Hostname: page-component-f554764f5-nwwvg Total loading time: 0 Render date: 2025-04-21T05:06:09.888Z Has data issue: false hasContentIssue false
  • English
  • Français

On irreducible representations of Fuchsian groups

Part of: Algebraic groups Families, fibrations

Published online by Cambridge University Press:  27 August 2024

Vikraman Balaji Open the ORCID record for Vikraman Balaji [Opens in a new window]  and
Yashonidhi Pandey
Vikraman Balaji*
Affiliation:
Chennai Mathematical Institute, H1 Sipcot IT Park, Siruseri, Kelambakkam 603103, India
Yashonidhi Pandey
Affiliation:
Indian Institute of Science Education and Research Mohali, Mohali Knowledge city, Sector 81, SAS Nagar, Manauli PO 140306, India e-mail: [email protected] [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 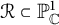${\mathcal {R}} \subset \mathbb {P}^1_{\mathbb {C}}$ be a finite subset of markings. Let G be an almost simple simply-connected algebraic group over 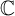$\mathbb {C}$. Let 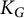$K_G$ denote the compact real form of G. Suppose for each lasso l around the marked point, a conjugacy class 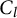$C_l$ in 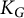$K_G$ is prescribed. The aim of this paper is to give verifiable criteria for the existence of an irreducible homomorphism of 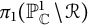$\pi _{1}(\mathbb P^1_{\mathbb {C}} \,{\backslash}\, {\mathcal {R}})$ into 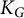$K_G$ such that the image of l lies in 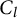$C_l$.

Keywords

Bruhat–Tits group schemeparahoric groupModuli stackGromov–Wittenstability

MSC classification

Primary: 14L15: Group schemes 14D23: Stacks and moduli problems 14D20: Algebraic moduli problems, moduli of vector bundles
Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 4 , December 2024 , pp. 970 - 990
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

To Apurv Pandey

The support of Science and Engineering Research Board under Mathematical Research Impact Centric Support File number: MTR/2017/000229 is gratefully acknowledged.

References

Agnihotri, S. and Woodward, C., Eigenvalues of products of unitary matrices and quantum Schubert calculus . Math. Res. Lett. 5(1998), no. 6, 817–836.CrossRefGoogle Scholar
Balaji, V., Biswas, I., and Pandey, Y., Connections on parahoric torsors on curves . Publ. Res. Inst. Math. Sci. 53(2017), 551–585.CrossRefGoogle Scholar
Balaji, V. and Seshadri, C. S., Moduli of parahoric   $\mathcal{G}$ -torsors on a compact Riemann surface. J. Algebraic Geom. 24(2015), no. 1, 1–49.Google Scholar
Bauer, S., Parabolic bundles, elliptic surfaces and SU (2)-representation spaces of genus zero Fuchsian groups . Math. Ann. 290(1991), no. 3, 509–526.CrossRefGoogle Scholar
Belkale, P., Local systems on ${\mathbb{P}}^1-S$ for $S$ a finite set . Compos. Math. 129(2001), no. 1, 67–86.CrossRefGoogle Scholar
Biswas, I., A criterion for the existence of a parabolic stable bundle of rank two over the projective line . Internat. J. Math. 9(1998), no. 5, 523–533.CrossRefGoogle Scholar
Biswas, I., On the existence of unitary flat connections over the punctured sphere with given local monodromy around the punctures . Asian J. Math. 3(1999), 333–344.CrossRefGoogle Scholar
Bruhat, F. and Tits, J., Groupes réductifs Sur un corps local. II. Schémas en groupes. Existence d’une donnée radicielle valuée . Inst. Hautes Études Sci. Publ. Math. 60(1984), 197–376.Google Scholar
Klyachko, A. A., Stable bundles, representation theory and Hermitian operators . Selecta Math. 4(1998), 419–445.CrossRefGoogle Scholar
Knutson, A. and Tao, T., The honeycomb model of GLn(C) tensor products. I. Proof of the saturation conjecture . J. Amer. Math. Soc. 12(1999), no. 4, 1055–1090.Google Scholar
Maruyama, M. and Yokogawa, K., Moduli of parabolic stable sheaves . Math. Ann. 293(1992), no. 1, 77–99.CrossRefGoogle Scholar
Mehta, V. B. and Seshadri, C. S., Moduli of vector bundles on curves with parabolic structures . Math. Ann. 248(1980), no. 3, 205–239.CrossRefGoogle Scholar
Meinrenken, E. and Woodward, C., Hamiltonian loop group actions and Verlinde factorization . J. Differential Geom. 50(1998), no. 3, 417–469.Google Scholar
Morgan, J. W., Holomorphic bundles over elliptic manifolds . In: Göttsche, Lothar (ed.), School on algebraic geometry (Trieste, 1999), ICTP Lecture Notes, 1, Abdus Salam International Centre for Theoretical Physics, Trieste, 2000, pp. 135–203.Google Scholar
Pandey, Y., Criteria for existence of stable parahoric $\mathrm{SO}_n$ , ${Sp}_n$ and spin bundles on ${\mathbb{P}}^1$ . J. Ramanujan Math. Soc. 29(2012), no. 1, 93–117.Google Scholar
Ramanathan, A., Stable principal bundles on a compact Riemann surface . Math. Ann. 213(1975), 129–152.CrossRefGoogle Scholar
Ramanathan, A., Deformations of principal bundles on the projective line . Invent. Math. 71(1983), no. 1, 165–191.CrossRefGoogle Scholar
Springer, T. A., Linear algebraic groups. 2nd ed., Modern Birkhäuser Classics, Birkhäuser Boston, Inc., Boston, MA, 2009.Google Scholar
Teleman, C. and Woodward, C., Parabolic bundles, products of conjugacy classes and Gromov–Witten invariants . Ann. Inst. Fourier (Grenoble). 53(2003), no. 3, 713–748.CrossRefGoogle Scholar