In certain technical problems it is necessary to know the mass concentration of snow in the air ρ s and the effective air density ρ ea during periods of snow-fall. Defining ρ s as ice mass per unit volume of snow-filled air (as is done for deposited snow):
where ρ i is ice density (≈ 0.92 × 103 kg/m3) and ρ a is the density of clear air (≈ 1.3 kg/m3).
In calm weather, the vertical flux of snow q v is easy to measure, e.g. by weighing the snow collected on a tray over a short time period. Representative fall velocities of snow particles u t are also fairly easy to measure if the complications of fall velocity variation within the dispersion are ignored. In principle, it is easy to estimate ρ s, since
However, while measurement of q v is routine, corresponding measurements of u t are seldom made.
At any given location. q v can vary by two or three orders of magnitude during a winter season (say in the range 0.002 to 2.0 g/cm2 h). By contrast, u t is unlikely to change by more than a factor of four for the whole range of snow crystals and snow-flakes. Thus, variations in ρ s must be controlled mainly by variations of q v.
Reference MellorMellor (1966) sampled a range of snow-falls, recording q v, u t, ρ s, and characteristics of the snow crystals. If the values of u t(cm/s) are plotted against those of q v(g/cm2 h), there is a weak correlation (Fig. 1) which can be described by

Fig. 1. Fall velocity u t plotted against accumulation rate q v.
The coefficient of determination r 2 for the power-relation regression is 0.3. Since u t does not vary much, there must be a strong correlation between ρ s and q v (Fig. 2). The data can be described by

Fig. 2. Snow density ρ s plotted against accumulation rate q v.
where q v is in g/cm2 h (which is equivalent to the accumulation rate expressed in centimetres of water per hour). The coefficient of determination r 2 is 0.969. A result that is essentially the same as Equation (4) is obtained by substituting Equation (3) into Equation (2) and adjusting the units.
The most basic quantitative description of a snow-fall is q v. Knowing q v, an estimate of ρ s that is sufficiently accurate for many practical purposes can be obtained from a relation such as Equation (4).
This is very convenient, and so it would be useful to have more field observations of q v, u t, and ρ s, especially for very heavy snow-falls.


 with
with 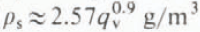 with
with 

