Published online by Cambridge University Press: 12 March 2014
Let 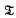 be a standard formalization of type theory. In [6] Kreisel introduced N-models for
be a standard formalization of type theory. In [6] Kreisel introduced N-models for 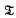 . These are general models in the sense of [1] in which the numerals have their standard denotations.
. These are general models in the sense of [1] in which the numerals have their standard denotations.
If ξ is a closed term of 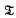 we shall denote the object denoted by ξ in the N-model M by ξM. In particular, ξ* is the object denoted by ξ in the standard model of
we shall denote the object denoted by ξ in the N-model M by ξM. In particular, ξ* is the object denoted by ξ in the standard model of 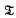 .
.
Please note a has been issued for this article.