Introduction
It is generally recognized that dry slab avalanche release can be initiated by the expansion in shearing mode of a “basal”crack at the slab/substrate interface (Reference McClungMcClung, 1981; Reference Gubler and BrugnotGubler, 1992), followed by the formation and expansion of a crown crack in the slab itself. Most models dealing with this problem are based on a comparison of the load resulting from the snow weight with the fracture strength of the medium. Some approaches, however (Reference McClungMcClung, 1981; Reference Jamieson and JohnstonJamieson and Johnston, 1992), incorporate the concept of crack stability in terms of Griffith’s model (Reference GriffithGriffith, 1920). In this model, the crack starts expanding in an unstable way when the stress concentration factor
![]() at the crack tip (where a is the stress and a the crack size) exceeds a critical value Kc
named toughness. This is equivalent to saying that, above this critical value, the release of stored elastic energy during a slight expansion da of the crack exceeds the energy dissipation related to crack opening.
at the crack tip (where a is the stress and a the crack size) exceeds a critical value Kc
named toughness. This is equivalent to saying that, above this critical value, the release of stored elastic energy during a slight expansion da of the crack exceeds the energy dissipation related to crack opening.
We also analyze here the stability of an incipient basal crack as a Griffith problem. We show, in contrast to previous models, that the slab avalanche is expected to behave in quite a different way according to whether or not the basal crack fulfils Griffith’s instability criterion before crown crack opening. For this purpose, snow is treated as a brittle ice foam (personal communication from G. Michot, 1999) that behaves in a purely elastic way (i.e. below the brittle-ductile transition temperature) on a time-scale comparable to that necessary for a skier to travel across the slab.
The present approach is illustrated using typical values for the mechanical properties of snow (Table 1) found in the literature, except for toughness values (Kc) which are deduced from ice data (Reference Nixon and SchulsonNixon and Schulson, 1987) using a relation obtained for open-cells porous media (Reference Gibson and AshbyGibson and Ashby, 1987).
Table 1. Snow density p, toughness Kc and tensile failure stress a,

Loading Stresses
Let us consider a snow layer of uniform thickness h (measured vertically) or h⊥ =hcosa (measured perpendicular to the slope) lying on a hard substrate (usually old transformed snow) with a slope a (Fig. 1). We shall use h rather than h⊥ because h represents the thickness of snow actually deposited by a steady snowfall, whatever the slope, provided snow transportation by wind is neglected. The “interface” between the slab and the substrate experiences a shear stress:
where p is the snow density. This shear stress obviously goes through a maximum for a = 45°, which is a compromise between a large slope angle that increases the shear component along the interface (proportional to sin a) and a small one that favours a large volume of snow (proportional to h⊥ = hcos α at constant snow thickness h deposited vertically). The shear stress τ increases linearly with snow thickness.

Fig. 1. Snow slab on a slope inclined at an angle a. The thickness of the snow slab can be measured vertically (h), or perpendicular to the slope (h⊥). Relaxation of shear stresses at the interface (basal crack) results in a tensile load at the top of the relaxed area, that can nucleate a crown crack across the slab.
An additional local overload induced by the fall of a cornice or the crossing of the slab by a skier may induce collapse of part of the weak interfacial zone, followed by relaxation of the shear stress through a slight downhill translation of the slab in the collapsed zone. The relaxed area is equivalent to a shear “basal” crack, assumed to have a circular shape. If the residual friction stress τ0 on free basal crack surfaces is neglected, the load transfer due to relaxation of interfacial shear stresses results in a tensile stress in the slab at the upper tip of the sheared zone, given by
where a is the diameter of the basal crack. Since snow thickness appears in both the total snow weight and the surface experiencing the tensile load, this tensile stress is independent of snow thickness, in contrast to the shear stress given by Equation (1). The role of residual friction stress at the interface, neglected at first for the sake of clarity, does not drastically change the qualitative conclusions of the present approach, and is examined at the end of the paper.
Crack Instability and Avalanche Triggering Scenarios
Let us focus on the case of an avalanche triggered by a skier, transposition to the other cases being straightforward in principle. A first release scenario is as follows: the basal crack gradually expands as the skier progresses across the slab. At some stage, tensile failure can take place in the slab at the uphill crack tip, either because of a transfer of the shear stress at the interface into a tensile load in the slab, or because of deflection of the shear crack into a mode I crack across the slab. For the sake of brevity, we shall restrict ourselves here to the former case, which can be shown to be preferred to the latter in the particular example discussed in Figure 3 (shown later), and more especially as the slab is less compliant than the weak layer. Yet the latter opening mode may operate for larger slab thicknesses and smaller slab-failure stresses (see Appendix). In the former case of “pure” tensile failure, a tensile “crown” crack starts opening across the slab when the tensile stress a in the slab at the upper basal crack tip reaches the tensile failure stress σf given inTable 1,
where σT is the corresponding size of the basal crack. The crown crack then grows quasi-statically in mode I (i.e. tensile opening) at the skier’s velocity. At this stage, the crack propagation starts being controlled by the energy balance between relaxation of stored elastic energy and free surface creation for both basal and crown cracks taken as a whole.
When the system made by the two coupled cracks meets its instability criterion, the crown crack starts propagating horizontally in mode I (tensile opening) at a speed of the order of sound velocity. The slab toughness KIIc for shear fracture (mode II) being only slightly larger than the toughness KIc in mode I (tension), the system readily meets the conditions for downhill deflection of the crown crack in mode II. The whole slab starts moving downhill, behind the skier’s position (Fig. 2a). If slab cohesion is large enough, it may subsequently break off into large fragments. In the following, this type of triggering will be referred to as a type A or undercritical.

Fig. 2. The destabilized zone is located behind the skier position in the case of an undercritical triggering (a), but encompasses it in the case of an overcritical triggering (b).
A second possible scenario is that the basal crack meets alone Griffith’s condition for unstable growth before the tensile stress a at the crown reaches the critical value σf for tensile failure. For the sake of simplicity, the shear stress concentration factor is approximated by
![]() The basal crack becomes unstable when this factor exceeds the interface shear toughness
The basal crack becomes unstable when this factor exceeds the interface shear toughness
![]() :
:
where as is the critical value of the basal crack diameter a satisfying this condition, which can be written as
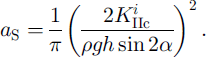
This condition can be met, for instance, during a snowfall (increase of τ) or during the skier’s propagation across the slab (increase of a). The basal crack then starts expanding in an unstable way along the interface, at a velocity which may be close to sound velocity in snow. This fast expansion causes a rapid increase of the basal crack size from as to αT, where condition (3) is in turn satisfied. By contrast with the first case, the basal crack is already overcritical at the crown crack opening. Even if it might be somewhat slowed down by crown crack expansion, basal crack propagation is likely to proceed at high velocity more especially as the difference (aT – as) is large. Condition (3) thus becomes satisfied over large distances in a very short time. A large crown crack thus suddenly opens, instantaneously relaxing most of the elastic energy stored in the slab. The suddenness of the release may explain the often observed horseshoe shape of the rupture line, at least on rather smooth and planar slopes: the instability condition is met almost simultaneously on the whole upper half-perimeter of the basal crack, from which the avalanche starts, in mode I at the upper part of the breaking line and in mode II on both sides of it. This type of triggering may be significantly more dangerous than the previous one, particularly because the destabilized area widely encompasses the skier position (Fig. 2b). In the following, this type of triggering will be referred to as a type B or overcritical.
Transition between the Two Triggering Modes
The competition between under- and overcritical modes is illustrated in Figure 3a where as and aT are plotted against slope in the case of a snow of 400 kg m–3. For a given slope, the type of avalanche is determined by the smaller of these two parameters. For the sake of simplicity, Killc has been taken in this example equal to the snow fracture toughness Kc given in Table 1. Figure 3a shows that for a snow thickness of lm, for instance, the triggering will be of the overcritical type for slopes of 15–58° and of the undercritical type outside this slope “window”. This window shrinks for smaller snow thicknesses, and vanishes in the present example for a snow thickness of about 0.8 m. Below this critical thickness, avalanches are expected to be of the under-critical type, whatever the slope. Yet, and despite the lack of in situ toughness measurements, the weak-layer toughness may be significantly less than Kc in the case of buried surface-hoar layers, ice crusts or radiation recrystallized layers, or in the case of flat grains or of hoar-frost resulting from temperature-gradient metamorphism. Equation (5) shows, however, that this effect may be balanced by slab thickness. This means that, for the slab-thickness range considered here, undercritical release would be restricted to significantly low or high slope angles, and the transition between the two modes would take place at smaller top-layer depths.

Fig. 3. (a) Calculated critical sizes of the basal crack for its unstable propagation in shear (as) and for tensile crown failure (aT), if residual friction is neglected, and for three different slab thicknesses (0.6, 0.8 and lm), plotted vs slope, with a snow density of 400 kgm3. (b) Same as (a), but with a residual friction coefficient A = 0.2.
Since an increase of slab tensile failure stress σr delays tensile rupture by shifting the aT curve upwards, stronger slabs favour wider avalanches. They also obviously promote overcritical avalanche triggering.
The transition between the situation where triggering is undercritical whatever the slope, and that where triggering becomes overcritical in an intermediate slope range, takes place for critical values of slope a0 and snow thickness h0 satisfying the tangency of both curves, i.e. the two following conditions:
From Equations (3) and (5), this system can be written as
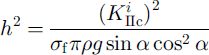
and

Eliminating h2 between Equations (8) and (9) gives
This result is quite general, i.e. independent of the characteristics of snow (toughness, failure stress, density).
The corresponding critical snow thickness h0 is given by
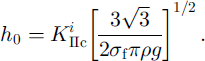
In contrast with α0, it depend on snow characteristics that can be expressed through slab density and weak-layer toughness.
A number of avalanche reports fit reasonably well with type B releases. This may be the case for avalanches of 5 January 1994 at Oscar River, British Columbia, Canada, and of 19 March 1995 at Telkwa Range, British Columbia, for instance Reference Jamieson and GeldsetzerJamieson and Geldsetzer, 1996). The reason may be that most of these reports mention slopes around 35–40°: these slope angles are both the most favoured ones for this type of triggering, and not unusual for ski practice. In contrast, type A triggenings are more favoured by weak layers than by thick slabs, and by large slope angles. The avalanche of 19 March 1995 at Doctor River, Purcell Range, British Columbia, reported by Reference Jamieson and GeldsetzerJamieson and Geldsetzer (1996), for which the fracture line started very close to the two snowmobiles responsible for the triggering, may be of type A. Some experimental triggennings on sand layers are also consistent with a type A scenario (personal communications from C. Abiteboul, 2000, and from L. Vidal, 2000).
Effect of a Residual Friction on Basal Crack Surfaces
Let us now assume that basal crack surfaces experience a residual friction τF verifying Amonton’s law (i.e. friction stress proportional to the normal load),
where the dimensionless friction coefficient A is comprised between 0 and 1. This friction modifies the shear stress given by Equation (1), which becomes
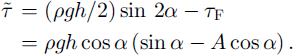
The load transfer to the upper crack tip results in a tensile stress that can be easily shown to be
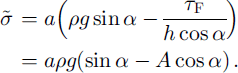
The critical sizes aT and as of the basal crack corresponding to crown crack opening and to basal crack instability respectively become
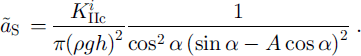
It can be easily shown through a calculation similar to that of Equations (6–11) that the critical transition angle a0 becomes
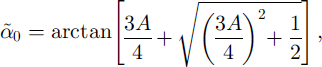
which is larger than α0, and reduces to a0
when A → 0 since
![]() is equivalent to Equation (10). The variations with slope of aT
and as are shown in Figure 3b for a value of the friction coefficient A of 0.2. Overcritical triggering is expected between 20° and 70° for a slab thickness of 1.5 m. The transition between the two regimes takes place for a slab thickness of about 0.9 m, at an angle of 41°. Residual friction thus shifts the window corresponding to overcritical triggering toward larger slopes, while smallest slopes (<10° in the present case) become totally safe.
is equivalent to Equation (10). The variations with slope of aT
and as are shown in Figure 3b for a value of the friction coefficient A of 0.2. Overcritical triggering is expected between 20° and 70° for a slab thickness of 1.5 m. The transition between the two regimes takes place for a slab thickness of about 0.9 m, at an angle of 41°. Residual friction thus shifts the window corresponding to overcritical triggering toward larger slopes, while smallest slopes (<10° in the present case) become totally safe.
Conclusions
Though the present approach relies on simplifying assumptions, the following conclusions can be formulated:
-
(i) Both under- and overcritical avalanche triggerings can result from shear crack nucleation and propagation at the interface with the old snow substrate, followed by tensile failure of the upper part of the slab. Strong interfaces hinder triggering of both types of slab avalanches, which are in contrast favoured by hoar-frost formation, for instance after a clear cold night. Rocky outcrops are preferential sites for tensile failure, owing to the local thickness reduction of the snow layer.
-
(ii) Undercritical triggering, resulting from a gradual extension of the basal crack, is favoured by steep slopes and poor interfacial cohesion, but does not depend on snow thickness.
-
(iii) Overcritical triggering, resulting from unstable propagation of the basal crack, is also promoted by a poor cohesion of the interfacial layer, but is significantly favoured by large snow thicknesses: the critical travel distance of a skier for overcritical triggering increases as the square of both shear toughness of the interface and reciprocal snow thickness. This type of avalanche release preferentially occurs on intermediate slopes, with a maximum risk around 35.3° (if residual friction is neglected). Moderate slopes are thus not necessarily safer than steep ones, mainly after heavy snowfalls.
-
(iv) An increase of snow density reduces the critical snow thickness ho below which overcritical triggering cannot occur (whatever the slope), but increases the corresponding critical path of the skier (everything else held equal).
-
(v) A residual friction at basal crack surfaces makes the lowest slopes safer, and shifts the overcritical triggering window to larger slopes.
Similar conclusions could be drawn in the case of spontaneous triggering, the instability of the shear crack being in this case related to either an increase of snow thickness, or a gradual weakening of the interface due, for instance, to strain softening of the interface during creep, or to metamorphism.
The present approach is based on some simplifying assumptions, so as to allow an analytical treatment of the problem. In order to be directly used for avalanche hazard forecast, it should be improved in several ways. The influence of variations of snow characteristics along or across the slab, the particular features of the slopes, as well as the role of plastic dissipation that may influence both crack stability and quasistatic propagation, for instance, should be treated using numerical simulations. The interest of the present model is nevertheless to describe analytically two extreme cases of triggering mechanisms that may result in quite different avalanche propagation types, and to give the main trends of the influence of slope and of snow thickness and mechanical properties on the occurrence of these triggering modes, thus giving a physical basis for further simulations.
Acknowledgements
The author is grateful to D. Daudon, P. Duval, D. Issler and I. Schmidt for very helpful comments.
Appendix: Grown Crack Tensile Opening Vs Basal Crack Deflection&/B;
Grown crack opening may result from either tensile opening or basal crack deflection by an angle 9 into the slab. In the latter case, if the basal crack is loaded in mode II with a stress intensity factor KIh the stress intensity factor k*l in the deflection direction is (Bui, 1985)
where
![]() is maximum (around –1.22) for 9 = 70–80°. Deflection of the basal crack therefore takes place if
is maximum (around –1.22) for 9 = 70–80°. Deflection of the basal crack therefore takes place if
In contrast, tensile failure takes place if
where τ and a are, respectively, the shear stress and the tensile stress given by Equations (1) and (2), and σf is the slab tensile-failure stress.
Deflection will thus be preferred to tensile failure if
![]() at failure. Using Equation (3), this is equivalent to
at failure. Using Equation (3), this is equivalent to
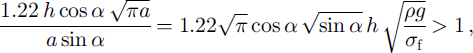
where a = adeflection = aT is the critical basal crack size at failure. The deflection mode is therefore favoured by large slab depths h (that increase τ but not a) and low slab-failure stresses, the latter result being equivalent to saying that this mode is favoured by small a values at failure. Using typical figures fromTable 1 and a slope angle of 35°, for instance, the last expression gives a critical value of h = 3.76 m. This means that for the example of Figure 3, where slab thicknesses do not exceed 1 m, tensile failure should be preferred to basal crack deflection. In addition, the above calculation assumes that elastic properties of the slab and of the weak layer are similar, whereas in real life the former may be significantly less compliant than the latter, which hinders crack deflection even more (Reference He and HutchinsonHe and Hutchinson, 1989). Yet this alternative scenario may arise in some extreme situations.






