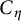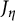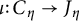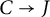1 Introduction
Let K be a field equipped with a nontrivial, non-Archimedean valuation
${\mathrm {val}\colon K\to {\mathbf {R}}\cup \{\infty \}}$
. Let R be the (potentially non-Noetherian) valuation ring of K, and let k be its residue field. We assume for simplicity that k is algebraically closed. Let
$C\to \mathrm {Spec}(R)$
be a proper, flat relative curve, with generic fiber
$C_\eta $
and special fiber
$C_s$
. We suppose that
$C_{\eta }$
is smooth and geometrically connected, and that
$C_s$
is reduced with (at worst) nodal singularities. Our first goal is to prove the following extension theorem.
Theorem 1.1 Let X be a proper, flat R-scheme of finite presentation whose special fiber
$X_s$
is reduced and contains no rational k-curves. Then any morphism
$f_\eta \colon C_\eta \to X_\eta $
on generic fibers extends (uniquely) to a morphism
$f\colon C\to X$
.
Suppose now that
$C_s$
of compact type, which means that removing any node disconnects
$C_s$
. Let
$\{C_v\}_v$
denote the irreducible components of
$C_s$
(the subscript v is meant to denote a vertex in the incidence graph of
$C_s$
). Let
$J = \mathrm {Pic}^0_{C/R}$
be the identity component of the relative Picard scheme of C; this is smooth and separated over R by [Reference Bosch, Lütkebohmert and RaynaudBLR90, Theorem 9.4/1]. Its generic fiber is the Jacobian of
$C_\eta $
. Let
$J(C_v)$
be the Jacobian of
$C_v$
. By [Reference Bosch, Lütkebohmert and RaynaudBLR90, Section 9.2, Example 8], we have an isomorphism on special fibers
$$\begin{align*}J_s = \mathrm{Pic}^0_{C_s/k} \overset\sim\longrightarrow \prod_v J(C_v), \end{align*}$$
which is functorially induced by the inclusions
$C_v\hookrightarrow C_s$
. Since
$J_s$
is an abelian variety, it follows from [Reference GrothendieckGr61, Corollaire 5.5.2] that
$J\to \mathrm {Spec}(R)$
is proper (the generic fiber
$J_\eta $
is connected, so the
$Z'$
in the statement of that result must be empty). Hence, J is an abelian scheme. It follows that when R is Noetherian, then J is the Néron model of its generic fiber
$J_\eta $
.
Suppose that
$C(K)\neq \emptyset $
. Let
$\iota _\eta \colon C_\eta \to J_\eta $
be an Abel–Jacobi map defined by some choice of base point. This extends to a morphism
$\iota \colon C\to J$
by Theorem 1.1. In this situation, we will show the following.
Theorem 1.2 The morphism
$\iota \colon C\to J$
is a closed immersion if
$C_s$
has no rational components.
This result is known to experts using moduli-theoretic techniques, at least when R is Noetherian (see, for instance, [Reference CaporasoCap07, Reference Caporaso and EstevesCE07, Reference Caporaso and HarrisCH98], and especially [Reference EdixhovenEdi98, Section 9]). (When R is not Noetherian, then there is no good notion of regularity for C, so existing results are not immediately applicable.)
We will prove Theorems 1.1 and 1.2 by passing to a formal-analytic category and using Bosch–Lütkebohmert’s careful analysis of reductions of curves and Jacobians. More specifically, we show in Proposition 2.2 that a morphism f between the generic fibers of formal analytic varieties extends to a morphism of integral models if and only if f takes formal fibers into formal fibers. We then use results of Bosch–Lütkebohmert to the effect that every formal fiber of a semistable curve is an open disk or an open annulus, and we will show that every disk or annulus in the analytification of a scheme X as in the statement of Theorem 1.1 is contained in a single formal fiber. An advantage of working in this context is that our proof avoids Noetherian hypotheses. It also avoids the modular interpretation of J: indeed, Theorem 1.1 works for much more general schemes X.
Remark 1.3 When R is Noetherian, then the Néron mapping property implies that
$C_\eta \to J_\eta $
extends to the smooth locus of C. One can interpret Theorem 1.1 as a kind of “log Néron mapping property” for maps of curves to abelian schemes. See Proposition 3.1 and the paragraph after.
1.1 Reduction step
Our analytic criteria are geometric in nature, so first, we reduce to the case when the ground field is complete and algebraically closed.
Lemma 1.4 Let
$K'$
be a valued field extension of K, and let
$R'$
be the ring of integers of
$K'$
. Let
$X,Y$
be flat R-schemes, and let
$X' = X\otimes _R R'$
and
$Y' = Y\otimes _R R'$
. Let
$f_\eta \colon X_\eta \to Y_\eta $
be a morphism on generic fibers. Then
$f_\eta $
extends, necessarily uniquely, to a morphism
$f\colon X\to Y$
, if and only if the base change
$f^{\prime }_\eta \colon X^{\prime }_\eta \to Y^{\prime }_\eta $
extends to a morphism
$f'\colon X'\to Y'$
. If
$f'$
is a closed immersion, then so is f.
Proof Since X is R-flat,
$X_\eta $
is dense in X, so if f exists then it is unique. Suppose that there exists
$f'\colon X'\to Y'$
extending
$f_\eta '$
. The two compositions
$X'\times _X X'\rightrightarrows Y'\to Y$
coincide when restricted to
$(X'\times _X X')\otimes _{R}K$
because
$f^{\prime }_\eta = f_\eta \otimes _K K'$
, so since
$X'\times _X X'$
is
$R'$
-flat, the maps
$X'\times _X X'\rightrightarrows Y$
coincide. Thus, f exists by faithfully flat descent of morphisms. The property of being a closed immersion can also be checked after faithfully flat base change.
Replacing K by the completion of an algebraic closure of the completion of K, we may and do assume from now on that K is complete and algebraically closed.
2 A fiberwise criterion for a morphism to extend to models
Let X be a proper, flat R-scheme. The valuative criterion of properness provides us with a functorial reduction map
$\pi \colon X(K)\to X(k)$
. A fiber of
$\pi $
is called a formal fiber. By functoriality, if
$f\colon X\to Y$
is a morphism of proper, flat R-schemes, then
$f_\eta $
takes formal fibers of X into formal fibers of Y. In this section, we prove a partial converse statement: that if
$f_\eta \colon X_\eta \to Y_\eta $
is a morphism that takes formal fibers of X to formal fibers of Y, then
$f_\eta $
extends to a morphism
$f\colon X\to Y$
, assuming the special fibers of X and Y are reduced.
2.1 Admissible formal schemes
In the situation discussed above, we wish to work more generally with admissible formal R-schemes.
Fix
$\varpi \in K$
with
$0 < \mathrm {val}(\varpi ) < \infty $
. Let X be a proper, flat R-scheme of finite presentation. Then the
$\varpi $
-adic completion
$\hat X$
of X is a proper admissible formal R-scheme in the sense of [Reference Bosch and LütkebohmertBL93]. That is, X is covered by formal affines
$\mathrm {Spf}(A)$
for A a flat,
$\varpi $
-adically complete R-algebra of topological finite presentation. The admissible formal R-scheme X has a “generic fiber”
$X_\eta $
, which is a rigid analytic variety over K. The generic fiber is locally given by
$\mathrm {Spf}(A)_\eta = \mathrm {Sp}(A\otimes _{R}K)$
, which makes sense as
$A_{K}:=A\otimes _{R}K$
is a quotient of a Tate algebra over K. When
$X\to \mathrm {Spec}(R)$
is proper, the analytic generic fiber
$\hat X_\eta $
is canonically isomorphic to
$X_\eta ^{\mathrm {an}}$
, the analytification of the generic fiber of X (see [Reference ConradCon99, Theorem A.3.1]).
Lemma 2.1 Let X and Y be proper, flat R-schemes of finite presentation, and let
$f_\eta \colon X_\eta \to Y_\eta $
be a morphism on generic fibers. Then
$f_\eta $
extends to a morphism
$f\colon X\to Y$
if and only if
$f_\eta ^{\mathrm {an}}\colon X_\eta ^{\mathrm {an}}\to Y_\eta ^{\mathrm {an}}$
extends to a morphism
$\hat f\colon \hat X\to \hat Y$
. More precisely,
$f_\eta $
extends if and only if there exists
$\hat f\colon \hat X\to \hat Y$
such that
$f_\eta ^{\mathrm {an}}$
is the generic fiber of
$\hat f$
under the identification
$\hat X_\eta \cong X_\eta ^{\mathrm {an}}$
.
Proof Consider the following commutative square:
All arrows arise from functoriality of the operations of completion, analytification, and passing to the analytic generic fiber, along with the identifications
$X_\eta ^{\mathrm {an}}\cong \hat X_\eta $
and
$Y_\eta ^{\mathrm {an}}\cong \hat Y_\eta $
. The left vertical arrow is a bijection by admissible formal GAGA [Reference Fujiwara and KatoFK14, Proposition 10.3.1], and the right vertical arrow is a bijection by rigid analytic GAGA. This proves the lemma.
2.2 Formal analytic varieties
For our purposes, we define a formal analytic variety over R to be a separated admissible formal R-scheme X with reduced special fiber
$X_s$
. We regard the analytic generic fiber
$X_\eta $
as a rigid space over K as above, and we regard the special fiber
$X_s$
as a variety over k and not as a scheme – that is, we only consider the closed points of
$X_s$
. With these conventions, there exists a canonical, functorial, surjective reduction map, which we denote by
$\pi \colon X_\eta \to X_s$
. A formal fiber of X is the
$\pi $
-inverse image of a (closed) point of
$X_s$
. It is known that for every formal affine
$U = \mathrm {Spf}(A)\subset X$
, the generic fiber
$U_\eta = \mathrm {Sp}(A_{K})\subset X_\eta $
is an affinoid domain with underlying set
$\pi ^{-1}(U_s)$
, and that A coincides with the ring
$A_{K}^\circ $
of power-bounded elements in the affinoid algebra
$A_{K}$
(see, for example, [Reference Bosch and LütkebohmertBL85, Section 1]). In this situation, we say
$\mathrm {Spf}(A)$
is the canonical model of
$\mathrm {Sp}(A_{K})$
. It follows that X is obtained by gluing the canonical models of a number of affinoid domains in
$X_\eta $
.
We have the following useful criterion for a morphism of rigid spaces to extend to a morphism of formal analytic varieties.
Proposition 2.2 Let X and Y be formal analytic varieties over R, and let
$f_\eta \colon X_\eta \to Y_\eta $
be a morphism. Then
$f_\eta $
extends to a morphism of formal analytic varieties
$f\colon X\to Y$
if and only if there exists a set-theoretic map
$f_s\colon X_s\to Y_s$
making the following square commute:
In this case,
$f_s$
coincides with the special fiber of f.
In other words,
$f_\eta $
extends to a morphism of formal analytic varieties if and only if it takes formal fibers of X into formal fibers of Y. It will be clear from the proof that the extension f is unique if it exists.
We will need the following straightforward lemma.
Lemma 2.3 Let
$f\colon {{\mathscr {X}}}\to {{\mathscr {Y}}}$
be a morphism of rigid analytic varieties over K. Suppose that
${{\mathscr {Y}}}$
is separated. Then for any affinoid domains
${{\mathscr {V}}}\subset {{\mathscr {Y}}}$
and
${{\mathscr {U}}}\subset {{\mathscr {X}}}$
, the intersection
$f{^{-1}}({{\mathscr {V}}})\cap {{\mathscr {U}}}$
is affinoid.
Proof Replacing
${{\mathscr {X}}}$
by
${{\mathscr {U}}}$
, we are reduced to showing that
$f{^{-1}}({{\mathscr {V}}})$
is affinoid when
${{\mathscr {X}}}$
is affinoid. As
${{\mathscr {Y}}}$
is separated, the graph
$\Gamma \colon {{\mathscr {X}}}\to {{\mathscr {X}}}\times {{\mathscr {Y}}}$
is a closed immersion. We have
$f{^{-1}}({{\mathscr {V}}}) = \Gamma {^{-1}}({{\mathscr {X}}}\times {{\mathscr {V}}})$
, and
${{\mathscr {X}}}\times {{\mathscr {V}}}$
is affinoid, so
$f{^{-1}}({{\mathscr {V}}})$
is too.
Proof of Proposition 2.2
The stated condition is necessary by functoriality of the reduction map. Suppose now that such
$f_s$
exists. First, we claim that
$f_s$
is continuous. Let
$V\subset Y$
be a formal affine, and let
$U_s = f_s^{-1}(V_s)$
and
$U_\eta = f_\eta ^{-1}(V_\eta ) = \pi ^{-1}(U_s)$
. Let
$U'\subset X$
be a formal affine. Then
$U^{\prime }_\eta \cap U_\eta $
is an affinoid subdomain of
$U^{\prime }_\eta $
by Lemma 2.3, and it is a union of formal fibers. It follows from [Reference Bosch and LütkebohmertBL84, Lemma 5.7] that
$U^{\prime }_\eta \cap U_\eta $
is the
$\pi $
-inverse image of a Zariski-open subset of
$U^{\prime }_s$
, so that
$U_s'\cap U_s$
is open. As
$U'$
was arbitrary, this establishes continuity of
$f_s$
.
Let
$V = \mathrm {Spf}(B)\subset Y$
be a formal affine, and let
$U = \mathrm {Spf}(A)$
be a formal affine with
$U_s\subset f_s^{-1}(V_s)$
. Then
$U_\eta \subset f_\eta ^{-1}(V_\eta )$
, so
$f_\eta $
induces a homomorphism
${\varphi }\colon B_{K}\to A_{K}$
. A homomorphism of affinoid algebras is automatically continuous, so
${\varphi }$
takes
$B = B_{K}^\circ $
into
$A = A_{K}^\circ $
, and thus induces a morphism
$U\to V$
. This construction is compatible with restriction, so it glues to a map
$f\colon X\to Y$
.
Remark 2.4 A formal analytic variety X may be regarded as a ringed space with underlying set
$X_\eta $
, whose open sets are the
$\pi $
-inverse images of Zariski-open subsets of
$X_s$
, and whose structure sheaf when evaluated on
$\pi ^{-1}(U_s)$
is the ring of power-bounded analytic functions on
$U_\eta $
for a formal affine
$U\subset X$
(see [Reference Bosch and LütkebohmertBL85, Section 1]). The second paragraph of the proof of Proposition 2.2 is the simple fact that a morphism of rigid spaces
$f_\eta \colon X_\eta \to Y_\eta $
extends to a morphism
$f\colon X\to Y$
if and only if
$f_\eta $
is continuous with respect to the corresponding formal analytic topologies.
3 Formal schemes with no rational curves in the special fiber
We assume still that K is complete and algebraically closed. The following result is the main geometric input into the proof of Theorem 1.1.
Proposition 3.1 Let
${{\mathscr {U}}}$
be a connected quasi-compact subdomain in
${{\mathbf {P}}}^1$
, and let X be an admissible formal R-scheme whose special fiber
$X_s$
contains no rational k-curves. Then the image of any morphism
$f\colon {{\mathscr {U}}}\to X_\eta $
is contained in a single formal fiber.
Example 3.2 If X is the completion of an abelian scheme, then
$X_s$
contains no rational curves: indeed,
$X_s$
is an abelian variety, and any morphism
${{\mathbf {P}}}^1_k\to X_s$
factors through
$J({{\mathbf {P}}}^1_k) = \{\star \}$
.
Proof of Proposition 3.1
By Raynaud’s theory [Reference Bosch and LütkebohmertBL93, Theorem 4.1], there exists an admissible formal scheme U with generic fiber
$U_\eta = {{\mathscr {U}}}$
and a morphism
$f\colon U\to X$
extending
$f\colon {{\mathscr {U}}}\to X_\eta $
. As
${{\mathscr {U}}}$
is an analytic domain in
${{\mathbf {P}}}^1$
, all of the irreducible components of
$U_s$
are rational curves. Since
$X_s$
contains no rational curves, the proposition follows from the commutativity of the square
as
$U_s$
collapses to a point.
Note that Proposition 3.1 applies equally well to a subdomain
${{\mathscr {U}}}\subset {{\mathbf {P}}}^1$
that can be expressed as an increasing union of connected quasi-compact subdomains; in particular, we can take
${{\mathscr {U}}}$
to be an open disk or an open annulus.
Proof of Theorem 1.1
By Lemma 2.1, we may replace C and X by their completions to work in the category of formal analytic varieties. The theorem then follows from Propositions 2.2 and 3.1 because all formal fibers of C are open disks and open annuli, by [Reference Bosch and LütkebohmertBL85, Propositions 2.2 and 2.3].
Remark 3.3 In particular, any morphism from
$C_\eta $
to an abelian variety with good reduction extends to C (see Example 3.2).
We assume now that
$C_s$
is of compact type. We let
$\iota \colon C\to J = \mathrm {Pic}^0_{C/R}$
be the morphism extending an Abel–Jacobi map
$\iota _\eta \colon C_\eta \to J(C_\eta )$
, as in the introduction. Now, we know that
$\iota $
exists, we can describe
$\iota _s\colon C_s\to J_s$
. As passing to the completion of an algebraic closure of the completion of a field does not affect special fibers, the conclusions of Proposition 3.4 are valid when K is not complete and algebraically closed.
Proposition 3.4 Let
$\iota \colon C\to J$
be the extension of an Abel–Jacobi map on the generic fiber, as provided by Theorem 1.1. Let
$\iota _v\colon C_v\to J_s$
be the restriction of
$\iota _s$
to the component
$C_v$
. Under the identification
$J_s = \prod _v J(C_v)$
, for any component
$C_w$
, the morphism
$$\begin{align*}\iota_w\colon C_w\to\prod_v J(C_v) \quad\text{is } \begin{cases} \text{zero}, & \text{in the}\ v{-}\text{coordinate for}\ v\neq w,\ \text{and} \\ \text{an Abel--Jacobi map}, & C_w\hookrightarrow J(C_w) \text{ in the}\ w{-}\text{coordinate,} \end{cases}\end{align*}$$
up to translation on
$J_s$
.
Proof This is a statement about smooth varieties over an algebraically closed field, so it may be checked on closed points. After translation, we may assume that
$\iota _\eta $
is the Abel–Jacobi map defined by a base point
$P_0\in C(K)$
whose reduction
$\widetilde {P}_0\in C(k)$
is a smooth point of
$C_w$
. For any other point
$P\in C(K)$
whose reduction
$\widetilde {P}$
is in
$C_w^{\mathrm {sm}}$
, the reduction
$\iota _w(\widetilde {P})$
of
$\iota _\eta (P) = [P-P_0]$
has w-coordinate
$[\widetilde {P}-\widetilde {P}_0]\in J(C_w)$
and has v-coordinate zero for
$v\neq w$
(see [Reference Bosch and LütkebohmertBL84, Theorem 5.1(c)]). Since every point of
$C_w^{\mathrm {sm}}$
is the reduction of some point
$P\in C(K)$
, this shows that
$C_w^{\mathrm {sm}}\to J(C_w)$
is the restriction of an Abel–Jacobi map, and that
$C_w^{\mathrm {sm}}\to J(C_v)$
is zero for
$v\neq w$
. The assertion follows because
$C_w^{\mathrm {sm}}$
is dense in
$C_w$
.
Proof of Theorem 1.2
Suppose that
$C_s$
has no rational components. First, we show that
$\iota $
is injective on closed points. Fix an irreducible component
$C_w$
of
$C_s$
, and translate
$\iota $
so that
$\iota _w\colon C_w\to \prod _v J(C_v)$
is as described in Proposition 3.4. In particular, the v-coordinate of
$\iota _w(\widetilde {P})$
is zero for
$\widetilde {P}\in C_w$
and
$v\neq w$
. We claim that this condition characterizes
$C_w$
: i.e., that if
$\widetilde {P}\in C(k)$
and
$\iota _s(\widetilde {P})$
has zero v-coordinate for all
$v\neq w$
, then
$\widetilde {P}\in C_w$
. This is enough to prove injectivity.
Let
$\widetilde {P}\in C_{w'}(k)$
for
$w\neq w'$
. Since the incidence graph of
$C_s$
is a tree, there is a unique chain of components
$C_w = C_{w_0},\,C_{w_1},\ldots ,C_{w_r}=C_{w'}$
connecting
$C_w$
and
$C_{w'}$
. Suppose first that
$r=1$
, so that
$C_w$
intersects
$C_{w'}$
. Since
$\widetilde {P}\notin C_w$
and since
$\iota _{w_1}$
is injective, we have that the
$w_1$
-coordinate of
$\iota _s(\widetilde {P})$
is nonzero, as claimed. If
$r> 1$
, then let
$\widetilde {P}'$
be the point where
$C_{w_1}$
and
$C_{w_2}$
intersect. Then
$\widetilde {P}'\notin C_w$
, so the
$w_1$
-coordinate of
$\iota _s(\widetilde {P}')$
is nonzero, as above. But
$\iota _{w_i}$
has constant
$w_1$
-coordinate for
$i> 1$
, so the
$w_1$
-coordinates of
$\iota _s(\widetilde {P})$
and
$\iota _s(\widetilde {P}')$
coincide. This completes the proof of injectivity.
Since
$\iota $
is quasi-finite and proper (as C is proper), it is finite. We now pass to formal completions to prove it is a closed immersion. Both
$\hat C$
and
$\hat J$
are formal analytic varieties, and
$\hat \iota \colon \hat C\to \hat J$
is an affine morphism. By [Reference Bosch, Güntzer and RemmertBGR84, Proposition 6.4.2/1], it is enough to prove that
$\iota _s$
is a closed immersion. This is a statement about a morphism of varieties over an algebraically closed field; we already know that
$\iota _s$
is injective on points, so it suffices to show it is injective on tangent vectors. This is clear for smooth points of
$C_s$
by Proposition 3.4. Let
$\widetilde {P}\in C(k)$
be a singular point, and let
$C_v,C_w$
be the irreducible components containing
$\widetilde {P}$
. The tangent space at
$\widetilde {P}$
is two-dimensional, generated by tangent vectors in the
$C_v$
- and
$C_w$
-directions. But these map to tangent vectors with zero
$J(C_w)$
- and
$J(C_v)$
-components, respectively, so their images under
$\iota _s$
are linearly independent.
Acknowledgments
The authors are very grateful to Jesse Kass for many helpful comments on an early draft, and to Lucia Caporaso for her expertise. The authors would also like to thank a referee for suggesting the current statement of Theorem 1.1.
