Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T13:05:29.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Hydrodynamic damping of an oscillating cylinder at small Keulegan–Carpenter numbers

Published online by Cambridge University Press:  02 March 2021

Chengjiao Ren Open the ORCID record for Chengjiao Ren [Opens in a new window] ,
Lin Lu Open the ORCID record for Lin Lu [Opens in a new window] ,
Liang Cheng Open the ORCID record for Liang Cheng [Opens in a new window]  and
Tingguo Chen
Chengjiao Ren
Affiliation:
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian116024, PR China Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian116024, PR China
Lin Lu*
Affiliation:
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian116024, PR China Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian116024, PR China
Liang Cheng*
Affiliation:
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian116024, PR China Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian116024, PR China School of Engineering, The University of Western Australia, 35 Stirling Hwy, Crawley, WA6009, Australia
Tingguo Chen
Affiliation:
Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian116024, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations (DNS) of oscillatory flow around a cylinder show that the Stokes–Wang (S–W) solution agrees exceptionally well with DNS results over a much larger parameter space than the constraints of $\beta K^2\ll 1$ and $\beta \gg 1$ specified by the S–W solution, where $K$ is the Keulegan–Carpenter number and $\beta$ is the Stokes number. 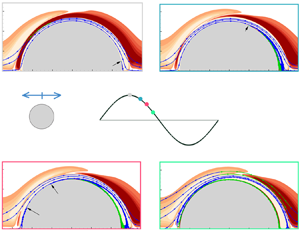The ratio of drag coefficients predicted by DNS and the S–W solution, $\varLambda _K$, mapped out in the $K\text {--}\beta$ space, shows that $\varLambda _K < 1.05$ for $K\leq {\sim }0.8$ and $1 \leq \beta \leq 10^6$, which contradicts its counterpart based on experimental results. The large $\varLambda _K$ values are primarily induced by the flow separation on the cylinder surface, rather than the development of three-dimensional (Honji) instabilities. The difference between two-dimensional and three-dimensional DNS results is less than 2 % for $K$ smaller than the corresponding $K$ values on the iso-line of $\varLambda _K = 1.1$ with $\beta = 200\text {--}20\,950$. The flow separation actually occurs over the parameter space where $\varLambda _K\approx 1.0$. It is the spatio-temporal extent of flow separation rather than separation itself that causes large $\varLambda _K$ values. The proposed measure for the spatio-temporal extent, which is more sensitive to $K$ than $\beta$, correlates extremely well with $\varLambda _K$. The conventional Morison equation with a quadratic drag component is fundamentally incorrect at small $K$ where the drag component is linearly proportional to the incoming velocity with a phase difference of ${\rm \pi} /4$. A general form of the Morison equation is proposed by considering both viscous and form drag components and demonstrated to be superior to the conventional equation for $K < {\sim }2.0$.

JFM classification

Boundary Layers: Boundary layer separation Wakes/Jets: Separated flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 913 , 25 April 2021 , A36
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

An, H., Cheng, L. & Zhao, M. 2011 Direct numerical simulation of oscillatory flow around a circular cylinder at low Keulegan–Carpenter number. J. Fluid Mech. 666, 77–103.CrossRefGoogle Scholar
Bearman, P.W., Downie, M.J., Graham, J.M.R. & Obasaju, E.D. 1985 Forces on cylinders in viscous oscillatory flow at low Keulegan–Carpenter numbers. J. Fluid Mech. 154, 337–356.CrossRefGoogle Scholar
Bearman, P.W & Mackwood, P.R 1992 Measurements of the hydrodynamic damping of oscillating cylinders. In Proceedings of the 6th International Conference on the Behaviour of Offshore Structures (BOSS’92), vol. 1, pp. 405–414. BPP Tech Services Ltd.Google Scholar
Blackburn, H.M. & Sherwin, S.J. 2004 Formulation of a Galerkin spectral element–Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.CrossRefGoogle Scholar
Bolis, A. 2013 Fourier spectral/$hp$ element method: investigation of time-stepping and parallelisation strategies. PhD thesis, Imperial College London.Google Scholar
Cantwell, C.D., Moxey, D., Comerford, A., Bolis, A., Rocco, G., Mengaldo, G., De Grazia, D., Yakovlev, S., Lombard, J.E., Ekelschot, D., et al. . 2015 Nektar++: an open-source spectral/$hp$ element framework. Comput. Phys. Commun. 192, 205–219.CrossRefGoogle Scholar
Chaplin, J.R. 2000 Hydrodynamic damping of a cylinder at $\beta \simeq 10^6$. J. Fluids Struct. 14 (8), 1101–1117.CrossRefGoogle Scholar
Elston, J.R., Blackburn, H.M. & Sheridan, J. 2006 The primary and secondary instabilities of flow generated by an oscillating circular cylinder. J. Fluid Mech. 550, 359–389.CrossRefGoogle Scholar
Gao, Z., Efthymiou, M., Cheng, L., Zhou, T., Minguez, M. & Zhao, W. 2020 Hydrodynamic damping of a circular cylinder at low $KC$: experiments and an associated model. Mar. Struct. 72, 102777.CrossRefGoogle Scholar
Guermond, J. & Shen, J. 2003 Velocity-correction projection methods for incompressible flows. SIAM J. Numer. Anal. 41 (1), 112–134.CrossRefGoogle Scholar
Hall, P. 1984 On the stability of the unsteady boundary layer on a cylinder oscillating transversely in a viscous fluid. J. Fluid Mech. 146, 347–367.CrossRefGoogle Scholar
Justesen, P. 1989 Hydrodynamic forces on large cylinders in oscillatory flow. J. Waterways Port Coast. Ocean Engng 115 (4), 497–514.CrossRefGoogle Scholar
Karniadakis, G.E., Israeli, M. & Orszag, S.A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.CrossRefGoogle Scholar
Keulegan, G. & Carpenter, L. 1958 Forces on cylinders and plates in an oscillating fluid. J. Res. Natl Bur. Stand. 60 (5), 423–440.CrossRefGoogle Scholar
Morison, J.R., Johnson, J.W. & Schaaf, S.A. 1950 The force exerted by surface waves on piles. J. Petrol. Tech. 2 (05), 149–154.CrossRefGoogle Scholar
Nehari, D., Armenio, V. & Ballio, F. 2004 Three-dimensional analysis of the unidirectional oscillatory flow around a circular cylinder at low Keulegan–Carpenter and $\beta$ numbers. J. Fluid Mech. 520, 157–186.CrossRefGoogle Scholar
Rashid, F., Vartdal, M. & Grue, J. 2011 Oscillating cylinder in viscous fluid: calculation of flow patterns and forces. J. Engng Maths 70 (1), 281–295.CrossRefGoogle Scholar
Ren, C., Cheng, L., Tong, F., Xiong, C. & Chen, T. 2019 Oscillatory flow regimes around four cylinders in a diamond arrangement. J. Fluid Mech. 877, 955–1006.CrossRefGoogle Scholar
Saghafian, M., Stansby, P.K., Saidi, M.S. & Apsley, D.D. 2003 Simulation of turbulent flows around a circular cylinder using nonlinear eddy-viscosity modelling: steady and oscillatory ambient flows. J. Fluids Struct. 17 (8), 1213–1236.CrossRefGoogle Scholar
Sarpkaya, T. 1986 Force on a circular cylinder in viscous oscillatory flow at low Keulegan–Carpenter numbers. J. Fluid Mech. 165 (1), 61–71.CrossRefGoogle Scholar
Sarpkaya, T. 2001 Hydrodynamic damping and quasi-coherent structures at large Stokes numbers. J. Fluids Struct. 15 (7), 909–928.CrossRefGoogle Scholar
Sarpkaya, T. 2002 Experiments on the stability of sinusoidal flow over a circular cylinder. J. Fluid Mech. 457, 157–180.CrossRefGoogle Scholar
Sarpkaya, T. 2006 a Hydrodynamic damping. Report. Naval Postgraduate School.Google Scholar
Sarpkaya, T. 2006 b Structures of separation on a circular cylinder in periodic flow. J. Fluid Mech. 567, 281–297.CrossRefGoogle Scholar
Sarpkaya, T. 2010 Wave Forces on Offshore Structures. Cambridge University Press.CrossRefGoogle Scholar
Stokes, G.G. 1851 On the Effect of the Internal Friction of Fluids on the Motion of Pendulums. Cambridge Library Collection — Mathematics, vol. 3. Cambridge University Press.Google Scholar
Sumer, B.M. & Fredsøe, J. 1997 Hydrodynamics Around Cylindrical Structures, Advanced Series on Ocean Engineering, vol. 26. World Scientific.CrossRefGoogle Scholar
Suthon, P. & Dalton, C. 2011 Streakline visualization of the structures in the near wake of a circular cylinder in sinusoidally oscillating flow. J. Fluids Struct. 27 (7), 885–902.CrossRefGoogle Scholar
Tong, F., Cheng, L., Zhao, M. & An, H. 2015 Oscillatory flow regimes around four cylinders in a square arrangement under small kc and re conditions. J. Fluid Mech. 769, 298–336.CrossRefGoogle Scholar
Vos, P. E.J., Eskilsson, C., Bolis, A., Chun, S., Kirby, R. M. & Sherwin, S. J. 2011 A generic framework for time-stepping partial differential equations (PDEs): general linear methods, object-oriented implementation and application to fluid problems. Intl J. Comput. Fluid Dyn. 25 (3), 107–125.CrossRefGoogle Scholar
Wang, C. 1968 On high-frequency oscillatory viscous flows. J. Fluid Mech. 32 (1), 55–68.CrossRefGoogle Scholar
Xiong, C., Cheng, L., Tong, F. & An, H. 2018 a Influence of plane boundary proximity on the Honji instability. J. Fluid Mech. 852, 226–256.CrossRefGoogle Scholar
Xiong, C., Cheng, L., Tong, F. & An, H. 2018 b On regime C flow around an oscillating circular cylinder. J. Fluid Mech. 849, 968–1008.CrossRefGoogle Scholar
Xiong, C., Cheng, L., Tong, F. & An, H. 2018 c Oscillatory flow regimes for a circular cylinder near a plane boundary. J. Fluid Mech. 844, 127–161.CrossRefGoogle Scholar
Zhao, M. & Cheng, L. 2014 Two-dimensional numerical study of vortex shedding regimes of oscillatory flow past two circular cylinders in side-by-side and tandem arrangements at low Reynolds numbers. J. Fluid Mech. 751, 1–37.CrossRefGoogle Scholar