No CrossRef data available.
Published online by Cambridge University Press: 02 October 2023
Let 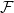 $\mathcal{F}$ be an intersecting family. A
$\mathcal{F}$ be an intersecting family. A 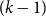 $(k-1)$-set
$(k-1)$-set 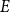 $E$ is called a unique shadow if it is contained in exactly one member of
$E$ is called a unique shadow if it is contained in exactly one member of 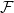 $\mathcal{F}$. Let
$\mathcal{F}$. Let 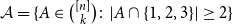 ${\mathcal{A}}=\{A\in \binom{[n]}{k}\colon |A\cap \{1,2,3\}|\geq 2\}$. In the present paper, we show that for
${\mathcal{A}}=\{A\in \binom{[n]}{k}\colon |A\cap \{1,2,3\}|\geq 2\}$. In the present paper, we show that for 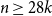 $n\geq 28k$,
$n\geq 28k$, 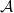 $\mathcal{A}$ is the unique family attaining the maximum size among all intersecting families without unique shadow. Several other results of a similar flavour are established as well.
$\mathcal{A}$ is the unique family attaining the maximum size among all intersecting families without unique shadow. Several other results of a similar flavour are established as well.