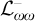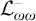1 Introduction
In the 1960s, Per Lindström [Reference Lindström25] showed that first-order logic is maximal (in terms of expressive power) among its extensions satisfying certain combinations of model-theoretic properties. The best known of these combinations are:
$$\begin{align*}&\text{L}\ddot{\mathrm{o}}\text{wenheim--Skolem theorem} \ +\ \text{Compactness,}\\ \text{L}\ddot{\mathrm{o}}\text{wenheim--}&\text{Skolem theorem} \ +\ \text{Recursively enumerable set of validities}. \end{align*}$$
This list is by no means exhaustive though (the reader can consult the encyclopaedic monograph [Reference Barwise and Feferman3] for a thorough treatment of this topic). Philosophically, these results have been interpreted as providing a case for first-order logic being the “right” logic in contrast to higher-order, infinitary, or logics with generalized quantifiers, which can be argued to be more mathematical beasts (see [Reference Kennedy and Väänänen21, Reference Tharp29]). An implicit assumption of Lindström’s work is that identity (
$=$
) belongs in the base logic.
The classical Lindström theorems clearly fail for first-order logic without identity (
$\mathcal {L}_{\omega \omega }^{-}$
) since first-order logic with identity (
$\mathcal {L}_{\omega \omega }$
) is a proper extension of
$\mathcal {L}_{\omega \omega }^{-}$
. In fact, there are continuum-many logics between the former and the latter satisfying the compactness and Löwenheim–Skolem properties, and with recursively enumerable sets of validities (see Example 2.1).
In this article, we aim at finding a way to amend Lindström’s two central theorems so that they apply in the identity-free context.Footnote
1
Our proofs make heavy use of a property that is not available in the presence of identity, namely, an unrestricted upwards Löwenheim–Skolem theorem that applies even to finite models. We also observe other maximality results: a very simple one for the monadic version of the logic (i.e., restricted to vocabularies that only have unary predicates),
$\mathcal {L}_{\omega \omega }^{1-}$
, as well as results for both
$\mathcal {L}_{\infty \omega }^{-}$
and
$\mathcal {L}_{\omega \omega }^{-} $
in terms of a suitable variant of the Karp property. A simple by-product will be a preservation theorem characterizing the identity-free fragment of first-order logic (essentially [Reference Casanovas, Dellunde and Jansana11, Corollary 2.10] obtained by a rather different method).
$\mathcal {L}_{\omega \omega }^{-}$
has attracted mathematical attention in other works such as [Reference Keisler and Miller20] where the problem of categoricity of theories in that logic is studied. Moreover, the results in the present paper may provide new insight on the philosophical discussion whether
$\mathcal {L}_{\omega \omega }^{-}$
is suitable as a contender for the title of the “right logic” against
$\mathcal {L}_{\omega \omega }$
. After all, the logicality of the
$=$
predicate is not obvious (cf. [Reference Feferman16]). So, if the criteria were to involve only indisputably logical operators (thus more than what
$\mathcal {L}_{\omega \omega }$
already involves), be reasonably expressive (quite a bit can be formalized already in
$\mathcal {L}_{\omega \omega }^{-}$
, including set theory), and satisfying a neat Lindström-style characterization,
$\mathcal {L}_{\omega \omega }^{-}$
would appear to be as good an option as any. However, we will not pursue those issues here.
We use the notion of an abstract logic from [Reference Barwise and Feferman3, Definition II.1.1.1] which presents logics as model-theoretic languages [Reference Feferman15] (see also [Reference Barwise2, Reference Flum17, Reference Lindström25]), not as consequence relations or collections of theorems. Furthermore, we assume logics to have the basic closure properties from [Reference Barwise and Feferman3, Definition II.1.2.1], except that in the atom property we use
$\mathcal {L}_{\omega \omega }^{-} $
as the base logic, and demand that
$\top $
be an atomic formula of every vocabulary. For greater generality, we do not require the relativization property. As usual, if
$\mathcal {L}$
and
$\mathcal {L}'$
are logics, we write
$\mathcal {L} \leq \mathcal {L'}$
if, for any vocabulary
$\tau $
and any formula
$\varphi \in \mathcal {L}(\tau )$
, we can find an equivalent formula
$\varphi ' \in \mathcal {L'}(\tau )$
.
For vocabularies containing a binary relation symbol,
$\mathcal {L}_{\omega \omega }^{-} $
is, properly speaking, a fragment of
$\mathcal {L}_{\omega \omega }$
that includes the guarded fragment corresponding to basic modal logic. In this setting, the most fruitful approach has been to use bisimulations as a modal analogue of potential isomorphisms in first-order logic [Reference Benthem, Cate and Väänänen5]. In the present context all we require is the notion of weak (partial) isomorphism introduced in [Reference Casanovas, Dellunde and Jansana11], which is stronger than bisimulation.Footnote
2
Interestingly, the presence of identity can make a substantial difference regarding compactness. For example, monadic first-order logic with the Henkin quantifier,
$\mathcal {L}^1_{\omega \omega }(Q^H)$
, is not compact and not contained in (monadic) first-order logic with identity for it can express the quantifier “there are at least
$\aleph _0$
-many elements”; however, the identity-free fragment of the very same logic admits the effective elimination of the quantifier
$Q^H$
and, hence, it is compact [Reference Krynicki and Lachlan23, Theorem 1.5].Footnote
3
The paper is arranged as follows: in Section 2 we start with the preliminary observation that there is a continuum of abstract logics between
$\mathcal {L}_{\omega \omega }^{-} $
and
$\mathcal {L}_{\omega \omega }$
, and we recall the definitions of the properties of abstract logics employed in the paper, while referring to the literature for some particular technical notions. In Section 3 we present our main new results, that is, Lindström-style characterizations of the identity-free first-order logic and its monadic fragment, together with instrumental observations regarding the logical relations of the involved properties and a useful form of upwards Löwenheim–Skolem theorem. In Section 4 we examine a few interesting particular extensions of
$\mathcal {L}_{\omega \omega }^{-} $
that help us understand the role of compactness and the Löwenheim–Skolem property in our characterizations. Finally, in Section 5, we collect some open problems that arise from this investigation.
2 Preliminaries
We begin this section by noting that there are continuum-many pairwise non-equivalent abstract logics between
$\mathcal {L}_{\omega \omega }^{-} $
and
$\mathcal {L}_{\omega \omega }$
(actually, already between their monadic fragments).
Example 2.1. Consider quantifiers
$\exists ^{\geq n}$
with semantics
$\mathfrak {A} \models {{\exists ^{\geq n}x} \,} \varphi $
iff there are at least n elements a such that
$\mathfrak {A} \models \varphi [a]$
. For each non-empty
$X \subsetneq \omega \setminus \{0,1\}$
, we can prove that the logic
$\mathcal {L}_{\omega \omega }^{-} (\{\exists ^{\geq n} \mid n\in X \})$
indeed lies properly between
$\mathcal {L}_{\omega \omega }^{-} $
and
$\mathcal {L}_{\omega \omega }$
in terms of expressive power and, moreover, there is a continuum of such intermediate abstract logics.
For distinct
$X, Y \subseteq \omega \setminus \{0,1\}$
, the corresponding logics
$\mathcal {L}_{\omega \omega }^{-} (\{\exists ^{\geq n} \mid n\in X \})$
and
$ \mathcal {L}_{\omega \omega }^{-} (\{\exists ^{\geq n} \mid n\in Y \})$
are also distinct. To see this, it suffices to focus our attention on a monadic vocabulary
$\tau =\{P\}$
. Suppose, without loss of generality, that we have an element
$r \in X \setminus Y$
. We abbreviate, for
$n < m$
,
${{\exists ^{\geq n}x}\,}\theta \wedge \lnot {{\exists ^{\geq m}x}\,} \theta $
as
$\exists ^{\lbrack n,m)}x\,\theta $
, and, for each n,
$\exists ^{\geq n}x\,\theta $
as
$\exists ^{\lbrack n,\infty )}x\,\theta $
. Then, using results from [Reference Caicedo and Lesmes9], any sentence
$\varphi $
from the logic
$\mathcal {L}_{\omega \omega }^{-} (\{\exists ^{\geq n} \mid n\in Y \})$
over the vocabulary
$\tau $
is equivalent to a disjunction
$\theta _1 \vee \dots \vee \theta _q$
involving only quantifiers from
$\varphi $
where each
$\theta _{i}$
is of one of the three following forms:
-
•
$\exists ^{\lbrack n_{i},m_{i})}x\, P(x)\wedge \exists ^{\lbrack r_{i},s_{i})}x\,\lnot P(x)$
, -
•
$\exists ^{\lbrack n_{i},m_{i})}x\, P(x)$
, -
•
$\exists ^{\lbrack r_{i},s_{i})}x\,\lnot P(x)$
,
where
$n_{i} \leq m_{i}$
and
$r_{i} \leq s_{i}$
belong to
$Y\cup \{1,\infty \}.$
Thus,
$\varphi $
just describes an array of possible cardinalities for the interpretations of P and its complement, and clearly,
${{\exists {}^{\geq r}x}\,} P(x)$
is equivalent to this disjunction if and only if
$[r,\infty )=\bigcup _{n_i < m_i}[n_{i},m_{i})$
, or
$r=n_{i}$
for the least
$n_{i},$
which is impossible as
$r\not \in Y\cup \{1\}.$
We use the definitions from [Reference Casanovas, Dellunde and Jansana11]:
$\mathfrak {A} \sim \mathfrak {B} $
means that there is a relativeness correspondence between the structures [Reference Casanovas, Dellunde and Jansana11, Definition 2.5] (we prefer to call this a weak isomorphism);
$\mathfrak {A}\sim _p\mathfrak {B}$
means that there is a back-and-forth system I of partial relativeness correspondences between the models [Reference Casanovas, Dellunde and Jansana11, Definition 4.7] (we will say that these structures are partially weakly isomorphic); and we denote by
$\sim _n$
the finite approximation of
$\sim _p$
[Reference Casanovas, Dellunde and Jansana11, Definition 4.2]. In the setting of first-order logic without identity, the relation
$ \sim $
behaves like a weak notion of isomorphism [Reference Casanovas, Dellunde and Jansana11], which motivates the name for the third property defined below.Footnote
4
The properties of abstract logics that we consider in this article are:
-
• Compactness property: for any vocabulary
$\tau $
,
$\Phi \subseteq \mathcal {L}(\tau )$
, if every finite subset of
$\Phi $
has a model, then
$\Phi $
has a model. -
• Löwenheim–Skolem property: for any vocabulary
$\tau $
and sentence
$\varphi \in \mathcal {L}(\tau )$
,
$\varphi $
has a countable model if it has an infinite model. -
• Weak isomorphism property: for any structures
$\mathfrak {A}$
and
$ \mathfrak {B}$
,
$\mathfrak {A} \sim \mathfrak {B} $
only if
$ \mathfrak {A} \equiv _{\mathcal {L}} \mathfrak {B}$
. -
• Finite weak dependence property: for any vocabulary
$\tau $
and any
$\varphi \in \mathcal {L}(\tau )$
, there is a finite
$\tau _0\subseteq \tau $
s.t. for any
$\tau $
-structures
$\mathfrak {A}$
and
$\mathfrak {B}$
, if
$\mathfrak {A}\upharpoonright \tau _0\sim \mathfrak {B} \upharpoonright \tau _0$
, then
$\mathfrak {A}\models \varphi $
iff
$\mathfrak {B} \models \varphi $
. -
• Karp
$^-$
property: for any structures
$\mathfrak {A}$
and
$ \mathfrak {B}$
,
$\mathfrak {A} \sim _p \mathfrak {B}$
only if
$\mathfrak {A} \equiv _{\mathcal {L}} \mathfrak {B}$
. -
• Boundedness property: any sentence
$\varphi (<, \dots )$
which for arbitrary large ordinal type
$\alpha $
has a model where the interpretation of
$<$
is an irreflexive and transitive binary relation containing a chain of order type
$\alpha $
has a model where the interpretation of
$<$
contains an infinite descending chain.
All these properties, with the exception of Karp
$^-$
and weak isomorphism, hold in
$\mathcal {L}_{\omega \omega }.$
Given a structure
$\mathfrak {A}$
, we denote by
$\mathfrak {A}^*$
the reduction of
$\mathfrak {A}$
[Reference Casanovas, Dellunde and Jansana11, Definition 2.4], i.e., the quotient structure
obtained from the Leibniz congruence relation.
Proposition 2.2 [Reference Casanovas, Dellunde and Jansana11]
Let
$\mathfrak {A}$
and
$\mathfrak {B}$
be structures. Then:
-
(i) If
$\mathfrak {A}$
and
$ \mathfrak {B}$
are countable, then
$\mathfrak {A} \sim _p \mathfrak {B}$
iff
$\mathfrak {A} \sim \mathfrak {B}$
. -
(ii)
$\mathfrak {A} \sim \mathfrak {B}$
iff
$\mathfrak {A}^* \cong \mathfrak {B}^*$
.
Thanks to Proposition 2.2, the weak isomorphism property can be equivalently formulated as follows: for any structures
$\mathfrak {A}$
and
$ \mathfrak {B}$
,
$\mathfrak {A}^* \cong \mathfrak {B}^*$
only if
$\mathfrak {A} \equiv _{\mathcal {L}} \mathfrak {B}$
. Observe that
$\mathfrak {A}^*\cong \mathfrak {A}^{**}$
, so by Proposition 2.2,
$\mathfrak {A} \sim \mathfrak {A}^*$
.
3 Maximality results
We start this section by showing a form of upwards Löwenheim–Skolem theorem, which will be heavily used in the arguments below:
Lemma 3.1. Let
$\mathcal {L}$
be an abstract logic with the weak isomorphism property. Then, a theory
$T \subseteq \mathcal {L}(\tau )$
has a model
$\mathfrak {A}$
of cardinality
$\lambda $
only if, for any
$\kappa>\lambda $
, there is a model
$\mathfrak {B}$
of T with cardinality
$\kappa $
and a surjective strict homomorphism
$($
in the sense of [Reference Casanovas, Dellunde and Jansana11, Definition 2.1]
$)$
, and hence a weak isomorphism, from
$\mathfrak {B}$
onto
$\mathfrak {A}$
.
Proof It follows by inspection of the proof of [Reference Bridge7, Lemma 2.24] or [Reference Ackermann1, Chapter IV, §1] (which is only formulated for relational languages but can be easily generalized to languages with function symbols). For any structure
$\mathfrak {A}$
of cardinality
$\lambda $
, in that proof one builds a model
$\mathfrak {B}$
of size
$\kappa $
and a mapping
$B \longrightarrow A$
which is, in fact, a surjective strict homomorphism.
Remark 3.2. Lemma 3.1 allows us to see that a plethora of logics do not have the weak isomorphism property, e.g., the logics in Example 2.1. Interestingly, the usual Lindström quantifiers may destroy the property, in particular in the logics
$\mathcal {L}_{\omega \omega }^{-}(Q_{\alpha })$
. However, as we will see in Example 4.1, all of these logics have counterparts which do have the weak isomorphism property. On the other hand, as we will see below, the Henkin quantifier
$Q^H$
is a curious case of a natural Lindström quantifier that has the weak isomorphism property.
Now we can provide an analogue of (1) from [Reference Barwise and Feferman3, Theorem III.1.1.1].
Lemma 3.3. Let
$\mathcal {L}$
be an abstract logic such that
$\mathcal {L}_{\omega \omega }^{-} \leq \mathcal {L}$
. If
$\mathcal {L}$
has the compactness and weak isomorphism properties, then it also has the finite weak dependence property.
Proof Given a vocabulary
$\tau ,$
let
$\tau ^{\prime }$
be a disjoint copy and consider the theory
$\Phi (\tau ,R)$
:
$$ \begin{align*} &\{\forall x_{1}\dots x_{n}\forall y_{1}\dots y_{n}[\bigwedge _{i}Rx_{i}y_{i}\rightarrow (\theta (x_{1}\dots)\leftrightarrow \theta ^{\prime }(y_{1}\dots))]\mid \theta \in \tau \text{, }\theta ^{\prime }\in \tau ^{\prime } \text{ its copy} \}\\ &\cup \{ {{\forall{{ x_{1}, \dots, x_{n}}}}\,} \,{{\forall{{y_{1}, \dots,y_{n}}}}\,} [\bigwedge _{i}Rx_{i}y_{i} \rightarrow Rt(x_1\dots)t'(y_{1} \dots)] \mid t \ \text{a term of} \ \tau\} \\ &\cup \ \{\text{"}R\text{ and }R^{-1}\text{are surjective"}\}. \end{align*} $$
For any
$\varphi \in \mathcal {L(\tau )}$
, let
$\varphi ^{\prime }$
denote its renaming in the type
$\tau ^{\prime }$
. Then,
$\Phi (\tau ,R)\models \varphi \leftrightarrow \varphi ^{\prime }$
by closure of the logic
$\mathcal {L}$
under weak isomorphisms, and by compactness
$$ \begin{align*} \Phi (\tau _{0},R)\models \varphi \leftrightarrow \varphi ^{\prime } \end{align*} $$
for some finite
$\tau _{0}\subseteq \tau $
.
Assume now that
$\mathfrak {A}\upharpoonright \tau _{0}\sim \mathfrak {B} \upharpoonright \tau _{0}$
by some
$\tau _{0}$
-weak isomorphism
$r\subseteq (A\cup B)^{2},$
and
$|A|<|B|.$
By Lemma 3.1, there is a
$\mathfrak {C}$
of power
$ |B|$
and a surjective strict homomorphism
$h:C\rightarrow A$
. Thus,
$r\circ h$
is a
$\tau _{0}$
-weak isomorphism from
$\mathfrak {C}$
onto
$\mathfrak {B}.$
Renaming the last structure as
$\mathfrak {B}^{\prime }$
with
$\tau ^{\prime }$
we may put
$\mathfrak {C}$
and
$\mathfrak {B}^{\prime }$
together in a structure
$\mathfrak {C}+\mathfrak {B}^{\prime }$
sharing the same domain. Then,
${\langle {{\mathfrak {C}+\mathfrak {B}^{\prime },r\circ h}}\rangle }\models \Phi (\tau _{0},R),$
and hence,
${\langle {{\mathfrak {C}+\mathfrak {B}^{\prime }, r\circ h}}\rangle }\models \varphi \leftrightarrow \varphi ^{\prime }$
this implies:
$ \mathfrak {C}\models \varphi \space $
iff
$\mathfrak {B}\models \varphi .$
But
$ \mathfrak {A}\sim \mathfrak {C}$
with respect to full
$\tau ,$
then
$\mathfrak {A}\models \varphi \space $
iff
$\mathfrak {B}\models \varphi .$
If
$|A|=|B|$
, we apply the construction directly with
$\mathfrak {A}$
and
$\mathfrak {B}$
.
We are now ready to provide the main result of this paper:
Theorem 3.4. Let
$\mathcal {L}$
be an abstract logic such that
$\mathcal {L}_{\omega \omega }^{-} \leq \mathcal {L}$
. If
$\mathcal {L}$
has the weak isomorphism, compactness, and Löwenheim–Skolem properties, then
$\mathcal {L} \leq \mathcal {L}_{\omega \omega }^{-}$
.
Proof Assume
$\varphi \in \mathcal {L}(\tau )\setminus \mathcal {L}_{\omega \omega }^{-}(\tau )$
and
$\varphi $
depends on a finite vocabulary
$\tau _{0}\subseteq \tau $
(by compactness and Lemma 3.3). Notice that there are only finitely many sentences of rank
$\leq n$
in
$\mathcal {L}_{\omega \omega }^{-}(\tau _{0})$
[Reference Casanovas, Dellunde and Jansana11, Lemma 4.4]; thus, the relation
$\mathfrak {A}\upharpoonright \tau _{0}\equiv _{n}^{-}\mathfrak {B}\upharpoonright \tau _{0}$
has finitely many equivalence classes of structures of type
$\tau $
and the equivalence class of a structure
$\mathfrak {A}$
coincides with
$\mathrm {Mod}_{\tau }(\Theta _{\mathfrak {A}})$
for the sentence
$$\begin{align*}\Theta_{\mathfrak{A}}=\bigwedge\{\theta\text{ of rank}\leq n\mid \mathfrak{A\models}\theta\}. \end{align*}$$
Therefore,
$\mathrm {Mod}_{\tau }(\varphi )$
cannot be a union of these classes (it would be equivalent to a finite disjunction of sentences in
$\mathcal {L}_{\omega \omega }^{-}(\tau _{0}))$
and it must cut some equivalence class in two non-emtpy pieces. In other words, there are
$\tau $
-structures
$\mathfrak {A}_{n}$
and
$\mathfrak {B}_{n}$
such that
$$\begin{align*}\mathfrak{A}_{n}\upharpoonright\tau_{0}\equiv_{n}^{-}\mathfrak{B}_{n}\upharpoonright\tau_{0},\ \ \mathfrak{A}_{n}\models \varphi,\mathfrak{B}_{n}\models\lnot\varphi. \end{align*}$$
By Lemma 3.1, we may assume that
$\mathfrak {A}_{n}$
and
$\mathfrak {B}_{n}$
have the same infinite power and share the same domain
$A_{n}.$
By [Reference Casanovas, Dellunde and Jansana11, Lemma 4.4 and Proposition 4.5],
$\mathfrak {A}_{n}\upharpoonright \tau _{0}\sim _{n}\mathfrak {B}_{n}\upharpoonright \tau _{0};$
that is, there are sets
$I_{0},\ldots ,I_{n}$
of weak finite
$\tau _{0}$
-partial isomorphisms from
$\mathfrak {A}_{n}$
to
$\mathfrak {B}_{n}$
such that
$I_{n}\not =\emptyset $
and, for each
$p\in I_{j+1}$
,
$a\in A_{n}, b\in B_{n}$
, there are
$q,q^{\prime }\in I_{j}$
such that
$q,q^{\prime }\supseteq r$
and
$a\in \textit {dom}(q)$
,
$b\in \textit {rg}(q^{\prime }),$
and further extension properties guaranteeing that constants and functions are eventually preserved. The set of all finite weak
$\tau _{0}$
-partial isomorphisms has the same power as
$D,$
so we may enumerate them as
$\{R_{p}\mid p\in A_{n}\};$
moreover, we may assume
$\{0,\ldots ,n\}\subseteq A_{n}.$
Then, renaming
$\mathfrak {B}_{n}$
as
$\mathfrak {B}_{n}^{\prime }$
on the vocabulary
$\tau ^{\prime },$
as in the proof of Lemma 3.3, and defining in
$A_{n}$
:
-
$<^{\ast }=$
usual order of
$\{0,\ldots ,n\}$
,
-
$c_{0}^{\ast }=n$
,
-
${\langle {{j,p}}\rangle }\in I^{\ast }\Leftrightarrow R_{p}\in I_{j}$
,
-
${\langle {{p,x,y}}\rangle }\in G^{\ast }\Leftrightarrow {\langle {{x,y}}\rangle }\in R_{p},$
the structure
${\langle {{\mathfrak {A}_{n}+\mathfrak {B}_{n},<^{\ast },c_{0}^{\ast },I^{\ast },G^{\ast }}}\rangle }$
satisfies the following finite theory
$\Psi $
in the vocabulary:
$$\begin{align*}\tau_{0}\cup\tau_{0}^{\prime}\cup\{<,c_{0},I,G\}, \end{align*}$$
where
$c_{0}$
is a constant,
$<$
and I are binary relations, and G is a ternary relation (all fresh symbols; moreover, for each formula
$\psi \in \mathcal {L}(\tau _{0})$
, we denote by
$\psi ^{\prime }$
its renaming in the vocabulary
$\tau _{0}^{\prime }$
):
-
1.
$\varphi $
,
$\lnot \varphi ^{\prime }$
. -
2.
$\exists p \ Ic_{0}p$
. -
3.
$\forall p\,\overrightarrow {x}\overrightarrow {y}({\textstyle \bigwedge \nolimits _{i}} Gpx_{i}y_{i}\rightarrow (\chi (\overrightarrow {x})\leftrightarrow \chi ^{\prime }(\overrightarrow {y}))),$
-
for each relation symbol
$\chi \in \tau _{0}$
of arity
$|\overrightarrow {x}|$
. -
4.
$\forall uvp\overrightarrow {x}\overrightarrow {y}(u<v\wedge Ivp\wedge {\textstyle \bigwedge \nolimits _{i}} Gpx_{i}y_{i}\rightarrow \exists q[Iuq\wedge Gqf(\overrightarrow {x})f^{\prime }(\overrightarrow {y})$
-
$\wedge \forall zw(Gpzw\rightarrow Gqzw)])$
,
-
for each function symbol
$f\in \tau _{0}$
of arity
$|\overrightarrow {x}|$
. -
5.
$\forall uvp(u<v\wedge Ivp\rightarrow \exists q[Iuq\wedge Gqcc^{\prime }\wedge \forall zw(Gpxw\rightarrow Gqzw)])$
, -
for each constant symbol
$c\in \tau _{0}$
. -
6.
$\forall uvp(u<v\wedge Ivp\rightarrow \forall x\exists qq^{\prime }yy^{\prime }[Iuq\wedge Iuq^{\prime }\wedge Gqxy\wedge Gq^{\prime }y^{\prime }x$
-
$\wedge \forall zw(Gpxw\rightarrow Gqzw\wedge Gq^{\prime }zw)]$
.
The second sentence states that
$I_{n}$
is non-empty. Sentences 3–6 describe a sequence
$I_{0},\ldots ,I_{n}$
of sets of weak
$\tau _{0}$
-partial isomorphisms in the sense of [Reference Casanovas, Dellunde and Jansana11, Definition 4.2].
As the above holds for any n, we have models for any finite part of the infinite theory with additional constants
$c_{1},c_{2},\ldots $
:
$$\begin{align*}\Psi(\tau_{0},<,I,G)\cup\{\varphi,\lnot\varphi^{\prime}\}\cup\{c_{j+1}<c_{j}\mid j\in\omega\}. \end{align*}$$
By compactness, we have a model
${\langle {{\mathfrak {C},<^{\mathfrak {C}},I^{\mathfrak {C} },G^{\mathfrak {C}},{\langle {{c_{j}^{\mathfrak {C}}}}\rangle }_{j\in \omega }}}\rangle }$
of this theory. By the axioms, each
$p\in C$
encodes a weak
$\tau _{0}$
-partial isomorphism
$R_{p}=\{{\langle {{x,y}}\rangle }\in A^{2}\mid {\langle {{p,x,y}}\rangle }\in G^{\mathfrak {C}}\}$
between
$\mathfrak {C}\upharpoonright \tau _{0}$
and
$\mathfrak {C}\upharpoonright \tau _{0}^{\prime },$
and the sequence
$$\begin{align*}I_{j}=\{R_{p}\in C\mid{\langle{{p,c_{j}}\rangle}^{\mathfrak{C}}}\in I^{\mathfrak{C}}\}, j=0,1,\ldots \end{align*}$$
has the back-and-forth extension property with respect to increasing subindexes: if
$R_{p}\in I_{j}$
and
$c\in C$
, then there is a
$R_{q}\in I_{j+1}$
such that
$c\in \textit {dom}(R_{p}),$
etc. Hence,
$K^{\mathfrak {C}}=\bigcup _{j}I_{j}$
has the unrestricted extension property and becomes a Karp system of weak
$\tau _{0}$
-isomorphisms. This is expressible by the finite theory
$\Phi (\tau _{0},K,G)$
which results of changing the back-and-forth axioms of
$\Psi (\tau _{0},<,c_{0},I,G)$
to
$$\begin{align*}\forall px(Kp\rightarrow\exists q\,q^{\prime}\,\exists yy^{\prime}[Kq\wedge Kq^{\prime}\wedge Gqxy\wedge Gq^{\prime}y^{\prime}x\wedge\forall z\forall w(Gpzw\rightarrow Gqzw\wedge Gq^{\prime}zw)]. \end{align*}$$
In sum,
${\langle {{\mathfrak {C},K^{\mathfrak {C}},G^{\mathfrak {C}}}}\rangle } \models \Phi (\tau _{0},K,G)\cup \{\varphi ,\lnot \varphi \}$
which means
$$\begin{align*}\mathfrak{C}\upharpoonright\tau_{0}\sim_{p}\mathfrak{C}\upharpoonright\tau _{0}^{\prime}, \mathfrak{C}\upharpoonright\tau\models\varphi ,\mathfrak{C}\upharpoonright\tau^{\prime}\models\lnot\varphi^{\prime}. \end{align*}$$
By the Löwenheim–Skolem property, we may assume that
$\mathfrak {C}$
is countable. Hence, by Proposition 2.2,
$\mathfrak {C\upharpoonright \tau }_{0}\sim \mathfrak {C}\upharpoonright \tau _{0}^{\prime }$
and thus
$\mathfrak {C\mathfrak {\upharpoonright \tau }\models \varphi \Longleftrightarrow C\mathfrak {\upharpoonright \tau }}^{\prime }\mathfrak {\models \varphi }$
by the choice of
$\tau ,$
a contradiction.
Remark 3.5. The Karp
$^-$
property may replace the Löwenheim–Skolem hypothesis in the above theorem because the proof yields before the last step a model of
$\Phi (\tau _{0},K,G)\cup \{\varphi ,\lnot \varphi \}$
for any finite
$\tau _{0}\subseteq \tau ,$
which by an additional use of compactness gives a model
${\langle {{\mathfrak {C},K^{\mathfrak {C}},G^{\mathfrak {C}}}}\rangle }$
of
$\Phi (\tau ,K,G)\cup \{\varphi ,\lnot \varphi \};$
that is, the weak isomorphisms encoded by
$K,G$
are weak
$\tau $
-isomorphisms, thus we have
$$\begin{align*}\mathfrak{C\upharpoonright\tau\sim}_{p}\text{ }\mathfrak{C\upharpoonright\tau }^{\prime},\text{ }\mathfrak{C\mathfrak{\upharpoonright\tau}\models\varphi ,}\text{ }\mathfrak{C\mathfrak{\upharpoonright\tau}}^{\prime}\mathfrak{\models \lnot\varphi}^{\prime}, \end{align*}$$
which, by the Karp
$^-$
property, gives directly the contradiction
$\mathfrak {C\mathfrak {\upharpoonright \tau }\hspace{-0.5pt}\models\hspace{-0.5pt} \varphi \Leftrightarrow \mathfrak {C\mathfrak {\upharpoonright \tau }}^{\prime }} {\hspace{-0.5pt}\models\hspace{-0.5pt} \varphi ^{\prime }}$
.
Remark 3.6. Note that the boundedness property for
$\mathcal {L}_{\infty \omega }^{-}$
is essentially a corollary of the classical one from [Reference Barwise and Kunen4, Theorem 1.8]. Then, if we use our approach in encoding weak partial isomorphisms in Theorem 3.4 and working with the Karp
$^-$
property, it is straightforward to modify the argument from [Reference Barwise and Feferman3, Theorem III.3.1] to show that
$\mathcal {L}_{\infty \omega }^{-}$
is maximal among its extensions in having the boundedness, and Karp
$^-$
properties. In fact, all we need from the boundedness property is that it will give us a model where
$<$
is not well founded.
Remark 3.7. As a referee suggests, a small modification of the given proof of Lindström’s result permits to prove the following separation theorem: if
$\varphi $
,
$\varphi ^{\ast }\in \mathcal {L}(\tau )$
,
$\mathcal {L}$
is an extension of
$\mathcal {L}_{\omega \omega }^{-}$
satisfying the conditions of Theorem 3.4 except for closure, and the classes of structures
$\mathrm {Mod}(\varphi )$
and
$\mathrm {Mod}(\varphi ^{\ast })$
are disjoint, then they are separable by some
$\theta \in \mathcal {L}_{\omega \omega }^{-}(\tau )$
, i.e.,
$\mathrm {Mod}(\varphi )\subseteq \mathrm {Mod}(\theta )$
and
$\mathrm {Mod}(\varphi ^{\ast })\subseteq \mathrm {Mod}(\lnot \theta )$
. Just make
$\varphi ^{\ast }$
play the role of
$\mathfrak {\lnot \varphi }$
in the proof (for a thorough discussion of the case with identity, see [Reference García-Matos18]). Applying this property to second-order existential logic without identity
$\mathcal {L}_{\omega \omega }^{-II\exists },$
yields Craig interpolation theorem for
$\mathcal {L}_{\omega \omega }^{-}$
[Reference Craig13, Theorem 5]. Assume
$\varphi \models \psi $
with
$\varphi \in \mathcal {L}_{\omega \omega } ^{-}(\tau )$
,
$\psi \in \mathcal {L}_{\omega \omega }^{-}(\mu )$
, and
$\rho =\tau \cap \mu $
. Then,
$\exists _{\tau \smallsetminus \rho }\varphi \models \forall _{\mu \smallsetminus \rho }\psi ,$
where
$\exists _{\tau \smallsetminus \rho }$
,
$\forall _{\mu \smallsetminus \rho }$
are second-order quantifier binding the symbols in
$\tau \smallsetminus \rho $
and
$\mu \smallsetminus \rho ,$
respectively. Now,
$\exists _{\tau \smallsetminus \rho }\varphi $
and
$\exists _{\mu \smallsetminus \rho }\lnot \psi $
define disjoint model classes belonging to
$\mathcal {L}_{\omega \omega }^{-II\exists }(\rho )$
and, by the separation property, we obtain
$\theta \in \mathcal {L}_{\omega \omega }^{-}(\rho )$
such that
$\exists _{\tau \smallsetminus \rho }\varphi \models \theta \models \forall _{\mu \smallsetminus \rho }\psi .$
That is,
$\varphi \models \theta \models \psi .$
Comparing the proof of Theorem 3.4 with that of its classical counterpart with identity, the reader should note that our approach makes a substantial use of the strong upwards Löwenheim–Skolem theorem given by Lemma 3.1. This allows us to deal with cardinality situations that in the classical context are dealt with the expressive power of identity.
One may wonder whether we can obtain a Lindström-style characterization for identity-free monadic first-order logic,
$\mathcal {L}_{\omega \omega }^{1-}$
, analogous to Tharp’s result [Reference Tharp28, Theorem 1] for monadic first-order logic. The answer is yes and the result does not require, surprisingly, any form of the Löwenheim–Skolem theorem (not even the other two properties if we assume the finite weak dependence property; see Remark 3.9).
Theorem 3.8. Let
$\mathcal {L}$
be a monadic logic such that
$\mathcal {L}_{\omega \omega }^{1-}\leq \mathcal {L}$
. If
$\mathcal {L}$
satisfies the compactness and weak isomorphism properties, then
$\mathcal {L}\leq \mathcal {L}_{\omega \omega }^{1-}$
.
Proof Assume
$\varphi \in \mathcal {L}(\tau )\setminus \mathcal {L}_{\omega \omega }^{-}(\tau )$
,
$\tau =\{P_{i} \mid i\in I\}$
. As in the proof of Theorem 3.4, we have for each finite
$\tau _{0}\subseteq \tau $
:
$$\begin{align*}\mathfrak{A}\upharpoonright\tau_{0}\equiv_{1}^{-}\mathfrak{B}\upharpoonright \tau_{0},\ \ \mathfrak{A}\models\varphi,\text{ }\models \lnot\varphi, \end{align*}$$
and by compactness
$$\begin{align*}\mathfrak{A}\equiv_{1}^{-}\mathfrak{B},\ \ \mathfrak{A}\models\varphi,\mathfrak{B}\models\lnot\varphi. \end{align*}$$
By Lemma 3, we may assume
$\mathfrak {A}$
and
$\mathfrak {B}$
share the same domain A.
Each map
$\delta \colon I\rightarrow \{0,1\}$
determines a type
$$\begin{align*}t_{\delta}(x)=\{P_{i}(x) \mid \delta(i)=1\}\cup\{\lnot P_{i}(x) \mid \delta(i)=0\}. \end{align*}$$
A type
$t_{\delta }$
is consistent with
$\mathfrak {A}$
if for each finite
$J\subseteq I$
,
$\mathfrak {A}\models \exists x\wedge (t_{\delta }(x)\upharpoonright J)$
. Clearly,
$\mathfrak {A}$
and
$\mathfrak {B}$
above have the same consistent types and, if
$t_{\delta }$
is not consistent with
$\mathfrak {A}$
, there is a witness
$\eta _{\delta }$
of the form
$\lnot \exists x\wedge (t_{\delta \upharpoonright J_{\delta }}(x))$
,
$J_{\delta }\subseteq _{fin}I,$
true in both
$\mathfrak {A}\space $
and
$\mathfrak {B}$
.
Consider the following theory on the vocabulary
$\tau \cup \tau ^{\prime }\cup \{P_{\delta },P_{\delta }^{\prime }\mid \delta \in 2^{I}\}$
:
-
–
$\varphi ,\lnot \varphi ^{\prime }$
. -
For each
$t_{\delta }$
consistent with
$\mathfrak {A}$
and each finite
$J\subseteq I$
: -
–
$\exists xP_{\delta }(x)$
,
$\forall x(P_{\delta }(x)\rightarrow \wedge (t_{\delta \upharpoonright J}(x))$
. -
–
$\exists xP_{\delta }^{\prime }(x)$
,
$\forall x (P_{\delta }^{\prime }(x)\rightarrow \wedge (t_{\delta \upharpoonright J}^{\prime }(x))$
. -
For each
$t_{\delta }$
inconsistent with
$\mathfrak {A}$
: -
–
$\eta _{\delta }$
,
$\eta _{\delta }^{\prime }.$
Then,
$\mathfrak {C=A}+\mathfrak {B}^{\prime }$
may be expanded to a model
${\langle {{\mathfrak {A}+\mathfrak {B}^{\prime }, P_{\delta }^{\mathfrak {C} },P_{\delta }^{\prime \mathfrak {C}}}}\rangle }_{\delta \in 2^{J}}$
of each finite part
$\Sigma $
of this theory, taking
$P_{\delta }^{\mathfrak {C}}=\{a\in A\mid \mathfrak {A\models }t_{\delta \upharpoonright J}(a)\}$
and
$P_{\delta }^{\prime \mathfrak {C}}=\{b\in A\mid \mathfrak {B}^{\prime }\mathfrak {\models }t_{\delta \upharpoonright J}^{\prime }(a)\}$
for
$J=\{i \mid P_{i}$
or
$P_{i}^{\prime }$
occur in
$\Sigma \}$
.
By compactness, there is a model
${\langle {{\widehat {\mathfrak {A}}+\widehat {\mathfrak {B}}^{\prime },P_{\delta }^{\mathfrak {A}},P_{\delta }^{\prime \mathfrak {B}^{\prime }}}}\rangle }_{\delta \in 2^{J}}$
of the full theory. Then,
$\widehat {\mathfrak {A}}$
and
$\widehat {\mathfrak {B}}$
realize exactly the same types
$t_{\delta }$
(those originally consistent) and thus
$\widehat {\mathfrak {A}}\sim \widehat {\mathfrak {B}},$
defining
$aRb$
iff a and b realize the same type
$t_{\delta }.$
This contradicts the weak isomorphism property since
$\widehat {\mathfrak {A}}\models \varphi $
and
$\widehat {\mathfrak {B}}\models \lnot \varphi .$
Remark 3.9. If
$\mathcal {L}$
has the finite weak dependence property, then the compactness and weak isomorphism properties are not needed in the previous theorem. Indeed, if
$\varphi $
depends on finite
$\tau _{0}\subseteq \tau $
, the first step of the proof
$\mathfrak {A}\upharpoonright \tau _{0}\equiv _{1}^{-}\mathfrak {B}\upharpoonright \tau _{0}$
,
$\mathfrak {A}\models \varphi $
,
$\mathfrak {B}\models \lnot \varphi ,$
yields already a contradiction, since
$\mathfrak {A}$
and
$\mathfrak {B}$
realize trivially the same
$t_{\delta }$
types based on
$\tau _{0},$
and thus
$\mathfrak {A}\upharpoonright \tau _{0}\sim \mathfrak {B}\upharpoonright \tau _{0}.$
Since
$\mathcal {L}_{\omega \omega }$
and
$\mathcal {L}^1_{\omega \omega }$
have both the compactness and the Löwenheim–Skolem properties, then we can obtain the following preservation result from Theorems 3.4 and 3.8 (which is essentially [Reference Casanovas, Dellunde and Jansana11, Corollary 2.10]Footnote
5
proved by a rather different method):
Corollary 3.10.
$\mathcal {L}_{\omega \omega }^{-}$
(resp.
$\mathcal {L}_{\omega \omega }^{1-}$
) is the fragment of
$\mathcal {L}_{\omega \omega }$
(resp.
$\mathcal {L}^1_{\omega \omega }$
) preserved under weak isomorphisms.
We proceed now to obtain an analogue of the second Lindström theorem from [Reference Lindström25]. First, we need the following lemma:
Lemma 3.11.
Footnote
6
Let
$\mathcal {L}$
be an abstract logic such that
$\mathcal {L}_{\omega \omega }^-\leq \mathcal {L}$
satisfying the finite weak dependence and weak isomorphism properties. If
$\mathcal {L}$
extends properly
$\mathcal {L}_{\omega \omega }^-$
, then there exist a finite vocabulary
$\sigma $
containing at least one unary relation U and, for each finite vocabulary
$\rho \supseteq \sigma $
, a sentence
$\theta \in \mathcal {L}(\rho )$
such that:
-
(1) For each
$n\geq 1$
, there is a model
$\mathfrak {A}\models \theta $
with
$|U^{\mathfrak {A}}|=n$
. -
(2) If
$\mathfrak {A}\models \theta $
and A is countably infinite, then
$U^{\mathfrak {A}^{\ast }}$
is finite and non-empty.
Proof Assume
$\varphi \in \mathcal {L}(\tau )\setminus \mathcal {L}_{\omega \omega }^{-}(\tau )$
and
$\varphi $
depends on finite
$\tau _{0}\subseteq \tau $
. Let
$\tau _{0}^{\prime }$
be a disjoint copy of
$\tau _{0}$
, and set
$$\begin{align*}\sigma=\tau_{0}\ \cup\ \tau_{0}^{\prime}\ \cup\ \{<,c_{0},I,G,U,E\}, \end{align*}$$
which results of adding to the vocabulary in the proof of Theorem 3.4 a unary predicate symbol U and a binary predicated symbol
$E.$
Next, let
$\rho \supseteq \alpha $
be finite and consider the sentence
$\theta \in \mathcal {L}(\rho )$
which is the conjunction of the theory
$\Psi $
introduced in the proof of Theorem 3.4 plus the following new sentences:
-
7.
$\forall x(Ux\leftrightarrow \exists y(x<y\vee y<x)$
“U is the field of
$<$
”. -
8.
$\forall xExx$
-
$\forall xy\forall \overrightarrow {w}(Exy\rightarrow (\chi (\overrightarrow {w})\leftrightarrow \chi (\overrightarrow {w}(y/x)))\wedge Ef(\overrightarrow {w})f(\overrightarrow {w}(y/x)))$
,
$\ \ \chi ,f\in \rho .$
-
This says that E satisfies the finite list of axioms of identity for the vocabulary
$\rho $
, and guarantees that E is the Leibniz congruence relation (this is enough by -
[Reference Kleene22, Section 73, Theorem 41]) with respect to
$\rho $
. -
9.
$\forall x\lnot (x<x)$
,
$\forall xyz(x<y\wedge y<z\rightarrow x<z),$
-
$\forall xy(Ux\wedge Uy\rightarrow x<y\vee y<x\vee Exy)$
,
-
$Uc_{0}\wedge \forall x(Ux\rightarrow x<c_{0}\vee xEc_{0}),$
-
$\forall xy(Ux\wedge Uy\wedge x<y\rightarrow \exists z(z<y\wedge \forall w(w<y\rightarrow w<z\vee Ewz))$
.
-
These axioms say, with E replacing
$=:$
“
$<$
is a strict linear order of U with last -
element
$c_{0}$
and immediate predecesor for non-minimal elements”.
Using [Reference Casanovas, Dellunde and Jansana11, Lemma 4.4 and Proposition 4.5] and Lemma 3.1 as in Theorem 3.4, for each
$n<\omega $
, we get a model
$\mathfrak {C}={\langle {{\mathfrak {A}_{n}+\mathfrak {B}_{n}^{\prime },<^{\ast }, c_{0}^{\ast },I^{\ast },G^{\ast },U^{\ast },E^{\ast }}}\rangle }\models \theta $
where
$U^{\mathfrak {A}}=\{0,\dots ,n\}$
, and
$E^{\mathfrak {A}}$
is true identity.
All that is left to show is that if for a countably infinite structure
$\mathfrak {A}$
we have
$\mathfrak {A}\models \theta $
, then
$U^{\mathfrak {A}^{\ast }}$
is finite and non-empty. The first thing to notice is that
$<^{\mathfrak {A}^{\ast }} $
is a strict linear ordering with last element
$[c_{0}]$
and immediate predecessors for non-minimal elements, because E collapses to true identity in
$\mathfrak {A}^{\ast }$
. Now, suppose that
$U^{\mathfrak {A}^{\ast }}$
is infinite, then we have an infinite descending sequence
$$\begin{align*}\dots<^{\mathfrak{A}^{\ast}}[a_{2}]<^{\mathfrak{A}^{\ast}}[a_{1}]<^{\mathfrak{A}^{\ast }}[a_{0}]=[c_{0}] \end{align*}$$
in
$U^{\mathfrak {A}^{\ast }}$
, where
$[a_{n+1}]$
is the immediate predecessor of
$[a_{n}].$
But then we have the sequence
$\dots<^{\mathfrak{A}}a_{2}<^{\mathfrak{A}}a_{1}<^{\mathfrak{A}}a_{0}$
in
$\mathfrak {A}$
. Reasoning as in the proof of Theorem 3.4 (i),
$\mathfrak {A}\upharpoonright \tau _{0}\sim _{p}(\mathfrak {A}\upharpoonright \tau _{0}^{\prime })^{-^{\prime }}$
and, since
$\mathfrak {A}$
is countable,
$\mathfrak {A}\upharpoonright \tau _{0}\sim (\mathfrak {A}\upharpoonright \tau _{0}^{\prime })^{-^{\prime }}$
but
$\mathfrak {A}\upharpoonright \tau _{0}\models \varphi ,(\mathfrak {A}\upharpoonright \tau _{0}^{\prime })^{-^{\prime }}\models \lnot \varphi ^{\prime }$
, contradicting the weak isomorphism property.
Theorem 3.12. Let
$\mathcal {L}$
be an effectively regular abstract logic [Reference Barwise and Feferman3, Definition II.1.2.4] such that
$\mathcal {L}_{\omega \omega }^{-} \leq \mathcal {L}$
. Then,
$\mathcal {L}$
has the weak isomorphism property, is recursively enumerable for validity, and has the Löwenheim–Skolem property only if
$\mathcal {L} \leq \mathcal {L}_{\omega \omega }^{-}$
.
Proof Assume for a contradiction that
$\mathcal {L}\not \leq \mathcal {L}_{\omega \omega }^{-}.$
Using Vaught’s generalization of Trakhtenbrot theorem to
$\mathcal {L}_{\omega \omega }^{-}$
[Reference Vaught31], we obtain a finite purely relational vocabulary
$\tau ^{\prime }$
such that the set
$V_{\text {fin}}\ \subseteq \mathcal {L}_{\omega \omega }^{-}(\tau ^{\prime })$
of sentences valid on finite models is not recursively enumerable. Let
$\theta \in \mathcal {L}_{\omega \omega }^{-}(\sigma \cup \tau ^{\prime })$
where
$\sigma $
and
$\theta $
are given by Lemma 3.11 (we may obviously assume
$\sigma \cap \tau ^{\prime }=\emptyset ).$
Now we may observe that
$$\begin{align*}\psi\in V_{\text{fin}}\ \ \text{iff}\ \vDash\theta\rightarrow\psi^{U}\!, \end{align*}$$
where
$\psi ^{U}$
is the relativization in
$\mathcal {L}_{\omega \omega }^{-}$
of
$\psi $
to the unary predicate U (which is possible since
$\mathcal {L}_{\omega \omega }^{-}$
has the relativization property). If
$\psi \in V_{\text {fin}}$
, then whenever
$\mathfrak {A}$
is a countably infinite
$\sigma \cup \tau ^{\prime }$
-structure such that
$\mathfrak {A}\models \theta $
we must have that
$U^{\mathfrak {A}^{\ast }}$
is finite and non-empty by Lemma 3.11, thus
$\mathfrak {A}^{\ast }\models \psi ^{U}$
, and by the weak isomorphism property,
$\mathfrak {A}\models \psi ^{U}$
as desired (given that
$\mathfrak {A}\sim \mathfrak {A}^{\ast }$
). But for any sentence
$\chi $
of
$\mathcal {L}$
,
$\vDash \chi $
iff
$\chi $
is valid on countably infinite structures: if
$\not \vDash \chi $
, a countably infinite countermodel for
$\chi $
can be found by either applying the Löwenheim–Skolem property or Lemma 3.1 as needed.Footnote
7
On the other hand, if
$\vDash \theta \rightarrow \psi ^{U}$
and
$\mathfrak {A}$
is a
$\tau ^{\prime }$
-model of size n, say, we may assume (since
$\tau ^{\prime }\cap \sigma =\emptyset $
) that
$\mathfrak {A}\cong (\mathfrak {A}^{\prime }|U)\upharpoonright \tau ^{\prime }$
for a model
$\mathfrak {A}^{\prime }$
that comes from extending and expanding
$\mathfrak {A}$
to a
$\tau ^{\prime }\cup \sigma $
-model of
$\theta $
given by (1) of Lemma 3.11 in a suitable way. Hence,
$\mathfrak {A}^{\prime }\models \psi ^{U}$
and thus
$\mathfrak {A}\models \psi .$
Since, by hypothesis,
$\mathcal {L}$
is effectively regular and recursively enumerable for validity, we must have then that
$V_{\text {fin}}$
is recursively enumerable after all, which is a contradiction.
Remark 3.13. Proper extensions of
$\mathcal {L}_{\omega \omega }^-$
which are recursively enumerable for validity and have the weak isomorphism property are given in Examples 4.1 and 4.2. Notice that an analogous theorem for the monadic case is trivial by Remark 3.9 because, in the presence of the weak isomorphism property, the effectivity of the logic implies the finite weak dependence property.
Remark 3.14. Other maximality results can be obtained by similar methods to those in this paper. For example,
$\mathcal {L}_{\omega \omega }^{-}$
is the maximal logic with the weak isomorphism property, compactness and the so called Tarski union property. This can be seen by adapting the argument of [Reference Barwise and Feferman3, Theorem III.2.2.1] for
$\mathcal {L}_{\omega \omega }$
to the context without identity with the help of [Reference Dellunde14, Proposition 2.8]. We conjecture that the
$\lambda $
-omitting types theorem also provides a characterization of the maximality of
$\mathcal {L}_{\omega \omega }^{-}$
(cf. [Reference Lindström26]).
4 Extensions of
$\mathcal {L}_{\omega \omega }^-$
In this section, we collect a number of interesting examples of identity-free logics that help answer some questions posed by our results, e.g., is there a proper extension of
$\mathcal {L}_{\omega \omega }^-$
satisfying both the compactness and weak isomorphism properties?
Footnote
8
Notice that the infinitary logic
$\mathcal {L}_{\omega _1\omega }^-$
is an example of an abstract logic with the weak isomorphism and Löwenheim–Skolem properties, but without compactness.
Our examples will rely on the addition of suitable Lindström quantifiers which conveniently differ from usual definitions found in the literature. Indeed, adding a Lindström quantifier to
$\mathcal {L}_{\omega \omega }^-$
usually destroys the weak isomorphism property, as is the case with cardinality and cofinality quantifiers. However, each quantifier has a natural version closed under weak isomorphisms.
Example 4.1 (The logic
$\mathcal {L}_{\omega \omega }^-(Q_{\alpha }^-)$
)
Consider the Lindström quantifier
$Q_{\alpha }^-$
defined as:
The satisfaction condition for this operator then is
The quantifier
$Q_{\alpha }$
may be recovered by letting E be the true identity relation
$=$
.
The first observation we wish to make is that
$Q_1^- $
(seen as a Lindström quantifier) is closed under weak isomorphisms, i.e., if
${\langle {{A, M, E}}\rangle } \in Q_1^- $
and
${\langle {{A, M, E}}\rangle } \sim {\langle {A', M', E'}\rangle }$
, then
${\langle {{A', M', E'}}\rangle }\in Q_1^- $
. To see this, suppose that
${\langle {{A, M, E}}\rangle }\in Q_1^- $
and R is a weak isomorphism from
${\langle {{A, M, E}}\rangle }$
onto
${\langle {{A', M', E'}}\rangle }$
.
$E'$
is an equivalence relation on
$A'$
compatible with
$M'$
because that fact can be expressed as a formula in
$\mathcal {L}_{\omega \omega }^-$
. We wish to show then that R induces a bijection
. Consider the relation
$R'$
defined as
$[x]R'[y]$
iff
$xRy$
. We wish to show that
$R'$
is in fact a bijection. It is obviously surjective since R is. For functionality: assume that
$x\in M$
,
$xRy_1$
and
$xRy_2$
, then, since
$xEx$
, we must have that
$y_1E'y_2$
, which then means that if
$[x]R'[y_1]$
and
$[x]R'[y_2]$
,
$[y_1]=[y_2]$
. Injectivity is obtained by an analogous argument in reverse. Hence,
as desired.
$\mathcal {L}_{\omega \omega }^-(Q_1^- )$
is clearly more expressive than
$\mathcal {L}_{\omega \omega }^-$
since the latter has the Löwenheim–Skolem property but the former does not (thus, the quantifier
$Q_1^-$
is not definable in
$\mathcal {L}_{\omega \omega }^-$
). Recall that a logic
$\mathcal {L}$
is said to be congruence closed [Reference Makowsky and Shelah27] if, for any
$\varphi \in \mathcal {L}(\tau )$
, there is a sentence
$\varphi _E \in \mathcal {L}(\tau \cup \{E\})$
(where E is a new binary predicate) such that
for any structure
$\mathfrak {A}$
and any equivalence relation
$\overline {E}$
on A. We will follow the notation of [Reference Caicedo8] in using
$q\mathcal {L}$
to denote the congruence closure of a given logic
$\mathcal {L}$
, obtained by adjoining to
$\mathcal {L}$
the sentences defined by
$(*)$
as new quantifiers (see [Reference Makowsky and Shelah27]). Then it is not difficult to observe that the logic
$\mathcal {L}_{\omega \omega }^-(Q_1^- )$
is contained in the logic (with identity)
$q \mathcal {L}_{\omega \omega }(Q_1)$
. By the definition above,
can be expressed by the relativized sentence
$((Q_1x(x=x))_{\theta })^{\{x \mid \varphi (x)\}}$
. Recall a logic is
$(\kappa , \lambda )$
-compact if every set of sentences of cardinality
$\leq \kappa $
which has models for each of its subsets of cardinality
$<\lambda $
, has itself a model. By [Reference Makowsky and Shelah27, Proposition 3.2], for any
$\mathcal {L}$
, if
$\mathcal {L}$
is
$(\kappa , \lambda )$
-compact, so is
$q\mathcal {L}$
, and hence
$q \mathcal {L}_{\omega \omega }(Q_1)$
is
$(\omega , \omega )$
-compact since
$\mathcal {L}_{\omega \omega }(Q_1)$
is, which means that
$\mathcal {L}_{\omega \omega }^-(Q_1^- )$
also inherits this property. Once more, by [Reference Makowsky and Shelah27, Proposition 3.2], since
$\mathcal {L}_{\omega \omega }(Q_1)$
is recursively enumerable for validity,
$q\mathcal {L}_{\omega \omega }(Q_1)$
is too, and hence, so is the logic
$\mathcal {L}_{\omega \omega }^-(Q_1^- )$
.
Example 4.2 (The logic
$\mathcal {L}_{\omega \omega }^-(Q^{\text {cf}\omega -})$
)
Consider now the following Lindström quantifier:
Then, we have that
$\mathfrak {A} \models Q^{\text {cf}\omega -} xyzw[\varphi (x,y), \theta (z, w)]$
iff:
-
•
$\theta ^{\mathfrak {A}}=\{ {\langle {{a, b}}\rangle } \in A^2 \mid \mathfrak {A} \models \theta [a, b]\} \ \text {is an equivalence relation on} \ A,$
-
•
$\mathfrak {A} \models \forall xy ((\theta (x,y) \wedge \theta (z,w)) \rightarrow (\varphi (x,z) \rightarrow \varphi (y, w))),$
-
•
$\mathfrak {A} \models \text {"}\varphi (x,y) \ \text {is an irreflexive transitive relation"},$
-
•
$\mathfrak {A} \models {{\forall {{xy}}}\,} (\varphi (x,y) \vee \varphi (y,x) \vee \theta (x,y)),$
and -
•
Once more, the quantifier
$Q^{\text {cf}\omega }$
can be defined as above by letting E be the true identity relation
$=$
.
We can show that the quantifier
$Q^{\text {cf}\omega -}$
is closed under weak isomorphisms. Suppose that
${\langle {{A, M, E}}\rangle }\in Q^{\text {cf}\omega -}$
and R is a weak isomorphism from
${\langle {{A, M, E}}\rangle }$
onto
${\langle {{A', M', E'}}\rangle }$
. As in Example 4.1,
$R'$
defined as
$[x]R'[y]$
iff
$xRy$
gives a bijection from
to
. Furthermore,
$R'$
preserves the order: assume that
$[x_1]R'[y_1]$
,
$[x_2]R'[y_2]$
and
, so
${\langle {{x_1, x_2}}\rangle } \in M$
and, since
$x_1Ry_1$
and
$x_2Ry_2$
, we have
${\langle {{y_1, y_2}}\rangle } \in M'$
, and thus
. Hence, the cofinality of
must be
$\omega $
as well.
Shelah’s logic
$\mathcal {L}_{\omega \omega }(Q^{\text {cf}\omega })$
is
$(\infty , \omega )$
-compactFootnote
9
and, by [Reference Makowsky and Shelah27, Proposition 3.2], so is
$q\mathcal {L}_{\omega \omega }(Q^{\text {cf}\omega })$
. But, given that
$\mathcal {L}_{\omega \omega }^-(Q^{\text {cf}\omega -})$
is included in
$q\mathcal {L}_{\omega \omega }(Q^{\text {cf}\omega })$
, the former is also
$(\infty , \omega )$
-compact. Similarly,
$\mathcal {L}_{\omega \omega }^-(Q^{\text {cf}\omega -})$
is recursively enumerable for validity. Moreover, we can observe that
$\mathcal {L}_{\omega \omega }^-(Q^{\text {cf}\omega -})$
does not have a Löwenheim–Skolem theorem. For example, the sentence in the signature
$\{ E, <\}$
with two binary relation symbols,
-
$\neg Q^{\text {cf}\omega -} xyzw[x<y, E(z, w)] \wedge \text {"}E \ \text {is an equivalence relation"}$
-
$\wedge \ \forall xy ((E(x,y) \wedge E(z,w)) \rightarrow (x<z \rightarrow y<w))$
-
$\wedge \text {"}< \ \text {is an irreflexive transitive relation"}$
-
$\wedge \ {{\forall {{xy}}}\,} (x <y \vee y<x \vee E(x,y)) \wedge \ {{\forall {{x}}}\,} {{\exists {y}}\,}(x<y)$
has no countable models since it produces in the quotient model an infinite linear order without last element with cofinality
$\neq \omega $
, and hence
$\geq \omega _1$
.
Interestingly enough, some known quantifiers can be shown to preserve the weak isomorphism property:
Example 4.3 (The logic
$\mathcal {L}_{\omega \omega }^-(Q^H)$
)
Recall the Henkin quantifier
$Q^H$
which is defined as follows:
$$\begin{align*}Q^H = \{{\langle{{A, M}}\rangle} \mid M \subseteq A^4, M \supseteq f \times g \ \text{for some} \ f,g \colon A \longrightarrow A\}. \end{align*}$$
Then, we have that
$\mathfrak {A} \models Q^{H} xyzw \varphi (x,y, z, w)$
iff for some
$f,g \colon A \longrightarrow A$
and for each
$a,b \in A$
,
$\mathfrak {A} \models \varphi [a,f(a), b, g(b)]$
iff
$\mathfrak {A} \models {{\exists {f,g}}\,} {{\forall {{x,y}}}\,} \varphi [x,f(x), y, g(y)]$
.
First, we must show that
$Q^H$
is closed under weak isomorphisms. Assume then that
${\langle {{A, M, E}}\rangle } \in Q^H$
and R is a weak isomorphism from
${\langle {{A, M}}\rangle }$
onto
${\langle {A', M'}\rangle }$
. Then
$M \subseteq A^4$
,
$M \supseteq f \times g$
for some
$f, g \colon A \longrightarrow A$
. All we need to do now is define
$f', g' \colon A' \longrightarrow A'$
such that
$M' \supseteq f' \times g'$
. Define
$f'$
as follows: take any
$a_1 \in A'$
, we know then that
$Ra_0a_1$
for some
$a_0\in A$
, so let
$f'(a_1)$
be some
$b_1\in A'$
such that
$Rf(a_0)b_1$
. Do a similar thing for
$g'$
. Now, for any
${\langle {{a_1, f'(a_1), b_1, g'(b_1)}}\rangle } \in f' \times g'$
, there are
$a_0, b_0 \in A$
s.t.
$Ra_0a_1, Rf(a_0)f'(a_1), Rb_0b_1, Rg(b_0)g'(b_1)$
, and since R is a weak isomorphism and
${\langle {{a_0, f(a_0), b_0, g(b_0)}}\rangle } \in M$
by hypothesis,
${\langle {{a_1, f'(a_1), b_1, g'(b_1)}}\rangle } \in M'$
, as desired.
Take now the sentence
$\varphi _{\text {inf}} \in \mathcal {L}_{\omega \omega }^-(Q^H)(\tau )$
where
$\tau = \{E\}$
and E is binary:
$$\begin{align*}\text{"}E \ \text{is an equivalence relation"} \wedge {{\exists{{z}}}\,}{{\exists{{f,g}}}\,}{{\forall{{x,y}}}\,} (\neg z E f(x) \wedge (f(x) E y \rightarrow g(y) E x)). \end{align*}$$
Since
$Q^H $
is closed under weak isomorphisms,
in the vocabulary
$\tau $
, and
, we have that
$\mathfrak {A}\models \varphi _{\text {inf}}$
only if
. The latter sentence says that
is infinite. On the other hand, for a
$\tau $
-structure
$\mathfrak {A}$
, if
$\mathfrak {A}\models \text {"}E \ \text {is an equivalence relation"}$
and
is infinite,
, so, reversing the previous reasoning,
$\mathfrak {A} \models \varphi _{\text {inf}}$
.
Hence, we might consider the following theory T in the vocabulary
$\tau $
:
$$\begin{align*}\{\neg \varphi_{\text{inf}}\} \cup \{{{\exists{{x_0, \dots, x_n}}}\,}\bigwedge_{i<j \leq n} \neg x_i E x_j \mid 1 \leq n < \omega\} \cup \{\text{"}E \ \text{is an equivalence relation"}\}. \end{align*}$$
This theory says that E is an equivalence relation with infinitely many equivalence classes, so for any model
$\mathfrak {A}\models T$
,
is infinite and then
, which is impossible, since
$\mathfrak {A}\models \neg \varphi _{\text {inf}}$
. Hence, T has no models. However, T is finitely satisfiable. Thus, compactness fails for the logic
$\mathcal {L}_{\omega \omega }^-(Q^H)$
, which is then obviously a proper extension of
$\mathcal {L}_{\omega \omega }^-$
.
To see that
$\mathcal {L}_{\omega \omega }^-(Q^H)$
does not have the Löwenheim–Skolem property, consider first the formula
$\theta (x,y)$
in the vocabulary
$\{E, <\}$
:
-
$ \text {"}E \ \text {is an equivalence relation congruent with } <\text {"} $
,
-
$ \exists f, g \, \forall u, v ((E (u, v) \leftrightarrow E(f(u), g(v))) \wedge (u<x \rightarrow f(v) < y)) $
,
-
$\wedge \ \exists f, g \, \forall u, v ((E (u, v) \leftrightarrow E(f(u), g(v))) \wedge (u<y \rightarrow f(v) < x)).$
Now, if
$\mathfrak {A} \models \theta [a,b]$
, since
, and given that
,
-
,
-
.
This implies that
. Hence,
$\theta (x,y)$
is an instance of a Härtig quantifier in the quotient by E. We can then use this methodology to adapt the typical counterexample for the Löwenheim–Skolem property for the Härtig quantifier [Reference Herre, Krynicki, Pinus and Väänänen19, Sentence (1.2)], axiomatizing infinite linear orderings of successor cardinalities.
Incidentally, the expressive power on finite models of fragments of existential second-order logic without identity, but containing the Henkin quantifier (in particular Independence Friendly logic), has been studied in great detail in [Reference Kuusisto24].
5 Conclusions
We have fulfilled our aim of finding Lindström-style characterizations for the maximality of (variants of) the identity-free first-order logic. The properties we have employed are collected in Table 1. Our work, however, still leaves a number of interesting open questions, including:
Table 1 Summary of properties of some logics.
Problem 5.1. Is there a proper extension of
$\mathcal {L}_{\omega \omega }^-$
satisfying both the Löwenheim–Skolem and compactness properties that is not contained in
$\mathcal {L}_{\omega \omega }$
?
Problem 5.2. Is there a compact extension of
$\mathcal {L}_{\omega \omega }^-$
which does not remain compact when adding identity to the logic?
Acknowledgments
We would like to thank various people who offered remarks that helped to improve the presentation of the paper, particularly Grigory Olkhovikov and Lloyd Humberstone. In addition, we are grateful to an anonymous reviewer for this journal who provided useful comments.
Funding
Badia was supported by the Australian Research Council grant DE220100544. Badia and Noguera were also supported by the European Union’s Marie Sklodowska–Curie grant no. 101007627 (MOSAIC project).
Open access
