Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-17T05:15:58.014Z Has data issue: false hasContentIssue false
  • English
  • Français

The role of coherent structures and inhomogeneity in near-field interscale turbulent energy transfers

Published online by Cambridge University Press:  01 June 2020

F. Alves Portela Open the ORCID record for F. Alves Portela [Opens in a new window] ,
G. Papadakis Open the ORCID record for G. Papadakis [Opens in a new window]  and
J. C. Vassilicos Open the ORCID record for J. C. Vassilicos [Opens in a new window]
F. Alves Portela*
Affiliation:
School of Engineering Sciences, University of Southampton, SouthamptonSO17 1BJ, UK
G. Papadakis
Affiliation:
Department of Aeronautics, Imperial College London, LondonSW7 2AZ, UK
J. C. Vassilicos*
Affiliation:
University of Lille, CNRS, ONERA, Arts et Métiers ParisTech, Centrale Lille, UMR 9014 – LMFL – Laboratoire de Mécanique des fluides de Lille – Kampé de Feriet, F-59000Lille, France
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

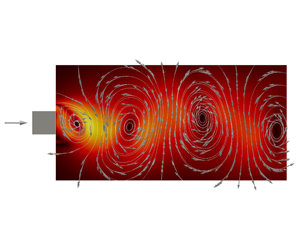
We use direct numerical simulation data to study interscale and interspace energy exchanges in the near field of a turbulent wake of a square prism in terms of a Kármán–Howarth–Monin–Hill (KHMH) equation written for a triple decomposition of the velocity field which takes into account the presence of quasi-periodic vortex shedding coherent structures. Concentrating attention on the plane of the mean flow and on the geometric centreline, we calculate orientation averages of every term in the KHMH equation. The near field considered here ranges between two and eight times the width $d$ of the square prism and is very inhomogeneous and out of equilibrium so that non-stationarity and inhomogeneity contributions to the KHMH balance are dominant. The mean flow produces kinetic energy which feeds the vortex shedding coherent structures. In turn, these coherent structures transfer their energy to the stochastic turbulent fluctuations over all length scales $r$ from the Taylor length $\unicode[STIX]{x1D706}$ to $d$ and dominate spatial turbulent transport of small-scale two-point stochastic turbulent fluctuations. The orientation-averaged nonlinear interscale transfer rate $\unicode[STIX]{x1D6F1}^{a}$ which was found to be approximately independent of $r$ by Alves Portela et al. (J. Fluid Mech., vol. 825, 2017, pp. 315–352) in the range $\unicode[STIX]{x1D706}\leqslant r\leqslant 0.3d$ at a distance $x_{1}=2d$ from the square prism requires an interscale transfer contribution of coherent structures for this approximate constancy. However, the near constancy of $\unicode[STIX]{x1D6F1}^{a}$ in the range $\unicode[STIX]{x1D706}\leqslant r\leqslant d$ at $x_{1}=8d$ which was also found by Alves Portela et al. (2017) is mostly attributable to stochastic fluctuations. Even so, the proximity of $-\unicode[STIX]{x1D6F1}^{a}$ to the turbulence dissipation rate $\unicode[STIX]{x1D700}$ in the range $\unicode[STIX]{x1D706}\leqslant r\leqslant d$ at $x_{1}=8d$ does require interscale transfer contributions of the coherent structures. Spatial inhomogeneity also makes a direct and distinct contribution to $\unicode[STIX]{x1D6F1}^{a}$, and the constancy of $-\unicode[STIX]{x1D6F1}^{a}/\unicode[STIX]{x1D700}$ close to $1$ would not have been possible without it either in this near-field flow. Finally, the pressure-velocity term is also an important contributor to the KHMH balance in this near field, particularly at scales $r$ larger than approximately $0.4d$, and appears to correlate with the purely stochastic nonlinear interscale transfer rate when the orientation average is lifted.

JFM classification

Turbulent Flows: Turbulence theory Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 896 , 10 August 2020 , A16
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves Portela, F., Papadakis, G. & Vassilicos, J. C. 2017 The turbulence cascade in the near wake of a square prism. J. Fluid Mech. 825, 315–352.CrossRefGoogle Scholar
Alves Portela, F., Papadakis, G. & Vassilicos, J. C. 2018 Turbulence dissipation and the role of coherent structures in the near wake of a square prism. Phys. Rev. Fluids 3, 124609.CrossRefGoogle Scholar
Braza, M., Perrin, R. & Hoarau, Y. 2006 Turbulence properties in the cylinder wake at high Reynolds numbers. J. Fluids Struct. 22 (6-7), 757–771.CrossRefGoogle Scholar
Davies, M. E. 1976 A comparison of the wake structure of a stationary and oscillating bluff body, using a conditional averaging technique. J. Fluid Mech. 75 (02), 209–231.CrossRefGoogle Scholar
Duchon, J. & Robert, R. 2000 Inertial energy dissipation for weak solutions of incompressible Euler and Navier–Stokes equations. Nonlinearity 13 (1), 249–255.CrossRefGoogle Scholar
Feldman, M. 2011 Hilbert Transform Applications in Mechanical Vibration, Wiley.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov, Cambridge University Press.CrossRefGoogle Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2015 The energy cascade in near-field non-homogeneous non-isotropic turbulence. J. Fluid Mech. 771, 676–705.CrossRefGoogle Scholar
Goto, S. & Vassilicos, J. C. 2016 Unsteady turbulence cascades. Phys. Rev. E 94 (5), 1–3.CrossRefGoogle ScholarPubMed
Hill, R. J. 1997 Applicability of Kolmogorov’s and Monin’s equations of turbulence. J. Fluid Mech. 353, 67–81.CrossRefGoogle Scholar
Hill, R. J. 2001 Equations relating structure functions of all orders. J. Fluid Mech. 434, 379–388.CrossRefGoogle Scholar
Hill, R. J. 2002a Exact second-order structure-function relationships. J. Fluid Mech. 468, 317–326.CrossRefGoogle Scholar
Hill, R. J.2002b The approach of turbulence to the locally homogeneous asymptote as studied using exact structure-function equations, pp. 1–24, arXiv:0206034.Google Scholar
Hussain, A. K. M. F. 1983 Coherent structures–reality and myth. Phys. Fluids 26 (10), 2816–2850.CrossRefGoogle Scholar
Hussain, A. K. M. F., Jeong, J. & Kim, J. 1987 Studying turbulence using numerical simulation databases. In Proceedings of the 1987 Summer Program, pp. 273–290. Stanford University.Google Scholar
Hussain, A. K. M. F. & Reynolds, W. C. 1970 The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 41 (02), 241–258.CrossRefGoogle Scholar
Lyn, D. A., Einav, S., Rodi, W. & Park, J. H. 1995 A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder. J. Fluid Mech. 304, 285–319.CrossRefGoogle Scholar
Marati, N., Casciola, C. M. & Piva, R. 2004 Energy cascade and spatial fluxes in wall turbulence. J. Fluid Mech. 521, 191–215.CrossRefGoogle Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (02), 263–288.CrossRefGoogle Scholar
Thiesset, F., Danaila, L. & Antonia, R. A. 2014 Dynamical interactions between the coherent motion and small scales in a cylinder wake. J. Fluid Mech. 749 (April 2016), 201–226.CrossRefGoogle Scholar
Valente, P. C. & Vassilicos, J. C. 2015 The energy cascade in grid-generated non-equilibrium decaying turbulence. Phys. Fluids 27 (4), 045103.CrossRefGoogle Scholar
Wlezien, R. W. & Way, J. L. 1979 Techniques for the experimental investigation of the near wake of a circular cylinder. AIAA J. 17 (6), 563–570.CrossRefGoogle Scholar
Yasuda, T. & Vassilicos, J. C. 2018 Spatio-temporal intermittency of the turbulent energy cascade. J. Fluid Mech. 853, 235–252.CrossRefGoogle Scholar