Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-16T22:33:17.623Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffeomorphism groups of tame Cantor sets and Thompson-like groups

Part of: Connections with other structures, applications Special aspects of infinite or finite groups Low-dimensional topology Smooth dynamical systems: general theory

Published online by Cambridge University Press:  03 April 2018

Louis Funar  and
Yurii Neretin
Louis Funar
Affiliation:
Institute Fourier, UMR 5582, Department of Mathematics, University Grenoble Alpes, CS40700, 38058 Grenoble, CEDEX 9, France email [email protected]
Yurii Neretin
Affiliation:
Mathematics Department, University of Vienna, Nordbergstrasse 15, Vienna, Austria Institute for Theoretical and Experimental Physics, Mech. Math. Department, Moscow State University, Kharkevich Institute for Information Transmission Problems, Moscow, Russia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The group of 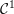${\mathcal{C}}^{1}$ -diffeomorphisms of any sparse Cantor subset of a manifold is countable and discrete (possibly trivial). Thompson’s groups come out of this construction when we consider central ternary Cantor subsets of an interval. Brin’s higher-dimensional generalizations 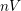$nV$ of Thompson’s group 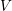$V$ arise when we consider products of central ternary Cantor sets. We derive that the 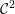${\mathcal{C}}^{2}$ -smooth mapping class group of a sparse Cantor sphere pair is a discrete countable group and produce this way versions of the braided Thompson groups.

Keywords

mapping class groupinfinite type surfacesbraided Thompson groupdiffeomorphism groupCantor setself-similar setsiterated function systems

MSC classification

Primary: 20F36: Braid groups; Artin groups 37C85: Dynamics of group actions other than ${bf Z}$ and ${bf R}$, and foliations 57S05: Topological properties of groups of homeomorphisms or diffeomorphisms 57M50: Geometric structures on low-dimensional manifolds 54H15: Transformation groups and semigroups
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 5 , May 2018 , pp. 1066 - 1110
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alvarez, S., Filimonov, D., Kleptsyn, V., Malicet, D., Cotón, C. M., Navas, A. and Triestino, M., Groups with infinitely many ends acting analytically on the circle , J. Topol. , to appear. Preprint (2015), arXiv:1506.03839.Google Scholar
Aramayona, J. and Funar, L., Asymptotic mapping class groups of closed surfaces punctured along Cantor sets, Preprint (2017), arXiv:1701.08132.Google Scholar
Bamón, R., Moreira, C. G., Plaza, S. and Vera, J., Differentiable structures of central Cantor sets , Ergodic Theory Dynam. Systems 17 (1997), 1027–1042.Google Scholar
Bieri, R. and Strebel, R., Groups of PL homeomorphisms of the real line, Mathematical Surveys and Monographs, vol. 215 (American Mathematical Society, Providence, RI, 2016).CrossRefGoogle Scholar
Blankenship, W. A., Generalization of a construction of Antoine , Ann. of Math. (2) 53 (1951), 276–297.Google Scholar
Bleak, C. and Lanoue, D., A family of non-isomorphism results , Geom. Dedicata 146 (2010), 21–26.Google Scholar
Bonatti, C., Monteverde, I., Navas, A. and Rivas, C., Rigidity for C1 actions on the interval arising from hyperbolicity I: solvable groups , Math. Z. 286 (2017), 919–949.Google Scholar
Brin, M. G., Higher dimensional Thompson groups , Geom. Dedicata 108 (2004), 163–192.Google Scholar
Brin, M. G., The algebra of strand splitting. I. A braided version of Thompson’s group V , J. Group Theory 10 (2007), 757–788.Google Scholar
Brin, M. G., On the baker’s map and the simplicity of the higher dimensional Thompson groups nV , Publ. Mat. 54 (2010), 433–439.CrossRefGoogle Scholar
Brown, K. S. and Geoghegan, R., An infinite-dimensional torsion-free FP ∞ group , Invent. Math. 77 (1984), 367–381.CrossRefGoogle Scholar
Brown, K. S., Finiteness properties of groups , J. Pure Appl. Algebra 44 (1987), 45–75.Google Scholar
Cannon, J. W., Floyd, W. J. and Parry, W. R., Introductory notes in Richard Thompson’s groups , Enseign. Math. 42 (1996), 215–256.Google Scholar
Castro, G., Jorquera, E. and Navas, A., Sharp regularity of certain nilpotent group actions on the interval , Math. Ann. 359 (2014), 101–152.Google Scholar
Cooper, D. and Pignataro, T., On the shape of Cantor sets , J. Differential Geom. 28 (1988), 203–221.Google Scholar
Dehornoy, P., The group of parenthesized braids , Adv. Math. 205 (2006), 354–409.Google Scholar
Deroin, B., Kleptsyn, V. and Navas, A., On the question of ergodicity for minimal group actions on the circle , Mosc. Math. J. 9 (2009), 263–303.CrossRefGoogle Scholar
Deroin, B., Kleptsyn, V. and Navas, A., Sur la dynamique unidimensionnelle en régularité intermédiaire , Acta Math. 199 (2007), 199–262.Google Scholar
Deroin, B., Kleptsyn, V. and Navas, A., On the ergodic theory of free group actions by real-analytic circle diffeomorphisms, Invent. Math., to appear. Preprint (2013),arXiv:1312.4133.Google Scholar
Dijkstra, J. J. and van Mill, J., Erdös space and homeomorphism groups of manifolds , Mem. Amer. Math. Soc. 208 (2010), no. 979.Google Scholar
Dippolito, P. R., Codimension one foliations of closed manifolds , Ann. of Math. (2) 107 (1978), 403–453.Google Scholar
Falconer, K. J., Fractal geometry: mathematical foundations and applications (Wiley, Chichester, 2003).Google Scholar
Falconer, K. J. and Marsh, D. T., On the Lipschitz equivalence of Cantor sets , Mathematika 39 (1992), 223–233.Google Scholar
Funar, L. and Kapoudjian, C., On a universal mapping class group of genus zero , Geom. Funct. Anal. 14 (2004), 965–1012.Google Scholar
Funar, L. and Kapoudjian, C., The braided Ptolemy–Thompson group is finitely presented , Geom. Topol. 12 (2008), 475–530.Google Scholar
Funar, L. and Nguyen, M., On the automorphisms group of the asymptotic pants complex of an infinite surface of genus zero , Math. Nachr. 289 (2016), 1189–1207.CrossRefGoogle Scholar
Ghys, É. and Sergiescu, V., Sur un groupe remarquable de difféomorphismes du cercle , Comment. Math. Helv. 62 (1987), 185–239.Google Scholar
Greenberg, P., Projective aspects of the Higman–Thompson group , in Group Theory from a Geometrical Viewpoint, Proceedings of ICTP workshop, Trieste, 1990 (World Scientific, Singapore, 1991), 633–644.Google Scholar
Greenberg, P. and Sergiescu, V., An acyclic extension of the braid group , Comment. Math. Helv. 66 (1991), 109–138.Google Scholar
Hennig, J. and Matucci, F., Presentations for the higher-dimensional Thompson groups nV , Pacific J. Math. 257 (2012), 53–74.Google Scholar
Higman, G., Finitely presented infinite simple groups, Notes on Pure Mathematics, vol. 8 (Australian National University, Canberra, 1974).Google Scholar
Hurtado, S. and Militon, E., Distortion and Tits alternative in smooth mapping class groups, Preprint (2015), arXiv:1506.02877.Google Scholar
Hutchinson, J. E., Fractals and self-similarity , Indiana Univ. Math. J. 30 (1981), 713–747.Google Scholar
Jorquera, E., A universal nilpotent group of C1 -diffeomorphisms of the interval , Topol. Appl. 159 (2012), 2115–2126.CrossRefGoogle Scholar
Kapoudjian, C. and Sergiescu, V., An extension of the Burau representation to a mapping class group associated to Thompson’s group T , in Geometry and dynamics, Contemporary Mathematics, vol. 389 (American Mathematical Society, Providence, RI, 2005), 141–164.Google Scholar
Laget, G., Groupes de Thompson projectifs en genre 0, PhD thesis, University of Grenoble (2004), available at:http://tel.archives-ouvertes.fr/docs/00/04/71/79/PDF/tel-00006388.pdf.Google Scholar
McDuff, D., C1 -minimal subset of the circle , Ann. Inst. Fourier 31 (1981), 177–193.Google Scholar
McMillan, D. R. Jr., Taming Cantor sets in E n , Bull. Amer. Math. Soc. 70 (1964), 706–708.Google Scholar
Moreira, C. G., There are no C1 -stable intersections of regular Cantor sets , Acta Math. 206 (2011), 311–323.Google Scholar
Navas, A., On uniformly quasisymmetric groups of circle diffeomorphisms , Ann. Acad. Sci. Fenn. Math. 31 (2006), 437–462.Google Scholar
Navas, A., Growth of groups and diffeomorphisms of the interval , Geom. Funct. Anal. 18 (2008), 988–1028.Google Scholar
Neretin, Y., Combinatorial analogues of the group of diffeomorphisms of the circle , Izv. Ross. Akad. Nauk Ser. Mat. 56 (1992), 1072–1085; Engl. transl. Russian Acad. Sci. Izv. Math. 41(2) (1993), 337–349.Google Scholar
Portela, A., Regular interval Cantor sets of S 1 and minimality , Bull. Braz. Math. Soc. 40 (2009), 53–75.Google Scholar
Rao, H., Ruan, H.-J. and Yang, W., Lipschitz equivalence of Cantor sets and algebraic properties of contraction ratios , Trans. Amer. Math. Soc. 364 (2012), 1109–1126.Google Scholar
Rubin, M., On the reconstruction of topological spaces from their groups of homeomorphisms , Trans. Amer. Math. Soc. 312 (1989), 487–538.Google Scholar
Rubin, M., Locally moving groups and reconstruction problems, ordered groups and infinite permutation groups (Kluwer Academic, Dordrecht, 1996), 121–157.Google Scholar
Sacksteder, R., Foliations and pseudogroups , Amer. J. Math. 87 (1965), 79–102.Google Scholar
Shilepsky, A. C., A rigid Cantor set in E 3 , Bull. Acad. Polon. Sci. 22 (1974), 223–224.Google Scholar
Stein, M., Groups of piecewise linear homeomorphisms , Trans. Amer. Math. Soc. 332 (1992), 477–514.CrossRefGoogle Scholar
Sullivan, D., Differentiable structures on fractal-like sets, determined by intrinsic scaling functions on dual Cantor sets , in The Mathematical Heritage of Hermann Weyl (Durham, NC, 1987), Proceedings of Symposia in Pure Mathematics, vol. 48 (American Mathematical Society, Providence, RI, 1988), 15–23.Google Scholar
Thurston, W. P., A generalization of the Reeb stability theorem , Topology 13 (1974), 347–352.Google Scholar
Tsuboi, T., Homological and dynamical study on certain groups of Lipschitz homeomorphisms of the circle , J. Math. Soc. Japan 47 (1995), 1–30.Google Scholar
Wright, D. G., Rigid sets in E n , Pacific J. Math. 121 (1986), 245–256.Google Scholar
Xi, L.-F. and Xiong, Y., Lipschitz equivalence class, ideal class and the gauss class number problem, Preprint (2013), arXiv:1304.0103.Google Scholar