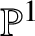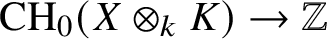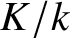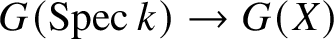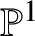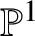1 Introduction
A proper smooth variety X over a field k is said to be universally 
${\mathrm {CH}}_0$-trivial if for any field extension 
$K/k$, the degree map of the Chow group of 
$0$-cycles induces an isomorphism 
$\deg \colon {\mathrm {CH}}_0(X\otimes _kK)\xrightarrow {\simeq }\mathbb {Z}$. Basic examples of universally 
${\mathrm {CH}}_0$-trivial varieties include rational (and more generally stably rational) varieties, and this property may be considered a near-rationality condition. The condition plays a crucial role in the degeneration method established by Voisin [Reference Voisin32] and Colliot-Thélène and Pirutka [Reference Colliot-Thélène and Pirutka9], where counterexamples to the Lüroth problem are produced.
Now it is natural to ask how to disprove the universal 
${\mathrm {CH}}_0$-triviality for a given variety X. In this direction, Merkurjev [Reference Merkurjev23, Theorem 2.11] proved that X is universally 
${\mathrm {CH}}_0$-trivial if and only if the function field 
$k(X)$ has trivial unramified cohomology – that is, 
$M_*(k)\simeq M_*(k(X))_{{\mathrm {ur}}}$ for all Rost’s cycle modules 
$M_*$ over k. As a consequence, if 
$\ell $ is a prime number different from the characteristic p of k, then 
$\ell $-primary torsion elements of the Brauer group 
$\operatorname {Br}(X):=H^2_{{\mathrm {\acute {e}t}}}(X,\mathbb {G}_m)$ not coming from 
$\operatorname {Br}(k)$ obstruct the universal 
${\mathrm {CH}}_0$-triviality. This is because the 
$\ell $-primary torsion subgroups 
$\operatorname {Br}(K)[\ell ^{\infty }]\simeq H^2_{{\mathrm {\acute {e}t}}}(K,\mathbb {Q}_{\ell }/\mathbb {Z}_{\ell }(1))$ for all field extensions 
$K/k$ give rise to a cycle module 
$M_*\colon K\mapsto \bigoplus _{i=0}^{\infty }H^{i+1}_{{\mathrm {\acute {e}t}}}(K,\mathbb {Q}_{\ell }/\mathbb {Z}_{\ell }(i))$, to which the theorem of Merkurjev can be applied.
There are, however, more obstructions other than cycle modules. In [Reference Totaro28], Totaro adopted as an obstruction the sheaves of differential forms 
$\Omega ^i_{X/k}$ to disprove the universal 
${\mathrm {CH}}_0$-triviality for a wide class of hypersurfaces. In [Reference Auel, Bigazzi, Böhning and Graf von Bothmer3], Auel et al. used 
$\operatorname {Br}(-)[2^\infty ]$ in characteristic 
$p=2$ to obtain a similar result for conic bundles over 
$\mathbb {P}^2$. Neither 
$\Omega ^i$ nor 
$\operatorname {Br}(-)[p^\infty ]$ in characteristic 
$p>0$ constitutes a cycle module. In fact, it is not straightforward to extend Merkurjev’s result to 
$\operatorname {Br}(-)[p^\infty ]$. This gap was filled in by the previous work of Auel et al. [Reference Auel, Bigazzi, Böhning and Graf von Bothmer2]:
Theorem 1.1 [1, Theorem 1.1]
Let X be a smooth proper variety over a field k which is universally 
${\mathrm {CH}}_0$-trivial. Then the structure morphism 
$X\to \operatorname {Spec} k$ induces an isomorphism 
$\operatorname {Br}(k)\xrightarrow {\simeq }\operatorname {Br}(X)$.
Our main result extends this theorem to more general invariants:
Theorem 1.2 see Corollary 3.3
Let X be a smooth proper variety over a field k which is universally 
${\mathrm {CH}}_0$-trivial. Then the structure morphism 
$X\to \operatorname {Spec} k$ induces an isomorphism 
$G(k)\xrightarrow {\simeq }G(X)$ for any 
$\mathbb {P}^1$-invariant Nisnevich sheaf with transfers G in the sense of Definition 3.1.
This theorem generalises Theorem 1.1, since the Brauer group has a structure of a 
$\mathbb {P}^1$-invariant Nisnevich sheaf with transfers (see Remark 1.5(1)). The conclusion of Theorem 1.2 for homotopy-invariant sheaves with transfers follows from Merkurjev’s result already cited. More recently, Binda et al. proved the same conclusion for another class of Nisnevich sheaves with transfers, called reciprocity sheaves [Reference Binda, Rülling and Saito5, Theorem 10.13, Remark 10.14]. Our main theorem also covers their result, since we have by [Reference Kahn, Saito and Yamazaki18, Theorems 3, 8]
$$ \begin{align} \text{homotopy invariant} \Rightarrow \text{reciprocity} \Rightarrow \mathbb{P}^1\text{-invariant} \\[-15pt]\nonumber \end{align} $$Both implications are strict (see Remark 3.4). Note also that 
$\Omega ^i$ is a reciprocity sheaf by [Reference Kahn, Saito and Yamazaki18, Theorem A.6.2], hence Totaro’s method can be explained either by our results or those of Binda et al. The main technical issue in the proof of Theorem 1.2 is the comparison of 
$G(X)$ and 
$h^0(G)(X)$, where 
$h^0(G)$ is the maximal homotopy-invariant subsheaf with transfers of G. We rephrase the problem in terms of algebraic cycles, and settle it by establishing a new moving lemma (Theorem 3.5).
The unramified logarithmic Hodge–Witt cohomology 
$H^1_{\mathrm {ur}}\left (-, W_n \Omega ^i_{\log }\right )$ (see Section 6 for the definition) satisfies the hypothesis of Theorem 1.2. Although this fact can also be deduced from known results on reciprocity sheaves (see Remark 6.2), we will give a direct proof which depends on classical results [Reference Gros and Suwa12, Reference Izhboldin15] but not on reciprocity sheaves.
Proposition 1.3 see Proposition 6.1
The unramified logarithmic Hodge–Witt cohomology 
$H^1_{\mathrm {ur}}\left (-, W_n \Omega ^i_{\log }\right )$ is a 
$\mathbb {P}^1$-invariant Nisnevich sheaf with transfers (over a field of positive characteristic) for any integers 
$n \ge 1$ and 
$i \ge 0$.
As a corollary, we obtain a new proof of the following (known) result:
Theorem 1.4. Let X be a smooth proper variety over a field k of characteristic 
$p>0$. Assume that X is universally 
${\mathrm {CH}}_0$-trivial. Then the canonical map
$$ \begin{align*} H^1_{\mathrm{ur}}\left(\operatorname{Spec} k, W_n \Omega^i_{\log}\right) \to H^1_{\mathrm{ur}}\left(X, W_n \Omega^i_{\log}\right) \\[-15pt]\end{align*} $$is an isomorphism for any integers 
$n \ge 1$ and 
$i \ge 0$.
(1) Since
$H^1_{{\mathrm {ur}}}\left (X,W_n\Omega ^1_{\log }\right )\simeq \operatorname {Br}(X)[p^n]$, Theorem 1.4 for $i=1$ follows from Theorem 1.1. For general i, Theorem 1.4 was posed as a problem by Auel et al. in [Reference Auel, Bigazzi, Böhning and Graf von Bothmer2, Problem 1.2] and previously proved in [Reference Binda, Rülling and Saito5] and [Reference Otabe24], as explained in the following.(2) Theorem 1.4 was shown by Binda et al. in [Reference Binda, Rülling and Saito5, Theorem 10.13, Remark 10.14] as a consequence of their general result on reciprocity sheaves already mentioned, along with the fact that
$H^1_{{\mathrm {ur}}}\left (-,W_n\Omega ^i_{\log }\right )$ has a structure of reciprocity sheaf.(3) Independent of [Reference Binda, Rülling and Saito5], almost at the same time, Otabe also obtained Theorem 1.4 for
$n=1$ [Reference Otabe24, Theorem 1.2]. His proof is somewhat close to ours, but it is more cycle-module-theoretical. A tame subgroup of the unramified cohomology is used in place of $h^0(G)$ in the present paper. The relation between these two subgroups is left for future research.(4) A similar statement to Theorem 1.4 holds when
$H^1_{\mathrm {ur}}$ is replaced by $H^j_{\mathrm {ur}}$ for any $j \in \mathbb {Z}$. Indeed, the cohomology groups in question are trivial unless $j = 0, 1$, because the natural map $H^j_{\mathrm {ur}}\left (X, W_n \Omega ^i_{\log }\right ) \to H^j_{\mathrm {ur}}\left (k(X), W_n \Omega ^i_{\log }\right )$ is injective (if X is connected), and the p-cohomology dimension of any field of characteristic $p>0$ is at most $1$. The case $j=0$ follows from the results of Bloch, Gabber and Kato [Reference Bloch and Kato6, Theorem 2.1] and Merkurjev [Reference Merkurjev23, Theorem 2.11].
The organisation of this paper is as follows. In Section 2, we revisit the proof of Theorem 1.2 for homotopy-invariant Nisnevich sheaves with transfers due to Merkurjev [Reference Merkurjev23] and Kahn [Reference Kahn16] (see Corollary 2.4). In Section 3, we state the main result in a slightly more general form (see Theorem 3.2) and prove it while admitting the key moving lemma (Theorem 3.5). The proof of Theorem 3.5 occupies the next two sections.
In Section 4, we rephrase the problem in terms of algebraic cycles. To do so, we consider the Suslin complex 
$C_{\bullet }(X)$ and its variant 
$\overline {C}_{\bullet }(X)$, where the latter is defined by replacing 
$\mathbb {A}^n$ with 
$\mathbb {P}^n$ in the former. Theorem 3.5 is then reduced to a comparison, up to Zariski sheafification, of their 
$0$th homology presheaves (see Theorem 4.1). Its proof is given in Section 5, which is pivotal in our work.
In Section 6, we give a proof of Proposition 1.3. Finally, Appendix A provides a proof of basic properties of universally 
$H_0^S$-trivial correspondences (see Definition 2.1).
We close this introduction with a brief discussion of related works. Shimizu [Reference Shimizu27] and Koizumi [Reference Koizumi21] have obtained some results resembling our moving lemma (Theorem 3.5) in 
$\mathbb {A}^1$-homotopy theory. Ayoub [Reference Ayoub4] has considered the notion of 
$\mathbb {P}^1$-localisation, which is much more sophisticated than our 
$\mathbb {P}^n$-Suslin complex introduced in Section 4. The relation of their works to ours is to be explored. Kahn has communicated to us that Theorem 3.5 has implications in the theory of birational sheaves [Reference Kahn and Sujatha19], which should be an interesting topic for future research (see a brief comment in Remark 3.6).
2 Reminders on homotopy-invariant sheaves with transfers
We fix a field k. Let 
$\mathbf {Sch}$ be the category of separated k-schemes of finite type, and 
$\mathbf {Sm}$ its full subcategory of smooth k-schemes. We write 
$\mathbf {Fld}_k$ for the category of fields over k, and 
$\mathbf {Fld}_k^{\mathrm {gm}}$ for its full subcategory consisting of the k-fields which are isomorphic to the function field of some (irreducible) 
$U \in \mathbf {Sm}$. For 
$K \in \mathbf {Fld}_k$ and 
$X \in \mathbf {Sch}$, we write 
$X_K := X \otimes _k K$.
Let 
$\mathbf {Cor}$ be Voevodsky’s category of finite correspondences. By definition it has the same objects as 
$\mathbf {Sm}$, and for 
$U, V \in \mathbf {Sm}$ the space of morphisms 
$\operatorname {\mathbf {Cor}}(U, X)$ from U to V is the free abelian group on the set of integral closed subschemes of 
$U \times X$ which is finite and surjective over an irreducible component of U. An additive functor 
$F : \mathbf {Cor}^{\mathrm {op}} \to \mathbf {Ab}$ is called a presheaf with transfers. Denote by 
$\mathbf {PST}$ the category of presheaves with transfers. If S is a k-scheme that is written as a filtered limit 
$S=\varprojlim _i S_i$ where 
$S_i \in \mathbf {Sm}$ and all transition maps are open immersions, then we define
$$ \begin{align} F(S) = \varinjlim_i F(S_i) \quad (F \in \mathbf{PST}). \end{align} $$ We abbreviate 
$F(R)=F(\operatorname {Spec} R)$ for a k-algebra R (when 
$F(\operatorname {Spec} R)$ is defined). In particular, we may speak of 
$F(K)$ for 
$K \in \mathbf {Fld}_k^{\mathrm {gm}}$ and 
$F\left (\mathcal {O}_{X, x}\right )$ for 
$x \in X \in \mathbf {Sm}$. We set 
$\mathbb {Z}_{\mathrm {tr}}(X):=\operatorname {\mathbf {Cor}}(-, X) \in \mathbf {PST}$ for 
$X \in \mathbf {Sm}$.
We say 
$F \in \mathbf {PST}$ is homotopy-invariant if the projection 
$\mathrm {pr} : X \times \mathbb {A}^1 \to X$ induces an isomorphism 
$\mathrm {pr}^* : F(X) \cong F\left (X \times \mathbb {A}^1\right )$ for any 
$X \in \mathbf {Sm}$. We write 
$\mathbf {HI}$ for the full subcategory of 
$\mathbf {PST}$ of homotopy-invariant presheaves with transfers. We say 
$F \in \mathbf {PST}$ is a Nisnevich sheaf with transfers if F composed with the inclusion (graph) functor 
$\mathbf {Sm} \to \mathbf {Cor}$ is a Nisnevich sheaf on 
$\mathbf {Sm}$. We write 
$\mathbf {NST}$ for the full subcategory of 
$\mathbf {PST}$ of Nisnevich sheaves with transfers. Set 
$\mathbf {HI}_{\mathrm {Nis}}:=\mathbf {HI} \cap \mathbf {NST}$.
We will use the following facts:
(V1) The inclusion functor
$\mathbf {NST} \hookrightarrow \mathbf {PST}$ admits a left adjoint $a_{\mathrm {Nis}} : \mathbf {PST} \to \mathbf {NST}$ and $a_{\mathrm {Nis}}(\mathbf {HI}) \subset \mathbf {HI}_{\mathrm {Nis}}$ holds [Reference Mazza, Voevodsky and Weibel22, Corollary 11.2, Theorem 22.3]. We write $F_{\mathrm {Nis}} := a_{\mathrm {Nis}}(F)$. We have $F_{\mathrm {Nis}}(K)=F(K)$ for any $K \in \mathbf {Fld}_k^{\mathrm {gm}}$ (because fields are Henselian local).(V2) The inclusion functor
$\mathbf {HI} \hookrightarrow \mathbf {PST}$ has a left adjoint $h_0$ given by the formula where we write$$ \begin{align*} h_0(F)(U)=\operatorname{Coker}\left(i_0^* - i_1^* : F\left(U \times \mathbb{A}^1\right) \to F(U)\right) \quad (F \in \mathbf{PST}, \ U \in \mathbf{Sm}), \end{align*} $$$i_\varepsilon ^*$ for the pullback along $U \to U \times \mathbb {A}^1,\, x \mapsto (x, \varepsilon )$, for $\varepsilon =0, 1$. This is the maximal homotopy-invariant quotient of F [Reference Mazza, Voevodsky and Weibel22, Example 2.20]. For $X \in \mathbf {Sm}$, we write $h_0(X):=h_0(\mathbb {Z}_{\mathrm {tr}}(X))$. We call the$$ \begin{align*} H_0^S(X_K):=h_0(X)(K) = h_0(X)_{\mathrm{Nis}}(K) \end{align*} $$$0$th Suslin homology of $X_K$ for $K \in \mathbf {Fld}_k^{\mathrm {gm}}$. There is a canonical surjective map $H_0^S(X_K) \to {\mathrm {CH}}_0(X_K)$, which is isomorphic if X is proper over k [Reference Mazza, Voevodsky and Weibel22, Exercise 2.21].(V3) The inclusion functor
$\mathbf {HI} \hookrightarrow \mathbf {PST}$ has a right adjoint $h^0$, given by the formula for$$ \begin{align*} h^0(F)(U)={\operatorname{\mathbf{PST}}}(h_0(U), F) \end{align*} $$$F \in \mathbf {PST}, U \in \mathbf {Sm}$. This is the maximal homotopy-invariant subobject of F [Reference Rülling and Saito25, Section 4.34].(V4) Let
$f : F \to G$ be a morphism in $\mathbf {HI}_{\mathrm {Nis}}$. If f induces an isomorphism $f^* : F(K) \cong G(K)$ for any $K \in \mathbf {Fld}^{\mathrm {gm}}_k$, then f is an isomorphism in $\mathbf {HI}_{\mathrm {Nis}}$ [Reference Mazza, Voevodsky and Weibel22, Corollary 11.2].(V5) Given
$F \in \mathbf {PST}$, we denote by $F_{\mathrm {Zar}}$ the Zariski sheaf associated to the presheaf on $\mathbf {Sm}$ obtained by restricting F along the graph functor $\mathbf {Sm} \to \mathbf {Cor}$. In general, it does not admit a structure of presheaf with transfers, but if $F \in \mathbf {HI}$, then we have $F_{\mathrm {Zar}}=F_{\mathrm {Nis}}$ by [Reference Mazza, Voevodsky and Weibel22, Theorem 22.2], and hence $F_{\mathrm {Zar}}$ acquires transfers by (V1). We say $F \in \mathbf {PST}$ is a Zariski sheaf with transfers if $F=F_{\mathrm {Zar}}$.
Another important fact can be stated as 
$H^i_{\mathrm {Zar}}(-, F_{\mathrm {Zar}})=H^i_{\mathrm {Nis}}(-, F_{\mathrm {Nis}}) \in \mathbf {HI}$ for 
$F \in \mathbf {HI}$, assuming k is perfect [Reference Voevodsky30, Theorems 5.6, 5.7]. We will not use this in the sequel.
Definition 2.1. Let 
$X, Y \in \operatorname {\mathbf {Sm}}$. We say 
$f \in \operatorname {\mathbf {Cor}}(X, Y)$ is universally 
$H_0^S$-trivial if the induced map 
$f_{K*} : H_0^S(X_K) \to H_0^S(Y_K)$ is an isomorphism for each 
$K \in \operatorname {\mathbf {Fld}}^{\operatorname {gm}}_k$.
Remark 2.2. This is an analogue of [Reference Colliot-Thélène and Pirutka9, Définition 1.1], where a proper morphism 
$f : X \to Y$ is said to be universally 
${\mathrm {CH}}_0$-trivial if the induced map 
$f_{K*} : {\mathrm {CH}}_0(X_K) \to {\mathrm {CH}}_0(Y_K)$ is an isomorphism for each 
$K \in \mathbf {Fld}_k$. When X and Y are proper over k, a universally 
${\mathrm {CH}}_0$-trivial morphism is also universally 
$H_0^S$-trivial by (V2). (We tacitly identify a morphism with its graph.) Note also that a smooth proper variety X is universally 
${\mathrm {CH}}_0$-trivial (in the sense of Theorem 1.4) if and only if the structure map 
$X \to \operatorname {Spec} k$ is universally 
${\mathrm {CH}}_0$-trivial.
The following result is due to Merkurjev [Reference Merkurjev23, Theorem 2.11] and Kahn [Reference Kahn16, Corollary 4.7]. We include a short proof here to keep self-containedness.
Proposition 2.3. Set 
$X, Y \in \mathbf {Sm}$. The following conditions are equivalent for 
$f \in \operatorname {\mathbf {Cor}}(X, Y)$:
(1) The finite correspondence f is universally
$H_0^S$-trivial.(2) The induced map
$f_* : h_0(X)_{\mathrm {Nis}} \to h_0(Y)_{\mathrm {Nis}}$ is an isomorphism in $\mathbf {HI}_{\mathrm {Nis}}$.(3) The induced map
$f^* : F(Y) \to F(X)$ is an isomorphism for each $F \in \mathbf {HI}_{\mathrm {Nis}}$.
(Thanks to (V5), we may replace 
${\mathrm {Nis}}$ by 
${\mathrm {Zar}}$ in this statement.)
Proof. The equivalence of (1) and (2) is a consequence of (V4). We have
$$ \begin{align*} F(X) = {\operatorname{\mathbf{PST}}}(\mathbb{Z}_{\mathrm{tr}}(X), F) = {\operatorname{\mathbf{HI}}}(h_0(X), F) = {\operatorname{\mathbf{HI}}}_{\mathrm{Nis}}(h_0(X)_{\mathrm{Nis}}, F) \end{align*} $$for any 
$F \in \mathbf {HI}_{\mathrm {Nis}}$. Here we used, in order, Yoneda’s lemma, (V2) and (V1). Now another use of Yoneda’s lemma shows the equivalence of (2) and (3).
Corollary 2.4. Let X be a smooth and proper scheme over a field k. If X is universally 
${\mathrm {CH}}_0$-trivial, then we have 
$F(k) \cong F(X)$ for any 
$F \in \mathbf {HI}_{\mathrm {Nis}}$.
We will generalise this result in Corollary 3.3.
Remark 2.5. We collect basic properties of universally 
$H_0^S$-trivial correspondences. Since they are not used in the sequel, the proof will be given in Appendix A.
(1) If
$f, g$ are composable finite correspondences and if two out of $f, g , f \circ g$ are universally $H_0^S$-trivial, then so is the third.(2) If
$f : X \to Y$ and $f' : X' \to Y'$ are universally $H_0^S$-trivial finite correspondences, then so is $f \times f' : X \times X' \to Y \times Y'$.(3) Suppose k is perfect. Let
$j : U \hookrightarrow X$ be an open dense immersion in $\mathbf {Sm}$. If $X \setminus j(U)$ is of codimension $\ge 2$, then j is universally $H_0^S$-trivial.(4) Suppose k is perfect. A proper birational morphism in
$\mathbf {Sm}$ is universally $H_0^S$-trivial.
3 $\mathbb {P}^1$-invariance and the main result
Recall from [Reference Voevodsky31, Section 3.2] that 
$\mathbf {PST}$ is equipped with a symmetric monoidal structure 
$\otimes $ which is uniquely characterised by the facts that it is right exact and the Yoneda functor is monoidal (that is, 
$\mathbb {Z}_{\mathrm {tr}}(X) \otimes \mathbb {Z}_{\mathrm {tr}}(Y)=\mathbb {Z}_{\mathrm {tr}}(X \times Y)$ for 
$X, Y \in \mathbf {Sm}$). It admits a right adjoint 
$\mathrm {\underline {Hom}}$ given by the formula
$$ \begin{align} \operatorname{\underline{Hom}}(F, G)(X) = {\operatorname{\mathbf{PST}}}(F \otimes \mathbb{Z}_{\mathrm{tr}}(X), G) \quad (F, G \in \mathbf{PST}, \ X \in \mathbf{Sm}). \end{align} $$Definition 3.1. We say 
$G \in \mathbf {PST}$ is 
$\mathbb {P}^1$-invariant if the structure map 
$\sigma : \mathbb {P}^1 \to \operatorname {Spec} k$ induces an isomorphism 
$G \overset {\cong }{\longrightarrow } \operatorname {\underline {Hom}}\left (\mathbb {Z}_{\mathrm {tr}}\left (\mathbb {P}^1\right ), G\right )$ – that is, 
$\sigma $ induces isomorphisms 
$G(U) \overset {\cong }{\longrightarrow } G\left (U \times \mathbb {P}^1\right )$ for all 
$U \in \mathbf {Sm}$. Denote by 
$\mathbf {PI}_{\mathrm {Nis}}$ the full subcategory of 
$\mathbf {PST}$ consisting of all Nisnevich sheaves with transfers which are 
$\mathbb {P}^1$-invariant.
Theorem 3.2. Suppose that 
$X, Y$ are smooth and proper schemes over a field k and 
$f \in \operatorname {\mathbf {Cor}}(X, Y)$. Then the conditions in Proposition 2.3 are equivalent to the following:
(4) The induced map
$f^* : G(Y) \to G(X)$ is an isomorphism for each $G \in \mathbf {PI}_{\mathrm {Nis}}$.
As with Corollary 2.4, Theorem 3.2 has an immediate consequence:
Corollary 3.3. Let X be a smooth proper scheme over a field k. If X is universally 
${\mathrm {CH}}_0$-trivial, then we have 
$G(k) \cong G(X)$ for any 
$G \in \mathbf {PI}_{\mathrm {Nis}}$.
Remark 3.4. Let T be a smooth quasi-affine scheme over k. It follows from [Reference Kahn, Miyazaki, Saito and Yamazaki17, Theorem 6.4.1] that 
$\mathbb {Z}_{\mathrm {tr}}(T) \in \mathbf {PI}_{\mathrm {Nis}}$. On the other hand, 
$\mathbb {Z}_{\mathrm {tr}}(T)$ does not have reciprocity in general. (This follows, for example, from [Reference Kahn, Saito and Yamazaki18, Proposition 9.4.4].) We conclude that 
$\mathbb {P}^1$-invariance does not imply reciprocity (i.e., the converse of the second arrow in formula (1.1) does not hold). On the other hand, the conclusion of Corollary 3.3 is obvious for 
$G=\mathbb {Z}_{\mathrm {tr}}(T)$. Indeed, it is not difficult to show 
$\operatorname {\mathbf {Cor}}(\operatorname {Spec} k, T) \cong \operatorname {\mathbf {Cor}}(X, T)$ for any 
$X \in \mathbf {Sm}$ which is connected and proper over k (but not necessary universally 
${\mathrm {CH}}_0$-trivial).
For 
$F \in \mathbf {PST}$ we define
$$ \begin{align} \overline{h}_0(F) := \operatorname{Coker}\left(i_0^* - i_1^* : \operatorname{\underline{Hom}}\left(\mathbb{Z}_{\mathrm{tr}}\left(\mathbb{P}^1\right), F\right) \to F\right). \end{align} $$We write 
$\overline {h}_0(X):=\overline {h}_0(\mathbb {Z}_{\mathrm {tr}}(X))$ for 
$X \in \mathbf {Sm}$. The main part in the proof of Theorem 3.2 is the following:
Theorem 3.5 A moving lemma
The natural map 
$\overline {h}_0(X) \to h_0(X)$ yields an isomorphism 
$\overline {h}_0(X)_{\mathrm {Zar}} \cong h_0(X)_{\mathrm {Zar}}$ for any smooth proper scheme X over a field k. (Hence we have 
$\overline {h}_0(X)_{\mathrm {Nis}} \cong h_0(X)_{\mathrm {Nis}}$ as well.)
The proof of Theorem 3.5 occupies the next two sections. In the rest of this section, we deduce Theorem 3.2 assuming Theorem 3.5.
Remark 3.6. For X as in Theorem 3.5, we have an explicit formula:
$$ \begin{align*} \overline{h}_0(X)_{\mathrm{Zar}}(U) \cong {\mathrm{CH}}_0(X \otimes_k k(U)) \quad \text{for any connected } U \in \mathbf{Sm}, \end{align*} $$because we know 
$h_0(X)_{\mathrm {Nis}}(U) \cong {\mathrm {CH}}_0(X \otimes _k k(U))$ by [Reference Kahn and Sujatha19, Theorem 3.1.2] (and we have 
$h_0(X)_{\mathrm {Zar}} \cong h_0(X)_{\mathrm {Nis}}$ by (V2) and (V5)). In particular, 
$\overline {h}_0(X)_{\mathrm {Zar}}$ is birational in the sense of [Reference Kahn and Sujatha19, Definition 2.3.1] – that is, any open dense immersion 
$V \hookrightarrow W$ induces an isomorphism 
$\overline {h}_0(X)_{\mathrm {Zar}}(W) \cong \overline {h}_0(X)_{\mathrm {Zar}}(V)$.
Denote by 
$i_\varepsilon : \operatorname {Spec} k \to \mathbb {P}^1$ the closed immersion defined by a rational point 
$\varepsilon \in \mathbb {P}^1(k)$.
Definition 3.7. Set 
$F \in \mathbf {PST}$. We say F is 
$\mathbb {P}^1$-rigid if the two induced maps
$$ \begin{align*} i_0^*, ~i_1^* : F\left(U \times \mathbb{P}^1\right) \to F(U) \end{align*} $$are equal for any 
$U \in \mathbf {Sm}$. Denote by 
$\mathbf {PRig}$ the full subcategory of 
$\mathbf {PST}$ consisting of all 
$\mathbb {P}^1$-rigid presheaves with transfers.
Lemma 3.8. If 
$F \in \mathbf {PST}$ is 
$\mathbb {P}^1$-invariant, then it is 
$\mathbb {P}^1$-rigid. The converse holds if F is separated for Zariski topology.
Proof. See [Reference Kahn, Saito and Yamazaki18, Proposition 6.1.4].
(1) For
$F \in \mathbf {PST}$, the following conditions are equivalent:(a) F is
$\mathbb {P}^1$-rigid.(b) The two induced maps
$i_0^*, ~i_1^* : \operatorname {\underline {Hom}}\left (\mathbb {Z}_{\mathrm {tr}}\left (\mathbb {P}^1\right ), F\right ) \to F$ are equal.(c) The canonical surjection
$F \to \overline {h}_0(F)$ is an isomorphism.(d) The canonical injection
${\operatorname {\mathbf {PST}}}\left (\overline {h}_0(U), F\right ) \to {\operatorname {\mathbf {PST}}}(\mathbb {Z}_{\mathrm {tr}}(U), F)$ is an isomorphism for each $U \in \mathbf {Sm}$.
(2) Rormula (3.2) defines a left adjoint
$\overline {h}_0 : \mathbf {PST} \to \mathbf {PRig}$ of the inclusion functor $\mathbf {PRig} \hookrightarrow \mathbf {PST}$.(3) We have
$\mathbf {HI}_{\mathrm {Nis}} \subset \mathbf {PI}_{\mathrm {Nis}}$.
Proof. (1) The equivalence of (a), (b) and (c) follows from formulas (3.1) and (3.2). If (c) holds, then any morphism 
$\mathbb {Z}_{\mathrm {tr}}(U) \to F$ factors as 
$\mathbb {Z}_{\mathrm {tr}}(U) \twoheadrightarrow \overline {h}_0(U) \to \overline {h}_0(F) \cong F$, whence (d). If (d) holds, then any morphism 
$\mathbb {Z}_{\mathrm {tr}}(U) \to F$ factors as 
$\mathbb {Z}_{\mathrm {tr}}(U) \twoheadrightarrow \overline {h}_0(U) \to F$, whence (b).
(2) We need to show 
${\operatorname {\mathbf {PST}}}\left (\overline {h}_0(G), F\right ) \cong {\operatorname {\mathbf {PST}}}(G, F)$ for any 
$F \in \mathbf {PRig}$ and 
$G \in \mathbf {PST}$. This is (d) if 
$G=\mathbb {Z}_{\mathrm {tr}}(U)$ for 
$U \in \mathbf {Sm}$, to which the general case is reduced by taking a resolution of the form
$$ \begin{align*} \bigoplus_\beta \mathbb{Z}_{\mathrm{tr}}\left(V_\beta\right) \to \bigoplus_\alpha \mathbb{Z}_{\mathrm{tr}}(U_\alpha) \to G \to 0, \end{align*} $$where 
$U_\alpha , V_\beta \in \mathbf {Sm}$ [Reference Voevodsky31, Section 3.2].
(3) Given 
$F \in \mathbf {PST}$, we have a chain of canonical surjections 
$F \twoheadrightarrow \overline {h}_0(F) \twoheadrightarrow h_0(F)$, and F is homotopy-invariant if and only if the composition is an isomorphism. It follows from (1) that 
$\mathbf {HI} \subset \mathbf {PRig}$. Now the assertion follows from Lemma 3.8.
Lemma 3.10. Suppose 
$G \in \mathbf {PST}$ is a Zariski sheaf. Then 
$h^0(G)$ is a Nisnevich sheaf.
Proof. This is essentially shown in [Reference Rülling and Saito25, Section 4.34], but we include a short proof for the sake of completeness. We consider a commutative diagram
The bottom arrow is injective, since the sheafification is exact. This shows the injectivity of j. Fact (V5) shows that 
$h^0(G)_{\mathrm {Zar}}=h^0(G)_{\mathrm {Nis}}$, and (V1) shows that it is homotopy-invariant. Hence j must be isomorphic, since 
$h^0(G) \subset G$ is the maximal subobject in 
$\mathbf {HI}$.
Proof of Theorem 3.2, admitting Theorem 3.5. That (4) implies (3) follows from Lemma 3.9(3). To show the converse, we assume (3) and take 
$G \in \mathbf {PI}_{\mathrm {Nis}}$. Set 
$F:=h^0(G)$. By Lemma 3.10 we find 
$F \in \mathbf {HI}_{\mathrm {Nis}}$, and hence we have 
$f^* : F(Y) \cong F(X)$ by assumption (3). It remains to show 
$G(X)=F(X)$ for any proper 
$X \in \mathbf {Sm}$. By Theorem 3.5 we have 
$\overline {h}_0(X)_{\mathrm {Nis}}=h_0(X)_{\mathrm {Nis}} \in \mathbf {HI}_{\mathrm {Nis}} \subset \mathbf {PST}$. We now proceed as follows:
$$\begin{align*}\hspace{35pt}G(X) &={\operatorname{\mathbf{PST}}}(\mathbb{Z}_{\mathrm{tr}}(X), G)\kern-0.2pt\!\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad{\text{(Yoneda)}} \\ &={\operatorname{\mathbf{PST}}}\left(\overline{h}_0(X), G\right) \kern-0.8pt\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\, {\text{(Lemma 3.9(d))}} \\ &={\operatorname{\mathbf{PST}}}\left(\overline{h}_0(X)_{\mathrm{Nis}}, G\right) \kern-0.8pt\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\!{\text{(}G\ \text{is a Nisnevich sheaf)}} \\ &={\operatorname{\mathbf{PST}}}\left(h_0(X)_{\mathrm{Nis}}, G\right) \quad\qquad\qquad\qquad\qquad\qquad{\text{(}\overline{h}_0(X)_{\mathrm{Nis}}=h_0(X)_{\mathrm{Nis}}, \text{by Theorem~3.5)}} \\ &={\operatorname{\mathbf{PST}}}(h_0(X), G)\qquad\qquad\qquad\qquad\quad\quad\qquad\qquad\qquad\qquad\!{\text{(}G\ \text{is a Nisnevich sheaf)}} \\ &={\operatorname{\mathbf{HI}}}(h_0(X), F) \qquad\qquad\qquad\qquad\qquad\qquad\quad\ \kern0.5pt\,{\text{(}h^0\ \text{is a right adjoint to the inclusion)}} \\ &={\operatorname{\mathbf{PST}}}(\mathbb{Z}_{\mathrm{tr}}(X), F) \qquad\qquad\qquad\qquad\ \quad\qquad\qquad{\text{(}h_0\ \text{is a left adjoint to the inclusion)}} \\ &=F(X) \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \qquad\qquad\qquad\ \ \quad{\text{(Yoneda)}}. \end{align*}$$This completes the proof.
4 Projective Suslin complex
Fix 
$X \in \mathbf {Sm}$ in this section. After a brief review of the definition of the Suslin complex of X, we define its variant using the projective spaces 
$\mathbb {P}^n$. This will be used in the proof of the moving lemma in the next section. (We will use them only up to degree 
$2$.)
For each nonnegative integer n, we write
$$ \begin{align*} \Delta^n :=\operatorname{Spec} k[t_0, \dotsc, t_n]/(t_0+\dotsb+t_n-1) \cong \mathbb{A}^n. \end{align*} $$For 
$j=0, \dotsc , n$, we define
$$ \begin{align} i_{n, j} : \Delta^{n-1} \to \Delta^n; \quad (t_0, \dotsc, t_{n-1}) \mapsto \left(t_0, \dotsc, t_{j-1}, 0, t_j, \dotsc, t_{n-1}\right). \end{align} $$The Suslin complex 
$C_\bullet (X)$ of X is a complex in 
$\mathbf {PST}$ defined by
$$ \begin{align*} C_n(X)&:=\operatorname{\underline{Hom}}(\mathbb{Z}_{\mathrm{tr}}(\Delta^n), \mathbb{Z}_{\mathrm{tr}}(X)), \\ {\partial}_n &:= \sum_{j=0}^n (-1)^j i_{n, j}^* : C_n(X) \to C_{n-1}(X). \end{align*} $$Its homology is denoted by 
$h_n(X) \in \mathbf {PST}$. For 
$n=0$, it recovers 
$h_0(X)$ from (V2).
For each nonnegative integer n, we set
$$ \begin{align*} \overline{\Delta}^n:= \operatorname{Proj} k[t_0, \dotsc, t_{n+1}]/(t_0+\dotsb+t_n-t_{n+1}) \cong \mathbb{P}^n. \end{align*} $$We have a canonical open immersion 
$\iota _n : \Delta ^n \hookrightarrow \overline {\Delta }^n$, which is isomorphic to 
$\mathbb {A}^n \hookrightarrow \mathbb {P}^n$. It induces a map in 
$\mathbf {PST}$
$$ \begin{align} \overline{C}_n(X):=\operatorname{\underline{Hom}}\left(\mathbb{Z}_{\mathrm{tr}}\left(\overline{\Delta}^n\right), \mathbb{Z}_{\mathrm{tr}}(X)\right) \hookrightarrow C_n(X), \end{align} $$which is injective for any n and isomorphic for 
$n=0$. Indeed, its section over 
$U \in \mathbf {Sm}$ is given by
$$ \begin{align*} ({\mathrm{Id}}_U \times \iota_n)^* : \operatorname{\mathbf{Cor}}\left(U \times \overline{\Delta}^n, X\right) \to \operatorname{\mathbf{Cor}}(U \times \Delta^n, X), \end{align*} $$which is injective in general and isomorphic for 
$n=0$. We regard 
$\overline {C}_n(X)$ as a subobject in 
$\mathbf {PST}$ of 
$C_n(X)$. Since the morphisms 
$i_{n, j}$ from formula (4.1) extend (uniquely) to morphisms 
$\overline {\Delta }^{n-1} \to \overline {\Delta }^{n}$, we obtain a subcomplex 
$\overline {C}_\bullet (X)$ of 
$C_\bullet (X)$. We write its homology by 
$\overline {h}_n(X) \in \mathbf {PST}$. For 
$n=0$, it recovers 
$\overline {h}_0(X)$ from formula (3.2).
We write
$$ \begin{align} Q_\bullet(X):=C_\bullet(X)/\overline{C}_\bullet(X) \end{align} $$for the quotient complex, and its homology presheaf is denoted by 
$H_n(Q_\bullet (X)) \in \mathbf {PST}$. We have 
$H_0(Q_\bullet (X))=0$, for formula (4.2) is isomorphic for 
$n=0$. Since the sheafification is exact, we obtain an exact sequence
$$ \begin{align*} H_1(Q_\bullet(X))_{\mathrm{Zar}} \to \overline{h}_0(X)_{\mathrm{Zar}} \to h_0(X)_{\mathrm{Zar}} \to H_0(Q_\bullet(X))_{\mathrm{Zar}}=0. \end{align*} $$Theorem 3.5 is now reduced to the following:
Theorem 4.1. If 
$X \in \mathbf {Sm}$ is proper, then we have 
$H_1(Q_\bullet (X))_{\mathrm {Zar}}=0$.
(1) In general,
$\overline {h}_n(X)_{\mathrm {Zar}} \to h_n(X)_{\mathrm {Zar}}$ is not isomorphic for $n>0$. Indeed, one easily checks $H_2\left (Q_\bullet \left (\mathbb {P}^1\right )\right )_{\mathrm {Zar}}(k)=H_2\left (Q_\bullet \left (\mathbb {P}^1\right )\right )(k) \not = 0$.(2) The properness assumption on X is essential. Indeed, it follows from [Reference Kahn, Miyazaki, Saito and Yamazaki17, Theorem 6.4.1] that if X is quasiaffine, then all the boundary maps of
$\overline {C}_\bullet (X)$ are the zero maps.
5 Moving lemma
We shall prove Theorem 4.1 in the following (equivalent) form:
Theorem 5.1. Let 
$X\in \mathbf {Sm} $ be proper. For every irreducible affine 
$V\in \mathbf {Sm} $ and local scheme U at a closed point of V, the restriction map
$$ \begin{align*} H_1(Q_\bullet (X) )(V) \to H_1(Q_\bullet (X) )(U)\\[-15pt] \end{align*} $$is the zero map. (The target 
$H_1(Q_\bullet (X) )(U)$ is defined as a colimit – see equation (2.1).)
Note that in proving Theorem 5.1, we may assume k is infinite; for if k is finite, we can use the usual norm argument.
5.1 The bad locus
In the notation of Theorem 5.1, let 
$\Gamma \subset V\times X\times \Delta ^n$ be an irreducible closed subset which is finite and surjective over 
$V\times \Delta ^n$. Let 
$\overline \Gamma $ be its closure in 
$V\times X\times {\overline \Delta }^{n}$. We call
$$ \begin{align} B(\Gamma ):=\left\{ p\in V\times {\overline\Delta}^{n} \,\middle\vert\, \overline\Gamma \to V\times {\overline\Delta}^{n} \text{ is not finite over}\ p \right\} \\[-15pt]\nonumber\end{align} $$the bad locus of 
$\Gamma $, which witnesses how far 
$\Gamma $ is from being a member of 
$\overline C _n(X)(V)$.
(1) We have
$\Gamma \in C_n(X)(V)$ if and only if $B(\Gamma )=\emptyset $.(2) The bad locus
$B(\Gamma )$ is a closed proper subset of $V\times \left ({\overline \Delta }^{n}\setminus \Delta ^n\right )$.(3) If
$n\le 1$, the image of the projection $B(\Gamma )\to V$ is a closed proper subset.
Proof. Assertion (1) is clear from definitions, and put for later reference.
To prove (2), consider the set upstairs:
$$ \begin{align*} \widetilde B\left(\overline\Gamma \right):= \left\{ x\in \overline\Gamma \,\middle\vert\, \text{locally around}\ x, \text{the fibre of}\ \overline\Gamma \to V\times {\overline\Delta}^{n}\ \text{has dimension}\ \ge 1 \right\}.\\[-15pt] \end{align*} $$It is a closed subset of 
$V\times X\times {\overline \Delta }^{n}$ by Chevalley’s theorem [Reference Dieudonné and Grothendieck11, IV3 13.1.3]. It is contained in 
$\overline \Gamma \setminus \Gamma $:
$$ \begin{align} \widetilde{B}\left(\overline\Gamma \right) \subset \overline\Gamma \setminus \Gamma ,\\[-15pt]\nonumber \end{align} $$because 
$\Gamma $ is assumed to be finite over 
$V\times \Delta ^n$. Since 
$B(\Gamma )$ is by definition the image of the map 
$\widetilde B\left (\overline \Gamma \right )\to V\times {\overline \Delta }^{n}$ which is proper because X is, it follows that 
$B(\Gamma )$ is a closed subset of 
$V\times \left ({\overline \Delta }^{n}\setminus \Delta ^n\right )$.
To show that 
$B(\Gamma )$ is a proper subset of 
$V\times \left ({\overline \Delta }^{n}\setminus \Delta ^n\right )$, let 
$\xi \in \widetilde B\left (\overline \Gamma \right )$ be an arbitrary point and 
$\eta \in B(\Gamma )$ its image. By formula (5.2) we have
$$ \begin{align*} \dim \left(\overline\Gamma \setminus \Gamma \right)&\ge \operatorname{\mathbf{trdeg}} (k(\xi )/k) \\ &=\operatorname{\mathbf{trdeg}} (k(\xi )/k(\eta ) ) +\operatorname{\mathbf{trdeg}} (k(\eta )/k) \\ &\ge 1+\operatorname{\mathbf{trdeg}} (k(\eta )/k ),\\[-15pt] \end{align*} $$and by 
$\dim (V)+n-1 \ge \dim \left (\overline \Gamma \setminus \Gamma \right ) $ we obtain
$$ \begin{align} \dim (V)+(n-2) \ge \operatorname{\mathbf{trdeg}} (k(\eta )/k).\\[-15pt]\nonumber \end{align} $$Since 
$\dim (B(\Gamma ))= \sup _{\eta \in B(\Gamma )} \operatorname {\mathbf {trdeg}} (k(\eta )/k)$, we conclude 
$\dim \left (V\times \left ({\overline \Delta }^{n} \setminus \Delta ^n\right )\right )>\dim (B(\Gamma ))$. We are done.
Assertion (3) is a direct consequence of (2) (or of formula (5.3)).
5.2 Affine-space case
In this subsection we consider the case 
$V=\mathbb {A} ^N$ of Theorem 5.1, with 
$N\ge 0$ an integer. Recall that we may assume k is infinite, which we do here.
Let 
$\Gamma \in C_1(X)\left (\mathbb {A} ^N\right )$ be an arbitrary irreducible cycle. By a diagram chase in the following diagram (see formula (4.3) for the definition of 
$Q_\bullet (X)$), it suffices to find 
$\widetilde \Gamma \in C_2(X)\left (\mathbb {A} ^N\right )$ such that 
$\left (\Gamma -\partial _2 \widetilde \Gamma \right )\rvert _U \in \overline C_1(X)(U)$:
For a vector 
$\boldsymbol{v}\in \mathbb {A}^N(k)$, consider the translation 
$+\boldsymbol{v} : \mathbb {A}^N \to \mathbb {A}^N$ by 
$\boldsymbol{v}$. The next assertion suggests how it can be useful:
Lemma 5.3. There is a closed proper subset 
$B\subset \mathbb {A}^N$ such that for every vector 
$\boldsymbol{v}\in \mathbb {A}^N(k)\setminus B$, if we denote by 
$\tau _{\boldsymbol{v}}\colon \mathbb {A} ^N\times X\times \mathbb {A}^1\to \mathbb {A}^N\times X\times \mathbb {A}^1$ the base change of the translation 
$\mathbb {A}^N \xrightarrow {+\boldsymbol{v}} \mathbb {A}^N$, then we have
$$ \begin{align*} \left(\tau _{\boldsymbol{v}}^*\Gamma \right)\rvert_U \in \overline C_1(X)(U).\\[-18pt] \end{align*} $$Proof. Let 
$s\in U$ be the unique closed point of V contained in U. Let 
$B(\Gamma )\subset V\times {\overline \Delta }^{1}$ be as in formula (5.1). By Lemma 5.2 we know that its projection 
$\operatorname {pr}_V (B(\Gamma ))\subset V=\mathbb {A} ^N $ is a closed proper subset. Consider the closed subset
$$ \begin{align*} B_0:=\operatorname{pr}_V \left(B(\Gamma )_{k(s)}\right)-s = \left\{ \boldsymbol{v}\in \mathbb{A}^N_{k(s)} \,\middle\vert\, \boldsymbol{v}+s \in \operatorname{pr}_V B(\Gamma ) _{k(s)} \right\} \subsetneq \mathbb{A}^N_{k(s)}\\[-18pt] \end{align*} $$and let B be its image by the finite projection 
$\pi \colon \mathbb {A}^N_{k(s)}\to \mathbb {A}^N$:
$$ \begin{align} B:= \pi (B_0) \subsetneq \mathbb{A}^N.\\[-18pt]\nonumber \end{align} $$Take an arbitrary 
$\boldsymbol{v}\in \mathbb {A}^N(k) \setminus B$. By definitions, we know 
$s+ \boldsymbol{v} \in \mathbb {A}^N\setminus \operatorname {pr}_V B(\Gamma )$. Since the right-hand side is an open subset of 
$\mathbb {A}^N$, this relation remains true if we replace s by any point specialising to s. In particular,
$$ \begin{align} U+\boldsymbol{v}\subset \mathbb{A} ^N\setminus \operatorname{pr}_V B(\Gamma ).\\[-18pt]\nonumber \end{align} $$ Let us denote by 
$\overline \tau _{\boldsymbol{v}}$ the endomorphism of 
$\mathbb {A}^N \times X\times {\overline \Delta }^{1}$ obtained as the base change of the translation 
$+\boldsymbol{v}$. By formula (5.5), the maps 
$\tau _{\boldsymbol{v}}$ and 
$\overline \tau _{\boldsymbol{v}}$ restrict themselves as in the following commutative diagram:
The slanted arrow is finite because 
$\overline \Gamma \to \mathbb {A}^N\times {\overline \Delta }^{1}$ is finite outside 
$B(\Gamma )$ precisely by definition (5.1), and we have the inclusion 
$\left (\mathbb {A}^N\setminus \operatorname {pr}_V B(\Gamma )\right )\times {\overline \Delta }^{1} \subset \left (\mathbb {A}^N\times {\overline \Delta }^{1}\right )\setminus B(\Gamma )$. It follows that 
$\overline \tau _{\boldsymbol{v}}^* \overline \Gamma $ is finite over 
$U\times {\overline \Delta }^{1}$. As a general fact about closure and continuity, we have the inclusion 
$\overline {\left (\tau _{\boldsymbol{v}}^*\Gamma \right )}\subset \overline \tau _{\boldsymbol{v}}^* \overline \Gamma $. We conclude that 
$\left (\tau _{\boldsymbol{v}}^*\Gamma \right )\rvert _{U}$ belongs to 
$\overline C_1(X)(U)$, and this completes the proof.
Let B be as in Lemma 5.2 and fix a vector 
$\boldsymbol{v}\in \mathbb {A}^N(k)\setminus B$. Let 
$\varphi _{\boldsymbol{v}}\colon \mathbb {A}^N \times \mathbb {A}^1\to \mathbb {A}^N$ be the map 
$(a,t)\mapsto a+t\boldsymbol{v}$ and let
$$ \begin{align*} \Phi _{\boldsymbol{v},n}\colon \mathbb{A}^N\times X\times \mathbb{A}^1\times \Delta ^n\to \mathbb{A}^N\times X\times \Delta ^n \end{align*} $$be its base change by 
$X\times \Delta ^n \to \operatorname {Spec} k$. Since finite morphisms are stable under base change, we know that
$$ \begin{align} \text{the inverse image }\Phi _{\boldsymbol{v},1}^{-1}\Gamma \subset \mathbb{A}^N\times X\times \mathbb{A}^1\times \Delta ^1 \text{ is finite over }\mathbb{A}^N\times \mathbb{A}^1\times \Delta ^1 .\end{align} $$We shall use the following triangulation maps, as in Figure 1:
$$ \begin{align} \sigma _1,\sigma _2 \colon \Delta ^2 \xrightarrow{\cong } \mathbb{A}^1 \times \Delta ^1. \end{align} $$
Figure 1 Triangulation.
Explicitly, the maps 
$\sigma _1, \sigma _2$ are the unique affine-linear ones satisfying
$$ \begin{align*} &\sigma _1(u_0)=(v_0,0),& &\sigma _1(u_1)=(v_1,0),& &\sigma _1(u_2)=(v_1,1),& \\ &\sigma _2(u_0)=(v_0,0),& &\sigma _2(u_1)=(v_0,1),& &\sigma _2(u_2)=(v_1,1)& \end{align*} $$in 
$\left (\Delta ^1\times \mathbb {A}^1\right )(k)$, where 
$v_j=i_{1, j}\left (\Delta ^0\right )$ for 
$j=0, 1$ and 
$u_0=i_{2, 2}(v_1), u_1=i_{2, 0}(v_1), u_2=i_{2, 1}(v_0)$.
Let 
$\Phi ^{(1)}_{\boldsymbol{v},1}, \Phi ^{(2)}_{\boldsymbol{v},1}\colon \mathbb {A}^N\times X\times \Delta ^2 \to \mathbb {A}^N\times X\times \Delta ^1$ be the composite maps 
$\Phi _{\boldsymbol{v},1}\circ \left ({\mathrm {Id}} _{\mathbb {A}^N\times X}\times \sigma _i\right )$ (
$i=1,2$). By fact (5.6), we conclude 
$\Phi ^{(1)*}_{\boldsymbol{v},1} \Gamma , \Phi ^{(2)*}_{\boldsymbol{v},1} \Gamma \in C_2(X)\left (\mathbb {A}^N\right )$. Now set
$$ \begin{align*} \widetilde{\Gamma }:= \Phi ^{(1)*}_{\boldsymbol{v},1} \Gamma -\ \Phi ^{(2)*}_{\boldsymbol{v},1} \Gamma. \end{align*} $$We want to show 
$\left (\Gamma -\partial _2 \widetilde {\Gamma }\right )\rvert _U \in \overline C_1(X)(U)$.
By a routine calculation of 
$\partial _2 \widetilde {\Gamma }$, we have
$$ \begin{align} \Gamma - \partial_2 \widetilde\Gamma = \tau _{\boldsymbol{v}}^*\Gamma +\Phi _{\boldsymbol{v},0}^*\left(i_{1,1}^*\Gamma \right) -\Phi _{\boldsymbol{v},0}^*\left(i_{1,0}^*\Gamma \right) .\end{align} $$By Lemma 5.3, for 
$\boldsymbol{v}\in \mathbb {A}^N(k)\setminus B $ we know that the first term of the right-hand side maps into 
$\overline C_1(X)(U)$. So it suffices to show the following, which we apply to 
$\gamma := i_{1,j}^*\Gamma $:
Lemma 5.4. For every 
$\gamma \in C_0(X)\left (\mathbb {A}^N \right ) $, there is a closed proper subset 
$C\subsetneq \mathbb {A}^N$ such that for all 
$\boldsymbol{v}\in \mathbb {A}^N(k)\setminus C$, the cycle 
$\Phi _{\boldsymbol{v},0}^*\gamma $ on 
$\mathbb {A}^N\times X\times \Delta ^1$ belongs to 
$\overline C_1(X)\left (\mathbb {A}^N\right )$.
Proof. Let us observe that as long as 
$\boldsymbol{v}\neq 0$, the morphism 
$\varphi _{\boldsymbol{v}}$ extends (uniquely) to a morphism
$$ \begin{align} \overline\varphi _{\boldsymbol{v}}\colon \mathbb{A}^N\times \mathbb{P} ^1 &\to \mathbb{P}^N \notag\\ (a,[t_0:t_1])&\mapsto [t_0:t_0a+t_1\boldsymbol{v}]. \end{align} $$ For this proof, we may assume 
$\gamma $ is irreducible. Let 
$\overline \gamma \subset \mathbb {P}^N\times X$ be the closure of 
$\gamma $. Consider the set
$$ \begin{align} C_\infty := \left\{ a\in \mathbb{P}^N\setminus \mathbb{A}^N \,\middle\vert\, \overline\gamma \to \mathbb{P}^N \text{ is not finite over }a \right\}. \end{align} $$By the 
$V=\operatorname {Spec} (k)$ case of Lemma 5.2(2) (via 
$X\times {\overline \Delta }^{n} \cong \mathbb {P} ^N\times X$), we find that 
$C_\infty $ is a closed proper subset of 
$\mathbb {P}^N\setminus \mathbb {A}^N$. Let 
$C\subset \mathbb {A}^N$ be the cone associated to 
$C_\infty $, namely,
$$ \begin{align*} C:= \begin{cases} \{ 0 \} \cup q^{-1}(C_\infty) \subset \mathbb{A}^N & (N>0), \\ \emptyset & (N=0), \end{cases} \end{align*} $$where 
$q : \mathbb {A}^N\setminus \left \{ 0 \right \} \to \mathbb {P}^N\setminus \mathbb {A}^N$ is the projection with centre 
$0$. This is a closed proper subset of 
$\mathbb {A}^N$.
Now suppose 
$\boldsymbol{v}\in \mathbb {A}^N(k)\setminus C$. Then by formula (5.9) we see that 
$\overline \varphi _{\boldsymbol{v}}$ maps 
$\mathbb {A}^N \times \mathbb {P}^1$ into 
$\mathbb {P}^N\setminus C_\infty $. We obtain the following commutative diagram:
Since the slanted arrow is finite by the definition (5.10) of 
$C_\infty $, the inverse image 
$\left (\overline \varphi _{\boldsymbol{v}}\times {\mathrm {Id}} _X\right )^*\overline \gamma $ is finite over 
$\mathbb {A}^N \times \mathbb {P}^1$. By the inclusion 
$\overline {\left (\Phi _{\boldsymbol{v},0}^*\gamma \right )}\subset \left (\overline \varphi _{\boldsymbol{v}}\times {\mathrm {Id}} _X\right )^*\overline \gamma $ of subsets of 
$\mathbb {A}^N\times X\times \mathbb {P}^1$, we conclude that 
$\Phi _{\boldsymbol{v},0}^*\gamma $ belongs to 
$\overline C_1(X)\left (\mathbb {A}^N\right )$, completing the proof.
Lemmas 5.3 and 5.4 applied to equation (5.8) prove Theorem 5.1 in the case 
$V=\mathbb {A}^N$.
5.3 The general case
Let 
$V\in \mathbf {Sm} $ be affine and irreducible. Let 
$N=\dim (V)$ be its dimension. Fix a closed embedding 
$V\hookrightarrow \mathbb {A}^{N'}$ into an affine space. For a technical reason (see Proposition 5.6), we assume it is obtained as the composition of a preliminary one 
$V\hookrightarrow \mathbb {A} ^{N^{\prime }_0}$ and the 
$2$-fold Veronese embedding 
$\mathbb {A} ^{N^{\prime }_0}\hookrightarrow \mathbb {A} ^{N'}$, 
$N':= \begin {pmatrix} N^{\prime }_0+2 \\ 2 \end {pmatrix} -1 $ defined by
$$ \begin{align} (x_i)_{i=1,\dotsc ,N^{\prime}_0} \mapsto \left(x_1,\dotsc ,x_{N^{\prime}_0}; \left(x_ix_j\right)_{i\le j} \right). \end{align} $$Let 
$M_{NN'}\cong \mathbb {A}^{NN'}$ be the k-scheme parametrising 
$N\times N'$ matrices. The choice of a k-rational point 
$f\in M_{NN'}(k)$ determines a morphism, which we denote by the same symbol 
$f\colon \mathbb {A}^{N'}\to \mathbb {A}^N$.
Proposition 5.5 Noether’s normalisation lemma
There is a closed proper subset 
$D_1\subset M_{NN'}$ such that the composite map
$$ \begin{align*} \pi _f \colon V\hookrightarrow \mathbb{A}^{N'}\xrightarrow[]{f}\mathbb{A}^N \end{align*} $$is finite and flat whenever 
$f\in M_{NN'}(k)\setminus D_1$.
Proof. For the existence of 
$D_1$ which guarantees finiteness, see, for example, [Reference Atiyah and Macdonald1, p. 69] or [Reference Kai20, Section 3.1]. Flatness is then automatic by the smoothness of V and 
$\mathbb {A}^N$; see [Reference Hartshorne13, Exercise III-10.9, p. 276].
By Proposition 5.5, for 
$f\in M_{NN'}(k)\setminus D_1$ we have push-forward maps 
$\pi _{f*}\colon H_n(X)(V)\to H_n(X)\left (\mathbb {A}^N\right )$. Let 
$s\in U$ be the unique closed point of V contained in U. Let 
$U_0\subset \mathbb {A}^N$ be the local scheme at 
$\pi _f (s)$. Since 
$\pi _f$ carries U into 
$U_0$, we have the following commutative diagram:
Here the restriction map 
$(-)\rvert _{U_0}$ is the zero map by the conclusion of Section 5.2.
Now toward the proof of Theorem 5.1, let
$$ \begin{align*} \Gamma \in C_1(X)(V) \end{align*} $$be an irreducible cycle. The commutative diagram shows that 
$ \left (\pi _f^*\pi _{f*} \Gamma \right )\rvert _U =0$ in 
$H_1(Q_\bullet (X))(U)$. In other words, we have
$$ \begin{align} \Gamma \rvert_U = \left(\Gamma - \pi _f^*\pi _{f*} \Gamma \right)\rvert_U \quad\text{in }H_1(Q_\bullet(X))(U). \end{align} $$This right-hand side turns out to be easier to handle.
Let 
$\overline \Gamma \subset V\times X\times \overline \Delta ^1$ be the closure and let 
$B(\Gamma )\subset V\times {\overline \Delta }^{1}$ be the bad locus in formula (5.1). By Lemma 5.2, we know it is a closed proper subset of 
$V\times \left \{ \infty \right \} $. Let 
$\overline B (\Gamma )\subsetneq V$ be its projection (which is isomorphic to 
$B(\Gamma )$).
Proposition 5.6. There is a closed proper subset 
$D_2\subsetneq M_{NN'}$ such that whenever 
$f\in M_{NN'}(k)\setminus (D_2\cup D_1)$, we have the equality of zero cycles:
$$ \begin{align} \pi _f^*\pi _{f*}s = s+\sum _{i=1}^m x_i \quad\text{on }V, \end{align} $$where 
$s,x_1,\dotsc ,x_m$ are distinct and 
$x_i\in V\setminus \overline B(\Gamma )$ for all i.
Proof. This can be shown using Chow’s techniques [Reference Chow8, pp. 458–460], [Reference Chevalley7, p. 3-08, Lemma 2]. We present a proof based on a more recent account [Reference Kai20].
First, since we are using the Veronese embedding (5.11), we can invoke [Reference Kai20, Propositions 3.2 and 3.3], which state that there is a closed proper subset 
$D'\subsetneq M_{NN'}$ such that for all 
$f\in M_{NN'}(k)\setminus (D'\cup D_1)$, the map 
$\pi _f\colon V\to \mathbb {A}^N $ is étale over 
$\pi _f(s)$ and the restriction 
$s\to \pi _f(s)$ is an isomorphism. This gives an equality of the form (5.14), with s and 
$x_i$s distinct.
It remains to show that 
$x_i\in V\setminus \overline B(\Gamma )$. We need the following statement:
Proposition 5.7 a special case of [Reference Kai20, Proposition 3.5]
Let 
$B\subset V$ be a proper closed subset and 
$s\in V$ a closed point. Then there is a closed proper subset 
$D''\subsetneq M_{NN'}$ such that for all 
$f\in M_{NN'}(k)\setminus D ''$, we have the equality of subsets of V:
$$ \begin{align*} \left(\pi _f^{-1}\pi _f (s) \setminus \{ s \} \right) \cap B = \emptyset. \end{align*} $$ (To extract Proposition 5.7 from [Reference Kai20, Proposition 3.5], set 
$X:= V$, 
$Y:= \operatorname {Spec} (k)$, 
$p=0$, 
$W:=B$ and 
$V:=\{ s \}$. Also note that the only topological space having dimension 
$\le -1$ is the empty set.)
Now set 
$D_2:= D'\cup D'' $ and suppose 
$f\in M_{NN'}(k)\setminus (D_1\cup D_2)$. Then we know 
$\pi _f^{-1}\pi _f (s) \setminus \{ s \} = \left \{ x_1,\dotsc ,x_m \right \}$, by the first half of this proof. Applying Proposition 5.7 to 
$B:= \overline B(\Gamma )$, we get the desired result. This completes the proof of Proposition 5.6.
Corollary 5.8. Take any 
$f\in M_{NN'}(k)\setminus (D_1\cup D_2)$ and form the fibre product 
$V\times _{\mathbb {A}^N} U$ of 
$\pi _f\colon V\to \mathbb {A}^N$ and 
$\pi _f\rvert _U \colon U\to \mathbb {A}^N$. Then it decomposes as
$$ \begin{align*} V\times _{\mathbb{A}^N }U \cong U\sqcup T, \end{align*} $$where 
$T $ is finite and étale over U by the second projection and maps into 
$V\setminus \overline B(\Gamma )$ along the first projection.
Proof. Since 
$\pi _f $ is finite and étale over 
$U_0$ by Proposition 5.6 and U maps into 
$U_0$, the second projection 
$V\times _{\mathbb {A}^N} U \to U$ is étale (and finite by default, because 
$f\in M_{NN'}(k)\setminus D_1$). Since it has the diagonal splitting 
$U\to V\times _{\mathbb {A}^N}U$, we have 
$V\times _{\mathbb {A}^N}U\cong U\sqcup T $. By Proposition 5.6, the set of its closed points can be computed as 
$V\times _{\mathbb {A}^N} \{ s \} \cong \left \{ s,x_1,\dotsc ,x_m \right \}$, with the right-hand side having the reduced structure, and we know that 
$x_i$s map into 
$V\setminus \overline B(\Gamma )$ by the first projection. This completes the proof.
Consider the following Cartesian diagram, where 
${\mathrm {Id}} $ denotes 
${\mathrm {Id}} _{X\times \Delta ^1}$:
The element 
$\left (\pi _f^*\pi _{f*} \Gamma \right )\rvert _U $ in equation (5.13) is represented by the cycle 
$\left (\left (\pi _f\rvert _U\right )\times {\mathrm {Id}} \right )^*\left (\pi _f \times {\mathrm {Id}} \right )_* \Gamma $ on 
$U\times X\times \Delta ^1$. By a slight abuse of notation, let us omit 
${\mathrm {Id}}$s from the notation in what follows; for example, the previous expression is shortened as 
$\left (\pi _f\rvert _U\right )^*\pi _{f*} \Gamma $. By the base-change formula for flat pullback and proper push-forward of algebraic cycles, we know this equals 
$\mathrm {pr} _{2*}\mathrm {pr} _1^*\Gamma $. Via the vertical isomorphism in diagram (5.15), if we write 
$\mathrm {pr} _{iU}$ and 
$\mathrm {pr} _{iT }$ (
$i=1,2$) for the restrictions of the projections, we get
$$ \begin{align} \left(\pi _f^*\pi _{f*} \Gamma \right)\rvert_U = \mathrm{pr} _{2U*}\mathrm{pr} _{1U} ^*\Gamma + \mathrm{pr} _{2T *}\mathrm{pr} _{1T } ^*\Gamma. \end{align} $$ We know that 
$\mathrm {pr} _{1U} \colon U\to V$ is the inclusion map and 
$\mathrm {pr} _{2U}\colon U\to U$ is the identity map. Thus the first term is 
$\Gamma \rvert _U$. Therefore we can compute the right-hand side in equation (5.13) as
$$ \begin{align} \left(\Gamma - \pi _f^*\pi _{f*} \Gamma \right)\rvert_U = -\mathrm{pr} _{2T *} \mathrm{pr} _{1T } ^*\Gamma. \end{align} $$ By Corollary 5.8, we know that 
$\mathrm {pr} _{1T }$ maps 
$T $ into 
$V\setminus \overline B(\Gamma ) \subset V$. In the resulting commutative diagram
we know that 
$\Gamma \rvert _{V\setminus \overline B(\Gamma )}$ belongs to the subgroup 
$ \overline C_1(X)\left (V\setminus \overline B(\Gamma )\right )$ by the definition of 
$B (\Gamma )$. It follows that 
$\mathrm {pr} _{1T }^*\Gamma \in \overline C_1(X)(T )$. Since 
$\mathrm {pr} _{2T }\colon T \to U$ is finite, we conclude 
$\mathrm {pr} _{2T *}\mathrm {pr} _{1T }^*\Gamma \in \overline C_1(X)(U)$.
Combined with equations (5.13) and (5.17), this shows that 
$\Gamma \rvert _U =0 $ in 
$H_1(Q_\bullet (X))(U)$. This completes the proof of Theorem 5.1.
6 The unramified cohomology $H_{\mathrm {ur}}^1\left (-, W_n\Omega ^j_{\log }\right )$
The aim of this short section is to prove Proposition 6.1.
Let X be a scheme over 
$\mathbb {F}_p$. For any integer 
$n\ge 1$, let 
$W_n\Omega ^{\bullet }_{X}$ denote the de Rham–Witt complex of 
$X/\mathbb {F}_p$ (see [Reference Illusie14, I, 1.3]). For any morphism of 
$\mathbb {F}_p$-schemes 
$f\colon Y\to X$, there exists a natural morphism of complexes of 
$W_n(\mathcal {O}_Y)$-modules,
$$ \begin{align} f^{-1}W_n\Omega_X^{\bullet}\to W_n\Omega_Y^{\bullet} \end{align} $$(see [Reference Illusie14, I, (1.12.3)]), which is an isomorphism if f is étale (see [Reference Illusie14, I, Proposition 1.14]).
For any 
$i\ge 0$, we denote by 
$W_n\Omega ^i_{X,\log }$ the logarithmic Hodge–Witt sheaf of X in the sense of [Reference Shiho26, Definition 2.6]. Namely, it is the étale sheaf on X defined as the image
$$ \begin{align*} W_n\Omega^i_{X,\log}:= \mathrm{im}\left(\left(\mathcal{O}_X^{\times}\right)^{\otimes i}\to W_n\Omega^i_X\right) \end{align*} $$of the map 
$\left (\mathcal {O}_X^{\times }\right )^{\otimes i}\to W_n\Omega ^i_X$; 
$x_1\otimes \dotsm \otimes x_i\mapsto d\log [x_1]\wedge \dotsb \wedge d\log [x_i]$, where 
$[x]\in W_n\mathcal {O}_X$ is the Teichmüller representative of any local section 
$x\in \mathcal {O}_X$. If 
$f\colon Y\to X$ is a morphism of 
$\mathbb {F}_p$-schemes, by the functoriality of the de Rham–Witt complexes (6.1) there exists a natural morphism of étale sheaves on Y,
$$ \begin{align} f^{-1}W_n\Omega_{X,\log}^i\to W_n\Omega^i_{Y,\log}. \end{align} $$Proposition 6.1. Fix 
$n>0$ and 
$i \ge 0$. We denote by 
$H_{\mathrm {ur}}^1\left (-, W_n \Omega ^i_{\log }\right )$ the Zariski sheaf on 
$\mathbf {Sm}$ associated to
$$ \begin{align*} H^1\left(-, W_n \Omega^i_{\log}\right) : X \mapsto H_{\mathrm{\acute{e}t}}^1\left(X, W_n \Omega^i_{X, \log}\right). \end{align*} $$Then 
$H_{\mathrm {ur}}^1\left (-, W_n \Omega ^i_{\log }\right )$ is a 
$\mathbb {P}^1$-invariant Nisnevich sheaf, and has a structure of presheaf with transfers.
Remark 6.2. As mentioned in the introduction, it is known that 
$H_{\mathrm {ur}}^1\left (-, W_n \Omega ^i_{\log }\right )$ has reciprocity [Reference Binda, Rülling and Saito5, Section 11.1 (5)], hence it is 
$\mathbb {P}^1$-invariant by [Reference Kahn, Saito and Yamazaki18, Theorem 8]. We shall give a direct proof of Proposition 6.1 which makes no use of the theory of reciprocity sheaves.
To ease the notation, for 
$q=0,1$ we set
$$ \begin{align*} F^{q,i} := H^q\left(-, W_n \Omega^i_{\log}\right), \qquad F^{q,i}_{\mathrm{ur}} := H^q_{\mathrm{ur}}\left(-, W_n \Omega^i_{\log}\right). \end{align*} $$We have 
$F^{q,i}(S)=F^{q,i}_{\mathrm {ur}}(S)$ for any local S.
Theorem 6.3. For any 
$X \in \mathbf {Sm}$ and any 
$q=0,1$, we have an exact sequence
$$ \begin{align*} 0 \to F^{q,i}_{\mathrm{ur}}(X) \to \bigoplus_{x \in X^{(0)}} F^{q,i}(x) \to \bigoplus_{x \in X^{(1)}} G^{q,i}_x(X), \end{align*} $$where we set 
$G_x^{q,i}(X):=H^{q+1}_x\left (X, W_n \Omega ^i_{X, \log }\right )$. Moreover, if 
$q=0$ there exists a canonical isomorphism
$$ \begin{align*} \theta^{i}_x\colon F^{0,i-1}(k(x))\xrightarrow{\simeq}G_x^{0,i}(X) \end{align*} $$for any codimension 
$1$ point 
$x\in X^{(1)}$.
Proof. For the first assertion, see [Reference Gros and Suwa12, Theorem 1.4] or [Reference Shiho26, Theorem 4.1]. For the last assertion, see [Reference Shiho26, Theorem 3.2].
Proposition 6.4. The étale sheaf 
$W_n\Omega _{\log }^i$ on 
$\mathbf {Sm}$ has a structure of presheaf with transfers. Hence so does the étale cohomology group 
$H^j\left (-,W_n\Omega _{\log }^i\right )$ for any 
$j\ge 0$.
Proof. According to [Reference Mazza, Voevodsky and Weibel22, 6.21], the second assertion is immediate from the first one. Therefore, it suffices to show that 
$W_n\Omega ^i_{\log }\in \mathbf {PST}$. However, thanks to Theorem 6.3 together with the theorem of Bloch, Gabber and Kato [Reference Bloch and Kato6], for any 
$X\in \mathbf {Sm}$ we have a natural exact sequence
$$ \begin{align*} 0\to H^0\left(X,W_n\Omega^i_{\log}\right)\to\bigoplus_{x \in X^{(0)}} K^{\textrm{M}}_i(k(x))/p^n \xrightarrow{\left(\partial^{\textrm{M}}_x\right)} \bigoplus_{x \in X^{(1)}}K_{i-1}^{\textrm{M}}(k(x))/p^n, \end{align*} $$where 
$\partial _x^{\textrm {M}}$ is the tame symbol at each 
$x\in X^{(1)}$. This implies that the sheaf 
$W_n\Omega ^i_{\log }$ has a structure of (homotopy-invariant) presheaf with transfers (see [Reference Kahn16]). This completes the proof of the proposition.
Proposition 6.5. Let 
$f : Y \to X$ be an étale morphism in 
$\mathbf {Sm}$ which induces an isomorphism 
$k(y) \cong k(x)$ for some 
$y \in Y^{(1)}$ and 
$x:=f(y)$. Then for 
$q=0,1$, in the commutative diagram
all maps are bijective.
Proof. For 
$q=0$, the assertion follows from the last claim of Theorem 6.3. So let us assume that 
$q=1$. Then the bijectivity of the left vertical map is a consequence of the localisation sequence
$$ \begin{align*} F^{1,i}\left(\mathcal{O}_{X, x}\right) \to F^{1,i}\left(\operatorname{Frac} \mathcal{O}_{X, x}\right) \to G_x^{1,i}(X) \to H^2\left(\mathcal{O}_{X, x}, W_n \Omega^i_{X, \log}\right)=0, \end{align*} $$and the same for the right vertical map. The statement for the upper horizontal map in the case when 
$n=1$ is a consequence of [Reference Totaro29, Theorem 4.3]. Indeed, given any discrete valuation ring over k, the cited theorem shows that there is an exhaustive filtration 
$F^{1,i}(R)=U_{-1} \subset U_0 \subset U_1 \subset \dotsb \subset F^{1,i}(\operatorname {Frac} R)$ whose graded quotients are described solely in terms of the residue field. In our situation, 
$F^{1,i}\left (\operatorname {Frac} \mathcal {O}_{X, x}\right ) \to F^{1,i}\left (\operatorname {Frac} \mathcal {O}_{Y, y}\right )$ respects this filtration because 
$\mathcal {O}_{X, x} \to \mathcal {O}_{Y, y}$ is étale. Hence the desired bijectivity follows from the assumption 
$k(y) \cong k(x)$. For 
$n>1$, thanks to the exact sequence
$$ \begin{align*} 0\to W_{n-1}\Omega^i_{X,\log}\to W_{n}\Omega^i_{X,\log}\to \Omega^i_{X,\log}\to 0 \end{align*} $$for any regular scheme X over 
$\mathbb {F}_p$ (see [Reference Shiho26, Proposition 2.12]), one can inductively see the bijectivity of the map 
$F^{1,i}\left (\operatorname {Frac} \mathcal {O}_{X, x}\right )/F^{1,i}\left (\mathcal {O}_{X, x}\right )\to F^{1,i}\left (\operatorname {Frac} \mathcal {O}_{Y, y}\right )/F^{1,i}\left (\mathcal {O}_{Y, y}\right )$. This completes the proof.
Proof of Proposition 6.1. We first show that 
$F^{1,i}_{\mathrm {ur}}$ is a sheaf for Nisnevich topology. For this, we take a Cartesian diagram in 
$\mathbf {Sm}$
where j is an open dense immersion and f is an étale morphism that is an isomorphism over 
$X \setminus j(U)$. By [Reference Mazza, Voevodsky and Weibel22, 12.7], it suffices to prove the exactness of the upper row in the commutative diagram
The second row is exact for obvious reason, and all columns are exact by Theorem 6.3. The map 
$(*)$ is injective by Proposition 6.5 (and the assumption on f). Now the claim follows by diagram chasing. As a consequence, we can find that 
$F^{1,i}_{{\mathrm {ur}}}$ is the same as the Nisnevich sheaf associated with 
$F^{1,i}\in \mathbf {PST}$ (see Proposition 6.4). Therefore, we conclude that 
$F^{1,i}_{\mathrm {ur}} \in \mathbf {PST}$ by [Reference Mazza, Voevodsky and Weibel22, 13.1].
Finally, to show that 
$F^{1,i}_{{\mathrm {ur}}}$ is 
$\mathbb {P}^1$-invariant, we apply Lemma 6.6. Condition (1) is due to Izhboldin [Reference Izhboldin15] (see also [Reference Totaro29, Theorem 4.4]), and (2) is a part of Theorem 6.3.
Lemma 6.6. Set 
$F \in \mathbf {PST}$. Suppose the following conditions hold:
(1) For any
$K \in \mathbf {Fld}_k^{\mathrm {gm}}$, $\sigma _K^* : F(\operatorname {Spec} K) \cong F\left (\mathbb {P}^1_K\right )$ is an isomorphism, where $\sigma _K$ denotes the base change of the structure morphism $\sigma : \mathbb {P}^1 \to \operatorname {Spec} k$.(2) Any open immersion
$U \hookrightarrow V$ in $\mathbf {Sm}$ induces an injection $F(V) \to F(U)$.
Then F is 
$\mathbb {P}^1$-invariant.
Proof. Define 
$G \in \mathbf {PST}$ by the formula
$$ \begin{align} G(U) := \operatorname{Coker}\left(\sigma^* : F(U) \to \operatorname{\underline{Hom}}\left(\mathbb{Z}_{\mathrm{tr}}\left(\mathbb{P}^1\right), F\right)(U)=F\left(U \times \mathbb{P}^1\right)\right) \quad (U \in \mathbf{Sm}). \end{align} $$We have a direct sum decomposition 
$\operatorname {\underline {Hom}}\left (\mathbb {Z}_{\mathrm {tr}}\left (\mathbb {P}^1\right ), F\right ) \cong F \oplus G$ (provided by a k-rational point of 
$\mathbb {P}^1$), and 
$G(U)=0$ holds if and only if the map in formula (6.3) is an isomorphism. By (1), we have 
$G(\operatorname {Spec} K)=0$ for any 
$K \in \mathbf {Fld}_k^{\mathrm {gm}}$. Property (2) for F implies the same property for 
$\operatorname {\underline {Hom}}\left (\mathbb {Z}_{\mathrm {tr}}\left (\mathbb {P}^1\right ), F\right )$ and hence for G. We conclude that 
$G(U) \hookrightarrow G(k(U))=0$ for any (irreducible) 
$U \in \mathbf {Sm}$, which means F is 
$\mathbb {P}^1$-invariant.
A Proof of Remark 2.5
We give a proof of Remark 2.5. Property (1) is obvious. Property (2) is a consequence of the formula 
$h_0(X \times X')=h_0(X) \otimes h_0(X')$. For (3) and (4), we shall freely use Voevodsky’s triangulated category 
$\operatorname {\mathbf {DM}}^-_{\mathrm {eff}}(k) \subset D^-(\mathbf {NST})$ of effective motivic complexes over k [Reference Voevodsky31]. For 
$V \in \mathbf {Sm}$, we denote the motivic complex of V by 
$M(V):=C_*(\mathbb {Z}_{\mathrm {tr}}(V)) \in \operatorname {\mathbf {DM}}^-_{\mathrm {eff}}(k)$. Recall that its homology sheaves 
$h_n(V):=H_n(M(V))$ are trivial if 
$n<0$, and for 
$n=0$ it recovers 
$h_0(V)$ defined in (V2).
Lemma A.1. Let 
$c>0$ be a positive integer and let 
$j : U \to X$ be an open immersion in 
$\mathbf {Sm}$. Define 
$M(X/U)$ to be the cone of 
$j_*:M(U) \to M(X)$. If each component of 
$Z := (X \setminus U)_{\mathrm {red}}$ is of codimension 
$\ge c$ in X, then 
$h_n(X/U):=H_n(M(X/U))$ vanishes for any 
$n<c$.
Proof. If Z is smooth over k, then by the Gysin triangle [Reference Mazza, Voevodsky and Weibel22, Theorem 15.15] we have
$$ \begin{align*} M(X/U) \cong M(Z)(c)[2c] \cong M(Z) \otimes (\mathbb{G}_m[0])^{\otimes c}[c], \end{align*} $$from which the statement follows. In general, let 
$Z' \subset Z$ be the singular locus of Z, and define 
$U':=X \setminus Z'$. There is a distinguished triangle
$$ \begin{align*} M(U'/U) \to M(X/U) \to M(X/U') \to M(U'/U)[1]. \end{align*} $$Since each component of 
$Z'$ has codimension 
$\ge c+1$ in X, we may assume 
$h_n(X/U')=0$ for any 
$n \le c$ by induction. Since 
$U' \setminus U = Z \setminus Z'$ is smooth over k, we have shown 
$h_n(U'/U)=0$ for 
$n<c$. It follows that 
$h_n(X/U)=0$ for 
$n<c$.
Now (3) immediately follows from Lemma A.1. To show (4), let 
$f : X \to Y$ be a proper birational morphism in 
$\mathbf {Sm}$. Let 
$V \subset Y$ be the open dense subset on which 
$f^{-1}$ is defined. Then f restricts to an isomorphism 
$U:=f^{-1}(V) \overset {\cong }{\longrightarrow } V$ and 
$Y \setminus V$ has codimension 
$\ge 2$ in Y. We have a commutative diagram
in which we used Lemma A.1 for the vanishing. This proves (4).
Acknowledgments
The second author would like to thank Tomoyuki Abe for fruitful discussions and suggestions, which brought him into Voevodsky’s theory of motives. Without that, this joint project would have never started. The authors thank Bruno Kahn for his intriguing comments on birational sheaves.
The first author is supported by a JSPS KAKENHI Grant (JP18K13382). The second author is supported by JSPS KAKENHI Grants (JP19J00366, JP21K20334). The third author is supported by JSPS KAKENHI Grants (JP18K03232, JP21K03153).
Conflict of Interest
None.
Open access
