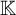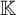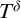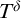1. Introduction
Let
![]() ${\mathbb K}$
be a structure expanding a field of characteristic 0. Recall that
${\mathbb K}$
be a structure expanding a field of characteristic 0. Recall that
![]() ${\mathbb K}$
is algebraically bounded if the model-theoretic algebraic closure and the field-theoretic algebraic closure coincide in every structure elementarily equivalent to
${\mathbb K}$
is algebraically bounded if the model-theoretic algebraic closure and the field-theoretic algebraic closure coincide in every structure elementarily equivalent to
![]() ${\mathbb K}$
. Algebraically closed, real closed, p-adically closed, pseudo-finite fields, and algebraically closed valued fields are examples of algebraically bounded structures; for more details, examples, and main properties, see [Reference van den Dries10] and Section 2. Van den Dries in his paper introduced a notion of dimension for any definable set with parameters, which is relevant in our context.
${\mathbb K}$
. Algebraically closed, real closed, p-adically closed, pseudo-finite fields, and algebraically closed valued fields are examples of algebraically bounded structures; for more details, examples, and main properties, see [Reference van den Dries10] and Section 2. Van den Dries in his paper introduced a notion of dimension for any definable set with parameters, which is relevant in our context.
Let L be the language of
![]() ${\mathbb K}$
, and let T be its theory. In order to study derivations on
${\mathbb K}$
, and let T be its theory. In order to study derivations on
![]() ${\mathbb K}$
, we denote by
${\mathbb K}$
, we denote by
![]() $\delta $
a new unary function symbol, and by
$\delta $
a new unary function symbol, and by
![]() $T^{\delta }$
the
$T^{\delta }$
the
![]() $L^\delta $
-theory expanding T by saying that
$L^\delta $
-theory expanding T by saying that
![]() $\delta $
is a derivation. Let
$\delta $
is a derivation. Let
![]() ${\mathbb K}$
be algebraically bounded. We remark that being algebraically bounded is not a first-order notion (since an ultraproduct of algebraically bounded structures is not necessarily algebraically bounded). We define an
${\mathbb K}$
be algebraically bounded. We remark that being algebraically bounded is not a first-order notion (since an ultraproduct of algebraically bounded structures is not necessarily algebraically bounded). We define an
![]() $L^\delta $
-theory
$L^\delta $
-theory
![]() $T^{\delta }_g$
extending
$T^{\delta }_g$
extending
![]() $T^{\delta }$
, with three equivalent axiomatizations (see Sections 3 and 7); one of them is given by
$T^{\delta }$
, with three equivalent axiomatizations (see Sections 3 and 7); one of them is given by
![]() $T^{\delta }$
, plus the following axiom scheme:
$T^{\delta }$
, plus the following axiom scheme:
-
For every
 $X \subseteq {\mathbb K}^{n} \times {\mathbb K}^{n}$
which is L-definable with parameters, if the dimension of the projection of X onto the first n coordinates, which we denote by
$X \subseteq {\mathbb K}^{n} \times {\mathbb K}^{n}$
which is L-definable with parameters, if the dimension of the projection of X onto the first n coordinates, which we denote by
 $\Pi _{n}(X),$
is n, then there exists
$\Pi _{n}(X),$
is n, then there exists
 $\bar a \in {\mathbb K}^{n}$
such that
$\bar a \in {\mathbb K}^{n}$
such that
 $\langle \bar a, \delta \bar a \rangle \in X$
.
$\langle \bar a, \delta \bar a \rangle \in X$
.
One of the main result of the paper is the following:
Theorem 1.1. If T is model complete, then
![]() $T^{\delta }_g$
is the model completion of
$T^{\delta }_g$
is the model completion of
![]() $T^{\delta }$
.
$T^{\delta }$
.
We also endow
![]() ${\mathbb K}$
with several derivations
${\mathbb K}$
with several derivations
![]() $\delta _{1}, \dotsc , \delta _{m}$
and we consider both the case when they commute and when we don’t impose any commutativity. We obtain two theories:
$\delta _{1}, \dotsc , \delta _{m}$
and we consider both the case when they commute and when we don’t impose any commutativity. We obtain two theories:
-
 $T^{\bar \delta }$
: the expansion of T saying that the
$T^{\bar \delta }$
: the expansion of T saying that the
 $\delta _{i}$
are derivations which commute with each other.
$\delta _{i}$
are derivations which commute with each other. -
 $T^{\bar \delta ,nc}$
: the expansion of T saying that the
$T^{\bar \delta ,nc}$
: the expansion of T saying that the
 $\delta _{i}$
are derivations without any further conditions.
$\delta _{i}$
are derivations without any further conditions.
Both theories have a model completion (if T is model complete) (see Sections 4 and 5). For convenience, we use
![]() $T^{\bar \delta ,?}_g$
to denote either of the model completions, both for commuting derivations and the non-commuting case. Many of the model-theoretic properties of T are inherited by
$T^{\bar \delta ,?}_g$
to denote either of the model completions, both for commuting derivations and the non-commuting case. Many of the model-theoretic properties of T are inherited by
![]() $T^{\bar \delta ,?}_g$
:
$T^{\bar \delta ,?}_g$
:
Theorem 1.2 (Section 6)
Assume that T is stable/NIP. Then
![]() $T^{\bar \delta ,?}_g$
is stable/NIP.
$T^{\bar \delta ,?}_g$
is stable/NIP.
In a work in preparation, we will prove that if T is simple, then
![]() $T^{\bar \delta ,?}_g$
is simple (see [Reference Mohamed33, Reference Moosa and Scanlon36] for particular cases); we will also characterize when
$T^{\bar \delta ,?}_g$
is simple (see [Reference Mohamed33, Reference Moosa and Scanlon36] for particular cases); we will also characterize when
![]() $T^{\bar \delta ,?}_g$
is
$T^{\bar \delta ,?}_g$
is
![]() $\omega $
-stable. Moreover, we will prove that
$\omega $
-stable. Moreover, we will prove that
![]() $T^{\bar \delta ,?}_g$
is uniformly finite. Finally, if
$T^{\bar \delta ,?}_g$
is uniformly finite. Finally, if
![]() ${\mathbb K}$
extends either a Henselian valued field with a definable valuation or a real closed field, then, under some additional assumptions, T is the open core of
${\mathbb K}$
extends either a Henselian valued field with a definable valuation or a real closed field, then, under some additional assumptions, T is the open core of
![]() $T^{\bar \delta ,?}_g$
.
$T^{\bar \delta ,?}_g$
.
On the other hand, in [Reference Fornasiero and Terzo15] we show that exponential fields do not admit generic derivations (notice that exponential fields are not algebraically bounded).
1.1. A brief model theoretic history
From a model theoretic point of view, differential fields have been studied at least since Robinson [Reference Robinson45] proved that the theory of fields of characteristic 0 with one derivation has a model completion, the theory
![]() $\textrm {DCF}_{0}$
of differentially closed fields of characteristic
$\textrm {DCF}_{0}$
of differentially closed fields of characteristic
![]() $0$
.
$0$
.
Blum gave a simpler sets of axioms for
![]() $\textrm {DCF}_{0}$
, saying that
$\textrm {DCF}_{0}$
, saying that
![]() ${\mathbb K}$
is a field of characteristic
${\mathbb K}$
is a field of characteristic
![]() $0$
, and, whenever p and q are differential polynomials in one variable, with q not zero and of order strictly less than the order of p, then there exists a in
$0$
, and, whenever p and q are differential polynomials in one variable, with q not zero and of order strictly less than the order of p, then there exists a in
![]() ${\mathbb K}$
such that
${\mathbb K}$
such that
![]() $p(a) = 0$
and
$p(a) = 0$
and
![]() $q(a) \neq 0$
(see [Reference Blum, Bass, Cassidy and Kovacic2, Reference Sacks46] for more details). Pierce and Pillay [Reference Pierce and Pillay39] gave yet another axiomatization for
$q(a) \neq 0$
(see [Reference Blum, Bass, Cassidy and Kovacic2, Reference Sacks46] for more details). Pierce and Pillay [Reference Pierce and Pillay39] gave yet another axiomatization for
![]() $\textrm {DCF}_{0}$
, which has been influential in the axiomatizations of other structures (see Section 7).
$\textrm {DCF}_{0}$
, which has been influential in the axiomatizations of other structures (see Section 7).
The theory
![]() $\textrm {DCF}_{0}$
(and its models) has been studied intensively, both for its own sake, for applications, and as an important example of many “abstract” model theoretic properties: it is
$\textrm {DCF}_{0}$
(and its models) has been studied intensively, both for its own sake, for applications, and as an important example of many “abstract” model theoretic properties: it is
![]() $\omega $
-stable of rank
$\omega $
-stable of rank
![]() $\omega $
, it eliminates imaginaries, it is uniformly finite, etc. For some surveys, see [Reference Blum, Bass, Cassidy and Kovacic2, Reference Chatzidakis, Villaveces, Hirvonen, Kontinen, Kossak and Villaveces6, Reference Hart and Valeriote20, Reference Marker, Messmer and Pillay31, Reference Moosa35].
$\omega $
, it eliminates imaginaries, it is uniformly finite, etc. For some surveys, see [Reference Blum, Bass, Cassidy and Kovacic2, Reference Chatzidakis, Villaveces, Hirvonen, Kontinen, Kossak and Villaveces6, Reference Hart and Valeriote20, Reference Marker, Messmer and Pillay31, Reference Moosa35].
Models of
![]() $\textrm {DCF}_{0}$
, as fields, are algebraically closed fields of characteristic
$\textrm {DCF}_{0}$
, as fields, are algebraically closed fields of characteristic
![]() $0$
; their study has been extended in several directions. An important extension, which however goes beyond the scope of this article, is Wood’s work [Reference Wood55] on fields of finite characteristic.
$0$
; their study has been extended in several directions. An important extension, which however goes beyond the scope of this article, is Wood’s work [Reference Wood55] on fields of finite characteristic.
From now on, all fields are of characteristic
![]() $0$
. More close to the goal of this article is the passage from one derivation to several commuting ones: McGrail [Reference McGrail32] axiomatized
$0$
. More close to the goal of this article is the passage from one derivation to several commuting ones: McGrail [Reference McGrail32] axiomatized
![]() $\textrm {DCF}_{0,\textrm {m}}$
(the model completion of the theory of fields of characteristic 0 with m commuting derivations). While the axiomatization is complicate (see Section 5 for an easier axiomatization, and [Reference León Sánchez27, Reference Pierce38] for alternative ones), from a model theoretic point of view
$\textrm {DCF}_{0,\textrm {m}}$
(the model completion of the theory of fields of characteristic 0 with m commuting derivations). While the axiomatization is complicate (see Section 5 for an easier axiomatization, and [Reference León Sánchez27, Reference Pierce38] for alternative ones), from a model theoretic point of view
![]() $\textrm {DCF}_{0,\textrm {m}}$
is quite similar to
$\textrm {DCF}_{0,\textrm {m}}$
is quite similar to
![]() $\textrm {DCF}_{0}$
: its models are algebraically closed (as fields), it is
$\textrm {DCF}_{0}$
: its models are algebraically closed (as fields), it is
![]() $\omega $
-stable of rank
$\omega $
-stable of rank
![]() $\omega ^{m}$
, it eliminates imaginaries, it is uniformly finite, etc.
$\omega ^{m}$
, it eliminates imaginaries, it is uniformly finite, etc.
Moosa and Scanlon followed a different path in [Reference Moosa and Scanlon36], where they studied a general framework of fields with non-commuting operators; for this introduction, the relevant application is that they proved that the theory of m non-commuting derivations has a model completion (see [Reference Moosa and Scanlon36] and Section 4), which we denote by
![]() $\textrm {DCF}_{0,\textrm {m,nc}}$
. Here the model theory is more complicate:
$\textrm {DCF}_{0,\textrm {m,nc}}$
. Here the model theory is more complicate:
![]() $\textrm {DCF}_{0,\textrm {m,nc}}$
is stable, but not
$\textrm {DCF}_{0,\textrm {m,nc}}$
is stable, but not
![]() $\omega $
-stable; however, it still eliminates imaginaries and it is uniformly finite.
$\omega $
-stable; however, it still eliminates imaginaries and it is uniformly finite.
Surprisingly, we can give three axiomatizations for
![]() $\textrm {DCF}_{0,\textrm {m,nc}}$
which are much simpler than the known axiomatizations for
$\textrm {DCF}_{0,\textrm {m,nc}}$
which are much simpler than the known axiomatizations for
![]() $\textrm {DCF}_{0,\textrm {m}}$
(including the one given in this article), see Sections 4 and 7. We guess that the reason why this has not been observed before is that people were deceived by the rich algebraic structure of
$\textrm {DCF}_{0,\textrm {m}}$
(including the one given in this article), see Sections 4 and 7. We guess that the reason why this has not been observed before is that people were deceived by the rich algebraic structure of
![]() $\textrm {DCF}_{0,\textrm {m}}$
.
$\textrm {DCF}_{0,\textrm {m}}$
.
Indeed, from an algebraic point of view,
![]() $\textrm {DCF}_{0,\textrm {m}}$
has been studied extensively (see [Reference Kolchin25] for a starting point) and is much simpler than
$\textrm {DCF}_{0,\textrm {m}}$
has been studied extensively (see [Reference Kolchin25] for a starting point) and is much simpler than
![]() $\textrm {DCF}_{0,\textrm {m,nc}}.$
The underlying combinatorial fact is that the free commutative monoid on m generators
$\textrm {DCF}_{0,\textrm {m,nc}}.$
The underlying combinatorial fact is that the free commutative monoid on m generators
![]() $\Theta $
, with the partial ordering given by
$\Theta $
, with the partial ordering given by
![]() $\alpha \preceq \beta \alpha $
for every
$\alpha \preceq \beta \alpha $
for every
![]() $\alpha , \beta \in \Theta $
, is a well-partial-order (by Dickson’s Lemma); this fact is a fundamental ingredient in Ritt–Raudenbush Theorem, asserting that there is no infinite ascending chain of radical differential ideals in the ring of differential polynomials with m commuting derivations with coefficients in some differential field; moreover, every radical differential ideal is a finite intersection of prime differential ideals. Since in models of
$\alpha , \beta \in \Theta $
, is a well-partial-order (by Dickson’s Lemma); this fact is a fundamental ingredient in Ritt–Raudenbush Theorem, asserting that there is no infinite ascending chain of radical differential ideals in the ring of differential polynomials with m commuting derivations with coefficients in some differential field; moreover, every radical differential ideal is a finite intersection of prime differential ideals. Since in models of
![]() $\textrm {DCF}_{0,\textrm {m}}$
there is a natural bijection between prime differential ideals and complete types, this in turns implies that
$\textrm {DCF}_{0,\textrm {m}}$
there is a natural bijection between prime differential ideals and complete types, this in turns implies that
![]() $\textrm {DCF}_{0,\textrm {m}}$
is
$\textrm {DCF}_{0,\textrm {m}}$
is
![]() $\omega $
-stable as we mentioned before.
$\omega $
-stable as we mentioned before.
Very different is the situation for the free monoid on m generators
![]() $\Gamma $
, with the same partial ordering.
$\Gamma $
, with the same partial ordering.
![]() $\Gamma $
is well-founded, but (when m is at least 2) not a well-partial-order. Given an infinite anti-chain in
$\Gamma $
is well-founded, but (when m is at least 2) not a well-partial-order. Given an infinite anti-chain in
![]() $\Gamma $
, it is easy to build an infinite ascending chain of radical differential ideals (in the corresponding ring of non-commuting differential polynomials), and therefore Ritt–Raudenbush does not hold in this situation.
$\Gamma $
, it is easy to build an infinite ascending chain of radical differential ideals (in the corresponding ring of non-commuting differential polynomials), and therefore Ritt–Raudenbush does not hold in this situation.
Some limited form of non-commutativity was considered already in [Reference Pierce38, Reference Singer53, Reference Yaffe56], where the derivations live in a finite-dimensional Lie algebra.
People have extended
![]() $\textrm {DCF}_{0}$
in another direction by considering fields which are not algebraically closed: Singer, and later others [Reference Brihaye, Michaux and Rivière4, Reference Brouette, Kovacsics and Point5, Reference Point41, Reference Rivière44, Reference Singer52] studied real closed fields with one generic derivation, and [Reference Rivière43] extended to m commuting derivations (see also [Reference Fornasiero and Kaplan14] for a different approach); [Reference Cubides Kovacsics and Point8, Reference Guzy and Point17–Reference Guzy and Rivière19] studied more general topological fields with one generic derivation. In [Reference Rivière42] the author studied fields with m independent orderings and one generic derivation and in [Reference Fornasiero and Kaplan14] they studied o-minimal structures with several commuting generic “compatible” derivations. In her Ph.D. thesis, Borrata [Reference Borrata3] studied ordered valued fields and “tame” pairs of real closed fields endowed with one generic derivation.
$\textrm {DCF}_{0}$
in another direction by considering fields which are not algebraically closed: Singer, and later others [Reference Brihaye, Michaux and Rivière4, Reference Brouette, Kovacsics and Point5, Reference Point41, Reference Rivière44, Reference Singer52] studied real closed fields with one generic derivation, and [Reference Rivière43] extended to m commuting derivations (see also [Reference Fornasiero and Kaplan14] for a different approach); [Reference Cubides Kovacsics and Point8, Reference Guzy and Point17–Reference Guzy and Rivière19] studied more general topological fields with one generic derivation. In [Reference Rivière42] the author studied fields with m independent orderings and one generic derivation and in [Reference Fornasiero and Kaplan14] they studied o-minimal structures with several commuting generic “compatible” derivations. In her Ph.D. thesis, Borrata [Reference Borrata3] studied ordered valued fields and “tame” pairs of real closed fields endowed with one generic derivation.
The results in [Reference Cubides Kovacsics and Point8, Reference Guzy and Point17, Reference Guzy and Point18, Reference Rivière42, Reference Rivière43] extend the one in [Reference Singer52] and are mostly subsumed in this article (because the structures they study are mostly algebraically bounded).
Tressl in [Reference Tressl54] studied generic derivations on fields that are “large” in the sense of Pop, and Mohamed in [Reference Mohamed33] extended his work to operators in the sense of [Reference Moosa and Scanlon36]. They assume that their fields are model-complete in the language of rings with additional constants, and therefore they are algebraically bounded (see [Reference Junker and Koenigsmann24, Theorem 5.4]).Footnote 1 Thus, our results extend their result on the existence of a model companion for large fields with finitely many derivations (either commuting as in [Reference Tressl54] or non-commuting as in [Reference Mohamed33]). Moreover, in this paper we consider fields which are not pure fields, such as algebraically closed valued fields (see Section 2 for more examples).
It turns out that, while in practice many of the fields studied in model theory are both large and algebraically bounded (and therefore their generic derivations can be studied by using either our framework or the one of Tressl et al.), there exist large fields which are not algebraically bounded (the field
![]() $\mathbb C((X,Y))$
is large but not algebraically bounded, see [Reference Fehm12, Example 8]), and there exist algebraically bounded fields which are not large (see [Reference Johnson and Ye23]). Tressl and Leòn Sánchez [Reference León Sánchez and Tressl29, Reference León Sánchez and Tressl30] later introduce the notion of “differentially large fields”.
$\mathbb C((X,Y))$
is large but not algebraically bounded, see [Reference Fehm12, Example 8]), and there exist algebraically bounded fields which are not large (see [Reference Johnson and Ye23]). Tressl and Leòn Sánchez [Reference León Sánchez and Tressl29, Reference León Sánchez and Tressl30] later introduce the notion of “differentially large fields”.
Often the fields considered have a topology (e.g., they are ordered fields or valued fields): however, the theories described above do not impose any continuity on the derivation (and the corresponding “generic” derivations are not continuous at any point). In [Reference Scanlon47, Reference Scanlon48] and [Reference Aschenbrenner, van den Dries and van der Hoeven1] the authors consider the case of a valued field endowed with a “monotone” derivation (i.e., a derivation
![]() $\delta $
such that
$\delta $
such that
![]() $v(\delta x) \geq v(x);$
in particular,
$v(\delta x) \geq v(x);$
in particular,
![]() $\delta $
is continuous) and prove a corresponding Ax–Kochen–Ersov principle.
$\delta $
is continuous) and prove a corresponding Ax–Kochen–Ersov principle.
2. Algebraically boundedness and dimension
We fix an L-structure
![]() ${\mathbb K}$
expanding a field of characteristic
${\mathbb K}$
expanding a field of characteristic
![]() $0$
.
$0$
.
We recall the following definition in [Reference van den Dries10], as refined in [Reference Johnson and Ye23]:
Definition 2.1. Let F be a subring of
![]() ${\mathbb K}$
. We say that
${\mathbb K}$
. We say that
![]() ${\mathbb K}$
is algebraically bounded over F if, for any formula
${\mathbb K}$
is algebraically bounded over F if, for any formula
![]() $\phi (\bar x, y)$
, there exist finitely many polynomials
$\phi (\bar x, y)$
, there exist finitely many polynomials
![]() $p_1, \ldots , p_m \in F[\bar x, y]$
such that for any
$p_1, \ldots , p_m \in F[\bar x, y]$
such that for any
![]() $\bar a,$
if
$\bar a,$
if
![]() $\phi (\bar a, {\mathbb K})$
is finite, then
$\phi (\bar a, {\mathbb K})$
is finite, then
![]() $\phi (\bar a, {\mathbb K})$
is contained in the zero set of
$\phi (\bar a, {\mathbb K})$
is contained in the zero set of
![]() $p_i(\bar a, y)$
for some i such that
$p_i(\bar a, y)$
for some i such that
![]() $p_i(\bar a, y)$
doesn’t vanish.
$p_i(\bar a, y)$
doesn’t vanish.
![]() ${\mathbb K}$
is algebraically bounded if it is algebraically bounded over
${\mathbb K}$
is algebraically bounded if it is algebraically bounded over
![]() ${\mathbb K}$
.
${\mathbb K}$
.
Since we assumed that
![]() ${\mathbb K}$
has characteristic
${\mathbb K}$
has characteristic
![]() $0$
, in the above definition we can replace “
$0$
, in the above definition we can replace “
![]() $p_i(\bar a, y)$
doesn’t vanish” with the following:
$p_i(\bar a, y)$
doesn’t vanish” with the following:
“
![]() $p_i(\bar a, b) = 0$
and
$p_i(\bar a, b) = 0$
and
![]() $\frac {\partial p_{i}}{\partial y}(\bar a, b) \neq 0$
”.
$\frac {\partial p_{i}}{\partial y}(\bar a, b) \neq 0$
”.
Fact 2.2 [Reference Johnson and Ye23], see also [Reference Fornasiero13]
-
(1)
 ${\mathbb K}$
is algebraically bounded iff it is algebraically bounded over
${\mathbb K}$
is algebraically bounded iff it is algebraically bounded over  .
. -
(2)
 ${\mathbb K}$
is algebraically bounded over F iff the model theoretic algebraic closure coincide with the field theoretic algebraic closure over F in every elementary extension of
${\mathbb K}$
is algebraically bounded over F iff the model theoretic algebraic closure coincide with the field theoretic algebraic closure over F in every elementary extension of
 ${\mathbb K}$
(it suffices to check it in the monster model).
${\mathbb K}$
(it suffices to check it in the monster model).
Remark 2.3. Junker and Koenigsmann in [Reference Junker and Koenigsmann24] defined
![]() ${\mathbb K}$
to be “very slim” if in the monster model the field-theoretic algebraic closure over the prime field coincide with the model-theoretic algebraic closure: thus,
${\mathbb K}$
to be “very slim” if in the monster model the field-theoretic algebraic closure over the prime field coincide with the model-theoretic algebraic closure: thus,
![]() ${\mathbb K}$
is very slim iff
${\mathbb K}$
is very slim iff
![]() ${\mathbb K}$
is algebraically bounded over
${\mathbb K}$
is algebraically bounded over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Let ![]() and we consider
and we consider
![]() ${\mathbb K}$
algebraically bounded over F.
${\mathbb K}$
algebraically bounded over F.
When we refer to the algebraic closure, unless specified otherwise, we will mean the T-algebraic closure; similarly,
![]() $\operatorname {\mathrm {acl}}$
will be the T-algebraic closure, and by “algebraically independent” we will mean according to T (or equivalently algebraically independent over F in the field-theoretic meaning).
$\operatorname {\mathrm {acl}}$
will be the T-algebraic closure, and by “algebraically independent” we will mean according to T (or equivalently algebraically independent over F in the field-theoretic meaning).
From the assumptions it follows that
![]() ${\mathbb K}$
is geometric: that is, in the monster model
${\mathbb K}$
is geometric: that is, in the monster model
![]() $\mathbb M \succ {\mathbb K}$
, the algebraic closure has the exchange property, and therefore it is a matroid; moreover, T is Uniformly Finite, that is it eliminates the quantifier
$\mathbb M \succ {\mathbb K}$
, the algebraic closure has the exchange property, and therefore it is a matroid; moreover, T is Uniformly Finite, that is it eliminates the quantifier
![]() $\exists ^{\infty }$
. In fact, a definable set
$\exists ^{\infty }$
. In fact, a definable set
![]() $X \subseteq {\mathbb K}$
is infinite iff for all
$X \subseteq {\mathbb K}$
is infinite iff for all
![]() $a \in K$
there exist
$a \in K$
there exist
![]() $x, y, x', y' \in X$
such that
$x, y, x', y' \in X$
such that
![]() $x \not = x'$
and
$x \not = x'$
and
![]() $a = (y-y')/(x'-x);$
(see [Reference Fornasiero13, Reference Johnson and Ye23]).
$a = (y-y')/(x'-x);$
(see [Reference Fornasiero13, Reference Johnson and Ye23]).
Moreover,
![]() ${\mathbb K}$
is endowed with a dimension function
${\mathbb K}$
is endowed with a dimension function
![]() $\dim ,$
associating to every set X definable with parameters some natural number, satisfying the axioms in [Reference van den Dries10]. This function
$\dim ,$
associating to every set X definable with parameters some natural number, satisfying the axioms in [Reference van den Dries10]. This function
![]() $\dim $
is invariant under automorphisms of the ambient structure: equivalently,
$\dim $
is invariant under automorphisms of the ambient structure: equivalently,
![]() $\dim $
is “code-definable” in the sense of [Reference Brouette, Kovacsics and Point5].
$\dim $
is “code-definable” in the sense of [Reference Brouette, Kovacsics and Point5].
We will also use the rank, denoted by
![]() $\operatorname {\mathrm {rk}},$
associated with the matroid
$\operatorname {\mathrm {rk}},$
associated with the matroid
![]() $\operatorname {\mathrm {acl}}$
:
$\operatorname {\mathrm {acl}}$
:
![]() $\operatorname {\mathrm {rk}}(V/B)$
is the cardinality of a basis of V over B. Thus, if
$\operatorname {\mathrm {rk}}(V/B)$
is the cardinality of a basis of V over B. Thus, if
![]() $X \subseteq \mathbb M^{n}$
is definable with parameters
$X \subseteq \mathbb M^{n}$
is definable with parameters
![]() $\bar b$
,
$\bar b$
,
2.1. Examples
Some well known examples of fields which are algebraically bounded structures as pure fields are: algebraically closed fields, p-adics and more generally Henselian fields (see [Reference Junker and Koenigsmann24, Theorem 5.5]), real closed fields, pseudo-finite fields; curve-excluding fields in the sense of [Reference Johnson and Ye22] are also algebraically bounded. Other examples of algebraically bounded structures which are not necessarily pure fields are:
-
• Algebraically closed valued fields.
-
• Henselian fields (of characteristic 0) with arbitrary relations on the value group and the residue field (see [Reference van den Dries10]).
-
• All models of “open theories of topological fields”, as defined in [Reference Cubides Kovacsics and Point8].
-
• The expansion of an algebraically bounded structure by a generic predicate (in the sense of [Reference Chatzidakis and Pillay7]) is still algebraically bounded (see [Reference Chatzidakis and Pillay7, Corollary 2.6]).
-
• The theory of fields with several independent orderings and valuations has a model companion, whose models are algebraically bounded (see [Reference van den Dries and van Dalen9], [Reference Johnson21, Corollary 3.12]).
Johnson and Ye in a recent paper [Reference Johnson and Ye22] produced examples of an infinite algebraically bounded field with a decidable first-order theory which is not large (in the Pop sense), and of a pure field that is algebraically bounded but not very slim.
2.2. Assumptions
Our assumptions for the whole article are the following:
-
•
 ${\mathbb K}$
is a structure expanding a field of characteristic
${\mathbb K}$
is a structure expanding a field of characteristic
 $0$
.
$0$
. -
• L is the language of
 ${\mathbb K}$
and T is its L-theory.
${\mathbb K}$
and T is its L-theory. -
•
 .
. -
•
 ${\mathbb K}$
is algebraically bounded over F.
${\mathbb K}$
is algebraically bounded over F. -
•
 $\dim $
is the dimension function on
$\dim $
is the dimension function on
 ${\mathbb K}$
(or on any model of T),
${\mathbb K}$
(or on any model of T),
 $\operatorname {\mathrm {acl}}$
is the T-algebraic closure, and
$\operatorname {\mathrm {acl}}$
is the T-algebraic closure, and
 $\operatorname {\mathrm {rk}}$
the rank of the corresponding matroid.
$\operatorname {\mathrm {rk}}$
the rank of the corresponding matroid.
3. Generic derivation
We fix a derivation
![]() $\eta : F \to F$
(if F is contained in the algebraic closure of
$\eta : F \to F$
(if F is contained in the algebraic closure of
![]() $\mathbb {Q}$
in
$\mathbb {Q}$
in
![]() ${\mathbb K}$
, that we denote by
${\mathbb K}$
, that we denote by
![]() $\overline {\mathbb {Q}},$
then
$\overline {\mathbb {Q}},$
then
![]() $\eta $
must be equal to
$\eta $
must be equal to
![]() $0$
). We denote by
$0$
). We denote by
![]() $T^{\delta }$
the expansion of T, saying that
$T^{\delta }$
the expansion of T, saying that
![]() $\delta $
is a derivation on
$\delta $
is a derivation on
![]() ${\mathbb K}$
extending
${\mathbb K}$
extending
![]() $\eta $
.
$\eta $
.
In the most important case,
![]() $F = \overline {\mathbb {Q}}$
and therefore
$F = \overline {\mathbb {Q}}$
and therefore
![]() $\eta = 0$
, and
$\eta = 0$
, and
![]() $T^{\delta }$
is the expansion of T saying that
$T^{\delta }$
is the expansion of T saying that
![]() $\delta $
is a derivation on
$\delta $
is a derivation on
![]() ${\mathbb K}$
.
${\mathbb K}$
.
3.1. Model completion
A. Robinson introduced the notion of model completion in relation with solvability of systems of equations. For convenience we recall the definition:
Definition 3.1. Let U and
![]() $U^{*}$
be theories in the same language
$U^{*}$
be theories in the same language
![]() $L.$
$L.$
![]() $U^{*}$
is a model completion of U if the following hold:
$U^{*}$
is a model completion of U if the following hold:
-
(1) If
 $A \models U^{*},$
then
$A \models U^{*},$
then
 $A \models U.$
$A \models U.$
-
(2) If
 $A \models U,$
then there exists a
$A \models U,$
then there exists a
 $B \supset A$
such that
$B \supset A$
such that
 $B \models U^{*}.$
$B \models U^{*}.$
-
(3) If
 $A \models U$
,
$A \models U$
,
 $A \subset B$
,
$A \subset B$
,
 $A \subset C,$
where
$A \subset C,$
where
 $B, C \models U^{*},$
then B is elementary equivalent to C over A.
$B, C \models U^{*},$
then B is elementary equivalent to C over A.
We give the following general criteria for model completion. In our context we use (3).
Proposition 3.2. Let U and
![]() $U^{*}$
be theories in the same language L such that
$U^{*}$
be theories in the same language L such that
![]() $U \subseteq U^{*}$
. The following are equivalent:
$U \subseteq U^{*}$
. The following are equivalent:
-
(1)
 $U^{*}$
is the model completion of U and
$U^{*}$
is the model completion of U and
 $U^{*}$
eliminates quantifiers.
$U^{*}$
eliminates quantifiers. - (2)
-
(a) For every
 $A \models U$
, for every
$A \models U$
, for every
 $\sigma _{1}, \dotsc , \sigma _{n} \in U^{*}$
, there exists
$\sigma _{1}, \dotsc , \sigma _{n} \in U^{*}$
, there exists
 $B \models U$
such that
$B \models U$
such that
 $A \subseteq B$
and
$A \subseteq B$
and
 $B \models \sigma _{1} \wedge \dots \wedge \sigma _{n}$
.
$B \models \sigma _{1} \wedge \dots \wedge \sigma _{n}$
. -
(b) For every L-structures
 $A, B, C$
such that
$A, B, C$
such that
 $B \models U$
,
$B \models U$
,
 $C \models U^{*}$
, and A is a common substructure, for every quantifier-free
$C \models U^{*}$
, and A is a common substructure, for every quantifier-free
 $L(A)$
-formula
$L(A)$
-formula
 $\phi (\bar x)$
, for every
$\phi (\bar x)$
, for every
 $\bar b \in B^n$
such that
$\bar b \in B^n$
such that
 $B \models \phi (\bar b)$
, there exists
$B \models \phi (\bar b)$
, there exists
 $\bar c \in C^n$
such that
$\bar c \in C^n$
such that
 $C \models \phi (\bar c)$
.
$C \models \phi (\bar c)$
.
-
- (3)
-
(a) For every
 $A \models U$
, for every
$A \models U$
, for every
 $\sigma _{1}, \dotsc , \sigma _{n} \in U^{*}$
, there exists
$\sigma _{1}, \dotsc , \sigma _{n} \in U^{*}$
, there exists
 $B \models U$
such that
$B \models U$
such that
 $A \subseteq B$
and
$A \subseteq B$
and
 $B \models \sigma _{1} \wedge \dots \wedge \sigma _{n}$
.
$B \models \sigma _{1} \wedge \dots \wedge \sigma _{n}$
. -
(b) For every L-structures
 $A, B, C$
such that
$A, B, C$
such that
 $B \models U$
,
$B \models U$
,
 $C \models U^{*}$
, and A is a common substructure, for every quantifier-free
$C \models U^{*}$
, and A is a common substructure, for every quantifier-free
 $L(A)$
-formula
$L(A)$
-formula
 $\phi (x)$
, and for every
$\phi (x)$
, and for every
 $b \in B$
such that
$b \in B$
such that
 $B \models \phi (b)$
, there exists
$B \models \phi (b)$
, there exists
 $c \in C$
such that
$c \in C$
such that
 $C \models \phi (c)$
.
$C \models \phi (c)$
.
-
-
(4) For all models A of
 $U_{\forall }$
we have:
$U_{\forall }$
we have:-
(a)
 $\operatorname {\mathrm {Diag}}(A) \cup U^{*}$
is consistent,
$\operatorname {\mathrm {Diag}}(A) \cup U^{*}$
is consistent, -
(b)
 $\operatorname {\mathrm {Diag}}(A) \cup U^{*}$
is complete,
$\operatorname {\mathrm {Diag}}(A) \cup U^{*}$
is complete,
where
 $\operatorname {\mathrm {Diag}}(A)$
is the L-diagram of
$\operatorname {\mathrm {Diag}}(A)$
is the L-diagram of
 $A.$
$A.$
-
-
(5) (Blum criterion)
-
(a) Any model of
 $U_{\forall }$
can be extended to some model of
$U_{\forall }$
can be extended to some model of
 $U^{*}$
.
$U^{*}$
. -
(b) For any
 $A, A(b) \models U_{\forall }$
and for all
$A, A(b) \models U_{\forall }$
and for all
 $C^{*} \models U^{*},$
where
$C^{*} \models U^{*},$
where
 $C^{*}$
is
$C^{*}$
is
 $|A|^+$
-saturated, there exists an immersion of
$|A|^+$
-saturated, there exists an immersion of
 $A(b)$
in
$A(b)$
in
 $C^{*}$
.
$C^{*}$
.
-
-
(6)
 $U^{*}$
is the model completion of
$U^{*}$
is the model completion of
 $U_{\forall }$
.
$U_{\forall }$
.
Proof. First we prove that (1) is equivalent to (6): if
![]() $U^{*}$
is the model completion of
$U^{*}$
is the model completion of
![]() $U_{\forall },$
trivially
$U_{\forall },$
trivially
![]() $U^{*}$
is a model completion of U and by [Reference Sacks46, Theorem 13.2], we have that
$U^{*}$
is a model completion of U and by [Reference Sacks46, Theorem 13.2], we have that
![]() $U^{*}$
eliminates quantifiers.
$U^{*}$
eliminates quantifiers.
For the converse, we have trivially that any models of
![]() $U^{*}$
is a model of
$U^{*}$
is a model of
![]() $U_{\forall }$
. Moreover, if
$U_{\forall }$
. Moreover, if
![]() $A \models U_{\forall }$
then there exists
$A \models U_{\forall }$
then there exists
![]() $C \models U$
such that there exists an immersion of A in C. But by (6) there exists
$C \models U$
such that there exists an immersion of A in C. But by (6) there exists
![]() $B \models U_{\forall }$
such that there exists an immersion of C in
$B \models U_{\forall }$
such that there exists an immersion of C in
![]() $B,$
and so an immersion of A in B. It is trivial to verify (3) in Definition 3.1. (1) is equivalent to (4): see [Reference Sacks46]. Also for the equivalence between (5) and (6) see [Reference Sacks46].
$B,$
and so an immersion of A in B. It is trivial to verify (3) in Definition 3.1. (1) is equivalent to (4): see [Reference Sacks46]. Also for the equivalence between (5) and (6) see [Reference Sacks46].
It remains to prove the equivalence between (1) and (2).
![]() $(1) \Rightarrow (2) \Rightarrow (3)$
is easy. For
$(1) \Rightarrow (2) \Rightarrow (3)$
is easy. For
![]() $(3) \Rightarrow (1)$
, in order to obtain that
$(3) \Rightarrow (1)$
, in order to obtain that
![]() $U^{*}$
is the model completion of U, we prove that
$U^{*}$
is the model completion of U, we prove that
![]() $\operatorname {\mathrm {Diag}}(A) \cup U^{*}$
is consistent, but it is enough to see that it is finitely consistent. By (a) we have finite consistency. To prove that
$\operatorname {\mathrm {Diag}}(A) \cup U^{*}$
is consistent, but it is enough to see that it is finitely consistent. By (a) we have finite consistency. To prove that
![]() $U^{*}$
eliminates quantifiers it is equivalent to prove that
$U^{*}$
eliminates quantifiers it is equivalent to prove that
![]() $\operatorname {\mathrm {Diag}}(A) \cup U^{*}$
is complete, which follows easily from (b).
$\operatorname {\mathrm {Diag}}(A) \cup U^{*}$
is complete, which follows easily from (b).
3.2. The axioms
We introduce the following notation:
Let
![]() $\delta : {\mathbb K} \to {\mathbb K}$
be some function,
$\delta : {\mathbb K} \to {\mathbb K}$
be some function,
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $a \in {\mathbb K}$
and
$a \in {\mathbb K}$
and
![]() $\bar a$
tuple of
$\bar a$
tuple of
![]() ${\mathbb K}^m.$
We denote by:
${\mathbb K}^m.$
We denote by:

Definition 3.3. Let
![]() $X \subseteq {\mathbb K}^{n}$
be L-definable with parameters. We say that X is large if
$X \subseteq {\mathbb K}^{n}$
be L-definable with parameters. We say that X is large if
![]() $\dim (X) = n$
.
$\dim (X) = n$
.
Two possible axiomatizations for the model completion
![]() $T^{\delta }_g$
are given by
$T^{\delta }_g$
are given by
![]() $T^{\delta }$
and either of the following axiom schemas:
$T^{\delta }$
and either of the following axiom schemas:
-
(Deep) For every
 $Z \subseteq {\mathbb K}^{n+1}$
$Z \subseteq {\mathbb K}^{n+1}$
 $L({\mathbb K})$
-definable, if
$L({\mathbb K})$
-definable, if
 $\Pi _{n}(Z)$
is large, then there exists
$\Pi _{n}(Z)$
is large, then there exists
 $c \in {\mathbb K}$
such that
$c \in {\mathbb K}$
such that
 $\operatorname {\mathrm {Jet}}^n_{\delta }(c) \in Z$
.
$\operatorname {\mathrm {Jet}}^n_{\delta }(c) \in Z$
. -
(Wide) For every
 $W \subseteq {\mathbb K}^{n} \times {\mathbb K}^{n}$
$W \subseteq {\mathbb K}^{n} \times {\mathbb K}^{n}$
 $L({\mathbb K})$
-definable, if
$L({\mathbb K})$
-definable, if
 $\Pi _{n}(W)$
is large, then there exists
$\Pi _{n}(W)$
is large, then there exists
 $\bar c \in {\mathbb K}^{n}$
such that
$\bar c \in {\mathbb K}^{n}$
such that
 $\langle \bar c, \delta \bar c \rangle \in W$
.
$\langle \bar c, \delta \bar c \rangle \in W$
.
Definition 3.4. We denote by
We will show that both
![]() ${T^{\delta }_{\mathrm {deep}}}$
and
${T^{\delta }_{\mathrm {deep}}}$
and
![]() ${T^{\delta }_{\mathrm {wide}}}$
are axiomatizations for the model completion of
${T^{\delta }_{\mathrm {wide}}}$
are axiomatizations for the model completion of
![]() $T^{\delta }$
. Notice that the axiom scheme
$T^{\delta }$
. Notice that the axiom scheme
![]() $(\texttt {Wide})$
deals with many variables at the same time, but has only one iteration of the map
$(\texttt {Wide})$
deals with many variables at the same time, but has only one iteration of the map
![]() $\delta $
, while
$\delta $
, while
![]() $(\texttt {Deep})$
deals with only one variable at the same time, but many iteration of
$(\texttt {Deep})$
deals with only one variable at the same time, but many iteration of
![]() $\delta $
.
$\delta $
.
Theorem 3.5. Assume that the theory T is model complete. Then the model completion
![]() $T^{\delta }_g$
of
$T^{\delta }_g$
of
![]() $T^{\delta }$
exists, and the theories
$T^{\delta }$
exists, and the theories
![]() ${T^{\delta }_{\mathrm {deep}}}$
and
${T^{\delta }_{\mathrm {deep}}}$
and
![]() ${T^{\delta }_{\mathrm {wide}}}$
are two possible axiomatizations of
${T^{\delta }_{\mathrm {wide}}}$
are two possible axiomatizations of
![]() $T^{\delta }_g$
.
$T^{\delta }_g$
.
3.3. Proof preliminaries
In order to prove the main result we first introduce the following notation: given a polynomial
![]() $p(\bar x,y)$
we write
$p(\bar x,y)$
we write
Let S be a field of characteristic 0 and
![]() $\varepsilon $
be a derivation on it. Let I be a set of indexes (possibly, infinite). Denote
$\varepsilon $
be a derivation on it. Let I be a set of indexes (possibly, infinite). Denote ![]() , and
, and ![]() .
.
Definition 3.6. There exists a unique derivation
![]() $S[\bar x] \to S[\bar x,\bar y]$
,
$S[\bar x] \to S[\bar x,\bar y]$
,
![]() $p \mapsto p^{[\varepsilon ]}$
such that:
$p \mapsto p^{[\varepsilon ]}$
such that:
such derivation extends uniquely to a derivation
![]() $S(\bar x) \to S(\bar x)[\bar y]$
,
$S(\bar x) \to S(\bar x)[\bar y]$
,
![]() $q \mapsto q^{[\varepsilon ]}$
.
$q \mapsto q^{[\varepsilon ]}$
.
Moreover, the map
![]() $S(\bar x) \to S(\bar x)$
defined by
$S(\bar x) \to S(\bar x)$
defined by
is the unique derivation on
![]() $S(\bar x)$
such that:
$S(\bar x)$
such that:
when
![]() $p \in S[\bar x]$
,
$p \in S[\bar x]$
,
![]() $p^{\varepsilon }$
is the polynomial obtained by p by applying
$p^{\varepsilon }$
is the polynomial obtained by p by applying
![]() $\varepsilon $
to each coefficient.
$\varepsilon $
to each coefficient.
Remark 3.7. For every
![]() $q \in S(\bar x)$
and
$q \in S(\bar x)$
and
![]() $\bar a \in S^{n}$
,
$\bar a \in S^{n}$
,
 $$ \begin{align} q^{[\varepsilon]}(\bar x, \bar y) &= q^{\varepsilon}(\bar x) + \sum_{i \in I} \frac{\partial q}{\partial x_{i}}(\bar x) y_{i}; \end{align} $$
$$ \begin{align} q^{[\varepsilon]}(\bar x, \bar y) &= q^{\varepsilon}(\bar x) + \sum_{i \in I} \frac{\partial q}{\partial x_{i}}(\bar x) y_{i}; \end{align} $$
If moreover
![]() $S'$
is a field containing S and
$S'$
is a field containing S and
![]() $\varepsilon ': S(\bar x) \to S'$
is a derivation extending
$\varepsilon ': S(\bar x) \to S'$
is a derivation extending
![]() $\varepsilon $
, then
$\varepsilon $
, then
 $$ \begin{align} \varepsilon'(q) = q^{[\varepsilon]}(\bar x, \varepsilon'(\bar x)) = q^{\varepsilon}(\bar x) + \sum_{i \in I} \frac{\partial q}{\partial x_{i}}(\bar x) \varepsilon'(x_{i}). \end{align} $$
$$ \begin{align} \varepsilon'(q) = q^{[\varepsilon]}(\bar x, \varepsilon'(\bar x)) = q^{\varepsilon}(\bar x) + \sum_{i \in I} \frac{\partial q}{\partial x_{i}}(\bar x) \varepsilon'(x_{i}). \end{align} $$
We will often also use the following fundamental fact, without further mentions.
Fact 3.8. Let
![]() $S'$
be a field containing S (as in Definition 3.6). Let
$S'$
be a field containing S (as in Definition 3.6). Let ![]() be a (possibly, infinite) tuple of elements of
be a (possibly, infinite) tuple of elements of
![]() $S'$
which are algebraically independent over S, and
$S'$
which are algebraically independent over S, and ![]() be a tuple of elements of
be a tuple of elements of
![]() $S'$
(of the same length as
$S'$
(of the same length as
![]() $\bar a$
). Then, there exists a derivation
$\bar a$
). Then, there exists a derivation
![]() $\varepsilon '$
on
$\varepsilon '$
on
![]() $S'$
extending
$S'$
extending
![]() $\varepsilon $
and such that
$\varepsilon $
and such that
![]() $\varepsilon '(\bar a) = \bar b$
. If moreover
$\varepsilon '(\bar a) = \bar b$
. If moreover
![]() $\bar a$
is a transcendence basis of
$\bar a$
is a transcendence basis of
![]() $S'$
over S, then
$S'$
over S, then
![]() $\varepsilon '$
is unique.
$\varepsilon '$
is unique.
Proof. W.l.o.g.,
![]() $\bar a$
is a transcendence basis of
$\bar a$
is a transcendence basis of
![]() $S'$
over S. By [Reference Zariski and Samuel57, Chapter II, Section 17, Theorem 39], there exists a unique derivation
$S'$
over S. By [Reference Zariski and Samuel57, Chapter II, Section 17, Theorem 39], there exists a unique derivation
![]() $\varepsilon ": S(\bar a) \to S'$
extending
$\varepsilon ": S(\bar a) \to S'$
extending
![]() $\varepsilon $
and such that
$\varepsilon $
and such that
![]() $\varepsilon "(\bar a) = \bar b$
; we can also prove it directly, by defining, for every
$\varepsilon "(\bar a) = \bar b$
; we can also prove it directly, by defining, for every
![]() $q \in S(\bar x)$
,
$q \in S(\bar x)$
,
Given
![]() $c \in S'$
, let
$c \in S'$
, let
![]() $p(y) \in S(\bar a)[y]$
be the (monic) minimal polynomial of c over S. Let
$p(y) \in S(\bar a)[y]$
be the (monic) minimal polynomial of c over S. Let ![]() . Let
. Let
Any derivation on
![]() $\varepsilon '$
on
$\varepsilon '$
on
![]() $S'$
extending
$S'$
extending
![]() $\varepsilon "$
must satisfy
$\varepsilon "$
must satisfy
![]() $\varepsilon '(c) = d$
, and by [Reference Zariski and Samuel57, Chapter II, Section 17, Theorem 39] again, there exists a unique derivation
$\varepsilon '(c) = d$
, and by [Reference Zariski and Samuel57, Chapter II, Section 17, Theorem 39] again, there exists a unique derivation
![]() $\varepsilon "': S" \to S'$
extending
$\varepsilon "': S" \to S'$
extending
![]() $\varepsilon "$
and such that
$\varepsilon "$
and such that
![]() $\varepsilon "'(c) = d$
.
$\varepsilon "'(c) = d$
.
By iterating the above construction, we find a unique derivation
![]() $\varepsilon '$
on
$\varepsilon '$
on
![]() $S'$
extending
$S'$
extending
![]() $\varepsilon "$
.
$\varepsilon "$
.
We need the following preliminary lemmas.
Lemma 3.9. Let
![]() $\alpha (x, \bar y)$
be an L-formula and
$\alpha (x, \bar y)$
be an L-formula and
![]() $(B, \delta ) \models T^{\delta }$
. Then there exists a function
$(B, \delta ) \models T^{\delta }$
. Then there exists a function
![]() $ \alpha ^{[\eta ]}$
definable in T such that
$ \alpha ^{[\eta ]}$
definable in T such that
![]() $\delta a = \alpha ^{[\eta ]}(a, \overline b, \delta \overline b)$
, for every
$\delta a = \alpha ^{[\eta ]}(a, \overline b, \delta \overline b)$
, for every
![]() $a, \overline b \in B$
with
$a, \overline b \in B$
with
![]() $B \models \alpha (a, \overline b)$
and
$B \models \alpha (a, \overline b)$
and
![]() $| \alpha ( a, B) | < \infty .$
$| \alpha ( a, B) | < \infty .$
Proof. Let
![]() $\alpha (x, \bar y)$
be an L-formula. Since
$\alpha (x, \bar y)$
be an L-formula. Since
![]() ${\mathbb B}$
is algebraically bounded over F and of characteristic 0, there exist polynomials
${\mathbb B}$
is algebraically bounded over F and of characteristic 0, there exist polynomials
![]() $p_1(x, \bar y), \ldots , p_k(x, \bar y) \in F[x,\bar y]$
associated with the formula
$p_1(x, \bar y), \ldots , p_k(x, \bar y) \in F[x,\bar y]$
associated with the formula
![]() $\alpha (x, \bar y)$
and formulas
$\alpha (x, \bar y)$
and formulas
![]() $\beta _i(x, \bar y) ="p_i(x, \bar y) =^{x} 0"$
such that
$\beta _i(x, \bar y) ="p_i(x, \bar y) =^{x} 0"$
such that
![]() $T \vdash (\alpha (x, \bar y) ) \wedge |\alpha (x, \cdot )| < \infty ) \rightarrow \bigvee _{i=1}^{k} \beta _i(x, \bar y)$
. Now we can associate to each polynomial
$T \vdash (\alpha (x, \bar y) ) \wedge |\alpha (x, \cdot )| < \infty ) \rightarrow \bigvee _{i=1}^{k} \beta _i(x, \bar y)$
. Now we can associate to each polynomial
![]() $p_i$
the partial function
$p_i$
the partial function
 $$\begin{align*}f_i(x, \bar y, \delta \bar y) := \frac{\frac{\partial p_i}{\partial \bar y}\cdot \delta \bar y + p^{\eta}}{\frac{\partial p_i}{\partial x}}, \end{align*}$$
$$\begin{align*}f_i(x, \bar y, \delta \bar y) := \frac{\frac{\partial p_i}{\partial \bar y}\cdot \delta \bar y + p^{\eta}}{\frac{\partial p_i}{\partial x}}, \end{align*}$$
where
![]() $p^{\eta }$
is the polynomial defined in 3.6 obtained by p by applying
$p^{\eta }$
is the polynomial defined in 3.6 obtained by p by applying
![]() $\eta $
to each coefficients.
$\eta $
to each coefficients.
So now we have a total T-definable function
![]() $f(x, \bar y, \delta \bar y)$
whose graph is defined in the following way:
$f(x, \bar y, \delta \bar y)$
whose graph is defined in the following way:
 $$ \begin{align*} z = &f(x, \bar y, \delta y ) \ \Leftrightarrow\ \big( \beta_1(x, \bar y) \wedge z=f_1(x, \bar y, \delta y) \big) \vee \big( \neg \beta_1(x, \bar y) \wedge \beta_2(x, \bar y) \wedge z=\\ &\qquad\qquad\qquad\qquad\qquad\quad =f_2(x, \bar y, \delta y) \big)\ \vee\\ &\ \vee\ \dots \vee \big( \neg \beta_1(x, \bar y) \wedge \dots \wedge \neg \beta_{k-1}(x, \bar y) \wedge \beta_{k}(x, \bar y) \wedge z=f_k(x, \bar y, \delta y) \big) \vee \\ &\qquad\qquad\qquad\quad \vee\ \big( \neg \beta_1(x, \bar y) \wedge \dots \wedge \neg \beta_{k-1}(x, \bar y) \wedge \neg \beta_{k}(x, \bar y) \wedge z= 0 \big). \end{align*} $$
$$ \begin{align*} z = &f(x, \bar y, \delta y ) \ \Leftrightarrow\ \big( \beta_1(x, \bar y) \wedge z=f_1(x, \bar y, \delta y) \big) \vee \big( \neg \beta_1(x, \bar y) \wedge \beta_2(x, \bar y) \wedge z=\\ &\qquad\qquad\qquad\qquad\qquad\quad =f_2(x, \bar y, \delta y) \big)\ \vee\\ &\ \vee\ \dots \vee \big( \neg \beta_1(x, \bar y) \wedge \dots \wedge \neg \beta_{k-1}(x, \bar y) \wedge \beta_{k}(x, \bar y) \wedge z=f_k(x, \bar y, \delta y) \big) \vee \\ &\qquad\qquad\qquad\quad \vee\ \big( \neg \beta_1(x, \bar y) \wedge \dots \wedge \neg \beta_{k-1}(x, \bar y) \wedge \neg \beta_{k}(x, \bar y) \wedge z= 0 \big). \end{align*} $$
Corollary 3.10. For any T-definable function
![]() $f(\bar x)$
there exists a T-definable function
$f(\bar x)$
there exists a T-definable function
![]() $f^{[\eta ]}$
such that
$f^{[\eta ]}$
such that
![]() $\delta (f(\bar x)) = f^{[\eta ]}(\bar x, \operatorname {\mathrm {Jet}}( \bar x)).$
$\delta (f(\bar x)) = f^{[\eta ]}(\bar x, \operatorname {\mathrm {Jet}}( \bar x)).$
Lemma 3.11. Let
![]() $t(\bar x)$
be an
$t(\bar x)$
be an
![]() $L^{\delta }$
-term. Then there is a T-definable function
$L^{\delta }$
-term. Then there is a T-definable function
![]() $f(\bar x, \bar y)$
such that
$f(\bar x, \bar y)$
such that
![]() $t(\bar x) = f(\bar x, \operatorname {\mathrm {Jet}}(\bar x))$
.
$t(\bar x) = f(\bar x, \operatorname {\mathrm {Jet}}(\bar x))$
.
Proof. We prove by induction on the complexity of the term
![]() $t(\bar x).$
If
$t(\bar x).$
If
![]() $t(\bar x)$
is a variable it is trivial. Suppose that
$t(\bar x)$
is a variable it is trivial. Suppose that
![]() $t(\bar x) = h(s(\bar x)).$
By induction there exists a T-definable function g such that
$t(\bar x) = h(s(\bar x)).$
By induction there exists a T-definable function g such that
![]() $s(\bar x) =g( \bar x, \operatorname {\mathrm {Jet}}(\bar x))$
. If the function h is in L we can conclude. Otherwise
$s(\bar x) =g( \bar x, \operatorname {\mathrm {Jet}}(\bar x))$
. If the function h is in L we can conclude. Otherwise
![]() $h = \delta $
and we obtain
$h = \delta $
and we obtain
![]() $t(\bar x) = \delta (g(\bar x, \operatorname {\mathrm {Jet}}(\bar x)))$
. By Corollary 3.10 we conclude the proof.
$t(\bar x) = \delta (g(\bar x, \operatorname {\mathrm {Jet}}(\bar x)))$
. By Corollary 3.10 we conclude the proof.
Lemma 3.12. Let
![]() $\phi (\bar x)$
be a quantifier free
$\phi (\bar x)$
be a quantifier free
![]() $L^{\delta }$
-formula. Then there exists an L-formula
$L^{\delta }$
-formula. Then there exists an L-formula
![]() $\psi $
such that
$\psi $
such that
![]() $T^{\delta } \vdash \phi (\bar x) \leftrightarrow \psi (\bar x, \operatorname {\mathrm {Jet}}(\bar x)).$
$T^{\delta } \vdash \phi (\bar x) \leftrightarrow \psi (\bar x, \operatorname {\mathrm {Jet}}(\bar x)).$
Proof. Follows from Lemma 3.11.
3.4. Proof of Theorem 3.5
We can finally prove that both
![]() ${T^{\delta }_{\mathrm {deep}}}$
and
${T^{\delta }_{\mathrm {deep}}}$
and
![]() ${T^{\delta }_{\mathrm {wide}}}$
axiomatize
${T^{\delta }_{\mathrm {wide}}}$
axiomatize
![]() $T^{\delta }_g$
. The proof is in three steps: firstly we show that
$T^{\delta }_g$
. The proof is in three steps: firstly we show that
![]() ${T^{\delta }_{\mathrm {wide}}} \vdash {T^{\delta }_{\mathrm {deep}}}$
, and later we prove that the conditions (3) of Proposition 3.2 hold for
${T^{\delta }_{\mathrm {wide}}} \vdash {T^{\delta }_{\mathrm {deep}}}$
, and later we prove that the conditions (3) of Proposition 3.2 hold for
![]() $U = T^{\delta }$
and, more precisely, (a) holds for
$U = T^{\delta }$
and, more precisely, (a) holds for
![]() $U^{*}$
equal to
$U^{*}$
equal to
![]() ${T^{\delta }_{\mathrm {wide}}}$
(i.e., that every model of
${T^{\delta }_{\mathrm {wide}}}$
(i.e., that every model of
![]() $T^{\delta }$
can be embedded in a model of
$T^{\delta }$
can be embedded in a model of
![]() ${T^{\delta }_{\mathrm {wide}}}$
), and (b) for
${T^{\delta }_{\mathrm {wide}}}$
), and (b) for
![]() $U^{*}$
equal
$U^{*}$
equal
![]() ${T^{\delta }_{\mathrm {deep}}}$
(i.e., if
${T^{\delta }_{\mathrm {deep}}}$
(i.e., if
![]() $B \models T^{\delta }$
and
$B \models T^{\delta }$
and
![]() $C \models {T^{\delta }_{\mathrm {deep}}}$
have a common substructure A, then every quantifier-free
$C \models {T^{\delta }_{\mathrm {deep}}}$
have a common substructure A, then every quantifier-free
![]() $L^\delta (A)$
-formula with one free variable having a solution in B also has a solution in C).
$L^\delta (A)$
-formula with one free variable having a solution in B also has a solution in C).
Lemma 3.13.
![]() ${T^{\delta }_{\mathrm {wide}}} \vdash {T^{\delta }_{\mathrm {deep}}}$
.
${T^{\delta }_{\mathrm {wide}}} \vdash {T^{\delta }_{\mathrm {deep}}}$
.
Proof. Let
![]() $Z \subseteq {\mathbb K}^{n+1}$
be
$Z \subseteq {\mathbb K}^{n+1}$
be
![]() $L({\mathbb K})$
-definable such that
$L({\mathbb K})$
-definable such that
![]() $\Pi _{n}(Z)$
is large. Define
$\Pi _{n}(Z)$
is large. Define
 $$\begin{align*}W := \{\langle \bar x, \bar y \rangle \in {\mathbb K}^{n} \times {\mathbb K}^{n}: \langle \bar x, y_{n} \rangle \in Z \wedge \bigwedge_{i=1}^{n-1} y_{i} = x_{i+1}\}. \end{align*}$$
$$\begin{align*}W := \{\langle \bar x, \bar y \rangle \in {\mathbb K}^{n} \times {\mathbb K}^{n}: \langle \bar x, y_{n} \rangle \in Z \wedge \bigwedge_{i=1}^{n-1} y_{i} = x_{i+1}\}. \end{align*}$$
Clearly,
![]() $\Pi _{n}(W) = \Pi _{n}(Z)$
, and therefore
$\Pi _{n}(W) = \Pi _{n}(Z)$
, and therefore
![]() $\Pi _{n}(W)$
is large. By
$\Pi _{n}(W)$
is large. By
![]() $(\texttt {Wide})$
, there exists
$(\texttt {Wide})$
, there exists
![]() $\bar c \in {\mathbb K}^{n}$
such that
$\bar c \in {\mathbb K}^{n}$
such that
![]() $\langle \bar c, \delta \bar c \rangle \in W$
. Then,
$\langle \bar c, \delta \bar c \rangle \in W$
. Then,
![]() $\operatorname {\mathrm {Jet}}^n_{\delta }(c_{1}) \in Z$
.
$\operatorname {\mathrm {Jet}}^n_{\delta }(c_{1}) \in Z$
.
Lemma 3.14. Let
![]() $(A, \delta ) \models T^{\delta }$
. Let
$(A, \delta ) \models T^{\delta }$
. Let
![]() $Z \subseteq A^{n} \times A^{n}$
be L-definable with parameters in A, such that
$Z \subseteq A^{n} \times A^{n}$
be L-definable with parameters in A, such that
![]() $\Pi _{n}(Z)$
is large. Then, there exists
$\Pi _{n}(Z)$
is large. Then, there exists
![]() $\langle B, \varepsilon \rangle \supseteq \langle A, \delta \rangle $
and
$\langle B, \varepsilon \rangle \supseteq \langle A, \delta \rangle $
and
![]() $\bar b \in B^{n}$
such that
$\bar b \in B^{n}$
such that
![]() $B \succeq A$
,
$B \succeq A$
,
![]() $\langle B,\varepsilon \rangle \models T^{\delta }$
, and
$\langle B,\varepsilon \rangle \models T^{\delta }$
, and
![]() $\langle \bar b, \varepsilon \bar b \rangle \in Z_{B}$
(the interpretation of Z in B).
$\langle \bar b, \varepsilon \bar b \rangle \in Z_{B}$
(the interpretation of Z in B).
Proof. Let
![]() $B \succ A$
(as L-structures) be such that B is
$B \succ A$
(as L-structures) be such that B is
![]() $\lvert A\rvert ^{+}$
-saturated. By definition of dimension, there exists
$\lvert A\rvert ^{+}$
-saturated. By definition of dimension, there exists
![]() $\bar b \in \Pi _{n}(Z_{B})$
which is algebraically independent over A. Let
$\bar b \in \Pi _{n}(Z_{B})$
which is algebraically independent over A. Let
![]() $\bar d \in B^{n}$
be such that
$\bar d \in B^{n}$
be such that
![]() $\langle \bar b, \delta \bar b \rangle \in Z_{B}$
. Let
$\langle \bar b, \delta \bar b \rangle \in Z_{B}$
. Let
![]() $\varepsilon $
be any derivation on B which extends
$\varepsilon $
be any derivation on B which extends
![]() $\delta $
and such that, by Fact 3.8,
$\delta $
and such that, by Fact 3.8,
![]() $\varepsilon (\bar b) = \bar d.$
$\varepsilon (\bar b) = \bar d.$
Lemma 3.15. Let
![]() $\langle B,\delta \rangle \models T^{\delta }$
,
$\langle B,\delta \rangle \models T^{\delta }$
,
![]() $\langle C,\delta \rangle \models {T^{\delta }_{\mathrm {deep}}}$
, and
$\langle C,\delta \rangle \models {T^{\delta }_{\mathrm {deep}}}$
, and
![]() $\langle A,\delta \rangle $
be an
$\langle A,\delta \rangle $
be an
![]() $L^{\delta }$
-substructures of both models, such that B and C have the same
$L^{\delta }$
-substructures of both models, such that B and C have the same
![]() $L(A)$
-theory. Let
$L(A)$
-theory. Let
![]() $b \in B$
be such that
$b \in B$
be such that
![]() $\langle B, \delta \rangle \models \theta (b)$
, where
$\langle B, \delta \rangle \models \theta (b)$
, where
![]() $\theta (x)$
is a quantifier free
$\theta (x)$
is a quantifier free
![]() $L^{\delta }$
-formula with parameters in A. Then, there exists
$L^{\delta }$
-formula with parameters in A. Then, there exists
![]() $c \in C$
such that
$c \in C$
such that
![]() $\langle C,\delta \rangle \models \theta (c)$
.
$\langle C,\delta \rangle \models \theta (c)$
.
Proof. By Lemma 3.12 there exist
![]() $n \in \mathbb {N}$
and an
$n \in \mathbb {N}$
and an
![]() $L(A)$
-formula
$L(A)$
-formula
![]() $\psi $
such that
$\psi $
such that
![]() $\theta (x) = \psi (\operatorname {\mathrm {Jet}}^n_{\delta }(x))$
.
$\theta (x) = \psi (\operatorname {\mathrm {Jet}}^n_{\delta }(x))$
.
Let
![]() $Y^{B} := \psi (B) = \{\bar d \in B^{n+1}: B \models \psi (\bar d)\}$
, and
$Y^{B} := \psi (B) = \{\bar d \in B^{n+1}: B \models \psi (\bar d)\}$
, and
![]() $Y^{C} := \psi (C)$
.
$Y^{C} := \psi (C)$
.
Let d be the smallest integer such that
![]() $\delta ^d (b)$
is algebraically dependent over
$\delta ^d (b)$
is algebraically dependent over
![]() $\operatorname {\mathrm {Jet}}^{d-1}(b) \cup A$
(or
$\operatorname {\mathrm {Jet}}^{d-1}(b) \cup A$
(or
![]() $d = + \infty $
if
$d = + \infty $
if
![]() $\operatorname {\mathrm {Jet}}^{\infty }_{\delta }(b)$
is algebraically independent over A). We distinguish two cases:
$\operatorname {\mathrm {Jet}}^{\infty }_{\delta }(b)$
is algebraically independent over A). We distinguish two cases:
(1)
![]() $d \geq n$
: in this case,
$d \geq n$
: in this case,
![]() $\Pi _{n}(Y^C)$
is large because
$\Pi _{n}(Y^C)$
is large because
![]() $\operatorname {\mathrm {Jet}}^{n-1}(b) \in \Pi _{n}(Y^{B})$
, therefore, by
$\operatorname {\mathrm {Jet}}^{n-1}(b) \in \Pi _{n}(Y^{B})$
, therefore, by
![]() $(\texttt {Deep})$
, there exists
$(\texttt {Deep})$
, there exists
![]() $c \in C$
such that
$c \in C$
such that
![]() $C \models \theta (\operatorname {\mathrm {Jet}}^n_{\delta }(c)).$
$C \models \theta (\operatorname {\mathrm {Jet}}^n_{\delta }(c)).$
(2)
![]() $d < n$
: this means that
$d < n$
: this means that
![]() $\delta ^{d}b \in \operatorname {\mathrm {acl}}(\operatorname {\mathrm {Jet}}^{d-1}(b)),$
so there exists a polynomial
$\delta ^{d}b \in \operatorname {\mathrm {acl}}(\operatorname {\mathrm {Jet}}^{d-1}(b)),$
so there exists a polynomial
![]() $p(\bar y, x) \in A[\bar y,x]$
such that
$p(\bar y, x) \in A[\bar y,x]$
such that
![]() $p(\operatorname {\mathrm {Jet}}^{d-1}(b), \delta ^{d} b) =^{x} 0$
. By Lemma 3.9 there exist
$p(\operatorname {\mathrm {Jet}}^{d-1}(b), \delta ^{d} b) =^{x} 0$
. By Lemma 3.9 there exist
![]() $L(A)$
-definable functions
$L(A)$
-definable functions
![]() $f_{d+1}, f_{d+2}, \ldots , f_n$
such that
$f_{d+1}, f_{d+2}, \ldots , f_n$
such that
![]() $\delta ^{i} = f_i(\operatorname {\mathrm {Jet}}^{d}(b))$
where
$\delta ^{i} = f_i(\operatorname {\mathrm {Jet}}^{d}(b))$
where
![]() $i = d + 1, d + 2, \ldots , n.$
Let
$i = d + 1, d + 2, \ldots , n.$
Let
Notice that
![]() $\Pi _{d}(Z^{C})$
is large, because
$\Pi _{d}(Z^{C})$
is large, because
![]() $\operatorname {\mathrm {Jet}}^{d-1}(b) \in \Pi _{d}(Z^{B})$
, and therefore by axiom
$\operatorname {\mathrm {Jet}}^{d-1}(b) \in \Pi _{d}(Z^{B})$
, and therefore by axiom
![]() $(\texttt {Deep})$
there exists
$(\texttt {Deep})$
there exists
![]() $c \in C$
such that
$c \in C$
such that
![]() $\operatorname {\mathrm {Jet}}^{d}(c) \in Z^{C}$
and so
$\operatorname {\mathrm {Jet}}^{d}(c) \in Z^{C}$
and so
![]() $\operatorname {\mathrm {Jet}}^{n}(c) \in Y^{C}$
.
$\operatorname {\mathrm {Jet}}^{n}(c) \in Y^{C}$
.
3.5. Corollaries
Corollary 3.16. Assume that T eliminates quantifiers. Then,
![]() ${T^{\delta }_{\mathrm {deep}}}$
and
${T^{\delta }_{\mathrm {deep}}}$
and
![]() ${T^{\delta }_{\mathrm {wide}}}$
are axiomatizations for the model completion
${T^{\delta }_{\mathrm {wide}}}$
are axiomatizations for the model completion
![]() $T^{\delta }_g$
of
$T^{\delta }_g$
of
![]() $T^{\delta }$
.
$T^{\delta }$
.
Moreover,
![]() $T^{\delta }_g$
admits elimination of quantifiers, and for every
$T^{\delta }_g$
admits elimination of quantifiers, and for every
![]() $L^\delta $
-formula
$L^\delta $
-formula
![]() $\alpha (\bar x)$
there exists a quantifier-free L-formula
$\alpha (\bar x)$
there exists a quantifier-free L-formula
![]() $\beta (\bar y)$
such that
$\beta (\bar y)$
such that
Finally,
![]() $T^{\delta }_g$
is complete.
$T^{\delta }_g$
is complete.
Corollary 3.17. Assume that T is model complete. Then,
![]() ${T^{\delta }_{\mathrm {deep}}}$
and
${T^{\delta }_{\mathrm {deep}}}$
and
![]() ${T^{\delta }_{\mathrm {wide}}}$
are axiomatizations for the model completion
${T^{\delta }_{\mathrm {wide}}}$
are axiomatizations for the model completion
![]() $T^{\delta }_g$
of
$T^{\delta }_g$
of
![]() $T^{\delta }$
.
$T^{\delta }$
.
The next corollary is without any further assumptions on T.
Corollary 3.18.
![]() ${T^{\delta }_{\mathrm {deep}}}$
and
${T^{\delta }_{\mathrm {deep}}}$
and
![]() ${T^{\delta }_{\mathrm {wide}}}$
are equivalent consistent theories (which we denote by
${T^{\delta }_{\mathrm {wide}}}$
are equivalent consistent theories (which we denote by
![]() $T^{\delta }_g$
).
$T^{\delta }_g$
).
Moreover, for every
![]() $L^\delta $
-formula
$L^\delta $
-formula
![]() $\alpha (\bar x)$
there exists an L-formula
$\alpha (\bar x)$
there exists an L-formula
![]() $\beta (\bar y)$
such that
$\beta (\bar y)$
such that
Finally,
![]() $T^{\delta }_g$
is complete.
$T^{\delta }_g$
is complete.
4. Several non-commuting derivations
We analyze first the case when there are several not commuting derivations
![]() $\delta _{1}, \dotsc , \delta _{k}$
because it is simpler in terms of axiomatization, as we observed in Section 1.1, and later in Section 5 we examine the harder case of commuting derivations.
$\delta _{1}, \dotsc , \delta _{k}$
because it is simpler in terms of axiomatization, as we observed in Section 1.1, and later in Section 5 we examine the harder case of commuting derivations.
Let
![]() $\bar \delta := \langle \delta _{1}, \dotsc , \delta _{k} \rangle $
. Let
$\bar \delta := \langle \delta _{1}, \dotsc , \delta _{k} \rangle $
. Let
![]() $\eta _{1}, \dotsc , \eta _{k}$
be derivations on F. We denote by
$\eta _{1}, \dotsc , \eta _{k}$
be derivations on F. We denote by
![]() $T^{\bar \delta ,nc}$
the
$T^{\bar \delta ,nc}$
the
![]() $L^{\bar \delta }$
-expansion of T saying that each
$L^{\bar \delta }$
-expansion of T saying that each
![]() $\delta _{i}$
is a derivation and that
$\delta _{i}$
is a derivation and that
![]() $\delta _{i}$
extends
$\delta _{i}$
extends
![]() $\eta _{i}$
for
$\eta _{i}$
for
![]() $i \leq k$
.
$i \leq k$
.
Theorem 4.1. Assume that T is model complete. Then,
![]() $T^{\bar \delta ,nc}$
has a model completion
$T^{\bar \delta ,nc}$
has a model completion
![]() $T^{\bar \delta ,nc}_g$
.
$T^{\bar \delta ,nc}_g$
.
To give the axioms for
![]() $T^{\bar \delta ,nc}_g$
we need some more definitions and notations. We fix
$T^{\bar \delta ,nc}_g$
we need some more definitions and notations. We fix
![]() $\langle {\mathbb K}, \bar \delta \rangle \models T^{\bar \delta ,nc}$
.
$\langle {\mathbb K}, \bar \delta \rangle \models T^{\bar \delta ,nc}$
.
Let
![]() $\Gamma $
be the free non-commutative monoid generated by
$\Gamma $
be the free non-commutative monoid generated by
![]() $\bar \delta $
, with the canonical partial order
$\bar \delta $
, with the canonical partial order
![]() $\preceq $
given by
$\preceq $
given by
![]() $\beta \preceq \alpha \beta $
, for all
$\beta \preceq \alpha \beta $
, for all
![]() $\alpha , \beta \in \Gamma .$
We fix the total order on
$\alpha , \beta \in \Gamma .$
We fix the total order on
![]() $\Gamma $
, given by
$\Gamma $
, given by
where
![]() $<_{lex}$
is the lexicographic order, and
$<_{lex}$
is the lexicographic order, and
![]() $\lvert \theta \rvert $
is the length of
$\lvert \theta \rvert $
is the length of
![]() $\theta $
as a word in the alphabet
$\theta $
as a word in the alphabet
![]() $\bar \delta $
.
$\bar \delta $
.
Remark 4.2.
![]() $\preceq $
is a well-founded partial order on
$\preceq $
is a well-founded partial order on
![]() $\Gamma $
, but it is not a well-partial-order (i.e., there exist infinite anti-chains).
$\Gamma $
, but it is not a well-partial-order (i.e., there exist infinite anti-chains).
Remark 4.3.
-
(1) As an ordered set,
 $\langle \Gamma , \leq \rangle $
is isomorphic to
$\langle \Gamma , \leq \rangle $
is isomorphic to
 $\langle \mathbb {N}, \leq \rangle $
.
$\langle \mathbb {N}, \leq \rangle $
. -
(2)
 (i.e., the empty word, corresponding to the identity function on
(i.e., the empty word, corresponding to the identity function on
 ${\mathbb K}$
) is the minimum of
${\mathbb K}$
) is the minimum of
 $\Gamma $
.
$\Gamma $
. -
(3) If
 $\alpha \preceq \beta $
, then
$\alpha \preceq \beta $
, then
 $\alpha \leq \beta $
.
$\alpha \leq \beta $
. -
(4) If
 $\alpha \leq \beta $
, then
$\alpha \leq \beta $
, then
 $\gamma \alpha \leq \gamma \beta $
and
$\gamma \alpha \leq \gamma \beta $
and
 $\alpha \gamma \leq \beta \gamma $
, for all
$\alpha \gamma \leq \beta \gamma $
, for all
 $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
For every variable x and every
![]() $\gamma \in \Gamma $
we introduce the variable
$\gamma \in \Gamma $
we introduce the variable
![]() $x_{\gamma }$
. Given
$x_{\gamma }$
. Given
![]() $V \subseteq \Gamma $
, we denote
$V \subseteq \Gamma $
, we denote ![]() and
and ![]() . We remark that
. We remark that
![]() $a^V$
is an analogue of the notion of Jet in one derivation, i.e.,
$a^V$
is an analogue of the notion of Jet in one derivation, i.e.,
![]() $\operatorname {\mathrm {Jet}}^n(a) = a^{\{0, 1, \ldots ,\ n\}}.$
Moreover, we denote
$\operatorname {\mathrm {Jet}}^n(a) = a^{\{0, 1, \ldots ,\ n\}}.$
Moreover, we denote
![]() $\Pi _{A}$
the projection from
$\Pi _{A}$
the projection from
![]() ${\mathbb K}^{B}$
to
${\mathbb K}^{B}$
to
![]() ${\mathbb K}^{A}$
(for some
${\mathbb K}^{A}$
(for some
![]() $A, B \subseteq \Gamma $
and
$A, B \subseteq \Gamma $
and
![]() $B \supseteq A$
), mapping
$B \supseteq A$
), mapping
![]() $\langle a_{\mu }: \mu \in B \rangle $
to
$\langle a_{\mu }: \mu \in B \rangle $
to
![]() $\langle a_{\mu }: \mu \in A \rangle $
.
$\langle a_{\mu }: \mu \in A \rangle $
.
We give now two alternative axiomatizations for
![]() $T^{\bar \delta ,nc}_g$
.
$T^{\bar \delta ,nc}_g$
.
-
(nc-Deep) Let
 $\mathcal V \subset \Gamma $
be finite and
$\mathcal V \subset \Gamma $
be finite and
 $\preceq $
-initial. Let
$\preceq $
-initial. Let
 $\mathcal P \subseteq \mathcal V$
be the set of
$\mathcal P \subseteq \mathcal V$
be the set of
 $\preceq $
-maximal elements of
$\preceq $
-maximal elements of
 $\mathcal V$
, and
$\mathcal V$
, and  . Let
. Let
 $Z \subseteq {\mathbb K}^{\mathcal V}$
be
$Z \subseteq {\mathbb K}^{\mathcal V}$
be
 $L(A)$
-definable. If
$L(A)$
-definable. If
 $\Pi _{\mathcal F }(Z)$
is large, then there exists
$\Pi _{\mathcal F }(Z)$
is large, then there exists
 $c \in {\mathbb K}$
such that
$c \in {\mathbb K}$
such that
 $c^{\mathcal V} \in Z$
.
$c^{\mathcal V} \in Z$
. -
(nc-Wide) Let
 $W \subseteq {\mathbb K}^{n} \times {\mathbb K}^{k \times n} $
be
$W \subseteq {\mathbb K}^{n} \times {\mathbb K}^{k \times n} $
be
 $L({\mathbb K})$
-definable, such that
$L({\mathbb K})$
-definable, such that
 $\Pi _{n}(W)$
is large. Then, there exists
$\Pi _{n}(W)$
is large. Then, there exists
 $\bar c \in {\mathbb K}^{n}$
such that
$\bar c \in {\mathbb K}^{n}$
such that
 $\langle \bar c, \delta _{1} \bar c, \dotsc , \delta _{k} \bar c \rangle \in W$
.
$\langle \bar c, \delta _{1} \bar c, \dotsc , \delta _{k} \bar c \rangle \in W$
.
Definition 4.4. We denote by
Theorem 4.5.
-
(1)
 $T^{\bar \delta ,nc}_{deep}$
and
$T^{\bar \delta ,nc}_{deep}$
and
 $T^{\bar \delta ,nc}_{wide}$
are consistent and equivalent to each other.
$T^{\bar \delta ,nc}_{wide}$
are consistent and equivalent to each other. -
(2) If T is model-complete, then the model completion
 $T^{\bar \delta ,nc}_g$
of
$T^{\bar \delta ,nc}_g$
of
 $T^{\bar \delta ,nc}$
exists, and the theories
$T^{\bar \delta ,nc}$
exists, and the theories
 $T^{\bar \delta ,nc}_{deep}$
and
$T^{\bar \delta ,nc}_{deep}$
and
 $T^{\bar \delta ,nc}_{wide}$
are two possible axiomatizations of
$T^{\bar \delta ,nc}_{wide}$
are two possible axiomatizations of
 $T^{\bar \delta ,nc}_g$
.
$T^{\bar \delta ,nc}_g$
. -
(3) If T eliminates quantifiers, then
 $T^{\bar \delta ,nc}_g$
eliminates quantifiers.
$T^{\bar \delta ,nc}_g$
eliminates quantifiers. -
(4) For every
 $L^{\bar \delta }$
-formula
$L^{\bar \delta }$
-formula
 $\alpha (\bar x)$
there exists an L-formula
$\alpha (\bar x)$
there exists an L-formula
 $\beta (\bar x)$
such that
$\beta (\bar x)$
such that  $$\begin{align*}T^{\bar \delta,nc}_g \models \forall \bar x\ \bigl( \alpha(\bar x) \leftrightarrow \beta(\bar x^{\Gamma}) \bigr). \end{align*}$$
$$\begin{align*}T^{\bar \delta,nc}_g \models \forall \bar x\ \bigl( \alpha(\bar x) \leftrightarrow \beta(\bar x^{\Gamma}) \bigr). \end{align*}$$
For the proof, we proceed as in Section 3.4, i.e., it is in three steps:
Lemma 4.6.
![]() $T^{\bar \delta ,nc}_{wide} \vdash T^{\bar \delta ,nc}_{deep}$
.
$T^{\bar \delta ,nc}_{wide} \vdash T^{\bar \delta ,nc}_{deep}$
.
Proof. Let
![]() $Z, \mathcal F, \mathcal P, \mathcal V$
be as in
$Z, \mathcal F, \mathcal P, \mathcal V$
be as in
![]() $(\texttt {nc-Deep})$
.
$(\texttt {nc-Deep})$
.
Claim 1. W.l.o.g., we may assume that
![]() $\mathcal P$
is equal to the set of
$\mathcal P$
is equal to the set of
![]() $\preceq $
-minimal elements of
$\preceq $
-minimal elements of
![]() $\Gamma \setminus \mathcal F$
.
$\Gamma \setminus \mathcal F$
.
In fact, let
![]() $\mathcal P'$
be the set of
$\mathcal P'$
be the set of
![]() $\preceq $
-minimal elements of
$\preceq $
-minimal elements of
![]() $\Gamma \setminus \mathcal F$
; notice that
$\Gamma \setminus \mathcal F$
; notice that
![]() $\mathcal P \subseteq \mathcal P'$
. We can replace
$\mathcal P \subseteq \mathcal P'$
. We can replace
![]() $\mathcal V$
with
$\mathcal V$
with ![]() , and Z with
, and Z with ![]() , where the function
, where the function
![]() $\Pi $
is defined as:
$\Pi $
is defined as:
 $$ \begin{align*} {\Pi} : {{\mathbb K}^{\mathcal V'}} & \longrightarrow {{\mathbb K}^{\mathcal V}} \\ {\bar x} &\longmapsto\! {\langle x_{\mu}: \mu \in \mathcal V \rangle.} \end{align*} $$
$$ \begin{align*} {\Pi} : {{\mathbb K}^{\mathcal V'}} & \longrightarrow {{\mathbb K}^{\mathcal V}} \\ {\bar x} &\longmapsto\! {\langle x_{\mu}: \mu \in \mathcal V \rangle.} \end{align*} $$
Then,
![]() $\Pi _{\mathcal F}(Z') = \Pi _{\mathcal F}(Z)$
, and if
$\Pi _{\mathcal F}(Z') = \Pi _{\mathcal F}(Z)$
, and if
![]() $a^{\mathcal V'} \in Z'$
, then
$a^{\mathcal V'} \in Z'$
, then
![]() $a^{\mathcal V} \in Z$
.
$a^{\mathcal V} \in Z$
.
We introduce variables
![]() $x_{0}, x_{1}, \dotsc , x_{k}$
and corresponding variable
$x_{0}, x_{1}, \dotsc , x_{k}$
and corresponding variable
![]() $x_{i,\gamma }$
, which for readability we denote by
$x_{i,\gamma }$
, which for readability we denote by
![]() $x(i,\gamma )$
such that
$x(i,\gamma )$
such that
![]() $0 \leq i \leq k, \gamma \in \Gamma $
. For brevity, we denote
$0 \leq i \leq k, \gamma \in \Gamma $
. For brevity, we denote
We also denote
 $$ \begin{align*} {\Pi_{0}} : {({\mathbb K}^{\mathcal V})^{k+1}} & \longrightarrow {{\mathbb K}^{\mathcal V}} \\ {\bar x} &\longmapsto\! {\bar x_0.} \end{align*} $$
$$ \begin{align*} {\Pi_{0}} : {({\mathbb K}^{\mathcal V})^{k+1}} & \longrightarrow {{\mathbb K}^{\mathcal V}} \\ {\bar x} &\longmapsto\! {\bar x_0.} \end{align*} $$
For each
![]() $\pi \in \mathcal P$
, we choose
$\pi \in \mathcal P$
, we choose
![]() $\mu _{\pi } \in \mathcal F$
and
$\mu _{\pi } \in \mathcal F$
and
![]() $i_{\pi } \in \{1, \dotsc , k\}$
such that
$i_{\pi } \in \{1, \dotsc , k\}$
such that
![]() $\delta _{i_{\pi }} \mu _{i} = \pi $
. Moreover, given
$\delta _{i_{\pi }} \mu _{i} = \pi $
. Moreover, given
![]() $\bar a \in ({\mathbb K}^{\mathcal F})^{k+1}$
, we define
$\bar a \in ({\mathbb K}^{\mathcal F})^{k+1}$
, we define
![]() $\bar a' \in K^{\mathcal V}$
as the tuple with coordinates
$\bar a' \in K^{\mathcal V}$
as the tuple with coordinates

We define
Notice that
![]() $\Pi _{0}(W)$
is equal to
$\Pi _{0}(W)$
is equal to
![]() $\Pi _{\mathcal F}(Z)$
, and therefore it is large. Thus, by
$\Pi _{\mathcal F}(Z)$
, and therefore it is large. Thus, by
![]() $(\texttt {nc-Wide})$
, there exists
$(\texttt {nc-Wide})$
, there exists
![]() $\bar a \in {\mathbb K}^{\mathcal F}$
such that
$\bar a \in {\mathbb K}^{\mathcal F}$
such that
![]() $\langle \bar a, \delta _{1}(\bar a), \dotsc , \delta _{k}(\bar a) \rangle \in W$
. Finally, taking
$\langle \bar a, \delta _{1}(\bar a), \dotsc , \delta _{k}(\bar a) \rangle \in W$
. Finally, taking ![]() , we get
, we get
![]() $a^{\mathcal V} \in Z$
.
$a^{\mathcal V} \in Z$
.
Lemma 4.7. Let
![]() $(A, \bar \delta ) \models T^{\bar \delta ,nc}$
. Let
$(A, \bar \delta ) \models T^{\bar \delta ,nc}$
. Let
![]() $Z \subseteq A^{n} \times (A^{n})^{k}$
be L-definable with parameters in A, such that
$Z \subseteq A^{n} \times (A^{n})^{k}$
be L-definable with parameters in A, such that
![]() $\Pi _{n}(Z)$
is large. Then, there exists
$\Pi _{n}(Z)$
is large. Then, there exists
![]() $\langle B, \bar \varepsilon \rangle \supseteq \langle A, \bar \delta \rangle $
and
$\langle B, \bar \varepsilon \rangle \supseteq \langle A, \bar \delta \rangle $
and
![]() $\bar b \in B^{n}$
such that
$\bar b \in B^{n}$
such that
![]() $B \succeq A$
,
$B \succeq A$
,
![]() $\langle B,\bar \varepsilon \rangle \models T^{\bar \delta ,nc}$
, and
$\langle B,\bar \varepsilon \rangle \models T^{\bar \delta ,nc}$
, and
![]() $\langle \bar b, \bar \varepsilon \bar b \rangle \in Z_{B}$
.
$\langle \bar b, \bar \varepsilon \bar b \rangle \in Z_{B}$
.
Proof. Same proof as for Lemma 3.14.
Lemma 4.8. Let
![]() $\langle B,\bar \delta \rangle \models T^{\bar \delta ,nc}$
,
$\langle B,\bar \delta \rangle \models T^{\bar \delta ,nc}$
,
![]() $\langle C,\bar \delta \rangle \models T^{\bar \delta ,nc}_{deep}$
, and
$\langle C,\bar \delta \rangle \models T^{\bar \delta ,nc}_{deep}$
, and
![]() $\langle A,\bar \delta \rangle $
be an
$\langle A,\bar \delta \rangle $
be an
![]() $L(\bar \delta )$
-substructures of both models, such that B and C have the same
$L(\bar \delta )$
-substructures of both models, such that B and C have the same
![]() $L(A)$
-theory. Let
$L(A)$
-theory. Let
![]() $b \in B$
be such that
$b \in B$
be such that
![]() $\langle B, \bar \delta \rangle \models \theta (b)$
, where
$\langle B, \bar \delta \rangle \models \theta (b)$
, where
![]() $\theta (x)$
is a quantifier free
$\theta (x)$
is a quantifier free
![]() $L(\bar \delta )$
-formula with parameters in A. Then, there exists
$L(\bar \delta )$
-formula with parameters in A. Then, there exists
![]() $c \in C$
such that
$c \in C$
such that
![]() $\langle C, \bar \delta \rangle \models \theta (c)$
.
$\langle C, \bar \delta \rangle \models \theta (c)$
.
Proof. By Lemma 3.12 there exists U finite subset of
![]() $\Gamma $
and an
$\Gamma $
and an
![]() $L(A)$
-formula
$L(A)$
-formula
![]() $\psi (\bar y)$
such that U is
$\psi (\bar y)$
such that U is
![]() $\preceq $
-initial and that
$\preceq $
-initial and that
![]() $T^{\bar \delta ,nc} \models \theta (x) = \psi (x^{U})$
. Let
$T^{\bar \delta ,nc} \models \theta (x) = \psi (x^{U})$
. Let ![]() and
and ![]() . Let
. Let
Define ![]() and
and
![]() $\mathcal P$
be the set of
$\mathcal P$
be the set of
![]() $\preceq $
-minimal elements of
$\preceq $
-minimal elements of
![]() $\mathcal B$
(notice that
$\mathcal B$
(notice that
![]() $\mathcal P$
might be infinite). As usual, define
$\mathcal P$
might be infinite). As usual, define ![]() .
.
For every
![]() $\gamma \in \Gamma $
there exists
$\gamma \in \Gamma $
there exists
![]() $q_{\gamma } \in A(x_{\mathcal V \leq \gamma })$
such that
$q_{\gamma } \in A(x_{\mathcal V \leq \gamma })$
such that
![]() $\gamma b = q_{\gamma }(b^{\mathcal V \leq \gamma })$
. Let
$\gamma b = q_{\gamma }(b^{\mathcal V \leq \gamma })$
. Let
![]() $\beta $
be the following
$\beta $
be the following
![]() $L(A)$
-formula:
$L(A)$
-formula:
Notice that
![]() $\langle B, \bar \delta \rangle \models \beta (b^{\mathcal V})$
. Let
$\langle B, \bar \delta \rangle \models \beta (b^{\mathcal V})$
. Let
![]() $\mathcal V_{0} \subseteq \mathcal V$
be the set of indexes of the variables of
$\mathcal V_{0} \subseteq \mathcal V$
be the set of indexes of the variables of
![]() $\beta $
: w.l.o.g., we may assume that
$\beta $
: w.l.o.g., we may assume that
![]() $\mathcal V_{0}$
is a
$\mathcal V_{0}$
is a
![]() $\preceq $
-initial subset of
$\preceq $
-initial subset of
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $\mathcal P_{0}$
be the set of
$\mathcal P_{0}$
be the set of
![]() $\preceq $
-maximal elements of
$\preceq $
-maximal elements of
![]() $\mathcal V_{0}$
. Define
$\mathcal V_{0}$
. Define
Notice that
![]() $\Pi _{\mathcal F_{0}}(Z)$
contains
$\Pi _{\mathcal F_{0}}(Z)$
contains
![]() $b^{\mathcal F_{0}}$
, and therefore it is large. Thus, by
$b^{\mathcal F_{0}}$
, and therefore it is large. Thus, by
![]() $(\texttt {nc-Deep})$
, there exists
$(\texttt {nc-Deep})$
, there exists
![]() $c \in C$
such that
$c \in C$
such that
![]() $c^{\mathcal V_{0}} \in Z$
, and therefore
$c^{\mathcal V_{0}} \in Z$
, and therefore
![]() $c^{U}$
satisfies
$c^{U}$
satisfies
![]() $\psi $
.
$\psi $
.
5. Several commuting derivations
We now deal with the case when there are several commuting derivations
![]() $\delta _{1}, \dotsc , \delta _{k}$
. The technique used here for the treatment of the study of several derivations are a variant of [Reference Fornasiero and Kaplan14]. In particular, we avoid as much as possible the algebraic approach in [Reference Kolchin25] based on autoreduced sets.
$\delta _{1}, \dotsc , \delta _{k}$
. The technique used here for the treatment of the study of several derivations are a variant of [Reference Fornasiero and Kaplan14]. In particular, we avoid as much as possible the algebraic approach in [Reference Kolchin25] based on autoreduced sets.
Let
![]() $\bar \delta := \langle \delta _{1}, \dotsc , \delta _{k} \rangle $
and let
$\bar \delta := \langle \delta _{1}, \dotsc , \delta _{k} \rangle $
and let
![]() $\eta _{1}, \dotsc , \eta _{k}$
be commuting derivations on F. Let
$\eta _{1}, \dotsc , \eta _{k}$
be commuting derivations on F. Let
![]() $T^{\bar \delta }$
be the
$T^{\bar \delta }$
be the
![]() $L^{\bar \delta }$
-expansion of T saying that each
$L^{\bar \delta }$
-expansion of T saying that each
![]() $\delta _{i}$
is a derivation, that
$\delta _{i}$
is a derivation, that
![]() $\delta _{i}$
extends
$\delta _{i}$
extends
![]() $\eta _{i}$
for
$\eta _{i}$
for
![]() $i \leq k$
, and that
$i \leq k$
, and that
![]() $\delta _{i} \circ \delta _{j} = \delta _{j} \circ \delta _{i}$
, for
$\delta _{i} \circ \delta _{j} = \delta _{j} \circ \delta _{i}$
, for
![]() $i, j \leq k$
.
$i, j \leq k$
.
Theorem 5.1. Assume that T is model complete. Then,
![]() $T^{\bar \delta }$
has a model completion
$T^{\bar \delta }$
has a model completion
![]() $T^{\bar \delta }_g$
.
$T^{\bar \delta }_g$
.
5.1. Configurations
In order to give axioms for
![]() $T^{\bar \delta }_g$
, we first need some more definitions and notations. We fix
$T^{\bar \delta }_g$
, we first need some more definitions and notations. We fix
![]() $\langle {\mathbb K}, \bar \delta \rangle \models T^{\bar \delta }$
. We denote by K the field underlying
$\langle {\mathbb K}, \bar \delta \rangle \models T^{\bar \delta }$
. We denote by K the field underlying
![]() ${\mathbb K}$
.
${\mathbb K}$
.
Let
![]() $\Theta $
be the free commutative monoid generated by
$\Theta $
be the free commutative monoid generated by
![]() $\bar \delta $
, with the canonical partial order
$\bar \delta $
, with the canonical partial order
![]() $\preceq $
(notice that
$\preceq $
(notice that
![]() $\Theta $
is isomorphic to
$\Theta $
is isomorphic to
![]() $\mathbb {N}^{k}$
).
$\mathbb {N}^{k}$
).
Notice that
![]() $\Theta $
is, canonically, a quotient of the free monoid
$\Theta $
is, canonically, a quotient of the free monoid
![]() $\Gamma $
. For every
$\Gamma $
. For every
![]() $v \in \Gamma $
we denote by
$v \in \Gamma $
we denote by
![]() $[v]\in \Theta $
the equivalence class of v.
$[v]\in \Theta $
the equivalence class of v.
We fix the total order on
![]() $\Theta $
, given by
$\Theta $
, given by
where
![]() $<_{lex}$
is the lexicographic order, and
$<_{lex}$
is the lexicographic order, and ![]() .
.
Given
![]() $a \in {\mathbb K}$
and
$a \in {\mathbb K}$
and
![]() $\theta \in \Theta $
, we denote by
$\theta \in \Theta $
, we denote by ![]() , and similarly
, and similarly ![]() , and
, and ![]() . Moreover, for each
. Moreover, for each
![]() $\theta \in \Theta $
we have a variable
$\theta \in \Theta $
we have a variable
![]() $x_{\theta }$
, and we denote
$x_{\theta }$
, and we denote ![]() . Moreover, given a set
. Moreover, given a set
![]() $A \subseteq \Theta $
, we denote
$A \subseteq \Theta $
, we denote ![]() , and
, and ![]() . Given a rational function
. Given a rational function
![]() $q \in K(x_{\Theta })$
and
$q \in K(x_{\Theta })$
and
![]() $\bar a \in K^{\Theta }$
, we denote by
$\bar a \in K^{\Theta }$
, we denote by

Let
![]() $K_{0}$
be a differential subfield of K (i.e., such that
$K_{0}$
be a differential subfield of K (i.e., such that
![]() $\bar \delta (K_{0}) \subseteq K_{0}$
).
$\bar \delta (K_{0}) \subseteq K_{0}$
).
A configuration
![]() $\mathfrak S$
with parameters in
$\mathfrak S$
with parameters in
![]() $K_{0}$
is given by the following data.
$K_{0}$
is given by the following data.
(1) A
![]() $\preceq $
-anti-chain
$\preceq $
-anti-chain
![]() $\mathcal P \subset \Theta $
. Notice that, by Dickson’s Lemma,
$\mathcal P \subset \Theta $
. Notice that, by Dickson’s Lemma,
![]() $\mathcal P$
must be finite.
$\mathcal P$
must be finite.
We distinguish two sets:
-
•
 , the set of leaders.Footnote
2
, the set of leaders.Footnote
2
-
•
 , the set of free elements. Moreover, we define:
, the set of free elements. Moreover, we define: -
•
 .
.
Notice that
![]() $\mathcal P$
is the set of
$\mathcal P$
is the set of
![]() $\preceq $
-minimal elements of
$\preceq $
-minimal elements of
![]() $\mathcal B$
. We assume that
$\mathcal B$
. We assume that
![]() $\mathcal F$
is non-empty (equivalently, that
$\mathcal F$
is non-empty (equivalently, that
![]() $0 \in \mathcal F$
).
$0 \in \mathcal F$
).
(2) For every
![]() $\pi \in \mathcal P$
we are given a nonzero polynomial
$\pi \in \mathcal P$
we are given a nonzero polynomial
![]() $p_{\pi } \in K_{0}[x_{\pi }, x_{\mathcal F < \pi }]$
which depends on
$p_{\pi } \in K_{0}[x_{\pi }, x_{\mathcal F < \pi }]$
which depends on
![]() $x_{\pi }$
(i.e., its degree in
$x_{\pi }$
(i.e., its degree in
![]() $x_{\pi }$
is nonzero).
$x_{\pi }$
is nonzero).
Consider the quasi-affine variety (defined over
![]() $K_{0}$
)
$K_{0}$
)
(by quasi-affine variety we simply mean a subset of
![]() $K^{n}$
which is locally closed in the Zariski topology. We don’t consider its spectrum).
$K^{n}$
which is locally closed in the Zariski topology. We don’t consider its spectrum).
(3) Finally, we are given
![]() $W \subseteq W_{0}$
, which is Zariski closed in
$W \subseteq W_{0}$
, which is Zariski closed in
![]() $W_{0}$
, such that W is defined (as a quasi-affine variety) over
$W_{0}$
, such that W is defined (as a quasi-affine variety) over
![]() $K_{0}$
and such that
$K_{0}$
and such that
![]() $\Pi _{\mathcal F}(W)$
is large (where
$\Pi _{\mathcal F}(W)$
is large (where
![]() $\Pi _{\mathcal F}: K^{\mathcal V} \to K^{\mathcal F}$
is the canonical projection).
$\Pi _{\mathcal F}: K^{\mathcal V} \to K^{\mathcal F}$
is the canonical projection).
For the remainder of this section, we are given a configuration:
We want to impose some commutativity on
![]() $\mathfrak S$
.
$\mathfrak S$
.
We define now some induced data.
For every
![]() $\alpha \in \Theta $
we define a rational function
$\alpha \in \Theta $
we define a rational function
![]() $f_{\alpha } \in K_{0}(x_{\mathcal V})$
and a tuple of rational functions
$f_{\alpha } \in K_{0}(x_{\mathcal V})$
and a tuple of rational functions
![]() $F_{\alpha }$
.
$F_{\alpha }$
.
-
• If
 $\alpha \in \mathcal V$
, then
$\alpha \in \mathcal V$
, then  and
and
 $F_{\alpha } = \{f_{\alpha }\}$
.
$F_{\alpha } = \{f_{\alpha }\}$
. -
• For every
 $\pi \in \mathcal P$
and
$\pi \in \mathcal P$
and
 $v \in \Gamma $
, we define
$v \in \Gamma $
, we define
 $f_{v, \pi }$
by induction on v, and then and
$f_{v, \pi }$
by induction on v, and then and $$\begin{align*}F_{\alpha} := \{f_{v, \pi}: v \in \Gamma, \pi \in \mathcal P, [v]\pi = \alpha\}, \end{align*}$$
$$\begin{align*}F_{\alpha} := \{f_{v, \pi}: v \in \Gamma, \pi \in \mathcal P, [v]\pi = \alpha\}, \end{align*}$$
 $f_{\alpha }$
is an arbitrary function in
$f_{\alpha }$
is an arbitrary function in
 $F_{\alpha }$
.
$F_{\alpha }$
.
If
 $v = 0$
, then
$v = 0$
, then  .
.If
 $v = \delta $
for some
$v = \delta $
for some
 $\delta \in \bar \delta $
, define (5)If
$\delta \in \bar \delta $
, define (5)If
 $v = \delta w$
with
$v = \delta w$
with
 $0 \neq w \in \Gamma $
, define where
$0 \neq w \in \Gamma $
, define where
 when
when
 $\mu \in \mathcal F$
.
$\mu \in \mathcal F$
.
We also define
![]() $g_{\alpha }$
and
$g_{\alpha }$
and
![]() $g_{w, \pi }$
as the restriction to W of
$g_{w, \pi }$
as the restriction to W of
![]() $f_{\alpha }$
and
$f_{\alpha }$
and
![]() $f_{w, \pi }$
, respectively, and
$f_{w, \pi }$
, respectively, and
![]() $G_{\alpha }$
the family
$G_{\alpha }$
the family
![]() $\{ g_{w, \pi }: w \in \Gamma , \pi \in \mathcal P, [w]\pi = \alpha \}$
.
$\{ g_{w, \pi }: w \in \Gamma , \pi \in \mathcal P, [w]\pi = \alpha \}$
.
Let
![]() $\theta \in \Theta $
be the
$\theta \in \Theta $
be the
![]() $\preceq $
-l.u.b. of
$\preceq $
-l.u.b. of
![]() $\mathcal P$
and d be the dimension of W. We say that
$\mathcal P$
and d be the dimension of W. We say that
![]() $\mathfrak S$
commutes at
$\mathfrak S$
commutes at
![]() $\alpha \in \Theta $
if, for every
$\alpha \in \Theta $
if, for every
![]() $g,g' \in G_{\alpha }$
, g and
$g,g' \in G_{\alpha }$
, g and
![]() $g'$
coincide outside a subset of W of dimension less than d (i.e., they coincide “almost everywhere” on W). We say that
$g'$
coincide outside a subset of W of dimension less than d (i.e., they coincide “almost everywhere” on W). We say that
![]() $\mathfrak S$
commutes locally if it commutes at every
$\mathfrak S$
commutes locally if it commutes at every
![]() $\alpha \leq \theta $
, and it commutes globally if it commutes at every
$\alpha \leq \theta $
, and it commutes globally if it commutes at every
![]() $\alpha \in \Theta $
.
$\alpha \in \Theta $
.
The main result that makes the machinery work is the following.
Theorem 5.2.
![]() $\mathfrak S$
commutes locally iff it commutes globally.
$\mathfrak S$
commutes locally iff it commutes globally.
We will say then that
![]() $\mathfrak S$
commutes if it commutes locally (equivalently, globally).
$\mathfrak S$
commutes if it commutes locally (equivalently, globally).
In order to prove the above theorem, we need some preliminary definitions and results. It suffices to prove the theorem for every
![]() $K_{0}$
-irreducible component of W of dimension d. Thus, w.l.o.g. we may assume for the remainder of this subsection that W is
$K_{0}$
-irreducible component of W of dimension d. Thus, w.l.o.g. we may assume for the remainder of this subsection that W is
![]() $K_{0}$
-irreducible. Then, the condition that W commutes at a certain
$K_{0}$
-irreducible. Then, the condition that W commutes at a certain
![]() $\alpha $
becomes that
$\alpha $
becomes that
![]() $G_{\alpha }$
is a singleton.
$G_{\alpha }$
is a singleton.
We denote by
![]() $K_{0}[W]$
the ring of regular functions on W (that is, the restriction to W of polynomial maps
$K_{0}[W]$
the ring of regular functions on W (that is, the restriction to W of polynomial maps
![]() $K_{0}^{\mathcal V} \to K_{0}$
). Since we are assuming that W is
$K_{0}^{\mathcal V} \to K_{0}$
). Since we are assuming that W is
![]() $K_{0}$
-irreducible,
$K_{0}$
-irreducible,
![]() $K_{0}[W]$
is an integral domain. Therefore, we can consider its fraction field
$K_{0}[W]$
is an integral domain. Therefore, we can consider its fraction field
![]() $K_{0}(W)$
. An element of
$K_{0}(W)$
. An element of
![]() $K_{0}(W)$
is the restriction to W of a rational function in
$K_{0}(W)$
is the restriction to W of a rational function in
![]() $K_{0}(x_{\mathcal V})$
; in particular, the functions
$K_{0}(x_{\mathcal V})$
; in particular, the functions
![]() $g_{\alpha }$
and
$g_{\alpha }$
and
![]() $g_{w, \pi }$
are in
$g_{w, \pi }$
are in
![]() $K_{0}(W)$
.
$K_{0}(W)$
.
Given
![]() $\delta \in \bar \delta $
, we define the following function:
$\delta \in \bar \delta $
, we define the following function:
 $$ \begin{align*} {R^{\delta}_{0}} : {K_0(x_{\mathcal V})} & \longrightarrow {K_0(x_{\mathcal V})} \\ h &\longmapsto\! {h^{\delta} + \sum_{\mu \in \mathcal V} \frac{\partial h}{\partial \mu} \cdot f_{\delta, \mu}.} \end{align*} $$
$$ \begin{align*} {R^{\delta}_{0}} : {K_0(x_{\mathcal V})} & \longrightarrow {K_0(x_{\mathcal V})} \\ h &\longmapsto\! {h^{\delta} + \sum_{\mu \in \mathcal V} \frac{\partial h}{\partial \mu} \cdot f_{\delta, \mu}.} \end{align*} $$
Notice that
![]() $R^{\delta }_{0}$
is the unique derivation extending
$R^{\delta }_{0}$
is the unique derivation extending
![]() $\delta $
such that
$\delta $
such that
![]() $R^{\delta }_{0}(x_{\mu }) = f_{\delta , \mu }$
, for every
$R^{\delta }_{0}(x_{\mu }) = f_{\delta , \mu }$
, for every
![]() $\mu \in \mathcal V$
. Given
$\mu \in \mathcal V$
. Given
![]() $w = w_{1} \dots w_{\ell } \in \Gamma $
, we can define
$w = w_{1} \dots w_{\ell } \in \Gamma $
, we can define
![]() $R^{w}_{0}: K_{0}(x_{\mathcal V}) \to K_{0}(x_{\mathcal V})$
as the composition
$R^{w}_{0}: K_{0}(x_{\mathcal V}) \to K_{0}(x_{\mathcal V})$
as the composition ![]() .
.
We have, for every
![]() $v,w \in \Gamma $
and every
$v,w \in \Gamma $
and every
![]() $\pi \in \mathcal P$
,
$\pi \in \mathcal P$
,
If we restrict
![]() $R^{\delta }_{0}$
to
$R^{\delta }_{0}$
to
![]() $K_{0}(x_{\mathcal F}) $
and compose with the restriction to W, we obtain a derivation
$K_{0}(x_{\mathcal F}) $
and compose with the restriction to W, we obtain a derivation
![]() $R^{\delta }_{1}: K_{0}(x_{\mathcal F}) \to K_{0}(W)$
. An equivalent definition is that
$R^{\delta }_{1}: K_{0}(x_{\mathcal F}) \to K_{0}(W)$
. An equivalent definition is that
![]() $R^{\delta }_{1}$
is the unique derivation extending
$R^{\delta }_{1}$
is the unique derivation extending
![]() $\delta $
such that
$\delta $
such that
![]() $R^{\delta }_{1}(x_{\mu }) = g_{\delta \mu }$
for every
$R^{\delta }_{1}(x_{\mu }) = g_{\delta \mu }$
for every
![]() $\mu \in \mathcal F$
. Finally, observe that
$\mu \in \mathcal F$
. Finally, observe that
![]() $K_{0}(W)$
is an algebraic extension of
$K_{0}(W)$
is an algebraic extension of
![]() $K_{0}(x_{\mathcal F})$
. So,
$K_{0}(x_{\mathcal F})$
. So,
![]() $R^{\delta }_{1}$
extends uniquely to a derivation
$R^{\delta }_{1}$
extends uniquely to a derivation
![]() $R^{\delta }$
from
$R^{\delta }$
from
![]() $K_{0}(W)$
to the algebraic closure of
$K_{0}(W)$
to the algebraic closure of
![]() $K_{0}(W)$
.
$K_{0}(W)$
.
We will consider the objects
![]() $x_{\mu }$
both as variables and as functions. Observe that, for every
$x_{\mu }$
both as variables and as functions. Observe that, for every
![]() $\mu \in \mathcal V$
,
$\mu \in \mathcal V$
,
![]() $g_{\mu }$
is the restriction of
$g_{\mu }$
is the restriction of
![]() $x_{\mu }$
to W.
$x_{\mu }$
to W.
Remark 5.3. Let
![]() $f \in K_{0}(x_{\mathcal V})$
and
$f \in K_{0}(x_{\mathcal V})$
and
![]() $h \in K_{0}(W)$
be the restriction of f to W. Then, we have
$h \in K_{0}(W)$
be the restriction of f to W. Then, we have
![]() $h = f(g_{\mathcal V})$
(we are seeing f as a rational function). Therefore,
$h = f(g_{\mathcal V})$
(we are seeing f as a rational function). Therefore,
 $$\begin{align*}R^{\delta}(h) = f^{\delta}(g_{\mathcal V}) + \sum_{\mu \in \mathcal V} \frac{\partial f}{\partial \mu}\upharpoonright_{W} \cdot R^{\delta}(g_{\mu}) = f^{\delta} \upharpoonright_W + \sum_{\mu \in \mathcal V} \frac{\partial f}{\partial \mu}\upharpoonright_{W} \cdot g_{\delta, \mu}. \end{align*}$$
$$\begin{align*}R^{\delta}(h) = f^{\delta}(g_{\mathcal V}) + \sum_{\mu \in \mathcal V} \frac{\partial f}{\partial \mu}\upharpoonright_{W} \cdot R^{\delta}(g_{\mu}) = f^{\delta} \upharpoonright_W + \sum_{\mu \in \mathcal V} \frac{\partial f}{\partial \mu}\upharpoonright_{W} \cdot g_{\delta, \mu}. \end{align*}$$
Lemma 5.4. Let
![]() $\mu \in \mathcal V$
. Then,
$\mu \in \mathcal V$
. Then,
Proof. If
![]() $\mu \in \mathcal F$
, the conclusion follows by definition of
$\mu \in \mathcal F$
, the conclusion follows by definition of
![]() $R^{\delta }_{1}$
.
$R^{\delta }_{1}$
.
If
![]() $\mu = \pi \in \mathcal P$
, observe that
$\mu = \pi \in \mathcal P$
, observe that
![]() $g_{\pi }$
satisfies the algebraic condition
$g_{\pi }$
satisfies the algebraic condition
Therefore,
 $$\begin{align*}R^{\delta}(g_{\pi}) = {{-}\frac{p_{\pi}^{\delta} + \sum_{\beta \in \mathcal F < \pi} \frac{\partial p_{\pi}}{\partial \beta} \cdot R^{\delta}(g_{\beta})} {\frac{\partial p_{\pi}}{\partial \pi}}}(g_{\pi}, g_{\mathcal F<\pi}) = f_{\delta, \pi} \upharpoonright_{W} = g_{\delta, \pi}.\\[-42pt] \end{align*}$$
$$\begin{align*}R^{\delta}(g_{\pi}) = {{-}\frac{p_{\pi}^{\delta} + \sum_{\beta \in \mathcal F < \pi} \frac{\partial p_{\pi}}{\partial \beta} \cdot R^{\delta}(g_{\beta})} {\frac{\partial p_{\pi}}{\partial \pi}}}(g_{\pi}, g_{\mathcal F<\pi}) = f_{\delta, \pi} \upharpoonright_{W} = g_{\delta, \pi}.\\[-42pt] \end{align*}$$
Remark 5.5. The image of
![]() $R^{\delta }$
is already in
$R^{\delta }$
is already in
![]() $K_{0}(W)$
(no need to take the algebraic closure). Indeed, as a
$K_{0}(W)$
(no need to take the algebraic closure). Indeed, as a
![]() $K_{0}$
-algebra,
$K_{0}$
-algebra,
![]() $K_{0}(W)$
is generated by
$K_{0}(W)$
is generated by
![]() $(g_{\mu }: \mu \in \mathcal V)$
. Thus, it suffices to show that
$(g_{\mu }: \mu \in \mathcal V)$
. Thus, it suffices to show that
![]() $R^{\delta }(g_{\mu }) \in K_{0}(W)$
, which follows from Lemma 5.4.
$R^{\delta }(g_{\mu }) \in K_{0}(W)$
, which follows from Lemma 5.4.
Lemma 5.6. For all
![]() $w \in \Gamma $
,
$w \in \Gamma $
,
![]() $R^w(g_{v, \pi }) = g_{wv, \pi }$
.
$R^w(g_{v, \pi }) = g_{wv, \pi }$
.
Lemma 5.7. Let
![]() $\delta , \varepsilon \in \bar \delta $
,
$\delta , \varepsilon \in \bar \delta $
,
![]() $f \in K_{0}(x_{\mathcal V})$
, and
$f \in K_{0}(x_{\mathcal V})$
, and
![]() $h \in K_{0}(W)$
be the restriction of f to W. Then,
$h \in K_{0}(W)$
be the restriction of f to W. Then,
 $$ \begin{align} [R^{\varepsilon}, R^{\delta}]h = \sum_{\mu \in \mathcal V} \frac{\partial f }{\partial \mu}\upharpoonright _{W} \cdot (R^{\varepsilon} g_{\delta, \mu} - R^{\delta} g_{\varepsilon, \mu}). \end{align} $$
$$ \begin{align} [R^{\varepsilon}, R^{\delta}]h = \sum_{\mu \in \mathcal V} \frac{\partial f }{\partial \mu}\upharpoonright _{W} \cdot (R^{\varepsilon} g_{\delta, \mu} - R^{\delta} g_{\varepsilon, \mu}). \end{align} $$
Proof.
(First proof) Let
![]() $\lambda = [\varepsilon , \delta ]$
be the Lie bracket of
$\lambda = [\varepsilon , \delta ]$
be the Lie bracket of
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\delta $
, and
$\delta $
, and
![]() $R^{\lambda } = [R^{\varepsilon }, R^{\delta }]$
be corresponding Lie bracket. We can write
$R^{\lambda } = [R^{\varepsilon }, R^{\delta }]$
be corresponding Lie bracket. We can write
![]() $h = f(g_{\mathcal V})$
, where we see f as a rational function: therefore, since
$h = f(g_{\mathcal V})$
, where we see f as a rational function: therefore, since
![]() $R^{\lambda }$
is a derivation, we have
$R^{\lambda }$
is a derivation, we have
 $$\begin{align*}R^{\lambda} h = h^{\lambda} + \sum_{\mu \in \mathcal V} \frac{\partial f}{\partial \mu}(g_{\mathcal V}) \cdot R^{\lambda}(g_{\mu}) = \sum_{\mu \in \mathcal V} \frac{\partial f }{\partial \mu}\upharpoonright _{W} \cdot (R^{\varepsilon} g_{\delta, \mu} - R^{\delta} g_{\varepsilon, \mu}). \end{align*}$$
$$\begin{align*}R^{\lambda} h = h^{\lambda} + \sum_{\mu \in \mathcal V} \frac{\partial f}{\partial \mu}(g_{\mathcal V}) \cdot R^{\lambda}(g_{\mu}) = \sum_{\mu \in \mathcal V} \frac{\partial f }{\partial \mu}\upharpoonright _{W} \cdot (R^{\varepsilon} g_{\delta, \mu} - R^{\delta} g_{\varepsilon, \mu}). \end{align*}$$
(Second proof) Since both the LHS and the RHS of (8) define a derivation on
![]() $K_{0}(W)$
, it suffices to show that they are equal when
$K_{0}(W)$
, it suffices to show that they are equal when
![]() $f = x_{\mu }$
for some
$f = x_{\mu }$
for some
![]() $\mu \in \mathcal F$
.
$\mu \in \mathcal F$
.
Then, RHS is equal to
![]() $R^{\varepsilon } g_{\delta , \mu } - R^{\delta } g_{\varepsilon , \mu }$
, which is equal to
$R^{\varepsilon } g_{\delta , \mu } - R^{\delta } g_{\varepsilon , \mu }$
, which is equal to
![]() $R^{\varepsilon } R^{\delta } g_{\mu } - R^{\delta } R^{\varepsilon } g_{\mu }$
, i.e., the LHS.
$R^{\varepsilon } R^{\delta } g_{\mu } - R^{\delta } R^{\varepsilon } g_{\mu }$
, i.e., the LHS.
We can finally prove the theorem.
Proof of Theorem 5.2
Assume that
![]() $\mathfrak S$
commutes locally (and that W is
$\mathfrak S$
commutes locally (and that W is
![]() $K_{0}$
-irreducible). Let
$K_{0}$
-irreducible). Let
![]() $\alpha \in \mathcal B$
: we show, by induction on
$\alpha \in \mathcal B$
: we show, by induction on
![]() $\alpha $
, that
$\alpha $
, that
![]() $\mathfrak S$
commutes at
$\mathfrak S$
commutes at
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $\pi , \pi ' \in \mathcal P$
and
$\pi , \pi ' \in \mathcal P$
and
![]() $w, w' \in \Gamma $
be such that
$w, w' \in \Gamma $
be such that
![]() $[w] \pi = [w'] \pi ' = \alpha $
: we need to show that
$[w] \pi = [w'] \pi ' = \alpha $
: we need to show that
![]() $g_{w, \pi } = g_{w', \pi '}$
.
$g_{w, \pi } = g_{w', \pi '}$
.
If
![]() $\pi = \pi '$
, we can reduce to the case when
$\pi = \pi '$
, we can reduce to the case when
![]() $w= v \delta \varepsilon u$
and
$w= v \delta \varepsilon u$
and
![]() $w' = v \varepsilon \delta u$
for some
$w' = v \varepsilon \delta u$
for some
![]() $\delta , \varepsilon \in \bar \delta $
,
$\delta , \varepsilon \in \bar \delta $
,
![]() $v, u \in \Gamma $
.
$v, u \in \Gamma $
.
If
![]() $u \neq 0$
, we have, by inductive hypothesis, that
$u \neq 0$
, we have, by inductive hypothesis, that
![]() $g_{v \delta \varepsilon , \pi } = g_{v \varepsilon \delta , \pi }$
and therefore
$g_{v \delta \varepsilon , \pi } = g_{v \varepsilon \delta , \pi }$
and therefore
which is the thesis.
If instead
![]() $u = 0$
, we have
$u = 0$
, we have
 $$\begin{align*}g_{w, \pi} - g_{w', \pi} = [R^{\varepsilon}, R^{\delta}] g_{v, \pi} = \sum_{\mu \in \mathcal V} \frac{\partial f_{v, \pi} }{\partial \mu}\upharpoonright _{W} \cdot (R^{\varepsilon} g_{\delta, \mu} - R^{\delta} g_{\varepsilon, \mu}). \end{align*}$$
$$\begin{align*}g_{w, \pi} - g_{w', \pi} = [R^{\varepsilon}, R^{\delta}] g_{v, \pi} = \sum_{\mu \in \mathcal V} \frac{\partial f_{v, \pi} }{\partial \mu}\upharpoonright _{W} \cdot (R^{\varepsilon} g_{\delta, \mu} - R^{\delta} g_{\varepsilon, \mu}). \end{align*}$$
Fix some
![]() $\mu $
in the above sum. Notice that
$\mu $
in the above sum. Notice that
![]() $\mu < [v]\delta $
, and therefore
$\mu < [v]\delta $
, and therefore
![]() $\delta \varepsilon \mu = \varepsilon \delta \mu < \alpha $
. Therefore, by inductive hypothesis,
$\delta \varepsilon \mu = \varepsilon \delta \mu < \alpha $
. Therefore, by inductive hypothesis,
![]() $R^{\varepsilon } g_{\delta , \mu } = g_{\varepsilon \delta \mu } = R^{\delta } g_{\varepsilon , \mu }$
. Thus, all summands are
$R^{\varepsilon } g_{\delta , \mu } = g_{\varepsilon \delta \mu } = R^{\delta } g_{\varepsilon , \mu }$
. Thus, all summands are
![]() $0$
and
$0$
and
![]() $g_{w, \pi } - g_{w', \pi } = 0$
, and we are done.
$g_{w, \pi } - g_{w', \pi } = 0$
, and we are done.
If
![]() $\pi \neq \pi '$
, let
$\pi \neq \pi '$
, let ![]() ; by definition,
; by definition,
![]() $\beta \leq \theta $
, and therefore, by assumption,
$\beta \leq \theta $
, and therefore, by assumption,
![]() $G_{\beta } = \{g_{\beta }\}$
. Let
$G_{\beta } = \{g_{\beta }\}$
. Let
![]() $u, u', w \in \Gamma $
be such that
$u, u', w \in \Gamma $
be such that
By the previous case, we have
Remark 5.8. If
![]() $\mathfrak S$
commutes globally, then the derivations
$\mathfrak S$
commutes globally, then the derivations
![]() $R^{\delta _{1}}, \dotsc , R^{\delta _{k}}$
commute with each other.
$R^{\delta _{1}}, \dotsc , R^{\delta _{k}}$
commute with each other.
The following remark motivates the definition of the functions
![]() $g_{\mu }$
.
$g_{\mu }$
.
Remark 5.9. Let
![]() $b \in K$
be such that
$b \in K$
be such that
![]() $b^{\mathcal V} \in W$
. Then, for every
$b^{\mathcal V} \in W$
. Then, for every
![]() $w \in \Gamma $
and
$w \in \Gamma $
and
![]() $\pi \in \mathcal P,$
$\pi \in \mathcal P,$
Therefore, for every
![]() $\mu \in \Theta $
,
$\mu \in \Theta $
,
Proof. By induction on
![]() $w $
.
$w $
.
Corollary 5.10. Let
![]() $b \in K$
be such that
$b \in K$
be such that
![]() $b^{\mathcal V} \in W$
and
$b^{\mathcal V} \in W$
and
![]() $b^{\mathcal F}$
is algebraically independent over
$b^{\mathcal F}$
is algebraically independent over
![]() $K_{0}$
. Then,
$K_{0}$
. Then,
![]() $\mathfrak S$
commutes.
$\mathfrak S$
commutes.
Proof. Remember that we are assuming that W is
![]() $K_{0}$
-irreducible. By Remark 5.9, for every
$K_{0}$
-irreducible. By Remark 5.9, for every
![]() $\mu \in \Theta $
and
$\mu \in \Theta $
and
![]() $g, g' \in G_{\mu }$
,
$g, g' \in G_{\mu }$
,
![]() $g(b^{\mathcal V}) = g'(b^{\mathcal V})$
. Since W is irreducible and
$g(b^{\mathcal V}) = g'(b^{\mathcal V})$
. Since W is irreducible and
![]() $b^{\mathcal V}$
is generic in W (over
$b^{\mathcal V}$
is generic in W (over
![]() $K_{0}$
), we have that
$K_{0}$
), we have that
![]() $g = g'$
.
$g = g'$
.
5.2. The axioms
Definition 5.11. The axioms of
![]() $T^{\bar \delta }_g$
are the axioms of
$T^{\bar \delta }_g$
are the axioms of
![]() $T^{\bar \delta }$
plus the following axiom scheme:
$T^{\bar \delta }$
plus the following axiom scheme:
-
(k -Deep) Let
 $\mathfrak S = (W; p_{\pi }: \pi \in \mathcal P)$
be a commutative configuration.Footnote
3
Let
$\mathfrak S = (W; p_{\pi }: \pi \in \mathcal P)$
be a commutative configuration.Footnote
3
Let
 $X \subseteq {\mathbb K}^{\mathcal V}$
be
$X \subseteq {\mathbb K}^{\mathcal V}$
be
 $L({\mathbb K})$
-definable, such that
$L({\mathbb K})$
-definable, such that
 $\Pi _{\mathcal F}(X)$
is large. Then, there exists
$\Pi _{\mathcal F}(X)$
is large. Then, there exists
 $a \in {\mathbb K}$
such that
$a \in {\mathbb K}$
such that
 $a^{\mathcal V} \in X$
.
$a^{\mathcal V} \in X$
.
Notice that the above is the analogue of the axiom scheme
![]() $(\texttt {Deep})$
. We don’t have an analogue for the axiom scheme
$(\texttt {Deep})$
. We don’t have an analogue for the axiom scheme
![]() $(\texttt {Wide})$
. Notice also that the axiom scheme (k
-Deep) is first-order expressible thanks to Theorem 5.2.
$(\texttt {Wide})$
. Notice also that the axiom scheme (k
-Deep) is first-order expressible thanks to Theorem 5.2.
Theorem 5.12.
-
(1)
 $T^{\bar \delta }_g$
is a consistent and complete extension of
$T^{\bar \delta }_g$
is a consistent and complete extension of
 $T^{\bar \delta }$
.
$T^{\bar \delta }$
. -
(2) If T is model-complete, then
 $T^{\bar \delta }_g$
is an axiomatization for the model completion of
$T^{\bar \delta }_g$
is an axiomatization for the model completion of
 $T^{\bar \delta }$
.
$T^{\bar \delta }$
. -
(3) If T eliminates quantifiers, then
 $T^{\bar \delta }_g$
eliminates quantifiers.
$T^{\bar \delta }_g$
eliminates quantifiers. -
(4) For every
 $L^{\bar \delta }$
-formula
$L^{\bar \delta }$
-formula
 $\alpha (\bar x)$
there exists an L-formula
$\alpha (\bar x)$
there exists an L-formula
 $\beta (\bar x)$
such that
$\beta (\bar x)$
such that  $$\begin{align*}T^{\bar \delta}_g \models \forall \bar x \bigl( \alpha(\bar x) \leftrightarrow \beta(\bar x^{\Theta}) \bigr). \end{align*}$$
$$\begin{align*}T^{\bar \delta}_g \models \forall \bar x \bigl( \alpha(\bar x) \leftrightarrow \beta(\bar x^{\Theta}) \bigr). \end{align*}$$
-
(5) For every
 $\langle {\mathbb K}, \bar \delta \rangle \models T^{\bar \delta }_g$
, for every
$\langle {\mathbb K}, \bar \delta \rangle \models T^{\bar \delta }_g$
, for every
 $\bar a$
tuple in
$\bar a$
tuple in
 ${\mathbb K}$
and
${\mathbb K}$
and
 $B \subseteq {\mathbb K}$
, the
$B \subseteq {\mathbb K}$
, the
 $L^{\bar \delta }$
-type of
$L^{\bar \delta }$
-type of
 $\bar a$
over B is determined by the L-type of
$\bar a$
over B is determined by the L-type of
 $\bar a^{\Theta }$
over
$\bar a^{\Theta }$
over
 $B^{\Theta }$
.
$B^{\Theta }$
.
We assume that T eliminates quantifiers. We use the criterion in Proposition 3.2(3) to show that
![]() $T^{\bar \delta }_g$
is the model completion of
$T^{\bar \delta }_g$
is the model completion of
![]() $T^{\bar \delta }$
and it eliminates quantifiers. We will do it in two lemmas.
$T^{\bar \delta }$
and it eliminates quantifiers. We will do it in two lemmas.
Lemma 5.13. Let
![]() $\langle A, \bar \delta \rangle \models T^{\bar \delta }$
. Let
$\langle A, \bar \delta \rangle \models T^{\bar \delta }$
. Let
![]() $\mathfrak S = (W; p_{\pi }: \pi \in \mathcal P)$
be a commutative configuration with parameters in A, and
$\mathfrak S = (W; p_{\pi }: \pi \in \mathcal P)$
be a commutative configuration with parameters in A, and
![]() $X \subseteq {\mathbb K}^{\mathcal V}$
be an
$X \subseteq {\mathbb K}^{\mathcal V}$
be an
![]() $L(A)$
-definable set, such that
$L(A)$
-definable set, such that
![]() $\Pi _{\mathcal F}(X)$
is large.
$\Pi _{\mathcal F}(X)$
is large.
Then, there exists
![]() $\langle B, \bar \delta \rangle \supseteq \langle A, \bar \delta \rangle $
and
$\langle B, \bar \delta \rangle \supseteq \langle A, \bar \delta \rangle $
and
![]() $b \in B$
such that
$b \in B$
such that
![]() $B \succeq A$
,
$B \succeq A$
,
![]() $\langle B, \bar \delta \rangle \models T^{\bar \delta }$
, and
$\langle B, \bar \delta \rangle \models T^{\bar \delta }$
, and
![]() $b^{\mathcal V} \in X$
.
$b^{\mathcal V} \in X$
.
Proof. Let
![]() $B \succeq A$
be
$B \succeq A$
be
![]() $\lvert A\rvert ^{+}$
-saturated. Let
$\lvert A\rvert ^{+}$
-saturated. Let
![]() $\bar b = (b_{\nu }: \nu \in \mathcal V) \in X_{B}$
be such that
$\bar b = (b_{\nu }: \nu \in \mathcal V) \in X_{B}$
be such that
![]() $b_{\mathcal F} := \Pi _{\mathcal F}(\bar b)$
is algebraically independent over A. Let
$b_{\mathcal F} := \Pi _{\mathcal F}(\bar b)$
is algebraically independent over A. Let
![]() $I \subset B$
be such that I is disjoint from
$I \subset B$
be such that I is disjoint from
![]() $b_{\mathcal F}$
and
$b_{\mathcal F}$
and ![]() is a transcendence basis of B over A. We extend each derivation
is a transcendence basis of B over A. We extend each derivation
![]() $\delta \in \bar \delta $
to B in the following way. It suffices to specify the value of
$\delta \in \bar \delta $
to B in the following way. It suffices to specify the value of
![]() $\delta $
on each
$\delta $
on each
![]() $c \in D$
.
$c \in D$
.
If
![]() $c \in I$
, we define
$c \in I$
, we define ![]() .
.
If
![]() $c = b_{\mu }$
for some
$c = b_{\mu }$
for some
![]() $\mu \in \mathcal F$
, we define
$\mu \in \mathcal F$
, we define ![]() .
.
By definition, it is clear that
![]() $b_{0}^{\mathcal V} = \bar b \in X$
. Thus, it suffices to show that the extensions of
$b_{0}^{\mathcal V} = \bar b \in X$
. Thus, it suffices to show that the extensions of
![]() $\bar \delta $
commute on all B. Again, it suffices to show that, for every
$\bar \delta $
commute on all B. Again, it suffices to show that, for every
![]() $c \in D$
and every
$c \in D$
and every
![]() $\delta , \varepsilon \in \bar \delta $
,
$\delta , \varepsilon \in \bar \delta $
,
If
![]() $c \in I$
, then both sides are equal to
$c \in I$
, then both sides are equal to
![]() $0$
, and we are done.
$0$
, and we are done.
Suppose now that
![]() $c = b_{\mu }$
for some
$c = b_{\mu }$
for some
![]() $\mu \in \mathcal F$
, we have to show that
$\mu \in \mathcal F$
, we have to show that
Since the argument is delicate we prefer to give two different proofs with two different approaches.
(First proof) For this first proof, we replace W with its A-irreducible component containing
![]() $\bar b$
. Thus, we may assume that W is A-irreducible. Since
$\bar b$
. Thus, we may assume that W is A-irreducible. Since
![]() $\bar b$
is generic in W, the map
$\bar b$
is generic in W, the map
![]() $A(W) \to A(\bar b)$
,
$A(W) \to A(\bar b)$
,
![]() $h \mapsto h(\bar b)$
is an isomorphism of A-algebras. Via the above isomorphism, the derivation
$h \mapsto h(\bar b)$
is an isomorphism of A-algebras. Via the above isomorphism, the derivation
![]() $R^{\delta }$
on
$R^{\delta }$
on
![]() $A(W)$
corresponds to the derivation
$A(W)$
corresponds to the derivation
![]() $\delta $
on
$\delta $
on
![]() $A(\bar b)$
. The assumptions plus Theorem 5.2 and Remark 5.8 imply that
$A(\bar b)$
. The assumptions plus Theorem 5.2 and Remark 5.8 imply that
![]() $R^{\delta }$
and
$R^{\delta }$
and
![]() $R^{\varepsilon }$
commute: therefore, also
$R^{\varepsilon }$
commute: therefore, also
![]() $\delta $
and
$\delta $
and
![]() $\varepsilon $
commute on
$\varepsilon $
commute on
![]() $A(\bar b)$
.
$A(\bar b)$
.
(Second proof) Since
![]() $\bar b \in W$
, we have that
$\bar b \in W$
, we have that
![]() $\delta b_{\pi } = f_{\delta , \pi }(\bar b)$
for every
$\delta b_{\pi } = f_{\delta , \pi }(\bar b)$
for every
![]() $\pi \in \mathcal P$
. Thus, by definition, for every
$\pi \in \mathcal P$
. Thus, by definition, for every
![]() $\nu \in \mathcal V$
,
$\nu \in \mathcal V$
,
Denote ![]() . By definition, the LHS of (9) is equal to
. By definition, the LHS of (9) is equal to
 $$ \begin{align} \begin{aligned} \delta g_{\varepsilon \mu}(\bar b)= \delta f(\bar b)= f^{\delta}(\bar b) &+ \sum_{\nu \in \mathcal V} \frac{\partial f}{\partial \nu}(\bar b) \cdot \delta b_{\nu} = \\ &= f^{\delta}(\bar b) + \sum_{\nu \in \mathcal V} \frac{\partial f}{\partial \nu}(\bar b) \cdot f_{\delta, \nu}(\bar b) = f_{\delta, \varepsilon \mu}(\bar b) = g_{\delta, \varepsilon \mu}(\bar b). \end{aligned}\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \begin{aligned} \delta g_{\varepsilon \mu}(\bar b)= \delta f(\bar b)= f^{\delta}(\bar b) &+ \sum_{\nu \in \mathcal V} \frac{\partial f}{\partial \nu}(\bar b) \cdot \delta b_{\nu} = \\ &= f^{\delta}(\bar b) + \sum_{\nu \in \mathcal V} \frac{\partial f}{\partial \nu}(\bar b) \cdot f_{\delta, \nu}(\bar b) = f_{\delta, \varepsilon \mu}(\bar b) = g_{\delta, \varepsilon \mu}(\bar b). \end{aligned}\\[-15pt]\nonumber \end{align} $$
Similarly, the RHS of (9) is equal to
![]() $g_{\varepsilon , \delta \mu }(\bar b)$
. Finally, since
$g_{\varepsilon , \delta \mu }(\bar b)$
. Finally, since
![]() $\mathfrak S$
commutes,
$\mathfrak S$
commutes,
![]() $g_{\delta , \varepsilon \mu } = g_{\varepsilon , \delta \mu }$
, and we are done.
$g_{\delta , \varepsilon \mu } = g_{\varepsilon , \delta \mu }$
, and we are done.
Lemma 5.14. Let
![]() $\langle B, \bar \delta \rangle \models T^{\bar \delta }$
,
$\langle B, \bar \delta \rangle \models T^{\bar \delta }$
,
![]() $\langle C,\bar \delta \rangle \models T^{\bar \delta }_g$
, and
$\langle C,\bar \delta \rangle \models T^{\bar \delta }_g$
, and
![]() $\langle A, \bar \delta \rangle $
be a common substructure, such that B and C have the same
$\langle A, \bar \delta \rangle $
be a common substructure, such that B and C have the same
![]() $L(A)$
-theory. Let
$L(A)$
-theory. Let
![]() $\gamma (x)$
be a quantifier-free
$\gamma (x)$
be a quantifier-free
![]() $L^{\bar \delta }$
-formula with parameters in A. Let
$L^{\bar \delta }$
-formula with parameters in A. Let
![]() $b \in B$
be such that
$b \in B$
be such that
![]() $\langle B, \bar \delta \rangle \models \gamma (b)$
. Then, there exists
$\langle B, \bar \delta \rangle \models \gamma (b)$
. Then, there exists
![]() $c \in C$
such that
$c \in C$
such that
![]() $\langle C, \bar \delta \rangle \models \gamma (c)$
.
$\langle C, \bar \delta \rangle \models \gamma (c)$
.
Proof. W.l.o.g., we may assume that the only constants in the language L are the elements of F, the only function symbols are
![]() $+$
and
$+$
and
![]() $\cdot $
, thus, an
$\cdot $
, thus, an
![]() $L(\bar \delta )$
-substructure is a differential subring containing F. Let
$L(\bar \delta )$
-substructure is a differential subring containing F. Let
![]() $A'$
(resp.,
$A'$
(resp.,
![]() $A"$
) be the relative algebraic closure (as fields, or equivalently as L-structures) of A inside B (resp., C). Since A has the same L-type in B and C, there exists an isomorphism
$A"$
) be the relative algebraic closure (as fields, or equivalently as L-structures) of A inside B (resp., C). Since A has the same L-type in B and C, there exists an isomorphism
![]() $\phi $
of L-structures between of
$\phi $
of L-structures between of
![]() $A'$
and
$A'$
and
![]() $A"$
extending the identity on A. Moreover, any derivations on A extends uniquely to
$A"$
extending the identity on A. Moreover, any derivations on A extends uniquely to
![]() $A'$
and
$A'$
and
![]() $A"$
: thus,
$A"$
: thus,
![]() $\phi $
is also an isomorphism of
$\phi $
is also an isomorphism of
![]() $L^{\bar \delta }$
-structures. Thus, w.l.o.g. we may assume that A is relatively algebraically closed in B and in C.
$L^{\bar \delta }$
-structures. Thus, w.l.o.g. we may assume that A is relatively algebraically closed in B and in C.
Let
and ![]() . If
. If
![]() $\mathcal F$
is empty, then
$\mathcal F$
is empty, then
![]() $b \in \operatorname {\mathrm {acl}}(A) = A$
, and we are done.
$b \in \operatorname {\mathrm {acl}}(A) = A$
, and we are done.
Otherwise, let
![]() $\mathcal P$
be the set of
$\mathcal P$
be the set of
![]() $\preceq $
-minimal elements of
$\preceq $
-minimal elements of
![]() $\mathcal B$
. For every
$\mathcal B$
. For every
![]() $\pi \in \mathcal P$
, let
$\pi \in \mathcal P$
, let
![]() $p_{\pi } \in A[x_{\pi }, x_{\mathcal F< \pi }]$
be such that
$p_{\pi } \in A[x_{\pi }, x_{\mathcal F< \pi }]$
be such that
![]() $p_{\pi }(\pi b, b^{\mathcal F < \pi }) =^{\pi } 0$
. Let W be the A-irreducible component of
$p_{\pi }(\pi b, b^{\mathcal F < \pi }) =^{\pi } 0$
. Let W be the A-irreducible component of
containing
![]() $b^{\mathcal V}$
.
$b^{\mathcal V}$
.
Claim 2.
![]() is a commutative configuration (over A).
is a commutative configuration (over A).
Again, we prefer to give two different proofs.
(First proof) Since
![]() $b^{\mathcal V}$
is generic (over A) in the A-irreducible variety W, the map
$b^{\mathcal V}$
is generic (over A) in the A-irreducible variety W, the map
![]() $\Phi : A(W) \mapsto A(b^{\mathcal V})$
,
$\Phi : A(W) \mapsto A(b^{\mathcal V})$
,
![]() $h \mapsto h(b^{\mathcal V})$
is an isomorphism of A-algebrae. Via the above isomorphism,
$h \mapsto h(b^{\mathcal V})$
is an isomorphism of A-algebrae. Via the above isomorphism,
![]() $R^{\delta }$
corresponds to the derivation
$R^{\delta }$
corresponds to the derivation
![]() $\delta $
on
$\delta $
on
![]() $A(b^{\mathcal V})= A(b^{\Theta })$
: thus, the maps
$A(b^{\mathcal V})= A(b^{\Theta })$
: thus, the maps
![]() $R^{\delta }$
commute with each other. Therefore, for every
$R^{\delta }$
commute with each other. Therefore, for every
![]() $\pi , \pi ' \in \mathcal P$
and
$\pi , \pi ' \in \mathcal P$
and
![]() $w,w' \in \Gamma $
with
$w,w' \in \Gamma $
with
![]() $[w] \pi = [w'] \pi '$
,
$[w] \pi = [w'] \pi '$
,
(Second proof) By Corollary 5.10.
Let
![]() $\beta (z_{\Theta })$
be a quantifier-free
$\beta (z_{\Theta })$
be a quantifier-free
![]() $L(A)$
-formula such that
$L(A)$
-formula such that
Let
Since
![]() $b^{\mathcal V} \in X$
, and X is
$b^{\mathcal V} \in X$
, and X is
![]() $L(A)$
-definable, we have that
$L(A)$
-definable, we have that
![]() $\Pi _{\mathcal F}(X)$
is large. Thus, there exists
$\Pi _{\mathcal F}(X)$
is large. Thus, there exists
![]() $c \in C$
such that
$c \in C$
such that
![]() $c^{\mathcal V} \in X$
. Since
$c^{\mathcal V} \in X$
. Since
![]() $c^{\mathcal V} \in W$
, by Remark 5.9 for every
$c^{\mathcal V} \in W$
, by Remark 5.9 for every
![]() $\mu \in \Theta $
we have
$\mu \in \Theta $
we have
![]() $c^{\mu } = g_{\mu }(c^{\mathcal V})$
. Therefore,
$c^{\mu } = g_{\mu }(c^{\mathcal V})$
. Therefore,
![]() $\langle C, \bar \delta \rangle \models \beta ( c^{\Theta })$
.
$\langle C, \bar \delta \rangle \models \beta ( c^{\Theta })$
.
5.2.1. Addendum
Call a configuration
![]() $\mathfrak S =(W; p_{\pi }: \pi \in \mathcal P)$
“
$\mathfrak S =(W; p_{\pi }: \pi \in \mathcal P)$
“
![]() $K_0$
-irreducible” if W is
$K_0$
-irreducible” if W is
![]() $K_{0}$
-irreducible. In the definition of a configuration we did not impose that it is irreducible. However, by the proof of the Amalgamation Lemma 5.14, it seems that it would suffice to impose in Axiom (k
-Deep) that only irreducible configurations need to be satisfied. The reason why we did not restrict ourselves to irreducible configurations is that we don’t know if we can impose irreducibility in a first-order way.
$K_{0}$
-irreducible. In the definition of a configuration we did not impose that it is irreducible. However, by the proof of the Amalgamation Lemma 5.14, it seems that it would suffice to impose in Axiom (k
-Deep) that only irreducible configurations need to be satisfied. The reason why we did not restrict ourselves to irreducible configurations is that we don’t know if we can impose irreducibility in a first-order way.
Question 5.15. Let
![]() $(W_{i}: i \in I)$
be an L-definable family of varieties in
$(W_{i}: i \in I)$
be an L-definable family of varieties in
![]() $K^{n}$
. Is the set
$K^{n}$
. Is the set
definable?
6. Stability and NIP
In this section we see that some of the model theoretic properties of T are inherited by
![]() $T^{\bar \delta ,?}_g.$
In a following paper we will consider other properties. We assume basic knowledge about stable and NIP theories: see [Reference Pillay40, Reference Simon51].
$T^{\bar \delta ,?}_g.$
In a following paper we will consider other properties. We assume basic knowledge about stable and NIP theories: see [Reference Pillay40, Reference Simon51].
Theorem 6.1.
-
(1) If T is stable, then
 $T^{\bar \delta ,?}_g$
is stable.
$T^{\bar \delta ,?}_g$
is stable. -
(2) If T is NIP, then
 $T^{\bar \delta ,?}_g$
is NIP.
$T^{\bar \delta ,?}_g$
is NIP.
The above theorem follows immediately from the following one.
Theorem 6.2. Let U be an L-theory. Let
![]() $\bar \delta $
be a set of new unary function symbols. Let
$\bar \delta $
be a set of new unary function symbols. Let
![]() $U'$
be an
$U'$
be an
![]() $L^{\bar \delta }$
-theory expanding U. Assume that, for every
$L^{\bar \delta }$
-theory expanding U. Assume that, for every
![]() $L^{\bar \delta }$
-formula
$L^{\bar \delta }$
-formula
![]() $\alpha (\bar x)$
there exists and L-formula
$\alpha (\bar x)$
there exists and L-formula
![]() $\beta (\bar y)$
such that
$\beta (\bar y)$
such that
where
![]() $\bar x^{\Gamma }$
is the set of
$\bar x^{\Gamma }$
is the set of
![]() $\bar \delta $
-terms in the variables
$\bar \delta $
-terms in the variables
![]() $\bar x$
.
$\bar x$
.
Then, for every
![]() $(M, \bar \delta ) \models U'$
and every
$(M, \bar \delta ) \models U'$
and every
![]() $\bar a$
tuple in M and B subset of M, the
$\bar a$
tuple in M and B subset of M, the
![]() $L^{\bar \delta }$
-type of
$L^{\bar \delta }$
-type of
![]() $\bar a$
over B is uniquely determined by the L-type of
$\bar a$
over B is uniquely determined by the L-type of
![]() $\bar a^{\Gamma }$
over
$\bar a^{\Gamma }$
over
![]() $B^{\Gamma }$
.
$B^{\Gamma }$
.
Moreover:
-
(1) If U is stable, then
 $U'$
is stable.
$U'$
is stable. -
(2) If U NIP, then
 $U'$
is NIP.
$U'$
is NIP.
Proof. The results follow easily by applying the following criteria.
(1) [Reference Shelah50, Theorem II. 2.13] A theory U is stable iff, for every subset A of a model M of U, and for every sequence
![]() $(\bar a_{n})_{n \in \mathbb {N}}$
of tuples in M, if
$(\bar a_{n})_{n \in \mathbb {N}}$
of tuples in M, if
![]() $(\bar a_{n})_{n \in \mathbb {N}}$
is an indiscernible sequence, then it is totally indiscernible.
$(\bar a_{n})_{n \in \mathbb {N}}$
is an indiscernible sequence, then it is totally indiscernible.
(2) [Reference Simon51, Proposition 2.8] A theory U is NIP iff, for every formula
![]() $\phi (\bar x; \bar y)$
and for any indiscernible sequence
$\phi (\bar x; \bar y)$
and for any indiscernible sequence
![]() $(\bar a_{i} : i \in I)$
and tuple
$(\bar a_{i} : i \in I)$
and tuple
![]() $\bar b$
, there is some end segment
$\bar b$
, there is some end segment
![]() $I_{0} \subseteq I$
such that
$I_{0} \subseteq I$
such that
![]() $\phi (a_{i}; b)$
is “constant” on
$\phi (a_{i}; b)$
is “constant” on
![]() $I_{0}$
: that is, either for every
$I_{0}$
: that is, either for every
![]() $i \in I_{0}$
$i \in I_{0}$
![]() $\phi (\bar a_{i}; \bar b)$
holds, or for every
$\phi (\bar a_{i}; \bar b)$
holds, or for every
![]() $i \in I_{0}$
$i \in I_{0}$
![]() $\neg \phi (\bar a_{i}; \bar b)$
holds.
$\neg \phi (\bar a_{i}; \bar b)$
holds.
7. Pierce–Pillay axioms
We give now an extra axiomatization for
![]() $T^{\delta }_g$
, in the “geometric” style of Pierce and Pillay [Reference Pierce and Pillay39]. We won’t use this axiomatization, but it may be of interest.
$T^{\delta }_g$
, in the “geometric” style of Pierce and Pillay [Reference Pierce and Pillay39]. We won’t use this axiomatization, but it may be of interest.
Let
![]() $\langle {\mathbb K}, \delta \rangle \models T^{\delta }$
.
$\langle {\mathbb K}, \delta \rangle \models T^{\delta }$
.
Let
![]() $W \subseteq {\mathbb K}^{n}$
be an algebraic variety defined over
$W \subseteq {\mathbb K}^{n}$
be an algebraic variety defined over
![]() ${\mathbb K}$
. We define the twisted tangent bundle
${\mathbb K}$
. We define the twisted tangent bundle
![]() $\tau W$
of W w.r.t.
$\tau W$
of W w.r.t.
![]() $\delta $
in the same way as in [Reference Pierce and Pillay39] (see also [Reference Moosa35], where it is called “prolongation”).
$\delta $
in the same way as in [Reference Pierce and Pillay39] (see also [Reference Moosa35], where it is called “prolongation”).
Let ![]() . Let
. Let
![]() ${\mathbb K}^{*} \succeq {\mathbb K}$
and
${\mathbb K}^{*} \succeq {\mathbb K}$
and ![]() . We define:
. We define:

Let
![]() $\bar p = (p_{1}, \dotsc , p_{\ell }) \in {\mathbb K}[\bar x]^{\ell }$
. Define
$\bar p = (p_{1}, \dotsc , p_{\ell }) \in {\mathbb K}[\bar x]^{\ell }$
. Define
and
![]() $(\bar p)_{{\mathbb K}}$
to be the ideal of
$(\bar p)_{{\mathbb K}}$
to be the ideal of
![]() ${\mathbb K}[\bar x]$
generated by
${\mathbb K}[\bar x]$
generated by
![]() $p_{1}, \dotsc , p_{\ell }$
.
$p_{1}, \dotsc , p_{\ell }$
.
Definition 7.1. Assume that
![]() $I(W/{\mathbb K}) = (p_{1}, \dotsc , p_{\ell })_{{\mathbb K}}$
. The twisted tangent bundle of W (w.r.t.
$I(W/{\mathbb K}) = (p_{1}, \dotsc , p_{\ell })_{{\mathbb K}}$
. The twisted tangent bundle of W (w.r.t.
![]() $\delta $
) is the algebraic variety
$\delta $
) is the algebraic variety
![]() $\tau ^{\delta } W \subseteq {\mathbb K}^{n} \times {\mathbb K}^{n}$
$\tau ^{\delta } W \subseteq {\mathbb K}^{n} \times {\mathbb K}^{n}$
where
![]() $p^{[\delta ]}$
was introduced in Definition 3.6.
$p^{[\delta ]}$
was introduced in Definition 3.6.
Notice that the definition of
![]() $\tau ^{\delta } W$
does not depend on the choice of polynomials
$\tau ^{\delta } W$
does not depend on the choice of polynomials
![]() $\bar p$
such that
$\bar p$
such that
![]() $I(W/{\mathbb K}) = (\bar p)_{{\mathbb K}}$
. Notice also that, when
$I(W/{\mathbb K}) = (\bar p)_{{\mathbb K}}$
. Notice also that, when
![]() $\delta = 0$
, the twisted tangent bundle
$\delta = 0$
, the twisted tangent bundle
![]() $\tau ^{0}W$
coincides with the tangent bundle.
$\tau ^{0}W$
coincides with the tangent bundle.
The importance in this context of the twisted tangent bundle is due to the following two facts:
Remark 7.2. If
![]() $\bar a \in W$
, then
$\bar a \in W$
, then
![]() $\langle \bar a, \delta \bar a \rangle \in \tau ^{\delta } W$
.
$\langle \bar a, \delta \bar a \rangle \in \tau ^{\delta } W$
.
Fact 7.3. Let
![]() $L \supset {\mathbb K}$
be a field. Let
$L \supset {\mathbb K}$
be a field. Let
![]() $\bar b \in W$
be (as interpreted in L) such that
$\bar b \in W$
be (as interpreted in L) such that
![]() $\bar b$
is generic in W over
$\bar b$
is generic in W over
![]() ${\mathbb K}$
(that is,
${\mathbb K}$
(that is,
![]() $\operatorname {\mathrm {rk}}(\bar b / {\mathbb K}) = \dim (W)$
). Let
$\operatorname {\mathrm {rk}}(\bar b / {\mathbb K}) = \dim (W)$
). Let
![]() $\bar c \in L^{n}$
be such that
$\bar c \in L^{n}$
be such that
![]() $\langle \bar b,\bar c \rangle \in \tau ^{\delta } W$
.
$\langle \bar b,\bar c \rangle \in \tau ^{\delta } W$
.
Then, there exists a derivation
![]() $\varepsilon $
on L extending
$\varepsilon $
on L extending
![]() $\delta $
and such that
$\delta $
and such that
![]() $\varepsilon \bar b = \bar c$
.
$\varepsilon \bar b = \bar c$
.
Proof. It is a known result: see [Reference Zariski and Samuel57, Chapter II, Section 17, Theorem 39]. See also [Reference Lang26, Theorem VIII.5.1], [Reference Pierce and Pillay39], and [Reference Guzy and Rivière19, Lemma 1.1].
We want to write an axiom scheme generalizing Pierce–Pillay to
![]() $T^{\delta }_g$
.
$T^{\delta }_g$
.
An idea would be to use the following:
-
(PP-wrong) Let
 $W \subseteq {\mathbb K}^{n}$
be an algebraic variety which is defined over
$W \subseteq {\mathbb K}^{n}$
be an algebraic variety which is defined over
 ${\mathbb K}$
and
${\mathbb K}$
and
 ${\mathbb K}$
-irreducible. Let
${\mathbb K}$
-irreducible. Let
 $U \subseteq \tau ^{\delta } W$
be an
$U \subseteq \tau ^{\delta } W$
be an
 $L({\mathbb K})$
-definable set, such that the projection of U over W is large in W (i.e., of the same dimension as W). Then, there exists
$L({\mathbb K})$
-definable set, such that the projection of U over W is large in W (i.e., of the same dimension as W). Then, there exists
 $\bar a \in W$
such that
$\bar a \in W$
such that
 $\langle \bar a, \delta \bar a \rangle \in U$
.
$\langle \bar a, \delta \bar a \rangle \in U$
.
However, there is an issue with the above axiom scheme: we don’t know how to express it in a first-order way! The reason is the following: given a definable family of tuples of polynomials
![]() $(\bar p_{i}: i \in I)$
, while each
$(\bar p_{i}: i \in I)$
, while each
![]() $\tau ^{\delta }(V_{{\mathbb K}}(\bar p_{i}))$
is definable, we do not know whether the family
$\tau ^{\delta }(V_{{\mathbb K}}(\bar p_{i}))$
is definable, we do not know whether the family
![]() $\bigl ( \tau ^{\delta }(V_{{\mathbb K}}(\bar p_{i})): i \in I \bigr )$
is definable. We leave it as an open problem, and we will use a different axiom scheme.
$\bigl ( \tau ^{\delta }(V_{{\mathbb K}}(\bar p_{i})): i \in I \bigr )$
is definable. We leave it as an open problem, and we will use a different axiom scheme.
Question 7.4. Let
![]() $\bigl ( \bar p_{i}: i \in I \bigr )$
be a definable family of tuples of polynomials. Is there a definable family
$\bigl ( \bar p_{i}: i \in I \bigr )$
be a definable family of tuples of polynomials. Is there a definable family
![]() $\bigl ( \bar q_{i}: i \in I \bigr )$
of tuples of polynomials, such that
$\bigl ( \bar q_{i}: i \in I \bigr )$
of tuples of polynomials, such that
![]() $I(V_{{\mathbb K}}(\bar p_{i})/{\mathbb K}) = (\bar q_{i})_{{\mathbb K}}$
for every
$I(V_{{\mathbb K}}(\bar p_{i})/{\mathbb K}) = (\bar q_{i})_{{\mathbb K}}$
for every
![]() $i \in I$
?
$i \in I$
?
The above question is related to Question 5.15: notice that “W is
![]() ${\mathbb K}$
-irreducible” is equivalent to “
${\mathbb K}$
-irreducible” is equivalent to “
![]() $I(W/{\mathbb K})$
is prime”, and the latter, by [Reference van den Dries and Schmidt11] (see also [Reference Schoutens49]), is a definable property of the parameters of the formula defining
$I(W/{\mathbb K})$
is prime”, and the latter, by [Reference van den Dries and Schmidt11] (see also [Reference Schoutens49]), is a definable property of the parameters of the formula defining
![]() $I(W/{\mathbb K})$
.
$I(W/{\mathbb K})$
.
We need some additional definitions and results before introducing the true axiom scheme. Fix
![]() $\bar p \in {\mathbb K}[\bar x]^{\ell }$
, and let
$\bar p \in {\mathbb K}[\bar x]^{\ell }$
, and let ![]() . Given
. Given
![]() $\bar a \in W$
, the twisted tangent space of
$\bar a \in W$
, the twisted tangent space of
![]() $\bar p$
at
$\bar p$
at
![]() $\bar a$
is
$\bar a$
is
Moreover,
![]() $\tau ^{0}(\bar p)$
is the usual tangent space at
$\tau ^{0}(\bar p)$
is the usual tangent space at
![]() $\bar a$
of
$\bar a$
of
![]() $V_{{\mathbb K}}(\bar p)$
.
$V_{{\mathbb K}}(\bar p)$
.
Remark 7.5. Let
![]() $\bar a \in ({K^{*}})^{n}$
, we define
$\bar a \in ({K^{*}})^{n}$
, we define ![]() and
and ![]() . Let
. Let
![]() $J'$
be the ideal of
$J'$
be the ideal of
![]() $F[\bar x]$
generated by J and let
$F[\bar x]$
generated by J and let ![]() be the tangent space at
be the tangent space at
![]() $\bar a$
(as an F-vector space). Then, the dimension of S as an F-vector space is equal to
$\bar a$
(as an F-vector space). Then, the dimension of S as an F-vector space is equal to
![]() $\operatorname {\mathrm {rk}}(\bar a/{\mathbb K})$
. Indeed, let
$\operatorname {\mathrm {rk}}(\bar a/{\mathbb K})$
. Indeed, let
![]() $S'$
be the set of derivations on F which are
$S'$
be the set of derivations on F which are
![]() $0$
on
$0$
on
![]() ${\mathbb K}$
: then, by Fact 7.3, S and
${\mathbb K}$
: then, by Fact 7.3, S and
![]() $S'$
are isomorphic as F-vector spaces. By [Reference Zariski and Samuel57, Chapter II, Section 17, Theorem 41], the dimension of
$S'$
are isomorphic as F-vector spaces. By [Reference Zariski and Samuel57, Chapter II, Section 17, Theorem 41], the dimension of
![]() $S'$
as F-vector space is equal to
$S'$
as F-vector space is equal to
![]() $\operatorname {\mathrm {rk}}(\bar a/{\mathbb K})$
.
$\operatorname {\mathrm {rk}}(\bar a/{\mathbb K})$
.
Let ![]() ; the following lemma shows that, under suitable conditions, we can replace
; the following lemma shows that, under suitable conditions, we can replace
![]() $I(W/{\mathbb K})$
with
$I(W/{\mathbb K})$
with
![]() $I(\bar p/{\mathbb K})$
. We need to introduce some notations:
$I(\bar p/{\mathbb K})$
. We need to introduce some notations:
Let ![]() and for every
and for every
![]() $d \in \mathbb {N}$
, we define
$d \in \mathbb {N}$
, we define
and ![]() .
.
Lemma 7.6. Let
![]() $\bar a \in ({{\mathbb K}^{*}})^{n}$
be such that
$\bar a \in ({{\mathbb K}^{*}})^{n}$
be such that
![]() $\bar a \in \operatorname {\mathrm {Reg}}(\bar p)$
and
$\bar a \in \operatorname {\mathrm {Reg}}(\bar p)$
and
![]() $rk(\bar a/{\mathbb K}) \geq d_{0}$
. Let
$rk(\bar a/{\mathbb K}) \geq d_{0}$
. Let ![]() and
and ![]() .
.
Then,
-
(1)
 $\dim (\operatorname {\mathrm {Reg}}(\bar p)) = \operatorname {\mathrm {rk}}(\bar a/{\mathbb K}) = d_{0}$
;
$\dim (\operatorname {\mathrm {Reg}}(\bar p)) = \operatorname {\mathrm {rk}}(\bar a/{\mathbb K}) = d_{0}$
; -
(2)
 $\tau ^{0}_{\bar a}(\bar p) = \tau ^{0}_{\bar a}(J)$
;
$\tau ^{0}_{\bar a}(\bar p) = \tau ^{0}_{\bar a}(J)$
; -
(3)
 $\tau ^{\delta }_{\bar a}(\bar p) = \tau ^{\delta }_{\bar a}(J)$
;
$\tau ^{\delta }_{\bar a}(\bar p) = \tau ^{\delta }_{\bar a}(J)$
; -
(4) for every
 $\bar b \in ({{\mathbb K}^{*}})^{n}$
such that
$\bar b \in ({{\mathbb K}^{*}})^{n}$
such that
 $\langle \bar a, \bar b \rangle \in \tau ^{\delta }(\bar p)$
there exists
$\langle \bar a, \bar b \rangle \in \tau ^{\delta }(\bar p)$
there exists
 $\delta '$
derivation on
$\delta '$
derivation on
 ${\mathbb K}^{*}$
extending
${\mathbb K}^{*}$
extending
 $\delta $
and such that
$\delta $
and such that
 $\delta '(\bar a) = \bar b$
.
$\delta '(\bar a) = \bar b$
.
Proof. (1) It is clear:
(2) Since
![]() $\bar p(\bar a) = 0$
, we have
$\bar p(\bar a) = 0$
, we have
![]() $(\bar p)_{{\mathbb K}} \subseteq J$
, and therefore
$(\bar p)_{{\mathbb K}} \subseteq J$
, and therefore
Thus,
![]() $\dim (V_{{\mathbb K}}(J)) \leq \dim W = d_{0}$
. Therefore,
$\dim (V_{{\mathbb K}}(J)) \leq \dim W = d_{0}$
. Therefore,
![]() $\bar a$
is also a generic point of
$\bar a$
is also a generic point of
![]() $V_{{\mathbb K}}(J)$
. So, by Remark 7.5,
$V_{{\mathbb K}}(J)$
. So, by Remark 7.5,
Therefore, the vector space
![]() $\tau ^{0}_{\bar a}(\bar p)$
contains
$\tau ^{0}_{\bar a}(\bar p)$
contains
![]() $\tau ^{0}_{\bar a}(J)$
and has the same dimension
$\tau ^{0}_{\bar a}(J)$
and has the same dimension
![]() $d_{0}$
: thus, they are equal.
$d_{0}$
: thus, they are equal.
(3) Notice that
![]() $\tau ^{0}_{\bar a}(\bar p)$
and
$\tau ^{0}_{\bar a}(\bar p)$
and
![]() $\tau ^{\delta }_{\bar a}(\bar p)$
are vector spaces of the same dimension, and the same happens for
$\tau ^{\delta }_{\bar a}(\bar p)$
are vector spaces of the same dimension, and the same happens for
![]() $\tau ^{\delta }_{\bar a}(J)$
. Moreover,
$\tau ^{\delta }_{\bar a}(J)$
. Moreover,
![]() $\tau ^{\delta }_{\bar a}(\bar p)$
contains
$\tau ^{\delta }_{\bar a}(\bar p)$
contains
![]() $\tau ^{\delta }_{\bar a}(J)$
and has the same dimension, and therefore
$\tau ^{\delta }_{\bar a}(J)$
and has the same dimension, and therefore
![]() $\tau ^{\delta }_{\bar a}(\bar p) = \tau ^{\delta }_{\bar a}(J)$
.
$\tau ^{\delta }_{\bar a}(\bar p) = \tau ^{\delta }_{\bar a}(J)$
.
(4) It follows from Fact 7.3.
Given
![]() $m, n, d \in \mathbb {N}$
, let
$m, n, d \in \mathbb {N}$
, let
be a parameterization (definable in the language of rings) of all m-tuples of polynomials in
![]() ${\mathbb K}[x_{1}, \dotsc , x_{n}]$
of degree at most d. We will write
${\mathbb K}[x_{1}, \dotsc , x_{n}]$
of degree at most d. We will write
![]() $\bar p$
instead of
$\bar p$
instead of
![]() $\bar p_{m,n,d}$
.
$\bar p_{m,n,d}$
.
For each
![]() $\bar a \in {\mathbb K}^{\ell }$
, let
$\bar a \in {\mathbb K}^{\ell }$
, let ![]() and
and ![]() . Let
. Let
![]() $\Pi _{n}: {\mathbb K}^{n} \times {\mathbb K}^{n} \to {\mathbb K}^{n}$
be the canonical projection onto the first n coordinates.
$\Pi _{n}: {\mathbb K}^{n} \times {\mathbb K}^{n} \to {\mathbb K}^{n}$
be the canonical projection onto the first n coordinates.
We can finally write the axiom scheme.
-
 $(\texttt {PP})$
Let
$(\texttt {PP})$
Let
 $m,n,d \in \mathbb {N}$
and
$m,n,d \in \mathbb {N}$
and  . Let
. Let
 $\bar a \in {\mathbb K}^{\ell }$
and
$\bar a \in {\mathbb K}^{\ell }$
and
 $X \subseteq \tau ^{\delta }(\bar p(\bar x, \bar a))$
be
$X \subseteq \tau ^{\delta }(\bar p(\bar x, \bar a))$
be
 $L({\mathbb K})$
-definable. Assume that
$L({\mathbb K})$
-definable. Assume that
 $\Pi _{n}(X) \subseteq U_{\bar a}$
and
$\Pi _{n}(X) \subseteq U_{\bar a}$
and
 $\dim (\Pi _{n}(X)) = \dim (W_{\bar a})$
. Then, there exists
$\dim (\Pi _{n}(X)) = \dim (W_{\bar a})$
. Then, there exists
 $\bar c \in {\mathbb K}^{n}$
such that
$\bar c \in {\mathbb K}^{n}$
such that
 $\langle \bar c, \delta \bar c \rangle \in X$
.
$\langle \bar c, \delta \bar c \rangle \in X$
.
Theorem 7.7.
![]() is an axiomatization of
is an axiomatization of
![]() $T^{\delta }_g$
.
$T^{\delta }_g$
.
Proof. Since we can take
![]() $\bar p$
to be the empty tuple, and therefore
$\bar p$
to be the empty tuple, and therefore ![]() , it is clear that
, it is clear that
![]() $(\texttt {PP})$
implies
$(\texttt {PP})$
implies
![]() $(\texttt {Wide})$
.
$(\texttt {Wide})$
.
We have to prove the opposite. Since
![]() $T^{\delta }_g$
is complete, it suffices to show that
$T^{\delta }_g$
is complete, it suffices to show that
![]() ${T^{\delta }_{\mathrm {PP}}}$
is consistent. W.l.o.g., we may assume that T has elimination of quantifiers. To show that
${T^{\delta }_{\mathrm {PP}}}$
is consistent. W.l.o.g., we may assume that T has elimination of quantifiers. To show that
![]() ${T^{\delta }_{\mathrm {PP}}}$
is consistent, it suffices to prove the following:
${T^{\delta }_{\mathrm {PP}}}$
is consistent, it suffices to prove the following:
Claim 3. Let
![]() $m,n,d, \bar p, \bar a, X$
be as in
$m,n,d, \bar p, \bar a, X$
be as in
![]() $(\texttt {PP})$
. Then there exists
$(\texttt {PP})$
. Then there exists
![]() $\mathbb{K}^{*} \succeq {\mathbb K}$
and
$\mathbb{K}^{*} \succeq {\mathbb K}$
and
![]() $\bar b \in ({{\mathbb K}^{*}})^{n}$
such that
$\bar b \in ({{\mathbb K}^{*}})^{n}$
such that
![]() $\langle \bar b, \delta \bar b \rangle \in X$
.
$\langle \bar b, \delta \bar b \rangle \in X$
.
Let
![]() $\mathbb{K}^{*} \succ {\mathbb K}$
be sufficiently saturated and
$\mathbb{K}^{*} \succ {\mathbb K}$
be sufficiently saturated and
![]() $\bar b \in {{\mathbb K}^{*}}^{n}$
such that
$\bar b \in {{\mathbb K}^{*}}^{n}$
such that
![]() $\bar b \in \Pi _{n}(X)$
and
$\bar b \in \Pi _{n}(X)$
and
![]() $\operatorname {\mathrm {rk}}(\bar b/K) = \dim (\Pi _{n}(X)) = \dim (W_{\bar a})$
. Let
$\operatorname {\mathrm {rk}}(\bar b/K) = \dim (\Pi _{n}(X)) = \dim (W_{\bar a})$
. Let
![]() $\bar c \in {{\mathbb K}^{*}}^{n}$
be such that
$\bar c \in {{\mathbb K}^{*}}^{n}$
be such that
![]() $\langle \bar b, \bar c \rangle \in X$
. By Lemma 7.6 there exists
$\langle \bar b, \bar c \rangle \in X$
. By Lemma 7.6 there exists
![]() $\delta '$
derivation on
$\delta '$
derivation on
![]() ${\mathbb K}^{*}$
extending
${\mathbb K}^{*}$
extending
![]() $\delta $
and such that
$\delta $
and such that
![]() $\delta (\bar b) = \bar c$
.
$\delta (\bar b) = \bar c$
.
Giving the analogue axiomatization for
![]() $T^{\bar \delta ,nc}_g$
is not difficult and the reader can provide the details.
$T^{\bar \delta ,nc}_g$
is not difficult and the reader can provide the details.
On the other hand, we won’t try to give a similar axiomatization for
![]() $T^{\bar \delta }_g$
, since already when
$T^{\bar \delta }_g$
, since already when
![]() $T= ACF$
it is an arduous task: see [Reference León Sánchez27, Reference Pierce37, Reference Pierce38].
$T= ACF$
it is an arduous task: see [Reference León Sánchez27, Reference Pierce37, Reference Pierce38].
8. Conjectures and open problems
We conclude the paper with a list of open problems, remarks and some ideas.
8.1. Elimination of imaginaries
Conjecture 8.1.
![]() $T^{\bar \delta ,?}_g$
has elimination of imaginaries modulo
$T^{\bar \delta ,?}_g$
has elimination of imaginaries modulo
![]() $T^{eq}$
.
$T^{eq}$
.
A few particular cases are known, when
![]() $T^{\bar \delta ,?}_g$
is one of the following:
$T^{\bar \delta ,?}_g$
is one of the following:
-
•
 $\textrm {DCF}_{0,\textrm {m}}$
: see [Reference McGrail32].
$\textrm {DCF}_{0,\textrm {m}}$
: see [Reference McGrail32]. -
•
 $\textrm {RCF}$
or certain theories of Henselian valued fields, endowed with m commuting generic derivations: see [Reference Cubides Kovacsics and Point8, Reference Fornasiero and Kaplan14] for a proof based on M. Tressl’s idea; see also [Reference Brouette, Kovacsics and Point5, Reference Montenegro and Rideau-Kikuchi34, Reference Point41] for different proofs.
$\textrm {RCF}$
or certain theories of Henselian valued fields, endowed with m commuting generic derivations: see [Reference Cubides Kovacsics and Point8, Reference Fornasiero and Kaplan14] for a proof based on M. Tressl’s idea; see also [Reference Brouette, Kovacsics and Point5, Reference Montenegro and Rideau-Kikuchi34, Reference Point41] for different proofs. -
•
 $\textrm {DCF}_{0,\textrm {m,nc}}$
(see [Reference Moosa and Scanlon36]).
$\textrm {DCF}_{0,\textrm {m,nc}}$
(see [Reference Moosa and Scanlon36]).
We have also established the validity of the above conjecture for certain topological structures. Drawing upon established techniques, it is probable that the conjecture can be proven for T simple (as proved in [Reference Mohamed33, Reference Moosa and Scanlon36]). However, for the general case, we believe that novel approaches are required (although some progress has been made in [Reference Brouette, Kovacsics and Point5]).
8.2. Definable types
Let
![]() $\langle {\mathbb K}, \bar \delta \rangle \models T^{\bar \delta ,?}_g$
. Given a type
$\langle {\mathbb K}, \bar \delta \rangle \models T^{\bar \delta ,?}_g$
. Given a type
![]() $p \in S_{L^\delta }^{n}({\mathbb K})$
, let
$p \in S_{L^\delta }^{n}({\mathbb K})$
, let
![]() $\bar a$
be a realization of p; we define
$\bar a$
be a realization of p; we define
![]() $\tilde p \in S_{L}^{n\times \Gamma }({\mathbb K})$
as the L-type of
$\tilde p \in S_{L}^{n\times \Gamma }({\mathbb K})$
as the L-type of
![]() $\bar a^{\Gamma }$
over
$\bar a^{\Gamma }$
over
![]() ${\mathbb K}$
.
${\mathbb K}$
.
Open problem 8.2. Is it true that p is definable iff
![]() $\tilde p$
is definable? We conjecture that it is true when
$\tilde p$
is definable? We conjecture that it is true when
![]() $T^{\bar \delta ,?}_g = T^{\bar \delta }_g$
.
$T^{\bar \delta ,?}_g = T^{\bar \delta }_g$
.
8.3. Zariski closure
Given
![]() $X \subseteq {\mathbb K}^{n}$
, denote by
$X \subseteq {\mathbb K}^{n}$
, denote by
![]() $X^{Zar}$
be the Zariski closure of X.
$X^{Zar}$
be the Zariski closure of X.
Open problem 8.3 (See [Reference Freitag, Sánchez and Li16])
(1) Let
![]() $\bigl ( X_{i}: i \in I \bigr )$
be an L-definable family of subsets of
$\bigl ( X_{i}: i \in I \bigr )$
be an L-definable family of subsets of
![]() ${\mathbb K}^{n}$
. Is
${\mathbb K}^{n}$
. Is
![]() $\bigl ( X_{i}^{Zar}: i \in I \bigr )$
also L-definable?
$\bigl ( X_{i}^{Zar}: i \in I \bigr )$
also L-definable?
(2) Assume that (1) holds for
![]() ${\mathbb K}$
. Let
${\mathbb K}$
. Let
![]() $\langle {\mathbb K}, \bar \delta \rangle \models T^{\bar \delta ,?}_g$
. Let
$\langle {\mathbb K}, \bar \delta \rangle \models T^{\bar \delta ,?}_g$
. Let
![]() $\bigl ( X_{i}: i \in I \bigr )$
be an
$\bigl ( X_{i}: i \in I \bigr )$
be an
![]() $L^\delta $
-definable family of subsets of
$L^\delta $
-definable family of subsets of
![]() ${\mathbb K}^{n}$
. Is
${\mathbb K}^{n}$
. Is
![]() $\bigl ( X_{i}^{Zar}: i \in I \bigr )$
also
$\bigl ( X_{i}^{Zar}: i \in I \bigr )$
also
![]() $L^\delta $
-definable?
$L^\delta $
-definable?
8.4. Monoid actions
Let
![]() $\Lambda $
be a monoid generated by a k-tuple
$\Lambda $
be a monoid generated by a k-tuple
![]() $\bar \delta $
: we consider
$\bar \delta $
: we consider
![]() $\Lambda $
as a quotient of the free monoid
$\Lambda $
as a quotient of the free monoid
![]() $\Gamma $
. We can consider actions of
$\Gamma $
. We can consider actions of
![]() $\Lambda $
on models of T such that each
$\Lambda $
on models of T such that each
![]() $\delta _{i}$
is a derivation: we have a corresponding theory
$\delta _{i}$
is a derivation: we have a corresponding theory
![]() $T^{\Lambda }$
whose language is
$T^{\Lambda }$
whose language is
![]() $L^\delta $
and with axioms given by T, the conditions that each
$L^\delta $
and with axioms given by T, the conditions that each
![]() $\delta _{i}$
is a derivation, and, for every
$\delta _{i}$
is a derivation, and, for every
![]() $\gamma , \gamma ' \in \Gamma $
which induce the same element of
$\gamma , \gamma ' \in \Gamma $
which induce the same element of
![]() $\Lambda $
, the axiom
$\Lambda $
, the axiom
![]() $\forall x\, \gamma x = \gamma 'x$
.
$\forall x\, \gamma x = \gamma 'x$
.
Open problem 8.4. Under which conditions on
![]() $\Lambda $
the theory
$\Lambda $
the theory
![]() $T^{\Lambda }$
has a model completion?
$T^{\Lambda }$
has a model completion?
Conjecture 8.5. Let
![]() $\Gamma _{\ell }$
be the free monoid in
$\Gamma _{\ell }$
be the free monoid in
![]() $\ell $
generators, and
$\ell $
generators, and
![]() $\Theta _{k}$
be the free commutative monoid in k generators. Then, for
$\Theta _{k}$
be the free commutative monoid in k generators. Then, for
![]() $\Lambda $
equal either to
$\Lambda $
equal either to
![]() $\Gamma _{\ell } \times \Theta _{k}$
or to
$\Gamma _{\ell } \times \Theta _{k}$
or to
![]() $\Gamma _{\ell } * \theta _{k}$
,
$\Gamma _{\ell } * \theta _{k}$
,
![]() $T^{\Lambda }$
has a model completion (where
$T^{\Lambda }$
has a model completion (where
![]() $\times $
is the Cartesian product, and
$\times $
is the Cartesian product, and
![]() $*$
is the free product). More generally, for
$*$
is the free product). More generally, for
![]() $\Gamma $
equal to a combination of free and Cartesian products of finitely many copies of
$\Gamma $
equal to a combination of free and Cartesian products of finitely many copies of
![]() $\mathbb {N}$
,
$\mathbb {N}$
,
![]() $T^{\Lambda }$
has a model completion.
$T^{\Lambda }$
has a model completion.
As a consequence of [Reference León Sánchez and Moosa28], when
![]() $T = ACF_{0}$
and
$T = ACF_{0}$
and
![]() $\Lambda = \Gamma _{\ell }\times \Theta _{k}$
,
$\Lambda = \Gamma _{\ell }\times \Theta _{k}$
,
![]() $T^{\Lambda }$
has a model companion.
$T^{\Lambda }$
has a model companion.
Maybe the following conditions on
![]() $\Lambda $
suffice for
$\Lambda $
suffice for
![]() $T^{\Lambda }$
to have a model completion:
$T^{\Lambda }$
to have a model completion:
Let
![]() $\preceq $
be the canonical quasi ordering on
$\preceq $
be the canonical quasi ordering on
![]() $\Lambda $
given by
$\Lambda $
given by
![]() $\alpha \preceq \beta \alpha $
for every
$\alpha \preceq \beta \alpha $
for every
![]() $\alpha ,\beta \in \Lambda $
; we assume that:
$\alpha ,\beta \in \Lambda $
; we assume that:
-
•
 $\preceq $
is a well-founded partial ordering;
$\preceq $
is a well-founded partial ordering; -
• for every
 $\lambda \in \Lambda $
, the set
$\lambda \in \Lambda $
, the set
 $\{\alpha \in \Lambda : \alpha \preceq \lambda \}$
is finite;
$\{\alpha \in \Lambda : \alpha \preceq \lambda \}$
is finite; -
• for every
 $\alpha , \beta \in \Lambda $
, if they have an upper bound, then they have a least upper bound;
$\alpha , \beta \in \Lambda $
, if they have an upper bound, then they have a least upper bound; -
• let
 $X \subset \Lambda $
be finite; assume that X is
$X \subset \Lambda $
be finite; assume that X is
 $\preceq $
-initial in
$\preceq $
-initial in
 $\Lambda $
; then,
$\Lambda $
; then,
 $\Lambda \setminus X$
has finitely many
$\Lambda \setminus X$
has finitely many
 $\preceq $
-minimal elements;
$\preceq $
-minimal elements; -
• if
 $\alpha _{1} \delta _{1} = \alpha _{2} \delta _{2}$
for some
$\alpha _{1} \delta _{1} = \alpha _{2} \delta _{2}$
for some
 $\alpha _{i} \in \Lambda $
and
$\alpha _{i} \in \Lambda $
and
 $\delta _{i} \in \bar \delta $
, then
$\delta _{i} \in \bar \delta $
, then
 $\delta _{1}$
and
$\delta _{1}$
and
 $\delta _{2}$
commute with each other; moreover, there exists
$\delta _{2}$
commute with each other; moreover, there exists
 $\beta \in \Lambda $
such that
$\beta \in \Lambda $
such that
 $\alpha _{1} = \delta _{2} \beta $
and
$\alpha _{1} = \delta _{2} \beta $
and
 $\alpha _{2} = \delta _{1} \beta $
.
$\alpha _{2} = \delta _{1} \beta $
.
Acknowledgements
The authors thank Noa Lavi, Giorgio Ottaviani, Françoise Point, Silvain Rideau-Kikuchi, Omar León Sánchez, and Marcus Tressl for the interesting discussions on the topic.
Funding
Both authors are members of the “National Group for Algebraic and Geometric Structures, and their Applications” (GNSAGA - INdAM). This research is part of the project PRIN 2022 “Models, sets and classification”.