Geology and geothermal conditions of the Pannonian basin

The heat flow density of the Pannonian basin ranges from 50 to 130 mW m⁻² with a mean value of 90–100 mW m⁻² (Hurter & Haenel, Reference Hurter and Haenel2002; Lenkey et al., Reference Lenkey, Dövényi, Horváth and Cloetingh2002; Horváth et al., Reference Horváth, Musitz, Balázs, Végh, Uhrin, Nádor, Koroknai, Pap, Tóth and Wórum2015). The wide range of values is explained by the presence of recharge areas and the cooling effect of the infiltrating meteoric waters. The overall positive geothermal character of the Pannonian basin with a geothermal gradient of about 45°C km⁻¹ (Dövényi and Horváth, Reference Dövényi, Horváth, Royden and Horváth1988) is related to the Early–Middle Miocene crustal extension. As a result of mid-Miocene rifting (Horváth and Royden Reference Horváth and Royden1981; Horváth Reference Horváth1993), deep basins originated with the deposition of thick offshore pelagic sediments in the rapidly sinking basin interiors, and coarse-grained brackish littoral facies sediments at the margins and on the tilting basement highs. This was followed by a significant thermal subsidence since the Late Miocene (Royden et al., Reference Royden, Horváth and Rumpler1983), when a huge inland lake (Lake Pannon) with a brackish water body formed about 11 Ma as a remnant of the Middle Miocene Paratethys Sea (Magyar et al., Reference Magyar, Geary and Müller1999; Harzhauser and Piller, Reference Harzhauser and Piller2007). This giant lake basin was gradually filled up by forward accretion of sediment packages during the Late Miocene and Early Pliocene, originating in the surrounding uplifting Alpine and Carpathian mountain belts. The resulting siliciclastic sequences with low thermal conductivity (the ‘Pannonian’ sedimentary succession) can be as thick as several thousand metres in the deepest sub-basins (Figures 1 and 2). The ‘Lower Pannonian’ sedimentary package consists of coarse material on basin floors deposited by turbidity currents with subsequent sedimentation of silt and argillaceous marl on the slopes. Prograding shelf sedimentation resulted in the deposition of thick sand bodies in the shelf front environment, overlain by fine-grained sediments of the shelf and alluvial plain, representing the latest stages of the filling-up of the lake basin, referred to as ‘Upper Pannonian’ (Bérczi and Phillips, Reference Bérczi and Phillips1985; Magyar et al., Reference Magyar, Geary and Müller1999, Reference Magyar, Radivojević, Sztanó, Synak, Ujszászi and Pócsik2013). The most favourable porous geothermal aquifers are formed in these ‘Upper Pannonian’ shelf front sands at depths from 500 to 2000 m, where the temperature ranges from 40 to 110°C (Szanyi and Kovács Reference Szanyi and Kovács2010; Nádor et al., Reference Nádor, Lapanje, Tóth, Rman, Szőcs, Prestor, Uhrin, Rajver, Fodor, Muráti and Székely2012; Rman, Reference Rman2014; Horváth et al., Reference Horváth, Musitz, Balázs, Végh, Uhrin, Nádor, Koroknai, Pap, Tóth and Wórum2015).

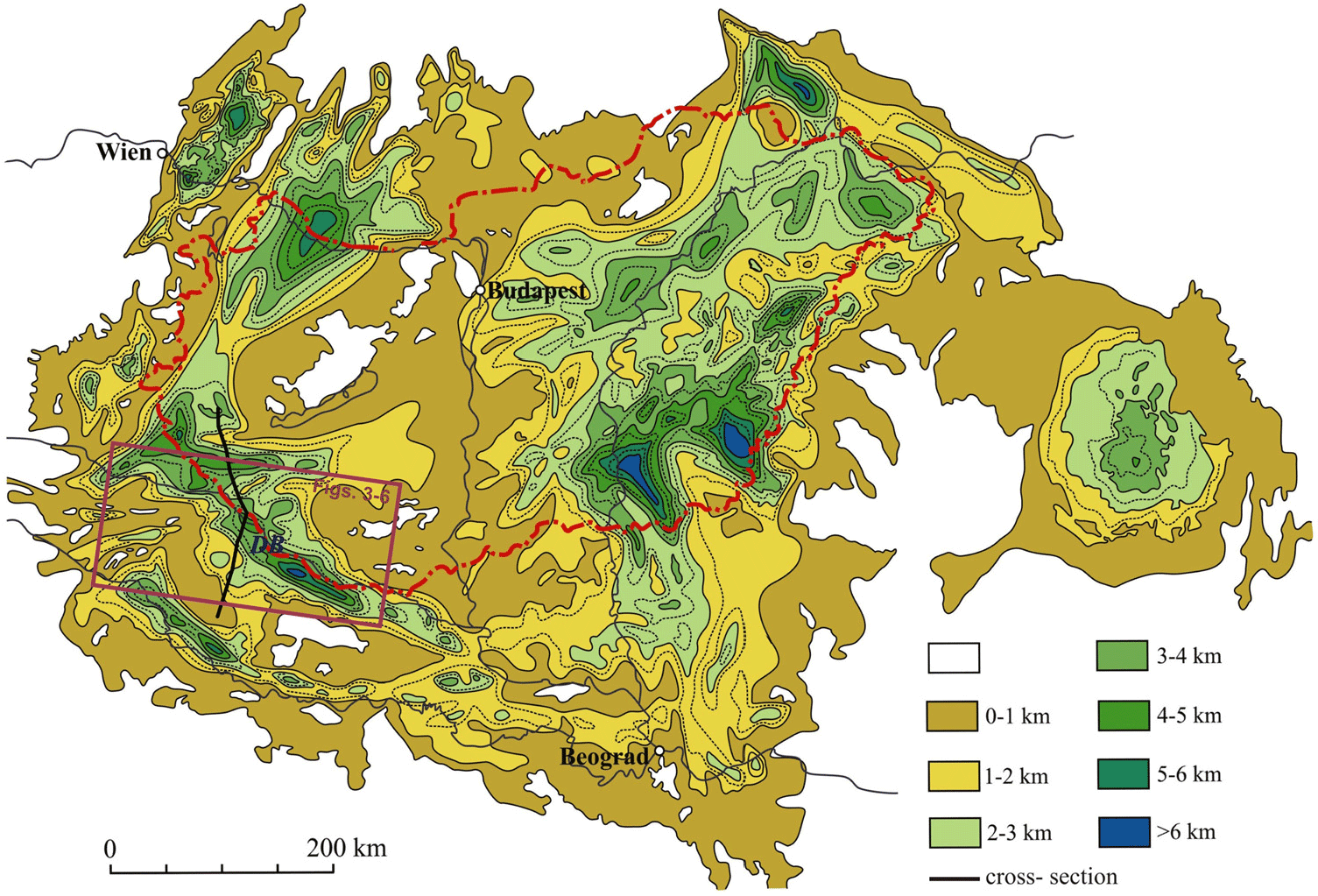
Figure 1. Thickness of Neogene sediments in the Pannonian basin (Horváth, Reference Horváth, Royden and Horváth1988). DB refers to the Dráva basin case study area, the top and bottom surfaces of whose most important potential porous geothermal reservoirs are displayed in Figures 3–6, also showing the location of the regional geological cross section in Figure 2.

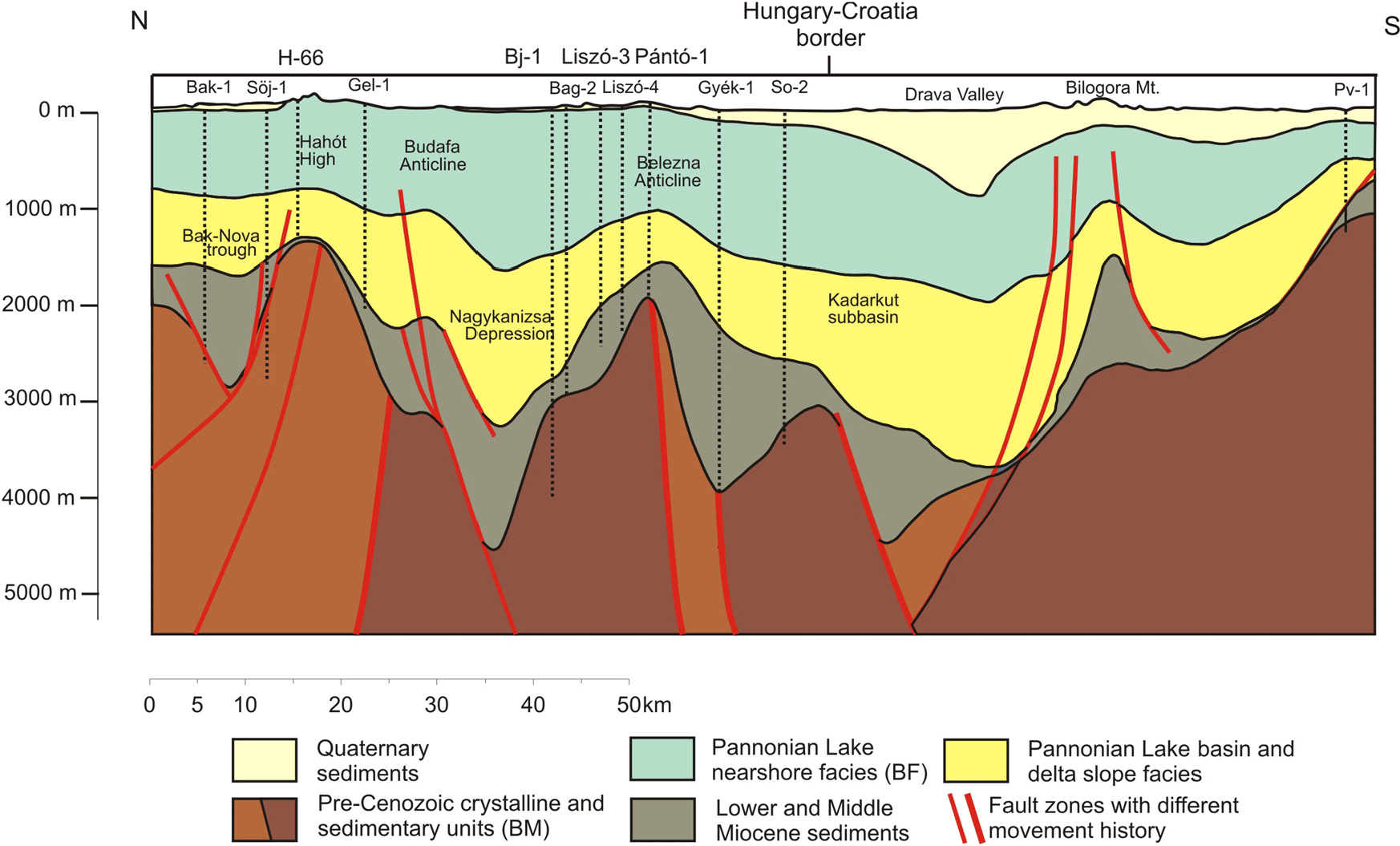
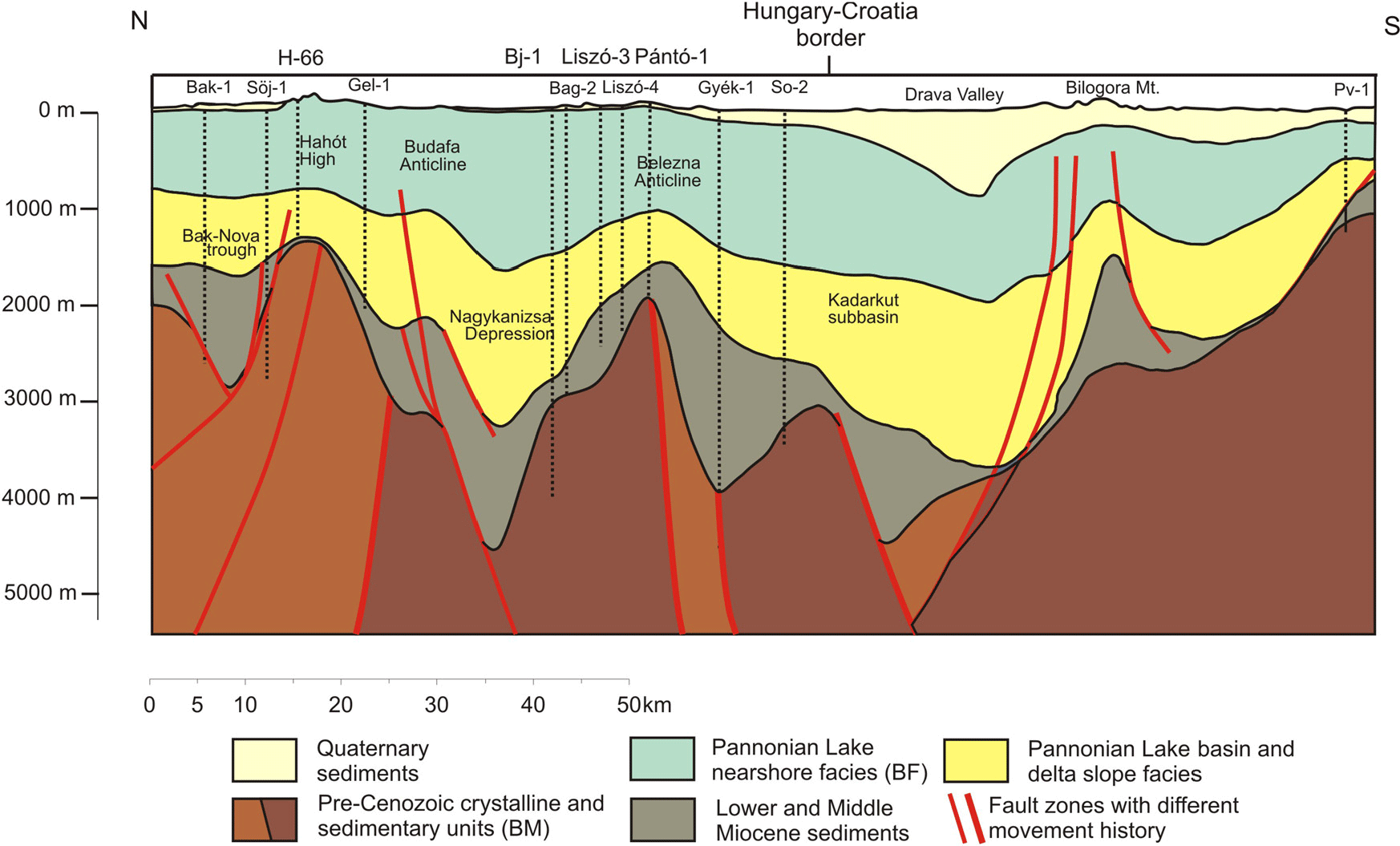
Figure 2. Geological cross section of the Dráva basin (Rotár-Szalkai et al., Reference Rotár-Szalkai, Maros, Bereczki, Markos, Babinszki, Zilahi-Sebess, Gulyás, Kun, Szőcs, Kerékgyártó, Nádor, Rajver, Lapanje, Šram, Marković, Vranješ, Farnoaga, Samardžić, Hrvatović, Skopljak and Jolović2018). Location is shown in Figure 1.

Under the several kilometres thick Neogene sedimentary sequences the basement of the Pannonian basin is extremely diverse and shows a complex structure, built up of various metamorphic and non-metamorphic Palaeo- and Mesozoic crystalline and carbonate rocks whose formation was associated with the Alpine–Carpathian orogene. They are arranged into nappes along thrust sheets, dissected by strike-slip and normal faults, associated with the multiphase tectonic development of the basin (Fodor et al., Reference Fodor, Csontos, Bada, Györfi, Benkovics, Durand, Jolivet, Horváth and Séranne1999; Csontos and Vörös Reference Csontos and Vörös2004; Horváth et al., Reference Horváth, Bada, Szafián, Tari, Ádám, Cloetingh, Gee and Stephenson2006; Schmid et al., Reference Schmid, Bernoulli, Fügenschuh, Matenco, Schefer, Schuster, Tischler and Ustaszewski2008; Haas et al., Reference Haas, Hámor, Jámbor, Kovács, Nagymarosy and Szederkényi2012; Haas & Budai, Reference Haas and Budai2014). These rocks also form some outcropping mountain regions, so-called ‘inselbergs’. The permeability of some basement carbonate rocks is enhanced by karstification that affected them during their geological evolution. The crystalline basement rocks might also serve as potential geothermal reservoirs, especially along regional tectonic zones with increased fissure permeability, or in their uppermost weathered-altered zones of 15–30 m average thickness. At the basement depth (around 2000 m or more) temperature can exceed 100–150°C (Dövényi et al., Reference Dövényi, Horváth, Drahos, Hurter and Haenel2002).

Methods of reservoir delineation

The method for delineating ‘potential reservoirs’ within the several thousand metre thick Pannonian (especially Upper Pannonian) sedimentary succession has been elaborated previously (Rotár-Szalkai et al., Reference Rotár-Szalkai, Nádor, Szőcs, Maros, Goetzl and Zekiri2017). It is based on the combination of representative geological horizons (top and bottom bounding surfaces of a given hydrogeological unit, potentially storing thermal water) by various subsurface isotherm maps by applying SURFER and ArcGIS softwares. As the regional thermal water flow systems of the Pannonian basin often cut across national borders, editing of such geological and geothermal model horizons requires massive data harmonisation among countries sharing the same transboundary geothermal reservoirs (Maros et al Reference Maros, Albert, Szeiler, Fodor, Gyalog, Jocha-Edelényi, Kercsmár, Magyari, Maigut, Maros, Nádor, Orosz, Palotás, Selmeczi, Uhrin, Vikor, Atzenhofer, Berka, Bottig, Brüstle, Hörfarter, Schubert, Weilbold, Baráth, Fordinál, Kronome, Maglay, Nagy, Jelen, Lapanje, Rifelj, Rižnar and Trajanova2012; Nádor et al., Reference Nádor, Lapanje, Tóth, Rman, Szőcs, Prestor, Uhrin, Rajver, Fodor, Muráti and Székely2012; Tóth et al., Reference Tóth, Rman, Rotár-Szalkai, Kerékgyártó, Szőcs, Lapanje, Černák, Remsík, Schubert and Nádor2016; Szőcs et al., Reference Szőcs, Rman, Rotár-Szalkai, Tóth, Lapanje, Černák and Nádor2018).

Despite the lower permeability of the clayey–marly strata within the thick shelf front to alluvial plain sedimentary sequences of the Pannonian basin-fill complex, hydraulic connection exists between the regionally extended sandy aquifer layers with a hydraulic conductivity of about 4 × 10⁻⁶ to 5 × 10⁻⁵ m s⁻¹. This makes the entire sedimentary series one large hydrostratigraphic unit (i.e. a unit encompassing different rock formations but possessing similar hydrogeological features) characterised by an almost uniform hydrostatic pressure.

The further subdivision of this large hydrostratigraphic unit into potential basin-fill geothermal reservoirs was done in three consecutive steps. First the bottom surface of the shelf-front sandy deposits and the top surface of the fine-grained alluvial sediments as bounding geological horizons of the main geothermal aquifers were edited.

Than various isotherm surfaces were selected to represent different temperature ranges of various utilisation schemes important in this region: thermal waters with temperatures of 30–50°C are mainly used for balneology; temperatures between 50 and 100°C are primarily suitable for direct heat utilisation, whereas the 75–100°C subcategory represents the temperature range in which thermal water can be economically used for larger district heating systems. Reservoirs having temperatures above 100°C have the potential for combined heat and power generation (CHP) projects using binary technologies. The various subsurface isotherm surfaces were edited on the basis of a simplified conductive model (details discussed in Rotár-Szalkai et al., Reference Rotár-Szalkai, Maros, Bereczki, Markos, Babinszki, Zilahi-Sebess, Gulyás, Kun, Szőcs, Kerékgyártó, Nádor, Rajver, Lapanje, Šram, Marković, Vranješ, Farnoaga, Samardžić, Hrvatović, Skopljak and Jolović2018), which was established for the entire southern part of the Pannonian basin in the DARLINGe project. The basic hypothesis of the calculation method was that the higher heat flow (higher values than world average) in the Pannonian basin is caused by the thinning of the lithosphere that resulted from lithosphere stretching coeval with the formation of the basin (Royden et al., Reference Royden, Horváth and Rumpler1983; Dövényi & Horváth Reference Dövényi, Horváth, Royden and Horváth1988). The relief of the pre-Pannonian basement evolved parallel with the intensive inflow of sediments due to thermal subsidence, i.e. the depth of the basin is proportional to the degree of thinning of the crust. The spatial variation of heat-flow density therefore reflects changes in the basin depth. Calculations of the depth value of the isotherm surfaces (grids) in the basin-fill sediments were performed by multiplying the basin depth by the average geothermal gradient. To validate the modelled temperature distribution, we compared them with the real temperature measurement data from wells. The comparison showed very close statistical agreement, but locally some differences occurred. Differences are expected in the regions where convection (modifying effect of groundwater flow) has an important role in spatial subsurface distribution of temperature, or is caused by uncertainty of temperature measurements.

As a last step the different basin-fill reservoirs were spatially outlined by combining the grids of the geological bounding horizons and the respective isotherms. For example, the combination of the geological horizon representing the top of the the fine-grained alluvial sediments and the 50°C isotherm surface designates the minimum depth of available thermal water with temperature higher than 50°C (top of BF50–75 reservoir). Similarly, the combination of the same geological horizon and the 75°C isotherm surface defines the minimum depth of available thermal water with temperature higher than 75°C (top of BF75–100 reservoir) and so on. It has to be highlighted that coming from the nature of sedimentary units, the basin-fill reservoirs are lens-shaped 3D bodies, whose top and bottom bounding horizons are bent surfaces which join each other, therefore they do not have ‘side walls’. Therefore the top (plan) view of a reservoir visualises the spatial distribution of both the top and bottom bounding surfaces.

Methods for potential assessment

When assessing the technical potential of a given geothermal reservoir, we want to express in a quantitative way the amount of geothermal energy to be potentially exploited. The first limit is the maximum realisable drilling depth which is 5–7 km (Muffler & Cataldi, Reference Muffler and Cataldi1978). It is also important to provide reliable values for the ‘recovery factor’ (the ratio of heat recoverable versus heat in place) that are needed to convert theoretical potentials into technical potentials. According to practical experience, its value is rather uncertain and varies in wide ranges. Depending on the geology and permeability, it is between 0.1 and 0.25 in porous systems and between 0.08 and 0.2 in fractured systems in the Pannonian basin (Nádor, Reference Nádor2016).

Since in large sedimentary basins, such as the Pannonian basin, the extraction of heat from the rock generally occurs by the production of thermal water (carrier of the heat energy), only the heat content of the ‘moveable fluid’ (fluid situated in the effective pore space) provides realistic values of the exploitable heat amount. In our study we considered this heat content as equivalent to the theoretical potential (physically usable energy as defined by Rybach, Reference Rybach2010) and performed calculations based on the classical formula of heat-in-place (i.e. volumetric method) (Muffler and Cataldi Reference Muffler and Cataldi1978), such as the following:

(1) $${Q_{{\rm{effpor}}}} = C \times m \times {\rm \Delta} T$$

• C = 4,187,106 J/(1000 kg·°C) is the specific heat capacity of water

• m = mass of moveable water (effective porosity) in reservoirs (kg)

• ΔT = T _average – T _reference is the excess temperature over 30°C (°C).

In our study we paid special attention to the determination of the effective porosity (which stores the moveable water that can be exploited), therefore the mass of moveable water in the reservoirs was calculated according to:

(2) $$m = \rho \times {\rm\Phi_{{\rm{eff}}}} \times {\rm{ }}{\rm \Delta} H \times A$$

• ρ = 1.0 [1000kg m⁻³] = specific density of water

• Φ_eff = average effective porosity of the reservoir (V_{eff pore}/V_total, no unit)

• ΔH = average thickness of the reservoir (m)

• A = area of the reservoir (m²)

where the effective porosity is:

(3) $${{\rm \Phi} _{{\rm{eff}}}} = (1 - {\rm{SH}}){\rm{ }} \times {{\rm \Phi} _{\rm{t}}}$$

• SH = average clay content of the reservoir (V _clay/V _total, no unit)

• Φ_t = average total porosity of the reservoir (V _pore/V _total, no unit).

Effective porosity is derived from total porosity. Its value is the function of actual basin depth (effect of compaction) and of the clay content. The clay content in our model was handled as laminar clay (the lithology consists of 100% sand and 100% clay layers, no disseminated clay). Lacking detailed geological information on the exact facies distribution of the Upper Pannonian shelf front, shelf and alluvial plain sequences in the southern part of the Pannonian basin, the clay content in the model was considered as varying between 20 and 60% (based on expert estimation and literature of the previous regional geological and hydrogeological modelling (Tóth et al., Reference Tóth, Rman, Rotár-Szalkai, Kerékgyártó, Szőcs, Lapanje, Černák, Remsík, Schubert and Nádor2016), with an average value of 40% for the entire sequence.

Results: Dráva basin case study

The Pannonian basin, as a large sedimentary basin complex, is composed of several sub-basins (Figure 1). The Dráva basin, situated along the border of Hungary and Croatia (Figure 1), is such a sub-basin, where the Neogene sedimentary succession is up to 5–7 km in total thickness (Figure 2) and is composed of three second-order megacycles separated by four major erosional unconformities (Stafic et al., Reference Stafic, Velic, Sztanó, Juhász and Ikovic2003).

In this very thick basin-fill complex we focused only on the Upper Pannonian – Pontian shelf front, shelf-plain, coastal plain to alluvial plain sedimentary succession (Pannonian Lake nearshore facies (BF) in Figure 2), as this is the major thermal-water bearing unit of the Dráva basin, which accumulated in an aggradational style due to the persistent high rate of subsidence coupled with an enormous rate of sediment supply. The top and bottom bounding horizons of this sedimentary unit – as characteristic facies, thus lithological boundaries – could be mapped from well logs and seismic sections, which were partly available for the study area (Horváth et al., Reference Horváth, Pap, Reményi and Tóth2012). The various isotherms (subsurface temperature maps) of 30, 50, 75, 100, 125 and 150°C derived from the conductive geothermal model. The top and bottom surfaces of the different basin-fill reservoirs were than edited by combining the geological bounding horizons and the respective isotherms. The top and bottom surfaces of the most important reservoirs of the Dráva basin (BF50–75, i.e. reservoirs storing thermal water with temperature higher than 50°C, and BF75–100, i.e. reservoirs storing thermal water with temperature higher than 75°C) are shown in Figures 3, 4, 5 and 6.

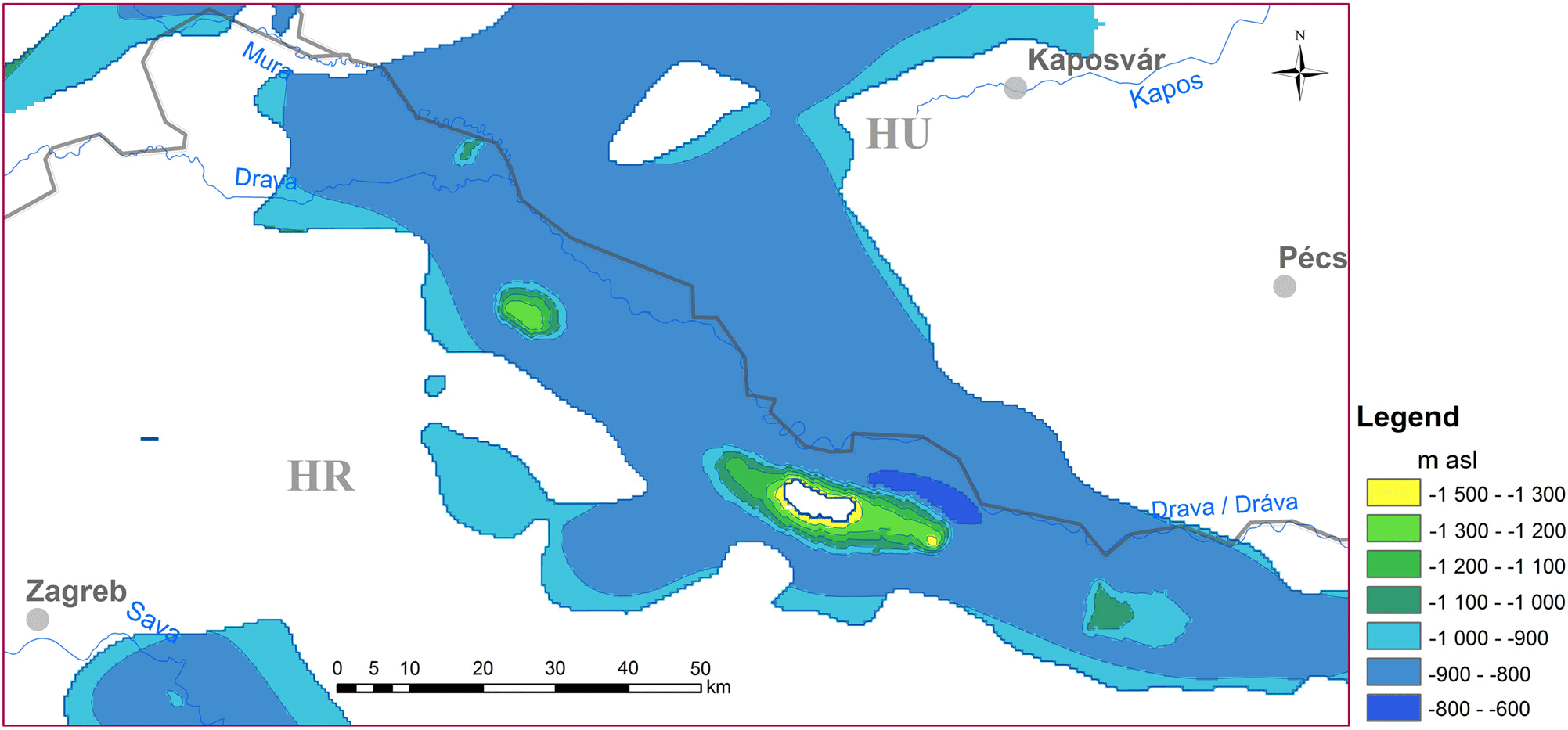
Figure 3. Top surface of the BF50–75 reservoir. The white patch indicates that the 50°C isotherm is most probably found in the very thick Quaternary sediments in the central depression of the Dráva basin (Figure 2), which is not considered as a sensu stricto ‘basin-fill reservoir’ due to its relatively low temperature.

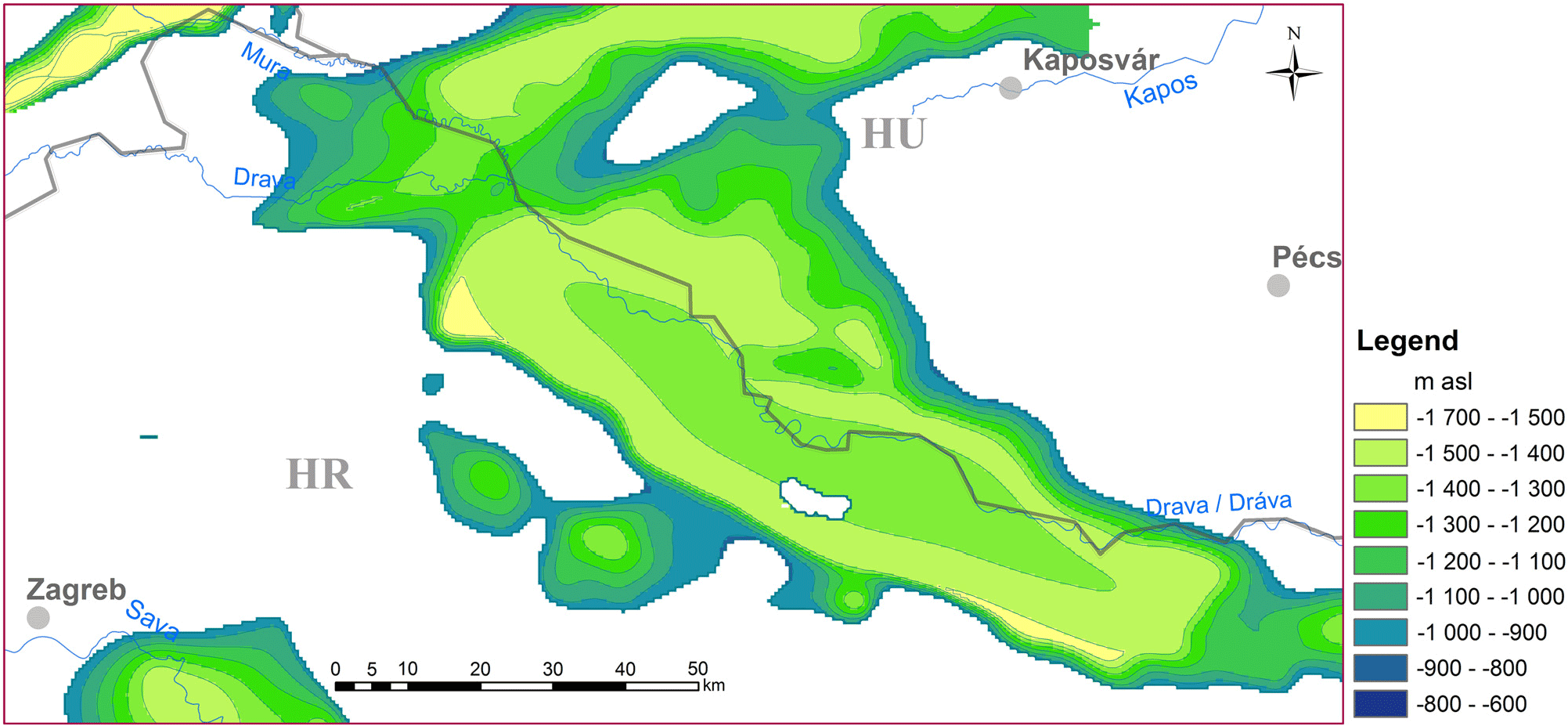
Figure 4. Bottom surface of the BF50–75 reservoir.

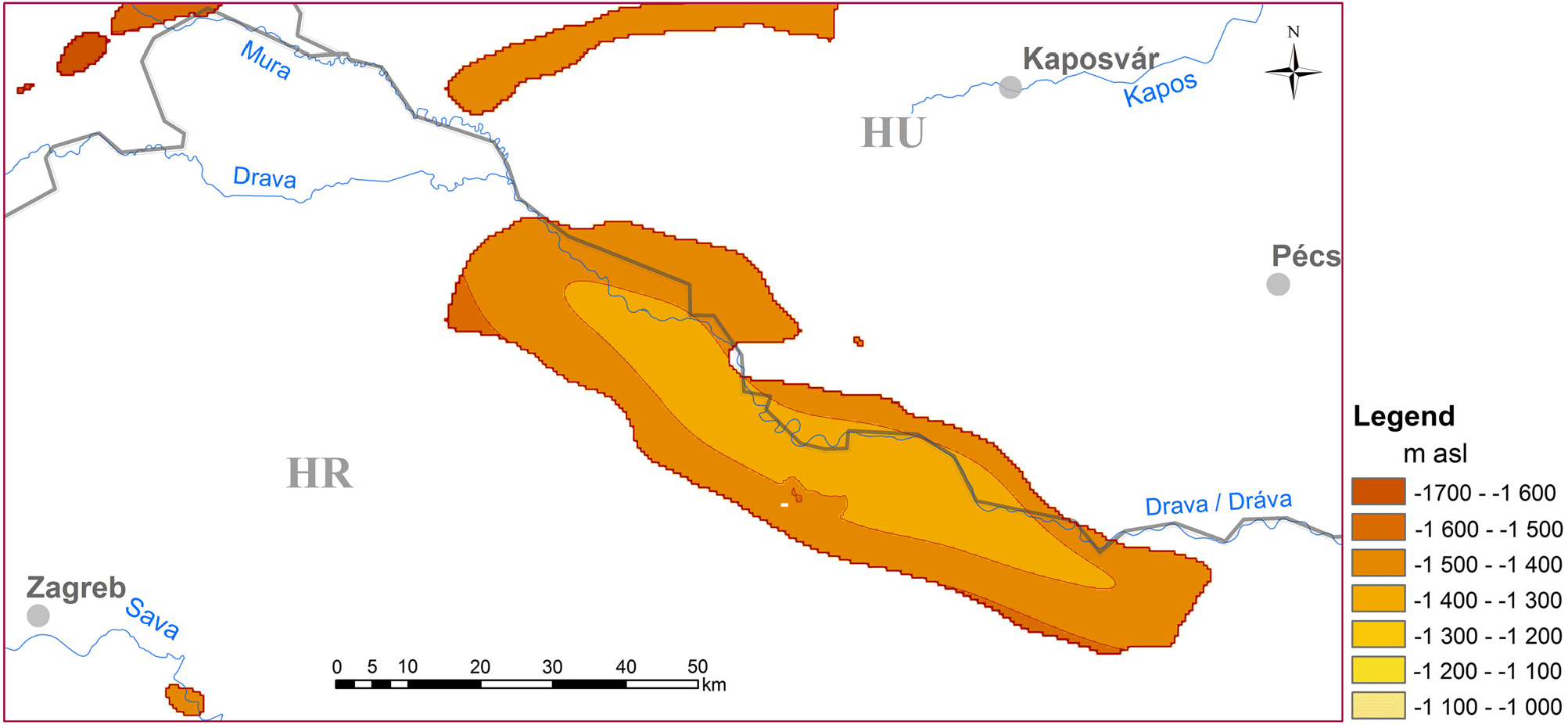
Figure 5. Top surface of the BF75–100 reservoir.

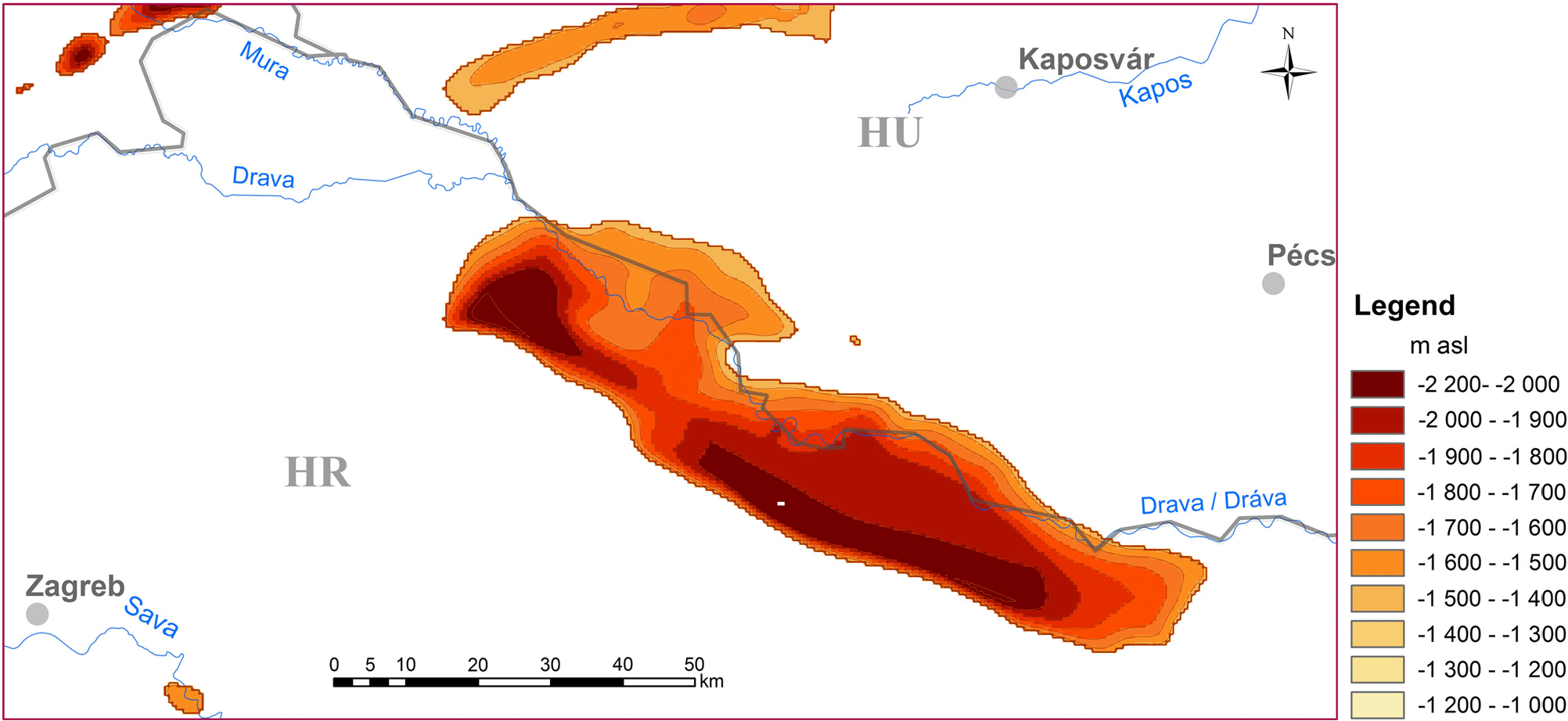
Figure 6. Bottom surface of the BF75–100 reservoir.

Once the reservoirs were spatially delineated, the next step was to calculate the effective porosity heat content and the recoverable heat for each reservoir category according to Equations 1, 2 and 3, summarised in Table 2. The distinctive parameters of a geothermal reservoir (area, thickness, porosity, and reservoir temperature) vary within a certain range of values, which can best be assessed by probabilistic approaches. Quantification of uncertainties in the parameters of the probability distribution can be dealt with quite well using the Monte Carlo simulation method (e.g. Shaha et al., Reference Shaha, Waidya and Sicar2018). The Monte Carlo simulation is a stochastic method, which uses randomness to solve problems that might be deterministic in principle. The computerised mathematical technique relies on repeated random sampling of input data series.

Table 2. Input and calculated parameters for quantifying the technical potential

In the Dráva basin case we applied the Monte Carlo simulation during the calculations of the effective porosity (Equation 3), where an average value and a standard deviation for the error of the estimated total porosity (±10%) and for the estimated clay content (±20%) were applied. For the rest of the parameters, static values were used: the area of the reservoirs was determined as the surface projection of the top of the reservoirs. The thicknesses of the reservoirs vary from place to place, and were individually determined in a 500 × 500 m grid from the geological model horizons as the distance between the top and bottom horizons. Temperature was estimated from the conductive model as an average for the given reservoir considering the depth and the thickness. These input parameters are summarised in Table 3.

Table 3. Input parameter values for the Dráva basin

Heat energy stored in the effective pore space (Equation 1) was also calculated by the Monte Carlo method where all the possible results were obtained with a cumulative distribution function in the form of P90, P50 and P10 cases representing high, medium and low levels of confidence. Two types of estimation were done: calculating the total heat content of moveable fluids (theoretical potential), and calculating the technical potential considering the recovery factor with a conservative value of 0.1 (Table 4). An example of the distribution of theoretical potential according to the various probability distributions is shown for one selected reservoir (BF75–100°C) in Figure 7, while Figure 8 summarises the calculated total heat content of moveable fluids for all of the BF reservoir types in the Dráva basin.

Table 4. Estimated heat content of effective porosity, at confidence levels P90, P50, P10, with and without applying the recovery factor of 0,1

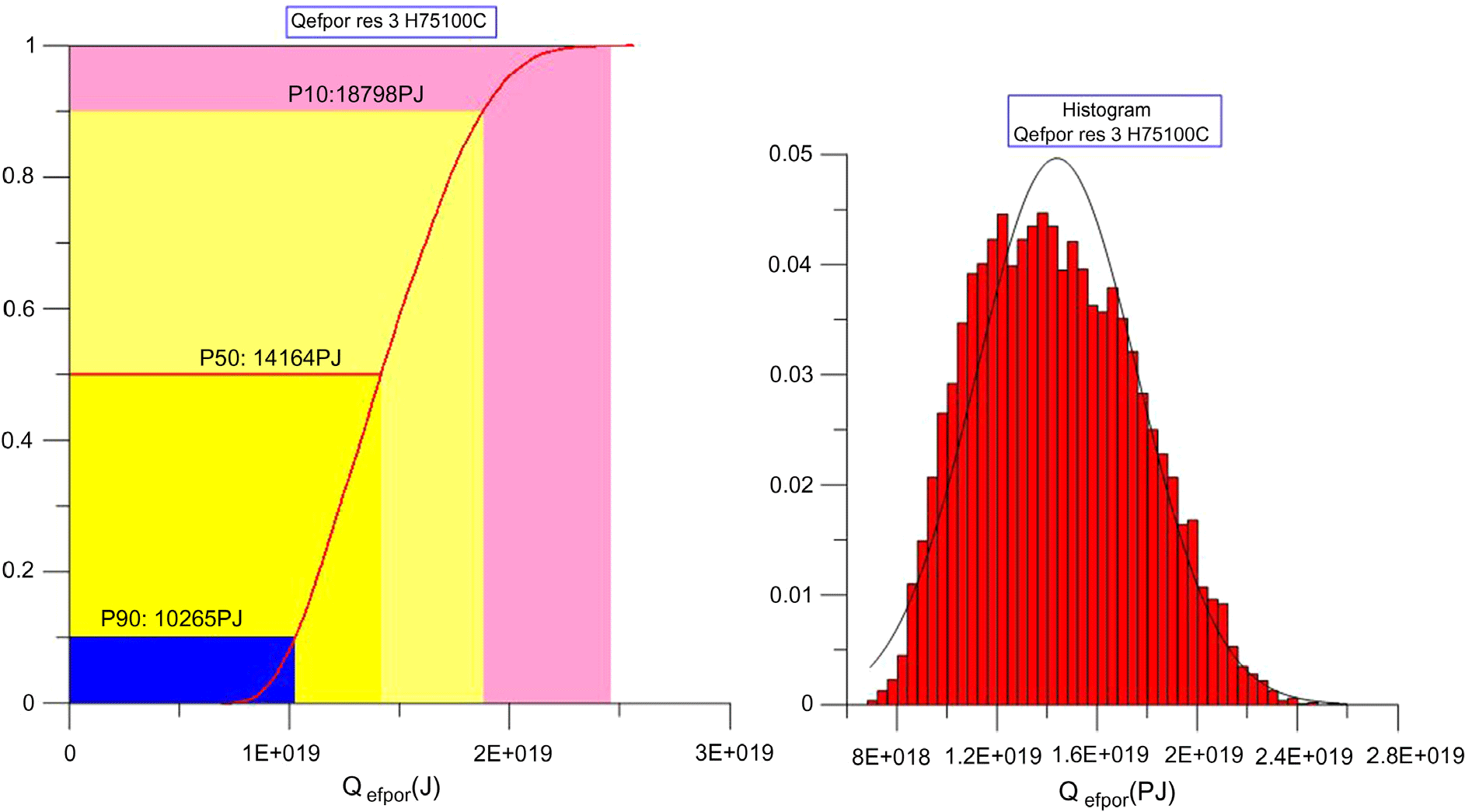
Figure 7. Distribution of the estimated theoretical potential according to P90, P50 and P10 for the BF75–100 reservoir in the Dráva basin.

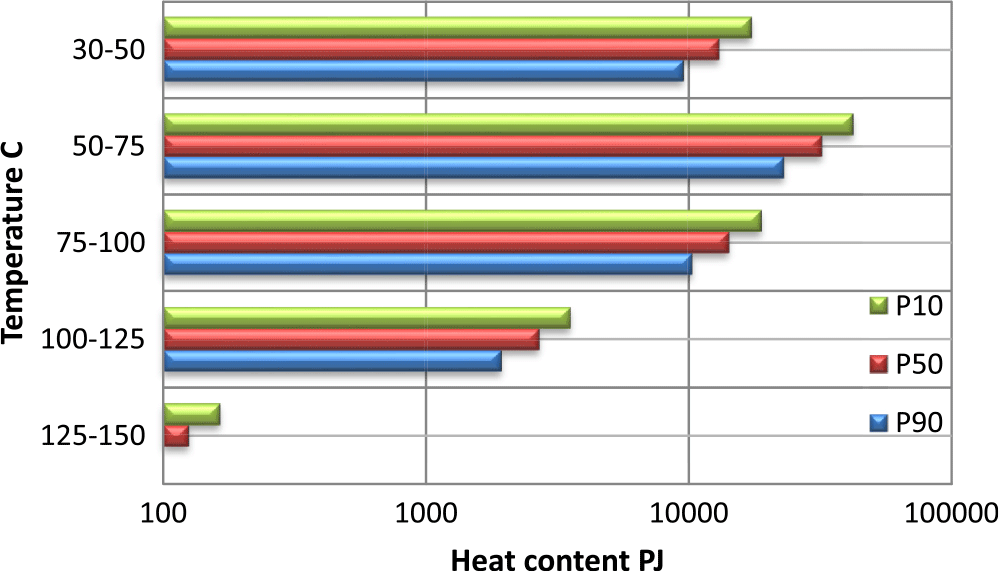
Figure 8. Calculated heat content of the BF reservoirs in the Dráva basin. Note that the BF50–75 reservoir is the most propitious in terms of P10, P50 and P90 values.

Discussion and conclusions

The paper has presented novel approaches to geothermal resource estimation at regional scales in two aspects: (1) it introduced methods for delineating potential geothermal reservoirs at basin scales, even extending beyond the political borders of neighbouring countries, and (2) it highlighted the importance of the extractable amount of geothermal energy stored in the effective porosity, and presented a probabilistic approach for its quantification.

(1) In the case of large, extended transboundary geothermal aquifers with multiple users having cumulative impacts by their thermal water abstractions, it is of utmost importance to have a joint and regional understanding of the reservoir dimensions and properties irrespective of state borders in order to guarantee sustainable production levels. The Pannonian basin in Central Europe is a typical case, where clarifications of the same reservoirs vary in the neighbouring countries due to the use of different geological nomenclatures for the same formation, different understandings of the thermal water flow systems, dissimilar models of the subsurface temperature field, etc. Although some promising progress in terms of common models has been achieved in the western part of the Pannonian basin (e.g; Rman et al. Reference Rman, Gál, Marcin, Weilbold, Schubert, Lapanje, Rajver, Benková and Nádor2016; Rotár-Szalkai et al., Reference Rotár-Szalkai, Nádor, Szőcs, Maros, Goetzl and Zekiri2017; Nádor et al., Reference Nádor, Kujbus and Tóth2019), the southern part remained a great challenge due to the highly uneven data distribution, and lack of FAIR principles (Findable, Accessible, Interoperable and Reusable) for data policies (Nádor, Reference Nádor2019). Nevertheless through the joint efforts of geoscientists from the DARLINGe project countries (Hungary, Slovenia, Croatia, Serbia, Bosnia and Herzegovina, and Romania) it was possible to edit some harmonised geological and geothermal model horizons (the latter based on a simplified conductive model), which served as the basic input information to delineate common, transboundary geothermal reservoirs within the several thousand meters thick Neogene sedimentary succession of the Pannonian basin. The simple but efficient method of reservoir delineation was based on the spatial combination of the bounding geological surfaces of the main geothermal aquifers with the respective isotherms, which made it possible to define a series of reservoir categories i.e. porous sediment bodies that store thermal water in temperature ranges of 30–50°C (BF 30–50), 50–75°C (BF 50–75), 75–100°C (BF 75–100), etc.

(2) The second group of new results is associated with the resource assessment of the delineated reservoirs. Estimations of geothermal resources – even for areas with well-acknowledged geothermal potential, such as the Pannonian basin – are often exaggerated. To provide scientifically based and reliable information, it has to be emphasised that potential investors should consider only the extractable amount of geothermal energy, which depends on many technical and non-technical limiting factors. In the case of sedimentary basins, one such aspect is the effective pore space, which stores the moveable (thermal) groundwater, i.e. the carrying medium of geothermal energy to be exploited. While the total porosity depends on a series of controlling factors, such as the original sediment composition and structure, grain size, etc., all determined by the former depositional environment, the effective porosity is rather governed by diagenetic processes, and its value is the function of actual basin depth (effect of compaction) and of the clay content.

All these novel methodological approaches were tested and presented through a case study of the Dráva basin, part of the Pannonian basin along the Hungarian–Croatian border. Figure 8 and Tables 3 and 4 let us draw the conclusion that both in volume and stored heat content, the BF50–75 reservoir (i.e. the part of the sandy Upper Pannonian sedimentary succession that stores exploitable thermal water with temperature between 50 and 75°C) is the most important in the Dráva basin. Its top surface is found around −800 to −900 m a.s.l. (Figure 3), representing an easy and relatively cheap drilling target. Although the BF30–50 reservoir is almost as extensive in volume (1,669,707 km³) as the BF50–75reservoir (1,819,788 km³), it has only about half as much stored heat content, due to its shallower depth (Table 4). The BF75–100 reservoir, situated at an average of −1400 to −1500 m depth (Figure 5), is more restricted in dimensions (associated with the central depression of the Dráva basin), but its heat content is still significant (about half of the BF50–75 reservoir’s; Table 4). These numbers underline the region’s great potential for space and district heating, which at the moment exists only at a few locations. Even though reservoirs storing thermal water above 100°C are limited to relatively small areas and bigger depths (below 2000 m), they represent a potential for CHP applications.