No CrossRef data available.
Article contents
COUNTING TO INFINITY: GRADED MODAL LOGIC WITH AN INFINITY DIAMOND
Published online by Cambridge University Press: 08 July 2022
Abstract
We extend the languages of both basic and graded modal logic with the infinity diamond, a modality that expresses the existence of infinitely many successors having a certain property. In both cases we define a natural notion of bisimilarity for the resulting formalisms, that we dub 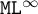 $\mathtt {ML}^{\infty }$ and
$\mathtt {ML}^{\infty }$ and 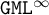 $\mathtt {GML}^{\infty }$, respectively. We then characterise these logics as the bisimulation-invariant fragments of the naturally corresponding predicate logic, viz., the extension of first-order logic with the infinity quantifier. Furthermore, for both
$\mathtt {GML}^{\infty }$, respectively. We then characterise these logics as the bisimulation-invariant fragments of the naturally corresponding predicate logic, viz., the extension of first-order logic with the infinity quantifier. Furthermore, for both 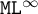 $\mathtt {ML}^{\infty }$ and
$\mathtt {ML}^{\infty }$ and 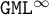 $\mathtt {GML}^{\infty }$ we provide a sound and complete axiomatisation for the set of formulas that are valid in every Kripke frame, we prove a small model property with respect to a widened class of weighted models, and we establish decidability of the satisfiability problem.
$\mathtt {GML}^{\infty }$ we provide a sound and complete axiomatisation for the set of formulas that are valid in every Kripke frame, we prove a small model property with respect to a widened class of weighted models, and we establish decidability of the satisfiability problem.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic



