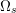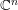1 Introduction
Let ![]() $(M,ds^{2})$ be a Kähler manifold of complex dimension
$(M,ds^{2})$ be a Kähler manifold of complex dimension ![]() $n$ with the Kähler metric
$n$ with the Kähler metric ![]() $ds^{2}=\sum g_{j\bar{k}}dz_{j}\otimes d\bar{z}_{k}$ in local coordinates. Let
$ds^{2}=\sum g_{j\bar{k}}dz_{j}\otimes d\bar{z}_{k}$ in local coordinates. Let ![]() ${\it\omega}=\sqrt{-1}/2{\it\pi}\sum g_{j\bar{k}}dz_{j}\wedge d\bar{z}_{k}$ be the positive
${\it\omega}=\sqrt{-1}/2{\it\pi}\sum g_{j\bar{k}}dz_{j}\wedge d\bar{z}_{k}$ be the positive ![]() $(1,1)$-form associated to the Kähler metric
$(1,1)$-form associated to the Kähler metric ![]() $ds^{2}$, and let
$ds^{2}$, and let ![]() $Ric({\it\omega})=-\sqrt{-1}/2{\it\pi}\partial \bar{\partial }\log \det (g_{j\bar{k}})$ be the Ricci form of
$Ric({\it\omega})=-\sqrt{-1}/2{\it\pi}\partial \bar{\partial }\log \det (g_{j\bar{k}})$ be the Ricci form of ![]() ${\it\omega}$. Then
${\it\omega}$. Then ![]() $ds^{2}$ is called Kähler–Einstein if
$ds^{2}$ is called Kähler–Einstein if ![]() $Ric({\it\omega})$ is proportional to the Kähler form
$Ric({\it\omega})$ is proportional to the Kähler form ![]() ${\it\omega}$.
${\it\omega}$.
In the present paper, we focus ourselves on the explicit Kähler–Einstein metrics of certain bounded pseudoconvex domains in ![]() $\mathbb{C}^{n}$. It is proved that for any domain of holomorphy, there is a unique complete Kähler–Einstein metric, with the Ricci curvature
$\mathbb{C}^{n}$. It is proved that for any domain of holomorphy, there is a unique complete Kähler–Einstein metric, with the Ricci curvature ![]() $-{\it\lambda}$, whose generating function
$-{\it\lambda}$, whose generating function ![]() $g$ satisfies the following Monge–Ampère equation with Dirichlet boundary condition:
$g$ satisfies the following Monge–Ampère equation with Dirichlet boundary condition:
where ![]() $(\partial ^{2}g/\partial z_{j}\partial \overline{z}_{k})=(g_{j\bar{k}})$ (see [Reference Cheng and Yau6], [Reference Mok and Yau12], [Reference Wu and Fornaess19]).
$(\partial ^{2}g/\partial z_{j}\partial \overline{z}_{k})=(g_{j\bar{k}})$ (see [Reference Cheng and Yau6], [Reference Mok and Yau12], [Reference Wu and Fornaess19]).
Usually, it is difficult to solve the above nonlinear partial differential equation (1) for general bounded pseudoconvex domains in ![]() $\mathbb{C}^{n}$. It is well known that, for any bounded homogeneous domain in
$\mathbb{C}^{n}$. It is well known that, for any bounded homogeneous domain in ![]() $\mathbb{C}^{n}$, the Bergman metric has constant Ricci curvature
$\mathbb{C}^{n}$, the Bergman metric has constant Ricci curvature ![]() $-1$ [Reference Bergman4]. Thus, the Bergman metric is identical to the Kähler–Einstein metric constructed by Cheng and Yau in [Reference Cheng and Yau6]. For nonhomogeneous cases, it was Bland who first described the Kähler–Einstein metric for the Thullen domain
$-1$ [Reference Bergman4]. Thus, the Bergman metric is identical to the Kähler–Einstein metric constructed by Cheng and Yau in [Reference Cheng and Yau6]. For nonhomogeneous cases, it was Bland who first described the Kähler–Einstein metric for the Thullen domain ![]() ${\rm\Omega}_{p}:=\{(z,w)\in \mathbb{C}^{n-1}\times \mathbb{C}:|w|^{2}<(1-\Vert z\Vert ^{2})^{1/p}\}$,
${\rm\Omega}_{p}:=\{(z,w)\in \mathbb{C}^{n-1}\times \mathbb{C}:|w|^{2}<(1-\Vert z\Vert ^{2})^{1/p}\}$, ![]() $p>0$ in [Reference Bland5], where the Monge–Ampère equation was reduced to an ordinary differential equation. Later, Yin and Roos generalized the Thullen domain to Cartan–Hartogs domains (see [Reference Wang, Yin, Zhang and Zhang18] for the definition). With Wang and Zhang, they obtained the explicit Kähler–Einstein metrics for Cartan–Hartogs domains in some critical cases [Reference Wang, Yin, Zhang and Roos17, Reference Wang, Yin, Zhang and Zhang18]. In general, the Cartan–Hartogs domains are not homogeneous due to [Reference Ahn, Byun and Park1] and [Reference Roos14], where the full holomorphic automorphism groups have been described explicitly already.
$p>0$ in [Reference Bland5], where the Monge–Ampère equation was reduced to an ordinary differential equation. Later, Yin and Roos generalized the Thullen domain to Cartan–Hartogs domains (see [Reference Wang, Yin, Zhang and Zhang18] for the definition). With Wang and Zhang, they obtained the explicit Kähler–Einstein metrics for Cartan–Hartogs domains in some critical cases [Reference Wang, Yin, Zhang and Roos17, Reference Wang, Yin, Zhang and Zhang18]. In general, the Cartan–Hartogs domains are not homogeneous due to [Reference Ahn, Byun and Park1] and [Reference Roos14], where the full holomorphic automorphism groups have been described explicitly already.
One observation of the above special domains is that both of them can be regarded as certain kinds of Hartogs domains, which are based on the unit ball or, more generally, bounded symmetric domains. The right-hand side of the defining inequality for either the Thullen domain or Cartan–Hartogs domains is exactly some negative power of the Bergman kernel (up to a constant). Besides, it is well known that bounded symmetric domains are special kinds of homogeneous domains. Therefore, we consider a more general type of Hartogs domain in this paper, named the Bergman–Hartogs domain, which is based on a bounded homogeneous domain. The setting of the Bergman–Hartogs domain is as follows.
Let ![]() $D$ be a bounded homogeneous domain in
$D$ be a bounded homogeneous domain in ![]() $\mathbb{C}^{n}$, and let
$\mathbb{C}^{n}$, and let ![]() $K_{D}(z,{\it\zeta})$ denote the Bergman kernel off the diagonal for
$K_{D}(z,{\it\zeta})$ denote the Bergman kernel off the diagonal for ![]() $D$. Then we define the Bergman–Hartogs domain as
$D$. Then we define the Bergman–Hartogs domain as
where ![]() $z=(z_{1},\ldots ,z_{n})\in D$, and
$z=(z_{1},\ldots ,z_{n})\in D$, and ![]() $s$ is a positive real number.
$s$ is a positive real number.
It is known that ![]() $D$ is Bergman exhaustive since
$D$ is Bergman exhaustive since ![]() $D$ is homogeneous, that is,
$D$ is homogeneous, that is, ![]() $K_{D}(z,z)\rightarrow +\infty$ as
$K_{D}(z,z)\rightarrow +\infty$ as ![]() $z\rightarrow \partial D$ (see [Reference Kobayashi9], Proposition 5.2), then
$z\rightarrow \partial D$ (see [Reference Kobayashi9], Proposition 5.2), then ![]() ${\rm\Omega}_{s}$ is a bounded domain in
${\rm\Omega}_{s}$ is a bounded domain in ![]() $\mathbb{C}^{n+1}$. Note that
$\mathbb{C}^{n+1}$. Note that ![]() $D$ is pseudoconvex and
$D$ is pseudoconvex and ![]() $\log K_{D}(z,z)$ is plurisubharmonic; we know that
$\log K_{D}(z,z)$ is plurisubharmonic; we know that ![]() ${\rm\Omega}_{s}$ is a bounded pseudoconvex domain in
${\rm\Omega}_{s}$ is a bounded pseudoconvex domain in ![]() $\mathbb{C}^{n+1}$(see [Reference Saitoh, Alpay, Ball and Ohsawa15, p. 142]). Consequently, there exists a unique complete Kähler–Einstein metric on
$\mathbb{C}^{n+1}$(see [Reference Saitoh, Alpay, Ball and Ohsawa15, p. 142]). Consequently, there exists a unique complete Kähler–Einstein metric on ![]() ${\rm\Omega}_{s}$ due to Mok and Yau [Reference Mok and Yau12], and we have the following result.
${\rm\Omega}_{s}$ due to Mok and Yau [Reference Mok and Yau12], and we have the following result.
Theorem 1.1. Let ![]() ${\rm\Omega}_{s}$ be the Bergman–Hartogs domain defined as in (3). Assume that the Bergman kernel on
${\rm\Omega}_{s}$ be the Bergman–Hartogs domain defined as in (3). Assume that the Bergman kernel on ![]() $D$ satisfies
$D$ satisfies ![]() $K_{D}(z,0)=K_{D}(0,0)$, then the generating function
$K_{D}(z,0)=K_{D}(0,0)$, then the generating function ![]() $g$ for the complete Kähler–Einstein metric of
$g$ for the complete Kähler–Einstein metric of ![]() ${\rm\Omega}_{s_{0}}$ is given by
${\rm\Omega}_{s_{0}}$ is given by
where ![]() $s_{0}=1/(n+1)$ and the constant
$s_{0}=1/(n+1)$ and the constant ![]() $C$ is given by
$C$ is given by
The notations ![]() $K_{D}(0,0)$ and
$K_{D}(0,0)$ and ![]() $T_{D}(0,0)$ denote the Bergman kernel and the Bergman metric matrix of
$T_{D}(0,0)$ denote the Bergman kernel and the Bergman metric matrix of ![]() $D$ at the point
$D$ at the point ![]() $0$, respectively.
$0$, respectively.
Notice that the condition for the Bergman kernel ![]() $K_{D}(z,0)=K_{D}(0,0)$ holds true when
$K_{D}(z,0)=K_{D}(0,0)$ holds true when ![]() $D$ is the Harish-Chandra realization of a bounded symmetric domain, especially when
$D$ is the Harish-Chandra realization of a bounded symmetric domain, especially when ![]() $D$ is one of the classical domains. This means that Theorem 1.1 generalizes the conclusions in [Reference Bland5] and [Reference Wang, Yin, Zhang and Roos17]. A complex domain
$D$ is one of the classical domains. This means that Theorem 1.1 generalizes the conclusions in [Reference Bland5] and [Reference Wang, Yin, Zhang and Roos17]. A complex domain ![]() $D$ whose Bergman kernel satisfies the condition
$D$ whose Bergman kernel satisfies the condition ![]() $K_{D}(z,0)=K_{D}(0,0)$ is said to be a minimal domain with center 0 (see, e.g., [Reference Ishi and Kai8] for the definition of minimal domain). In 2010, Ishi and Kai proved that any bounded homogeneous domain is holomorphically equivalent to a minimal domain because a homogeneous representative domain is minimal [Reference Ishi and Kai8, Proposition 3.8]. As an application of the above arguments and Theorem 1.1, we have the following corollary.
$K_{D}(z,0)=K_{D}(0,0)$ is said to be a minimal domain with center 0 (see, e.g., [Reference Ishi and Kai8] for the definition of minimal domain). In 2010, Ishi and Kai proved that any bounded homogeneous domain is holomorphically equivalent to a minimal domain because a homogeneous representative domain is minimal [Reference Ishi and Kai8, Proposition 3.8]. As an application of the above arguments and Theorem 1.1, we have the following corollary.
Corollary 1.2. Let ![]() ${\mathcal{U}}$ be a bounded homogeneous representative domain in
${\mathcal{U}}$ be a bounded homogeneous representative domain in ![]() $\mathbb{C}^{n}$, and let
$\mathbb{C}^{n}$, and let ![]() $\widehat{{\rm\Omega}}_{s}$ be the corresponding Bergman–Hartogs domain based on
$\widehat{{\rm\Omega}}_{s}$ be the corresponding Bergman–Hartogs domain based on ![]() ${\mathcal{U}}$. Then the Kähler–Einstein metric for
${\mathcal{U}}$. Then the Kähler–Einstein metric for ![]() $\widehat{{\rm\Omega}}_{s_{0}}$ is generated by
$\widehat{{\rm\Omega}}_{s_{0}}$ is generated by
where ![]() $s_{0}=1/(n+1)$, and the constant
$s_{0}=1/(n+1)$, and the constant ![]() $C^{\prime }$ is given similarly to (4).
$C^{\prime }$ is given similarly to (4).
The authors knew the definition of the Bergman–Hartogs domain in the winter of 2012, communicated by Roos. Recently, the full holomorphic automorphism group ![]() $\text{Aut}({\rm\Omega}_{s})$ was given by Roos in [Reference Roos14]. Therefore, we know that
$\text{Aut}({\rm\Omega}_{s})$ was given by Roos in [Reference Roos14]. Therefore, we know that ![]() ${\rm\Omega}_{s}$ is not homogeneous in general, except for when
${\rm\Omega}_{s}$ is not homogeneous in general, except for when ![]() ${\rm\Omega}_{s}$ is the Euclidean unit ball in
${\rm\Omega}_{s}$ is the Euclidean unit ball in ![]() $\mathbb{C}^{n+1}$. Park and Yamamori [Reference Park and Yamamori13] have computed the Bergman kernel for
$\mathbb{C}^{n+1}$. Park and Yamamori [Reference Park and Yamamori13] have computed the Bergman kernel for ![]() ${\rm\Omega}_{s}$ and considered the corresponding Lu Qikeng problem. The authors would like to thank Professor Roos for giving them the preprint [Reference Roos14] and Park for showing them the preprint [Reference Park and Yamamori13].
${\rm\Omega}_{s}$ and considered the corresponding Lu Qikeng problem. The authors would like to thank Professor Roos for giving them the preprint [Reference Roos14] and Park for showing them the preprint [Reference Park and Yamamori13].
The paper is organized as follows. In Section 2, we give a subgroup of the holomorphic automorphism group ![]() $\text{Aut}({\rm\Omega}_{s})$ for the Bergman–Hartogs domain
$\text{Aut}({\rm\Omega}_{s})$ for the Bergman–Hartogs domain ![]() ${\rm\Omega}_{s}$. This allows us to reduce the Monge–Ampère equation to an ordinary differential equation in Section 3, following the method used in [Reference Wang, Yin, Zhang and Roos17], where
${\rm\Omega}_{s}$. This allows us to reduce the Monge–Ampère equation to an ordinary differential equation in Section 3, following the method used in [Reference Wang, Yin, Zhang and Roos17], where ![]() $D$ is one of the classical domains in the sense of Loo-Keng Hua. The reduced ordinary equation can be solved explicitly for a special value
$D$ is one of the classical domains in the sense of Loo-Keng Hua. The reduced ordinary equation can be solved explicitly for a special value ![]() $s_{0}$ of the parameter
$s_{0}$ of the parameter ![]() $s$. In Section 4, we consider the minimality of bounded representative homogeneous domains introduced by Ishi and Kai in [Reference Ishi and Kai8], and give a sufficient condition for a bounded homogeneous domain to be minimal by comparing the Jacobi of the representative mapping and the automorphism transformation of the domain. Finally, we give some examples of Bergman–Hartogs domains, on which the Kähler–Einstein metrics are calculated explicitly.
$s$. In Section 4, we consider the minimality of bounded representative homogeneous domains introduced by Ishi and Kai in [Reference Ishi and Kai8], and give a sufficient condition for a bounded homogeneous domain to be minimal by comparing the Jacobi of the representative mapping and the automorphism transformation of the domain. Finally, we give some examples of Bergman–Hartogs domains, on which the Kähler–Einstein metrics are calculated explicitly.
2 Holomorphic automorphism subgroup
In this section, we present a holomorphic automorphism subgroup for the Bergman–Hartogs domain ![]() ${\rm\Omega}_{s}$.
${\rm\Omega}_{s}$.
Recall that the domain ![]() $D$ in the definition of
$D$ in the definition of ![]() ${\rm\Omega}_{s}$ is homogeneous, that is, for any two points
${\rm\Omega}_{s}$ is homogeneous, that is, for any two points ![]() $p,q\in D$, there exists
$p,q\in D$, there exists ![]() ${\it\psi}\in \text{Aut}(D)$ such that
${\it\psi}\in \text{Aut}(D)$ such that ![]() ${\it\psi}(p)=q$. Without loss of generality, we may assume that
${\it\psi}(p)=q$. Without loss of generality, we may assume that ![]() $0\in D$. Then, for any
$0\in D$. Then, for any ![]() $z\in D$, there exists
$z\in D$, there exists ![]() ${\it\psi}\in \text{Aut}(D)$ such that
${\it\psi}\in \text{Aut}(D)$ such that ![]() ${\it\psi}(z)=0$.
${\it\psi}(z)=0$.
Proposition 2.1. Let ![]() ${\rm\Omega}_{s}$ be the Bergman–Hartogs domain in
${\rm\Omega}_{s}$ be the Bergman–Hartogs domain in ![]() $\mathbb{C}^{n+1}$. Let
$\mathbb{C}^{n+1}$. Let
where ![]() ${\it\phi}_{{\it\psi},{\it\theta}}(z,z_{n+1}):=({\it\psi}(z),(\det J_{{\it\psi}}(z))^{s}e^{\sqrt{-1}{\it\theta}}z_{n+1})$ for
${\it\phi}_{{\it\psi},{\it\theta}}(z,z_{n+1}):=({\it\psi}(z),(\det J_{{\it\psi}}(z))^{s}e^{\sqrt{-1}{\it\theta}}z_{n+1})$ for ![]() $(z,z_{n+1})\in {\rm\Omega}_{s}$, and
$(z,z_{n+1})\in {\rm\Omega}_{s}$, and ![]() $\det J_{{\it\psi}}(z)$ denotes the Jacobian of
$\det J_{{\it\psi}}(z)$ denotes the Jacobian of ![]() ${\it\psi}$ at
${\it\psi}$ at ![]() $z$, then
$z$, then ![]() $G$ is a subgroup of
$G$ is a subgroup of ![]() $\text{Aut}({\rm\Omega}_{s})$.
$\text{Aut}({\rm\Omega}_{s})$.
It is known that any bounded homogeneous domain is simply connected [Reference Vinberg, Gindikin and Pjateckii-Šapiro16], hence one can take a branch of ![]() $(\det J_{{\it\psi}}(z))^{s}$ to be a single-valued holomorphic function on
$(\det J_{{\it\psi}}(z))^{s}$ to be a single-valued holomorphic function on ![]() $D$ since
$D$ since ![]() $\det J_{{\it\psi}}(z)$ is a nonzero holomorphic function on
$\det J_{{\it\psi}}(z)$ is a nonzero holomorphic function on ![]() $D$, and other branches can be obtained by multiplying
$D$, and other branches can be obtained by multiplying ![]() $e^{\sqrt{-1}{\it\theta}}$ by appropriate constants
$e^{\sqrt{-1}{\it\theta}}$ by appropriate constants ![]() ${\it\theta}$.
${\it\theta}$.
Proof of Proposition 2.1.
A direct calculation shows that
where ![]() $K_{D}$ denotes the Bergman kernel of the bounded homogeneous domain
$K_{D}$ denotes the Bergman kernel of the bounded homogeneous domain ![]() $D$. This means that
$D$. This means that ![]() ${\it\phi}(z,z_{n+1})\in {\rm\Omega}_{s}$ for any point
${\it\phi}(z,z_{n+1})\in {\rm\Omega}_{s}$ for any point ![]() $(z,z_{n+1})\in {\rm\Omega}_{s}$.
$(z,z_{n+1})\in {\rm\Omega}_{s}$.
It is obvious that ![]() ${\it\phi}$ is invertible and
${\it\phi}$ is invertible and ![]() ${\it\phi}_{1}\circ {\it\phi}_{2}\in G$ for any
${\it\phi}_{1}\circ {\it\phi}_{2}\in G$ for any ![]() ${\it\phi}_{1},{\it\phi}_{2}\in G$, since
${\it\phi}_{1},{\it\phi}_{2}\in G$, since ![]() ${\it\psi}\in \text{Aut}(D)$. Therefore,
${\it\psi}\in \text{Aut}(D)$. Therefore, ![]() $G$ is a subgroup of
$G$ is a subgroup of ![]() $\text{Aut}({\rm\Omega}_{s})$.◻
$\text{Aut}({\rm\Omega}_{s})$.◻
Remark 2.1. In [Reference Roos14], Roos proved that ![]() $G=\text{Aut}({\rm\Omega}_{s})$, that is,
$G=\text{Aut}({\rm\Omega}_{s})$, that is, ![]() $G$ is the full holomorphic automorphism group unless
$G$ is the full holomorphic automorphism group unless ![]() ${\rm\Omega}_{s}$ is the Euclidean unit ball. The method is almost the same as in [Reference Ahn, Byun and Park1] (see [Reference Ahn, Byun and Park1] and [Reference Roos14] for more details).
${\rm\Omega}_{s}$ is the Euclidean unit ball. The method is almost the same as in [Reference Ahn, Byun and Park1] (see [Reference Ahn, Byun and Park1] and [Reference Roos14] for more details).
Remark 2.2. Since ![]() $D$ is homogeneous, we know from Proposition 2.1 that for any point
$D$ is homogeneous, we know from Proposition 2.1 that for any point ![]() $(z,z_{n+1})\in {\rm\Omega}_{s}$, there exists
$(z,z_{n+1})\in {\rm\Omega}_{s}$, there exists ![]() ${\it\phi}\in G$ such that
${\it\phi}\in G$ such that ![]() ${\it\phi}(z,z_{n+1})=(0,w_{n+1})$.
${\it\phi}(z,z_{n+1})=(0,w_{n+1})$.
Now we define a ![]() $G$-invariant function on
$G$-invariant function on ![]() ${\rm\Omega}_{s}$, which is used frequently in the following text for convenience.
${\rm\Omega}_{s}$, which is used frequently in the following text for convenience.
Proposition 2.2. For any point ![]() $(z,z_{n+1})\in {\rm\Omega}_{s}$, we define
$(z,z_{n+1})\in {\rm\Omega}_{s}$, we define
Then ![]() $x$ is invariant under the holomorphic automorphism subgroup
$x$ is invariant under the holomorphic automorphism subgroup ![]() $G$, that is,
$G$, that is, ![]() $x({\it\phi}(z,z_{n+1}))=x(z,z_{n+1})$ for any element
$x({\it\phi}(z,z_{n+1}))=x(z,z_{n+1})$ for any element ![]() ${\it\phi}\in G$.
${\it\phi}\in G$.
Proof. This is obviously due to the formula (7).
One can immediately see that the real-valued function ![]() $x$ takes values in the interval
$x$ takes values in the interval ![]() $[0,1)$ by the definition of the Bergman–Hartogs domain
$[0,1)$ by the definition of the Bergman–Hartogs domain ![]() ${\rm\Omega}_{s}$.
${\rm\Omega}_{s}$.
In order to simplify the computations in Section 3, we present the Jacobian determinant of ![]() ${\it\phi}\in G$ here.
${\it\phi}\in G$ here.
Proposition 2.3. For ![]() $Z=(z,z_{n+1})\in {\rm\Omega}_{s}$, the Jacobian of
$Z=(z,z_{n+1})\in {\rm\Omega}_{s}$, the Jacobian of ![]() ${\it\phi}={\it\phi}_{{\it\psi},{\it\theta}}\in G$ is given by
${\it\phi}={\it\phi}_{{\it\psi},{\it\theta}}\in G$ is given by
where ![]() ${\it\psi}\in \text{Aut}(D)$. In particular, one can choose one
${\it\psi}\in \text{Aut}(D)$. In particular, one can choose one ![]() ${\it\psi}_{z}\in \text{Aut}(D)$ such that
${\it\psi}_{z}\in \text{Aut}(D)$ such that ![]() ${\it\psi}_{z}(z)=0$, and the Jacobian of the corresponding
${\it\psi}_{z}(z)=0$, and the Jacobian of the corresponding ![]() ${\it\phi}_{z}\in G$ is
${\it\phi}_{z}\in G$ is
Proof. Let ![]() $Z=(z,z_{n+1})\in {\rm\Omega}_{s}$. Because
$Z=(z,z_{n+1})\in {\rm\Omega}_{s}$. Because
we have
where ![]() ${\rm\Phi}(Z)=(\det J_{{\it\psi}}(z))^{s}e^{\sqrt{-1}{\it\theta}}z_{n+1}$. Thus, the conclusion (9) follows immediately from the well-known formula
${\rm\Phi}(Z)=(\det J_{{\it\psi}}(z))^{s}e^{\sqrt{-1}{\it\theta}}z_{n+1}$. Thus, the conclusion (9) follows immediately from the well-known formula
and
In particular, for any point ![]() $Z=(z,z_{n+1})\in {\rm\Omega}_{s}$, we can choose a special
$Z=(z,z_{n+1})\in {\rm\Omega}_{s}$, we can choose a special ![]() ${\it\psi}_{z}\in \text{Aut}(D)$ such that
${\it\psi}_{z}\in \text{Aut}(D)$ such that ![]() ${\it\psi}_{z}(z)=0$ since
${\it\psi}_{z}(z)=0$ since ![]() $\text{Aut}(D)$ acts on
$\text{Aut}(D)$ acts on ![]() $D$ transitively. Therefore, there exists a corresponding
$D$ transitively. Therefore, there exists a corresponding ![]() ${\it\phi}_{z}\in G$ satisfying
${\it\phi}_{z}\in G$ satisfying ![]() ${\it\phi}_{z}(z,z_{n+1})=(0,w_{n+1})$, and consequently the Jacobian of
${\it\phi}_{z}(z,z_{n+1})=(0,w_{n+1})$, and consequently the Jacobian of ![]() ${\it\phi}_{z}$ is
${\it\phi}_{z}$ is
3 Reduction of the Monge–Ampère equation
In this section, by using the holomorphic automorphism subgroup ![]() $G$, we reduce the complex Monge–Ampère equation to an ordinary differential equation with respect to the invariant function
$G$, we reduce the complex Monge–Ampère equation to an ordinary differential equation with respect to the invariant function ![]() $x$, which was introduced in Proposition 2.2. Then we solve the ordinary differential equation when the parameter
$x$, which was introduced in Proposition 2.2. Then we solve the ordinary differential equation when the parameter ![]() $s$ of the Bergman–Hartogs domain
$s$ of the Bergman–Hartogs domain ![]() ${\rm\Omega}_{s}$ takes some critical value.
${\rm\Omega}_{s}$ takes some critical value.
3.1 Reduction of the complex Monge–Ampère equation
Let ![]() $D$ be any bounded homogeneous domain in
$D$ be any bounded homogeneous domain in ![]() $\mathbb{C}^{n}$, and let
$\mathbb{C}^{n}$, and let ![]() $K_{D}(z,z)$ denote the Bergman kernel for
$K_{D}(z,z)$ denote the Bergman kernel for ![]() $D$. The Bergman–Hartogs domain is
$D$. The Bergman–Hartogs domain is
where ![]() $z=(z_{1},\ldots ,z_{n})\in D$ and
$z=(z_{1},\ldots ,z_{n})\in D$ and ![]() $s$ is a positive real number. According to the arguments before Theorem 1.1, we know that
$s$ is a positive real number. According to the arguments before Theorem 1.1, we know that ![]() ${\rm\Omega}_{s}$ is bounded and pseudoconvex. Thanks to Mok and Yau [Reference Mok and Yau12], we know that the Bergman–Hartogs domain
${\rm\Omega}_{s}$ is bounded and pseudoconvex. Thanks to Mok and Yau [Reference Mok and Yau12], we know that the Bergman–Hartogs domain ![]() ${\rm\Omega}_{s}$ admits a unique complete Kähler–Einstein metric with the Ricci curvature
${\rm\Omega}_{s}$ admits a unique complete Kähler–Einstein metric with the Ricci curvature ![]() $-(n+2)$, and the generating function, say
$-(n+2)$, and the generating function, say ![]() $g$, of the complete Kähler–Einstein metric satisfies the following complex Monge–Ampère equation with Dirichlet boundary condition:
$g$, of the complete Kähler–Einstein metric satisfies the following complex Monge–Ampère equation with Dirichlet boundary condition:
For simplicity of the notation, we write ![]() $Z:=(z,z_{n+1})$ and the image
$Z:=(z,z_{n+1})$ and the image ![]() ${\it\phi}(Z)=(w,w_{n+1})=:W$ for
${\it\phi}(Z)=(w,w_{n+1})=:W$ for ![]() ${\it\phi}\in G$.
${\it\phi}\in G$.
For any holomorphic automorphism transformation ![]() ${\it\phi}\in G$,
${\it\phi}\in G$, ![]() $W={\it\phi}(Z)$, we have
$W={\it\phi}(Z)$, we have
where ![]() $j,k$ run from
$j,k$ run from ![]() $1$ to
$1$ to ![]() $n+1$. According to the Monge–Ampère equation (11), Equation (13) is equivalent to
$n+1$. According to the Monge–Ampère equation (11), Equation (13) is equivalent to
That is,
Now we fix a point ![]() $Z=(z,z_{n+1})\in {\rm\Omega}_{s}$ for a moment. As explained in the proof of Proposition 2.3, we can take a special
$Z=(z,z_{n+1})\in {\rm\Omega}_{s}$ for a moment. As explained in the proof of Proposition 2.3, we can take a special ![]() ${\it\phi}_{z}\in G$ such that
${\it\phi}_{z}\in G$ such that ![]() ${\it\phi}_{z}(Z)=(0,w_{n+1})$. By Proposition 2.3, we know that
${\it\phi}_{z}(Z)=(0,w_{n+1})$. By Proposition 2.3, we know that
then Equation (15) yields
As ![]() $Z$ varies in
$Z$ varies in ![]() ${\rm\Omega}_{s}$, Equation (17) holds true on
${\rm\Omega}_{s}$, Equation (17) holds true on ![]() ${\rm\Omega}_{s}$ since we can always take
${\rm\Omega}_{s}$ since we can always take ![]() ${\it\phi}_{z}\in G$ such that
${\it\phi}_{z}\in G$ such that ![]() ${\it\phi}_{z}(Z)=(0,w_{n+1})$.
${\it\phi}_{z}(Z)=(0,w_{n+1})$.
To obtain ![]() $g(Z)$ explicitly, we need to know
$g(Z)$ explicitly, we need to know ![]() $g(0,w_{n+1})$. We want to express
$g(0,w_{n+1})$. We want to express ![]() $g(0,w_{n+1})$ in terms of the invariant function
$g(0,w_{n+1})$ in terms of the invariant function ![]() $x$, which is defined by
$x$, which is defined by
in Proposition 2.2. Note that ![]() $x$ is invariant under
$x$ is invariant under ![]() $G$, that is,
$G$, that is, ![]() $\forall {\it\phi}\in G,x({\it\phi}(Z))=x(Z)$, thus we have
$\forall {\it\phi}\in G,x({\it\phi}(Z))=x(Z)$, thus we have ![]() $x(Z)=x({\it\phi}_{z}(Z))=x(0,w_{n+1})$. It follows that
$x(Z)=x({\it\phi}_{z}(Z))=x(0,w_{n+1})$. It follows that
By taking a suitable ![]() ${\it\theta}$ in the automorphism
${\it\theta}$ in the automorphism ![]() ${\it\phi}_{z}$, say
${\it\phi}_{z}$, say ![]() ${\it\theta}_{z}$, we can assume that
${\it\theta}_{z}$, we can assume that ![]() $w_{n+1}$ is real. Therefore, one can regard
$w_{n+1}$ is real. Therefore, one can regard ![]() $g(0,w_{n+1})$ as a real-valued function of the real variable
$g(0,w_{n+1})$ as a real-valued function of the real variable ![]() $x$.
$x$.
Let ![]() $y(x):=g(0,w_{n+1})$, then Equation (17) becomes
$y(x):=g(0,w_{n+1})$, then Equation (17) becomes
Differentiating both sides of the above equation with respect to ![]() $Z=(z,z_{n+1})$, we have
$Z=(z,z_{n+1})$, we have
 $$\begin{eqnarray}\displaystyle \left(\frac{\partial ^{2}g}{\partial z_{j}\partial \overline{z}_{k}}\right) & = & \displaystyle \left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}g\nonumber\\ \displaystyle & = & \displaystyle \left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}y+\frac{s+1}{n+2}\left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}\log K_{D}(z,z),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\partial ^{2}g}{\partial z_{j}\partial \overline{z}_{k}}\right) & = & \displaystyle \left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}g\nonumber\\ \displaystyle & = & \displaystyle \left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}y+\frac{s+1}{n+2}\left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}\log K_{D}(z,z),\end{eqnarray}$$ where ![]() $\partial /\partial Z=(\partial /\partial z_{1},\ldots ,\partial /\partial z_{n},\partial /\partial z_{n+1})$ and
$\partial /\partial Z=(\partial /\partial z_{1},\ldots ,\partial /\partial z_{n},\partial /\partial z_{n+1})$ and ![]() $(\partial /\partial Z)^{t}$ denotes the transpose of
$(\partial /\partial Z)^{t}$ denotes the transpose of ![]() $\partial /\partial Z$. Notice that
$\partial /\partial Z$. Notice that
and
then Equation (20) can be reformulated as
 $$\begin{eqnarray}\displaystyle \left(\frac{\partial ^{2}g}{\partial z_{j}\partial \overline{z}_{k}}\right) & = & \displaystyle y^{\prime \prime }\left(\frac{\partial x}{\partial Z}\right)^{t}\frac{\partial x}{\partial \overline{Z}}+y^{\prime }\left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}x\nonumber\\ \displaystyle & & \displaystyle +\,\frac{s+1}{n+2}\left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}\log K_{D}(z,z)\nonumber\\ \displaystyle & := & \displaystyle I_{1}+I_{2}+I_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\partial ^{2}g}{\partial z_{j}\partial \overline{z}_{k}}\right) & = & \displaystyle y^{\prime \prime }\left(\frac{\partial x}{\partial Z}\right)^{t}\frac{\partial x}{\partial \overline{Z}}+y^{\prime }\left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}x\nonumber\\ \displaystyle & & \displaystyle +\,\frac{s+1}{n+2}\left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}\log K_{D}(z,z)\nonumber\\ \displaystyle & := & \displaystyle I_{1}+I_{2}+I_{3}.\end{eqnarray}$$ Next, we want to calculate the values of ![]() $I_{1},I_{2}$ and
$I_{1},I_{2}$ and ![]() $I_{3}$ at the point
$I_{3}$ at the point ![]() $(0,w_{n+1})$.
$(0,w_{n+1})$.
Recall that
then a routine computation shows that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial x}{\partial z_{j}}=sx\frac{\partial \log K_{D}(z,z)}{\partial z_{j}},\quad j=1,\ldots ,n;\nonumber\\ \displaystyle & & \displaystyle \frac{\partial x}{\partial z_{n+1}}=\overline{z}_{n+1}K_{D}(z,z)^{s}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial x}{\partial z_{j}}=sx\frac{\partial \log K_{D}(z,z)}{\partial z_{j}},\quad j=1,\ldots ,n;\nonumber\\ \displaystyle & & \displaystyle \frac{\partial x}{\partial z_{n+1}}=\overline{z}_{n+1}K_{D}(z,z)^{s}.\nonumber\end{eqnarray}$$ The second-order derivatives of ![]() $x$ give
$x$ give
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial ^{2}x}{\partial z_{j}\partial \overline{z}_{k}}=s^{2}x\frac{\partial \log K_{D}(z,z)}{\partial z_{j}}\frac{\partial \log K_{D}(z,z)}{\partial \overline{z}_{k}}+sx\frac{\partial ^{2}\log K_{D}(z,z)}{\partial z_{j}\partial \overline{z}_{k}},\nonumber\\ \displaystyle & & \displaystyle \frac{\partial ^{2}x}{\partial z_{j}\partial \overline{z}_{n+1}}=sz_{n+1}K_{D}(z,z)^{s}\frac{\partial \log K_{D}(z,z)}{\partial z_{j}},\nonumber\\ \displaystyle & & \displaystyle \frac{\partial ^{2}x}{\partial z_{n+1}\partial \overline{z}_{n+1}}=K_{D}(z,z)^{s},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial ^{2}x}{\partial z_{j}\partial \overline{z}_{k}}=s^{2}x\frac{\partial \log K_{D}(z,z)}{\partial z_{j}}\frac{\partial \log K_{D}(z,z)}{\partial \overline{z}_{k}}+sx\frac{\partial ^{2}\log K_{D}(z,z)}{\partial z_{j}\partial \overline{z}_{k}},\nonumber\\ \displaystyle & & \displaystyle \frac{\partial ^{2}x}{\partial z_{j}\partial \overline{z}_{n+1}}=sz_{n+1}K_{D}(z,z)^{s}\frac{\partial \log K_{D}(z,z)}{\partial z_{j}},\nonumber\\ \displaystyle & & \displaystyle \frac{\partial ^{2}x}{\partial z_{n+1}\partial \overline{z}_{n+1}}=K_{D}(z,z)^{s},\nonumber\end{eqnarray}$$ where ![]() $j$ and
$j$ and ![]() $k$ run from
$k$ run from ![]() $1$ to
$1$ to ![]() $n$.
$n$.
In order to get the values of the derivatives of ![]() $x$ at the point
$x$ at the point ![]() $(0,w_{n+1})$, we need the following lemma.
$(0,w_{n+1})$, we need the following lemma.
Lemma 3.1. Let ![]() $D$ be a bounded homogeneous domain in
$D$ be a bounded homogeneous domain in ![]() $\mathbb{C}^{n}$ containing the origin. Assume that the Bergman kernel
$\mathbb{C}^{n}$ containing the origin. Assume that the Bergman kernel ![]() $K_{D}(z,{\it\zeta})$ satisfies the condition
$K_{D}(z,{\it\zeta})$ satisfies the condition ![]() $K_{D}(z,0)=K_{D}(0,0)$, then
$K_{D}(z,0)=K_{D}(0,0)$, then
Proof of the Lemma.
The conclusion follows from the fact that
Applying Lemma 3.1, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial x}{\partial z_{j}}\Big|_{\left(0,w_{n+1}\right)}=sx\frac{\partial \log K_{D}(z,z)}{\partial z_{j}}\Big|_{\left(0,w_{n+1}\right)}=0,\quad j=1,\ldots ,n;\nonumber\\ \displaystyle & & \displaystyle \frac{\partial x}{\partial z_{n+1}}\Big|_{\left(0,w_{n+1}\right)}=\overline{w}_{n+1}K_{D}(0,0)^{s};\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial x}{\partial z_{j}}\Big|_{\left(0,w_{n+1}\right)}=sx\frac{\partial \log K_{D}(z,z)}{\partial z_{j}}\Big|_{\left(0,w_{n+1}\right)}=0,\quad j=1,\ldots ,n;\nonumber\\ \displaystyle & & \displaystyle \frac{\partial x}{\partial z_{n+1}}\Big|_{\left(0,w_{n+1}\right)}=\overline{w}_{n+1}K_{D}(0,0)^{s};\nonumber\end{eqnarray}$$and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial ^{2}x}{\partial z_{j}\partial \overline{z}_{k}}\Big|_{\left(0,w_{n+1}\right)}=sx\frac{\partial ^{2}\log K_{D}(z,z)}{\partial z_{j}\partial \overline{z}_{k}}\Big|_{z=0},\quad j,k=1,\ldots ,n;\nonumber\\ \displaystyle & & \displaystyle \frac{\partial ^{2}x}{\partial z_{j}\partial \overline{z}_{n+1}}\Big|_{\left(0,w_{n+1}\right)}=0;\nonumber\\ \displaystyle & & \displaystyle \frac{\partial ^{2}x}{\partial z_{n+1}\partial \overline{z}_{n+1}}\Big|_{\left(0,w_{n+1}\right)}=K_{D}(0,0)^{s}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial ^{2}x}{\partial z_{j}\partial \overline{z}_{k}}\Big|_{\left(0,w_{n+1}\right)}=sx\frac{\partial ^{2}\log K_{D}(z,z)}{\partial z_{j}\partial \overline{z}_{k}}\Big|_{z=0},\quad j,k=1,\ldots ,n;\nonumber\\ \displaystyle & & \displaystyle \frac{\partial ^{2}x}{\partial z_{j}\partial \overline{z}_{n+1}}\Big|_{\left(0,w_{n+1}\right)}=0;\nonumber\\ \displaystyle & & \displaystyle \frac{\partial ^{2}x}{\partial z_{n+1}\partial \overline{z}_{n+1}}\Big|_{\left(0,w_{n+1}\right)}=K_{D}(0,0)^{s}.\nonumber\end{eqnarray}$$Hence, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle I_{1}\big|_{(0,w_{n+1})}=y^{\prime \prime }\left(\frac{\partial x}{\partial Z}\right)^{t}\frac{\partial x}{\partial \overline{Z}}\Big|_{(0,w_{n+1})}=\left(\begin{array}{@{}cc@{}}0 & 0\\ 0 & xy^{\prime \prime }K_{D}(0,0)^{s}\end{array}\right),\nonumber\\ \displaystyle & & \displaystyle I_{2}\big|_{(0,w_{n+1})}=y^{\prime }\left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}x\Big|_{(0,w_{n+1})}=\left(\begin{array}{@{}cc@{}}sxy^{\prime }T_{D}(0,0) & 0\\ 0 & y^{\prime }K_{D}(0,0)^{s}\end{array}\right),\nonumber\\ \displaystyle & & \displaystyle I_{3}\big|_{(0,w_{n+1})}=\frac{s+1}{n+2}\left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}\log K_{D}(z,z)\Big|_{z=0}=\frac{s+1}{n+2}\left(\begin{array}{@{}cc@{}}T_{D}(0,0) & 0\\ 0 & 0\end{array}\right),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle I_{1}\big|_{(0,w_{n+1})}=y^{\prime \prime }\left(\frac{\partial x}{\partial Z}\right)^{t}\frac{\partial x}{\partial \overline{Z}}\Big|_{(0,w_{n+1})}=\left(\begin{array}{@{}cc@{}}0 & 0\\ 0 & xy^{\prime \prime }K_{D}(0,0)^{s}\end{array}\right),\nonumber\\ \displaystyle & & \displaystyle I_{2}\big|_{(0,w_{n+1})}=y^{\prime }\left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}x\Big|_{(0,w_{n+1})}=\left(\begin{array}{@{}cc@{}}sxy^{\prime }T_{D}(0,0) & 0\\ 0 & y^{\prime }K_{D}(0,0)^{s}\end{array}\right),\nonumber\\ \displaystyle & & \displaystyle I_{3}\big|_{(0,w_{n+1})}=\frac{s+1}{n+2}\left(\frac{\partial }{\partial Z}\right)^{t}\frac{\partial }{\partial \overline{Z}}\log K_{D}(z,z)\Big|_{z=0}=\frac{s+1}{n+2}\left(\begin{array}{@{}cc@{}}T_{D}(0,0) & 0\\ 0 & 0\end{array}\right),\nonumber\end{eqnarray}$$where
is the Bergman metric on ![]() $D$.
$D$.
Summarizing ![]() $I_{1},I_{2}$ and
$I_{1},I_{2}$ and ![]() $I_{3}$, we have
$I_{3}$, we have
 $$\begin{eqnarray}\displaystyle \left(\frac{\partial ^{2}g}{\partial z_{j}\partial \overline{z}_{k}}\right)\Big|_{(0,w_{n+1})} & = & \displaystyle (I_{1}+I_{2}+I_{3})\big|_{(0,w_{n+1})}\nonumber\\ \displaystyle & = & \displaystyle \left(\begin{array}{@{}cc@{}}\left(sxy^{\prime }+\frac{s+1}{n+2}\right)T_{D}(0,0) & 0\\ 0 & \left(xy^{\prime \prime }+y^{\prime }\right)K_{D}(0,0)^{s}\end{array}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\partial ^{2}g}{\partial z_{j}\partial \overline{z}_{k}}\right)\Big|_{(0,w_{n+1})} & = & \displaystyle (I_{1}+I_{2}+I_{3})\big|_{(0,w_{n+1})}\nonumber\\ \displaystyle & = & \displaystyle \left(\begin{array}{@{}cc@{}}\left(sxy^{\prime }+\frac{s+1}{n+2}\right)T_{D}(0,0) & 0\\ 0 & \left(xy^{\prime \prime }+y^{\prime }\right)K_{D}(0,0)^{s}\end{array}\right).\nonumber\end{eqnarray}$$Consequently, we have
 $$\begin{eqnarray}\displaystyle \det \left(\frac{\partial ^{2}g}{\partial z_{j}\partial \overline{z}_{k}}\right)\Big|_{(0,w_{n+1})} & = & \displaystyle \left(xy^{\prime \prime }+y^{\prime }\right)\left(xy^{\prime }+b\right)^{n}s^{n}K_{D}(0,0)^{s}\det T_{D}(0,0)\nonumber\\ \displaystyle & = & \displaystyle a\left[(xy^{\prime }+b)^{n+1}\right]^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \det \left(\frac{\partial ^{2}g}{\partial z_{j}\partial \overline{z}_{k}}\right)\Big|_{(0,w_{n+1})} & = & \displaystyle \left(xy^{\prime \prime }+y^{\prime }\right)\left(xy^{\prime }+b\right)^{n}s^{n}K_{D}(0,0)^{s}\det T_{D}(0,0)\nonumber\\ \displaystyle & = & \displaystyle a\left[(xy^{\prime }+b)^{n+1}\right]^{\prime },\end{eqnarray}$$ where ![]() $a=s^{n}/(n+1)K_{D}(0,0)^{s}\det T_{D}(0,0)$ and
$a=s^{n}/(n+1)K_{D}(0,0)^{s}\det T_{D}(0,0)$ and ![]() $b=(1+1/s)/(n+2)$ are positive constants.
$b=(1+1/s)/(n+2)$ are positive constants.
Considering the Monge–Ampère equation (11) at the point ![]() $(0,w_{n+1})\in {\rm\Omega}_{s}$, that is
$(0,w_{n+1})\in {\rm\Omega}_{s}$, that is
Equations (23) and (24) yield the following differential equation:
Let ![]() $u(x):=xy^{\prime }+b$; we summarize the above arguments by the following proposition.
$u(x):=xy^{\prime }+b$; we summarize the above arguments by the following proposition.
Proposition 3.2. If
is a solution of the Monge–Ampère equation
with the boundary condition ![]() $g(z,z_{n+1})\rightarrow \infty$ when
$g(z,z_{n+1})\rightarrow \infty$ when ![]() $(z,z_{n+1})\rightarrow \partial {\rm\Omega}_{s},$ then the function
$(z,z_{n+1})\rightarrow \partial {\rm\Omega}_{s},$ then the function ![]() $u(x)=xy^{\prime }+b$ satisfies the differential equation
$u(x)=xy^{\prime }+b$ satisfies the differential equation
with the initial condition ![]() $u(0)=b$.
$u(0)=b$.
Proof. The differential equation (26) results from Equations (23) and (24). Next, we give an illustration about the boundary condition. We know that ![]() $g(z,z_{n+1})\rightarrow \infty$
$g(z,z_{n+1})\rightarrow \infty$![]() $((z,z_{n+1})\rightarrow \partial {\rm\Omega}_{s})$ implies
$((z,z_{n+1})\rightarrow \partial {\rm\Omega}_{s})$ implies ![]() $y(x)=g(0,w_{n+1})\rightarrow \infty (x\rightarrow 1)$. From
$y(x)=g(0,w_{n+1})\rightarrow \infty (x\rightarrow 1)$. From
we deduce that ![]() $xy^{\prime }\rightarrow 0$ as
$xy^{\prime }\rightarrow 0$ as ![]() $w_{n+1}\rightarrow 0$, or equivalently
$w_{n+1}\rightarrow 0$, or equivalently ![]() $xy^{\prime }\rightarrow 0$ as
$xy^{\prime }\rightarrow 0$ as ![]() $x\rightarrow 0$.◻
$x\rightarrow 0$.◻
3.2 Solution of the Monge–Ampère equation
In what follows, we solve the above differential equation (26) and obtain the generating function ![]() $g$ for the complete Kähler–Einstein metric on
$g$ for the complete Kähler–Einstein metric on ![]() ${\rm\Omega}_{s}$.
${\rm\Omega}_{s}$.
Integrating on both sides of Equation (26) with respect to ![]() $x$, we have
$x$, we have
By the formula of integration by parts, the right-hand side yields
By Equation (26), we have
 $$\begin{eqnarray}\displaystyle \int xy^{\prime }e^{(n+2)y}dx & = & \displaystyle a\int xy^{\prime }\left(u^{n+1}\right)^{\prime }\,dx\nonumber\\ \displaystyle & = & \displaystyle a(n+1)\int (u-b)u^{n}\,du\nonumber\\ \displaystyle & = & \displaystyle \frac{a(n+1)}{n+2}u^{n+2}-abu^{n+1}+ac,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int xy^{\prime }e^{(n+2)y}dx & = & \displaystyle a\int xy^{\prime }\left(u^{n+1}\right)^{\prime }\,dx\nonumber\\ \displaystyle & = & \displaystyle a(n+1)\int (u-b)u^{n}\,du\nonumber\\ \displaystyle & = & \displaystyle \frac{a(n+1)}{n+2}u^{n+2}-abu^{n+1}+ac,\end{eqnarray}$$ where ![]() $c$ is a constant.
$c$ is a constant.
where ![]() $c_{1}$ is a constant to be determined.
$c_{1}$ is a constant to be determined.
Taking the initial condition in Proposition 3.2 into consideration, that is, ![]() $u(0)=b$ when
$u(0)=b$ when ![]() $x=0$, we have
$x=0$, we have ![]() $c_{1}=b^{n+1}(b-1)$.
$c_{1}=b^{n+1}(b-1)$.
Let
We have the following facts.
(2) For
 $x=0$, it is easy to check that
$x=0$, it is easy to check that  $f(u(0))=f(b)=0$.
$f(u(0))=f(b)=0$.(3)
 $f^{\prime }(b)=(n+1)b^{n}>0$, which means that
$f^{\prime }(b)=(n+1)b^{n}>0$, which means that  $\exists {\it\delta}>0$ such that
$\exists {\it\delta}>0$ such that  $f(u)<0$ for
$f(u)<0$ for  $b-{\it\delta}<u<b$.
$b-{\it\delta}<u<b$.
Claim:![]() $u(x)\geqslant b$ for
$u(x)\geqslant b$ for ![]() $0\leqslant x<1$.
$0\leqslant x<1$.
Proof of Claim.
Otherwise, assume ![]() $\exists x_{0}\in (0,1)$ such that
$\exists x_{0}\in (0,1)$ such that ![]() $u(x_{0})<b$. Then, by the continuity of
$u(x_{0})<b$. Then, by the continuity of ![]() $u$ (we know this since
$u$ (we know this since ![]() $g$ is
$g$ is ![]() $C^{2}$),
$C^{2}$), ![]() $\exists x_{1}\in (0,x_{0})$ such that
$\exists x_{1}\in (0,x_{0})$ such that ![]() $b-{\it\delta}<u(x_{1})<b$. Consequently, we have
$b-{\it\delta}<u(x_{1})<b$. Consequently, we have ![]() $f(u(x_{1}))<0$ by the fact
$f(u(x_{1}))<0$ by the fact ![]() $(3)$, which is in contradiction to the fact
$(3)$, which is in contradiction to the fact ![]() $(1)$.
$(1)$.
Note that Equation (26) shows that the derivative of ![]() $u^{n+1}$ is positive and tends to
$u^{n+1}$ is positive and tends to ![]() $\infty$ when
$\infty$ when ![]() $x\rightarrow 1$ (since
$x\rightarrow 1$ (since ![]() $y(x)\rightarrow \infty$ when
$y(x)\rightarrow \infty$ when ![]() $x\rightarrow 1$). Then, combined with the above claim, we have
$x\rightarrow 1$). Then, combined with the above claim, we have ![]() $u^{\prime }>0$. Therefore, the function
$u^{\prime }>0$. Therefore, the function ![]() $u$ is strictly increasing and maps
$u$ is strictly increasing and maps ![]() $[0,1)$ onto
$[0,1)$ onto ![]() $[b,+\infty )$.
$[b,+\infty )$.
In summary, we have the following proposition.
Proposition 3.3. Assume that
is a solution of the Monge–Ampère equation (11) with Dirichlet boundary condition, then the function ![]() $u(x)=xy^{\prime }+b$ is the solution of the following ordinary differential equation (ODE):
$u(x)=xy^{\prime }+b$ is the solution of the following ordinary differential equation (ODE):
where ![]() $f(u)$ is defined by (31).
$f(u)$ is defined by (31).
Now suppose that ![]() $u$ satisfies the ODE (32) with the boundary condition. From the above arguments, we know that
$u$ satisfies the ODE (32) with the boundary condition. From the above arguments, we know that ![]() $f(u)$ is positive on
$f(u)$ is positive on ![]() $(b,\infty )$, the function
$(b,\infty )$, the function ![]() $u:[0,1)\rightarrow [b,\infty )$ is monotone and its inverse function satisfies the differential equation
$u:[0,1)\rightarrow [b,\infty )$ is monotone and its inverse function satisfies the differential equation
The solution of this equation is given by
which gives ![]() $x$ as a function of
$x$ as a function of ![]() $u$, and
$u$, and ![]() $u$ as an implicit function of
$u$ as an implicit function of ![]() $x$. In general, it is difficult to get the explicit
$x$. In general, it is difficult to get the explicit ![]() $u$. In the next subsection, we prove that when the parameter
$u$. In the next subsection, we prove that when the parameter ![]() $s$ takes some special value then we can solve (32) with the boundary condition (32).
$s$ takes some special value then we can solve (32) with the boundary condition (32).
3.3 The critical exponent
Letting ![]() $b=1$, that is,
$b=1$, that is, ![]() $s=1/(n+1)$ in Equation (32), we have
$s=1/(n+1)$ in Equation (32), we have
The solution of the ODE (37) is
where ![]() $c_{2}$ is an arbitrary constant to be determined.
$c_{2}$ is an arbitrary constant to be determined.
Since ![]() $u\rightarrow \infty$ when
$u\rightarrow \infty$ when ![]() $x\rightarrow 1$, then
$x\rightarrow 1$, then ![]() $c_{2}$ has to be
$c_{2}$ has to be ![]() $1$. Substituting the unique solution (39) into Equation (25), we have
$1$. Substituting the unique solution (39) into Equation (25), we have
 $$\begin{eqnarray}\displaystyle g\left(0,w_{n+1}\right) & = & \displaystyle \frac{1}{n+2}\log \left[a(u^{n+1})^{\prime }\right]\nonumber\\ \displaystyle & = & \displaystyle -\!\log (1-x)+\frac{1}{n+2}\log (n+1)a,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g\left(0,w_{n+1}\right) & = & \displaystyle \frac{1}{n+2}\log \left[a(u^{n+1})^{\prime }\right]\nonumber\\ \displaystyle & = & \displaystyle -\!\log (1-x)+\frac{1}{n+2}\log (n+1)a,\nonumber\end{eqnarray}$$ where the constant ![]() $a=(n+1)^{-(n+1)}K_{D}(0,0)^{s_{0}}\det T_{D}(0,0)$ as in Equation (23). According to Equation (19), we have
$a=(n+1)^{-(n+1)}K_{D}(0,0)^{s_{0}}\det T_{D}(0,0)$ as in Equation (23). According to Equation (19), we have
where ![]() $C$ is a constant defined as
$C$ is a constant defined as
We claim that
 $$\begin{eqnarray}\displaystyle g(Z) & = & \displaystyle -\!\log (1-x)+\frac{1}{n+1}\log K_{D}(z,z)+C\nonumber\\ \displaystyle & = & \displaystyle -\!\log \left(K_{D}(z,z)^{-s_{0}}-|z_{n+1}|^{2}\right)+C\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g(Z) & = & \displaystyle -\!\log (1-x)+\frac{1}{n+1}\log K_{D}(z,z)+C\nonumber\\ \displaystyle & = & \displaystyle -\!\log \left(K_{D}(z,z)^{-s_{0}}-|z_{n+1}|^{2}\right)+C\end{eqnarray}$$ is the solution of the complex Monge–Ampère equation (11) with the boundary value condition on ![]() ${\rm\Omega}_{s_{0}}$, where
${\rm\Omega}_{s_{0}}$, where ![]() $s_{0}=1/(n+1)$.
$s_{0}=1/(n+1)$.
Proof. First, ![]() $g$ solves the complex Monge–Ampère equation (11) since the generating function
$g$ solves the complex Monge–Ampère equation (11) since the generating function ![]() $g$ for the Kähler–Einstein metric on
$g$ for the Kähler–Einstein metric on ![]() ${\rm\Omega}_{s_{0}}$ is a solution of the ODE (32) due to Proposition 3.3, while
${\rm\Omega}_{s_{0}}$ is a solution of the ODE (32) due to Proposition 3.3, while ![]() $u=(1-x)^{-1}$ is the unique solution of (32) with the boundary condition. (Of course, one can also check directly that
$u=(1-x)^{-1}$ is the unique solution of (32) with the boundary condition. (Of course, one can also check directly that ![]() $g$ satisfies the Monge–Ampère equation (11).) Now we need only to check that
$g$ satisfies the Monge–Ampère equation (11).) Now we need only to check that ![]() $g$ satisfies the boundary value condition, that is,
$g$ satisfies the boundary value condition, that is, ![]() $g\rightarrow \infty$ as
$g\rightarrow \infty$ as ![]() $(z,z_{n+1})\rightarrow \partial {\rm\Omega}_{s_{0}}$.
$(z,z_{n+1})\rightarrow \partial {\rm\Omega}_{s_{0}}$.
(1) When
 $(z,z_{n+1})$ goes to the strongly pseudoconvex boundary points
$(z,z_{n+1})$ goes to the strongly pseudoconvex boundary points  $\{(z,z_{n+1})\in D\times \mathbb{C}:|z_{n+1}|^{2}=K_{D}(z,z)^{-s_{0}},~z_{n+1}\neq 0\}$, we know that
$\{(z,z_{n+1})\in D\times \mathbb{C}:|z_{n+1}|^{2}=K_{D}(z,z)^{-s_{0}},~z_{n+1}\neq 0\}$, we know that  $(z,z_{n+1})\rightarrow \partial {\rm\Omega}_{s_{0}}$ implies
$(z,z_{n+1})\rightarrow \partial {\rm\Omega}_{s_{0}}$ implies  $x\rightarrow 1$. Obviously,
$x\rightarrow 1$. Obviously,  $g\rightarrow \infty$ as
$g\rightarrow \infty$ as  $x\rightarrow 1$.
$x\rightarrow 1$.(2) When
 $(z,z_{n+1})$ approaches the weakly pseudoconvex boundary points
$(z,z_{n+1})$ approaches the weakly pseudoconvex boundary points  $\partial D\times \{0\}$, we have
$\partial D\times \{0\}$, we have  $x\rightarrow 0$. In this case, the Bergman kernel
$x\rightarrow 0$. In this case, the Bergman kernel  $K_{D}(z,z)$ of the bounded homogeneous domain
$K_{D}(z,z)$ of the bounded homogeneous domain  $D$ blows up as
$D$ blows up as  $z\rightarrow \partial D$. Therefore, we still have
$z\rightarrow \partial D$. Therefore, we still have  $g\rightarrow \infty$ when
$g\rightarrow \infty$ when  $(z,z_{n+1})\rightarrow \partial D\times \{0\}$.
$(z,z_{n+1})\rightarrow \partial D\times \{0\}$.
Now we can say that
solves the complex Monge–Ampère equation with Dirichlet boundary value problem on ![]() ${\rm\Omega}_{s_{0}}$, where
${\rm\Omega}_{s_{0}}$, where
We call ![]() $s_{0}=1/(n+1)$ the critical exponent. The corresponding Kähler form of the unique complete Kähler–Einstein metric on
$s_{0}=1/(n+1)$ the critical exponent. The corresponding Kähler form of the unique complete Kähler–Einstein metric on ![]() ${\rm\Omega}_{s_{0}}$ is given by
${\rm\Omega}_{s_{0}}$ is given by
and we conclude the proof of Theorem 1.1. ◻
4 The homogeneous domains with  $K(z,0)=K(0,0)$
$K(z,0)=K(0,0)$
In this section, we turn back and take a look at the condition ![]() $K_{D}(z,0)=K_{D}(0,0)$ for the Bergman kernel
$K_{D}(z,0)=K_{D}(0,0)$ for the Bergman kernel ![]() $K_{D}(z,{\it\zeta})$ in Theorem 1.1.
$K_{D}(z,{\it\zeta})$ in Theorem 1.1.
The condition ![]() $K_{D}(z,0)=K_{D}(0,0)$ holds true when
$K_{D}(z,0)=K_{D}(0,0)$ holds true when ![]() $D$ is the Harish-Chandra realization of a bounded symmetric domain, especially when
$D$ is the Harish-Chandra realization of a bounded symmetric domain, especially when ![]() $D$ is one of the classical domains. In this case, the Bergman kernels were obtained by Hua [Reference Hua7] explicitly and one can verify the above condition directly.
$D$ is one of the classical domains. In this case, the Bergman kernels were obtained by Hua [Reference Hua7] explicitly and one can verify the above condition directly.
In general, we do not always know whether this condition does hold for homogeneous domains in ![]() $\mathbb{C}^{n}$. Ishi and Kai [Reference Ishi and Kai8, Proposition 3.8] proved that when
$\mathbb{C}^{n}$. Ishi and Kai [Reference Ishi and Kai8, Proposition 3.8] proved that when ![]() $D$ is a representative bounded homogeneous domain (see Section 4.1 for the definition of representative domains) in
$D$ is a representative bounded homogeneous domain (see Section 4.1 for the definition of representative domains) in ![]() $\mathbb{C}^{n}$, one has
$\mathbb{C}^{n}$, one has ![]() $K_{D}(z,0)=K_{D}(0,0)$. Before the statement of the corollary, let us recall the definition of the representative domain.
$K_{D}(z,0)=K_{D}(0,0)$. Before the statement of the corollary, let us recall the definition of the representative domain.
4.1 Representative domains
The representative domain of a bounded domain ![]() $D\subset \mathbb{C}^{n}$ was introduced by Bergman in [Reference Bergman3]. Let
$D\subset \mathbb{C}^{n}$ was introduced by Bergman in [Reference Bergman3]. Let ![]() $K_{D}(z,{\it\zeta})$ denote the Bergman kernel of
$K_{D}(z,{\it\zeta})$ denote the Bergman kernel of ![]() $D$. If
$D$. If ![]() $K_{D}(z,{\it\zeta})\neq 0$, then the Bergman representative mapping
$K_{D}(z,{\it\zeta})\neq 0$, then the Bergman representative mapping ![]() ${\it\rho}_{p}:D\rightarrow \mathbb{C}^{n}$ for a fixed point
${\it\rho}_{p}:D\rightarrow \mathbb{C}^{n}$ for a fixed point ![]() $p\in D$ is defined by
$p\in D$ is defined by
where ![]() $\frac{\partial }{\partial \overline{{\it\zeta}}^{t}}=(\frac{\partial }{\partial \overline{{\it\zeta}}_{1}},\ldots ,\frac{\partial }{\partial \overline{{\it\zeta}}_{n}})^{t}$, and
$\frac{\partial }{\partial \overline{{\it\zeta}}^{t}}=(\frac{\partial }{\partial \overline{{\it\zeta}}_{1}},\ldots ,\frac{\partial }{\partial \overline{{\it\zeta}}_{n}})^{t}$, and ![]() $T_{D}(z,{\it\zeta}):=(\frac{\partial ^{2}}{\partial z_{j}\partial \overline{{\it\zeta}}_{k}}\log K_{D}(z,{\it\zeta}))$ is an
$T_{D}(z,{\it\zeta}):=(\frac{\partial ^{2}}{\partial z_{j}\partial \overline{{\it\zeta}}_{k}}\log K_{D}(z,{\it\zeta}))$ is an ![]() $n\times n$ complex matrix. The image
$n\times n$ complex matrix. The image ![]() ${\it\rho}_{p}(D)$ is called the representative domain of the bounded domain
${\it\rho}_{p}(D)$ is called the representative domain of the bounded domain ![]() $D$. If
$D$. If ![]() ${\it\rho}_{p}$ is one-to-one, then the image
${\it\rho}_{p}$ is one-to-one, then the image ![]() ${\it\rho}_{p}(D)$, say
${\it\rho}_{p}(D)$, say ![]() ${\mathcal{U}}$, is indeed a domain.
${\mathcal{U}}$, is indeed a domain.
In general, Lu [Reference Lu10] pointed out that ![]() ${\it\rho}_{p}$ is not necessarily globally defined. Following this idea, he gave an alternative definition of the representative domain. A bounded domain
${\it\rho}_{p}$ is not necessarily globally defined. Following this idea, he gave an alternative definition of the representative domain. A bounded domain ![]() ${\mathcal{U}}$ is called a representative domain if there is a point
${\mathcal{U}}$ is called a representative domain if there is a point ![]() $p\in {\mathcal{U}}$ such that the Bergman metric matrix
$p\in {\mathcal{U}}$ such that the Bergman metric matrix ![]() $T_{{\mathcal{U}}}(z,p)$ is independent of
$T_{{\mathcal{U}}}(z,p)$ is independent of ![]() $z$. The point
$z$. The point ![]() $p$ is called the center of the representative domain
$p$ is called the center of the representative domain ![]() ${\mathcal{U}}$. For example, the Harish-Chandra realization of an irreducible bounded symmetric domain is a representative domain (up to a constant multiple). Any bounded circular domain with origin as the center is a representative domain with center
${\mathcal{U}}$. For example, the Harish-Chandra realization of an irreducible bounded symmetric domain is a representative domain (up to a constant multiple). Any bounded circular domain with origin as the center is a representative domain with center ![]() $0$. Recently, Yamamori proved that a normal quasi-circular domain in
$0$. Recently, Yamamori proved that a normal quasi-circular domain in ![]() $\mathbb{C}^{2}$ is a representative domain with the center at the origin (see [Reference Yamamori21, Proposition 3.2] and the definition of normal quasi-circular domains therein).
$\mathbb{C}^{2}$ is a representative domain with the center at the origin (see [Reference Yamamori21, Proposition 3.2] and the definition of normal quasi-circular domains therein).
4.2 Minimal domains
Let ![]() $D$ denote a domain in
$D$ denote a domain in ![]() $\mathbb{C}^{n}$ with finite volume, and fix
$\mathbb{C}^{n}$ with finite volume, and fix ![]() $p\in D$. We say that
$p\in D$. We say that ![]() $D$ is a minimal domain with a center
$D$ is a minimal domain with a center ![]() $p$ if for every biholomorphism
$p$ if for every biholomorphism ![]() ${\rm\Psi}:D\simeq \tilde{D}$ with
${\rm\Psi}:D\simeq \tilde{D}$ with ![]() $\det J_{{\rm\Psi}}(p)=1$, we have
$\det J_{{\rm\Psi}}(p)=1$, we have ![]() $vol(\tilde{D})\geqslant vol(D)$, where
$vol(\tilde{D})\geqslant vol(D)$, where ![]() $vol(D)$ denotes the Euclidean volume of
$vol(D)$ denotes the Euclidean volume of ![]() $D$, and
$D$, and ![]() $J_{{\rm\Psi}}(p)$ denotes the Jacobian matrix of
$J_{{\rm\Psi}}(p)$ denotes the Jacobian matrix of ![]() ${\rm\Psi}$ at
${\rm\Psi}$ at ![]() $p$.
$p$.
Theorem 4.1. [Reference Maschler11, Theorem 3.1]
Let ![]() $D\subset \mathbb{C}^{n}$ be a bounded univalent domain and
$D\subset \mathbb{C}^{n}$ be a bounded univalent domain and ![]() $p\in D$. Then
$p\in D$. Then ![]() $D$ is a minimal domain with a center
$D$ is a minimal domain with a center ![]() $p$ if and only if
$p$ if and only if ![]() $K_{D}(z,p)(z\in D)$ is constant on
$K_{D}(z,p)(z\in D)$ is constant on ![]() $D$.
$D$.
In general, Maschler [Reference Maschler11] proved that a representative domain is not necessarily minimal. Fortunately, for bounded homogeneous domains, Ishi and Kai [Reference Ishi and Kai8] proved the following theorem.
Corollary 4.2. [Reference Ishi and Kai8, Corollary 3.8]
The representative domain ![]() ${\mathcal{U}}$ of a bounded homogeneous domain
${\mathcal{U}}$ of a bounded homogeneous domain ![]() $D\in \mathbb{C}^{n}$ is minimal with a center
$D\in \mathbb{C}^{n}$ is minimal with a center ![]() $0$.
$0$.
Therefore, combined with Theorem 1.1 and Corollary 4.2, we have the following corollary.
Corollary 4.3. Assume that ![]() ${\mathcal{U}}$ is the representative domain of a bounded homogeneous domain
${\mathcal{U}}$ is the representative domain of a bounded homogeneous domain ![]() $D\subset \mathbb{C}^{n}$. Let
$D\subset \mathbb{C}^{n}$. Let ![]() $\widehat{{\rm\Omega}}_{s}$ be the corresponding Bergman–Hartogs domain built on
$\widehat{{\rm\Omega}}_{s}$ be the corresponding Bergman–Hartogs domain built on ![]() ${\mathcal{U}}$. Then the Kähler–Einstein metric for
${\mathcal{U}}$. Then the Kähler–Einstein metric for ![]() $\widehat{{\rm\Omega}}_{s_{0}}$ is generated by
$\widehat{{\rm\Omega}}_{s_{0}}$ is generated by
where ![]() $s_{0}=1/n+1$, and
$s_{0}=1/n+1$, and ![]() $C$ is a constant as in (40).
$C$ is a constant as in (40).
For general bounded domains in ![]() $\mathbb{C}^{n}$, even for homogeneous domains, we cannot expect
$\mathbb{C}^{n}$, even for homogeneous domains, we cannot expect ![]() $K_{D}(z,0)=K_{D}(0,0)$ any more. It was pointed out by the referee that
$K_{D}(z,0)=K_{D}(0,0)$ any more. It was pointed out by the referee that ![]() $K_{D}(z,0)=K_{D}(0,0)$ is actually equivalent to the domain
$K_{D}(z,0)=K_{D}(0,0)$ is actually equivalent to the domain ![]() $D$ being minimal with the center
$D$ being minimal with the center ![]() $0$. The authors are grateful to the referee for interpreting the following example. A simply connected domain
$0$. The authors are grateful to the referee for interpreting the following example. A simply connected domain ![]() ${\rm\Omega}\subset \mathbb{C}$ is symmetric because it is biholomorphic to the unit disc
${\rm\Omega}\subset \mathbb{C}$ is symmetric because it is biholomorphic to the unit disc ![]() ${\rm\Delta}$ by the Riemann mapping theorem, while
${\rm\Delta}$ by the Riemann mapping theorem, while ![]() ${\rm\Omega}$ is minimal with some center only if
${\rm\Omega}$ is minimal with some center only if ![]() ${\rm\Omega}$ is the image of
${\rm\Omega}$ is the image of ![]() ${\rm\Delta}$ by an affine map
${\rm\Delta}$ by an affine map ![]() $z\mapsto az+b$, thanks to [Reference Ishi and Kai8, Proposition 3.4]. Indeed, the minimality and the representativeness of
$z\mapsto az+b$, thanks to [Reference Ishi and Kai8, Proposition 3.4]. Indeed, the minimality and the representativeness of ![]() ${\rm\Omega}$ are equivalent in this case. Hence, there exist many bounded symmetric domains whose Bergman kernels do not satisfy the condition
${\rm\Omega}$ are equivalent in this case. Hence, there exist many bounded symmetric domains whose Bergman kernels do not satisfy the condition ![]() $K_{D}(z,0)=K_{D}(0,0)$.
$K_{D}(z,0)=K_{D}(0,0)$.
4.3 A sufficient condition for  $K_{D}(z,0)=K_{D}(0,0)$
$K_{D}(z,0)=K_{D}(0,0)$
From the above arguments, we know that the minimality of a bounded domain is not an intrinsic property, that is, it is not biholomorphically invariant. Therefore the Bergman kernel condition ![]() $K_{D}(z,0)=K_{D}(0,0)$ does not always hold even for homogeneous domains. In the following, we give a sufficient condition such that
$K_{D}(z,0)=K_{D}(0,0)$ does not always hold even for homogeneous domains. In the following, we give a sufficient condition such that ![]() $K_{D}(z,0)=K_{D}(0,0)$ holds for all bounded homogeneous domains
$K_{D}(z,0)=K_{D}(0,0)$ holds for all bounded homogeneous domains ![]() $D$ in
$D$ in ![]() $\mathbb{C}^{n}$.
$\mathbb{C}^{n}$.
Proposition 4.4. Let ![]() $D$ be a bounded homogeneous domain in
$D$ be a bounded homogeneous domain in ![]() $\mathbb{C}^{n}$ and
$\mathbb{C}^{n}$ and ![]() $0\in D$. Let
$0\in D$. Let ![]() ${\mathcal{U}}:={\it\rho}_{p}(D)$ be the representative domain of
${\mathcal{U}}:={\it\rho}_{p}(D)$ be the representative domain of ![]() $D$. Take
$D$. Take ![]() ${\it\psi}_{p}\in \text{Aut}(D)$ satisfying
${\it\psi}_{p}\in \text{Aut}(D)$ satisfying ![]() ${\it\psi}_{p}(p)=0$, then
${\it\psi}_{p}(p)=0$, then ![]() $K_{D}(z,0)=K_{D}(0,0)$ if
$K_{D}(z,0)=K_{D}(0,0)$ if
where ![]() $\det J_{{\it\psi}}(z)$ denotes the determinant of the Jacobian matrix of
$\det J_{{\it\psi}}(z)$ denotes the determinant of the Jacobian matrix of ![]() ${\it\psi}$ at
${\it\psi}$ at ![]() $z$.
$z$.
Proof. Under the assumptions in the proposition, it is well known that
Noting that ![]() $J_{{\it\rho}_{p}}(p)=I_{n}$, it follows that
$J_{{\it\rho}_{p}}(p)=I_{n}$, it follows that
Let ![]() $z=p$ in (48), then we have
$z=p$ in (48), then we have
By Proposition 4.2, we know that
Then (48) and (49) imply that ![]() $K_{D}({\it\psi}_{p}(z),0)=K_{D}(0,0)$ if and only if
$K_{D}({\it\psi}_{p}(z),0)=K_{D}(0,0)$ if and only if
This completes the proof. ◻
5 Applications of the main theorem
In this section, we give some examples of Bergman–Hartogs domains.
We first investigate the relation between two generating functions of the complete Kähler–Einstein metrics on two holomorphically equivalent domains. More precisely, let ![]() ${\rm\Phi}:{\rm\Omega}_{1}\simeq {\rm\Omega}_{2}$ be the biholomorphic mapping between two bounded pseudoconvex domains
${\rm\Phi}:{\rm\Omega}_{1}\simeq {\rm\Omega}_{2}$ be the biholomorphic mapping between two bounded pseudoconvex domains ![]() ${\rm\Omega}_{1}$ and
${\rm\Omega}_{1}$ and ![]() ${\rm\Omega}_{2}$ in
${\rm\Omega}_{2}$ in ![]() $\mathbb{C}^{n+1}$. Assume that
$\mathbb{C}^{n+1}$. Assume that ![]() $g_{1}$ and
$g_{1}$ and ![]() $g_{2}$ generate the complete Kähler–Einstein metrics on
$g_{2}$ generate the complete Kähler–Einstein metrics on ![]() ${\rm\Omega}_{1}$ and
${\rm\Omega}_{1}$ and ![]() ${\rm\Omega}_{2}$, respectively, then it follows that
${\rm\Omega}_{2}$, respectively, then it follows that
Since ![]() $g_{1}$ and
$g_{1}$ and ![]() $g_{2}$ satisfy the Monge–Ampère equations (11) on
$g_{2}$ satisfy the Monge–Ampère equations (11) on ![]() ${\rm\Omega}_{1}$ and
${\rm\Omega}_{1}$ and ![]() ${\rm\Omega}_{2}$, respectively, we have
${\rm\Omega}_{2}$, respectively, we have
which yields
5.1 Bergman–Hartogs domains over the unit ball
Denote by ![]() $B^{n}$ the unit ball in
$B^{n}$ the unit ball in ![]() $\mathbb{C}^{n}$. The Bergman–Hartogs domain over
$\mathbb{C}^{n}$. The Bergman–Hartogs domain over ![]() $B^{n}$ is
$B^{n}$ is
where ![]() $K_{B^{n}}(z,z)=(n!/{\it\pi}^{n})1/(1-\Vert z\Vert ^{2})^{n+1}$ is the Bergman kernel of the unit ball
$K_{B^{n}}(z,z)=(n!/{\it\pi}^{n})1/(1-\Vert z\Vert ^{2})^{n+1}$ is the Bergman kernel of the unit ball ![]() $B^{n}$. When
$B^{n}$. When ![]() $s_{0}=1/(n+1)$, we get the generating function of the complete Kähler–Einstein metric by Theorem 1.1 (see also (40)) as
$s_{0}=1/(n+1)$, we get the generating function of the complete Kähler–Einstein metric by Theorem 1.1 (see also (40)) as
where ![]() $C=-\!\log (n!/{\it\pi}^{n})/(n+2).$
$C=-\!\log (n!/{\it\pi}^{n})/(n+2).$
Notice that at the moment ![]() ${\rm\Omega}_{s_{0}}$ is biholomorphic to the unit ball
${\rm\Omega}_{s_{0}}$ is biholomorphic to the unit ball ![]() $B^{n+1}\subset \mathbb{C}^{n+1}$ via the following map:
$B^{n+1}\subset \mathbb{C}^{n+1}$ via the following map:
Hence, by the formula (52), the solution (53) actually gives the Kähler–Einstein metric of the unit ball ![]() $B^{n+1}$, that is
$B^{n+1}$, that is
which is exactly the Bergman metric of ![]() $B^{n+1}$ up to a factor
$B^{n+1}$ up to a factor ![]() $1/(n+2)$.
$1/(n+2)$.
5.2 Bergman–Hartogs domains over bounded symmetric domains
Let ![]() $R_{A}\;(A=I,II,III,IV)$ denote the Harish-Chandra realization of bounded symmetric domains. We take, for example, the first type
$R_{A}\;(A=I,II,III,IV)$ denote the Harish-Chandra realization of bounded symmetric domains. We take, for example, the first type
where ![]() $I$ is the identity matrix of order
$I$ is the identity matrix of order ![]() $p$,
$p$, ![]() $\bar{Z}$ denotes the conjugate matrix of
$\bar{Z}$ denotes the conjugate matrix of ![]() $Z$, and
$Z$, and ![]() $Z^{t}$ denotes the transposed matrix of
$Z^{t}$ denotes the transposed matrix of ![]() $Z$.
$Z$.
The corresponding Bergman–Hartogs domain is defined as
where the Bergman kernel ![]() $K_{R_{I}}(Z,Z)$ is [Reference Hua7]
$K_{R_{I}}(Z,Z)$ is [Reference Hua7]
and ![]() $vol(R_{I})$ is the volume of
$vol(R_{I})$ is the volume of ![]() $R_{I}$. According to Theorem 1.1, when the parameter
$R_{I}$. According to Theorem 1.1, when the parameter ![]() $s$ takes the critical value
$s$ takes the critical value ![]() $1/(pq+1)$, the generating function of the complete Kähler–Einstein metric is given by
$1/(pq+1)$, the generating function of the complete Kähler–Einstein metric is given by
 $$\begin{eqnarray}\displaystyle g(Z,W) & = & \displaystyle -\!\log \left(K_{R_{I}}(Z,Z)^{-1/(pq+1)}-|W|^{2}\right)+C\nonumber\\ \displaystyle & = & \displaystyle -\!\log \left(\det (I-Z\bar{Z}^{t})^{(p+q)/(pq+1)}-|W|^{2}\right)+\widetilde{C},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g(Z,W) & = & \displaystyle -\!\log \left(K_{R_{I}}(Z,Z)^{-1/(pq+1)}-|W|^{2}\right)+C\nonumber\\ \displaystyle & = & \displaystyle -\!\log \left(\det (I-Z\bar{Z}^{t})^{(p+q)/(pq+1)}-|W|^{2}\right)+\widetilde{C},\end{eqnarray}$$ which coincides with the Kähler–Einstein metric of the Cartan–Hartogs domain of the first type (see [Reference Wang, Yin, Zhang and Zhang18, page 47]). We omit ![]() $R_{II},R_{III}$ and
$R_{II},R_{III}$ and ![]() $R_{IV}$ here since the conclusions are almost the same.
$R_{IV}$ here since the conclusions are almost the same.
5.3 Bergman–Hartogs domains over a nonsymmetric bounded homogeneous domain
In this subsection, we consider the Bergman–Hartogs domains over a nonsymmetric bounded minimal homogeneous domain ![]() ${\mathcal{U}}$. It was Yamaji who observed this kind of
${\mathcal{U}}$. It was Yamaji who observed this kind of ![]() ${\mathcal{U}}$ (see [Reference Yamaji20, Section 7.2]) when he considered the compactness of composition operators on the weighted Bergman space of a minimal bounded homogeneous domain.
${\mathcal{U}}$ (see [Reference Yamaji20, Section 7.2]) when he considered the compactness of composition operators on the weighted Bergman space of a minimal bounded homogeneous domain.
Let ![]() $T_{V}:=\mathbb{R}^{5}+iV$ be the tube domain over the Vinberg cone
$T_{V}:=\mathbb{R}^{5}+iV$ be the tube domain over the Vinberg cone ![]() $V$(see [Reference Békollé and Nana2]), where
$V$(see [Reference Békollé and Nana2]), where
and
Let ![]() ${\mathcal{U}}$ be the representative domain of the tube
${\mathcal{U}}$ be the representative domain of the tube ![]() $T_{V}$. Then
$T_{V}$. Then ![]() ${\mathcal{U}}$ is a nonsymmetric minimal bounded homogeneous domain with center 0 by Proposition 4.2.
${\mathcal{U}}$ is a nonsymmetric minimal bounded homogeneous domain with center 0 by Proposition 4.2.
For ![]() $z:=(z_{1},z_{2},\ldots ,z_{5})\in T_{V}$, let
$z:=(z_{1},z_{2},\ldots ,z_{5})\in T_{V}$, let
Then the Bergman kernel for ![]() ${\mathcal{U}}$ on the diagonal was given by Yamaji in [Reference Yamaji20], that is,
${\mathcal{U}}$ on the diagonal was given by Yamaji in [Reference Yamaji20], that is,
 $$\begin{eqnarray}\displaystyle K_{{\mathcal{U}}}({\it\sigma}(z),{\it\sigma}(z)) & = & \displaystyle \frac{1}{vol({\mathcal{U}})}\left(1-{\mathcal{L}}_{1}(z_{1})\overline{{\mathcal{L}}_{1}(z_{1})}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{j=1}^{2}\left(\det (I-{\mathcal{L}}_{2}(z_{[j]})\overline{{\mathcal{L}}_{2}(z_{[j]})})\right)^{-3},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{{\mathcal{U}}}({\it\sigma}(z),{\it\sigma}(z)) & = & \displaystyle \frac{1}{vol({\mathcal{U}})}\left(1-{\mathcal{L}}_{1}(z_{1})\overline{{\mathcal{L}}_{1}(z_{1})}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{j=1}^{2}\left(\det (I-{\mathcal{L}}_{2}(z_{[j]})\overline{{\mathcal{L}}_{2}(z_{[j]})})\right)^{-3},\nonumber\end{eqnarray}$$ where ![]() ${\it\sigma}$ is the Bergman mapping from
${\it\sigma}$ is the Bergman mapping from ![]() $T_{V}$ to
$T_{V}$ to ![]() ${\mathcal{U}}$ at
${\mathcal{U}}$ at ![]() $p_{0}:=(i,i,i,0,0)$, and
$p_{0}:=(i,i,i,0,0)$, and ![]() ${\mathcal{L}}_{m}\;(m=1,2)$ denotes the Cayley transform
${\mathcal{L}}_{m}\;(m=1,2)$ denotes the Cayley transform ![]() ${\mathcal{L}}_{m}(Z):=(Z-iI_{m})$
${\mathcal{L}}_{m}(Z):=(Z-iI_{m})$![]() $(Z+iI_{m})^{-1}$ for
$(Z+iI_{m})^{-1}$ for ![]() $Z\in \text{Mat}(m,\mathbb{C})$.
$Z\in \text{Mat}(m,\mathbb{C})$.
The corresponding Bergman–Hartogs domains over the nonsymmetric homogeneous domain ![]() ${\mathcal{U}}$ are defined as
${\mathcal{U}}$ are defined as
where ![]() ${\it\xi}:={\it\sigma}(z)\in {\mathcal{U}}$. Since
${\it\xi}:={\it\sigma}(z)\in {\mathcal{U}}$. Since ![]() ${\mathcal{U}}$ is minimal with the center
${\mathcal{U}}$ is minimal with the center ![]() $0$, we have
$0$, we have ![]() $K_{{\mathcal{U}}}({\it\xi},0)=K_{{\mathcal{U}}}(0,0).$ (One can also check this fact directly from the explicit formula of the Bergman kernel of
$K_{{\mathcal{U}}}({\it\xi},0)=K_{{\mathcal{U}}}(0,0).$ (One can also check this fact directly from the explicit formula of the Bergman kernel of ![]() ${\mathcal{U}}$.) Therefore, according to Theorem 1.1 or Corollary 1.2, we have obtained the generating function of the complete Kähler–Einstein metric on
${\mathcal{U}}$.) Therefore, according to Theorem 1.1 or Corollary 1.2, we have obtained the generating function of the complete Kähler–Einstein metric on ![]() ${\rm\Omega}_{s}^{{\mathcal{U}}}$ when
${\rm\Omega}_{s}^{{\mathcal{U}}}$ when ![]() $s=1/6$. That is,
$s=1/6$. That is,
Acknowledgments
The authors are grateful to the referee for many valuable comments and suggestions, which essentially made the paper more readable.