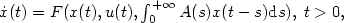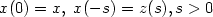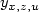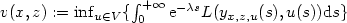Research Article
A sensitivity-based extrapolation techniquefor the numerical solution of state-constrained optimal control problems
-
- Published online by Cambridge University Press:
- 02 July 2009, pp. 503-522
-
- Article
- Export citation
A penalty method for topology optimization subject to a pointwise state constraint
-
- Published online by Cambridge University Press:
- 18 June 2009, pp. 523-544
-
- Article
- Export citation
Magnetic vortices for a Ginzburg-Landau type energywithdiscontinuous constraint
-
- Published online by Cambridge University Press:
- 18 June 2009, pp. 545-580
-
- Article
- Export citation
Recent advances in the analysis of pointwise state-constrainedelliptic optimal control problems
-
- Published online by Cambridge University Press:
- 02 July 2009, pp. 581-600
-
- Article
- Export citation
Metric subregularity for nonclosed convex multifunctions innormed spaces
-
- Published online by Cambridge University Press:
- 18 June 2009, pp. 601-617
-
- Article
- Export citation
On the ersatz material approximation in level-set methods
-
- Published online by Cambridge University Press:
- 31 July 2009, pp. 618-634
-
- Article
- Export citation
Mean variance and goal achieving portfoliofor discrete-time market with currently observable source of correlations
-
- Published online by Cambridge University Press:
- 18 June 2009, pp. 635-647
-
- Article
- Export citation
Bounds for the first Dirichlet eigenvalue of trianglesand quadrilaterals
-
- Published online by Cambridge University Press:
- 02 July 2009, pp. 648-676
-
- Article
- Export citation
Controllability of 3D incompressible Euler equationsby a finite-dimensional externalforce
-
- Published online by Cambridge University Press:
- 02 July 2009, pp. 677-694
-
- Article
- Export citation
Regularity properties of the distance functions to conjugate and cut loci for viscosity solutions of Hamilton-Jacobi equations and applicationsin Riemannian geometry
-
- Published online by Cambridge University Press:
- 02 July 2009, pp. 695-718
-
- Article
- Export citation
Relaxation of an optimal design problemin fracture mechanic: the anti-plane case
-
- Published online by Cambridge University Press:
- 02 July 2009, pp. 719-743
-
- Article
- Export citation
Hamilton-Jacobi-Bellman equations for the optimal control of a state equation with memory
-
- Published online by Cambridge University Press:
- 31 July 2009, pp. 744-763
-
- Article
- Export citation
Switching and stability propertiesof conewise linear systems
-
- Published online by Cambridge University Press:
- 02 July 2009, pp. 764-793
-
- Article
- Export citation
The squares of the Laplacian-Dirichlet eigenfunctionsare generically linearly independent
-
- Published online by Cambridge University Press:
- 02 July 2009, pp. 794-805
-
- Article
- Export citation
Correction
Erratum of “The squares of the Laplacian-Dirichlet eigenfunctions are generically linearly independent”
-
- Published online by Cambridge University Press:
- 04 December 2009, pp. 806-807
-
- Article
- Export citation