Introduction
Recent geodetic and gravimetric mass-balance studies show that the majority of glaciers in Alaska and northwestern Canada (referred to hereafter as ‘Alaska’ for brevity) have been experiencing overall retreat, surface lowering and mass loss over the last half-century (Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002; Reference Luthcke, Arendt, Rowlands, McCarthy and LarsenLuthcke and others, 2008; Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others, 2010). Further, the contribution to sea-level rise (SLR) from Alaskan glaciers has been shown to be among the largest from glaciated areas outside the Greenland and Antarctic ice sheets (Reference MeierMeier and others, 2007; Reference Luthcke, Arendt, Rowlands, McCarthy and LarsenLuthcke and others, 2008; Reference WuWu and others, 2010; Reference Jacob, Wahr, Pfeffer and SwensonJacob and others, 2012). In Alaska there are only a handful of glaciers with glaciological mass-balance records (Reference Pelto and MillerPelto and Miller, 1990; Reference Heinrichs, Mayo, Echelmeyer and HarrisonHeinrichs and others, 1996; Reference Hodge, Trabant, Krimmel, Heinrichs, March and JosbergerHodge and others, 1998; Reference Miller and PeltoMiller and Pelto, 1999; Reference Nolan, Arendt and Rabus Band HinzmanNolan and others, 2005; Reference Van Beusekom, O’Neel, March, Sass and CoxVan Beusekom and others, 2010), so it is difficult to place this recent thinning into a long-term context.
We focus on a region of glaciers and icefields surrounding Glacier Bay in southeast Alaska (Fig. 1). Glacier Bay has a particularly well-documented history of large-scale tidewater retreat since the end of the Little Ice Age (LIA), and the rapid crustal unloading associated with this ice loss has resulted in large rates of uplift (Reference Larsen, Motyka, Freymueller, Echelmeyer and IvinsLarsen and others, 2005; Reference Motyka, Larsen, Freymueller and EchelmeyerMotyka and others, 2007). In the Glacier Bay region, the University of Alaska Fairbanks (UAF) laser altimetry program has repeatedly surveyed 11 glaciers at least three times since 1995. We use these laser altimetry profiles of glacier surface elevation to: (1) estimate the change in ice mass of glaciers in the Glacier Bay area that have been surveyed with laser altimetry over four periods between 1995 and 2011; (2) examine the temporal and spatial variations in mass change for the entire Glacier Bay region since 1995; and (3) examine the extent to which this mass change is correlated with a climate model or other variables, such as glacier size, type or location. We assess the accuracy of the assumption that center-line altimetry measurements are representative of change across the width of a glacier using sequential, differenced digital elevation grids (difference DEM).
Fig. 1. Map of the Glacier Bay region showing the flight lines for airborne laser altimetry used in this study. Surveyed glaciers are in blue, unsurveyed glaciers are in red and laser altimetry flight lines are in black. The thin black curve is the border between Alaska, USA, and British Columbia, Canada. The location of the US Geological Survey (USGS) index glaciers is shown in the inset.
Study Area
The Glacier Bay region is located to the west of Haines, Alaska, and to the northwest of Juneau, Alaska, and had an ice-covered area of ∼6428 km2 as of August 2010 (Reference Raup, Racoviteanu, Khalsa, Helm, Armstrong and ArnaudRaup and others, 2007; Reference Arendt, Larsen, Loso, Murphy and RichArendt and others, 2012). The glaciated area is shaped like an arrowhead, and ranges from 58°19′ N to 59°45′ N and spans from 135°25′ W to 138°1 1′W (Fig. 1). There are two distinct areas of ice coverage: the western icefield glaciers located in the Fairweather Range, which include Grand Pacific and Brady Glaciers, and the glaciers of the eastern icefield that are located northeast of the West Arm of Glacier Bay in the Alsek and Chilkat Ranges, which include Carroll and Muir Glaciers. These two separate icefields were previously part of the much more extensive Glacier Bay Icefield that has experienced a massive glacial retreat since the end of the LIA (Reference Connor, Streveler, Post, Monteith and HowellConnor and others, 2009). The ice mass loss since the end of the LIA (∼ad 1770) was modeled by Reference Larsen, Motyka, Freymueller, Echelmeyer and IvinsLarsen and others (2005) and Reference Motyka, Larsen, Freymueller and EchelmeyerMotyka and others (2007). They mapped geomorphologic features, such as trimlines and moraines, and fitted an icefield surface to the data in order to reconstruct the LIA glacier maximum. This surface was then differenced with a recent digital elevation model (DEM) to determine the total ice mass loss since the LIA, which was found to be ∼3450 Gt.
Overall, glaciers in the Glacier Bay region (Fig. 1) are losing mass (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007; Reference Luthcke, Arendt, Rowlands, McCarthy and LarsenLuthcke and others, 2008). However, there are a few glaciers there that are currently gaining mass and advancing (Johns Hopkins, Lituya, South and North Crillion, and Margerie). There are eight tidewater glaciers in the Glacier Bay region; at present none of the tidewater glaciers are experiencing the rapid retreat observed in tidewater glaciers elsewhere in Alaska (e.g. Columbia Glacier (Reference Walter, O’Neel, McNamara, Pfeffer, Bassis and FrickerWalter and others, 2010) and South Sawyer Glacier). Most of the largest glaciers in the Glacier Bay area are included in the surveying. Glaciers with areas >100 km2 that are unsurveyed are Johns Hopkins (254 km2), Alsek (244 km2), LaPerouse (124 km2) and McBride glaciers (119 km2). The total area of the surveyed glaciers is 3328 km2, 52% of the total glaciated area of the Glacier Bay region.
Data
Laser altimetry
UAF has acquired laser altimetry data with two general types of systems: (1) nadir fixed lasers that collect a single track of point measurements along the flight track and (2) a system that sweeps the laser beam ±30° off-nadir to produce a swath of point measurements along the flight track. Herein, we refer to these two types of systems as (1) profiler and (2) scanner, although such usage may not reflect a general definition of these terms. The profiler systems have been described in previous publications (Reference EchelmeyerEchelmeyer and others, 1996; Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002). In the late summer of 2009 the scanner system replaced the profiler. The current laser scanner is a Riegl LMS-Q240i, which has a sampling rate of 10 000 Hz. As with the profiler, this scanner has a 905 nm wavelength laser. The average spacing of laser returns both along and perpendicular to the flight path from an optimal aircraft elevation of 500m above the glacier surface is ∼1 m × 1 m, with a swath width of 500 m. Each laser shot has a footprint diameter of ∼20 cm. The earlier profiler system had along-track laser shot point spacing of ∼1.2 m and a similar-sized footprint of 20 cm.
The glaciers were surveyed very close to the same calendar date in 1995, 2000, 2005, 2009 and 2011. The difference between each repeat survey date is <10 days. The data are reported in the fixed date system, wherein the first day of the mass-balance year occurs on the same calendar date. Based on the available data, there are four mass-balance periods: 1995–2000 (period 1), 2000–05 (period 2), 2005–09 (period 3) and 2009–11 (period 4). The selection of surveyed glaciers includes a wide variety of geometries, sizes and glacier types, i.e. tidewater, lake-terminating, land-terminating and surge-type (Table 1).
Table 1. Glaciers surveyed with laser altimetry in the Glacier Bay region with attributes for glacier type, August 2010 area, area-weighted mean elevation, elevation range and the years surveyed. Glacier types are land-terminating (L), lake-terminating (LK), tidewater (T) and surge-type (S). Reid Glacier is likely now land-terminating, however it appears that high tides do still reach the terminus on occasion. Fairweather Glacier calves into a lake that is located in the middle of the stagnant terminus of the glacier. Dashes between years surveyed indicate years that were differenced to obtain mass balances (where 95 is 1995, 00 is 2000, etc.)
We derived glacier surface elevations from the combination of airplane positioning and attitude data from the onboard global positioning system–inertial navigation system (GPS–INS), and the distance to and direction of the laser point returns from the glacier surface. The combination of these data determines positions in three-dimensional space of the laser points on the glacier surface. We referenced the points in International Terrestrial reference Frame 2000 (ITRF00) and projected the coordinates to World Geodetic System 1984 (WGS84)/Universal Transverse Mercator (UTM) zone 8N, with elevation data referenced as height above ellipsoid. GPS processing of the aircraft position uses both L1/L2 data and is processed with the Gamit–Globk differential phase kinematic positioning program ‘Track’ (Reference ChenChen, 1999; Reference KingKing, 2009). All data acquired during earlier missions have been reprocessed to create a consistent dataset for the entire UAF laser altimetry program. The Operation IceBridge data (2009–12) are available from the US National Snow and Ice Data Center (NSIDC) and earlier data are available upon request
Glacier hypsometries
Glacier hypsometries, also known as the area–altitude distribution (AAD), are derived from the Shuttle Radar Topography Mission (SRTM) DEM that was acquired in February 2000. We do not calculate any elevation changes directly from this DEM rather we use it solely to find the reference AAD. The surface area of each glacier is derived from glacier outlines distributed by the Global Land Ice Measurements from Space (GLIMS) project (Reference Raup, Racoviteanu, Khalsa, Helm, Armstrong and ArnaudRaup and others, 2007). Glacier outlines are based on Landsat 7 ETM+ images from August 2010; we explore the effects on our analysis of changing glacier extents by using outlines from other dates in the error analysis section.
Methods
Estimating elevation changes with time
The glacier surface elevation profiles from each year were differenced to find the surface elevation change, Δh, divided by the time elapsed between profiles to give the rate of elevation change, Δh/Δt. We extrapolated the measured surface elevation changes along each of the flight lines to the entire surface area of the glacier, in order to estimate volume change from center-line surface elevation changes on each surveyed glacier (Reference Arendt, Luthcke, Larsen, Abdalati, Krabill and BeedleArendt and others, 2008). We converted the glacier volume change to water equivalent (w.e.) to give mass balance, 
, in km3 w.e. a−1(equivalent to Gt a−1) or in specific mass-balance units, mw.e. a−1 . The method for finding the elevation change between repeated profiles differed slightly, depending on whether the profiler (1995–2009) or scanner (2011) systems were used. For profiler-toprofiler comparisons, we selected all points that are located within 10 m of each other in the map plane as common points between the different years. If more than three points were located within that 10 m grid, we calculated the mode of the elevation for each gridcell by binning the points. Using the mode instead of the mean elevation serves to reduce the sensitivity of the elevation profile data to small-scale topographic features (e.g. crevasses or sastrugi) that are unlikely to be present at the same location every flight year. We then differenced the elevations of common gridcells to find Δh/Δt. Since only a single track of data points was recorded with the profiler, it is critical that these earlier tracks were repeated as closely as possible to obtain a large number of common points. However, sometimes, because of wind and turbulence, the flights were not repeated precisely enough to provide sufficient elevation change measurements. For example, the elevation profile of Muir Glacier between 2005 and 2009 has only five common gridcells with data points over a large area between 1275 and 1800 m elevation (Reference JohnsonJohnson, 2012). Sparsely repeated flight lines, such as this, can limit the robustness of the interpolated Δh/Δt fitted to the data.
To compare scanner to profiler for surface elevation differencing, we created a 10 m resolution DEM from the scanner data. The gridded elevations were derived from the mode of the scanner data within each gridcell. We used the coordinates from each point in the earlier profile to extract an elevation from this DEM using bilinear interpolation. We then differenced this interpolated DEM elevation with the profiler elevation at that point.
The series of Δh/Δt values vs elevation over the glacier was modeled using a moving median to smooth the Δh/Δt values (see smoothed example in Fig. 2). The use of the mean or median was found to give similar results in this model, but the presence of occasional outliers in the data series suggested the median would be more robust. This moving median sequentially travels through the elevation range of the glacier over which there are Δh/Δt data. The elevation range over which the median traverses was variable: it typically used 12 Δh/Δt points, but used fewer points (4 or 8) on profiles with sparse data coverage and more points (>20) for profiles with a larger number of Δh/Δt points (>10 000 points). In Glacier Bay the variations in thinning rates between different branches of a given glacier were observed to be on the order of the scatter normally found in these data. Here we combined the elevation change profiles when multiple branches of a single glacier were surveyed. This approach would be problematic on some glaciers, such as Columbia Glacier where large differences in thinning are found at the same elevation on different branches (Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others, 2010).
Fig. 2. Change in elevation vs elevation from repeated altimetry profiles of Casement Glacier during periods 3 (2005–09) and 4 (2009–11). The red curve is the modeled Δh /Δt vs elevation curve that is defined by the median quartile, while the dashed blue curves are the estimated uncertainty defined by the lower and upper quartiles. The bottom plot (solid blue curve) shows the AAD of the glacier. The glacier-wide mass balance is calculated by integrating each modeled Δh/Δt vs elevation curve over the area–altitude distribution. The appearance of larger scatter during period 4 is due to use of the scanner system during 2011, which produces an order of magnitude more crossover locations.
We interpolated the second quartile (median) values to elevation steps of 30m to create the modeled line for the Δh/Δt vs elevation curve. This method preserved the shape of the curve and was able to interpolate through elevations where there were sparse data points. We approximated the rate of volume change, Δv/Δt, by numerical integration of the modeled Δh/Δt vs elevation curve over the glacier-specific SRTM AAD. This approximation relies on several assumptions, discussed below. An example of this analysis over two time periods on Casement Glacier is shown in Figure 2.
We assigned a value of zero to Δh/Δt at both the lower and upper elevation limits of the glacier outline. This assumption is based on previous observations that have shown that the thickness changes at a glacier’s head are generally near zero over time for glaciers undergoing overall thinning and mass loss (Reference Schwitter and RaymondSchwitter and Raymond, 1993; Reference ArendtArendt and others, 2006). This assumption does not hold for glaciers or icefields that have an equilibrium-line altitude (ELA) above the glacier head (e.g. Yakutat Glacier (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007; Reference Trüssel, Motyka, Truffer and LarsenTrüssel and others, 2013)). In these cases, nonzero thinning can be observed at the highest elevation range of the glaciers. The 6 km2 Burroughs Glacier remnant is the only glacier in Glacier Bay that presently has this geometry.
Estimating mass balance
There were no density measurements associated with the mass-balance results presented herein, a common situation for geodetic measurements of mass balance (Reference CogleyCogley, 2009). This required that we invoke the assumption of a constant (in time) vertical density profile, i.e. Sorge’s law (Reference BaderBader, 1954). We calculated the mass-balance rate, , by assuming that the volume changes of the glacier are entirely ice. The calculated Δv/Δt was converted to water equivalent volume change, and hence mass balance, assuming a constant glacier density, where ρ
ice = 900 kg m−3. The specific mass-balance rate (m w.e. a−1) is useful for comparing the changes that occur on glaciers of various sizes and is found by dividing by the corresponding glacier surface area.
Regionalization methods
To estimate the regional mass balance and contribution to SLR, we extrapolated the results from the surveyed glaciers to the entire Glacier Bay region. We compared three different regionalization methods. The first regional extrapolation method produced a single, normalized mean elevation change vs elevation curve for all the glaciers surveyed during a particular time period. We then integrated this curve over the AAD of the unsurveyed glaciers to estimate the remaining, unmeasured mass balance. The other two methods applied a mean (area-weighted or simple average) specific mass balance of the surveyed glaciers to the remaining unmeasured glaciers.
Normalized elevation (NE)
The NE method exploits the common signatures of Δh/Δt variations with elevation for a glacier that is thinning and losing mass, wherein elevation losses are greatest at the current glacier terminus and decrease with elevation to near zero at the glacier head (Reference Schwitter and RaymondSchwitter and Raymond, 1993). However, prior to regionalizing Δh/Δt variations with elevation it is important to normalize individual glacier elevation ranges, because of the variations in these ranges across the region. This is similar to the use of normalized elevations in the ‘toe–headwall altitude ratio’ approach in studies of regional glacier ELAs (Reference MeierdingMeierding, 1982; Reference Leonard and FountainLeonard and Fountain, 2003). Reference ArendtArendt and others (2006) presented a regionalization method that normalized both Δh/Δt and the elevation range. However, applying this regionalization based on normalizing both Δh/Δt and the elevation range to unmeasured glaciers requires knowledge of the rate of thickness change at the termini of the unmeasured glaciers. Lacking such data on the unsurveyed glaciers, we used a simplified version of ‘Method B’ of Reference ArendtArendt and others (2006) (personal communication from R. Hock, 2011, wherein only the elevation range is normalized using
where h was derived from the SRTM AAD and h term and h head are the elevations of the glacier terminus and head.
A mean Δh/Δt vs normalized elevation curve was calculated for each altimetry time period, which was then integrated over the AAD of unsurveyed glaciers to estimate the of those glaciers. We applied this NE method individually to the eastern and western icefields of Glacier Bay. We separated the eastern and western icefields because of the significantly different AADs of the two areas. In the eastern icefield, the elevation of the maximum in glaciated area is within 50m of the median elevation, but in the western icefield a larger portion of the glaciated area is at the lower end of the elevation range. The western icefield also contains glaciers at higher elevations than those in the eastern icefield (4670 cf. 2500 m). Due to this difference in the AADs, integrating the mean Δh/Δt vs normalized elevation over the entire Glacier Bay region would give unrealistic mass change results. However, this method relies on the assumption that the surveyed and unsurveyed glaciers are located in a similar climate regime.
Area-weighted average 
(area avg ) and simple average (simple avg )
The second regionalization method (area avg ) is ‘Method C′ of Reference ArendtArendt and others (2006). It applies the area-weighted average of all the surveyed glaciers (m w.e. a−1) to all of the unsurveyed glaciers in Glacier Bay for a particular time period. This method is particularly useful if the AAD of the unsurveyed glaciers is not well known, as it only requires knowledge of the total surface area of the unsurveyed glaciers. The third method (simple avg ) only differs in that it uses a simple average instead of an area-weighted average.
Sensitivity analysis
One challenge in performing a robust regionalization of the total ice mass change of an area is to determine whether the surveyed glaciers are representative of the region. To examine this issue, we carried out sensitivity analyses by iteratively removing surveyed glaciers one at a time from the regionalization of a given time period. This simulates what the measured would have been if that particular glacier had not been surveyed. Comparing the amount of variation within the results of the sensitivity analyses to the mass change estimates gives us an idea of whether the selected glaciers as a group are representative of the entire glaciated area.
The flights in 2005, 2009 and 2011 included more glaciers than earlier years, and thus a comprehensive sensitivity analysis was more meaningful for period 3 (9 glaciers) and period 4 (14 glaciers). The Glacier Bay region contains a wide variety of glacier geometries, so applying the most representative normalized elevation change function to the unsurveyed glaciers is important to accurately determine the mass-balance rate of those glaciers. For example, previous authors (e.g. Reference ArendtArendt and others, 2006) have shown that it is inappropriate to apply the thickness change profile of a rapidly calving tidewater glacier to a terrestrial glacier. This limitation may not necessarily hold for tidewater or previously tidewater glaciers that are not currently undergoing rapid retreat.
Errors and Uncertainties in Mass-Balance Estimations
Positioning errors
The dominant source of measurement error of airborne altimetry is associated with the positioning and orientation (attitude) of the aircraft along its trajectory from the GPS–INS solution (Reference KingKing, 2009). We estimated the effect of the GPS–INS errors by analyzing repeat profiles over fixed objects. These errors are independent, and result in a net vertical and horizontal positioning error of ±0.2 m. These errors are correlated with range and angle of incidence of the laser shots. Attitude measurement errors were larger with the profiler system than with the scanner system, and the more accurate GPS–INS of the scanner system leads to higher laser point positioning accuracy than the profiler system at the typical flight altitudes of each system. Trajectory errors are on the order of ±0.2 m, and the effect of attitude errors can lead to a laser profiler shot point coordinate error of ±0.2 m. By comparison, the laser ranging error is two orders of magnitude smaller (±0.002 m). In both systems, the greatest effect of attitude error occurs when the laser angle of incidence with the glacier surface is large. Typically, the profiler system (attitude accuracy ±0.2°) was flown at a height of 250 m above the glacier surface, a geometry that could result in an attitude-induced positioning error of ±0.58 m if the angle of incidence is 30° relative to the glacier surface. The scanner system (attitude accuracy ±0.02°) at a typical height above the surface of 500m would have a vertical and horizontal point positioning error of ±0.19 m with the same angle of incidence to the surface. The effects of attitude measurement errors on laser point positioning are minimized when the aircraft’s attitude is nearly parallel to the glacier surface. For example, the profiler at a typical height above ground (250m) will have an attitude positioning error of only ±0.002 m under level flight conditions over a flat glacier.
Aircraft positioning errors from the GPS solution are dependent on a number of variables that change with time and can be difficult to quantify. These variables include atmospheric delays, geometric strength of GPS constellations, ionosphere characteristics and variable distances from the reference station to the kinematic GPS on board the aircraft (Reference KingKing, 2009). A complete error analysis of the coordinates of laser returns would incorporate the full covariance matrix from the GPS–INS solution, along with the geometry of each laser shot and the angle of incidence iteratively derived from the surface slope and aircraft orientation. However, this analysis was not done here. Instead, through repeated surveying of fixed objects (e.g. paved runways and airport buildings) with independently derived coordinates, we empirically determined the error in the point measurements to be of the order of ±0.2 m, in good agreement with earlier studies (Reference EchelmeyerEchelmeyer and others, 1996; Reference Arendt, Luthcke, Larsen, Abdalati, Krabill and BeedleArendt and others, 2008; Reference KingKing, 2009).
Modeled Δh/Δt uncertainties
We estimated the uncertainty of the modeled Δh /Δt vs elevation curve by examining the data variance. We calculated the upper and lower quartiles Δh /Δt as a function of the elevation range for each glacier. We then used the upper and lower quartiles of the Δh /Δt instead of the median to calculate upper and lower estimates of Δv /Δt by numerically integrating these values over the AAD (Fig. 2). The lower and upper quartiles are not always equally spaced from the median, and so the upper and lower uncertainties will not necessarily have the same difference from the median. We determined the Δh /Δt uncertainty for elevations above which there are no Δh /0394t data by applying the full interquartile range of all Δh/Δt data for all elevations. This approach results in a typical uncertainty of ±1.0 m a-1 at the glacier’s head.
Uncertainties in modeling across glacier Δh/Δt
Our glacier-wide mass-balance extrapolation method of laser altimetry relies on the assumption that elevation changes measured along the center line are constant across the width of the glacier. Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010) questioned the validity of this assumption when they compared the results of differencing elevations of sequential DEMs with center-line-derived volume changes. Their study suggested that Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others (2002) overestimated total ice loss Alaska-wide by 34%. To find the source of this discrepancy, Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010) compared DEM-derived ice loss with simulated laser altimetry (referred to as ‘simu-laser’ by Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others, 2010, and herein) ice loss on ten large Alaska glaciers using elevation changes along center lines. These elevation changes were extracted from the difference DEM, and were assumed to represent thickness changes across the full width of the glacier. These Δh /Δt were then integrated over the AAD to calculate mass balance, , following the same methodology as laser altimetry mass-balance estimates of Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others (2002). Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010) found that the simu-laser ice loss for the ten selected Alaskan glaciers exceeded the sequential-DEM-derived ice loss by 22%.
We applied the simu-laser methodology to the Glacier Bay region in order to further test the laser altimetry centerline method. We used the difference DEM of Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007), a difference of the SRTM and a modified National Elevation Dataset (NED). The dates of the glacier outlines used in this difference DEM are 1948/87 (US Geological Survey (USGS) maps), so the thinning at the glacier margins is included. The simu-laser elevation changes are extracted from the difference DEM along the altimetry flight paths in Glacier Bay. We included all of the 16 glaciers with laser altimetry results in Glacier Bay in this analysis. The analysis was extended to an additional 24 unsurveyed glaciers with simulated flight lines that generally followed the glacier’s center line, resulting in a total of 40 glaciers used in our simu-laser analysis. The distribution of the 16 surveyed glaciers is biased toward the larger glaciers, with 11 glaciers that have areas >100 km2. In contrast, the 24 unsurveyed glaciers only have four glaciers with areas >100 km2. The total area in our simu-laser analysis is 5143 km2, which represents 80% of the total glaciated area of the Glacier Bay region.
Although the magnitude and sign of the relative difference between 
and 
is variable for individual
glaciers, we find that the simu-laser method underestimates the full difference DEM derived ice loss by only 6% for the 40 glaciers that were tested (Fig. 3). The 
and 
cumulative mass changes were −3.91 and −3:68 Gt a−1, respectively. We tested the effect of using 2010 glacier outlines on our analysis and found the 
and 
cumulative mass changes were −2.84 and −2.68 Gt a−1, also a 6% difference. Finally, the 
and 
estimates were within 1% over the 16 surveyed glaciers in Glacier Bay. The agreement between the DEM and simulaser methods (Fig. 3) lends strong support to the validity of scaling center-line altimetry-derived elevation changes to the entire Glacier Bay area.
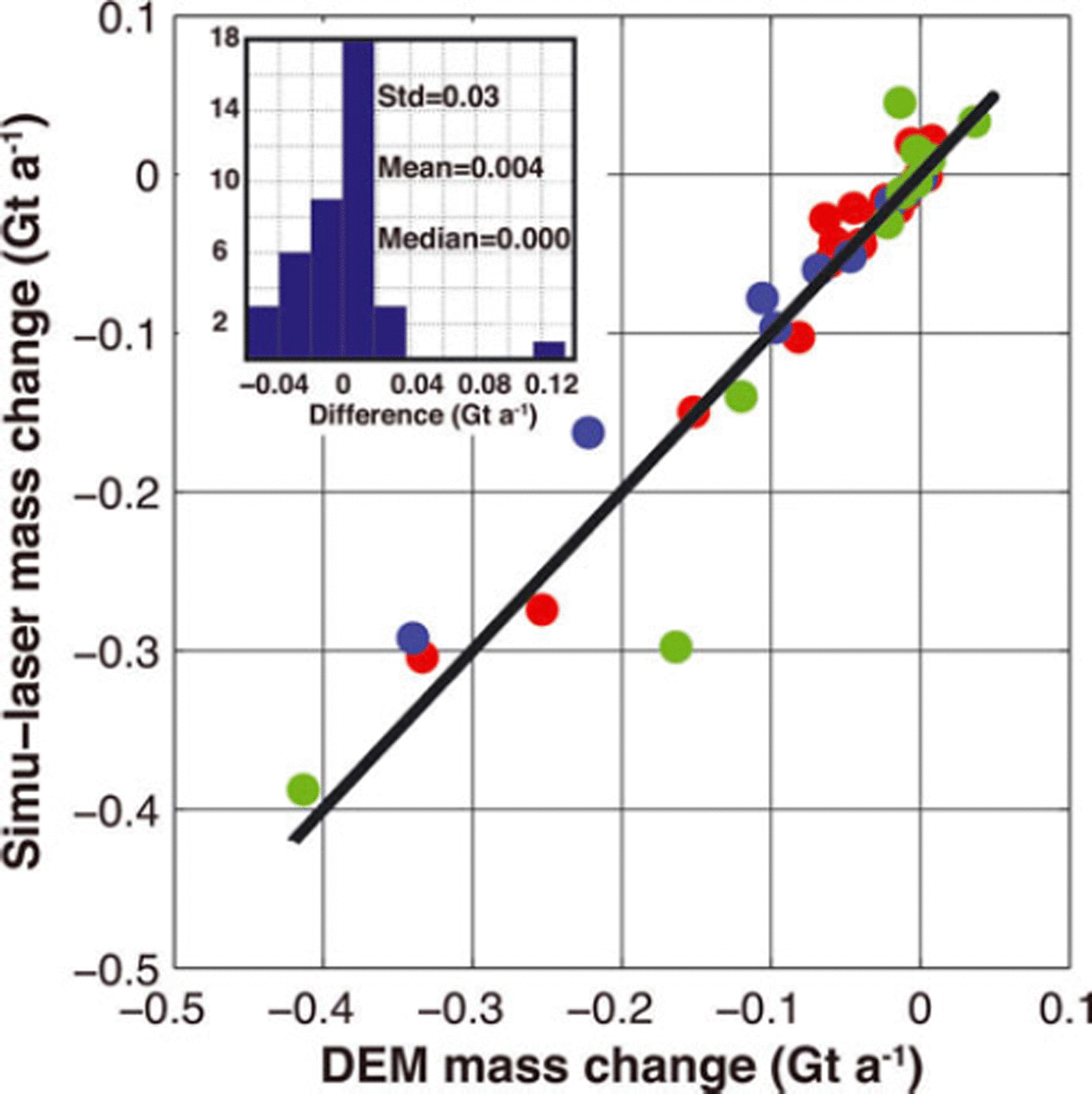
Fig. 3. Comparison of mass change from DEM differencing and the simu-laser method for 40 glaciers in Glacier Bay. Different colors distinguish between glacier types (red: land-terminating, blue: lake-terminating; and green: tidewater), and the solid black line represents a one-to-one mass change, i.e. results that fall on this line indicate agreement between DEM mass change and simu-laser mass change. The inset shows the distribution of differences between the two methods (DEM differencing minus simu-laser), and statistics of this distribution are noted. An outlier can be observed in both the scatter plot and the histogram. This outlier is Muir Glacier, and removing it from the distribution shown in the histogram results in a mean difference of 0.000Gt a−1.
Outline and AAD uncertainties
We use a single set of outlines to determine the surface area of glaciers in Glacier Bay. By using a fixed outline, the calculated mass balance presented here is a reference-surface balance (Reference Elsberg, Harrison, Echelmeyer and KrimmelElsberg and others, 2001). The effect of using glacier outlines from different dates is tested by using regional glacier outlines from August 2010, August 1999 and 1948/87 to determine how the estimates vary by only changing the representative glacier surface area. Older outlines from 1948 coverthe USA portion of Glacier Bay, while 1987 outlines are used forthe Canadian portion. This affects both the amount of area over which the mass change is calculated and the spatial extent of the DEM that is used to determine the AAD. The difference in that results from using the most recent glacier outlines from 1999 and 2010 and the SRTM DEM is within the uncertainties for the four different periods. The uncertainty of period 4 is ±0.54 Gt a−1 for the surveyed glaciers, while the of the same glaciers was only 0.15 Gt a−1, or 4%, more negative when using 1999 outlines as compared to using 2010 outlines. The total area lost between 1999 and 2010 was 130 km2 (6558 to 6428 km2), an actual change in glacier extent not attributable to variances in the quality of the outline data. Our analysis shows that using different outlines during the period of altimetry measurements has little effect on the mass-balance estimates and thus a minimal effect on both conventional and reference-surface balances. This error assessment does not account for changes in surface elevation that would accompany glacier area changes. We tested the worst-case scenario of this potential error using AADs from the DEM based on air photographs from the 1948/ 87 NED DEM and glacier outlines from topographic maps based on the same photographs (47 years before the first altimetry profiles for the USA portion). In this case, the for period 4 using the NED DEM and 1948/87 outlines was 0.54 Gt a−1, or 13%, more negative than using 2010 outlines.
Density assumption
To convert from observed changes in volume to estimates of changes in mass, we assumed a constant bulk density of the material involved in the volume changes, i.e. Sorge’s law (Reference BaderBader, 1954). Sorge’s law must be applied to the whole glacier assuming a single bulk density because flow, accumulation and ablation all occur as a continuum between the dates of surface elevation measurements. In general, this assumption of Sorge’s law could have increasing impacts on mass-balance estimates when invoked over shorter time intervals, for example as could be caused by seasonal to annual variations in firn density. Shorter time intervals also require effort to minimize seasonal effects of snow depth on this assumption, accomplished herein by repeating the surveys as closely as possible to the same calendar date. Unfortunately, regional changes in firn density and seasonal variations in snowpack depth are not monitored in our study area, and these additional uncertainties cannot be formally constrained. However, we find that for the majority of glaciers studied herein, most of the mass loss occurs in the ablation area, where variations in column-averaged ice density are smaller. These temperate glaciers are also unlikely to have the ongoing process of rapid and dramatic firn densification, as observed in the polythermal glaciers of Canada’s Baffin and Bylot Islands, which prompted Reference Gardner, Moholdt, Arendt and WoutersGardner and others (2012) to assign an additional uncertainty to areas above the firn line. Without any evidence for this process in Glacier Bay, we do not assign a similar additional uncertainty above the firn line. We do, however, examine the effect on caused by assuming different bulk glacier densities(ρ
ice = 830 and 917 kg m−3), in a similar way to previous studies (e.g. Reference Arendt, Luthcke, Larsen, Abdalati, Krabill and BeedleArendt and others, 2008), in place of the average bulk density assumed herein (900 kgm−3). The difference in calculated using these different densities is ∼10%. The effect of using these minimum and maximum densities tends to be less than the uncertainties caused by the other assumptions and errors discussed above. For example, period 4 has a uncertainty of ±0.54 Gt a−1 for the surveyed glaciers. The estimate of varies by ±0.36 Gt a−1 when using the different ice densities of 830 and 917 kg m−3.
Effects upon regionalization caused by a temporally varying set of surveyed glaciers
Each of the four periods has a different set of surveyed glaciers, leading to changes in the spatial sampling of data used in the regionalization. We test the effects of this temporal variation using two approaches. In the first, we perform simulated regional izations using the difference DEM map of Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007). In the second approach, we create a homogenized time series in which we regionalize using altimetry data only from the three glaciers (Brady, Lamplugh and Reid) that were surveyed in all four time periods.
The simulated regional izations begin with a known answer (i.e. the full mass change as found in the difference DEM map), and we try to estimate this mass change using data extracted from this difference map only from each subset of glaciers as were surveyed in each of the four periods. For example, a simulated regionalization using period 1’s glaciers would extract data from only Brady, Reid, Lamplugh, Grand Pacific and Little Jarvis glaciers, and then use those data to estimate the full mass change in the difference map using all three regionalization methods (NE, area avg and simple avg ). The results are shown in Table 2.
Table 2. Tests of regionalization methods. Simulated regional izations are performed using subsets of the DEM difference map of Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007). The four subsets of glaciers used are the same glaciers surveyed in periods 1, 2, 3 and 4. Using the three regionalization methods, the data from each of these subsets are extracted from the DEM difference map and then used to estimate the total mass change. These estimates are compared to the known value of total mass change from the full DEM difference result of −4.62 Gt a−1
Notably, the NE method works very well with the full set of glaciers, as were surveyed in period 4, suggesting that this set of glaciers is a reasonable representation of the whole area. Wide-ranging estimates from the NE method in periods 1 and 2 appear to be driven by too few glaciers in the subset, combined with the extreme behavior of Muir Glacier during the time frame of the difference DEM (1948–2000). Note that Muir Glacier is not present in the period 1 subset, but is present in the subsets of periods 2, 3 and 4. Muir Glacier underwent a rapid tidewater calving retreat during this time, and including (or not including) the associated rapid elevation changes strongly biases the regionalization if only a few glaciers are present. However, the subsets of periods 3 and 4 appear to overcome this bias with a greater number of glaciers. The two averaging methods, area avg and simple avg , appear to perform better than the NE method when fewer glaciers are surveyed, yet they both consistently overestimate the total mass loss in all but the period 1 subset. In the period 1 subset, the absence of data from rapidly retreating Muir Glacier causes all methods to underestimate the total mass loss.
During the time period covered by the altimetry data presented herein, there are no glaciers in our study area that exhibit extreme calving retreat dynamics and rapid elevation changes similar to Muir Glacier in the DEM difference time period. As such, it is difficult to directly quantify the results of these simulated regional izations into our error budget. Using a homogenized time series can offer a quantifiable uncertainty for our results, as it is based upon the actual altimetry data. Using just data from Brady, Lamplugh and Reid glaciers, the estimated for the entire Glacier Bay area with the NE method is -2:73 ± 0:91 Gt a−1 during period 1, −6.00 ± 1:48 Gt a−1 during period 2, -2.48 ± 0.48 Gt a−1 during period 3, and −5.37 ± 0.57Gt a−1 during period 4. As shown in the results section below, these homogenized NE results were within ±0.30Gt a−1 of the regional NE estimates that were based upon all available data. We thus assign an additional uncertainty of ±0.30Gt a−1 for periods 1 and 2 to account for the limited spatial sampling during those periods.
Total error estimation
For each glacier surveyed, the uncertainties of the modeled Δh /Δt vs elevation curve are propagated in quadrature sum along with the positioning errors, across glacier Δh /Δt uncertainties, area uncertainties and density uncertainties to estimate the mass change error. These individual glacier uncertainties are then similarly propagated into the regionalization error estimates, which additionally include ±0.30Gt a−1 for periods 1 and 2, associated with the limited spatial sampling then.
Results and Discussion
Glacier mass balance and mass changes
The mass-balance (), record is widely variable between periods and individual glaciers; however, most glaciers lost more mass during 2000–05 (period 2) and 2009–11 (period 4) than in 1995–2000 (period 1) and 2005–09 (period 3). For example, Brady Glacier had a of −1.01 ± 0.13 mw.e. a−1 during period 1, 
mw.e.a-1 during period 2, 
mw.e. a−1 during period 3, and 
m w.e.a−1 during period 4. The total mass balance of Brady Glacier between 1995 and 2011 is -9.91 ± 0.02 Gt when the from each period is summed, which compares closely to the when the 2011 scanner swath is compared directly to the 1995 profile (−9.93 ± 0.03 Gt). Results are shown as maps (Fig. 4) and as time series of (Fig. 5).
Fig. 4. (a–d) Altimetry-derived rate of surface elevation change for all surveyed glaciers, with flight lines shown on glacier surfaces in black. For comparison, the rate of thinning from differencing of DEMs from 2000 and 1948/87 (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007) is shown in (e). Land is shown as light brown and unsurveyed glaciers are shown as light gray.
Fig. 5. Mass balance of every glacier that has been surveyed with altimetry, separated by type (land-terminating, tidewater, lake-terminating). Width of the box is the time-span of each period, while height is the uncertainty of the mass-balance estimate
The most negative Δh /Δt values in Glacier Bay during the periods for which we have the greatest number of surveyed glaciers (periods 3 and 4) occurred on Casement and Grand Plateau Glaciers. Casement Glacier is a land-terminating glacier and had a Δh /Δt of −6m a−1 near the terminus during period 3, which then became more negative than -8ma−1 during period 4 (Fig. 2). Grand Plateau Glacier is a lake-terminating glacier and has a broad and relatively flat terminus that calves into multiple lakes. The Δh /Δt over this low-elevation area of Grand Plateau Glacier was −5ma−1 during period 3 and became more negative, −8ma−1, during period 4. Thinning was observed over most of the elevation range of the glacier during period 4, with a Δh/Δt that was more negative than −1.5 m a-1 up to 3400 m (Fig. 4d). The for Grand Plateau Glacier during period 4 was 
mw.e. a−1, which is by far the most negative of all the surveyed glaciers in Glacier Bay for any period and was much more negative than the of −1.02 ± 0.38 mw.e.a−1 observed during period 3. Such behavior could be associated with lake calving dynamics, such as are occurring on nearby Yakutat Glacier (Reference Trüssel, Motyka, Truffer and LarsenTrüssel and others, 2013).
A couple of glaciers that are adjacent to each other had different spatial thinning patterns. During periods 3 and 4 Riggs Glacier had a thinning profile that is similar to Muir Glacier below 1100 m. However, Riggs Glacier had no thickening above this elevation, whereas Muir Glacier did (Fig. 4c and d). This response is intriguing, as the accumulation areas of the two glaciers are directly adjacent to each other (Fig. 1), and it implies that ice dynamics are involved. Riggs Glacier also had a more negative during period 4 when compared with period 3, which follows the same pattern as Brady and Grand Plateau Glaciers.
Davidson and Casement Glaciers share a flow divide at an elevation of ∼1200m, with Casement Glacier flowing west and Davidson Glacier flowing east (Fig. 1). Both glaciers had a Δh /Δt of around −1 m a−1 at the flow divide during period 3; however, Casement Glacier had a much more negative Δh /Δt below 600m than Davidson Glacier (−6 m a−1 vs 0 m a−1 at the terminus). The thinning at the flow divide during period 4 (−1.5ma−1) was similar to period 3, but with increased thinning at the lower elevations of both glaciers, that resulted in a more negative during period 4. However, the thinning at the terminus of Casement Glacier was again greater than at Davidson Glacier (−8 and −3 m a−1, respectively).
There is some indication of a minor surge occurring in the upper region of Carroll Glacier during period 4, with a drawdown of ∼3 m a−1at 1800 m and thickening of ∼2 m a-1 between 1200 and 1500 m. However, the surge front did not reach the lower elevations of Carroll Glacier, as Δh /Δt was around −8 m a−1 near the terminus. Margerie Glacier, a surge-type, tidewater glacier that last surged during the 1980s (Reference Molnia, Williams and FerrignoMolnia, 2008), does not fit the study area’s pattern of increased thinning and mass loss during period 4. Margerie Glacier had thickening below 1000m (−2 ma−1 at the terminus) during period 3 (Fig. 4c) and had a slightly positive , which is not consistent with most of the other surveyed glaciers. During period 4 Margerie Glacier had thickening that was sustained from the terminus up to 1200 m (Fig. 4d) and had the most positive for any glacier in Glacier Bay during any period (0.36 
). During both periods there are no laser data on Margerie Glacier between 1300 and 2200m (39% of its area), due to an icefall with a surface slope steeper than the aircraft can descend or climb. The Δh /Δt uncertainties associated with this data gap are large, which contributes to the large uncertainty for Margerie Glacier.
Konamoxt Glacier is a lake-terminating glacier in the northern Glacier Bay region (Fig. 1) that was surveyed only in 1996 and 2011 and had a of 
over that period. It had a significantly negative Δh /Δt just up-glacier of the 2010 calving terminus, −7m a−1 at an elevation of 400m, which equates to a total thinning of 105 m between 1996 and 2011.
Regionalization
The different regionalization methods (NE, area avg and simple avg ) gave different results for periods 1 through 4 (Table 3). The area of the unsurveyed glaciers (i.e. the area extrapolated to) varies significantly between periods: period 1 has an unsurveyed glacier area of 5136 km2, period 2 of 5572 km2, period 3 of 4624 km2 and period 4 of 3174 km2. With a total glaciated area in Glacier Bay of 6428 km2, the percentages of extrapolated area for periods 1 through 4 are 80%, 87%, 74% and 49%. The estimated for the entire Glacier Bay area with the NE method is −2.66 ± 0.89 Gt a-1 during period 1, −5.14 ± 1.27Gt a−1 during period 2, −2.96 ± 0.54Gt a−1 during period 3 and −6.06 ± 0.65Gt a−1 during period 4.
Table 3. Mass-balance rates of the Glacier Bay region. ‘Surveyed glaciers area avg’ is an area-weighted average mass balance that is used in the area avg method, and ‘Surveyed glaciers simple avg’ is a simple average mass balance that is used in the simple avg method. The mean normalized elevation curves are used in the NE method. Numbers in bold are ice mass change for the entire Glacier Bay region using the the preferred regionalization method (NE)
The NE method is preferred here because of the reliability of the precise glacier outlines used, which allows for a precise AAD to be calculated for unsurveyed glaciers. The results of the simulated regional izations (above) based upon the difference DEM of Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) show that the NE method can very accurately reproduce a regional mass change, provided there is sufficient spatial sampling. As discussed below, a close correlation between the regional NE and GRACE results, the wide variability in glacier and the limited number of glaciers that were surveyed during the earlier altimetry periods are also factors in this preference. In the absence of high-quality glacier outlines and accurate AADs the avg methods would be preferred and would ideally be used with a dataset wherein many glacier were known (Reference ArendtArendt and others, 2006). Results for the NE method are presented as a time series over the four periods in Figure 6a.
Fig. 6. Total regional mass change in Glacier Bay (a) between 1995 and 2011 and (b) since the LIA. (a) Regionalized altimetry results are presented for the NE method. Width of the box is the time-span of each period, while height is the uncertainty of the mass-balance estimate. Laser altimetry results are shown with solid lines; difference DEM results that overlap from the earlier period (covered by (b)) are shown with dashed lines. (b) Mass-balance estimates, 1770–1948 (Reference Larsen, Motyka, Freymueller, Echelmeyer and IvinsLarsen and others, 2005; Reference Motyka, Larsen, Freymueller and EchelmeyerMotyka and others, 2007) and 1948–2000 (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007).
Periods 1 and 3 have nearly the same magnitude of estimated e, with a regional NE mass change near −3Gt a−1. Periods 2 and 4 have a regional NE that is around twice as negative as in the other two periods (Fig. 6a). The total estimates vary depending on whether the NE or avg regional izations are used, with both the avg methods resulting in a more negative regional for all periods. During periods 1 and 2, the regional using the area avg method was >50% more negative than using the NE method, and was ∼25% more negative during periods 3 and 4. The larger difference in between these two methods during periods 1 and 2 is likely because Brady Glacier dominates the area-weighted average e, in those periods, due to the small number of glaciers surveyed and the large area of Brady Glacier compared with the other glaciers. The simple avg regional results are closer to the NE results than those from the area avg method.
A sensitivity analysis was carried out for periods 3 and 4 to examine the effect that removing a single glacier from the NE regionalization had on the of unsurveyed glaciers. The results of the sensitivity analyses for period 3 are generally within ±0.1 mw.e.a−1 and ±0.20Gt a−1, with the exception of the case where Casement Glacier was excluded. Casement Glacier had the most negative during this period. Its removal meant the NE was 0.44Gt a−1 higher than any of the other estimates and was the only case where was outside the estimated error. The results from period 4 are generally within ±0.05 m w.e.a-1 and ±0.15Gt a−1. As with period 3, the removal of Casement Glacier had a large impact on the NE estimates, second only to the impact of Grand Plateau Glacier (removal of Grand Plateau Glacier resulted in a NE that was 0.16Gta−1 higher than any of the other estimates excluding Casement Glacier). However, both cases were still within the estimated error of the calculated for period 4.
Temporal variability of mass balance prior to these altimetry results
Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) differenced the 2000 SRTM DEM from a composite DEM based on air photographs from 1948 (USA) and 1987 (Canada) to estimate glacier mass change in southeast Alaska. Here we subsampled the surface elevation change grid of Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) to include just the glaciers located in the Glacier Bay region, and found that was −4.62 ±1.22 Gt a−1 (−0.7 ± 0.2 m w.e. a−1). This is more negative than the regionalized average NE of −3.93 ± 0.89 Gt a−1 between 1995 and 2011. The highest rate of thinning occurred at Muir Glacier (Fig. 4e), which experienced a rapid tidewater retreat during this period and prior to the altimetry data presented here ( of −0.46 Gt a−1 or −2.45 mw.e. a−1 from DEM differencing). The decrease in the regional mass loss rate is likely due to the termination of the rapid tidewater retreat of Muir Glacier up the West Arm, with the rapid retreat ending ∼1980 (for a complete discussion, see Reference JohnsonJohnson, 2012). There was also rapid retreat of Melbern and Konamoxt Glaciers, which had created the 20 km long Lake Melbern by ∼2000. Additionally, Grand Plateau and Alsek Glaciers, which are both calving into lakes, have also experienced rapid retreat which continues at present.
The of −4.62 ± 1.22 Gt a−1 from DEM differencing is equivalent to a total mass loss of 240 ± 63Gt over the 52 years between 1948 and 2000, using the assumption that the area in Canada that is covered by the 1987 DEM had a mass loss rate between 1948 and 1987 that was the same as between 1987 and 2000. Adding this to the regionalized altimetry data using the NE method, a mass loss of 49.6 ± 9.6 Gt between 2000 and 2011 gives a total mass loss of 289.8 ± 73.0 Gt since 1948, and an equivalent total SLR of 0.801 ± 0.202 mm. To put this into perspective, the total ice mass loss since 1770 (Fig. 6b) is about an order of magnitude larger, modeled at ∼3450 Gt, which is equivalent to a total SLR of ∼10 mm (Reference Larsen, Motyka, Freymueller, Echelmeyer and IvinsLarsen and others, 2005; Reference Motyka, Larsen, Freymueller and EchelmeyerMotyka and others, 2007). The inferred 8 between 1770 and 1948 is −17.8 Gt a−1, which is almost four times greater than the of −4.6 Gt a−1 between 1948 and 2011.
Comparison with the GRACE mass-balance record
Gravity data from the GRACE (Gravity Recovery and Climate Experiment) mission provide another mass change estimate that can be compared with the laser altimetry mass change. The GRACE mission uses tandem satellites to map temporal variations in the Earth’s geoid, and senses all components of the atmosphere, ocean and land systems. The geophysical signal of interest (e.g. change in ice mass) is identified from the complete gravity signal by forward-modeling all non-glacier mass changes using terrestrial water storage, glacial isostatic adjustment and other datasets. The fundamental resolution is limited by the orbital height of the satellite, accelerometer accuracy and other variables. Although numerous GRACE solutions exist for Alaska, the mascon approach of Reference Luthcke, Arendt, Rowlands, McCarthy and LarsenLuthcke and others (2008) is used here, because it provides exceptionally high resolution, that has been shown to compare well with independent airborne altimetry observations in Alaska (Reference Arendt, Luthcke, Larsen, Abdalati, Krabill and BeedleArendt and others, 2008). GRACE cumulative mass balances from this mascon solution are currently available from the middle of 2003 through late 2010, which coincides with the end of altimetry period 2, all of altimetry period 3 and most of altimetry period 4. We use a new 1° × 1° product derived from a new NASA Goddard Space Flight Center global solution optimized for retrieval of glacier mass balance (Reference Pritchard, Luthcke and FlemingPritchard and others, 2010). The equal-area mascons are used as the domain over which spatial and temporal constraints are applied on the gravity signal that is recorded from GRACE. The mass change is estimated over successive time intervals of 10 days. The errors for individual mascon solutions can be large due to smearing of the signal between neighboring mascons; however, we do not quantify this error here.
The current mascon that includes the Glacier Bay region covers most of the region’s glaciated area, with parts of the eastern glaciers and the southern part of Brady Glacier located in neighboring mascons that also include glaciers outside Glacier Bay. Following Reference Arendt, Luthcke, Larsen, Abdalati, Krabill and BeedleArendt and others (2008), we estimate cumulative mass balances for those areas by finding the percentage of ice in the adjoining mascons that are located within the Glacier Bay region, and then adjusting the cumulative mass balance of the adjoining mascons by the same percentage. The time period covered by the GRACE gravity data is from April 2003 through December 2010 (Fig. 7). The trend in the Glacier Bay GRACE signal over this period was −3.05 Gt a−1, which includes parts of laser altimetry periods 2, 3 and 4. Selecting the GRACE cumulative mass balance from the end of May during each year allows the GRACE-derived mass loss to be calculated over the annual balance year that is used here in laser altimetry. The trend was −2.47 Gt a−1 when the GRACE signal was restricted to period 3 from altimetry. This is much closer to the period 3 NE estimate of −2.96 ± 0.54 Gt a−1 than the area avg of −3.78 ± 0.73 Gt a−1. The year 2009/10 had the most negative annual mass change at −6.34 Gt a−1, while 2006/ 07 and 2008/09 had much less negative annual mass changes, −0.99 and −1.16 Gt a−1, respectively. The wide variability in GRACE annual mass balances echoes the variability that is seen in the various laser altimetry periods.
Fig. 7. GRACE cumulative mass balance of the Glacier Bay region during 2003–10, from an updated series of Reference Luthcke, Arendt, Rowlands, McCarthy and LarsenLuthcke and others (2008) (Luthcke and others, in press). The red line represents the mass change trend for the entire period of the GRACE observations. The trend is calculated through simultaneous estimations of tidal al iasing period and bias, trend, annual and semi-annual sinusoids. Balance year GRACE mass losses are 2004/05: −5.27Gt a−1; 2005/06: − 3.60Gt a−1; 2006/07: −0.99Gt a−1; 2007/08: −4.29Gt a−1; 2008/09 −1.16 Gt a−1; 2009/10: −6.34 Gt a−1.
Relationship to climate
The Glacier Bay laser altimetry mass-balance record shows large temporal and spatial variations in e, with increased ice loss during periods 2 and 4 when compared with periods 1 and 3. To place these variations in context with other Alaska mass-balance records, we compare our results with the USGS index glaciers. The USGS has been using the glaciological method to monitor the mass balance of two Alaska glaciers since 1966: Gulkana Glacier in the eastern Alaska Range and Wolverine Glacier on the Kenai Peninsula (Reference Van Beusekom, O’Neel, March, Sass and CoxVan Beusekom and others, 2010). Annual mass balances for these glaciers are calculated through conventional mass-balance measurements carried out in spring near the beginning of the melt season, and in autumn at the end of the melt season. For comparison with our May altimetry acquisitions, we calculate average annual mass balances at the USGS glaciers from spring to spring seasons of each measurement period. Glacier Bay and Wolverine Glacier are both located in a maritime setting, while Gulkana Glacier is located in an interior continental setting. Reference-surface mass-balance data from the USGS were used to find the average of these glaciers during the altimetry time periods (Table 4). The average for both of these glaciers is most negative during altimetry period 2. This temporal evolution is similar to both the record of Brady Glacier and the regional record in Glacier Bay, which had around twice as much mass loss during period 2 compared with periods 1 and 3. This general agreement in temporal mass-balance variations suggests a broadly regional, multi-annual synoptic relationship. To further explore a connection to climate, we compare the temporal variation in mass balance within Glacier Bay to positive degree-days and winter precipitation.
Table 4. Average reference-surface mass-balance rates for Wolverine and Gulkana Glaciers during each altimetry time period. The Glacier Bay mass-balance rate is the regional total using the NE method
There is a dearth of long-term climate stations within the study area, with the closest sites located in Juneau, Yakutat and Sitka, Alaska. We used a gridded climate product that interpolates anomalies of station data from 1971–2000 climate normals over a 2 km × 2 km grid (personal communication fom D.F. Hill and S.E. Calos, 2011). Hill and Calos interpolated absolute (for temperature) and proportional (for precipitation) anomalies because these are assumed to be less spatially variable than the raw observations. We then sampled this gridded dataset over the Glacier Bay region to obtain monthly temperature and precipitation data. We calculated the change in annual average temperature over time using linear regression. Annual mean temperatures increased by 1.7°C from 1961 to 2009 in Glacier Bay, with summer temperatures (May–September) increasing by 1.4°C and winter temperatures (October–April) by 1.9°C.
We used the gridded average monthly temperature to calculate annual, spatially averaged, positive degree-months, which we converted to positive degree-days, or PDD (the sum of daily temperatures above a certain threshold). We summed the PDD over the entire region using a temperature threshold of 0°C and then normalized by the number of gridcells. Here the average PDD does not have a direct physical interpretation, but it can be used to examine temporal and spatial trends in the amount of energy that is available to contribute to the melting of snow and ice. We calculated the winter precipitation, or the amount of precipitation that fell as solid precipitation or snow (mmw.e.), by extracting gridcells that had temperatures below 0°C, summing the amount of precipitation over those gridcells and then normalizing by the number of gridcells. The average annual PDD in Glacier Bay was calculated over the time-span of the four altimetry mass-balance periods (Table 5). The average PDD suggests higher ablation during periods 2 and 4 than in period 3, which is reflected in the record (periods 2 and 4 had a mass loss rate that was approximately twice that of period 3). The summer of 2004 had the highest PDD during periods 2–4 (Fig. 8), which correlates with the record negative summer mass balance measured in Alaska during 2004 (Truffer a0nd others, 2005) and the increased mass loss during period 2. However, the relationship between annually averaged PDD and does not hold for period 1, which had a mass loss rate similar to period 3. Period 1 had an average PDD that was significantly higher than that of the other three periods and was particularly high in 1997. This suggests that period 1 would have had the most ablation of all the periods, which is contrary to the altimetry record. Additionally, 1997 and 2004 had the highest annually averaged PDD in the Glacier Bay region, which corresponds to years that had the most negative on Wolverine and Gulkana Glaciers since 1995.
Fig. 8. (a) 1961–2009 spatially averaged total winter precipitation in Glacier Bay. (b) Spatially averaged annual positive degree-days in Glacier Bay calculated from monthly air temperatures. Precipitation and temperature data are from D.F. Hill and S.E Calos (personal communication, 2011). Solid black curves are 10 year running averages.
Table 5. Annual average of positive degree-days (PDD) and the annual average of precipitation that fell when the average monthly temperature was <0°C. Data are calculated over the duration of each altimetry time period. ‘All’ is calculated over the entire Glacier Bay domain, while ‘East’ and ‘West’ were sampled separately over the two distinct glaciated regions of Glacier Bay
The winter precipitation record does not appear to be correlated at all with the altimetry measurements. The average winter precipitation during each period increased over time (Table 5), which does not correspond with the fluctuations seen in the record nor in the Wolverine and Gulkana Glacier records. If winter precipitation was directly related to we would expect to see decreased winter precipitation during the periods with the most negative (periods 2 and 4), and increased winter precipitation during periods with less negative (periods 1 and 3).
Looking at both PDD and winter precipitation together, the correlation of the climate data with the record becomes even more tenuous. For instance, based upon the lower mass loss that is observed with altimetry during period 1, we would expect to see the high average PDD during period 1 being balanced by higher winter precipitation. The exact opposite response is observed, with period 1 showing the lowest winter precipitation.
Previous studies have demonstrated that alpine glaciers are sensitive to small changes in climate, and are able to respond quickly to short-term changes in climate (Reference OerlemansOerlemans and others, 1998). We therefore expect to see a clear relationship between and the climate data, based upon the similar patterns in that are observed in Glacier Bay. There are a number of possible explanations for the discrepancy between the climate data and records. Glacier Bay is located in a maritime, temperate climate that results in precipitation being very sensitive to freezing thresholds. Also, precipitation is very difficult to measure, particularly in high mountain areas (Reference Nesbitt and AndersNesbitt and Anders, 2009). The climate data used here only employ a limited number of low-altitude weather stations in southeast Alaska, so the model may not be correctly extrapolating temperature and precipitation in the mountainous Glacier Bay region. Temperature and precipitation are calculated at monthly resolution, which does not capture shorter-term variability. This variability will have the largest effect during spring and fall, when the temperature is close to the freezing point. Finally, temperature may not be an appropriate proxy for melt during some years, when radiative effects may dominate. For example, it has been indicated that the 2009 eruption of Mount Redoubt, which is located to the west of Cook Inlet, Alaska, reduced albedo and increased melt, even though summer temperatures were not high during 2009 (Reference Arendt, Luthcke, O’Neel, Gardner and HillArendt and others, 2011).
Relationship to glacier dynamics
The glaciers that have been surveyed are generally large, but are these glaciers representative of the rest of the Glacier Bay area? Glaciers of differing size respond with differing sensitivities and response times to changes in climate. We examine this question by testing the relationship between and glacier area for the surveyed glaciers. Figure 9 shows that the region’s large glaciers generally have a more negative specific , although the relationship does not appear very robust. This indicates that the surveyed glaciers, which tend to be larger than average, may not represent the entire Glacier Bay area, and could explain why our altimetry mass loss is slightly higher than the mass loss observed by GRACE. There appears to be no relationship between and the area-averaged elevation of the surveyed glaciers (Fig. 9). Our data also do not demonstrate a relationship between and glacier type, i.e. land-terminating, lake-terminating or tidewater. We performed the same analysis on the eastern and western icefields, and found no significant difference between the glaciated regions.
Fig. 9. (a) Specific mass balance vs area-averaged elevation for glaciers surveyed in Glacier Bay between 2009 and 2011. (b) Mass balance vs 2010 glacier surface area for the same period.
Tidewater glaciers can be strongly influenced by ice dynamics associated with the tidewater glacier cycle (Reference Meier and PostMeier and Post, 1987). In many cases, mass balance of calving glaciers may appear to be independent of climate. These glaciers may contribute markedly to a region’s overall ice loss, especially if they are in a state of rapid calving, as was certainly the case in Glacier Bay’s rapid post-LIA retreat. It is important to monitor as many tidewater glaciers as possible, including advancing, retreating and stable tidewater glaciers, to determine present volume change rates, and to avoid the complications of regionalizing tidewater glaciers (Reference ArendtArendt and others, 2006).
The tidewater glaciers of the Glacier Bay area are relatively stable when compared with other dramatically retreating Alaska tidewater glaciers (e.g. Columbia Glacier (Reference Walter, O’Neel, McNamara, Pfeffer, Bassis and FrickerWalter and others, 2010); Icy Bay (Reference Muskett, Lingle, Sauber, Rabus and TangbornMuskett and others, 2008); and South Sawyer Glacier (unpublished data from UAF)). This raises the question of whether the tidewater glaciers in Glacier Bay can be included in a regionalization without adversely affecting the estimated ice loss. The sensitivity analysis that was carried out shows that removing individual tidewater glaciers from the regionalization does not have a significant effect on the mass balance of the remaining glaciers, compared with the removal of a non-tidewater glacier. The rapid tidewater retreat that Glacier Bay experienced after the LIA has ended, and at present the fastest- retreating glaciers generally include both land-terminating and lake-terminating glaciers.
Conclusions
We estimated mass-balance rates for glaciers located in the Glacier Bay area of Alaska and Canada with airborne laser altimetry. Mass balances are estimated by differencing glacier surface elevations acquired during repeat laser altimetry flights in 1995, 2000, 2005, 2009 and 2011. The mass-balance record generally shows a more negative mass balance for the periods 2000–05 (period 2) and 2009–11 (period 4) as compared with periods 1995–2000 (period 1) and 2005–09 (period 3), with significant local variability. Thinning of up to 8 m a−1 is observed at lower elevations on some glaciers.
We validated the laser altimetry method using DEM differencing for glaciers located in the Glacier Bay area. The simu-laser method, wherein surface elevation changes along laser altimetry flight lines are extracted from a difference DEM, shows good agreement with whole-DEM differencing. Reference Berthier, Schiefer, Clarke, Menounos and RémyBerthier and others (2010) found that the simu-laser ice loss was overestimated by 22% compared with DEM differencing for ten Alaskan glaciers; here we find the simu-laser method underestimates ice loss in Glacier Bay by 6% compared with DEM differencing.
Three regionalization methods were used to extrapolate mass-balance results from glaciers with measurements to those without, in order to estimate the mass balance of the entire Glacier Bay region. Over the entire 16 year time-span of altimetry measurements (1995–2011) the average mass change for the entire Glacier Bay glaciated area, using the NE method, is −3.93 ± 0.89 Gt a−1 (−0.6 ± 0.1 m w.e. a−1), resulting in a total SLR of 0.174 ± 0.039 mm over this period. There are wide variations from this average between individual time periods. Both area avg a and simple avg e methods yield mass-balance estimates that are more negative than those estimated with the NE method. Over the time-span of altimetry measurements in Glacier Bay, the area’s glaciers generally follow a relationship where more-negative balance rates are found on glaciers with greater areas. The closer agreement between the regionalization methods during the later two periods is probably associated with the greater number of surveyed glaciers and an improvement in the distribution of glacier sizes. Independent support for the NE method comes from the closer correlation found between the regional NE and GRACE results than that with the area-weighted method. Simulated regional izations of the difference DEM of Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007) were used to test the three methods over the various subsets of glaciers surveyed here. These tests show that the NE method can very accurately reproduce the regional mass changes given observations from a sufficient number of glaciers. We conclude that the NE method is generally more accurate than averaging methods (area avg a and simple avg e), yet it is important to note that the normalized elevation approach is only practical when precise glacier outlines and an accurate DEM are available for the study area.
To put these changes in the context of mass losses across the entire Gulf of Alaska (GOA) region, we assembled all available GRACE estimates for Alaska spanning at least the 2003–09 period. These estimates vary due to differences in methods of processing GRACE data between various centers, different choices of models to correct for non-glacier sources of mass variability in the region and different sampling periods. Reference Sasgen, Klemann and MartinecSasgen and others (2012) report changes ranging from −47 to −76 ± 4 Gt a−1 for the period August 2002–09, derived from four different processing centers. An updated series of Luthcke and others (in press) for the period January 2004–10 is −65 ± 15 Gt a−1, while Reference Jacob, Wahr, Pfeffer and SwensonJacob and others (2012) report −47 ± 7 Gt a−1for the period December 2003 to January 2010. While it would be preferable to adjust these estimates to a common time window, only the Reference Luthcke, Arendt, Rowlands, McCarthy and LarsenLuthcke and others (2008) values are reported on an annual basis, allowing for such a computation. Therefore we take the arithmetic average of all values and the root-sum-square of the errors to obtain −64 ± 18 Gt−1. The Glacier Bay region between 2005 and 2011 (periods 3 and 4) averaged a loss of 4.0 ± 0.6 Gt a−1, and thus comprises ∼6 ± 1% of the total mass loss of GOA glaciers over these roughly coinciding time frames.
Finally, we found a weak to non-existent relationship between climate data and the mass-balance record in Glacier Bay, with poor correlation of the mass-balance time series with the time series of positive degree-days and winter precipitation. The positive degree-day record shows a weak correlation to the altimetry mass balance during periods 2–4; however, there appears to be no correlation with period 1. There also appears to be no correlation with winter precipitation, which steadily increases over the time period covered by altimetry measurements. The altimetry mass balance of the Glacier Bay region does, however, correspond to the USGS mass-balance records of Gulkana and Wolverine Glaciers over the same time periods. All three areas (Glacier Bay, and Wolverine and Gulkana Glaciers) have a more negative mass balance during period 2 than in periods 1 and 3. This suggests an Alaska-wide regional mass-balance pattern that can only be explained by climate, yet is not captured here by the simple proxies of positive degree-days and winter precipitation.
Acknowledgements
Support for this work was provided by NASA’s Operation IceBridge (N N X 1 1 A C 2 4 G, N N H 0 9 Z D A 0 0 1 N, NNX09AP54G), by NASA’s Cryospheric Sciences Program (NNH10ZDA001 N, NNH07ZDA001 N), by the US National Science Foundation (NSF) (ARC-0612537) and by the US National Park Service (CESU (Cooperative Ecosystem Studies Units) agreement No. H9911080028). The late Keith Echelmeyer initiated the UAF altimetry program, piloted the aircraft and collected the 1995 and 2000 data. Paul Claus took over pilot duties in 2002. David Hill provided the climate dataset. Logistical support provided by the Claus family at Ultima Thule Outfitters is especially appreciated. Dave Burns reprocessed all the kinematic GPS data and scanner data. Justin Rich contributed updated glacier outlines and sampled the climate data to the Glacier Bay area. Tim Bartholomaus and Martin Truffer provided valuable suggestions and comments.
