Published online by Cambridge University Press: 15 December 2022
This article presents the results of the first AIAA Stability and Control Prediction Workshop obtained at the U.S. Air Force Academy using the kCFD flow solver of the
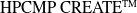 ${\rm{HPCMP}}\;{\rm{CREAT}}{{\rm{E}}^{{\rm{TM}}}}$
-AV Kestrel simulation tools. The test case considered is a large-scale Common Research Model (CRM) tested at the ONERA S1MA wind tunnel at different transonic speeds and fixed lift coefficient values at zero and non-zero side-slip angles. The computational results include a grid sensitivity analysis and validation with available experimental data. In addition, the Mach number and sting effects on the predicted stability and control values of the test case are investigated. Finally, a system identification method using a regression model is developed and used for prediction of stability and control data. The regression coefficients are estimated from an input signal with varying-frequency changes in the angle-of-attack, pitch rate, and side-slip angle. Once the model was created, it was used to predict the static and dynamic aerodynamic data of the test cases. The results show that the model predictions match very well with calculated CFD data at discrete flow conditions.
${\rm{HPCMP}}\;{\rm{CREAT}}{{\rm{E}}^{{\rm{TM}}}}$
-AV Kestrel simulation tools. The test case considered is a large-scale Common Research Model (CRM) tested at the ONERA S1MA wind tunnel at different transonic speeds and fixed lift coefficient values at zero and non-zero side-slip angles. The computational results include a grid sensitivity analysis and validation with available experimental data. In addition, the Mach number and sting effects on the predicted stability and control values of the test case are investigated. Finally, a system identification method using a regression model is developed and used for prediction of stability and control data. The regression coefficients are estimated from an input signal with varying-frequency changes in the angle-of-attack, pitch rate, and side-slip angle. Once the model was created, it was used to predict the static and dynamic aerodynamic data of the test cases. The results show that the model predictions match very well with calculated CFD data at discrete flow conditions.
Distribution A. Approved for Public Release. Distribution unlimited.