1. Introduction
Interfacial fluid phenomena are of interest in a wide range of applications including biological materials such as membranes formed by lipid bilayers and two-dimensional liquid crystal films. The development of a theoretical framework that describes the governing equations for these interfaces has been of long-standing interest to both the fluids and biophysics community. The dynamics of a fluid interface for a Newtonian fluid is concisely given in Scriven (Reference Scriven1960). Inspired by these works and by the observations that lipid bilayers behave as fluid membranes (Singer & Nicolson Reference Singer and Nicolson1972), the governing equations for deformable membranes with bending elasticity and viscous flow were derived a few years ago (Arroyo & DeSimone Reference Arroyo and DeSimone2009; Rangamani et al. Reference Rangamani, Agrawal, Mandadapu, Oster and Steigmann2013). These studies have led to multiple insights into how the viscosity of the fluid film can interact with the bending elasticity, foremost of which is the description of the Scriven–Love number and its implications (Al-Izzi, Sens & Turner Reference Al-Izzi, Sens and Turner2020; Sahu et al. Reference Sahu, Glisman, Tchoufag and Mandadapu2020). This dimensionless number captures the competition between the viscous and bending forces in the membrane. Building on these prior works, we now focus on the two-dimensional active nematic fluids and their governing equations as described in Al-Izzi & Morris (Reference Al-Izzi and Morris2023).
2. Overview
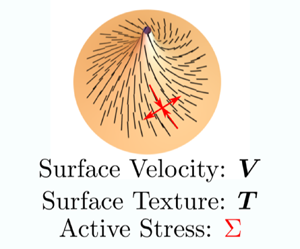
Nematic liquid crystals are rod-shaped molecules that do not have a translational order but instead have a long-range orientational order, which is represented by a director field (figure 1a). A specific biological example of such systems in three dimensions is bacterial suspensions, shown in figure 1(b), (Dombrowski et al. Reference Dombrowski, Cisneros, Chatkaew, Goldstein and Kessler2004). The coupling of nematic liquid crystals and thin film deformation has been studied by different groups with varying degrees of complexity (Nitschke, Reuther & Voigt Reference Nitschke, Reuther and Voigt2020). Coupling deformation with a director field is a challenging mathematical problem, particularly for two-dimensional films. The effect of surface geometry on the order parameter was explored in detail in Napoli & Vergori (Reference Napoli and Vergori2012). Steigmann (Reference Steigmann2013) worked out a detailed theory for lipid membranes with tilt and distension based on three-dimensional liquid crystal theory, and explored how the deformation and the director field exhibit coupled behaviours in special cases (Rangamani & Steigmann Reference Rangamani and Steigmann2014; Rangamani et al. Reference Rangamani, Benjamini, Agrawal, Smit, Steigmann and Oster2014) (figure 1c). These prior studies did not consider the interactions of the director field with the surface flows or the role played by the activity of the inclusions on the surface.
Figure 1. (a) Three-dimensional nematic liquid crystals have long-range orientational order but no positional order. The director is the black arrow and represents the average orientation of the liquid crystals. Presence of activity (represented by yellow) leads to hydrodynamic flows as shown in a bacterial suspension in (b), scale bar  $35\,\mathrm {\mu }{\rm m}$. Image adapted with permission from Dombrowski et al. (Reference Dombrowski, Cisneros, Chatkaew, Goldstein and Kessler2004). (c) Two-dimensional liquid crystals with activity also have a director field associated with them and presence of activity on such surfaces can lead to flow patterns as observed in panel (d). These experiments were conducted using active nematic liquid crystals on lipid bilayers; image adapted with permission from Keber et al. (Reference Keber, Loiseau, Sanchez, DeCamp, Giomi, Bowick, Marchetti, Dogic and Bausch2014). (e) Lipid bilayers with embedded motor proteins such as adenosine triphosphate (ATP) synthases shown as a schematic. (f) The interaction of the ATP synthases alters the surface curvature of the lipid membrane. The left image shows monomeric ATP synthases and the right image shows dimeric ATP synthases. Image adapted with permission from Davies et al. (Reference Davies, Anselmi, Wittig, Faraldo-Gomez and Kuhlbrandt2012). Figure created with BioRender.com.
$35\,\mathrm {\mu }{\rm m}$. Image adapted with permission from Dombrowski et al. (Reference Dombrowski, Cisneros, Chatkaew, Goldstein and Kessler2004). (c) Two-dimensional liquid crystals with activity also have a director field associated with them and presence of activity on such surfaces can lead to flow patterns as observed in panel (d). These experiments were conducted using active nematic liquid crystals on lipid bilayers; image adapted with permission from Keber et al. (Reference Keber, Loiseau, Sanchez, DeCamp, Giomi, Bowick, Marchetti, Dogic and Bausch2014). (e) Lipid bilayers with embedded motor proteins such as adenosine triphosphate (ATP) synthases shown as a schematic. (f) The interaction of the ATP synthases alters the surface curvature of the lipid membrane. The left image shows monomeric ATP synthases and the right image shows dimeric ATP synthases. Image adapted with permission from Davies et al. (Reference Davies, Anselmi, Wittig, Faraldo-Gomez and Kuhlbrandt2012). Figure created with BioRender.com.
Al-Izzi & Morris (Reference Al-Izzi and Morris2023) derive the governing equations for active nematic fluids on deformable curved surface for nematic liquid crystals in the one-constant limit of the Frank free energy and derive the general form of the tangential and normal force balance equations. The activity of these liquid crystals, which characterizes their ability to convert stored energy or energy from the environment into motion, is described using an active stress tensor. They obtain the full dynamical equations that describe the polarization dynamics, the constant director and incompressibility constraints and the tangential and normal balances. Analysis of these equations reveals both the dimensionless Scriven–Love number described above for isotropic coupling and a new ‘liquid crystalline Scriven–Love’ number that captures the anisotropic coupling terms. The dimensionless active stress, which results from comparing the tangential stresses with bending stress, is an analogue of the Föppl–von-Kármán number. These dimensionless numbers complete the analysis and allow for a comparison between isotropic fluid films and anisotropic fluids films for in-plane and out-of-plane stresses. Further, the authors apply their equations to some example cases. On tubes with active nematics, they find that contractile active stresses lead to the case of an ‘active pearling’ instability while extensile active stresses lead to ‘ruffles’.
There are many potential applications for the model developed in Al-Izzi & Morris (Reference Al-Izzi and Morris2023). Consider the field of membrane biophysics as a specific example. Cellular membranes contain many proteins that diffuse in the plane of the membrane. The dynamics of defects associated with active nematic liquid crystals on lipid vesicles was experimentally determined in Keber et al. (Reference Keber, Loiseau, Sanchez, DeCamp, Giomi, Bowick, Marchetti, Dogic and Bausch2014) (figure 1d). Deformation of the membrane in response to any curvature-inducing proteins is often modelled as a spontaneous curvature, a ‘catch-all’ input parameter that essentially forces the curvature of the surface. Coupling of the diffusion of such curvature-inducing proteins with membrane flow was discussed in Mahapatra, Saintillan & Rangamani (Reference Mahapatra, Saintillan and Rangamani2020, Reference Mahapatra, Saintillan and Rangamani2021). However, many of these proteins are active, undergoing conformational changes or phosphorylation state changes due to biochemical reactions or interactions with the environment. Active proteins in cellular membranes can act as hydrodynamic dipoles, and analysis of hydrodynamic collective effects of active proteins in lipid bilayers showed that this activity can contribute to the diffusion enhancement and drift in the plane of the membrane (Mikhailov & Kapral Reference Mikhailov and Kapral2015). The activity of these proteins could then influence the nematic order parameter and the deformation of the membrane without the need for specific-curvature-inducing domains on the bilayer. Al-Izzi & Morris (Reference Al-Izzi and Morris2023) discuss active pearling of a cylindrical tube. Such active pearling could be relevant to the function of membrane-embedded motor proteins in cellular systems. Prominent examples of such a system are the ATP synthases on mitochondrial membranes, which produce ATP in cells (figure 1e) (Nirody, Budin & Rangamani Reference Nirody, Budin and Rangamani2020). Applications of models such as those developed in Al-Izzi & Morris (Reference Al-Izzi and Morris2023) can shed light into how the activity of ATP synthases and local lipid environment may be coupled. Davies et al. (Reference Davies, Anselmi, Wittig, Faraldo-Gomez and Kuhlbrandt2012) showed that the curvature of the mitochondrial membranes depends on the interactions between ATP synthases (figure 1f). The long-range effects of active inclusions in deformable surfaces and the effect of non-uniform distribution of inclusion in local and long-range transport will be important to understand in general conditions and with applications to specific examples. Thus, this study paves the path forward for us to gain fundamental insight into some extremely complex, small length scale (nm– $\mathrm {\mu }$m), active nematic thin fluid films.
$\mathrm {\mu }$m), active nematic thin fluid films.
3. Outlook
Deformable nematic shells appear in a wide range of biological systems ranging across length scales from tissues to subcellular components such as cellular membranes. Many of these components also carry activity and deform their shape in response to activity. Recent experiments described in Guillamat et al. (Reference Guillamat, Blanch-Mercader, Pernollet, Kruse and Roux2022) and simulations described in Zhang & Yeomans (Reference Zhang and Yeomans2023) highlight the role of active forces in determining tissue architecture. The development of governing equations that describe the interaction of the activity with the nematic order parameter, such as the work done in Al-Izzi & Morris (Reference Al-Izzi and Morris2023), is a step forward in our ability to investigate multiple physics, particularly in complex biological systems. These predictions set the stage for the investigation of both long-range interactions in these fluid films and short length scale molecular dynamic simulations to identify how the interactions between order parameter and activity can perturb the system. There now arises an exciting possibility of even making comparisons with experimental measurements; see Watkins et al. (Reference Watkins, Miller, Majewski and Kuhl2011) for beautiful grazing incidence X-ray diffraction measurements of textures induced on a lipid bilayer surface by cholera toxin molecules. For further in-depth investigation and generation of quantitative results, computational tools, including numerical schemes to solve the governing equations and molecular dynamic simulations to obtain small length scale parameters, will be needed (see Huang et al. Reference Huang, Kapral, Mikhailov and Chen2013; Sauer Reference Sauer2018).

 $35\,\mathrm {\mu }{\rm m}$. Image adapted with permission from Dombrowski et al. (2004). (c) Two-dimensional liquid crystals with activity also have a director field associated with them and presence of activity on such surfaces can lead to flow patterns as observed in panel (d). These experiments were conducted using active nematic liquid crystals on lipid bilayers; image adapted with permission from Keber et al. (2014). (e) Lipid bilayers with embedded motor proteins such as adenosine triphosphate (ATP) synthases shown as a schematic. (f) The interaction of the ATP synthases alters the surface curvature of the lipid membrane. The left image shows monomeric ATP synthases and the right image shows dimeric ATP synthases. Image adapted with permission from Davies et al. (2012). Figure created with BioRender.com.
$35\,\mathrm {\mu }{\rm m}$. Image adapted with permission from Dombrowski et al. (2004). (c) Two-dimensional liquid crystals with activity also have a director field associated with them and presence of activity on such surfaces can lead to flow patterns as observed in panel (d). These experiments were conducted using active nematic liquid crystals on lipid bilayers; image adapted with permission from Keber et al. (2014). (e) Lipid bilayers with embedded motor proteins such as adenosine triphosphate (ATP) synthases shown as a schematic. (f) The interaction of the ATP synthases alters the surface curvature of the lipid membrane. The left image shows monomeric ATP synthases and the right image shows dimeric ATP synthases. Image adapted with permission from Davies et al. (2012). Figure created with BioRender.com.



1. Introduction
Interfacial fluid phenomena are of interest in a wide range of applications including biological materials such as membranes formed by lipid bilayers and two-dimensional liquid crystal films. The development of a theoretical framework that describes the governing equations for these interfaces has been of long-standing interest to both the fluids and biophysics community. The dynamics of a fluid interface for a Newtonian fluid is concisely given in Scriven (Reference Scriven1960). Inspired by these works and by the observations that lipid bilayers behave as fluid membranes (Singer & Nicolson Reference Singer and Nicolson1972), the governing equations for deformable membranes with bending elasticity and viscous flow were derived a few years ago (Arroyo & DeSimone Reference Arroyo and DeSimone2009; Rangamani et al. Reference Rangamani, Agrawal, Mandadapu, Oster and Steigmann2013). These studies have led to multiple insights into how the viscosity of the fluid film can interact with the bending elasticity, foremost of which is the description of the Scriven–Love number and its implications (Al-Izzi, Sens & Turner Reference Al-Izzi, Sens and Turner2020; Sahu et al. Reference Sahu, Glisman, Tchoufag and Mandadapu2020). This dimensionless number captures the competition between the viscous and bending forces in the membrane. Building on these prior works, we now focus on the two-dimensional active nematic fluids and their governing equations as described in Al-Izzi & Morris (Reference Al-Izzi and Morris2023).
2. Overview
Nematic liquid crystals are rod-shaped molecules that do not have a translational order but instead have a long-range orientational order, which is represented by a director field (figure 1a). A specific biological example of such systems in three dimensions is bacterial suspensions, shown in figure 1(b), (Dombrowski et al. Reference Dombrowski, Cisneros, Chatkaew, Goldstein and Kessler2004). The coupling of nematic liquid crystals and thin film deformation has been studied by different groups with varying degrees of complexity (Nitschke, Reuther & Voigt Reference Nitschke, Reuther and Voigt2020). Coupling deformation with a director field is a challenging mathematical problem, particularly for two-dimensional films. The effect of surface geometry on the order parameter was explored in detail in Napoli & Vergori (Reference Napoli and Vergori2012). Steigmann (Reference Steigmann2013) worked out a detailed theory for lipid membranes with tilt and distension based on three-dimensional liquid crystal theory, and explored how the deformation and the director field exhibit coupled behaviours in special cases (Rangamani & Steigmann Reference Rangamani and Steigmann2014; Rangamani et al. Reference Rangamani, Benjamini, Agrawal, Smit, Steigmann and Oster2014) (figure 1c). These prior studies did not consider the interactions of the director field with the surface flows or the role played by the activity of the inclusions on the surface.
Figure 1. (a) Three-dimensional nematic liquid crystals have long-range orientational order but no positional order. The director is the black arrow and represents the average orientation of the liquid crystals. Presence of activity (represented by yellow) leads to hydrodynamic flows as shown in a bacterial suspension in (b), scale bar $35\,\mathrm {\mu }{\rm m}$. Image adapted with permission from Dombrowski et al. (Reference Dombrowski, Cisneros, Chatkaew, Goldstein and Kessler2004). (c) Two-dimensional liquid crystals with activity also have a director field associated with them and presence of activity on such surfaces can lead to flow patterns as observed in panel (d). These experiments were conducted using active nematic liquid crystals on lipid bilayers; image adapted with permission from Keber et al. (Reference Keber, Loiseau, Sanchez, DeCamp, Giomi, Bowick, Marchetti, Dogic and Bausch2014). (e) Lipid bilayers with embedded motor proteins such as adenosine triphosphate (ATP) synthases shown as a schematic. (f) The interaction of the ATP synthases alters the surface curvature of the lipid membrane. The left image shows monomeric ATP synthases and the right image shows dimeric ATP synthases. Image adapted with permission from Davies et al. (Reference Davies, Anselmi, Wittig, Faraldo-Gomez and Kuhlbrandt2012). Figure created with BioRender.com.
$35\,\mathrm {\mu }{\rm m}$. Image adapted with permission from Dombrowski et al. (Reference Dombrowski, Cisneros, Chatkaew, Goldstein and Kessler2004). (c) Two-dimensional liquid crystals with activity also have a director field associated with them and presence of activity on such surfaces can lead to flow patterns as observed in panel (d). These experiments were conducted using active nematic liquid crystals on lipid bilayers; image adapted with permission from Keber et al. (Reference Keber, Loiseau, Sanchez, DeCamp, Giomi, Bowick, Marchetti, Dogic and Bausch2014). (e) Lipid bilayers with embedded motor proteins such as adenosine triphosphate (ATP) synthases shown as a schematic. (f) The interaction of the ATP synthases alters the surface curvature of the lipid membrane. The left image shows monomeric ATP synthases and the right image shows dimeric ATP synthases. Image adapted with permission from Davies et al. (Reference Davies, Anselmi, Wittig, Faraldo-Gomez and Kuhlbrandt2012). Figure created with BioRender.com.
Al-Izzi & Morris (Reference Al-Izzi and Morris2023) derive the governing equations for active nematic fluids on deformable curved surface for nematic liquid crystals in the one-constant limit of the Frank free energy and derive the general form of the tangential and normal force balance equations. The activity of these liquid crystals, which characterizes their ability to convert stored energy or energy from the environment into motion, is described using an active stress tensor. They obtain the full dynamical equations that describe the polarization dynamics, the constant director and incompressibility constraints and the tangential and normal balances. Analysis of these equations reveals both the dimensionless Scriven–Love number described above for isotropic coupling and a new ‘liquid crystalline Scriven–Love’ number that captures the anisotropic coupling terms. The dimensionless active stress, which results from comparing the tangential stresses with bending stress, is an analogue of the Föppl–von-Kármán number. These dimensionless numbers complete the analysis and allow for a comparison between isotropic fluid films and anisotropic fluids films for in-plane and out-of-plane stresses. Further, the authors apply their equations to some example cases. On tubes with active nematics, they find that contractile active stresses lead to the case of an ‘active pearling’ instability while extensile active stresses lead to ‘ruffles’.
There are many potential applications for the model developed in Al-Izzi & Morris (Reference Al-Izzi and Morris2023). Consider the field of membrane biophysics as a specific example. Cellular membranes contain many proteins that diffuse in the plane of the membrane. The dynamics of defects associated with active nematic liquid crystals on lipid vesicles was experimentally determined in Keber et al. (Reference Keber, Loiseau, Sanchez, DeCamp, Giomi, Bowick, Marchetti, Dogic and Bausch2014) (figure 1d). Deformation of the membrane in response to any curvature-inducing proteins is often modelled as a spontaneous curvature, a ‘catch-all’ input parameter that essentially forces the curvature of the surface. Coupling of the diffusion of such curvature-inducing proteins with membrane flow was discussed in Mahapatra, Saintillan & Rangamani (Reference Mahapatra, Saintillan and Rangamani2020, Reference Mahapatra, Saintillan and Rangamani2021). However, many of these proteins are active, undergoing conformational changes or phosphorylation state changes due to biochemical reactions or interactions with the environment. Active proteins in cellular membranes can act as hydrodynamic dipoles, and analysis of hydrodynamic collective effects of active proteins in lipid bilayers showed that this activity can contribute to the diffusion enhancement and drift in the plane of the membrane (Mikhailov & Kapral Reference Mikhailov and Kapral2015). The activity of these proteins could then influence the nematic order parameter and the deformation of the membrane without the need for specific-curvature-inducing domains on the bilayer. Al-Izzi & Morris (Reference Al-Izzi and Morris2023) discuss active pearling of a cylindrical tube. Such active pearling could be relevant to the function of membrane-embedded motor proteins in cellular systems. Prominent examples of such a system are the ATP synthases on mitochondrial membranes, which produce ATP in cells (figure 1e) (Nirody, Budin & Rangamani Reference Nirody, Budin and Rangamani2020). Applications of models such as those developed in Al-Izzi & Morris (Reference Al-Izzi and Morris2023) can shed light into how the activity of ATP synthases and local lipid environment may be coupled. Davies et al. (Reference Davies, Anselmi, Wittig, Faraldo-Gomez and Kuhlbrandt2012) showed that the curvature of the mitochondrial membranes depends on the interactions between ATP synthases (figure 1f). The long-range effects of active inclusions in deformable surfaces and the effect of non-uniform distribution of inclusion in local and long-range transport will be important to understand in general conditions and with applications to specific examples. Thus, this study paves the path forward for us to gain fundamental insight into some extremely complex, small length scale (nm– $\mathrm {\mu }$m), active nematic thin fluid films.
$\mathrm {\mu }$m), active nematic thin fluid films.
3. Outlook
Deformable nematic shells appear in a wide range of biological systems ranging across length scales from tissues to subcellular components such as cellular membranes. Many of these components also carry activity and deform their shape in response to activity. Recent experiments described in Guillamat et al. (Reference Guillamat, Blanch-Mercader, Pernollet, Kruse and Roux2022) and simulations described in Zhang & Yeomans (Reference Zhang and Yeomans2023) highlight the role of active forces in determining tissue architecture. The development of governing equations that describe the interaction of the activity with the nematic order parameter, such as the work done in Al-Izzi & Morris (Reference Al-Izzi and Morris2023), is a step forward in our ability to investigate multiple physics, particularly in complex biological systems. These predictions set the stage for the investigation of both long-range interactions in these fluid films and short length scale molecular dynamic simulations to identify how the interactions between order parameter and activity can perturb the system. There now arises an exciting possibility of even making comparisons with experimental measurements; see Watkins et al. (Reference Watkins, Miller, Majewski and Kuhl2011) for beautiful grazing incidence X-ray diffraction measurements of textures induced on a lipid bilayer surface by cholera toxin molecules. For further in-depth investigation and generation of quantitative results, computational tools, including numerical schemes to solve the governing equations and molecular dynamic simulations to obtain small length scale parameters, will be needed (see Huang et al. Reference Huang, Kapral, Mikhailov and Chen2013; Sauer Reference Sauer2018).
Acknowledgements
The author would like to thank Dr A. Chandrasekaran, S. Llewellyn Smith and D. Saintillan, and Y. Chen for their feedback and many discussions on this topic.
Declaration of interests
The author reports no conflict of interest.