I. INTRODUCTION
Acoustic noise problems have become serious with the increased use of industrial equipment, such as engines, fans, blowers, transformers, and compressors. It is especially prominent in transportation systems (e.g., vehicles, trains, airplanes, and ships), manufacturing plants, electrical appliances (e.g., air-conditioners, refrigerators, washing machines, and vacuum cleaners), medical equipment (e.g., magnetic resonance imaging (MRI) systems, and infant incubators), and human activities (e.g., crowded public spaces, offices, and bedrooms). Traditional acoustic noise reduction techniques are based on passive noise control, such as earplugs, ear-protectors, sound insulation walls, mufflers, and sound-absorbing materials. These passive techniques are effective for reducing noise over a wide frequency range. However, they require relatively large and costly materials, and are ineffective at low frequencies. Therefore, the active noise control (ANC) [Reference Nelson and Elliott1–Reference Kuo and Morgan8] proposed in the early 20th century, has gained intensive development in the last two decades to reduce low-frequency noise.
The ANC technique using a loudspeaker to generate anti-noise sound was first proposed in the 1936 patent by Lueg [Reference Lueg9]. ANC is an electro-acoustical technique based on the principle of superposition, that is, an anti-noise with the same amplitude but opposite phase is generated by secondary source(s) to cancel unwanted (primary) noise acoustically, thus resulting in reduced residual noise. The ANC system is very efficient for attenuating low-frequency noise in environments where the passive noise control techniques are expensive, bulky, and ineffective.
In practical applications, the characteristics of the noise source and acoustic environment are changing, and thus the frequency content, amplitude, and phase of the primary noise are also changing. The noise reduction performance is mainly dependent on the accuracy of the amplitude and phase of the anti-noise generated by a signal processing algorithm. To deal with these time-varying issues, most ANC systems utilize adaptive filters [Reference Widrow and Stearns10–Reference Lee, Gan and Kuo12] to track these variations and unknown plants. The most commonly used adaptive filters are realized using a finite impulse response (FIR) filter with the least-mean-square (LMS) algorithm [Reference Widrow and Stearns10].
The development of powerful, low-cost digital signal processors (DSPs) [Reference Kuo and Gan13–Reference Gan and Kuo15] encourages the implementation of advanced adaptive algorithms to achieve faster convergence, increased robustness to interference, and improved system performance for practical ANC applications.
The control structure of ANC is generally classified into two classes: feedforward control and feedback control. In the feedforward control case, a reference noise is assumed to be available for the adaptive filter. Feedforward ANC systems can be categorized as either a broadband or a narrowband depending on the type of primary noise that can be reduced. In the broadband feedforward control case, a reference noise is detected by a reference sensor (e.g., microphone), and thus noise correlating with the reference noise can be reduced. On the other hand, in the narrowband feedforward control case, a reference signal is internally generated using information available from a reference sensor (e.g., accelerometer) that is not affected by a control field. The feedforward ANC scheme utilizes a secondary loudspeaker (e.g., actuator) to generate anti-noise and an error sensor (e.g., microphone) to pick up residual noise, which serves as the error signal for updating the adaptive filter. The single-channel feedforward ANC scheme, which consists of two sensors (reference and error) and an actuator, is widely used for industrial applications such as reducing duct noise [Reference Burgess16].
The feedback ANC system uses only an error sensor and a secondary source, not using an “upstream” reference sensor. Analog feedback control based on a simple negative feedback is widely used in headphone applications [Reference Usagawa, Shimada, Nishimura and Ebata17–Reference Chang and Li20]. Unfortunately, the controllable bandwidth is limited by the throughput of the overall control system; thus, it is difficult to reduce broadband noise. Digital feedback control generally utilizes internal model control (IMC) [Reference Datta21,Reference Elliott and Sutton22], which minimizes residual noise using predicted primary noise as the reference signal. Hence, the IMC-based feedback ANC system can reduce only predictable noise (including sinusoidal, narrowband, and color noises). The bandwidth that can be controlled by the feedback ANC system is limited because of the large delay due to the analog-to-digital converter (ADC) and digital-to-analog converter (DAC).
Today, successful real-world ANC application is still limited owing to the effectiveness of signal processing algorithms, physical implementation constraints, and economical consideration. Recently, many advanced signal processing algorithms, implementation techniques, and successful applications of ANC have been reported. In this overview paper, we will focus on introducing some new signal processing algorithms, discussing challenges for innovative applications, and proposing open issues for further research and development of ANC systems.
This paper is organized as follows. In Section II, the basic structures and algorithms of ANC will be introduced. ANC systems include broadband and narrowband feedforward ANC, adaptive feedback ANC, hybrid ANC, multiple-channel ANC, and audio-integrated ANC. Convergence analysis of the filtered-x LMS (FXLMS) algorithm including recent published works will be given. Different algorithms and structures including nonlinear ANC will be briefly overviewed, while citing many important recent works. Furthermore, some new approaches including active noise equalization, psychoacoustics, and virtual sensing will be introduced. In Section III, the basic principles of and recent works on online secondary-path modeling, and ANC algorithms that do not require a secondary-path model will be discussed. Finally, several real-world ANC applications with challenging issues will be introduced in Section IV. In this paper, we choose topics related to our works in this field. Some important results may be omitted owing to page limitation. Readers can therefore refer to many recent works reported in the last decade that are cited as references.
II. OVERVIEW OF ANC
In this section, we briefly present basic ANC concepts, algorithms, analyses, problems, solutions, and recent works with focus on signal processing algorithms.
A) Broadband feedforward ANC
The single-channel broadband feedforward ANC system is illustrated in Fig. 1 [Reference Kuo and Morgan2], where acoustic, analog, and digital regions are clearly distinguished. Noise propagating from the noise source is picked up by a reference sensor such as a microphone, and then the digital (sampled-time) reference signal x(n) is obtained through a preamplifier, an anti-aliasing filter, and an ADC. The reference signal is processed by the control filter W(z) to generate the sampled-time anti-noise signal y(n) that drives a secondary source such as a loudspeaker through a DAC, a reconstruction filter, and a power amplifier. The error sensor (microphone) is used to monitor the performance of the ANC system by the sampled-time residual noise signal e(n), which is obtained through a preamplifier, an anti-aliasing filter, and ADC. The primary path P(z) consists of the acoustic response from the reference sensor to the error sensor, as shown in Fig. 1. The adaptive filter W(z) minimizes the error signal e(n) by adapting filter coefficients automatically using the LMS algorithm. The use of the adaptive filter for the ANC application shown in Fig. 1 is necessary to compensate for the secondary-path transfer function S(z) from y(n) to e(n), which includes the DAC, reconstruction filter, power amplifier, loudspeaker, acoustic path from the loudspeaker to the error microphone, preamplifier, anti-aliasing filter, and ADC. Here, Fig. 1 shows the exact block diagram including the acoustic, analog, and digital regions. On the other hand, the equivalent sampled-time block diagram shown in Fig. 2 is generally used for understanding and analyzing the system and its performance. Henceforth, we utilize equivalent sampled-time block diagrams to explain other ANC structures, unless otherwise noted.
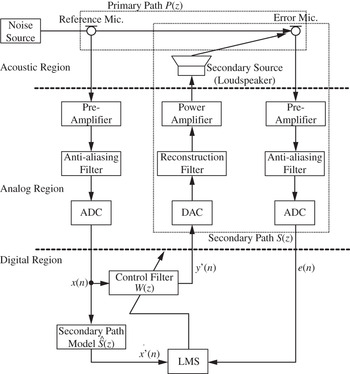
Fig. 1. Block diagram of broadband feedforward ANC system that includes acoustic, analog, and digital regions. This block diagram shows a single-channel feedforward ANC system with one reference microphone, one error microphone, and one secondary source (loudspeaker).
The optimal solution of the adaptive filter W(z) is given by the following optimal transfer function in the steady state:
Therefore, the adaptive filter W(z) has to simultaneously model P(z) and inversely model S(z). The performance of an ANC system largely depends on the transfer function of the secondary path S(z) [Reference Kuo and Morgan2].
As illustrated in Fig. 2, after the reference sensor picks up the reference noise, the controller needs time to calculate the anti-noise and send it to the secondary loudspeaker. If this delay becomes longer than the acoustic delay from the reference microphone to the secondary loudspeaker, the performance of the ANC system to cancel broadband random noise will be degraded because the action to exactly cancel the noise would require it to be non-causal. However, even if the causality condition is not met, the ANC system is still capable of canceling narrowband periodic noise.
B) The FXLMS algorithm
The presence of the secondary-path transfer function S(z) after the controller, shown in Fig. 2, will generally cause instability of the LMS algorithm. This is because the error signal is not correctly “aligned” in time with the reference signal owing to the presence of S(z). Morgan suggested placing a secondary-path estimate Ŝ(z) to filter the reference signal x(n) for the weight update of the LMS algorithm, which results in the FXLMS algorithm [Reference Morgan23]. The FXLMS algorithm was independently derived by Widrow and Stearns [Reference Widrow and Stearns10] in the context of adaptive control and by Burgess [Reference Burgess16] for ANC applications.
The block diagram of an ANC system using the FXLMS algorithm is illustrated in Fig. 2. The secondary signal y(n) is computed as
where w(n) = [w 0(n) w 1(n) … w L−1(n)]T and x(n) = [x(n) x(n − 1) … x(n − L + 1)]T are the coefficient and signal vectors of W(z), respectively, and L is the filter length. The FXLMS algorithm updates the coefficient vector expressed as
where μ is the step size (or convergence factor) that determines the convergence speed,
is the filtered reference signal vector and ŝ(n) is the impulse response of the secondary-path estimation filter, Ŝ(z). Therefore, the ANC system using the FXLMS algorithm requires the accurate estimation of the secondary-path model.
Under the limitation of slow adaptation, the FXLMS algorithm will converge within ±90° of the phase error between Ŝ(z) and S(z). Therefore, the offline modeling of the secondary path using adaptive system identification with the LMS algorithm and white noise as an excitation signal can be used to estimate S(z) during an initial training stage before the operation of noise control for most ANC applications. However, for applications that have a significant time-varying secondary path and require high performance, online modeling during the ANC operation may be required. Therefore, updating of the secondary-path model is important in some ANC applications. Detailed online secondary-path modeling algorithms [Reference Eriksson and Allie24–Reference Jin, Yang, Xiao and Liu45] and associated problems will be presented in Section III. Moreover, ANC systems that require no secondary-path models [Reference Maeda and Yoshida46–Reference Yuan65] will also be introduced in Section III.
C) Feedback path
The acoustic ANC system shown in Fig. 1 uses a reference microphone to pick up the reference noise and generates anti-noise to cancel primary noise acoustically. Unfortunately, anti-noise from a loudspeaker also radiates upstream to the reference microphone, resulting in an undesired acoustic feedback that may cause instability. The simple approach to solving the feedback problem is to use a feedback cancellation (or neutralization) filter that models the feedback path from the secondary loudspeaker to the reference sensor, which is exactly the same technique used in acoustic echo cancellation [Reference Kuo and Morgan2]. Since primary noise highly correlates with anti-noise, the adaptation of the feedback neutralization filter must be inhibited when the ANC system is in operation. Thus, the feedback neutralization filter is usually obtained using an offline adaptive modeling of the feedback path at the training stage, which can be performed simultaneously with the offline secondary-path modeling. An online feedback path modeling technique [Reference Kuo and Luan66] is developed in [Reference Kuo67] using adaptive predictor. Moreover, some modified techniques have recently been developed in [Reference Iwamatsu, Fujii and Muneyasu68], which utilize a simultaneous equation estimation method, and in [Reference Akhtar, Abe and Kawamata69–Reference Akhtar and Mitsuhashi72], which utilize adaptive noise cancellation.
In the broadband feedforward ANC, when a feedback path is present, the optimal solution is generally an infinite impulse response (IIR) function with poles and zeros. Moreover, the use of the IIR filter can be considerably more efficient for the realization than FIR filters because an IIR filter may require much fewer coefficients than an FIR filter to model any resonance systems. Hence, an IIR-based ANC is often effective for broadband feedforward control. In [Reference Eriksson, Allie and Greiner73,Reference Eriksson74], the filtered-u recursive LMS algorithm has been proposed to realize an IIR-based ANC system. In [Reference Crawford and Stewart75], the full-gradient and simplified-gradient versions of the filtered-u algorithm called the filtered-v algorithms have been proposed to minimize the mean square error. In [Reference Wang and Ren76,Reference Fraanje, Verhaegen and Doelman77], the performance of the filtered-u LMS algorithm has been analyzed. Other novel adaptive IIR ANC systems have also been proposed in [Reference Mosquera, Gomez, Perez and Sobreira78–Reference Yuan86].
D) Narrowband feedforward ANC
A narrowband ANC system reduces periodic and narrow band noises using a signal generator to synthesize the reference signal x(n). This technique has several advantages: (1) prevents acoustic feedback from the secondary loudspeaker back to the reference microphone, (2) avoids nonlinearities and aging problems associated with the reference microphone, (3) relaxes causality constraint, (4) can control individual harmonics independently, and (5) is only necessary to model plants at frequencies of the harmonics, thus, an FIR filter with a lower order may be sufficient.
The reference signal generator is triggered by a synchronization pulse from a non-acoustic sensor, such as a tachometer signal from an automotive engine. Two types of reference signal are commonly used in narrowband ANC systems: (1) an impulse train with a period equal to the inverse of the fundamental frequency of the periodic noise [Reference Elliott and Darlington87], and (2) sine waves of the same frequencies as the corresponding harmonics to be canceled. The first technique is called the waveform synthesis method, whereas the second technique embodies the adaptive notch filter, which was originally developed for the cancellation of tonal interference [Reference Widrow88].
The adaptive notch filter offers easy control of bandwidth, an infinite null, and the capability to adaptively track the exact frequency of narrowband noise. In practical applications, periodic noise usually contains multiple tones at a fundamental frequency and several harmonic frequencies. In general, the realization of multiple notches requires a higher-order filter, which can be realized in direct, parallel, direct/parallel, or cascade form [Reference Kuo and Morgan2]. The convergence analysis of the direct and direct/parallel forms related to the frequency separation between the adjacent harmonics is presented in [Reference Kuo and Puvvala89]. It is shown that the convergence rate of the direct form can be increased using the direct/parallel form, which increases the frequency separation.
The narrowband feedforward ANC utilizes the synchronization signal, which is obtained by timing signal sensors such as a tachometer. However, actual sensors contain some errors because of aging and fatigue damage accumulation. These errors consequently cause frequency mismatch between the reference signal and the primary noise to be canceled. In [Reference Xiao, Ma, Khorasani and Ikuta90], the noise reduction of the narrowband feedforward ANC system degrades significantly even for a 1% frequency mismatch. Recently, some approaches considering the frequency mismatch have been proposed [Reference Shimada, Nishimura, Usagawa and Ebata91–Reference Niedzwiecki and Meller94], which utilize a frequency adjuster or estimate the correct frequencies.
A convergence analysis of narrowband ANC systems has been conducted [Reference Kuo, Puvvala and Gan95–Reference Jeon, Chang, Yu and Kuo103], resulting in the development of some novel algorithms, which can improve the convergence property and/or the noise reduction ability.
E) Adaptive feedback ANC
Several non-adaptive feedback ANC systems have been described in [Reference Elliott and Nelson7]. A block diagram of the single-channel adaptive feedback ANC system is presented in Fig. 3 [Reference Kuo and Morgan2]. This technique synthesizes (or regenerates) the reference signal x(n) using only the error signal and the adaptive filter output filtered by the secondary-path model; thus, this technique is also known as IMC [Reference Datta21,Reference Elliott and Sutton22]. As shown in Fig. 3, the primary noise estimate ![]() (n) ≈ d(n), if Ŝ(z) ≈ S(z). Because the current estimate of d(n) is used as the reference signal for the next iteration, i.e., at time n + 1, the reference signal synthesis process is functioned as a one-step predictor. This principle clearly indicates that the adaptive feedback ANC can cancel predictable noise. As shown in Fig. 3, the primary noise d(n) is generated by filtering the original noise with the primary path P(z) so primary noise can be predicted.
(n) ≈ d(n), if Ŝ(z) ≈ S(z). Because the current estimate of d(n) is used as the reference signal for the next iteration, i.e., at time n + 1, the reference signal synthesis process is functioned as a one-step predictor. This principle clearly indicates that the adaptive feedback ANC can cancel predictable noise. As shown in Fig. 3, the primary noise d(n) is generated by filtering the original noise with the primary path P(z) so primary noise can be predicted.
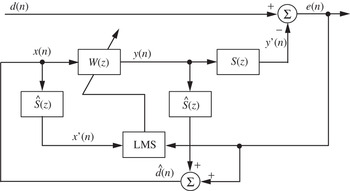
Fig. 3. Equivalent sampled-time block diagram of adaptive feedback ANC system. In this figure, S(z) is the secondary path, W(z) is the control filter, and Ŝ(z) is the secondary-path model. The input signal of the control filter W(z) is internally generated in this system.
The single-channel adaptive feedback ANC algorithm has been applied to the global control of manufacturing plant noise generated by vibratory bowls [Reference Kuo, Kong and Gan104] and active headsets for noise protection [Reference Gan, Mitra and Kuo18–Reference Chang and Li20,Reference Meurers, Veres and Elliott105]. The convergence property has been analyzed [Reference Kuo, Kong and Gan104,Reference Sakai and Miyagi106]. In [Reference Bouchard and Paillard107], a new adaptive feedback active control structure is proposed. This method utilizes the IMC structure to estimate periodic noise, but does not require the filtering of the reference signal with the secondary-path model; thus, this method can achieve fast convergence and high noise reduction. In [Reference Wang, Gan and Kuo108], the effects of frequency separation in feedback ANC systems are discussed.
F) Hybrid ANC
The hybrid ANC system [Reference Kuo and Morgan2] is a combination of both feedforward and feedback ANC systems, as individually described in Sections II(A) and II(E), respectively. The canceling signal y(n) is generated on the basis of the outputs of both the reference and error sensors, as shown in Fig. 4. The hybrid ANC system plays a dual role in canceling the primary noise picked up by the reference sensor of the feedforward ANC, A(z), and the residual noise component (or plant noise) that is only picked up by the error sensor of the feedback ANC, C(z). The hybrid ANC, therefore, offers better performance in terms of both narrowband and broadband noise cancellations, and provides higher flexibility than either the feedforward or feedback ANC system [Reference Ray, Solbeck, Streeter and Collier109–Reference Xiao and Wang115]. The computational complexity of the hybrid ANC can be reduced because a lower order of FIR or IIR filters [Reference Kuo and Morgan2] can be used to achieve the same performance as that using the feedforward or feedback ANC system alone.
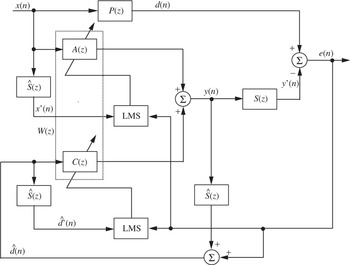
Fig. 4. Equivalent sampled-time block diagram of hybrid ANC system using FIR filters. In this figure, P(z) is the primary path, S(z) is the secondary path, A(z) is the control filter for the feedforward part, C(z) is the control filter for the feedback part, and Ŝ(z) is the secondary-path model.
G) Multiple-channel ANC
A noise field is more complicated in an enclosure or three-dimensional space than in a narrow duct. It is generally necessary to use a multiple-channel ANC system with several secondary sources, error sensors, and perhaps even several reference sensors to achieve global cancellation, or to create a large-size quiet zone. The locations of error sensors are very important to obtain the best estimate of the total acoustic potential energy.
A general multiple-reference/multiple-output ANC system using the FXLMS algorithm has been proposed [Reference Elliott, Stothers and Nelson116]. The convergence behavior of the multiple-channel ANC system is analyzed in the frequency domain in terms of the convergence of individual secondary signals, cost function, and control effort [Reference Elliott, Boucher and Nelson117]. This frequency-domain analysis can be applied to narrowband ANC systems that control one or more harmonics of periodic noise.
Suppose the multi-channel ANC system uses a single reference sensor, M secondary sources, and N error sensors. Then, the corresponding multi-channel FXLMS algorithm consists of M adaptive filters and M × N secondary-path models. Therefore, the computational complexity of the multi-channel ANC system increases significantly with more transducers deployed, and this represents one of the major challenges for applying multi-channel ANC systems in large-scale applications. Recent works have suggested more efficient realization of multichannel ANC systems [Reference Douglas118–Reference Thomas, Lovstedt, Blotter and Sommerfeldt123].
H) Analysis of the FXLMS algorithm
The maximum step size for the FXLMS algorithm in the case of a white reference signal was derived by Elliott and Nelson [Reference Elliott and Nelson7] as
where P′x is the power of the filtered reference signal x′(n) and Δ is the number of samples corresponding to the overall delay in the secondary path. The longer delay of the secondary path reduces the maximum step size, thus decreasing the convergence speed of the FXLMS algorithm.
Various methods have been proposed to analyze the FXLMS algorithm theoretically. Feintuch et al. [Reference Feintuch, Bershad and Lo124] and Bjarnason [Reference Bjarnason125] used the independence assumption to analyze the convergence behavior. It is assumed that successive signal vectors of the tapped delay line x(n) are independently generated at each time step. In [Reference Bjarnason125], the maximum step size in the sinusoidal reference case is derived as
Analytical results based on the independence assumption cannot precisely or generally explain the experimental results in [Reference Takenouchi, Suzuki and Omoto126]. Tobias et al. [Reference Tobias, Bermudez and Bershad127] and Miyagi and Sakai [Reference Miyagi and Sakai128] assumed that the step size is small. In this case, the theoretical results agree with the corresponding experimental results. Analysis for the periodic signals is conducted in [Reference Vicente and Masgrau129–Reference Hinamoto and Sakai131]. In [Reference Ardekani and Abdulla132–Reference Ardekani and Abdulla134], the closed-form expressions of the FXLMS algorithm are proposed, which can apply to a relatively general case with an arbitrary secondary path, acoustic noise with an arbitrary bandwidth, and arbitrary (imperfect) secondary-path model. These expressions give a more accurate maximum step size. In [Reference Miyoshi and Kajikawa135], the dynamical behaviors of the FXLMS algorithm are derived using the statistical–mechanical method. The analysis is conducted without using the independence assumption, the small step-size condition, and the assumption of a small number of taps.
In [Reference Boucher, Elliott and Nelson136–Reference Chen, Wang, Chen and Muto141], the effects of secondary-path estimation error on optimum step size and convergence rate are discussed. The analysis shows that if the phase error of the secondary-path model is within ±90°, the FXLMS algorithm can remain stable, but the step size must be set to small values. In [Reference Fraanje, Verhaegen and Doelman142–Reference Fraanje, Elliott and Verhaegen144], a strictly positive real condition on the model error for which the FXLMS algorithm asymptotically converges to the mean is analyzed, and regularization methods to increase the robustness of the FXLMS algorithm are proposed.
Other analyses on the convergence behaviors of the ANC systems include the presence of a feedback path [Reference Jacobson, Johnson, McCormick and Sethares145], the ANC dealing with moving noise sources [Reference Omoto, Morie and Fujiwara146], the modified FXLMS algorithm [Reference Lopes and Piedade147], the leaky FXLMS algorithm [Reference Tobias and Seara148,Reference Tobias and Seara149], and the filtered-x adaptive filter with an averaging algorithm [Reference Tobias and Seara150].
I) Audio-integrated ANC systems
The ANC systems using the FXLMS algorithm are effective in reducing low-frequency noise. However, residual noise is still present in the steady state after the ANC systems have converged. Residual noise may be masked using audio signals such as music or nature sounds. Furthermore, in some applications such as headphones, the secondary emitter of the ANC system is also used to play intended audio signals (such as speech and music) during the ANC operation. To prevent the ANC system from canceling the desired audio signal and to avoid the audio signal acting as interference that degrades the ANC performance, the audio-integrated ANC algorithm was proposed in [Reference Kuo and Finn151–Reference Wang, Gan and Kuo159].
The single-channel audio-integrated ANC system is shown in Fig. 5, where the comfort audio a(n) is added to the adaptive filter output y(n), and the mixed signal y′(n) is output to the secondary loudspeaker to cancel the primary noise d(n). Thus, the signal e(n) picked up by the error microphone contains both the residual noise and the desired audio component. To estimate the audio component picked up by the error microphone, a(n) is filtered by the adaptive secondary-path estimation filter Ŝ(z). The estimated audio component a′ (n) is subtracted from e(n) to obtain the true error signal e′(n) if Ŝ(z) = S(z). This audio-free error signal is then used to update the adaptive filter W(z). Therefore, the adaptive filter Ŝ(z) performs the online canceling of the audio component using the LMS algorithm.
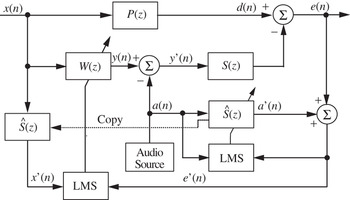
Fig. 5. Equivalent sampled-time block diagram of integration of audio with the single-channel ANC systems. In this figure, P(z) is the primary path, S(z) is the secondary path, W(z) is the control filter, and Ŝ(z) is the secondary-path model. The audio signal is combined with the anti-noise signal y(n) and used for modeling the secondary-path model Ŝ(z).
As shown in Fig. 5, the adaptive filter Ŝ(z) performs the adaptive system identification of the secondary path S(z) using the audio signal a(n) as the excitation signal. In general, when the audio signal is uncorrelated with the anti-noise y(n), a perfect model can be obtained, i.e., Ŝ(z) = S(z). Thus, the error signal is the true residual noise used for the FXLMS algorithm. Therefore, the performance of the FXLMS algorithm will not degrade with the additional audio signal, and the ANC system will not cancel the desired audio component because the audio component is not fed back to the LMS algorithm. The additional benefit of using the audio-integrated algorithm is that the adaptive filter Ŝ(z) performs the online modeling of the secondary path using the broadband audio signal as an excitation signal. Because the audio-integrated ANC system uses the same secondary loudspeaker and amplifier to play the intended audio, it adds value to an integrated system without increasing the overall system cost.
This audio-integrated feedforward ANC system can be extended to the adaptive feedback ANC system, which will be introduced in Section IV. The application to the helmet, snore, and incubator ANC systems will also be presented in Section IV. The selection of audio signal depends on the characteristics of residual noise and may be guided by psychoacoustic principles, which require interdisciplinary effort.
J) Active noise equalization and psychoacoustic ANC
The goal of the conventional ANC system is to reduce residual noise. However, in some applications, it is desired to retain perceivable residual noise with a desired spectral shape or a different signature so as to aid humans in operating machines or vehicles safely. The use of an active noise equalizer (ANE) [Reference Kuo and Ji160] or active sound profiling [Reference Rees and Elliott161], which changes the amplitude of noise components with predetermined values, is a useful and important extension of ANC. The narrowband ANE [Reference Kuo and Ji162–Reference Kuo, Yenduri and Gupta166] can be implemented to individually control each harmonic of a periodic noise, and further extends to become a broadband ANE [Reference Kuo and Yang167,Reference Yenduri and Kuo168] using a shaping filter to shape the desired broadband noise spectrum. Wang and Gan [Reference Wang and Gan96,Reference Wang and Gan99] investigate the sensitivity of the ANE under an imperfect secondary-path estimation.
It was found that the noise level is not the sole contribution of irritation [Reference Rees and Elliott169]. In many instances when the low-frequency components are actively attenuated, high-frequency noise components increase the level of irritation as the sharpness of noise becomes more obvious. Therefore, a better noise control approach is to provide a mechanism that can realize psychoacoustic considerations. A class of psychoacoustic ANC systems [Reference Wang, Gan and Chong170–Reference Bao and Panahi172] improves performance from a psychoacoustic point of view. For example, noise loudness is used as the psychoacoustic criterion, and this psychoacoustic ANC system can match the hearing threshold of individuals to form a personalized ANC system.
K) Virtual sensing ANC
In many practical applications, error microphones cannot be placed near intended locations to achieve maximum cancellation in the desired quiet zone (e.g., near the listener's ears). To form quiet zones away from error microphones, a technique known as virtual sensing [Reference Haneda173,Reference Kestell, Cazzolato and Hansen174] must be deployed. The challenge is to create quiet zones at the locations of virtual sensors by placing physical sensors away from the desired quiet zones.
Currently, two classes of algorithms have been developed. The first class [Reference Bonito, Elliott and Boucher175–Reference Kuo, Gan and Kalluri178] requires system models to process data acquired from physical sensors. A training (offline) stage is required to measure the system model from physical sensors to virtual sensors, which will be used in the online operation of the virtual sensing ANC algorithm. However, this class of algorithms is highly dependent on the accuracy of the system model obtained offline; it is also very sensitive to the environmental change and locations of physical sensors. In some cases, offline modeling may not be possible. The second class of algorithms requires no offline training to obtain the system model, and thus can be more flexible in its deployment. For example, Moreau et al. [Reference Moreau, Ghan, Cazzolato and Zander179] developed stochastically optimal tonal diffuse field virtual sensing method for a spatially fixed target zone, and extended it to moving targets.
In many practical ANC applications, especially in consumer electronics and medical instruments, it is desired to create quiet zones at the desired virtual locations away from the locations of physical error sensors for optimum performance. Therefore, the development of effective virtual sensing techniques for ANC systems is a very important and challenging work that deserves further research and development.
L) Other ANC algorithms and structures
The FXLMS algorithm is widely used in ANC systems owing to its simplicity and robustness. However, the convergence rate of LMS-type algorithms depends on the characteristics of the input signal, that is, it becomes slow for colored signals. The slow convergence is a major concern for fast-changing noise such as automobile noise. In ANC systems, the original noise from a source is filtered by the physical path before being sensed by the reference sensor; thus, the reference signal becomes a colored noise even if the original noise is white. Hence, the convergence rate needs to be improved using more advanced algorithms, such as variable step-size LMS algorithms, affine projection (AP) algorithms, and recursive least square (RLS) algorithms. The filtered-x sign LMS algorithm is proposed and the convergence behaviors are analyzed [Reference Orosz, Sujbert and Peceli180]. Recently, an AP algorithm has been proposed for ANC systems [Reference Bouchard181]. However, AP algorithms require excessive computational cost for high projection orders. Thus, computationally efficient algorithms have been proposed [Reference Albu182–Reference Carini and Sicuranza185]. Moreover, their transient and steady-state behaviors are analyzed [Reference Carini and Sicuranza186–Reference Ferrer, Gonzalez, de Diego and Pinero188]. Multichannel filtered-x RLS, modified filtered-x RLS and adjoin-RLS algorithms, and their low computational fast-transversal-filter-based versions are proposed [Reference Bouchard and Quednau189].
Broadband ANC often requires an adaptive FIR filter with hundreds of taps. Subband structures [Reference Lee, Gan and Kuo12] can reduce the computational burden by using a large number of subbands because the adaptive filter length and sampling rate can be decimated in each subband. Moreover, the subband structures can achieve faster convergence because the spectral dynamic range is greatly reduced in each subband. For ANC application, the processing delay must be eliminated because of the causality problem discussed in the previous section. Therefore, a delayless subband ANC system is proposed [Reference Morgan and Thi190]. The basic idea is that wideband anti-noise is generated by the adaptive FIR filter to eliminate delay caused by (analysis and synthesis) filter banks, whereas filter coefficients are updated by a subband adaptive algorithm in the background to achieve faster convergence. Various delayless subband ANC systems are proposed [Reference DeBrunner, DeBrunner and Wang191–Reference Milani, Kannan, Panahi and Briggs198].
In some practical ANC applications, non-target noise (including intended signals such as speech and white noise for online modeling of secondary path) often corrupts residual noise sensed by the error sensor. Non-target noise reduces the convergence rates of the ANC algorithm and online modeling of the secondary path. It even leads to the instability of the IMC-based feedback ANC in some cases. Hence, non-target noise must be considered in order to improve the convergence rate and system stability. In [Reference Bao, Sas and Brussel25], a prediction error filter is utilized to improve the convergence rate in online secondary-path modeling. In [Reference Lan, Zhang and Ser199,Reference Akhtar, Abe and Kawamata200], weight-constrained FXLMS algorithm and the weight-averaged FXLMS algorithm are proposed to improve the system stability and convergence rate, respectively. In [Reference Sun and Kuo201], the cascading adaptive algorithm is proposed to remove non-target noise and improve the steady-state performance of ANC systems. In [Reference Kajikawa and Hirayama202], a linear prediction filter is utilized to improve the system stability in the IMC-based feedback ANC system when broadband noise corrupts the error signal.
In practical ANC systems, there are several sources of nonlinearity that can affect the system performance. For example, the reference noise may be a nonlinear deterministic process, possibly chaotic. The acoustic paths involved may also show nonlinearity, e.g., owing to the high sound pressure and saturation in some transducers of the control system [Reference Kuo, Wu, Chen and Gunnala203,Reference Chen and Chen204]. Overdriving the electronics or the loudspeakers may also cause relevant nonlinear effects, e.g., generating unwanted nonlinear distortions. Hence, ANC systems that can handle such nonlinearity are often needed. Nonlinear ANC systems utilize various types of nonlinear filters, such as multilayer artificial neural networks [Reference Snyder and Tanaka205–Reference Chang and Luoh209], truncated Volterra expansions [Reference Strauch and Mulgrew210–Reference Russo and Sicuranza215], radial basis functions [Reference Strauch and Mulgrew210], functional link artificial neural networks [Reference Das and Panda216–Reference Sicuranza and Carini224], adaptive bilinear filters [Reference Kuo and Wu225], general function expansion nonlinear filters [Reference Zhou and DeBrunner226], and polynomial nonlinear autoregressive models with exogenous variables model [Reference Napoli and Piroddi227]. In [Reference Costa, Bermudez and Bershad228–Reference Costa, Ximenes and Bermudez230], the performance of the FXLMS algorithm with a nonlinear secondary path in ANC systems is analyzed.
III. NEW APPROACHES RELATED TO SECONDARY-PATH MODEL
As discussed in Section II(B), the secondary-path model can be estimated offline before the operation of the ANC in situations where no primary noise exists. In many practical applications, however, primary noise always exists and the secondary path may be changed, such that the phase error between the current secondary path and its offline model exceeds 90°. The secondary-path modeling error may lead to system instability, slow convergence, or suboptimal performance [Reference Boucher, Elliott and Nelson136–Reference Chen, Wang, Chen and Muto141]. Hence, the online modeling of a time-varying secondary path may be required to guarantee the stability of the FXLMS algorithm and to improve its noise reduction performance. In general, there are two different techniques for online secondary-path modeling: the additive random noise technique and the overall modeling technique.
A) Online modeling using additive random noise
Figure 6 shows the online secondary-path modeling technique using additive random noise proposed in [Reference Eriksson and Allie24]. The zero-mean white noise v(n), which is uncorrelated with the primary noise x(n), is internally generated and added to the secondary signal y(n) to drive the secondary source. In this technique, the adaptive filter Ŝ(z) is added in parallel with the secondary path S(z) to estimate it online. In the presence of primary noise and the operation of the ANC controller, the error signal e(n) consists of u(n) and v′(n), where u(n) = d(n) − y′(n) is the residual noise (the error signal) without using v(n) for the secondary-path modeling and v′(n) is the filtered v(n). Because u(n) is uncorrelated with v′(n), the LMS solution for the secondary-path modeling is unaffected by the presence of the interference u(n). However, it can be shown that u(n) will degrade the convergence rate of the adaptive filter Ŝ(z) because u(n) is large before the convergence of the noise control filter W(z). On the other hand, the noise control filter updated by the FXLMS algorithm will be degraded by the extra noise v′(n), which is proportional to the power of v(n).
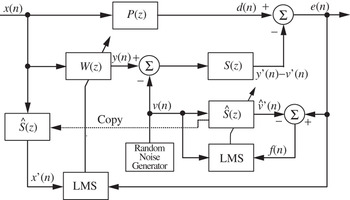
Fig. 6. Equivalent sampled-time block diagram of Erikson's method for online secondary-path modeling [23]. In this figure, P(z) is the primary path, S(z) is the secondary path, W(z) is the control filter, and Ŝ(z) is the secondary-path model. Random noise is combined with the anti-noise signal y(n) and used for modeling the secondary-path model Ŝ(z).
In summary, the true error signal u(n) becomes the interference for the secondary-path modeling filter Ŝ(z), and the additive random noise v(n) becomes the interference for the ANC filter W(z). These interferences must be isolated to simultaneously improve the performance of both processes in ANC systems with online secondary-path modeling. The power scheduling of additive random noise to accurately detect secondary-path changes and the adjustment of step size are required. Another potential solution is to replace annoying white noise with a wideband audio signal, as discussed in Section II. In fact, the block diagram in Fig. 6 is very similar to that in Fig. 5, which shows the audio-integration ANC system. In Fig. 5, the additive random noise in Fig. 6 is substituted for an audio signal. The only difference between both systems is the purpose, that is, the purpose of the system in Fig. 6 is to model the secondary path online, in contrast, the purpose of the system in Fig. 5 is to deliver an audio signal to the user and to remove the audio signal from the error signal to improve system performance.
B) Methods for improvement
To solve the problems discussed in the previous section, various approaches were proposed. These approaches can be classified into three types. The first type is to introduce another adaptive filter into the ANC system to remove the interference from the secondary-path modeling process [Reference Bao, Sas and Brussel25,Reference Kuo and Vijayan26], or the mutual interference between the noise control process and the secondary-path modeling process [Reference Zhang, Lan and Ser27]. The second type is to improve the adaptive algorithm with the weight-averaged approach for the noise control filter [Reference Akhtar, Abe and Kawamata28] without introducing any extra adaptive filter into the ANC system. The averaging of the adaptive filter, which removes the effect of additive random noise, leads to an increase in convergence rate. The third type is to control the power of additive noise or/and step size in the online modeling process [Reference Lan, Zhang and Ser29–Reference Davari and Hassanpour35]. In this approach, the power of additive noise is initially set large for the fast convergence of the secondary-path modeling filter and is subsequently reduced to a small value. Moreover, the step size used for online modeling varies according to the power of additive noise. The convergence analysis of the ANC with online secondary-path modeling is examined in [Reference Liu, Xiao, Sun and Xu36,Reference Wu, Qiu, Xu and Li37], and the multi-channel ANC with online modeling of secondary paths is proposed in [Reference Akhtar, Abe, Kawamata and Nishihara38]. In this section, we focus on the first type, in particular, Zhang's method [Reference Zhang, Lan and Ser27].
Figure 7 shows the block diagram of Zhang's method [Reference Zhang, Lan and Ser27] for online secondary-path modeling. This method utilizes an additional filter, H(z), to remove the interference ![]() for the online secondary-path modeling process as Bao's method [Reference Bao, Sas and Brussel25]. In this system, three adaptive filters, W(z), H(z), and Ŝ(z), are cross-updated. If S(n) ≈ Ŝ(n), then e′(n) ≈ u(n). The new signal e′(n), which is used as the error signal for W(z) and as the desired signal for H(z), does not include the additive random noise v(n). Therefore, the noise control filter can converge fast. Moreover, the convergence rate of the additional adaptive filter can be improved. Furthermore, z(n) is subtracted from e(n), and g(n) ≈ v′(n) if
for the online secondary-path modeling process as Bao's method [Reference Bao, Sas and Brussel25]. In this system, three adaptive filters, W(z), H(z), and Ŝ(z), are cross-updated. If S(n) ≈ Ŝ(n), then e′(n) ≈ u(n). The new signal e′(n), which is used as the error signal for W(z) and as the desired signal for H(z), does not include the additive random noise v(n). Therefore, the noise control filter can converge fast. Moreover, the convergence rate of the additional adaptive filter can be improved. Furthermore, z(n) is subtracted from e(n), and g(n) ≈ v′(n) if ![]() . In this case, the new signal g(n), which is used as the desired signal for the secondary-path modeling filter Ŝ(z), does not include the primary and secondary noises so the secondary-path modeling can converge fast. It has been demonstrated in [Reference Zhang, Lan and Ser39] that Zhang's method gives the best performance among the above methods.
. In this case, the new signal g(n), which is used as the desired signal for the secondary-path modeling filter Ŝ(z), does not include the primary and secondary noises so the secondary-path modeling can converge fast. It has been demonstrated in [Reference Zhang, Lan and Ser39] that Zhang's method gives the best performance among the above methods.
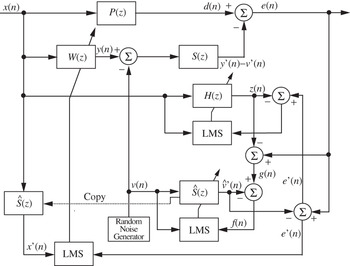
Fig. 7. Equivalent sampled-time block diagram of Zhang's method for online secondary-path modeling [26]. In this figure, P(z) is the primary path, S(z) is the secondary path, W(z) is the control filter, H(z) is the overall system model, and Ŝ(z) is the secondary-path model. The overall system model H(z) is used for improving the convergence performance of both the control filter W(z) and the secondary-path model Ŝ(z).
In summary, online secondary-path modeling methods using additive noise have many disadvantages. Several algorithms using additional adaptive filters were developed to solve such problems with increased computational complexity. They include the overall online modeling algorithm [Reference Kuo and Wang40–Reference Zhang and Gan42] and simultaneous equations methods [Reference Fujii and Ohga43–Reference Jin, Yang, Xiao and Liu45], which do not use an additive random noise. The overall online secondary-path modeling algorithm introduces an additional adaptive filter for estimating the primary path. Some simulation results demonstrated that the additional adaptive filter and online secondary-path modeling filter can track slow changes in both the primary and secondary paths online [Reference Kuo, Wang and Chen41]. In simultaneous equation methods, an additional adaptive filter is also used like the overall online method, but the secondary path is estimated through algebraic calculation [Reference Fujii and Ohga43–Reference Jin, Yang, Xiao and Liu45].
C) ANC systems without secondary path model
A class of algorithms that do not require secondary-path modeling utilizes the simultaneous perturbation (SP) method originally proposed for neural networks. The SP method can simultaneously estimate all elements of the gradient vector using only two values of the objective function J(w(k)). The SP method is given by
where Δw i(k) is the modification at the kth iteration for the ith element of the parameter vector w(k), c is the magnitude of the perturbation, μ is the step size, and s(k) is the fundamental vector at the kth iteration and its ith element s i(k) is either 1 or −1. The sign of s i(k) is randomly determined. Moreover, the sign of s i(k) is independent of the sign of the jth element s j(k) of the sign vector. Let us briefly consider the SP method. If J(w(k) + c s(k)) on the right-hand side of (7) is expanded at the point w(k), its expectation is taken, and the conditions of the sign vector s(k) are considered, we obtain
That is, Δ w i becomes a good estimate of the true gradient vector. In other words, the SP method is a different type of the stochastic gradient method [Reference Maeda and Yoshida46].
Next, let us consider the ANC system using the SP method. The SP method requires two measurements in every iteration to obtain the objective function. The objective function (mean squared error) is replaced with the sum of squared errors defined as
Therefore, the coefficients of the adaptive filter are updated by two error signals in the SP method: one is the difference between the filter output and the target noise, and the other is the error between the filter output with perturbation and the target noise. However, the ANC system cannot obtain two error signals simultaneously because only one output signal from the noise control filter with or without perturbation can propagate through the physical secondary path. Therefore, the SP method requires that the reference signal x(n) is stationary for a short time.
Figure 8 shows the block diagram of the ANC system using the SP method [Reference Maeda and Yoshida46,Reference Kajikawa and Nomura47], where Q(z) is the perturbation filter that generates the perturbation o(n) and has the same filter length L as the adaptive filter W(z), that is, Q(z) corresponds to c s(k) in (7), thus the output o(n) is given by
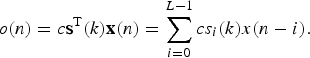
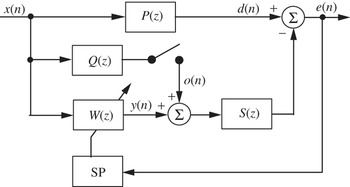
Fig. 8. Equivalent sampled-time block diagram of the TDSP method [45,46]. In this figure, P(z) is the primary path, S(z) is the secondary path, W(z) is the control filter, and Q(z) is the perturbation filter. The perturbation filter Q(z) is used for estimating the gradient vector of the objective function.
The switch in Fig. 8 is closed (so the perturbation is added) at the first half of a given block and is opened (so the anti-noise without perturbation) at the second half of the block to obtain the two objective functions in (7). The sums of squared errors for these two half blocks are calculated. If the signal is stationary within the block, these sums are approximately equal to the corresponding squared errors at the same time. Hence, the SP method can be applied to ANC by block processing.
The updating algorithm at the kth block is expressed as
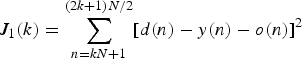
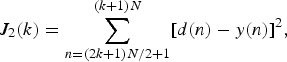
where N is the block length and s(k) is a sign vector whose elements are either −1 or 1; it has the following properties:
where s i(k) is the ith element of the vector s(k) and E[ ] is the expectation operator. Thus, the elements s i(k) are variables that have a zero-mean and are uncorrelated with other elements and the same element at different times. A pseudo-random (PN) sequence is generally used as the coefficients for the perturbation filter because the PN sequence satisfies the above conditions and can be easily generated. Furthermore, the same PN sequence is used for the perturbation filter Q(z) in every block, but is shifted by one tap in every block to satisfy the above conditions.
The computational complexity of the SP method is similar to the FXLMS algorithm because the secondary-path model is replaced with the perturbation filter. However, the original time-domain simultaneous perturbation (TDSP) method converges slowly owing to the perturbation and the step size. In the TDSP method, the magnitude of the perturbation and step size must be set small to achieve good performance. To mitigate this problem, the frequency-domain simultaneous perturbation (FDSP) and frequency domain time difference simultaneous perturbation (FDTDSP) methods were proposed in [Reference Kajikawa and Nomura48,Reference Mori, Kajikawa and Nomura49], respectively. Moreover, the FDSP and FDTDSP methods with variable perturbation were also proposed in [Reference Tokoro, Kajikawa and Nomura50]. However, the convergence rate is still lower than that in the FXLMS algorithm. Therefore, the challenge for the use of these algorithms for practical application is to improve their convergence rate. In [Reference Zhou, Zhang, Li and Gan51], the feedback ANC system using the SP method is proposed and applied to the duct ANC system.
Another approach that requires no secondary-path model uses the simultaneous equation method [Reference Fujii, Muneyasu and Ohga52]. In the simultaneous equation method, an auxiliary adaptive filter is utilized similarly to the overall online modeling method. The simultaneous equations method computes a noise control filter without requiring the secondary-path model. In [Reference Fujii, Muneyasu and Ohga52,Reference Fujii, Yamaguchi, Hashimoto, Fujita and Muneyasu53], it was demonstrated that the convergence rate of the simultaneous equation method is higher than that of the FXLMS algorithm. However, the original simultaneous equation method requires a higher computational cost than the FXLMS algorithm owing to the auxiliary adaptive filter and background system identification. To mitigate this problem, the frequency-domain simultaneous equation method and the simultaneous equation method without auxiliary filters were proposed in [Reference Fujii, Hashimoto and Muneyasu54,Reference Muneyasu, Hisayasu, Fujii and Hinamoto55], respectively. Moreover, they were applied to the hybrid ANC systems [Reference Muneyasu, Wakasugi, Hisayasu, Fujii and Hinamoto56], narrowband ANC systems [Reference Fujii, Nakatani and Muneyasu57], IIR-based ANC systems [Reference Fujii, Kashihara, Muneyasu and Morimoto58], and multi-channel ANC systems [Reference Muneyasu, Wakasugi, Kagawa, Fujii and Hinamoto59–Reference Okamoto, Kashihara, Fujii, Muneyasu and Morimoto61].
Other ANC techniques that do not require the secon-dary-path model include methods based on the strict positive real (SPR) property of the FXLMS algorithm [Reference Zhou and DeBrunner62,Reference Wu, Chen and Qiu63], adaptive genetic algorithm [Reference Chang and Chen64], and self-learning [Reference Yuan65]. Among these algorithms, the SPR-based method is the most attractive owing to its simple implementation and good performance. However, the convergence rate of this method is lower than that of the FXLMS algorithm. Therefore, it is still a challenge to improve the convergence rate of these ANC algorithms without the secondary-path model for practical applications.
IV. SOME NEW APPLICATIONS
In this section, some recent applications including motorcycle helmet ANC, snore ANC, MRI ANC, infant incubator ANC, and new attempts to use highly directional loudspeakers for ANC are introduced to explain challenges and suggest some open issues for further research and development of ANC systems.
A) Motorcycle helmet ANC systems
Motorcycle noise mainly consists of engine noise, wind noise, tire noise, and road noise. Predominantly, the low-frequency engine noise produced from the motorcycle can range from 80–90 dBA at 30 mph to 116 dBA at 120 mph depending on the type of motorcycle and on the road conditions [Reference Lower, Hurst, Claughton and Thomas231]. Prolonged listening to this high-level noise will result in hearing loss, and may even distract the concentration of the rider and make it difficult to hear or communicate any emergency signal on the road, which may potentially be life threatening. In general, a motorcycle helmet's liner can act as a passive barrier and provides good noise (such as wind noise) attenuation at a frequency above 500 Hz. Therefore, combining ANC with passive noise control from the helmet liner can provide broadband noise control for motorcycle riders.
The conventional feedforward ANC has been successfully applied to reduce motorcycle engine noise by 40 dB in the frequency range up to 200 Hz, and by 15 dB in the frequency range from 200 to 600 Hz [Reference Raghunathan, Kuo and Gan232]. An extension of this work has also been reported in [Reference Wang, Gan and Kuo233], whereby a subband-based ANE based on the psychoacoustic shaping of residual noise spectra is proposed to better match human preference in noise perception. The use of hybrid ANC to cancel motorcycle noise is reported in [Reference Castae-Selga and Pea234].
To further add to the audio/speech listening capability to allow motorcycle riders to listen to music/speech from audio devices using the same loudspeakers that are installed inside the helmet to generate anti-noise for noise attenuation, the feedback audio-integrated ANC system was proposed in [Reference Gan and Kuo156,Reference Gan and Kuo158]. Furthermore, when communicating in a noisy environment, there is also a need to remove near-end noise picked up by the reference microphone before sending it to the far-end. A simple adaptive noise-canceling filter H(z) using the LMS algorithm can be added to the audio-integrated ANC system, as shown in Fig. 9. The reference microphone is used to pick up the near-end speech from the speaker, but also to sense near-end noise. Correlated noise derived from the output of the feedback active noise controller W(z) can be used as the reference input to H(z). The operation and functionality of the integrated audio and ANC system remain the same. Experimental results show that the acoustic noise cancellation of 30–40 dB in the frequency range of 500 Hz, and the near-end speech enhancement of 25 dB [Reference Gan and Kuo158] can be achieved.
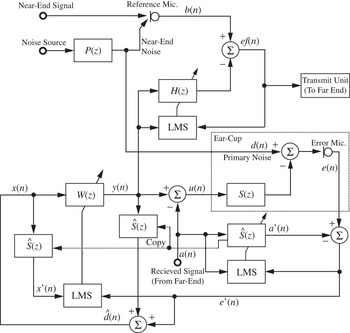
Fig. 9. Equivalent sampled-time block diagram of an audio-integrated ANC system with near-end noise cancellation for speech communication. In this figure, P(z) is the primary path, S(z) is the secondary path, W(z) is the control filter, H(z) is the adaptive noise canceling filter, and Ŝ(z) is the secondary-path model. The adaptive noise canceling filter H(z) is added to the audio-integrated ANC system in Fig. 5 to cancel near-end noise.
B) Snore ANC systems
Snoring is an acoustic phenomenon generated by vibrating tissue structures owing to obstruction in the upper airway during sleep, and is a prominent problem in modern society. The annoying intermittent nature of snoring disrupts the sleep of the snorer's bed partner, causing stress, excessive daytime sleepiness, and social nuisance. For low-frequency snoring noise, passive methods such as earmuffs or earplugs are either ineffective or uncomfortable to wear during sleep.
The application of ANC to reduce snoring noise was reported in [Reference Chakravarthy and Kuo235,Reference Chakrovorthy236]. A snore ANC system installed on a traditional headboard has potential benefits of retrofitting, convenience, and non-obtrusiveness. As shown in Fig. 10, two secondary loudspeakers and two error microphones are mounted on the headboard. A model of a human torso called KEMAR (Knowles Electronics Mannequin for Acoustics Research) is used as the bed partner. Two microphones inside the ear cavities of KEMAR are used to evaluate the performance of the system at the ears of the bed partner, which mimics real performance perceived by humans. Both single-channel and multiple-channel ANC structures using adaptive IIR filters and FIR filters have been developed and tested to evaluate their performance for canceling snore.

Fig. 10. Experimental setup for the snore ANC inside an acoustic chamber.
Real-time experiments based on the 1 × 2 × 2 (which consists of a single reference sensor, two secondary sources, and two error sensors) FXLMS algorithm using recorded snore samples show that the average noise reduction at the left error microphone is about 10–20 dB. However, the noise reduction at the left ear of KEMAR is about 5–10 dB. These results clearly suggest that better snore ANC performance can be achieved by placing the error microphones close to the ears of KEMAR, especially in the high-frequency region with a smaller quiet zone. Therefore, one of the challenges for practical application is to create quiet zones at the locations of virtual sensors (i.e., ears of the bed partner) by placing physical error sensors on the headboard as shown in Fig. 10. This problem can be solved using virtual sensing techniques [Reference Haneda173–Reference Moreau, Ghan, Cazzolato and Zander179], which are also critical for many practical ANC applications that have to place error sensors away from the desired control locations.
Another challenge is that a snore is a fast time-varying and intermittent noise. This requires fast convergence algorithms such as those introduced in Section II(L). Owing to the broadband nature of snore, feedforward ANC with a reference sensor is required. This may cause causality problems if the snorer and bed partner are too close to shorten the acoustic delay. In addition, a snorer does not always snore so a robust snore detector to turn the ANC algorithm on and off is needed.
Furthermore, ANC systems do not completely reduce primary noise owing to many physical limitations. In the snore ANC application, which is often used in quiet bedrooms, still annoying residual noise may need special treatment. One effective solution based on psychoacoustic principles is to mask residual noise using suitable masking signals, such as music or nature sound. This can be done using audio-integrated ANC algorithms [Reference Kuo and Finn151–Reference Wang, Gan and Kuo159]. Properly selected audio sound for snore ANC systems can create a very soothing atmosphere to help a person relax and sleep. In addition, the same audio can be used as a training signal (instead of annoying white noise) for offline secondary-path modeling, and can continue to function in the online secondary-path modeling shown in Fig. 6, where a random noise generator is replaced with an audio player. Many online secondary-path modeling algorithms introduced in Section III may be modified to improve the performance of audio-integrated ANC systems.
C) MRI ANC systems
Recently, MRI equipment, which is used to take images of human organs, has been in use in many medical institutions. Some MRI devices have also been introduced to conduct microwave coagulation therapy using near-real-time MR images. However, MRI equipment generates intense noise because the gradient coil vibrates owing to Lorentz force. Exposure to the intense noise may cause patients and medical staff to suffer extreme stress and may prevent verbal communication between them [Reference McJury, Stewart, Crawford and Toma237].
Many approaches to reducing MRI noise have been developed. These approaches include passive noise control, the design of silent MRI pulse sequences, and ANC. Passive noise control uses earplugs or ear protection, which is only effective for high-frequency noise. Unfortunately, MRI noise has a high sound pressure level (SPL) at low frequencies. Moreover, passive noise control devices prevent verbal communication among patients and medical staff during operation. The design of silent MRI pulse sequences relies on selecting imaging parameters to reduce related acoustic noise, which results in an approximately 20 dB attenuation of the SPL. However, this technique limits imaging sequences and reduces image resolution.
The ANC system offers an effective technique for reducing MRI noise. The application of ANC to MRI noise has been reported in [Reference McJury, Stewart, Crawford and Toma237–Reference Kannan, Milani, Panahi and Briggs246], and an approximately 15–30 dB noise reduction has been achieved. However, these studies have some limitations. Firstly, the experiment was conducted using computer simulations or in a laboratory setup, not in actual MRI rooms. Secondly, these studies used a headset-based system that has problems of preventing verbal communication between the medical staff and the patients, causing pressure on the user's ears, and separating the patient from the outside acoustical environment. Finally, most of the studies utilized the feedforward ANC system with the FXLMS algorithm. The feedforward ANC system requires at least two microphones (reference and error) and sufficient distance between the two microphones to ensure causality, thus increasing the size of the system. Moreover, the reference noise sensed at the reference microphone must highly correlate with the noise picked up by the error microphone. In practical applications, it is very difficult to determine the reference microphone position because the MRI equipment is very large and the noise source is unknown.
A novel ANC structure that can achieve high noise reduction regardless of the user's movements that allows for clear verbal communication, and that can be comfortably mounted without pressure on the ears is proposed in [Reference Kumamoto, Kida, Hirayama, Kajikawa, Tani and Kurumi245]. The ANC structure consists of two microphones arranged near the opening of the user's external auditory canal and two loudspeakers located close to the user's ears, as shown in Fig. 11. This structure is called a head-mounted ANC system to distinguish it from the headset-based ANC systems. That is, the head-mounted ANC system does not cover the user's ears, so that the user can verbally communicate with other people while reducing unwanted MRI noise. Hence, this ANC system is utilized for medical staff working in the MRI room. The head-mounted ANC system utilizes optical microphones and piezo-electric loudspeakers to realize noise reduction in a high magnetic field and compensate the low SPL of the piezo-electric loudspeakers because the loudspeakers are close to the user's ears. This ANC system uses the IMC-based feedback system (introduced in Section II(E)), which can reduce predictable noise, is independent of the direction of arrival of noise, and is small in physical size as compared with the feedforward ANC system because the reference sensor is not needed. This ANC system can effectively reduce MRI noise in the frequency range between 500 and 2500 Hz. Experimental results demonstrated that the ANC system can reduce MRI noise by approximately 20 dB at a high magnetic field in an actual MRI room.
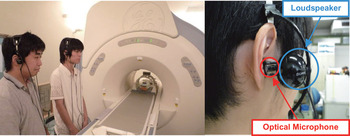
Fig. 11. Experimental setup for the MRI ANC in an MRI room and the head-mounted ANC system.
A challenging problem for MRI ANC is that the MRI noise contains periodical and impulse-like noise. Periodic components can be minimized by feedback ANC, but impulse-like components cannot be minimized. This problem can be solved by means of some advanced algorithms using the probability density function of impulse-like noise [Reference Sun, Kuo and Meng247–Reference Bergamasco, Rossa and Piroddi252] for canceling impulse-like noise included in MRI noise. The second challenge is that MRI equipment generates intense magnetic fields. Therefore, it is necessary for transducers in the ANC system to satisfy several conditions: the transducer must work normally in an intense magnetic field and must not affect the MR image. Hence, transducers containing magnetic materials cannot be used for the MRI ANC system. In [Reference Kumamoto, Kida, Hirayama, Kajikawa, Tani and Kurumi245], an optical microphone and a piezo-electric loudspeaker were used to satisfy these conditions. However, a piezo-electric loudspeaker cannot generate sufficient SPL at low frequencies. Therefore, further development of an appropriate transducer is required.
D) Infant incubator ANC systems
Medical and technological advancements including the use of infant incubators in neonatal intensive care units (NICUs) have significantly increased the survival of premature and ill infants. The infant incubator is an enclosure designed to hold an infant with transparent sections for viewing. The incubator consists of sensors and devices for monitoring the vital statistics of a baby, and for the environmental control of temperature, humidity, supplementary gas and other parameters. However, high levels of noise generated by medical equipment and human activities inside NICU results in numerous adverse health effects including sleep disturbance and other forms of stress. There is also evidence that NICU noise exposure has significant long-term consequences of hearing loss. Unfortunately, there are few developed methods that are effective in reducing incubator noise. The performance of passive noise reduction techniques in the low-frequency range is limited. Furthermore, most passive techniques either occupy limited incubator space or block the view of an infant to caregivers, or both. These difficulties motivated the development of ANC systems to cancel low-frequency noise inside incubators, as shown in Fig. 12 [Reference Yu, Gujjula and Kuo253,Reference Kuo, Liu and Gujjula254].
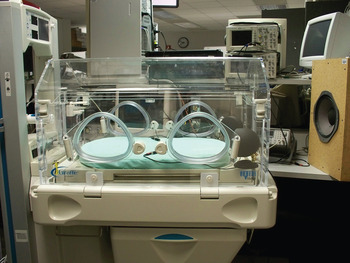
Fig. 12. Experimental setup for the infant incubator ANC system.
A challenging problem for incubator ANC is that there is a lot of impulse-like noise produced by pumps and human activities. This problem can be solved by means of some advanced algorithms using the probability density function of impulse-like noise [Reference Sun, Kuo and Meng247,Reference Akhtar and Mitsuhashi248,Reference Wu, He and Qiu250–Reference Bergamasco, Rossa and Piroddi252] to cancel impulse-like noise in infant incubators. The second challenge is that noise inside an incubator comes from multiple noise sources inside and outside the incubator. Since NICU noise is broadband in nature, the broadband feedforward ANC system introduced in Section II(A) is needed. In general, a reference microphone is placed outside the incubator, as shown in Fig. 12, to satisfy causality constraint. This configuration can cancel noise outside the incubator, but is ineffective for canceling noise inside the incubator. This problem may be solved using hybrid ANC systems [Reference Ray, Solbeck, Streeter and Collier109–Reference Xiao and Wang115]. Finally, the number and locations of noise sources inside an NICU is generally unknown to achieve effective incubator ANC; thus, it is very challenging to determine the number and locations of reference microphones and the corresponding FXLMS algorithm for such a configuration.
In addition, intrauterine (womb-like) sound provides infants with the ambience of the mother's womb, which has been proved to relieve stress and improve learning and neurological development for preterm infants – it helps in infant neurological development and improves infants' understanding of rhythm and melody. Thus, it is necessary to design audio-integrated ANC systems [Reference Kuo and Finn151–Reference Wang, Gan and Kuo159] that not only cancel harmful NICU noise, but also play intrauterine sound inside incubators to recreate the in utero experience for infants. The audio-integrated ANC system introduced in Section II(I) can be used for incubator ANC.
E) ANC using directional loudspeakers
Noise cancellation is generally carried out using conventional omnidirectional loudspeakers. Recently, there has been some interest to exploit the use of highly directional loudspeakers, such as parametric loudspeakers [Reference Gan, Tan and Kuo255]. Parametric loudspeakers modulate an audible sound signal onto an ultrasonic carrier, and project the modulated signal via special types of ultrasonic emitter to generate a nonlinear acoustic effect in air, such that audible sound can travel in a column of sound beams.
The main motivation in using a directional secondary sound source is to attenuate primary noise to achieve focused noise control at a local zone of quiet with little spill over outside this zone. A special feature of directional loudspeakers is their ability to project highly directional sound sources, just like a spotlight. Furthermore, the pressure decay within the Rayleigh distance of a parametric loudspeaker is less than that of a conventional omnidirectional loudspeaker. These unique characteristics of parametric loudspeakers allow for noise control to be confined within the directional beamwidth of the parametric loudspeakers. A comparison of noise control performance based on the sound pressure distribution between an omnidirectional voice coil loudspeaker and a directional parametric loudspeaker is conducted in [Reference Tanaka and Tanaka256].
Another work [Reference Tanaka and Tanaka257] conducted by the same research group used a steerable parametric loudspeaker, which can electronically steer a control sound source to the target control point. This steerable feature is useful in canceling a moving noise source such as a vehicle; the tracking of the noise source may be implemented using a camera and locality information can be fed back into the system to generate a directional and steerable control sound at the target noise source. The current challenge is to develop effective and low-cost tracking algorithms for moving targets.
However, one current drawback of parametric loudspeakers is their inability to efficiently control a low-frequency noise source lower than 500 Hz. This is due to the poorer frequency response of the parametric acoustic array generation of a directional sound field at low frequencies [Reference Gan, Tan and Kuo255].
V. CONCLUSION AND FUTURE TRENDS OF ANC
In this paper, we briefly reviewed broadband and narrowband feedforward and adaptive feedback ANC systems with focus on signal processing algorithms. We focused on the introduction of the recent research and development in the last decade after detailed tutorial publications [Reference Nelson and Elliott1–Reference Kuo and Morgan8]. In particular, we introduced the audio-integrated algorithm and the concepts of psychoacoustics and virtual sensing for ANC. In this paper, we also comprehensively reviewed online secondary-path modeling techniques and ANC without the secondary-path model, which remain critical for some practical applications. Finally, we highlighted some ANC applications in medical and consumer electronics fields, which are important for motivating new ANC applications in addition to traditional applications in industry and transportation. We also identified many related difficulties and open research issues in each section.
There are many challenges [Reference Kuo, Kuo and Gan258] in developing successful ANC applications: (1) theory of associated acoustics related to ANC algorithms and the positioning of transducers for optimum performance; (2) development of fast convergence and robust algorithms to achieve maximum noise reduction at desired locations in time-varying environments; and (3) implementation considerations including system complexity, physical constraints, and cost reduction. In addition to these requirements, integrating value-added functions, such as audio and communications into ANC can further promote the development of other applications. Finally, many consumer products may prefer ANC systems to mask and control the spectral contents of residual noise over simple noise reduction.















