Article contents
Measure transfer and S-adic developments for subshifts
Published online by Cambridge University Press: 11 March 2024
Abstract
Based on previous work of the authors, to any S-adic development of a subshift X a ‘directive sequence’ of commutative diagrams is associated, which consists at every level 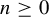 $n \geq 0$ of the measure cone and the letter frequency cone of the level subshift
$n \geq 0$ of the measure cone and the letter frequency cone of the level subshift 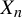 $X_n$ associated canonically to the given S-adic development. The issuing rich picture enables one to deduce results about X with unexpected directness. For instance, we exhibit a large class of minimal subshifts with entropy zero that all have infinitely many ergodic probability measures. As a side result, we also exhibit, for any integer
$X_n$ associated canonically to the given S-adic development. The issuing rich picture enables one to deduce results about X with unexpected directness. For instance, we exhibit a large class of minimal subshifts with entropy zero that all have infinitely many ergodic probability measures. As a side result, we also exhibit, for any integer 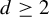 $d \geq 2$, an S-adic development of a minimal, aperiodic, uniquely ergodic subshift X, where all level alphabets
$d \geq 2$, an S-adic development of a minimal, aperiodic, uniquely ergodic subshift X, where all level alphabets 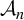 $\mathcal A_n$ have cardinality
$\mathcal A_n$ have cardinality 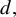 $d,$ while none of the
$d,$ while none of the 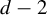 $d-2$ bottom level morphisms is recognizable in its level subshift
$d-2$ bottom level morphisms is recognizable in its level subshift 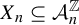 $X_n \subseteq \mathcal A_n^{\mathbb {Z}}$.
$X_n \subseteq \mathcal A_n^{\mathbb {Z}}$.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 1
- Cited by



