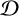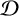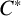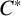1 Introduction
Given an inverse semigroup S, we denote by
![]() $E(S)$
its semilattice of idempotents and by
$E(S)$
its semilattice of idempotents and by
![]() $\leq $
its natural partial order (hence,
$\leq $
its natural partial order (hence,
![]() $a \leq b$
if and only if
$a \leq b$
if and only if
![]() $a = eb$
for some
$a = eb$
for some
![]() $e \in E(S)$
). Given
$e \in E(S)$
). Given
![]() $s \in S$
, let
$s \in S$
, let
![]() $\lambda _S(s) = \{ t \in S \mid t \leq s\}$
and let
$\lambda _S(s) = \{ t \in S \mid t \leq s\}$
and let
![]() $\mu _S(s)$
denote the set of maximal elements of
$\mu _S(s)$
denote the set of maximal elements of
![]() $\lambda _S(s) \cap E(S)$
for
$\lambda _S(s) \cap E(S)$
for
![]() $\leq $
.
$\leq $
.
Paterson [Reference Paterson5] associated an étale groupoid
![]() $\mathcal G(S)$
to every inverse semigroup S, called its universal groupoid, and showed that the
$\mathcal G(S)$
to every inverse semigroup S, called its universal groupoid, and showed that the
![]() $C^{*}$
-algebra of the inverse semigroup is isomorphic to the
$C^{*}$
-algebra of the inverse semigroup is isomorphic to the
![]() $C^{*}$
-algebra of its universal groupoid. The second author later generalized Paterson’s result by showing that if K is any commutative ring with unit, then the semigroup algebra
$C^{*}$
-algebra of its universal groupoid. The second author later generalized Paterson’s result by showing that if K is any commutative ring with unit, then the semigroup algebra
![]() $KS$
of S is isomorphic to a certain convolution algebra of K-valued functions on the groupoid
$KS$
of S is isomorphic to a certain convolution algebra of K-valued functions on the groupoid
![]() $\mathcal G(S)$
[Reference Steinberg8]. There is now a well-developed theory of étale groupoid algebras which has proven useful for studying inverse semigroup algebras. Both the algebra and
$\mathcal G(S)$
[Reference Steinberg8]. There is now a well-developed theory of étale groupoid algebras which has proven useful for studying inverse semigroup algebras. Both the algebra and
![]() $C^{*}$
-algebra of an étale groupoid are best behaved when the groupoid is Hausdorff. In particular, the theory of traces on groupoid
$C^{*}$
-algebra of an étale groupoid are best behaved when the groupoid is Hausdorff. In particular, the theory of traces on groupoid
![]() $C^{*}$
-algebras seems to only be well developed in the Hausdorff case where there is a faithful conditional expectation mapping to the algebra of continuous functions vanishing at infinity on the unit space. Universal groupoids of inverse semigroups are not always Hausdorff. It was shown in [Reference Steinberg8] that
$C^{*}$
-algebras seems to only be well developed in the Hausdorff case where there is a faithful conditional expectation mapping to the algebra of continuous functions vanishing at infinity on the unit space. Universal groupoids of inverse semigroups are not always Hausdorff. It was shown in [Reference Steinberg8] that
![]() $\mathcal G(S)$
is Hausdorff if and only if
$\mathcal G(S)$
is Hausdorff if and only if
![]() $\lambda _S(s)\cap E(S)$
is finitely generated as an ideal in
$\lambda _S(s)\cap E(S)$
is finitely generated as an ideal in
![]() $E(S)$
, that is, there is a finite set
$E(S)$
, that is, there is a finite set
![]() $F\subseteq \lambda _S(s)\cap E(S)$
such that if
$F\subseteq \lambda _S(s)\cap E(S)$
such that if
![]() $e\in \lambda _S(s)\cap E(S)$
, then
$e\in \lambda _S(s)\cap E(S)$
, then
![]() $e\leq f$
for some
$e\leq f$
for some
![]() $f\in F$
. In particular, if
$f\in F$
. In particular, if
![]() $\mathcal G(S)$
is Hausdorff, then
$\mathcal G(S)$
is Hausdorff, then
![]() $\mu _S(s)$
is finite. For example, if G is a nontrivial group and E is the semilattice consisting of a zero element and a countably infinite set of orthogonal idempotents, then
$\mu _S(s)$
is finite. For example, if G is a nontrivial group and E is the semilattice consisting of a zero element and a countably infinite set of orthogonal idempotents, then
![]() $S=G\cup E$
is an inverse monoid, where G acts trivially on the left and right of E, with a non-Hausdorff universal groupoid. Indeed, if
$S=G\cup E$
is an inverse monoid, where G acts trivially on the left and right of E, with a non-Hausdorff universal groupoid. Indeed, if
![]() $1\neq g\in G$
, then
$1\neq g\in G$
, then
![]() $\lambda _S(g)\cap E(S)=E$
which has infinitely many maximal elements. Note that S is a Clifford inverse monoid: each
$\lambda _S(g)\cap E(S)=E$
which has infinitely many maximal elements. Note that S is a Clifford inverse monoid: each
![]() $\mathcal D$
-class of S contains a single idempotent. However, S is not finitely generated and each of its finitely generated inverse subsemigroups does have a Hausdorff universal groupoid and hence S is a direct limit of Clifford monoids with Hausdorff universal groupoids.
$\mathcal D$
-class of S contains a single idempotent. However, S is not finitely generated and each of its finitely generated inverse subsemigroups does have a Hausdorff universal groupoid and hence S is a direct limit of Clifford monoids with Hausdorff universal groupoids.
The second author has recently initiated a study of stable finiteness of étale groupoid algebras [Reference Steinberg9] and, in particular, recovered a result of Munn showing that if S is an inverse semigroup whose
![]() $\mathcal D$
-classes have finitely many idempotents, then
$\mathcal D$
-classes have finitely many idempotents, then
![]() $KS$
is stably finite for any field K of characteristic
$KS$
is stably finite for any field K of characteristic
![]() $0$
[Reference Munn4]. Recall that a ring R is stably finite if
$0$
[Reference Munn4]. Recall that a ring R is stably finite if
![]() $M_n(R)$
does not contain a copy of the bicyclic monoid as a subsemigroup for any
$M_n(R)$
does not contain a copy of the bicyclic monoid as a subsemigroup for any
![]() $n\geq 1$
. In the case where S has a Hausdorff universal groupoid, this can be deduced using the theory of
$n\geq 1$
. In the case where S has a Hausdorff universal groupoid, this can be deduced using the theory of
![]() $C^{*}$
-algebras, but in the non-Hausdorff case, one needs to work around this. However, since the stable finiteness result can be reduced to the case of finitely generated inverse semigroups with finitely many idempotents in each
$C^{*}$
-algebras, but in the non-Hausdorff case, one needs to work around this. However, since the stable finiteness result can be reduced to the case of finitely generated inverse semigroups with finitely many idempotents in each
![]() $\mathcal D$
-class, it becomes of interest to know whether there are examples of such finitely generated inverse semigroups with non-Hausdorff universal groupoids. The easiest way to guarantee that each
$\mathcal D$
-class, it becomes of interest to know whether there are examples of such finitely generated inverse semigroups with non-Hausdorff universal groupoids. The easiest way to guarantee that each
![]() $\mathcal D$
-class of S contains finitely many idempotents is to impose the stronger condition that each
$\mathcal D$
-class of S contains finitely many idempotents is to impose the stronger condition that each
![]() ${\mathcal {R}}$
-class of S is finite (since each idempotent f in the
${\mathcal {R}}$
-class of S is finite (since each idempotent f in the
![]() $\mathcal D$
-class of e is of the form
$\mathcal D$
-class of e is of the form
![]() $s^{-1}s$
with s in the
$s^{-1}s$
with s in the
![]() ${\mathcal {R}}$
-class of e).
${\mathcal {R}}$
-class of e).
This paper is then motivated by the following question.
Problem 1.1. Is there a finitely generated inverse semigroup S such that:
-
(i) every
 ${\mathcal {R}}$
-class of S is finite; and
${\mathcal {R}}$
-class of S is finite; and -
(ii)
 $\mu _S(s)$
is infinite for some
$\mu _S(s)$
is infinite for some
 $s \in S$
?
$s \in S$
?
In Section 3, we present a construction that provides uncountably many nonisomorphic 3-generated inverse monoids satisfying the conditions of Problem 1.1.
In Section 4, we present a construction which provides infinitely many nonisomorphic finitely presented 3-generated inverse monoids satisfying the conditions of Problem 1.1.
It is not difficult to show (see [Reference Steinberg9]) that if S is finitely presented and has a non-Hausdorff universal groupoid, then S cannot be written as a direct limit of inverse semigroups with Hausdorff universal groupoids. Since stable finiteness is preserved under direct limits, to really show that we cannot reduce stable finiteness of
![]() $KS$
to the case that S has a Hausdorff universal groupoid, it is important to have a finitely presented inverse semigroup satisfying the conditions of Problem 1.1.
$KS$
to the case that S has a Hausdorff universal groupoid, it is important to have a finitely presented inverse semigroup satisfying the conditions of Problem 1.1.
2 Preliminaries
The reader is assumed to have basic knowledge of inverse semigroup theory and automata theory, being respectively referred to [Reference Lawson2, Reference Sakarovitch6] for that purpose. Since the inverse semigroups we construct are actually inverse monoids, all the relevant definitions are presented in the monoid version.
2.1 Inverse automata
Given a finite alphabet A, we denote by
![]() $A^{-1}$
a set of formal inverses of A and write
$A^{-1}$
a set of formal inverses of A and write
![]() $\widetilde {A} = A\cup A^{-1}$
. An inverse automaton over the alphabet
$\widetilde {A} = A\cup A^{-1}$
. An inverse automaton over the alphabet
![]() $\widetilde {A}$
is a structure of the form
$\widetilde {A}$
is a structure of the form
![]() ${\cal {A}} = (Q,i,t,E)$
, where:
${\cal {A}} = (Q,i,t,E)$
, where:
-
• Q is the set of vertices;
-
•
 $i, t \in Q$
are the initial and terminal vertices, respectively;
$i, t \in Q$
are the initial and terminal vertices, respectively; -
•
 $E \subseteq Q \times \widetilde {A} \times Q$
is the set of edges,
$E \subseteq Q \times \widetilde {A} \times Q$
is the set of edges,
satisfying the following properties:
-
• deterministic,
 $(p,a,q),(p,a,q') \in E \Rightarrow q = q'$
;
$(p,a,q),(p,a,q') \in E \Rightarrow q = q'$
; -
• involutive,
 $(p,a,q) \in E \Leftrightarrow (q,a^{-1},p) \in E$
;
$(p,a,q) \in E \Leftrightarrow (q,a^{-1},p) \in E$
; -
• trim, every vertex lies in some path from i to t.
If
![]() $i = t$
, we refer to it as the basepoint of
$i = t$
, we refer to it as the basepoint of
![]() ${\cal {A}}$
. If we do not specify the initial and terminal vertices, we have an inverse graph.
${\cal {A}}$
. If we do not specify the initial and terminal vertices, we have an inverse graph.
Assume now that
![]() ${\cal {A}}$
is involutive and trim, but not deterministic. A folding operation on
${\cal {A}}$
is involutive and trim, but not deterministic. A folding operation on
![]() ${\cal {A}}$
consists of identifying two distinct edges of the form
${\cal {A}}$
consists of identifying two distinct edges of the form
![]() $p \xleftarrow {a} q \xrightarrow {a} r$
(identifying also the inverse edges
$p \xleftarrow {a} q \xrightarrow {a} r$
(identifying also the inverse edges
![]() $p \xrightarrow {a^{-1}} q \xleftarrow {a^{-1}} r$
). If
$p \xrightarrow {a^{-1}} q \xleftarrow {a^{-1}} r$
). If
![]() ${\cal {A}}$
is finite and we fold enough edges, we end up obtaining a finite inverse automaton
${\cal {A}}$
is finite and we fold enough edges, we end up obtaining a finite inverse automaton
![]() ${\cal {A}}'$
, which we say is obtained from
${\cal {A}}'$
, which we say is obtained from
![]() ${\cal {A}}$
by complete folding.
${\cal {A}}$
by complete folding.
Is this operation confluent? That is, does the inverse automaton depend on the sequence of foldings? Given
![]() $u,v \in \widetilde {A}^{*}$
, write
$u,v \in \widetilde {A}^{*}$
, write
![]() $u \xrightarrow {*} v$
if v can be obtained from u by successively erasing factors of the form
$u \xrightarrow {*} v$
if v can be obtained from u by successively erasing factors of the form
![]() $aa^{-1}$
$aa^{-1}$
![]() $(a \in \widetilde {A})$
. It is easy to check that
$(a \in \widetilde {A})$
. It is easy to check that
Hence, the language of the inverse automaton
![]() ${\cal {A}}'$
is completely determined by
${\cal {A}}'$
is completely determined by
![]() ${\cal {A}}$
. Since inverse automata are known to be minimal (see for example [Reference Bartholdi, Silva and Pin1]), it follows that
${\cal {A}}$
. Since inverse automata are known to be minimal (see for example [Reference Bartholdi, Silva and Pin1]), it follows that
![]() ${\cal {A}}'$
is itself determined by
${\cal {A}}'$
is itself determined by
![]() ${\cal {A}}$
and so the folding process is confluent.
${\cal {A}}$
and so the folding process is confluent.
A Dyck word on
![]() $\widetilde {A}$
is some
$\widetilde {A}$
is some
![]() $w \in \widetilde {A}^{*}$
satisfying
$w \in \widetilde {A}^{*}$
satisfying
![]() $w \xrightarrow {*} 1$
. These are the words representing the identity in the free group on A, and also play an important role in the theory of inverse semigroups as we soon see.
$w \xrightarrow {*} 1$
. These are the words representing the identity in the free group on A, and also play an important role in the theory of inverse semigroups as we soon see.
2.2 Free inverse monoids
Let A be a nonempty alphabet. We extend
![]() $^{-1}\colon A \to A^{-1}: a \mapsto a^{-1}$
to an involution on the free monoid
$^{-1}\colon A \to A^{-1}: a \mapsto a^{-1}$
to an involution on the free monoid
![]() $\widetilde {A}^{*}$
through
$\widetilde {A}^{*}$
through
The free inverse monoid on A is the quotient
![]() $FIM_A = \widetilde {A}^{*}/\rho $
, where
$FIM_A = \widetilde {A}^{*}/\rho $
, where
![]() $\rho $
is the congruence on
$\rho $
is the congruence on
![]() $\widetilde {A}^{*}$
generated by the relation
$\widetilde {A}^{*}$
generated by the relation
known as the Wagner congruence on
![]() $\widetilde {A}^{*}$
.
$\widetilde {A}^{*}$
.
Munn provided in [Reference Munn3] an elegant normal form for
![]() $FIM_A$
using inverse automata (see also [Reference Scheiblich7] by Scheiblich).
$FIM_A$
using inverse automata (see also [Reference Scheiblich7] by Scheiblich).
Given
![]() $w = a_1\cdots a_n \in \widetilde {A}^{*}$
$w = a_1\cdots a_n \in \widetilde {A}^{*}$
![]() $(a_i \in \widetilde {A})$
, let
$(a_i \in \widetilde {A})$
, let
![]() $\mathrm {Lin}(w)$
denote the linear automaton of w:
$\mathrm {Lin}(w)$
denote the linear automaton of w:
that contains also the inverse edges (to make it involutive). The Munn tree of w is the finite inverse automaton
![]() $\mbox {MT}(w)$
obtained by completely folding
$\mbox {MT}(w)$
obtained by completely folding
![]() $\mathrm {Lin}(w)$
. This provides the following solution for the word problem of
$\mathrm {Lin}(w)$
. This provides the following solution for the word problem of
![]() $FIM_A$
.
$FIM_A$
.
Theorem 2.1 [Reference Munn3].
For all
![]() $u,v \in \widetilde {A}^{*}$
, the following conditions are equivalent:
$u,v \in \widetilde {A}^{*}$
, the following conditions are equivalent:
-
(i)
 $u\rho = v\rho $
;
$u\rho = v\rho $
; -
(ii)
 $\mathrm {MT}(u) \cong \mathrm {MT}(v)$
;
$\mathrm {MT}(u) \cong \mathrm {MT}(v)$
; -
(iii)
 $u \in L(\mathrm {MT}(v))$
and
$u \in L(\mathrm {MT}(v))$
and
 $v \in L(\mathrm {MT}(u))$
.
$v \in L(\mathrm {MT}(u))$
.
Such Munn trees are precisely those finite inverse automata on
![]() $\widetilde {A}$
whose underlying undirected graph is a tree (when we consider only the edges labeled by A).
$\widetilde {A}$
whose underlying undirected graph is a tree (when we consider only the edges labeled by A).
It is easy to see that, given
![]() $w \in \widetilde {A}^{*}$
,
$w \in \widetilde {A}^{*}$
,
2.3 Inverse monoid presentations
A (finite) inverse monoid presentation is a formal expression of the form
![]() ${\cal {P}} = \langle A \mid R\rangle $
, where A is a (finite) alphabet and R is a (finite) subset of
${\cal {P}} = \langle A \mid R\rangle $
, where A is a (finite) alphabet and R is a (finite) subset of
![]() $\widetilde {A}^{*} \times \widetilde {A}^{*}$
. We usually describe the relations in R as formal equalities
$\widetilde {A}^{*} \times \widetilde {A}^{*}$
. We usually describe the relations in R as formal equalities
![]() $r = s$
.
$r = s$
.
Let
![]() $\tau = (\rho \cup R)^{\sharp }$
be the congruence on
$\tau = (\rho \cup R)^{\sharp }$
be the congruence on
![]() $\widetilde {A}^{*}$
generated by the relation
$\widetilde {A}^{*}$
generated by the relation
![]() $\rho \cup R$
. The quotient
$\rho \cup R$
. The quotient
![]() $S = \widetilde {A}^{*}/\tau $
is the inverse monoid defined by
$S = \widetilde {A}^{*}/\tau $
is the inverse monoid defined by
![]() ${\cal {P}}$
. Equivalently, we might write
${\cal {P}}$
. Equivalently, we might write
![]() $S = FIM_A/R^{\sharp }$
, viewing R as a relation on
$S = FIM_A/R^{\sharp }$
, viewing R as a relation on
![]() $FIM_A$
. We denote by
$FIM_A$
. We denote by
![]() $\varphi \colon \widetilde {A}^{*} \to S$
the canonical homomorphism.
$\varphi \colon \widetilde {A}^{*} \to S$
the canonical homomorphism.
Stephen devised in [Reference Stephen10] an approach which is the most useful tool known to date to deal with inverse monoid presentations. The Cayley graph of S with respect to the generating set A, denoted by Cay
![]() $_A(S)$
, has vertex set S and edges of the form
$_A(S)$
, has vertex set S and edges of the form
![]() $s \xrightarrow {a} s(a\varphi )$
for all
$s \xrightarrow {a} s(a\varphi )$
for all
![]() $s \in S$
and
$s \in S$
and
![]() $a \in \widetilde {A}$
. This is not in general an involutive graph (it would be if S is a group). However, the strongly connected components of Cay
$a \in \widetilde {A}$
. This is not in general an involutive graph (it would be if S is a group). However, the strongly connected components of Cay
![]() $_A(S)$
are actually inverse automata. Additionally, these correspond to the various
$_A(S)$
are actually inverse automata. Additionally, these correspond to the various
![]() ${\mathcal {R}}$
-classes of S (so there exist paths
${\mathcal {R}}$
-classes of S (so there exist paths

in Cay
![]() $_A(S)$
for some
$_A(S)$
for some
![]() $u,v \in \widetilde {A}^{*}$
if and only if
$u,v \in \widetilde {A}^{*}$
if and only if
![]() $s_1s_1^{-1} = s_2s_2^{-1}$
). The Schützenberger graph of
$s_1s_1^{-1} = s_2s_2^{-1}$
). The Schützenberger graph of
![]() $w \in \widetilde {A}^{*}$
, denoted by
$w \in \widetilde {A}^{*}$
, denoted by
![]() $S\Gamma (w)$
, is the strongly connected component of Cay
$S\Gamma (w)$
, is the strongly connected component of Cay
![]() $_A(S)$
containing
$_A(S)$
containing
![]() $w\varphi $
(that is, the induced subgraph having the
$w\varphi $
(that is, the induced subgraph having the
![]() ${\mathcal {R}}$
-class of
${\mathcal {R}}$
-class of
![]() $w\varphi $
as a set of vertices). The Schützenberger automaton of
$w\varphi $
as a set of vertices). The Schützenberger automaton of
![]() $w \in \widetilde {A}^{*}$
, denoted by
$w \in \widetilde {A}^{*}$
, denoted by
![]() ${\cal {A}}(w)$
, is obtained from
${\cal {A}}(w)$
, is obtained from
![]() $S\Gamma (w)$
by setting
$S\Gamma (w)$
by setting
![]() $(ww^{-1})\varphi $
as initial vertex and
$(ww^{-1})\varphi $
as initial vertex and
![]() $w\varphi $
as terminal vertex. We may also write
$w\varphi $
as terminal vertex. We may also write
![]() $S\Gamma (u\varphi ) = S\Gamma (u)$
or
$S\Gamma (u\varphi ) = S\Gamma (u)$
or
![]() ${\cal {A}}(u\varphi ) = {\cal {A}}(u)$
if it suits us.
${\cal {A}}(u\varphi ) = {\cal {A}}(u)$
if it suits us.
Stephen proved the following theorems, which generalize those of Munn.
Theorem 2.2 [Reference Stephen10].
For all
![]() $u,v \in \widetilde {A}^{*}$
, the following conditions are equivalent:
$u,v \in \widetilde {A}^{*}$
, the following conditions are equivalent:
-
(i)
 $u\varphi \geq v\varphi $
;
$u\varphi \geq v\varphi $
; -
(ii)
 $u \in L({\cal {A}}(v))$
.
$u \in L({\cal {A}}(v))$
.
Theorem 2.3 [Reference Stephen10].
For all
![]() $u,v \in \widetilde {A}^{*}$
, the following conditions are equivalent:
$u,v \in \widetilde {A}^{*}$
, the following conditions are equivalent:
-
(i)
 $u\varphi = v\varphi $
;
$u\varphi = v\varphi $
; -
(ii)
 ${\cal {A}}(u) \cong {\cal {A}}(v)$
;
${\cal {A}}(u) \cong {\cal {A}}(v)$
; -
(iii)
 $u \in L({\cal {A}}(v))$
and
$u \in L({\cal {A}}(v))$
and
 $v \in L({\cal {A}}(u))$
.
$v \in L({\cal {A}}(u))$
.
Since
![]() $u\varphi \in E(S)$
if and only if
$u\varphi \in E(S)$
if and only if
![]() $(uu^{-1})\varphi = u\varphi $
, it follows that the idempotents of S are characterized by having a basepoint at their Schützenberger automaton.
$(uu^{-1})\varphi = u\varphi $
, it follows that the idempotents of S are characterized by having a basepoint at their Schützenberger automaton.
It follows from Theorem 2.3 that the word problem is decidable for
![]() ${\cal {P}}$
if membership is decidable in the languages of its Schützenberger automata. In general, it is not. However, Stephen devised a procedure which brings positive results in many important cases. We describe it now.
${\cal {P}}$
if membership is decidable in the languages of its Schützenberger automata. In general, it is not. However, Stephen devised a procedure which brings positive results in many important cases. We describe it now.
Suppose that
![]() ${\cal {A}}$
is a finite involutive automaton and
${\cal {A}}$
is a finite involutive automaton and
![]() $r = s$
is a relation in R such that there exists in
$r = s$
is a relation in R such that there exists in
![]() ${\cal {A}}$
a path of the form
${\cal {A}}$
a path of the form
![]() $p \xrightarrow {r} q$
but no path
$p \xrightarrow {r} q$
but no path
![]() $p \xrightarrow {s} q$
(or vice versa). If we glue to
$p \xrightarrow {s} q$
(or vice versa). If we glue to
![]() ${\cal {A}}$
a ‘path’
${\cal {A}}$
a ‘path’
![]() $p \xrightarrow {s} q$
with the corresponding inverse edges (to keep it involutive), we say that this new automaton
$p \xrightarrow {s} q$
with the corresponding inverse edges (to keep it involutive), we say that this new automaton
![]() ${\cal {A}}'$
is obtained from
${\cal {A}}'$
is obtained from
![]() ${\cal {A}}$
by an expansion (expanding through the relation
${\cal {A}}$
by an expansion (expanding through the relation
![]() $r = s$
).
$r = s$
).
If
![]() $L({\cal {A}}) \subseteq L({\cal {A}}(w))$
and
$L({\cal {A}}) \subseteq L({\cal {A}}(w))$
and
![]() ${\cal {A}}'$
is obtained from
${\cal {A}}'$
is obtained from
![]() ${\cal {A}}$
by either folding or through an expansion through some relation in R, then
${\cal {A}}$
by either folding or through an expansion through some relation in R, then
![]() $L({\cal {A}}') \subseteq L({\cal {A}}(w))$
. We call any finite involutive automaton
$L({\cal {A}}') \subseteq L({\cal {A}}(w))$
. We call any finite involutive automaton
![]() ${\cal {A}}$
such that
${\cal {A}}$
such that
![]() $w \in L({\cal {A}}) \subseteq L({\cal {A}}(w))$
an approximate automaton of w (for the presentation
$w \in L({\cal {A}}) \subseteq L({\cal {A}}(w))$
an approximate automaton of w (for the presentation
![]() ${\cal {P}}$
). This is the case of any finite inverse automaton obtained from
${\cal {P}}$
). This is the case of any finite inverse automaton obtained from
![]() $\mbox {MT}(w)$
through a finite sequence of foldings and expansions. If
$\mbox {MT}(w)$
through a finite sequence of foldings and expansions. If
![]() ${\cal {A}}$
is an approximate automaton of w that admits neither foldings nor expansions, then
${\cal {A}}$
is an approximate automaton of w that admits neither foldings nor expansions, then
![]() ${\cal {A}} \cong {\cal {A}}(w)$
.
${\cal {A}} \cong {\cal {A}}(w)$
.
Assume now that the
![]() ${\mathcal {R}}$
-classes of S are all finite. Then the Schützenberger automata are all finite as well. Can we compute them? If R is finite, the answer is given through Stephen’s sequence, which provides a systematic way of building approximate automata. Take
${\mathcal {R}}$
-classes of S are all finite. Then the Schützenberger automata are all finite as well. Can we compute them? If R is finite, the answer is given through Stephen’s sequence, which provides a systematic way of building approximate automata. Take
![]() ${\cal {A}}_1(w) = \mbox {MT}(w)$
. If
${\cal {A}}_1(w) = \mbox {MT}(w)$
. If
![]() ${\cal {A}}_n(w)$
is defined, let
${\cal {A}}_n(w)$
is defined, let
![]() ${\cal {A}}^{\prime }_{n+1}(w)$
be obtained by performing simultaneously all the possible expansions of
${\cal {A}}^{\prime }_{n+1}(w)$
be obtained by performing simultaneously all the possible expansions of
![]() ${\cal {A}}_n(w)$
. Since R is finite,
${\cal {A}}_n(w)$
. Since R is finite,
![]() ${\cal {A}}^{\prime }_{n+1}(w)$
is a finite involutive automaton. Now define
${\cal {A}}^{\prime }_{n+1}(w)$
is a finite involutive automaton. Now define
![]() ${\cal {A}}_{n+1}(w)$
by completely folding
${\cal {A}}_{n+1}(w)$
by completely folding
![]() ${\cal {A}}^{\prime }_{n+1}(w)$
. We get then a sequence
${\cal {A}}^{\prime }_{n+1}(w)$
. We get then a sequence
![]() $({\cal {A}}_n(w))_n$
of approximate automata of w. If
$({\cal {A}}_n(w))_n$
of approximate automata of w. If
![]() ${\cal {A}}(w)$
is finite, it will eventually show up as a member of the sequence.
${\cal {A}}(w)$
is finite, it will eventually show up as a member of the sequence.
This is still true for infinite R if:
-
• we are sure of S having only finite
 ${\mathcal {R}}$
-classes;
${\mathcal {R}}$
-classes; -
• only finitely many expansions can be applied to each
 ${\cal {A}}_n(w)$
.
${\cal {A}}_n(w)$
.
Anyway, in the general case of an arbitrary presentation,
![]() $v \in L({\cal {A}}_T(u))$
implies that v is recognized by some approximate automaton of u; in fact, given any approximate automaton of u, one can perform a finite sequence of foldings and expansions to obtain an approximate automaton recognizing v.
$v \in L({\cal {A}}_T(u))$
implies that v is recognized by some approximate automaton of u; in fact, given any approximate automaton of u, one can perform a finite sequence of foldings and expansions to obtain an approximate automaton recognizing v.
The results in this subsection are used throughout the paper without further reference. The reader is referred to [Reference Stephen10] for more details on Schützenberger automata and Stephen’s sequences.
3 Finitely generated examples
In this section, we present a construction which provides uncountably many nonisomorphic 3-generated inverse monoids satisfying the conditions of Problem 1.1.
We start by proving the following proposition.
Proposition 3.1. Let S be an inverse monoid where every
![]() ${\mathcal {R}}$
-class is finite. Let
${\mathcal {R}}$
-class is finite. Let
![]() $\langle A \mid R\rangle $
be an inverse monoid presentation of S. Let
$\langle A \mid R\rangle $
be an inverse monoid presentation of S. Let
![]() $E \subseteq E(S)\setminus \{ 1\}$
and let
$E \subseteq E(S)\setminus \{ 1\}$
and let
![]() $w_e \in \widetilde {A}^+$
be a Dyck word representing e for every
$w_e \in \widetilde {A}^+$
be a Dyck word representing e for every
![]() $e \in E$
. Let T be the inverse semigroup defined by the inverse monoid presentation
$e \in E$
. Let T be the inverse semigroup defined by the inverse monoid presentation
where b is a new letter. Then:
-
(i) every
 ${\mathcal {R}}$
-class of T is finite;
${\mathcal {R}}$
-class of T is finite; -
(ii) if no two distinct elements of E are
 ${\mathcal J}$
-comparable in S and E is infinite, then
${\mathcal J}$
-comparable in S and E is infinite, then
 $\mu _T(b)$
is infinite.
$\mu _T(b)$
is infinite.
Proof. (i) Note that an idempotent e can always be represented by some Dyck word since
![]() $e = ee^{-1}$
. Write
$e = ee^{-1}$
. Write
![]() $B = A \cup \{ b\}$
and let
$B = A \cup \{ b\}$
and let
![]() $\psi \colon \widetilde {A}^{*} \to S$
and
$\psi \colon \widetilde {A}^{*} \to S$
and
![]() $\varphi \colon \widetilde {B}^{*} \to T$
be the canonical homomorphisms.
$\varphi \colon \widetilde {B}^{*} \to T$
be the canonical homomorphisms.
We use the notation
![]() ${\cal {A}}_S(u)$
and
${\cal {A}}_S(u)$
and
![]() ${\cal {A}}_T(u)$
to denote the Schützenberger automata of u relative to the presentation of S and T, respectively.
${\cal {A}}_T(u)$
to denote the Schützenberger automata of u relative to the presentation of S and T, respectively.
Let
![]() $u \in \widetilde {B}^{*}$
. Then
$u \in \widetilde {B}^{*}$
. Then
![]() $\mbox {MT}(u)$
is essentially the disjoint union of finitely many Munn trees for some words in
$\mbox {MT}(u)$
is essentially the disjoint union of finitely many Munn trees for some words in
![]() $\widetilde {A}^{*}$
, connected by b-trees to each other in a way that results in a tree. Let
$\widetilde {A}^{*}$
, connected by b-trees to each other in a way that results in a tree. Let
![]() $Q'$
be the set of vertices of
$Q'$
be the set of vertices of
![]() $\mbox {MT}(u)$
that admit a b-loop (at their image) in
$\mbox {MT}(u)$
that admit a b-loop (at their image) in
![]() ${\cal {A}}_T(u)$
. Let
${\cal {A}}_T(u)$
. Let
![]() ${\cal {A}}_1$
be the finite inverse automaton obtained from
${\cal {A}}_1$
be the finite inverse automaton obtained from
![]() $\mbox {MT}(u)$
by adjoining a b-loop at each
$\mbox {MT}(u)$
by adjoining a b-loop at each
![]() $q \in Q'$
followed by complete folding. Adding a b-loop and folding can absorb b-trees into that vertex creating possibly a wedge of Munn trees with
$q \in Q'$
followed by complete folding. Adding a b-loop and folding can absorb b-trees into that vertex creating possibly a wedge of Munn trees with
![]() $\widetilde {A}$
-edges at that vertex. Such a wedge of
$\widetilde {A}$
-edges at that vertex. Such a wedge of
![]() $\widetilde {A}$
-trees is itself an
$\widetilde {A}$
-trees is itself an
![]() $\widetilde {A}$
-tree, and hence an approximate automaton for some
$\widetilde {A}$
-tree, and hence an approximate automaton for some
![]() $\widetilde {A}$
-word for
$\widetilde {A}$
-word for
![]() $FIM_A$
, folding therefore into a Munn tree. Thus,
$FIM_A$
, folding therefore into a Munn tree. Thus,
![]() ${\cal {A}}_1$
is a finite inverse automaton consisting of Munn trees with edges in
${\cal {A}}_1$
is a finite inverse automaton consisting of Munn trees with edges in
![]() $\widetilde {A}$
, say
$\widetilde {A}$
, say
![]() $\mbox {MT}(u_1),\ldots ,\mbox {MT}(u_n)$
, connected by b-edges and having some b-loops adjoined. Moreover,
$\mbox {MT}(u_1),\ldots ,\mbox {MT}(u_n)$
, connected by b-edges and having some b-loops adjoined. Moreover,
![]() ${\cal {A}}_1$
is an approximate automaton of u with the property that each b-edge that is not a loop comes from
${\cal {A}}_1$
is an approximate automaton of u with the property that each b-edge that is not a loop comes from
![]() $\mbox {MT}(u)$
.
$\mbox {MT}(u)$
.
We start now what we call the iterative process. Since every
![]() ${\mathcal {R}}$
-class of S is finite, we can turn each of these Munn trees
${\mathcal {R}}$
-class of S is finite, we can turn each of these Munn trees
![]() $\mbox {MT}(u_i)$
inside
$\mbox {MT}(u_i)$
inside
![]() ${\cal {A}}_1$
into a finite inverse automaton admitting no R-expansions by a finite series of R-expansions and foldings. The resulting automaton (which contains the same b-edges as
${\cal {A}}_1$
into a finite inverse automaton admitting no R-expansions by a finite series of R-expansions and foldings. The resulting automaton (which contains the same b-edges as
![]() ${\cal {A}}_1$
) is a finite inverse automaton admitting no R-expansions, and is still an approximate automaton of u. However, vertices of the Munn trees
${\cal {A}}_1$
) is a finite inverse automaton admitting no R-expansions, and is still an approximate automaton of u. However, vertices of the Munn trees
![]() $\mbox {MT}(u_i)$
may have been identified in the process, so now folding of b-edges may become possible. After folding the b-edges, different
$\mbox {MT}(u_i)$
may have been identified in the process, so now folding of b-edges may become possible. After folding the b-edges, different
![]() $\widetilde {A}$
-components may now share a vertex, but we claim that these new
$\widetilde {A}$
-components may now share a vertex, but we claim that these new
![]() $\widetilde {A}$
-components may still be viewed as approximate automata for some word on
$\widetilde {A}$
-components may still be viewed as approximate automata for some word on
![]() $\widetilde {A}$
.
$\widetilde {A}$
.
Indeed, assume that
![]() $\cal {B}$
and
$\cal {B}$
and
![]() $\cal {C}$
are subautomata of
$\cal {C}$
are subautomata of
![]() ${\cal {A}}_1$
corresponding to approximate automata of
${\cal {A}}_1$
corresponding to approximate automata of
![]() $v,w \in \widetilde {A}^{*}$
, respectively. If we identify the vertex p of
$v,w \in \widetilde {A}^{*}$
, respectively. If we identify the vertex p of
![]() $\cal {B}$
with the vertex q of
$\cal {B}$
with the vertex q of
![]() $\cal {C}$
, we may modify
$\cal {C}$
, we may modify
![]() $v,w$
to assume that p and q were, respectively, the terminal and initial vertices of
$v,w$
to assume that p and q were, respectively, the terminal and initial vertices of
![]() $\cal {B}$
and
$\cal {B}$
and
![]() $\cal {C}$
. It follows easily that, by identifying p and q, we get an approximate automaton of
$\cal {C}$
. It follows easily that, by identifying p and q, we get an approximate automaton of
![]() $vw \in \widetilde {A}^{*}$
.
$vw \in \widetilde {A}^{*}$
.
We may now restart the process. At each iteration, the number of b-edges decreases, so we are bound to eventually halt by obtaining some finite inverse automaton
![]() ${\cal {A}}_2$
admitting no R-expansions, which is still an approximate automaton of u.
${\cal {A}}_2$
admitting no R-expansions, which is still an approximate automaton of u.
Now let
![]() ${\cal {A}}_3$
be obtained from
${\cal {A}}_3$
be obtained from
![]() ${\cal {A}}_2$
by adjoining a b-loop at each vertex p admitting a path
${\cal {A}}_2$
by adjoining a b-loop at each vertex p admitting a path
![]() $p \xrightarrow {w_e^{-1}} \cdots $
for some
$p \xrightarrow {w_e^{-1}} \cdots $
for some
![]() $e \in E$
(if it does not exist already). Adjoining these new b-loops does not allow any folding: if
$e \in E$
(if it does not exist already). Adjoining these new b-loops does not allow any folding: if
![]() $p \xrightarrow {b^{\varepsilon }} q \neq p$
would be an edge of
$p \xrightarrow {b^{\varepsilon }} q \neq p$
would be an edge of
![]() ${\cal {A}}_2$
for
${\cal {A}}_2$
for
![]() $\varepsilon = \pm 1$
, then we have necessarily
$\varepsilon = \pm 1$
, then we have necessarily
![]() $p \in Q'$
because p is doomed to host a b-loop in
$p \in Q'$
because p is doomed to host a b-loop in
![]() ${\cal {A}}_T(u)$
, and then we already have a b-loop at p in
${\cal {A}}_T(u)$
, and then we already have a b-loop at p in
![]() ${\cal {A}}_1$
. Hence,
${\cal {A}}_1$
. Hence,
![]() ${\cal {A}}_3$
admits no folding and it certainly admits no expansions of any sort. Since
${\cal {A}}_3$
admits no folding and it certainly admits no expansions of any sort. Since
![]() ${\cal {A}}_3$
is an approximate automaton of u, it follows that
${\cal {A}}_3$
is an approximate automaton of u, it follows that
![]() ${\cal {A}}_3 = {\cal {A}}_T(u)$
, which is therefore finite.
${\cal {A}}_3 = {\cal {A}}_T(u)$
, which is therefore finite.
Therefore,
![]() ${\cal {A}}_T(u)$
must be finite in all cases and so is
${\cal {A}}_T(u)$
must be finite in all cases and so is
![]() ${\mathcal {R}}_{u\varphi }$
.
${\mathcal {R}}_{u\varphi }$
.
(ii) We start by noting that the homomorphism
![]() $\eta \colon S \to T$
extending the identity mapping on A is an embedding. It is immediate that we have a homomorphism
$\eta \colon S \to T$
extending the identity mapping on A is an embedding. It is immediate that we have a homomorphism
![]() ${\theta \colon T \to S}$
defined by
${\theta \colon T \to S}$
defined by
Then
![]() $\theta \eta =1_S$
(as it is the identity on A), and so
$\theta \eta =1_S$
(as it is the identity on A), and so
![]() $\eta $
is an embedding of S into T.
$\eta $
is an embedding of S into T.
Let
![]() $e \in E$
. To construct
$e \in E$
. To construct
![]() ${\cal {A}}_T(w_e)$
, we start by turning
${\cal {A}}_T(w_e)$
, we start by turning
![]() $\mbox {MT}(w_e)$
into
$\mbox {MT}(w_e)$
into
![]() ${\cal {A}}_S(w_e)$
, which is an approximate automaton of
${\cal {A}}_S(w_e)$
, which is an approximate automaton of
![]() $w_e$
for the presentation in Equation (3-1). Expanding through the relation
$w_e$
for the presentation in Equation (3-1). Expanding through the relation
![]() $w_eb = w_e$
and subsequent folding produces a b-loop at the basepoint i and possibly at other vertices where a path labeled by
$w_eb = w_e$
and subsequent folding produces a b-loop at the basepoint i and possibly at other vertices where a path labeled by
![]() $w_e$
(necessarily a loop) can be read.
$w_e$
(necessarily a loop) can be read.
Suppose now that we have some path of the form
![]() $p \xrightarrow {w_{e'}} q$
in
$p \xrightarrow {w_{e'}} q$
in
![]() ${\cal {A}}_S(w_e)$
with
${\cal {A}}_S(w_e)$
with
![]() $e'\hspace{-0.5pt} \in\hspace{-0.5pt} E \setminus \{ e\}$
. Then
$e'\hspace{-0.5pt} \in\hspace{-0.5pt} E \setminus \{ e\}$
. Then
![]() $uw_{e'}v\hspace{-0.5pt} \in\hspace{-0.5pt} L({\cal {A}}_S(w_e))$
for some
$uw_{e'}v\hspace{-0.5pt} \in\hspace{-0.5pt} L({\cal {A}}_S(w_e))$
for some
![]() $u,v\hspace{-0.5pt} \in\hspace{-0.5pt} \widetilde {A}^{*}$
and so
$u,v\hspace{-0.5pt} \in\hspace{-0.5pt} \widetilde {A}^{*}$
and so
![]() $(u\psi )e'(v\psi )e\hspace{-0.5pt} =\hspace{-0.5pt} e$
, yielding
$(u\psi )e'(v\psi )e\hspace{-0.5pt} =\hspace{-0.5pt} e$
, yielding
![]() $e' \geq _{{\mathcal J}} e$
. This contradicts the assumption that no two distinct elements of E are
$e' \geq _{{\mathcal J}} e$
. This contradicts the assumption that no two distinct elements of E are
![]() ${\mathcal J}$
-comparable in S, and hence
${\mathcal J}$
-comparable in S, and hence
![]() ${\cal {A}}_S(w_e)$
admits no path of the form
${\cal {A}}_S(w_e)$
admits no path of the form
![]() $p \xrightarrow {w_{e'}} q$
and so
$p \xrightarrow {w_{e'}} q$
and so
![]() ${\cal {A}}_T(w_e)$
is indeed
${\cal {A}}_T(w_e)$
is indeed
![]() ${\cal {A}}_S(w_e)$
with a few b-loops attached (namely at the basepoint).
${\cal {A}}_S(w_e)$
with a few b-loops attached (namely at the basepoint).
In view of the relation
![]() $w_eb = w_e$
, we get
$w_eb = w_e$
, we get
![]() $w_e\varphi \leq b\varphi $
and so
$w_e\varphi \leq b\varphi $
and so
![]() $w_e\varphi \in \lambda _T(b\varphi ) \cap E(T)$
. Suppose now that
$w_e\varphi \in \lambda _T(b\varphi ) \cap E(T)$
. Suppose now that
![]() $w_e\varphi \leq f \in \lambda _T(b\varphi ) \cap E(T)$
. Let
$w_e\varphi \leq f \in \lambda _T(b\varphi ) \cap E(T)$
. Let
![]() $v \in \widetilde {B}^{*}$
be a Dyck word representing f.
$v \in \widetilde {B}^{*}$
be a Dyck word representing f.
On the one hand,
![]() $w_e\varphi \leq v\varphi $
implies
$w_e\varphi \leq v\varphi $
implies
![]() $L({\cal {A}}_T(v)) \subseteq L({\cal {A}}_T(w_e))$
. On the other hand, since
$L({\cal {A}}_T(v)) \subseteq L({\cal {A}}_T(w_e))$
. On the other hand, since
![]() $f \leq b\varphi $
, we have
$f \leq b\varphi $
, we have
![]() $v\varphi =f = f(b\varphi ) = (v\varphi )(b\varphi ) =(vb)\varphi $
. Thus,
$v\varphi =f = f(b\varphi ) = (v\varphi )(b\varphi ) =(vb)\varphi $
. Thus,
![]() ${\cal {A}}_T(vb) \cong {\cal {A}}_T(v)$
and so there exists a b-loop at i in
${\cal {A}}_T(vb) \cong {\cal {A}}_T(v)$
and so there exists a b-loop at i in
![]() ${\cal {A}}_T(vb)$
.
${\cal {A}}_T(vb)$
.
It follows that at some point in the Stephen’s sequence of
![]() $vb$
, we must have had some expansion through some relation of the form
$vb$
, we must have had some expansion through some relation of the form
![]() $w_{e'}b = w_{e'}$
. Hence,
$w_{e'}b = w_{e'}$
. Hence,
![]() $w_{e'}$
labels some path in
$w_{e'}$
labels some path in
![]() ${\cal {A}}_T(v)$
and so
${\cal {A}}_T(v)$
and so
![]() $xw_{e'}y \in L({\cal {A}}_T(v)) \subseteq L({\cal {A}}_T(w_e))$
for some
$xw_{e'}y \in L({\cal {A}}_T(v)) \subseteq L({\cal {A}}_T(w_e))$
for some
![]() $x,y \in \widetilde {B^{*}}$
.
$x,y \in \widetilde {B^{*}}$
.
We have seen above that there is no path in
![]() ${\cal {A}}_S(w_e)$
(and consequently none in
${\cal {A}}_S(w_e)$
(and consequently none in
![]() ${\cal {A}}_T(w_e)$
) labeled by some
${\cal {A}}_T(w_e)$
) labeled by some
![]() $w_{e'}$
for
$w_{e'}$
for
![]() $e' \in E \setminus \{ e\}$
, and hence
$e' \in E \setminus \{ e\}$
, and hence
![]() ${\cal {A}}_T(v)$
must admit some loop labeled by
${\cal {A}}_T(v)$
must admit some loop labeled by
![]() $w_e$
at some vertex
$w_e$
at some vertex
![]() $q_1$
.
$q_1$
.
Let
![]() $i = q_0 \xrightarrow {w} q_1$
be a path in
$i = q_0 \xrightarrow {w} q_1$
be a path in
![]() ${\cal {A}}_T(v)$
. For those familiar with the bicyclic monoid, if we put
${\cal {A}}_T(v)$
. For those familiar with the bicyclic monoid, if we put
![]() $x=(vww_e)\varphi $
, then
$x=(vww_e)\varphi $
, then
![]() $xx^{-1} =f$
and
$xx^{-1} =f$
and
![]() $x^{-1} x = e(w^{-1}\varphi )f(w\varphi ) e \leq e\leq f$
. So if
$x^{-1} x = e(w^{-1}\varphi )f(w\varphi ) e \leq e\leq f$
. So if
![]() $e<f$
, then
$e<f$
, then
![]() $x,x^{-1}$
generate a copy of the bicyclic monoid with identity f and hence the
$x,x^{-1}$
generate a copy of the bicyclic monoid with identity f and hence the
![]() ${\mathcal {R}}$
-class of f is infinite, contradicting part (i). For those not familiar with the bicyclic monoid, here is a direct proof. Here,
${\mathcal {R}}$
-class of f is infinite, contradicting part (i). For those not familiar with the bicyclic monoid, here is a direct proof. Here,
![]() $ww_ew^{-1} \in L({\cal {A}}_T(v)) \subseteq L({\cal {A}}_T(w_e))$
and so
$ww_ew^{-1} \in L({\cal {A}}_T(v)) \subseteq L({\cal {A}}_T(w_e))$
and so
![]() $(ww_ew^{-1})\varphi \geq w_e\varphi $
. Assume that there exists a path
$(ww_ew^{-1})\varphi \geq w_e\varphi $
. Assume that there exists a path

in
![]() ${\cal {A}}_T(v)$
for some
${\cal {A}}_T(v)$
for some
![]() $j \geq 1$
. Then
$j \geq 1$
. Then
![]() $w^jw_ew^{-j} \in L({\cal {A}}_T(v))$
yields
$w^jw_ew^{-j} \in L({\cal {A}}_T(v))$
yields
![]() $(w^jw_ew^{-j})\varphi \geq v\varphi $
and so
$(w^jw_ew^{-j})\varphi \geq v\varphi $
and so
Thus,
![]() $w^{j+1}w_ew^{-(j+1)} \in L({\cal {A}}_T(v))$
. By induction, it follows that we have a path of the above form in
$w^{j+1}w_ew^{-(j+1)} \in L({\cal {A}}_T(v))$
. By induction, it follows that we have a path of the above form in
![]() ${\cal {A}}_T(v)$
for every
${\cal {A}}_T(v)$
for every
![]() $j \geq 1$
. Since
$j \geq 1$
. Since
![]() ${\cal {A}}_T(v)$
is finite by part (i) and is an inverse automaton, we must have
${\cal {A}}_T(v)$
is finite by part (i) and is an inverse automaton, we must have
![]() $q_j = q_0$
for some
$q_j = q_0$
for some
![]() $j \geq 1$
. However, then
$j \geq 1$
. However, then
![]() $w_e$
labels a loop at
$w_e$
labels a loop at
![]() $q_0 = i$
in
$q_0 = i$
in
![]() ${\cal {A}}_T(v)$
and so
${\cal {A}}_T(v)$
and so
![]() $w_e\varphi \geq v\varphi = f$
.
$w_e\varphi \geq v\varphi = f$
.
Thus,
![]() $f = w_e\varphi $
and so
$f = w_e\varphi $
and so
![]() $w_e\varphi \in \mu _T(b\varphi )$
for every
$w_e\varphi \in \mu _T(b\varphi )$
for every
![]() $e \in E$
.
$e \in E$
.
Since E is infinite and
![]() $\eta \colon S\to T$
induced by the identity on A is an embedding,
$\eta \colon S\to T$
induced by the identity on A is an embedding,
![]() $\{ w_e\varphi \mid e \in E\}$
is an infinite subset of
$\{ w_e\varphi \mid e \in E\}$
is an infinite subset of
![]() $\mu _T(b\varphi )$
.
$\mu _T(b\varphi )$
.
Now we can use Proposition 3.1 to produce examples which answer positively Problem 1.1.
Example 3.2. Let
![]() $I \subseteq \mathbb {N} \setminus \{ 0 \}$
be infinite and let
$I \subseteq \mathbb {N} \setminus \{ 0 \}$
be infinite and let
![]() $T_I$
be defined by the inverse monoid presentation
$T_I$
be defined by the inverse monoid presentation
Then:
-
(i) all the
 ${\mathcal {R}}$
-classes of
${\mathcal {R}}$
-classes of
 $T_I$
are finite;
$T_I$
are finite; -
(ii)
 $\mu _{T_I}(c)$
is infinite.
$\mu _{T_I}(c)$
is infinite.
Indeed, let
![]() $S = FIM_{\{ a,b\}}$
, which has finite
$S = FIM_{\{ a,b\}}$
, which has finite
![]() ${\mathcal {R}}$
-classes [Reference Munn3]. Then
${\mathcal {R}}$
-classes [Reference Munn3]. Then
is an infinite subset of
![]() $E(S)$
. If
$E(S)$
. If
![]() $i,j \in I$
are distinct, then there is no path labeled by
$i,j \in I$
are distinct, then there is no path labeled by
![]() $ab^ia$
in
$ab^ia$
in
![]() $\mbox {MT}(ab^ja)$
and vice versa, so no two distinct elements of
$\mbox {MT}(ab^ja)$
and vice versa, so no two distinct elements of
![]() $E_I$
are
$E_I$
are
![]() ${\mathcal J}$
-comparable in S. Consider now the inverse monoid presentation
${\mathcal J}$
-comparable in S. Consider now the inverse monoid presentation
In any inverse semigroup,
![]() $u = uc$
is equivalent to
$u = uc$
is equivalent to
![]() $u^{-1} u = u^{-1} uc$
, and hence this presentation is equivalent to Equation (3-2).
$u^{-1} u = u^{-1} uc$
, and hence this presentation is equivalent to Equation (3-2).
Now it follows from Proposition 3.1 that all the
![]() ${\mathcal {R}}$
-classes of
${\mathcal {R}}$
-classes of
![]() $T_I$
are finite and
$T_I$
are finite and
![]() $\mu _{T_I}(c)$
is infinite.
$\mu _{T_I}(c)$
is infinite.
We can now use Example 3.2 to prove the following proposition.
Proposition 3.3. There exist uncountably many nonisomorphic
![]() $3$
-generated inverse monoids satisfying the conditions of Problem 1.1.
$3$
-generated inverse monoids satisfying the conditions of Problem 1.1.
Proof. For each infinite
![]() $I \subseteq \mathbb {N} \setminus \{ 0 \}$
, let
$I \subseteq \mathbb {N} \setminus \{ 0 \}$
, let
![]() $T_I$
be defined by the inverse monoid presentation in Equation (3-2). We have shown in Example 3.2 that
$T_I$
be defined by the inverse monoid presentation in Equation (3-2). We have shown in Example 3.2 that
![]() $T_I$
satisfies the conditions of Problem 1.1. Since a countably infinite set contains uncountably many infinite subsets, it suffices to show that
$T_I$
satisfies the conditions of Problem 1.1. Since a countably infinite set contains uncountably many infinite subsets, it suffices to show that
![]() $T_I \not \cong T_J$
for distinct
$T_I \not \cong T_J$
for distinct
![]() $I,J \subseteq \mathbb {N} \setminus \{ 0 \}$
.
$I,J \subseteq \mathbb {N} \setminus \{ 0 \}$
.
Out of symmetry, we may assume that
![]() $i \in I\setminus J$
. Suppose that
$i \in I\setminus J$
. Suppose that
![]() $\theta \colon T_I \to T_J$
is an isomorphism. It is easy to see that each generating set of
$\theta \colon T_I \to T_J$
is an isomorphism. It is easy to see that each generating set of
![]() $T_J$
must contain:
$T_J$
must contain:
-
• a or
 $a^{-1}$
;
$a^{-1}$
; -
• b or
 $b^{-1}$
;
$b^{-1}$
; -
• c or
 $c^{-1}$
.
$c^{-1}$
.
Hence, any minimal generating set of
![]() $T_J$
is necessarily of the form
$T_J$
is necessarily of the form
![]() $\{ a^{\varepsilon },b^{\delta }, c^{\gamma } \}$
with
$\{ a^{\varepsilon },b^{\delta }, c^{\gamma } \}$
with
![]() $\varepsilon , \delta , \gamma = \pm 1$
. Thus, we may assume that
$\varepsilon , \delta , \gamma = \pm 1$
. Thus, we may assume that
![]() $\theta $
is induced by some bijection
$\theta $
is induced by some bijection
![]() $\{ a,b,c\} \to \{ a^{\varepsilon },b^{\delta }, c^{\gamma } \}$
.
$\{ a,b,c\} \to \{ a^{\varepsilon },b^{\delta }, c^{\gamma } \}$
.
Since
![]() $ab^ia = ab^iac$
is a relation of the presentation of
$ab^ia = ab^iac$
is a relation of the presentation of
![]() $T_I$
, then
$T_I$
, then
![]() $(ab^ia)\theta = (ab^iac)\theta $
holds in
$(ab^ia)\theta = (ab^iac)\theta $
holds in
![]() $T_J$
. Hence,
$T_J$
. Hence,
![]() $c\theta $
labels a loop in
$c\theta $
labels a loop in
![]() ${\cal {A}}_{T_J}((ab^ia)\theta )$
and so
${\cal {A}}_{T_J}((ab^ia)\theta )$
and so
![]() $c\theta = c^{\gamma }$
necessarily.
$c\theta = c^{\gamma }$
necessarily.
Since
![]() $ab^ia = ab^iac$
holds in
$ab^ia = ab^iac$
holds in
![]() $T_I$
, then
$T_I$
, then
![]() $(ab^ia)\theta = (ab^ia)\theta c^{\gamma }$
must hold in
$(ab^ia)\theta = (ab^ia)\theta c^{\gamma }$
must hold in
![]() $T_J$
. The only way of enabling an expansion in
$T_J$
. The only way of enabling an expansion in
![]() $\mbox {MT}((ab^ia)\theta )$
is if
$\mbox {MT}((ab^ia)\theta )$
is if
![]() $a\theta = a$
,
$a\theta = a$
,
![]() $b\theta = b$
, and
$b\theta = b$
, and
![]() $i \in J$
, which is a contradiction. Therefore,
$i \in J$
, which is a contradiction. Therefore,
![]() $T_I \not \cong T_J$
.
$T_I \not \cong T_J$
.
4 Finitely presented examples
In this section, we present a construction which provides infinitely many nonisomorphic finitely presented 3-generated inverse monoids satisfying the conditions of Problem 1.1.
Example 4.1. For each
![]() $t \geq 2$
, let
$t \geq 2$
, let
![]() $S_t$
be defined by the inverse monoid presentation
$S_t$
be defined by the inverse monoid presentation
Then:
-
(i) every
 ${\mathcal {R}}$
-class of
${\mathcal {R}}$
-class of
 $S_t$
is finite;
$S_t$
is finite; -
(ii)
 $\mu _{S_t}(aca^{-1})$
is infinite.
$\mu _{S_t}(aca^{-1})$
is infinite.
Let us check these facts.
(i) Write
![]() $S = S_t$
and
$S = S_t$
and
![]() $A = \{ a,b,c\}$
. Let
$A = \{ a,b,c\}$
. Let
![]() $\varphi \colon \widetilde {A}^{*} \to S$
be the canonical homomorphism. For every
$\varphi \colon \widetilde {A}^{*} \to S$
be the canonical homomorphism. For every
![]() $x \in A$
, let
$x \in A$
, let
![]() $\pi _x\colon \widetilde {A}^{*} \to \mathbb {Z}$
be the homomorphism defined by
$\pi _x\colon \widetilde {A}^{*} \to \mathbb {Z}$
be the homomorphism defined by
 $$ \begin{align*}y\pi_x = \begin{cases} 1&\mbox{if }y = x,\\ -1&\mbox{if }y = x^{-1},\\ 0&\mbox{if }y \in \widetilde{A} \setminus \{ x,x^{-1}\}. \end{cases} \end{align*} $$
$$ \begin{align*}y\pi_x = \begin{cases} 1&\mbox{if }y = x,\\ -1&\mbox{if }y = x^{-1},\\ 0&\mbox{if }y \in \widetilde{A} \setminus \{ x,x^{-1}\}. \end{cases} \end{align*} $$
Let
![]() $u \in \widetilde {A}^{*}$
. It suffices to show that
$u \in \widetilde {A}^{*}$
. It suffices to show that
![]() $S\Gamma (u)$
possesses only finitely many edges labeled by
$S\Gamma (u)$
possesses only finitely many edges labeled by
![]() $a,b,c$
.
$a,b,c$
.
If we perform an expansion involving the letter a, the subsequent folding prevents the number of a-edges to increase. Hence, the number of a-edges in
![]() $S\Gamma (u)$
is bounded by the number of a-edges in
$S\Gamma (u)$
is bounded by the number of a-edges in
![]() $\mbox {MT}(u)$
.
$\mbox {MT}(u)$
.
Dealing with the b-edges is harder because its number may increase through the Stephen’s sequence of u. We start by proving a few remarks.
Inspection of the defining relations shows that
![]() $\pi _b$
induces a homomorphism
$\pi _b$
induces a homomorphism
![]() $\overline \pi _b\colon S_t\to \mathbb Z$
. If v reads a loop in
$\overline \pi _b\colon S_t\to \mathbb Z$
. If v reads a loop in
![]() $S\Gamma (u)$
, then
$S\Gamma (u)$
, then
![]() $s(v\varphi ) =s$
for some
$s(v\varphi ) =s$
for some
![]() $s\in S_t$
, and so
$s\in S_t$
, and so
![]() $s\overline \pi _b +v\pi _b = s\overline \pi _b$
, whence
$s\overline \pi _b +v\pi _b = s\overline \pi _b$
, whence
![]() $v\pi _b=0$
.
$v\pi _b=0$
.
Let
![]() $v \in \widetilde {A}^+$
. We call a vertex (respectively edge) of
$v \in \widetilde {A}^+$
. We call a vertex (respectively edge) of
![]() $S\Gamma (v)$
original if it corresponds to some vertex (respectively edge) of
$S\Gamma (v)$
original if it corresponds to some vertex (respectively edge) of
![]() $\mbox {MT}(v)$
. We show that:
$\mbox {MT}(v)$
. We show that:
Once again, this property holds trivially for
![]() $\mbox {MT}(u)$
and is preserved through folding. What about expansions? If we expand through the relation
$\mbox {MT}(u)$
and is preserved through folding. What about expansions? If we expand through the relation
![]() $ca = a$
and fold once to make the new c label a loop, the property still holds. Hence, we may assume that we are expanding through the relation
$ca = a$
and fold once to make the new c label a loop, the property still holds. Hence, we may assume that we are expanding through the relation
![]() $cb^{-t}c^{-1} b^{t} = cb^{-t}b^{t}c^{-1} $
. The only way of getting new vertices is described by the following picture (where some appropriate folding is also assumed to limit the appearance of new vertices to a minimum):
$cb^{-t}c^{-1} b^{t} = cb^{-t}b^{t}c^{-1} $
. The only way of getting new vertices is described by the following picture (where some appropriate folding is also assumed to limit the appearance of new vertices to a minimum):

If the property holds for the vertex
![]() $p_0$
, it must also hold for the new vertices (
$p_0$
, it must also hold for the new vertices (
![]() $p_4$
and
$p_4$
and
![]() $p_5$
in the picture), thus the property is preserved through both sorts of expansions. It follows that the property holds throughout the whole Stephen’s sequence of u. Since every vertex p of
$p_5$
in the picture), thus the property is preserved through both sorts of expansions. It follows that the property holds throughout the whole Stephen’s sequence of u. Since every vertex p of
![]() $S\Gamma (u)$
must originate from some term of the Stephen’s sequence, then Equation (4-2) holds.
$S\Gamma (u)$
must originate from some term of the Stephen’s sequence, then Equation (4-2) holds.
Let X be the set of b-edges of
![]() $S\Gamma (u)$
. Let
$S\Gamma (u)$
. Let
![]() $\sigma $
be the equivalence relation on X generated by relating edges
$\sigma $
be the equivalence relation on X generated by relating edges
whenever
![]() $S\Gamma (u)$
admits a path
$S\Gamma (u)$
admits a path
for some
![]() $s \in \mathbb {Z}$
. Since the unique expansions that increase the number of b-edges involve the relation
$s \in \mathbb {Z}$
. Since the unique expansions that increase the number of b-edges involve the relation
![]() $cb^{-t}c^{-1} b^{t} = cb^{-t}b^{t}c^{-1}$
, it follows easily by induction on the usual expansion/folding scheme that every edge in X is
$cb^{-t}c^{-1} b^{t} = cb^{-t}b^{t}c^{-1}$
, it follows easily by induction on the usual expansion/folding scheme that every edge in X is
![]() $\sigma $
-equivalent to some original edge. Thus,
$\sigma $
-equivalent to some original edge. Thus,
![]() $\sigma $
has only finitely many equivalence classes and we only need to show that the size of each equivalence class can be bounded. Let k be the number of vertices in
$\sigma $
has only finitely many equivalence classes and we only need to show that the size of each equivalence class can be bounded. Let k be the number of vertices in
![]() $\mbox {MT}(u)$
. Suppose that some equivalence class of
$\mbox {MT}(u)$
. Suppose that some equivalence class of
![]() $\sigma $
possesses
$\sigma $
possesses
![]() $k+1$
different edges
$k+1$
different edges
![]() $p_i \xrightarrow {b} q_i$
for
$p_i \xrightarrow {b} q_i$
for
![]() $i = 0,\ldots ,k$
. By Equation (4-2), for each
$i = 0,\ldots ,k$
. By Equation (4-2), for each
![]() $i = 0,\ldots ,k$
, there is a path
$i = 0,\ldots ,k$
, there is a path
![]() $q_i \xrightarrow {b^{m_i}} r_i$
in
$q_i \xrightarrow {b^{m_i}} r_i$
in
![]() $S\Gamma (u)$
with
$S\Gamma (u)$
with
![]() $m_i \geq 0$
and
$m_i \geq 0$
and
![]() $r_i$
original. Hence, there exist
$r_i$
original. Hence, there exist
![]() $0 \leq i < j \leq k$
such that
$0 \leq i < j \leq k$
such that
![]() $r_i = r_j$
. Since
$r_i = r_j$
. Since
![]() $q_i \neq q_j$
, we get
$q_i \neq q_j$
, we get
![]() $m_i \neq m_j$
. However, it is easy to see that since
$m_i \neq m_j$
. However, it is easy to see that since
![]() $p_i \xrightarrow {b} q_i$
and
$p_i \xrightarrow {b} q_i$
and
![]() $p_j \xrightarrow {b} q_j$
are
$p_j \xrightarrow {b} q_j$
are
![]() $\sigma $
-equivalent, there exists some path
$\sigma $
-equivalent, there exists some path
![]() $q_i \xrightarrow {w} q_j$
in
$q_i \xrightarrow {w} q_j$
in
![]() $S\Gamma (u)$
with
$S\Gamma (u)$
with
![]() $w\pi _b = 0$
. However, then
$w\pi _b = 0$
. However, then

is a loop in
![]() $S\Gamma (u)$
with
$S\Gamma (u)$
with
![]() $(wb^{m_j}b^{-m_i})\pi _b \neq 0$
, contradicting Equation (4-1). Therefore, each equivalence class of
$(wb^{m_j}b^{-m_i})\pi _b \neq 0$
, contradicting Equation (4-1). Therefore, each equivalence class of
![]() $\sigma $
has at most k elements and so
$\sigma $
has at most k elements and so
![]() $S\Gamma (u)$
has finitely many b-edges.
$S\Gamma (u)$
has finitely many b-edges.
It remains to bound the number of c-edges. Suppose that we remove all the a-edges and b-edges from
![]() $S\Gamma (u)$
to get the automaton
$S\Gamma (u)$
to get the automaton
![]() ${\cal {A}}$
. Each time we remove an edge, the number of connected components increases at most by one. Hence, the number of connected components of
${\cal {A}}$
. Each time we remove an edge, the number of connected components increases at most by one. Hence, the number of connected components of
![]() ${\cal {A}}$
is bounded and it suffices to show that all of them are finite.
${\cal {A}}$
is bounded and it suffices to show that all of them are finite.
Now for every edge
![]() $p_i \xrightarrow {c} q_i \neq p_i$
appearing for the first time in
$p_i \xrightarrow {c} q_i \neq p_i$
appearing for the first time in
![]() ${\cal {A}}_i(u)$
in the Stephen’s sequence, there exist necessarily some edge
${\cal {A}}_i(u)$
in the Stephen’s sequence, there exist necessarily some edge
![]() $p_{i-1} \xrightarrow {c} q_{i-1} \neq p_{i-1}$
in
$p_{i-1} \xrightarrow {c} q_{i-1} \neq p_{i-1}$
in
![]() ${\cal {A}}_{i-1}(u)$
and paths
${\cal {A}}_{i-1}(u)$
and paths

in
![]() ${\cal {A}}_i(u)$
because the expansion
${\cal {A}}_i(u)$
because the expansion
![]() $ca = a$
could never produce the straight edge
$ca = a$
could never produce the straight edge
![]() $p_i \xrightarrow {c} q_i$
. It follows that, for every edge
$p_i \xrightarrow {c} q_i$
. It follows that, for every edge
![]() $p \xrightarrow {c} q \neq p$
in
$p \xrightarrow {c} q \neq p$
in
![]() $S\Gamma (u)$
, there exist some edge
$S\Gamma (u)$
, there exist some edge
![]() $p_1 \xrightarrow {c} q_{1}$
in
$p_1 \xrightarrow {c} q_{1}$
in
![]() $\mbox {MT}(u)$
and paths
$\mbox {MT}(u)$
and paths

in
![]() ${\cal {A}}(u)$
for some
${\cal {A}}(u)$
for some
![]() $m \geq 0$
. Since
$m \geq 0$
. Since
![]() $\mbox {MT}(u)$
is finite and
$\mbox {MT}(u)$
is finite and
![]() $S\Gamma (u)$
has finitely many b-edges, then we can bound the size of each connected component of
$S\Gamma (u)$
has finitely many b-edges, then we can bound the size of each connected component of
![]() ${\cal {A}}$
. Thus,
${\cal {A}}$
. Thus,
![]() $S\Gamma (u)$
possesses only finitely many c-edges and we are done.
$S\Gamma (u)$
possesses only finitely many c-edges and we are done.
(ii) For every
![]() $n \geq 1$
, let
$n \geq 1$
, let
![]() $e_n = ((ab^{tn}a)(ab^{tn}a)^{-1})\varphi $
. We claim that
$e_n = ((ab^{tn}a)(ab^{tn}a)^{-1})\varphi $
. We claim that

is
![]() $S\Gamma (e_n)$
. Here an edge
$S\Gamma (e_n)$
. Here an edge
![]() $p\xrightarrow {b^t}q$
is shorthand for a sequence of t edges in a straightline from p to q, labeled by b, (together with their inverse edges) and with no other edges incident on any vertex other than
$p\xrightarrow {b^t}q$
is shorthand for a sequence of t edges in a straightline from p to q, labeled by b, (together with their inverse edges) and with no other edges incident on any vertex other than
![]() $p,q$
.
$p,q$
.
It is clear that
![]() $\mbox {MT}(e_n)$
is
$\mbox {MT}(e_n)$
is
Expanding through the relation
![]() $ca = a$
, we can produce the first and the last c-loops. Then we expand through the relation
$ca = a$
, we can produce the first and the last c-loops. Then we expand through the relation
![]() $cb^{-t}c^{-1} b^{t} = cb^{-t}b^{t}c^{-1}$
to successively produce the c-loops at
$cb^{-t}c^{-1} b^{t} = cb^{-t}b^{t}c^{-1}$
to successively produce the c-loops at
![]() $p_{n}, p_{n-1}, \ldots , p_1$
. Since Equation (4-3) is an inverse automaton and admits no expansions, it must be
$p_{n}, p_{n-1}, \ldots , p_1$
. Since Equation (4-3) is an inverse automaton and admits no expansions, it must be
![]() $S\Gamma (e_n)$
, which has therefore
$S\Gamma (e_n)$
, which has therefore
![]() $tn+3$
vertices.
$tn+3$
vertices.
Now
![]() ${\cal {A}}(e_n)$
is obtained from
${\cal {A}}(e_n)$
is obtained from
![]() $S\Gamma (e_n)$
by declaring
$S\Gamma (e_n)$
by declaring
![]() $p_0$
the basepoint. Since
$p_0$
the basepoint. Since
![]() $aca^{-1} \in L({\cal {A}}(e_n))$
, then
$aca^{-1} \in L({\cal {A}}(e_n))$
, then
![]() $(aca^{-1})\varphi \geq e_n$
and so
$(aca^{-1})\varphi \geq e_n$
and so
![]() $e_n \in \lambda ((aca^{-1})\varphi ) \cap E(S)$
. We show that
$e_n \in \lambda ((aca^{-1})\varphi ) \cap E(S)$
. We show that
![]() $e_n \in \mu _S((aca^{-1})\varphi )$
.
$e_n \in \mu _S((aca^{-1})\varphi )$
.
Suppose now that
![]() $f \in \lambda ((aca^{-1})\varphi ) \cap E(S)$
satisfies
$f \in \lambda ((aca^{-1})\varphi ) \cap E(S)$
satisfies
![]() $e_n \leq f$
. Let
$e_n \leq f$
. Let
![]() $v \in \widetilde {A}^{*}$
be a Dyck word representing f.
$v \in \widetilde {A}^{*}$
be a Dyck word representing f.
First we note that
![]() $f \in \lambda ((aca^{-1})\varphi )$
implies
$f \in \lambda ((aca^{-1})\varphi )$
implies
![]() $f \leq (aca^{-1})\varphi $
. Hence,
$f \leq (aca^{-1})\varphi $
. Hence,
![]() $aca^{-1} \in L({\cal {A}}(v))$
.
$aca^{-1} \in L({\cal {A}}(v))$
.
Write
![]() $B = \{ b,c\}$
. We show that
$B = \{ b,c\}$
. We show that
First note that if
![]() $u\in \widetilde {B}^{*}$
, then u does not represent the same element of
$u\in \widetilde {B}^{*}$
, then u does not represent the same element of
![]() $S_t$
as any word z containing a or
$S_t$
as any word z containing a or
![]() $a^{-1}$
since the relation
$a^{-1}$
since the relation
![]() $ca=a$
cannot be applied to any word in
$ca=a$
cannot be applied to any word in
![]() $\widetilde {B}^{*}$
. It then follows that the inverse subsemigroup
$\widetilde {B}^{*}$
. It then follows that the inverse subsemigroup
![]() $T_t$
of
$T_t$
of
![]() $S_t$
generated by B is defined by the relation
$S_t$
generated by B is defined by the relation
![]() $cb^{-t}c^{-1} b^{t}=cb^{-t}b^{t}c^{-1}$
. It also follows that a cannot label an edge in
$cb^{-t}c^{-1} b^{t}=cb^{-t}b^{t}c^{-1}$
. It also follows that a cannot label an edge in
![]() $S\Gamma (w)$
for any
$S\Gamma (w)$
for any
![]() $w\in \widetilde {B}^{*}$
since if a labels an edge in
$w\in \widetilde {B}^{*}$
since if a labels an edge in
![]() $S\Gamma (w)$
, then
$S\Gamma (w)$
, then
![]() $w\varphi = z\varphi $
for some word
$w\varphi = z\varphi $
for some word
![]() $z\in \widetilde {A}^+$
containing an a or
$z\in \widetilde {A}^+$
containing an a or
![]() $a^{-1}$
. Thus, the Schützenberger graphs of w in
$a^{-1}$
. Thus, the Schützenberger graphs of w in
![]() $S_t$
and
$S_t$
and
![]() $T_t$
coincide. From the presentation for
$T_t$
coincide. From the presentation for
![]() $T_t$
,
$T_t$
,
![]() $\pi _c|_{\widetilde {B}^{*}}$
factors through a homomorphism
$\pi _c|_{\widetilde {B}^{*}}$
factors through a homomorphism
![]() $T_t\to \mathbb Z$
. Since
$T_t\to \mathbb Z$
. Since
![]() $\mathbb Z$
is a group, it follows that if
$\mathbb Z$
is a group, it follows that if
![]() $z\in \widetilde {B}^{*}$
labels a loop in
$z\in \widetilde {B}^{*}$
labels a loop in
![]() $S\Gamma (w)$
, then
$S\Gamma (w)$
, then
![]() $z\pi _c=0$
, and so Equation (4-4) holds.
$z\pi _c=0$
, and so Equation (4-4) holds.
Since
![]() $e_n \leq f = v\varphi $
, then
$e_n \leq f = v\varphi $
, then
![]() $v \in L({\cal {A}}(e_n))$
. Let
$v \in L({\cal {A}}(e_n))$
. Let
![]() ${\cal {A}}$
be obtained by removing the vertex
${\cal {A}}$
be obtained by removing the vertex
![]() $p_{2n+2}$
from
$p_{2n+2}$
from
![]() ${\cal {A}}(e_n)$
(in the notation given in Equation (4-3) for
${\cal {A}}(e_n)$
(in the notation given in Equation (4-3) for
![]() $S\Gamma (e_n)$
). Suppose that
$S\Gamma (e_n)$
). Suppose that
![]() $v \in L({\cal {A}})$
. We can factor
$v \in L({\cal {A}})$
. We can factor
with
![]() $m\geq 1$
,
$m\geq 1$
,
![]() $i_j \in \mathbb {Z}$
, and
$i_j \in \mathbb {Z}$
, and
![]() $w_j \in B^{*}$
. Expanding
$w_j \in B^{*}$
. Expanding
![]() $\mathrm {Lin}(v)$
through the relation
$\mathrm {Lin}(v)$
through the relation
![]() $ca = a$
and folding to get c-loops, we get the automaton
$ca = a$
and folding to get c-loops, we get the automaton

Applying expansions and folds to the part corresponding to
![]() $\mathrm {Lin}(w_1\cdots w_m)$
, the graph we get is
$\mathrm {Lin}(w_1\cdots w_m)$
, the graph we get is
![]() $S\Gamma (w_1\cdots w_m)$
(which contains no c-loops by Equation (4-4)) with finitely many subgraphs
$S\Gamma (w_1\cdots w_m)$
(which contains no c-loops by Equation (4-4)) with finitely many subgraphs  adjoined. No further expansion applies to this graph, and hence what we get is really
adjoined. No further expansion applies to this graph, and hence what we get is really
![]() ${\cal {A}}(v)$
. However, we have remarked before that
${\cal {A}}(v)$
. However, we have remarked before that
![]() $aca^{-1} \in L({\cal {A}}(v))$
, contradicting the nonexistence of c-loops in
$aca^{-1} \in L({\cal {A}}(v))$
, contradicting the nonexistence of c-loops in
![]() $S\Gamma (w_1\cdots w_m)$
. Thus,
$S\Gamma (w_1\cdots w_m)$
. Thus,
![]() $v \in L({\cal {A}}(e_n)) \setminus L({\cal {A}}')$
.
$v \in L({\cal {A}}(e_n)) \setminus L({\cal {A}}')$
.
It follows that we can factor
![]() $v = v'v"$
so that
$v = v'v"$
so that
![]() $v'$
labels a path of the form
$v'$
labels a path of the form
in
![]() ${\cal {A}}(e_n)$
for some factorization
${\cal {A}}(e_n)$
for some factorization
![]() $v' = v_0av_1v_2\cdots v_{2n+1}a$
such that
$v' = v_0av_1v_2\cdots v_{2n+1}a$
such that
![]() $v_{2j} \,\rho \, b^t$
for
$v_{2j} \,\rho \, b^t$
for
![]() $j = 1,\ldots ,n$
. And we may assume that
$j = 1,\ldots ,n$
. And we may assume that
For
![]() $j = 0,\ldots ,n$
, let
$j = 0,\ldots ,n$
, let
![]() ${\cal {A}}_j$
denote the inverse automaton depicted by
${\cal {A}}_j$
denote the inverse automaton depicted by

We show that
We use induction on j. The case
![]() $j = 0$
is immediate in view of the relation
$j = 0$
is immediate in view of the relation
![]() $ca = a$
. Hence, we assume that
$ca = a$
. Hence, we assume that
![]() $j> 0$
and Equation (4-6) holds for
$j> 0$
and Equation (4-6) holds for
![]() $j-1$
.
$j-1$
.
Let
![]() $w \in L({\cal {A}}_{n-j})$
. Then we may write
$w \in L({\cal {A}}_{n-j})$
. Then we may write
![]() $w = w'xw"$
with
$w = w'xw"$
with
![]() $x\,\rho \,b^t$
and
$x\,\rho \,b^t$
and
![]() $w" \in L({\cal {A}}_{n-(j-1)})$
. By the induction hypothesis, we get
$w" \in L({\cal {A}}_{n-(j-1)})$
. By the induction hypothesis, we get
![]() ${\cal {A}}(w") = {\cal {A}}_{n-(j-1)}$
. Folding the b-edges and expanding through the relation
${\cal {A}}(w") = {\cal {A}}_{n-(j-1)}$
. Folding the b-edges and expanding through the relation
![]() $cb^{-t}c^{-1} b^{t} = cb^{-t}b^{t}c^{-1}$
, we obtain
$cb^{-t}c^{-1} b^{t} = cb^{-t}b^{t}c^{-1}$
, we obtain
![]() ${\cal {A}}(b^tw") = {\cal {A}}_{n-j}$
. However,
${\cal {A}}(b^tw") = {\cal {A}}_{n-j}$
. However,
![]() $w \in L({\cal {A}}_{n-j})$
and
$w \in L({\cal {A}}_{n-j})$
and
![]() $xw"\rho = b^tw"\rho $
, and thus
$xw"\rho = b^tw"\rho $
, and thus
![]() $w\varphi \geq xw"\varphi $
. Therefore,
$w\varphi \geq xw"\varphi $
. Therefore,
and so
![]() ${\cal {A}}(w) = {\cal {A}}(b^tw") = {\cal {A}}_{n-j}$
, whence Equation (4-6) holds.
${\cal {A}}(w) = {\cal {A}}(b^tw") = {\cal {A}}_{n-j}$
, whence Equation (4-6) holds.
In particular,
![]() ${\cal {A}}(z) = {\cal {A}}_0$
for
${\cal {A}}(z) = {\cal {A}}_0$
for
![]() $z = v_1b^tv_3b^t\cdots b^t v_{2n+1}a$
in view of Equation (4-5). Expanding through the relation
$z = v_1b^tv_3b^t\cdots b^t v_{2n+1}a$
in view of Equation (4-5). Expanding through the relation
![]() $ca = a$
and folding, it is easy to see that
$ca = a$
and folding, it is easy to see that
![]() ${\cal {A}}(az)$
is just
${\cal {A}}(az)$
is just
![]() ${\cal {A}}(e_n)$
with
${\cal {A}}(e_n)$
with
![]() $p_{2n+2}$
as terminal vertex. Since
$p_{2n+2}$
as terminal vertex. Since
![]() $v_0$
labels a loop at
$v_0$
labels a loop at
![]() $p_0$
, we have
$p_0$
, we have
![]() $v_0\varphi \geq (az)(az)^{-1}\varphi $
and so
$v_0\varphi \geq (az)(az)^{-1}\varphi $
and so
![]() $v_0az\varphi = az\varphi $
. Thus,
$v_0az\varphi = az\varphi $
. Thus,
![]() ${\cal {A}}(v') = {\cal {A}}(v_0az) = {\cal {A}}(az)$
. Hence,
${\cal {A}}(v') = {\cal {A}}(v_0az) = {\cal {A}}(az)$
. Hence,
![]() ${\cal {A}}(v'(v')^{-1}) = {\cal {A}}(e_n)$
and so
${\cal {A}}(v'(v')^{-1}) = {\cal {A}}(e_n)$
and so
![]() $(v'(v')^{-1})\varphi = e_n$
. However, then
$(v'(v')^{-1})\varphi = e_n$
. However, then
yields
![]() $v\varphi = e_n$
and so
$v\varphi = e_n$
and so
![]() $e_n \in \mu _S((aca^{-1})\varphi )$
for every
$e_n \in \mu _S((aca^{-1})\varphi )$
for every
![]() $n \geq 1$
. Since we have established before that
$n \geq 1$
. Since we have established before that
![]() $S\Gamma (e_n)$
has
$S\Gamma (e_n)$
has
![]() $tn+3$
vertices, it follows that
$tn+3$
vertices, it follows that
![]() $\mu _S((aca^{-1})\varphi )$
is infinite.
$\mu _S((aca^{-1})\varphi )$
is infinite.
We can now use Example 4.1 to prove the following proposition.
Proposition 4.2. There exist infinitely many nonisomorphic finitely presented
![]() $3$
-generated inverse monoids satisfying the conditions of Problem 1.1.
$3$
-generated inverse monoids satisfying the conditions of Problem 1.1.
Proof. We have shown in Example 4.1 that
![]() $S_t$
satisfies the conditions of Problem 1.1 for every
$S_t$
satisfies the conditions of Problem 1.1 for every
![]() $t \geq 2$
. Thus, it suffices to show that
$t \geq 2$
. Thus, it suffices to show that
![]() $S_t \not \cong S_n$
for distinct
$S_t \not \cong S_n$
for distinct
![]() $t,n \geq 2$
.
$t,n \geq 2$
.
Suppose that
![]() $\theta \colon S_t \to S_n$
is an isomorphism. It is easy to see that each generating set of
$\theta \colon S_t \to S_n$
is an isomorphism. It is easy to see that each generating set of
![]() $S_n$
must contain:
$S_n$
must contain:
-
•
 $a^{\alpha }$
with
$a^{\alpha }$
with
 $\alpha = \pm 1$
;
$\alpha = \pm 1$
; -
•
 $b^{\varepsilon }$
with
$b^{\varepsilon }$
with
 $\varepsilon = \pm 1$
;
$\varepsilon = \pm 1$
; -
•
 $c^{\delta }$
with
$c^{\delta }$
with
 $\delta = \pm 1$
.
$\delta = \pm 1$
.
Hence, any minimal generating set of
![]() $S_n$
consists necessarily of three elements of this form. Thus, we may assume that
$S_n$
consists necessarily of three elements of this form. Thus, we may assume that
![]() $\theta $
is induced by some bijection
$\theta $
is induced by some bijection
![]() $\{ a,b,c\} \to \{ a^{\alpha },b^{\varepsilon },c^{\delta } \}$
.
$\{ a,b,c\} \to \{ a^{\alpha },b^{\varepsilon },c^{\delta } \}$
.
Since
![]() $ca = a$
is a relation of the presentation of
$ca = a$
is a relation of the presentation of
![]() $S_t$
, then
$S_t$
, then
![]() $(c\theta )(a\theta ) = a\theta $
holds in
$(c\theta )(a\theta ) = a\theta $
holds in
![]() $S_n$
, yielding successively
$S_n$
, yielding successively
![]() $c\theta = c^{\delta }$
(since a and b never label loops),
$c\theta = c^{\delta }$
(since a and b never label loops),
![]() $a\theta = a^{\alpha }$
, and
$a\theta = a^{\alpha }$
, and
![]() $b\theta = b^{\varepsilon }$
.
$b\theta = b^{\varepsilon }$
.
However,
![]() $cb^{-t}c^{-1} b^{t} = cb^{-t}b^{t}c$
is also a relation of the presentation of
$cb^{-t}c^{-1} b^{t} = cb^{-t}b^{t}c$
is also a relation of the presentation of
![]() $S_t$
, and hence
$S_t$
, and hence
![]() $c^{\delta }b^{-\varepsilon t}c^{-\delta }b^{\varepsilon t} = c^{\delta }b^{-\varepsilon t}b^{\varepsilon t}c^{-\delta }$
holds in
$c^{\delta }b^{-\varepsilon t}c^{-\delta }b^{\varepsilon t} = c^{\delta }b^{-\varepsilon t}b^{\varepsilon t}c^{-\delta }$
holds in
![]() $S_n$
. Since
$S_n$
. Since
![]() $\mbox {MT}(c^{\delta }b^{-\varepsilon t}c^{-\delta }b^{\varepsilon t})$
admits no expansion for the presentation of
$\mbox {MT}(c^{\delta }b^{-\varepsilon t}c^{-\delta }b^{\varepsilon t})$
admits no expansion for the presentation of
![]() $S_n$
, we have reached a contradiction. Therefore,
$S_n$
, we have reached a contradiction. Therefore,
![]() $S_t \not \cong S_n$
.
$S_t \not \cong S_n$
.