INTRODUCTION
Salmonella spp. are important foodborne and direct-contact zoonoses with a major impact on both human and animal health [Reference Akkina1–Reference Wray, Davies, Wray and Wray3]. Salmonella spp. can be subdivided into over 2400 serovars, some of which are species-specific. Of the ten most commonly reported Salmonella serovars in human beings in 2000, seven were also reported in cattle by routine statutory surveillance [4].
Our understanding of the ecology and infection dynamics of Salmonella spp. in dairy cattle is limited; this hampers efforts to control and prevent disease [Reference Kabagambe5, Reference Warnick6]. Dairy cattle are exposed to Salmonella spp. through persistently contaminated environments, feed, water, and wildlife faeces. At the farm level, persistent infection may be evident for years, probably as the result of a continuous cycle of environmental contamination, cattle infection and faecal shedding [Reference Davies7, Reference Huston, Wittum and Love8]. This may lead to recurrent outbreaks of clinical disease.
The epidemiology of Salmonella serotypes is diverse. Endemic persistence at a fluctuating level within the national dairy herd is evident for many strains of serovars such as S. enterica serovar Agama and S. enterica serovar Dublin. Other strains show a more epidemic pattern of spread. For example, an emergent multidrug-resistant strain of S. enterica serovar Typhimurium, which was classified as definitive type (DT)104, was identified in the United Kingdom in 1984. This strain was first recorded on dairy farms in 1988. Few human and animal cases of infection were reported up to 1990 [Reference Gibbens9]. Subsequently, S. Typhimurium DT104 caused an epidemic in both humans and cattle, with elevated morbidity and mortality compared to other serovars. The number of cases peaked in 1996, subsequently declining without targeted intervention measures. To date, there is little understanding of why Salmonella infections display such variation in their epidemiology [Reference Sato10].
Quantitative description of the spatial pattern of the Salmonella serovars of interest will inform knowledge of the underlying epidemiology and biological processes. For example, large-scale regional variations in infection may indicate risk factors operating on a similar spatial scale such as the presence of suitable habitats for wildlife populations acting as a reservoir of infection [Reference Wilson11]. Similarly, smaller-scale excess spatial clustering – or the tendency for case farms to be closer together than would be expected based on the distribution of all farms – may result from localized contagious spread or highly localized risk factors such as local feed suppliers [Reference Anderson12, Reference Davis13] and environmental contamination [Reference Jones14]. For example, runoff from pastures, direct contamination of surface water, leakage or overflow from slurry lagoons and wastewater disposal can all contribute to local water contamination, which in turn may result in localized spread between cattle herds [Reference Murray, Wray and Wray15].
The aim of this study was to investigate both large- and small-scale spatial and temporal patterns of infection of three commonly identified S. enterica serovars (Agama, Dublin and Typhimurium) on dairy farms in England and Wales. Detailed information on clustering in space and time may lead to enhanced understanding of the different epidemiological traits of these serovars. Such information may prove useful for the design and implementation of specific and effective control strategies, for instance by targeting both surveillance and control activities towards high-risk farms.
MATERIALS AND METHODS
Study design and population sampled
Data were taken from a cohort study of all known Salmonella serovars on dairy farms in England and Wales conducted by the Veterinary Laboratories Agency (VLA) between October 1999 and February 2001. As described elsewhere, the study estimated the national herd prevalence, incidence and spatial epidemiology of S. Agama, S. Dublin and S. Typhimurium [Reference Davison16], as well as risk factors associated with Salmonella status [Reference Davison17]. A brief description of the study population and relevant findings follows.
Dairy farms were enrolled through five milk companies, which bought from 1224 dairy farms (representing 63% of the total) in Great Britain. A total of 872 farms agreed to the release of their name and address. Of 547 farms that were randomly selected and asked to participate, 499 met the defined selection criteria: they had at least 30 milking cows, did not sell directly to the public, did not produce unpasteurized products, were not open to public visitors on a commercial basis, and were not primarily cattle dealers. A further 50 farms declined to participate; the remaining 449 farms were enrolled. The geographical distribution of these study farms appeared, on visual inspection, representative of the wider geographical distribution of dairy farms throughout England and Wales.
Farms were sampled on up to four visits separated by around 3-monthly intervals. At visit 1 (October 1999 to February 2000), all enrolled farms were sampled. Of these farms, 272 farms consented to continued participation in the study, and were sampled at visit 2 (March–July 2000). There were 251 farms sampled at visit 3 (June–October 2000), and 243 farms at visit 4 (September 2000 to January 2001). At each visit, 20 pooled 50-g samples of freshly voided faeces were collected from nine defined sites, following a standardized sampling protocol to minimize variations between visits and between farms. Samples were bacteriologically cultured for Salmonella following a standardized method. Suspect Salmonella colonies were confirmed serologically and biochemically, and were serotyped and/or phage-typed.
Case farms were classified as those having a positive result for a particular Salmonella serovar from at least one sample on any of the visits. For optimum confidence that control farms were truly negative, all samples on all four visits were required to be negative (n=132). For the spatial analysis, information regarding the date of visit was ignored; the time element was included for an analysis of changes in infection status over time, and over space and time.
Statistical analysis
Spatial K-function
Spatial clustering of cases of each of the three Salmonella serovars in turn was assessed using a technique proposed by Diggle & Chetwynd [Reference Diggle and Chetwynd18], which allows estimation of the nature and physical scale of clustering, rather than just determination of the existence of any such effect. Their approach corrects for the underlying spatial variation in farm density by comparing case locations with the locations of a randomly selected group of controls from the population at risk, so that any apparent clustering of cases may be attributed to genuine spatial anomalies, rather than simply reflecting the underlying geographical population structure.
The data for analysis were the farm locations, with a farm labelled as a case if it had positive disease status, and as a control otherwise. Assessment of spatial clustering was then based on the second-order properties of the process, using the K-function,
where λ is the intensity, or mean number of events per unit area [Reference Ripley19]. The K-functions for cases and controls were evaluated at a set of equally spaced distances s k: k=1, …, m. The K-function was estimated using the khat( ) routine of the Splancs library [Reference Rowlingson and Diggle20] in R version 2.4.0 (http://www.r-project.org), which implements the estimator of Ripley [Reference Ripley19] given by
where t is the distance of interest, I( ) is an indicator of whether the distance d ij between point i and j is less than t, n is the number of points in the region, |A| is the area of the study region and w ij is the edge correction factor. This latter is necessary to allow for potential biases in studying distances between pairs of events, one or more of which lies close to the boundary of the study region. (For a detailed description of K-function estimation and the associated edge correction, see Diggle [21, pp. 50–51].)
Under the null hypothesis of no spatial clustering the cases and controls form independent random samples from the same underlying population at risk, in which case the K-functions of cases and controls are identical [Reference Diggle21]. Diggle & Chetwynd [Reference Diggle and Chetwynd18] therefore considered the function
where subscripts 1 and 0 correspond to case and control farms, respectively. Significantly positive values of the test statistic D(s) constitute evidence of spatial clustering above that explained by the underlying spatial distribution of at-risk farms. D(s) is therefore interpretable as excess clustering after this underlying spatial distribution has been taken into account. Diggle & Chetwynd [Reference Diggle and Chetwynd18] then proposed a formal test of significance for spatial clustering based upon the test statistic
which combines the information from the values of D(s k) over the m distances, and the variance is calculated under the null hypothesis of no spatial clustering. Statistical significance of an observed D can then be assessed using a Monte Carlo test. Under the null hypothesis, cases are a random sample from the superposition of cases and controls. The Monte Carlo procedure ranks the observed value D 1 of D from the data amongst values D 2, …, D r obtained from r−1 random permutations of the case and control labels under the null hypothesis. For D 1 ranking the kth largest, the exact P value is then given by k/r [Reference Diggle and Chetwynd18, Reference Barnard22, Reference Besag and Diggle23]. A priori, to balance the geographical scale of interest with the fact that the K-function is most effective at detecting small-scale spatial interaction, we set a maximum distance of interest of 30 km.
To correctly interpret the possible spatial clustering of Salmonella infection over the study period, the analysis was adjusted for the underlying distribution of farms sampled by comparing the spatial distribution of case farms to that of control farms. We initially conducted an analysis at the country level. With a single realization of a point process over a geographical scale of this magnitude, we acknowledge that the possibility cannot be excluded that any identifiable clustering is due to geographical heterogeneity alone. Accordingly, we conducted a subsidiary analysis of three internally homogeneous sub-regions to obtain supplementary evidence in favour of anomalous clustering (as opposed to purely geographical heterogeneity).
Allowing for temporal effects
As sampling of Salmonella spp. on the dairy farms was conducted during four sampling intervals over the 17-month study period, the evidence for a temporally varying prevalence over the study period was examined.
Let X K,T denote the disease status of farm K at visit T, and write P ij(t) for the probability that farm k moves from state i at time t−1 to state j at time t. Denote a positive (infected) farm status as 1, and a negative farm as 0. The sequence of test results for each farm can then be modelled using a two-state Markov Chain [Reference Cox and Miller24], defined by the 2×2 transition matrices
![P_{ij} \lpar t\rpar \equals {\rm Pr\lsqb }X_{k\comma t} \equals j\vert X_{k\comma t \minus \setnum{1}} \equals i{\rm \rsqb } \equals \left[ {\matrix{ {1 \minus P_{\setnum{01}} \lpar t\rpar } \tab {P_{\setnum{01}} \lpar t\rpar } \cr {P_{\setnum{10}} \lpar t\rpar } \tab {1 \minus P_{\setnum{10}} \lpar t\rpar } \cr} } \right].](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160921000156093-0261:S0950268808001349:S0950268808001349_eqnU5.gif?pub-status=live){kind=small}
Under this model, the likelihood of P ij(t) is given by
where n ij(t) denotes the number of transitions that occur from state i at visit (t−1) to state j at visit t. Conditioning on visit 1, the maximum-likelihood estimates (MLEs) for the transition probabilities 
ij(t) at t=2, 3 and 4 are ij(t)=[n ij(t)/n i(t)]. We compared the null hypothesis that no visit effect exists (equating to transition probabilities being temporally homogeneous, i.e. ij(t)=ij), with the alternative hypothesis of a visit effect [a separate ij(t) being required for each visit] using standard likelihood ratio tests (i.e. comparing twice the difference in likelihoods with a χ2 distribution on the appropriate degrees of freedom).
If there was evidence for a visit effect, a formal test was conducted to determine whether specification of separate transition probabilities for each visit was required, or whether a more parsimonious model would suffice. The number of parameters in the model was varied by adjusting the transition probability structure, resulting in different models; comparison of the outputs was again performed using likelihood ratio tests. First, the original model which assumed separate transition probabilities for positive to negative, and negative to positive at each visit (i.e. containing six parameters) was compared to the simplest model, which fitted two parameters (i.e. specified common negative to positive, and positive to negative transition probabilities at all visits). The six-parameter model was also compared to models which allowed for a seasonal effect, containing four parameters (common negative to positive, and positive to negative transition probabilities at visits 2 and 4, and different transition probabilities at visit 3) and three parameters (with a negative to positive transition probability that was the same at visits 2 and 4 and different at visit 3, and a common positive to negative transition probability).
Spatio-temporal analysis
After the examination of temporal relationships, we allowed for the presence of spatial effects. Specifically, we investigated whether farms which move from negative at time (t−1) to positive at time t were close to farms that were positive at time (t−1). A covariate x i was introduced as a measure of risk of infection from neighbouring farms, here defined as the number of farms that were positive for any serovar within a 25 km radius. The distance of 25 km was chosen to include both short- and middle-range spatial effects which may reflect first-order and second-order infections. This model, relating the transition probability 01(t) to the status of neighbouring farms, was fitted within the generalized linear model framework [Reference McCullagh and Nelder25]. The response Y i is a binary variable representing the disease status of farm i at time t conditional on the premises being negative at time (t−1), taking the value 1 if the farm is positive and 0 if negative. The model is written as
where t again denotes visit (2, 3 or 4) and x i the measure of risk from neighbouring farms calculated at visit (t−1). The estimated coefficients, α and β, represent the effects of visit and spatial risk respectively. The measure of spatial risk x i did not differentiate between serovars due to the small numbers in each group; however, the analysis was still of benefit in that clusters of farms which were infected in the same time period might be exposed to some common underlying risk factors.
To assess the effect of varying the neighbourhood definition, the spatial risk function was calculated at various distances and the effects on the residual deviance of the model and the exponents of the coefficient values were considered.
RESULTS
Spatial analysis
Of the 449 farms that were initially enrolled into the cohort study, Salmonella spp. were isolated from 159 farms on at least one occasion. The most common serovars identified were S. Agama (n=46 farms), S. Dublin (n=34) and S. Typhimurium (n=31). Detailed information on estimates of prevalence and incidence of Salmonella on the dairy farms can be found in Davison et al. [Reference Davison16]. There appeared to be a degree of spatial clustering of Salmonella infection during the study period (Fig. 1). S. Agama was seen only in Southern England, Wales and the Midlands whereas S. Dublin was found more commonly in Northern England, Wales and the Midlands. Clustering was not apparent for S. Typhimurium. Multivariable analysis showed a statistically significant association between region and Salmonella status [Reference Davison17].
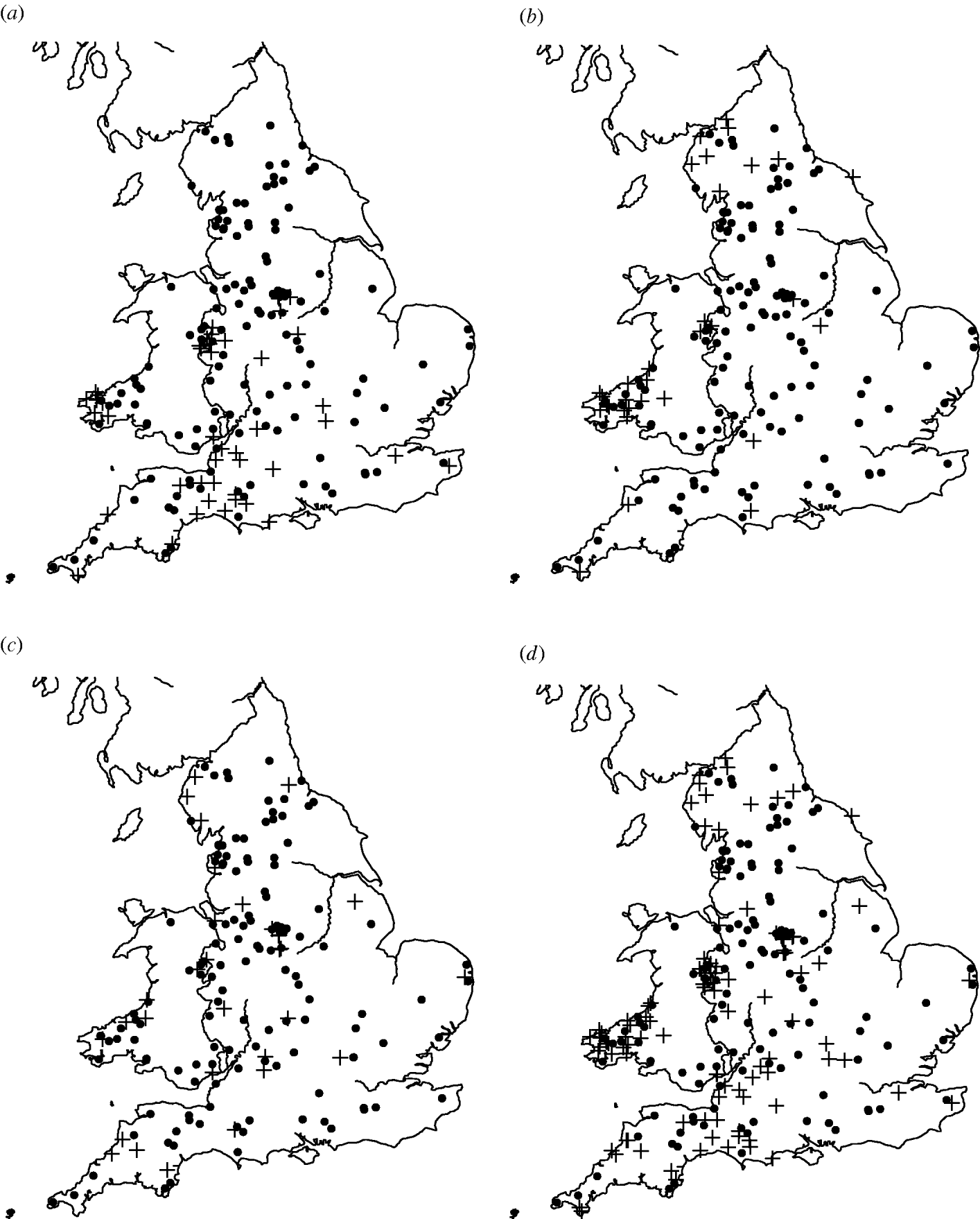
Fig. 1. Maps of England and Wales showing the dairy farms sampled and their (a) S. Agama status, (b) S. Dublin status, (c) S. Typhimurium status, (d) status for all three serovars combined. +, Case; •, control.
First, considering the countrywide analysis, Figure 2 shows D(s) for each serovar evaluated at distances s up to 30 km, together with approximate 95% tolerance limits 
constructed under the null hypothesis of no spatial heterogeneity of each of the three serotypes. Figure 2 provides evidence for spatial heterogeneity of S. Agama, S. Dublin and S. Typhimurium, having taken the underlying farm density into account, indicated by the departure of the function D(s) at a range of distances from 95% tolerance limits constructed under the null hypothesis of no excess clustering. This may suggest localized variation in the occurrence of each serotype. Formal Monte Carlo tests of the significance of spatial heterogeneity, using the statistic D which summarizes spatial heterogeneity across all scales studied, gave P values for S. Agama (P=0·001), S. Dublin (P=0·001) and S. Typhimurium (P=0·077). The first two of these provide significant evidence against the null hypothesis that the cases and controls are random samples from the same underlying population, and are suggestive of heterogeneity in the occurrence of these two serotypes over and above that which would be explained by the density of cattle farms alone. The evidence for heterogeneity of S. Typhimurium is marginal. The Monte Carlo P values are consistent with Figure 2: the smallest (most significant) P values are associated with S. Agama and S. Dublin, for which the departure from the 95% tolerance limits was most pronounced; in contrast, S. Typhimurium only deviated from the envelopes at small distances.
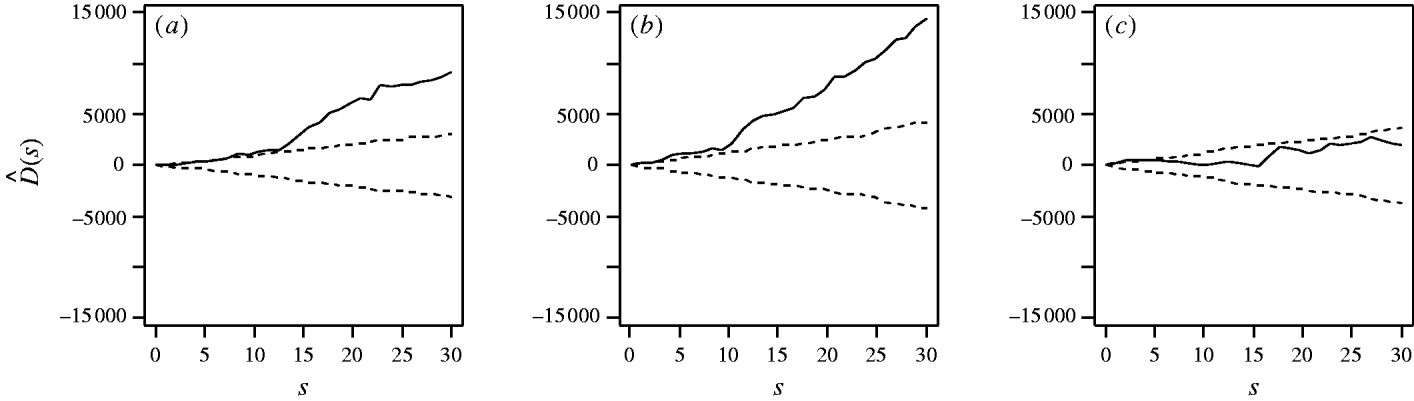
Fig. 2. Estimated excess risk attributable to spatial clustering, D(s) (––), and approximate 95% tolerance limits for D(s)=0 (– – –), calculated at distances s=1, …, 30 km for (a) S. Agama, (b) S. Dublin and (c) S. Typhimurium.
The function λD(s) estimates the expected number of cases (positive farms) within distance s of a reference case which are attributable to excess spatial clustering (Fig. 3). From Figure 3 it was seen that within 20 km of a case of S. Agama, a further 1·8 cases would be expected due to excess spatial clustering; within 20 km of a S. Dublin case, a further 1·7 cases; and within 20 km of a S. Typhimurium case, a further 0·3 cases (although the last of these was not statistically significant).
Fig. 3. Expected number of positive farms within distance s (km) of an arbitrary positive farm which were attributable to spatial clustering for (a) S. Agama, (b) S. Dublin (c) S. Typhimurium.
We subsequently estimated D(s) within three sub-regions of England and Wales: North West England (Cheshire and North Midlands), South West England (Devon and Cornwall), and Pembroke, Wales. The numbers of cases of each serotype in each region are shown in Table 1. Figure 4 shows the estimates of D(s) with approximate pointwise 95% tolerance limits (constructed as ±2 s.d.) under the null hypothesis of random labelling of cases and controls within each region. The final row of Figure 4 shows pooled estimates obtained as weighted averages over the three regions, with weights proportional to the numbers of cases shown in Table 1.
Fig. 4. Estimated excess risk attributable to spatial clustering, by region and pooled across regions. In each panel the solid line represents D(s) and the dotted lines approximate pointwise 95% tolerance limits under a null hypothesis of random labelling, within which D(s)=0. D(s) is evaluated at distances s=1, …, 30 km. (a)–(c) D-functions in the North West for S. Agama, S. Dublin and S. Typhimurium, respectively; (d)–(f) D-functions for these same serotypes in the South West; (g)–(i) D-functions for these serotypes in Pembroke; (j)–(l) the pooled D-functions for S. Agama, S.Dublin and S. Typhimurium, respectively.
Table 1. Numbers of cases of each serotype in each of three regions
For S. Dublin, the results show significant clustering in the North West (P=0·010), no significant departure from random labelling in the South West (P=0·696) and no evidence of clustering in Pembroke (P=0·258). The non-significant result in the South West is unsurprising as this region includes only four cases. The pooled estimate of D(s) shows significant clustering (P=0·010).
For S. Typhimurium the results are qualitatively similar: significant clustering in the North West (P=0·021), no significant departure from random labelling in either the South West (P=0·275) or Pembroke (P=0·571), where the numbers of cases are again small (5 and 4, respectively), and significant clustering in the pooled analysis (P=0·021).
For S. Agama, the results once more indicate clustering, significantly so in the North West (P=0·012), Pembroke (P=0·029) and pooled (P=0·001) analyses, whilst a non-significant result was observed in the South West (P=0·302).
In principle, the shapes of the estimated functions D(s) can indicate the nature and scale of the clustering [21, section 6.3.1]. However, in the present study their capacity to do so is limited by the relatively small numbers of cases, as is reflected in the widths of the tolerance intervals shown in Figure 4.
Temporal analysis
Comparison of outputs of the Markov Chain models indicated that the model incorporating different transition probabilities at all visits (i.e. six parameters) best represented the data: it had a significantly better fit than the simplest, two-parameter model (D=21·00, P=0·0003), as well as the intermediate models with four parameters (D=7·30, P=0·02) and three parameters (D=12·59, P=0·006).
Figure 5 shows the time-varying transition probabilities estimated via maximum likelihood (a) for a farm becoming infected with Salmonella (any serovar) and (b) for a farm returning to a negative Salmonella status. Considering all serovars together, the transition probabilities of negative to positive (and vice versa) were similar at visits 2 and 4. For visit 3 there was an increase in the chance of a farm becoming positive and a decrease in the likelihood of farms returning from a positive to negative status.
Fig. 5. Maximum-likelihood for transition probabilities divided into serovars: (a) probability of a farm moving from a negative to positive status, 01(t). (b) probability of a positive farm returning to a negative status, 10(t).
Stronger evidence for transmission dynamics ought to be obtained from serovar-specific analyses. When this was done, significant time inhomogeneity was found for new infections of S. Agama (P=0·026). There was, however, no evidence of time inhomogeneity for S. Dublin (P=0·230) or for S. Typhimurium (P=0·953). Lack of evidence for time inhomogeneity may in part be due to a lack of power induced by the reduced sample size (Table 2), and may also explain the large differences seen between serovars, particularly for P 10(t), shown in Figure 5.
Table 2. The number of farms with a new infection, and the number remaining negative from the previous visit, at visits 2–4
Values given are number (%).
Spatio-temporal analysis
Results of the generalized linear model relating the probability of a control farm becoming infected to the number of positive neighbouring farms within a 25 km radius, after adjustment for the temporal visit effect, are shown in Table 3. It can be seen that the estimated probability for a farm becoming positive at visit 2 (P=0·083) was very similar to the MLE of the transition probability from the earlier Markov Chain analysis considering all serovars together [01(2)=0·075] shown in Figure 5. The effects of visits 3 and 4 were different from the MLEs (0·198, 0·158), due to the spatial effect explaining a part of the residual deviance.
Table 3. Risk factors associated with a farm becoming positive for all Salmonella serovars
The effects of varying the neighbourhood distance on the residual deviance of the model and the exponents of the coefficient values are shown in Figure 6. Figure 6 a shows that the spatial risk function reduced the residual deviance by the greatest amount when neighbourhoods of 22–25 km and 35–40 km were used. Since the measure of risk was a cumulative count of infected farms over the distances defined, the peak between these two ranges was difficult to explain and may simply reflect random variation in the data.
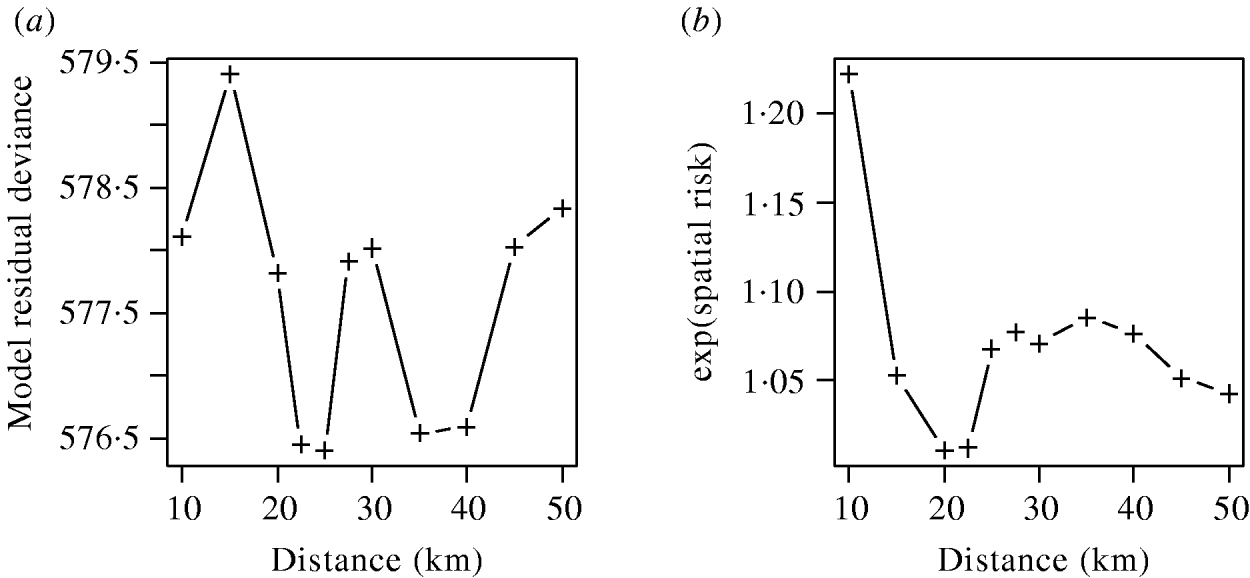
Fig. 6. (a) Residual deviance and (b) exponent of the coefficients value for the spatial risk function calculated from models including time element and spatial risk function calculated at varying distances.
The exponents of the estimated coefficients for the spatial risk function are shown in Figure 6 b where it was seen that the spatial risk was always >1, indicating that a farm was more likely to become positive if it had a positive neighbour at the previous visit. There was a general trend for the value to decrease as distance increased, albeit with a minimum around 20 km, which may again reflect random variation. Results from Figure 6 are suggestive of the underlying process of transmission, but given their borderline significance (P=0·065), should be interpreted with caution.
DISCUSSION
The study provided evidence for spatial clustering of S. Agama and S. Dublin at the country level, above that explained by variations in farm density and geographical distribution of cases. The results of the sub-regional analysis collectively demonstrate that all three serotypes show evidence of spatial clustering that cannot be attributed solely to regional scale variation in risk.
The temporal and spatio-temporal analysis provided further evidence for a higher than expected number of cases arising within a defined time period and distance. The temporal analysis indicated that the risk of a farm becoming infected with Salmonella was not constant over time and was higher during visit 3; note that this corresponded to samples being taken in the months of June–October, a time when certain Salmonella strains have been reported to be at their most prevalent [Reference Davison16]. Unfortunately, it was difficult to assign meaning to results of serovar-specific analysis due to the limited sample size. The spatio-temporal analysis suggested that at visits 3 and 4, a farm was more likely to become positive if there were more positive farms within 25 km of that farm at the time of the previous visit.
This clustering suggests evidence for either a contagious process (e.g. through direct or indirect farm-to-farm transmission) or for geographically localized environmental and/or farm factors which increase the risk of infection [Reference Graham26]. In support of the former, previous studies have demonstrated evidence for farm-to-farm spread of Salmonella serovars [Reference Wray, Davies, Wray and Wray3, Reference Wray27]. In terms of common risk factors, studies have suggested common sources for Salmonella infections in cattle, e.g. feed [Reference Anderson12, Reference Davis13], other animals (including birds [Reference Čížek28, Reference Fenlon29], rodents [Reference Daniels, Hutchings and Greig30], badger reservoirs [Reference Wilson11]), and environmental contamination [Reference Davies7, Reference Jones14].
These results emphasize the different epidemiology of the three Salmonella serovars. S. Agama and S. Dublin show similar behaviour in terms of the nature and scale of spatial clustering (Fig. 2 a, b), although their geographical distributions were clearly different. In contrast, S. Typhimurium was found throughout England and Wales, and with the current dataset does not demonstrate significant spatial clustering. This may in part be due to the known differences in the serovars: endemic and epidemic strains might be expected to behave differently in terms of virulence, host adaptation and survival in the environment. A recent study in The Netherlands estimated a higher basic reproduction ratio (R 0) for S. Dublin than for S. Typhimurium [Reference Van Schaik31]. This related to the higher probability that S. Dublin outbreaks led to more severe clinical signs and mortality, and resulted in persistence more often, than S. Typhimurium outbreaks. The reasons for the emergence and subsequent decline in the 1990s of the more virulent, epidemic S. Typhimurium DT104 strain have not yet been explained; the in vitro invasiveness of this strain does not appear to be greater than for other Salmonella strains. The results of the present study support a more epidemic pattern of behaviour of S. Typhimurium, although it must be borne in mind that S. Typhimurium generates the smallest dataset of the three serovars studied, and analyses for S. Typhimurium DT104 were not possible because of the small number of cases.
This study, although longitudinal in nature, spans just a short window in the full timescale of persistence of these serotypes in the population. It is therefore possible that any observed differences in the spatial and temporal properties are the result of sampling serotypes at different stages in their epidemic/endemic profiles, and that over a longer timescale they may be more similar. Such variations in the nature and extent of spatial and temporal clustering between different serotypes have been observed in other studies [Reference Sato10].
Possible biases in the design of the study were described in Pascoe [Reference Pascoe32] and Davison et al. [Reference Davison16]. The 449 dairy herds initially sampled at visit 1 were randomly selected through five large commercial milk companies which represented 63% of the dairy herds in England and Wales. Of these 449 farms, 272 were enrolled into the cohort study (out of 362 farms requested to continue) and sampled on up to three further occasions, and 243 farms were sampled at all four visits. To achieve a consistent sampling interval of about 3 months, farms which were sampled at visit 1 in October and early November (mostly one milk company) were excluded, and a potential association between milk company and farms recruited was therefore introduced. Pascoe [Reference Pascoe32] concludes that this potential bias was unlikely to have influenced results and states there had been no significant association between milk company and the outcomes of interest (a farm being positive or becoming positive). Moreover since the controls were taken from within the study population the conclusions reached should be valid and be applicable to all dairies in England and Wales that fulfil the study selection criteria.
The use of the K-function technique in detecting and describing spatial clustering has been used previously for sporadic cases of human disease [Reference Prince33]. The K-function approach is receiving increasing attention in veterinary epidemiology [Reference Wilson11, Reference O'Brien34]. In this application, the approach enables not only the use of D(s) to test the null hypothesis of no spatial clustering, but also estimation of the size and scale of the clustering present due to the novel interpretation of 
(s) as a scaled expectation. The Markov Chain approach presents a further example of the innovative application of a well-founded probabilistic technique within the veterinary epidemiology field. It provides an objective method for making inference from spatial-temporal disease surveillance data and, in particular, for assessing the evidence in favour of particular disease transmission mechanisms and underlying aetiologies.
ACKNOWLEDGEMENTS
The Veterinary Laboratories Agency are acknowledged for collecting and providing the data for the analysis, and Richard Smith (Centre for Epidemiology and Risk Analysis at VLA) for transfer of the data. Financial funding for this work, and the VLA data collection, was provided by the Department for Environment Food and Rural Affairs.
DECLARATION OF INTEREST
None.
