INTRODUCTION
The total potential global sea-level contribution from the West Antarctic Ice Sheet (WAIS) is ~4.3 m (Fretwell and others, Reference Fretwell2013), and recent work suggests that Antarctica could contribute 0.15–0.62 m of sea-level rise in the next century (Solomon and others, Reference Solomon2007; Pfeffer and others, Reference Pfeffer, Harper and O'Neel2008; Joughin and others, Reference Joughin, Smith and Holland2010, Reference Joughin, Smith and Medley2014; Gladstone and others, Reference Gladstone2012; Mouginot and others, Reference Mouginot, Rignot and Scheuchl2014). However, projections of the stability of the WAIS are hampered by the complexity of ice/ocean dynamics and uncertainty in the current and projected environmental changes (Joughin and Alley, Reference Joughin and Alley2011; Nowicki and others, Reference Nowicki2013). Here, we combine recent observations of ice thickness, basal topography and surface velocity (Rignot and others, Reference Rignot2008, Reference Rignot, Mouginot and Scheuchl2011; Fretwell and others, Reference Fretwell2013) with advances in theoretical understanding of ice-sheet-shelf/ocean interactions (Schoof, Reference Schoof2007; Gagliardini and others, Reference Gagliardini, Durand, Zwinger, Hindmarsh and Le Meur2010; Drouet and others, Reference Drouet2012) to gain perspective on the stability of the WAIS, using a numerical study of a shelf-terminating ice stream. The results are qualitatively extrapolated to determine implications for other WAIS ice streams.
In steady state, the flux of ice from the margins of an ice sheet is balanced by the accumulation rate integrated over the upstream catchment area. In reality, because an ice sheet is never truly in steady state, the mass balance is controlled mainly by changes in the activity of fast-flowing outlet glaciers and ice streams. These outlet glaciers respond to changing conditions at the grounding line, the transition between the grounded ice sheet and the floating ice shelf. The grounding line is, in turn, highly sensitive to changes in sea level and the melting/freezing of ice shelves. Because the ice shelves are confined by an embayment and may have some contact with the bed, they exert longitudinal compressive forces on the grounded ice that are greater than those expected from free-floating ice tongues. This additional compression, or buttressing, modifies the shape and flow of the upstream grounded ice (Alley and Whillans, Reference Alley and Whillans1991; Payne and others, Reference Payne, Vieli, Shepherd, Wingham and Rignot2004; Joughin and others, Reference Joughin, Smith and Holland2010; Pritchard and others, Reference Pritchard2012; Shepherd and others, Reference Shepherd2012).
Recent studies of the Thwaites and Pine Island glaciers in the Amundsen Sea sector indicate that present-day grounding line retreat is driven by ice-shelf melt and the associated decrease in buttressing (Joughin and others, Reference Joughin, Smith and Medley2014; Rignot and others, Reference Rignot, Mouginot, Morlighem, Seroussi and Scheuchl2014). In contrast, our research focuses on an ice stream with a very different basal topography and shelf buttressing, Foundation Ice Stream (FIS) in the Weddell Sea sector. We use a numerical model to test the sensitivity of the FIS's grounding line to changes in sea level, accumulation and shelf buttressing, then extrapolate these findings to make a qualitative evaluation of ice streams in other sectors of the WAIS.
MODEL
Schoof (Reference Schoof2007) provided an elegant theory for calculating the flux of ice across grounding lines. With several simplifying assumptions, the flux per unit width across a grounding line, q(x g), can be approximated by:
 $$\eqalign{q(x_{\rm g}) = & \left[ {\displaystyle{{\bar A{(\rho _{\rm i}g)}^{n + 1}{(1 - (\rho _{\rm i}/\rho _{\rm w}))}^n} \over {4^nC}}} \right]^{1/(m + 1)} \cr & \theta ^{n/(m + 1)}H_{\rm g}^{(m + n + 3)/(m + 1)} ,} $$
$$\eqalign{q(x_{\rm g}) = & \left[ {\displaystyle{{\bar A{(\rho _{\rm i}g)}^{n + 1}{(1 - (\rho _{\rm i}/\rho _{\rm w}))}^n} \over {4^nC}}} \right]^{1/(m + 1)} \cr & \theta ^{n/(m + 1)}H_{\rm g}^{(m + n + 3)/(m + 1)} ,} $$
where x is the distance along a flowline, ρ
i,w are the densities of ice and sea water, respectively, g is the acceleration due to gravity,
![]() $\bar A$
is the depth-averaged temperature-dependent rheological parameter in Glen's flow law and n is the corresponding exponent on the shear stress. C and m are parameters used to relate the basal shear stress and sliding speed: τ
b = C|u
b|
m−1
u
b, a formulation frequently used in ice-stream studies (Pattyn and others, Reference Pattyn2012). H
g is the ice thickness at the grounding line. Equation (1) implicitly includes the effect of an ice shelf, requiring both force- and mass-balance across the interface. The θ parameterizes the effects of ice-shelf buttressing on the longitudinal stress gradients, and varies between 0 (fully buttressed) and 1 (no buttressing). In reality, changes in buttressing depend on the evolution of the geometry of the surrounding ice shelf. While a single parameter, θ, cannot capture the complexities of the dynamic stresses that the shelf imposes on the grounded ice stream, it provides a simple way to describe the back stress from buttressing and the resultant modification of the flux of ice across the grounding line.
$\bar A$
is the depth-averaged temperature-dependent rheological parameter in Glen's flow law and n is the corresponding exponent on the shear stress. C and m are parameters used to relate the basal shear stress and sliding speed: τ
b = C|u
b|
m−1
u
b, a formulation frequently used in ice-stream studies (Pattyn and others, Reference Pattyn2012). H
g is the ice thickness at the grounding line. Equation (1) implicitly includes the effect of an ice shelf, requiring both force- and mass-balance across the interface. The θ parameterizes the effects of ice-shelf buttressing on the longitudinal stress gradients, and varies between 0 (fully buttressed) and 1 (no buttressing). In reality, changes in buttressing depend on the evolution of the geometry of the surrounding ice shelf. While a single parameter, θ, cannot capture the complexities of the dynamic stresses that the shelf imposes on the grounded ice stream, it provides a simple way to describe the back stress from buttressing and the resultant modification of the flux of ice across the grounding line.
Model parameters representing ice flow and sliding are not well constrained, but values of n = 3, and
![]() $\bar A = 10^{ - 25} \,{\rm s}^{ - 1} \,{\rm Pa}^{ - 3} $
(appropriate for depth-averaged temperatures of −20°C) are reasonable for ice streams (Cuffey and Paterson, Reference Cuffey and Paterson2010). Reported values for C vary by more than an order of magnitude, ranging from ~ 6 × 105 Pa s1/3 m−1/3 for the fast-flowing Siple Coast Ice Streams to 107 Pa s1/3 m−1/3 for basally resisted ice streams (Cuffey and Paterson, Reference Cuffey and Paterson2010). Values for the sliding parameter, m, range from 1/3 for ice that is resisted laterally, to 4 for basally resisted ice. For this range of m, the exponent on H
g varies from 2 to 4.75. Thus, in terms of fractional changes, q(x
g) is much more sensitive to H
g than to either buttressing (θ, exponent of 0.6–2.25) or flow and sliding parameters (A and C, exponent of 0.2–0.75).
$\bar A = 10^{ - 25} \,{\rm s}^{ - 1} \,{\rm Pa}^{ - 3} $
(appropriate for depth-averaged temperatures of −20°C) are reasonable for ice streams (Cuffey and Paterson, Reference Cuffey and Paterson2010). Reported values for C vary by more than an order of magnitude, ranging from ~ 6 × 105 Pa s1/3 m−1/3 for the fast-flowing Siple Coast Ice Streams to 107 Pa s1/3 m−1/3 for basally resisted ice streams (Cuffey and Paterson, Reference Cuffey and Paterson2010). Values for the sliding parameter, m, range from 1/3 for ice that is resisted laterally, to 4 for basally resisted ice. For this range of m, the exponent on H
g varies from 2 to 4.75. Thus, in terms of fractional changes, q(x
g) is much more sensitive to H
g than to either buttressing (θ, exponent of 0.6–2.25) or flow and sliding parameters (A and C, exponent of 0.2–0.75).
For simplicity, hereafter we adopt a value of m = 1/3 for the entire model domain; higher values of m increase the importance of H g relative to other variables, making 1/3 a conservative choice for sensitivity tests. Equation (1) has been used for several modeling experiments (Pollard and DeConto, Reference Pollard and DeConto2009; Docquier and others, Reference Docquier, Perichon and Pattyn2011), and is broadly supported by comparisons with numerical models with idealized geometries (Pattyn and others, Reference Pattyn2012). The power law dependence on H g in Eqn (1) also has a similar exponent to earlier theoretical work (Lingle, Reference Lingle1984).
Assuming hydrostatic equilibrium at the grounding line, the dominant term H g is:
where z
b is the bed elevation above sea level. Together, Eqns (1) and (2) suggest that
![]() $q(x_{\rm g} ){\rm \sim} z_{\rm b}^{2\,{\rm to}\,5} $
. The acute sensitivity of the flux to changes of z
b emphasizes the importance of basal topography in the vicinity of the grounding line as a first-order control on discharge from the ice sheet. The importance of basal topography (in particular for marine ice sheets where the bed deepens inland) has been widely recognized (Weertman, Reference Weertman1974; Lingle, Reference Lingle1984; Schoof, Reference Schoof2007; Cofaigh and others, Reference Cofaigh, Dowdeswell, Evans and Larter2008; Pollard and DeConto, Reference Pollard and DeConto2009; Joughin and others, Reference Joughin, Smith and Medley2014).
$q(x_{\rm g} ){\rm \sim} z_{\rm b}^{2\,{\rm to}\,5} $
. The acute sensitivity of the flux to changes of z
b emphasizes the importance of basal topography in the vicinity of the grounding line as a first-order control on discharge from the ice sheet. The importance of basal topography (in particular for marine ice sheets where the bed deepens inland) has been widely recognized (Weertman, Reference Weertman1974; Lingle, Reference Lingle1984; Schoof, Reference Schoof2007; Cofaigh and others, Reference Cofaigh, Dowdeswell, Evans and Larter2008; Pollard and DeConto, Reference Pollard and DeConto2009; Joughin and others, Reference Joughin, Smith and Medley2014).
We first investigate the sensitivity of the grounding line of FIS in the Weddell Sea sector to changes in accumulation rate, sea level and buttressing at the grounding line, then discuss the implications for other outlet glaciers and ice streams. The grounding line is the location where the ice flux equals q(x g) in Eqn (1). The ice flux is the upstream integral of the present-day accumulation, here obtained from a regional climate model (Le Brocq and others, Reference Le Brocq, Payne and Vieli2010). We calculate the ice-stream profile upstream of the grounding line using a dynamic 1.5-D flowband model (Eqn (A1) in Appendix). The grounding-line position, our main focus here, does not depend on the details of the upstream ice flow model, only on Eqn (1) and the specified accumulation. Our sensitivity experiments show that the grounding-line physics exert strong control on the advance and retreat of the ice stream.
The upper catchment of FIS is located in East Antarctica, but the ice stream flows through West Antarctica and discharges into the Filchner-Ronne Ice Shelf (Fig. 1). Like many of the ice streams in the Weddell Sea sector, the grounding line of the FIS lies in a deep (up to 1900 m below sea level) trench, which extends around the embayment and shoals gently out to the edge of the continental shelf (Ross and others, Reference Ross2012; Fretwell and others, Reference Fretwell2013). Basal relief just inland of the FIS grounding line rises 1400 m over 150 km (Fig. 2). Values for the sliding law C (8.0 × 106 Pa s1/3 m−(1/3)) and θ = 0.2 were chosen to match the modern surface elevation profile and grounding-line position, respectively. Tuning θ and C in this way assumes that the ice stream is now in equilibrium, which is consistent with recent results from cosmogenic exposure-age dating that indicate the ice stream has not thinned significantly over the past 4000 ka (Balco and others, Reference Balco2016). Model velocities vary from 0 near the divide to more than 500 m a−1 near the grounding line (consistent with observations, Rignot and others (Reference Rignot, Mouginot and Scheuchl2011)), where the assumption of plug-like sliding, rather than internal shearing deformation, accounts for more than 80% of the ice flux. Figure 2 shows that the mismatch between the modeled and observed present-day profile and the grounding-line position is small; any differences are likely due to spatial variations in bed conditions and ice flow parameters, or the three-dimensional effects that are unaccounted for in our model.

Fig. 1. Major West Antarctic ice-stream catchment areas, outlined in black (data from personal communication from I. Joughin). A characteristic flowline for each catchment area (from Byrd Polar Research Center, 1997) is overlain on Antarctica's bed elevation (Fretwell and others, Reference Fretwell2013). Red flowlines drain to the Weddell Sea, purple to the Amundsen Sea and blue to the Ross Sea. The flowline routing beyond the present-day ice-shelf extent is drawn as a continuation of the flowline. Brown colors indicate elevations above the present-day sea level, and blue colors indicate elevations below sea level. Transition from solid to pixelated area marks the edge of the continental shelf.
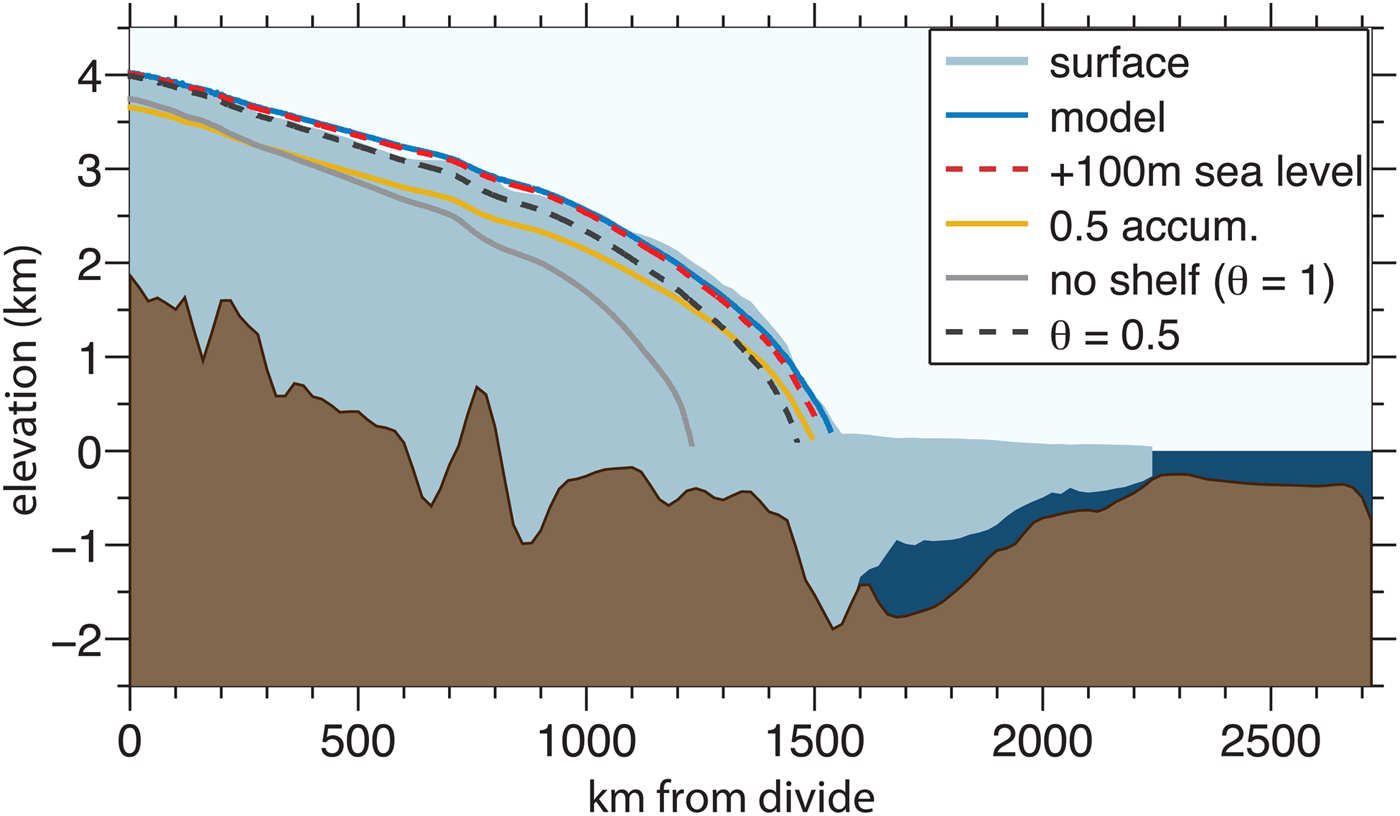
Fig. 2. FIS profile and model results. The FIS flowline from Figure 1 is interpolated onto BEDMAP2 surface elevation, bed elevation and thickness data (Fretwell and others, Reference Fretwell2013), with the profile shown in solid colors. The bed topography has been smoothed for visual clarity, but was kept at a 1 km grid spacing for the model runs. The blue curve shows the initial steady-state model profile (C = 8 × 106 Pa s1/3 m−1/3, θ = 0.2). The other curves show new steady-state profiles, under different environmental constraints: for sea-level rise of 100 m (red dashed curve); half of the present-day accumulation (yellow curve); no ice-shelf buttressing (θ = 1) (solid gray curve); and partial buttressing (θ = 0.5) (dashed black curve).
RESULTS: FIS
In all experiments,
![]() $\bar A$
, C and m are kept constant. Results are for steady-state conditions; we do not show transient states, though internal variability and hysteresis may explain some ice stream behavior (Robel and others, Reference Robel, DeGiuli, Schoof and Tziperman2013). Elevations throughout the text are referenced to the modern sea level. We do not correct for isostatic response or local gravitational effects (Gomez and others, Reference Gomez, Mitrovica, Huybers and Clark2010), both of which would tend to reduce grounding-line changes (and so our estimates are thus upper bounds in this regard), but neither would change the relative importance of different climatic factors.
$\bar A$
, C and m are kept constant. Results are for steady-state conditions; we do not show transient states, though internal variability and hysteresis may explain some ice stream behavior (Robel and others, Reference Robel, DeGiuli, Schoof and Tziperman2013). Elevations throughout the text are referenced to the modern sea level. We do not correct for isostatic response or local gravitational effects (Gomez and others, Reference Gomez, Mitrovica, Huybers and Clark2010), both of which would tend to reduce grounding-line changes (and so our estimates are thus upper bounds in this regard), but neither would change the relative importance of different climatic factors.
We caution that the calculations are not intended as projections or recreations of historical grounding-line positions and upstream ice profiles; parametrizations of deformation and sliding are uncertain and full thermomechanical details are not included. Rather, our results are a quantitative demonstration of the physical principles embodied in Eqns (1), (2), (A1) and (A2).
First, we consider forcings that would cause the grounding line of the FIS to retreat. An unrealistically large sea-level increase of 100 m requires grounding-line retreat of only 5 km to restore balance (Fig. 2, dashed red line). The steep basal topography inland of the grounding line can accommodate this change over relatively short horizontal scales, and is accompanied by very little change in ice thickness.
Halving the upstream accumulation rate is balanced by a grounding-line retreat of only ~18 km (Fig. 2, yellow line). In contrast to sea-level rise, the reduced accumulation causes interior thinning that averages 180 m over the domain of the grounded ice.
Complete removal of buttressing (setting θ = 1 in Eqn (1)) causes the largest change. The grounding line retreats ~300 km before re-stabilizing near the edge of the trench, and the interior thins, reducing the volume of ice by 28% (Fig. 2, dark gray line). Smaller changes in buttressing have less effect – setting θ = 0.5 causes the grounding line to retreat by only 75 km, with an ice-volume loss of ~5% (Fig. 2, dashed black line).
We now turn to the factors that might cause an advance of FIS. Because the FIS's grounding line presently lies in the deepest part of its domain, an increase in the flux cannot be accommodated by an advance in the grounding line due to the shallowing topography (Eqn (1)). Lowering the sea level by only 23 m (well above the Last Glacial Maximum (LGM) sea level) or increasing the accumulation uniformly by 6% results in a grounding line advance to the edge of the continental shelf. Although model uncertainties are high, this highlights how complex grounding-line dynamics might produce counter-intuitive consequences to environmental change. They serve as a quantitative demonstration of the physical principle embodied in Eqn (1): that a large forcing is necessary to induce retreat from the trench in which the present-day grounding line resides, but a relatively small forcing is sufficient to advance the grounding line on a long, reverse-slope bed.
The location of the FIS grounding line is key to its current stability with respect to retreat. Because the upstream gradient of the bed is so steep, relatively small changes in the grounding-line position can accommodate large changes in ice flux. While the modern FIS geometry suggests it is stable to retreat, we note that the long reverse-slope seaward of the present-day grounding line cannot sustain a stable grounding-line position, implying that the FIS is relatively unstable to advances, and that during glacial periods the grounding line could readily push well beyond its present location, advancing to the edge of the continental shelf. This theoretical argument for a significant advancement during the last glacial period is corroborated by marine-geological evidence (Hillenbrand and others, Reference Hillenbrand, Melles, Kuhn and Larter2012), and other modeling efforts (Stolldorf and others, Reference Stolldorf, Schenke and Anderson2012; Whitehouse and others, Reference Whitehouse, Bentley and Le Brocq2012) and by glacial geological data from the Williams Hills 50 km upstream from the grounding line that show the ice stream there was 500 m thicker during the LGM (Balco and others, Reference Balco2016). However, our model cannot establish for how long such an advance would be stable; for instance, the added ice volume would further depress the bed, raising relative sea level higher and mitigating runaway advance. Moreover, the redistribution of ice shelves would impact buttressing, an effect that is also omitted here.
APPLICATION TO OTHER ICE STREAMS AND SECTORS
The analyses from the previous section underscore the predominant importance of basal topography for grounding-line sensitivity, and motivate exploring the potential implications for the sensitivity of other ice streams. It should be emphasized that such an evaluation is only a qualitative interpretation.
FIS's position in a deep trench is characteristic of several other outlets. Many of the other ice streams that flow into the Ronne-Filchner Ice Shelf are also grounded within the deep asymmetrical trench that rings the Weddell Sea embayment. Support-Force, Recovery, Rutford, and Evans Ice Streams all have beds that rise steeply inland immediately behind the present-day position of the grounding line (Figs 1, 3b, c, h, i), implying that they are also stable to plausible future sea-level rise or decreases in shelf buttressing. Moreover, with the exception of Recovery Ice Stream, the bed generally shoals toward the continental shelf, indicating the potential for expansion of the ice sheet when sea level lowered during glacial periods. The grounding lines of Slessor, Bailey, Möller and Institute Ice Streams (Figs 1, 3d, e, f, g) lie just beyond the deep trench. For these ice streams, a relatively small external forcing may cause an initial grounding retreat on the order of ~100 km, but stability would be re-acquired in the deep trenches. Note that Slessor Ice Stream is currently grounded on a reverse slope; this potentially unstable position implies a more complex role for buttressing than is represented by Eqn (1). One possibility is lateral communication of buttressing between adjacent ice streams through thickness changes on lightly grounded ice plains, as inferred by Hulbe and Fahnestock (Reference Hulbe and Fahnestock2007).

Fig. 3. Weddell Sea sector (red, a–i), Ross Sea sector (blue, j–n) and Amundsen Sea sector (yellow, o, p), ice-stream and bed profiles, from Figure 1, interpolated onto the BEDMAP2 surface elevation, bed elevation and thickness data (Fretwell and others, Reference Fretwell2013).
In contrast, the variations in basal topography beneath the ice streams in the Ross Sea sector are small (Figs 1, 3j–n). Over regional scales (a few hundred kilometers), the ice streams are grounded on gentle reverse slopes that extend in both directions from the current grounding line. The large-scale basal topography suggests that both advances and retreats would be determined by the complex interplay of basal topography, external forcing factors and influence from adjacent ice streams, mediated by ice-shelf buttressing and competition for upstream catchment area. Further, thermomechanical feedbacks that control basal sliding of the Ross Ice Streams (Raymond, Reference Raymond1996) may lead to stagnation and reactivation of flow over century scales (Hulbe and Fahnestock, Reference Hulbe and Fahnestock2007; Robel and others, Reference Robel, DeGiuli, Schoof and Tziperman2013) and even switches of flow direction (Conway and others, Reference Conway2002), adding complexity to projections of future behaviors. In addition, small-scale sea mounts and lateral buttressing from interstream ridges along the Siple Coast influence grounding-line advance and retreat (Gagliardini and others, Reference Gagliardini, Durand, Zwinger, Hindmarsh and Le Meur2010; Drouet and others, Reference Drouet2012).
The Amundsen Sea sector is currently well out of balance (−64 Gt a−1, Rignot and others (Reference Rignot2008)). Further, the current grounding lines of Thwaites and Pine Island Glaciers are positioned at the edge of an overdeepening that extends below sea level more than 400 km inland (Figs 1, 3o, p). If the current rates of melting and disintegration of surrounding ice shelves continues (Pritchard and others, Reference Pritchard2012), the glaciers could retreat more than 300 km inland, perhaps temporarily held up at numerous small bedrock bumps.
CONCLUSIONS
Quantitative projections of the future of the WAIS and a detailed understanding of past changes are hampered by uncertainties relating to the complex interactions in the ice, ocean and atmospheric dynamics in the region. Key factors are ice-sliding rheology, buttressing and isostatic response. It is yet to be established whether such projections and reconstructions are a tractable goal. While accurate predictions may remain elusive, the robust physical constraints embodied in Eqn (1), together with new bedrock data, can provide insight into relative stability of the ice streams in the Weddell, Amundsen and Ross Sea sectors of Antarctica to the same environmental forcing.
The focus in this study has been the acute functional sensitivity of the grounding-line flux to basal topography (
![]() $q(x_{\rm g} ){\rm \sim} z_{\rm b}^{2\,{\rm to}\,5} $
). This implies that ice streams like FIS that are grounded in bathymetric trenches may be quite stable to retreat, but relatively unstable to advance. It also implies that even small topographic ridges can locally anchor grounding lines, even if the larger scale topography is a reverse slope (Schoof, Reference Schoof2007). Our evaluation reaffirms that the greatest concerns for WAIS retreat are locations of reverse slopes, muted basal topography and limited lateral support.
$q(x_{\rm g} ){\rm \sim} z_{\rm b}^{2\,{\rm to}\,5} $
). This implies that ice streams like FIS that are grounded in bathymetric trenches may be quite stable to retreat, but relatively unstable to advance. It also implies that even small topographic ridges can locally anchor grounding lines, even if the larger scale topography is a reverse slope (Schoof, Reference Schoof2007). Our evaluation reaffirms that the greatest concerns for WAIS retreat are locations of reverse slopes, muted basal topography and limited lateral support.
SUPPLEMENTARY MATERIAL
The supplementary material for this article can be found at https://doi.org/10.1017/aog.2017.9.
ACKNOWLEDGEMENTS
Funding was provided by the US National Science Foundation (ANT-083783, ANT-0838784, and ANT-0838256). We thank Greg Balco, Claire Todd, Seth Campbell and Ed Waddington for thoughtful discussions and insights. We also thank Raytheon Polar Services, Ken Borek Air, UNAVCO and the New York Air National Guard, for logistical support in Antarctica.





