Introduction

Most large glaciers in the Nepal Himalaya have ablation areas covered with debris. In contrast with debris-free glaciers, which are rather small, debris-covered glaciers several kilometers long are unique landscapes in the glaciated area. The change or evolution of these glaciers is of great interest and importance for water resources, as well as for tourism, particularly for assessing the effect of global warming on runoff in Himalayan catchments.

The melt rate of glacier ice underneath a supraglacial debris layer is rather small and it is difficult to detect changes to such glaciers by short-term observations. It is also relatively dangerous and difficult to carry out field observations because many big boulders are distributed over steep sloping surfaces and the debris thickness varies tremendously from place to place. Previous studies on debris- covered glaciers are hence very limited.

This paper discusses changes in a debris-covered glacier based on an estimate of the ablation rate underneath the debris layer using a heat-budget approach, and of the velocity distribution derived from analysis of satellite data.

Previous Work

Khumbu Glacier, a typical debris-covered glacier more than 15 km long, drains mainly from the West Cwm between Mts Everest (Mt. Sagarmatha or Mt. Qomolangma), Lhotse and Nuptse in eastern Nepal. The elevation of the apparent terminus is about 4900 m a.s.l. The glacier has attracted much attention because it is located along a route to the highest peak of the world. The amount of information on the glacier is therefore large compared to other debris-covered glaciers.

Figure 1 shows a satellite image of the lower half of the glacier, covering the ablation area. West Cwm, the main accumulation basin lies to the east, and the glacier flows to the ablation area through an icefall just above Everest Base Camp (EBC; 5300 m a.s.l.), where bare ice is exposed. The equilibrium line is just above EBC. There are many ice pinnacles up to 10 m high which extend downstream 2–3 km below EBC. In the middle of the pinnacle zone, there is a transverse debris layer formed by a big landslide event, according to local people. Along the center-line of the glacier, supraglacial debris appears at the end of the pinnacle zone, increasing its thickness downstream (Reference Nakawo, Iwata, Watanabe and YbshidaNakawo and others, 1986). The debris consists of schistic rocks around the pinnacle zone and for a few kilometers downstream, but becomes granitic further downstream (Reference Fushimi, Yoshida, Watanabe and UpadhyayFushimi and others, 1980). The topographical characteristics of the glacier surface have been reported by Reference Iwata, Watanabe and FushimiIwata and others (1980) and Reference Watanabe, Iwata and FushimiWatanabe and others (1986). Ice thickness was estimated by Reference Kodama and MaeKodama and Mae (1976) from surface velocity, and by Reference Higuchi, Mae and KodamaHiguchi and others (1978) with an empirical equation. A direct measurement was made by Reference MoribayashiMoribayashi (1978) using gravimetry.

Fig. 1. Satellite multi-spectral image of Khumbu Glacier (SPOT HRV) taken 7 November 1995 (Scene ID: 3 227294, 04:52:301 xs). The pinnacle zone appears white extending downstream from Everest Base Camp (EBC) near the center of the glacier.

Based on structural observations (Reference FushimiFushimi, 1977), the active terminus was considered to be about 3 km upstream from the apparent one, with a dead ice body in between. The velocity of the glacier has been measured by triangulation (Reference MüllerMüller, 1968; Reference Kodama and MaeKodama and Mae, 1976) at several upstream sites. Recently, Reference Seko, Yabuki, Nakawo, Sakai, Kadota and YamadaSeko and others (1998) obtained the velocity around EBC and the pinnacle zone by analyzing satellite images, and found, in comparison with previous results, that the velocity was decreasing.

The ablation rate observed by Reference MüllerMüller (1968) was 0.020–03 m d^-1 1at sites with bare ice surface and/or with very thin debris cover. Reference Inoue and YbshidaInoue and Yoshida (1980) reported an average ablation rate of about 0.02 m d^-1, a similar value to Müller’s, obtained at similar sites. They measured the ablation rate under a 1.2 m thick debris cover as well, and found it to be about 0.0015 m d^-1, smaller by one order of magnitude. Although they noted much higher ablation at ice cliffs with thick debris, which generally surround supraglacial lakes in the area, they estimated an average ablation rate of 0.0020–004 m d^-1 where thick debris cover was present.

Analysis of Satellite Data

Ablation

The heat balance equation at the debris surface is given by

(1)

where C, F, H and E are conductive heat flux into the debris, radiation flux, sensible heat flux and latent heat flux, respectively. The values of F, H and E can be estimated with conventional equations using global radiation, air temperature, humidity, wind speed and cloud amount data, if surface temperature T _s is known (Reference Nakawo and YoungNakawo and Young, 1981; 1982). Assuming a linear temperature gradient in the debris layer and 0°C at the debris-ice interface, C is given by

(2)

where T_s is in °C and R is the thermal resistance of the debris layer, defined as debris thickness divided by the thermal conductivity. The value for R can be estimated by combining Equations (1) and (2). Once R is known, the conductive heat flux C, for ice ablation for different periods, can be calculated by the same equations with meteorological data alone; without knowing T_s , since R can be regarded as constant at a site for a rather long time. This method for estimating ablation rate under a debris layer, proposed by Reference Nakawo, Morohoshi and UeharaNakawo and others (1993), was tested successfully for Lirung Glacier, Nepal Himalaya, by Reference RanaRana and others (1997), who estimated the surface temperature using satellite thermal-band data (e.g. Reference Hall, Ormsby, Bindschadler and SiddalingaiahHall and others, 1987).

Figure 2 shows the longitudinal distribution of the surface temperature of the debris layer along the center-line of Khumbu Glacier derived from satellite thermal imagery (Landsat TM band 6, 12 April 1988). Unfortunately, the midstream of the glacier was covered with a small patch of cloud which caused the low temperatures found 3.5-6 km from EBC. The linear interpolation is shown with a dotted line (Fig. 2) and the result used in the following calculation.

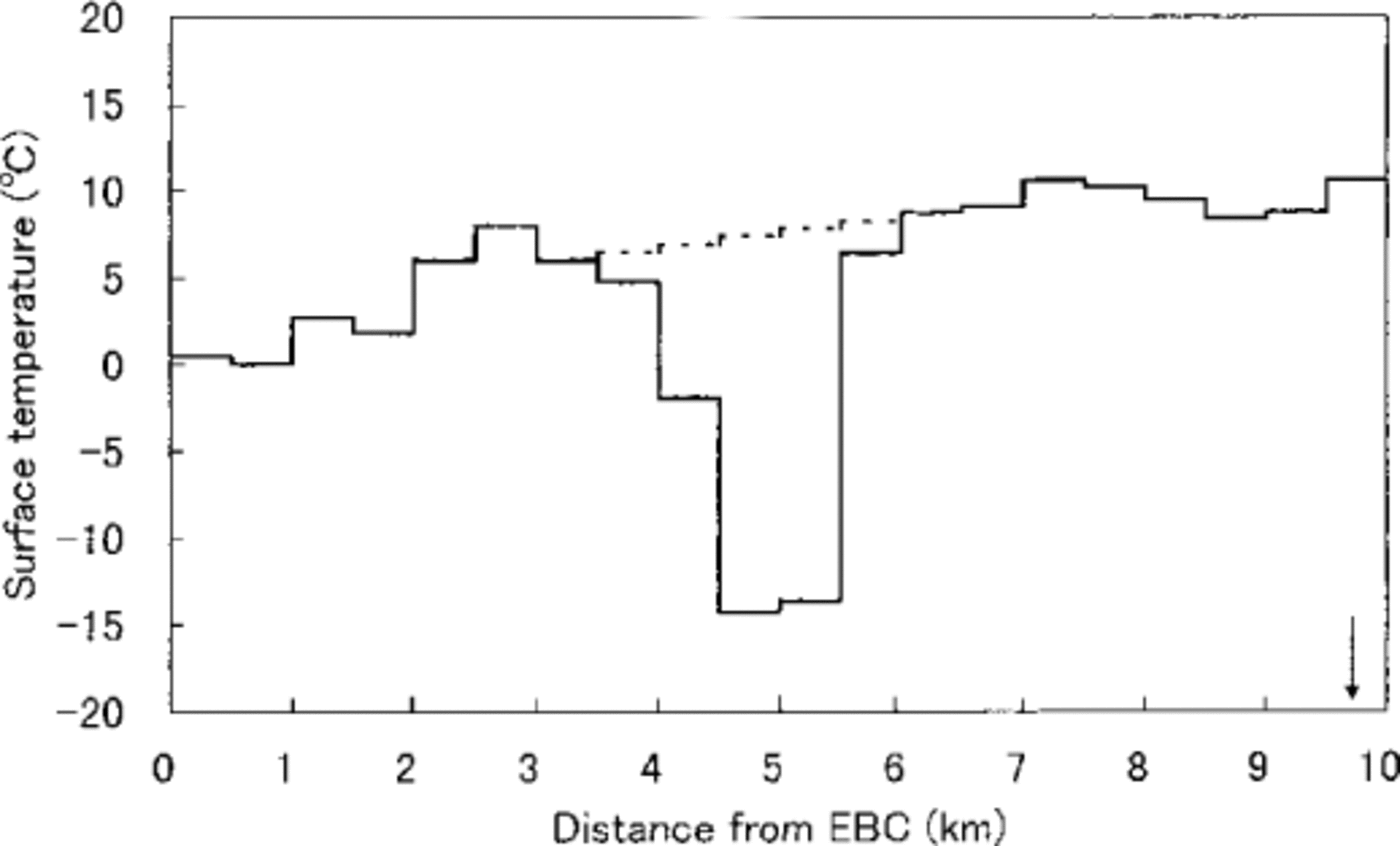
Fig. 2. Surface temperature averaged for every 0.5 km interval (TM Band 6 of Landsat, 12 April 1988). Dotted line indicates interpolation for area shaded by cloud cover. Arrow shows apparent terminus of the glacier.

The surface temperature was close to 0°C near EBC, where bare ice was exposed or there was a very thin debris layer, increasing gradually toward the terminus with a small peak at the 2.5-3 km range. This peak corresponded with a transverse debris band separating the pinnacle zone into two (Fig. 1). The spatial pattern of surface temperature reflects the distribution of thermal resistance of the debris layer, which is roughly proportional to the debris thickness. The thickness increases with the distance from EBC (Reference Nakawo, Iwata, Watanabe and YbshidaNakawo and others, 1986). There is an area with relatively lower temperature 8-9.5 km from EBC, where paradoxically the debris thickness was considered to be very large. It was observed in the field that the debris of the terminal area was partly covered with vegetation and rather fine soil particles. During in situ observations, it seemed to be wetter than the other sites of the debris. The lower temperature could be caused by reduced latent heat associated with evapotranspiration from the surface, which would be much more intense than where the debris surface appeared to be dry.

The thermal resistance along the center-line of the ablation area was estimated by Equations (1) and (2), for which unpublished meteorological data, measured by the Glaciological Expedition in Nepal (GEN) from 1973 to 1976 (Reference HiguchiHiguchi, 1993), was used. It was assumed in the estimation that meteorological conditions at the time of satellite data retrieval were the same as those averaged for the same time in the same season in different years, since no data were available for that particular time. Based on the distribution of thermal resistance R, ablation under the debris layer was calculated for one year. Meteorological data were taken from limited data given by the Nepal Department of Hydrology and Meteorology (DHM, 1993), Reference InoueInoue (1976) and unpublished data by GEN, since no consistent continuous data covering one full year are available. In the calculation, latent-heat flux was neglected since the debris surface is mostly dry. Different albedo values were used: 0.5 for bare ice; 0.1 for schistic debris; 0.2 for granitic debris.

The longitudinal distribution of thermal resistance and annual ablation along the center-line are shown with a solid line in Figures 3 and 4, respectively. The annual ablation is very low near EBC, but increases downstream, having a maximum value of about 5 m 3.5–4 km from EBC, then decreases towards the terminus. Near the terminus, another peak can be seen which is probably caused by neglecting the latent-heat flux, since the area was rather wet in contrast to the other area. Re-calculation of thermal resistance, as well as ablation rate, taking into account the latent-heat flux, resulted in the dotted line shown in the figures. Thermal resistance increases gradually toward the terminus. The ablation rate roughly agrees with both the observations by Reference MüllerMüller (1968) and Reference Inoue and YbshidaInoue and Yoshida (1980).

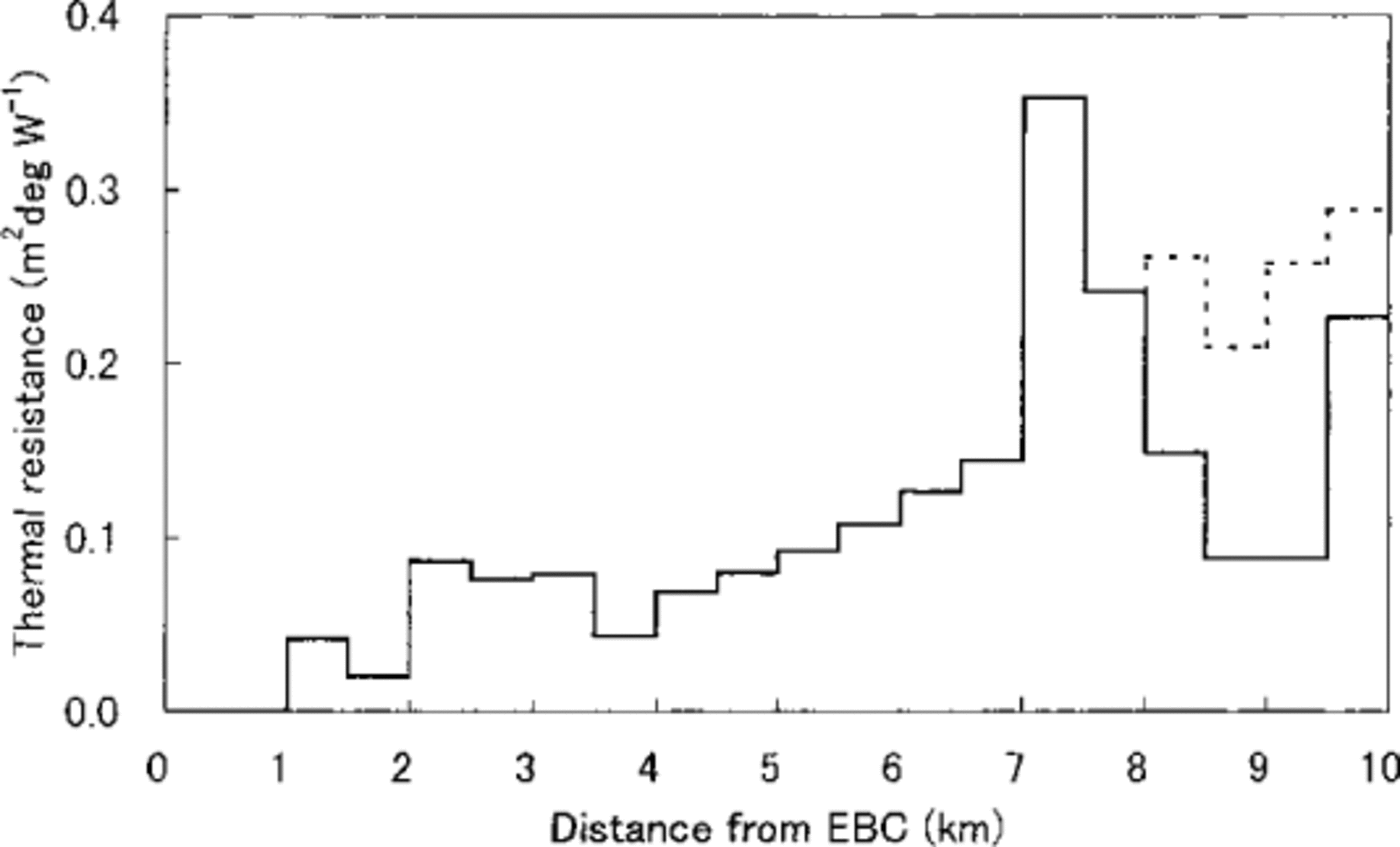
Fig. 3. Thermal resistance for every 0.5 km interval. Solid line shows calculation neglecting latent-heat flux. Dotted line that when latent-heat flux in wet areas is accounted for.

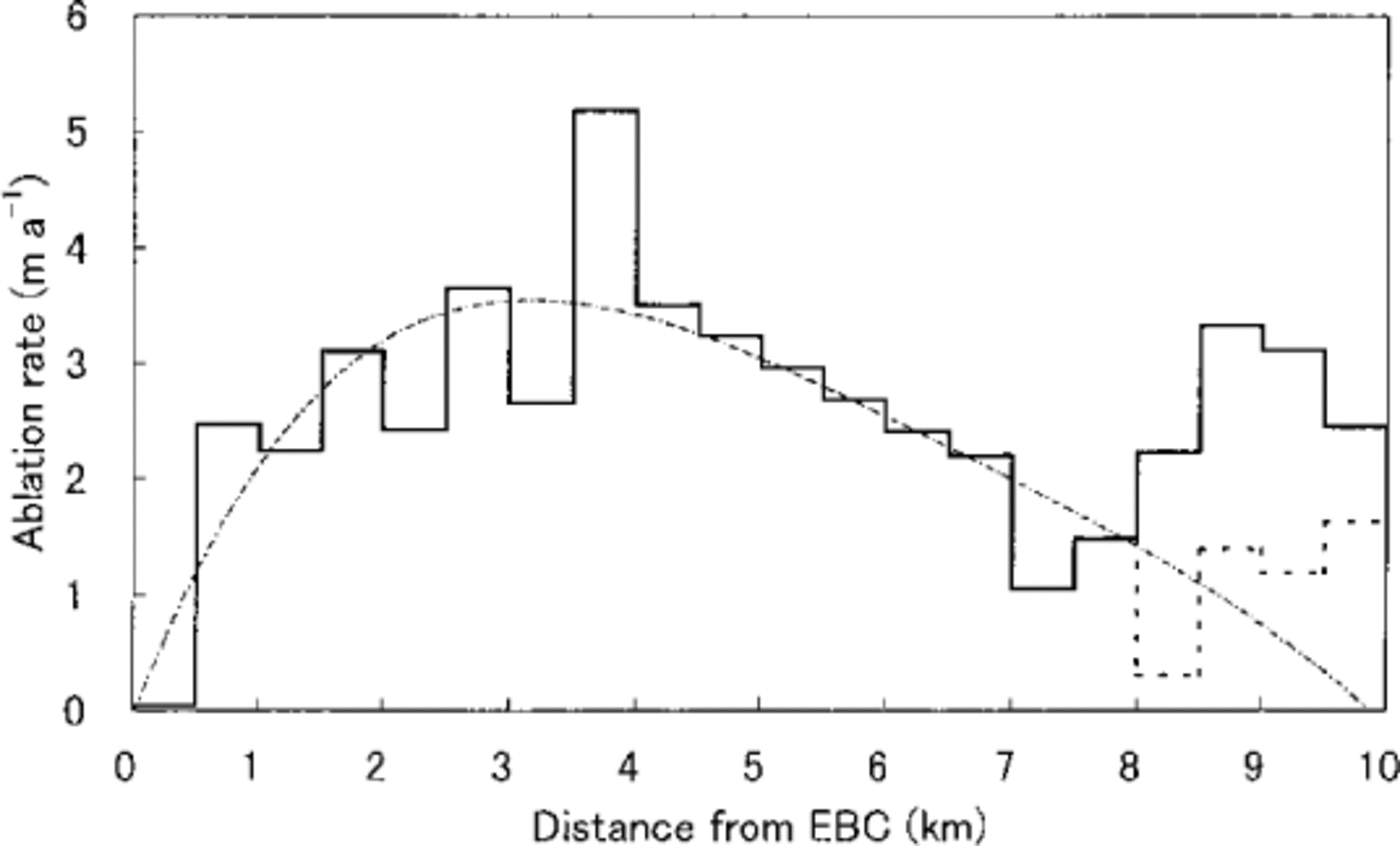
Fig. 4. Annual ablation estimated for every 0.5 km interval. Solid line shows calculation neglecting latent-heat flux. Dotted line that when latent-heat flux in wet areas is accounted for. The approximation of the profile is shown with the dash-and-dot line which is used for further calculation.

Ice flow

Various surface micromorphologies were identified over the ablation area of the glacier on SPOT (systeme probatoire pour l’observation de la terre) HRV (high resolution visual) panchromatic images (10 m spatial resolution, 19 January 1987 and 9 November 1993). By comparing the location of the same feature in two images, the distribution of the surface velocity was estimated. In the process, a different feature may be misread as the same feature when comparing the two images. Hence, flow vectors whose direction differed from that of the center-line of the glacier by more than 30 degrees were discarded; this accounted for roughly one- third of the data. Among the flow vectors obtained, those near the center-line of the glacier were selected and are presented in Figure 5 with dark spots.

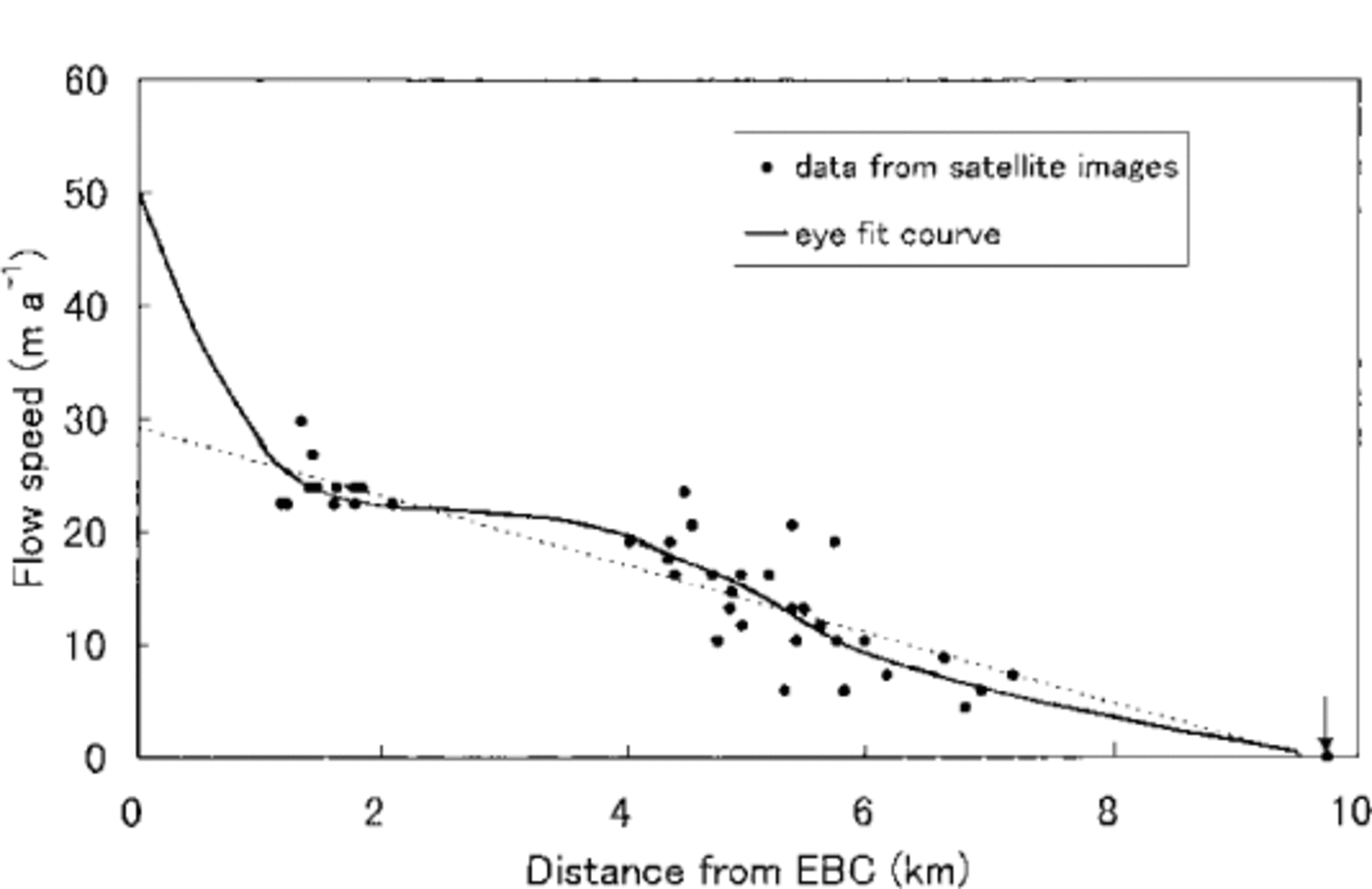
Fig. 5. Surface velocity estimated from SPOT HRV panchromatic images, 19 January 1987 and 9 November1993. Visually fitted curve and linear regression line are shown with solid and dotted lines, respectively. Arrow indicates apparent terminus.

Flow speed was 20–30 m a^-1 1 to 2 km from EBC and decreased down-glacier almost linearly with the increase in distance from EBC. These values are roughly compatible with, but slightly smaller than, the earlier data obtained at sites around the pinnacle zone. At downstream sites, only two survey data are available (Reference Kodama and MaeKodama and Mae, 1976). They observed velocities of about 20 m a^-1 and 1m a^-1 at about 5 km and 8.5 km from EBC respectively, which compare with our result. The solid line in Figure 5 represents a visual fit to the data, taking into account the velocity of about 50 m a^-1 near EBC recently obtained by Reference Seko, Yabuki, Nakawo, Sakai, Kadota and YamadaSeko and others (1998), which is smaller than but almost consistent with the survey data of Reference MüllerMüller (1968) and Reference Kodama and MaeKodama and Mae (1976).

Change in ice thickness

Ice-thickness data obtained by Reference MoribayashiMoribayashi (1978) are plotted in Figure 6, with the widths of the glacier and the area between the side moraines measured from the topographical map published by the National Geographic Society (1988). With these data, combined with ablation rate data and satellite-derived velocities, the change in ice thickness can be estimated with the following continuity equation:

(3)

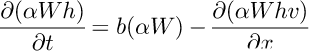
where W is the width of glacier surface, h is ice thickness, b is the surface balance which is equivalent to ablation rate in our calculation, v is mean velocity, x is longitudinal distance taken positive downward, and t is time. The calculation was made for a central part of the glacier along the center-line, and α is the proportionality constant of the width of the central part in question to the glacier width W. For simplicity, it was assumed that the mean velocity was not much different from the surface velocity. In the calculation, made for every 0.5 km increment, the approximation curve, shown with the dash-and-dot line in Figure 4, was used for b, and the velocity curve v was fitted by eye.

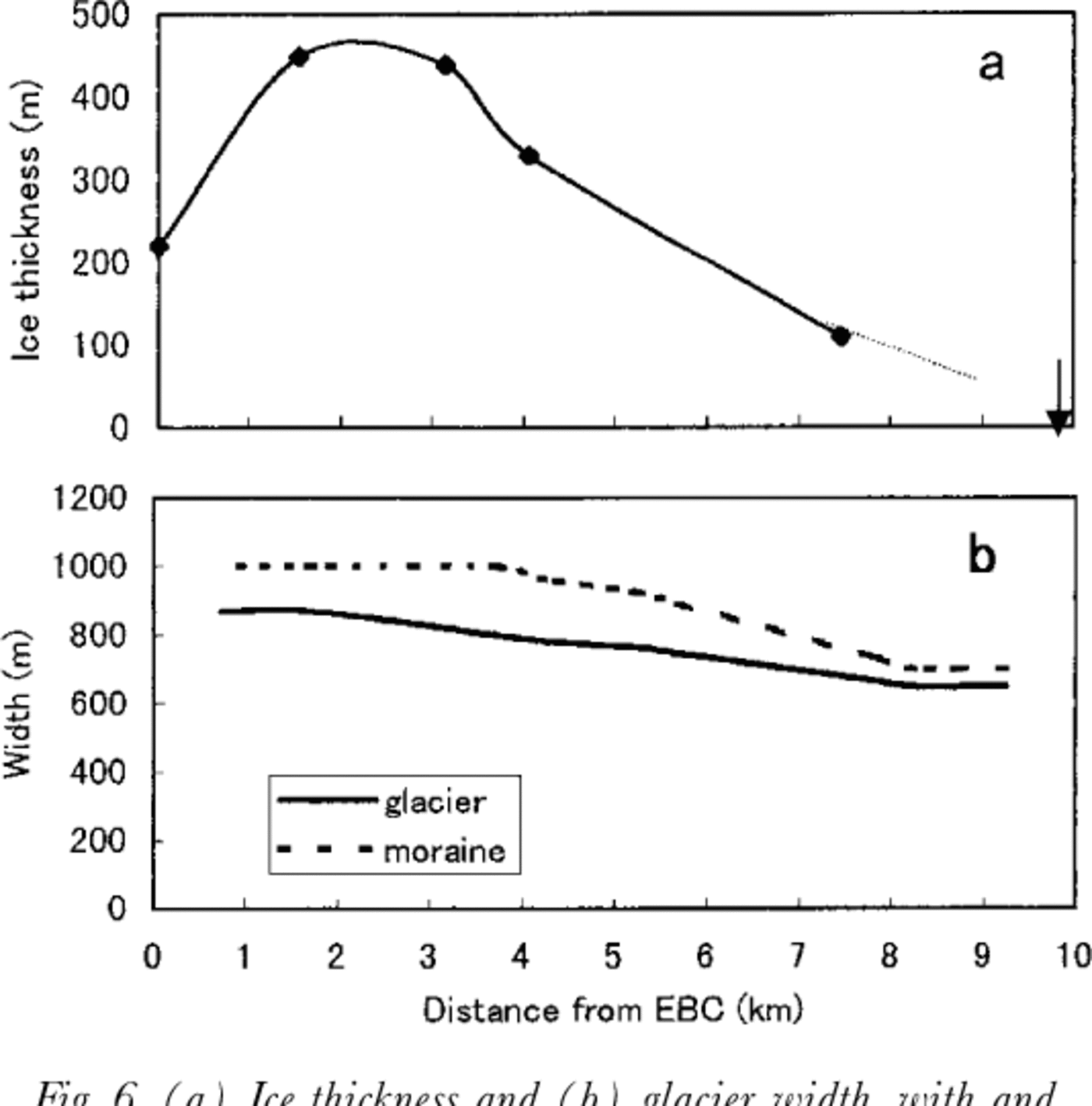
Fig. 6. (a) Ice thickness and (b) glacier width, with and without side moraines. Ice-thickness data (♦) are from Reference MoribayashiMoribayashi (1978). Solid line is interpolated and dotted line extrapolated toward the terminus. Both lines were used to calculate surface lowering Arrow indicates apparent terminus.

The result shown in Figure 7 indicates the glacier surface is lowering throughout the ablation area. The rate is large near EBC, roughly 1–2 ma^-1, and decreases down-glacier with a peak 3–5 km from EBC. In the area with thick supra-glacial debris, the rate is not much different from place to place, about 1m a^-1.

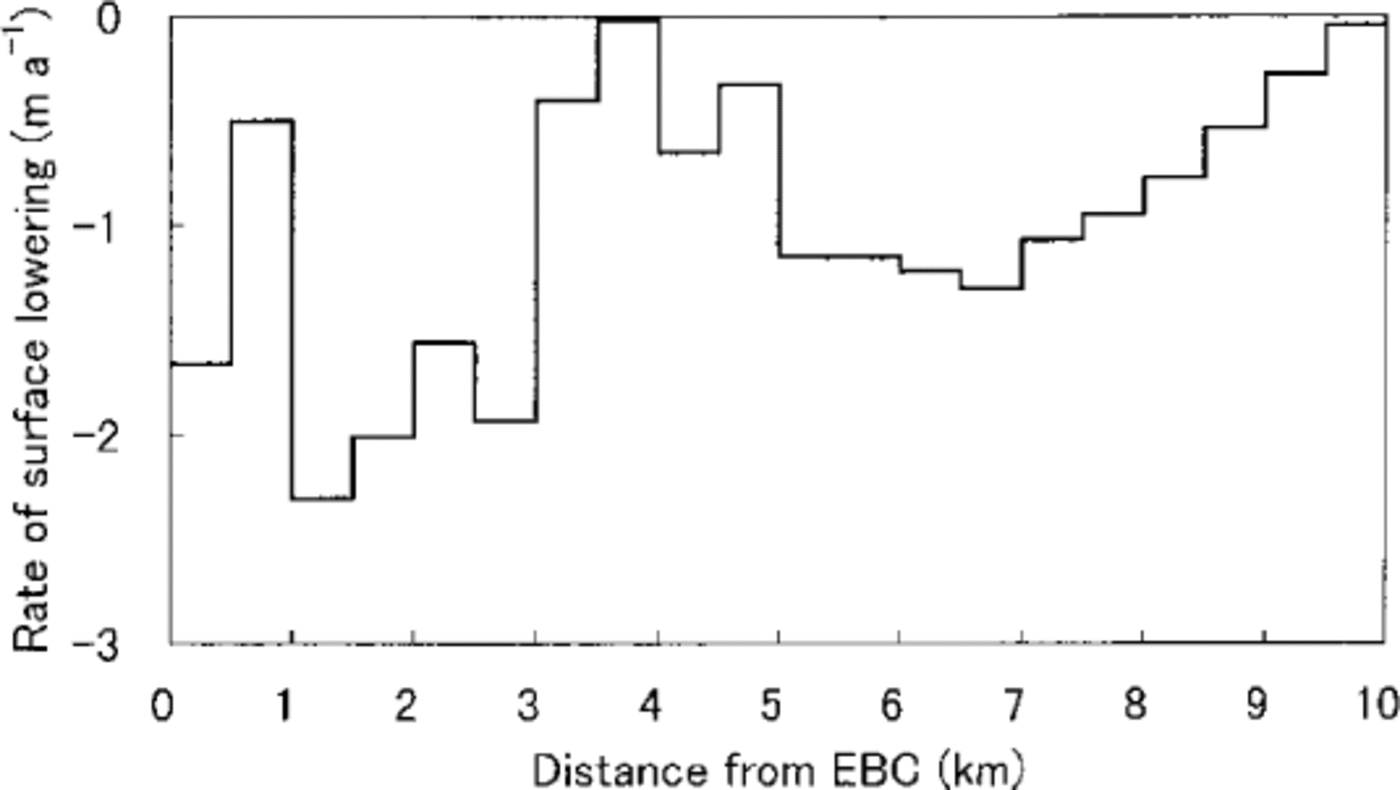
Fig. 7. Surface lowering Visually fitted curve in Figure 5 was used for velocity.

Discussion

At debris-free glaciers, the ablation rate increases with decreasing elevation downstream. The longitudinal distribution of ablation on debris-covered glacier is quite different (Fig. 4). This is considered a result of the insulating effect of the supraglacial debris layer. The trend of decrease in ablation with distance, however, is rather gentle. Earlier investigations showed that the ablation rate under debris, about 0.1 m thick, was roughly one-tenth of that for bare ice; under about 1 m thick the ablation became negligible (e.g. Reference Mattson, Gardner and YoungMattson and others, 1993). The ratio is dependent on both the thermal properties of the debris and the meteorological parameters (Reference Nakawo and TakahashiNakawo and Takahashi, 1982).This was confirmed by Reference Inoue and YbshidaInoue and Yoshida (1980) in the ablation area of Khumbu Glacier. Therefore, the ablation rate should decrease very rapidly with the distance, since debris thickness was more than 1 m in the lower half of the ablation area of Khumbu Glacier (Reference Nakawo, Iwata, Watanabe and YbshidaNakawo and others, 1986).

Reference Sakai, Nakawo and FujitaSakai and others (1998) assessed the contribution of the ablation at ice cliffs surrounding supraglacial lakes to the total ablation of the debris-covered area of a glacier in the Nepal Himalaya. It was concluded recently that melting at ice cliffs accounted for 20% of the total ablation of the debris-covered area, although the ratio of the cliffs was only 2% of the total area. For Khumbu Glacier, where the area of ice cliffs accounts for 2.6% of the total, melting at ice cliffs should also contribute significantly to the average ablation of the debris-covered area (Reference Inoue and YbshidaInoue and Yoshida, 1980), and the decreasing trend downstream should be small. In the area with thick debris, there are many supraglacial lakes, which change their locations frequently (Reference Seko, Yabuki, Nakawo, Sakai, Kadota and YamadaSeko and others, 1998). One of the advantages of estimating ablation under a debris layer from the surface temperature data is that the averaged surface temperature can lead to a realistic averaged ablation rate over a heterogeneous surface, such as a mixture of ice cliffs, lakes and debris-covered surfaces, where ablation rates differ significantly from place to place (Reference Nakawo, Morohoshi and UeharaNakawo and others, 1993).

Satellite imagery for estimating surface-flow velocity is useful and advantageous for debris-covered glaciers where in situ observations are difficult or dangerous. Reference Seko, Yabuki, Nakawo, Sakai, Kadota and YamadaSeko and others (1998) have also estimated ice velocity from satellite images in the pinnacle zone, which generally agrees with our result. They compared the velocity data obtained with the earlier survey data by Reference MüllerMüller (1968) and Reference Kodama and MaeKodama and Mae (1976), and concluded that flow rates seem to have decreased in the last few decades in the area down to about 3 km from EBC, although appreciable temporal change was not detected with our data at downstream sites, where velocities were rather small.

The thinning of the glacier could be the cause of the decrease in velocity, since surface flow is roughly proportional to the 4th power of ice thickness. According to Reference Seko, Yabuki, Nakawo, Sakai, Kadota and YamadaSeko and others (1998), the rate of decrease in velocity was about 13 m a^-1 around EBC, and about 6 m a^-1 2 km from EBC, over three decades shown in Figure 8. Near EBC, where the ice is 200–300 m thick, the rate of velocity decrease could be caused by the thinning rate of about 0.5 m a^-1, assuming no basal sliding and constant surface slope. For the site 2 km from EBC, the rate of velocity decrease can be attributed to a thinning of about 1m a^-1. These values are of the same order of magnitude for surface lowering rate as those shown in Figure 7. Also the rate is roughly twice as large at the lower site than near EBC, similar to Figure 7.

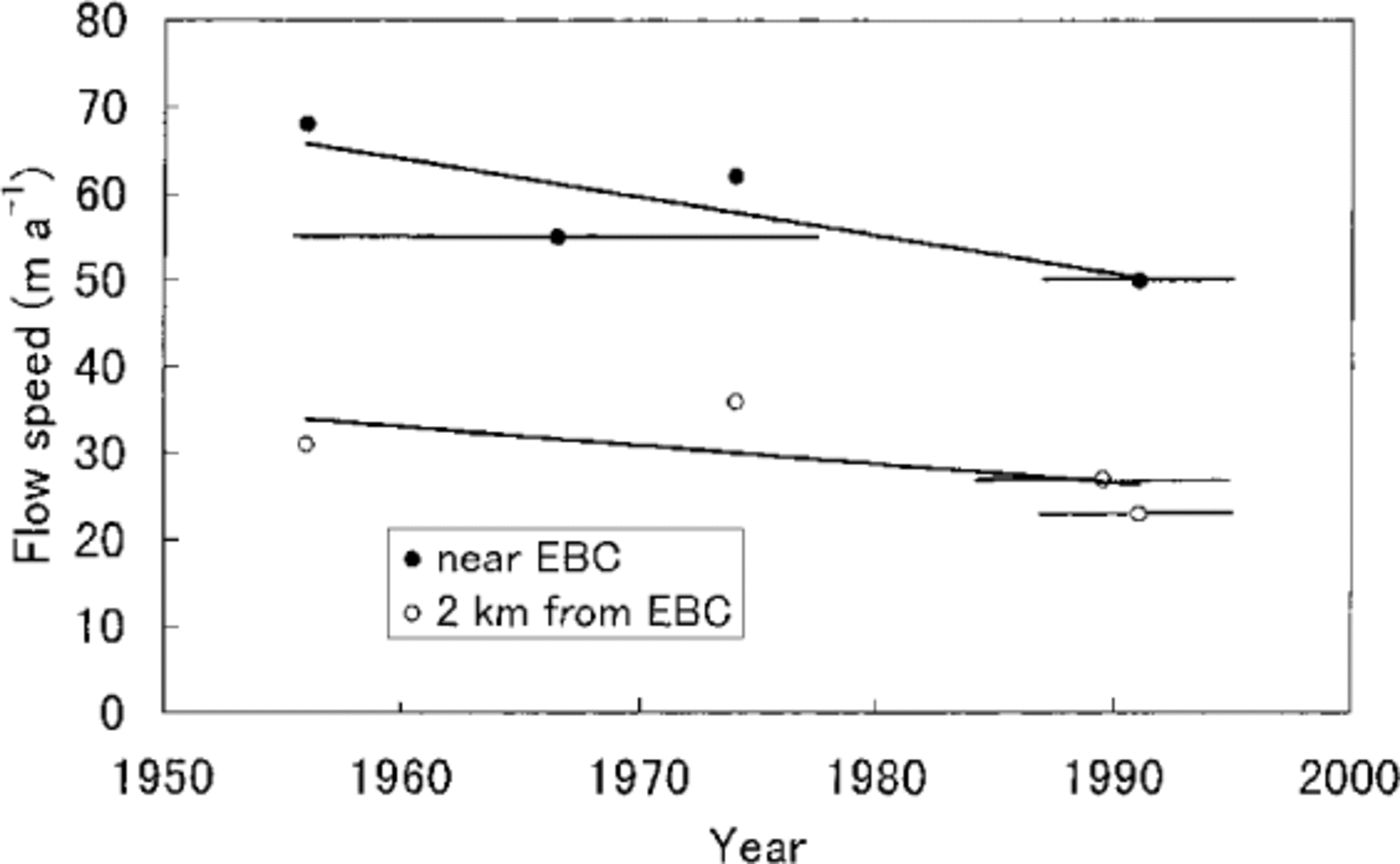
Fig. 8. Decreasing trend of velocity near EBC and around ice- pinnacle zone. Data are from Reference Seko, Yabuki, Nakawo, Sakai, Kadota and YamadaSeko and others (1998). The period of observation is marked by a horizontal bar with a symbol in the middle of the time.

Detailed surface mapping was carried out in 1978 (Reference WatanabeWatanabe and others, 1980), and the glacier was resurveyed in 1995. The surface lowering detected over the 17 years was (personal communication from T. Kadota, 1998): in the pinnacle zone 10–30 m (0.6–1.8ma^-1 on average); 4 km from EBC about 8 m (0.5 m a^-1 on average); 6 km from EBC about 10 m (0.6 m a^-1 on average); and 9 km from EBC about 3 m (0.15 m a^-1 on average). The spatial distribution of thinning is very similar to our calculation, although the magnitude is not the same.

The difference in magnitude is caused mainly by uncertainty in meteorological conditions in the ablation-rate calculations, because continuous year-round meteorological data were not available. When the meteorological conditions were changed, the resultant rate of lowering altered accordingly. It is considered, therefore, that absolute values of calculated surface lowering may be in error. The characteristics of the longitudinal distribution, however, should be comparatively reliable, since the spatial variation in meteorological conditions, although not known exactly, would be small.

One of the characteristics shown in Figure 7 is that the lowering takes place almost uniformly in the debris-covered area, particularly where debris thickness is large, even though debris thickness increases down-glacier quite rapidly. This would be due mainly to the contribution of melting at ice cliffs as discussed previously. This indicates that this part of the glacier, whose ice thickness is a few hundred meters in the ablation area, might disappear in a century or so, even with the current meteorological conditions. We are not sure whether the air temperature has increased lately in the Himalaya in association with global warming. If this did happen, but precipitation remained the same, the glaciers would retreat much more rapidly.

In the Lirung drainage basin, the amount of river discharge exceeded the total precipitation into the basin by about 30% (Reference RanaRana, 1997). It was augmented by shrinkage of Lirung Glacier, a debris-covered glacier. Debris-covered glaciers are thus playing a role in supplying additional water, without which the discharge would be much smaller. Disappearance of the glaciers would also damage the scenery which attracts many tourists. Therefore, careful attention needs to be paid to the evolution of debris-covered glaciers, since they account for more than half of the total glacierized area in the Nepal Himalaya.