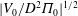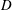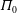1 Introduction
McCreary, Zhang & Shetye (Reference McCreary, Zhang and Shetye1997) note that although river water typically turns to the right in the northern hemisphere as it flows into the ocean, as in the outflow from Delaware Bay (Münchow & Garvine Reference Münchow and Garvine1993), there are also indications that river water can turn to the left, with the presence of a coastally trapped plume just north of the Changjiang River mouth suggested both by salinity and suspended sediment, and a similarly leftward bending of the Yellow River plume which can be inferred from the accumulation of clay in sediments upstream from the river mouth. This paper aims to show how the consideration of the vorticity dynamics offers a possible explanation of the difference in the leftward and rightward fluxes. Fluid from an outflow gains positive or negative relative vorticity through the stretching and squashing of the expelled vortex columns. This vorticity generation has been discussed for observations by Lake, Borenäs & Lundberg (Reference Lake, Borenäs and Lundberg2005) and in numerical modelling by Beardsley et al. (Reference Beardsley, Limeburner, Yu and Cannon1985), Spall & Price (Reference Spall and Price1998) and Marques et al. (Reference Marques, Padman, Springer, Howard and Özgökmen2014). The analysis here isolates the vorticity dynamics of outflows by presenting a model that retains sufficient physics to capture the essential nonlinearity of the flow but is sufficiently simple that explicit analytical solutions can be given for the fully nonlinear outflow evolution. Southwick, Johnson & McDonald (Reference Southwick, Johnson and McDonald2017) describe extensions of the model to unsteady sources, external currents, winds and tides and place the work in the context of additional oceanographic observations and previous analyses of ocean outflows.

Figure 1. Looking downwards on the current formed when dyed buoyant fluid is discharged from a side wall source into fluid in solid-body rotation (from Thomas & Linden Reference Thomas and Linden2007). The current is interpreted here as a bulge surrounding the outlet with an everywhere-unsteady lengthening tongue of fluid propagating anticlockwise around the tank wall. The pale dashed line (blue online) indicates the width at inception of the tongue which, it is suggested in § 6, may be related to the long-wave dynamics of the source region.
Outflows have also been modelled in the laboratory by Lane-Serff & Baines (Reference Lane-Serff and Baines2000), Horner-Devine et al. (Reference Horner-Devine, Fong, Monismith and Maxworthy2006) and Thomas & Linden (Reference Thomas and Linden2007). Figure 1, from Thomas & Linden (Reference Thomas and Linden2007), shows the current formed when dyed buoyant fluid is discharged from a side wall source into fluid in solid-body rotation in a rapidly rotating constant-depth cylindrical tank. The identification added here, of a bulge expanding upstream and downstream of the source and an everywhere-unsteady lengthening tongue of fluid propagating anticlockwise around the tank wall, follows from the theory below and is discussed in § 6. Most analyses of experiments concern two-dimensional (offshore and depth) steady shallow-water predictions of the current profiles and observations scale well with theory. The approach here is to focus on the temporal development in the two-dimensional (offshore and alongshore) horizontal plane by considering a
![]() $1(1/2)$
-layer quasi-geostrophic model with piecewise-constant potential vorticity (PV). Stern & Pratt (Reference Stern and Pratt1985) introduced a one-layer (rigid interface) version of this to model eddy formation on PV fronts using contour dynamics (CD) and a leading-order long-wave theory, subsequently extending it to
$1(1/2)$
-layer quasi-geostrophic model with piecewise-constant potential vorticity (PV). Stern & Pratt (Reference Stern and Pratt1985) introduced a one-layer (rigid interface) version of this to model eddy formation on PV fronts using contour dynamics (CD) and a leading-order long-wave theory, subsequently extending it to
![]() $1(1/2)$
-layers (Pratt & Stern Reference Pratt and Stern1986). Kubokawa (Reference Kubokawa1991) used this model to discuss an outflow where half the exiting fluid had zero PV anomaly and half had negative PV anomaly, presenting only CD integrations. McCreary et al. (Reference McCreary, Zhang and Shetye1997) integrated a full-physics version of the
$1(1/2)$
-layers (Pratt & Stern Reference Pratt and Stern1986). Kubokawa (Reference Kubokawa1991) used this model to discuss an outflow where half the exiting fluid had zero PV anomaly and half had negative PV anomaly, presenting only CD integrations. McCreary et al. (Reference McCreary, Zhang and Shetye1997) integrated a full-physics version of the
![]() $1(1/2)$
-layer model obtaining results that supported those of Kubokawa (Reference Kubokawa1991) in the small Rossby number limit. Johnson & McDonald (Reference Johnson and McDonald2006) discuss vortical outflows for one-layer flows, presenting CD integrations and an exact closed-form solution for the asymptotic steady state solution which proves useful below in giving the behaviour in the vorticity-dominated limit for the flows discussed here.
$1(1/2)$
-layer model obtaining results that supported those of Kubokawa (Reference Kubokawa1991) in the small Rossby number limit. Johnson & McDonald (Reference Johnson and McDonald2006) discuss vortical outflows for one-layer flows, presenting CD integrations and an exact closed-form solution for the asymptotic steady state solution which proves useful below in giving the behaviour in the vorticity-dominated limit for the flows discussed here.
Section 2 describes the
![]() $1(1/2)$
-layer model in the present context. Two effects drive the flow: a straightforward linear turning of the flow to the right (for positive rotation) due to the Coriolis force and the advection along the wall of the vortical current by image (in the wall) vorticity of the opposite sign to the current vorticity. These effects reinforce when the expelled fluid gains positive relative vorticity and compete when the expelled fluid gains negative relative vorticity. Section 2.1 discusses the linear turning flow and § 2.2 derives both the leading-order, hydraulic, long-wave equation and the next term in the expansion, which introduces long dispersive waves, as for vortical currents in Johnson & Clarke (Reference Johnson and Clarke1999, Reference Johnson and Clarke2001). Section 3 describes the steady flow that is set up across the source region in the hydraulic limit, introducing hydraulically controlled solutions as for vortical flow past topography in Haynes, Johnson & Hurst (Reference Haynes, Johnson and Hurst1993), and also presents solutions for the unsteady rarefactions that propagate away from the source region. Section 4 gives the full analytical unsteady evolution of the hydraulic model for an impulsively switched-on uniform source and § 5 compares the analytical solution with CD integrations. Section 6 discusses the results.
$1(1/2)$
-layer model in the present context. Two effects drive the flow: a straightforward linear turning of the flow to the right (for positive rotation) due to the Coriolis force and the advection along the wall of the vortical current by image (in the wall) vorticity of the opposite sign to the current vorticity. These effects reinforce when the expelled fluid gains positive relative vorticity and compete when the expelled fluid gains negative relative vorticity. Section 2.1 discusses the linear turning flow and § 2.2 derives both the leading-order, hydraulic, long-wave equation and the next term in the expansion, which introduces long dispersive waves, as for vortical currents in Johnson & Clarke (Reference Johnson and Clarke1999, Reference Johnson and Clarke2001). Section 3 describes the steady flow that is set up across the source region in the hydraulic limit, introducing hydraulically controlled solutions as for vortical flow past topography in Haynes, Johnson & Hurst (Reference Haynes, Johnson and Hurst1993), and also presents solutions for the unsteady rarefactions that propagate away from the source region. Section 4 gives the full analytical unsteady evolution of the hydraulic model for an impulsively switched-on uniform source and § 5 compares the analytical solution with CD integrations. Section 6 discusses the results.

Figure 2. The flow geometry near the inlet. (a) A side elevation of a vertical cut through the inlet region. Before the inlet is switched on the ambient fluid in
![]() $y>0$
is a two-layer quiescent fluid with density
$y>0$
is a two-layer quiescent fluid with density
![]() $\unicode[STIX]{x1D70C}_{1}<\unicode[STIX]{x1D70C}_{2}$
. Here the depth
$\unicode[STIX]{x1D70C}_{1}<\unicode[STIX]{x1D70C}_{2}$
. Here the depth
![]() $D_{s}$
of the inlet source is less than the depth
$D_{s}$
of the inlet source is less than the depth
![]() $D$
of the upper-layer ambient fluid and so the expelled fluid has positive PV anomaly,
$D$
of the upper-layer ambient fluid and so the expelled fluid has positive PV anomaly,
![]() $\unicode[STIX]{x1D6F1}_{0}>0$
. It stretches vertically to join the exterior flow and so acquires positive relative vorticity. The disturbance to the interface height is given by
$\unicode[STIX]{x1D6F1}_{0}>0$
. It stretches vertically to join the exterior flow and so acquires positive relative vorticity. The disturbance to the interface height is given by
![]() $h(x,y,t)$
. (b) As for (a) but for
$h(x,y,t)$
. (b) As for (a) but for
![]() $D_{s}>D$
so the expelled fluid has negative PV anomaly,
$D_{s}>D$
so the expelled fluid has negative PV anomaly,
![]() $\unicode[STIX]{x1D6F1}_{0}<0$
. It squashes vertically and acquires negative relative vorticity. A sill is present in the inlet to maintain the exterior ambient state. (c) A plan view in the horizontal
$\unicode[STIX]{x1D6F1}_{0}<0$
. It squashes vertically and acquires negative relative vorticity. A sill is present in the inlet to maintain the exterior ambient state. (c) A plan view in the horizontal
![]() $(x,y)$
plane showing, at some time
$(x,y)$
plane showing, at some time
![]() $t>0$
, the boundary
$t>0$
, the boundary
![]() ${\mathcal{C}}$
, where
${\mathcal{C}}$
, where
![]() $y=Y(x,t)$
, of the vortical expelled fluid which occupies the region
$y=Y(x,t)$
, of the vortical expelled fluid which occupies the region
![]() ${\mathcal{D}}$
.
${\mathcal{D}}$
.
2 The model and governing equations
Consider flow relative to a frame rotating about a vertical axis
![]() $Oz$
with constant angular speed
$Oz$
with constant angular speed
![]() $f/2>0$
. Take Cartesian axes
$f/2>0$
. Take Cartesian axes
![]() $Oxyz$
fixed in the rotating frame and consider flow in the half-space
$Oxyz$
fixed in the rotating frame and consider flow in the half-space
![]() $y>0$
, with
$y>0$
, with
![]() $Ox$
directed along the bounding wall
$Ox$
directed along the bounding wall
![]() $y=0$
. At time
$y=0$
. At time
![]() $t=0$
the half-space is occupied by a quiescent two-layer fluid with a thin layer of fluid of constant depth
$t=0$
the half-space is occupied by a quiescent two-layer fluid with a thin layer of fluid of constant depth
![]() $D$
and density
$D$
and density
![]() $\unicode[STIX]{x1D70C}_{1}$
overlying an infinitely deep layer of density
$\unicode[STIX]{x1D70C}_{1}$
overlying an infinitely deep layer of density
![]() $\unicode[STIX]{x1D70C}_{2}$
, where
$\unicode[STIX]{x1D70C}_{2}$
, where
![]() $\unicode[STIX]{x1D70C}_{2}>\unicode[STIX]{x1D70C}_{1}$
with the difference
$\unicode[STIX]{x1D70C}_{2}>\unicode[STIX]{x1D70C}_{1}$
with the difference
![]() $\unicode[STIX]{x1D70C}_{2}-\unicode[STIX]{x1D70C}_{1}$
sufficiently small that the Boussinesq approximation applies. For
$\unicode[STIX]{x1D70C}_{2}-\unicode[STIX]{x1D70C}_{1}$
sufficiently small that the Boussinesq approximation applies. For
![]() $t>0$
fluid is injected into the half-space from a source region occupying a depth
$t>0$
fluid is injected into the half-space from a source region occupying a depth
![]() $D_{s}$
and lying between
$D_{s}$
and lying between
![]() $x=-L$
and
$x=-L$
and
![]() $x=L$
on the wall
$x=L$
on the wall
![]() $y=0$
. Two cases can be distinguished depending on whether
$y=0$
. Two cases can be distinguished depending on whether
![]() $D_{s}$
is less or greater than
$D_{s}$
is less or greater than
![]() $D$
. If
$D$
. If
![]() $D_{s}<D$
then source fluid deepens as it adjusts to the ambient, as in figure 2(a). Through conservation of angular momentum this stretching of vortex columns generates positive relative vorticity, modelled here by taking the expelled fluid to have uniform positive PV anomaly (PVa),
$D_{s}<D$
then source fluid deepens as it adjusts to the ambient, as in figure 2(a). Through conservation of angular momentum this stretching of vortex columns generates positive relative vorticity, modelled here by taking the expelled fluid to have uniform positive PV anomaly (PVa),
![]() $\unicode[STIX]{x1D6F1}_{0}>0$
, i.e. the value of the expelled PV,
$\unicode[STIX]{x1D6F1}_{0}>0$
, i.e. the value of the expelled PV,
![]() $f/D_{s}$
, minus the ambient PV,
$f/D_{s}$
, minus the ambient PV,
![]() $f/D$
, is positive. If
$f/D$
, is positive. If
![]() $D_{s}>D$
then source fluid shallows as it adjusts to the ambient. Through conservation of angular momentum this squashing of vortex columns generates negative relative vorticity, modelled here by taking the expelled fluid to have uniform negative PVa,
$D_{s}>D$
then source fluid shallows as it adjusts to the ambient. Through conservation of angular momentum this squashing of vortex columns generates negative relative vorticity, modelled here by taking the expelled fluid to have uniform negative PVa,
![]() $\unicode[STIX]{x1D6F1}_{0}<0$
. To maintain this ambient state in a geophysical flow requires some form of sill in the inlet, as in figure 2(b). The expelled fluid is taken to form a connected region
$\unicode[STIX]{x1D6F1}_{0}<0$
. To maintain this ambient state in a geophysical flow requires some form of sill in the inlet, as in figure 2(b). The expelled fluid is taken to form a connected region
![]() ${\mathcal{D}}$
whose boundary is the material surface
${\mathcal{D}}$
whose boundary is the material surface
![]() ${\mathcal{C}}$
, as in figure 2(c). The disturbed interface depth due to the fluid incursion is denoted by
${\mathcal{C}}$
, as in figure 2(c). The disturbed interface depth due to the fluid incursion is denoted by
![]() $h(x,y,t)$
, and the analysis below is concerned with evolution of
$h(x,y,t)$
, and the analysis below is concerned with evolution of
![]() $h(x,y,t)$
as a time-dependent problem for
$h(x,y,t)$
as a time-dependent problem for
![]() $t>0$
in the horizontal
$t>0$
in the horizontal
![]() $(x,y)$
plane. Note that
$(x,y)$
plane. Note that
![]() $h$
needs only to satisfy the equation for constant PV in the interior of the flow domain, i.e. in
$h$
needs only to satisfy the equation for constant PV in the interior of the flow domain, i.e. in
![]() $y>0$
. Along
$y>0$
. Along
![]() $y=0$
the value of
$y=0$
the value of
![]() $h$
is determined by the boundary condition.
$h$
is determined by the boundary condition.
The depth difference
![]() $D-D_{s}$
is taken to be sufficiently small that the flow is geostrophic everywhere. Moreover since the flow is taken to be Boussinesq the upper, free surface is effectively rigid and the dynamics of the motion is confined to the interface. Thus consider a
$D-D_{s}$
is taken to be sufficiently small that the flow is geostrophic everywhere. Moreover since the flow is taken to be Boussinesq the upper, free surface is effectively rigid and the dynamics of the motion is confined to the interface. Thus consider a
![]() $1(1/2)$
-layer quasi-geostrophic free-surface flow driven when a source of total volume flux
$1(1/2)$
-layer quasi-geostrophic free-surface flow driven when a source of total volume flux
![]() $Q_{0}D$
(giving area flux
$Q_{0}D$
(giving area flux
![]() $Q_{0}$
) is switched on impulsively at time
$Q_{0}$
) is switched on impulsively at time
![]() $t=0$
and maintained for
$t=0$
and maintained for
![]() $t>0$
(although the analysis extends immediately to unsteady sources). A natural scaling that retains the vorticity-dominated limit, for which analytical solutions are known (Johnson & McDonald Reference Johnson and McDonald2006), is to scale horizontal lengths on the vortex-source length
$t>0$
(although the analysis extends immediately to unsteady sources). A natural scaling that retains the vorticity-dominated limit, for which analytical solutions are known (Johnson & McDonald Reference Johnson and McDonald2006), is to scale horizontal lengths on the vortex-source length
![]() $L_{v}=(Q_{0}/|\unicode[STIX]{x1D6F1}_{0}|D)^{1/2}$
. This effectively ensures that vortical currents have widths of order unity on this scale. The flow is determined by two non-dimensional parameters. The first can be chosen to be the ratio of the internal Rossby radius to the vortical length,
$L_{v}=(Q_{0}/|\unicode[STIX]{x1D6F1}_{0}|D)^{1/2}$
. This effectively ensures that vortical currents have widths of order unity on this scale. The flow is determined by two non-dimensional parameters. The first can be chosen to be the ratio of the internal Rossby radius to the vortical length,
![]() $a=c/fL_{v}=(g^{\prime }D^{2}|\unicode[STIX]{x1D6F1}_{0}|/f^{2}Q_{0})^{1/2}$
, where
$a=c/fL_{v}=(g^{\prime }D^{2}|\unicode[STIX]{x1D6F1}_{0}|/f^{2}Q_{0})^{1/2}$
, where
![]() $g^{\prime }$
is the reduced gravity and
$g^{\prime }$
is the reduced gravity and
![]() $c=(g^{\prime }D)^{1/2}$
is the linear long-wave speed on the interface. It is the important parameter in determining the form of the outflow evolution, measuring the relative strength of the flow driven by image vorticity compared to the strength of the linear turning flow set up by the initial Kelvin wave (KW), with large
$c=(g^{\prime }D)^{1/2}$
is the linear long-wave speed on the interface. It is the important parameter in determining the form of the outflow evolution, measuring the relative strength of the flow driven by image vorticity compared to the strength of the linear turning flow set up by the initial Kelvin wave (KW), with large
![]() $a$
corresponding to vortically dominated evolutions as in Johnson & McDonald (Reference Johnson and McDonald2006) and small
$a$
corresponding to vortically dominated evolutions as in Johnson & McDonald (Reference Johnson and McDonald2006) and small
![]() $a$
corresponding to KW-advected zero PVa evolutions. It is noted in § 2.1, and in greater detail in § 4.5, that the parameter
$a$
corresponding to KW-advected zero PVa evolutions. It is noted in § 2.1, and in greater detail in § 4.5, that the parameter
![]() $a$
gives the ratio of the scale for the speed of the image-vorticity-driven flow to that of the KW-driven flow. For brevity, the parameter
$a$
gives the ratio of the scale for the speed of the image-vorticity-driven flow to that of the KW-driven flow. For brevity, the parameter
![]() $a$
will be described simply as the speed ratio herein and will be taken to be of order unity compared to the second parameter. This second parameter measures the ratio of the current width to the scale of flow variations along the boundary and is required to be small in the long-wave analysis of §§ 3 and 4. For sources wide compared to current widths, and for clarity of exposition, it can be taken as
$a$
will be described simply as the speed ratio herein and will be taken to be of order unity compared to the second parameter. This second parameter measures the ratio of the current width to the scale of flow variations along the boundary and is required to be small in the long-wave analysis of §§ 3 and 4. For sources wide compared to current widths, and for clarity of exposition, it can be taken as
![]() $\unicode[STIX]{x1D716}=L_{v}/L$
. This is however overly restrictive, particularly for small
$\unicode[STIX]{x1D716}=L_{v}/L$
. This is however overly restrictive, particularly for small
![]() $a$
when currents are thin compared to
$a$
when currents are thin compared to
![]() $L_{v}$
, and comparisons below with unapproximated integrations of the full problem in § 5 show that the assumption of currents slowly varying along the boundary remains accurate even for the most extreme case of point sources.
$L_{v}$
, and comparisons below with unapproximated integrations of the full problem in § 5 show that the assumption of currents slowly varying along the boundary remains accurate even for the most extreme case of point sources.
In the quasi-geostrophic limit the interface displacement provides a streamfunction,
![]() $\unicode[STIX]{x1D702}(x,y,t)=g^{\prime }h/fQ_{0}$
, for the flow with velocity components given by the geostrophic relations
$\unicode[STIX]{x1D702}(x,y,t)=g^{\prime }h/fQ_{0}$
, for the flow with velocity components given by the geostrophic relations
![]() $(u,v)=(-\unicode[STIX]{x1D702}_{y},\unicode[STIX]{x1D702}_{x})$
, where lengths have been non-dimensionalised on
$(u,v)=(-\unicode[STIX]{x1D702}_{y},\unicode[STIX]{x1D702}_{x})$
, where lengths have been non-dimensionalised on
![]() $L_{v}$
, speeds on
$L_{v}$
, speeds on
![]() $Q_{0}/L_{v}$
,
$Q_{0}/L_{v}$
,
![]() $\unicode[STIX]{x1D702}$
on the flux
$\unicode[STIX]{x1D702}$
on the flux
![]() $Q_{0}$
and, subsequently,
$Q_{0}$
and, subsequently,
![]() $t$
on the advective, vortex time
$t$
on the advective, vortex time
![]() ${L_{v}}^{2}/Q_{0}=|D\unicode[STIX]{x1D6F1}_{0}|^{-1}$
. The non-dimensional half-width of the source is thus
${L_{v}}^{2}/Q_{0}=|D\unicode[STIX]{x1D6F1}_{0}|^{-1}$
. The non-dimensional half-width of the source is thus
![]() $W=L/L_{v}=\unicode[STIX]{x1D716}^{-1}$
and is formally large. The PVa then satisfies the non-dimensional equation,
$W=L/L_{v}=\unicode[STIX]{x1D716}^{-1}$
and is formally large. The PVa then satisfies the non-dimensional equation,
where
![]() $\unicode[STIX]{x1D6F1}=\pm 1$
, depending on the sign of the PVa of the expelled fluid. The fluid is taken to be impulsively set into motion at time
$\unicode[STIX]{x1D6F1}=\pm 1$
, depending on the sign of the PVa of the expelled fluid. The fluid is taken to be impulsively set into motion at time
![]() $t=0$
with efflux profile on the wall
$t=0$
with efflux profile on the wall
![]() $y=0$
given by
$y=0$
given by
where
![]() $\unicode[STIX]{x1D702}(-W)=Q(-W)=0$
and
$\unicode[STIX]{x1D702}(-W)=Q(-W)=0$
and
![]() $\unicode[STIX]{x1D702}(W)=Q(W)=1$
. An interfacial KW of non-dimensional amplitude unity, and so dimensional amplitude
$\unicode[STIX]{x1D702}(W)=Q(W)=1$
. An interfacial KW of non-dimensional amplitude unity, and so dimensional amplitude
![]() $Q_{0}\,f/g^{\prime }$
, propagates along the wall
$Q_{0}\,f/g^{\prime }$
, propagates along the wall
![]() $y=0$
, to the right,
$y=0$
, to the right,
![]() $x>W$
, at
$x>W$
, at
![]() $t=0^{+}$
at effectively infinite speed (of order the long-wave speed
$t=0^{+}$
at effectively infinite speed (of order the long-wave speed
![]() $c$
) setting the boundary condition on the interface at the wall as in the vortical adjustment problem of Hermann, Rhines & Johnson (Reference Hermann, Rhines and Johnson1989). Thus
$c$
) setting the boundary condition on the interface at the wall as in the vortical adjustment problem of Hermann, Rhines & Johnson (Reference Hermann, Rhines and Johnson1989). Thus
with
![]() $Q=0$
for
$Q=0$
for
![]() $x\leqslant -W$
and
$x\leqslant -W$
and
![]() $Q=1$
for
$Q=1$
for
![]() $x\geqslant W$
, giving the total dimensional source strength
$x\geqslant W$
, giving the total dimensional source strength
![]() $Q_{0}$
. For definiteness, the direction of KW propagation will be described here as ‘downstream’, following McCreary et al. (Reference McCreary, Zhang and Shetye1997). The flow remains at rest sufficiently far from the wall and so
$Q_{0}$
. For definiteness, the direction of KW propagation will be described here as ‘downstream’, following McCreary et al. (Reference McCreary, Zhang and Shetye1997). The flow remains at rest sufficiently far from the wall and so
At each instant the velocity field is determined by boundary conditions (2.3) and (2.4) and the PVa distribution (2.1) which is in turn determined completely by knowledge of the material curve
![]() ${\mathcal{C}}$
that forms its boundary. The unapproximated evolution can thus be followed accurately numerically using contour dynamics.
${\mathcal{C}}$
that forms its boundary. The unapproximated evolution can thus be followed accurately numerically using contour dynamics.
2.1 The zero PVa component
If the inlet and ambient upper-layer depths are equal then the PVa is zero, there is no vortex stretching or squashing and the expelled fluid has zero relative vorticity. The flow adjusts instantaneously, on the quasi-geostrophic time scale, to the solution of the linear problem given by field equation (2.1) with
![]() $\unicode[STIX]{x1D6F1}=0$
, subject to the boundary conditions (2.3) and (2.4). For the finite-width uniform source of § 4 the zero PVa component for a source of half-width unity can be written as
$\unicode[STIX]{x1D6F1}=0$
, subject to the boundary conditions (2.3) and (2.4). For the finite-width uniform source of § 4 the zero PVa component for a source of half-width unity can be written as
for
![]() $\unicode[STIX]{x1D6FE}=(l^{2}+1/a^{2})^{1/2}$
, and rapidly evaluated by fast Fourier transforms. Downstream of the source the non-dimensional flow speed along the wall approaches
$\unicode[STIX]{x1D6FE}=(l^{2}+1/a^{2})^{1/2}$
, and rapidly evaluated by fast Fourier transforms. Downstream of the source the non-dimensional flow speed along the wall approaches
![]() $1/a$
, giving a dimensional speed of
$1/a$
, giving a dimensional speed of
![]() $Q_{0}\,f/c$
which, in the quasi-geostrophic limit, is small compared to the long-wave speed
$Q_{0}\,f/c$
which, in the quasi-geostrophic limit, is small compared to the long-wave speed
![]() $c$
. The boundary
$c$
. The boundary
![]() ${\mathcal{C}}$
of expelled zero PVa fluid is advected as a passive material line by the steady KW flow and the nose of the expelled fluid moves downstream at constant dimensional speed
${\mathcal{C}}$
of expelled zero PVa fluid is advected as a passive material line by the steady KW flow and the nose of the expelled fluid moves downstream at constant dimensional speed
![]() $Q_{0}\,f/c$
. This flow remains as a component of the flow for non-zero PVa outflows and, for brevity, this KW-initiated, zero PVa component is referred to here simply as the KW flow. The parameter
$Q_{0}\,f/c$
. This flow remains as a component of the flow for non-zero PVa outflows and, for brevity, this KW-initiated, zero PVa component is referred to here simply as the KW flow. The parameter
![]() $a$
thus gives the ratio of the scale
$a$
thus gives the ratio of the scale
![]() $Q_{0}/L_{v}$
for the speed of vorticity-driven flow to the KW flow speed,
$Q_{0}/L_{v}$
for the speed of vorticity-driven flow to the KW flow speed,
![]() $Q_{0}\,f/c$
. Figure 3(a) shows contours of
$Q_{0}\,f/c$
. Figure 3(a) shows contours of
![]() $\unicode[STIX]{x1D702}$
, and thus streamlines, of this steady component for
$\unicode[STIX]{x1D702}$
, and thus streamlines, of this steady component for
![]() $a=3$
, plotted for non-zero PVa with horizontal distances scaled here, as elsewhere, on the vortex length scale,
$a=3$
, plotted for non-zero PVa with horizontal distances scaled here, as elsewhere, on the vortex length scale,
![]() $L_{v}$
. The flow is relatively broad and weak on the vortex scale. Figure 3(b) gives streamlines for
$L_{v}$
. The flow is relatively broad and weak on the vortex scale. Figure 3(b) gives streamlines for
![]() $a=1/3$
, showing that the current is relatively narrow and strong (since both currents carry the same unit flux) on the vortex scale and far more asymmetrically turned downstream on this scale. Sections 4 and 5 discuss how the KW flow reinforces image vorticity advection for positive PVa outflows, described here as reinforcing dynamics, and competes with image vorticity in negative PVa flows, described as opposing dynamics.
$a=1/3$
, showing that the current is relatively narrow and strong (since both currents carry the same unit flux) on the vortex scale and far more asymmetrically turned downstream on this scale. Sections 4 and 5 discuss how the KW flow reinforces image vorticity advection for positive PVa outflows, described here as reinforcing dynamics, and competes with image vorticity in negative PVa flows, described as opposing dynamics.

Figure 3. Evenly spaced contours of surface elevation (and thus streamlines) for the zero PVa component of non-zero PVa flow for uniform outflow from an inlet of half-width unity, plotted with horizontal distances scaled on the vortex length scale,
![]() $L_{v}$
. The total efflux in each case is one. (a)
$L_{v}$
. The total efflux in each case is one. (a)
![]() $a=3$
. For larger
$a=3$
. For larger
![]() $a$
the flow is relatively broad and slow and closer to upstream–downstream symmetric vorticity-dominated flow. (b)
$a$
the flow is relatively broad and slow and closer to upstream–downstream symmetric vorticity-dominated flow. (b)
![]() $a=1/3$
. For smaller
$a=1/3$
. For smaller
![]() $a$
the flow is relatively narrow and fast, turning rapidly downstream.
$a$
the flow is relatively narrow and fast, turning rapidly downstream.
2.2 The long-wave equations
If the evolution is sufficiently gentle that the interface
![]() ${\mathcal{C}}$
does not overturn,
${\mathcal{C}}$
does not overturn,
![]() ${\mathcal{C}}$
can be expressed as the curve
${\mathcal{C}}$
can be expressed as the curve
![]() $y=Y(x,t)$
for
$y=Y(x,t)$
for
![]() $Y$
a single-valued function of
$Y$
a single-valued function of
![]() $x$
. The condition that the interface
$x$
. The condition that the interface
![]() ${\mathcal{C}}$
between expelled fluid and the ambient is a material surface then can be written
${\mathcal{C}}$
between expelled fluid and the ambient is a material surface then can be written
i.e.
Equation (2.6b
) is the equation for the conservation of mass for the outflow and consequently also for the conservation of PVa. For steady solutions (2.6b
) gives immediately that
![]() $\unicode[STIX]{x1D702}$
is constant on
$\unicode[STIX]{x1D702}$
is constant on
![]() ${\mathcal{C}}$
, i.e. that the material line is a streamline as expected. As in contour dynamics, knowledge of
${\mathcal{C}}$
, i.e. that the material line is a streamline as expected. As in contour dynamics, knowledge of
![]() $Y(x,t)$
gives the entire flow evolution. Now suppose that the interface
$Y(x,t)$
gives the entire flow evolution. Now suppose that the interface
![]() ${\mathcal{C}}$
varies only slowly along the current compared to cross-current variations in
${\mathcal{C}}$
varies only slowly along the current compared to cross-current variations in
![]() $\unicode[STIX]{x1D702}$
and look for solutions of the form
$\unicode[STIX]{x1D702}$
and look for solutions of the form
The speed ratio
![]() $a$
is taken to be of order unity as
$a$
is taken to be of order unity as
![]() $\unicode[STIX]{x1D716}\rightarrow 0$
to retain the effects of both vortical and KW advection at leading order.
$\unicode[STIX]{x1D716}\rightarrow 0$
to retain the effects of both vortical and KW advection at leading order.
2.2.1 The non-dispersive, hydraulic limit
Substituting (2.7) in (2.1) gives the leading-order field equation
subject to the boundary condition that
![]() $\unicode[STIX]{x1D702}^{(0)}(X,0)=Q(x)$
on the wall
$\unicode[STIX]{x1D702}^{(0)}(X,0)=Q(x)$
on the wall
![]() $y=0$
, thus implicitly requiring that
$y=0$
, thus implicitly requiring that
![]() $Q$
be a slowly varying function of
$Q$
be a slowly varying function of
![]() $x$
. The current boundary
$x$
. The current boundary
![]() $y=Y$
is a slowly varying function of
$y=Y$
is a slowly varying function of
![]() $x$
and
$x$
and
![]() $t$
but for clarity this explicit dependence is suppressed here and subsequently. The leading-order (oceanic) flow outside the vortical layer (i.e.
$t$
but for clarity this explicit dependence is suppressed here and subsequently. The leading-order (oceanic) flow outside the vortical layer (i.e.
![]() $y>Y$
) can be written
$y>Y$
) can be written
giving the downstream current
Here
![]() $Q_{e}(x,t)$
gives the leading-order instantaneous downstream flux (of oceanic, zero PVa water) exterior to the vortical layer so
$Q_{e}(x,t)$
gives the leading-order instantaneous downstream flux (of oceanic, zero PVa water) exterior to the vortical layer so
![]() $Q(x)-Q_{e}(x,t)$
gives the leading-order instantaneous downstream flux of vortical fluid at any station
$Q(x)-Q_{e}(x,t)$
gives the leading-order instantaneous downstream flux of vortical fluid at any station
![]() $x$
. In the irrotational flow region
$x$
. In the irrotational flow region
and so, by continuity of
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $\unicode[STIX]{x1D702}_{y}$
across
$\unicode[STIX]{x1D702}_{y}$
across
![]() $y=Y$
, equation (2.11) gives the leading-order outer boundary condition at the edge of the vortical fluid.
$y=Y$
, equation (2.11) gives the leading-order outer boundary condition at the edge of the vortical fluid.
The general solution of the field equation (2.8) inside the vortical layer (i.e.
![]() $y<Y$
) can be written
$y<Y$
) can be written
where
![]() $A$
and
$A$
and
![]() $B$
are determined by the boundary conditions. Substituting (2.12) into (2.11) gives
$B$
are determined by the boundary conditions. Substituting (2.12) into (2.11) gives
![]() $A$
with (2.3) determining
$A$
with (2.3) determining
![]() $B$
so
$B$
so
with the leading-order solution for the vortical current in
![]() $y\leqslant Y$
,
$y\leqslant Y$
,
Evaluating (2.14) at the current edge
![]() $y=Y$
gives
$y=Y$
gives
Substituting (2.15) into (2.6b
) then gives a first-order quasi-linear hyperbolic inhomogeneous equation for the leading-order evolution of the interface displacement
![]() $Y(x,t)$
. As is typical for such equations, for some forcings the interface can overturn. At the order here such overturnings can then be incorporated by allowing jumps in
$Y(x,t)$
. As is typical for such equations, for some forcings the interface can overturn. At the order here such overturnings can then be incorporated by allowing jumps in
![]() $Y$
. These solutions are discussed in § 4 below.
$Y$
. These solutions are discussed in § 4 below.
2.2.2 Dispersive effects
The jumps present in the leading-order solutions are smoothed by dispersion at the next order. The field equation at
![]() $O(\unicode[STIX]{x1D716}^{2})$
becomes
$O(\unicode[STIX]{x1D716}^{2})$
becomes
whose solution in
![]() $y>Y$
, bounded as
$y>Y$
, bounded as
![]() $y\rightarrow \infty$
, can be written
$y\rightarrow \infty$
, can be written
where
![]() $C(X,T)$
remains to be determined. Now (2.17) satisfies
$C(X,T)$
remains to be determined. Now (2.17) satisfies
and so, again by continuity of
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $\unicode[STIX]{x1D702}_{y}$
across
$\unicode[STIX]{x1D702}_{y}$
across
![]() $y=Y$
, equation (2.18) forms the boundary condition at
$y=Y$
, equation (2.18) forms the boundary condition at
![]() $y=Y$
for vortical flow at this order.
$y=Y$
for vortical flow at this order.
The solution of (2.16) in
![]() $0\leqslant y\leqslant Y$
, vanishing on
$0\leqslant y\leqslant Y$
, vanishing on
![]() $y=0$
to satisfy (2.3), can be written
$y=0$
to satisfy (2.3), can be written
where
![]() $D(X,T)$
is determined from substituting in (2.18) as
$D(X,T)$
is determined from substituting in (2.18) as
Summing (2.15), (2.19) and (2.20) then gives the governing equation for the current edge as (2.6b
) with
![]() $\unicode[STIX]{x1D702}(x,Y(x,t))$
given with error of order
$\unicode[STIX]{x1D702}(x,Y(x,t))$
given with error of order
![]() $\unicode[STIX]{x1D716}^{4}$
by
$\unicode[STIX]{x1D716}^{4}$
by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}(x,Y(x,t)) & = & \displaystyle Q_{e}(x,t)-[(1/2)aY\exp (Y/a)-a(a+2Y)\sinh (Y/a)]A_{xx}\nonumber\\ \displaystyle & & \displaystyle -\,[(1/2)aY\exp (-Y/a)+(1/2)a^{2}\exp (-2Y/a)\sinh (Y/a)]B_{xx}\nonumber\\ \displaystyle & & \displaystyle +\,(1/2)a^{2}\exp (-2Y/a)[Q_{e}\exp (Y/a)]_{xx}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}(x,Y(x,t)) & = & \displaystyle Q_{e}(x,t)-[(1/2)aY\exp (Y/a)-a(a+2Y)\sinh (Y/a)]A_{xx}\nonumber\\ \displaystyle & & \displaystyle -\,[(1/2)aY\exp (-Y/a)+(1/2)a^{2}\exp (-2Y/a)\sinh (Y/a)]B_{xx}\nonumber\\ \displaystyle & & \displaystyle +\,(1/2)a^{2}\exp (-2Y/a)[Q_{e}\exp (Y/a)]_{xx}.\end{eqnarray}$$
As is typical for these expansions (Johnson & Clarke Reference Johnson and Clarke1999, Reference Johnson and Clarke2001),
![]() $\unicode[STIX]{x1D716}$
no longer appears explicitly although (2.21) formally requires that variations in
$\unicode[STIX]{x1D716}$
no longer appears explicitly although (2.21) formally requires that variations in
![]() $x$
are slow. In practice the long-wave equations can be accurate even when variations are not slow, as demonstrated by comparison with numerical integrations of the full equations in § 5. The dispersive aspects of solutions of (2.21) follow closely those for the evolution of vortical currents past coastal perturbations in Clarke & Johnson (Reference Clarke and Johnson1997a
,Reference Clarke and Johnson
b
) with shocks in the leading-order equations smoothed through spreading dispersive wave trains, as in § 5.
$x$
are slow. In practice the long-wave equations can be accurate even when variations are not slow, as demonstrated by comparison with numerical integrations of the full equations in § 5. The dispersive aspects of solutions of (2.21) follow closely those for the evolution of vortical currents past coastal perturbations in Clarke & Johnson (Reference Clarke and Johnson1997a
,Reference Clarke and Johnson
b
) with shocks in the leading-order equations smoothed through spreading dispersive wave trains, as in § 5.
3 Hydraulic solutions
The leading-order hydraulic solutions are conveniently discussed by nonlinearly scaling the current width by writing
so that
![]() $0\leqslant Z\leqslant 1$
with
$0\leqslant Z\leqslant 1$
with
![]() $Z=1$
when
$Z=1$
when
![]() $Y=0$
and
$Y=0$
and
![]() $Z\rightarrow 0$
as
$Z\rightarrow 0$
as
![]() $Y\rightarrow \infty$
. Since also
$Y\rightarrow \infty$
. Since also
![]() $Z_{t}=(-Z/a)Y_{t}$
, the governing equation (2.6b
) with (2.15) becomes, to leading order,
$Z_{t}=(-Z/a)Y_{t}$
, the governing equation (2.6b
) with (2.15) becomes, to leading order,
where
and
![]() $\unicode[STIX]{x1D6FC}(x)=Q(x)/a^{2}\unicode[STIX]{x1D6F1}$
. This can be written in the flux form
$\unicode[STIX]{x1D6FC}(x)=Q(x)/a^{2}\unicode[STIX]{x1D6F1}$
. This can be written in the flux form
where
Equation (3.3) is a forced first-order partial differential equation with disturbance propagation speed
![]() ${\mathcal{F}}^{\prime }(Z)=-a\unicode[STIX]{x1D6F1}Z[Z-(1+\unicode[STIX]{x1D6FC})]$
, to be solved subject to the initial condition of no initial disturbance, i.e.
${\mathcal{F}}^{\prime }(Z)=-a\unicode[STIX]{x1D6F1}Z[Z-(1+\unicode[STIX]{x1D6FC})]$
, to be solved subject to the initial condition of no initial disturbance, i.e.
![]() $Z=1$
at
$Z=1$
at
![]() $t=0$
for all
$t=0$
for all
![]() $x$
. Note that
$x$
. Note that
![]() ${\mathcal{F}}^{\prime \prime }(Z)$
can change sign in the interval
${\mathcal{F}}^{\prime \prime }(Z)$
can change sign in the interval
![]() $0<Z<1$
for some
$0<Z<1$
for some
![]() $a$
and
$a$
and
![]() $\unicode[STIX]{x1D6F1}$
, so for some parameter values the flux function is non-convex (Leveque Reference Leveque2002) and non-standard shocks and rarefactions can appear, and are visible in the integrations of the full equations in § 5.
$\unicode[STIX]{x1D6F1}$
, so for some parameter values the flux function is non-convex (Leveque Reference Leveque2002) and non-standard shocks and rarefactions can appear, and are visible in the integrations of the full equations in § 5.
Differentiating (2.12) with respect to
![]() $y$
and setting
$y$
and setting
![]() $y=0$
gives the along-wall velocity at
$y=0$
gives the along-wall velocity at
![]() $y=0^{+}$
as
$y=0^{+}$
as
There is thus a flux of
![]() $x$
-momentum through the source into the flow of
$x$
-momentum through the source into the flow of
using (3.4) and
![]() $v\,\text{d}x=Q_{x}\,\text{d}x=\text{d}Q$
. The final integral is positive as its integrand is non-negative. Thus
$v\,\text{d}x=Q_{x}\,\text{d}x=\text{d}Q$
. The final integral is positive as its integrand is non-negative. Thus
![]() $\unicode[STIX]{x0394}M_{s}>0$
for
$\unicode[STIX]{x0394}M_{s}>0$
for
![]() $\unicode[STIX]{x1D6F1}>0$
: positive PVa sources inject positive downstream momentum and current turns downstream under the joint effect of the KW flow and image vorticity. For negative PVa, opposing dynamics,
$\unicode[STIX]{x1D6F1}>0$
: positive PVa sources inject positive downstream momentum and current turns downstream under the joint effect of the KW flow and image vorticity. For negative PVa, opposing dynamics,
The integrand is again positive and so
![]() $\unicode[STIX]{x0394}M_{s}>0$
for
$\unicode[STIX]{x0394}M_{s}>0$
for
![]() $a<1/\surd 2$
. Negative PVa outflows can be expected to flow predominantly downstream when
$a<1/\surd 2$
. Negative PVa outflows can be expected to flow predominantly downstream when
![]() $a<1/\surd 2$
and the downstream KW flow dominates upstream advection by image vorticity. For negative PVa and
$a<1/\surd 2$
and the downstream KW flow dominates upstream advection by image vorticity. For negative PVa and
![]() $a$
sufficiently greater than
$a$
sufficiently greater than
![]() $1/\surd 2$
, upstream advection by image vorticity dominates the downstream KW flow and currents can be expected to turn upstream. In the large
$1/\surd 2$
, upstream advection by image vorticity dominates the downstream KW flow and currents can be expected to turn upstream. In the large
![]() $-a$
, vorticity-dominated limit
$-a$
, vorticity-dominated limit
The injected momentum flux is negative and the current turns upstream as in the vorticity-dominated solutions of Johnson & McDonald (Reference Johnson and McDonald2006). Southwick et al. (Reference Southwick, Johnson and McDonald2017) discuss these effects in greater detail showing explicitly for steady hydraulic solutions that the flux of momentum from the source exactly balances the increase of downstream momentum in the current and how this result and its extension to quasi-geostrophic flows helps resolve the momentum paradox of Pichevin & Nof (Reference Pichevin and Nof1997) and Nof (Reference Nof2005).

Figure 4. Contours of the hydraulic function
![]() $f(\unicode[STIX]{x1D6FC},Z)$
of (3.8) in
$f(\unicode[STIX]{x1D6FC},Z)$
of (3.8) in
![]() $(\unicode[STIX]{x1D6FC},Z)$
space. Each contour gives a possible steady solution for the leading-order flow. The bold curve and the dashed line determine the controlled solutions for positive and negative PVa, respectively. The bold straight line gives the limiting solution for negative PVa.
$(\unicode[STIX]{x1D6FC},Z)$
space. Each contour gives a possible steady solution for the leading-order flow. The bold curve and the dashed line determine the controlled solutions for positive and negative PVa, respectively. The bold straight line gives the limiting solution for negative PVa.
3.1 Steady hydraulic solutions
Before considering the unsteady evolutions it is useful to discuss the solutions of equations (3.2) that are steady across the source region as these appear later as asymptotically steady states in most parameter regimes. For steady solutions the exterior flux
![]() $Q_{e}$
is constant and (2.15) can be written, using (3.2), as
$Q_{e}$
is constant and (2.15) can be written, using (3.2), as
where
![]() $\unicode[STIX]{x1D6FC}_{e}=Q_{e}/a^{2}\unicode[STIX]{x1D6F1}$
. Figure 4 shows contours of
$\unicode[STIX]{x1D6FC}_{e}=Q_{e}/a^{2}\unicode[STIX]{x1D6F1}$
. Figure 4 shows contours of
![]() $f(\unicode[STIX]{x1D6FC},Z)$
. Steady solutions are given by the contours joining
$f(\unicode[STIX]{x1D6FC},Z)$
. Steady solutions are given by the contours joining
![]() $\unicode[STIX]{x1D6FC}=0$
(corresponding to
$\unicode[STIX]{x1D6FC}=0$
(corresponding to
![]() $Q=0$
at
$Q=0$
at
![]() $x=-W$
) to
$x=-W$
) to
![]() $\unicode[STIX]{x1D6FC}=1/a^{2}\unicode[STIX]{x1D6F1}$
(corresponding to
$\unicode[STIX]{x1D6FC}=1/a^{2}\unicode[STIX]{x1D6F1}$
(corresponding to
![]() $Q=1$
at
$Q=1$
at
![]() $x=W$
). As is standard in steady hydraulic solutions,
$x=W$
). As is standard in steady hydraulic solutions,
![]() $x$
appears only parametrically, through
$x$
appears only parametrically, through
![]() $\unicode[STIX]{x1D6FC}$
which determines
$\unicode[STIX]{x1D6FC}$
which determines
![]() $Q(x)$
which, in turn, determines
$Q(x)$
which, in turn, determines
![]() $x$
for a given
$x$
for a given
![]() $Z$
.
$Z$
.
For positive PVa, i.e.
![]() $\unicode[STIX]{x1D6F1}=1$
, a unique contour, corresponding to
$\unicode[STIX]{x1D6F1}=1$
, a unique contour, corresponding to
![]() $\unicode[STIX]{x1D6FC}_{e}=0$
and shown bold in figure 4, joins
$\unicode[STIX]{x1D6FC}_{e}=0$
and shown bold in figure 4, joins
![]() $\unicode[STIX]{x1D6FC}=0$
,
$\unicode[STIX]{x1D6FC}=0$
,
![]() $Z=1$
to any
$Z=1$
to any
![]() $\unicode[STIX]{x1D6FC}=1/a^{2}>0$
. The fluid outside the vortical current is stagnant and current width increases monotonically across the source from zero at
$\unicode[STIX]{x1D6FC}=1/a^{2}>0$
. The fluid outside the vortical current is stagnant and current width increases monotonically across the source from zero at
![]() $x=-W$
(where
$x=-W$
(where
![]() $\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}Z=0$
so the long-wave speed vanishes and the flow is critically controlled) to have width
$\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}Z=0$
so the long-wave speed vanishes and the flow is critically controlled) to have width
at
![]() $x=W$
. As
$x=W$
. As
![]() $a\rightarrow \infty$
,
$a\rightarrow \infty$
,
![]() $Y_{hp}^{d}\rightarrow \surd 2$
, the non-dimensional current width in the vorticity-dominated limit (Johnson & McDonald Reference Johnson and McDonald2006).
$Y_{hp}^{d}\rightarrow \surd 2$
, the non-dimensional current width in the vorticity-dominated limit (Johnson & McDonald Reference Johnson and McDonald2006).
For negative PVa, i.e.
![]() $\unicode[STIX]{x1D6F1}=-1$
, steady solutions require a contour joining
$\unicode[STIX]{x1D6F1}=-1$
, steady solutions require a contour joining
![]() $\unicode[STIX]{x1D6FC}=0$
to
$\unicode[STIX]{x1D6FC}=0$
to
![]() $\unicode[STIX]{x1D6FC}=-1/a^{2}<0$
. The contour crossing the line
$\unicode[STIX]{x1D6FC}=-1/a^{2}<0$
. The contour crossing the line
![]() $\unicode[STIX]{x1D6FC}=0$
that extends furthest into negative
$\unicode[STIX]{x1D6FC}=0$
that extends furthest into negative
![]() $\unicode[STIX]{x1D6FC}$
is that originating from
$\unicode[STIX]{x1D6FC}$
is that originating from
![]() $\unicode[STIX]{x1D6FC}=0$
,
$\unicode[STIX]{x1D6FC}=0$
,
![]() $Z=0$
and so has
$Z=0$
and so has
![]() $f(\unicode[STIX]{x1D6FC},Z)=1$
. The contour consists of the lines
$f(\unicode[STIX]{x1D6FC},Z)=1$
. The contour consists of the lines
![]() $Z=0$
and
$Z=0$
and
![]() $Z=2(1+\unicode[STIX]{x1D6FC})$
, also shown bold in figure 4. Thus no steady solution can connect
$Z=2(1+\unicode[STIX]{x1D6FC})$
, also shown bold in figure 4. Thus no steady solution can connect
![]() $\unicode[STIX]{x1D6FC}=0$
to
$\unicode[STIX]{x1D6FC}=0$
to
![]() $\unicode[STIX]{x1D6FC}\leqslant -1$
and so if
$\unicode[STIX]{x1D6FC}\leqslant -1$
and so if
![]() $\unicode[STIX]{x1D6FC}\leqslant -1$
, i.e.
$\unicode[STIX]{x1D6FC}\leqslant -1$
, i.e.
![]() $a\leqslant 1$
, the flow cannot be steady for negative PVa: no steady flow is possible for KW-flow-dominated, opposing dynamics. It is shown in §§ 3.2 and 4 that this corresponds to the current expanding monotonically in the neighbourhood of the source. For
$a\leqslant 1$
, the flow cannot be steady for negative PVa: no steady flow is possible for KW-flow-dominated, opposing dynamics. It is shown in §§ 3.2 and 4 that this corresponds to the current expanding monotonically in the neighbourhood of the source. For
![]() $a>1$
a continuum of contours crosses the source region. The narrowest current (that with largest
$a>1$
a continuum of contours crosses the source region. The narrowest current (that with largest
![]() $Z$
) terminates in
$Z$
) terminates in
![]() $\unicode[STIX]{x1D6FC}<0$
with
$\unicode[STIX]{x1D6FC}<0$
with
![]() $Q=1$
when
$Q=1$
when
![]() $\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}Z=0$
and the long-wave speed vanishes, i.e. on the line
$\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}Z=0$
and the long-wave speed vanishes, i.e. on the line
![]() $Z=1+\unicode[STIX]{x1D6FC}=1-1/a^{2}$
shown dashed in figure 4. This current is critically controlled at the downstream edge of the source, giving a flow with flux
$Z=1+\unicode[STIX]{x1D6FC}=1-1/a^{2}$
shown dashed in figure 4. This current is critically controlled at the downstream edge of the source, giving a flow with flux
![]() $Q_{e}=1-1/2a^{2}$
of zero PVa (oceanic) fluid external to the outflowing current. This external flux has been observed by McCreary et al. (Reference McCreary, Zhang and Shetye1997) in their numerical integrations, where they describe outflow water flowing upstream before reversing direction and, together with fresher oceanic water, flowing downstream as a current straddling the density front between the fresher and salty waters. Away from the source the upstream and downstream vortical flows have widths
$Q_{e}=1-1/2a^{2}$
of zero PVa (oceanic) fluid external to the outflowing current. This external flux has been observed by McCreary et al. (Reference McCreary, Zhang and Shetye1997) in their numerical integrations, where they describe outflow water flowing upstream before reversing direction and, together with fresher oceanic water, flowing downstream as a current straddling the density front between the fresher and salty waters. Away from the source the upstream and downstream vortical flows have widths
(with
![]() $Y_{hn}^{u}\rightarrow \surd 2$
in the vorticity-dominated limit) shown as functions of the speed ratio
$Y_{hn}^{u}\rightarrow \surd 2$
in the vorticity-dominated limit) shown as functions of the speed ratio
![]() $a$
in figure 5. The critical solution is the steady state flow that evolves from the unsteady hydraulic initial value problem discussed below. The full CD integrations in § 5 show that for narrower sources, where along-shore variations become significant, other steady solutions can be selected.
$a$
in figure 5. The critical solution is the steady state flow that evolves from the unsteady hydraulic initial value problem discussed below. The full CD integrations in § 5 show that for narrower sources, where along-shore variations become significant, other steady solutions can be selected.

Figure 5. The upstream current width
![]() $Y_{hn}^{u}$
(upper curve) and the downstream critical-point current width
$Y_{hn}^{u}$
(upper curve) and the downstream critical-point current width
![]() $Y_{hn}^{d}$
(lower) of the critical hydraulic solution for a negative PVa outflow as a function of speed ratio for
$Y_{hn}^{d}$
(lower) of the critical hydraulic solution for a negative PVa outflow as a function of speed ratio for
![]() $a>1$
.
$a>1$
.
3.2 Unsteady hydraulic solutions: simple rarefactions
The unsteady, lengthening tongue of expelled fluid visible in figure 1, and the corresponding regions in the full integrations of § 5, can be regarded as rarefactions of the coastal flow. A rarefaction in gas dynamics, where the density smoothly decreases from a region where the density is larger to one where it is smaller, lengthens when the local propagation speed, being a function of density, is faster at the leading edge of the rarefaction than at its trailing edge. In the flow here a rarefaction smoothly joins two regions of differing current width, again lengthening when its leading edge travels faster than its trailing edge. The simplest rarefaction solutions of (3.2) are the self-similar solutions in terms of the speed variable
![]() $s=x/at$
, with
$s=x/at$
, with
![]() $s$
giving the rarefaction propagation speed non-dimensionalised on
$s$
giving the rarefaction propagation speed non-dimensionalised on
![]() $(|\unicode[STIX]{x1D6F1}_{0}|D/f)c$
which, in the quasi-geostrophic limit, is small compared to the KW speed
$(|\unicode[STIX]{x1D6F1}_{0}|D/f)c$
which, in the quasi-geostrophic limit, is small compared to the KW speed
![]() $c$
. These require
$c$
. These require
![]() $Q$
to be a function of
$Q$
to be a function of
![]() $s$
alone and so for an impulsively switched on source require
$s$
alone and so for an impulsively switched on source require
![]() $Q(s)=\text{H}(s)$
, a Heaviside function, corresponding to a point source at the origin. Away from the origin
$Q(s)=\text{H}(s)$
, a Heaviside function, corresponding to a point source at the origin. Away from the origin
![]() $Q$
is a constant and the governing equation (3.2) becomes
$Q$
is a constant and the governing equation (3.2) becomes
Thus either
![]() $\text{d}Z/\text{d}s=0$
and the current has constant width or
$\text{d}Z/\text{d}s=0$
and the current has constant width or
i.e.
For positive PVa (
![]() $\unicode[STIX]{x1D6F1}=1$
), reinforcing dynamics, image vorticity reinforces the KW flow, shown from (3.12b
) by noting that solutions with
$\unicode[STIX]{x1D6F1}=1$
), reinforcing dynamics, image vorticity reinforces the KW flow, shown from (3.12b
) by noting that solutions with
![]() $0\leqslant Z\leqslant 1$
are possible only downstream where
$0\leqslant Z\leqslant 1$
are possible only downstream where
![]() $Q=1$
. Introducing
$Q=1$
. Introducing
and writing
![]() $Z=\unicode[STIX]{x1D706}\hat{Z}$
,
$Z=\unicode[STIX]{x1D706}\hat{Z}$
,
![]() $s=\unicode[STIX]{x1D706}^{2}{\hat{s}}$
, gives the universal form
$s=\unicode[STIX]{x1D706}^{2}{\hat{s}}$
, gives the universal form
with
![]() $0\leqslant {\hat{s}}\leqslant 1/4$
. The maximum value of
$0\leqslant {\hat{s}}\leqslant 1/4$
. The maximum value of
![]() $Z=\unicode[STIX]{x1D706}/2$
, which gives the minimum current width, occurs when
$Z=\unicode[STIX]{x1D706}/2$
, which gives the minimum current width, occurs when
![]() ${\hat{s}}=1/4$
. For
${\hat{s}}=1/4$
. For
![]() $a<1$
, when the KW flow dominates, the minimum is negative and so the rarefaction terminates downstream against the wall, driven by the narrow, intense flow of figure 3(b). For
$a<1$
, when the KW flow dominates, the minimum is negative and so the rarefaction terminates downstream against the wall, driven by the narrow, intense flow of figure 3(b). For
![]() $a>1$
image vorticity dominates the broad, weak KW flow of figure 3(a) decreasing the speed at the wall: the maximum value of
$a>1$
image vorticity dominates the broad, weak KW flow of figure 3(a) decreasing the speed at the wall: the maximum value of
![]() $Z$
occurs for
$Z$
occurs for
![]() $Z<1$
and the downstream edge of the rarefaction does not reach the wall, with instead the rarefaction terminating in a shock. This is discussed in greater detail for the finite-width source in § 4.2 and these behaviours can be seen in the solutions for finite-width sources there with figure 8(a) showing a downstream rarefaction terminating at the wall and figure 8(b) showing a downstream rarefaction terminating at a shock.
$Z<1$
and the downstream edge of the rarefaction does not reach the wall, with instead the rarefaction terminating in a shock. This is discussed in greater detail for the finite-width source in § 4.2 and these behaviours can be seen in the solutions for finite-width sources there with figure 8(a) showing a downstream rarefaction terminating at the wall and figure 8(b) showing a downstream rarefaction terminating at a shock.
For negative PVa (
![]() $\unicode[STIX]{x1D6F1}=-1$
), opposing dynamics, image vorticity opposes the KW flow. The form of the downstream rarefaction (with
$\unicode[STIX]{x1D6F1}=-1$
), opposing dynamics, image vorticity opposes the KW flow. The form of the downstream rarefaction (with
![]() $Q=1$
) depends on the value of
$Q=1$
) depends on the value of
![]() $a$
. For
$a$
. For
![]() $a=1$
,
$a=1$
,
![]() $Z=\surd s$
with the range
$Z=\surd s$
with the range
![]() $0\leqslant s\leqslant 1$
covering all possible values of current width and so joining any current smoothly to the wall. For
$0\leqslant s\leqslant 1$
covering all possible values of current width and so joining any current smoothly to the wall. For
![]() $a<1$
, KW flow dominated, the rarefaction has universal form
$a<1$
, KW flow dominated, the rarefaction has universal form
Since
![]() $Z\rightarrow 0$
as
$Z\rightarrow 0$
as
![]() $s\rightarrow 0$
and
$s\rightarrow 0$
and
![]() $Z\rightarrow \infty$
as
$Z\rightarrow \infty$
as
![]() $s\rightarrow \infty$
, the rarefaction can join any current smoothly to the wall, as can be seen in the downstream rarefaction for finite-width sources in figure 9(a). For
$s\rightarrow \infty$
, the rarefaction can join any current smoothly to the wall, as can be seen in the downstream rarefaction for finite-width sources in figure 9(a). For
![]() $a>1$
, image vorticity dominated, equation (3.12b
) becomes
$a>1$
, image vorticity dominated, equation (3.12b
) becomes
with
![]() $Z\rightarrow \infty$
as
$Z\rightarrow \infty$
as
![]() $s\rightarrow \infty$
and
$s\rightarrow \infty$
and
![]() $Z=\unicode[STIX]{x1D706}$
when
$Z=\unicode[STIX]{x1D706}$
when
![]() $s=0$
, giving a current of width fixed for all time at the downstream edge of the source region precisely equal to
$s=0$
, giving a current of width fixed for all time at the downstream edge of the source region precisely equal to
![]() $Y_{hn}^{d}$
of (3.10), the width at the downstream edge of the source region of the unique hydraulic solution that is critically controlled when
$Y_{hn}^{d}$
of (3.10), the width at the downstream edge of the source region of the unique hydraulic solution that is critically controlled when
![]() $Q=1$
. Thus the rarefaction smoothly joins this controlled hydraulic solution to the wall for all time, as can be seen for finite-width sources in figure 9(b,c). For negative PVa, upstream rarefactions (with
$Q=1$
. Thus the rarefaction smoothly joins this controlled hydraulic solution to the wall for all time, as can be seen for finite-width sources in figure 9(b,c). For negative PVa, upstream rarefactions (with
![]() $Q=0$
) are also possible with
$Q=0$
) are also possible with
giving a universal form defined for
![]() $-{\textstyle \frac{1}{4}}\leqslant s\leqslant 0$
. Figure 6 shows the current widths of upstream and downstream negative PVa rarefactions from (3.15), (3.17). The universal forms (3.14)–(3.17) may prove useful in collapsing time-dependent data from experiments and observations onto a single curve.
$-{\textstyle \frac{1}{4}}\leqslant s\leqslant 0$
. Figure 6 shows the current widths of upstream and downstream negative PVa rarefactions from (3.15), (3.17). The universal forms (3.14)–(3.17) may prove useful in collapsing time-dependent data from experiments and observations onto a single curve.

Figure 6. The width
![]() $Y/a=-\text{log}\,Z$
of a self-similar rarefaction in a negative PVa current as a function of the speed variable
$Y/a=-\text{log}\,Z$
of a self-similar rarefaction in a negative PVa current as a function of the speed variable
![]() $s=x/at$
. (a) The upstream rarefaction in
$s=x/at$
. (a) The upstream rarefaction in
![]() $x<0$
. This is the universal form for all
$x<0$
. This is the universal form for all
![]() $a$
. (b) A downstream rarefaction in
$a$
. (b) A downstream rarefaction in
![]() $x>0$
. This form is not universal in these variables and is given here for
$x>0$
. This form is not universal in these variables and is given here for
![]() $a=0.5$
.
$a=0.5$
.
4 A finite-width uniform source
The entire evolution in the unsteady hydraulic limit can be obtained explicitly for the top-hat velocity profile given by
with
![]() $Q=0$
in
$Q=0$
in
![]() $x<W$
and
$x<W$
and
![]() $Q=1$
in
$Q=1$
in
![]() $x>W$
, so that the outflow velocity vanishes outside
$x>W$
, so that the outflow velocity vanishes outside
![]() $|x|\leqslant W$
and takes the constant value
$|x|\leqslant W$
and takes the constant value
![]() $1/2W$
across the source. In characteristic form (3.2) becomes
$1/2W$
across the source. In characteristic form (3.2) becomes
4.1 The source region
For the uniform source (4.1), the right-hand side of (4.2) is piecewise constant and, in particular, can be integrated directly in
![]() $|x|\leqslant W$
to give the scaled current width across the source region,
$|x|\leqslant W$
to give the scaled current width across the source region,
on applying the initial condition that
![]() $Z_{S}=1$
when
$Z_{S}=1$
when
![]() $t=0$
, shown in figure 7. Note that
$t=0$
, shown in figure 7. Note that
![]() $Y_{S}\rightarrow t/2W~\text{as}~t\rightarrow 0$
as fluid in the source region is swept uniformly away from the wall at speed
$Y_{S}\rightarrow t/2W~\text{as}~t\rightarrow 0$
as fluid in the source region is swept uniformly away from the wall at speed
![]() $1/2W$
. The integrations of the full equations in § 5 indicate that the growth of the current in the source region is relatively insensitive to the precise exit profile and so formula (4.3) will closely estimate the current width for other profiles provided the scale
$1/2W$
. The integrations of the full equations in § 5 indicate that the growth of the current in the source region is relatively insensitive to the precise exit profile and so formula (4.3) will closely estimate the current width for other profiles provided the scale
![]() $W$
of the source width is chosen appropriately. The current width for this exit profile is the same on all characteristics issuing from the source region and so is constant (in
$W$
of the source width is chosen appropriately. The current width for this exit profile is the same on all characteristics issuing from the source region and so is constant (in
![]() $x$
) across the source region.
$x$
) across the source region.

Figure 7. The temporal development of the scaled width
![]() $Y_{S}/a$
of the constant (in
$Y_{S}/a$
of the constant (in
![]() $x$
) width current in the neighbourhood of the source forced by the uniform discharge (4.1) as a function of the scaled time
$x$
) width current in the neighbourhood of the source forced by the uniform discharge (4.1) as a function of the scaled time
![]() $t/2aW$
, as given by the formula (4.3). For positive PVa and negative PVa with
$t/2aW$
, as given by the formula (4.3). For positive PVa and negative PVa with
![]() $a\geqslant 1$
, the expansion terminates in the formation of a steady hydraulic solution. For negative PVa with
$a\geqslant 1$
, the expansion terminates in the formation of a steady hydraulic solution. For negative PVa with
![]() $a<1$
, so KW flow dominates, the expansion continues indefinitely but slows dramatically at larger times.
$a<1$
, so KW flow dominates, the expansion continues indefinitely but slows dramatically at larger times.

Figure 8. The evolution of the boundary of a positive PVa outflow, reinforcing dynamics, from a uniform source occupying the region
![]() $|x|<1$
. In this and subsequent figures the coast
$|x|<1$
. In this and subsequent figures the coast
![]() $y=0$
is shown as a thick line and the edges of the source region as dashed lines with the thin line indicating the locus in time of the junction between the rarefaction and its leading jump. Each panel shows the outflow boundary at times
$y=0$
is shown as a thick line and the edges of the source region as dashed lines with the thin line indicating the locus in time of the junction between the rarefaction and its leading jump. Each panel shows the outflow boundary at times
![]() $t=2$
, 5 and 12. (a) For speed ratio
$t=2$
, 5 and 12. (a) For speed ratio
![]() $a=1$
, typical of all KW-flow-dominated evolutions with
$a=1$
, typical of all KW-flow-dominated evolutions with
![]() $a\leqslant 1$
. (b) For
$a\leqslant 1$
. (b) For
![]() $a=1.6$
so
$a=1.6$
so
![]() $1<a<a_{m}$
. (c) For
$1<a<a_{m}$
. (c) For
![]() $a=5$
, so
$a=5$
, so
![]() $a>a_{m}$
, typical of image-vorticity-dominated evolutions.
$a>a_{m}$
, typical of image-vorticity-dominated evolutions.

Figure 9. As in figure 8 but for a negative PVa, opposing dynamics outflow. (a) For speed ratio
![]() $a=0.75$
, typical of all KW-flow-dominated evolutions with
$a=0.75$
, typical of all KW-flow-dominated evolutions with
![]() $a\leqslant 1$
, at times
$a\leqslant 1$
, at times
![]() $t=2$
, 5 and 15. (b) For
$t=2$
, 5 and 15. (b) For
![]() $a=1.8$
, so
$a=1.8$
, so
![]() $1<a<a_{m}$
, at times
$1<a<a_{m}$
, at times
![]() $t=1$
, 5 and 15. (c) For
$t=1$
, 5 and 15. (c) For
![]() $a=5$
, so
$a=5$
, so
![]() $a>a_{m}$
, at times
$a>a_{m}$
, at times
![]() $t=2$
, 5 and 8. In (b), (c), as in all vortically dominated flows, the maximum width of the downstream current is determined by hydraulic control at the downstream edge of the source.
$t=2$
, 5 and 8. In (b), (c), as in all vortically dominated flows, the maximum width of the downstream current is determined by hydraulic control at the downstream edge of the source.
For positive PVa, reinforcing dynamics, § 3.1 shows that, for all
![]() $a$
, a steady, critical, hydraulic solution, controlled from the upstream edge (
$a$
, a steady, critical, hydraulic solution, controlled from the upstream edge (
![]() $x=-W$
), set up by characteristics spreading downstream from
$x=-W$
), set up by characteristics spreading downstream from
![]() $x=-W$
, extends across the source region. Within the source region the unsteady constant-width current expands until it meets this steady solution as can be seen in each frame of figure 8. The controlled solution is established across the whole source region by time
$x=-W$
, extends across the source region. Within the source region the unsteady constant-width current expands until it meets this steady solution as can be seen in each frame of figure 8. The controlled solution is established across the whole source region by time
![]() $t_{2p}$
, given from (3.9) and (4.3) by
$t_{2p}$
, given from (3.9) and (4.3) by
![]() $Y_{S}(t_{2p})=Y_{hp}^{d}$
.
$Y_{S}(t_{2p})=Y_{hp}^{d}$
.
For negative PVa, opposing dynamics, a steady, critical, hydraulic solution, controlled from the downstream edge (
![]() $x=W$
) of the source region, extends across the source region provided
$x=W$
) of the source region, extends across the source region provided
![]() $a>1$
, so vorticity dynamics dominates the KW flow. As for positive PVa, the unsteady constant-width current expands until it meets the steady solution as in figure 9(b,c). The controlled solution originates from
$a>1$
, so vorticity dynamics dominates the KW flow. As for positive PVa, the unsteady constant-width current expands until it meets the steady solution as in figure 9(b,c). The controlled solution originates from
![]() $x=W$
and
$x=W$
and
![]() $y=Y_{hn}^{d}>0$
and is established over times
$y=Y_{hn}^{d}>0$
and is established over times
![]() $t>t_{1n}$
, where
$t>t_{1n}$
, where
![]() $Y_{S}(t_{1n})=Y_{hn}^{d}$
, by characteristics spreading upstream from
$Y_{S}(t_{1n})=Y_{hn}^{d}$
, by characteristics spreading upstream from
![]() $x=W$
, with all characteristics that exit downstream (and form the rarefaction described in § 4.2) having done so by time
$x=W$
, with all characteristics that exit downstream (and form the rarefaction described in § 4.2) having done so by time
![]() $t_{1n}$
. The controlled solution is fully established by time
$t_{1n}$
. The controlled solution is fully established by time
![]() $t_{2n}$
when
$t_{2n}$
when
![]() $Y_{S}(t_{2n})=Y_{hn}^{u}$
. For a negative PVa outflow with
$Y_{S}(t_{2n})=Y_{hn}^{u}$
. For a negative PVa outflow with
![]() $a\leqslant 1$
, so KW flow dominates, all characteristics exit downstream establishing the rarefaction of § 4.2, there is no steady hydraulic solution crossing the source region and the constant-width current grows indefinitely as in figure 9(a), where
$a\leqslant 1$
, so KW flow dominates, all characteristics exit downstream establishing the rarefaction of § 4.2, there is no steady hydraulic solution crossing the source region and the constant-width current grows indefinitely as in figure 9(a), where
![]() $a=0.75$
.
$a=0.75$
.
4.2 The downstream (
 $x>W$
) region for positive PVa
$x>W$
) region for positive PVa
The upstream and downstream currents for both positive and negative PVa outflows are led by rarefactions similar to those of § 3.2. Equations (4.2) show that characteristics for
![]() $|x|>W$
, outside the source region, are straight lines along which
$|x|>W$
, outside the source region, are straight lines along which
![]() $Z$
remains constant. On each characteristic the value of the constant is given by the value of
$Z$
remains constant. On each characteristic the value of the constant is given by the value of
![]() $Z$
on the characteristic when it crosses
$Z$
on the characteristic when it crosses
![]() $x=\pm W$
. For the uniform source here the value of
$x=\pm W$
. For the uniform source here the value of
![]() $Z$
on all characteristics in
$Z$
on all characteristics in
![]() $|x|<W$
is simply
$|x|<W$
is simply
![]() $Z_{S}(t)$
and so the value of
$Z_{S}(t)$
and so the value of
![]() $Z$
on any characteristic in
$Z$
on any characteristic in
![]() $|x|>W$
is determined by the time
$|x|>W$
is determined by the time
![]() $t$
when the characteristic crosses
$t$
when the characteristic crosses
![]() $x=\pm W$
.
$x=\pm W$
.
For positive PVa, consider a characteristic in
![]() $x>W$
and suppose that it crossed
$x>W$
and suppose that it crossed
![]() $x=W$
at a crossing time,
$x=W$
at a crossing time,
![]() $t=t_{c}$
. Then on this characteristic
$t=t_{c}$
. Then on this characteristic
![]() $Z(x,t)=Z_{S}(t_{c})=Z_{c}$
(say). Since the speed is constant on the characteristic (4.2) gives, equating expressions for the characteristic slope,
$Z(x,t)=Z_{S}(t_{c})=Z_{c}$
(say). Since the speed is constant on the characteristic (4.2) gives, equating expressions for the characteristic slope,
Inverting (4.3) for the crossing time
![]() $t_{c}$
in terms of
$t_{c}$
in terms of
![]() $Z_{c}$
and substituting in (4.4) gives the implicit equation for the boundary of the downstream rarefaction as
$Z_{c}$
and substituting in (4.4) gives the implicit equation for the boundary of the downstream rarefaction as
The solution of this quadratic equation for
![]() $Z_{c}$
gives the scaled width
$Z_{c}$
gives the scaled width
![]() $Z_{c}$
in terms of
$Z_{c}$
in terms of
![]() $x$
and
$x$
and
![]() $t$
. Equation (4.4) can also be regarded as giving the parametric representation
$t$
. Equation (4.4) can also be regarded as giving the parametric representation
with
![]() $Z_{c}=Z_{S}(t_{c})$
and the rarefaction at any time
$Z_{c}=Z_{S}(t_{c})$
and the rarefaction at any time
![]() $t$
given by taking all values of
$t$
given by taking all values of
![]() $t_{c}$
in the interval
$t_{c}$
in the interval
![]() $0\leqslant t_{c}\leqslant t$
, i.e. over all earlier crossing times. For
$0\leqslant t_{c}\leqslant t$
, i.e. over all earlier crossing times. For
![]() $t\leqslant t_{2p}$
these rarefactions join smoothly to the unsteady growing current in the source region as can be seen in figure 8. For
$t\leqslant t_{2p}$
these rarefactions join smoothly to the unsteady growing current in the source region as can be seen in figure 8. For
![]() $t\geqslant t_{2p}$
, form (4.6) continues to give the rarefaction provided the parameter
$t\geqslant t_{2p}$
, form (4.6) continues to give the rarefaction provided the parameter
![]() $t_{c}$
is restricted to the interval
$t_{c}$
is restricted to the interval
![]() $0\leqslant t_{c}\leqslant t_{2p}$
, so the minimum value of
$0\leqslant t_{c}\leqslant t_{2p}$
, so the minimum value of
![]() $Z_{c}$
is
$Z_{c}$
is
![]() $Z_{c}=Z_{S}(t_{2p})$
, giving a maximum current width of
$Z_{c}=Z_{S}(t_{2p})$
, giving a maximum current width of
![]() $Y_{c}=Y_{hp}^{d}$
. The rarefaction joins smoothly to the downstream end of the constant-width, hydraulically controlled current growing from the downstream edge (
$Y_{c}=Y_{hp}^{d}$
. The rarefaction joins smoothly to the downstream end of the constant-width, hydraulically controlled current growing from the downstream edge (
![]() $x=W$
) of the source region at times
$x=W$
) of the source region at times
![]() $t\geqslant t_{2p}$
, visible in all panels of figure 8. For
$t\geqslant t_{2p}$
, visible in all panels of figure 8. For
![]() $a\leqslant 1$
, where the KW flow reinforces but dominates the vortical flow, as in figure 8(a) where
$a\leqslant 1$
, where the KW flow reinforces but dominates the vortical flow, as in figure 8(a) where
![]() $a=1$
, this completes the solution.
$a=1$
, this completes the solution.
The slope of the nose of the rarefaction follows from differentiating (4.5) with respect to
![]() $x$
at fixed time and setting
$x$
at fixed time and setting
![]() $Z_{c}=1$
to give the value of the slope at the wall as
$Z_{c}=1$
to give the value of the slope at the wall as
The initial slope is
![]() $-a/2W$
and remains constant for
$-a/2W$
and remains constant for
![]() $a=1$
as in figure 8(a). For
$a=1$
as in figure 8(a). For
![]() $a<1$
, KW flow dominated, the nose slope decreases (in magnitude) as
$a<1$
, KW flow dominated, the nose slope decreases (in magnitude) as
![]() $t$
increases but for
$t$
increases but for
![]() $a>1$
, vortically dominated flow, the slope becomes progressively more negative, with the front steepening and becoming vertical when
$a>1$
, vortically dominated flow, the slope becomes progressively more negative, with the front steepening and becoming vertical when
![]() $t=t_{b}=2aW/(a^{2}-1)$
. At any subsequent time,
$t=t_{b}=2aW/(a^{2}-1)$
. At any subsequent time,
![]() $t>t_{b}$
, as for the positive PVa point source of § 3.2, the maximum downstream extent of the rarefaction occurs at
$t>t_{b}$
, as for the positive PVa point source of § 3.2, the maximum downstream extent of the rarefaction occurs at
![]() $Y>0$
, away from the wall. The downstream edge of the rarefaction does not reach the wall and instead terminates in a shock as in figure 8(b,c). Let the shock have position
$Y>0$
, away from the wall. The downstream edge of the rarefaction does not reach the wall and instead terminates in a shock as in figure 8(b,c). Let the shock have position
![]() $x_{J}(t)$
and the current there have width
$x_{J}(t)$
and the current there have width
![]() $Y_{J}(t)$
. Then, by conservation of mass, the shock moves at speed
$Y_{J}(t)$
. Then, by conservation of mass, the shock moves at speed
the change in downstream flux divided by the current width, where, as usual,
![]() $Z_{J}=\exp (-Y_{J}/a)$
. Differentiating (4.5) with respect to
$Z_{J}=\exp (-Y_{J}/a)$
. Differentiating (4.5) with respect to
![]() $t$
and setting
$t$
and setting
![]() $Z_{c}=Z_{J}$
gives a second expression for the speed of the downstream edge of the rarefaction. Equating this with (4.8) gives the ordinary differential equation for
$Z_{c}=Z_{J}$
gives a second expression for the speed of the downstream edge of the rarefaction. Equating this with (4.8) gives the ordinary differential equation for
![]() $Z_{J}(t)$
,
$Z_{J}(t)$
,
This equation is to be solved subject to the condition of a jump initiated at
![]() $t=t_{b}$
, i.e.
$t=t_{b}$
, i.e.
![]() $Z_{J}(t_{b})=1$
. The jump height
$Z_{J}(t_{b})=1$
. The jump height
![]() $Z_{J}(t)$
can be obtained as an implicit function of
$Z_{J}(t)$
can be obtained as an implicit function of
![]() $t$
but it is more straightforward to compute
$t$
but it is more straightforward to compute
![]() $Z_{J}(t)$
directly by numerically integrating (4.9). The locus of the point
$Z_{J}(t)$
directly by numerically integrating (4.9). The locus of the point
![]() $(x_{c},Z_{c})$
where the downstream rarefaction meets the jump is shown as the thin line in each of figure 8(b,c), growing from
$(x_{c},Z_{c})$
where the downstream rarefaction meets the jump is shown as the thin line in each of figure 8(b,c), growing from
![]() $x\sim 2.2$
in figure 8(b) where
$x\sim 2.2$
in figure 8(b) where
![]() $a=1.6$
and almost immediately in figure 8(c) where
$a=1.6$
and almost immediately in figure 8(c) where
![]() $a=5$
. The jump can grow until the right-hand side of (4.9) vanishes, so that
$a=5$
. The jump can grow until the right-hand side of (4.9) vanishes, so that
![]() $\text{d}Z_{J}/\text{d}t=0$
. This occurs for a maximum jump height
$\text{d}Z_{J}/\text{d}t=0$
. This occurs for a maximum jump height
![]() $Y_{m}=-a\log Z_{m}$
where
$Y_{m}=-a\log Z_{m}$
where
![]() $0\leqslant Z_{m}\leqslant 1$
solves
$0\leqslant Z_{m}\leqslant 1$
solves
The root is simple and thus the jump asymptotes to its maximum height as a decaying exponential. As
![]() $a$
increases,
$a$
increases,
![]() $Y_{m}$
increases monotonically from zero when
$Y_{m}$
increases monotonically from zero when
![]() $a=1$
, until
$a=1$
, until
![]() $Y_{m}=Y_{hp}^{d}$
, when
$Y_{m}=Y_{hp}^{d}$
, when
![]() $a=a_{m}\sim 1.8684$
, given by substituting (3.9) in (4.10). In figure 8(b),
$a=a_{m}\sim 1.8684$
, given by substituting (3.9) in (4.10). In figure 8(b),
![]() $1<a<a_{m}$
so
$1<a<a_{m}$
so
![]() $0<Y_{m}<Y_{hp}^{d}$
and the jump asymptotes downstream to height
$0<Y_{m}<Y_{hp}^{d}$
and the jump asymptotes downstream to height
![]() $Y_{m}$
, terminating the rarefaction at all times. The jump speed is faster than the speed of the junction with the constant-width current at the rear of the rarefaction and so the rarefaction elongates and flattens with increasing time. In figure 8(c), typical of all vortically dominated reinforcing flows,
$Y_{m}$
, terminating the rarefaction at all times. The jump speed is faster than the speed of the junction with the constant-width current at the rear of the rarefaction and so the rarefaction elongates and flattens with increasing time. In figure 8(c), typical of all vortically dominated reinforcing flows,
![]() $a>a_{m}$
so
$a>a_{m}$
so
![]() $Y_{m}>Y_{hp}^{d}$
. The jump speed is slower than the speed of the junction with the constant-width current and so the rarefaction contracts with increasing time until it is extinguished at time
$Y_{m}>Y_{hp}^{d}$
. The jump speed is slower than the speed of the junction with the constant-width current and so the rarefaction contracts with increasing time until it is extinguished at time
![]() $t_{J}$
when
$t_{J}$
when
![]() $Y_{J}=Y_{hp}^{d}$
, with the current then continuing downstream with constant width
$Y_{J}=Y_{hp}^{d}$
, with the current then continuing downstream with constant width
![]() $Y_{hp}^{d}$
terminating in a full-width jump.
$Y_{hp}^{d}$
terminating in a full-width jump.
4.3 The downstream (
 $x>W$
) region for negative PVa
$x>W$
) region for negative PVa
For negative PVa, the downstream rarefaction follows similarly to (4.5), equation (4.6) with (4.2) giving the slope-speed equation
and so the implicit equation for the boundary of the rarefaction as
and the parametric representation
with the parameter
![]() $t_{c}$
covering the interval
$t_{c}$
covering the interval
![]() $0\leqslant t_{c}\leqslant t$
. Differentiating (4.12) and setting
$0\leqslant t_{c}\leqslant t$
. Differentiating (4.12) and setting
![]() $Z_{c}=1$
shows that, for all
$Z_{c}=1$
shows that, for all
![]() $a$
, the slope of the nose of the rarefaction decreases with increasing
$a$
, the slope of the nose of the rarefaction decreases with increasing
![]() $t$
and so no shock forms at the leading edge of the downstream rarefaction for negative PVa. Thus (4.13) gives the solution for all times for
$t$
and so no shock forms at the leading edge of the downstream rarefaction for negative PVa. Thus (4.13) gives the solution for all times for
![]() $a\leqslant 1$
, giving a rarefaction that matches smoothly to the indefinitely widening current in the source region, as in figure 9(a). For
$a\leqslant 1$
, giving a rarefaction that matches smoothly to the indefinitely widening current in the source region, as in figure 9(a). For
![]() $a>1$
the source region flow becomes controlled from its downstream edge (
$a>1$
the source region flow becomes controlled from its downstream edge (
![]() $x=W$
) at times
$x=W$
) at times
![]() $t\geqslant t_{1n}$
. Form (4.13) continues to describe the rarefaction at times
$t\geqslant t_{1n}$
. Form (4.13) continues to describe the rarefaction at times
![]() $t\geqslant t_{1n}$
provided the parameter
$t\geqslant t_{1n}$
provided the parameter
![]() $t_{c}$
is restricted to the interval
$t_{c}$
is restricted to the interval
![]() $0\leqslant t_{c}\leqslant t_{1n}$
, giving a maximum rarefaction width of
$0\leqslant t_{c}\leqslant t_{1n}$
, giving a maximum rarefaction width of
![]() $Y_{c}=Y_{hn}^{d}$
which joins smoothly to the controlled solution in the source region as in figure 9(b,c).
$Y_{c}=Y_{hn}^{d}$
which joins smoothly to the controlled solution in the source region as in figure 9(b,c).
4.4 The upstream (
 $x<-W$
) region for negative PVa
$x<-W$
) region for negative PVa
The upstream current for negative PVa shares many properties with the downstream current for positive PVa and so simply the differences are noted here. The slope-speed equation
gives the implicit equation for the boundary the rarefaction as
and the parametric representation
with the parameter
![]() $t_{c}$
covering the interval
$t_{c}$
covering the interval
![]() $0\leqslant t_{c}\leqslant t$
. For all
$0\leqslant t_{c}\leqslant t$
. For all
![]() $a$
, for
$a$
, for
![]() $t<t_{2n}$
, the downstream edge (
$t<t_{2n}$
, the downstream edge (
![]() $x=-W$
) of the rarefaction joins smoothly to the growing constant-width current in the source region. For
$x=-W$
) of the rarefaction joins smoothly to the growing constant-width current in the source region. For
![]() $a\leqslant 1$
the source region width grows indefinitely and so to does the rarefaction width, as in figure 9(a). For
$a\leqslant 1$
the source region width grows indefinitely and so to does the rarefaction width, as in figure 9(a). For
![]() $a>1$
steady flow, hydraulically controlled from the downstream edge, is established across the whole source region by
$a>1$
steady flow, hydraulically controlled from the downstream edge, is established across the whole source region by
![]() $t=t_{2n}$
. Form (4.16) continues to describe the rarefaction at times
$t=t_{2n}$
. Form (4.16) continues to describe the rarefaction at times
![]() $t\geqslant t_{2n}$
provided the parameter
$t\geqslant t_{2n}$
provided the parameter
![]() $t_{c}$
is restricted to the interval
$t_{c}$
is restricted to the interval
![]() $0\leqslant t_{c}\leqslant t_{2n}$
, giving a maximum rarefaction width of
$0\leqslant t_{c}\leqslant t_{2n}$
, giving a maximum rarefaction width of
![]() $Y_{c}=Y_{hn}^{u}$
which joins smoothly to the controlled solution in the source region as in figure 9(b,c). Differentiating (4.15) and setting
$Y_{c}=Y_{hn}^{u}$
which joins smoothly to the controlled solution in the source region as in figure 9(b,c). Differentiating (4.15) and setting
![]() $Z_{c}=1$
shows that, for all
$Z_{c}=1$
shows that, for all
![]() $a$
, the rarefaction immediately has infinite slope at
$a$
, the rarefaction immediately has infinite slope at
![]() $x=-W$
,
$x=-W$
,
![]() $t=0$
. The breaking time
$t=0$
. The breaking time
![]() $t_{b}$
for negative PVa outflows is thus zero for all
$t_{b}$
for negative PVa outflows is thus zero for all
![]() $a$
in contrast to positive PVa outflows where
$a$
in contrast to positive PVa outflows where
![]() $t_{b}>0$
for
$t_{b}>0$
for
![]() $a>1$
and rarefactions do not break for
$a>1$
and rarefactions do not break for
![]() $a\leqslant 1$
. A shock thus leads the rarefaction upstream for all
$a\leqslant 1$
. A shock thus leads the rarefaction upstream for all
![]() $t>0$
. Similar considerations to those giving (4.9) give the governing equation for the jump height,
$t>0$
. Similar considerations to those giving (4.9) give the governing equation for the jump height,
subject to the initial condition
![]() $Z_{J}(0)=1$
. Again a numerical solution is more convenient than the implicit analytical solution. The locus of the point
$Z_{J}(0)=1$
. Again a numerical solution is more convenient than the implicit analytical solution. The locus of the point
![]() $(x_{c},Z_{c})$
where the upstream rarefaction meets the jump is shown as the thin line in figure 9. The jump can grow until the right side of (4.17) vanishes, giving a maximum jump height
$(x_{c},Z_{c})$
where the upstream rarefaction meets the jump is shown as the thin line in figure 9. The jump can grow until the right side of (4.17) vanishes, giving a maximum jump height
![]() $Y_{m}$
satisfying
$Y_{m}$
satisfying
i.e.
![]() $Y_{m}\approx 1.25643a$
, with the jump asymptoting exponentially with increasing
$Y_{m}\approx 1.25643a$
, with the jump asymptoting exponentially with increasing
![]() $-x$
or
$-x$
or
![]() $t$
to its maximum height. The maximum increases linearly with
$t$
to its maximum height. The maximum increases linearly with
![]() $a$
until
$a$
until
![]() $Y_{m}=Y_{hn}^{u}$
which occurs first when
$Y_{m}=Y_{hn}^{u}$
which occurs first when
If
![]() $a\leqslant a_{m}$
, as in figure 9(a,b), then the shock height asymptotes upstream to
$a\leqslant a_{m}$
, as in figure 9(a,b), then the shock height asymptotes upstream to
![]() $Y_{m}$
with the rarefaction lengthening and flattening as for the positive PVa outflow of figure 8(b). If
$Y_{m}$
with the rarefaction lengthening and flattening as for the positive PVa outflow of figure 8(b). If
![]() $a\geqslant a_{m}$
, as in figure 9(c),
$a\geqslant a_{m}$
, as in figure 9(c),
![]() $Y_{m}>Y_{hn}^{u}$
and, as in figure 8(c), the rarefaction is eventually extinguished with the upstream-flowing controlled current led by a full-width jump.
$Y_{m}>Y_{hn}^{u}$
and, as in figure 8(c), the rarefaction is eventually extinguished with the upstream-flowing controlled current led by a full-width jump.
Figure 9(b) gives the current boundary for
![]() $a=1.8$
. The initial evolution follows that of figure 9(a) for
$a=1.8$
. The initial evolution follows that of figure 9(a) for
![]() $a\leqslant 1$
with an expanding current in the source region bordered by upstream and downstream rarefactions with a jump terminating the upstream-propagating rarefaction. However (4.3) shows that at time
$a\leqslant 1$
with an expanding current in the source region bordered by upstream and downstream rarefactions with a jump terminating the upstream-propagating rarefaction. However (4.3) shows that at time
![]() $t_{1}=2a[\exp (-Y_{hn}^{d})-1]$
the current width has grown to equal
$t_{1}=2a[\exp (-Y_{hn}^{d})-1]$
the current width has grown to equal
![]() $Y_{hn}^{d}$
. All characteristics that exit the source region downstream have done so by time
$Y_{hn}^{d}$
. All characteristics that exit the source region downstream have done so by time
![]() $t_{1}$
and characteristics spread upstream from the point
$t_{1}$
and characteristics spread upstream from the point
![]() $(t,x)=(t_{1},W)$
to give the hydraulic solution (3.8) controlled from the downstream edge of the source. This form of solution holds until time
$(t,x)=(t_{1},W)$
to give the hydraulic solution (3.8) controlled from the downstream edge of the source. This form of solution holds until time
![]() $t_{2}=2a[\exp (-Y_{hn}^{u})-1]$
when the hydraulic solution is established across the whole source region and the constant-width current in the source region has disappeared. The region of controlled flow then expands upstream at constant speed
$t_{2}=2a[\exp (-Y_{hn}^{u})-1]$
when the hydraulic solution is established across the whole source region and the constant-width current in the source region has disappeared. The region of controlled flow then expands upstream at constant speed
![]() $aZ_{hn}^{u}(1-Z_{hn}^{u})$
, led by the rarefaction.
$aZ_{hn}^{u}(1-Z_{hn}^{u})$
, led by the rarefaction.
Figure 9(c) gives an example of the current boundary in this case for
![]() $a=5$
, so
$a=5$
, so
![]() $a>a_{m}$
. The evolution initially follows that shown in figure 9(a,b) for evolutions with
$a>a_{m}$
. The evolution initially follows that shown in figure 9(a,b) for evolutions with
![]() $a<a_{m}$
. A constant-width current in the source region expands until time
$a<a_{m}$
. A constant-width current in the source region expands until time
![]() $t_{1}$
when it becomes progressively squeezed from downstream as controlled flow is established in
$t_{1}$
when it becomes progressively squeezed from downstream as controlled flow is established in
![]() $x<W$
from the critical point at
$x<W$
from the critical point at
![]() $x=W$
. By time
$x=W$
. By time
![]() $t_{2}$
this controlled flow is established across the whole source region and expands at constant speed into
$t_{2}$
this controlled flow is established across the whole source region and expands at constant speed into
![]() $x<-W$
as a constant-width current led by a rarefaction terminated by a growing jump. However when
$x<-W$
as a constant-width current led by a rarefaction terminated by a growing jump. However when
![]() $a>a_{m}$
the limiting height of this jump exceeds the maximum width of the controlled solution. The junction between the downstream-edge-controlled solution and the rarefaction is non-dissipative and so moves at the controlled solution speed until it overtakes the slower-moving dissipative jump that terminates the rarefaction upstream. Thus at some finite time
$a>a_{m}$
the limiting height of this jump exceeds the maximum width of the controlled solution. The junction between the downstream-edge-controlled solution and the rarefaction is non-dissipative and so moves at the controlled solution speed until it overtakes the slower-moving dissipative jump that terminates the rarefaction upstream. Thus at some finite time
![]() $t_{3}>t_{2}$
the rarefaction disappears and the hydraulic solution simply terminates at a dissipative jump.
$t_{3}>t_{2}$
the rarefaction disappears and the hydraulic solution simply terminates at a dissipative jump.
4.5 Terminal speeds of the leading edges of the anomalies
The speeds of the leading edges of the PV anomalies are of observational interest. The solutions here show that these speeds vary as the flow evolves but asymptote to a steady terminal velocity,
![]() $u_{e}$
(say), at large times. Figure 10(a) shows
$u_{e}$
(say), at large times. Figure 10(a) shows
![]() $u_{e}$
of the downstream edge for positive PVa as a function of
$u_{e}$
of the downstream edge for positive PVa as a function of
![]() $a$
. For
$a$
. For
![]() $a<1$
, KW flow dominated, this is the speed of the leading edge of the rarefaction and is given by substituting
$a<1$
, KW flow dominated, this is the speed of the leading edge of the rarefaction and is given by substituting
![]() $Z_{c}=1$
into (4.4) as
$Z_{c}=1$
into (4.4) as
![]() $u_{e}=a(\unicode[STIX]{x1D706}-1)=1/a$
, precisely the speed, downstream from the source, of the zero PVa component of § 2.1. For
$u_{e}=a(\unicode[STIX]{x1D706}-1)=1/a$
, precisely the speed, downstream from the source, of the zero PVa component of § 2.1. For
![]() $1<a<a_{m}$
, moderately vorticity-dominated flow, the current is led by a jump of height
$1<a<a_{m}$
, moderately vorticity-dominated flow, the current is led by a jump of height
![]() $Y_{m}$
at speed given by substituting
$Y_{m}$
at speed given by substituting
![]() $Z_{m}$
from (4.10) into (4.4). With increasing
$Z_{m}$
from (4.10) into (4.4). With increasing
![]() $a$
the speed decreases as the width
$a$
the speed decreases as the width
![]() $Y_{m}$
increases. For
$Y_{m}$
increases. For
![]() $a\geqslant a_{m}$
, strongly vortex-dominated flow, the current width is the controlled width
$a\geqslant a_{m}$
, strongly vortex-dominated flow, the current width is the controlled width
![]() $Y_{hp}^{d}$
and so
$Y_{hp}^{d}$
and so
![]() $u_{e}=1/Y_{hp}^{d}$
. In the limit
$u_{e}=1/Y_{hp}^{d}$
. In the limit
![]() $a\rightarrow \infty$
,
$a\rightarrow \infty$
,
![]() $Y_{hp}^{d}\rightarrow \surd 2$
and
$Y_{hp}^{d}\rightarrow \surd 2$
and
![]() $u_{e}\rightarrow 1/\surd 2$
, as in the vorticity-dominated limit (Johnson & McDonald Reference Johnson and McDonald2006). The speeds, here and elsewhere, are non-dimensionalised on
$u_{e}\rightarrow 1/\surd 2$
, as in the vorticity-dominated limit (Johnson & McDonald Reference Johnson and McDonald2006). The speeds, here and elsewhere, are non-dimensionalised on
![]() $Q_{0}/L_{v}=(Q_{0}|\unicode[STIX]{x1D6F1}_{0}|D)^{1/2}$
, appropriate for vorticity-dominated flows. The dashed curve in figure 10(a) shows
$Q_{0}/L_{v}=(Q_{0}|\unicode[STIX]{x1D6F1}_{0}|D)^{1/2}$
, appropriate for vorticity-dominated flows. The dashed curve in figure 10(a) shows
![]() $au_{e}$
, the speed non-dimensionalised on
$au_{e}$
, the speed non-dimensionalised on
![]() $Q_{0}\,f/c$
, appropriate for the KW flow. In both cases the speed is proportional to the area flux
$Q_{0}\,f/c$
, appropriate for the KW flow. In both cases the speed is proportional to the area flux
![]() $Q_{0}$
divided by an appropriate length, related to the current width, where the length is the dimensional Rossby radius in KW flow and the vortex scale
$Q_{0}$
divided by an appropriate length, related to the current width, where the length is the dimensional Rossby radius in KW flow and the vortex scale
![]() $L_{v}$
in vorticity-dominated flow, with the non-dimensional parameter
$L_{v}$
in vorticity-dominated flow, with the non-dimensional parameter
![]() $a$
giving the ratio of the velocity scale for vorticity-driven flow to that for the KW flow. In the quasi-geostrophic limit both velocity scales are small compared to the long-wave speed
$a$
giving the ratio of the velocity scale for vorticity-driven flow to that for the KW flow. In the quasi-geostrophic limit both velocity scales are small compared to the long-wave speed
![]() $c$
.
$c$
.

Figure 10. The terminal speeds,
![]() $u_{e}$
, of the leading edges of the anomalies as a function of
$u_{e}$
, of the leading edges of the anomalies as a function of
![]() $a$
. (a) Positive PVa,
$a$
. (a) Positive PVa,
![]() $\unicode[STIX]{x1D6F1}>0$
, so KW flow and image vorticity reinforce. The solid line gives
$\unicode[STIX]{x1D6F1}>0$
, so KW flow and image vorticity reinforce. The solid line gives
![]() $u_{e}$
normalised on
$u_{e}$
normalised on
![]() $(Q_{0}|\unicode[STIX]{x1D6F1}_{0}|D)^{1/2}$
, the vortex velocity scale, and approaches
$(Q_{0}|\unicode[STIX]{x1D6F1}_{0}|D)^{1/2}$
, the vortex velocity scale, and approaches
![]() $1/\surd 2$
as
$1/\surd 2$
as
![]() $a\rightarrow \infty$
. The dashed line gives
$a\rightarrow \infty$
. The dashed line gives
![]() $au_{e}$
, the speed normalised on
$au_{e}$
, the speed normalised on
![]() $Q_{0}\,f/c$
, the KW flow velocity scale, and so approaches 1 as
$Q_{0}\,f/c$
, the KW flow velocity scale, and so approaches 1 as
![]() $a\rightarrow 0$
. (b) Negative PVa,
$a\rightarrow 0$
. (b) Negative PVa,
![]() $\unicode[STIX]{x1D6F1}<0$
, so KW flow and image vorticity oppose, with speeds normalised on the vortex velocity scale, as elsewhere. The dashed line gives the downstream speed which is precisely the KW flow speed
$\unicode[STIX]{x1D6F1}<0$
, so KW flow and image vorticity oppose, with speeds normalised on the vortex velocity scale, as elsewhere. The dashed line gives the downstream speed which is precisely the KW flow speed
![]() $1/a$
and the solid line gives the upstream speed which approaches
$1/a$
and the solid line gives the upstream speed which approaches
![]() $1/\surd 2$
as
$1/\surd 2$
as
![]() $a\rightarrow \infty$
.
$a\rightarrow \infty$
.
For negative PVa outflows the terminal speed of the downstream leading edge is the speed of the rarefaction at the wall and so follows from substituting
![]() $Z_{c}=1$
into (4.11) yielding, once again,
$Z_{c}=1$
into (4.11) yielding, once again,
![]() $u_{e}=1/a$
, precisely the speed, downstream from the source, of the zero PVa component of § 2.1, shown dashed in figure 10(b). The terminal speed of the downstream leading edge is given by the jump speed. For
$u_{e}=1/a$
, precisely the speed, downstream from the source, of the zero PVa component of § 2.1, shown dashed in figure 10(b). The terminal speed of the downstream leading edge is given by the jump speed. For
![]() $a<a_{m}$
, KW flow dominated and also moderately vortically dominated flow, the terminal jump height is given by (4.18) with the terminal speed following from substituting
$a<a_{m}$
, KW flow dominated and also moderately vortically dominated flow, the terminal jump height is given by (4.18) with the terminal speed following from substituting
![]() $Z_{m}$
into (4.11). For
$Z_{m}$
into (4.11). For
![]() $a\geqslant a_{m}$
, strongly vortex-dominated flow, the current width is the controlled width
$a\geqslant a_{m}$
, strongly vortex-dominated flow, the current width is the controlled width
![]() $Y_{hn}^{u}$
and so
$Y_{hn}^{u}$
and so
![]() $u_{e}=Q_{e}/Y_{hn}^{u}=(1-1/2a^{2})/Y_{hn}^{u}$
, from § 3.1. In the limit
$u_{e}=Q_{e}/Y_{hn}^{u}=(1-1/2a^{2})/Y_{hn}^{u}$
, from § 3.1. In the limit
![]() $a\rightarrow \infty$
,
$a\rightarrow \infty$
,
![]() $Y_{hn}^{u}\rightarrow \surd 2$
and
$Y_{hn}^{u}\rightarrow \surd 2$
and
![]() $u_{e}\rightarrow 1/\surd 2$
, as in the vorticity-dominated limit (Johnson & McDonald Reference Johnson and McDonald2006). The solid line in figure 10(b) shows this upstream terminal speed, which is small compared to the downstream KW flow speed when vortex effects are weak (
$u_{e}\rightarrow 1/\surd 2$
, as in the vorticity-dominated limit (Johnson & McDonald Reference Johnson and McDonald2006). The solid line in figure 10(b) shows this upstream terminal speed, which is small compared to the downstream KW flow speed when vortex effects are weak (
![]() $a\lesssim 2$
) but exceeds the KW flow speed for strong vortex effects (
$a\lesssim 2$
) but exceeds the KW flow speed for strong vortex effects (
![]() $a\gtrsim 2$
).
$a\gtrsim 2$
).
5 The full problem
5.1 Positive PVa outflows
The full problem (2.1)–(2.4) can be solved numerically with extreme accuracy, using the CD implementation of Dritschel (Reference Dritschel1988) and simply replacing the logarithmic Green’s function in Johnson & McDonald (Reference Johnson and McDonald2006) by the appropriate Green’s function for (2.1), i.e.
![]() $\text{K}_{0}([(x-x_{0})^{2}+(y-y_{0})^{2}]^{1/2}/a)$
where
$\text{K}_{0}([(x-x_{0})^{2}+(y-y_{0})^{2}]^{1/2}/a)$
where
![]() $\text{K}_{0}$
is the modified Bessel function of the second kind of order zero. The analysis of § 4 formally requires that the source width is large, i.e.
$\text{K}_{0}$
is the modified Bessel function of the second kind of order zero. The analysis of § 4 formally requires that the source width is large, i.e.
![]() $W\gg 1$
, but, as suggested above, this is overly restrictive in practice. Figure 11 compares CD integrations of the unapproximated problem with long-wave solutions for a point source of positive PVa, obtained by setting
$W\gg 1$
, but, as suggested above, this is overly restrictive in practice. Figure 11 compares CD integrations of the unapproximated problem with long-wave solutions for a point source of positive PVa, obtained by setting
![]() $W=0$
in § 4.2. Even for this most extreme case, the agreement is remarkable. The exit velocity is infinite so the controlled solution is set up instantaneously giving a crossing time of
$W=0$
in § 4.2. Even for this most extreme case, the agreement is remarkable. The exit velocity is infinite so the controlled solution is set up instantaneously giving a crossing time of
![]() $t_{c}=0$
. For
$t_{c}=0$
. For
![]() $a<1$
and
$a<1$
and
![]() $t>0$
, equation (4.7) shows that both the rarefaction and its nose flatten as they propagate downstream. For
$t>0$
, equation (4.7) shows that both the rarefaction and its nose flatten as they propagate downstream. For
![]() $a=1$
the rarefaction again flattens as it propagates downstream with however the nose meeting the wall at right angles, as in figure 11(a), similarly to figure 8(a). In figure 11(b),
$a=1$
the rarefaction again flattens as it propagates downstream with however the nose meeting the wall at right angles, as in figure 11(a), similarly to figure 8(a). In figure 11(b),
![]() $1<a<a_{m}$
, as in figure 8(b) so the leading jump in the long-wave solution asymptotes to a value less than the constant width of the hydraulically controlled current. Dispersion in the full problem means that the nose of the flow is rounded and waves appear on the boundary of the controlled current. In figure 11(c),
$1<a<a_{m}$
, as in figure 8(b) so the leading jump in the long-wave solution asymptotes to a value less than the constant width of the hydraulically controlled current. Dispersion in the full problem means that the nose of the flow is rounded and waves appear on the boundary of the controlled current. In figure 11(c),
![]() $a>a_{m}$
, as in figure 8(c) so the constant-width, hydraulically controlled current is set-up immediately. The flow development closely follows the vorticity-dominated solution of Johnson & McDonald (Reference Johnson and McDonald2006), corresponding to
$a>a_{m}$
, as in figure 8(c) so the constant-width, hydraulically controlled current is set-up immediately. The flow development closely follows the vorticity-dominated solution of Johnson & McDonald (Reference Johnson and McDonald2006), corresponding to
![]() $a\gg 1$
. Rossby waves on the current boundary originate from small fluctuations near the source and propagate downstream, with high PV to their right, towards the nose of the current. The speed of the waves decreases as they propagate towards the nose and so their amplitude increases to conserve wave action flux. Johnson & McDonald (Reference Johnson and McDonald2006) give exact solutions for linear waves on the steady asymptotic flow in the vorticity-dominated limit and the increase in amplitude is discussed there and in Haynes et al. (Reference Haynes, Johnson and Hurst1993). The finite amplitude waves are governed by (2.6b
) and (2.21). The development of a leading eddy in the vorticity-dominated limit is discussed in Stern & Pratt (Reference Stern and Pratt1985). Note that the hydraulic solution does not exceed
$a\gg 1$
. Rossby waves on the current boundary originate from small fluctuations near the source and propagate downstream, with high PV to their right, towards the nose of the current. The speed of the waves decreases as they propagate towards the nose and so their amplitude increases to conserve wave action flux. Johnson & McDonald (Reference Johnson and McDonald2006) give exact solutions for linear waves on the steady asymptotic flow in the vorticity-dominated limit and the increase in amplitude is discussed there and in Haynes et al. (Reference Haynes, Johnson and Hurst1993). The finite amplitude waves are governed by (2.6b
) and (2.21). The development of a leading eddy in the vorticity-dominated limit is discussed in Stern & Pratt (Reference Stern and Pratt1985). Note that the hydraulic solution does not exceed
![]() $Y_{hp}^{d}$
and so
$Y_{hp}^{d}$
and so
![]() ${\mathcal{F}}^{\prime \prime }(Z)$
remains single-signed along the entire current boundary. The disturbance speed is a monotonic function of the current width throughout the evolution and so only classical shocks and rarefactions are present in positive PVa outflows. For all
${\mathcal{F}}^{\prime \prime }(Z)$
remains single-signed along the entire current boundary. The disturbance speed is a monotonic function of the current width throughout the evolution and so only classical shocks and rarefactions are present in positive PVa outflows. For all
![]() $a$
, from (3.5), throughout the evolution of the current the injected momentum flux in the hydraulic limit is positive,
$a$
, from (3.5), throughout the evolution of the current the injected momentum flux in the hydraulic limit is positive,
![]() $\unicode[STIX]{x0394}M_{s}>0$
, and the current turns downstream.
$\unicode[STIX]{x0394}M_{s}>0$
, and the current turns downstream.

Figure 11. CD integrations for the full problem (thin lines, blue online) and the analytical long-wave solutions (thick lines, red online) for positive PVa outflows from a point source at times
![]() $t=10$
, 50, and 100 for non-dimensional Rossby radii of (top to bottom) (a)
$t=10$
, 50, and 100 for non-dimensional Rossby radii of (top to bottom) (a)
![]() $a=1$
, (b)
$a=1$
, (b)
![]() $a=1.3$
, (c)
$a=1.3$
, (c)
![]() $a=2$
.
$a=2$
.
5.2 Negative PVa outflows
Figure 12 compares CD integrations with long-wave solutions for a point source of negative PVa, obtained by setting
![]() $W=0$
in §§ 4.3 and 4.4. As for the positive PVa point source, the exit speed is infinite and so in the long-wave solution the asymptotic values on
$W=0$
in §§ 4.3 and 4.4. As for the positive PVa point source, the exit speed is infinite and so in the long-wave solution the asymptotic values on
![]() $x=0$
are set up instantly. For figure 12(a), where
$x=0$
are set up instantly. For figure 12(a), where
![]() $a=0.75$
, so
$a=0.75$
, so
![]() $a\leqslant 1$
as in figure 9(a), this means that the upstream and downstream rarefactions have infinite width at
$a\leqslant 1$
as in figure 9(a), this means that the upstream and downstream rarefactions have infinite width at
![]() $x=0$
. Away from the origin the downstream rarefaction of the long-wave solution is indistinguishable from the full integration and the upstream rarefaction and jump model the full solution, where again sharp changes in the boundary are smoothed by dispersion. In figure 12(b),
$x=0$
. Away from the origin the downstream rarefaction of the long-wave solution is indistinguishable from the full integration and the upstream rarefaction and jump model the full solution, where again sharp changes in the boundary are smoothed by dispersion. In figure 12(b),
![]() $1<a<a_{m}$
, as in figure 9(b) so the long-wave solution asymptotes to a jump of height less than the constant width of the hydraulically controlled current. The long-wave solutions capture much of the flow behaviour but differences are visible. The large exit velocity at the origin means that the full solution overshoots the minimal controlled solution. The full solution adjusts to a steady solution with upstream and downstream heights linked through (3.8) but the upstream current is wider and the downstream narrower than for the minimal solution. The downstream rarefaction joins to a constant-width current issuing from the downstream control and the upstream rarefaction joins to a constant-width current terminating in a jump. Both these effects are the result of the non-convexity of the flux function
$1<a<a_{m}$
, as in figure 9(b) so the long-wave solution asymptotes to a jump of height less than the constant width of the hydraulically controlled current. The long-wave solutions capture much of the flow behaviour but differences are visible. The large exit velocity at the origin means that the full solution overshoots the minimal controlled solution. The full solution adjusts to a steady solution with upstream and downstream heights linked through (3.8) but the upstream current is wider and the downstream narrower than for the minimal solution. The downstream rarefaction joins to a constant-width current issuing from the downstream control and the upstream rarefaction joins to a constant-width current terminating in a jump. Both these effects are the result of the non-convexity of the flux function
![]() ${\mathcal{F}}(Z)$
.
${\mathcal{F}}(Z)$
.

Figure 12. As for figure 11 but for a negative PVa outflow. (a)
![]() $a=0.75$
at times
$a=0.75$
at times
![]() $t=10$
, 20 and 100. (b)
$t=10$
, 20 and 100. (b)
![]() $a=1.3$
at times
$a=1.3$
at times
![]() $t=30$
, 150 and 500.
$t=30$
, 150 and 500.

Figure 13. As for figure 12 but for a uniform source of half-width
![]() $W=20$
. (a)
$W=20$
. (a)
![]() $a=1.3$
at times
$a=1.3$
at times
![]() $t=30$
, 150 and 500. (b)
$t=30$
, 150 and 500. (b)
![]() $a=2$
at times
$a=2$
at times
![]() $t=10$
, 50 and 200.
$t=10$
, 50 and 200.
The question arises as to how much of the deviation seen in figure 12 is due to choosing the extreme of point-source forcing
![]() $(W=0)$
. Figure 13 compares full integrations with long-wave solutions for a uniform source of negative PVa of width
$(W=0)$
. Figure 13 compares full integrations with long-wave solutions for a uniform source of negative PVa of width
![]() $W=20$
. The agreement is much closer, particularly at early times when the full and analytical solutions are almost indistinguishable. As in § 4.1, the current width across the source region grows uniformly until it reaches the controlled solution, which is established from the downstream edge,
$W=20$
. The agreement is much closer, particularly at early times when the full and analytical solutions are almost indistinguishable. As in § 4.1, the current width across the source region grows uniformly until it reaches the controlled solution, which is established from the downstream edge,
![]() $x=W$
. At later times, as for positive PVa, boundary Rossby waves originating from small fluctuations near the source propagate, here upstream with low PVa to the left, towards the nose of the current, again slowing and increasing in amplitude. Lengthening the source region means that the hydraulic theory becomes more accurate near the source but the introduction of a definite length scale, and thus a particular value of
$x=W$
. At later times, as for positive PVa, boundary Rossby waves originating from small fluctuations near the source propagate, here upstream with low PVa to the left, towards the nose of the current, again slowing and increasing in amplitude. Lengthening the source region means that the hydraulic theory becomes more accurate near the source but the introduction of a definite length scale, and thus a particular value of
![]() $\unicode[STIX]{x1D716}$
, introduces dispersive waves that are absent in the point-source solutions of figure 12. At the latest times, a small shelf grows from the downstream edge, a manifestation of the non-convex flux function.
$\unicode[STIX]{x1D716}$
, introduces dispersive waves that are absent in the point-source solutions of figure 12. At the latest times, a small shelf grows from the downstream edge, a manifestation of the non-convex flux function.
In figure 12(a)
![]() $a=0.75$
and so (3.7) suggests that throughout the evolution of the current the injected momentum flux in is positive,
$a=0.75$
and so (3.7) suggests that throughout the evolution of the current the injected momentum flux in is positive,
![]() $\unicode[STIX]{x0394}M_{s}>0$
, and the current should turn predominantly downstream, dominated by the KW flow. With increasing
$\unicode[STIX]{x0394}M_{s}>0$
, and the current should turn predominantly downstream, dominated by the KW flow. With increasing
![]() $a$
, as in figure 12(b), the injected momentum flux decreases, becoming negative, and the current turns upstream, dominated by image-vorticity driving. This upstream current with weak downstream KW flow is clearly visible in the full-physics integrations in figure 3 of McCreary et al. (Reference McCreary, Zhang and Shetye1997).
$a$
, as in figure 12(b), the injected momentum flux decreases, becoming negative, and the current turns upstream, dominated by image-vorticity driving. This upstream current with weak downstream KW flow is clearly visible in the full-physics integrations in figure 3 of McCreary et al. (Reference McCreary, Zhang and Shetye1997).
6 Discussion
A simple, fully nonlinear, dispersive, quasi-geostrophic model has been put forward to isolate the vorticity dynamics of coastal outflows. The model retains sufficient physics to capture the essential nonlinearity of the flow but is sufficiently simple so as to allow highly accurate numerical integration of the full problem and also fully nonlinear explicit solutions for the evolution of a uniform velocity outflow in the hydraulic limit. The flow evolution depends strongly on the sign of the PVa of the expelled fluid and on the ratio of the internal Rossby radius to the vortex-source scale of the flow. Comparison of the explicit hydraulic solutions with the numerical integrations shows that the analytical solutions predict the flow development well with differences ascribable to the effects of dispersion and the non-convex flux function. In particular, the height of the downstream shelf in figure 13(a) differs from the shelf height for the same value of
![]() $a$
for the point source of figure 12(b) and so is a function of the width
$a$
for the point source of figure 12(b) and so is a function of the width
![]() $W$
of the source and hence of the strength of dispersion. As in Johnson & Clarke (Reference Johnson and Clarke1999, Reference Johnson and Clarke2001), the form of the jump depends on the kink-soliton solutions of the nonlinear dispersive problem (2.6b
) and (2.21) can be related to the conservation of momentum. The technical details of these transitions are of great interest but lie beyond the scope of this present paper and will be considered at length elsewhere.
$W$
of the source and hence of the strength of dispersion. As in Johnson & Clarke (Reference Johnson and Clarke1999, Reference Johnson and Clarke2001), the form of the jump depends on the kink-soliton solutions of the nonlinear dispersive problem (2.6b
) and (2.21) can be related to the conservation of momentum. The technical details of these transitions are of great interest but lie beyond the scope of this present paper and will be considered at length elsewhere.
Quantitative comparison with the observations of Thomas & Linden (Reference Thomas and Linden2007), TL here, is not straightforward. The experiment differs from the model here in having no ambient layer of density
![]() $\unicode[STIX]{x1D70C}_{1}$
fluid outside the source region. The depth of the expelled fluid vanishes at the current edge and so even the full shallow-water equations do not rigorously apply there, let alone the quasi-geostrophic model here. TL show however that the shallow-water model captures the offshore depth profile well with the region of non-uniformity at the current edge proving irrelevant. TL further argue that as their source is small the expelled fluid can be taken to have zero PV and this also accords well with their observations. In the present model this corresponds to large negative PVa equal to
$\unicode[STIX]{x1D70C}_{1}$
fluid outside the source region. The depth of the expelled fluid vanishes at the current edge and so even the full shallow-water equations do not rigorously apply there, let alone the quasi-geostrophic model here. TL show however that the shallow-water model captures the offshore depth profile well with the region of non-uniformity at the current edge proving irrelevant. TL further argue that as their source is small the expelled fluid can be taken to have zero PV and this also accords well with their observations. In the present model this corresponds to large negative PVa equal to
![]() $-f/D$
, giving
$-f/D$
, giving
![]() $L_{v}=(Q_{0}f)^{1/2}$
, and so the most relevant results here would appear to be those or for negative PVa in figures 9, 10(b) and 12. In the particular, the coastal current in figure 1 here (reproduced from figure 3(a) of TL) appears to manifest the elongated, unsteady, downstream rarefaction of the long-wave solutions of figure 9(a) and, more closely, the full point-source solution of a figure 12(a), which also seems to capture the slow spreading at, and upstream of, the source. The expelled fluid spreads significantly more rapidly downstream than upstream. Section 4.5 estimates the downstream speed as
$L_{v}=(Q_{0}f)^{1/2}$
, and so the most relevant results here would appear to be those or for negative PVa in figures 9, 10(b) and 12. In the particular, the coastal current in figure 1 here (reproduced from figure 3(a) of TL) appears to manifest the elongated, unsteady, downstream rarefaction of the long-wave solutions of figure 9(a) and, more closely, the full point-source solution of a figure 12(a), which also seems to capture the slow spreading at, and upstream of, the source. The expelled fluid spreads significantly more rapidly downstream than upstream. Section 4.5 estimates the downstream speed as
![]() $Q_{0}/a^{\ast }$
, where
$Q_{0}/a^{\ast }$
, where
![]() $a^{\ast }$
is the dimensional Rossby radius, and the upstream speed as of order
$a^{\ast }$
is the dimensional Rossby radius, and the upstream speed as of order
![]() $Q_{0}/L_{v}$
, and thus it appears that the speed ratio
$Q_{0}/L_{v}$
, and thus it appears that the speed ratio
![]() $a=a^{\ast }/L_{v}$
can be regarded as small in this experiment, in line with the evolutions of figures 9(a) and 12(a). Comparing figure 1 with figure 3(b) of TL (not reproduced here) shows that the width at inception of the downstream current, i.e. the current width where it leaves the neighbourhood of the source, is a strong function of the external parameters. Section 4.3 shows that in the quasi-geostrophic limit this width at inception grows without limit for
$a=a^{\ast }/L_{v}$
can be regarded as small in this experiment, in line with the evolutions of figures 9(a) and 12(a). Comparing figure 1 with figure 3(b) of TL (not reproduced here) shows that the width at inception of the downstream current, i.e. the current width where it leaves the neighbourhood of the source, is a strong function of the external parameters. Section 4.3 shows that in the quasi-geostrophic limit this width at inception grows without limit for
![]() $a\leqslant 1$
, KW flow dominated, but for
$a\leqslant 1$
, KW flow dominated, but for
![]() $a>1$
, vorticity-dominated flow, the inception width is given by
$a>1$
, vorticity-dominated flow, the inception width is given by
![]() $Y_{hn}^{d}$
, plotted in figure 5, derived from a criticality condition at the downstream edge of the source region. A similar determination might occur in the experiments. TL note that the currents in their figure 3(a,b) do not have constant width, suggesting that this might be due to the Ekman number’s being too large. The solutions here raise the possibility that the narrowing is a manifestation of an unsteady downstream rarefaction. The generation in the laboratory of coastal flows with positive PVa has been discussed by Thivolle-Cazat & Sommeria (Reference Thivolle-Cazat and Sommeria2006) who concentrate on the instability of the coastal current but also postulate a downstream constant-width current led by a lengthening tongue of fluid as in the long-wave solution of figure 8(a) and the full solution of figure 11(a).
$Y_{hn}^{d}$
, plotted in figure 5, derived from a criticality condition at the downstream edge of the source region. A similar determination might occur in the experiments. TL note that the currents in their figure 3(a,b) do not have constant width, suggesting that this might be due to the Ekman number’s being too large. The solutions here raise the possibility that the narrowing is a manifestation of an unsteady downstream rarefaction. The generation in the laboratory of coastal flows with positive PVa has been discussed by Thivolle-Cazat & Sommeria (Reference Thivolle-Cazat and Sommeria2006) who concentrate on the instability of the coastal current but also postulate a downstream constant-width current led by a lengthening tongue of fluid as in the long-wave solution of figure 8(a) and the full solution of figure 11(a).
The extension of the present methods to full shallow-water dynamics is ongoing and straightforward as is the modelling of tides, winds, external currents and unsteady sources (Southwick et al. Reference Southwick, Johnson and McDonald2017). The geometry of the coast and its topography can also dramatically alter the propagation of the outflow. Sadoux et al. (Reference Sadoux, Baey, Fincham and Renouard2000), experimentally, and Clarke & Johnson (Reference Clarke and Johnson1997a ,Reference Clarke and Johnson b ), in theory and CD integrations, discuss vortical flows interacting with capes. McDonald & Johnson (Reference McDonald and Johnson2009) present closed-form analytical solutions and CD integrations for vortical currents passing through gaps and An & McDonald (Reference An and McDonald2004) discuss the additional turning caused by topographic steering on a step shelf.
Acknowledgements
E.R.J. is grateful to J.-B. Flor and J. Sommeria for their helpful comments on experimental observations of these flows during a visit to the Laboratoire des Écoulements Géophysiques et Industriels, Grenoble. O.R.S. was supported by a DTA studentship under the EPSRC grant EP/J500331/1.