Hostname: page-component-f554764f5-rvxtl Total loading time: 0 Render date: 2025-04-21T05:01:45.266Z Has data issue: false hasContentIssue false
  • English
  • Français

AN EFFECTIVE BOUND FOR GENERALISED DIOPHANTINE m-TUPLES

Part of: Multiplicative number theory Diophantine equations

Published online by Cambridge University Press:  06 November 2023

SAUNAK BHATTACHARJEE Open the ORCID record for SAUNAK BHATTACHARJEE [Opens in a new window] ,
ANUP B. DIXIT Open the ORCID record for ANUP B. DIXIT [Opens in a new window]  and
DISHANT SAIKIA Open the ORCID record for DISHANT SAIKIA [Opens in a new window]
SAUNAK BHATTACHARJEE
Affiliation:
IISER Tirupati, C/O Sree Rama Engineering College, (Transit Campus), Tirupati, Andhra Pradesh 517507, India e-mail: [email protected]
ANUP B. DIXIT*
Affiliation:
Institute of Mathematical Sciences (HBNI), CIT Campus, Taramani, Chennai, Tamil Nadu 600113, India
DISHANT SAIKIA
Affiliation:
Freie Universität Berlin, Kaiserswerther Str. 16-18, Berlin 14195, Germany e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For 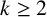$k\geq 2$ and a nonzero integer n, a generalised Diophantine m-tuple with property 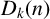$D_k(n)$ is a set of m positive integers 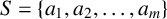$S = \{a_1,a_2,\ldots , a_m\}$ such that 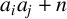$a_ia_j + n$ is a kth power for 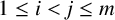$1\leq i< j\leq m$. Define 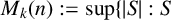$M_k(n):= \text {sup}\{|S| : S$ having property 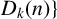$D_k(n)\}$. Dixit et al. [‘Generalised Diophantine m-tuples’, Proc. Amer. Math. Soc. 150(4) (2022), 1455–1465] proved that 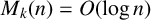$M_k(n)=O(\log n)$, for a fixed k, as n varies. In this paper, we obtain effective upper bounds on 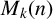$M_k(n)$. In particular, we show that for 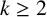$k\geq 2$, 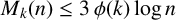$M_k(n) \leq 3\,\phi (k) \log n$ if n is sufficiently large compared to k.

Keywords

Diophantine m-tuplesGallagher’s sievegap principlequantitative Roth’s theorem

MSC classification

Primary: 11D45: Counting solutions of Diophantine equations
Secondary: 11D72: Equations in many variables 11N36: Applications of sieve methods
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 2 , April 2024 , pp. 242 - 253
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The research of the second author is partially supported by the Inspire Faculty Fellowship. The research of the first and third authors was supported by a summer research program in IMSc, Chennai.

References

Arkin, J., Hoggatt, V. E. Jr and Straus, E. G., ‘On Euler’s solution of a problem of Diophantus’, Fibonacci Quart. 17(4) (1979), 333–339.Google Scholar
Baker, A. and Davenport, H., ‘The equations $3{x}^2-2={y}^2$ and $8{x}^2-7={z}^2$ ’, Q. J. Math. Oxford Ser. (2) 20 (1969), 129–137.CrossRefGoogle Scholar
Becker, R. and Murty, M. R., ‘Diophantine $m$ -tuples with the property $D(n)$ ’, Glas. Mat. Ser. III 54 (2019), 65–75.CrossRefGoogle Scholar
Bennett, M. A., Martin, G., O’Bryant, K. and Rechnitzer, A., ‘Explicit bounds for primes in arithmetic progressions’, Illinois J. Math. 62(1–4) (2018), 427–532.CrossRefGoogle Scholar
Bérczes, A., Dujella, A., Hajdu, L. and Luca, F., ‘On the size of sets whose elements have perfect power $n$ -shifted products’, Publ. Math. Debrecen 79(3–4) (2011), 325–339.CrossRefGoogle Scholar
Bugeaud, Y. and Dujella, A., ‘On a problem of Diophantus for higher powers’, Math. Proc. Cambridge Philos. Soc. 135 (2003), 1–10.CrossRefGoogle Scholar
Cojocaru, A. and Murty, M. R., An Introduction to Sieve Methods and Their Applications, London Mathematical Society Student Texts, 66 (Cambridge University Press, Cambridge, 2005).CrossRefGoogle Scholar
Dixit, A. B., Kim, S. and Murty, M. R., ‘Generalised Diophantine $m$ -tuples’, Proc. Amer. Math. Soc. 150(4) (2022), 1455–1465.CrossRefGoogle Scholar
Dujella, A., ‘Bounds for the size of sets with the property $D(n)$ ’, Glas. Mat. Ser. III 39(2) (2004), 199–205.CrossRefGoogle Scholar
Dujella, A., ‘There are only finitely many Diophantine quintuples’, J. reine angew. Math. 566 (2004), 183–214.Google Scholar
Evertse, J.-H., ‘On the quantitative subspace theorem’, J. Math. Sci. (N.Y.) 171(6) (2010), 824–837.CrossRefGoogle Scholar
Faltings, G., ‘Endlichkeitssätze für abelsche Varietäten über Zählkorpern’, Invent. Math. 73 (1983), 349–366. Erratum: ibid., 75 (1984), 381.CrossRefGoogle Scholar
Gallagher, P. X., ‘A larger sieve’, Acta Arith. 18 (1971), 77–81.CrossRefGoogle Scholar
Gyarmati, K., ‘On a problem of Diophantus’, Acta Arith. 97 (2001), 53–65.CrossRefGoogle Scholar
He, B., Togbé, A. and Ziegler, V., ‘There is no Diophantine quintuple’, Trans. Amer. Math. Soc. 371(9) (2019), 6665–6709.CrossRefGoogle Scholar
Vinogradov, I. M., Elements of Number Theory (Dover Publications, Inc., New York, 1954), translated by S. Kravetz.Google Scholar