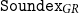1. Introduction
Misspelled and mispronounced words can negatively affect various tasks in Information Retrieval (IR), and Natural Language Processing (NLP) tasks such as indexing, retrieval, autocompletion (Fafalios et al. Reference Fafalios, Kitsos and Tzitzikas2012), entity recognition (Yadav and Bethard Reference Yadav and Bethard2018), question answering (Dimitrakis et al. Reference Dimitrakis, Sgontzos and Tzitzikas2019), structured data integration (Mountantonakis and Tzitzikas Reference Mountantonakis and Tzitzikas2019), and phonetic interfaces in general (Kaur et al. Reference Kaur, Singh and Kadyan2020). Moreover, the existing approaches for producing word embeddings (like Word2Vec Mikolov et al. (Reference Mikolov, Sutskever, Chen, Corrado and Dean2013), Glove Pennington et al. (Reference Pennington, Socher and Manning2014), and BERT Devlin et al. (Reference Devlin, Chang, Lee and Toutanova2018)) have limited applicability to malformed texts, which contain a non-negligible amount of out-of-vocabulary words (Piktus et al. Reference Piktus, Edizel, Bojanowski, Grave, Ferreira and Silvestri2019), meaning that they cannot provide embeddings for words that have not been observed at training time.
To tackle such cases, stemming and edit-related distances (e.g., the Levenstein distance Levenshtein (Reference Levenshtein1966)) are usually employed (e.g., Medhat et al. (Reference Medhat, Hassan and Salama2015)). However, these methods are not always sufficient: we cannot apply stemming to person and location names, while the edit distance between a word and a misspelled one (that has more than one misspellings) can be too big (e.g., the edit distance between “Schumacher” and “Soumaher” is 4), thus limiting the value of edit distance-based matching. Another family of algorithms to deal with this issue is the family of phonetic matching algorithms. Indeed, phonetic codes have been used in various contexts, for example, for indexing and retrieving names from a large dataset (Koneru et al. Reference Koneru, Pulla and Varol2016), for SMS retrieval (Pinto et al. Reference Pinto, Vilarino, Alemán, Gómez and Loya2012), for link discovery (Ahmed et al. Reference Ahmed, Sherif and Ngonga Ngomo2019), for duplicate record detection (Elmagarmid et al. Reference Elmagarmid, Ipeirotis and Verykios2006), and for preserving privacy (Karakasidis and Verykios Reference Karakasidis and Verykios2009) and others.
The first implementation of phonetic algorithms dates back to 1918, with the Soundex algorithm (Russell Reference Russell1918; Russell Reference Russell1922), which attempts to encode words based on how they sound. Although there is a plethora of proposed solutions for tackling this issue in the English language (Soundex, Metaphone, Double Metaphone, Metaphone 3, NYSIIS and others), this is not the case for the Greek language. In this paper, we propose and evaluate an algorithm that falls to that family and aims at dealing with such issues for the Greek language. Such an algorithm should be able to tackle a wider variety of errors with high accuracy. For example, for the word ![]() (which is spelled correctly and sounds [étimos]), it should be able to retrieve (match) misspelled variations of the same word and word sense, like
(which is spelled correctly and sounds [étimos]), it should be able to retrieve (match) misspelled variations of the same word and word sense, like ![]() ([étimos]),
([étimos]), ![]() ([étims]),
([étims]), ![]() ([étimos]), or similar terms of a different sense like
([étimos]), or similar terms of a different sense like ![]() ([éntimos]). Hereafter, we shall use [ ] to enclose both phonetic and phonemic word transcriptions.
([éntimos]). Hereafter, we shall use [ ] to enclose both phonetic and phonemic word transcriptions.
Our approach for designing such an algorithm is to adapt the basic idea of Soundex to the characteristics of the Greek language, for having a baseline method, and then to widen its rules, like most modern (post-Soundex) phonetic algorithms have done, for accommodating the Greek language’s phonetic rules. To this end, we introduce a family of algorithms that we call
![]() ${\tt Soundex}_{GR}$
. With
${\tt Soundex}_{GR}$
. With
![]() ${\tt Soundex}_{GR}$
, we achieve assigning the same code to set of words that should match, like the set of words
${\tt Soundex}_{GR}$
, we achieve assigning the same code to set of words that should match, like the set of words
![]() $\{$
$\{$
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() $\}$
, the set
$\}$
, the set
![]() $\{$
$\{$
![]() ,
, ![]()
![]() $\}$
and the set
$\}$
and the set
![]() $\{$
$\{$
![]() ,
, ![]() ,
, ![]()
![]() $\}$
.
$\}$
.
Then, we report comparative experimental results that show which variation/configuration of the algorithm behaves better in the evaluation over datasets with various kinds of errors. Specifically, the original Soundex algorithm, modified for corresponding to the Greek Alphabet, achieves an average F-Score equal to 0.64 across different type of errors (letter addition, deletion, or substitution). The enhanced version that takes into consideration also the Greek phonetic rules achieves an average F-Score of 0.66. The variation that uses both of the previous versions to find a match achieves an average F-Score of 0.70, while in a dataset that contains similar sounded words it reaches F-Score equal to 0.91, while
![]() ${\tt Soundex}_{GR}$
achieves F-Score equal to 0.97. In addition, we report comparative experimental results with stemming and full phonetic transcription that show that the proposed algorithm performs better. We also evaluate how the code length affects the F-Score in datasets of different sizes, types of errors, and word lengths, and we measure efficiency by applying it over a Greek dictionary. Overall, the effectiveness, the simplicity, and the efficiency of the proposed family of algorithms makes it applicable to a wide range of tasks.
${\tt Soundex}_{GR}$
achieves F-Score equal to 0.97. In addition, we report comparative experimental results with stemming and full phonetic transcription that show that the proposed algorithm performs better. We also evaluate how the code length affects the F-Score in datasets of different sizes, types of errors, and word lengths, and we measure efficiency by applying it over a Greek dictionary. Overall, the effectiveness, the simplicity, and the efficiency of the proposed family of algorithms makes it applicable to a wide range of tasks.
Although there are works about the phonetic (and phonemic) transcription of Greek words (e.g., Themistocleous (Reference Themistocleous2011)), to the best of our knowledge, there is no work on using and evaluating such codes for matching Greek text.
The rest of this paper is organized as follows. Section 2 describes the background and discusses related work. Section 3 describes the proposed family of algorithms and provides various application examples for revealing the differences of these variations. Section 4 focuses on evaluation, presents extensive comparative results (for various datasets, codes sizes, and matching methods including stemming, full phonetic transcription, and edit distance), and discusses applications. Finally, Section 5 concludes the paper and identifies issues that are worth further work and research.
2. Background and related work
A wide variety of phonetic algorithms exist, many if not all, are descendants of the Soundex algorithm (described in detail in Section 2.1), like Philips (Reference Philips1990); Hood (Reference Hood2002). These algorithms aim at retrieving misspelled words and improving IR, by generating a coding of the query based on phonetic pronunciation rules. They are in use mainly in Database Systems to aid in the retrieval process, as well as in various IR tasks, such as indexing, query autocompletion, and retrieval. They are also useful in NLP tasks like Named Entity Recognition and Linking and word sense disambiguation in general. Unfortunately, most of them provide at best minimal or no support at all for the Greek language.
The works that concern the processing of the Greek language in general are not excessive (see Papantoniou and Tzitzikas (Reference Papantoniou and Tzitzikas2020) for a recent survey), in comparison to the English language. However, there are quite a few works on the phonetics of the Greek language which are described in brief below.
The 1972 book Newton (Reference Newton1972) studies Greek phonology in general, while Epitropakis et al. (Reference Epitropakis, Yiourgalis and Kokkinakis1993) presents an algorithm for the generation of intonation (F0 contours) for the Greek Text-To-Speech system. Fourakis et al. (Reference Fourakis, Botinis and Katsaiti1999) analyzes the acoustic characteristics of the Greek vowels (duration, fundamental frequency, amplitude, and others). Along the same line, Sfakianaki (Reference Sfakianaki2002) analyzes the acoustic characteristics of Greek vowels produced by adults and children, while Trudgill (Reference Trudgill2009) focuses on the Greek dialect vowel systems. Arvaniti (Reference Arvaniti2007) describes the 2007 state of the art in greek phonetics.
IPAGreek (Themistocleous Reference Themistocleous2011) is an implementation (available at Themistocleous (Reference Themistocleous2017)) of Standard Modern Greek and Cypriot Greek “phonological grammar.” The application enables users to transcribe text written in Greek orthography into the International Phonetics Alphabet (IPA).
Karanikolas (Reference Karanikolas2019) proposes an automatic machine learning approach that learns rules of how to transcribe Greek words into the International Phonetics Association’s (IPA’s) phonetic alphabet; however, the suggested method has not been implemented, nor evaluated.
Finally, Themistocleous (Reference Themistocleous2019) describes classification approaches based on deep neural networks for distinguishing two Greek dialects, namely Athenian Greek, the prototypical form of Standard Modern Greek and Cypriot Greek. That work is based on the acoustic features of spoken language.
Most of the above works focus on acoustic aspects of the language, fewer on the management of Greek text, and in particular on the problem of retrieval and matching. One algorithm that could be used for the Greek language, and for the tasks that we mentioned, that is, for matching over Greek text, is the Beider-Morse Beider (Reference Beider2008), by changing Greek letters to their equivalent English letters, without taking into consideration Greek phonetic rules, but based on how they would sound in the American dialect. Another approach would be to take a phonemic transcription method, like the one described in Themistocleous (Reference Themistocleous2017), and truncate and/or modify it (i.e., group different letters to the same code as a means to assist matching), for being suitable for approximate matching.
In this paper, we attempt to fill this gap in the literature, that is, propose a general purpose algorithm for phonetic matching for Greek text, and we evaluate its potential for matching in various datasets and under different configurations.
2.1 The original Soundex algorithm
As mentioned in the introduction, our approach for designing an algorithm for phonetic matching for the Greek language is to adapt the basic idea of Soundex to the characteristics of the Greek language, for having a baseline method, and then to widen its rules for accommodating the Greek language’s phonetic rules.
Originating back in 1918, developed by Robert C. Russell and Margaret King Odell, Soundex algorithm had a simple set of rules. It generates a code by ignoring vowels and the letter h if not at the start of the word, and encoding consonants based on how they sound, generating a code of just four characters length. Specifically, the steps of the original Soundex algorithm are
-
(i) keep the first letter unencoded,
-
(ii) remove all occurrences of a, e, h, i, o, u, w, y, except when they appear as the first letter of the word,
-
(iii) replace consonants after the first letter as shown in Table 1,
-
(iv) remove adjacent duplicate digits,
-
(v) produce a code of the form Letter Digit Digit Digit by ignoring digits after the third one (if needed), or by appending zeros (if needed).
Table 1. Consonants Replacement in the Soundex

For example,the name SMITH will be encoded to S530 as well as the names SCHMIDT and SMYTH, while both ROBERT and RUPERT yield R163. However, imprecise results are possible, for example, BLACK and BAILS yield the code B420.
Christian (Reference Christian1998) described the problems to the original Soundex, ignoring different spellings of letters in different contexts and letter combinations. Other issues include the ignoring of vowels if not at the start of the word and the short generated code. All these issues greatly harm Soundex precision levels.
The first usage of the algorithm was to retrieve people names from a large dataset, while today Soundex algorithm or its descendants can be found in various systems, for example, for SMS retrieval (Pinto et al. Reference Pinto, Vilarino, Alemán, Gómez and Loya2012), for indexing names (Raghavan and Allan Reference Raghavan and Allan2004), for link discovery (Ahmed et al. Reference Ahmed, Sherif and Ngonga Ngomo2019), for duplicate record detection (Elmagarmid et al. Reference Elmagarmid, Ipeirotis and Verykios2006), for record linkage (da Silva et al. Reference da Silva, da Silva Leite, Sampaio, Lynn and Endo2020), etc.
Moreover, it has been adapted for various languages, including the Thai language (Karoonboonyanan et al. Reference Karoonboonyanan, Sornlertlamvanich and Meknavin1997), the Arabic language (Yahia et al. Reference Yahia, Saeed and Salih2006; Shedeed and Abdel Reference Shedeed and Abdel2011; Ousidhoum and Bensaou Reference Ousidhoum and Bensaou2013), the Vietnamese language (Nguyen et al. Reference Nguyen, Ngo, Phan, Dinh and Huynh2008), the Chinese language (Li and Peng Reference Li and Peng2011), the Indian language (Shah Reference Shah2014; Gautam et al. Reference Gautam, Pipal and Arora2019), the Assamese language (Baruah and Mahanta Reference Baruah and Mahanta2015), the Spanish language (del Pilar Angeles et al. Reference del Pilar Angeles, Espino-Gamez and Gil-Moncada2015), and others.
2.2 Other related algorithms
Several algorithms after Soundex, sprawled from the core idea of it, group letters by their pronunciation, aiming at improving the original algorithm. Some of the most renownedones are
Metaphone (Philips Reference Philips1990): Applies a transformation to the original word, before the word is encoded through letter pronunciation buckets and a vast set of phonetic rules. Subsequently, various improvements were made to it: Philips (Reference Philips2000) creates a primary and a secondary encoding for a given word and applies rules based on the origin language of the input word, while Philips (Reference Philips2013) added configurable rules to the algorithm, as well as it further improved foreign word retrieval.
Caverphone (Hood Reference Hood2002): Applies transformations to the word that may be larger than 2-gram at a time to produce an encoding. It was originally created based on accents in a specific area of New Zealand.
BMPM (Beider Reference Beider2008): Before a set of phonetic rules are applied to the word, there is an identification process of the origin of the word, and then the corresponding language rules are applied.
MRA (Match Rating Approach) developed by Western Airlines in 1977 had a simple set of phonetic rules, providing through a set of comparison rules to go along the encoding.
Other phonetic algorithms produce more than one encoding to the word in order to enhance Soundex retrieval. In general, these algorithms aimed to cope with the shortcomings of the original Soundex that were described in Section 2.1 and improved it, as Koneru et al. (Reference Koneru, Pulla and Varol2016) suggest, in terms of precision which is the main shortcoming of the Soundex algorithm.
3. The algorithm
 ${\boldsymbol{\tt Soundex}}_{GR}$
(and variations)
${\boldsymbol{\tt Soundex}}_{GR}$
(and variations)
This section is organized as follows: at first, in Section 3.1, we describe in brief the requirements. Then in Section 3.2, we describe the basic idea of the new algorithm that we call
![]() ${\tt Soundex}_{GR}$
, while in Section 3.3 we detail the exact steps of this algorithm. For reasons of comparative evaluation, in Section 3.4, we define a variation that we call
${\tt Soundex}_{GR}$
, while in Section 3.3 we detail the exact steps of this algorithm. For reasons of comparative evaluation, in Section 3.4, we define a variation that we call
![]() ${\tt{Soundex}}^{naive}_{GR}$
that shares the same principles of the original Soundex algorithm but without any word preprocessing before the encoding of the word. Finally, in Section 3.5, we introduce another variation for phonetic matching (
${\tt{Soundex}}^{naive}_{GR}$
that shares the same principles of the original Soundex algorithm but without any word preprocessing before the encoding of the word. Finally, in Section 3.5, we introduce another variation for phonetic matching (
![]() ${\tt{Soundex}}^{comp}_{GR}$
) that uses both
${\tt{Soundex}}^{comp}_{GR}$
) that uses both
![]() ${\tt Soundex}_{GR}$
and
${\tt Soundex}_{GR}$
and
![]() ${\tt{Soundex}}^{naive}_{GR}$
.
${\tt{Soundex}}^{naive}_{GR}$
.
3.1 Requirements for the Greek language
The basic idea of the original Soundex algorithm can be easily translated to a Greek version. Indeed, a simple version would be to adopt the exact same rules as Soundex, as described in section 2.1, with Greek consonants. However, we wanted to tackle the shortcomings of the original Soundex (described in Section 2.1), hence to consider letter contexts, letter combinations, and generally grammar rules specific to Greek. Moreover, while the original Soundex was implemented for use mainly on names, we would like an algorithm for regular words as well. This means that we would like to achieve high precision for regular (frequent) words (to avoid having a lot of words having the same code), while for names we would like to achieve high recall (i.e., low percentage of false-positives), since they occur more rarely.
For example, we would like an algorithm that would correctly group ![]() with
with ![]() (both sound [θálasa]),
(both sound [θálasa]), ![]() with
with ![]() (both sound [mínima]),
(both sound [mínima]), ![]() with
with ![]() or
or ![]() (all sound [étima]), and
(all sound [étima]), and ![]() with
with ![]() (both sound [efkola]). The algorithm should retrieve all such cases with minimal noise and as high recall as possible.
(both sound [efkola]). The algorithm should retrieve all such cases with minimal noise and as high recall as possible.
3.2 The basic idea of
 ${\boldsymbol{\tt Soundex}}_{GR}$
${\boldsymbol{\tt Soundex}}_{GR}$
Here, we describe our algorithm that we call
![]() ${\tt Soundex}_{GR}$
. As in the original Soundex, we keep an encoding length of just four characters. As we shall see in the experiments reported in Section 4.5, if we increase the length from 4 to 5 we get a higher precision by 5–10% percent; however, the recall is decreased 10–15%. However, in larger datasets, a bigger length can be more appropriate (detailed experimental results are given in Section 4.10).
${\tt Soundex}_{GR}$
. As in the original Soundex, we keep an encoding length of just four characters. As we shall see in the experiments reported in Section 4.5, if we increase the length from 4 to 5 we get a higher precision by 5–10% percent; however, the recall is decreased 10–15%. However, in larger datasets, a bigger length can be more appropriate (detailed experimental results are given in Section 4.10).
As discussed in Section 2.1, Soundex has a precision issue, which originates from the combination of short code of just four characters and not taking in to account any lexical context. In order to improve the precision levels of the Soundex algorithm, we have to focus on these. On the contrary to Soundex, in
![]() ${\tt Soundex}_{GR}$
, we take into account a more rich set of rules, corresponding to the phonetic rules of Greek language. Below we describe the key points and subsequently we describe the exact steps.
${\tt Soundex}_{GR}$
, we take into account a more rich set of rules, corresponding to the phonetic rules of Greek language. Below we describe the key points and subsequently we describe the exact steps.
Before a word is encoded, we preprocess it and generate a different word form. The preprocessing operations include identification of the cases when a vowel sounds as a consonant in Greek, grouping of pairs of vowels based on how they sound, intonation removal, and dismantling of digrams to single letters. When this procedure finishes, the word is encoded.
For example, ![]() that sounds [béno], will be transformed to
that sounds [béno], will be transformed to ![]() and finally it will be encoded to
and finally it will be encoded to
![]() ${\tt{b}}^{\tt\ast}\tt{7\$} $
, while the name
${\tt{b}}^{\tt\ast}\tt{7\$} $
, while the name ![]() (that sounds [jánis]) will be transformed to
(that sounds [jánis]) will be transformed to ![]() and then it will be encoded to
and then it will be encoded to ![]() (more examples will be given later on).
(more examples will be given later on).
Another difference is that Soundex ignores vowels; however,
![]() ${\tt Soundex}_{GR}$
does not ignore vowels, instead it groups them into three categories based on how they sound, in particular to
${\tt Soundex}_{GR}$
does not ignore vowels, instead it groups them into three categories based on how they sound, in particular to ![]() ,
, ![]() ,
, ![]() , in order to improve the precision of the algorithm.
, in order to improve the precision of the algorithm.
The last letter of the word is ignored if it is a consonant, specifically if it is a ![]() or
or ![]() , as it does not add much value to the word.
, as it does not add much value to the word.
3.3 The exact steps of
 ${\boldsymbol{\tt Soundex}}_{GR}$
${\boldsymbol{\tt Soundex}}_{GR}$
The
![]() ${\tt Soundex}_{GR}$
algorithm and the procedures that are used by the algorithm are given in pseudocode in Alg. 1.
${\tt Soundex}_{GR}$
algorithm and the procedures that are used by the algorithm are given in pseudocode in Alg. 1.


In the first part, we preprocess the word, applying to it syntax and grammar rules of the Greek language. Specifically, in UnwrapConsonantBigrams(word), we change common Greek consonant digrams with their equivalent, identically pronounced single letters. This is based on the substitutions shown in Table 2 (top part).
Table 2. Phonetic rules

Table 3.
![]() ${\tt Soundex}_{GR}$
buckets
${\tt Soundex}_{GR}$
buckets

Then, in TransformVowelsToConsonant(word), we continue with identifying if the Greek Letter ![]() is acting as a vowel or as a consonant. This distinction needs to be made only if the letter before is
is acting as a vowel or as a consonant. This distinction needs to be made only if the letter before is ![]() or
or ![]() , and the subsequent consonant falls in the category of Tables 4 and 5. For example,
, and the subsequent consonant falls in the category of Tables 4 and 5. For example,
![]() [áfkson] (
[áfkson] (![]() : consonant-
: consonant-
![]() $\unicode{x03C6}$
),
$\unicode{x03C6}$
),
![]() [aftós] (
[aftós] (![]() : consonant-
: consonant-
![]() $\unicode{x03C6}$
),
$\unicode{x03C6}$
),
![]() [avlí] (
[avlí] (![]() : consonant-
: consonant-
![]() $\unicode{x03B2}$
),
$\unicode{x03B2}$
),
![]() [éfksinos] (
[éfksinos] (![]() : consonant-
: consonant-
![]() $\unicode{x03C6}$
),
$\unicode{x03C6}$
),
![]() [évdoksos] (
[évdoksos] (![]() : consonant-
: consonant-
![]() $\unicode{x03B2}$
),
$\unicode{x03B2}$
),
![]() [eveksa] (
[eveksa] (![]() : consonant-
: consonant-
![]() $\unicode{x03B2}$
).
$\unicode{x03B2}$
).
Table 4. Loud consonants in Greek

Table 5. Silent consonants in Greek

After that, we remove letters ![]() or
or ![]() if they are the last letter of the word, as such letters do not add much value to the world.
if they are the last letter of the word, as such letters do not add much value to the world.
In GroupVowels, we change common Greek vowel digrams with their equivalent, identically pronounced, single letters. This is based on the substitutions shown in Table 2 (bottom part).
In RemoveIntonation(word) (line 6), we remove possible remaining tones (if any); this is the last step of the word preprocessing phase.
In SoundexEncode(word) (line 7), we encode the word through the letter-digit pairs in Table 3. After translating the original word to a code, we remove adjacent duplicate digits in RemoveDuplicates(code) (line 8) and trim length to four characters or assign 0s to the end of the code if the code is smaller than four characters in trimLength(code,4) (line 9).
A few examples that show the outcome after each step of the algorithm are shown inTable 6.
Table 6. Examples of
![]() ${\tt Soundex}_{GR}$
code generation, through different stages
${\tt Soundex}_{GR}$
code generation, through different stages

To summarize the rules applied, Table 2 shows the 2-gram groups that produce similar sounds to a single letter, and as a result they are transformed to the corresponding single letter in the word preprocessing operation. Table 3 shows the complete set of phonetic buckets that are applied to the word as the final step in the encoding of the word. Table 4 shows the Loud category of the consonants in Greek which are used in order to identify if ![]() acts as a consonant, specifically a
acts as a consonant, specifically a ![]() , while Table 5 shows the Silent category of the consonants in Greek which are used in order to identify if
, while Table 5 shows the Silent category of the consonants in Greek which are used in order to identify if ![]() acts as a consonant, specifically a
acts as a consonant, specifically a ![]() . Note that the distinction to Loud and Silent concerns consonant phonemes. The silent ones contain those of Table 5 plus
. Note that the distinction to Loud and Silent concerns consonant phonemes. The silent ones contain those of Table 5 plus ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; however, the last three are not needed for understanding the interpretation of
; however, the last three are not needed for understanding the interpretation of ![]() , and this is the reason why they are not included in Table 5.
, and this is the reason why they are not included in Table 5.
3.4 The algorithm
 ${\boldsymbol{\tt{Soundex}}}^{naive}_{GR}$
${\boldsymbol{\tt{Soundex}}}^{naive}_{GR}$
For reasons of comparative evaluation, here we define another algorithm, that we call
![]() ${\tt{Soundex}}^{naive}_{GR}$
, that shares the same principles of the original Soundex algorithm, but without any word preprocessing before the encoding of the word. Specifically, the algorithm ignores vowels, has an encoding length of four characters, and does not encode the first letter. The only common aspect between this algorithm and
${\tt{Soundex}}^{naive}_{GR}$
, that shares the same principles of the original Soundex algorithm, but without any word preprocessing before the encoding of the word. Specifically, the algorithm ignores vowels, has an encoding length of four characters, and does not encode the first letter. The only common aspect between this algorithm and
![]() ${\tt Soundex}_{GR}$
is that it uses the same buckets from which the final encoding is generated, as shown in Table 3. Similarly to the original Soundex, we adopt the following steps:
${\tt Soundex}_{GR}$
is that it uses the same buckets from which the final encoding is generated, as shown in Table 3. Similarly to the original Soundex, we adopt the following steps:
-
(i) keep the first letter unencoded,
-
(ii) remove all occurrences of
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  except when they appear as the first letter of the word,
except when they appear as the first letter of the word, -
(iii) replace consonants after the first letter as shown in Table 7,
-
(iv) remove adjacent duplicate digits,
-
(v) produce a code of the form Letter Digit Digit Digit by ignoring digits after the third one (if needed), or by appending zeros (if needed).
Table 7. Consonants Replacement in the
![]() ${\tt{Soundex}}^{naive}_{GR}$
${\tt{Soundex}}^{naive}_{GR}$

For example, this algorithm would encode ![]() to
to ![]() and
and ![]() to
to ![]() , which are two identically sounded words, but with different encoding results. This evidences the superiority of
, which are two identically sounded words, but with different encoding results. This evidences the superiority of
![]() ${\tt Soundex}_{GR}$
in comparison to
${\tt Soundex}_{GR}$
in comparison to
![]() ${\tt{Soundex}}^{naive}_{GR}$
(more such examples are included in Section 4.1).
${\tt{Soundex}}^{naive}_{GR}$
(more such examples are included in Section 4.1).
3.5 Phonetic matching with
 ${\boldsymbol{\tt{Soundex}}}^{comp}_{GR}$
${\boldsymbol{\tt{Soundex}}}^{comp}_{GR}$
With
![]() ${\tt Soundex}_{GR}$
we consider that two words w and w
′ match, denoted by
${\tt Soundex}_{GR}$
we consider that two words w and w
′ match, denoted by
![]() $w \Leftrightarrow w'$
, if they have the same code, that is, if
$w \Leftrightarrow w'$
, if they have the same code, that is, if
![]() ${\tt Soundex}_{GR}$
(w) =
${\tt Soundex}_{GR}$
(w) =
![]() ${\tt Soundex}_{GR}$
(w
′). Analogously, with
${\tt Soundex}_{GR}$
(w
′). Analogously, with
![]() ${\tt{Soundex}}^{naive}_{GR}$
.
${\tt{Soundex}}^{naive}_{GR}$
.
In order to maintain both precision and recall levels as high as possible, here we introduce another variation for phonetic matching, that we call
![]() ${\tt{Soundex}}^{comp}_{GR}$
. The idea is to use both
${\tt{Soundex}}^{comp}_{GR}$
. The idea is to use both
![]() ${\tt Soundex}_{GR}$
and
${\tt Soundex}_{GR}$
and
![]() ${\tt{Soundex}}^{naive}_{GR}$
for keeping recall levels as high possible, without precision dropping. Specifically, this method uses both
${\tt{Soundex}}^{naive}_{GR}$
for keeping recall levels as high possible, without precision dropping. Specifically, this method uses both
![]() ${\tt Soundex}_{GR}$
and
${\tt Soundex}_{GR}$
and
![]() ${\tt{Soundex}}^{naive}_{GR}$
in combination during the matching process, that is, the query and the text are encoded with both the implementations, and if either one of them matches, then it is considered a match, that is:
${\tt{Soundex}}^{naive}_{GR}$
in combination during the matching process, that is, the query and the text are encoded with both the implementations, and if either one of them matches, then it is considered a match, that is:
4. Evaluation
At first (in Section 4.1), we provide some indicative examples showcasing the merits of the codes and the differences between
![]() ${\tt{Soundex}}^{naive}_{GR}$
and
${\tt{Soundex}}^{naive}_{GR}$
and
![]() ${\tt Soundex}_{GR}$
. Then (in Section 4.2), we describe an evaluation collection that we have created containing datasets (Dataset A - Dataset D) with various types of errors and the metrics that we use for comparing the performance of various options (in Section 4.3). Subsequently (in Section 4.4), we report the evaluation results and discuss the related trade-offs (in Section 4.5). For further understanding of the performance of these codes, we also compare them with the lemmas produced by Greek stemmer (in Section 4.6), and we report measurements over a Greek dictionary (in Section 4.7). Furthermore (in Section 4.8), we provide and evaluate a method that yields a full phonetic transcription. In Section 4.9, we compare all methods, including the full phonemic transcription, plus edit distance-based methods, over an extended dataset of similarly sounded words
${\tt Soundex}_{GR}$
. Then (in Section 4.2), we describe an evaluation collection that we have created containing datasets (Dataset A - Dataset D) with various types of errors and the metrics that we use for comparing the performance of various options (in Section 4.3). Subsequently (in Section 4.4), we report the evaluation results and discuss the related trade-offs (in Section 4.5). For further understanding of the performance of these codes, we also compare them with the lemmas produced by Greek stemmer (in Section 4.6), and we report measurements over a Greek dictionary (in Section 4.7). Furthermore (in Section 4.8), we provide and evaluate a method that yields a full phonetic transcription. In Section 4.9, we compare all methods, including the full phonemic transcription, plus edit distance-based methods, over an extended dataset of similarly sounded words
![]() ${\tt Dataset\ D}^{ext}$
, while in Section 4.10 we report the results of a series of experiments at different scales for understanding the factors that determine the optimal code length (Dataset E -
${\tt Dataset\ D}^{ext}$
, while in Section 4.10 we report the results of a series of experiments at different scales for understanding the factors that determine the optimal code length (Dataset E -
![]() ${\tt Dataset\ H}$
). Subsequently (in Section 4.11), we discuss efficiency, and finally (in Section 4.12) we discuss applicability and describe an application that showcases the benefits of
${\tt Dataset\ H}$
). Subsequently (in Section 4.11), we discuss efficiency, and finally (in Section 4.12) we discuss applicability and describe an application that showcases the benefits of
![]() ${\tt Soundex}_{GR}$
for approximate matching.
${\tt Soundex}_{GR}$
for approximate matching.
An overview of the datasets that are used for evaluation purposes are given in Figure 1.

Figure 1. An overview of the datasets used for evaluation purposes.
4.1 Indicative examples
Here, we provide a few indicative examples for understanding the behavior of
![]() ${\tt{Soundex}}^{naive}_{GR}$
and
${\tt{Soundex}}^{naive}_{GR}$
and
![]() ${\tt Soundex}_{GR}$
. Specifically, Table 8 provides examples where both
${\tt Soundex}_{GR}$
. Specifically, Table 8 provides examples where both
![]() ${\tt{Soundex}}^{naive}_{GR}$
and
${\tt{Soundex}}^{naive}_{GR}$
and
![]() ${\tt Soundex}_{GR}$
tackle correctly various misspellings, that is, they assign the same code to all word variations.
${\tt Soundex}_{GR}$
tackle correctly various misspellings, that is, they assign the same code to all word variations.
Table 8. Indicative good examples for both
![]() ${\tt{Soundex}}^{naive}_{GR}$
and
${\tt{Soundex}}^{naive}_{GR}$
and
![]() ${\tt Soundex}_{GR}$
${\tt Soundex}_{GR}$

Now Table 9 provides examples where
![]() ${\tt{Soundex}}^{naive}_{GR}$
fails to assign the same code, while
${\tt{Soundex}}^{naive}_{GR}$
fails to assign the same code, while
![]() ${\tt Soundex}_{GR}$
succeeds on providing the same code to all relevant word variations.
${\tt Soundex}_{GR}$
succeeds on providing the same code to all relevant word variations.
Table 9. Indicative examples where
![]() ${\tt{Soundex}}^{naive}_{GR}$
fails while
${\tt{Soundex}}^{naive}_{GR}$
fails while
![]() ${\tt Soundex}_{GR}$
succeeds
${\tt Soundex}_{GR}$
succeeds

4.2 Evaluation datasets (
 ${\boldsymbol{\tt{Dataset\ A}}} - {\boldsymbol{\tt{Dataset\ D}}}$
)
${\boldsymbol{\tt{Dataset\ A}}} - {\boldsymbol{\tt{Dataset\ D}}}$
)
There are various kinds of errors, for more see the extensive survey Kukich (Reference Kukich1992), below we summarize the main ones. Human-generated misspellings sometimes tend to reflect typewriter keyboard adjacencies, for example, the substitution of “b” for “n” (in Greek
![]() $\unicode{x03B2}$
and
$\unicode{x03B2}$
and
![]() $\unicode{x03BD}$
). However, errors introduced by Optical Character Recognition (OCR) are more likely to be based on confusions due to featural similarities between letters (depending on the font), for example, the substitution of “D” for “O” (in Greek, we may encounter analogous problems with various groups of letters like
$\unicode{x03BD}$
). However, errors introduced by Optical Character Recognition (OCR) are more likely to be based on confusions due to featural similarities between letters (depending on the font), for example, the substitution of “D” for “O” (in Greek, we may encounter analogous problems with various groups of letters like
![]() $\mathrm{O},\Theta,\Omega $
, as well as
$\mathrm{O},\Theta,\Omega $
, as well as
![]() $ \mathrm{A},\Lambda,\Delta $
, and
$ \mathrm{A},\Lambda,\Delta $
, and
![]() $ \mathrm{E},\Sigma $
and
$ \mathrm{E},\Sigma $
and
![]() $ \Upsilon,\Psi $
). We may also have the so-called typographic errors, for example, “spell” and “speel” (in greek
$ \Upsilon,\Psi $
). We may also have the so-called typographic errors, for example, “spell” and “speel” (in greek ![]() and
and ![]() ), where it is assumed that the writer knows the correct spelling but simply makes a motor coordination slip. There are also cognitive errors, for example, “receive” and “recieve” (in Greek
), where it is assumed that the writer knows the correct spelling but simply makes a motor coordination slip. There are also cognitive errors, for example, “receive” and “recieve” (in Greek ![]() and
and ![]() each having a different meaning), due to a misconception or a lack of knowledge on the part of the writer. We can also encounter phonetic errors, for example, “abyss” and “abiss” (in Greek
each having a different meaning), due to a misconception or a lack of knowledge on the part of the writer. We can also encounter phonetic errors, for example, “abyss” and “abiss” (in Greek ![]() and
and ![]() and
and ![]() and
and ![]() ) that are a special class of cognitive errors in which the writer substitutes a phonetically correct but orthographically incorrect sequence of letters for the intended word.
) that are a special class of cognitive errors in which the writer substitutes a phonetically correct but orthographically incorrect sequence of letters for the intended word.
Apart from mistakes, there are words with more than one correct form, for example, ![]() and
and ![]() , and the same applies also for entity names, for example, the city of Heraklion is written as
, and the same applies also for entity names, for example, the city of Heraklion is written as ![]() but also as
but also as ![]() , while the city of Athens is written
, while the city of Athens is written ![]() but also
but also ![]() .
.
Overall, according to Kukich (Reference Kukich1992), nearly 80% of problems of misspelled words can be addressed either by addition of a single letter, or replacement of a single letter or swapping of letters. As the authors of Koneru et al. (Reference Koneru, Pulla and Varol2016) propose in their evaluation of various phonetic matching algorithms, we provide a similar evaluation collection for the Greek language that consists of datasets that contain words corresponding to various kinds of errors. Specifically, below we describe each of the four evaluation datasets that we have created. The set of words in each of these datasets contains verbs, nouns, adjectives, and proper names. The first three datasets, Dataset A , Dataset B , and Dataset C , were created for checking how the algorithms behave in various kinds of errors (additions, deletions, and replacements) that can occur to a word, while last one, Dataset D , was created for evaluating letter buckets, that is, for testing the behavior of the matching in common errors.
In particular,
Dataset A
contains words produced by a single random letter addition to a random position in a word, for example, from the set of words ![]() we produce words like
we produce words like ![]() Errors of this kind can happen by typing an extra keystroke. In
Dataset B
, the same procedure is used for deletions, that is, a letter is deleted from a random position, for the same set of words, for example, this dataset contains words like
Errors of this kind can happen by typing an extra keystroke. In
Dataset B
, the same procedure is used for deletions, that is, a letter is deleted from a random position, for the same set of words, for example, this dataset contains words like ![]() . Again errors of this kind can happen during typing, that is, by a missing keystroke, or a typo (missing double letter). In
Dataset C
, we have random letter substitution in a random position, for example, in our example, we get words like
. Again errors of this kind can happen during typing, that is, by a missing keystroke, or a typo (missing double letter). In
Dataset C
, we have random letter substitution in a random position, for example, in our example, we get words like ![]() . Again errors of this kind can happen during typing by one wrong keystroke (recall keyboard adjacencies, OCR errors, typographic, and cognitive errors).
. Again errors of this kind can happen during typing by one wrong keystroke (recall keyboard adjacencies, OCR errors, typographic, and cognitive errors).
Each of the above datasets contains 2500 words, generated from the same 293 unique words, that is, 7500 words in total. The generation of the erroneous words is random, that is, it does not consider any context or expected errors or typos. Finally,
Dataset D
contains 150 words comprising groups of similarly pronounced words, such as ![]()
![]() and
and ![]() , created manually. The motivation for creating this dataset was to capture some common errors, that is, frequently occurring spelling mistakes.
, created manually. The motivation for creating this dataset was to capture some common errors, that is, frequently occurring spelling mistakes.
4.3 Evaluation metrics
We shall use two basic metrics to evaluate the effectiveness of the algorithms, namely Precision and Recall. Precision is the portion of words that are retrieved and are relevant to the query, while Recall is the portion of relevant words that were retrieved, formally:
![]() $Precision =\frac{ |(relevant) \cap (retrieved)|}{|(retrieved)|}$
,
$Precision =\frac{ |(relevant) \cap (retrieved)|}{|(retrieved)|}$
,
![]() $Recall =\frac{ |(relevant) \cap (retrieved)|}{|(relevant)|}$
. Let us now explain what “query”, “retrieved”, and “relevant” mean in our context. Each of the 293 unique words (of the first three datasets) is considered as query. For each such word w, the corresponding set of words in each dataset, that is, the words derived by making one modification, is considered as the set of relevant words.
$Recall =\frac{ |(relevant) \cap (retrieved)|}{|(relevant)|}$
. Let us now explain what “query”, “retrieved”, and “relevant” mean in our context. Each of the 293 unique words (of the first three datasets) is considered as query. For each such word w, the corresponding set of words in each dataset, that is, the words derived by making one modification, is considered as the set of relevant words.
For example, for the word ![]() , the set of relevant words is
, the set of relevant words is ![]() (from Dataset A),
(from Dataset A), ![]() (from Dataset B), and
(from Dataset B), and ![]() (from Dataset C). For each query word, the set of retrieved words is considered the set of all words in all datasets that have the same code. Then, for each dataset individually, we calculate the average Precision and average Recall, based on the Recall and Precision of each of the N queries, that is,
(from Dataset C). For each query word, the set of retrieved words is considered the set of all words in all datasets that have the same code. Then, for each dataset individually, we calculate the average Precision and average Recall, based on the Recall and Precision of each of the N queries, that is,
![]() $Precision_{avg} = \frac{\Sigma_{i=1}^{N} Precision_i}{N}$
and
$Precision_{avg} = \frac{\Sigma_{i=1}^{N} Precision_i}{N}$
and
![]() $Recall_{avg} = \frac{\Sigma_{i=1}^{N} Recall_i}{N}$
.
$Recall_{avg} = \frac{\Sigma_{i=1}^{N} Recall_i}{N}$
.
4.4 Evaluation results over
 ${\boldsymbol{\tt{Dataset\ A}}} - {\boldsymbol{\tt{Dataset\ D}}}$
${\boldsymbol{\tt{Dataset\ A}}} - {\boldsymbol{\tt{Dataset\ D}}}$
At first, we should note that if instead of applying any approximate algorithm, we apply exact match, then obviously we get Precision equal to 1, but the Recall is very low (around 0.1), as only one of the “relevant” words is fetched (of course the bigger the buckets of the group of words is in the evaluation datasets are, the lower the recall becomes). In Dataset A (the letter addition collection),
![]() ${\tt Soundex}_{GR}$
achieved 0.83 precision and 0.42 recall, while
${\tt Soundex}_{GR}$
achieved 0.83 precision and 0.42 recall, while
![]() ${\tt{Soundex}}^{naive}_{GR}$
0.80 and 0.45, respectively, while
${\tt{Soundex}}^{naive}_{GR}$
0.80 and 0.45, respectively, while
![]() ${\tt{Soundex}}^{comp}_{GR}$
achieved precision 0.74 and recall 0.56, as seen in Figure 2 (for precision) and Figure 3 (for recall).
${\tt{Soundex}}^{comp}_{GR}$
achieved precision 0.74 and recall 0.56, as seen in Figure 2 (for precision) and Figure 3 (for recall).

Figure 2. Precision levels for each collection.

Figure 3. Recall levels for each collection.
In Dataset B (the letter deletion collection),
![]() ${\tt{Soundex}}^{naive}_{GR}$
had a slight drop in precision to 0.75, and an increase in recall that reached to 0.57, while
${\tt{Soundex}}^{naive}_{GR}$
had a slight drop in precision to 0.75, and an increase in recall that reached to 0.57, while
![]() ${\tt Soundex}_{GR}$
remained on the same level, with 0.82 and 0.45, respectively.
${\tt Soundex}_{GR}$
remained on the same level, with 0.82 and 0.45, respectively.
![]() ${\tt{Soundex}}^{comp}_{GR}$
maintained a high precision level of 0.70 and achieved the higher recall 0.68, as seen in Figure 2 (precision) and Figure 3 (recall). The drop in the precision of
${\tt{Soundex}}^{comp}_{GR}$
maintained a high precision level of 0.70 and achieved the higher recall 0.68, as seen in Figure 2 (precision) and Figure 3 (recall). The drop in the precision of
![]() ${\tt{Soundex}}^{naive}_{GR}$
with the recall increasing is quite expected, since
${\tt{Soundex}}^{naive}_{GR}$
with the recall increasing is quite expected, since
![]() ${\tt{Soundex}}^{naive}_{GR}$
ignores some letters and therefore it can handle better the deletion of a letter, while
${\tt{Soundex}}^{naive}_{GR}$
ignores some letters and therefore it can handle better the deletion of a letter, while
![]() ${\tt Soundex}_{GR}$
is more rigid to such errors.
${\tt Soundex}_{GR}$
is more rigid to such errors.
In Dataset C (the letter substitution collection),
![]() ${\tt{Soundex}}^{naive}_{GR}$
achieved precision 0.69 and recall 0.34. The lower scores are due to the more narrow set of phonetic rules. On the other hand, albeit a drop in the scores, the
${\tt{Soundex}}^{naive}_{GR}$
achieved precision 0.69 and recall 0.34. The lower scores are due to the more narrow set of phonetic rules. On the other hand, albeit a drop in the scores, the
![]() ${\tt Soundex}_{GR}$
algorithm maintained the same level of score as in all three sets, with precision 0.80 and recall 0.39. In substitution,
${\tt Soundex}_{GR}$
algorithm maintained the same level of score as in all three sets, with precision 0.80 and recall 0.39. In substitution,
![]() ${\tt{Soundex}}^{comp}_{GR}$
did not manage to make a difference, as it combined the better results of
${\tt{Soundex}}^{comp}_{GR}$
did not manage to make a difference, as it combined the better results of
![]() ${\tt Soundex}_{GR}$
with the worse of
${\tt Soundex}_{GR}$
with the worse of
![]() ${\tt{Soundex}}^{naive}_{GR}$
, achieving precision 0.67 and recall 0.49, as seen in Figure 2 (precision) and Figure 3 (recall). Generally, the algorithms behave better when the error is ordinary to the common Greek Language, meaning that the word is still sounding as the correct one.
${\tt{Soundex}}^{naive}_{GR}$
, achieving precision 0.67 and recall 0.49, as seen in Figure 2 (precision) and Figure 3 (recall). Generally, the algorithms behave better when the error is ordinary to the common Greek Language, meaning that the word is still sounding as the correct one.
In Dataset D, the collection of similarly pronounced words, which comprises the main cases that a phonetic algorithm should be able to tackle both
![]() ${\tt{Soundex}}^{naive}_{GR}$
and
${\tt{Soundex}}^{naive}_{GR}$
and
![]() ${\tt Soundex}_{GR}$
got similar high scores, specifically
${\tt Soundex}_{GR}$
got similar high scores, specifically
![]() ${\tt{Soundex}}^{naive}_{GR}$
achieved precision 0.88 and recall 0.92, while the
${\tt{Soundex}}^{naive}_{GR}$
achieved precision 0.88 and recall 0.92, while the
![]() ${\tt Soundex}_{GR}$
achieved precision 0.96 and recall 0.98, as seen in Figure 2 (precision) and in Figure 3 (recall). The combination of the above algorithms, that is,
${\tt Soundex}_{GR}$
achieved precision 0.96 and recall 0.98, as seen in Figure 2 (precision) and in Figure 3 (recall). The combination of the above algorithms, that is,
![]() ${\tt{Soundex}}^{comp}_{GR}$
, manages to maintain the high scores specifically precision 0.86 and recall 0.98, as its scores are dependent on the two implementations. These scores show that the buckets are sufficient, with
${\tt{Soundex}}^{comp}_{GR}$
, manages to maintain the high scores specifically precision 0.86 and recall 0.98, as its scores are dependent on the two implementations. These scores show that the buckets are sufficient, with
![]() ${\tt Soundex}_{GR}$
having slightly greater precision and recall score.
${\tt Soundex}_{GR}$
having slightly greater precision and recall score.
To sum upthe results, we can see in Figure 4, that
![]() ${\tt{Soundex}}^{naive}_{GR}$
achieves F-Score (note that F-Score, else called F-Measure, is the harmonic mean of precision and recall, that is, F-Score =
${\tt{Soundex}}^{naive}_{GR}$
achieves F-Score (note that F-Score, else called F-Measure, is the harmonic mean of precision and recall, that is, F-Score =
![]() $2 \frac{Precision*Recall}{Precision \mbox{+} Recall}$
) equal to 0.57, 0.65, 0.46, and 0.90 in Dataset A, Dataset B, Dataset C, and Dataset D, respectively.
$2 \frac{Precision*Recall}{Precision \mbox{+} Recall}$
) equal to 0.57, 0.65, 0.46, and 0.90 in Dataset A, Dataset B, Dataset C, and Dataset D, respectively.
![]() ${\tt Soundex}_{GR}$
achieves F-Score scores equal to 0.56, 0.58, 0.53, and 0.97, respectively, and the combination of the two
${\tt Soundex}_{GR}$
achieves F-Score scores equal to 0.56, 0.58, 0.53, and 0.97, respectively, and the combination of the two
![]() ${\tt{Soundex}}^{comp}_{GR}$
achieves 0.64, 0.69, 0.56, and 0.91, respectively, which shows that the
${\tt{Soundex}}^{comp}_{GR}$
achieves 0.64, 0.69, 0.56, and 0.91, respectively, which shows that the
![]() ${\tt{Soundex}}^{comp}_{GR}$
behaves better in general.
${\tt{Soundex}}^{comp}_{GR}$
behaves better in general.

Figure 4. F-measure levels for each collection.
Both
![]() ${\tt Soundex}_{GR}$
and
${\tt Soundex}_{GR}$
and
![]() ${\tt{Soundex}}^{naive}_{GR}$
achieved similar results. They work well when the error does not alter the generated code at a crucial point for the code. Both crucial points would be bellow four characters, and the error involving a consonant for
${\tt{Soundex}}^{naive}_{GR}$
achieved similar results. They work well when the error does not alter the generated code at a crucial point for the code. Both crucial points would be bellow four characters, and the error involving a consonant for
![]() ${\tt{Soundex}}^{naive}_{GR}$
, and a random, unexpected consonant or vowel that is not handled in the preprocessing of the word for the
${\tt{Soundex}}^{naive}_{GR}$
, and a random, unexpected consonant or vowel that is not handled in the preprocessing of the word for the
![]() ${\tt Soundex}_{GR}$
. Since
${\tt Soundex}_{GR}$
. Since
![]() ${\tt{Soundex}}^{comp}_{GR}$
includes both implementations in the retrieval process, it shares the same issues but manages to have higher recall values while not sacrificing greatly in precision. Using both codes can increase recall levels by 0.05 to 0.20, while the precision suffers a drop from 0.10 to 0.20, comparing to
${\tt{Soundex}}^{comp}_{GR}$
includes both implementations in the retrieval process, it shares the same issues but manages to have higher recall values while not sacrificing greatly in precision. Using both codes can increase recall levels by 0.05 to 0.20, while the precision suffers a drop from 0.10 to 0.20, comparing to
![]() ${\tt Soundex}_{GR}$
. The algorithms work well in retrieving words, if the error in a word is based on the same phonetic rules (of Table 3) or are caught in the preprocessing stage, when we make both the query and the text as mispronounced as possible, especially
${\tt Soundex}_{GR}$
. The algorithms work well in retrieving words, if the error in a word is based on the same phonetic rules (of Table 3) or are caught in the preprocessing stage, when we make both the query and the text as mispronounced as possible, especially
![]() ${\tt Soundex}_{GR}$
. For example, for a query like
${\tt Soundex}_{GR}$
. For example, for a query like ![]() , it would correctly retrieve
, it would correctly retrieve ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() but not
but not ![]() ,
, ![]() ,
, ![]() . This is the case because, a single letter addition/deletion/substitution will change the Soundex code, and Soundex does not have a similarity metric in the comparison process.
. This is the case because, a single letter addition/deletion/substitution will change the Soundex code, and Soundex does not have a similarity metric in the comparison process.
4.5 Discussion of the revealed trade-offs as Regards the Length of the Codes (over
 ${\boldsymbol{\tt{Dataset\ A}}} - {\boldsymbol{\tt{Dataset\ D}}}$
)
${\boldsymbol{\tt{Dataset\ A}}} - {\boldsymbol{\tt{Dataset\ D}}}$
)
While testing the algorithm, we observed that simple changes affect the achieved precision and recall. For instance, changing the length of the encoding of
![]() ${\tt Soundex}_{GR}$
from 4 to 6 would greatly improve precision from 0.80 to over 0.90, while dropping recall from 0.40–0.45 to 0.25–0.30. Although Soundex algorithms are used mainly in context where recall matters the most, it is wise to choose the algorithm that suits better the requirements of the application context, that is, whether emphasis should be given to precision or recall. We also noticed that by leaving the first letter unencoded, as the original Soundex, we get a slight increase in the precision (by 0.05–0.10), and a decrease in the recall by 0.05. Finally, splitting all the letters to more categories would also increase precision and decrease recall.
${\tt Soundex}_{GR}$
from 4 to 6 would greatly improve precision from 0.80 to over 0.90, while dropping recall from 0.40–0.45 to 0.25–0.30. Although Soundex algorithms are used mainly in context where recall matters the most, it is wise to choose the algorithm that suits better the requirements of the application context, that is, whether emphasis should be given to precision or recall. We also noticed that by leaving the first letter unencoded, as the original Soundex, we get a slight increase in the precision (by 0.05–0.10), and a decrease in the recall by 0.05. Finally, splitting all the letters to more categories would also increase precision and decrease recall.
To better understand how the length of the
![]() ${\tt Soundex}_{GR}$
codes affects the obtained F-Score, we computed the F-Score over all datasets for code length starting from 1 up to 10, and the length 15. The results are shown in Table 10. The rightmost column shows the average F-Score over each of the four datasets. We can see that length 4 yields the best average F-Score.
${\tt Soundex}_{GR}$
codes affects the obtained F-Score, we computed the F-Score over all datasets for code length starting from 1 up to 10, and the length 15. The results are shown in Table 10. The rightmost column shows the average F-Score over each of the four datasets. We can see that length 4 yields the best average F-Score.
Table 10. Average F-Score (over Dataset A, Dataset B, Dataset C, Dataset D) for different lengths of
![]() ${\tt Soundex}_{GR}$
${\tt Soundex}_{GR}$

To better understand how Precision and Recall are affected by the length of the code, Figure 5 shows for each dataset the Precision, Recall, and F-Score for each length from 1 to 10. In the datasets that correspond to various kinds of errors, that is, in Dataset A (the letter addition collection), Dataset B (the letter deletion collection), and Dataset C (the letter substitution collection), we can see clearly that as the code length increases, the precision increases but the recall decreases. The code length where the F-Score is maximized in these three datasets is 3. In Dataset D (the collection of similarly pronounced words), we can see that as the length increases, the precision increases as well, reaching its maximum at length 5. The recall level does not decrease as the code length increases (as it happens in the previous three datasets) because, even with big code length, the set of all relevant words are those that sound the same and all of them are retrieved because
![]() ${\tt Soundex}_{GR}$
succeeds in assigning them the same code. In this dataset, the length that maximizes F-Score is 5 and any bigger length.
${\tt Soundex}_{GR}$
succeeds in assigning them the same code. In this dataset, the length that maximizes F-Score is 5 and any bigger length.

Figure 5. Precision, Recall, and F-Score evaluation metrics on Dataset A (top left), Dataset B (top right), Dataset C (bottom left), and Dataset D (bottom right) for
![]() ${\tt Soundex}_{GR}$
code lengths 1 to 10.
${\tt Soundex}_{GR}$
code lengths 1 to 10.
More experiments on the selection of the codes’ length are given and analyzed in Section 4.10.
4.6 Comparison with stemming
Apart from comparing the various variations of
![]() ${\tt Soundex}_{GR}$
we decided to compare the grouping of words that it is obtained through
${\tt Soundex}_{GR}$
we decided to compare the grouping of words that it is obtained through
![]() ${\tt Soundex}_{GR}$
, with the grouping that it is obtained by a Stemmer for the Greek language. In general, stemming refers to the process of reducing inflected (or derived) words to their word base or root form. Note that the stem is not necessarily the morphological root of the word in the sense that if two related words map to the same step, then even this stem is not a valid rootFootnote
a
, and it is sufficient for the task of matching and retrieval. Consequently, the strong point of using a stemmer for the problem of matching is that it can successfully identify morphological variations of the same word, and thus it can match word forms that are orthographically and phonetically quite different; however, the weak point of using a stemmer for matching is that it cannot tackle typos (stemmers have not been designed for overcoming typing mistakes) and cannot be applied to named entities (persons, addresses, places, companies, etc).
${\tt Soundex}_{GR}$
, with the grouping that it is obtained by a Stemmer for the Greek language. In general, stemming refers to the process of reducing inflected (or derived) words to their word base or root form. Note that the stem is not necessarily the morphological root of the word in the sense that if two related words map to the same step, then even this stem is not a valid rootFootnote
a
, and it is sufficient for the task of matching and retrieval. Consequently, the strong point of using a stemmer for the problem of matching is that it can successfully identify morphological variations of the same word, and thus it can match word forms that are orthographically and phonetically quite different; however, the weak point of using a stemmer for matching is that it cannot tackle typos (stemmers have not been designed for overcoming typing mistakes) and cannot be applied to named entities (persons, addresses, places, companies, etc).
We used one stemmer of the Greek language, specifically the Mitos Greek Stemmer (Karamaroudis and Markidakis Reference Karamaroudis and Markidakis2006) described in Papadakos et al. (Reference Papadakos, Vasiliadis, Theoharis, Armenatzoglou, Kopidaki, Marketakis, Daskalakis, Karamaroudis, Linardakis and Makrydakis2008) and applied it over the same datasets. The results for Precision, Recall, and F-Score are shown in Figure 6, 7, and 8 respectively.

Figure 6. Precision levels for each collection (also for stemming).

Figure 7. Recall levels for each collection (also for stemming).

Figure 8. F-measure levels for each collection (also for stemming).
We can see that stemming has higher precision (as expected), that is, if two words have the same stem then with high probability they belong to same category of words; however, the recall is very low (as expected), since it cannot tackle misspellings that sound the same. Consequently, stemming has a poor F-Score in comparison to
![]() ${\tt Soundex}_{GR}$
; only in Dataset C stemming has comparable performance (with performance similar to that of
${\tt Soundex}_{GR}$
; only in Dataset C stemming has comparable performance (with performance similar to that of
![]() ${\tt{Soundex}}^{naive}_{GR}$
). Overall,
${\tt{Soundex}}^{naive}_{GR}$
). Overall,
![]() ${\tt Soundex}_{GR}$
is significantly better for the problem at hand, in comparison to using an ordinary stemmer.
${\tt Soundex}_{GR}$
is significantly better for the problem at hand, in comparison to using an ordinary stemmer.
Finally, we should note that we tried also the scenario where we first apply stemming and then apply the Soundex (over the stemmed words); however, the results were worse.
More comparative experiments with stemmer-based matching are given in Section 4.9, as well as in the series of experiments described in Section 4.10.
4.7 Measurements over a Greek dictionary
A dictionary is not a kind of dataset for evaluating phonetic algorithms, since it neither contains misspelled words nor persons’ last names, location names, etc. However, we decided to perform some measurements for getting one idea about the distribution of codes (and for measuring efficiency). For this purpose, we used the WinEdt Unicode dictionary for GreekFootnote
b
. That dictionary contains Greek words and their morphological variations, as well as fist names and acronyms, for example, it contains ![]() AEI. It is actually a list of words, and in total it contains more than half a million Greek words (specifically 574,883). The total number of characters of these words is 6,279,813; hence, the average word size is 10.92 characters and the smallest word(s) have a length 3, while the bigger one has a length 27 (
AEI. It is actually a list of words, and in total it contains more than half a million Greek words (specifically 574,883). The total number of characters of these words is 6,279,813; hence, the average word size is 10.92 characters and the smallest word(s) have a length 3, while the bigger one has a length 27 (![]() ).
).
Since the average number of characters per word is 10.92, while each
![]() ${\tt Soundex}_{GR}$
code comprises four characters, the size of these codes correspond to the 36% of the size of the original dictionary (or we will have 36% increase in the dictionary size if we decide to store also the
${\tt Soundex}_{GR}$
code comprises four characters, the size of these codes correspond to the 36% of the size of the original dictionary (or we will have 36% increase in the dictionary size if we decide to store also the
![]() ${\tt Soundex}_{GR}$
code for each word). Using the stemmer that we mentioned in Section 4.6, the average stem size is 7.46. That means that the size of these stems correspond to the 68% of the size of the original dictionary (or we will have 68% increase in the dictionary size if we decide to store also the stem for each word).
${\tt Soundex}_{GR}$
code for each word). Using the stemmer that we mentioned in Section 4.6, the average stem size is 7.46. That means that the size of these stems correspond to the 68% of the size of the original dictionary (or we will have 68% increase in the dictionary size if we decide to store also the stem for each word).
The number of distinct
![]() ${\tt Soundex}_{GR}$
codes is 7577, that is, in average each code corresponds to 574,883/7577 = 75.87 words. The number of distinct stems is 109,453, that is, each stem corresponds to 574,883/ 109,453 = 5,25 words. In comparison to
${\tt Soundex}_{GR}$
codes is 7577, that is, in average each code corresponds to 574,883/7577 = 75.87 words. The number of distinct stems is 109,453, that is, each stem corresponds to 574,883/ 109,453 = 5,25 words. In comparison to
![]() ${\tt Soundex}_{GR}$
, the number of lemmas is 109,4530/7577 = 14.44 times more than the number of
${\tt Soundex}_{GR}$
, the number of lemmas is 109,4530/7577 = 14.44 times more than the number of
![]() ${\tt Soundex}_{GR}$
codes.
${\tt Soundex}_{GR}$
codes.
The distribution of neither
![]() ${\tt Soundex}_{GR}$
codes, nor stems, is uniform, as expected. There are codes with only one word, while the more “populated” code corresponds to 11,681 words (corresponding to words starting from
${\tt Soundex}_{GR}$
codes, nor stems, is uniform, as expected. There are codes with only one word, while the more “populated” code corresponds to 11,681 words (corresponding to words starting from ![]() , a frequent prefix in Greek). Analogously, the min number of words per stem is 1, while the max number of words per stem is 257 (corresponding to the lemma
, a frequent prefix in Greek). Analogously, the min number of words per stem is 1, while the max number of words per stem is 257 (corresponding to the lemma ![]() ). The distributions of the frequencies of
). The distributions of the frequencies of
![]() ${\tt Soundex}_{GR}$
codes, and stemmer lemmas, over the distionary, are shown in Figure 9, where both Y-axes (of the left and right plot) are in log scale. The 10 more frequent codes are shown in Table 11, while the 10 more frequent stems at Table 12.
${\tt Soundex}_{GR}$
codes, and stemmer lemmas, over the distionary, are shown in Figure 9, where both Y-axes (of the left and right plot) are in log scale. The 10 more frequent codes are shown in Table 11, while the 10 more frequent stems at Table 12.

Figure 9. Frequency of
![]() ${\tt Soundex}_{GR}$
codes (left), and lemmas of the stemmer (right) over the dictionary.
${\tt Soundex}_{GR}$
codes (left), and lemmas of the stemmer (right) over the dictionary.
Table 11. More frequent
![]() ${\tt Soundex}_{GR}$
codes
${\tt Soundex}_{GR}$
codes

Of course, and based on the task at hand, one might decide to use longer
![]() ${\tt Soundex}_{GR}$
codes if he wants to improve precision over recall, as discussed in Section 4.5.
${\tt Soundex}_{GR}$
codes if he wants to improve precision over recall, as discussed in Section 4.5.
Table 12. More frequent stems

4.8 Other variations: Full phonemic transcription
It is not hard to see that the same rules, with small changes, can be used for deriving the full phonemic transcription of a Greek word. With “phonemes,” we refer to the mental categories that a speaker uses, rather than the actual spoken variants of those phonemes that are produced in the context of a particular word (note that phonetic transcription specifies the finer details of how sounds are actually made).
Specifically, we can use only the following three steps of Alg. 1:
-
 $w \gets $
UnwrapConsonantBigrams(word)
$w \gets $
UnwrapConsonantBigrams(word) -
 $w \gets $
TransformVowelsToConsonants(w)
$w \gets $
TransformVowelsToConsonants(w) -
 $w \gets $
GroupVowels(w)
$w \gets $
GroupVowels(w)
The rest steps of Alg. 1 are not needed, that is, we skip the step of removing last chars (RemoveLast), the step of encoding (SoundexEncode), and the step of duplicate elimination (RemoveDuplicates).
With the above three steps, the changes that are required for producing a full phonetic transcription of Greek words are minimal. The first change is that in GroupVowels(w) the grouping is a bit different, specifically we group “ou” to“u” (instead of “o”). The second change is that instead of mapping both ![]() and
and ![]() to “c” we map the first to “ts” and the second to “dz”. Finally, instead of using greek letters for the phonetic transcription we can use latin letters whenever possible, in any case the selection of the characters in the phonetic transcription does not affect the matching process. A few examples are given in Figure 10:
to “c” we map the first to “ts” and the second to “dz”. Finally, instead of using greek letters for the phonetic transcription we can use latin letters whenever possible, in any case the selection of the characters in the phonetic transcription does not affect the matching process. A few examples are given in Figure 10:

Figure 10. Indicative examples of full phonemic transcription.
We have implemented the above version, and it is included in the public release of the SoundexGR family of algorithms (described in Section 4.11). Another important question is how the exact phonetic (phonemic) transcription would behave in the evaluation datasets (described in Section 4.2). The results are not that good, specifically:
in Dataset A (the letter addition collection) we got F-Score = 0.17,
in Dataset B (the letter deletion collection) we got F-Score = 0.31,
in Dataset C (the letter substitution collection) we got F-Score = 0.23, and
in Dataset D (the collection of similarly pronounced words) we got F-Score = 0.93. We observe that full phonetic transcription behaves well only in Dataset D achieving F-Score 0.93; however, that score is lower than 0.97 that is achieved by by
![]() ${\tt{Soundex}}^{naive}_{GR}$
. As expected, in the rest evaluation datasets, the exact phonetic transcription behaves much worse since it cannot tackle the cases of letter additions, deletions, and substitutions.
${\tt{Soundex}}^{naive}_{GR}$
. As expected, in the rest evaluation datasets, the exact phonetic transcription behaves much worse since it cannot tackle the cases of letter additions, deletions, and substitutions.
Overall, the average F-Score across all evaluation datasets of
![]() ${\tt Soundex}_{GR}$
for length 4 is equal to 0.66 (as shown in Table 5), while the average F-Score across all evaluation datasets of full phonemic transcription is 0.41 (=(0.17+0.31+0.23+0.93)/4).
${\tt Soundex}_{GR}$
for length 4 is equal to 0.66 (as shown in Table 5), while the average F-Score across all evaluation datasets of full phonemic transcription is 0.41 (=(0.17+0.31+0.23+0.93)/4).
Additional experiments with matching using full phonemic transcription are given in Section 4.9, and in the series of experiments described in Section 4.10.
4.9 Comparing all variations over
 ${\boldsymbol{\tt Dataset\ D}}^{ext}$
${\boldsymbol{\tt Dataset\ D}}^{ext}$
To provide an overview of the effectiveness of the aforementioned methods, we decided to prepare an extended version of Dataset D for containing more variations for each word. The derived dataset, denoted by
![]() ${\tt Dataset\ D}^{ext}$
, contains in total 500 words, in particular it contains 125 words in their orthographically correct form plus 3 misspellings for each one of these. All of the misspellings sound the same with the correct one. We have tried to include words that are frequently misspelled as well as typographic errors that do not, however, change the way they would sound. An excerpt of this dataset is shown in Figure 11.
${\tt Dataset\ D}^{ext}$
, contains in total 500 words, in particular it contains 125 words in their orthographically correct form plus 3 misspellings for each one of these. All of the misspellings sound the same with the correct one. We have tried to include words that are frequently misspelled as well as typographic errors that do not, however, change the way they would sound. An excerpt of this dataset is shown in Figure 11.

Figure 11. Excerpt from
![]() ${\rm{Dataset }}{{\rm{D}}^{ext}}$
.
${\rm{Dataset }}{{\rm{D}}^{ext}}$
.
Over this dataset, we evaluated all aforementioned methods, plus some more, 10 in total methods, in particular exact match,
![]() ${\tt{Soundex}}^{naive}_{GR}$
,
${\tt{Soundex}}^{naive}_{GR}$
,
![]() ${\tt Soundex}_{GR}$
,
${\tt Soundex}_{GR}$
,
![]() ${\tt{Soundex}}^{comp}_{GR}$
, stemming (as described in Section 4.6),
${\tt{Soundex}}^{comp}_{GR}$
, stemming (as described in Section 4.6),
![]() ${\tt Soundex}_{GR}$
over the results of stemming, full phonemic transcription (as described in Section 4.8), and matching based on the edit distance Levenshtein (Reference Levenshtein1966) with tolerance K ranging from 1 to 3. For instance, edit distance with
${\tt Soundex}_{GR}$
over the results of stemming, full phonemic transcription (as described in Section 4.8), and matching based on the edit distance Levenshtein (Reference Levenshtein1966) with tolerance K ranging from 1 to 3. For instance, edit distance with
![]() $K=2$
means that two words match if their edit distance is less than or equal to 2. The code length for
$K=2$
means that two words match if their edit distance is less than or equal to 2. The code length for
![]() ${\tt{Soundex}}^{naive}_{GR}$
,
${\tt{Soundex}}^{naive}_{GR}$
,
![]() ${\tt Soundex}_{GR}$
, and
${\tt Soundex}_{GR}$
, and
![]() ${\tt{Soundex}}^{comp}_{GR}$
was equal to 4. The results are shown in Table 13, where the highest values of Precision, Recall, and F-Score are written in bold. By inspecting the values, we can understand the behavior of these methods, and we can see that
${\tt{Soundex}}^{comp}_{GR}$
was equal to 4. The results are shown in Table 13, where the highest values of Precision, Recall, and F-Score are written in bold. By inspecting the values, we can understand the behavior of these methods, and we can see that
![]() ${\tt Soundex}_{GR}$
achieves the highest F-Score (0.97).
${\tt Soundex}_{GR}$
achieves the highest F-Score (0.97).
Table 13. Evaluating 10 matching methods over
![]() ${\tt Dataset\ D}^{ext}$
${\tt Dataset\ D}^{ext}$

4.10 Experiments at different scales—On selecting the length of the codes (over
 ${\boldsymbol{\tt Dataset\ E}}$
-
${\boldsymbol{\tt Dataset\ E}}$
-
 ${\boldsymbol{\tt Dataset\ H}}$
)
${\boldsymbol{\tt Dataset\ H}}$
)
In Section 4.5, we have seen that the length 4 yields the best average F-Score over the four evaluation datasets. Questions that arise are: Does the optimal length depend on the size of the dataset? Should we use shorter codes in smaller datasets, and larger codes in larger collections? One approach for tackling these questions is to make the experiments (like those reported in Table 10) but instead of considering the entire evaluation datasets, to consider only parts of these datasets starting from very small parts and reaching to the entire evaluation datasets. For this purpose, we performed experiments after having limited the number of words to be considered from each dataset, starting from 200 words up to 2000 words with increment step equal to 200.
For each such dataset size, we have evaluated
![]() ${\tt Soundex}_{GR}$
code lengths starting from 2 up to 12. The experimental results, as regards average F-Score, are shown in Figure 12(top plot). The left Y-axis corresponds to the code length (from 2 to 12), while the right Y-axis corresponds to the average F-Score (across the four evaluation dataset parts). The X-axis shows the dataset sizes (from 200 to 2000 words with step equal to 200), and for each such size the X-axis has 11 ticks each corresponding to one code length (from 2 to 12).
${\tt Soundex}_{GR}$
code lengths starting from 2 up to 12. The experimental results, as regards average F-Score, are shown in Figure 12(top plot). The left Y-axis corresponds to the code length (from 2 to 12), while the right Y-axis corresponds to the average F-Score (across the four evaluation dataset parts). The X-axis shows the dataset sizes (from 200 to 2000 words with step equal to 200), and for each such size the X-axis has 11 ticks each corresponding to one code length (from 2 to 12).

Figure 12. Average F-Score (top), Precision (middle), and Recall (bottom) as a function of code length (left Y-axis, blue dots) and dataset size (X-axis) of
![]() ${\tt Soundex}_{GR}$
in Dataset A, Dataset B, Dataset C, and Dataset D.
${\tt Soundex}_{GR}$
in Dataset A, Dataset B, Dataset C, and Dataset D.
Figure 12(top plot) reveals the following general pattern: as the code length increases, theF-Score increases reaching a peak around 0.7 (usually for code length 3 or 4) and then it is decreased and ends up to 0.5. Figure 12 (middle and bottom plot) shows the average Precision and average Recall that helps us to explain the distribution of the average F-Score. From these measurements, we could say that the size of the dataset is not very decisive (at least for the considered sizes in this experiment, i.e., for 200 to 2000), since we can see that the size of the dataset does not affect significantly the F-Score. It is not hard to see that it is not only the size of the dataset that matters, but also the length of the words, a quantity that does not depend on the dataset size: even in small datasets too, short codes or too long codes harm the F-Score that we achieve and this is evidenced by the measurements, that is, through the low F-Score values that we get for very short and very long codes in Figure 12(top plot). To test this hypothesis, and further understand what affects performance, we designed the experiment that follows.
Datasets with bigger word size variations. By exploiting the experience from creating (manually) the
![]() ${\tt Dataset\ D}^{ext}$
, we decided to use the dictionary of Greek words (mentioned in Section 4.7 that contains 574,883 distinct words) for producing larger datasets for further evaluation and experimentation related to the size of the codes. For each word of that dictionary, we produce a bucket that contains variations of the word with various kinds of errors. We decided to include words that contain more than one errors, not only because there are many frequent misspellings that contain more than one error, for example,
${\tt Dataset\ D}^{ext}$
, we decided to use the dictionary of Greek words (mentioned in Section 4.7 that contains 574,883 distinct words) for producing larger datasets for further evaluation and experimentation related to the size of the codes. For each word of that dictionary, we produce a bucket that contains variations of the word with various kinds of errors. We decided to include words that contain more than one errors, not only because there are many frequent misspellings that contain more than one error, for example, ![]() instead of
instead of ![]() ,
, ![]() instead of
instead of ![]() , but also for evaluating cases that cannot be captured easily by the edit distance. Therefore, we have included various errors that do not affect the way the word sounds, so the emphasis is given on orthographic errors.
, but also for evaluating cases that cannot be captured easily by the edit distance. Therefore, we have included various errors that do not affect the way the word sounds, so the emphasis is given on orthographic errors.
Specifically, for producing such errors, we have created around 40 rules for capturing various cases. Most of them are replacement rules, with conditions on the characters that should not appear before or after the character to be replaced. For instance, the rule Rule ![]() replaces
replaces ![]() with
with ![]() only if the letter before
only if the letter before ![]() is not one of
is not one of ![]() since in that case we have a diphthong and such an error would not be common. Analogously, the rule Rule (
since in that case we have a diphthong and such an error would not be common. Analogously, the rule Rule (![]() ) replaces
) replaces ![]() with
with ![]() only if the character after
only if the character after ![]() is not one of the lists, since in that case we have a diphthong too. The set of rules is not supposed to produce all possible errors, but they can capture pretty well various kind of common errors; therefore, the variations they produce can be used for the evaluation of approximate matching. To ensure that for each word (also for the very small ones) we have at least one misspelled word, we have included one rule that doubles a middle consonant. Let call this dataset Dataset E.
is not one of the lists, since in that case we have a diphthong too. The set of rules is not supposed to produce all possible errors, but they can capture pretty well various kind of common errors; therefore, the variations they produce can be used for the evaluation of approximate matching. To ensure that for each word (also for the very small ones) we have at least one misspelled word, we have included one rule that doubles a middle consonant. Let call this dataset Dataset E.
The words in the original dictionary are ordered by their size. To create a dataset that covers all word sizes we used step 400, that is, we peek one word every 400 words of the dictionary. The resulting dataset, that we will denote by
![]() ${\tt Dataset\ E}_{1.4K-7.6K}$
, has 1438 distinct correct words 7608 words in total, and the average size of the blocks is 5.29, that is, in average the dataset contains more than four misspellings per word. A small excerpt from the produced dataset is shown in Figure 13.
${\tt Dataset\ E}_{1.4K-7.6K}$
, has 1438 distinct correct words 7608 words in total, and the average size of the blocks is 5.29, that is, in average the dataset contains more than four misspellings per word. A small excerpt from the produced dataset is shown in Figure 13.

Figure 13. Excerpt from
![]() ${\tt Dataset\ E}_{1.4K-7.6K}$
.
${\tt Dataset\ E}_{1.4K-7.6K}$
.
Over this dataset, denoted by
![]() ${\tt Dataset\ E}_{1.4K-7.6K}$
, we run the experiments and the results are shown in Table 14. At first, we observe that exact match achieves F-Score 0.37, stemming 0.40, while full phonemic transcription 0.86. Edit distance achieves its maximum F-Score, that is, 0.9, with
${\tt Dataset\ E}_{1.4K-7.6K}$
, we run the experiments and the results are shown in Table 14. At first, we observe that exact match achieves F-Score 0.37, stemming 0.40, while full phonemic transcription 0.86. Edit distance achieves its maximum F-Score, that is, 0.9, with
![]() $K\leq3$
. Notice that
$K\leq3$
. Notice that
![]() ${\tt Soundex}_{GR}$
is better than all the above options for any code length equal or greater than 6. The optimal F-Score is, that is, 0.98, is achieved with
${\tt Soundex}_{GR}$
is better than all the above options for any code length equal or greater than 6. The optimal F-Score is, that is, 0.98, is achieved with
![]() ${\tt{Soundex}}^{comp}_{GR}$
and code length equal to 10. This length is longer than what we expected; however, this can be explained by the fact that the dictionary contains a lot of big words.
${\tt{Soundex}}^{comp}_{GR}$
and code length equal to 10. This length is longer than what we expected; however, this can be explained by the fact that the dictionary contains a lot of big words.
Table 14. Evaluating 10 methods over
![]() ${\tt Dataset\ E}_{1.4K-7.6K}$
${\tt Dataset\ E}_{1.4K-7.6K}$

To produce a larger dataset, we reduced the step to 200 and we produced
![]() ${\tt Dataset\ F}_{2.8K-15.2K}$
that contains 2875 correct words and 15,297 total words (average bucket size 5.32). The results of the experiments are shown in Table 15. We observe a slight drop in precision and F-Score for length 4; however
${\tt Dataset\ F}_{2.8K-15.2K}$
that contains 2875 correct words and 15,297 total words (average bucket size 5.32). The results of the experiments are shown in Table 15. We observe a slight drop in precision and F-Score for length 4; however
![]() ${\tt Soundex}_{GR}$
with code length equal to 12 preserves the very high F-Score (0.97).
${\tt Soundex}_{GR}$
with code length equal to 12 preserves the very high F-Score (0.97).
To produce an even larger dataset, we further reduced the step to 100 and produced
![]() ${\tt Dataset\ G}_{5.7K-30.4K}$
that contains 5749 correct words and 30,824 words in total (average bucket size 5.36). The results of the experiments and the results are shown in Table 16. We observe a further drop in precision and F-Score for length 4; however, for code length equal to 12,
${\tt Dataset\ G}_{5.7K-30.4K}$
that contains 5749 correct words and 30,824 words in total (average bucket size 5.36). The results of the experiments and the results are shown in Table 16. We observe a further drop in precision and F-Score for length 4; however, for code length equal to 12,
![]() ${\tt Soundex}_{GR}$
preserves the very high F-Score (0.97).
${\tt Soundex}_{GR}$
preserves the very high F-Score (0.97).
Table 15. Evaluating 10 methods over
![]() ${\tt Dataset\ F}_{2.8K-15.2K}$
${\tt Dataset\ F}_{2.8K-15.2K}$

Table 16. Evaluating 10 methods over
![]() ${\tt Dataset\ G}_{5.7K-30.4K}$
${\tt Dataset\ G}_{5.7K-30.4K}$

The previous datasets (
![]() ${\tt Dataset\ E}_{1.4K-7.6K}-{\tt Dataset\ G}_{5.7K-30.4K}$
), which were derived by picking words from the beginning up to the end of the dictionary, covered the entire spectrum of word lengths. However, longer words are less frequent; therefore, it is sensible to make experiments starting from the beginning and without gaps, for considering all short- and medium-sized words, which are expected to contain the frequent ones. The resulting dataset is probably harder for matching, not only because there are many small words making precision hard to achieve, but also because many morphological variations of the included words will be included (since Step 1 was used), so it is more challenging to achieve high precision. For this reason, we performed experiments of
${\tt Dataset\ E}_{1.4K-7.6K}-{\tt Dataset\ G}_{5.7K-30.4K}$
), which were derived by picking words from the beginning up to the end of the dictionary, covered the entire spectrum of word lengths. However, longer words are less frequent; therefore, it is sensible to make experiments starting from the beginning and without gaps, for considering all short- and medium-sized words, which are expected to contain the frequent ones. The resulting dataset is probably harder for matching, not only because there are many small words making precision hard to achieve, but also because many morphological variations of the included words will be included (since Step 1 was used), so it is more challenging to achieve high precision. For this reason, we performed experiments of
![]() ${\tt Soundex}_{GR}$
for all code lengths from 2 up to 12 for dataset sizes starting from 1000 words to 29,000 words with dataset increment step 2000 (words, not rows). The resulting series of 15 datasets contain letters with words up to 6 letters.
${\tt Soundex}_{GR}$
for all code lengths from 2 up to 12 for dataset sizes starting from 1000 words to 29,000 words with dataset increment step 2000 (words, not rows). The resulting series of 15 datasets contain letters with words up to 6 letters.
The results are given in Figure 14. Notice that the right vertical axes start from 0.5 for F-Score, 0.3 for Precision, 0.8 for Recall, to make more evident the differences. In Figure 14(top plot), we observe that Recall is not essentially affected by neither dataset size nor code length. In Figure 14 (middle plot), we observe that (as expected) the Precision is lower and it is affected by the size of the collection. In Figure 14 (bottom plot), we observe that F-Score is affected by the size of the collection (i.e., it decreases as the dataset size increases) but achieves 0.7 for code lenghs
![]() $\geq 8$
. In general, we observe (as expected) that in this series of datasets that contains small words, the F-Score is lower than what in
$\geq 8$
. In general, we observe (as expected) that in this series of datasets that contains small words, the F-Score is lower than what in
![]() ${\tt Dataset\ G}_{5.7K-30.4K}$
. This evidences that not only the size of the vocabulary and the kind of errors but also the size of the words affect the effectiveness of matching.
${\tt Dataset\ G}_{5.7K-30.4K}$
. This evidences that not only the size of the vocabulary and the kind of errors but also the size of the words affect the effectiveness of matching.

Figure 14. Recall (top), Precision (middle), and F-Score (bottom) as a function of code length (left Y-axis, blue dots) and dataset size (X-axis) of
![]() ${\tt Soundex}_{GR}$
in
${\tt Soundex}_{GR}$
in
![]() ${\tt Dataset\ H}$
.
${\tt Dataset\ H}$
.
Synopsis and general remarks. Figure 15 illustrates the main results, that is, it shows each dataset and its characteristics, as well as the best F-Scores obtained by
![]() ${\tt Soundex}_{GR}$
and other matching methods.
${\tt Soundex}_{GR}$
and other matching methods.

Figure 15. A synopsis of the main evaluation results.
A few general remarks follow:
-
The bigger the collection is, and the longer words it contains, the longer the codes should be (to preserve precision). The same is true for the tolerance of edit distance-based matching. In a context where retrieval of high precision is required (e.g., in the retrieval of user comments within a voice-based conversational interaction, as in Dimitrakis et al. (Reference Dimitrakis, Sgontzos, Papadakos, Marketakis, Papangelis, Stylianou and Tzitzikas2018)), longer codes can be selected, while in an application context where recall is more important (e.g., in patent search), shorter ones could be more appropriate. The performance also depends on the kind of errors that expect and their relative percentage (e.g., long codes are good if we have several orthographic errors, not random errors).
-
If one wants to select the best option in a particular application setting, apart from the above analysis, one can perform ad hoc experiments, and for this reason the code for running the aforementioned experiments with various sizes of codes has been made publicly available. Moreover, and to facilitate comparative results, we have uploaded the full dataset that contains 574,883 distinct Greek words and 4.32 misspellings per word in average, in total more than 3 million forms of Greek words (3,063,143) at Tzitzikas (Reference Tzitzikas2021).
4.11 Implementation and efficiency
As regards efficiency, using a machine with 1.8 GHz i7, 4MB cache, and 16 GB of RAM,
![]() ${\tt Soundex}_{GR}$
encodes the words of each set of 2500 words in 2.5 s, meaning each word takes 1 ms to be encoded, while
${\tt Soundex}_{GR}$
encodes the words of each set of 2500 words in 2.5 s, meaning each word takes 1 ms to be encoded, while
![]() ${\tt{Soundex}}^{naive}_{GR}$
in 0.4 s, meaning that it needs 0.016 ms per word. Since
${\tt{Soundex}}^{naive}_{GR}$
in 0.4 s, meaning that it needs 0.016 ms per word. Since
![]() ${\tt{Soundex}}^{comp}_{GR}$
uses both the implementations to encode a word, it needs 1.016 ms per word.
${\tt{Soundex}}^{comp}_{GR}$
uses both the implementations to encode a word, it needs 1.016 ms per word.
To compute the
![]() ${\tt Soundex}_{GR}$
codes for each word of the dictionary described in Section 4.7, that is, for more than half a million words, our implementation (using Java 8) takes less than 2 s (specifically 1,684 msecs) using a machine with 1.9 GHz i7, 8MB cache, and 16 GB of RAM.
${\tt Soundex}_{GR}$
codes for each word of the dictionary described in Section 4.7, that is, for more than half a million words, our implementation (using Java 8) takes less than 2 s (specifically 1,684 msecs) using a machine with 1.9 GHz i7, 8MB cache, and 16 GB of RAM.
An implementation of all algorithms, as well as the evaluation datasets, are publicly available at https://github.com/YannisTzitzikas/SoundexGR. Moreover, a tool (editor) for aiding the designer to select the method to be applied is also provided: it shows all codes for the words of the input text, a screenshot is given in Figure 16.

Figure 16. A tool for visual inspection of the produced codes, approximate matching, and others.
4.12 Applications
The simplicity and efficiency of the proposed algorithm makes it applicable to a wide range of tasks. It can be exploited whenever we want to find matchings between (written or spoken) descriptions in Greek. In general, these phonetic codes can be used for tackling Out-Of-Vocabulary (OOV) words, a problem that occurs frequently and in various contexts. Indeed, the phonetic codes can be exploited for supporting various kinds of matching, depending on the context. As shown in Section 4.10, the way to handle the OOV problem depends on various factors (collection size, kind and percentage of errors, and word lengths). To verify it in a pure matching context, we implemented a prototype matching service where the user enters a word, and the system performs lookup in the dictionary of Greek words (mentioned in Section 4.7 that contains 574,883 distinct words), and if the word is not found, then it suggests to the user a number of approximate matches. Note that this problem is easier in a context where also the frequencies of words are available (e.g., in query autocompletion in web searching); however, we wanted to inspect the behavior of matching if no usage information is available. We implemented the approximate matching by returning all words of the dictionary that have the same
![]() ${\tt Soundex}_{GR}$
code with the word entered by the user. As expected, the returned words depend on the length of the codes that are used. For instance, for the mispelled word
${\tt Soundex}_{GR}$
code with the word entered by the user. As expected, the returned words depend on the length of the codes that are used. For instance, for the mispelled word ![]() the system, with
the system, with
![]() ${\tt Soundex}_{GR}$
code length equal to 12, returns two suggestions
${\tt Soundex}_{GR}$
code length equal to 12, returns two suggestions ![]() . Notice that the edit distance of these words is 4 and 5, making clear the differentiation (and benefit) of this matching in comparison to edit distance-based matching. We obtain the same two suggestions for any code length between 7 and 12.
. Notice that the edit distance of these words is 4 and 5, making clear the differentiation (and benefit) of this matching in comparison to edit distance-based matching. We obtain the same two suggestions for any code length between 7 and 12.
However, if we further reduce the length to 6, then we get the 23 suggestions shown in Figure 17.

Figure 17. Suggestions for the mispelled word ![]() based on length code = 6.
based on length code = 6.
This suggests that the phonetic codes can be used for more sophisticated services as well, for example, if the number of words with the same code is high then we can rank them according to their edit distance. The returned ranked list will include words that sound the same but may have several orthographic mistakes (therefore would be not returned by the edit distance) which will be subsequently ranked with respect to edit distance allowing in this way to control the number of suggestions. An example for the word ![]() is shown in Figure 18, demonstrating that ranking with edit distance over the
is shown in Figure 18, demonstrating that ranking with edit distance over the
![]() ${\tt Soundex}_{GR}$
codes gives better results than applying directly edit distance, as the latter includes totally irrelevant words.
${\tt Soundex}_{GR}$
codes gives better results than applying directly edit distance, as the latter includes totally irrelevant words.

Figure 18. Demonstrating approximate matching methods.
Furthermore, since the codes can be computed once (something that is not possible with the edit distance), this offers a more efficient method for computing approximate matches.
To support the process of designing such services, the application allows testing the above services using various code lengths. It also offers a method that takes as input one word and produces various misspellings, enabling the user to easily pick misspellings for checking the approximate matching (as shown in the bottom part of Figure 16).
4.12.1 Indicative Application Contexts
Below, we sketch how these codes can be used for tackling the problem of Out-Of-Vocabulary (OOV) words in various contexts.
-
Autocompletion Services. Each work w in the list of possible query completions (corresponding to the frequent queries according to the query logs) can be accompanied by its
 ${\tt Soundex}_{GR}$
code. If the user’s input contains a word w
′ that is not in C, instead of searching for words with small edit distance, the words that have the same
${\tt Soundex}_{GR}$
code. If the user’s input contains a word w
′ that is not in C, instead of searching for words with small edit distance, the words that have the same
 ${\tt Soundex}_{GR}$
can be prompted as well. To support letter-based suggestions, a trie data structure (like the one in Fafalios and Tzitzikas (Reference Fafalios and Tzitzikas2015)) of
${\tt Soundex}_{GR}$
can be prompted as well. To support letter-based suggestions, a trie data structure (like the one in Fafalios and Tzitzikas (Reference Fafalios and Tzitzikas2015)) of
 ${\tt Soundex}_{GR}$
codes can be used for parallel traversal as well, that is, for each letter that is typed by the user we traverse both the trie of frequent queries and the trie of the
${\tt Soundex}_{GR}$
codes can be used for parallel traversal as well, that is, for each letter that is typed by the user we traverse both the trie of frequent queries and the trie of the
 ${\tt Soundex}_{GR}$
codes of these queries, and eventually we suggest to the user completions based on the contents of both tries.
${\tt Soundex}_{GR}$
codes of these queries, and eventually we suggest to the user completions based on the contents of both tries. -
Retrieval Services. Each work w in the Vocabulary V of an Inverted File can be accompanied by its
 ${\tt Soundex}_{GR}$
code. If the user’s query contains a word w
′ that is not in V (for instance, Cucerzan and Brill (Reference Cucerzan and Brill2004) reports that misspellings appear in up to 15% of web search queries), instead of searching only for words with small edit distance, the words that have the same
${\tt Soundex}_{GR}$
code. If the user’s query contains a word w
′ that is not in V (for instance, Cucerzan and Brill (Reference Cucerzan and Brill2004) reports that misspellings appear in up to 15% of web search queries), instead of searching only for words with small edit distance, the words that have the same
 ${\tt Soundex}_{GR}$
can be used as well. Subsequently, the
${\tt Soundex}_{GR}$
can be used as well. Subsequently, the
 ${\tt Soundex}_{GR}$
codes of the words can also be exploited for producing the snippets of the hits that will be displayed in the search results. The snippet of a hit is a small excerpt of that document that contains most of the query words that is computed at query time using sequential text search. Consequently, if the locally stored textual contents of the indexed documents are encoded using
${\tt Soundex}_{GR}$
codes of the words can also be exploited for producing the snippets of the hits that will be displayed in the search results. The snippet of a hit is a small excerpt of that document that contains most of the query words that is computed at query time using sequential text search. Consequently, if the locally stored textual contents of the indexed documents are encoded using
 ${\tt Soundex}_{GR}$
, then that would speed up the sequential search required for selecting the snippet to display. Other modern applications of real-time searching, for example, methods for linking text to a knowledge base of fact-checked claims (as in Maliaroudakis et al. (Reference Maliaroudakis, Boland, Dietze, Todorov, Tzitzikas and Fafalios2021)), for aiding the detection of fake news, can also be benefited by phonetic matching.
${\tt Soundex}_{GR}$
, then that would speed up the sequential search required for selecting the snippet to display. Other modern applications of real-time searching, for example, methods for linking text to a knowledge base of fact-checked claims (as in Maliaroudakis et al. (Reference Maliaroudakis, Boland, Dietze, Todorov, Tzitzikas and Fafalios2021)), for aiding the detection of fake news, can also be benefited by phonetic matching. -
Named Entity Identification. Modern methods for Named Entity Extraction rely on pure NLP methods and knowledge-based methods (Mountantonakis and Tzitzikas Reference Mountantonakis and Tzitzikas2020). The extraction of named entities is usually based on lists of entities (e.g., Countries, etc) which comprise the names of the entities (and alternative names, as in Linked Open Data). Such lists can also contain the phonetic codes of these names to speed up matching and to tackle morphological variations. Indeed, the recent survey by Singh et al. (Reference Singh, Lytra, Radhakrishna, Shekarpour, Vidal and Lehmann2020) shows that the components of modern Question Answering systems (that heavily rely on entity identification) are very vulnerable to the morphological variations of the words in the questions that refer to entities.
-
Word Embeddings and ML. As mentioned in Piktus et al. (Reference Piktus, Edizel, Bojanowski, Grave, Ferreira and Silvestri2019), the existing approaches for producing word embeddings cannot provide embeddings for words that have not been observed at training time. For instance, for the English language, Satapathy et al. (Reference Satapathy, Guerreiro, Chaturvedi and Cambria2017) used the Soundex algorithm to convert out-of-vocabulary to in-vocabulary and analyzed its impact on the sentiment analysis task, while Satapathy et al. (Reference Satapathy, Singh and Cambria2019) proposed a concept-based lexicon that exploits phonetic features to normalize the out-of-vocabulary concepts to in-vocabulary concepts (Huang et al. Reference Huang, Zhuang and Wang2020). An analogous direction could be investigated for the Greek language, since there are already proposals for creating embeddings for the Greek language, for example, the ensemble method described in Lioudakis et al. (Reference Lioudakis, Outsios and Vazirgiannis2019), the method for named entity recognition from Greek legislation described in Angelidis et al. (Reference Angelidis, Chalkidis and Koubarakis2018), while an evaluation of Greek Word Embeddings is described in Outsios et al. (Reference Outsios, Karatsalos, Skianis and Vazirgiannis2019), that does not include the more recent Greek BERT Koutsikakis et al. (Reference Koutsikakis, Chalkidis, Malakasiotis and Androutsopoulos2020). Out-Of-Vocabulary (OOV) words need to be tackled in all cases, for instance, the dictionary that we used contains around 500K Greek words, while Greek BERT Koutsikakis et al. (Reference Koutsikakis, Chalkidis, Malakasiotis and Androutsopoulos2020) contains embeddings for only 35K words.
In general, applications of phonetic encoding algorithms are widely used in modern information technology, both in the original and modified forms, a detailed list is given in Vykhovanets et al. (Reference Vykhovanets, Du and Sakulin2020).
5. Conclusion
We introduced a family of phonetic algorithms for the Greek Language by adapting the original Soundex to the characteristics of the Greek Language, and widening the rules, as most modern phonetic algorithms have done. In particular, we introduced
![]() ${\tt Soundex}_{GR}$
and a simpler variation called
${\tt Soundex}_{GR}$
and a simpler variation called
![]() ${\tt{Soundex}}^{naive}_{GR}$
, both producing codes of four characters. In brief, before a word is encoded, it is preprocessed and this preprocessing includes identification of cases when a vowel sounds as a consonant in Greek, grouping of vowels that make a different sound when paired together, intonation removal, and dismantling digrams to single letters. Moreover, we defined
${\tt{Soundex}}^{naive}_{GR}$
, both producing codes of four characters. In brief, before a word is encoded, it is preprocessed and this preprocessing includes identification of cases when a vowel sounds as a consonant in Greek, grouping of vowels that make a different sound when paired together, intonation removal, and dismantling digrams to single letters. Moreover, we defined
![]() ${\tt{Soundex}}^{comp}_{GR}$
that combines the previous two in the matching process.
${\tt{Soundex}}^{comp}_{GR}$
that combines the previous two in the matching process.
To identify which rules have a positive impact on the algorithm, in different error scenarios, we comparatively evaluated these algorithms. To this end, we constructed four evaluation datasets: one with similarly sounded Greek words and three more depending on the kind of error that can happen to a word (letter addition, deletion, or substitution), containing 7650 words in total. The algorithms achieve (precision, recall) metrics that range in (0.90–0.96, 0.40-0.98) for
![]() ${\tt Soundex}_{GR}$
, (0.69–0.88, 0.34–0.92) for
${\tt Soundex}_{GR}$
, (0.69–0.88, 0.34–0.92) for
![]() ${\tt{Soundex}}^{naive}_{GR}$
, and (0.66–0.86, 0.50–0.98) for
${\tt{Soundex}}^{naive}_{GR}$
, and (0.66–0.86, 0.50–0.98) for
![]() ${\tt{Soundex}}^{comp}_{GR}$
. To synopsize,
${\tt{Soundex}}^{comp}_{GR}$
. To synopsize,
![]() ${\tt{Soundex}}^{comp}_{GR}$
achieves F-Score equal to 0.91 in the dataset with the similar-sounded words. We have also seen that these algorithms behave better (over the evaluation collection) than a Greek stemmer, and we have tested their efficiency over a Greek dictionary comprising more than half a million words. Furthermore, we have seen that the
${\tt{Soundex}}^{comp}_{GR}$
achieves F-Score equal to 0.91 in the dataset with the similar-sounded words. We have also seen that these algorithms behave better (over the evaluation collection) than a Greek stemmer, and we have tested their efficiency over a Greek dictionary comprising more than half a million words. Furthermore, we have seen that the
![]() ${\tt Soundex}_{GR}$
performs much better in comparison to a full phonetic transcription. In an extended dataset that contains common errors, we have seen that
${\tt Soundex}_{GR}$
performs much better in comparison to a full phonetic transcription. In an extended dataset that contains common errors, we have seen that
![]() ${\tt Soundex}_{GR}$
achieves the highest F-Score (0.97), outperforming also edit distance-based matching. In bigger datasets (that include long words),
${\tt Soundex}_{GR}$
achieves the highest F-Score (0.97), outperforming also edit distance-based matching. In bigger datasets (that include long words),
![]() ${\tt Soundex}_{GR}$
preserves its superiority but with code length equal or greater than 6, while the length that gives the optimal F-Score is 12. The effectiveness, the simplicity, and the efficiency of the proposed algorithm makes it applicable to a wide range of tasks. The length of the codes can be configured according to the desired precision–recall performance, and we believe that the experimental results reported in this paper provide help for such configuration; we have seen that the size of the vocabulary, the distribution of word sizes, and the type and percentage of errors determine the code length that gives the optimal performance. Moreover, we have seen that these codes can be used in combination with other methods for approximate matching for achieving more sophisticated matching methods that can be more effective, and even more efficient. The implementation of the algorithm, a stand-alone application for approximate matching that can support the designer on selecting the code length to use, as well as the evaluation datasets, are available at https://github.com/YannisTzitzikas/SoundexGR. Moreover, and to facilitate comparative results, we have created and made public the GMW (Greek Misspelled Words) dataset Tzitzikas (Reference Tzitzikas2021), a dataset that contains 574,883 distinct Greek words and 4.32 misspellings per word in average, in total more than 3 million forms of Greek words.
${\tt Soundex}_{GR}$
preserves its superiority but with code length equal or greater than 6, while the length that gives the optimal F-Score is 12. The effectiveness, the simplicity, and the efficiency of the proposed algorithm makes it applicable to a wide range of tasks. The length of the codes can be configured according to the desired precision–recall performance, and we believe that the experimental results reported in this paper provide help for such configuration; we have seen that the size of the vocabulary, the distribution of word sizes, and the type and percentage of errors determine the code length that gives the optimal performance. Moreover, we have seen that these codes can be used in combination with other methods for approximate matching for achieving more sophisticated matching methods that can be more effective, and even more efficient. The implementation of the algorithm, a stand-alone application for approximate matching that can support the designer on selecting the code length to use, as well as the evaluation datasets, are available at https://github.com/YannisTzitzikas/SoundexGR. Moreover, and to facilitate comparative results, we have created and made public the GMW (Greek Misspelled Words) dataset Tzitzikas (Reference Tzitzikas2021), a dataset that contains 574,883 distinct Greek words and 4.32 misspellings per word in average, in total more than 3 million forms of Greek words.
One direction that is worth research is to investigate whether these phonetic codes could be exploited in various deep learning models for NLP for the Greek language (e.g., Lioudakis et al. (Reference Lioudakis, Outsios and Vazirgiannis2019) for word embeddings, Angelidis et al. (Reference Angelidis, Chalkidis and Koubarakis2018) for named entity recognition from Greek legislation), for making these models more tolerant to misspelled or mispronounced words. Another topic that is worth research is to compute n-grams of such phonetic codes over various corpora and then evaluate whether they can further improve the handling of Out-of-Vocabulary words. Along the same line, since our work is not for word sense disambiguation, for example, the word ![]() in the two phrases “
in the two phrases “![]() ” and “
” and “![]() ” will be assigned the same phonemic code even if the meaning is different, N-grams and other more recent methods, either over the original words or over their phonemic transcription, could be investigated in the future for identifying the right sense of a word occurrence.
” will be assigned the same phonemic code even if the meaning is different, N-grams and other more recent methods, either over the original words or over their phonemic transcription, could be investigated in the future for identifying the right sense of a word occurrence.
Acknowledgment
The authors would like to thank Katerina Papantoniou for her feedback and for proof-reading the paper, and the anonymous reviewers for their fruitful comments and suggestions.