One of the major impediments to the development of a failure criterion for low-density snow has been the very large scatter of the various strength measurements. (Reference Bader,, Bader,, Haefeli,, Bucher,, Neher,, Eckel,, Thams, and Niggli,Bader and others, 1939; Reference Bucher,Bucher, 1948; Reference Butkovich,Butkovich, 1956; Reference Ramseier,Ramseier, 1963; Reference Roch,Roch, 1966; Reference Keeler, and Weeks,Keeler and Weeks, 1967; Reference Keeler,Keeler, 1969; Reference Martinelli,Martinelli, 1971). In most of the strength measurements and in the release of dry snow avalanches, the failure mechanism is brittle fracture. Brittle fracture is characterized by large scatter in strength measurements because stress concentrations near flaws in brittle materials are not relieved and the strength of any particular sample is determined not by its bulk properties but by the weakest flaw which is included in the sample (Reference Griffith,Griffith, 1920). Thus the large scatter in strength is an inherent property of snow and the development of a failure criterion is a statistical problem.
It has been shown that for brittle materials the probability of failure R is a function of the ratio of the applied stress σ to some characteristic stress σ m;
(Reference Weibull,Weibull, 1939; Reference Frenkel, and Kontorova,Frenkel and Kontorova, 1943). Also it seems reasonable to assume that σm is a function of the sample density ρ. The above hypotheses can be tested with available centrifugal tensile-strength data (Reference Butkovich,Butkovich, 1956; Reference Keeler, and Weeks,Keeler and Weeks, 1967; Reference Keeler,Keeler, 1969; Reference Martinelli,Martinelli, 1971).
Figures 1, 2, 3 and 4 are log-log plots of tensile strength versus density. It is apparent in Figures 1, 2 and 4 that an envelope of maximum strength exists. The data shown in Figure 3 do not have a wide enough spread in density to clearly show an envelope. The envelope drawn in the figures fits the equation
It agrees with the measurements of Reference Martinelli,Martinelli (1971), and Reference Keeler,Keeler (1969) and is not contradicted by those of Butkovitch (1956). However, the data of Reference Keeler, and Weeks,Keeler and Weeks (1967) require an envelope of steeper slope. It is interesting to note that reasonable envelopes drawn to the data predict the highest available measurements of the tensile strength of polycrystalline ice (Reference Butkovich,Butkovich, 1959). Reference Martinelli,Martinelli’s (1971) and Reference Keeler,Keeler’s (1969) measurements were on fairly young snow, while those of Reference Keeler, and Weeks,Keeler and Weeks (1967) included old, highly metamorphosed snow which may have experienced some melt-freeze cycles. Thus there is an indication that the maximum strength is a weak function of metamorphic grade or snow type.

Fig. 1. Logarithm of tensile strength (log σ) versus logarithm of density (log ρ) using data from Reference Martinelli,Martinelli (1971),

Fig. 2. Similar plot to Figure 1 using data from Reference Keeler,Keeler (1969).

Fig. 3. Similar plot to Figure 1 using data from Reference Butkovich,Butkovich (1956).

Fig. 4. Similar plot to Figure 1 using data from Reference Keeler, and Weeks,Keeler and Weeks (1967).
The probabilities of failure (cumulative frequencies) as functions of σ/σm were calculated from Reference Martinelli,Martinelli’s (1971) and Reference Keeler,Keeler’s (1969) measurements. σm was calculated from Equation (2); that is the characteristic stress was assumed to be given by the maximum strength envelope. Log-log plots of the results are shown in Figures 5 and 6. It is immediately apparent that there is a functional relationship which justifies the assumptions. Even more important, the data obtained at Berthoud Pass, Colorado, predict the probability of failure of snow at Alta, Utah, to an accuracy of better than ±0.05.

Fig. 5. Logarithm of probability of failure (log R) versus logarithm of normalized stress (log σ/σm) using results from calculations on Reference Martinelli,Martinelli’s (1971) data.

Fig. 6. Similar plot to Figure 5 using results from calculations on Reference Keeler,Keeler’s (1969) data.
All the data which were noted as “bad run” or “premature break” were assigned zero strength. It is probable that the subjective judgment involved in calling an experiment “bad” accounts for the slight disagreement in the cut-off approximately at log R = — 1 (R = 0.1). Reference Martinelli,Martinelli (1971) recorded lower strength readings than Reference Keeler,Keeler (1969). The cut-off indicates that about 10% of the flaws in the samples were about the same size as the sample diameter (57 mm) or larger.
The hypothesis that the maximum strength is a function of density also implies that, at least for similar snow types, there is a particular texture for each density which has the maximum strength. Evidence that such is the case is shown in Figure 7; a three-dimensional plot of density, permeability, and tensile strength for some of Reference Martinelli,Martinelli’s (1971) samples. The tensile-strength ridge indicates that for each density there is an optimum permeability. Since permeability and texture are related the conclusion can be drawn that there is an optimum texture for each density.

Fig. 7. Tensile strength contours on a plot of density versus permeability (Reference Martinelli,Martinelli, 1971).
The conclusions that can be drawn are:
-
(1) A maximum strength envelope given by the equation
characterizes centrifugal tensile strength–density measurements. For fairly young snow A = —4·3 and B = 3 when σ is in units of 102 N m–2 and ρ is kg m–3.
-
(2) The probability of failure is a function of the applied stress normalized for the density of the sample.
It should be noted that the constants in Equation (2) are the same for snows which are as different as those found at Berthoud Pass, Colorado, and Alta, Utah. Furthermore there is no apparent temperature dependence at least over the range at which the measurements were performed (c. — 1°C to — 15°C).
These results show that “weakest link” theories of brittle fracture can be applied to snow. In order to develop usable failure criteria for snow in avalanche tracks, it is necessary to extend this work by determining the dependence of strength on the sample volume. Since the larger the sample the more likely it is that a large flaw will be included, the strength will dependence of strength on metamorphic grade. This can be accomplished by accurately classifying the metamorphic grade of each tested sample.
Acknowledgement
The idea for this work grew out of a stimulating discussion with Mr R. Perla.


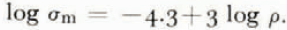 .
.







