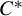 $C^*$ and von Neumann algebras
$C^*$ and von Neumann algebrasPublished online by Cambridge University Press: 04 November 2022
Given an irreducible lattice 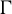 $\Gamma $ in the product of higher rank simple Lie groups, we prove a co-finiteness result for the
$\Gamma $ in the product of higher rank simple Lie groups, we prove a co-finiteness result for the 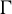 $\Gamma $-invariant von Neumann subalgebras of the group von Neumann algebra
$\Gamma $-invariant von Neumann subalgebras of the group von Neumann algebra 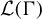 $\mathcal {L}(\Gamma )$, and for the
$\mathcal {L}(\Gamma )$, and for the 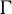 $\Gamma $-invariant unital
$\Gamma $-invariant unital 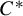 $C^*$-subalgebras of the reduced group
$C^*$-subalgebras of the reduced group 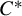 $C^*$-algebra
$C^*$-algebra 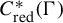 $C^*_{\mathrm {red}}(\Gamma )$. We use these results to show that: (i) every
$C^*_{\mathrm {red}}(\Gamma )$. We use these results to show that: (i) every 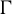 $\Gamma $-invariant von Neumann subalgebra of
$\Gamma $-invariant von Neumann subalgebra of 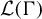 $\mathcal {L}(\Gamma )$ is generated by a normal subgroup; and (ii) given a weakly mixing unitary representation
$\mathcal {L}(\Gamma )$ is generated by a normal subgroup; and (ii) given a weakly mixing unitary representation 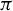 $\pi $ of
$\pi $ of 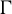 $\Gamma $, every
$\Gamma $, every 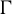 $\Gamma $-equivariant conditional expectation on
$\Gamma $-equivariant conditional expectation on  $C^*_\pi (\Gamma )$ is the canonical conditional expectation onto the
$C^*_\pi (\Gamma )$ is the canonical conditional expectation onto the 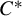 $C^*$-subalgebra generated by a normal subgroup.
$C^*$-subalgebra generated by a normal subgroup.