Hostname: page-component-f554764f5-246sw Total loading time: 0 Render date: 2025-04-20T08:30:14.292Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigidity of Lyapunov exponents for derived from Anosov diffeomorphisms

Part of: Dynamical systems with hyperbolic behavior Ergodic theory

Published online by Cambridge University Press:  14 October 2024

J. SANTANA COSTA  and
A. TAHZIBI
J. SANTANA COSTA
Affiliation:
DEMAT-UFMA, São Luis, MA, Brazil (e-mail: [email protected])
A. TAHZIBI*
Affiliation:
Departamento de Matemática, ICMC-USP, São Carlos, SP, Brazil
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a class of volume-preserving partially hyperbolic diffeomorphisms (or non-uniformly Anosov) 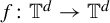$f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$ homotopic to linear Anosov automorphism, we show that the sum of the positive (negative) Lyapunov exponents of f is bounded above (respectively below) by the sum of the positive (respectively negative) Lyapunov exponents of its linearization. We show this for some classes of derived from Anosov (DA) and non-uniformly hyperbolic systems with dominated splitting, in particular for examples described by Bonatti and Viana [SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115(1) (2000), 157–193]. The results in this paper address a flexibility program by Bochi, Katok and Rodriguez Hertz [Flexibility of Lyapunov exponents. Ergod. Th. & Dynam. Sys. 42(2) (2022), 554–591].

Keywords

entropyLyapunov exponentspartial hyperbolicity

MSC classification

Primary: 37D30: Partially hyperbolic systems and dominated splittings 37A35: Entropy and other invariants, isomorphism, classification
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 45 , Issue 5 , May 2025 , pp. 1444 - 1460
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andersson, M., Carrasco, P. D. and Saghin, R.. Non-uniformly hyperbolic endomorphisms. Preprint, 2022, arXiv:2206.08295.Google Scholar
Barreira, L. and Pesin, Y. B.. Lyapunov Exponents and Smooth Ergodic Theory (University Lecture Series, 23). American Mathematical Society, Providence, RI, 2002.Google Scholar
Bochi, J.. Genericity of zero Lyapunov exponents. Ergod. Th. & Dynam. Sys. 22(6) (2002), 1667–1696.CrossRefGoogle Scholar
Bochi, J., Katok, A. and Rodriguez Hertz, F.. Flexibility of Lyapunov exponents. Ergod. Th. & Dynam. Sys. 42(2) (2022), 554–591.Google Scholar
Bochi, J. and Viana, M.. The Lyapunov exponents of generic volume-preserving and symplectic maps. Ann. of Math. (2) 161 (2005), 1423–1485.CrossRefGoogle Scholar
Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115(1) (2000), 157–193.Google Scholar
Brin, M. and Pesin, Y.. Partially hyperbolic dynamical systems. Math. USSR-Izv. 8 (1974), 177–218.Google Scholar
Buzzi, J. and Fisher, T.. Entropic stability beyond partial hyperbolicity. J. Mod. Dyn. 7(4) (2013), 527–552.Google Scholar
Carrasco, P. and Saghin, R.. Extended flexibility of lyapunov exponents for anosov diffeomorphisms. Trans. Amer. Math. Soc. 375 (2022), 3411–3449.Google Scholar
Costa, J. S. C. and Micena, F.. Pathological center foliation with dimension greater than one. Discrete Contin. Dyn. Syst. 39(2) (2019), 1049.CrossRefGoogle Scholar
Furstenberg, H. and Kesten, H.. Products of random matrices. Ann. Math. Stat. 31(2) (1960), 457–469.CrossRefGoogle Scholar
Hammerlindl, A.. Leaf conjugacies on the torus. Ergod. Th. & Dynam. Sys. 33(3) (2013), 896–933.Google Scholar
Hu, H., Hua, Y. and Wu, W.. Unstable entropies and variational principle for partially hyperbolic diffeomorphisms. Adv. Math. 321 (2017), 31–68.Google Scholar
Lyapunov, A. M.. The general problem of the stability of motion. Internat. J. Control 55(3) (1992), 531–534.CrossRefGoogle Scholar
Micena, F.. New derived from Anosov diffeomorphisms with pathological center foliation. J. Dynam. Differential Equations 29(3) (2017), 1159–1172.CrossRefGoogle Scholar
Micena, F. and Tahzibi, A.. Regularity of foliations and Lyapunov exponents of partially hyperbolic dynamics on 3-torus. Nonlinearity 26(4) (2013), 1071.CrossRefGoogle Scholar
Micena, F. and Tahzibi, A.. On the unstable directions and Lyapunov exponents of Anosov endomorphisms. Fund. Math. 235(1) (2016), 37–48.Google Scholar
Oseledec, V. I.. A multiplicative ergodic theorem. Lyapunov characteristic numbers for dynamical systems. Trans. Moscow Math. Soc. 19(2) (1968), 197–231.Google Scholar
Roldan, M.. Hyperbolic sets and entropy at the homological level. Discrete Contin. Dyn. Syst. 36(6) (2016), 3417.CrossRefGoogle Scholar
Saghin, R.. Volume growth and entropy for ${C}^1$ partially hyperbolic diffeomorphisms. Discrete Contin. Dyn. Syst. 34(9) (2014), 3798–3801.Google Scholar
Saghin, R., Valenzuela-Henríquez, P. and Vásquez, C. H.. Regularity of Lyapunov exponents for diffeomorphisms with dominated splitting. Preprint, 2020, arXiv:2002.08459.Google Scholar
Saghin, R. and Xia, Z.. Geometric expansion, Lyapunov exponents and foliations. Ann. Inst. H. Poincaré Anal. Non Linéaire 26 (2009), 689–704.CrossRefGoogle Scholar
Tahzibi, A.. Stably ergodic diffeomorphisms which are not partially hyperbolic. Israel J. Math. 142(1) (2004), 315–344.CrossRefGoogle Scholar