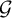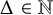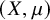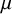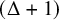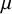1 Introduction
Vizing’s theorem is a fundamental result in graph theory that relates the number of colors needed to properly color edges of a given graph G, the so-called chromatic index
![]() $\chi '(G)$
of G, with its maximum degree; it states that if the maximum degree of G is
$\chi '(G)$
of G, with its maximum degree; it states that if the maximum degree of G is
![]() $\Delta \in \mathbb {N}$
, then
$\Delta \in \mathbb {N}$
, then
![]() $\chi '(G)\le \Delta +1$
. Together with König’s line coloring theorem (that states that
$\chi '(G)\le \Delta +1$
. Together with König’s line coloring theorem (that states that
![]() $\chi '(G)=\Delta $
under the additional assumption that G is bipartite), these classical results laid the foundation of edge-coloring, an important and active area of graph theory; see, for example, the recent book on edge-coloring by Stiebitz, Scheide, Toft and Favrholdt [Reference Stiebitz, Scheide, Toft and FavrholdtSSTF12].
$\chi '(G)=\Delta $
under the additional assumption that G is bipartite), these classical results laid the foundation of edge-coloring, an important and active area of graph theory; see, for example, the recent book on edge-coloring by Stiebitz, Scheide, Toft and Favrholdt [Reference Stiebitz, Scheide, Toft and FavrholdtSSTF12].
In this paper, we study Vizing’s theorem from the perspective of measurable graph combinatorics, a subfield of descriptive set theory that lies at the intersection of measure theory, random processes, dynamics, group theory, combinatorics and distributed computing; a (nonexhaustive) sample of results related to the field (and to our investigation) includes [Reference LaczkovichLac90, Reference Marks and UngerMU17, Reference Grabowski, Máthé and PikhurkoGMP17, Reference Dougherty and ForemanDF92, Reference Marks and UngerMU16, Reference GaboriauGab00, Reference Kechris, Solecki and TodorčevićKST99, Reference MarksMar16, Reference Conley and MillerCM17, Reference Conley, Jackson, Marks, Seward and Tucker-DrobCJM+23, Reference Csóka, Grabowski, Máthé, Pikhurko and TyrosCGM+17, Reference Grebík and PikhurkoGP20, Reference BernshteynBer23, Reference Brandt, Chang, Grebík, Grunau, Rozhoň and VidnyánszkyBCG+24]. In its most abstract form, measurable graph combinatorics systematically studies the existence of measurable or definable solutions to various graph coloring problems defined on so-called Borel graphs, graphs where the vertex set
![]() $(V,\mathcal {B})$
is a standard Borel space, for example, the unit interval, and the edge relation E is a Borel subset of
$(V,\mathcal {B})$
is a standard Borel space, for example, the unit interval, and the edge relation E is a Borel subset of
![]() $[V]^2$
, where
$[V]^2$
, where
![]() $[V]^2$
denotes the set of unordered pairs endowed with the canonical Borel structure coming from V. This study originated in the seminal paper of Kechris, Solecki and Todorčević [Reference Kechris, Solecki and TodorčevićKST99] and since then found many applications in various areas of central mathematics; see the surveys of Kechris and Marks [Reference Kechris and MarksKM20] and Pikhurko [Reference PikhurkoPik21].
$[V]^2$
denotes the set of unordered pairs endowed with the canonical Borel structure coming from V. This study originated in the seminal paper of Kechris, Solecki and Todorčević [Reference Kechris, Solecki and TodorčevićKST99] and since then found many applications in various areas of central mathematics; see the surveys of Kechris and Marks [Reference Kechris and MarksKM20] and Pikhurko [Reference PikhurkoPik21].
Basic questions about vertex colorings of bounded degree Borel graphs are well understood. Recall that the Borel chromatic number
![]() $\chi _{\mathcal {B}}(\mathcal {G})$
of a Borel graph
$\chi _{\mathcal {B}}(\mathcal {G})$
of a Borel graph
![]() $\mathcal {G}=(V,\mathcal {B},E)$
is the smallest
$\mathcal {G}=(V,\mathcal {B},E)$
is the smallest
![]() $k\in \mathbb {N}$
such that there is a decomposition
$k\in \mathbb {N}$
such that there is a decomposition
![]() $V=V_1\sqcup \dots \sqcup V_k$
, where
$V=V_1\sqcup \dots \sqcup V_k$
, where
![]() $V_i$
is a Borel subset of V that does not span any edge of
$V_i$
is a Borel subset of V that does not span any edge of
![]() $\mathcal {G}$
for every
$\mathcal {G}$
for every
![]() $i\in [k]$
. In the paper [Reference Kechris, Solecki and TodorčevićKST99], Kechris, Solecki and Todorčević showed that there is a Borel measurable version of the classical greedy algorithm for proper vertex coloring, thus proved that
$i\in [k]$
. In the paper [Reference Kechris, Solecki and TodorčevićKST99], Kechris, Solecki and Todorčević showed that there is a Borel measurable version of the classical greedy algorithm for proper vertex coloring, thus proved that
![]() $\chi _{\mathcal {B}}(\mathcal {G})\le \Delta +1$
for every Borel graph
$\chi _{\mathcal {B}}(\mathcal {G})\le \Delta +1$
for every Borel graph
![]() $\mathcal {G}=(V,\mathcal {B},E)$
of maximum degree
$\mathcal {G}=(V,\mathcal {B},E)$
of maximum degree
![]() $\Delta \in \mathbb {N}$
. In the groundbreaking paper [Reference MarksMar16], Marks found an example of acylic
$\Delta \in \mathbb {N}$
. In the groundbreaking paper [Reference MarksMar16], Marks found an example of acylic
![]() $\Delta $
-regular Borel graph
$\Delta $
-regular Borel graph
![]() $\mathcal {G}$
such that
$\mathcal {G}$
such that
![]() $\chi _{\mathcal {B}}(\mathcal {G})=\Delta +1$
for every
$\chi _{\mathcal {B}}(\mathcal {G})=\Delta +1$
for every
![]() $\Delta \in \mathbb {N}$
, thus concluding that there is no Borel analogue of the classical Brooks’ theorem from finite combinatorics. On the other hand, Conley, Marks and Tucker-Drob [Reference Conley, Marks and Tucker-DrobCMTD16] proved that Brooks’ theorem holds once Borel measurability is relaxed either in the sense of measure theory or topology. For example, if
$\Delta \in \mathbb {N}$
, thus concluding that there is no Borel analogue of the classical Brooks’ theorem from finite combinatorics. On the other hand, Conley, Marks and Tucker-Drob [Reference Conley, Marks and Tucker-DrobCMTD16] proved that Brooks’ theorem holds once Borel measurability is relaxed either in the sense of measure theory or topology. For example, if
![]() $\mathcal {G}=(V,\mathcal {B},E)$
is a Borel graph of degree bounded by
$\mathcal {G}=(V,\mathcal {B},E)$
is a Borel graph of degree bounded by
![]() $\Delta \ge 3$
that does not contain a clique on
$\Delta \ge 3$
that does not contain a clique on
![]() $\Delta +1$
vertices and
$\Delta +1$
vertices and
![]() $\mu $
is a Borel probability measure on
$\mu $
is a Borel probability measure on
![]() $(V,\mathcal {B})$
, then there is a
$(V,\mathcal {B})$
, then there is a
![]() $\mu $
-null Borel set Y such that
$\mu $
-null Borel set Y such that
![]() $\chi _{\mathcal {B}}(\mathcal {G}\upharpoonright (V\setminus Y))=\Delta $
. Recently, these results were refined by Bernshteyn [Reference BernshteynBer23] and Brandt, Chang, the author, Grunau, Rozhoň and Vidnyánszky [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and VidnyánszkyBCG+24] using ideas from the theory of distributed computing.
$\chi _{\mathcal {B}}(\mathcal {G}\upharpoonright (V\setminus Y))=\Delta $
. Recently, these results were refined by Bernshteyn [Reference BernshteynBer23] and Brandt, Chang, the author, Grunau, Rozhoň and Vidnyánszky [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and VidnyánszkyBCG+24] using ideas from the theory of distributed computing.
In contrast, similar questions about edge colorings are not yet fully understood. A Borel matching of a Borel graph
![]() $\mathcal {G}=(V,\mathcal {B},E)$
is a Borel subset
$\mathcal {G}=(V,\mathcal {B},E)$
is a Borel subset
![]() $M\subseteq E$
that is a matching, that is, every two edges
$M\subseteq E$
that is a matching, that is, every two edges
![]() $e, f\in M$
are either equal (as unordered pairs) or do not share a vertex. The Borel chromatic index
$e, f\in M$
are either equal (as unordered pairs) or do not share a vertex. The Borel chromatic index
![]() $\chi ^{\prime }_B(\mathcal {G})$
is defined to be the smallest
$\chi ^{\prime }_B(\mathcal {G})$
is defined to be the smallest
![]() $k\in \mathbb {N}$
such that there is a decomposition
$k\in \mathbb {N}$
such that there is a decomposition
![]() $E=E_1\sqcup \dots \sqcup E_k$
, where
$E=E_1\sqcup \dots \sqcup E_k$
, where
![]() $E_i$
is a Borel matching for every
$E_i$
is a Borel matching for every
![]() $i\in [k]$
. Equivalently, this can be stated in the language of edge colorings as finding the smallest
$i\in [k]$
. Equivalently, this can be stated in the language of edge colorings as finding the smallest
![]() $k\in \mathbb {N}$
such that there is a Borel map
$k\in \mathbb {N}$
such that there is a Borel map
![]() $c:E\to [k]$
that is a proper edge coloring, i.e.,
$c:E\to [k]$
that is a proper edge coloring, i.e.,
![]() $c(e)\not =c(f)$
whenever
$c(e)\not =c(f)$
whenever
![]() $e\not =f\in E$
share a vertex. The greedy upper bound [Reference Kechris, Solecki and TodorčevićKST99] implies that
$e\not =f\in E$
share a vertex. The greedy upper bound [Reference Kechris, Solecki and TodorčevićKST99] implies that
![]() $\chi ^{\prime }_B(\mathcal {G})\le 2\Delta -1$
for every Borel graph
$\chi ^{\prime }_B(\mathcal {G})\le 2\Delta -1$
for every Borel graph
![]() $\mathcal {G}$
of maximum degree bounded by
$\mathcal {G}$
of maximum degree bounded by
![]() $\Delta \in \mathbb {N}$
. In the same paper [Reference MarksMar16], Marks found an example of acylic
$\Delta \in \mathbb {N}$
. In the same paper [Reference MarksMar16], Marks found an example of acylic
![]() $\Delta $
-regular Borel graph
$\Delta $
-regular Borel graph
![]() $\mathcal {G}$
such that
$\mathcal {G}$
such that
![]() $\chi ^{\prime }_B(\mathcal {G})=2\Delta -1$
for every
$\chi ^{\prime }_B(\mathcal {G})=2\Delta -1$
for every
![]() $\Delta \in \mathbb {N}$
. This shows that Borel analogue of Vizing’s theorem does not hold. Similarly as in the case of vertex colorings, it is natural to ask if Vizing’s theorem hold once Borel measurability is relaxed either in the sense of measure theory or topology. This question (for both measure and topology) is explicitly stated in the survey of Kechris and Marks [Reference Kechris and MarksKM20, Problem 6.13]. Marks asked about the measurable relaxation for regular graphs [Reference MarksMar16, Question 4.9], and, in fact, the same question for invariant measures, so-called graphings, was raised earlier by Abért [Reference AbertAbe10].
$\Delta \in \mathbb {N}$
. This shows that Borel analogue of Vizing’s theorem does not hold. Similarly as in the case of vertex colorings, it is natural to ask if Vizing’s theorem hold once Borel measurability is relaxed either in the sense of measure theory or topology. This question (for both measure and topology) is explicitly stated in the survey of Kechris and Marks [Reference Kechris and MarksKM20, Problem 6.13]. Marks asked about the measurable relaxation for regular graphs [Reference MarksMar16, Question 4.9], and, in fact, the same question for invariant measures, so-called graphings, was raised earlier by Abért [Reference AbertAbe10].
In this paper, we completely resolve the measurable case; see Theorem 1.1. Before we state the result, we formalize the definitions and discuss relevant results from recent years. Recall that we always assume that the Borel graph
![]() $\mathcal {G}=(V,\mathcal {B},E)$
in question has degree uniformly bounded by
$\mathcal {G}=(V,\mathcal {B},E)$
in question has degree uniformly bounded by
![]() $\Delta \in \mathbb {N}$
. Given a Borel probability measure
$\Delta \in \mathbb {N}$
. Given a Borel probability measure
![]() $\mu $
on
$\mu $
on
![]() $(V,\mathcal {B})$
, we define the
$(V,\mathcal {B})$
, we define the
![]() $\mu $
-chromatic index of
$\mu $
-chromatic index of
![]() $\mathcal {G}$
,
$\mathcal {G}$
,
![]() $\chi _\mu '(\mathcal {G})$
, to be the minimal
$\chi _\mu '(\mathcal {G})$
, to be the minimal
![]() $k\in \mathbb {N}$
such that there is a Borel map
$k\in \mathbb {N}$
such that there is a Borel map
![]() $c:E\to [k]$
that satisfies
$c:E\to [k]$
that satisfies
where c is not proper at
![]() $v\in V$
if there are edges
$v\in V$
if there are edges
![]() $e\not =f \in E$
that are adjacent to v and
$e\not =f \in E$
that are adjacent to v and
![]() $c(e)=c(f)$
. In another words, c is a proper edge coloring at
$c(e)=c(f)$
. In another words, c is a proper edge coloring at
![]() $\mu $
-almost every vertex
$\mu $
-almost every vertex
![]() $v\in V$
. We say that
$v\in V$
. We say that
![]() $\mu $
is
$\mu $
is
![]() $\mathcal {G}$
-invariant, if
$\mathcal {G}$
-invariant, if
![]() $\mu (g(C))=\mu (C)$
for every
$\mu (g(C))=\mu (C)$
for every
![]() $C\in \mathcal {B}$
and every Borel injection
$C\in \mathcal {B}$
and every Borel injection
![]() $g:C\to V$
that satisfies that x and
$g:C\to V$
that satisfies that x and
![]() $g(x)$
are in the same connected component of
$g(x)$
are in the same connected component of
![]() $\mathcal {G}$
for every
$\mathcal {G}$
for every
![]() $x\in C$
. In that case, the quadruple
$x\in C$
. In that case, the quadruple
![]() $\mathcal {G}=(V,\mathcal {B},\mu ,E)$
is called a graphing.
$\mathcal {G}=(V,\mathcal {B},\mu ,E)$
is called a graphing.
Csóka, Lippner and Pikhurko [Reference Csóka, Lippner and PikhurkoCLP16] showed that
![]() $\chi ^{\prime }_\mu (\mathcal {G})\le \Delta +1$
for a graphing
$\chi ^{\prime }_\mu (\mathcal {G})\le \Delta +1$
for a graphing
![]() $\mathcal {G}=(V,\mathcal {B},\mu ,E)$
that does not contain odd cycles and proved an upper bound of
$\mathcal {G}=(V,\mathcal {B},\mu ,E)$
that does not contain odd cycles and proved an upper bound of
![]() $\Delta +O(\sqrt {\Delta })$
colors for graphings in general. In a related result, Bernshteyn [Reference BernshteynBer19, Theorem 1.3] proved that
$\Delta +O(\sqrt {\Delta })$
colors for graphings in general. In a related result, Bernshteyn [Reference BernshteynBer19, Theorem 1.3] proved that
![]() $\Delta +o(\Delta )$
colors are enough (even for the so-called list-coloring version) provided that the graphing factors to the shift action
$\Delta +o(\Delta )$
colors are enough (even for the so-called list-coloring version) provided that the graphing factors to the shift action
![]() $\Gamma \curvearrowright [0, 1]^\Gamma $
of a finitely generated group
$\Gamma \curvearrowright [0, 1]^\Gamma $
of a finitely generated group
![]() $\Gamma $
. Answering the question of Abért, the author and Pikhurko [Reference Grebík and PikhurkoGP20] proved a measurable version of Vizing’s theorem for graphings, that is,
$\Gamma $
. Answering the question of Abért, the author and Pikhurko [Reference Grebík and PikhurkoGP20] proved a measurable version of Vizing’s theorem for graphings, that is,
![]() $\chi ^{\prime }_\mu (\mathcal {G})\le \Delta +1$
for any graphing
$\chi ^{\prime }_\mu (\mathcal {G})\le \Delta +1$
for any graphing
![]() $\mathcal {G}=(V,\mathcal {B},\mu ,E)$
. Interestingly, the technique developed in [Reference Grebík and PikhurkoGP20] was greatly extended by Bernshteyn [Reference BernshteynBer22] who found striking applications to the LOCAL model of distributed computing; see [Reference BernshteynBer22, Reference ChristiansenChr23, Reference Bernshteyn and DhawanBD23] for a current development in that direction.
$\mathcal {G}=(V,\mathcal {B},\mu ,E)$
. Interestingly, the technique developed in [Reference Grebík and PikhurkoGP20] was greatly extended by Bernshteyn [Reference BernshteynBer22] who found striking applications to the LOCAL model of distributed computing; see [Reference BernshteynBer22, Reference ChristiansenChr23, Reference Bernshteyn and DhawanBD23] for a current development in that direction.
Bernshteyn [Reference BernshteynBer19], the author and Pikhurko [Reference Grebík and PikhurkoGP20], Tóth [Reference TóthT2́1] and the author [Reference GrebíkGre22] investigated weaker notion of approximate edge colorings. In this setting, we require to find for each probability measure
![]() $\mu $
and
$\mu $
and
![]() $\epsilon>0$
a coloring of edges that is not correct or undefined for at most
$\epsilon>0$
a coloring of edges that is not correct or undefined for at most
![]() $\epsilon $
fraction of all edges. Here, the analogues of Vizing’s theorem as well as König’s line coloring theorem hold; see [Reference Grebík and PikhurkoGP20] and [Reference GrebíkGre22].
$\epsilon $
fraction of all edges. Here, the analogues of Vizing’s theorem as well as König’s line coloring theorem hold; see [Reference Grebík and PikhurkoGP20] and [Reference GrebíkGre22].
Bowen and Weilacher [Reference Bowen and WeilacherBW23] investigated Vizing’s theorem in the context of (Borel) asymptotic dimension introduced in [Reference Conley, Jackson, Marks, Seward and Tucker-DrobCJM+23]. As an application they derived that
![]() $\Delta +1$
colors are enough for edge colorings of bipartite graphs in the topological relaxation sense and for measures that are hyperfinite. Stronger results in the special case of free Borel
$\Delta +1$
colors are enough for edge colorings of bipartite graphs in the topological relaxation sense and for measures that are hyperfinite. Stronger results in the special case of free Borel
![]() $\mathbb {Z}^d$
-actions, that is, Borel edge coloring with
$\mathbb {Z}^d$
-actions, that is, Borel edge coloring with
![]() $2d$
colors which is the analogue of König’s line coloring theorem in this setting, were obtained independently around the same time in [Reference Bencs, Hrušková and TóthBHT24, Reference Chandgotia and UngerCU22, Reference Grebík and RozhoňGR23, Reference WeilacherWei21].
$2d$
colors which is the analogue of König’s line coloring theorem in this setting, were obtained independently around the same time in [Reference Bencs, Hrušková and TóthBHT24, Reference Chandgotia and UngerCU22, Reference Grebík and RozhoňGR23, Reference WeilacherWei21].
Recently, Qian and Weilacher [Reference Qian and WeilacherQW22] found connections of the topological relaxation to computable combinatorics which allowed them to derive an upper bound of
![]() $\Delta +2$
colors for the Baire measurable analogue of Vizing’s theorem, the full topological analogue, that is,
$\Delta +2$
colors for the Baire measurable analogue of Vizing’s theorem, the full topological analogue, that is,
![]() $\Delta +1$
colors only, remains an interesting open problem.
$\Delta +1$
colors only, remains an interesting open problem.
Next, we state our main result, which is the full analogue of Vizing’s theorem in the measurable setting.
Theorem 1.1. Let
![]() $(V,\mathcal {B})$
be a standard Borel space,
$(V,\mathcal {B})$
be a standard Borel space,
![]() $\Delta \in \mathbb {N}$
,
$\Delta \in \mathbb {N}$
,
![]() $\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph of uniformly bounded degree by
$\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph of uniformly bounded degree by
![]() $\Delta \in \mathbb {N}$
and
$\Delta \in \mathbb {N}$
and
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() $(V,\mathcal {B})$
. Then
$(V,\mathcal {B})$
. Then
![]() $\chi _\mu '(\mathcal {G})\le \Delta +1$
, that is, there is a Borel map
$\chi _\mu '(\mathcal {G})\le \Delta +1$
, that is, there is a Borel map
![]() $c:E\to [\Delta +1]$
that is a proper edge coloring at
$c:E\to [\Delta +1]$
that is a proper edge coloring at
![]() $\mu $
-almost every vertex
$\mu $
-almost every vertex
![]() $v\in V$
.
$v\in V$
.
In the proof, we combine the technique of augmenting iterated Vizing chains introduced by the author and Pikhurko in [Reference Grebík and PikhurkoGP20] together with the following result, Theorem 1.2, that is interesting in its own right and might be useful for other applications as well.Footnote
1
Before we state the result, we need several definitions. Let
![]() $\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph and
$\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph and
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() $(V,\mathcal {B})$
. Recall that
$(V,\mathcal {B})$
. Recall that
![]() $\mu $
is called
$\mu $
is called
![]() $\mathcal {G}$
-quasi-invariant if
$\mathcal {G}$
-quasi-invariant if
![]() $\mu ([A]_{\mathcal {G}})=0$
, whenever
$\mu ([A]_{\mathcal {G}})=0$
, whenever
![]() $\mu (A)=0$
, where
$\mu (A)=0$
, where
![]() $[A]_{\mathcal {G}}$
is the union of all connected component of
$[A]_{\mathcal {G}}$
is the union of all connected component of
![]() $\mathcal {G}$
that have a nonempty intersection with A. It is a standard fact (see, e.g., [Reference Kechris and MillerKM04, Chapter II, Section 8], that if
$\mathcal {G}$
that have a nonempty intersection with A. It is a standard fact (see, e.g., [Reference Kechris and MillerKM04, Chapter II, Section 8], that if
![]() $\mu $
is
$\mu $
is
![]() $\mathcal {G}$
-quasi-invariant, then there is a function
$\mathcal {G}$
-quasi-invariant, then there is a function
![]() $\rho _\mu $
, called the Radon–Nikodym cocycle of
$\rho _\mu $
, called the Radon–Nikodym cocycle of
![]() $\mathcal {G}$
that takes values in
$\mathcal {G}$
that takes values in
![]() $(0,+\infty )$
, is defined for every ordered pair of points
$(0,+\infty )$
, is defined for every ordered pair of points
![]() $x,y\in V$
that are in the same connected component of
$x,y\in V$
that are in the same connected component of
![]() $\mathcal {G}$
and satisfies the following mass transport principle:
$\mathcal {G}$
and satisfies the following mass transport principle:
for every
![]() $C\subseteq V$
and an injective Borel map
$C\subseteq V$
and an injective Borel map
![]() $g:C\to X$
that satisfies for every
$g:C\to X$
that satisfies for every
![]() $x\in C$
that
$x\in C$
that
![]() $g(x)$
is in the same connected component of
$g(x)$
is in the same connected component of
![]() $\mathcal {G}$
as x. While in general
$\mathcal {G}$
as x. While in general
![]() $\rho _\mu $
can behave chaotically, the next result shows that one can always pass to an equivalent measure
$\rho _\mu $
can behave chaotically, the next result shows that one can always pass to an equivalent measure
![]() $\nu $
such that
$\nu $
such that
![]() $\rho _\nu $
is bounded on edges of
$\rho _\nu $
is bounded on edges of
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Theorem 1.2 (see also [Reference KuhnKuh94] Lemma 1).
Let
![]() $(V,\mathcal {B})$
be a standard Borel space,
$(V,\mathcal {B})$
be a standard Borel space,
![]() $\Delta \in \mathbb {N}$
,
$\Delta \in \mathbb {N}$
,
![]() $\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph of uniformly bounded degree by
$\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph of uniformly bounded degree by
![]() $\Delta \in \mathbb {N}$
and
$\Delta \in \mathbb {N}$
and
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() $(V,\mathcal {B})$
that is
$(V,\mathcal {B})$
that is
![]() $\mathcal {G}$
-quasi-invariant. Then there is an equivalent Borel probability measure
$\mathcal {G}$
-quasi-invariant. Then there is an equivalent Borel probability measure
![]() $\nu $
on
$\nu $
on
![]() $(V,\mathcal {B})$
such that
$(V,\mathcal {B})$
such that
for every edge
![]() $(x,y)\in E$
.
$(x,y)\in E$
.
In particular, if
![]() $\operatorname {dist}_{\mathcal {G}}(x,y)=k\in \mathbb {N}$
, then
$\operatorname {dist}_{\mathcal {G}}(x,y)=k\in \mathbb {N}$
, then
![]() $\rho _\nu (x,y)\le (4\Delta )^k$
, where
$\rho _\nu (x,y)\le (4\Delta )^k$
, where
![]() $\operatorname {dist}_{\mathcal {G}}$
is the graph distance on
$\operatorname {dist}_{\mathcal {G}}$
is the graph distance on
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Remark 1.3. Kuhn [Reference KuhnKuh94, Lemma 1] showed that if a countable group
![]() $\Gamma $
acts in a quasi-invariant fashion on a standard probability space
$\Gamma $
acts in a quasi-invariant fashion on a standard probability space
![]() $(X,\mu )$
, then there is an equivalent measure
$(X,\mu )$
, then there is an equivalent measure
![]() $\nu $
such that the cocycle
$\nu $
such that the cocycle
![]() $\rho _\nu ({-},\gamma \cdot {-})$
(as a function
$\rho _\nu ({-},\gamma \cdot {-})$
(as a function
![]() $X\to (0,\infty )$
) is bounded for every fixed
$X\to (0,\infty )$
) is bounded for every fixed
![]() $\gamma \in \Gamma $
. This result combined with the fact that every Borel graph
$\gamma \in \Gamma $
. This result combined with the fact that every Borel graph
![]() $\mathcal {G}$
of degree bounded by
$\mathcal {G}$
of degree bounded by
![]() $\Delta (\mathcal {G})<+\infty $
can be generated by
$\Delta (\mathcal {G})<+\infty $
can be generated by
![]() $2\Delta (\mathcal {G})-1$
involutions (which follows from the Lusin–Novikov uniformization theorem [Reference KechrisKec95, Theorem 18.10]) implies Theorem 1.2 possibly with a constant larger than
$2\Delta (\mathcal {G})-1$
involutions (which follows from the Lusin–Novikov uniformization theorem [Reference KechrisKec95, Theorem 18.10]) implies Theorem 1.2 possibly with a constant larger than
![]() $4\Delta $
.
$4\Delta $
.
Similar, stronger conditions on the cocycle was used by Conley and Tamuz [Reference Conley and TamuzCT21]. They designed a procedure for solving the unfriendly coloring problem on graphs of degree bounded by
![]() $\Delta $
and showed that this procedure terminates off of a
$\Delta $
and showed that this procedure terminates off of a
![]() $\mu $
-null set for every quasi-invariant Borel probability measure
$\mu $
-null set for every quasi-invariant Borel probability measure
![]() $\mu $
under the assumption that
$\mu $
under the assumption that
![]() $1-1/\Delta \le \rho _\mu (x,y)\le 1+1/\Delta $
for every edge
$1-1/\Delta \le \rho _\mu (x,y)\le 1+1/\Delta $
for every edge
![]() $\{x,y\}$
(this includes, for example, the case when
$\{x,y\}$
(this includes, for example, the case when
![]() $\mu $
is invariant). Finding a measurable unfriendly coloring for a general Borel probability measure remains an interesting open problem. In general, it would be nice to investigate if our condition has another applications in the context of local graph coloring problems.
$\mu $
is invariant). Finding a measurable unfriendly coloring for a general Borel probability measure remains an interesting open problem. In general, it would be nice to investigate if our condition has another applications in the context of local graph coloring problems.
The paper is structured as follows: In Section 2, we set the notation and recall basic results; in Section 3, we define the augmenting chains that we consider in this paper, so-called
![]() $3$
-step Vizing chains, and estimate how many of them can be attached to an uncolored edge; in Section 4, we describe an infinite procedure that improves a given coloring so that it does not contain augmenting chains of small weight; in Section 5, we prove Theorem 1.2, that is, we show how to modify a given quasi-invariant measure to an equivalent measure that has bounded cocycle on edges; in Section 6, we describe the double counting argument that estimates the number of uncolored edges; and finally in Section 7, we combine all the results to prove Theorem 1.1.
$3$
-step Vizing chains, and estimate how many of them can be attached to an uncolored edge; in Section 4, we describe an infinite procedure that improves a given coloring so that it does not contain augmenting chains of small weight; in Section 5, we prove Theorem 1.2, that is, we show how to modify a given quasi-invariant measure to an equivalent measure that has bounded cocycle on edges; in Section 6, we describe the double counting argument that estimates the number of uncolored edges; and finally in Section 7, we combine all the results to prove Theorem 1.1.
2 Preliminaries
Our basic descriptive set theory reference is [Reference KechrisKec95]; see also [Reference Kechris and MarksKM20, Reference PikhurkoPik21]. We mostly follow the notation developed in [Reference Grebík and PikhurkoGP20]. Let us point out that
![]() $\mathbb {N}$
contains
$\mathbb {N}$
contains
![]() $0$
. If
$0$
. If
![]() $k\in \mathbb {N}\setminus \{0\}$
, then we write
$k\in \mathbb {N}\setminus \{0\}$
, then we write
![]() $[k]=\{1,2,\dots ,k\}$
. If S is a set, then we write
$[k]=\{1,2,\dots ,k\}$
. If S is a set, then we write
![]() $[S]^k$
for the set of k-element subsets of S. In particular,
$[S]^k$
for the set of k-element subsets of S. In particular,
![]() $[S]^2$
is the set of unordered pairs of S. We follow a standard graph theoretic notation, that is, a graph is a pair
$[S]^2$
is the set of unordered pairs of S. We follow a standard graph theoretic notation, that is, a graph is a pair
![]() $G=(V,E)$
, where
$G=(V,E)$
, where
![]() $V\subseteq [E]^2$
,
$V\subseteq [E]^2$
,
![]() $\operatorname {deg}_G(x)$
is the number of neighbors of x in G,
$\operatorname {deg}_G(x)$
is the number of neighbors of x in G,
![]() $\operatorname {dist}_G(x,y)$
denotes the graph distance of
$\operatorname {dist}_G(x,y)$
denotes the graph distance of
![]() $x,y\in V$
in G, and
$x,y\in V$
in G, and
![]() $N_G(x)$
denotes the set of all edges of G that are adjacent to x, that is,
$N_G(x)$
denotes the set of all edges of G that are adjacent to x, that is,
![]() $N_G(x)=\{e\in E:x\in e\}$
.
$N_G(x)=\{e\in E:x\in e\}$
.
Borel graphs. A Borel graph is a triplet
![]() $\mathcal {G}=(V,\mathcal {B},E)$
, where
$\mathcal {G}=(V,\mathcal {B},E)$
, where
![]() $(V,\mathcal {B})$
is a standard Borel space,
$(V,\mathcal {B})$
is a standard Borel space,
![]() $(V,E)$
is a graph and E is a Borel subset of
$(V,E)$
is a graph and E is a Borel subset of
![]() $[V]^2$
(endowed with the natural
$[V]^2$
(endowed with the natural
![]() $\sigma $
-algebra inherited from the product
$\sigma $
-algebra inherited from the product
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {B}\times \mathcal {B}$
on
$\mathcal {B}\times \mathcal {B}$
on
![]() $V\times V$
). We say that
$V\times V$
). We say that
![]() $\mathcal {G}$
is of bounded maximum degree if there is
$\mathcal {G}$
is of bounded maximum degree if there is
![]() $\Delta \in \mathbb {N}$
such that
$\Delta \in \mathbb {N}$
such that
![]() $\operatorname {deg}_{\mathcal {G}}(x)\le \Delta $
for every
$\operatorname {deg}_{\mathcal {G}}(x)\le \Delta $
for every
![]() $x\in V$
. We write
$x\in V$
. We write
![]() $\Delta (\mathcal {G})$
for smallest such
$\Delta (\mathcal {G})$
for smallest such
![]() $\Delta $
. We denote the connectedness relation of
$\Delta $
. We denote the connectedness relation of
![]() $\mathcal {G}$
as
$\mathcal {G}$
as
![]() $F_{\mathcal {G}}$
. That is,
$F_{\mathcal {G}}$
. That is,
![]() $F_{\mathcal {G}}$
is an equivalence relation on X, and we write
$F_{\mathcal {G}}$
is an equivalence relation on X, and we write
![]() $[x]_{\mathcal {G}}$
for the
$[x]_{\mathcal {G}}$
for the
![]() $\mathcal {G}$
-connectivity component of
$\mathcal {G}$
-connectivity component of
![]() $x\in V$
. If
$x\in V$
. If
![]() $\Delta (\mathcal {G})<\infty $
, then
$\Delta (\mathcal {G})<\infty $
, then
![]() $F_{\mathcal {G}}$
is a Borel subset of
$F_{\mathcal {G}}$
is a Borel subset of
![]() $V\times V$
and
$V\times V$
and
![]() $|[x]_{\mathcal {G}}|$
is at most countable. Recall that an equivalence relation F on a standard Borel space
$|[x]_{\mathcal {G}}|$
is at most countable. Recall that an equivalence relation F on a standard Borel space
![]() $(X,\mathcal {D})$
that is Borel as a subset of
$(X,\mathcal {D})$
that is Borel as a subset of
![]() $X\times X$
and each F-equivalence class is at most countable is called a countable Borel equvialence relation (CBER) on X; see [Reference KechrisKec24]. In particular, if
$X\times X$
and each F-equivalence class is at most countable is called a countable Borel equvialence relation (CBER) on X; see [Reference KechrisKec24]. In particular, if
![]() $\Delta (\mathcal {G})<\infty $
, then
$\Delta (\mathcal {G})<\infty $
, then
![]() $F_{\mathcal {G}}$
is a CBER on V. Given
$F_{\mathcal {G}}$
is a CBER on V. Given
![]() $A\subseteq X$
, we write
$A\subseteq X$
, we write
![]() $[A]_F$
for the F-saturation of A in F, that is, the smallest F-invariant subset of X that contains A. If
$[A]_F$
for the F-saturation of A in F, that is, the smallest F-invariant subset of X that contains A. If
![]() $[A]_F=A$
, then we say that A is F-invariant. In case
$[A]_F=A$
, then we say that A is F-invariant. In case
![]() $F=F_{\mathcal {G}}$
, we write simply
$F=F_{\mathcal {G}}$
, we write simply
![]() $[A]_{\mathcal {G}}$
and say that A is
$[A]_{\mathcal {G}}$
and say that A is
![]() $\mathcal {G}$
-invariant if it is
$\mathcal {G}$
-invariant if it is
![]() $F_{\mathcal {G}}$
-invariant. Observe that if A is a Borel set, then so is
$F_{\mathcal {G}}$
-invariant. Observe that if A is a Borel set, then so is
![]() $[A]_F$
.
$[A]_F$
.
The line graph of a Borel graph
![]() $\mathcal {G}=(V,\mathcal {B},E)$
is the Borel graph
$\mathcal {G}=(V,\mathcal {B},E)$
is the Borel graph
![]() $\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
, where
$\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
, where
![]() $\mathcal {C}$
is the
$\mathcal {C}$
is the
![]() $\sigma $
-algebra on E inherited form
$\sigma $
-algebra on E inherited form
![]() $[V]^2$
and
$[V]^2$
and
![]() $(E,I_{\mathcal {G}})$
is the line graph of
$(E,I_{\mathcal {G}})$
is the line graph of
![]() $(V,E)$
, that is,
$(V,E)$
, that is,
![]() $\{e,f\}\in I_{\mathcal {G}}$
if and only if e and f share exactly one vertex. Observe that if
$\{e,f\}\in I_{\mathcal {G}}$
if and only if e and f share exactly one vertex. Observe that if
![]() $\Delta (\mathcal {G})<\infty $
, then
$\Delta (\mathcal {G})<\infty $
, then
![]() $\Delta (\mathcal {E})\le 2\Delta (\mathcal {G})-2$
. Similarly as above,
$\Delta (\mathcal {E})\le 2\Delta (\mathcal {G})-2$
. Similarly as above,
![]() $F_{\mathcal {E}}$
is the CBER on E induced by the connectivity components of
$F_{\mathcal {E}}$
is the CBER on E induced by the connectivity components of
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
A Borel chromatic number
![]() $\chi _{\mathcal {B}}(\mathcal {G})$
of a Borel graph
$\chi _{\mathcal {B}}(\mathcal {G})$
of a Borel graph
![]() $\mathcal {G}$
is the minimal
$\mathcal {G}$
is the minimal
![]() $k\in \mathbb {N}$
such that there is a Borel proper vertex coloring
$k\in \mathbb {N}$
such that there is a Borel proper vertex coloring
![]() $d:V\to [k]$
of
$d:V\to [k]$
of
![]() $\mathcal {G}$
. Note that the subscript
$\mathcal {G}$
. Note that the subscript
![]() $\chi _{\mathcal {B}}$
refers to the corresponding
$\chi _{\mathcal {B}}$
refers to the corresponding
![]() $\sigma $
-algebra. A Borel chromatic index
$\sigma $
-algebra. A Borel chromatic index
![]() $\chi ^{\prime }_{\mathcal {B}}(\mathcal {G})$
is defined as
$\chi ^{\prime }_{\mathcal {B}}(\mathcal {G})$
is defined as
![]() $\chi _{\mathcal {C}}(\mathcal {E})$
. That is
$\chi _{\mathcal {C}}(\mathcal {E})$
. That is
![]() $\chi ^{\prime }_{\mathcal {B}}(\mathcal {G})=k$
if there is a Borel proper vertex coloring
$\chi ^{\prime }_{\mathcal {B}}(\mathcal {G})=k$
if there is a Borel proper vertex coloring
![]() $c:E\to [k]$
of
$c:E\to [k]$
of
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
Measures. The set of all Borel probability measures on a standard Borel space
![]() $(X,\mathcal {B})$
is denoted as
$(X,\mathcal {B})$
is denoted as
![]() $\mathcal {P}(X)$
. Let F be a CBER on X and
$\mathcal {P}(X)$
. Let F be a CBER on X and
![]() $\mu \in \mathcal {P}(X)$
. We say that
$\mu \in \mathcal {P}(X)$
. We say that
![]() $\mu $
is F-quasi invariant if
$\mu $
is F-quasi invariant if
![]() $\mu ([A]_F)=0$
, whenever
$\mu ([A]_F)=0$
, whenever
![]() $\mu (A)=0$
. If
$\mu (A)=0$
. If
![]() $\mathcal {G}=(V,\mathcal {B},E)$
is a Borel graph, then we say that
$\mathcal {G}=(V,\mathcal {B},E)$
is a Borel graph, then we say that
![]() $\mu \in \mathcal {P}(V)$
is
$\mu \in \mathcal {P}(V)$
is
![]() $\mathcal {G}$
-quasi-invariant if it is
$\mathcal {G}$
-quasi-invariant if it is
![]() $F_{\mathcal {G}}$
-quasi-invariant
$F_{\mathcal {G}}$
-quasi-invariant
Proposition 2.1 (Propositions 3.1 and 3.2 in [Reference Grebík and PikhurkoGP20]).
Let
![]() $\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
$\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
![]() $\Delta (\mathcal {G})<\infty $
,
$\Delta (\mathcal {G})<\infty $
,
![]() $\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
be its line graph and
$\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
be its line graph and
![]() $\mu \in \mathcal {P}(V)$
. Then there is
$\mu \in \mathcal {P}(V)$
. Then there is
![]() $\hat \mu \in \mathcal {P}(E)$
that is
$\hat \mu \in \mathcal {P}(E)$
that is
![]() $\mathcal {E}$
-quasi-invariant and satisfies
$\mathcal {E}$
-quasi-invariant and satisfies
for every
![]() $A\subseteq E$
that satisfy
$A\subseteq E$
that satisfy
![]() $\hat \mu (A)=0$
.
$\hat \mu (A)=0$
.
Proof. By [Reference Grebík and PikhurkoGP20, Proposition 3.2], we find
![]() $\tilde \mu \in \mathcal {P}(V)$
that is
$\tilde \mu \in \mathcal {P}(V)$
that is
![]() $\mathcal {G}$
-quasi invariant and satisfies
$\mathcal {G}$
-quasi invariant and satisfies
![]() $\mu ([A]_{\mathcal {G}})=\tilde \mu ([A]_{\mathcal {G}})$
for every
$\mu ([A]_{\mathcal {G}})=\tilde \mu ([A]_{\mathcal {G}})$
for every
![]() $A\subseteq V$
. By [Reference Grebík and PikhurkoGP20, Proposition 3.1], we find
$A\subseteq V$
. By [Reference Grebík and PikhurkoGP20, Proposition 3.1], we find
![]() $\hat \mu \in \mathcal {P}(E)$
that is
$\hat \mu \in \mathcal {P}(E)$
that is
![]() $\mathcal {E}$
-quasi invariant and satisfies
$\mathcal {E}$
-quasi invariant and satisfies
for every
![]() $A\subseteq E$
that satisfies
$A\subseteq E$
that satisfies
![]() $\hat \mu (A)<\epsilon $
. In particular, if
$\hat \mu (A)<\epsilon $
. In particular, if
![]() $\hat \mu (A)=0$
, then
$\hat \mu (A)=0$
, then
 $$ \begin{align*} \mu\left(\left\{x\in V:\exists e\in A \ x\in e\right\}\right)\le & \ \mu\left(\left[\left\{x\in V:\exists e\in A \ x\in e\right\}\right]_{\mathcal{G}}\right)\\ = & \ \tilde \mu\left(\left[\left\{x\in V:\exists e\in A \ x\in e\right\}\right]_{\mathcal{G}}\right)=0 \end{align*} $$
$$ \begin{align*} \mu\left(\left\{x\in V:\exists e\in A \ x\in e\right\}\right)\le & \ \mu\left(\left[\left\{x\in V:\exists e\in A \ x\in e\right\}\right]_{\mathcal{G}}\right)\\ = & \ \tilde \mu\left(\left[\left\{x\in V:\exists e\in A \ x\in e\right\}\right]_{\mathcal{G}}\right)=0 \end{align*} $$
as
![]() $\tilde {\mu }\left (\left \{x\in V:\exists e\in A \ x\in e\right \}\right )=0$
.
$\tilde {\mu }\left (\left \{x\in V:\exists e\in A \ x\in e\right \}\right )=0$
.
A fundamental tool in the study of quasi-invariant measures is the Radon–Nikodym cocycle. Let
![]() $(X,\mathcal {B})$
be a standard Borel space, F be a CBER on X and
$(X,\mathcal {B})$
be a standard Borel space, F be a CBER on X and
![]() $\mu \in \mathcal {P}(X)$
be F-quasi-invariant. Then the Radon–Nikodym cocycle (of
$\mu \in \mathcal {P}(X)$
be F-quasi-invariant. Then the Radon–Nikodym cocycle (of
![]() $\mu $
with respect to F) is a Borel function
$\mu $
with respect to F) is a Borel function
![]() $\rho _{\mu ,F}:F\to \mathbb {R}_{>0}$
with the property that
$\rho _{\mu ,F}:F\to \mathbb {R}_{>0}$
with the property that
for every
![]() $C\in \mathcal {B}$
and injective Borel map
$C\in \mathcal {B}$
and injective Borel map
![]() $g:C\to X$
such that
$g:C\to X$
such that
![]() $(x,g(x))\in F$
. It is a standard fact that the Radon–Nikodym cocycle exists, and it is unique up to null-sets, that is, if
$(x,g(x))\in F$
. It is a standard fact that the Radon–Nikodym cocycle exists, and it is unique up to null-sets, that is, if
![]() $\rho $
and
$\rho $
and
![]() $\rho '$
are two Radon–Nikodym cocycles of
$\rho '$
are two Radon–Nikodym cocycles of
![]() $\mu $
with respect to F, then there is a
$\mu $
with respect to F, then there is a
![]() $\mu $
-conull F-invariant set
$\mu $
-conull F-invariant set
![]() $A\subseteq X$
such that
$A\subseteq X$
such that
see [Reference Kechris and MillerKM04]. The following statement summarizes the properties of cocycles that we need.
Proposition 2.2 (Chapter II, Section 8 in [Reference Kechris and MillerKM04]).
Let
![]() $(X,\mathcal {B})$
be a standard Borel space, F be a CBER on X and
$(X,\mathcal {B})$
be a standard Borel space, F be a CBER on X and
![]() $\mu \in \mathcal {P}(X)$
be F-quasi-invariant. Then the Radon–Nikodym cocycle
$\mu \in \mathcal {P}(X)$
be F-quasi-invariant. Then the Radon–Nikodym cocycle
![]() $\rho _{\mu ,F}:F\to \mathbb {R}_{>0}$
satisfies:
$\rho _{\mu ,F}:F\to \mathbb {R}_{>0}$
satisfies:
-
1. there is a
 $\mu $
-conull F-invariant set
$\mu $
-conull F-invariant set
 $A\in \mathcal {B}$
such that
$A\in \mathcal {B}$
such that
 $\rho _{\mu ,F}(x,y)\rho _{\mu ,F}(y,z)=\rho _{\mu ,F}(x,z)$
for any
$\rho _{\mu ,F}(x,y)\rho _{\mu ,F}(y,z)=\rho _{\mu ,F}(x,z)$
for any
 $x,y,z\in A$
such that
$x,y,z\in A$
such that
 $y,z\in [x]_F$
,
$y,z\in [x]_F$
, -
2. (mass transport) we have
for any function $$ \begin{align*}\int_{X} \sum_{x\in [y]_F}\mathbf{F}(x,y) \ d \mu(y)=\int_{X} \sum_{y\in [x]_F} \mathbf{F}(x,y)\rho_{\mu,F}(x,y) \ d \mu(x)\end{align*} $$
$$ \begin{align*}\int_{X} \sum_{x\in [y]_F}\mathbf{F}(x,y) \ d \mu(y)=\int_{X} \sum_{y\in [x]_F} \mathbf{F}(x,y)\rho_{\mu,F}(x,y) \ d \mu(x)\end{align*} $$
 $\mathbf {F}:F\to [0,\infty ]$
.
$\mathbf {F}:F\to [0,\infty ]$
.
In case that
![]() $F=F_{\mathcal {G}}$
, we write
$F=F_{\mathcal {G}}$
, we write
![]() $\rho _{\mu ,\mathcal {G}}$
instead of
$\rho _{\mu ,\mathcal {G}}$
instead of
![]() $\rho _{\mu ,F_{\mathcal {G}}}$
. If F is clear from context, then we write simply
$\rho _{\mu ,F_{\mathcal {G}}}$
. If F is clear from context, then we write simply
![]() $\rho _\mu $
.
$\rho _\mu $
.
Definition 2.3. Let
![]() $\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
$\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
![]() $\Delta (\mathcal {G})<\infty $
and
$\Delta (\mathcal {G})<\infty $
and
![]() $\mu \in \mathcal {P}(V)$
be
$\mu \in \mathcal {P}(V)$
be
![]() $\mathcal {G}$
-quasi-invariant. We say that
$\mathcal {G}$
-quasi-invariant. We say that
![]() $\mu $
is
$\mu $
is
![]() $\mathcal {G}$
-bounded if
$\mathcal {G}$
-bounded if
for every
![]() $\{x,y\}\in E$
.
$\{x,y\}\in E$
.
We show in Theorem 5.1 that every
![]() $\mathcal {G}$
-quasi-invariant
$\mathcal {G}$
-quasi-invariant
![]() $\mu \in \mathcal {P}(V)$
is equivalent with a
$\mu \in \mathcal {P}(V)$
is equivalent with a
![]() $\mathcal {G}$
-bounded measure
$\mathcal {G}$
-bounded measure
![]() $\nu \in \mathcal {P}(V)$
.
$\nu \in \mathcal {P}(V)$
.
3 Edge colorings
Let
![]() $\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
$\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
![]() $\Delta (\mathcal {G})<\infty $
. A partial (Borel proper edge) coloring of
$\Delta (\mathcal {G})<\infty $
. A partial (Borel proper edge) coloring of
![]() $\mathcal {G}$
is a partial Borel (with respect to the
$\mathcal {G}$
is a partial Borel (with respect to the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {C}$
on E, in particular,
$\mathcal {C}$
on E, in particular,
![]() $\operatorname {dom}(c)\in \mathcal {C}$
) map
$\operatorname {dom}(c)\in \mathcal {C}$
) map
![]() $c;E\to [\Delta (\mathcal {G})+1]$
that assigns different colors to different edges that share a vertex. Usually we use lower case Greek letters for colors,for example,
$c;E\to [\Delta (\mathcal {G})+1]$
that assigns different colors to different edges that share a vertex. Usually we use lower case Greek letters for colors,for example,
![]() $\alpha ,\beta \in [\Delta (\mathcal {G})+1]$
. Given a partial coloring c, we define
$\alpha ,\beta \in [\Delta (\mathcal {G})+1]$
. Given a partial coloring c, we define
![]() $m_c(x)$
to be the set of missing colors at
$m_c(x)$
to be the set of missing colors at
![]() $x\in V$
, that is,
$x\in V$
, that is,
![]() $m_c(x)=[\Delta (\mathcal {G})+1]\setminus \{c(e):e\in N_{\mathcal {G}}(x)\}$
. We also write
$m_c(x)=[\Delta (\mathcal {G})+1]\setminus \{c(e):e\in N_{\mathcal {G}}(x)\}$
. We also write
![]() $U_c$
for the set of uncolored edges, that is,
$U_c$
for the set of uncolored edges, that is,
![]() $U_c=E\setminus \operatorname {dom}(c)$
.
$U_c=E\setminus \operatorname {dom}(c)$
.
In order to improve a given partial coloring c, we utilize an idea from the proof of Vizing’s theorem, so-called Vizing chains. In general, given an uncolored edge
![]() $e\in U_c$
, we want to find an injective augmenting sequence of edges
$e\in U_c$
, we want to find an injective augmenting sequence of edges
![]() $W_c(e)=(e_i)_{i\le k}$
such that
$W_c(e)=(e_i)_{i\le k}$
such that
![]() $e_0=e$
,
$e_0=e$
,
![]() $e_i\cap e_{i+1}\not =\emptyset $
for
$e_i\cap e_{i+1}\not =\emptyset $
for
![]() $i\le k$
and
$i\le k$
and
![]() $e_i\not \in U_c$
for every
$e_i\not \in U_c$
for every
![]() $1\le i\le k$
with the property that keeping the colors outside of
$1\le i\le k$
with the property that keeping the colors outside of
![]() $W_{c}(e)$
intact, but shifting the colors from
$W_{c}(e)$
intact, but shifting the colors from
![]() $e_{i+1}$
to
$e_{i+1}$
to
![]() $e_i$
produces a different partial (proper) coloring
$e_i$
produces a different partial (proper) coloring
![]() $c'$
such that
$c'$
such that
![]() $m_{c'}(z_0)\cap m_{c'}(z_1)\not =\emptyset $
, where
$m_{c'}(z_0)\cap m_{c'}(z_1)\not =\emptyset $
, where
![]() $\{z_0,z_1\}=e_k$
is the last edge of
$\{z_0,z_1\}=e_k$
is the last edge of
![]() $W_{c}(e)$
. Extending
$W_{c}(e)$
. Extending
![]() $c'$
by assigning any color from
$c'$
by assigning any color from
![]() $m_{c'}(z_0)\cap m_{c'}(z_1)$
to
$m_{c'}(z_0)\cap m_{c'}(z_1)$
to
![]() $e_k$
then improves c as we decreased the number of uncolored edges. Observe that the difference between c and
$e_k$
then improves c as we decreased the number of uncolored edges. Observe that the difference between c and
![]() $c'$
is contained in
$c'$
is contained in
![]() $W_{c}(e)$
.
$W_{c}(e)$
.
Various types of sequences
![]() $W_{c}(e)$
have been used in the literature. In order to prove classical Vizing’s theorem, one chooses
$W_{c}(e)$
have been used in the literature. In order to prove classical Vizing’s theorem, one chooses
![]() $W_{c}(e)$
to be a concatenation of a so-called fan and an alternating path, also known as a Vizing chain. To prove an analogue of Vizing’s theorem for graphings, the author and Pikhurko [Reference Grebík and PikhurkoGP20] iterated this process two times. Namely, first we fix a Vizing chain, then truncate it at any edge on the alternating path, and then grow a second Vizing chain from that place; such a sequence is called an iterated Vizing chain. In order to devise efficient (both deterministic and randomized) local algorithms that produce a proper edge colorings with
$W_{c}(e)$
to be a concatenation of a so-called fan and an alternating path, also known as a Vizing chain. To prove an analogue of Vizing’s theorem for graphings, the author and Pikhurko [Reference Grebík and PikhurkoGP20] iterated this process two times. Namely, first we fix a Vizing chain, then truncate it at any edge on the alternating path, and then grow a second Vizing chain from that place; such a sequence is called an iterated Vizing chain. In order to devise efficient (both deterministic and randomized) local algorithms that produce a proper edge colorings with
![]() $\Delta +1$
colors on finite graphs, Bernshteyn [Reference BernshteynBer22] iterated this process
$\Delta +1$
colors on finite graphs, Bernshteyn [Reference BernshteynBer22] iterated this process
![]() $\log (n)$
times, where n is the number of vertices of the graph. Bernshteyn called the produced injective sequence a multistep Vizing chain. In this paper, being ideologically more closer to [Reference Grebík and PikhurkoGP20], we iterate the process three times. We follow the terminology of Bernshteyn and call this augmenting chain a
$\log (n)$
times, where n is the number of vertices of the graph. Bernshteyn called the produced injective sequence a multistep Vizing chain. In this paper, being ideologically more closer to [Reference Grebík and PikhurkoGP20], we iterate the process three times. We follow the terminology of Bernshteyn and call this augmenting chain a
![]() $3$
-step Vizing chain. The estimate for the number of
$3$
-step Vizing chain. The estimate for the number of
![]() $3$
-step Vizing chains that can be assigned to a given uncolored edge follows the computation from [Reference Grebík and PikhurkoGP20]. It seems plausible that one can get similar estimate by adapting the results from finite graphs, but we decided to follow the more direct path of generalizing [Reference Grebík and PikhurkoGP20].
$3$
-step Vizing chains that can be assigned to a given uncolored edge follows the computation from [Reference Grebík and PikhurkoGP20]. It seems plausible that one can get similar estimate by adapting the results from finite graphs, but we decided to follow the more direct path of generalizing [Reference Grebík and PikhurkoGP20].
3.1
 $3$
-step Vizing chains
$3$
-step Vizing chains
We recall the notation from [Reference Grebík and PikhurkoGP20, Section 2] and refer the reader there for basic results about this notation. Fix a Borel graph
![]() $\mathcal {G}=(V,\mathcal {B},E)$
such that
$\mathcal {G}=(V,\mathcal {B},E)$
such that
![]() $\Delta (\mathcal {G})<\infty $
and a partial edge coloring
$\Delta (\mathcal {G})<\infty $
and a partial edge coloring
![]() $c;E\to [\Delta (\mathcal {G})+1]$
. Set
$c;E\to [\Delta (\mathcal {G})+1]$
. Set
![]() $\Delta =\Delta (\mathcal {G})$
, and fix an ordering of the set of colors
$\Delta =\Delta (\mathcal {G})$
, and fix an ordering of the set of colors
![]() $[\Delta +1]$
.
$[\Delta +1]$
.
A chain is a sequence
![]() $P=(e_0,\dots )$
of edges of
$P=(e_0,\dots )$
of edges of
![]() $\mathcal {G}$
such that for every index
$\mathcal {G}$
such that for every index
![]() $i\in \mathbb {N}$
with
$i\in \mathbb {N}$
with
![]() $e_i,e_{i+1}$
being in P we have
$e_i,e_{i+1}$
being in P we have
![]() $e_i\cap e_{i+1}\not =\emptyset $
, that is, every two consecutive edges in P intersect. Let
$e_i\cap e_{i+1}\not =\emptyset $
, that is, every two consecutive edges in P intersect. Let
![]() $l(P)=|P|$
denote the length of the chain P, that is, the number of edges in P. Note that a chain can be finite (possibly empty) or infinite; thus,
$l(P)=|P|$
denote the length of the chain P, that is, the number of edges in P. Note that a chain can be finite (possibly empty) or infinite; thus,
![]() $l(P)\in \mathbb {N}\cup \{\infty \}$
and, if P is finite, then
$l(P)\in \mathbb {N}\cup \{\infty \}$
and, if P is finite, then
![]() $P=(e_0,\dots , e_{l(P)-1})$
. The convention of labeling the first edge as
$P=(e_0,\dots , e_{l(P)-1})$
. The convention of labeling the first edge as
![]() $e_0$
allows us to write
$e_0$
allows us to write
![]() $P=(e_i)_{i<l(P)}$
, regardless of whether P is finite or not. If
$P=(e_i)_{i<l(P)}$
, regardless of whether P is finite or not. If
![]() $l(P)=\infty $
, then we define
$l(P)=\infty $
, then we define
![]() $l(P)-1=\infty $
in order to avoid case by case statements in several places.
$l(P)-1=\infty $
in order to avoid case by case statements in several places.
We call
![]() $e_{i-1}$
the i-th edge of P. For an edge f that occurs exactly once in P, let its index
$e_{i-1}$
the i-th edge of P. For an edge f that occurs exactly once in P, let its index
![]() $i(f)$
be
$i(f)$
be
![]() $i\ge 1$
such that
$i\ge 1$
such that
![]() $f=e_{i-1}$
, that is, the index of the i-th edge is i. Also, for
$f=e_{i-1}$
, that is, the index of the i-th edge is i. Also, for
![]() $i\le l(P)$
, let
$i\le l(P)$
, let
![]() $P_i=(e_j)_{j<i}$
denote the i-th prefix of P (which consists of the first i edges from P). We have, for example, that
$P_i=(e_j)_{j<i}$
denote the i-th prefix of P (which consists of the first i edges from P). We have, for example, that
![]() $P_{l(P)}=P$
. For chains P and Q, we write
$P_{l(P)}=P$
. For chains P and Q, we write
![]() $P\sqsubseteq Q$
if
$P\sqsubseteq Q$
if
![]() $P=Q_{l(P)}$
, that is, P is a prefix of Q. If P is a finite chain with the last edge e and Q is a chain with the first edge f and
$P=Q_{l(P)}$
, that is, P is a prefix of Q. If P is a finite chain with the last edge e and Q is a chain with the first edge f and
![]() $e\cap f\not =\emptyset $
, then we write
$e\cap f\not =\emptyset $
, then we write
![]() $P^\frown Q$
for the chain that is the concatenation of P and Q.
$P^\frown Q$
for the chain that is the concatenation of P and Q.
Let us call a chain
![]() $P=(e_i)_{i<l(P)}$
a path if P is empty, or if every vertex
$P=(e_i)_{i<l(P)}$
a path if P is empty, or if every vertex
![]() $z\in V$
belongs to at most two edges from P and there is a vertex that belongs only to
$z\in V$
belongs to at most two edges from P and there is a vertex that belongs only to
![]() $e_0$
. (In other words, P is a finite path with a fixed direction on edges or an infinite one-sided ray, where no self-intersections are allowed.) Also, a chain P is called a cycle if P is nonempty and every vertex belongs to zero or two edges of P. (These are just finite cycles, having some edge and direction fixed.)
$e_0$
. (In other words, P is a finite path with a fixed direction on edges or an infinite one-sided ray, where no self-intersections are allowed.) Also, a chain P is called a cycle if P is nonempty and every vertex belongs to zero or two edges of P. (These are just finite cycles, having some edge and direction fixed.)
Definition 3.1 (Definition 2.2 in [Reference Grebík and PikhurkoGP20]).
We say that a chain
![]() $P=(e_i)_{i<l(P)}$
is
$P=(e_i)_{i<l(P)}$
is
-
1. edge injective if every edge appears at most once in P, that is, for every
 $0\le i<j< l(P)$
we have that
$0\le i<j< l(P)$
we have that
 $e_i\not =e_j$
,
$e_i\not =e_j$
, -
2. c-shiftable if
 $l(P)\ge 1$
, P is edge injective,
$l(P)\ge 1$
, P is edge injective,
 $e_0\in U_c$
and
$e_0\in U_c$
and
 $e_j\in \operatorname {dom}(c)$
for every
$e_j\in \operatorname {dom}(c)$
for every
 $1\le j<l(P)$
(that is, if P is nonempty with no edge repeated and
$1\le j<l(P)$
(that is, if P is nonempty with no edge repeated and
 $e_0$
is the unique uncolored edge of P);
$e_0$
is the unique uncolored edge of P); -
3. c-proper-shiftable if P is c-shiftable and
 $c_P;E\to [\Delta +1]$
is a partial coloring, where
$c_P;E\to [\Delta +1]$
is a partial coloring, where
 $c_P$
is the shift of c along P (or P-shift of c for short) which is defined as
$c_P$
is the shift of c along P (or P-shift of c for short) which is defined as-
○
 $\operatorname {dom}(c_P)=\operatorname {dom}(c)\cup \{e_0\}\setminus \{e_{l(P)-1}\}$
where we put
$\operatorname {dom}(c_P)=\operatorname {dom}(c)\cup \{e_0\}\setminus \{e_{l(P)-1}\}$
where we put
 $\{e_{l(P)-1}\}=\emptyset $
if
$\{e_{l(P)-1}\}=\emptyset $
if
 $l(P)=\infty $
,
$l(P)=\infty $
, -
○
 $c_P(e_i)=c(e_{i+1})$
for every
$c_P(e_i)=c(e_{i+1})$
for every
 $i+1<l(P)$
,
$i+1<l(P)$
, -
○
 $c_P(f)=c(f)$
for every
$c_P(f)=c(f)$
for every
 $f\in \operatorname {dom}(c)\setminus P$
;
$f\in \operatorname {dom}(c)\setminus P$
;
-
-
4. c-augmenting if P is c-proper-shiftable and either
 $l(P)=\infty $
or P is finite with
$l(P)=\infty $
or P is finite with
 $m_{c_P}(x)\cap m_{c_P}(y)\not =\emptyset $
, where
$m_{c_P}(x)\cap m_{c_P}(y)\not =\emptyset $
, where
 $x\not =y$
are the vertices of the last edge
$x\not =y$
are the vertices of the last edge
 $e_{l(P)-1}$
of P.
$e_{l(P)-1}$
of P.
Next, we describe the building blocks that will be used to build
![]() $3$
-step Vizing chains:
$3$
-step Vizing chains:
Alternating path. Let
![]() $x\in V$
and
$x\in V$
and
![]() $\alpha ,\beta \in [\Delta +1]$
be different colors such that
$\alpha ,\beta \in [\Delta +1]$
be different colors such that
![]() $\beta \in m_c(x)$
. Then there is a unique maximal chain
$\beta \in m_c(x)$
. Then there is a unique maximal chain
![]() $P=(e_i)_{i<l(P)}$
such that
$P=(e_i)_{i<l(P)}$
such that
![]() $x\in e_0$
if
$x\in e_0$
if
![]() $l(P)>0$
,
$l(P)>0$
,
![]() $x\not \in e_1$
if
$x\not \in e_1$
if
![]() $l(P)>1$
, and
$l(P)>1$
, and
![]() $c(e_{i})=\alpha $
(resp.
$c(e_{i})=\alpha $
(resp.
![]() $c(e_{i})=\beta $
) for every
$c(e_{i})=\beta $
) for every
![]() $i<l(P)$
that is even (resp. odd). We call this unique maximal chain the (alternating)
$i<l(P)$
that is even (resp. odd). We call this unique maximal chain the (alternating)
![]() $\alpha /\beta $
-path starting at
$\alpha /\beta $
-path starting at
![]() $x\in V$
and denote it as
$x\in V$
and denote it as
![]() $P_c(x,\alpha /\beta )$
. If
$P_c(x,\alpha /\beta )$
. If
![]() $P_c(x,\alpha /\beta )$
is finite and nonempty, then we call the unique
$P_c(x,\alpha /\beta )$
is finite and nonempty, then we call the unique
![]() $y\in V$
such that
$y\in V$
such that
![]() $|\{f\in P_c(x,\alpha /\beta ):y\in f\}|=1$
and
$|\{f\in P_c(x,\alpha /\beta ):y\in f\}|=1$
and
![]() $y\not =x$
the last vertex of
$y\not =x$
the last vertex of
![]() $P_c(x,\alpha /\beta )$
. If
$P_c(x,\alpha /\beta )$
. If
![]() $P_c(x,\alpha /\beta )$
is empty (which happens exactly when
$P_c(x,\alpha /\beta )$
is empty (which happens exactly when
![]() $\alpha \in m_c(x)$
), then the last vertex is x. Whenever we write
$\alpha \in m_c(x)$
), then the last vertex is x. Whenever we write
![]() $P_c(x,\alpha /\beta )$
, we always assume that the condition that
$P_c(x,\alpha /\beta )$
, we always assume that the condition that
![]() $\beta \in m_c(x)$
is satisfied. Observe that the colors on the chain alternate between
$\beta \in m_c(x)$
is satisfied. Observe that the colors on the chain alternate between
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
(starting with
$\beta $
(starting with
![]() $\alpha $
) and we never return to a vertex we have previously visited (and thus the edges in P form a path).
$\alpha $
) and we never return to a vertex we have previously visited (and thus the edges in P form a path).
Fan. Let
![]() $e\in U_c$
and
$e\in U_c$
and
![]() $x\in e$
. We define the maximal fan around x starting at e, in symbols
$x\in e$
. We define the maximal fan around x starting at e, in symbols
![]() $F_c(x,e)$
, as a (finite) chain
$F_c(x,e)$
, as a (finite) chain
![]() $P=(e_0,e_1,\dots ,e_k)$
such that
$P=(e_0,e_1,\dots ,e_k)$
such that
![]() $x\in e_i$
for every
$x\in e_i$
for every
![]() $i\le k$
and if we denote the other vertex in
$i\le k$
and if we denote the other vertex in
![]() $e_i$
by
$e_i$
by
![]() $v_i$
, then the following statements are satisfied
$v_i$
, then the following statements are satisfied
-
1.
 $e_0=e$
,
$e_0=e$
, -
2. P is edge injective,
-
3.
 $c(e_{i+1})\in m_c(v_i)$
for every
$c(e_{i+1})\in m_c(v_i)$
for every
 $i<k$
and
$i<k$
and
 $c(e_{i+1})$
is the minimal color available in the i-th step, where we say that a color
$c(e_{i+1})$
is the minimal color available in the i-th step, where we say that a color
 $\alpha $
is available in the i-th step if
$\alpha $
is available in the i-th step if
 $\alpha \in m_c(v_i)$
,
$\alpha \in m_c(v_i)$
, -
4.
 $(e_0,\dots ,e_k)$
is maximal with these properties.
$(e_0,\dots ,e_k)$
is maximal with these properties.
Conditional fan. We generalize, but only formally, the following definition from [Reference Grebík and PikhurkoGP20, Section 2.5]. Take
![]() $P_c(x,\alpha /\beta )$
for some
$P_c(x,\alpha /\beta )$
for some
![]() $x\in V$
. Let
$x\in V$
. Let
![]() $f\in P_c(x,\alpha /\beta )$
be a an edge that is not first nor last in
$f\in P_c(x,\alpha /\beta )$
be a an edge that is not first nor last in
![]() $P_c(x,\alpha /\beta )$
and
$P_c(x,\alpha /\beta )$
and
![]() $y\in V$
be the last vertex of
$y\in V$
be the last vertex of
![]() $P_c(x,e)_{i(f)}$
. We define the maximal
$P_c(x,e)_{i(f)}$
. We define the maximal
![]() $\alpha /\beta $
-conditional fan starting at f, denoted as
$\alpha /\beta $
-conditional fan starting at f, denoted as
![]() $F_c(x,\alpha /\beta ,y)$
, as a chain
$F_c(x,\alpha /\beta ,y)$
, as a chain
![]() $P=(g_0,\dots , g_m)$
such that
$P=(g_0,\dots , g_m)$
such that
![]() $y\in g_i$
for every
$y\in g_i$
for every
![]() $i\le m$
and, if we denote the other vertex of
$i\le m$
and, if we denote the other vertex of
![]() $g_i$
by
$g_i$
by
![]() $u_i$
, then the following is satisfied
$u_i$
, then the following is satisfied
-
1.
 $g_0=f$
,
$g_0=f$
, -
2. P is edge injective,
-
3.
 $c(g_{i+1})\in m_c(u_{i})$
and it is the minimal available color,
$c(g_{i+1})\in m_c(u_{i})$
and it is the minimal available color, -
4.
 $\alpha ,\beta \not \in m_c(u_i)$
for every
$\alpha ,\beta \not \in m_c(u_i)$
for every
 $i<m$
,
$i<m$
, -
5. if
 $\alpha ,\beta \not \in m_c(u_m)$
, then
$\alpha ,\beta \not \in m_c(u_m)$
, then
 $(g_0,\dots , g_m)$
is maximal with the properties above.
$(g_0,\dots , g_m)$
is maximal with the properties above.
Note that we should rather write
![]() $u_i^f$
,
$u_i^f$
,
![]() $g_i^f$
and
$g_i^f$
and
![]() $y^f$
to stress that those objects depend on the choice of f. This will be, however, omitted in the cases when we work with only one f.
$y^f$
to stress that those objects depend on the choice of f. This will be, however, omitted in the cases when we work with only one f.
Now, we are ready to for the main definition.
Definition 3.2 (
 $3$
-step Vizing chain).
$3$
-step Vizing chain).
Let
![]() $\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
$\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
![]() $\Delta (\mathcal {G})<\infty $
,
$\Delta (\mathcal {G})<\infty $
,
![]() $c;E\to [\Delta (\mathcal {G})+1]$
be a partial edge coloring and
$c;E\to [\Delta (\mathcal {G})+1]$
be a partial edge coloring and
![]() $e\in U_c$
. We say that a c-augmenting chain
$e\in U_c$
. We say that a c-augmenting chain
![]() $W_c(e)=(e_i)_{i< l(W_c(e))}$
, where
$W_c(e)=(e_i)_{i< l(W_c(e))}$
, where
![]() $l(W_c(e))\in \mathbb {N}\cup \{\infty \}$
, is a
$l(W_c(e))\in \mathbb {N}\cup \{\infty \}$
, is a
![]() $3$
-step Vizing chain (at e) if there are pairwise different vertices
$3$
-step Vizing chain (at e) if there are pairwise different vertices
![]() $y_1,y_2,y_3,z_1,z_2,z_3\in V$
, and colors
$y_1,y_2,y_3,z_1,z_2,z_3\in V$
, and colors
![]() $\alpha _i,\beta _i\in [\Delta (\mathcal {G})+1]$
for
$\alpha _i,\beta _i\in [\Delta (\mathcal {G})+1]$
for
![]() $i\in \{1,2,3\}$
such that
$i\in \{1,2,3\}$
such that
where
-
1.
 $F^1_c\sqsubseteq F_c(y_1,e)$
,
$F^1_c\sqsubseteq F_c(y_1,e)$
,
 $F^2_c\sqsubseteq F_c(z_1,\alpha _1/\beta _1,y_2)$
and
$F^2_c\sqsubseteq F_c(z_1,\alpha _1/\beta _1,y_2)$
and
 $F^3_c\sqsubseteq F_c(z_2,\alpha _2/\beta _2,y_3)$
,
$F^3_c\sqsubseteq F_c(z_2,\alpha _2/\beta _2,y_3)$
, -
2.
 $P^i_c\sqsubseteq P_c(z_i,\alpha _i/\beta _i)$
for every
$P^i_c\sqsubseteq P_c(z_i,\alpha _i/\beta _i)$
for every
 $i\in \{1,2,3\}$
,
$i\in \{1,2,3\}$
, -
3. if
 $T\in \{F^i_c\}_{i=1}^3\cup \{P^i_c\}_{i=1}^3$
satisfies
$T\in \{F^i_c\}_{i=1}^3\cup \{P^i_c\}_{i=1}^3$
satisfies
 $T=\emptyset $
, then every S to the right from T in the definition of
$T=\emptyset $
, then every S to the right from T in the definition of
 $W_c(e)$
is empty as well, that is,
$W_c(e)$
is empty as well, that is,
 $W_c(e)$
is built by at most three iterations of the ‘Vizing chain’ construction,
$W_c(e)$
is built by at most three iterations of the ‘Vizing chain’ construction,
3.2 Construction of
 $3$
-step Vizing chains
$3$
-step Vizing chains
Let
![]() $e\in U_c$
and
$e\in U_c$
and
![]() $x\in e$
be fixed. First, we describe a process that produces many chains of the form
$x\in e$
be fixed. First, we describe a process that produces many chains of the form
that satisfies (1)–(3) in Definition 3.2, then we investigate how many of these chains are
![]() $3$
-step Vizing chains, that is, which ones are c-augmenting. We handle each iteration separately.
$3$
-step Vizing chains, that is, which ones are c-augmenting. We handle each iteration separately.
Iteration I. We start with [Reference Grebík and PikhurkoGP20, Section 2.4]. Recall that the Vizing chain
![]() $V_c(x,e)$
either consists of the fan
$V_c(x,e)$
either consists of the fan
![]() $F_c(x,e)$
, in case it is augmenting, or we have
$F_c(x,e)$
, in case it is augmenting, or we have
where
![]() $i<l(F_c(x,e))$
(so-called first critical index) and
$i<l(F_c(x,e))$
(so-called first critical index) and
![]() $\{x,v_{i}\}$
is the last edge of the truncated fan
$\{x,v_{i}\}$
is the last edge of the truncated fan
![]() $F_c(x,e)_{i_1+1}$
.
$F_c(x,e)_{i_1+1}$
.
Claim 3.3 (Proposition 2.9 in [Reference Grebík and PikhurkoGP20]).
If
![]() $F_c(x,e)$
is not c-augmenting, then there is
$F_c(x,e)$
is not c-augmenting, then there is
![]() $i<l(F_c(x,e))$
such that
$i<l(F_c(x,e))$
such that
![]() ${F_c(x,e)_{i+1}}^\frown P_c(v_i, \alpha /\beta )$
is c-augmenting, where
${F_c(x,e)_{i+1}}^\frown P_c(v_i, \alpha /\beta )$
is c-augmenting, where
![]() $(x,v_i)$
is the last edge of the truncated fan
$(x,v_i)$
is the last edge of the truncated fan
![]() $F_c(x,e)_{i+1}$
and
$F_c(x,e)_{i+1}$
and
![]() $\beta $
is the smallest missing color at
$\beta $
is the smallest missing color at
![]() $v_i$
. In particular, the Vizing chain
$v_i$
. In particular, the Vizing chain
![]() $V_c(x,e)$
is a
$V_c(x,e)$
is a
![]() $3$
-step Vizing chain.
$3$
-step Vizing chain.
Moreover, if nonempty, then
![]() $P_c(v_{i}, \alpha /\beta )$
does not use the vertex x.
$P_c(v_{i}, \alpha /\beta )$
does not use the vertex x.
Suppose that
![]() $P_c(v_i, \alpha /\beta )$
is nonempty. Define
$P_c(v_i, \alpha /\beta )$
is nonempty. Define
![]() $F^1_c=F_c(x,e)_{{i_1}+1}$
,
$F^1_c=F_c(x,e)_{{i_1}+1}$
,
![]() $y_1=x$
,
$y_1=x$
,
![]() $z_1=v_{i}$
and
$z_1=v_{i}$
and
![]() $\alpha _1=\alpha $
,
$\alpha _1=\alpha $
,
![]() $\beta _1=\beta $
. This concludes the first iteration of the construction.
$\beta _1=\beta $
. This concludes the first iteration of the construction.
Iteration II. Recall that
![]() $f^1\in P_c(z_1, \alpha _1/\beta _1)$
is suitable [Reference Grebík and PikhurkoGP20, Definition 2.10] if it is of graph distance
$f^1\in P_c(z_1, \alpha _1/\beta _1)$
is suitable [Reference Grebík and PikhurkoGP20, Definition 2.10] if it is of graph distance
![]() $\ge 3$
from
$\ge 3$
from
![]() $F^1_c$
, it is not the last edge of
$F^1_c$
, it is not the last edge of
![]() $P_c(z_1, \alpha _1/\beta _1)$
and
$P_c(z_1, \alpha _1/\beta _1)$
and
![]() $c(f^1)=\alpha _1$
(we remark that the last condition only helps with the notation and is otherwise irrelevant). Let
$c(f^1)=\alpha _1$
(we remark that the last condition only helps with the notation and is otherwise irrelevant). Let
![]() $y_2$
be the last vertex of
$y_2$
be the last vertex of
![]() $P_c(z_1, \alpha _1/\beta _1)_{i(f^1)}$
, and set
$P_c(z_1, \alpha _1/\beta _1)_{i(f^1)}$
, and set
![]() $F_c(x,e\leadsto f^1)=F_c(z_1,\alpha _1/\beta _1,y_2)$
, where
$F_c(x,e\leadsto f^1)=F_c(z_1,\alpha _1/\beta _1,y_2)$
, where
![]() $F_c(z_1,\alpha _1/\beta _1,y_2)$
is the maximal
$F_c(z_1,\alpha _1/\beta _1,y_2)$
is the maximal
![]() $\alpha _1/\beta _1$
-conditional fan starting at
$\alpha _1/\beta _1$
-conditional fan starting at
![]() $f^1$
.
$f^1$
.
Claim 3.4 (Proposition 2.12 in [Reference Grebík and PikhurkoGP20]).
Let
![]() $f^1 \in P_c(z_1, \alpha /\beta )$
be suitable. Then
$f^1 \in P_c(z_1, \alpha /\beta )$
be suitable. Then
is c-proper-shiftable.
According to the type of
![]() $f^1$
, as defined in [Reference Grebík and PikhurkoGP20, Section 2.5], it is possible to assign an injective sequence of edges Q such that either
$f^1$
, as defined in [Reference Grebík and PikhurkoGP20, Section 2.5], it is possible to assign an injective sequence of edges Q such that either
![]() $Q=F_c(x,e\leadsto f^1)$
, or
$Q=F_c(x,e\leadsto f^1)$
, or
where
![]() $m<l(F_c(x,e\leadsto f^1))$
(the so-called second critical index),
$m<l(F_c(x,e\leadsto f^1))$
(the so-called second critical index),
![]() $\{y_2,u_m\}$
is the last edge of the truncated fan
$\{y_2,u_m\}$
is the last edge of the truncated fan
![]() $F_c(x,e\leadsto f^1)_{m+1}$
and
$F_c(x,e\leadsto f^1)_{m+1}$
and
![]() $\{\gamma ,\delta \}$
is either equal to or disjoint from
$\{\gamma ,\delta \}$
is either equal to or disjoint from
![]() $\{\alpha _1,\beta _1\}$
. Using the technical notion of superb edges, the following, again adapted to our terminology, is shown in [Reference Grebík and PikhurkoGP20].
$\{\alpha _1,\beta _1\}$
. Using the technical notion of superb edges, the following, again adapted to our terminology, is shown in [Reference Grebík and PikhurkoGP20].
Claim 3.5 (Propositions 2.15 and 2.17 in [Reference Grebík and PikhurkoGP20]).
Let
![]() $f^1\in P_c(z_1, \alpha _1/\beta _1)$
be suitable and superb. The chain
$f^1\in P_c(z_1, \alpha _1/\beta _1)$
be suitable and superb. The chain
is a
![]() $3$
-step Vizing chain.
$3$
-step Vizing chain.
Suppose that
![]() $P_c(u_m, \gamma /\delta )$
is nonempty. Define
$P_c(u_m, \gamma /\delta )$
is nonempty. Define
![]() $P^1_c=P_c(z_1, \alpha _1/\beta _1)_{i(f^1)-1}$
,
$P^1_c=P_c(z_1, \alpha _1/\beta _1)_{i(f^1)-1}$
,
![]() $F^2_c=F_c(x,e\leadsto f^1)_{m+1}$
,
$F^2_c=F_c(x,e\leadsto f^1)_{m+1}$
,
![]() $z_2=u_m$
and
$z_2=u_m$
and
![]() $\alpha _2=\gamma $
,
$\alpha _2=\gamma $
,
![]() $\beta _2=\delta $
. This concludes the second iteration of the construction.
$\beta _2=\delta $
. This concludes the second iteration of the construction.
Iteration III. We say that
![]() $f^2\in P_c(z_2,\alpha _2/\beta _2)$
is
$f^2\in P_c(z_2,\alpha _2/\beta _2)$
is
![]() $2$
-suitable if
$2$
-suitable if
-
○ the graph distance of f and
 $f^2$
is at least
$f^2$
is at least
 $3$
for every
$3$
for every
 $f\in (F^1_c)^\frown (P^1_c)^\frown (F^2_c)$
,
$f\in (F^1_c)^\frown (P^1_c)^\frown (F^2_c)$
, -
○ it is not the last edge of
 $P_c(z_2,\alpha _2/\beta _2)$
,
$P_c(z_2,\alpha _2/\beta _2)$
, -
○
 $c(f^2)=\alpha _2$
.
$c(f^2)=\alpha _2$
.
Let
![]() $y_3$
be the last vertex of
$y_3$
be the last vertex of
![]() $P_c(z_2, \alpha _2/\beta _2)_{i(f^2)}$
, and set
$P_c(z_2, \alpha _2/\beta _2)_{i(f^2)}$
, and set
where
![]() $F_c(z_2,\alpha _2/\beta _2,y_3)$
is the maximal
$F_c(z_2,\alpha _2/\beta _2,y_3)$
is the maximal
![]() $\alpha _2/\beta _2$
-conditional fan starting at
$\alpha _2/\beta _2$
-conditional fan starting at
![]() $f^2$
.
$f^2$
.
Proposition 3.6. Let
![]() $f^2 \in P_c(z_2,\alpha _2/\beta _2)$
be
$f^2 \in P_c(z_2,\alpha _2/\beta _2)$
be
![]() $2$
-suitable. Then
$2$
-suitable. Then
is c-proper-shiftable.
Proof. Suppose that
![]() $c_P$
is not a partial coloring. By the definition, we find a vertex
$c_P$
is not a partial coloring. By the definition, we find a vertex
![]() $v\in V$
such that
$v\in V$
such that
![]() $c_P\upharpoonright N_{\mathcal {G}}(v)$
is not proper. By the fact that
$c_P\upharpoonright N_{\mathcal {G}}(v)$
is not proper. By the fact that
![]() $f^2$
is
$f^2$
is
![]() $2$
-suitable together with [Reference Grebík and PikhurkoGP20, Proposition 2.12], we see that
$2$
-suitable together with [Reference Grebík and PikhurkoGP20, Proposition 2.12], we see that
![]() $v\not \in f$
for any
$v\not \in f$
for any
![]() $f\in (F^1_c)^\frown (P^1_c)^\frown (F^2_c)$
. Moreover, we must have
$f\in (F^1_c)^\frown (P^1_c)^\frown (F^2_c)$
. Moreover, we must have
![]() $v\in f$
for some
$v\in f$
for some
![]() $f\in F_c(x,e\leadsto f^1\leadsto f^2)$
as the colors used around vertices that lie only on the path
$f\in F_c(x,e\leadsto f^1\leadsto f^2)$
as the colors used around vertices that lie only on the path
![]() $P_c(z_2,\alpha _2/\beta _2)_{i(f^2)-1}$
do not change. Now, the definition of
$P_c(z_2,\alpha _2/\beta _2)_{i(f^2)-1}$
do not change. Now, the definition of
![]() $F_c(x,e\leadsto f^1\leadsto f^2)$
, as the maximal
$F_c(x,e\leadsto f^1\leadsto f^2)$
, as the maximal
![]() $\alpha _2/\beta _2$
-conditional fan starting at
$\alpha _2/\beta _2$
-conditional fan starting at
![]() $f^2$
, shows that no such
$f^2$
, shows that no such
![]() $v\in V$
can exist, the argument is literally the same as in [Reference Grebík and PikhurkoGP20, Proposition 2.12].
$v\in V$
can exist, the argument is literally the same as in [Reference Grebík and PikhurkoGP20, Proposition 2.12].
Suppose that
![]() $f^2$
is
$f^2$
is
![]() $2$
-suitable and set
$2$
-suitable and set
![]() $P^2_c=P_c(z_2,\alpha _2/\beta _2)_{i(f^2)-1}$
. Next, we define various types of
$P^2_c=P_c(z_2,\alpha _2/\beta _2)_{i(f^2)-1}$
. Next, we define various types of
![]() $2$
-suitable edges and the notion of an amazing edge. This is inspired by similar notions in [Reference Grebík and PikhurkoGP20, Section 2.5].
$2$
-suitable edges and the notion of an amazing edge. This is inspired by similar notions in [Reference Grebík and PikhurkoGP20, Section 2.5].
We say that a
![]() $2$
-suitable edge
$2$
-suitable edge
![]() $f^2\in P_c(z_2,\alpha _2/\beta _2)$
is of type (a) if
$f^2\in P_c(z_2,\alpha _2/\beta _2)$
is of type (a) if
is c-augmenting. Every edge of type (a) is said to be amazing. Define
![]() $F^3_c=F_c(x,e\leadsto f^1\leadsto f^2)$
, and set
$F^3_c=F_c(x,e\leadsto f^1\leadsto f^2)$
, and set
Then the following is immediate from the definitions.
Proposition 3.7. Let
![]() $f^2$
be of type (a). Then
$f^2$
be of type (a). Then
![]() $W_c(e,f^1,f^2)$
is a
$W_c(e,f^1,f^2)$
is a
![]() $3$
-step Vizing chain.
$3$
-step Vizing chain.
We say that a
![]() $2$
-suitable edge
$2$
-suitable edge
![]() $f^2\in P_c(z_2,\alpha _2/\beta _2)$
is of type (b) if it is not of type (a) and in the construction of the conditional fan
$f^2\in P_c(z_2,\alpha _2/\beta _2)$
is of type (b) if it is not of type (a) and in the construction of the conditional fan
![]() $F_c(x,e\leadsto f^1\leadsto f^2)$
we encountered
$F_c(x,e\leadsto f^1\leadsto f^2)$
we encountered
![]() $\alpha _2$
or
$\alpha _2$
or
![]() $\beta _2$
. Observe that as
$\beta _2$
. Observe that as
![]() $f^2$
is not of type (a), we must have
$f^2$
is not of type (a), we must have
![]() $\beta _2\in m_c(w_n)$
, where
$\beta _2\in m_c(w_n)$
, where
![]() $\{y_3,w_n\}$
is the last edge in
$\{y_3,w_n\}$
is the last edge in
![]() $F_c(x,e\leadsto f^1\leadsto f^2)$
. Following the previous notation, we say that n is the third critical index. Define
$F_c(x,e\leadsto f^1\leadsto f^2)$
. Following the previous notation, we say that n is the third critical index. Define
![]() $F^3_c=F_c(x,e\leadsto f^1\leadsto f^2)$
,
$F^3_c=F_c(x,e\leadsto f^1\leadsto f^2)$
,
![]() $y_3=w_n$
,
$y_3=w_n$
,
![]() $\alpha _3=\alpha _2$
,
$\alpha _3=\alpha _2$
,
![]() $\beta _3=\beta _2$
and
$\beta _3=\beta _2$
and
![]() $P^3_c=P_c(z_3,\alpha _3/\beta _3)$
. We say that
$P^3_c=P_c(z_3,\alpha _3/\beta _3)$
. We say that
![]() $f^2$
of type (b) is amazing, if
$f^2$
of type (b) is amazing, if
-
○
 $P_{c_{Q}}(z_3,\alpha _3/\beta _3)=P_c(z_3,\alpha _3/\beta _3)$
, where
$P_{c_{Q}}(z_3,\alpha _3/\beta _3)=P_c(z_3,\alpha _3/\beta _3)$
, where
 $Q=(F^1_c)^\frown (P^1_c)^\frown (F^2_c)^\frown (P^2_c)^\frown (F^3_c)$
.
$Q=(F^1_c)^\frown (P^1_c)^\frown (F^2_c)^\frown (P^2_c)^\frown (F^3_c)$
.
Proposition 3.8. Let
![]() $f^2$
be of type (b) and amazing. Then
$f^2$
be of type (b) and amazing. Then
is a
![]() $3$
-step Vizing chain.
$3$
-step Vizing chain.
Proof. It follows directly from the definitions that
![]() $W_c(e,f^1,f^2)$
satisfies (1)–(3) in Definition 3.2. It remains to show that
$W_c(e,f^1,f^2)$
satisfies (1)–(3) in Definition 3.2. It remains to show that
![]() $W_c(e,f^1,f^2)$
is c-augmenting. This can be done by the same argument as in [Reference Grebík and PikhurkoGP20, Proposition 2.15]. Namely, first observe that
$W_c(e,f^1,f^2)$
is c-augmenting. This can be done by the same argument as in [Reference Grebík and PikhurkoGP20, Proposition 2.15]. Namely, first observe that
![]() $c_Q$
, where
$c_Q$
, where
is a proper coloring by the same reasoning as in Proposition 3.6. Moreover, by the definition of
![]() $2$
-suitable edge, we must have
$2$
-suitable edge, we must have
![]() $\alpha _2\in m_{c_{Q}}(y_3)$
. As
$\alpha _2\in m_{c_{Q}}(y_3)$
. As
![]() $P_{c_{Q}}(z_3,\alpha _3/\beta _3)=P_c(z_3,\alpha _3/\beta _3)$
, we have that
$P_{c_{Q}}(z_3,\alpha _3/\beta _3)=P_c(z_3,\alpha _3/\beta _3)$
, we have that
![]() $W_c(e,f^1,f^2)$
is edge injective and
$W_c(e,f^1,f^2)$
is edge injective and
![]() $\beta _2\in m_{c_{Q}(z_3)}$
. This shows that
$\beta _2\in m_{c_{Q}(z_3)}$
. This shows that
![]() $\{y_3,z_3\}^\frown P^3_c$
is
$\{y_3,z_3\}^\frown P^3_c$
is
![]() $c_Q$
-augmenting as
$c_Q$
-augmenting as
![]() $y_3$
cannot be the last vertex of
$y_3$
cannot be the last vertex of
![]() $P^3_c$
(if it were, then
$P^3_c$
(if it were, then
![]() $P_{c_{Q}}(z_3,\alpha _3/\beta _3)\not =P_c(z_3,\alpha _3/\beta _3)$
as
$P_{c_{Q}}(z_3,\alpha _3/\beta _3)\not =P_c(z_3,\alpha _3/\beta _3)$
as
![]() $\alpha _2,\beta _2\not \in m_c(y_3)$
). Hence,
$\alpha _2,\beta _2\not \in m_c(y_3)$
). Hence,
![]() $W_c(e,f^1,f^2)$
is c-augmenting as desired.
$W_c(e,f^1,f^2)$
is c-augmenting as desired.
We say that a
![]() $2$
-suitable edge
$2$
-suitable edge
![]() $f^2\in P_c(z_2,\alpha _2/\beta _2)$
is of type (c) if it is not of type (a), or (b). Let
$f^2\in P_c(z_2,\alpha _2/\beta _2)$
is of type (c) if it is not of type (a), or (b). Let
![]() $\gamma $
be the smallest color in
$\gamma $
be the smallest color in
![]() $m_c(y_3)$
. The reason why we cannot extend
$m_c(y_3)$
. The reason why we cannot extend
![]() $F_c(x,e\leadsto f^1\leadsto f^2)$
is the same as when we build the standard Vizing chain; see [Reference Grebík and PikhurkoGP20, Proposition 2.8], or [Reference Grebík and PikhurkoGP20, Section2.5: Type II edge]. Namely, there is a color
$F_c(x,e\leadsto f^1\leadsto f^2)$
is the same as when we build the standard Vizing chain; see [Reference Grebík and PikhurkoGP20, Proposition 2.8], or [Reference Grebík and PikhurkoGP20, Section2.5: Type II edge]. Namely, there is a color
![]() $\delta $
and index
$\delta $
and index
such that
![]() $\delta $
is the minimal color available in both
$\delta $
is the minimal color available in both
![]() $m_c(w_j)$
and
$m_c(w_j)$
and
![]() $m_c(w_n)$
. It is clear that
$m_c(w_n)$
. It is clear that
![]() $\gamma \not =\delta $
because
$\gamma \not =\delta $
because
![]() $f^2$
is not of Type (a) and
$f^2$
is not of Type (a) and
![]() $\{\alpha _2,\beta _2\}\cap \{\gamma ,\delta \}=\emptyset $
because f is not of Type (b).
$\{\alpha _2,\beta _2\}\cap \{\gamma ,\delta \}=\emptyset $
because f is not of Type (b).
Consider now the alternating
![]() $\gamma /\delta $
-paths
$\gamma /\delta $
-paths
![]() $P_c(w_j,\gamma /\delta )$
and
$P_c(w_j,\gamma /\delta )$
and
![]() $P_c(w_n,\gamma /\delta )$
. Our aim is to choose one of them, call it Q, and then define
$P_c(w_n,\gamma /\delta )$
. Our aim is to choose one of them, call it Q, and then define
where
![]() $\ell \in \{i,m\}$
, depending on the choice of Q, is such that
$\ell \in \{i,m\}$
, depending on the choice of Q, is such that
![]() $W_c(x,f^1,f^2)$
is c-augmenting. As in the case of type (b), we need to rule out some edges. We say that a
$W_c(x,f^1,f^2)$
is c-augmenting. As in the case of type (b), we need to rule out some edges. We say that a
![]() $2$
-suitable
$2$
-suitable
![]() $f^2\in P_c(z_2,\alpha _2/\beta _2)$
of type (c) is amazing if, in the above notation, both of the following equalities hold
$f^2\in P_c(z_2,\alpha _2/\beta _2)$
of type (c) is amazing if, in the above notation, both of the following equalities hold
-
○
 $P_c(w_j,\gamma /\delta )=P_{c_R}(w_j,\gamma /\delta )$
,
$P_c(w_j,\gamma /\delta )=P_{c_R}(w_j,\gamma /\delta )$
, -
○
 $P_c(w_n,\gamma /\delta )=P_{c_R}(w_j,\gamma /\delta )$
,
$P_c(w_n,\gamma /\delta )=P_{c_R}(w_j,\gamma /\delta )$
,
where
![]() $R=(F^1_c)^\frown (P^1_c)^\frown (F^2_c)^\frown (P^2_c)$
.
$R=(F^1_c)^\frown (P^1_c)^\frown (F^2_c)^\frown (P^2_c)$
.
Let
![]() $f^2\in P_c(z_2,\alpha _2/\beta _2)$
be of type (c) and amazing. We take
$f^2\in P_c(z_2,\alpha _2/\beta _2)$
be of type (c) and amazing. We take
![]() $\ell \in \{j,n\}$
to be the index for which there is no
$\ell \in \{j,n\}$
to be the index for which there is no
![]() $h\in P_c(u_j,\delta /\epsilon )$
such that
$h\in P_c(u_j,\delta /\epsilon )$
such that
![]() $y_3\in h$
; see [Reference Grebík and PikhurkoGP20, Proposition 2.9]. If both indices j and n satisfy this, then we put
$y_3\in h$
; see [Reference Grebík and PikhurkoGP20, Proposition 2.9]. If both indices j and n satisfy this, then we put
![]() $\ell =j$
for definiteness. We call this index
$\ell =j$
for definiteness. We call this index
![]() $\ell $
the third critical index. We define
$\ell $
the third critical index. We define
![]() $F^3_c=F_c(x,e\leadsto f^1\leadsto f^2)_{\ell +1}$
,
$F^3_c=F_c(x,e\leadsto f^1\leadsto f^2)_{\ell +1}$
,
![]() $z_3=w_\ell $
,
$z_3=w_\ell $
,
![]() $\alpha _3=\gamma $
,
$\alpha _3=\gamma $
,
![]() $\beta _3=\delta $
and
$\beta _3=\delta $
and
![]() $P^3_c=P_c(w_\ell ,\alpha _3/\beta _3)$
.
$P^3_c=P_c(w_\ell ,\alpha _3/\beta _3)$
.
Proposition 3.9. Let
![]() $f^2$
be of type (c) and amazing. Then
$f^2$
be of type (c) and amazing. Then
is a
![]() $3$
-step Vizing chain.
$3$
-step Vizing chain.
Proof. It follows directly from the definitions that
![]() $W_c(e,f^1,f^2)$
satisfies (1)–(3) in Definition 3.2. It remains to show that
$W_c(e,f^1,f^2)$
satisfies (1)–(3) in Definition 3.2. It remains to show that
![]() $W_c(e,f^1,f^2)$
is c-augmenting. This can be done by the same argument as in [Reference Grebík and PikhurkoGP20, Proposition 2.17]. Namely, first observe that
$W_c(e,f^1,f^2)$
is c-augmenting. This can be done by the same argument as in [Reference Grebík and PikhurkoGP20, Proposition 2.17]. Namely, first observe that
![]() $c_Q$
, where
$c_Q$
, where
is c-proper shiftable by the same reasoning as in Proposition 3.6. In particular, Q is edge injective. As
![]() ${y_3\not \in f}$
for any
${y_3\not \in f}$
for any
![]() $f\in P^3_c$
by the definition of the third critical index and
$f\in P^3_c$
by the definition of the third critical index and
![]() $P_{c_{R}}(z_3,\alpha _3/\beta _3)=P_c(z_3,\alpha _3/\beta _3)$
, we infer that
$P_{c_{R}}(z_3,\alpha _3/\beta _3)=P_c(z_3,\alpha _3/\beta _3)$
, we infer that
![]() $W_c(e,f^1,f^2)$
is edge injective. Similar argument shows that
$W_c(e,f^1,f^2)$
is edge injective. Similar argument shows that
![]() $P_{c_{Q}}(z_3,\alpha _3/\beta _3)=P_{c_{R}}(z_3,\alpha _3/\beta _3)=P_c(z_3,\alpha _3/\beta _3)$
. Moreover, by the definition of
$P_{c_{Q}}(z_3,\alpha _3/\beta _3)=P_{c_{R}}(z_3,\alpha _3/\beta _3)=P_c(z_3,\alpha _3/\beta _3)$
. Moreover, by the definition of
![]() $2$
-suitable edge, we must have
$2$
-suitable edge, we must have
![]() $\alpha _3\in m_{c_{Q}}(y_3)$
. This shows that
$\alpha _3\in m_{c_{Q}}(y_3)$
. This shows that
![]() $\{y_3,z_3\}^\frown P^3_c$
is
$\{y_3,z_3\}^\frown P^3_c$
is
![]() $c_Q$
-augmenting. Hence,
$c_Q$
-augmenting. Hence,
![]() $W_c(e,f^1,f^2)$
is c-augmenting as desired.
$W_c(e,f^1,f^2)$
is c-augmenting as desired.
Altogether, we just proved the following statement.
Theorem 3.10. Let
![]() $e\in U_c$
,
$e\in U_c$
,
![]() $x\in e$
,
$x\in e$
,
![]() $f^1$
be superb and
$f^1$
be superb and
![]() $f^2$
be amazing as defined above. Then
$f^2$
be amazing as defined above. Then
![]() $W_c(e,f^1,f^2)$
is a
$W_c(e,f^1,f^2)$
is a
![]() $3$
-step Vizing chain.
$3$
-step Vizing chain.
3.3 How many
 $3$
-step Vizing chains are there
$3$
-step Vizing chains are there
Let
![]() $e\in U_c$
and
$e\in U_c$
and
![]() $x\in e$
. We say that e is K-bad for c, where
$x\in e$
. We say that e is K-bad for c, where
![]() $K\in \mathbb {N}$
, if every
$K\in \mathbb {N}$
, if every
![]() $3$
-step Vizing chain
$3$
-step Vizing chain
![]() $W_c(e)$
at e satisfies
$W_c(e)$
at e satisfies
![]() $l(W_c(e)))\ge 2K+2\Delta $
. In the following claims, we use the notation from previous section.
$l(W_c(e)))\ge 2K+2\Delta $
. In the following claims, we use the notation from previous section.
Proposition 3.11. Let
![]() $K\in \mathbb {N}$
,
$K\in \mathbb {N}$
,
![]() $e\in U_c$
be K-bad for c and
$e\in U_c$
be K-bad for c and
![]() $x\in e$
. Then
$x\in e$
. Then
-
○
 $l(P_c(v_i,\alpha /\beta ))\ge K$
, where
$l(P_c(v_i,\alpha /\beta ))\ge K$
, where
 $P_c(v_i,\alpha /\beta )$
is the alternating path from the first iteration,
$P_c(v_i,\alpha /\beta )$
is the alternating path from the first iteration, -
○
 $l(P_c(u_m,\gamma /\delta ))\ge \frac {K}{2}$
for every superb edge
$l(P_c(u_m,\gamma /\delta ))\ge \frac {K}{2}$
for every superb edge
 $f^1$
such that
$f^1$
such that
 $i(f^1)\le \frac {K}{2}$
, where
$i(f^1)\le \frac {K}{2}$
, where
 $P_c(u_m,\gamma /\delta )$
is the alternating path in the second iteration that corresponds to
$P_c(u_m,\gamma /\delta )$
is the alternating path in the second iteration that corresponds to
 $f^1$
.
$f^1$
.
Proof. Both chains from Claim 3.3 and Claim 3.5 are
![]() $3$
-step Vizing chains. As e is K-bad for c and both chains contain at most two fans that each contain at most
$3$
-step Vizing chains. As e is K-bad for c and both chains contain at most two fans that each contain at most
![]() $\Delta $
edges, we conclude that
$\Delta $
edges, we conclude that
![]() $l(P_c(v_i,\alpha /\beta ))\ge K$
and
$l(P_c(v_i,\alpha /\beta ))\ge K$
and
![]() $l(P_c(u_m,\gamma /\delta ))\ge \frac {K}{2}$
under the assumption that
$l(P_c(u_m,\gamma /\delta ))\ge \frac {K}{2}$
under the assumption that
![]() $f^1$
is superb and satisfies
$f^1$
is superb and satisfies
![]() $i(f^1)\le \frac {K}{2}$
.
$i(f^1)\le \frac {K}{2}$
.
Claim 3.12 (Proposition 2.20 in [Reference Grebík and PikhurkoGP20]).
Let
![]() $K\in \mathbb {N}$
,
$K\in \mathbb {N}$
,
![]() $e\in U_c$
be K-bad for c and
$e\in U_c$
be K-bad for c and
![]() $x\in e$
. Then there are colors
$x\in e$
. Then there are colors
![]() $\{\gamma ,\delta \}\subseteq [\Delta +1]$
and at least
$\{\gamma ,\delta \}\subseteq [\Delta +1]$
and at least
 $$ \begin{align*}\frac{1}{3(\Delta+1)^2}\left(\frac{K}{4}-\Delta^5-1\right)-2\Delta^3\end{align*} $$
$$ \begin{align*}\frac{1}{3(\Delta+1)^2}\left(\frac{K}{4}-\Delta^5-1\right)-2\Delta^3\end{align*} $$
many superb edges
![]() $f^1\in P_c(v_i,\alpha /\beta )$
such that
$f^1\in P_c(v_i,\alpha /\beta )$
such that
![]() $i(f^1)\le \frac {K}{2}$
and the alternating path in the second iteration that corresponds to
$i(f^1)\le \frac {K}{2}$
and the alternating path in the second iteration that corresponds to
![]() $f^1$
is a
$f^1$
is a
![]() $\gamma /\delta $
-path.
$\gamma /\delta $
-path.
Definition 3.13. Let
![]() $K\in \mathbb {N}$
,
$K\in \mathbb {N}$
,
![]() $e\in U_c$
be K-bad for c,
$e\in U_c$
be K-bad for c,
![]() $x\in e$
and
$x\in e$
and
![]() $\{\gamma ,\delta \}\subseteq [\Delta +1]$
be as in Claim 3.12. Define
$\{\gamma ,\delta \}\subseteq [\Delta +1]$
be as in Claim 3.12. Define
![]() $\mathcal {V}_c(e)$
to be the set of pairs
$\mathcal {V}_c(e)$
to be the set of pairs
![]() $(f^1,f^2)$
such that
$(f^1,f^2)$
such that
![]() $f^1\in P_c(v_i,\alpha /\beta )$
is superb and satisfies
$f^1\in P_c(v_i,\alpha /\beta )$
is superb and satisfies
![]() $i(f^1)\le \frac {K}{2}$
and
$i(f^1)\le \frac {K}{2}$
and
![]() $f^2\in P_c(u_m,\gamma /\delta )$
is amazing and satisfies
$f^2\in P_c(u_m,\gamma /\delta )$
is amazing and satisfies
![]() $i(f^2)\le \frac {K}{2}$
(where the index
$i(f^2)\le \frac {K}{2}$
(where the index
![]() $i(f^2)$
is taken with respect to
$i(f^2)$
is taken with respect to
![]() $P_c(u_m,\gamma /\delta )$
), where
$P_c(u_m,\gamma /\delta )$
), where
![]() $P_c(u_m,\gamma /\delta )$
is the alternating path in the second iteration that corresponds to
$P_c(u_m,\gamma /\delta )$
is the alternating path in the second iteration that corresponds to
![]() $f^1$
.
$f^1$
.
Our aim is to estimate the cardinality of
![]() $\mathcal {V}_c(e)$
as this gives a lower bound on the cardinality of the set of all
$\mathcal {V}_c(e)$
as this gives a lower bound on the cardinality of the set of all
![]() $3$
-step Vizing chains at e. In fact, we bound the cardinality of the projection of
$3$
-step Vizing chains at e. In fact, we bound the cardinality of the projection of
![]() $\mathcal {V}_c(e)$
to the second coordinate as this clearly gives a lower bound for the cardinality of
$\mathcal {V}_c(e)$
to the second coordinate as this clearly gives a lower bound for the cardinality of
![]() $\mathcal {V}_c(e)$
.
$\mathcal {V}_c(e)$
.
The following proposition gives a sufficient condition for an edge to be amazing.
Proposition 3.14. Let
![]() $K\in \mathbb {N}$
,
$K\in \mathbb {N}$
,
![]() $e\in U_c$
be K-bad for c,
$e\in U_c$
be K-bad for c,
![]() $x\in e$
and
$x\in e$
and
![]() $\{\gamma ,\delta \}\subseteq [\Delta +1]$
be as in Claim 3.12. Suppose that
$\{\gamma ,\delta \}\subseteq [\Delta +1]$
be as in Claim 3.12. Suppose that
![]() $f^1\in P_c(v_i,\alpha /\beta )$
is superb,
$f^1\in P_c(v_i,\alpha /\beta )$
is superb,
![]() $i(f^1)\le \frac {K}{2}$
, and pick
$i(f^1)\le \frac {K}{2}$
, and pick
![]() $f^2$
on the the alternating path
$f^2$
on the the alternating path
![]() $P_c(u_m,\gamma /\delta )$
(that corresponds to
$P_c(u_m,\gamma /\delta )$
(that corresponds to
![]() $f^1$
in the second iteration). Assume that
$f^1$
in the second iteration). Assume that
-
1.
 $f^2 $
is
$f^2 $
is
 $2$
-suitable,
$2$
-suitable, -
2. there is no alternating path
 $P_c(w,\iota /\kappa )$
such that, simultaneously,
$P_c(w,\iota /\kappa )$
such that, simultaneously,
 $w\in V$
is of
$w\in V$
is of
 $\mathcal {G}$
-distance
$\mathcal {G}$
-distance
 $1$
from
$1$
from
 $y_3\in f^2$
and
$y_3\in f^2$
and
 $P_c(w,\iota /\kappa )$
is of distance at most
$P_c(w,\iota /\kappa )$
is of distance at most
 $3$
from
$3$
from
 $(F^1_c)^\frown (P^1_c)^\frown (F^2_c)$
, where
$(F^1_c)^\frown (P^1_c)^\frown (F^2_c)$
, where
 $f^1$
is the first edge of
$f^1$
is the first edge of
 $F^2_c$
.
$F^2_c$
.
Then
![]() $f^2$
is amazing. In particular,
$f^2$
is amazing. In particular,
![]() $(f^1,f^2)\in \mathcal {V}_c(e)$
.
$(f^1,f^2)\in \mathcal {V}_c(e)$
.
Proof. Suppose that the conditions are satisfied. If
![]() $f^2$
is of type (a), then it is amazing.
$f^2$
is of type (a), then it is amazing.
If
![]() $f^2$
is of type (b), then we need to verify that
$f^2$
is of type (b), then we need to verify that
![]() $P_{c_{Q}}(z_3,\alpha _3/\beta _3)=P_c(z_3,\alpha _3/\beta _3)$
, where
$P_{c_{Q}}(z_3,\alpha _3/\beta _3)=P_c(z_3,\alpha _3/\beta _3)$
, where
![]() $Q=(F^1_c)^\frown (P^1_c)^\frown (F^2_c)^\frown (P^2_c)^\frown (F^3_c)$
. As
$Q=(F^1_c)^\frown (P^1_c)^\frown (F^2_c)^\frown (P^2_c)^\frown (F^3_c)$
. As
![]() $\operatorname {dist}_{\mathcal {G}}(y_3,z_3)=1$
, we have that
$\operatorname {dist}_{\mathcal {G}}(y_3,z_3)=1$
, we have that
![]() $P_c(z_3,\alpha _3/\beta _3)$
avoids
$P_c(z_3,\alpha _3/\beta _3)$
avoids
![]() $(F^1_c)^\frown (P^1_c)^\frown (F^2_c)$
. Hence, if
$(F^1_c)^\frown (P^1_c)^\frown (F^2_c)$
. Hence, if
![]() $P_{c_{Q}}(z_3,\alpha _3/\beta _3)\not =P_c(z_3,\alpha _3/\beta _3)$
it must be the case that
$P_{c_{Q}}(z_3,\alpha _3/\beta _3)\not =P_c(z_3,\alpha _3/\beta _3)$
it must be the case that
![]() $y_3$
is covered by
$y_3$
is covered by
![]() $P_c(z_3,\alpha _3/\beta _3)$
. This can only happen if
$P_c(z_3,\alpha _3/\beta _3)$
. This can only happen if
![]() $P_c(z_3,\alpha _3/\beta _3)$
contains
$P_c(z_3,\alpha _3/\beta _3)$
contains
![]() $P^2_c$
as
$P^2_c$
as
![]() $\alpha _3=\alpha _2$
and
$\alpha _3=\alpha _2$
and
![]() $\beta _3=\beta _2$
. But that is not possible as
$\beta _3=\beta _2$
. But that is not possible as
![]() $P^2_c$
is of distance
$P^2_c$
is of distance
![]() $1$
from
$1$
from
![]() $(F^1_c)^\frown (P^1_c)^\frown (F^2_c)$
.
$(F^1_c)^\frown (P^1_c)^\frown (F^2_c)$
.
If
![]() $f^2$
is of type (c), then we need to verify that
$f^2$
is of type (c), then we need to verify that
![]() $P_c(w_j,\gamma /\delta )=P_{c_R}(w_j,\gamma /\delta )$
and
$P_c(w_j,\gamma /\delta )=P_{c_R}(w_j,\gamma /\delta )$
and
![]() $P_c(w_n,\gamma /\delta )=P_{c_R}(w_j,\gamma /\delta )$
. This follows easily as
$P_c(w_n,\gamma /\delta )=P_{c_R}(w_j,\gamma /\delta )$
. This follows easily as
![]() $\{\gamma ,\delta \}\cap \{\alpha _2,\beta _2\}=\emptyset $
and both
$\{\gamma ,\delta \}\cap \{\alpha _2,\beta _2\}=\emptyset $
and both
![]() $P_c(w_j,\gamma /\delta )$
,
$P_c(w_j,\gamma /\delta )$
,
![]() $P_c(w_n,\gamma /\delta )$
avoid
$P_c(w_n,\gamma /\delta )$
avoid
![]() $(F^1_c)^\frown (P^1_c)^\frown (F^2_c)$
.
$(F^1_c)^\frown (P^1_c)^\frown (F^2_c)$
.
Proposition 3.15. Let
![]() $K\in \mathbb {N}$
,
$K\in \mathbb {N}$
,
![]() $e\in U_c$
be K-bad for c,
$e\in U_c$
be K-bad for c,
![]() $x\in e$
and
$x\in e$
and
![]() $\{\gamma ,\delta \}\subseteq [\Delta +1]$
be as in Claim 3.12. Define
$\{\gamma ,\delta \}\subseteq [\Delta +1]$
be as in Claim 3.12. Define
![]() $f^2\in \mathcal {S}_c(e)$
if
$f^2\in \mathcal {S}_c(e)$
if
![]() $c(f^2)=\gamma $
, and there is
$c(f^2)=\gamma $
, and there is
![]() $f^1\in P_c(v_i,\alpha /\beta )$
such that
$f^1\in P_c(v_i,\alpha /\beta )$
such that
![]() $f^1$
is superb,
$f^1$
is superb,
![]() $i(f^1)\le \frac {K}{2}$
,
$i(f^1)\le \frac {K}{2}$
,
![]() $f^2 \in P_c(u_m,\gamma /\delta )$
and
$f^2 \in P_c(u_m,\gamma /\delta )$
and
![]() $i(f^2)\le \frac {K}{2}$
(the index is taken with respect to
$i(f^2)\le \frac {K}{2}$
(the index is taken with respect to
![]() $P_c(u_m,\gamma /\delta )$
and
$P_c(u_m,\gamma /\delta )$
and
![]() $P_c(u_m,\gamma /\delta )$
corresponds to
$P_c(u_m,\gamma /\delta )$
corresponds to
![]() $f^1$
in the second iteration), and at least one of the items from Proposition 3.14 is not satisfied. Then we have
$f^1$
in the second iteration), and at least one of the items from Proposition 3.14 is not satisfied. Then we have
 $$ \begin{align*}|\mathcal{S}_c(e)|\le 4(\Delta+1)^4\sum_{r=0}^4 (2\Delta)^r\left(\frac{K}{2}+\Delta\right).\end{align*} $$
$$ \begin{align*}|\mathcal{S}_c(e)|\le 4(\Delta+1)^4\sum_{r=0}^4 (2\Delta)^r\left(\frac{K}{2}+\Delta\right).\end{align*} $$
Proof. Let
![]() $f^1$
and
$f^1$
and
![]() $f^2$
are as above and assume that item (1) from Proposition 3.14 is not satisfied. As
$f^2$
are as above and assume that item (1) from Proposition 3.14 is not satisfied. As
![]() $c(f^2)=\gamma $
, we know that either
$c(f^2)=\gamma $
, we know that either
![]() $f^2$
is the last edge on
$f^2$
is the last edge on
![]() $P_c(u_m,\gamma /\delta )$
or it is of distance at most
$P_c(u_m,\gamma /\delta )$
or it is of distance at most
![]() $4$
from
$4$
from
![]() $(F^1_c)^\frown P_c(v_i,\alpha /\beta )_{\frac {K}{2}+1}$
. There are at most
$(F^1_c)^\frown P_c(v_i,\alpha /\beta )_{\frac {K}{2}+1}$
. There are at most
![]() $\frac {K}{2}$
many edges that satisfy the former condition, and we have
$\frac {K}{2}$
many edges that satisfy the former condition, and we have
 $$ \begin{align} \left|\left\{f\in E:\operatorname{dist}_{\mathcal{E}}(f,(F^1_c)^\frown P_c(v_i,\alpha/\beta)_{\frac{K}{2}+1})\le 4\right\}\right|\le\sum_{r=0}^4 (2\Delta)^r\left(\frac{K}{2}+\Delta\right) \end{align} $$
$$ \begin{align} \left|\left\{f\in E:\operatorname{dist}_{\mathcal{E}}(f,(F^1_c)^\frown P_c(v_i,\alpha/\beta)_{\frac{K}{2}+1})\le 4\right\}\right|\le\sum_{r=0}^4 (2\Delta)^r\left(\frac{K}{2}+\Delta\right) \end{align} $$
which gives upper bound on the latter condition.
Suppose that (2) from Proposition 3.14 is not satisfied. That means that there is a path
![]() $P_c(w,\iota /\kappa )$
, where w is of distance one from
$P_c(w,\iota /\kappa )$
, where w is of distance one from
![]() $y_3$
, that intersect
$y_3$
, that intersect
Every edge from B is an element of
![]() $2(\Delta +1)^2$
many such paths. Together with Equation (3.1), we conclude that there are at most
$2(\Delta +1)^2$
many such paths. Together with Equation (3.1), we conclude that there are at most
 $$ \begin{align*}2(\Delta+1)^4\sum_{r=0}^4 (2\Delta)^r\left(\frac{K}{2}+\Delta\right)\end{align*} $$
$$ \begin{align*}2(\Delta+1)^4\sum_{r=0}^4 (2\Delta)^r\left(\frac{K}{2}+\Delta\right)\end{align*} $$
edges
![]() $f^2$
that do not satisfy (2) from Proposition 3.14.
$f^2$
that do not satisfy (2) from Proposition 3.14.
Summing these three bounds gives the desired estimate.
Proposition 3.16. Let
![]() $K\in \mathbb {N}$
,
$K\in \mathbb {N}$
,
![]() $e\in U_c$
be K-bad for c,
$e\in U_c$
be K-bad for c,
![]() $x\in e$
and
$x\in e$
and
![]() $\{\gamma ,\delta \}\subseteq [\Delta +1]$
be as in Claim 3.12. Define
$\{\gamma ,\delta \}\subseteq [\Delta +1]$
be as in Claim 3.12. Define
![]() $f^2\in \mathcal {T}_c(e)$
if
$f^2\in \mathcal {T}_c(e)$
if
![]() $c(f^2)=\gamma $
, and there is
$c(f^2)=\gamma $
, and there is
![]() $f^1\in P_c(v_i,\alpha /\beta )$
such that
$f^1\in P_c(v_i,\alpha /\beta )$
such that
![]() $f^1$
is superb,
$f^1$
is superb,
![]() $i(f^1)\le \frac {K}{2}$
,
$i(f^1)\le \frac {K}{2}$
,
![]() $f^2 \in P_c(u_m,\gamma /\delta )$
and
$f^2 \in P_c(u_m,\gamma /\delta )$
and
![]() $i(f^2)\le \frac {K}{2}$
(the index is taken with respect to
$i(f^2)\le \frac {K}{2}$
(the index is taken with respect to
![]() $P_c(u_m,\gamma /\delta )$
and
$P_c(u_m,\gamma /\delta )$
and
![]() $P_c(u_m,\gamma /\delta )$
corresponds to
$P_c(u_m,\gamma /\delta )$
corresponds to
![]() $f^1$
in the second iteration). Then we have
$f^1$
in the second iteration). Then we have
 $$ \begin{align*}|\mathcal{T}_c(e)|\ge \frac{K}{4\Delta^2} \left(\frac{1}{3(\Delta+1)^2}\left(\frac{K}{4}-\Delta^5-1\right)-2\Delta^3\right).\end{align*} $$
$$ \begin{align*}|\mathcal{T}_c(e)|\ge \frac{K}{4\Delta^2} \left(\frac{1}{3(\Delta+1)^2}\left(\frac{K}{4}-\Delta^5-1\right)-2\Delta^3\right).\end{align*} $$
Proof. By Claim 3.12, there is
![]() $\{\gamma ,\delta \}\subseteq [\Delta +1]$
and at least
$\{\gamma ,\delta \}\subseteq [\Delta +1]$
and at least
 $$ \begin{align*}\frac{1}{3(\Delta+1)^2}\left(\frac{K}{4}-\Delta^5-1\right)-2\Delta^3\end{align*} $$
$$ \begin{align*}\frac{1}{3(\Delta+1)^2}\left(\frac{K}{4}-\Delta^5-1\right)-2\Delta^3\end{align*} $$
many superb edges
![]() $f^1\in P_c(v_i,\alpha /\beta )$
such that
$f^1\in P_c(v_i,\alpha /\beta )$
such that
![]() $i(f^1)\le \frac {K}{2}$
and the alternating path in the second iteration that corresponds to
$i(f^1)\le \frac {K}{2}$
and the alternating path in the second iteration that corresponds to
![]() $f^1$
is a
$f^1$
is a
![]() $\gamma /\delta $
-path. For each such
$\gamma /\delta $
-path. For each such
![]() $f^1$
, there are at least
$f^1$
, there are at least
![]() $\frac {K}{4}$
edges of the corresponding
$\frac {K}{4}$
edges of the corresponding
![]() $P_c(u_m,\gamma /\delta )$
that have color
$P_c(u_m,\gamma /\delta )$
that have color
![]() $\gamma $
. This shows that there are at least
$\gamma $
. This shows that there are at least
 $$ \begin{align*}\frac{K}{4}\left(\frac{1}{3(\Delta+1)^2}\left(\frac{K}{4}-\Delta^5-1\right)-2\Delta^3\right)\end{align*} $$
$$ \begin{align*}\frac{K}{4}\left(\frac{1}{3(\Delta+1)^2}\left(\frac{K}{4}-\Delta^5-1\right)-2\Delta^3\right)\end{align*} $$
pairs
![]() $(f^1,f^2)$
that satisfy the conditions above. To estimate the size of
$(f^1,f^2)$
that satisfy the conditions above. To estimate the size of
![]() $\mathcal {T}_c(e)$
, we need to compute the number of pairs
$\mathcal {T}_c(e)$
, we need to compute the number of pairs
![]() $(f^1,f^2)$
to which a given edge
$(f^1,f^2)$
to which a given edge
![]() $f^2$
contributes.
$f^2$
contributes.
Every
![]() $f^2$
can reach
$f^2$
can reach
![]() $f_1$
by following the
$f_1$
by following the
![]() $\gamma /\delta $
path in one of its two directions, and then there are
$\gamma /\delta $
path in one of its two directions, and then there are
![]() $\Delta ^2$
many choices for
$\Delta ^2$
many choices for
![]() $f^1$
. Altogether,
$f^1$
. Altogether,
 $$ \begin{align*}|\mathcal{T}_c(e)|\ge\frac{K}{4\Delta^2} \left(\frac{1}{3(\Delta+1)^2}\left(\frac{K}{4}-\Delta^5-1\right)-2\Delta^3\right)\end{align*} $$
$$ \begin{align*}|\mathcal{T}_c(e)|\ge\frac{K}{4\Delta^2} \left(\frac{1}{3(\Delta+1)^2}\left(\frac{K}{4}-\Delta^5-1\right)-2\Delta^3\right)\end{align*} $$
as needed.
Finally, observe that the projection of
![]() $\mathcal {V}_c(e)$
to the second coordinate contains
$\mathcal {V}_c(e)$
to the second coordinate contains
![]() $\mathcal {T}_c(e)\setminus \mathcal {S}_c(e)$
by Proposition 3.14. Hence, the combination of Propositions 3.15 and 3.16, together with a trivial modification gives the main estimate.
$\mathcal {T}_c(e)\setminus \mathcal {S}_c(e)$
by Proposition 3.14. Hence, the combination of Propositions 3.15 and 3.16, together with a trivial modification gives the main estimate.
Theorem 3.17. Let
![]() $K\in \mathbb {N}$
,
$K\in \mathbb {N}$
,
![]() $e\in U_c$
be K-bad for c and
$e\in U_c$
be K-bad for c and
![]() $x\in e$
. Then we have
$x\in e$
. Then we have
 $$ \begin{align*}|\mathcal{V}_c(e)|\ge \frac{K^2}{(8\Delta)^4}-(16\Delta)^5K.\end{align*} $$
$$ \begin{align*}|\mathcal{V}_c(e)|\ge \frac{K^2}{(8\Delta)^4}-(16\Delta)^5K.\end{align*} $$
In particular, for every
![]() $e\in U_c$
that is K-bad and
$e\in U_c$
that is K-bad and
![]() $x\in e$
there are at least
$x\in e$
there are at least
![]() $\left (\frac {K^2}{(8\Delta )^4}-(16\Delta )^5K\right )$
many pairs
$\left (\frac {K^2}{(8\Delta )^4}-(16\Delta )^5K\right )$
many pairs
![]() $(f^1,f^2)$
such that
$(f^1,f^2)$
such that
![]() $W_c(e,f^1,f^2)$
is a
$W_c(e,f^1,f^2)$
is a
![]() $3$
-step Vizing chain.
$3$
-step Vizing chain.
4 Improving colorings
In this section, we describe one step of the algorithm that will, in Section 7, produce the desired
![]() $\Delta (\mathcal {G})+1$
edge coloring
$\Delta (\mathcal {G})+1$
edge coloring
![]() $\mu $
-almost everywhere. The step, and therefore the whole algorithm, can be run on any Borel graph
$\mu $
-almost everywhere. The step, and therefore the whole algorithm, can be run on any Borel graph
![]() $\mathcal {G}=(V,\mathcal {B},E)$
of degree bounded by
$\mathcal {G}=(V,\mathcal {B},E)$
of degree bounded by
![]() $\Delta (\mathcal {G})<\infty $
endowed with an
$\Delta (\mathcal {G})<\infty $
endowed with an
![]() $\mathcal {E}$
-quasi-invariant Borel probability measure
$\mathcal {E}$
-quasi-invariant Borel probability measure
![]() $\nu \in \mathcal {P}(E)$
, where
$\nu \in \mathcal {P}(E)$
, where
![]() $\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
is the corresponding line graph. However, in order to show that the algorithm terminates
$\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
is the corresponding line graph. However, in order to show that the algorithm terminates
![]() $\nu $
-almost everywhere, we need to assume additionally that
$\nu $
-almost everywhere, we need to assume additionally that
![]() $\nu $
is
$\nu $
is
![]() $\mathcal {G}$
-bounded; see Section 5.
$\mathcal {G}$
-bounded; see Section 5.
Fix
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\nu $
as above, and a Radon–Nikodym cocycle
$\nu $
as above, and a Radon–Nikodym cocycle
![]() $\rho _\nu $
of
$\rho _\nu $
of
![]() $\nu $
with respect to
$\nu $
with respect to
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
Definition 4.1. We say that a partial coloring
![]() $c;E\to [\Delta (\mathcal {G})+1]$
does not admit an improvement of weight
$c;E\to [\Delta (\mathcal {G})+1]$
does not admit an improvement of weight
![]() $L\in \mathbb {N}$
if
$L\in \mathbb {N}$
if
 $$ \begin{align*} \nu\left(\left\{e\in U_c: \exists \ 3\operatorname{-step \ Vizing \ chain} \ W_c(e) \ \operatorname{s. t.} \ \sum_{f\in W_c(e)} \rho_{\nu}(e,f)\le L\right\}\right)=0. \end{align*} $$
$$ \begin{align*} \nu\left(\left\{e\in U_c: \exists \ 3\operatorname{-step \ Vizing \ chain} \ W_c(e) \ \operatorname{s. t.} \ \sum_{f\in W_c(e)} \rho_{\nu}(e,f)\le L\right\}\right)=0. \end{align*} $$
If this condition is not satisfied, then we say that c admits an improvement of weight L.
Theorem 4.2. Let
![]() $c;E\to [\Delta (\mathcal {G})+1]$
be a partial coloring and
$c;E\to [\Delta (\mathcal {G})+1]$
be a partial coloring and
![]() $L\in \mathbb {N}$
. Then there is a partial coloring
$L\in \mathbb {N}$
. Then there is a partial coloring
![]() $c';E\to [\Delta (\mathcal {G})+1]$
that does not admit improvement of weight L with the property that
$c';E\to [\Delta (\mathcal {G})+1]$
that does not admit improvement of weight L with the property that
![]() $\nu (\operatorname {dom}(c)\setminus \operatorname {dom}(c'))=0$
and
$\nu (\operatorname {dom}(c)\setminus \operatorname {dom}(c'))=0$
and
where
![]() $c(e)\not = c'(e)$
also includes the situation when
$c(e)\not = c'(e)$
also includes the situation when
![]() $e\in \operatorname {dom}(c')\setminus \operatorname {dom}(c)$
.
$e\in \operatorname {dom}(c')\setminus \operatorname {dom}(c)$
.
Proof. The strategy of the proof follows closely [Reference Grebík and PikhurkoGP20, Proof of Proposition 5.4]. For a partial coloring
![]() $d;E\to [\Delta (\mathcal {G})+1]$
, define
$d;E\to [\Delta (\mathcal {G})+1]$
, define
![]() $A_d$
to be the set of those
$A_d$
to be the set of those
![]() $e\in U_d$
for which there exists a
$e\in U_d$
for which there exists a
![]() $3$
-step Vizing chain
$3$
-step Vizing chain
![]() $W_d(e)$
such that
$W_d(e)$
such that
 $$ \begin{align*}\sum_{f\in W_{d}(e)}\rho_\nu(e,f)\le L.\end{align*} $$
$$ \begin{align*}\sum_{f\in W_{d}(e)}\rho_\nu(e,f)\le L.\end{align*} $$
Clearly,
![]() $\nu (A_d)=0$
if and only if d does not admit improvement of weight L. Set
$\nu (A_d)=0$
if and only if d does not admit improvement of weight L. Set
![]() $c_0=c$
. We use induction to build a transfinite sequence of partial colorings
$c_0=c$
. We use induction to build a transfinite sequence of partial colorings
![]() $(c_{\alpha })_{\alpha <\aleph _1}$
that satisfy the following:
$(c_{\alpha })_{\alpha <\aleph _1}$
that satisfy the following:
-
1. for every
 $\alpha < \beta <\aleph _1$
, we have
$\alpha < \beta <\aleph _1$
, we have
 $\nu (\operatorname {dom}(c_\alpha )\setminus \operatorname {dom}(c_\beta ))=0$
,
$\nu (\operatorname {dom}(c_\alpha )\setminus \operatorname {dom}(c_\beta ))=0$
, -
2. for every
 $\alpha <\aleph _1$
, if
$\alpha <\aleph _1$
, if
 $\nu (A_{c_\alpha })\not = 0$
, then
$\nu (A_{c_\alpha })\not = 0$
, then
 $\nu (U_{c_{\alpha +1}})<\nu (U_{c_{\alpha }})$
,
$\nu (U_{c_{\alpha +1}})<\nu (U_{c_{\alpha }})$
, -
3. for every
 $\alpha <\beta <\aleph _1$
, if
$\alpha <\beta <\aleph _1$
, if
 $c_{\alpha }\not =c_{\beta }$
, then
$c_{\alpha }\not =c_{\beta }$
, then
 $\nu (U_{c_{\beta }})<\nu (U_{c_{\alpha }})$
,
$\nu (U_{c_{\beta }})<\nu (U_{c_{\alpha }})$
, -
4. if
 $c_{\alpha }=c_{\alpha +1}$
for some
$c_{\alpha }=c_{\alpha +1}$
for some
 $\alpha <\aleph _1$
, then
$\alpha <\aleph _1$
, then
 $c_{\alpha }=c_\beta $
for every
$c_{\alpha }=c_\beta $
for every
 $\alpha \le \beta <\aleph _1$
,
$\alpha \le \beta <\aleph _1$
, -
5. for every
 $\alpha < \beta <\aleph _1$
, where
$\alpha < \beta <\aleph _1$
, where $$ \begin{align*}\nu(\{e\in E:c_{\alpha}(e)\not=c_\beta(e)\})\le L\sum_{\alpha\le \alpha'<\beta}\nu(S_{\alpha'})=L\nu\left(\bigcup_{\alpha\le \alpha'<\beta} S_{\alpha'}\right)\le L\nu(U_c),\end{align*} $$
$$ \begin{align*}\nu(\{e\in E:c_{\alpha}(e)\not=c_\beta(e)\})\le L\sum_{\alpha\le \alpha'<\beta}\nu(S_{\alpha'})=L\nu\left(\bigcup_{\alpha\le \alpha'<\beta} S_{\alpha'}\right)\le L\nu(U_c),\end{align*} $$
 $S_{\alpha '}=U_{c_{\alpha '}}\setminus U_{c_{\alpha '+1}}$
.
$S_{\alpha '}=U_{c_{\alpha '}}\setminus U_{c_{\alpha '+1}}$
.
Once we build such a sequence, then we are done. Indeed, conditions (3) and (4) guarantee the existence of
![]() $\alpha <\aleph _1$
such that
$\alpha <\aleph _1$
such that
![]() $c_{\alpha }=c_{\beta }$
for every
$c_{\alpha }=c_{\beta }$
for every
![]() $\alpha \le \beta <\aleph _1$
as there are no strictly decreasing sequences of real numbers of length
$\alpha \le \beta <\aleph _1$
as there are no strictly decreasing sequences of real numbers of length
![]() $\aleph _1$
. Define
$\aleph _1$
. Define
![]() $c'=c_{\alpha _0}$
, where
$c'=c_{\alpha _0}$
, where
![]() $\alpha _0$
is the minimal ordinal with this property. Then (1) (with the choice
$\alpha _0$
is the minimal ordinal with this property. Then (1) (with the choice
![]() $0< \alpha _0$
) implies
$0< \alpha _0$
) implies
![]() $\nu (\operatorname {dom}(c)\setminus \operatorname {dom}(c'))=0$
, (2) implies that
$\nu (\operatorname {dom}(c)\setminus \operatorname {dom}(c'))=0$
, (2) implies that
![]() $c'=c_{\alpha _0}$
does not admit improvement of weight L and (5) (with the choice
$c'=c_{\alpha _0}$
does not admit improvement of weight L and (5) (with the choice
![]() $0< \alpha _0$
) implies that
$0< \alpha _0$
) implies that
![]() $\nu (\{e\in E:c(e)\not =c'(e)\})\le L\nu (U_c)$
.
$\nu (\{e\in E:c(e)\not =c'(e)\})\le L\nu (U_c)$
.
Successor stage
![]() $\mathbf {\alpha \mapsto \alpha +1}$
. Suppose that we have constructed a sequence of partial colorings
$\mathbf {\alpha \mapsto \alpha +1}$
. Suppose that we have constructed a sequence of partial colorings
![]() $(c_\beta )_{\beta \le \alpha }$
such that the property (1)–(5) hold for every (pair of) ordinal(s) less or equal than
$(c_\beta )_{\beta \le \alpha }$
such that the property (1)–(5) hold for every (pair of) ordinal(s) less or equal than
![]() $\alpha $
. If
$\alpha $
. If
![]() $\nu (A_{c_{\alpha }})=0$
, then setting
$\nu (A_{c_{\alpha }})=0$
, then setting
![]() $c_{\alpha +1}=c_{\alpha }$
clearly works. Suppose that
$c_{\alpha +1}=c_{\alpha }$
clearly works. Suppose that
![]() $\nu (A_{c_{\alpha }})>0$
, and pick any Borel assignemnt
$\nu (A_{c_{\alpha }})>0$
, and pick any Borel assignemnt
![]() $e\in A_{c_{\alpha }}\mapsto W_{c_{\alpha }}(e)$
with the property
$e\in A_{c_{\alpha }}\mapsto W_{c_{\alpha }}(e)$
with the property
![]() $W_{c_{\alpha }}(e)$
is a
$W_{c_{\alpha }}(e)$
is a
![]() $3$
-step Vizing chain and
$3$
-step Vizing chain and
![]() $\sum _{f\in W_c(e)}\rho _{\nu }(e,f)\le L$
for every
$\sum _{f\in W_c(e)}\rho _{\nu }(e,f)\le L$
for every
![]() $e\in A_{c_{\alpha }}$
.
$e\in A_{c_{\alpha }}$
.
Case I. There is
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
By [Reference Kechris, Solecki and TodorčevićKST99, Proposition 4.6] (applied on the
![]() $2k+2$
power graph of
$2k+2$
power graph of
![]() $\mathcal {E}$
that is of bounded degree), there is a set
$\mathcal {E}$
that is of bounded degree), there is a set
![]() $S_\alpha \subseteq A_{c_\alpha }$
with the property that
$S_\alpha \subseteq A_{c_\alpha }$
with the property that
-
(a)
 $\nu (S_\alpha )>0$
,
$\nu (S_\alpha )>0$
, -
(b)
 $e\not =e'\in S_\alpha $
are at least
$e\not =e'\in S_\alpha $
are at least
 $2k+2$
far apart in the graph distance of
$2k+2$
far apart in the graph distance of
 $\mathcal {E}$
,
$\mathcal {E}$
, -
(c)
 $|W_{c_{\alpha }}(e)|=k$
for every
$|W_{c_{\alpha }}(e)|=k$
for every
 $e\in S_{\alpha }$
.
$e\in S_{\alpha }$
.
Set
![]() $T_\alpha =\bigcup _{e\in S_\alpha }W_{c_{\alpha }}(e)$
, and observe that
$T_\alpha =\bigcup _{e\in S_\alpha }W_{c_{\alpha }}(e)$
, and observe that
 $$ \begin{align} \nu(T_\alpha)=\int_{e\in S_\alpha} \sum_{f\in W_{c_\alpha}(e)}\rho_{\nu} (e,f) \ d\nu \le L \nu(S_\alpha) \end{align} $$
$$ \begin{align} \nu(T_\alpha)=\int_{e\in S_\alpha} \sum_{f\in W_{c_\alpha}(e)}\rho_{\nu} (e,f) \ d\nu \le L \nu(S_\alpha) \end{align} $$
by item (2) in Proposition 2.2. As
![]() $\{W_{c_{\alpha }}(e)\}_{e\in S_\alpha }$
are pairwise of positive distance from each other by (b) and (c) and each
$\{W_{c_{\alpha }}(e)\}_{e\in S_\alpha }$
are pairwise of positive distance from each other by (b) and (c) and each
![]() $W_{c_{\alpha }}(e)$
is augmenting, there is a partial coloring
$W_{c_{\alpha }}(e)$
is augmenting, there is a partial coloring
![]() $c_{\alpha +1}$
with the property that
$c_{\alpha +1}$
with the property that
-
(i)
 $T_\alpha \subseteq \operatorname {dom}(c_{\alpha +1})$
,
$T_\alpha \subseteq \operatorname {dom}(c_{\alpha +1})$
, -
(ii)
 $c_\alpha \upharpoonright (\operatorname {dom} (c_{\alpha })\setminus T_\alpha )=c_{\alpha +1}\upharpoonright (\operatorname {dom} (c_{\alpha })\setminus T_\alpha )$
.
$c_\alpha \upharpoonright (\operatorname {dom} (c_{\alpha })\setminus T_\alpha )=c_{\alpha +1}\upharpoonright (\operatorname {dom} (c_{\alpha })\setminus T_\alpha )$
.
We claim that
![]() $c_{\alpha +1}$
works as required, namely, let
$c_{\alpha +1}$
works as required, namely, let
![]() $\alpha '<\alpha +1$
, then
$\alpha '<\alpha +1$
, then
-
1.
 $\nu (\operatorname {dom}(c_{\alpha '})\setminus \operatorname {dom}(c_{\alpha +1}))=0$
as
$\nu (\operatorname {dom}(c_{\alpha '})\setminus \operatorname {dom}(c_{\alpha +1}))=0$
as
 $\nu (\operatorname {dom}(c_{\alpha '})\setminus \operatorname {dom}(c_{\alpha }))=0$
and
$\nu (\operatorname {dom}(c_{\alpha '})\setminus \operatorname {dom}(c_{\alpha }))=0$
and
 $\operatorname {dom}(c_{\alpha +1})=\operatorname {dom}(c_{\alpha })\cup S_{\alpha }$
by (i) and (ii),
$\operatorname {dom}(c_{\alpha +1})=\operatorname {dom}(c_{\alpha })\cup S_{\alpha }$
by (i) and (ii), -
2. follows from
 $\operatorname {dom}(c_{\alpha +1})=\operatorname {dom}(c_{\alpha })\cup S_{\alpha }$
together with (a),
$\operatorname {dom}(c_{\alpha +1})=\operatorname {dom}(c_{\alpha })\cup S_{\alpha }$
together with (a), -
3. follows from (2) combined with inductive assumption (3),
-
4. if
 $c_{\alpha '}=c_{\alpha '+1}$
for some
$c_{\alpha '}=c_{\alpha '+1}$
for some
 ${\alpha '<\alpha }$
, then
${\alpha '<\alpha }$
, then
 $\nu (A_{c_{\alpha }})=0$
by the inductive assumption (4) and (2),
$\nu (A_{c_{\alpha }})=0$
by the inductive assumption (4) and (2), -
5. observe that
 $\nu \left (S_{\alpha }\cap S_{\beta }\right )=0$
for every
$\nu \left (S_{\alpha }\cap S_{\beta }\right )=0$
for every
 $\beta <\alpha $
by the inductive assumption (1); consequently, when combined with the inductive assumption (5) and (*), we have
$\beta <\alpha $
by the inductive assumption (1); consequently, when combined with the inductive assumption (5) and (*), we have  $$ \begin{align*} \nu(\{e\in E:c_{\alpha'}(e)\not=c_{\alpha+1}(e)\})\le & \ \nu(\{e\in E:c_{\alpha'}(e)\not=c_{\alpha}(e)\})\\ & \ +\nu(\{e\in E:c_{\alpha}(e)\not=c_{\alpha+1}(e)\})\\ \le & \ L\sum_{\alpha'\le \beta<\alpha}\nu(S_{\beta})+ \nu(T_{\alpha})\\ \le & \ L\sum_{\alpha'\le \beta<\alpha+1}\nu(S_{\beta})\\ = & \ L\nu\left(\bigcup_{\alpha'\le \beta<\alpha+1} S_{\alpha'}\right)\le L\nu(U_c). \end{align*} $$
$$ \begin{align*} \nu(\{e\in E:c_{\alpha'}(e)\not=c_{\alpha+1}(e)\})\le & \ \nu(\{e\in E:c_{\alpha'}(e)\not=c_{\alpha}(e)\})\\ & \ +\nu(\{e\in E:c_{\alpha}(e)\not=c_{\alpha+1}(e)\})\\ \le & \ L\sum_{\alpha'\le \beta<\alpha}\nu(S_{\beta})+ \nu(T_{\alpha})\\ \le & \ L\sum_{\alpha'\le \beta<\alpha+1}\nu(S_{\beta})\\ = & \ L\nu\left(\bigcup_{\alpha'\le \beta<\alpha+1} S_{\alpha'}\right)\le L\nu(U_c). \end{align*} $$
Case II. There is no
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
In another words,
![]() $\nu $
-almost every
$\nu $
-almost every
![]() $3$
-step Vizing chain is infinite. Observe that this can happen if and only if there is an assignment (defined for
$3$
-step Vizing chain is infinite. Observe that this can happen if and only if there is an assignment (defined for
![]() $\nu $
-almost every
$\nu $
-almost every
![]() $e\in A_{c_{\alpha }}$
)
$e\in A_{c_{\alpha }}$
)
![]() $e\in A_{c_\alpha }\mapsto (x_e,\alpha _e,\beta _e)$
, where
$e\in A_{c_\alpha }\mapsto (x_e,\alpha _e,\beta _e)$
, where
![]() $x_e\in V$
and
$x_e\in V$
and
![]() $\alpha _e,\beta _e\in [\Delta +1]$
such that
$\alpha _e,\beta _e\in [\Delta +1]$
such that
![]() $W_{c_{\alpha }}(e)=M(e)^\frown P_{c_{\alpha }}(x_e,\alpha _e/\beta _e)$
. Using finite additivity of
$W_{c_{\alpha }}(e)=M(e)^\frown P_{c_{\alpha }}(x_e,\alpha _e/\beta _e)$
. Using finite additivity of
![]() $\nu $
and [Reference Kechris, Solecki and TodorčevićKST99, Proposition 4.6], we find
$\nu $
and [Reference Kechris, Solecki and TodorčevićKST99, Proposition 4.6], we find
![]() $10<k\in \mathbb {N}$
,
$10<k\in \mathbb {N}$
,
![]() $\alpha ,\beta \in [\Delta +1]$
and
$\alpha ,\beta \in [\Delta +1]$
and
![]() $R_\alpha \subseteq A_{c_\alpha }$
such that
$R_\alpha \subseteq A_{c_\alpha }$
such that
-
(a)
 $\nu (R_\alpha )>0$
,
$\nu (R_\alpha )>0$
, -
(b)
 $|M(e)|=k$
,
$|M(e)|=k$
,
 $\alpha _e=\alpha $
and
$\alpha _e=\alpha $
and
 $\beta _e=\beta $
for every
$\beta _e=\beta $
for every
 $e\in R_\alpha $
,
$e\in R_\alpha $
, -
(c)
 $e\not =e'\in R_\alpha $
are at least
$e\not =e'\in R_\alpha $
are at least
 $5k$
far apart in the graph distance of
$5k$
far apart in the graph distance of
 $\mathcal {E}$
.
$\mathcal {E}$
.
Note that this implies that if
![]() $e\not = e'\in R_\alpha $
, then
$e\not = e'\in R_\alpha $
, then
-
○
 $x_e\not =x_{e'}$
and consequently
$x_e\not =x_{e'}$
and consequently
 $P_{c_{\alpha }}(x_e,\alpha /\beta )$
and
$P_{c_{\alpha }}(x_e,\alpha /\beta )$
and
 $P_{c_{\alpha }}(x_{e'},\alpha /\beta )$
are vertex disjoint,
$P_{c_{\alpha }}(x_{e'},\alpha /\beta )$
are vertex disjoint, -
○
 $M(e)$
and
$M(e)$
and
 $M(e')$
are at least
$M(e')$
are at least
 $2k$
apart in the graph distance of
$2k$
apart in the graph distance of
 $\mathcal {E}$
.
$\mathcal {E}$
.
However, it can happen that
![]() $M(e)\cap P_{c_{\alpha }}(x_{e'},\alpha /\beta )\not = \emptyset $
.
$M(e)\cap P_{c_{\alpha }}(x_{e'},\alpha /\beta )\not = \emptyset $
.
We address this issue as follows. Define an auxiliary directed graph
![]() $\mathcal {H}$
on
$\mathcal {H}$
on
![]() $R_\alpha $
as follows. For
$R_\alpha $
as follows. For
![]() $e\not =e'\in R_\alpha $
, let
$e\not =e'\in R_\alpha $
, let
![]() $(e,e')$
be an oriented edge if
$(e,e')$
be an oriented edge if
![]() $P_{c_{\alpha }}(x_{e'},\alpha /\beta )$
intersect
$P_{c_{\alpha }}(x_{e'},\alpha /\beta )$
intersect
![]() $B_{\mathcal {E}}(e,2k)$
, the ball of radius
$B_{\mathcal {E}}(e,2k)$
, the ball of radius
![]() $2k$
around e. Note that as
$2k$
around e. Note that as
![]() $|B_{\mathcal {E}}(e,2k)|\le (2\Delta )^{2k}$
for every
$|B_{\mathcal {E}}(e,2k)|\le (2\Delta )^{2k}$
for every
![]() $e\in R_\alpha $
, the graph
$e\in R_\alpha $
, the graph
![]() $\mathcal {H}$
has uniformly bounded outdegree. By [Reference Kechris, Solecki and TodorčevićKST99, Proposition 4.5], we can write
$\mathcal {H}$
has uniformly bounded outdegree. By [Reference Kechris, Solecki and TodorčevićKST99, Proposition 4.5], we can write
![]() $R_\alpha =\bigcup _{n\in \mathbb {N}} R_{\alpha ,n}$
, where each
$R_\alpha =\bigcup _{n\in \mathbb {N}} R_{\alpha ,n}$
, where each
![]() $R_{\alpha ,n}$
is
$R_{\alpha ,n}$
is
![]() $\mathcal {H}$
-independent. By
$\mathcal {H}$
-independent. By
![]() $\sigma $
-additivity of
$\sigma $
-additivity of
![]() $\nu $
, we find
$\nu $
, we find
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $\nu (R_{\alpha ,n})>0$
and set
$\nu (R_{\alpha ,n})>0$
and set
![]() $S_{\alpha }=R_{\alpha ,n}$
.
$S_{\alpha }=R_{\alpha ,n}$
.
Let
![]() $e\not =e'\in S_\alpha $
. By the definition, we have that
$e\not =e'\in S_\alpha $
. By the definition, we have that
![]() $W_{c_{\alpha }}(e)$
and
$W_{c_{\alpha }}(e)$
and
![]() $W_{c_{\alpha }}(e')$
are vertex disjoint. Moreover,
$W_{c_{\alpha }}(e')$
are vertex disjoint. Moreover,
![]() $(c_{\alpha })_e$
extends
$(c_{\alpha })_e$
extends
![]() $c_{\alpha }$
as
$c_{\alpha }$
as
![]() $e\in \operatorname {dom}((c_{\alpha })_e)$
and
$e\in \operatorname {dom}((c_{\alpha })_e)$
and
![]() $\operatorname {dom}(c_{\alpha })\subseteq \operatorname {dom}((c_{\alpha })_e)$
. Set
$\operatorname {dom}(c_{\alpha })\subseteq \operatorname {dom}((c_{\alpha })_e)$
. Set
![]() $T_{\alpha }=\bigcup _{e\in S_\alpha } W_{c_{\alpha }}(e)$
, and define
$T_{\alpha }=\bigcup _{e\in S_\alpha } W_{c_{\alpha }}(e)$
, and define
 $$\begin{align*}c_{\alpha+1}(f)= \begin{cases} c_\alpha(f) & \text{if } f\not\in T_{\alpha} \\(c_\alpha)_e(f) & \text{if } f\in W_{c_{\alpha}}(e), \text{where} e\in S_\alpha \text{is the unique such edge}. \end{cases} \end{align*}$$
$$\begin{align*}c_{\alpha+1}(f)= \begin{cases} c_\alpha(f) & \text{if } f\not\in T_{\alpha} \\(c_\alpha)_e(f) & \text{if } f\in W_{c_{\alpha}}(e), \text{where} e\in S_\alpha \text{is the unique such edge}. \end{cases} \end{align*}$$
It follows immediately that
-
(i)
 $T_\alpha \subseteq \operatorname {dom}(c_{\alpha +1})$
,
$T_\alpha \subseteq \operatorname {dom}(c_{\alpha +1})$
, -
(ii)
 $c_\alpha \upharpoonright (\operatorname {dom} (c_{\alpha })\setminus T_\alpha )=c_{\alpha +1}\upharpoonright (\operatorname {dom} (c_{\alpha })\setminus T_\alpha )$
.
$c_\alpha \upharpoonright (\operatorname {dom} (c_{\alpha })\setminus T_\alpha )=c_{\alpha +1}\upharpoonright (\operatorname {dom} (c_{\alpha })\setminus T_\alpha )$
.
Observe that
![]() $c_{\alpha +1}$
is a partial coloring. Indeed, if
$c_{\alpha +1}$
is a partial coloring. Indeed, if
![]() $x\in V$
is not covered by any edge of distance
$x\in V$
is not covered by any edge of distance
![]() $k+2$
to some
$k+2$
to some
![]() $e\in S_\alpha $
, then
$e\in S_\alpha $
, then
![]() $c_{\alpha +1}\upharpoonright N_{\mathcal {G}}(x) =c_\alpha \upharpoonright N_{\mathcal {G}}(x)$
(as the only modification is a shift of some of the infinite
$c_{\alpha +1}\upharpoonright N_{\mathcal {G}}(x) =c_\alpha \upharpoonright N_{\mathcal {G}}(x)$
(as the only modification is a shift of some of the infinite
![]() $\alpha /\beta $
-paths). On the other hand, if
$\alpha /\beta $
-paths). On the other hand, if
![]() $x\in V$
is of distance at most
$x\in V$
is of distance at most
![]() $k+2$
to some
$k+2$
to some
![]() $e\in S_{\alpha }$
, then
$e\in S_{\alpha }$
, then
![]() $c_{\alpha +1}\upharpoonright N_{\mathcal {G}}(x)=(c_\alpha )_e\upharpoonright N_{\mathcal {G}}(x)$
, hence
$c_{\alpha +1}\upharpoonright N_{\mathcal {G}}(x)=(c_\alpha )_e\upharpoonright N_{\mathcal {G}}(x)$
, hence
![]() $c_{\alpha +1}$
is a partial coloring. The same reasoning as above shows that
$c_{\alpha +1}$
is a partial coloring. The same reasoning as above shows that
 $$ \begin{align} \nu(T_\alpha)=\int_{e\in S_\alpha} \sum_{f\in W_{c_\alpha}(e)}\rho_{\nu} (e,f) \ d\nu \le L \nu(S_\alpha) \end{align} $$
$$ \begin{align} \nu(T_\alpha)=\int_{e\in S_\alpha} \sum_{f\in W_{c_\alpha}(e)}\rho_{\nu} (e,f) \ d\nu \le L \nu(S_\alpha) \end{align} $$
by item (2) in Proposition 2.2. Verifying the conditions (1)–(5) can be done mutatis mutandis as in the Case (I).
Limit stage
![]() $\mathbf {\beta \nearrow \alpha }$
. Suppose that
$\mathbf {\beta \nearrow \alpha }$
. Suppose that
![]() $\alpha <\aleph _1$
is a limit ordinal and we have constructed
$\alpha <\aleph _1$
is a limit ordinal and we have constructed
![]() $(c_\beta )_{\beta <\alpha }$
such that the property (1)–(5) hold for every (pair of) ordinal(s) strictly less than
$(c_\beta )_{\beta <\alpha }$
such that the property (1)–(5) hold for every (pair of) ordinal(s) strictly less than
![]() $\alpha $
. We claim that
$\alpha $
. We claim that
![]() $c_{\alpha }(e):=\lim _{\beta \to \alpha } c_{\beta }(e)$
is defined
$c_{\alpha }(e):=\lim _{\beta \to \alpha } c_{\beta }(e)$
is defined
![]() $\nu $
-almost everywhere, that is, the sequence of colors
$\nu $
-almost everywhere, that is, the sequence of colors
![]() $(c_\beta (e))_{\beta <\alpha }$
eventually stabilizes (in fact the colors in the sequence are changed only finitely many times) for
$(c_\beta (e))_{\beta <\alpha }$
eventually stabilizes (in fact the colors in the sequence are changed only finitely many times) for
![]() $\nu $
-almost every
$\nu $
-almost every
![]() $e\in E$
. This follows from the Borel–Cantelli lemma as, by the previous paragraph, the sequence
$e\in E$
. This follows from the Borel–Cantelli lemma as, by the previous paragraph, the sequence
![]() $(T_{\beta })_{\beta <\alpha }$
, where
$(T_{\beta })_{\beta <\alpha }$
, where
![]() $T_\beta $
is the set of edges that changed their color in the
$T_\beta $
is the set of edges that changed their color in the
![]() $\beta $
th step, satisfies
$\beta $
th step, satisfies
 $$ \begin{align*}\sum_{\beta<\alpha}\nu(T_\beta)\le \sum_{\beta<\alpha}L\nu(S_\beta)\le L\nu(U_c)<\infty.\end{align*} $$
$$ \begin{align*}\sum_{\beta<\alpha}\nu(T_\beta)\le \sum_{\beta<\alpha}L\nu(S_\beta)\le L\nu(U_c)<\infty.\end{align*} $$
Hence, the set of edges
![]() $e\in E$
for which
$e\in E$
for which
![]() $\{\beta <\alpha :e\in T_\beta \}$
is cofinal in
$\{\beta <\alpha :e\in T_\beta \}$
is cofinal in
![]() $\alpha $
has to be
$\alpha $
has to be
![]() $\nu $
-null.
$\nu $
-null.
It remains to show that (1)–(5) continuous to hold with
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $\alpha '<\alpha $
, then
$\alpha '<\alpha $
, then
-
1. by the fact that
 $\alpha <\aleph _1$
, the inductive assumption and construction of
$\alpha <\aleph _1$
, the inductive assumption and construction of
 $c_\alpha $
, we have consequently,
$c_\alpha $
, we have consequently, $$ \begin{align*}\nu(\{e\in \operatorname{dom}(c_{\alpha'}):\exists \alpha' <\beta'<\alpha \ e\not\in \operatorname{dom}(c_{\beta'}) \ \operatorname{or} \ \lim_{\beta\to\alpha} c_\beta(e) \ \operatorname{not \ defined}\})=0,\end{align*} $$
$$ \begin{align*}\nu(\{e\in \operatorname{dom}(c_{\alpha'}):\exists \alpha' <\beta'<\alpha \ e\not\in \operatorname{dom}(c_{\beta'}) \ \operatorname{or} \ \lim_{\beta\to\alpha} c_\beta(e) \ \operatorname{not \ defined}\})=0,\end{align*} $$
 $\nu (\operatorname {dom}(c_{\alpha '})\setminus \operatorname {dom}(c_\alpha ))=0$
,
$\nu (\operatorname {dom}(c_{\alpha '})\setminus \operatorname {dom}(c_\alpha ))=0$
,
-
2. is not relevant in limit stages,
-
3. if
 $c_{\alpha '}\not =c_{\alpha }$
, then
$c_{\alpha '}\not =c_{\alpha }$
, then
 $c_{\alpha '}\not =c_{\alpha '+1}$
(see (4)); this implies that as
$c_{\alpha '}\not =c_{\alpha '+1}$
(see (4)); this implies that as $$ \begin{align*}\nu(U_{c_{\alpha'}})>\nu(U_{c_{\alpha'+1}})\ge \nu(U_{c_\alpha})\end{align*} $$
$$ \begin{align*}\nu(U_{c_{\alpha'}})>\nu(U_{c_{\alpha'+1}})\ge \nu(U_{c_\alpha})\end{align*} $$
 $\nu (\operatorname {dom}(c_{\alpha '+1})\setminus \operatorname {dom}(c_\alpha ))=0$
by (1) (where the strict inequality follows from the inductive assumption (3)),
$\nu (\operatorname {dom}(c_{\alpha '+1})\setminus \operatorname {dom}(c_\alpha ))=0$
by (1) (where the strict inequality follows from the inductive assumption (3)),
-
4. if
 $c_{\beta '}=c_{\beta "}$
for some
$c_{\beta '}=c_{\beta "}$
for some
 $\beta '<\alpha $
and every
$\beta '<\alpha $
and every
 $\beta '\le \beta "<\alpha $
, then
$\beta '\le \beta "<\alpha $
, then
 $c_{\alpha }(e)=\lim _{\beta \to \alpha }c_{\beta (e)}=c_{\beta '}(e)$
, hence
$c_{\alpha }(e)=\lim _{\beta \to \alpha }c_{\beta (e)}=c_{\beta '}(e)$
, hence
 $c_{\alpha }=c_{\beta '}$
,
$c_{\alpha }=c_{\beta '}$
, -
5. if
 $c_{\alpha '}(e)\not = c_\alpha (e)$
, then there must be
$c_{\alpha '}(e)\not = c_\alpha (e)$
, then there must be
 $\alpha '\le \beta <\alpha $
such that
$\alpha '\le \beta <\alpha $
such that
 $e\in T_\beta $
as otherwise
$e\in T_\beta $
as otherwise
 $c_\alpha (e)=\lim _{\beta \to \alpha } c_\beta (e)=c_{\alpha '}(e)$
, consequently, we have by the definition of
$c_\alpha (e)=\lim _{\beta \to \alpha } c_\beta (e)=c_{\alpha '}(e)$
, consequently, we have by the definition of $$ \begin{align*} \nu(\{e\in E:c_{\alpha'}(e)\not=c_\alpha(e)\})\le & \ \sum_{\alpha'\le \beta<\alpha}\nu(T_\beta)\le \sum_{\alpha'\le \beta<\alpha}L\nu(S_\beta)\\ = & \ L\sum_{\alpha'\le \beta<\alpha}\nu(S_\beta)=L\nu\left(\bigcup_{\alpha'\le \beta<\alpha} S_\beta\right)\\ \le & \ L\nu\left(\bigcup_{\beta<\alpha} S_\beta\right)\le L\nu(U_c) \end{align*} $$
$$ \begin{align*} \nu(\{e\in E:c_{\alpha'}(e)\not=c_\alpha(e)\})\le & \ \sum_{\alpha'\le \beta<\alpha}\nu(T_\beta)\le \sum_{\alpha'\le \beta<\alpha}L\nu(S_\beta)\\ = & \ L\sum_{\alpha'\le \beta<\alpha}\nu(S_\beta)=L\nu\left(\bigcup_{\alpha'\le \beta<\alpha} S_\beta\right)\\ \le & \ L\nu\left(\bigcup_{\beta<\alpha} S_\beta\right)\le L\nu(U_c) \end{align*} $$
 $T_\beta $
and
$T_\beta $
and
 $S_\beta $
combined with the fact that
$S_\beta $
combined with the fact that
 $\nu (S_\beta \cap S_{\beta '})=0$
for every
$\nu (S_\beta \cap S_{\beta '})=0$
for every
 $\beta <\beta '<\alpha $
which follows by the inductive assumption (1).
$\beta <\beta '<\alpha $
which follows by the inductive assumption (1).
This finishes the proof.
5 Cocycle bounded on edges
Recall that two Borel probablity measures
![]() $\mu ,\nu \in \mathcal {P}(V)$
are equivalent if
$\mu ,\nu \in \mathcal {P}(V)$
are equivalent if
![]() $\mu (A)=0$
if and only if
$\mu (A)=0$
if and only if
![]() $\nu (A)=0$
for every
$\nu (A)=0$
for every
![]() $A\in \mathcal {B}$
. We restate Theorem 1.2 in a compact form for the convenience of the reader.
$A\in \mathcal {B}$
. We restate Theorem 1.2 in a compact form for the convenience of the reader.
Theorem 5.1. Let
![]() $\Delta \in \mathbb {N}$
,
$\Delta \in \mathbb {N}$
,
![]() $\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
$\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
![]() $\Delta (\mathcal {G})<\infty $
and
$\Delta (\mathcal {G})<\infty $
and
![]() $\mu \in \mathcal {P}(V)$
be a
$\mu \in \mathcal {P}(V)$
be a
![]() $\mathcal {G}$
-quasi-invariant. Then there is an equivalent
$\mathcal {G}$
-quasi-invariant. Then there is an equivalent
![]() $\mathcal {G}$
-bounded Borel probability measure
$\mathcal {G}$
-bounded Borel probability measure
![]() $\nu \in \mathcal {P}(V)$
.
$\nu \in \mathcal {P}(V)$
.
Proof. Let
![]() $\mathcal {G}^{[k]}$
denote the Borel graph on V, where
$\mathcal {G}^{[k]}$
denote the Borel graph on V, where
![]() $(x,y)$
form an edge if and only if
$(x,y)$
form an edge if and only if
![]() $\operatorname {dist}_{\mathcal {G}}(x,y)=k$
. Then
$\operatorname {dist}_{\mathcal {G}}(x,y)=k$
. Then
![]() $\mathcal {G}^{[1]}=\mathcal {G}$
and
$\mathcal {G}^{[1]}=\mathcal {G}$
and
![]() $\mathcal {G}^{[k]}$
has degree bounded by
$\mathcal {G}^{[k]}$
has degree bounded by
![]() $\Delta ^k$
. Use repeatedly [Reference Kechris, Solecki and TodorčevićKST99, Proposition 4.6] to find a Borel proper edge coloring
$\Delta ^k$
. Use repeatedly [Reference Kechris, Solecki and TodorčevićKST99, Proposition 4.6] to find a Borel proper edge coloring
![]() $\{A^k_i\}_{i=1}^{2\Delta ^k}$
of
$\{A^k_i\}_{i=1}^{2\Delta ^k}$
of
![]() $\mathcal {G}^{[k]}$
for each
$\mathcal {G}^{[k]}$
for each
![]() $k\in \mathbb {N}\setminus \{0\}$
. Using any Borel linear order on V, vertices covered by
$k\in \mathbb {N}\setminus \{0\}$
. Using any Borel linear order on V, vertices covered by
![]() $A^k_i$
can be split into two disjoint Borel sets
$A^k_i$
can be split into two disjoint Borel sets
![]() $A^k_{i,0}\subseteq V$
and
$A^k_{i,0}\subseteq V$
and
![]() $A^k_{i,1}\subseteq V$
together with Borel isomorphisms
$A^k_{i,1}\subseteq V$
together with Borel isomorphisms
![]() $f^{k}_{i,0}:A^k_{i,0}\to A^k_{i,1}$
and
$f^{k}_{i,0}:A^k_{i,0}\to A^k_{i,1}$
and
![]() $f^k_{i,1}:A^k_{i,1}\to A^k_{i,0}$
such that
$f^k_{i,1}:A^k_{i,1}\to A^k_{i,0}$
such that
![]() $\{x,f^{k}_{i,0}(x)\},\{y,f^{k}_{i,1}(y)\}\in A^{k}_{i}$
for every
$\{x,f^{k}_{i,0}(x)\},\{y,f^{k}_{i,1}(y)\}\in A^{k}_{i}$
for every
![]() $x\in A^{k}_{i,0}$
and
$x\in A^{k}_{i,0}$
and
![]() $y\in A^{k}_{i,1}$
. We also set
$y\in A^{k}_{i,1}$
. We also set
![]() $A^0_{0,0}=V$
and
$A^0_{0,0}=V$
and
![]() $f^0_{0,0}=\operatorname {id}_V$
. Observe that for every
$f^0_{0,0}=\operatorname {id}_V$
. Observe that for every
![]() $(x,y)\in F_{\mathcal {G}}$
there is exactly one triplet
$(x,y)\in F_{\mathcal {G}}$
there is exactly one triplet
![]() $(k,i,j)$
, where
$(k,i,j)$
, where
![]() $k=\operatorname {dist}_{\mathcal {G}}(x,y)$
,
$k=\operatorname {dist}_{\mathcal {G}}(x,y)$
,
![]() $i\in 2\Delta ^{\operatorname {dist}_{\mathcal {G}}(x,y)}$
and
$i\in 2\Delta ^{\operatorname {dist}_{\mathcal {G}}(x,y)}$
and
![]() $j\in \{0,1\}$
such that
$j\in \{0,1\}$
such that
![]() $f^k_{i,j}(x)=y$
.
$f^k_{i,j}(x)=y$
.
Denote as
![]() $\mu ^{k}_{i,j}$
the push-forward of
$\mu ^{k}_{i,j}$
the push-forward of
![]() $\mu \upharpoonright A^k_{i,1-j}$
via
$\mu \upharpoonright A^k_{i,1-j}$
via
![]() $\left (f^k_{i,j}\right )^{-1}$
, where
$\left (f^k_{i,j}\right )^{-1}$
, where
![]() $j\in \{0,1\}$
. We have
$j\in \{0,1\}$
. We have
for every
![]() $B\in \mathcal {B}$
, where
$B\in \mathcal {B}$
, where
![]() $\rho _\mu $
is the Radon–Nikodym cocycle with respect to
$\rho _\mu $
is the Radon–Nikodym cocycle with respect to
![]() $\mu $
. In particular,
$\mu $
. In particular,
![]() $\mu ^k_{i,j}(V)\le 1$
. Define
$\mu ^k_{i,j}(V)\le 1$
. Define
 $$ \begin{align} \tilde{\nu}=\mu+\sum_{k\in \mathbb{N}\setminus \{0\}}\frac{1}{2^k} \left(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mu^{k}_{i,0}+\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mu^{k}_{i,1}\right). \end{align} $$
$$ \begin{align} \tilde{\nu}=\mu+\sum_{k\in \mathbb{N}\setminus \{0\}}\frac{1}{2^k} \left(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mu^{k}_{i,0}+\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mu^{k}_{i,1}\right). \end{align} $$
Claim 5.2.
![]() $\tilde {\nu }$
is a finite Borel measure on V that is equivalent with
$\tilde {\nu }$
is a finite Borel measure on V that is equivalent with
![]() $\mu $
. The Radon–Nikodym derivative
$\mu $
. The Radon–Nikodym derivative
![]() $\Omega =\frac {d\tilde {\nu }}{d\mu }$
can be explicitly written as
$\Omega =\frac {d\tilde {\nu }}{d\mu }$
can be explicitly written as
 $$ \begin{align*}\Omega(x)=1+\sum_{k\in \mathbb{N}\setminus \{0\}}\frac{1}{2^k} \left(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{ 1}_{A^k_{i,0}}(x)\rho_\mu(x,f^k_{i,0}(x))+\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,1}}(x)\rho_\mu(x,f^k_{i,1}(x))\right)\end{align*} $$
$$ \begin{align*}\Omega(x)=1+\sum_{k\in \mathbb{N}\setminus \{0\}}\frac{1}{2^k} \left(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{ 1}_{A^k_{i,0}}(x)\rho_\mu(x,f^k_{i,0}(x))+\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,1}}(x)\rho_\mu(x,f^k_{i,1}(x))\right)\end{align*} $$
for
![]() $\mu $
(and
$\mu $
(and
![]() $\tilde {\nu }$
) almost every
$\tilde {\nu }$
) almost every
![]() $x\in V$
. In particular,
$x\in V$
. In particular,
![]() $\frac {1}{\Omega }=\frac {d\mu }{d\tilde {\nu }}$
.
$\frac {1}{\Omega }=\frac {d\mu }{d\tilde {\nu }}$
.
Proof. Let
![]() $n\in \mathbb {N}$
, and define
$n\in \mathbb {N}$
, and define
 $$ \begin{align*} \tilde{\nu}_n=\mu+\sum_{k=1}^n\frac{1}{2^k} \left(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mu^{k}_{i,0}+\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mu^{k}_{i,1}\right). \end{align*} $$
$$ \begin{align*} \tilde{\nu}_n=\mu+\sum_{k=1}^n\frac{1}{2^k} \left(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mu^{k}_{i,0}+\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mu^{k}_{i,1}\right). \end{align*} $$
As
![]() $\mu ^{k}_{i,j}(V)\le 1$
, we see that
$\mu ^{k}_{i,j}(V)\le 1$
, we see that
![]() $\tilde {\nu }_n$
is a finite Borel measure on V that is equivalent with
$\tilde {\nu }_n$
is a finite Borel measure on V that is equivalent with
![]() $\mu $
. Indeed, if
$\mu $
. Indeed, if
![]() $\mu (A)=0$
, then by the definition of
$\mu (A)=0$
, then by the definition of
![]() $\mathcal {G}$
-quasi-invariance we have that
$\mathcal {G}$
-quasi-invariance we have that
![]() $\tilde {\nu }_n(A)=0$
, and if
$\tilde {\nu }_n(A)=0$
, and if
![]() $\tilde {\nu }_n(A)=0$
, then
$\tilde {\nu }_n(A)=0$
, then
![]() $\mu (A)=0$
as
$\mu (A)=0$
as
![]() $\mu (A)\le \tilde {\nu }_n(A)$
for every
$\mu (A)\le \tilde {\nu }_n(A)$
for every
![]() $A\in \mathcal {B}$
. Moreover, it is easy to see that the Radon–Nikodym derivative
$A\in \mathcal {B}$
. Moreover, it is easy to see that the Radon–Nikodym derivative
![]() $\Omega _n=\frac {d\tilde {\nu }_n}{d\mu }$
satisfies
$\Omega _n=\frac {d\tilde {\nu }_n}{d\mu }$
satisfies
 $$ \begin{align*}\Omega_n(x)=1+\sum_{k=1}^n\frac{1}{2^k} \left(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,0}}(x)\rho_\mu(x,f^k_{i,0}(x))+\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{ 1}_{A^k_{i,1}}(x)\rho_\mu(x,f^k_{i,1}(x))\right)\end{align*} $$
$$ \begin{align*}\Omega_n(x)=1+\sum_{k=1}^n\frac{1}{2^k} \left(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,0}}(x)\rho_\mu(x,f^k_{i,0}(x))+\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{ 1}_{A^k_{i,1}}(x)\rho_\mu(x,f^k_{i,1}(x))\right)\end{align*} $$
by Equation (5.1).
Observe that the limit
![]() $\Omega (x)=\lim _{n\to \infty }\Omega _n(x)$
is defined for every
$\Omega (x)=\lim _{n\to \infty }\Omega _n(x)$
is defined for every
![]() $x\in V$
as
$x\in V$
as
![]() $\{\Omega _n(x)\}_{n\in \mathbb {N}}$
is increasing, and we have
$\{\Omega _n(x)\}_{n\in \mathbb {N}}$
is increasing, and we have
for every
![]() $A\in \mathcal {B}$
by the monotone convergence theorem. Note that by the definition of
$A\in \mathcal {B}$
by the monotone convergence theorem. Note that by the definition of
![]() $\Omega _n$
we have
$\Omega _n$
we have
for every
![]() $A\in \mathcal {B}$
.
$A\in \mathcal {B}$
.
The sequence
![]() $\{\tilde \nu _n\}_{n\in \mathbb {N}}$
is a Cauchy sequence in the total variation distance
$\{\tilde \nu _n\}_{n\in \mathbb {N}}$
is a Cauchy sequence in the total variation distance
![]() $\|.\|_{TV}$
. Indeed, we have
$\|.\|_{TV}$
. Indeed, we have
 $$ \begin{align*}\|\tilde{\nu}_m-\tilde{\nu}_n\|_{TV}=(\tilde{\nu}_m-\tilde{\nu}_n)(V)=\left(\sum_{k=n}^m\frac{1}{2^k} \left(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mu^{k}_{i,0}+\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mu^{k}_{i,1}\right)\right)(V)\le \frac{1}{2^{n-1}}\end{align*} $$
$$ \begin{align*}\|\tilde{\nu}_m-\tilde{\nu}_n\|_{TV}=(\tilde{\nu}_m-\tilde{\nu}_n)(V)=\left(\sum_{k=n}^m\frac{1}{2^k} \left(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mu^{k}_{i,0}+\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mu^{k}_{i,1}\right)\right)(V)\le \frac{1}{2^{n-1}}\end{align*} $$
as
![]() $\tilde {\nu }_m-\tilde {\nu }_n$
is a finite Borel (positive) measure for every
$\tilde {\nu }_m-\tilde {\nu }_n$
is a finite Borel (positive) measure for every
![]() $m>n>1$
. Consequently, there is a finite Borel measure
$m>n>1$
. Consequently, there is a finite Borel measure
![]() $\tilde {\nu }$
on
$\tilde {\nu }$
on
![]() $(V,\mathcal {B})$
such that
$(V,\mathcal {B})$
such that
![]() $\tilde {\nu }_n\xrightarrow {TV} \tilde {\nu }$
. In particular, we have
$\tilde {\nu }_n\xrightarrow {TV} \tilde {\nu }$
. In particular, we have
![]() $\tilde {\nu }_n(A)\to \tilde {\nu }(A)<\infty $
for every
$\tilde {\nu }_n(A)\to \tilde {\nu }(A)<\infty $
for every
![]() $A\in \mathcal {B}$
. Combined with Equation (5.3), we see that
$A\in \mathcal {B}$
. Combined with Equation (5.3), we see that
![]() $\Omega =\frac {d\tilde {\nu }}{d\mu }$
as desired.
$\Omega =\frac {d\tilde {\nu }}{d\mu }$
as desired.
It remains to show that
![]() $\mu $
and
$\mu $
and
![]() $\tilde {\nu }$
are equivalent. If
$\tilde {\nu }$
are equivalent. If
![]() $\mu (A)=0$
, then
$\mu (A)=0$
, then
![]() $\tilde {\nu }(A)=\lim _{n\to \infty } \tilde {\nu }_n(A)=0$
as in that case
$\tilde {\nu }(A)=\lim _{n\to \infty } \tilde {\nu }_n(A)=0$
as in that case
![]() $\tilde {\nu }_n(A)=0$
for every
$\tilde {\nu }_n(A)=0$
for every
![]() $n\in \mathbb {N}$
. On the other hand, if
$n\in \mathbb {N}$
. On the other hand, if
![]() $\tilde {\nu }(A)=0$
, then
$\tilde {\nu }(A)=0$
, then
![]() $\int _A \Omega (x) \ d \mu =0$
as
$\int _A \Omega (x) \ d \mu =0$
as
![]() $\Omega =\frac {d\tilde {\nu }}{d\mu }$
. This can only happen if
$\Omega =\frac {d\tilde {\nu }}{d\mu }$
. This can only happen if
![]() $\mu (A)=0$
as
$\mu (A)=0$
as
![]() $\Omega \ge 1$
.
$\Omega \ge 1$
.
Let
![]() $\nu $
be a normalization of
$\nu $
be a normalization of
![]() $\tilde {\nu }$
, that is,
$\tilde {\nu }$
, that is,
![]() $\nu =K\tilde {\nu }$
for some
$\nu =K\tilde {\nu }$
for some
![]() $0<K<\infty $
. It is easy to see that
$0<K<\infty $
. It is easy to see that
![]() $\nu $
and
$\nu $
and
![]() $\tilde {\nu }$
, hence also
$\tilde {\nu }$
, hence also
![]() $\nu $
and
$\nu $
and
![]() $\mu $
, are equivalent. Consequently,
$\mu $
, are equivalent. Consequently,
![]() $\nu $
is
$\nu $
is
![]() $\mathcal {G}$
-quasi-invariant. Write
$\mathcal {G}$
-quasi-invariant. Write
![]() $\rho _\nu $
for the Radon–Nikodym cocycle of
$\rho _\nu $
for the Radon–Nikodym cocycle of
![]() $\nu $
with respect to
$\nu $
with respect to
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Claim 5.3. There is a
![]() $\mu $
-conull
$\mu $
-conull
![]() $\mathcal {G}$
-invariant set
$\mathcal {G}$
-invariant set
![]() $A\subseteq V$
such that
$A\subseteq V$
such that
for every
![]() $x,y\in A$
such that
$x,y\in A$
such that
![]() $(x,y)\in F_{\mathcal {G}}$
.
$(x,y)\in F_{\mathcal {G}}$
.
Proof. Let
![]() $g:C\to V$
be a Borel injection such that
$g:C\to V$
be a Borel injection such that
![]() $(x,g(x))\in F_{\mathcal {G}}$
for every
$(x,g(x))\in F_{\mathcal {G}}$
for every
![]() $x\in C$
. Set
$x\in C$
. Set
![]() $g(C)=D$
, then
$g(C)=D$
, then
![]() $g:C\to D$
is a Borel bijection. As
$g:C\to D$
is a Borel bijection. As
![]() $\mu $
and
$\mu $
and
![]() $\nu $
are equivalent,
$\nu $
are equivalent,
![]() $\frac {\Omega }{K}= \frac {\nu }{\mu }$
and
$\frac {\Omega }{K}= \frac {\nu }{\mu }$
and
![]() $\rho _\mu (x,g(x))\frac {\Omega (g(x))}{\Omega (x)}$
are nonnegative. We have
$\rho _\mu (x,g(x))\frac {\Omega (g(x))}{\Omega (x)}$
are nonnegative. We have
 $$ \begin{align*} \int_{C} \rho_\mu(x,g(x))\frac{\Omega(g(x))}{\Omega(x)} \ d\nu(x)= & \ \int_{C} \rho_\mu(x,g(x))\frac{\Omega(g(x))}{\Omega(x)} \frac{\Omega(x)}{K}\ d\mu(x)\\ = & \ \int_{C} \rho_\mu(x,g(x))\frac{1}{K}\Omega(g(x)) \ d\mu(x). \end{align*} $$
$$ \begin{align*} \int_{C} \rho_\mu(x,g(x))\frac{\Omega(g(x))}{\Omega(x)} \ d\nu(x)= & \ \int_{C} \rho_\mu(x,g(x))\frac{\Omega(g(x))}{\Omega(x)} \frac{\Omega(x)}{K}\ d\mu(x)\\ = & \ \int_{C} \rho_\mu(x,g(x))\frac{1}{K}\Omega(g(x)) \ d\mu(x). \end{align*} $$
By (2) Proposition 2.2 applied to
![]() $f(x,y)$
that is defined as
$f(x,y)$
that is defined as
![]() $\frac {1}{K}\Omega (y)$
whenever
$\frac {1}{K}\Omega (y)$
whenever
![]() $g(x)=y$
and
$g(x)=y$
and
![]() $0$
otherwise, we have
$0$
otherwise, we have
 $$ \begin{align*} \int_{C} \rho_\mu(x,g(x))\frac{1}{K}\Omega(g(x)) \ d\mu(x)= & \ \int_{D} \frac{1}{K}\Omega(y) \ d\mu(y)\\ = & \ \nu (D)=\nu (g(C))\\ = & \ \int_{C} \rho_{\nu}(x,g(x)) \ d\nu(x) \end{align*} $$
$$ \begin{align*} \int_{C} \rho_\mu(x,g(x))\frac{1}{K}\Omega(g(x)) \ d\mu(x)= & \ \int_{D} \frac{1}{K}\Omega(y) \ d\mu(y)\\ = & \ \nu (D)=\nu (g(C))\\ = & \ \int_{C} \rho_{\nu}(x,g(x)) \ d\nu(x) \end{align*} $$
and the claim follows from the uniqueness of the Radon–Nikodym cocycle.
It remains to show that
![]() $\rho _{\mu }(x,y)\Omega (y)\le 4\Delta \Omega (x)$
for every
$\rho _{\mu }(x,y)\Omega (y)\le 4\Delta \Omega (x)$
for every
![]() $(x,y)\in E$
, as this clearly implies
$(x,y)\in E$
, as this clearly implies
![]() $\rho _{\nu }(x,y)=\rho _\mu (x,y)\frac {\Omega (y)}{\Omega (x)}\le 4\Delta $
. Let
$\rho _{\nu }(x,y)=\rho _\mu (x,y)\frac {\Omega (y)}{\Omega (x)}\le 4\Delta $
. Let
![]() $(x,y)\in E$
. Suppose that
$(x,y)\in E$
. Suppose that
![]() $y\in A^k_{i,j}$
, that is,
$y\in A^k_{i,j}$
, that is,
![]() $z=f^k_{i,j}(y)$
is well defined and satisfies
$z=f^k_{i,j}(y)$
is well defined and satisfies
![]() $\operatorname {dist}_{\mathcal {G}}(y,z)=k$
. We already observed that the triplet
$\operatorname {dist}_{\mathcal {G}}(y,z)=k$
. We already observed that the triplet
![]() $(k,i,j)$
is unique. As
$(k,i,j)$
is unique. As
![]() $(x,y)\in F_{\mathcal {G}}$
, there is exactly one triplet
$(x,y)\in F_{\mathcal {G}}$
, there is exactly one triplet
![]() $(k',i',j')$
such that
$(k',i',j')$
such that
![]() $x\in A^{k'}_{i',j'}$
and
$x\in A^{k'}_{i',j'}$
and
![]() $f^{k'}_{i',j'}(x)=z$
. Moreover, as
$f^{k'}_{i',j'}(x)=z$
. Moreover, as
![]() $(x,y)\in E$
we have that
$(x,y)\in E$
we have that
![]() $k'\le k+1$
. Indeed, we have
$k'\le k+1$
. Indeed, we have
![]() $\operatorname {dist}_{\mathcal {G}}(x,z)=k'\le \operatorname {dist}_{\mathcal {G}}(x,y)+\operatorname {dist}_{\mathcal {G}}(y,z)=k+1$
. The same reasoning with the roles of y and x interchanged implies that the assignment
$\operatorname {dist}_{\mathcal {G}}(x,z)=k'\le \operatorname {dist}_{\mathcal {G}}(x,y)+\operatorname {dist}_{\mathcal {G}}(y,z)=k+1$
. The same reasoning with the roles of y and x interchanged implies that the assignment
![]() $(k,i,j)\mapsto (k',i',j')$
is a bijection. Observe that
$(k,i,j)\mapsto (k',i',j')$
is a bijection. Observe that
holds whenever
![]() $y\in A^k_{i,j}$
. We have
$y\in A^k_{i,j}$
. We have
 $$ \begin{align*} \rho_\mu(x,y)\Omega(y)= & \ \rho_\mu(x,y)\Bigg(1+\sum_{k\in \mathbb{N}\setminus \{0\}}\frac{1}{2^k} \Bigg(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,0}}(y)\rho_\mu(y,f^k_{i,0}(y))\\ & \ +\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,1}}(y)\rho_\mu(y,f^k_{i,1}(y))\Bigg)\Bigg)\\ = & \ \rho_\mu(x,y)+\sum_{k\in \mathbb{N}\setminus \{0\}}\frac{1}{2^k} \Bigg(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,0}}(y)\rho_\mu(x,f^k_{i,0}(y))\\ & \ +\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,1}}(y)\rho_\mu(x,f^k_{i,1}(y))\Bigg)\\ \le & \ 4\Delta \Bigg(\frac{1}{4\Delta}\rho_\mu(x,f^0_{0,0}(y))+ \sum_{k\in \mathbb{N}\setminus \{0\}}\frac{1}{2^{k+1}} \Bigg(\frac{1}{2\Delta^{k+1}}\sum_{i=1}^{2\Delta^k}\mathbf{ 1}_{A^k_{i,0}}(y)\rho_\mu(x,f^k_{i,0}(y))\\ & \ + \frac{1}{2\Delta^{k+1}}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,1}}(y)\rho_\mu(x,f^k_{i,1}(y))\Bigg)\Bigg)\\ \le & \ 4\Delta\Bigg(1+\sum_{k'\in \mathbb{N}\setminus \{0\}}\frac{1}{2^{k'}} \Bigg(\frac{1}{2\Delta^{k'}}\sum_{i=1}^{2\Delta^{k'}}\mathbf{1}_{A^{k'}_{i',0}}(x)\rho_\mu(x,f^{k'}_{i',0}(x))\\ & \ +\frac{1}{2\Delta^{k'}}\sum_{i=1}^{2\Delta^{k'}}\mathbf{1}_{A^{k'}_{i',1}}(x)\rho_\mu(x,f^{k'}_{i',1}(x))\Bigg)\Bigg)\\ = & \ 4\Delta \Omega(x), \end{align*} $$
$$ \begin{align*} \rho_\mu(x,y)\Omega(y)= & \ \rho_\mu(x,y)\Bigg(1+\sum_{k\in \mathbb{N}\setminus \{0\}}\frac{1}{2^k} \Bigg(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,0}}(y)\rho_\mu(y,f^k_{i,0}(y))\\ & \ +\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,1}}(y)\rho_\mu(y,f^k_{i,1}(y))\Bigg)\Bigg)\\ = & \ \rho_\mu(x,y)+\sum_{k\in \mathbb{N}\setminus \{0\}}\frac{1}{2^k} \Bigg(\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,0}}(y)\rho_\mu(x,f^k_{i,0}(y))\\ & \ +\frac{1}{2\Delta^k}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,1}}(y)\rho_\mu(x,f^k_{i,1}(y))\Bigg)\\ \le & \ 4\Delta \Bigg(\frac{1}{4\Delta}\rho_\mu(x,f^0_{0,0}(y))+ \sum_{k\in \mathbb{N}\setminus \{0\}}\frac{1}{2^{k+1}} \Bigg(\frac{1}{2\Delta^{k+1}}\sum_{i=1}^{2\Delta^k}\mathbf{ 1}_{A^k_{i,0}}(y)\rho_\mu(x,f^k_{i,0}(y))\\ & \ + \frac{1}{2\Delta^{k+1}}\sum_{i=1}^{2\Delta^k}\mathbf{1}_{A^k_{i,1}}(y)\rho_\mu(x,f^k_{i,1}(y))\Bigg)\Bigg)\\ \le & \ 4\Delta\Bigg(1+\sum_{k'\in \mathbb{N}\setminus \{0\}}\frac{1}{2^{k'}} \Bigg(\frac{1}{2\Delta^{k'}}\sum_{i=1}^{2\Delta^{k'}}\mathbf{1}_{A^{k'}_{i',0}}(x)\rho_\mu(x,f^{k'}_{i',0}(x))\\ & \ +\frac{1}{2\Delta^{k'}}\sum_{i=1}^{2\Delta^{k'}}\mathbf{1}_{A^{k'}_{i',1}}(x)\rho_\mu(x,f^{k'}_{i',1}(x))\Bigg)\Bigg)\\ = & \ 4\Delta \Omega(x), \end{align*} $$
where we used (1) Proposition 2.2 to get the second equality and Equation (5.5) together with the fact that
![]() $(k,i,j)\mapsto (k',i',j')$
is a bijection to get the second inequality.
$(k,i,j)\mapsto (k',i',j')$
is a bijection to get the second inequality.
6 Double counting argument
In this section, we show that if a partial edge coloring c does not admit improvement of weight L, then the measure of uncolored edges has to be
![]() $O\left (\frac {1}{\log ^2 (L)L}\right )$
under the assumption that
$O\left (\frac {1}{\log ^2 (L)L}\right )$
under the assumption that
![]() $\nu $
is
$\nu $
is
![]() $\mathcal {G}$
-bounded.
$\mathcal {G}$
-bounded.
Theorem 6.1. Let
![]() $\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
$\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
![]() $\Delta (\mathcal {G})<\infty $
,
$\Delta (\mathcal {G})<\infty $
,
![]() $\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
be the corresponding line graph,
$\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
be the corresponding line graph,
![]() $\nu \in \mathcal {P}(E)$
be
$\nu \in \mathcal {P}(E)$
be
![]() $\mathcal {E}$
-bounded, that is,
$\mathcal {E}$
-bounded, that is,
![]() $\nu $
satisfy
$\nu $
satisfy
![]() $\rho _\nu (e,f)\le 8\Delta $
for every
$\rho _\nu (e,f)\le 8\Delta $
for every
![]() $e,f\in E$
such that
$e,f\in E$
such that
![]() $(e,f)\in I_{\mathcal {G}}$
, and
$(e,f)\in I_{\mathcal {G}}$
, and
![]() $c;E\to [\Delta (\mathcal {G})+1]$
be a partial coloring that does not admit improvement of weight
$c;E\to [\Delta (\mathcal {G})+1]$
be a partial coloring that does not admit improvement of weight
![]() $L\in \mathbb {N}$
, where
$L\in \mathbb {N}$
, where
![]() $\log _{8\Delta }(L)\ge (8\Delta )^{20}$
. Then
$\log _{8\Delta }(L)\ge (8\Delta )^{20}$
. Then
 $$ \begin{align*}\nu(U_c)\le \frac{64 (4\Delta)^7(\Delta!)^{14}}{\log_{8\Delta}^2(L) L}.\end{align*} $$
$$ \begin{align*}\nu(U_c)\le \frac{64 (4\Delta)^7(\Delta!)^{14}}{\log_{8\Delta}^2(L) L}.\end{align*} $$
Proposition 6.2. Let
![]() $\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
$\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
![]() $\Delta (\mathcal {G})<\infty $
,
$\Delta (\mathcal {G})<\infty $
,
![]() $\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
be the corresponding line graph and
$\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
be the corresponding line graph and
![]() $\nu \in \mathcal {P}(E)$
be
$\nu \in \mathcal {P}(E)$
be
![]() $\mathcal {E}$
-bounded. Suppose that
$\mathcal {E}$
-bounded. Suppose that
![]() $c;E\to [\Delta (\mathcal {G})+1]$
is a partial coloring that does not admit improvement of weight
$c;E\to [\Delta (\mathcal {G})+1]$
is a partial coloring that does not admit improvement of weight
![]() $L\in \mathbb {N}$
, where
$L\in \mathbb {N}$
, where
![]() $\frac {\log _{8\Delta }(L)}{2}-1\ge 2\Delta $
. Then
$\frac {\log _{8\Delta }(L)}{2}-1\ge 2\Delta $
. Then
![]() $\nu $
-almost every
$\nu $
-almost every
![]() $e\in U_c$
is
$e\in U_c$
is
![]() $\frac {\log _{8\Delta }(L)}{4}$
-bad for c.
$\frac {\log _{8\Delta }(L)}{4}$
-bad for c.
Proof. Let
![]() $W_c(e)$
be a
$W_c(e)$
be a
![]() $3$
-step Vizing chain at e. We have
$3$
-step Vizing chain at e. We have
 $$ \begin{align*}L\le \sum_{f\in W_c(e)} \rho_\nu(e,f)\le \sum_{k\le |W_c(e)|}(8\Delta)^k\le (8\Delta)^{|W_c(e)|+1}.\end{align*} $$
$$ \begin{align*}L\le \sum_{f\in W_c(e)} \rho_\nu(e,f)\le \sum_{k\le |W_c(e)|}(8\Delta)^k\le (8\Delta)^{|W_c(e)|+1}.\end{align*} $$
Consequently,
![]() $|W_c(e)|\ge \log _{8\Delta }(L)-1\ge \frac {\log _{8\Delta }(L)}{2}+2\Delta $
.
$|W_c(e)|\ge \log _{8\Delta }(L)-1\ge \frac {\log _{8\Delta }(L)}{2}+2\Delta $
.
We get an immediate corollary of Theorem 3.17.
Proposition 6.3. Let
![]() $\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
$\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
![]() $\Delta (\mathcal {G})<\infty $
,
$\Delta (\mathcal {G})<\infty $
,
![]() $\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
be the corresponding line graph and
$\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
be the corresponding line graph and
![]() $\nu \in \mathcal {P}(E)$
be
$\nu \in \mathcal {P}(E)$
be
![]() $\mathcal {E}$
-bounded. Suppose that
$\mathcal {E}$
-bounded. Suppose that
![]() $c;E\to [\Delta (\mathcal {G})+1]$
is a partial coloring that does not admit improvement of weight
$c;E\to [\Delta (\mathcal {G})+1]$
is a partial coloring that does not admit improvement of weight
![]() $L\in \mathbb {N}$
, where
$L\in \mathbb {N}$
, where
![]() $\log _{8\Delta }(L)\ge (8\Delta )^{20}$
. Then we have
$\log _{8\Delta }(L)\ge (8\Delta )^{20}$
. Then we have
for
![]() $\nu $
-almost every
$\nu $
-almost every
![]() $e\in U_c$
.
$e\in U_c$
.
Proposition 6.4. Let
![]() $\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
$\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
![]() $\Delta (\mathcal {G})<\infty $
,
$\Delta (\mathcal {G})<\infty $
,
![]() $\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
be the corresponding line graph and
$\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
be the corresponding line graph and
![]() $\nu \in \mathcal {P}(E)$
be
$\nu \in \mathcal {P}(E)$
be
![]() $\mathcal {E}$
-bounded. Suppose that
$\mathcal {E}$
-bounded. Suppose that
![]() $c;E\to [\Delta (\mathcal {G})+1]$
is a partial coloring that does not admit improvement of weight
$c;E\to [\Delta (\mathcal {G})+1]$
is a partial coloring that does not admit improvement of weight
![]() $L\in \mathbb {N}$
, where
$L\in \mathbb {N}$
, where
![]() $\log _{8\Delta }(L)\ge (8\Delta )^{20}$
. Then for
$\log _{8\Delta }(L)\ge (8\Delta )^{20}$
. Then for
![]() $\nu $
-almost every
$\nu $
-almost every
![]() $e\in U_c$
and every
$e\in U_c$
and every
![]() $(f^1,f^2)\in \mathcal {V}_c(e)$
, we have
$(f^1,f^2)\in \mathcal {V}_c(e)$
, we have
 $$ \begin{align*}\sum_{f\in P^3_c}\rho_\nu(e,f)\ge \frac{L}{2},\end{align*} $$
$$ \begin{align*}\sum_{f\in P^3_c}\rho_\nu(e,f)\ge \frac{L}{2},\end{align*} $$
where
![]() $W_c(e,f^1,f^2)=\left (F^1_c\right )^\frown \left (P^1_c\right )^\frown \left (F^2_c\right )^\frown \left (P^2_c\right )^\frown \left (F^3_c\right )^\frown \left (P^3_c\right )$
.
$W_c(e,f^1,f^2)=\left (F^1_c\right )^\frown \left (P^1_c\right )^\frown \left (F^2_c\right )^\frown \left (P^2_c\right )^\frown \left (F^3_c\right )^\frown \left (P^3_c\right )$
.
Proof. Set
![]() $P=\left (F^1_c\right )^\frown \left (P^1_c\right )^\frown \left (F^2_c\right )^\frown \left (P^2_c\right )^\frown \left (F^3_c\right )$
. It follows from the definition of
$P=\left (F^1_c\right )^\frown \left (P^1_c\right )^\frown \left (F^2_c\right )^\frown \left (P^2_c\right )^\frown \left (F^3_c\right )$
. It follows from the definition of
![]() $\mathcal {V}_c(e)$
that
$\mathcal {V}_c(e)$
that
![]() $s=l(P)\le 3\Delta +\frac {\log _{8\Delta }(L)}{2}$
. We have
$s=l(P)\le 3\Delta +\frac {\log _{8\Delta }(L)}{2}$
. We have
 $$ \begin{align*} L\le \sum_{f\in W_c(e,f^1,f^2)}\rho_\nu(e,f)= & \ \sum_{f\in P}\rho_\nu(e,f)+\sum_{f\in P^3_c}\rho_\nu(e,f)\\ \le & \ (8\Delta)^{3\Delta+\frac{\log_{8\Delta}(L)}{2}+2} + \sum_{f\in P^3_c}\rho_\nu(e,f). \end{align*} $$
$$ \begin{align*} L\le \sum_{f\in W_c(e,f^1,f^2)}\rho_\nu(e,f)= & \ \sum_{f\in P}\rho_\nu(e,f)+\sum_{f\in P^3_c}\rho_\nu(e,f)\\ \le & \ (8\Delta)^{3\Delta+\frac{\log_{8\Delta}(L)}{2}+2} + \sum_{f\in P^3_c}\rho_\nu(e,f). \end{align*} $$
Consequently,
![]() $\frac {L}{2}\le L-(8\Delta )^{3\Delta +2} L^{\frac {1}{2}}\le \sum _{f\in P^3_c}\rho _\nu (e,f)$
as needed.
$\frac {L}{2}\le L-(8\Delta )^{3\Delta +2} L^{\frac {1}{2}}\le \sum _{f\in P^3_c}\rho _\nu (e,f)$
as needed.
Define an auxiliary Borel oriented bipartite multigraph
![]() $\mathcal {H}_c$
with vertex set
$\mathcal {H}_c$
with vertex set
![]() $U_c\sqcup \operatorname {dom}(c)$
such that
$U_c\sqcup \operatorname {dom}(c)$
such that
![]() $(e,f)$
is an edge if
$(e,f)$
is an edge if
![]() $f\in P^3_c$
for some
$f\in P^3_c$
for some
where
![]() $(f^1,f^2)\in \mathcal {V}_c(e)$
. Note that
$(f^1,f^2)\in \mathcal {V}_c(e)$
. Note that
![]() $\mathcal {H}_c$
is in general a multigraph as there might be different
$\mathcal {H}_c$
is in general a multigraph as there might be different
![]() $3$
-step Vizing chains at the same edge e for which
$3$
-step Vizing chains at the same edge e for which
![]() $(e,f)\in \mathcal {H}_c$
for the same
$(e,f)\in \mathcal {H}_c$
for the same
![]() $f\in \operatorname {dom}(c)$
. The following is the crucial observation for the double counting argument; note that the right-hand side of the inequality does not depend on L.
$f\in \operatorname {dom}(c)$
. The following is the crucial observation for the double counting argument; note that the right-hand side of the inequality does not depend on L.
Proposition 6.5.
![]() $\operatorname {deg}_{\mathcal {H}_c}(f)\le 32 (\Delta !)^{14}$
for every
$\operatorname {deg}_{\mathcal {H}_c}(f)\le 32 (\Delta !)^{14}$
for every
![]() $f\in \operatorname {dom}(c)$
.
$f\in \operatorname {dom}(c)$
.
Proof. There are at most
![]() $2\Delta $
choices for
$2\Delta $
choices for
![]() $\alpha _3,\beta _3$
and
$\alpha _3,\beta _3$
and
![]() $z_3$
such that
$z_3$
such that
![]() $f\in P^3_c=P_c(z_3,\alpha _3/\beta _3)$
. There are at most
$f\in P^3_c=P_c(z_3,\alpha _3/\beta _3)$
. There are at most
![]() $\Delta $
choices for
$\Delta $
choices for
![]() $y_3$
, and at most
$y_3$
, and at most
![]() $\Delta !\Delta $
choices for a fan
$\Delta !\Delta $
choices for a fan
![]() $F^3_c$
at
$F^3_c$
at
![]() $x_3$
. For
$x_3$
. For
![]() $P^2_c$
, we deduce that there are at most
$P^2_c$
, we deduce that there are at most
![]() $4(\Delta +1)^2$
choices for
$4(\Delta +1)^2$
choices for
![]() $z_2$
and
$z_2$
and
![]() $\alpha _2,\beta _2$
as the last edge of
$\alpha _2,\beta _2$
as the last edge of
![]() $P^2_c$
has to intersect the first edge of
$P^2_c$
has to intersect the first edge of
![]() $F^3_c$
. Similar estimates hold for
$F^3_c$
. Similar estimates hold for
![]() $F^2_c$
,
$F^2_c$
,
![]() $P^1_c$
and
$P^1_c$
and
![]() $F^1_c$
. Altogether, we get that
$F^1_c$
. Altogether, we get that
as desired.
Proof of Theorem 6.1.
Define a function
![]() $\mathbf {F}(e,f)$
that counts the number of oriented edges from e to f in
$\mathbf {F}(e,f)$
that counts the number of oriented edges from e to f in
![]() $\mathcal {H}_c$
. By (2) Proposition 2.2, we have
$\mathcal {H}_c$
. By (2) Proposition 2.2, we have
 $$ \begin{align} \int_{E}\sum_{f\in [e]_{\mathcal{E}}}\mathbf{F}(e,f)\rho_{\nu}(e,f) \ d\nu(e)=\int_{E}\sum_{e\in [f]_{\mathcal{E}}}\mathbf{F}(e,f) \ d\nu(f). \end{align} $$
$$ \begin{align} \int_{E}\sum_{f\in [e]_{\mathcal{E}}}\mathbf{F}(e,f)\rho_{\nu}(e,f) \ d\nu(e)=\int_{E}\sum_{e\in [f]_{\mathcal{E}}}\mathbf{F}(e,f) \ d\nu(f). \end{align} $$
Using Proposition 6.5, we get an upper bound for the right-hand side of Equation (DC) as
 $$ \begin{align*}\int_{E}\sum_{e\in [f]_{\mathcal{E}}}\mathbf{F}(e,f) \ d\nu(f)\le \int_{\operatorname{dom}(c)}\operatorname{deg}_{\mathcal{H}_c}(f) \ d\nu(f)\le 32 (\Delta!)^{14}.\end{align*} $$
$$ \begin{align*}\int_{E}\sum_{e\in [f]_{\mathcal{E}}}\mathbf{F}(e,f) \ d\nu(f)\le \int_{\operatorname{dom}(c)}\operatorname{deg}_{\mathcal{H}_c}(f) \ d\nu(f)\le 32 (\Delta!)^{14}.\end{align*} $$
Using the definition of
![]() $\mathcal {V}_c(e)$
for
$\mathcal {V}_c(e)$
for
![]() $e\in U_c$
, Proposition 6.4 and Proposition 6.3, we get an lower bound for the left-hand side of Equation (DC) as
$e\in U_c$
, Proposition 6.4 and Proposition 6.3, we get an lower bound for the left-hand side of Equation (DC) as
 $$ \begin{align*} \int_{E}\sum_{f\in [e]_{\mathcal{E}}}\mathbf{F}(e,f)\rho_{\nu}(e,f) \ d\nu(e)= & \ \int_{U_c}\sum_{(f^1,f^2)\in \mathcal{V}_c(e)}\sum_{f\in P^3_c}\rho_{\nu}(e,f) \ d\nu(e)\\ \ge & \ \int_{U_c}\sum_{(f^1,f^2)\in \mathcal{V}_c(e)}\frac{L}{2} \ d\nu(e)\\ \ge & \ \int_{U_c} \frac{1}{(4\Delta)^7}\log^2_{8\Delta}(L)\frac{L}{2} \ d\nu(e)=\frac{1}{2(4\Delta)^7}\log^2_{8\Delta}(L)L\nu(U_c). \end{align*} $$
$$ \begin{align*} \int_{E}\sum_{f\in [e]_{\mathcal{E}}}\mathbf{F}(e,f)\rho_{\nu}(e,f) \ d\nu(e)= & \ \int_{U_c}\sum_{(f^1,f^2)\in \mathcal{V}_c(e)}\sum_{f\in P^3_c}\rho_{\nu}(e,f) \ d\nu(e)\\ \ge & \ \int_{U_c}\sum_{(f^1,f^2)\in \mathcal{V}_c(e)}\frac{L}{2} \ d\nu(e)\\ \ge & \ \int_{U_c} \frac{1}{(4\Delta)^7}\log^2_{8\Delta}(L)\frac{L}{2} \ d\nu(e)=\frac{1}{2(4\Delta)^7}\log^2_{8\Delta}(L)L\nu(U_c). \end{align*} $$
Altogether, we infer that
 $$ \begin{align*}\nu(U_c)\le \frac{64 (4\Delta)^7(\Delta!)^{14}}{\log^2_{8\Delta}(L)L}\end{align*} $$
$$ \begin{align*}\nu(U_c)\le \frac{64 (4\Delta)^7(\Delta!)^{14}}{\log^2_{8\Delta}(L)L}\end{align*} $$
as desired.
7 Proof of the main result
We restate Theorem 1.1, in a compact form, for the convenience of the reader.
Theorem 7.1. Let
![]() $\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
$\mathcal {G}=(V,\mathcal {B},E)$
be a Borel graph such that
![]() $\Delta (\mathcal {G})<\infty $
and
$\Delta (\mathcal {G})<\infty $
and
![]() $\mu \in \mathcal {P}(V)$
. Then there is a Borel map
$\mu \in \mathcal {P}(V)$
. Then there is a Borel map
![]() $c:E\to [\Delta (\mathcal {G})+1]$
that is a proper edge coloring
$c:E\to [\Delta (\mathcal {G})+1]$
that is a proper edge coloring
![]() $\mu $
-almost everywhere.
$\mu $
-almost everywhere.
Proof. Apply Proposition 2.1 to
![]() $\mathcal {G}$
to get
$\mathcal {G}$
to get
![]() $\hat \mu $
, then apply Theorem 5.1 to
$\hat \mu $
, then apply Theorem 5.1 to
![]() $\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
and
$\mathcal {E}=(E,\mathcal {C},I_{\mathcal {G}})$
and
![]() $\hat \mu $
to get
$\hat \mu $
to get
![]() $\nu \in \mathcal {P}(E)$
with the property that
$\nu \in \mathcal {P}(E)$
with the property that
![]() $\rho _\nu (e,f)\le 8\Delta $
for every
$\rho _\nu (e,f)\le 8\Delta $
for every
![]() $e,f\in E$
such that
$e,f\in E$
such that
![]() $(e,f)\in I_{\mathcal {G}}$
, and
$(e,f)\in I_{\mathcal {G}}$
, and
![]() $\mu (\{x\in V:\exists e\in A \ x\in e\})=0$
for every
$\mu (\{x\in V:\exists e\in A \ x\in e\})=0$
for every
![]() $A\in \mathcal {C}$
such that
$A\in \mathcal {C}$
such that
![]() $\nu (A)=0$
.
$\nu (A)=0$
.
Set
![]() $L_n=A\cdot (8\Delta )^n$
, where
$L_n=A\cdot (8\Delta )^n$
, where
![]() $A\in \mathbb {N}$
is such that
$A\in \mathbb {N}$
is such that
![]() $\log _{8\Delta }(L_n)\ge (8\Delta )^{20}$
for every
$\log _{8\Delta }(L_n)\ge (8\Delta )^{20}$
for every
![]() $n\in \mathbb {N}$
, and define inductively, using Theorem 4.2, a sequence
$n\in \mathbb {N}$
, and define inductively, using Theorem 4.2, a sequence
![]() $\{c_n\}_{n\in \mathbb {N}}$
such that
$\{c_n\}_{n\in \mathbb {N}}$
such that
![]() $c_n$
does not admit improvement of weight
$c_n$
does not admit improvement of weight
![]() $L_n$
for every
$L_n$
for every
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
for every
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
The Borel–Cantelli lemma implies that
![]() $c(e)=\lim _{n\to \infty } c_n(e)$
is defined
$c(e)=\lim _{n\to \infty } c_n(e)$
is defined
![]() $\nu $
-almost everywhere as
$\nu $
-almost everywhere as
 $$ \begin{align*} \sum_{n\in \mathbb{N}}L_{n+1}\nu(U_{c_n})\le & \ \sum_{n\in \mathbb{N}}\frac{64 (4\Delta)^7(\Delta!)^{14}L_{n+1}}{\log_{8\Delta}^2(L_n)L_n}\\ = & \ \sum_{n\in \mathbb{N}}\frac{64 (4\Delta)^7(\Delta!)^{14}(8\Delta)^{n+1}}{n^2 (8\Delta)^{n}}=\sum_{n\in \mathbb{N}}\frac{128 (4\Delta)^8(\Delta!)^{14}}{n^2}<\infty \end{align*} $$
$$ \begin{align*} \sum_{n\in \mathbb{N}}L_{n+1}\nu(U_{c_n})\le & \ \sum_{n\in \mathbb{N}}\frac{64 (4\Delta)^7(\Delta!)^{14}L_{n+1}}{\log_{8\Delta}^2(L_n)L_n}\\ = & \ \sum_{n\in \mathbb{N}}\frac{64 (4\Delta)^7(\Delta!)^{14}(8\Delta)^{n+1}}{n^2 (8\Delta)^{n}}=\sum_{n\in \mathbb{N}}\frac{128 (4\Delta)^8(\Delta!)^{14}}{n^2}<\infty \end{align*} $$
by Theorem 6.1. Altogether, this shows that c is correct at
![]() $\mu $
-almost every vertex by the definition of
$\mu $
-almost every vertex by the definition of
![]() $\nu $
.
$\nu $
.
Acknowledgments
I would like to thank Oleg Pikhurko for many insightful discussions and constant support, to Gábor Elek for pointing out the reference [Reference KuhnKuh94] and to the anonymous referee for valuable comments.
Competing interest
The authors have no competing interest to declare.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Financial support
The author was supported by Leverhulme Research Project Grant RPG-2018-424. The main part of this work was carried out while the author was affiliated with University of Warwick.