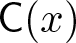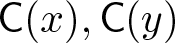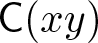1. Introduction
Hilbert’s syzygy theorem is one of the most beautiful theorems in commutative algebra and algebraic geometry. It is considered to be the introduction of homological methods into this area. In today’s language, Hilbert’s theorem states that over a polynomial ring with n variables over a field, any finitely generated module is quasi-isomorphic to a perfect complex of length at most n. During the first half of the twentieth century, the goal was to answer this question for other rings: over which rings can we say that any finitely generated module is quasi-isomorphic to a perfect complex? And during the second half of the century, with the language and the rising importance of derived categories, the question became: over which rings can we say that any bounded complex of finitely generated modules is quasi-isomorphic to a perfect complex? This question motivates the definition of the singularity category (or the stabilized derived category) of a Noetherian ring which is defined as the Verdier quotient of the bounded derived category of finitely generated modules by the (full) subcategory of perfect complexes. Note that this quotient vanishes if and only if every bounded complex of finitely generated modules is quasi-isomorphic to a perfect complex. The name singularity category suggests that there is a geometric connection. Indeed, due to the work of Auslander, Buchsbaum and Serre, we know that the singularity category ![]() $\mathsf{D_{sg}}(R)$ of a commutative Noetherian ring R vanishes if and only if R is regular. Thus, it provides a measure of the singularities of the affine space
$\mathsf{D_{sg}}(R)$ of a commutative Noetherian ring R vanishes if and only if R is regular. Thus, it provides a measure of the singularities of the affine space ![]() $\mathsf{Spec}(R)$.
$\mathsf{Spec}(R)$.
The goal of this paper is to further our understanding of the structure of the singularity category of a commutative Noetherian ring R. Our approach uses the annihilators of the singularity category and our main observation is the following: for any ![]() $x,y \in R$, we have
$x,y \in R$, we have
Let us explain the notation. For each ![]() $r\in R$ we denote by
$r\in R$ we denote by ![]() $\mathsf{C}(r)$ the subcategory of
$\mathsf{C}(r)$ the subcategory of ![]() $\mathsf{D_{sg}}(R)$ consisting of objects X such that the morphism
$\mathsf{D_{sg}}(R)$ consisting of objects X such that the morphism ![]() $X\xrightarrow{r}X$ in
$X\xrightarrow{r}X$ in ![]() $\mathsf{D_{sg}}(R)$ given by the multiplication by r is zero. The subcategory
$\mathsf{D_{sg}}(R)$ given by the multiplication by r is zero. The subcategory ![]() $\mathsf{C}(x) \ast \mathsf{C}(y)$ consists of all objects E that fit into an exact triangle
$\mathsf{C}(x) \ast \mathsf{C}(y)$ consists of all objects E that fit into an exact triangle ![]() $X \to E \to Y \to X[1] $ in
$X \to E \to Y \to X[1] $ in ![]() $\mathsf{D_{sg}}(R)$ with
$\mathsf{D_{sg}}(R)$ with ![]() $X \in \mathsf{C}(x)$ and
$X \in \mathsf{C}(x)$ and ![]() $Y \in \mathsf{C}(y)$. Finally, by
$Y \in \mathsf{C}(y)$. Finally, by ![]() $\operatorname{\mathsf{smd}}(\mathsf{C}(x) \ast \mathsf{C}(y))$, we denote the subcategory consisting of all direct summands of objects belonging to
$\operatorname{\mathsf{smd}}(\mathsf{C}(x) \ast \mathsf{C}(y))$, we denote the subcategory consisting of all direct summands of objects belonging to ![]() $\mathsf{C}(x) \ast \mathsf{C}(y)$. This observation is motivated by a result of Dugas and Leuschke [Reference Dugas and Leuschke8] who proved the special case
$\mathsf{C}(x) \ast \mathsf{C}(y)$. This observation is motivated by a result of Dugas and Leuschke [Reference Dugas and Leuschke8] who proved the special case ![]() $\mathsf{C}(z^{m+n}) = \operatorname{\mathsf{smd}}(\mathsf{C}(z^m) \ast \mathsf{C}(z^n))$ where
$\mathsf{C}(z^{m+n}) = \operatorname{\mathsf{smd}}(\mathsf{C}(z^m) \ast \mathsf{C}(z^n))$ where ![]() $R =S / (f+z^k)$ is the k-fold branched cover of a hypersurface singularity
$R =S / (f+z^k)$ is the k-fold branched cover of a hypersurface singularity ![]() $S/(f)$. We note that if
$S/(f)$. We note that if ![]() $\mathsf{C}(xy) = \mathsf{D_{sg}}(R)$, then (1.0.1) gives a decomposition of the singularity category. This is the first part of our main theorem. In fact, using the associativity of the
$\mathsf{C}(xy) = \mathsf{D_{sg}}(R)$, then (1.0.1) gives a decomposition of the singularity category. This is the first part of our main theorem. In fact, using the associativity of the ![]() $\ast$ operator, we have the following.
$\ast$ operator, we have the following.
Theorem A.
Let ![]() $x_1,\dots,x_n$ be elements of a commutative Noetherian ring R such that the product
$x_1,\dots,x_n$ be elements of a commutative Noetherian ring R such that the product ![]() $x_1\cdots x_n$ belongs to
$x_1\cdots x_n$ belongs to ![]() $\operatorname{ann}\mathsf{D_{sg}}(R)$. Then
$\operatorname{ann}\mathsf{D_{sg}}(R)$. Then
The second part of our main theorem concerns the dimension of the singularity category of a commutative Noetherian ring. Recall that the (Rouquier) dimension ![]() $\dim\mathcal{T}$ of a triangulated category
$\dim\mathcal{T}$ of a triangulated category ![]() $\mathcal{T}$ is an invariant which measures how much it costs to build it from a single object using the “free” operations of finite direct sums, direct summands and shift and the cone operation which costs “1 unit” each time it is applied.
$\mathcal{T}$ is an invariant which measures how much it costs to build it from a single object using the “free” operations of finite direct sums, direct summands and shift and the cone operation which costs “1 unit” each time it is applied.
Theorem B.
Let ![]() $x_1,\dots,x_n$ be elements of a commutative Noetherian ring R such that the product
$x_1,\dots,x_n$ be elements of a commutative Noetherian ring R such that the product ![]() $x_1\cdots x_n$ belongs to
$x_1\cdots x_n$ belongs to ![]() $\operatorname{ann}\mathsf{D_{sg}}(R)$. If no xi is a unit or a zerodivisor, then there is an inequality:
$\operatorname{ann}\mathsf{D_{sg}}(R)$. If no xi is a unit or a zerodivisor, then there is an inequality:
 \begin{equation*}
\dim\mathsf{D_{sg}}(R)\le\sum_{i=1}^n\dim\mathsf{D_{sg}}(R/x_iR)+n-1.
\end{equation*}
\begin{equation*}
\dim\mathsf{D_{sg}}(R)\le\sum_{i=1}^n\dim\mathsf{D_{sg}}(R/x_iR)+n-1.
\end{equation*} In these theorems, ![]() $\operatorname{ann}\mathsf{D_{sg}}(R)$ is the annihilator of the singularity category which is defined as the ideal of R consisting of elements r such that
$\operatorname{ann}\mathsf{D_{sg}}(R)$ is the annihilator of the singularity category which is defined as the ideal of R consisting of elements r such that ![]() $\mathsf{C}(r) = \mathsf{D_{sg}}(R)$. We prove these theorems in
$\mathsf{C}(r) = \mathsf{D_{sg}}(R)$. We prove these theorems in ![]() $\S$ 2 after providing the necessary background and preliminaries. It is worth comparing them with similar results shown in [Reference Iyengar and Takahashi10, Reference Shimada and Takahashi15].
$\S$ 2 after providing the necessary background and preliminaries. It is worth comparing them with similar results shown in [Reference Iyengar and Takahashi10, Reference Shimada and Takahashi15].
In ![]() $\S$ 3, we consider the case of a sequence elements. After proving a weaker version of Theorem A, we prove the following.
$\S$ 3, we consider the case of a sequence elements. After proving a weaker version of Theorem A, we prove the following.
Theorem C.
Let ![]() $\boldsymbol{x} = x_1, \ldots, x_n$ a regular sequence on R such that
$\boldsymbol{x} = x_1, \ldots, x_n$ a regular sequence on R such that ![]() $x_1^{m_1}, \ldots, x_n^{m_n} \in \operatorname{ann} \mathsf{D_{sg}}(R)$ for some positive integers
$x_1^{m_1}, \ldots, x_n^{m_n} \in \operatorname{ann} \mathsf{D_{sg}}(R)$ for some positive integers ![]() $m_1, \ldots, m_n$. Assume that
$m_1, \ldots, m_n$. Assume that ![]() $a_1, \cdots, a_n$ are non-negative integers such that
$a_1, \cdots, a_n$ are non-negative integers such that ![]() $x_1^{a_1}\cdots x_n^{a_n} \in \operatorname{ann} \mathsf{D_{sg}}(R)$. Put
$x_1^{a_1}\cdots x_n^{a_n} \in \operatorname{ann} \mathsf{D_{sg}}(R)$. Put  $\omega = m_1 \cdots m_n \left( \dfrac{a_1}{m_1} + \cdots + \dfrac{a_n}{m_n} \right)$. Then, we have
$\omega = m_1 \cdots m_n \left( \dfrac{a_1}{m_1} + \cdots + \dfrac{a_n}{m_n} \right)$. Then, we have
In particular, ![]() $\dim \mathsf{D_{sg}}(R) \leq m\,( \dim \mathsf{D_{sg}}(R/\boldsymbol{x} R) + 1) - 1$, where
$\dim \mathsf{D_{sg}}(R) \leq m\,( \dim \mathsf{D_{sg}}(R/\boldsymbol{x} R) + 1) - 1$, where ![]() $m=m_1\cdots m_n$.
$m=m_1\cdots m_n$.
We dedicate ![]() $\S$ 4 to examples and applications of these theorems. We compute several examples and discuss the case of isolated singularitie s: When
$\S$ 4 to examples and applications of these theorems. We compute several examples and discuss the case of isolated singularitie s: When ![]() $\dim \mathsf{D_{sg}}(R)$ is finite, the vanishing locus of
$\dim \mathsf{D_{sg}}(R)$ is finite, the vanishing locus of ![]() $\operatorname{ann} \mathsf{D_{sg}}(R)$ is the singular locus of R. In particular, if
$\operatorname{ann} \mathsf{D_{sg}}(R)$ is the singular locus of R. In particular, if ![]() $(R, \mathfrak{m})$ is a local ring with an isolated singularity for which
$(R, \mathfrak{m})$ is a local ring with an isolated singularity for which ![]() $\dim \mathsf{D_{sg}}(R) \lt \infty$, then
$\dim \mathsf{D_{sg}}(R) \lt \infty$, then ![]() $\operatorname{ann} \mathsf{D_{sg}}(R)$ is
$\operatorname{ann} \mathsf{D_{sg}}(R)$ is ![]() $\mathfrak{m}$-primary. In this case, for any
$\mathfrak{m}$-primary. In this case, for any ![]() $x \in \mathfrak{m}$, we have
$x \in \mathfrak{m}$, we have ![]() $x^n \in \operatorname{ann} \mathsf{D_{sg}}(R)$ for some positive integer n. If we define
$x^n \in \operatorname{ann} \mathsf{D_{sg}}(R)$ for some positive integer n. If we define ![]() $\alpha(x) = \min\{n \mid x^n \in \operatorname{ann} \mathsf{D_{sg}}(R) \}$, then we have the following corollary.
$\alpha(x) = \min\{n \mid x^n \in \operatorname{ann} \mathsf{D_{sg}}(R) \}$, then we have the following corollary.
Corollary D.
Let ![]() $(R, \mathfrak{m})$ be a commutative Noetherian local ring with an isolated singularity. If
$(R, \mathfrak{m})$ be a commutative Noetherian local ring with an isolated singularity. If ![]() $\dim \mathsf{D_{sg}}(R) \lt \infty$, then
$\dim \mathsf{D_{sg}}(R) \lt \infty$, then
where x runs over the non-zerodivisors in ![]() $\mathfrak{m}$. In particular, if
$\mathfrak{m}$. In particular, if ![]() $\dim \mathsf{D_{sg}}(R/xR) = 0$ for some non-zerodivisor
$\dim \mathsf{D_{sg}}(R/xR) = 0$ for some non-zerodivisor ![]() $x\in\mathfrak{m}$, then
$x\in\mathfrak{m}$, then ![]() $\dim \mathsf{D_{sg}}(R) \leq \alpha(x) - 1$.
$\dim \mathsf{D_{sg}}(R) \leq \alpha(x) - 1$.
2. Proof of the main theorem
In this section, we introduce and prove preliminaries about the subcategories which appear in our main observation 1.0.1. Let us start with the conventions and the definitions that we will use.
Convention 2.1.
Throughout the rest of this section, let R be a commutative Noetherian ring. Denote by ![]() $\operatorname{mod} R$ the category of finitely generated R-modules. Denote by
$\operatorname{mod} R$ the category of finitely generated R-modules. Denote by ![]() $\mathsf{D^b}(R)$ the bounded derived category of
$\mathsf{D^b}(R)$ the bounded derived category of ![]() $\operatorname{mod} R$. Let
$\operatorname{mod} R$. Let ![]() $\mathsf{D_{sg}}(R)$ stand for the singularity category of R, which is by definition the Verdier quotient of
$\mathsf{D_{sg}}(R)$ stand for the singularity category of R, which is by definition the Verdier quotient of ![]() $\mathsf{D^b}(R)$ by the perfect complexes. We assume that all R-modules are finitely generated and all subcategories are strictly full. We may omit subscripts/superscripts unless there is a danger of confusion.
$\mathsf{D^b}(R)$ by the perfect complexes. We assume that all R-modules are finitely generated and all subcategories are strictly full. We may omit subscripts/superscripts unless there is a danger of confusion.
(1) For an element
 $x\in R$, we denote by
$x\in R$, we denote by  $\mathsf{C}(x)$ the subcategory of
$\mathsf{C}(x)$ the subcategory of  $\mathsf{D_{sg}}(R)$ consisting of objects X such that the morphism
$\mathsf{D_{sg}}(R)$ consisting of objects X such that the morphism  $X\xrightarrow{x}X$ in
$X\xrightarrow{x}X$ in  $\mathsf{D_{sg}}(R)$ given by the multiplication by x is zero. Note that
$\mathsf{D_{sg}}(R)$ given by the multiplication by x is zero. Note that  $\mathsf{C}(x)$ is closed under finite direct sums, direct summands and shifts.
$\mathsf{C}(x)$ is closed under finite direct sums, direct summands and shifts.(2) Let
 $\mathcal{A}$ be an additive category. For a subcategory
$\mathcal{A}$ be an additive category. For a subcategory  $\mathcal{X}$ of
$\mathcal{X}$ of  $\mathcal{A}$, we denote by
$\mathcal{A}$, we denote by  $\operatorname{\mathsf{smd}}_\mathcal{A}\mathcal{X}$ the subcategory of
$\operatorname{\mathsf{smd}}_\mathcal{A}\mathcal{X}$ the subcategory of  $\mathcal{A}$ consisting of direct summands of objects in
$\mathcal{A}$ consisting of direct summands of objects in  $\mathcal{X}$.
$\mathcal{X}$.(3) Let
 $\mathcal{T}$ be a triangulated category. For subcategories
$\mathcal{T}$ be a triangulated category. For subcategories  $\mathcal{X},\mathcal{Y}$ of
$\mathcal{X},\mathcal{Y}$ of  $\mathcal{T}$, we denote by
$\mathcal{T}$, we denote by  $\mathcal{X}\ast\mathcal{Y}$ the subcategory of
$\mathcal{X}\ast\mathcal{Y}$ the subcategory of  $\mathcal{T}$ consisting of objects
$\mathcal{T}$ consisting of objects  $E\in\mathcal{T}$ such that there exists an exact triangle
$E\in\mathcal{T}$ such that there exists an exact triangle  $X\to E\to Y\to X[1]$ in
$X\to E\to Y\to X[1]$ in  $\mathcal{T}$ with
$\mathcal{T}$ with  $X\in\mathcal{X}$ and
$X\in\mathcal{X}$ and  $Y\in\mathcal{Y}$. Using the octahedral axiom, one easily sees that
$Y\in\mathcal{Y}$. Using the octahedral axiom, one easily sees that  $-\ast-$ is associative: the equality
$-\ast-$ is associative: the equality  $(\mathcal{X}\ast\mathcal{Y})\ast\mathcal{Z}=\mathcal{X}\ast(\mathcal{Y}\ast\mathcal{Z})$ holds for subcategories
$(\mathcal{X}\ast\mathcal{Y})\ast\mathcal{Z}=\mathcal{X}\ast(\mathcal{Y}\ast\mathcal{Z})$ holds for subcategories  $\mathcal{X},\mathcal{Y},\mathcal{Z}$ of
$\mathcal{X},\mathcal{Y},\mathcal{Z}$ of  $\mathcal{T}$. Hence there is no confusion in writing
$\mathcal{T}$. Hence there is no confusion in writing  $\mathcal{X}_1\ast\cdots\ast\mathcal{X}_n$ for subcategories
$\mathcal{X}_1\ast\cdots\ast\mathcal{X}_n$ for subcategories  $\mathcal{X}_1,\dots,\mathcal{X}_n$ of
$\mathcal{X}_1,\dots,\mathcal{X}_n$ of  $\mathcal{T}$.
$\mathcal{T}$.(4) For a sequence
 $\boldsymbol{x}=x_1,\dots,x_n$ of elements of R, we denote by
$\boldsymbol{x}=x_1,\dots,x_n$ of elements of R, we denote by  $\operatorname{K}(\boldsymbol{x})$ the Koszul complex of x over R.
$\operatorname{K}(\boldsymbol{x})$ the Koszul complex of x over R.
Remark 2.3. Let ![]() $T\in\mathsf{D^b}(R)$. In general, taking derived tensor product
$T\in\mathsf{D^b}(R)$. In general, taking derived tensor product ![]() $T\otimes^{\mathbf{L}}_R-$ does not preserve an isomorphism in
$T\otimes^{\mathbf{L}}_R-$ does not preserve an isomorphism in ![]() $\mathsf{D_{sg}}(R)$, but it does if T is isomorphic to a perfect complex. To be precise, let P be a perfect complex over R. Let
$\mathsf{D_{sg}}(R)$, but it does if T is isomorphic to a perfect complex. To be precise, let P be a perfect complex over R. Let  $(X\xleftarrow{s}Z\xrightarrow{f}Y)$ be a morphism in
$(X\xleftarrow{s}Z\xrightarrow{f}Y)$ be a morphism in ![]() $\mathsf{D_{sg}}(R)$, that is, s and f are morphisms in
$\mathsf{D_{sg}}(R)$, that is, s and f are morphisms in ![]() $\mathsf{D^b}(R)$ such that the mapping cone
$\mathsf{D^b}(R)$ such that the mapping cone ![]() $\operatorname{cone}(s)$ of s is isomorphic to a perfect complex. Then
$\operatorname{cone}(s)$ of s is isomorphic to a perfect complex. Then  $(P\otimes^{\mathbf{L}}_RX\xleftarrow{P\otimes^{\mathbf{L}}_Rs}P\otimes^{\mathbf{L}}_RZ\xrightarrow{P\otimes^{\mathbf{L}}_Rf}P\otimes^{\mathbf{L}}_RY)$ is a morphism in
$(P\otimes^{\mathbf{L}}_RX\xleftarrow{P\otimes^{\mathbf{L}}_Rs}P\otimes^{\mathbf{L}}_RZ\xrightarrow{P\otimes^{\mathbf{L}}_Rf}P\otimes^{\mathbf{L}}_RY)$ is a morphism in ![]() $\mathsf{D_{sg}}(R)$, since
$\mathsf{D_{sg}}(R)$, since ![]() $\operatorname{cone}(P\otimes^{\mathbf{L}}_Rs)$ is isomorphic to a perfect complex. One sees that the functor
$\operatorname{cone}(P\otimes^{\mathbf{L}}_Rs)$ is isomorphic to a perfect complex. One sees that the functor ![]() $P\otimes^{\mathbf{L}}_R-:\mathsf{D^b}(R)\to\mathsf{D^b}(R)$ induces a functor
$P\otimes^{\mathbf{L}}_R-:\mathsf{D^b}(R)\to\mathsf{D^b}(R)$ induces a functor ![]() $\mathsf{D_{sg}}(R)\to\mathsf{D_{sg}}(R)$. In particular, the implication:
$\mathsf{D_{sg}}(R)\to\mathsf{D_{sg}}(R)$. In particular, the implication:
holds for any objects ![]() $X,Y$ of
$X,Y$ of ![]() $\mathsf{D_{sg}}(R)$ and any sequence
$\mathsf{D_{sg}}(R)$ and any sequence ![]() $\boldsymbol{x}=x_1,\dots,x_n$ in R.
$\boldsymbol{x}=x_1,\dots,x_n$ in R.
The first part of the following lemma shows us the role that the Koszul complex plays in the rest of the section.
(1) Let
 $x\in R$. Then
$x\in R$. Then  $\mathsf{C}(x)=\operatorname{\mathsf{smd}}\{\operatorname{K}(x)\otimes X\mid X\in\mathsf{D_{sg}}(R)\}$.
$\mathsf{C}(x)=\operatorname{\mathsf{smd}}\{\operatorname{K}(x)\otimes X\mid X\in\mathsf{D_{sg}}(R)\}$.(2) Let
 $x,y\in R$. Let
$x,y\in R$. Let  $A\to B\to C\to A[1]$ be an exact triangle in
$A\to B\to C\to A[1]$ be an exact triangle in  $\mathsf{D_{sg}}(R)$. If
$\mathsf{D_{sg}}(R)$. If  $A\in\mathsf{C}(x)$ and
$A\in\mathsf{C}(x)$ and  $C\in\mathsf{C}(y)$, then
$C\in\mathsf{C}(y)$, then  $B\in\mathsf{C}(xy)$.
$B\in\mathsf{C}(xy)$.
(1) The chain map
 $\operatorname{K}(x)\xrightarrow{x}\operatorname{K}(x)$ given by multiplication by x is null-homotopic by [Reference Bruns and Herzog3, Proposition 1.6.5(a)], which shows the inclusion
$\operatorname{K}(x)\xrightarrow{x}\operatorname{K}(x)$ given by multiplication by x is null-homotopic by [Reference Bruns and Herzog3, Proposition 1.6.5(a)], which shows the inclusion  $(\supseteq)$. To show the inclusion
$(\supseteq)$. To show the inclusion  $(\subseteq)$, pick an object
$(\subseteq)$, pick an object  $Y\in\mathsf{C}(x)$. There is an exact triangle
$Y\in\mathsf{C}(x)$. There is an exact triangle  $R\xrightarrow{x}R\to\operatorname{K}(x)\to R[1]$ in
$R\xrightarrow{x}R\to\operatorname{K}(x)\to R[1]$ in  $\mathsf{D^b}(R)$. Tensoring the complex Y, we get an exact triangle:
(2.4.1)
$\mathsf{D^b}(R)$. Tensoring the complex Y, we get an exact triangle:
(2.4.1) \begin{equation}
Y\xrightarrow{x}Y\to\operatorname{K}(x)\otimes Y\to Y[1],
\end{equation}
\begin{equation}
Y\xrightarrow{x}Y\to\operatorname{K}(x)\otimes Y\to Y[1],
\end{equation}in
 $\mathsf{D^b}(R)$. Since
$\mathsf{D^b}(R)$. Since  $(Y\xrightarrow{x}Y)=0$ in
$(Y\xrightarrow{x}Y)=0$ in  $\mathsf{D_{sg}}(R)$, the image of (2.4.1) in
$\mathsf{D_{sg}}(R)$, the image of (2.4.1) in  $\mathsf{D_{sg}}(R)$ yields an isomorphism:
(2.4.2)
$\mathsf{D_{sg}}(R)$ yields an isomorphism:
(2.4.2) \begin{equation}
\operatorname{K}(x)\otimes Y\cong Y\oplus Y[1],
\end{equation}
\begin{equation}
\operatorname{K}(x)\otimes Y\cong Y\oplus Y[1],
\end{equation}in
 $\mathsf{D_{sg}}(R)$.
$\mathsf{D_{sg}}(R)$.(2) The argument given in [Reference Iyengar and Takahashi10, Remark 2.6] shows the assertion.
Before proving our main observation, we need one more technical lemma. This lemma is standard and a proof can be found in [Reference Bondal and van den Bergh2, Lemma 2.2.1].
Lemma 2.5. Let ![]() $\mathcal{T}$ be a triangulated category. Let
$\mathcal{T}$ be a triangulated category. Let ![]() $\mathcal{X},\mathcal{Y}$ be subcategories of
$\mathcal{X},\mathcal{Y}$ be subcategories of ![]() $\mathcal{T}$. Then, there are equalities:
$\mathcal{T}$. Then, there are equalities:
Now we are ready to prove our main observation. We note once again that this observation works in the generality of all commutative Noetherian rings.
Proposition 2.6. Let ![]() $x_1,\dots,x_n\in R$. Then there is an equality
$x_1,\dots,x_n\in R$. Then there is an equality
Proof. In view of Lemma 2.5, it suffices to show that ![]() $\mathsf{C}(xy)=\operatorname{\mathsf{smd}}(\mathsf{C}(x)\ast\mathsf{C}(y))$ for
$\mathsf{C}(xy)=\operatorname{\mathsf{smd}}(\mathsf{C}(x)\ast\mathsf{C}(y))$ for ![]() $x,y\in R$. Indeed, if we have done it and if
$x,y\in R$. Indeed, if we have done it and if ![]() $\mathsf{C}(x_1\cdots x_{n-1})=\operatorname{\mathsf{smd}}(\mathsf{C}(x_1)\ast\cdots\ast\mathsf{C}(x_{n-1}))$, then we will have:
$\mathsf{C}(x_1\cdots x_{n-1})=\operatorname{\mathsf{smd}}(\mathsf{C}(x_1)\ast\cdots\ast\mathsf{C}(x_{n-1}))$, then we will have:
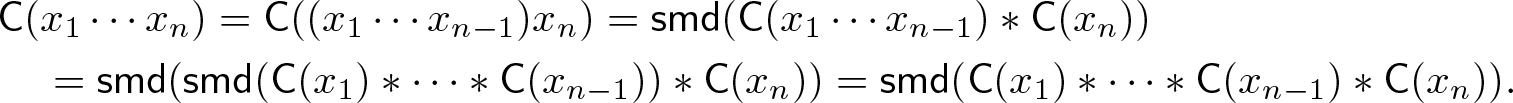 \begin{multline*}
\mathsf{C}(x_1\cdots x_n)
=\mathsf{C}((x_1\cdots x_{n-1})x_n)
=\operatorname{\mathsf{smd}}(\mathsf{C}(x_1\cdots x_{n-1})\ast\mathsf{C}(x_n))\\
=\operatorname{\mathsf{smd}}(\operatorname{\mathsf{smd}}(\mathsf{C}(x_1)\ast\cdots\ast\mathsf{C}(x_{n-1}))\ast\mathsf{C}(x_n))
=\operatorname{\mathsf{smd}}(\mathsf{C}(x_1)\ast\cdots\ast\mathsf{C}(x_{n-1})\ast\mathsf{C}(x_n)).
\end{multline*}
\begin{multline*}
\mathsf{C}(x_1\cdots x_n)
=\mathsf{C}((x_1\cdots x_{n-1})x_n)
=\operatorname{\mathsf{smd}}(\mathsf{C}(x_1\cdots x_{n-1})\ast\mathsf{C}(x_n))\\
=\operatorname{\mathsf{smd}}(\operatorname{\mathsf{smd}}(\mathsf{C}(x_1)\ast\cdots\ast\mathsf{C}(x_{n-1}))\ast\mathsf{C}(x_n))
=\operatorname{\mathsf{smd}}(\mathsf{C}(x_1)\ast\cdots\ast\mathsf{C}(x_{n-1})\ast\mathsf{C}(x_n)).
\end{multline*} Let us show the inclusion ![]() $\mathsf{C}(xy)\subseteq\operatorname{\mathsf{smd}}(\mathsf{C}(x)\ast\mathsf{C}(y))$. Pick an object
$\mathsf{C}(xy)\subseteq\operatorname{\mathsf{smd}}(\mathsf{C}(x)\ast\mathsf{C}(y))$. Pick an object ![]() $A\in\mathsf{C}(xy)$. Applying the octahedral axiom, we get a commutative diagram:
$A\in\mathsf{C}(xy)$. Applying the octahedral axiom, we get a commutative diagram:
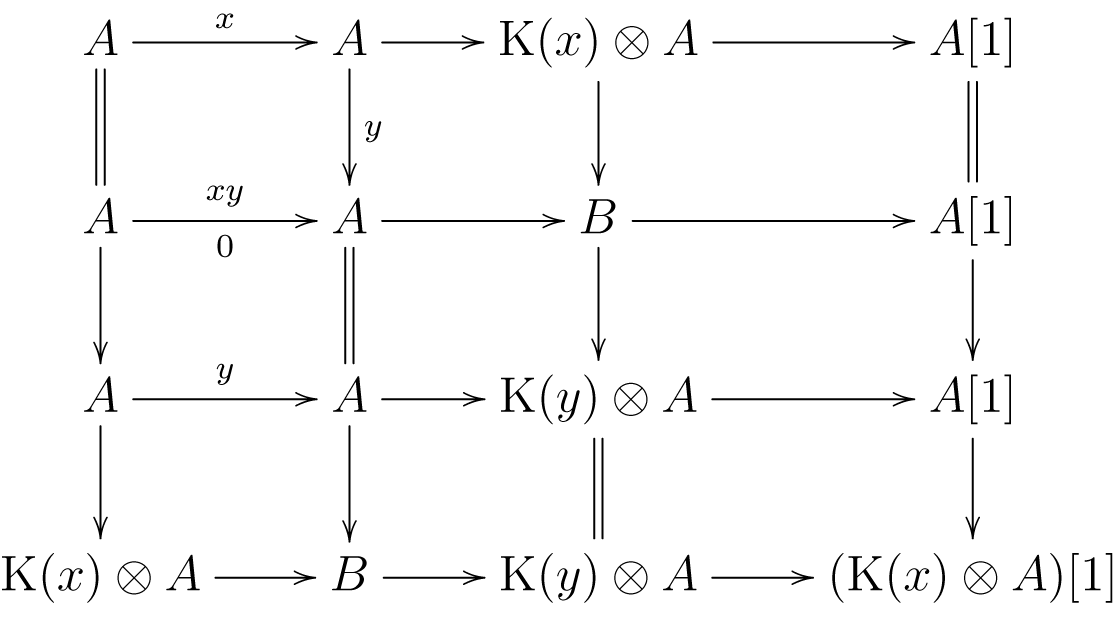
in ![]() $\mathsf{D_{sg}}(R)$ whose rows are exact triangles. The second row implies
$\mathsf{D_{sg}}(R)$ whose rows are exact triangles. The second row implies ![]() $B\cong A\oplus A[1]$, while the bottom row shows
$B\cong A\oplus A[1]$, while the bottom row shows ![]() $B\in\mathsf{C}(x)\ast\mathsf{C}(y)$ by Lemma 2.4(1). Therefore, A belongs to
$B\in\mathsf{C}(x)\ast\mathsf{C}(y)$ by Lemma 2.4(1). Therefore, A belongs to ![]() $\operatorname{\mathsf{smd}}(\mathsf{C}(x)\ast\mathsf{C}(y))$.
$\operatorname{\mathsf{smd}}(\mathsf{C}(x)\ast\mathsf{C}(y))$.
Let us show the inclusion ![]() $\mathsf{C}(xy)\supseteq\operatorname{\mathsf{smd}}(\mathsf{C}(x)\ast\mathsf{C}(y))$. Pick
$\mathsf{C}(xy)\supseteq\operatorname{\mathsf{smd}}(\mathsf{C}(x)\ast\mathsf{C}(y))$. Pick ![]() $A\in\operatorname{\mathsf{smd}}(\mathsf{C}(x)\ast\mathsf{C}(y))$. Then
$A\in\operatorname{\mathsf{smd}}(\mathsf{C}(x)\ast\mathsf{C}(y))$. Then ![]() $A\oplus B\in\mathsf{C}(x)\ast\mathsf{C}(y)$ for some
$A\oplus B\in\mathsf{C}(x)\ast\mathsf{C}(y)$ for some ![]() $B\in\mathsf{D_{sg}}(R)$, and there exists an exact triangle
$B\in\mathsf{D_{sg}}(R)$, and there exists an exact triangle ![]() $C\to A\oplus B\to D\to C[1]$ in
$C\to A\oplus B\to D\to C[1]$ in ![]() $\mathsf{D_{sg}}(R)$ such that
$\mathsf{D_{sg}}(R)$ such that ![]() $C\in\mathsf{C}(x)$ and
$C\in\mathsf{C}(x)$ and ![]() $D\in\mathsf{C}(y)$. Lemma 2.4(2) says that
$D\in\mathsf{C}(y)$. Lemma 2.4(2) says that ![]() $A\oplus B$ is in
$A\oplus B$ is in ![]() $\mathsf{C}(xy)$, and so is its direct summand A.
$\mathsf{C}(xy)$, and so is its direct summand A.
We are interested in the situation where the left hand side of the equality in the preceding proposition is the entire singularity category. That is, we would like to consider the case where for any object in the bounded derived category, multiplication by ![]() $x_1 \cdots x_n$ factors through a perfect complex. Let us make this more precise and introduce notation with the following definition.
$x_1 \cdots x_n$ factors through a perfect complex. Let us make this more precise and introduce notation with the following definition.
Definition 2.7. We introduce two kinds of annihilators as follows.
(1) The annihilator of an object
 $X\in\mathsf{D_{sg}}(R)$ is defined by:
$X\in\mathsf{D_{sg}}(R)$ is defined by:
 \begin{align*}
\operatorname{ann}_{\mathsf{D_{sg}}(R)}X
&=\{a\in R\mid(X\xrightarrow{a}X)=0\ \text{in }\mathsf{D_{sg}}(R)\}\\
&=\{a\in R\mid X\in\mathsf{C}(a)\}=\operatorname{ann}_R(\operatorname{End}_{\mathsf{D_{sg}}(R)}(X)).
\end{align*}
\begin{align*}
\operatorname{ann}_{\mathsf{D_{sg}}(R)}X
&=\{a\in R\mid(X\xrightarrow{a}X)=0\ \text{in }\mathsf{D_{sg}}(R)\}\\
&=\{a\in R\mid X\in\mathsf{C}(a)\}=\operatorname{ann}_R(\operatorname{End}_{\mathsf{D_{sg}}(R)}(X)).
\end{align*}(2) The annihilator
 $\operatorname{ann}\mathsf{D_{sg}}(R)$ of the category
$\operatorname{ann}\mathsf{D_{sg}}(R)$ of the category  $\mathsf{D_{sg}}(R)$ is defined by:
$\mathsf{D_{sg}}(R)$ is defined by:
 \begin{align*}
\operatorname{ann}\mathsf{D_{sg}}(R)&=\{a\in R\mid(X\xrightarrow{a}X)=0\ \text{for all }X\in\mathsf{D_{sg}}(R)\}\\
&=\{a\in R\mid\mathsf{C}(a)=\mathsf{D_{sg}}(R)\}
=\bigcap_{X\in\mathsf{D_{sg}}(R)}{\operatorname{ann}}_{\mathsf{D_{sg}}(R)}X.
\end{align*}
\begin{align*}
\operatorname{ann}\mathsf{D_{sg}}(R)&=\{a\in R\mid(X\xrightarrow{a}X)=0\ \text{for all }X\in\mathsf{D_{sg}}(R)\}\\
&=\{a\in R\mid\mathsf{C}(a)=\mathsf{D_{sg}}(R)\}
=\bigcap_{X\in\mathsf{D_{sg}}(R)}{\operatorname{ann}}_{\mathsf{D_{sg}}(R)}X.
\end{align*}
Note that both of the annihilators ![]() ${\operatorname{ann}}_{\mathsf{D_{sg}}(R)}X$ and
${\operatorname{ann}}_{\mathsf{D_{sg}}(R)}X$ and ![]() $\operatorname{ann}\mathsf{D_{sg}}(R)$ are ideals of R.
$\operatorname{ann}\mathsf{D_{sg}}(R)$ are ideals of R.
Now we recall the definition of the dimension of a triangulated category.
Definition 2.8. Let ![]() $\mathcal{T}$ be a triangulated category.
$\mathcal{T}$ be a triangulated category.
(1) Let
 $\mathcal{X}$ be a subcategory of
$\mathcal{X}$ be a subcategory of  $\mathcal{T}$. We denote by
$\mathcal{T}$. We denote by  $\langle \mathcal{X}\rangle$ the additive closure:
$\langle \mathcal{X}\rangle$ the additive closure:
 \begin{equation*}
\operatorname{add}\{X[i]\mid X\in\mathcal{X},i\in\mathbb{Z}\},
\end{equation*}
\begin{equation*}
\operatorname{add}\{X[i]\mid X\in\mathcal{X},i\in\mathbb{Z}\},
\end{equation*}in
 $\mathcal{T}$, that is, the smallest subcategory of
$\mathcal{T}$, that is, the smallest subcategory of  $\mathcal{T}$ containing
$\mathcal{T}$ containing  $\mathcal{X}$ and closed under finite direct sums, direct summands and shifts. We set
$\mathcal{X}$ and closed under finite direct sums, direct summands and shifts. We set  $\langle\mathcal{X}\rangle_0^{\mathcal{T}}=0$ and define
$\langle\mathcal{X}\rangle_0^{\mathcal{T}}=0$ and define  $\langle \mathcal{X} \rangle_n^\mathcal{T} = \langle\langle \mathcal{X} \rangle_{n-1}^\mathcal{T} \ast\langle\mathcal{X}\rangle\rangle$ by induction for any
$\langle \mathcal{X} \rangle_n^\mathcal{T} = \langle\langle \mathcal{X} \rangle_{n-1}^\mathcal{T} \ast\langle\mathcal{X}\rangle\rangle$ by induction for any  $n \geq 1$. Note that
$n \geq 1$. Note that  $\langle\mathcal{X}\rangle_1=\langle\mathcal{X}\rangle$. When
$\langle\mathcal{X}\rangle_1=\langle\mathcal{X}\rangle$. When  $\mathcal{X}$ consists of a single object T, we simply write
$\mathcal{X}$ consists of a single object T, we simply write  $\langle T\rangle_n$ instead of
$\langle T\rangle_n$ instead of  $\langle\mathcal{X}\rangle_n$.
$\langle\mathcal{X}\rangle_n$.(2) The (Rouquier) dimension of
 $\mathcal{T}$ is defined by:
$\mathcal{T}$ is defined by:
 \begin{equation*}
\dim\mathcal{T}=\inf\{n\ge0\mid\langle G\rangle_{n+1}=\mathcal{T}\ \text{for some}\ G\in\mathcal{T}\}.
\end{equation*}
\begin{equation*}
\dim\mathcal{T}=\inf\{n\ge0\mid\langle G\rangle_{n+1}=\mathcal{T}\ \text{for some}\ G\in\mathcal{T}\}.
\end{equation*}
We are now ready to give the main application of our main observation.
Theorem 2.9. Let ![]() $x_1,\dots,x_n$ be elements of R such that the product
$x_1,\dots,x_n$ be elements of R such that the product ![]() $x_1\cdots x_n$ belongs to
$x_1\cdots x_n$ belongs to ![]() $\operatorname{ann}\mathsf{D_{sg}}(R)$. Then
$\operatorname{ann}\mathsf{D_{sg}}(R)$. Then
If no xi is a unit or a zerodivisor, then there is an inequality:
 \begin{equation*}
\dim\mathsf{D_{sg}}(R)\le\sum_{i=1}^n\dim\mathsf{D_{sg}}(R/x_iR)+n-1.
\end{equation*}
\begin{equation*}
\dim\mathsf{D_{sg}}(R)\le\sum_{i=1}^n\dim\mathsf{D_{sg}}(R/x_iR)+n-1.
\end{equation*}Proof. It immediately follows from Proposition 2.6 that: ![]() $\mathsf{D_{sg}}(R)=\operatorname{\mathsf{smd}}(\mathsf{C}(x_1)\ast\cdots\ast\mathsf{C}(x_n))$. Let us show the dimension inequality. Since each xi is a non-unit,
$\mathsf{D_{sg}}(R)=\operatorname{\mathsf{smd}}(\mathsf{C}(x_1)\ast\cdots\ast\mathsf{C}(x_n))$. Let us show the dimension inequality. Since each xi is a non-unit, ![]() $R/x_iR$ is not a zero ring. We may assume
$R/x_iR$ is not a zero ring. We may assume ![]() $\dim\mathsf{D_{sg}}(R/x_iR)=:d_i \lt \infty$ for each i. There exists an object
$\dim\mathsf{D_{sg}}(R/x_iR)=:d_i \lt \infty$ for each i. There exists an object ![]() $G_i\in\mathsf{D_{sg}}(R/x_iR)$ such that
$G_i\in\mathsf{D_{sg}}(R/x_iR)$ such that  $\mathsf{D_{sg}}(R/x_iR)=\langle G_i\rangle_{d_i+1}^{\mathsf{D_{sg}}(R/x_iR)}$. Since xi is a non-zerodivisor, we have
$\mathsf{D_{sg}}(R/x_iR)=\langle G_i\rangle_{d_i+1}^{\mathsf{D_{sg}}(R/x_iR)}$. Since xi is a non-zerodivisor, we have
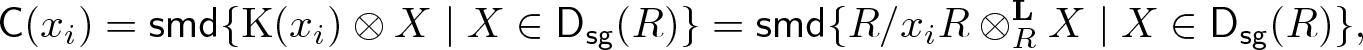 \begin{equation*}
\mathsf{C}(x_i)=\operatorname{\mathsf{smd}}\{\operatorname{K}(x_i)\otimes X\mid X\in\mathsf{D_{sg}}(R)\}=\operatorname{\mathsf{smd}}\{R/x_iR\otimes^{\mathbf{L}}_RX\mid X\in\mathsf{D_{sg}}(R)\},
\end{equation*}
\begin{equation*}
\mathsf{C}(x_i)=\operatorname{\mathsf{smd}}\{\operatorname{K}(x_i)\otimes X\mid X\in\mathsf{D_{sg}}(R)\}=\operatorname{\mathsf{smd}}\{R/x_iR\otimes^{\mathbf{L}}_RX\mid X\in\mathsf{D_{sg}}(R)\},
\end{equation*}by Lemma 2.4(1), and
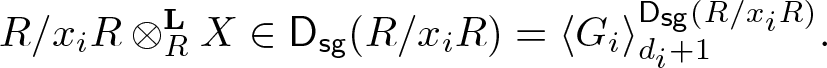 \begin{equation}
R/x_iR\otimes^{\mathbf{L}}_RX\in\mathsf{D_{sg}}(R/x_iR)=\langle G_i\rangle_{d_i+1}^{\mathsf{D_{sg}}(R/x_iR)}.
\end{equation}
\begin{equation}
R/x_iR\otimes^{\mathbf{L}}_RX\in\mathsf{D_{sg}}(R/x_iR)=\langle G_i\rangle_{d_i+1}^{\mathsf{D_{sg}}(R/x_iR)}.
\end{equation} As a perfect ![]() $R/x_iR$-complex is quasi-isomorphic to a perfect R-complex, the natural surjection
$R/x_iR$-complex is quasi-isomorphic to a perfect R-complex, the natural surjection ![]() $R\to R/x_iR$ induces an exact functor
$R\to R/x_iR$ induces an exact functor ![]() $\mathsf{D_{sg}}(R/x_iR)\to\mathsf{D_{sg}}(R)$. Applying this functor to (2.9.1), we observe that there is an inclusion
$\mathsf{D_{sg}}(R/x_iR)\to\mathsf{D_{sg}}(R)$. Applying this functor to (2.9.1), we observe that there is an inclusion  $\mathsf{C}(x_i)\subseteq\langle G_i\rangle_{d_i+1}^{\mathsf{D_{sg}}(R)}$. It follows that:
$\mathsf{C}(x_i)\subseteq\langle G_i\rangle_{d_i+1}^{\mathsf{D_{sg}}(R)}$. It follows that:
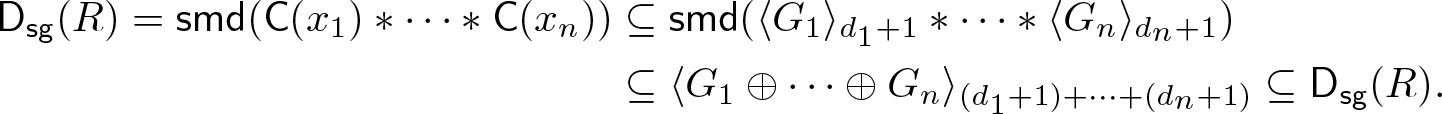 \begin{align*}
\mathsf{D_{sg}}(R)=\operatorname{\mathsf{smd}}(\mathsf{C}(x_1)\ast\cdots\ast\mathsf{C}(x_n))&\subseteq\operatorname{\mathsf{smd}}(\langle G_1\rangle_{d_1+1}\ast\cdots\ast\langle G_n\rangle_{d_n+1})\\
&\subseteq\langle G_1\oplus\cdots\oplus G_n\rangle_{(d_1+1)+\cdots+(d_n+1)}\subseteq\mathsf{D_{sg}}(R).
\end{align*}
\begin{align*}
\mathsf{D_{sg}}(R)=\operatorname{\mathsf{smd}}(\mathsf{C}(x_1)\ast\cdots\ast\mathsf{C}(x_n))&\subseteq\operatorname{\mathsf{smd}}(\langle G_1\rangle_{d_1+1}\ast\cdots\ast\langle G_n\rangle_{d_n+1})\\
&\subseteq\langle G_1\oplus\cdots\oplus G_n\rangle_{(d_1+1)+\cdots+(d_n+1)}\subseteq\mathsf{D_{sg}}(R).
\end{align*} Hence the equality ![]() $\mathsf{D_{sg}}(R)=\langle G_1\oplus\cdots\oplus G_n\rangle_{(d_1+\cdots+d_n)+n}$ holds, which yields the inequality
$\mathsf{D_{sg}}(R)=\langle G_1\oplus\cdots\oplus G_n\rangle_{(d_1+\cdots+d_n)+n}$ holds, which yields the inequality ![]() $\dim\mathsf{D_{sg}}(R)\le(d_1+\cdots+d_n)+n-1$.
$\dim\mathsf{D_{sg}}(R)\le(d_1+\cdots+d_n)+n-1$.
We should compare the above theorem with [Reference Iyengar and Takahashi10, Theorem 1.1 and Corollary 2.12], which have similar flavours.
3. The case of a sequence of elements
In the previous section, we considered the full subcategory of objects in the singularity category of a commutative Noetherian ring that are annihilated by a given ring element. In this section, we are going to further investigate such subcategories by considering their intersections. That is, we will consider the full subcategory of objects that are annihilated by a given sequence of ring elements.
(1) For a sequence
 $\boldsymbol{x}=x_1,\dots,x_n$ of elements of R, set
$\boldsymbol{x}=x_1,\dots,x_n$ of elements of R, set  $\mathsf{C}(\boldsymbol{x})=\bigcap_{i=1}^n\mathsf{C}(x_i)$. Namely,
$\mathsf{C}(\boldsymbol{x})=\bigcap_{i=1}^n\mathsf{C}(x_i)$. Namely,  $\mathsf{C}(\boldsymbol{x})$ is the subcategory of
$\mathsf{C}(\boldsymbol{x})$ is the subcategory of  $\mathsf{D_{sg}}(R)$ consisting of all objects X with
$\mathsf{D_{sg}}(R)$ consisting of all objects X with  $(X\xrightarrow{x_i}X)=0$ in
$(X\xrightarrow{x_i}X)=0$ in  $\mathsf{D_{sg}}(R)$ for all i.
$\mathsf{D_{sg}}(R)$ for all i.(2) For an ideal I of R, we set
 $\mathsf{C}(I)=\bigcap_{a\in I}\mathsf{C}(a)$. This is the subcategory of
$\mathsf{C}(I)=\bigcap_{a\in I}\mathsf{C}(a)$. This is the subcategory of  $\mathsf{D_{sg}}(R)$ consisting of those objects X which satisfy
$\mathsf{D_{sg}}(R)$ consisting of those objects X which satisfy  $(X\xrightarrow{a}X)=0$ in
$(X\xrightarrow{a}X)=0$ in  $\mathsf{D_{sg}}(R)$ for all
$\mathsf{D_{sg}}(R)$ for all  $a\in I$. Note that for any ideals
$a\in I$. Note that for any ideals  $I,J$ of R, if
$I,J$ of R, if  $I\subseteq J$, then
$I\subseteq J$, then  $\mathsf{C}(I)\supseteq\mathsf{C}(J)$.
$\mathsf{C}(I)\supseteq\mathsf{C}(J)$.
The second assertion of the following proposition is a generalization of Lemma 2.4(1).
(1) Let I be an ideal of R. Let
 $\boldsymbol{x}=x_1,\dots,x_n$ be a system of generators of I. Then
$\boldsymbol{x}=x_1,\dots,x_n$ be a system of generators of I. Then  $\mathsf{C}(I)=\mathsf{C}(\boldsymbol{x})$. In particular, the implication:
$\mathsf{C}(I)=\mathsf{C}(\boldsymbol{x})$. In particular, the implication:
 \begin{equation*}
(\boldsymbol{a})=(\boldsymbol{b})\implies\mathsf{C}(\boldsymbol{a})=\mathsf{C}(\boldsymbol{b}),
\end{equation*}
\begin{equation*}
(\boldsymbol{a})=(\boldsymbol{b})\implies\mathsf{C}(\boldsymbol{a})=\mathsf{C}(\boldsymbol{b}),
\end{equation*}holds for sequences of elements
 $\boldsymbol{a}=a_1,\dots,a_r$ and
$\boldsymbol{a}=a_1,\dots,a_r$ and  $\boldsymbol{b}=b_1,\dots,b_s$ in R.
$\boldsymbol{b}=b_1,\dots,b_s$ in R.(2) Let
 $\boldsymbol{x}=x_1,\dots,x_n$ be a sequence of elements of R. Then every object
$\boldsymbol{x}=x_1,\dots,x_n$ be a sequence of elements of R. Then every object  $C\in\mathsf{C}(\boldsymbol{x})$ satisfies:
$C\in\mathsf{C}(\boldsymbol{x})$ satisfies:
 \begin{equation*}
\operatorname{K}(\boldsymbol{x})\otimes C\cong\bigoplus_{i=0}^n(C[i])^{\oplus\binom{n}{i}},
\end{equation*}
\begin{equation*}
\operatorname{K}(\boldsymbol{x})\otimes C\cong\bigoplus_{i=0}^n(C[i])^{\oplus\binom{n}{i}},
\end{equation*}in
 $\mathsf{D_{sg}}(R)$. In particular, it holds that
$\mathsf{D_{sg}}(R)$. In particular, it holds that  $\mathsf{C}(\boldsymbol{x})=\operatorname{\mathsf{smd}}\{\operatorname{K}(\boldsymbol{x})\otimes X\mid X\in\mathsf{D_{sg}}(R)\}$.
$\mathsf{C}(\boldsymbol{x})=\operatorname{\mathsf{smd}}\{\operatorname{K}(\boldsymbol{x})\otimes X\mid X\in\mathsf{D_{sg}}(R)\}$.
(1) It is clear that
 $\mathsf{C}(I)$ is contained in
$\mathsf{C}(I)$ is contained in  $\mathsf{C}(\boldsymbol{x})$. To show the opposite inclusion, let
$\mathsf{C}(\boldsymbol{x})$. To show the opposite inclusion, let  $X\in\mathsf{C}(\boldsymbol{x})$. Take any
$X\in\mathsf{C}(\boldsymbol{x})$. Take any  $a\in I$. Then
$a\in I$. Then  $a=\sum_{i=1}^n{a_ix_i}$ for some
$a=\sum_{i=1}^n{a_ix_i}$ for some  $a_1,\dots,a_n\in R$. Note that
$a_1,\dots,a_n\in R$. Note that  $x_1,\dots,x_n$ are in
$x_1,\dots,x_n$ are in  $\mathrm{ann}_{\mathsf{D_{sg}}(R)}X$. Since
$\mathrm{ann}_{\mathsf{D_{sg}}(R)}X$. Since  $\mathrm{ann}_{\mathsf{D_{sg}}(R)}X$ is an ideal of R, the element a is also in
$\mathrm{ann}_{\mathsf{D_{sg}}(R)}X$ is an ideal of R, the element a is also in  $\mathrm{ann}_{\mathsf{D_{sg}}(R)}X$. Hence X belongs to
$\mathrm{ann}_{\mathsf{D_{sg}}(R)}X$. Hence X belongs to  $\mathsf{C}(I)$.
$\mathsf{C}(I)$.(2) The last assertion follows from the first assertion and the fact by Lemma 2.4(1) that:
 \begin{equation*}
\operatorname{K}(\boldsymbol{x})\otimes X\cong\operatorname{K}(x_i)\otimes(\operatorname{K}(x_1,\dots,x_{i-1},x_{i+1},\dots,x_n)\otimes X)\in\mathsf{C}(x_i),
\end{equation*}
\begin{equation*}
\operatorname{K}(\boldsymbol{x})\otimes X\cong\operatorname{K}(x_i)\otimes(\operatorname{K}(x_1,\dots,x_{i-1},x_{i+1},\dots,x_n)\otimes X)\in\mathsf{C}(x_i),
\end{equation*}for each
 $1\le i\le n$. To prove the first assertion, we use induction on n. The case n = 0 is obvious. Let n > 0. The induction hypothesis gives rise to an isomorphism
$1\le i\le n$. To prove the first assertion, we use induction on n. The case n = 0 is obvious. Let n > 0. The induction hypothesis gives rise to an isomorphism  $\operatorname{K}(x_1,\dots,x_{n-1})\otimes C\cong\bigoplus_{i=0}^{n-1}C[i]^{\oplus\binom{n-1}{i}}$ in
$\operatorname{K}(x_1,\dots,x_{n-1})\otimes C\cong\bigoplus_{i=0}^{n-1}C[i]^{\oplus\binom{n-1}{i}}$ in  $\mathsf{D_{sg}}(R)$. Tensoring with
$\mathsf{D_{sg}}(R)$. Tensoring with  $\operatorname{K}(x_n)$, we get isomorphisms:
$\operatorname{K}(x_n)$, we get isomorphisms:
 \begin{align*}
\operatorname{K}(\boldsymbol{x})\otimes C
&\cong\operatorname{K}(x_n)\otimes(\operatorname{K}(x_1,\dots,x_{n-1})\otimes C)
\cong\operatorname{K}(x_n)\otimes(\textstyle\bigoplus_{i=0}^{n-1}C[i]^{\oplus\binom{n-1}{i}})\\
&\cong\textstyle\bigoplus_{i=0}^{n-1}(\operatorname{K}(x_n)\otimes C)[i]^{\oplus\binom{n-1}{i}}
\cong\textstyle\bigoplus_{i=0}^{n-1}(C\oplus C[1])[i]^{\oplus\binom{n-1}{i}}\\
&\cong\textstyle\bigoplus_{i=0}^{n-1}(C[i]\oplus C[i+1])^{\oplus\binom{n-1}{i}}
\cong\textstyle\bigoplus_{i=0}^{n-1}(C[i]^{\oplus\binom{n-1}{i}}\oplus C[i+1]^{\oplus\binom{n-1}{i}})\\
&\cong C\oplus(\textstyle\bigoplus_{i=1}^{n-1}C[i]^{\oplus\binom{n-1}{i}})\oplus(\textstyle\bigoplus_{i=0}^{n-2}C[i+1]^{\binom{n-1}{i}})\oplus C[n]\\
&\cong C\oplus\textstyle\bigoplus_{i=1}^{n-1}C[i]^{\oplus\binom{n-1}{i}+\binom{n-1}{i-1}}\oplus C[n]
\cong\textstyle\bigoplus_{i=0}^n(C[i])^{\oplus\binom{n}{i}},
\end{align*}
\begin{align*}
\operatorname{K}(\boldsymbol{x})\otimes C
&\cong\operatorname{K}(x_n)\otimes(\operatorname{K}(x_1,\dots,x_{n-1})\otimes C)
\cong\operatorname{K}(x_n)\otimes(\textstyle\bigoplus_{i=0}^{n-1}C[i]^{\oplus\binom{n-1}{i}})\\
&\cong\textstyle\bigoplus_{i=0}^{n-1}(\operatorname{K}(x_n)\otimes C)[i]^{\oplus\binom{n-1}{i}}
\cong\textstyle\bigoplus_{i=0}^{n-1}(C\oplus C[1])[i]^{\oplus\binom{n-1}{i}}\\
&\cong\textstyle\bigoplus_{i=0}^{n-1}(C[i]\oplus C[i+1])^{\oplus\binom{n-1}{i}}
\cong\textstyle\bigoplus_{i=0}^{n-1}(C[i]^{\oplus\binom{n-1}{i}}\oplus C[i+1]^{\oplus\binom{n-1}{i}})\\
&\cong C\oplus(\textstyle\bigoplus_{i=1}^{n-1}C[i]^{\oplus\binom{n-1}{i}})\oplus(\textstyle\bigoplus_{i=0}^{n-2}C[i+1]^{\binom{n-1}{i}})\oplus C[n]\\
&\cong C\oplus\textstyle\bigoplus_{i=1}^{n-1}C[i]^{\oplus\binom{n-1}{i}+\binom{n-1}{i-1}}\oplus C[n]
\cong\textstyle\bigoplus_{i=0}^n(C[i])^{\oplus\binom{n}{i}},
\end{align*}where the fourth isomorphism follows from (2.4.2), and the last isomorphism holds since
 $\binom{n-1}{i}+\binom{n-1}{i-1}=\binom{n}{i}$.
$\binom{n-1}{i}+\binom{n-1}{i-1}=\binom{n}{i}$.
The following proposition is a weaker version of Proposition 2.6 for this setting.
Proposition 3.3. For any elements ![]() $x_1,\dots,x_n,y,z\in R$ with
$x_1,\dots,x_n,y,z\in R$ with ![]() $n\ge0$ one has:
$n\ge0$ one has:
Proof. Put ![]() $\boldsymbol{x}=x_1,\dots,x_n$. Let
$\boldsymbol{x}=x_1,\dots,x_n$. Let ![]() $X\in\mathsf{C}(\boldsymbol{x},yz)$. Applying the octahedral axiom, we get a commutative diagram:
$X\in\mathsf{C}(\boldsymbol{x},yz)$. Applying the octahedral axiom, we get a commutative diagram:
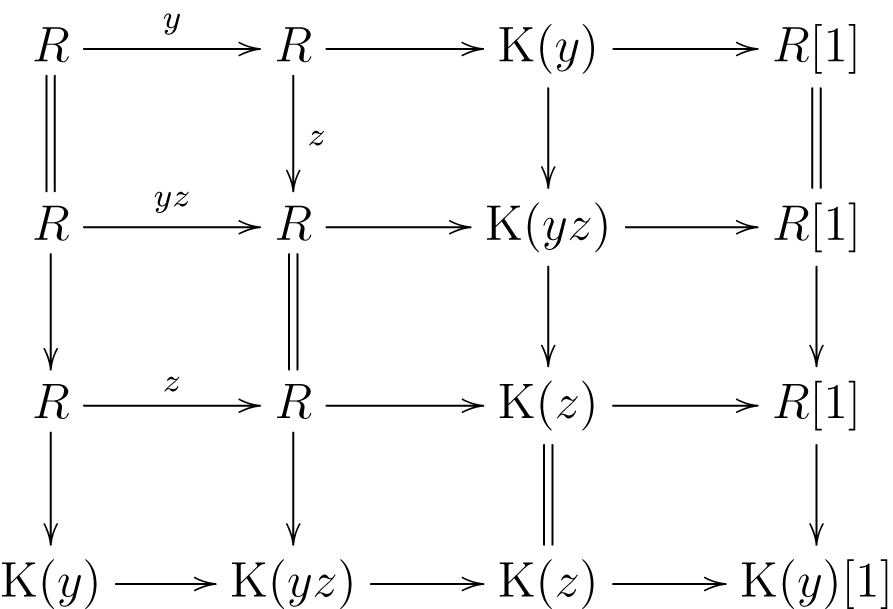
in ![]() $\mathsf{D^b}(R)$ whose rows are exact triangles. Tensoring
$\mathsf{D^b}(R)$ whose rows are exact triangles. Tensoring ![]() $\operatorname{K}(\boldsymbol{x})\otimes X$ with the bottom row induces an exact triangle:
$\operatorname{K}(\boldsymbol{x})\otimes X$ with the bottom row induces an exact triangle:
It follows from Proposition 3.2(2) that X is a direct summand in ![]() $\mathsf{D_{sg}}(R)$ of
$\mathsf{D_{sg}}(R)$ of ![]() $\operatorname{K}(\boldsymbol{x},yz)\otimes X$, and the latter object belongs to
$\operatorname{K}(\boldsymbol{x},yz)\otimes X$, and the latter object belongs to ![]() $\mathsf{C}(\boldsymbol{x},y)\ast\mathsf{C}(\boldsymbol{x},z)$ by (3.3.1). Therefore, X is in
$\mathsf{C}(\boldsymbol{x},y)\ast\mathsf{C}(\boldsymbol{x},z)$ by (3.3.1). Therefore, X is in ![]() $\operatorname{\mathsf{smd}}(\mathsf{C}(\boldsymbol{x},y)\ast\mathsf{C}(\boldsymbol{x},z))$.
$\operatorname{\mathsf{smd}}(\mathsf{C}(\boldsymbol{x},y)\ast\mathsf{C}(\boldsymbol{x},z))$.
The following proposition is an immediate consequence of Proposition 3.3.
Lemma 3.4. Let ![]() $x_1, \dots, x_n \in R$ and assume that
$x_1, \dots, x_n \in R$ and assume that ![]() $m_1,\dots, m_n$ are non-negative integers. Then, we have
$m_1,\dots, m_n$ are non-negative integers. Then, we have
where ![]() $m = m_1 \cdots m_n$.
$m = m_1 \cdots m_n$.
Proof. If ![]() $m_i=0$ for some
$m_i=0$ for some ![]() $1\le i\le n$, then
$1\le i\le n$, then  $\mathsf{C}(x_1^{m_1},\dots,x_n^{m_n})=\bigcap_{j=1}^n\mathsf{C}(x_j^{m_j})\subseteq\mathsf{C}(x_i^{m_i})=\mathsf{C}(1)=0$, and the assertion obviously holds. Assume that
$\mathsf{C}(x_1^{m_1},\dots,x_n^{m_n})=\bigcap_{j=1}^n\mathsf{C}(x_j^{m_j})\subseteq\mathsf{C}(x_i^{m_i})=\mathsf{C}(1)=0$, and the assertion obviously holds. Assume that ![]() $m_1,\dots,m_n$ are all positive. By induction on mn, it follows from Proposition 3.3 and Lemma 2.5 that we should have
$m_1,\dots,m_n$ are all positive. By induction on mn, it follows from Proposition 3.3 and Lemma 2.5 that we should have  $\mathsf{C}(x_1^{m_1}, \dots, x_n^{m_n}) \subseteq \langle \mathsf{C}(x_1^{m_1}, \dots, x_{n-1}^{m_{n-1}}, x_n) \rangle_{m_n}$. Then, the proof is finished by induction on n.
$\mathsf{C}(x_1^{m_1}, \dots, x_n^{m_n}) \subseteq \langle \mathsf{C}(x_1^{m_1}, \dots, x_{n-1}^{m_{n-1}}, x_n) \rangle_{m_n}$. Then, the proof is finished by induction on n.
As an application of Lemma 3.4, we get the following.
Lemma 3.5. Let ![]() $x_1, \dots, x_n \in R$ and assume that
$x_1, \dots, x_n \in R$ and assume that ![]() $m_1, \dots, m_n$ are such that
$m_1, \dots, m_n$ are such that ![]() $x_1^{m_1}, \dots, x_n^{m_n} \in \operatorname{ann} \mathsf{D_{sg}}(R)$. Let
$x_1^{m_1}, \dots, x_n^{m_n} \in \operatorname{ann} \mathsf{D_{sg}}(R)$. Let ![]() $m = m_1\cdots m_n$ and put
$m = m_1\cdots m_n$ and put  $\omega_i = \dfrac{m}{m_i}a_i$ where ai is a non-negative integer and
$\omega_i = \dfrac{m}{m_i}a_i$ where ai is a non-negative integer and ![]() $1 \leq i \leq n$. Then, we have
$1 \leq i \leq n$. Then, we have
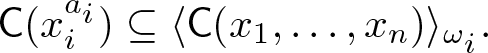 \begin{equation*}
\mathsf{C}(x_i^{a_i}) \subseteq \langle \mathsf{C}(x_1, \dots, x_n) \rangle_{\omega_i}.
\end{equation*}
\begin{equation*}
\mathsf{C}(x_i^{a_i}) \subseteq \langle \mathsf{C}(x_1, \dots, x_n) \rangle_{\omega_i}.
\end{equation*}Proof. Note that for any ![]() $1 \leq j \leq n$, we have
$1 \leq j \leq n$, we have  $\mathsf{C}(x_j^{m_j}) = \mathsf{D_{sg}}(R)$ as
$\mathsf{C}(x_j^{m_j}) = \mathsf{D_{sg}}(R)$ as  $x_j^{m_j} \in \operatorname{ann} \mathsf{D_{sg}}(R)$. Therefore, we have
$x_j^{m_j} \in \operatorname{ann} \mathsf{D_{sg}}(R)$. Therefore, we have  $\mathsf{C}(x_i^{a_i}) = \mathsf{C}(x_1^{m_1}, \dots, x_{i-1}^{m_{i-1}}, x_i^{a_i}, x_{i+1}^{m_{i+1}}, \dots, x_n^{m_n})$. Then, the result follows from Lemma 3.4.
$\mathsf{C}(x_i^{a_i}) = \mathsf{C}(x_1^{m_1}, \dots, x_{i-1}^{m_{i-1}}, x_i^{a_i}, x_{i+1}^{m_{i+1}}, \dots, x_n^{m_n})$. Then, the result follows from Lemma 3.4.
Combining our results, we have the following proposition.
Proposition 3.6. Let ![]() $x_1, \ldots, x_n \in R$ and assume that
$x_1, \ldots, x_n \in R$ and assume that ![]() $a_1, \ldots, a_n$ are non-negative integers. Let
$a_1, \ldots, a_n$ are non-negative integers. Let ![]() $\omega_1,\dots,\omega_n$ be as in Lemma 3.5. Then, we have
$\omega_1,\dots,\omega_n$ be as in Lemma 3.5. Then, we have
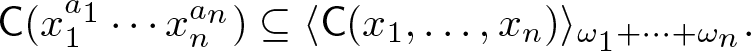 \begin{align*}
\mathsf{C}(x_1^{a_1} \cdots x_n^{a_n}) \subseteq \langle \mathsf{C}(x_1, \dots, x_n)\rangle_{\omega_1 + \cdots + \omega_n}.
\end{align*}
\begin{align*}
\mathsf{C}(x_1^{a_1} \cdots x_n^{a_n}) \subseteq \langle \mathsf{C}(x_1, \dots, x_n)\rangle_{\omega_1 + \cdots + \omega_n}.
\end{align*} In particular, if ![]() $a_1, \ldots, a_n$ are such that
$a_1, \ldots, a_n$ are such that ![]() $x_1^{a_1} \cdots x_n^{a_n} \in \operatorname{ann} \mathsf{D_{sg}}(R)$, then we have
$x_1^{a_1} \cdots x_n^{a_n} \in \operatorname{ann} \mathsf{D_{sg}}(R)$, then we have
Proof. Applying Proposition 2.6, we have ![]() $\mathsf{C}(x_1^{a_1}\cdots x_n^{a_n})=\operatorname{\mathsf{smd}}(\mathsf{C}(x_1^{a_1})\ast\cdots\ast\mathsf{C}(x_n^{a_n}))$. It follows from Lemma 3.5 that
$\mathsf{C}(x_1^{a_1}\cdots x_n^{a_n})=\operatorname{\mathsf{smd}}(\mathsf{C}(x_1^{a_1})\ast\cdots\ast\mathsf{C}(x_n^{a_n}))$. It follows from Lemma 3.5 that  $\mathsf{C}(x_i^{a_i})\subseteq\langle\mathsf{C}(x_1,\dots,x_n)\rangle_{\omega_i}$ for each
$\mathsf{C}(x_i^{a_i})\subseteq\langle\mathsf{C}(x_1,\dots,x_n)\rangle_{\omega_i}$ for each ![]() $1\le i\le n$. Therefore,
$1\le i\le n$. Therefore,  $\mathsf{C}(x_1^{a_1} \cdots x_n^{a_n}) \subseteq \langle \mathsf{C}(x_1, \dots, x_n)\rangle_{\omega_1 + \cdots + \omega_n}$.
$\mathsf{C}(x_1^{a_1} \cdots x_n^{a_n}) \subseteq \langle \mathsf{C}(x_1, \dots, x_n)\rangle_{\omega_1 + \cdots + \omega_n}$.
We are now ready to state our main theorem in this section. We should compare it with Theorem 2.9. Indeed, the second part of the theorem can be proved by induction using Theorem 2.9.
Theorem 3.7. Let ![]() $\boldsymbol{x} = x_1, \ldots, x_n$ a regular sequence on R such that
$\boldsymbol{x} = x_1, \ldots, x_n$ a regular sequence on R such that ![]() $x_1^{m_1}, \ldots, x_n^{m_n} \in \operatorname{ann} \mathsf{D_{sg}}(R)$ for some positive integers
$x_1^{m_1}, \ldots, x_n^{m_n} \in \operatorname{ann} \mathsf{D_{sg}}(R)$ for some positive integers ![]() $m_1, \ldots, m_n$. Assume that
$m_1, \ldots, m_n$. Assume that ![]() $a_1, \ldots, a_n$ are non-negative integers such that
$a_1, \ldots, a_n$ are non-negative integers such that ![]() $x_1^{a_1}\cdots x_n^{a_n} \in \operatorname{ann} \mathsf{D_{sg}}(R)$.
$x_1^{a_1}\cdots x_n^{a_n} \in \operatorname{ann} \mathsf{D_{sg}}(R)$.
(1) There is an inequality
 \begin{equation*}
\dim \mathsf{D_{sg}}(R) \leq \omega \left( \dim \mathsf{D_{sg}}(R/\boldsymbol{x} R) + 1 \right) - 1,
\end{equation*}
\begin{equation*}
\dim \mathsf{D_{sg}}(R) \leq \omega \left( \dim \mathsf{D_{sg}}(R/\boldsymbol{x} R) + 1 \right) - 1,
\end{equation*}where
 $\omega = m_1 \cdots m_n(\frac{a_1}{m_1} + \cdots + \frac{a_n}{m_n})$.
$\omega = m_1 \cdots m_n(\frac{a_1}{m_1} + \cdots + \frac{a_n}{m_n})$.(2) There is an inequality
 \begin{equation*}
\dim \mathsf{D_{sg}}(R) \leq m\,( \dim \mathsf{D_{sg}}(R/\boldsymbol{x} R) + 1) - 1,
\end{equation*}
\begin{equation*}
\dim \mathsf{D_{sg}}(R) \leq m\,( \dim \mathsf{D_{sg}}(R/\boldsymbol{x} R) + 1) - 1,
\end{equation*}where
 $m=m_1\cdots m_n$.
$m=m_1\cdots m_n$.
Proof. The second assertion follows from the first by letting ![]() $a_1=m_1$ and
$a_1=m_1$ and ![]() $a_2=\cdots=a_n=0$. In the following, we show the first assertion. The proof is similar to the proof of Theorem 2.9; we use Proposition 3.2(2) instead of Lemma 2.4(1). Let us assume that
$a_2=\cdots=a_n=0$. In the following, we show the first assertion. The proof is similar to the proof of Theorem 2.9; we use Proposition 3.2(2) instead of Lemma 2.4(1). Let us assume that ![]() $\dim\mathsf{D_{sg}}(R/\boldsymbol{x} R) = d \lt \infty$. Then, there exists an object
$\dim\mathsf{D_{sg}}(R/\boldsymbol{x} R) = d \lt \infty$. Then, there exists an object ![]() $G \in \mathsf{D_{sg}}(R/\boldsymbol{x} R)$ such that
$G \in \mathsf{D_{sg}}(R/\boldsymbol{x} R)$ such that  $\mathsf{D_{sg}}(R/\boldsymbol{x} R) = \langle G \rangle_{d+1}^{\mathsf{D_{sg}}(R/\boldsymbol{x} R)}$. Since x is a regular sequence, we have:
$\mathsf{D_{sg}}(R/\boldsymbol{x} R) = \langle G \rangle_{d+1}^{\mathsf{D_{sg}}(R/\boldsymbol{x} R)}$. Since x is a regular sequence, we have:
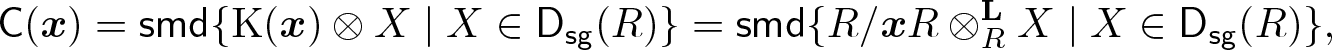 \begin{align*}
\mathsf{C}(\boldsymbol{x}) = \operatorname{\mathsf{smd}}\{\operatorname{K}(\boldsymbol{x}) \otimes X \mid X \in \mathsf{D_{sg}}(R) \}= \operatorname{\mathsf{smd}}\{R/\boldsymbol{x} R\otimes^{\mathbf{L}}_RX\mid X\in\mathsf{D_{sg}}(R)\},
\end{align*}
\begin{align*}
\mathsf{C}(\boldsymbol{x}) = \operatorname{\mathsf{smd}}\{\operatorname{K}(\boldsymbol{x}) \otimes X \mid X \in \mathsf{D_{sg}}(R) \}= \operatorname{\mathsf{smd}}\{R/\boldsymbol{x} R\otimes^{\mathbf{L}}_RX\mid X\in\mathsf{D_{sg}}(R)\},
\end{align*}and
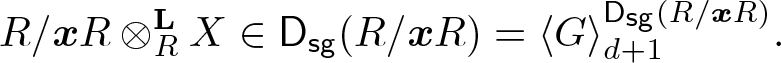 \begin{align*}
R/\boldsymbol{x} R\otimes^{\mathbf{L}}_RX\in\mathsf{D_{sg}}(R/\boldsymbol{x} R)=\langle G \rangle_{d+1}^{\mathsf{D_{sg}}(R/\boldsymbol{x} R)}.
\end{align*}
\begin{align*}
R/\boldsymbol{x} R\otimes^{\mathbf{L}}_RX\in\mathsf{D_{sg}}(R/\boldsymbol{x} R)=\langle G \rangle_{d+1}^{\mathsf{D_{sg}}(R/\boldsymbol{x} R)}.
\end{align*} By applying the exact functor ![]() $\mathsf{D_{sg}}(R/ \boldsymbol{x} R) \to \mathsf{D_{sg}}(R)$ induced by the natural projection
$\mathsf{D_{sg}}(R/ \boldsymbol{x} R) \to \mathsf{D_{sg}}(R)$ induced by the natural projection ![]() $R \to R/\boldsymbol{x} R$, we see that there is an inclusion
$R \to R/\boldsymbol{x} R$, we see that there is an inclusion  $\mathsf{C}(\boldsymbol{x}) \subseteq \langle G \rangle_{d+1}^{\mathsf{D_{sg}}(R)}$. Combining this with Proposition 3.6, we see that
$\mathsf{C}(\boldsymbol{x}) \subseteq \langle G \rangle_{d+1}^{\mathsf{D_{sg}}(R)}$. Combining this with Proposition 3.6, we see that ![]() $\mathsf{D_{sg}}(R) = \langle G \rangle_{\omega(d+1)}$ which finishes the proof.
$\mathsf{D_{sg}}(R) = \langle G \rangle_{\omega(d+1)}$ which finishes the proof.
Remark 3.8. If we have a regular sequence ![]() $x_1,x_2$ on R of length 2 such that
$x_1,x_2$ on R of length 2 such that ![]() $x_1x_2, x_1^{m_1}, x_2^{m_2} \in \operatorname{ann} \mathsf{D_{sg}}(R)$, then Theorem 3.7 gives us:
$x_1x_2, x_1^{m_1}, x_2^{m_2} \in \operatorname{ann} \mathsf{D_{sg}}(R)$, then Theorem 3.7 gives us:
as opposed to
which we would get by successive applications of Theorem 2.9. By using ![]() $m_1 + m_2$ instead of
$m_1 + m_2$ instead of ![]() $m_1 m_2$, Theorem 3.7 helps us reduce the dimension even further than simply using induction and Theorem 2.9. We illustrate this in Example 4.5.
$m_1 m_2$, Theorem 3.7 helps us reduce the dimension even further than simply using induction and Theorem 2.9. We illustrate this in Example 4.5.
4. Applications
In this section, we provide some applications of Theorems 2.9 and 3.7. These two results prove useful when the singularity categories of the quotients on the right hand side are in fact of dimension zero. We begin with recalling some definitions.
(1) Suppose that R is a Gorenstein local ring. By
 $\mathrm{MCM}(R)$ we denote the category of maximal Cohen–Macaulay modules and by
$\mathrm{MCM}(R)$ we denote the category of maximal Cohen–Macaulay modules and by  $\underline{\mathrm{MCM}}(R)$ the corresponding stable category. The celebrated theorem due to Buchweitz [Reference Buchweitz4, Theorem 4.4.1] asserts that the assignment
$\underline{\mathrm{MCM}}(R)$ the corresponding stable category. The celebrated theorem due to Buchweitz [Reference Buchweitz4, Theorem 4.4.1] asserts that the assignment  $M\mapsto M$ gives a triangle equivalence:
$M\mapsto M$ gives a triangle equivalence:
 \begin{equation*}
\Delta:\underline{\mathrm{MCM}}(R)\xrightarrow{\cong}\mathsf{D_{sg}}(R).
\end{equation*}
\begin{equation*}
\Delta:\underline{\mathrm{MCM}}(R)\xrightarrow{\cong}\mathsf{D_{sg}}(R).
\end{equation*}(2) Recall that the cohomology annihilator ideal
 $\mathrm{ca}(R)$ of a commutative Noetherian ring R is defined as:
$\mathrm{ca}(R)$ of a commutative Noetherian ring R is defined as:
 \begin{align*}
\mathrm{ca}(R) = \bigcup_{n =0}^\infty \{r \in R \mid r \in \mathrm{ann}_R \mathrm{Ext}_R^i(M,N)\ \text{for any } i \geq n\ \text{and } M, N \in \mathrm{mod}\ R \}.
\end{align*}
\begin{align*}
\mathrm{ca}(R) = \bigcup_{n =0}^\infty \{r \in R \mid r \in \mathrm{ann}_R \mathrm{Ext}_R^i(M,N)\ \text{for any } i \geq n\ \text{and } M, N \in \mathrm{mod}\ R \}.
\end{align*}When R is a Gorenstein local ring, it follows from [Reference Esentepe9] that:
 \begin{equation*}
\mathrm{ca}(R)=\mathrm{ann}\mathsf{D_{sg}}(R).
\end{equation*}
\begin{equation*}
\mathrm{ca}(R)=\mathrm{ann}\mathsf{D_{sg}}(R).
\end{equation*}More precisely, it is equal to the ideal consisting of those
 $r \in R$ which annihilate every Hom-set in the stable category of maximal Cohen–Macaulay modules.
$r \in R$ which annihilate every Hom-set in the stable category of maximal Cohen–Macaulay modules.
Corollary 4.2. Let ![]() $(R,\mathfrak{m})$ be a Gorenstein local ring. Let
$(R,\mathfrak{m})$ be a Gorenstein local ring. Let ![]() $x_1,\dots,x_n\in\mathfrak{m}$ be non-zerodivisors such that the product
$x_1,\dots,x_n\in\mathfrak{m}$ be non-zerodivisors such that the product ![]() $x_1\cdots x_n$ belongs to the cohomology annihilator
$x_1\cdots x_n$ belongs to the cohomology annihilator ![]() $\mathrm{ca}(R)$. Suppose that each
$\mathrm{ca}(R)$. Suppose that each ![]() $R/x_iR$ has finite CM-representation type. Then
$R/x_iR$ has finite CM-representation type. Then ![]() $\dim\underline{\mathrm{MCM}}(R)\le n-1$.
$\dim\underline{\mathrm{MCM}}(R)\le n-1$.
Proof. There is an equality ![]() $\mathrm{ca}(R)=\operatorname{ann}\mathsf{D_{sg}}(R)$. Since each
$\mathrm{ca}(R)=\operatorname{ann}\mathsf{D_{sg}}(R)$. Since each ![]() $R/x_iR$ has finite CM-representation type, we have
$R/x_iR$ has finite CM-representation type, we have ![]() $\dim\mathsf{D_{sg}}(R/x_iR)=\dim\underline{\mathrm{MCM}}(R/x_iR)\le0$. The assertion now follows from Theorem 2.9.
$\dim\mathsf{D_{sg}}(R/x_iR)=\dim\underline{\mathrm{MCM}}(R/x_iR)\le0$. The assertion now follows from Theorem 2.9.
Let ![]() $(S,\mathfrak{n})$ be a regular local ring, and let
$(S,\mathfrak{n})$ be a regular local ring, and let ![]() $R=S/(f)$, where
$R=S/(f)$, where ![]() $0\ne f\in\mathfrak{n}^2$. We say that R is a simple singularity if there exist only finitely many ideals I of S such that
$0\ne f\in\mathfrak{n}^2$. We say that R is a simple singularity if there exist only finitely many ideals I of S such that ![]() $f\in I^2$. When
$f\in I^2$. When ![]() $R=k[\![x_1,\dots,x_n]\!]/(f_1,\dots,f_m)$ with k a field, we denote by
$R=k[\![x_1,\dots,x_n]\!]/(f_1,\dots,f_m)$ with k a field, we denote by ![]() $\operatorname{jac} R$ the Jacobian ideal of R, which is defined as the ideal of R generated by the h-minors of the Jacobian matrix
$\operatorname{jac} R$ the Jacobian ideal of R, which is defined as the ideal of R generated by the h-minors of the Jacobian matrix  $(\frac{\partial f_i}{\partial x_j})$, where h is the height of the ideal
$(\frac{\partial f_i}{\partial x_j})$, where h is the height of the ideal ![]() $(f_1,\dots,f_m)$ of the formal power series ring
$(f_1,\dots,f_m)$ of the formal power series ring ![]() $k[\![x_1,\dots,x_n]\!]$.
$k[\![x_1,\dots,x_n]\!]$.
Corollary 4.3. Let ![]() $d\ge1$ and
$d\ge1$ and ![]() $e\ge2$ be integers. Let k be an algebraically closed field whose characteristic is neither
$e\ge2$ be integers. Let k be an algebraically closed field whose characteristic is neither ![]() $2,3,5$ nor divides e. Let
$2,3,5$ nor divides e. Let ![]() $f\in(x_1,\dots,x_d)^2k[\![x_1,\dots,x_d]\!]$ be such that
$f\in(x_1,\dots,x_d)^2k[\![x_1,\dots,x_d]\!]$ be such that ![]() $k[\![x_1,\dots,x_d]\!]/(f)$ is a simple singularity. Let
$k[\![x_1,\dots,x_d]\!]/(f)$ is a simple singularity. Let ![]() $R=k[\![x_0,\dots,x_d]\!]/(x_0^e+f)$. Then
$R=k[\![x_0,\dots,x_d]\!]/(x_0^e+f)$. Then ![]() $\dim\underline{\mathrm{MCM}}(R)\le e-2$.
$\dim\underline{\mathrm{MCM}}(R)\le e-2$.
Proof. We have ![]() $x_0^{e-1}=e^{-1}(ex_0^{e-1})\in\operatorname{jac} R\subseteq\mathrm{ca}(R)$ by [Reference Iyengar and Takahashi11, Example 2.7]. Also,
$x_0^{e-1}=e^{-1}(ex_0^{e-1})\in\operatorname{jac} R\subseteq\mathrm{ca}(R)$ by [Reference Iyengar and Takahashi11, Example 2.7]. Also, ![]() $R/x_0R=k[\![x_1,\dots,x_d]\!]/(f)$ is a simple singularity, so that it has finite CM-representation type by [Reference Leuschke and Wiegand12, Theorem 9.8]. By virtue of Corollary 4.2, we get
$R/x_0R=k[\![x_1,\dots,x_d]\!]/(f)$ is a simple singularity, so that it has finite CM-representation type by [Reference Leuschke and Wiegand12, Theorem 9.8]. By virtue of Corollary 4.2, we get ![]() $\dim\underline{\mathrm{MCM}}(R)\le(e-1)-1=e-2$.
$\dim\underline{\mathrm{MCM}}(R)\le(e-1)-1=e-2$.
Let ![]() $(R,\mathfrak{m})$ be a local ring. We denote by
$(R,\mathfrak{m})$ be a local ring. We denote by ![]() $\ell(R)$ the length of R as an R-module, and by
$\ell(R)$ the length of R as an R-module, and by ![]() $\ell\ell(R)$ the Loewy length of R, that is, the infimum of integers
$\ell\ell(R)$ the Loewy length of R, that is, the infimum of integers ![]() $n\ge0$ such that
$n\ge0$ such that ![]() $\mathfrak{m}^n=0$. For an
$\mathfrak{m}^n=0$. For an ![]() $\mathfrak{m}$-primary ideal I of R, we denote by
$\mathfrak{m}$-primary ideal I of R, we denote by ![]() $\operatorname{e}(I)$ the (Hilbert–Samuel) multiplicity of I, i.e.
$\operatorname{e}(I)$ the (Hilbert–Samuel) multiplicity of I, i.e.  $\operatorname{e}(I)=\lim_{n\to\infty}\frac{d!}{n^d}\ell(R/I^{n+1})\in\mathbb{N}$, where
$\operatorname{e}(I)=\lim_{n\to\infty}\frac{d!}{n^d}\ell(R/I^{n+1})\in\mathbb{N}$, where ![]() $d=\dim R$.
$d=\dim R$.
Example 4.4. Let ![]() $R=\mathbb{C}[\![x,y]\!]/(x^a-y^b)$ with
$R=\mathbb{C}[\![x,y]\!]/(x^a-y^b)$ with ![]() $2\le a\le b$. Then it is easy to observe that
$2\le a\le b$. Then it is easy to observe that ![]() $\mathbb{C}[\![y]\!]/(y^b)$ is a simple singularity. Corollary 4.3 gives rise to the inequality:
$\mathbb{C}[\![y]\!]/(y^b)$ is a simple singularity. Corollary 4.3 gives rise to the inequality:
Let ![]() $J=\operatorname{jac} R$ be the Jacobian ideal of R. Then we have
$J=\operatorname{jac} R$ be the Jacobian ideal of R. Then we have ![]() $J=(x^{a-1},y^{b-1})$ and
$J=(x^{a-1},y^{b-1})$ and ![]() $R/J=\mathbb{C}[\![x,y]\!]/(x^{a-1},y^{b-1})$. We easily see that
$R/J=\mathbb{C}[\![x,y]\!]/(x^{a-1},y^{b-1})$. We easily see that ![]() $\ell\ell(R/J)=(a-1)+(b-1)-1=a+b-3$. It follows from [Reference Ballard, Favero and Katzarkov1, Proposition 4.11] or [Reference Dao and Takahashi7, Corollary 1.3(1)] that
$\ell\ell(R/J)=(a-1)+(b-1)-1=a+b-3$. It follows from [Reference Ballard, Favero and Katzarkov1, Proposition 4.11] or [Reference Dao and Takahashi7, Corollary 1.3(1)] that
Take the parameter ideal ![]() $Q=(x^{a-1})$ of R contained in J. We claim that
$Q=(x^{a-1})$ of R contained in J. We claim that ![]() $J^a=QJ^{a-1}$. In fact, we have
$J^a=QJ^{a-1}$. In fact, we have ![]() $J^a=(x^{a-1},y^{b-1})^a=(\{(x^{a-1})^i(y^{b-1})^{a-i}\}_{i=1}^a)+(y^{(b-1)a})$, and
$J^a=(x^{a-1},y^{b-1})^a=(\{(x^{a-1})^i(y^{b-1})^{a-i}\}_{i=1}^a)+(y^{(b-1)a})$, and
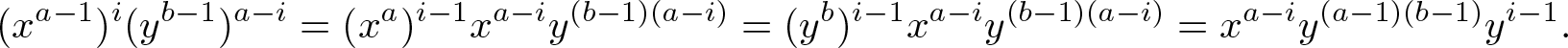 \begin{equation*}
(x^{a-1})^i(y^{b-1})^{a-i}=(x^a)^{i-1}x^{a-i}y^{(b-1)(a-i)}=(y^b)^{i-1}x^{a-i}y^{(b-1)(a-i)}=x^{a-i}y^{(a-1)(b-1)}y^{i-1}.
\end{equation*}
\begin{equation*}
(x^{a-1})^i(y^{b-1})^{a-i}=(x^a)^{i-1}x^{a-i}y^{(b-1)(a-i)}=(y^b)^{i-1}x^{a-i}y^{(b-1)(a-i)}=x^{a-i}y^{(a-1)(b-1)}y^{i-1}.
\end{equation*} As ![]() $a\le b$, we have
$a\le b$, we have ![]() $y^{b-1}\in(y^{a-1})$. There are equalities
$y^{b-1}\in(y^{a-1})$. There are equalities
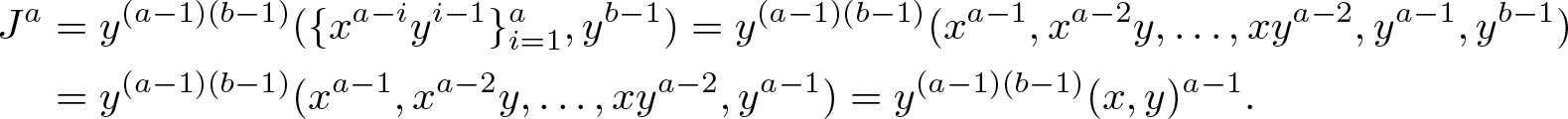 \begin{align*}
J^a&=y^{(a-1)(b-1)}(\{x^{a-i}y^{i-1}\}_{i=1}^a,y^{b-1})=y^{(a-1)(b-1)}(x^{a-1},x^{a-2}y,\dots,xy^{a-2},y^{a-1},y^{b-1})\\
&=y^{(a-1)(b-1)}(x^{a-1},x^{a-2}y,\dots,xy^{a-2},y^{a-1})=y^{(a-1)(b-1)}(x,y)^{a-1}.
\end{align*}
\begin{align*}
J^a&=y^{(a-1)(b-1)}(\{x^{a-i}y^{i-1}\}_{i=1}^a,y^{b-1})=y^{(a-1)(b-1)}(x^{a-1},x^{a-2}y,\dots,xy^{a-2},y^{a-1},y^{b-1})\\
&=y^{(a-1)(b-1)}(x^{a-1},x^{a-2}y,\dots,xy^{a-2},y^{a-1})=y^{(a-1)(b-1)}(x,y)^{a-1}.
\end{align*}Therefore, we get
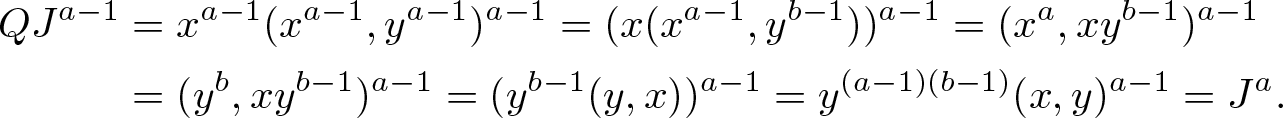 \begin{align*}
QJ^{a-1}&=x^{a-1}(x^{a-1},y^{a-1})^{a-1}=(x(x^{a-1},y^{b-1}))^{a-1}=(x^a,xy^{b-1})^{a-1}\\
&=(y^b,xy^{b-1})^{a-1}=(y^{b-1}(y,x))^{a-1}=y^{(a-1)(b-1)}(x,y)^{a-1}=J^a.
\end{align*}
\begin{align*}
QJ^{a-1}&=x^{a-1}(x^{a-1},y^{a-1})^{a-1}=(x(x^{a-1},y^{b-1}))^{a-1}=(x^a,xy^{b-1})^{a-1}\\
&=(y^b,xy^{b-1})^{a-1}=(y^{b-1}(y,x))^{a-1}=y^{(a-1)(b-1)}(x,y)^{a-1}=J^a.
\end{align*} This claim says that the parameter ideal Q is a reduction of J, and we obtain ![]() $\operatorname{e}(J)=\ell(R/Q)=\ell(\mathbb{C}[\![x,y]\!]/(x^{a-1},y^b))=(a-1)b$. It follows from [Reference Dao and Takahashi7, Corollary 1.3(2)] that:
$\operatorname{e}(J)=\ell(R/Q)=\ell(\mathbb{C}[\![x,y]\!]/(x^{a-1},y^b))=(a-1)b$. It follows from [Reference Dao and Takahashi7, Corollary 1.3(2)] that:
As ![]() $a,b$ are at least 2, both of the integers
$a,b$ are at least 2, both of the integers ![]() $a+2b-5$ and
$a+2b-5$ and ![]() $(a-1)(b-1)$ are positive. Therefore, the upper bound (4.4.1) for the dimension of the triangulated category
$(a-1)(b-1)$ are positive. Therefore, the upper bound (4.4.1) for the dimension of the triangulated category ![]() $\underline{\mathrm{MCM}}(R)$ produced by Corollary 4.3 is better than the upper bounds produced by [Reference Ballard, Favero and Katzarkov1, Reference Dao and Takahashi7]. Furthermore, we should notice that when a = 3 and
$\underline{\mathrm{MCM}}(R)$ produced by Corollary 4.3 is better than the upper bounds produced by [Reference Ballard, Favero and Katzarkov1, Reference Dao and Takahashi7]. Furthermore, we should notice that when a = 3 and ![]() $b\ge6$, the ring R is not of finite CM-representation type by [Reference Yoshino16, Chapter 9], so that (4.4.1) and [Reference Minamoto14, Theorem 1.2] imply
$b\ge6$, the ring R is not of finite CM-representation type by [Reference Yoshino16, Chapter 9], so that (4.4.1) and [Reference Minamoto14, Theorem 1.2] imply ![]() $\dim\underline{\mathrm{MCM}}(R)=1$. This also says that the inequality (4.4.1) is the best possible.
$\dim\underline{\mathrm{MCM}}(R)=1$. This also says that the inequality (4.4.1) is the best possible.
We should also compare Corollaries 4.2, 4.3 and Example 4.4 with [Reference Shimada and Takahashi15, Corollaries 1.2 and 1.3], which are stated in a similar context.
We present one more example, applying Theorem 3.7.
Example 4.5. Let ![]() $R = \mathbb{C}[\![x,y,z,w]\!]/(f)$, where
$R = \mathbb{C}[\![x,y,z,w]\!]/(f)$, where ![]() $f=x^3+y^3+xyz+w^2$. Then, the partial derivatives of f with respect to x, y and z are
$f=x^3+y^3+xyz+w^2$. Then, the partial derivatives of f with respect to x, y and z are ![]() $3x^2 + yz$,
$3x^2 + yz$, ![]() $3y^2+xz$ and xy, respectively. The equalities
$3y^2+xz$ and xy, respectively. The equalities  $x^3=\dfrac{1}{3}x(3x^2+yz)-\dfrac{1}{3}z(xy)$ and
$x^3=\dfrac{1}{3}x(3x^2+yz)-\dfrac{1}{3}z(xy)$ and  $y^3=\dfrac{1}{3}y(3y^2+xz)-\dfrac{1}{3}z(xy)$ hold in R. It follows from [Reference Iyengar and Takahashi11, Example 2.7] that x 3, y 3 and xy are in
$y^3=\dfrac{1}{3}y(3y^2+xz)-\dfrac{1}{3}z(xy)$ hold in R. It follows from [Reference Iyengar and Takahashi11, Example 2.7] that x 3, y 3 and xy are in ![]() $\mathrm{ca}(R)$. On the other hand, note that
$\mathrm{ca}(R)$. On the other hand, note that ![]() $x,y$ is a regular sequence on R and:
$x,y$ is a regular sequence on R and:
is a complete local hypersurface of countable CM-representation type by [Reference Buchweitz, Greuel and Schreyer5, Proposition 4.1] or [Reference Yoshino16, Example (6.5)] and thus ![]() $\dim \underline{\mathrm{MCM}}(R / (x,y)R) = 1$ by [Reference Dao and Takahashi6, Propositions 2.4 and 2.7]. Therefore, by Theorem 3.7, we conclude that:
$\dim \underline{\mathrm{MCM}}(R / (x,y)R) = 1$ by [Reference Dao and Takahashi6, Propositions 2.4 and 2.7]. Therefore, by Theorem 3.7, we conclude that:
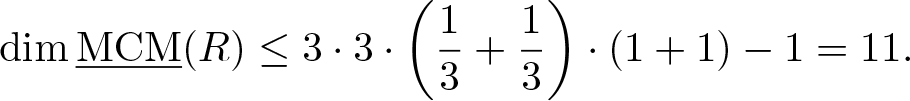 \begin{equation*}
\dim \underline{\mathrm{MCM}}(R) \le 3\cdot3\cdot\left(\frac{1}{3}+\frac{1}{3}\right)\cdot(1+1)-1=11.
\end{equation*}
\begin{equation*}
\dim \underline{\mathrm{MCM}}(R) \le 3\cdot3\cdot\left(\frac{1}{3}+\frac{1}{3}\right)\cdot(1+1)-1=11.
\end{equation*} Our results on the dimension of singularity categories require the condition that the product of some non-zerodivisors belong to ![]() $\operatorname{ann} \mathsf{D_{sg}}(R)$. Hence, it is reasonable to ask whether this condition is too strong or when it happens. Now we recall a recent result on the annihilation of singularity categories and formulate our results from this point of view in the case of isolated singularities.
$\operatorname{ann} \mathsf{D_{sg}}(R)$. Hence, it is reasonable to ask whether this condition is too strong or when it happens. Now we recall a recent result on the annihilation of singularity categories and formulate our results from this point of view in the case of isolated singularities.
Theorem 4.6. [[Reference Liu13, Theorem 4.6]] Let R be a commutative Noetherian ring. If ![]() $\dim \mathsf{D_{sg}}(R) \lt \infty$, then
$\dim \mathsf{D_{sg}}(R) \lt \infty$, then
Therefore, the annihilator of the singularity is not only a homological invariant, but also plays a role geometrically. For instance, it tells us that when the dimension of the singularity category of a commutative Noetherian ring is finite, then the singular locus is a closed subset.
We start with the finiteness condition on ![]() $\dim \mathsf{D_{sg}}(R)$ in Liu’s theorem. To this end, let us consider the following three conditions on a commutative Noetherian local ring
$\dim \mathsf{D_{sg}}(R)$ in Liu’s theorem. To this end, let us consider the following three conditions on a commutative Noetherian local ring ![]() $(R, \mathfrak{m})$:
$(R, \mathfrak{m})$:
A: There exists a non-zerodivisor
 $x \in \mathfrak{m}$ such that
$x \in \mathfrak{m}$ such that  $\dim \mathsf{D_{sg}}(R/x R) \lt \infty$ and
$\dim \mathsf{D_{sg}}(R/x R) \lt \infty$ and  $x^i \in \operatorname{ann} \mathsf{D_{sg}}(R)$ for some i > 0.
$x^i \in \operatorname{ann} \mathsf{D_{sg}}(R)$ for some i > 0.B:
 $\dim \mathsf{D_{sg}}(R) \lt \infty$.
$\dim \mathsf{D_{sg}}(R) \lt \infty$.C: For any
 $x \in \mathfrak{m}$, there is a positive integer
$x \in \mathfrak{m}$, there is a positive integer  $\ell_x$ such that
$\ell_x$ such that  $x^{\ell_x} \in \operatorname{ann} \mathsf{D_{sg}}(R)$.
$x^{\ell_x} \in \operatorname{ann} \mathsf{D_{sg}}(R)$.
Then, Theorem 3.7 immediately tells us that A implies B. If, moreover, R has only isolated singularities, then the above theorem due to Liu tells us that ![]() $\operatorname{ann} \mathsf{D_{sg}}(R)$ is
$\operatorname{ann} \mathsf{D_{sg}}(R)$ is ![]() $\mathfrak{m}$-primary, which tells us that B implies C. Note that the
$\mathfrak{m}$-primary, which tells us that B implies C. Note that the ![]() $\ell_x$ are bounded above by the Loewy length
$\ell_x$ are bounded above by the Loewy length ![]() $\ell\ell(R/\operatorname{ann} \mathsf{D_{sg}}(R))$ of
$\ell\ell(R/\operatorname{ann} \mathsf{D_{sg}}(R))$ of ![]() $R/\operatorname{ann} \mathsf{D_{sg}}(R)$.
$R/\operatorname{ann} \mathsf{D_{sg}}(R)$.
For any non-zerodivisor ![]() $x \in \mathfrak{m}$, let
$x \in \mathfrak{m}$, let ![]() $\ell_x$ be as above and put
$\ell_x$ be as above and put ![]() $d_x = \dim \mathsf{D_{sg}}(R/xR)$. Then, we have the following corollary of Theorem 3.7.
$d_x = \dim \mathsf{D_{sg}}(R/xR)$. Then, we have the following corollary of Theorem 3.7.
Corollary 4.7. Let ![]() $(R,\mathfrak{m})$ be an isolated singularity with
$(R,\mathfrak{m})$ be an isolated singularity with ![]() $\dim \mathsf{D_{sg}}(R) \lt \infty$. Then, for any non-zerodivisor
$\dim \mathsf{D_{sg}}(R) \lt \infty$. Then, for any non-zerodivisor ![]() $x \in \mathfrak{m}$, we have:
$x \in \mathfrak{m}$, we have:
Acknowledgements
The authors thank the anonymous referee for reading the paper carefully and giving useful comments and helpful suggestions.
Funding Statement
R.T. was partly supported by JSPS Grant-in-Aid for Scientific Research 23K03070. Ö.E. was supported by the Engineering and Physical Sciences Research Council [grant number EP/W007509/1].