1. Introduction
Glacierized basins play an important role in the hydrology of alpine watersheds (Röthlisberger and Lang, 1987). Runoff from seasonal snow and glacier ice can vary dramatically in both timing and magnitude, often making water-storage and stream-flow forecasting difficult. Indirect measurements are exploited to investigate the subsurface processes of water flow and include injection of hydrologic tracers (Hooke and others, 1988; Fountain, 1992b); measurements of stream electrical conductivity (EC), turbidity, pH and water quality (Collins, 1979; Tranter and others, 1998); and the use of isotopes of hydrogen and oxygen as natural tracers (Ambach and others, 1968; Behrens and others, 1971). Studies using isotopic methods have been successful in distinguishing variations in runoff on seasonal time-scales using a modest number of samples. EC indicates waters in long or short contact times with the glacier bed. This is useful for determining subglacial flow processes.
In this study, we measured water discharge, stable-isotopic concentrations and electrical conductivity in three streams flowing from South Cascade Glacier, Washington, USA, during a summer ablation season (Vaughn, 1994). These measurements are used to infer the drainage area, travel time, and water storage and location of storage within each drainage basin within the glacier.
2. Study Site
South Cascade Glacier is an alpine glacier about 2.6 km2 in area and about 3.4 km long at the time of study. It is located at 48˚21′ N, 121˚3′W, on the crest of the North Cascade Mountains Range. The glacier is in a maritime environment, with annual precipitation commonly reaching about 4.5 mw.e. and a mean annual temperature of about 1.3˚C (Meier and others, 1971). The glacier ranges in elevation from about 1600 to 2100 m. The bedrock is predominantly granodiorite under the lower glacier, with a schist and gneiss under the upper glacier (Reynolds and Johnson, 1972). Four streams emerge from the glacier ice at the terminus and are named from east to west as streams 1–4 (Fig. 1). Stream 1 primarily drains the basin on the margin of the glacier and is excluded from this study. Streams 2 and 3 are the primary outlets of South Cascade Glacier and drain from separate sub-basins within the glacier (Fountain, 1992b). Stream 4 drains a very small (∼0.1km2) area of the glacier, and, due to significant problems in monitoring this stream, caused by low flows and unstable stream banks, our efforts were not successful and the data are not included in this study. We also ignore any groundwater contributions. These contributions are probably small since the glacierized basin is bedrock and located on the flank of the mountain divide. Data were collected in late August and early September 1991 and 1992.
Fig. 1. South Cascade Glacier, Washington. Inset shows location of terminus streams 1–4, along with sites for stream gauging, sample collection and meteorological stations.
3. Methods
3.1. Isotopes
Isotopes in precipitation vary seasonally, with winter isotopic ratios generally heavier than summer, due to temperature differences, variations in the moisture sources, and atmospheric transport of the vapor (Dansgaard, 1964; Jouzel and Merlivat, 1984). Summer variations of δD in precipitation can vary widely, due in part to the addition of precipitation from convective storms (Craig, 1961; Gedzelman and others, 1987). Hourly samples of deuterium isotopes (δD) were collected using an automatic water sampler, with a small amount of mineral oil floating on top of the water in each sample to minimize evaporation of the sample stored overnight. Samples were collected from marginal streams, precipitation and seasonal snowpack to characterize their deuterium content. Additionally, snow, firn and ice samples were collected from along the center line of the glacier from the terminus (1600 m) to the head (2000 m). Two tipping-bucket rain gauges were employed, one at the terminus of the glacier (near stream 2; 1683 m) and a storage type at 1835 m, where isotope samples were taken during rainstorms. The samples were later analyzed for hydrogen/deuterium isotopes using dual-inlet mass spectrometry in conjunction with an automated uranium reduction preparation system (Vaughn and others, 1998). Isotopic values are expressed as deuterium per mil (δD%), relative to the Vienna Standard Mean Ocean Water (V-SMOW) standard using the normal notation:
where RSample and RStandard are the isotopic ratios derived from measurements of beam currents integrated over time for sample gas vs a hydrogen reference gas (Coplen, 1988). Intermediate laboratory water standards are included in each analysis run, insuring normalization to primary isotopic standards and the V-SMOW scale.
3.2. Electrical conductivity
The chemical composition of glacier runoff is controlled by complex weathering reactions affecting solute concentrations of water at the bed (Reynolds and Johnson, 1972; Collins, 1979; Tranter and Raiswell, 1991). Simply speaking, englacial water flow has a much lower solute concentration than water flowing along the bottom of the glacier, where meltwater acquires solutes from the glacier substrate (sediment or bedrock). Consequently, diurnal fluctuations in chemistry are interpreted as a proxy indicator of the relative amount of time water has spent in contact with the glacier bed (Collins, 1979). We use EC of the glacial stream water to infer qualitative solute concentrations. High EC indicates high solute concentrations and a longer contact period between the water and bedrock or sediments at the bed. Fluctuations in the chemical constituents may preclude a constant relation between solute concentration and EC, but the relation is sufficiently stable over the relatively short periods (days) used here. To measure EC we used a 
conductivity probe (YSI Incorporated, Yellow Springs, Ohio) in which the measured anode/cathode conductance generates a signal output voltage that changes proportionally with the concentration of dissolved ions in the water. The probes were calibrated during the season by periodically comparing the probe output (mV) with the conductivity of a standard solution. The two streams were measured for stage and EC at 15 min intervals using a data logger. Periodic measurements of discharge were made using a current meter and standard US Geological Survey methods to establish a rating curve between stage and discharge.
4. Results
The results of the stream measurements over a 6 day period are shown in Figure 2, which includes water discharge, EC and isotopes. Diurnal patterns in all three measurements are present in all streams, and isotopic variations are greater during the rainfall event.
Fig. 2. Plots over a 6 day period of (a) stream 2 discharge (bold curve) and EC (dashed curve); (b) stream 2 discharge (bold curve) and δD isotopes (points); (c) stream 3 discharge (bold curve) and EC (dashed curve); (d) stream 3 discharge (bold curve and δD isotopes (points); and (e) incoming solar radiation (light curve), and precipitation (bold).
4.1. Isotopes
Source waters for the two streams include melt from seasonal snow (–70%), firn and glacial ice (–100% to –70%), and rainfall (–80%). Surface samples showed that glacial ice near the terminus was isotopically the lightest, becoming heavier near the firn line and then lighter at the head of the glacier. These results support similar gradients found on other temperate glaciers (Holdsworth and others, 1991). About half of the glacier surface was covered by seasonal snow during the measurement period, with an average value of –90.5%. This value is based on measurements of samples from the top 15cm of the snow in the accumulation zone (1900–2100 m). On South Cascade Glacier in summer, melting occurs near-simultaneously at all elevations and on all facies – snow, firn, and glacial ice. This process, coupled with the elevational gradient in isotopic values, precludes distinguishing these facies from each other in stream flow. The most different isotopic tracer was a 12 hour rainfall event which differed as much as 15% from the isotopic values found in base-flow conditions, when there were no contributions from rainfall or daytime surface melt to the stream flow. The rainfall began with light rain, becoming intense at times; after a period of some 12 hours the temperature dropped, and it turned to graupel, ending the liquid input to the glacier. The rainfall was measured at discrete intervals through the event, beginning with a δD of –80% progressing to –85% as the air temperature cooled, with 24mm measured rainfall.
4.2. EC and water discharge
The EC varied inversely with water discharge, suggesting a dilution effect commonly observed in glacial runoff. The load (total solute mass flux) is estimated from the product of discharge ×EC and is an indicator of subglacial processes that is unaffected by meltwater dilution (Fountain, 1992b). The load and discharge are more directly related (Fig. 3), suggesting that more solute is transported during higher flows. A hysteresis was present in the record of stream 3, and to a lesser degree in stream 2, and is characterized by a higher load occurring on the rising limb of discharge than during the falling limb of discharge (clockwise on the plots in Fig. 3), consistent with results from other glaciers (Collins, 1979; Humphrey and others, 1986; Fountain, 1992b).
Fig. 3. Plots of discharge (Q), EC and load (L) over time in streams 2 and 3 during melt events and rainfall events. More hysteresis was present in stream 3, with higher load on the rising limb of the hydrograph and lower load on the falling limb (clockwise).
5. Mixing Model
Hydrologic mixing models have been widely used to separate a variety of constituents in surface and groundwater studies (Rodhe, 1987; Turner and others, 1987; McDonnell and others, 1990). Here we employ hydrograph separation using δD and EC to distinguish between melt and rainfall, and between surface and basal routing paths. Mass balance for the total water flux is
and the tracer flux (either δD or EC) is
where Q is discharge, C is the concentration and subscripts b, p and t are baseflow, precipitation (or melt) and total measured, respectively. Combining Equations (2) and (3) and solving for Q ▴, as an example, yields:
The model requires the end-members (subscripts b, p) are measurably different and remain constant throughout the experiment. These are reasonable assumptions for both δD and EC tracers in the englacial/subglacial waters and snowmelt, but not for δD of rainfall, which changes over time. To account for the change in δD during the rainfall, in place of C p in Equation (3) we use the time series of rainfall samples to characterize the δD as a linear function f (δp):
where JD is Julian day. The isotopic ratio of the minimum (baseflow), C b, was determined from the observed minimum isotopic value for each stream during low discharge.
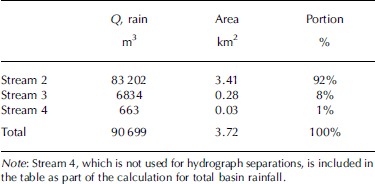
Table 1. Areas of stream drainage basins calculated from the volume of rainwater detected in stream discharge over the course of a 24mm rainfall event
The value of EC chosen to represent subglacial water is determined from the mean of the high peaks in EC over the hydrograph used. EC is plotted against the inverse of discharge (1/Q), and a linear fit of the data extrapolated back to the intercept to estimate the minimum value of EC to represent glacial meltwater. This approach is preferable to using the pure ice-melt value of EC (∼1 μScm–1), because even under the highest flow there is some minimum contact time with the glacier bed, which would raise this minimum value.
6. Analysis and Discussion
6.1. Drainage area
The rainwater portion of discharge integrated over time gives us the total volume of rainwater passing through each drainage basin. Using the measured amount of rainfall occurring during the period of the hydrograph separation, we calculate the catchment area for each stream basin as:
where A is the area (m2), Q R is the average rainwater component of discharge (m3 s–1) and In is the measured total rainfall (m) during the period t 1–t 2. Equation (6) assumes that rainfall is evenly distributed over the basin and discharge was accurately measured. Results (Table 1) showed that the total estimated area is 3.8 km2, close (2%) to the 3.76 km2 area, estimated from maps, that drains through the terminus streams (Krimmel, 1993). Using Equation (6) to estimate the drainage area of streams 2 and 3 resulted in areas of 3.4 km2 (91% of the basin area) and 0.3 km2 (˚%), respectively. The stream 2 basin had tripled in area, at the expense of the stream 3 basin, since 1987 when Fountain (1992b) first estimated the drainage area of each stream.
Table 2. Relative portions of water storage in two drainage basins of South Cascade Glacier
Note: Values are calculated from combined isotope and EC hydrograph separations, distinguishing water stored in contact with the bed from other water in the glacier.
6.2. Hydrograph analysis
For the melt event, the EC separations for stream 2 (Fig. 4a) are used to infer englacial and subglacial routing. The subglacial component peaks first, then decreases, whereas the englacial component peaks later. This suggests that the basal water is first flushed from the main routing pathways before they are dominated by the englacial water. Perhaps the englacial water is pressurized more quickly than the basal waters and therefore suppresses (but does not eliminate) basal flow to the glacier outlet. Isotopic analysis of the rain event exhibits the same behavior as the melt event, whereby the discharge peak in resident water precedes the rainwater peak. The discharge and englacial water flow (not shown) exhibits a double peak, reflecting the variation in rain input (Fig. 4b). Presumably, variations in water input cause transient pressure effects that are reflected in discharge variations. The unimodal appearance of the rain component indicates dispersion in the advection of the rainwater. This is probably the result of routing delays as the glacial water system fills with water. One delay is the temporary storage of rainwater on top of the resident meltwater in the firn water layer. The small variations in the basal flow hint at a response similar to the melt event, whereby basal water flow is limited by englacial input. However, the variations are slight compared to the melt event, which may result from the accumulation of subglacial waters during the morning of JD 245 (not shown) when little meltwater was generated and little basal flushing presumably occurred.
Fig. 4. (a) Hydrograph separations for stream 2 during a period of significant melt from high solar radiation. Total discharge is plotted along with rainfall and glacier components of discharge. (b) Hydrograph separation for stream 2 during a rainfall event. (c) Hydrograph separation for stream 3 during the same rainfall event.
The rain event exhibited in stream 3 (Fig. 4c) shows a somewhat different response (compared to stream 2) in the rain component. The rain component of discharge somewhat corresponds to the variations in rain. This may be due to the small area of the stream 3 basin, which was entirely snow-free. Variations in water input are directly expressed in the runoff with little delay. The basal water shows variations similar to those in stream 2 whereby peaks in englacial flow likely suppress basal water flow. Overall, the basal variations for streams 2 and 3 are small compared to those in the melt event.
6.3. Water volume
In all cases, examined data indicate that the water is pushed through the system in a first-in, first-out manner. Therefore we can estimate the storage volume in the glacier using our hydrographic separations. First, we estimate the transient storage for rainfall and glacier melt, and for basal and englacial storage.
Our approach is to estimate the volume from the transit time in the glacier and 
the discharge
where Vi is water volume for the storage of interest (englacial, melt or rain), Q is the total discharge measured at the terminus stream, t o is the onset time of surface melt or rain and t 1 is the arrival time of peak of the component of interest. We use total Q because we are interested in determining the storage volumes within the glacier, not the total event discharge. Table 2 summarizes calculated water volumes using Equation (7) and time intervals for each of the components as determined from Figure 4. No times were determined for the basal water flow during the rain events because the variability of the basal water flow was insufficient to clearly determine a peak. During a rainfall event, the stream 2 basin holds slightly more water volume at the glacier base (35%) than during a melt event (21%) (Table 2). Expressed as a layer of water over the entire bed of the stream 2 basin, the rain event stored a volume equivalent to about 10 mm, and about 4mm during the melt event. Stream 3 has significantly less overall storage than stream 2 (2.5 × 103m3 and 98.6 × 103m3 respectively), and the fractional volume stored at the bed is higher. About 55% of the water stored in the basin during a rainfall event was stored at the bed and is equivalent to a 4mm thick layer. However, the equivalent layer thickness (specific storage) at the bed during a rain event is half that of the stream 2 basin (more like the melt event), indicating the lack of storage zones or the lack of isolated pockets of solute-rich water at the bed. This result could also be explained by an increase in englacial storage regions, but there is nothing in the character of the ice that would suggest increased porosity or that implies spatial differences in subglacial storage.
7. Conclusions
Measurements of stable isotopes and electrical conductivity in waters draining South Cascade Glacier have provided insight into the timing, storage and volume of runoff on hourly time-scales. Significant differences in δD and EC found in stream flow were interpreted to represent the components of surface melt, basal water and rainfall. The measured δD value of rainfall was significantly different from background snow- and ice melt, and served as a tracer in the streams. This 24mm rainfall event provided a basin-wide isotopic tracer that was quantitatively accounted for in the hydrograph separations in the terminus streams, allowing calculation of drainage areas for each stream. Stream 2 had grown from 30% of the catchment basin in 1987 (Fountain, 1992a) to >90% in this study. Stream 3 drained ˚%, and stream 4 only 1% of the basin. This suggests that drainage divides within a glacier can rapidly shift over a few years’ time.
The combinations of EC and isotope hydrograph separations reveal lags between peaks in discharge and the arrival of waters from surface melt or rainfall events. This allows estimations of water volumes of the region at the bed of the glacier and, indirectly, the englacial storage system consisting of everything from the snow surface to the bed of the glacier. More water was stored in the glacier during a rainfall event than during a melt event. The total storage in the stream 2 basin for these two events was 98.6×103 and 59.4 × 103m3, respectively. During the rainfall event, 35% and 55% of the water was stored near the bed in streams 2 and 3, respectively. Stream 2 exhibited a higher proportion of storage at the bed of the glacier during a rainfall event than it did during a melt event. This suggests that the subglacial flow system is accommodating the extra burden of water input compared to the supraglacial or englacial portions of the glacial drainage. This may imply that the subglacial regions may be able to respond faster than englacial regions to accommodate the extra water volume. This should not be surprising if glacier sliding can react fast enough to enlarge cavities at the glacier base, thereby accommodating the extra water, and the fast water passages fill with water. In the englacial system, little extra accommodation is possible, except if the water backs up in the system.
Appendix
Error Analysis
The error in the hydrograph separation calculations is a function of the four variables in Equation (2): Q, C t , C b , C r . For example, the error in Q r, the rain component of total discharge Q, can be described as the square root of the sum of the error in each variable or
where ↑ is the error, Q is discharge, C is concentration, and the subscripts t b and r represent total, baseflow and rainfall respectively. Expanded, this equation becomes and is the error associated with each estimate of the rainfall component of discharge (Taylor, 1982). The primary source of error is the discharge measurement itself. Exact estimates of this type of error are difficult even under perfect stream-channel conditions anywhere. At South Cascade terminus streams, where channels are far from controlled, a generous estimate of discharge measurement error is given as ±15%. Plotting the stream 2 rainfall event with the 15% error bars on total discharge and the error estimates on rainfall component from Equation (7), it can be seen that the errors involved can be significant (Fig. 5). However, the drainage area and storage volume estimates depend more on the timing of the arrival of component peaks, and are less affected by the magnitude of the errors shown in Figure 5.
Fig. 5. Plotted error estimates for a rainfall component hydrograph separation in stream 2. Based on Equation (7) and ±15% estimate of error in discharge measurement.
