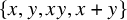1 Introduction
In this paper, we prove the following:
Theorem 1.1. Any finite coloring of
![]() $\mathbb {Q}$
contains monochromatic sets of the form
$\mathbb {Q}$
contains monochromatic sets of the form
![]() $\{x,y,xy,x+y\}$
with all terms distinct and nonzero.
$\{x,y,xy,x+y\}$
with all terms distinct and nonzero.
The classical theorem of Schur [Reference SchurSch16] states that any finite coloring of the set
![]() $\mathbb {N}$
of positive integers contains a monochromatic set of the form
$\mathbb {N}$
of positive integers contains a monochromatic set of the form
![]() $\{x,y,x+y\}$
and, as observed by Graham, this immediately implies the analogous result for sets of the form
$\{x,y,x+y\}$
and, as observed by Graham, this immediately implies the analogous result for sets of the form
![]() $\{x,y,xy\}.$
In 1974, Hindman [Reference HindmanHin74] proved a strong generalization of this theorem and showed that finite colorings of
$\{x,y,xy\}.$
In 1974, Hindman [Reference HindmanHin74] proved a strong generalization of this theorem and showed that finite colorings of
![]() $\mathbb {N}$
admit monochromatic sets which consist of all finite distinct sums of an infinite set. An enlightening proof of Hindman’s theorem using ultrafilters was found by Galvin and Glazer, see, for example, the book of Todorčević [Reference TodorcevicTod10, Chapter 2].
$\mathbb {N}$
admit monochromatic sets which consist of all finite distinct sums of an infinite set. An enlightening proof of Hindman’s theorem using ultrafilters was found by Galvin and Glazer, see, for example, the book of Todorčević [Reference TodorcevicTod10, Chapter 2].
In [Reference HindmanHin79], Hindman famously conjectured that any finite coloring of
![]() $\mathbb {N}$
contains monochromatic sets of the form
$\mathbb {N}$
contains monochromatic sets of the form
![]() $\{x,y,xy,x+y\}$
, see also the textbook [Reference Graham, Rothschild and SpencerGRS91] or the recent Quanta article on this conjecture and the recent advances in the field [Reference SlomanQua23]. In the two color case, Graham showed that any
$\{x,y,xy,x+y\}$
, see also the textbook [Reference Graham, Rothschild and SpencerGRS91] or the recent Quanta article on this conjecture and the recent advances in the field [Reference SlomanQua23]. In the two color case, Graham showed that any
![]() $2$
-coloring of
$2$
-coloring of
![]() $\{1,\ldots ,252\}$
contains a monochromatic configuration of the form
$\{1,\ldots ,252\}$
contains a monochromatic configuration of the form
![]() $\{x,y,xy,x+y\}$
, and Hindman showed the same for any
$\{x,y,xy,x+y\}$
, and Hindman showed the same for any
![]() $2$
-coloring of
$2$
-coloring of
![]() $\{2,\ldots ,990\}$
[Reference HindmanHin79]. However, even the three color case remains open.
$\{2,\ldots ,990\}$
[Reference HindmanHin79]. However, even the three color case remains open.
Hindman’s conjecture and its infinite versions have been studied also with
![]() $\mathbb {N}$
replaced by the rationals since at least the late 1990s, see, for example, the recent paper of Hindman et al. [Reference Hindman, Ivan and LeaderHIL23] for more background. The question of whether Hindman’s conjecture holds over the rationals has been also asked by Moreira [Reference MoreiraMor13]. Theorem 1.1 answers this in the affirmative.
$\mathbb {N}$
replaced by the rationals since at least the late 1990s, see, for example, the recent paper of Hindman et al. [Reference Hindman, Ivan and LeaderHIL23] for more background. The question of whether Hindman’s conjecture holds over the rationals has been also asked by Moreira [Reference MoreiraMor13]. Theorem 1.1 answers this in the affirmative.
In fact, in Theorem 5.1, we prove an extension of the above result involving arithmetic progressions and several variables. In particular, we can find monochromatic sets of the form
![]() $\{x,y,xy,x+iy:i\leq k\}$
and
$\{x,y,xy,x+iy:i\leq k\}$
and
![]() $\{x_i, \sum x_i, \prod x_i: i\leq k\}$
for any
$\{x_i, \sum x_i, \prod x_i: i\leq k\}$
for any
![]() $k\in \mathbb {N}$
.
$k\in \mathbb {N}$
.
Hindman’s conjecture with
![]() $\mathbb {N}$
replaced by a field has been the subject of significant study recently. In [Reference ShkredovShk10], Shkredov showed that finite colorings of large enough prime fields
$\mathbb {N}$
replaced by a field has been the subject of significant study recently. In [Reference ShkredovShk10], Shkredov showed that finite colorings of large enough prime fields
![]() $\mathbb {F}_p$
contain monochromatic sets of the form
$\mathbb {F}_p$
contain monochromatic sets of the form
![]() $\{x,xy,x+y\}$
and Green and Sanders [Reference Green and SandersGS16], building on this work, completely solved Hindman’s conjecture for colorings of finite prime fields, even obtaining good quantitative bounds on the number of solutions. For large enough finite fields, Cilleruelo [Reference CillerueloCil12], Hanson [Reference HansonHan13] and Bergelson and Moreira [Reference Bergelson and MoreiraBM17] gave different proofs that any large subset of the field, and, in particular, a color class in any finite coloring, contains sets of the form
$\{x,xy,x+y\}$
and Green and Sanders [Reference Green and SandersGS16], building on this work, completely solved Hindman’s conjecture for colorings of finite prime fields, even obtaining good quantitative bounds on the number of solutions. For large enough finite fields, Cilleruelo [Reference CillerueloCil12], Hanson [Reference HansonHan13] and Bergelson and Moreira [Reference Bergelson and MoreiraBM17] gave different proofs that any large subset of the field, and, in particular, a color class in any finite coloring, contains sets of the form
![]() $\{xy,x+y\}.$
For infinite fields, Bergelson and Moreira [Reference Bergelson and MoreiraBM17] proved that any finite coloring of an infinite field contains a monochromatic set of the form
$\{xy,x+y\}.$
For infinite fields, Bergelson and Moreira [Reference Bergelson and MoreiraBM17] proved that any finite coloring of an infinite field contains a monochromatic set of the form
![]() $\{x,xy,x+y\}$
. Later [Reference Bergelson and MoreiraBM18], they generalized this result to a wider class of rings.
$\{x,xy,x+y\}$
. Later [Reference Bergelson and MoreiraBM18], they generalized this result to a wider class of rings.
In [Reference MoreiraMor17], Moreira gave a beautiful proof that any finite coloring of
![]() $\mathbb {N}$
contains monochromatic sets of the form
$\mathbb {N}$
contains monochromatic sets of the form
![]() $\{x,xy,x+y\}$
. The first author [Reference BowenBow22] was also able to refine Moreira’s result to also include the y term in the two color case. Recently, Xiao [Reference XiaoXia22] used the structural technique of the present paper to obtain other extensions of Moreira’s theorem.
$\{x,xy,x+y\}$
. The first author [Reference BowenBow22] was also able to refine Moreira’s result to also include the y term in the two color case. Recently, Xiao [Reference XiaoXia22] used the structural technique of the present paper to obtain other extensions of Moreira’s theorem.
By a standard compactness argument, Theorem 1.1 extends to other fields, giving a (nonquantitative) extension of the Green and Sanders theorem [Reference Green and SandersGS16] to nonprime fields.
Corollary 1.2. For every n, there exists a prime p, such that whenever a field of characteristic at least p is colored with n colors, there exists a monochromatic set of the form
![]() $\{x,y,xy,x+y\}$
with all terms distinct and nonzero.
$\{x,y,xy,x+y\}$
with all terms distinct and nonzero.
In fact, our proof of Theorem 1.1 can be adapted to work for infinite fields of arbitrary characteristic through routine modifications, however, throughout the paper, we will work only with
![]() $\mathbb {Q}$
for ease of exposition.
$\mathbb {Q}$
for ease of exposition.
Our proof of Theorem 1.1 uses a recent result due to Bergelson and Glasscock [Reference Bergelson and GlasscockBG20] that is a quantitative version of Szemerédi’s theorem [Reference SzemerédiSze75] and is based on the density version of the Hales–Jewett theorem [Reference Furstenberg and KatznelsonFK91].
The proof of our result in the case of two colors is simpler than in the general case. Namely, in the case of two colors, we use an analysis of colorings where each class is thick, or each class is syndetic and apply the result of Bergelson and Glasscock [Reference Bergelson and GlasscockBG20]. However, for more than two colors, the complexity of the problem grows considerably, and we need a systematic analysis of how thick and syndetic sets interact with the partition classes of a given finite coloring.
The main new technique of our paper is devised to work with colorings with an arbitrary finite number of colors. It seeks to localize certain thick and syndetic sets with respect to the given finite coloring of the rationals. More precisely, in Section 3, we prove a structure result that decomposes a coloring into pieces that globally appear thick and locally appear syndetic, allowing us to extend the simpler proofs that apply to colorings where each class is thick or syndetic to colorings with arbitrary classes.
Such analysis of thick and syndetic sets is new in the context of [Reference HindmanHin79] conjecture, and it seems to not have been used before even outside of the scope of Ramsey theory. This result is stated in purely combinatorial terms in order to make the paper accessible to a wider audience. However, our original motivation was inspired by the ultrafilter methods of Galvin and Glazer (see [Reference Hindman and StraussHS12]) and was focused on analyzing how minimal left ideals in
![]() $(\beta \mathbb {Q},\cdot )$
interact with a given finite coloring of the rationals.
$(\beta \mathbb {Q},\cdot )$
interact with a given finite coloring of the rationals.
2 IP sets and a quantitative version of Szemerédi’s theorem
In this section, we recall several notions of size in the structure of the additive group
![]() $({\mathbb {Q}},+)$
that will be useful throughout the remainder of this paper.
$({\mathbb {Q}},+)$
that will be useful throughout the remainder of this paper.
For a finite sequence
![]() $(a_1,\ldots ,a_n)$
of elements of
$(a_1,\ldots ,a_n)$
of elements of
![]() ${\mathbb {Q}}$
, we use the notation
${\mathbb {Q}}$
, we use the notation
![]() $\sum (a_1,\ldots ,a_n)=a_1+\ldots +a_n$
. Given a sequence A of elements of
$\sum (a_1,\ldots ,a_n)=a_1+\ldots +a_n$
. Given a sequence A of elements of
![]() ${\mathbb {Q}}$
, we write
${\mathbb {Q}}$
, we write
The notion of IP sets, coined to abbreviate “infinite-dimensional parallelepiped” [Reference Furstenberg and WeissFW78], is defined in terms of the sets FS
![]() $(A)$
and can be considered in any semigroup. In this paper, we will always consider IP sets with respect to the additive structure
$(A)$
and can be considered in any semigroup. In this paper, we will always consider IP sets with respect to the additive structure
![]() $({\mathbb {Q}},+)$
. Since we will be also concerned with the multiplicative structure on the rationals, we make it explicit in the definition below that IP sets are considered with respect to the additive structure.
$({\mathbb {Q}},+)$
. Since we will be also concerned with the multiplicative structure on the rationals, we make it explicit in the definition below that IP sets are considered with respect to the additive structure.
Definition 2.1.
-
• A subset of
 ${\mathbb {Q}}$
is additively IP if it contains a set of the form FS(A) for some infinite sequence A of elements of
${\mathbb {Q}}$
is additively IP if it contains a set of the form FS(A) for some infinite sequence A of elements of
 ${\mathbb {Q}}$
.
${\mathbb {Q}}$
. -
• Given
 $r\in \mathbb {N}$
, a subset of
$r\in \mathbb {N}$
, a subset of
 ${\mathbb {Q}}$
is additively
${\mathbb {Q}}$
is additively
 $\mathbf {IP}_r$
if it contains a set of the form FS(A) for some finite sequence A of length r consisting of elements of
$\mathbf {IP}_r$
if it contains a set of the form FS(A) for some finite sequence A of length r consisting of elements of
 ${\mathbb {Q}}$
.
${\mathbb {Q}}$
. -
• A subset of
 ${\mathbb {Q}}$
is additively
${\mathbb {Q}}$
is additively
 $\mathbf {IP}_r^*$
if it has nonempty intersection with every IP
$\mathbf {IP}_r^*$
if it has nonempty intersection with every IP
 $_r$
subset of
$_r$
subset of
 ${\mathbb {Q}}$
.
${\mathbb {Q}}$
.
The classical Folkman theorem (see [Reference Graham, Rothschild and SpencerGRS91, Theorem 11]) ensures that any finite coloring of
![]() $\mathbb {N}$
contains a monochromatic additively IP
$\mathbb {N}$
contains a monochromatic additively IP
![]() $_r$
set, and Hindman’s theorem [Reference HindmanHin74], which has a particularly enlightening ultrafilter proof due to Galvin and Glazer (see, e.g., the textbook of Hindman–Strauss [Reference Hindman and StraussHS12] or of Todorčević [Reference TodorcevicTod10]), gives the same result for additively IP sets. The proof of Theorem 1.1 will use a colorful extension of the IP
$_r$
set, and Hindman’s theorem [Reference HindmanHin74], which has a particularly enlightening ultrafilter proof due to Galvin and Glazer (see, e.g., the textbook of Hindman–Strauss [Reference Hindman and StraussHS12] or of Todorčević [Reference TodorcevicTod10]), gives the same result for additively IP sets. The proof of Theorem 1.1 will use a colorful extension of the IP
![]() $_r$
version that applies to thick colorings (see Lemma 3.2, which is related to the monochromatic products of sums theorem given in [Reference BowenBow22, Theorem 3.1]).
$_r$
version that applies to thick colorings (see Lemma 3.2, which is related to the monochromatic products of sums theorem given in [Reference BowenBow22, Theorem 3.1]).
Definition 2.2. An invariant mean on
![]() $({\mathbb {Q}},+)$
is a positive linear functional d of norm
$({\mathbb {Q}},+)$
is a positive linear functional d of norm
![]() $1$
which is translation invariant on the space of all bounded, real-valued functions on
$1$
which is translation invariant on the space of all bounded, real-valued functions on
![]() ${\mathbb {Q}}$
with the
${\mathbb {Q}}$
with the
![]() $\|\cdot \|_\infty $
norm.
$\|\cdot \|_\infty $
norm.
The existence of an invariant mean on
![]() $({\mathbb {Q}},+)$
, or on any commutative semigroup, is a classical result, see e.g. [Reference GreenleafGre69, Theorem 1.2.1]. The following result of Bergelson and Glasscock [Reference Bergelson and GlasscockBG20, Theorem 7.5] is a quantitative strengthening of Szemerédi’s theorem that we will use in the inductive steps of our construction. We restate it here in the special case when the additive semigroup is
$({\mathbb {Q}},+)$
, or on any commutative semigroup, is a classical result, see e.g. [Reference GreenleafGre69, Theorem 1.2.1]. The following result of Bergelson and Glasscock [Reference Bergelson and GlasscockBG20, Theorem 7.5] is a quantitative strengthening of Szemerédi’s theorem that we will use in the inductive steps of our construction. We restate it here in the special case when the additive semigroup is
![]() $({\mathbb {Q}},+)$
and the homomorphisms are of the form
$({\mathbb {Q}},+)$
and the homomorphisms are of the form
![]() $\varphi _i(q)=q_i\cdot q$
for some
$\varphi _i(q)=q_i\cdot q$
for some
![]() $q_i\in {\mathbb {Q}}$
and the first one is the constant zero function.
$q_i\in {\mathbb {Q}}$
and the first one is the constant zero function.
Theorem 2.3 (Bergelson, Glasscock, [Reference Bergelson and GlasscockBG20] Theorem 7.5).
Let d be an invariant mean on
![]() $({\mathbb {Q}},+)$
and let
$({\mathbb {Q}},+)$
and let
![]() $s\in \mathbb {N}$
and
$s\in \mathbb {N}$
and
![]() $\alpha>0$
be given. There exists
$\alpha>0$
be given. There exists
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\alpha '>0$
for which the following holds. For any sequence of rational numbers
$\alpha '>0$
for which the following holds. For any sequence of rational numbers
![]() $q_1,\ldots ,q_n$
and
$q_1,\ldots ,q_n$
and
![]() $A\subseteq {\mathbb {Q}}$
with
$A\subseteq {\mathbb {Q}}$
with
![]() $d(A)\geq \alpha $
, the set
$d(A)\geq \alpha $
, the set
The key point in our application is that the numbers r and
![]() $\alpha '$
depend only on s and
$\alpha '$
depend only on s and
![]() $\alpha $
, and not on the particular choice of the numbers
$\alpha $
, and not on the particular choice of the numbers
![]() $q_1,\ldots ,q_n$
.
$q_1,\ldots ,q_n$
.
3 Localizing thick and syndetic sets in finite colorings
In this section, we recall some notions of size in semigroups, which will be stated and used only in terms of the multiplicative group
![]() $({\mathbb {Q}}\setminus \{0\},\cdot )$
throughout the paper. We then present two lemmas which will be crucial in the remainder of the paper. The first, Lemma 3.2, will be used together with Theorem 2.3 to control the term y in colorings where each color class is multiplicatively thick. The second, Lemma 3.3, is a structure result for colorings that will allow us to reduce the problem to the cases when either all color classes are multiplicatively syndetic or all color classes are multiplicatively thick.
$({\mathbb {Q}}\setminus \{0\},\cdot )$
throughout the paper. We then present two lemmas which will be crucial in the remainder of the paper. The first, Lemma 3.2, will be used together with Theorem 2.3 to control the term y in colorings where each color class is multiplicatively thick. The second, Lemma 3.3, is a structure result for colorings that will allow us to reduce the problem to the cases when either all color classes are multiplicatively syndetic or all color classes are multiplicatively thick.
We will state the results of this section in the group
![]() $({\mathbb {Q}}\setminus \{0\},\cdot )$
. The only reason why we choose to work with the group
$({\mathbb {Q}}\setminus \{0\},\cdot )$
. The only reason why we choose to work with the group
![]() $({\mathbb {Q}}\setminus \{0\},\cdot )$
rather than the semigroup
$({\mathbb {Q}}\setminus \{0\},\cdot )$
rather than the semigroup
![]() $({\mathbb {Q}},\cdot )$
is because we want to obtain nonzero elements in our main result. The results hold true for more general semigroups and semirings such as
$({\mathbb {Q}},\cdot )$
is because we want to obtain nonzero elements in our main result. The results hold true for more general semigroups and semirings such as
![]() $(\mathbb {N},+,\cdot )$
and may be useful in that context.
$(\mathbb {N},+,\cdot )$
and may be useful in that context.
For
![]() $A\subseteq {\mathbb {Q}}\setminus \{0\}$
and
$A\subseteq {\mathbb {Q}}\setminus \{0\}$
and
![]() $t\in {\mathbb {Q}}\setminus \{0\}$
, write
$t\in {\mathbb {Q}}\setminus \{0\}$
, write
![]() $A\ t=\{a\ t: a\in A\}$
.
$A\ t=\{a\ t: a\in A\}$
.
Definition 3.1.
-
• A set
 $T\subseteq {\mathbb {Q}}\setminus \{0\}$
is multiplicatively thick if for any finite
$T\subseteq {\mathbb {Q}}\setminus \{0\}$
is multiplicatively thick if for any finite
 $F\subseteq {\mathbb {Q}}\setminus \{0\}$
, there is an
$F\subseteq {\mathbb {Q}}\setminus \{0\}$
, there is an
 $a\in {\mathbb {Q}}\setminus \{0\}$
with
$a\in {\mathbb {Q}}\setminus \{0\}$
with
 $F\cdot a\subseteq T$
,
$F\cdot a\subseteq T$
, -
• A set
 $S\subseteq {\mathbb {Q}}\setminus \{0\}$
is multiplicatively syndetic if there is a finite
$S\subseteq {\mathbb {Q}}\setminus \{0\}$
is multiplicatively syndetic if there is a finite
 $F\subseteq {\mathbb {Q}}\setminus \{0\}$
, such that
$F\subseteq {\mathbb {Q}}\setminus \{0\}$
, such that
 ${\mathbb {Q}}\setminus \{0\}=\bigcup _{f\in F} S\ f$
.
${\mathbb {Q}}\setminus \{0\}=\bigcup _{f\in F} S\ f$
.
Note that a set is multiplicatively thick if and only if its complement is not multiplicatively syndetic. In the proof of our main result, we will use the following fact to control the color of the step sizes in the arithmetic progressions obtained from Theorem 2.3.
Lemma 3.2. Let
![]() $k, r, N\in \mathbb {N}$
and
$k, r, N\in \mathbb {N}$
and
![]() $T_1,\ldots ,T_k\subseteq {\mathbb {Q}}\setminus \{0\}$
be multiplicatively thick. For every
$T_1,\ldots ,T_k\subseteq {\mathbb {Q}}\setminus \{0\}$
be multiplicatively thick. For every
![]() $j<N$
, there are additively IP
$j<N$
, there are additively IP
![]() $_r$
sets
$_r$
sets
![]() $S_{1,j}\subseteq T_1,\ldots ,S_{k,j}\subseteq T_k$
, such that for any
$S_{1,j}\subseteq T_1,\ldots ,S_{k,j}\subseteq T_k$
, such that for any
![]() $i\leq j< N$
and for any
$i\leq j< N$
and for any
![]() $l_i,\ldots ,l_j\leq k$
, we have
$l_i,\ldots ,l_j\leq k$
, we have
Proof. First, observe that if
![]() $S\subseteq {\mathbb {Q}}\setminus \{0\}$
is additively IP
$S\subseteq {\mathbb {Q}}\setminus \{0\}$
is additively IP
![]() $_r$
and
$_r$
and
![]() $t\in {\mathbb {Q}}\setminus \{0\}$
, then
$t\in {\mathbb {Q}}\setminus \{0\}$
, then
![]() $St$
is additively IP
$St$
is additively IP
![]() $_r$
. This implies that any multiplicatively thick set is additively IP
$_r$
. This implies that any multiplicatively thick set is additively IP
![]() $_r$
. Next, note that if
$_r$
. Next, note that if
![]() $T\subseteq {\mathbb {Q}}\setminus \{0\}$
is multiplicatively thick and
$T\subseteq {\mathbb {Q}}\setminus \{0\}$
is multiplicatively thick and
![]() $F\subseteq {\mathbb {Q}}\setminus \{0\}$
is finite, then
$F\subseteq {\mathbb {Q}}\setminus \{0\}$
is finite, then
![]() $\{t\in T: tF\subseteq T\}$
is also multiplicatively thick. Using these two facts, we construct the sets
$\{t\in T: tF\subseteq T\}$
is also multiplicatively thick. Using these two facts, we construct the sets
![]() $S_{1,N-i},\ldots ,S_{k,N-i}$
by induction on
$S_{1,N-i},\ldots ,S_{k,N-i}$
by induction on
![]() $i\in \{0,\ldots ,N-1\}$
. Start with any additively IP
$i\in \{0,\ldots ,N-1\}$
. Start with any additively IP
![]() $_r$
sets
$_r$
sets
![]() $S_{1,N}\subseteq T_1,\ldots S_{k,N}\subseteq T_k$
. Having constructed
$S_{1,N}\subseteq T_1,\ldots S_{k,N}\subseteq T_k$
. Having constructed
![]() $S_{1,N-i},\ldots ,S_{k,N-i}$
, find additively IP
$S_{1,N-i},\ldots ,S_{k,N-i}$
, find additively IP
![]() $_r$
sets
$_r$
sets
![]() $S_{1,N-i-1},\ldots ,S_{k,N-i-1}$
, so that for each
$S_{1,N-i-1},\ldots ,S_{k,N-i-1}$
, so that for each
![]() $j\geq N-i$
and each F of the form
$j\geq N-i$
and each F of the form
![]() $S_{l_{N-i},N-i}\cdot \ldots \cdot S_{l_j,j}$
, we have
$S_{l_{N-i},N-i}\cdot \ldots \cdot S_{l_j,j}$
, we have
The following lemma is the main technical tool that allows us to analyze the structure of thick and syndetic sets within the colors in a finite coloring of
![]() ${\mathbb {Q}}$
. It will be the key ingredient in dealing with an arbitrary number of colors.
${\mathbb {Q}}$
. It will be the key ingredient in dealing with an arbitrary number of colors.
Lemma 3.3. Let
![]() ${\mathbb {Q}}\setminus \{0\}=\bigcup _{i=1}^n C_i$
be a finite coloring. There is
${\mathbb {Q}}\setminus \{0\}=\bigcup _{i=1}^n C_i$
be a finite coloring. There is
![]() $k\in \mathbb {N}$
, index sets
$k\in \mathbb {N}$
, index sets
![]() $Y_1,\ldots ,Y_k\subseteq [n],$
and a finite set
$Y_1,\ldots ,Y_k\subseteq [n],$
and a finite set
![]() $F\subseteq {\mathbb {Q}}\setminus \{0\}$
, such that
$F\subseteq {\mathbb {Q}}\setminus \{0\}$
, such that
-
(i) for each
 $l \leq k$
, the set
$l \leq k$
, the set
 $\bigcup _{m\in Y_l} C_m$
is multiplicatively thick,
$\bigcup _{m\in Y_l} C_m$
is multiplicatively thick, -
(ii) for each
 $x\in {\mathbb {Q}}\setminus \{0\}$
, there exists
$x\in {\mathbb {Q}}\setminus \{0\}$
, there exists
 $l\leq k$
, such that for each
$l\leq k$
, such that for each
 $m\in Y_l$
, we have
$m\in Y_l$
, we have
 $x\in \bigcup _{f\in F}C_m/ f$
.
$x\in \bigcup _{f\in F}C_m/ f$
.
Proof. For
![]() $Y\subseteq [n]$
, we denote
$Y\subseteq [n]$
, we denote
![]() $C_Y=\bigcup _{m\in Y}C_m$
. Write
$C_Y=\bigcup _{m\in Y}C_m$
. Write
and
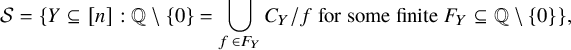 $$ \begin{align*}\mathcal{S}=\{Y\subseteq [n]: {\mathbb{Q}}\setminus\{0\}=\bigcup_{f\in F_Y} C_Y/ f\text{ for some finite }F_Y\subseteq {\mathbb{Q}}\setminus\{0\}\},\end{align*} $$
$$ \begin{align*}\mathcal{S}=\{Y\subseteq [n]: {\mathbb{Q}}\setminus\{0\}=\bigcup_{f\in F_Y} C_Y/ f\text{ for some finite }F_Y\subseteq {\mathbb{Q}}\setminus\{0\}\},\end{align*} $$
that is,
![]() $\mathcal {S}=\{Y\subseteq [n]: C_Y$
is syndetic
$\mathcal {S}=\{Y\subseteq [n]: C_Y$
is syndetic
![]() $\}$
. For each
$\}$
. For each
![]() $Y\in \mathcal {S}$
, choose an
$Y\in \mathcal {S}$
, choose an
![]() $F_Y$
, such that
$F_Y$
, such that
![]() ${\mathbb {Q}}\setminus \{0\}=\bigcup _{f\in F_Y} C_Y/ f$
. Since
${\mathbb {Q}}\setminus \{0\}=\bigcup _{f\in F_Y} C_Y/ f$
. Since
![]() $\mathcal {S}$
is a finite collection, we can choose a finite set
$\mathcal {S}$
is a finite collection, we can choose a finite set
![]() $F\subseteq {\mathbb {Q}}\setminus \{0\}$
which is a superset of all the finite sets
$F\subseteq {\mathbb {Q}}\setminus \{0\}$
which is a superset of all the finite sets
![]() $F_Y$
.
$F_Y$
.
For
![]() $x\in {\mathbb {Q}}\setminus \{0\}$
, write
$x\in {\mathbb {Q}}\setminus \{0\}$
, write
Note that by the definition of
![]() $\mathcal {S}$
, for every
$\mathcal {S}$
, for every
![]() $x\in {\mathbb {Q}}\setminus \{0\}$
, we have
$x\in {\mathbb {Q}}\setminus \{0\}$
, we have
Claim 3.4. For every
![]() $x\in {\mathbb {Q}}\setminus \{0\}$
, there exists
$x\in {\mathbb {Q}}\setminus \{0\}$
, there exists
![]() $Y_x\in \mathcal {T}$
, such that
$Y_x\in \mathcal {T}$
, such that
![]() $Y_x\subseteq A_x$
.
$Y_x\subseteq A_x$
.
Proof. For the sake of contradiction, suppose that no such set
![]() $Y_x$
exists. Then
$Y_x$
exists. Then
![]() $[n]\setminus A_x$
belongs to
$[n]\setminus A_x$
belongs to
![]() $\mathcal {S}$
, which contradicts (3.1).
$\mathcal {S}$
, which contradicts (3.1).
Finally, there are finitely many choices for
![]() $Y_x$
as in Claim 3.4, and so these choices correspond to the desired
$Y_x$
as in Claim 3.4, and so these choices correspond to the desired
![]() $Y_1,\ldots ,Y_k$
.
$Y_1,\ldots ,Y_k$
.
4 Finding the pattern
 $\{x,y,xy,x+y\}$
$\{x,y,xy,x+y\}$
Before giving the proof of Theorem 1.1, we discuss two special cases as a warm-up. Namely, we first present the proof in the case when each color class is syndetic, and next, we present the proof in the case when the color classes are all multiplicatively thick. In the proof of Theorem 1.1, we will carry out the arguments of these special cases simultaneously, using the ideas of Section 3.
4.1 Two special cases
We begin with the proof in the case that each color class is multiplicatively syndetic. Below, we use Moreira’s theorem [Reference MoreiraMor17, Theorem 7.5] in the general form that holds for any field (cf. the remarks after [Reference MoreiraMor17, Definition 7.1]). We also mention that this proof also works in
![]() $\mathbb {N}$
and can be adapted to show that any subset of
$\mathbb {N}$
and can be adapted to show that any subset of
![]() $\mathbb {N}$
which is both multiplicatively syndetic and central contains a subset of the form
$\mathbb {N}$
which is both multiplicatively syndetic and central contains a subset of the form
![]() $\{x,y,xy,x+y\}.$
$\{x,y,xy,x+y\}.$
Claim 4.1. Suppose that
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() ${\mathbb {Q}}\setminus \{0\}$
is colored as
${\mathbb {Q}}\setminus \{0\}$
is colored as
![]() $\bigcup _{i=1}^n C_i$
, where each
$\bigcup _{i=1}^n C_i$
, where each
![]() $C_i$
is multiplicatively syndetic. Then there are monochromatic sets of the form
$C_i$
is multiplicatively syndetic. Then there are monochromatic sets of the form
![]() $\{x,y,xy,x+y\}$
.
$\{x,y,xy,x+y\}$
.
Proof. By definition, for each
![]() $i\in [n]$
, there is a finite set
$i\in [n]$
, there is a finite set
![]() $F_i\subseteq {\mathbb {Q}}\setminus \{0\}$
so that
$F_i\subseteq {\mathbb {Q}}\setminus \{0\}$
so that
![]() ${\mathbb {Q}}\setminus \{0\}=\bigcup _{t\in F_i} (C_i\setminus \{0\})/ t$
. Let
${\mathbb {Q}}\setminus \{0\}=\bigcup _{t\in F_i} (C_i\setminus \{0\})/ t$
. Let
![]() $F=\bigcup _{i=1}^n F_i.$
Then for each
$F=\bigcup _{i=1}^n F_i.$
Then for each
![]() $x\in {\mathbb {Q}}\setminus \{0\}$
, we may pick
$x\in {\mathbb {Q}}\setminus \{0\}$
, we may pick
![]() $(f_{x,1},\ldots ,f_{x,n})\in F^n$
, such that for each
$(f_{x,1},\ldots ,f_{x,n})\in F^n$
, such that for each
![]() $i\in [n]$
, we have
$i\in [n]$
, we have
![]() $x\in C_i/ f_{x,i}$
. For
$x\in C_i/ f_{x,i}$
. For
![]() $\vec {f}\in F^n$
, let
$\vec {f}\in F^n$
, let
![]() $D_{\vec {f}}=\{x\in {\mathbb {Q}}\setminus \{0\}: (f_{x,1},\ldots ,f_{x,n})=\vec {f}\}$
. Then
$D_{\vec {f}}=\{x\in {\mathbb {Q}}\setminus \{0\}: (f_{x,1},\ldots ,f_{x,n})=\vec {f}\}$
. Then
![]() ${\mathbb {Q}}=\{0\}\cup \bigcup _{\vec {f}\in F^n} D_{\vec {f}}$
. For
${\mathbb {Q}}=\{0\}\cup \bigcup _{\vec {f}\in F^n} D_{\vec {f}}$
. For
![]() $f\in F$
, let
$f\in F$
, let
![]() $g_f\in {\mathbb {Q}}[x]$
be defined by
$g_f\in {\mathbb {Q}}[x]$
be defined by
![]() $g_f(x)=x/ f$
, and let
$g_f(x)=x/ f$
, and let
![]() $G=\{0\}\cup \{g_f:f\in F\}$
.
$G=\{0\}\cup \{g_f:f\in F\}$
.
Pick by [Reference MoreiraMor17, Theorem 7.5] some
![]() $\vec {f}=(f_1,\ldots ,f_n)\in F^n$
and
$\vec {f}=(f_1,\ldots ,f_n)\in F^n$
and
![]() $x_0,x_1\in {\mathbb {Q}}\setminus \{0\}$
, such that
$x_0,x_1\in {\mathbb {Q}}\setminus \{0\}$
, such that
![]() $\{x_0,x_1\}\cup \{x_0+g(x_1) : g \in G\}\subseteq D_{\vec {f}}$
. Then
$\{x_0,x_1\}\cup \{x_0+g(x_1) : g \in G\}\subseteq D_{\vec {f}}$
. Then
![]() $\{x_0 x_1, x_0\} \cup \{x_0 + x_1/ f : f \in F\}\subseteq D_{\vec {f}}$
. Pick j, such that
$\{x_0 x_1, x_0\} \cup \{x_0 + x_1/ f : f \in F\}\subseteq D_{\vec {f}}$
. Pick j, such that
![]() $x_1 \in C_j$
. Let
$x_1 \in C_j$
. Let
![]() $y=x_1$
and
$y=x_1$
and
![]() $x=x_0 f_j$
. Then
$x=x_0 f_j$
. Then
![]() $\{x,y,xy,x+y\}\subseteq C_j$
.
$\{x,y,xy,x+y\}\subseteq C_j$
.
The other extreme case is when the colors are all multiplicatively thick. For the sake of simplicity, we only present the two color case here; the proof extends naturally to more colors, albeit with more complicated notation.
Claim 4.2. Suppose that
![]() ${\mathbb {Q}}\setminus \{0\}=C_1\cup C_2$
, where both
${\mathbb {Q}}\setminus \{0\}=C_1\cup C_2$
, where both
![]() $C_i$
are multiplicatively thick in
$C_i$
are multiplicatively thick in
![]() $({\mathbb {Q}}\setminus \{0\},\cdot )$
. There are monochromatic sets of the form
$({\mathbb {Q}}\setminus \{0\},\cdot )$
. There are monochromatic sets of the form
![]() $\{x,y,xy,x+y\}.$
$\{x,y,xy,x+y\}.$
Proof. Let d be a left-invariant mean on
![]() $({\mathbb {Q}},+)$
. Without loss of generality, we may assume that
$({\mathbb {Q}},+)$
. Without loss of generality, we may assume that
![]() $d(C_1)>0$
. Let
$d(C_1)>0$
. Let
![]() $\alpha =d(C_1)$
. Apply Theorem 2.3 with
$\alpha =d(C_1)$
. Apply Theorem 2.3 with
![]() $\alpha =d(C_1)$
and
$\alpha =d(C_1)$
and
![]() $s=1$
, to get
$s=1$
, to get
![]() $r_1$
and
$r_1$
and
![]() $\alpha '$
, and apply it again with
$\alpha '$
, and apply it again with
![]() $\alpha '$
and
$\alpha '$
and
![]() $s=2$
to get
$s=2$
to get
![]() $r_2$
.
$r_2$
.
Since
![]() $C_2$
is multiplicatively thick, we can find an additively IP
$C_2$
is multiplicatively thick, we can find an additively IP
![]() $_{r_2}$
set
$_{r_2}$
set
![]() $S_2$
contained in
$S_2$
contained in
![]() $C_2$
. Using the fact that
$C_2$
. Using the fact that
![]() $C_1$
is multiplicatively thick, we can find an additively IP
$C_1$
is multiplicatively thick, we can find an additively IP
![]() $_{r_1}$
set
$_{r_1}$
set
![]() $S_1$
contained in
$S_1$
contained in
![]() $C_1$
, such that
$C_1$
, such that
Now, since
![]() $S_1$
is additively IP
$S_1$
is additively IP
![]() $_{r_1}$
, applying Theorem 2.3 to the homomorphism
$_{r_1}$
, applying Theorem 2.3 to the homomorphism
![]() $x\mapsto x$
, we find
$x\mapsto x$
, we find
![]() $C_1'\subseteq C_1$
with
$C_1'\subseteq C_1$
with
![]() $d(C_1')=\alpha '$
and
$d(C_1')=\alpha '$
and
![]() $y_1\in S_1$
, such that
$y_1\in S_1$
, such that
If
![]() $y_1C_1' \cap C_1\not =\emptyset $
, then pick any
$y_1C_1' \cap C_1\not =\emptyset $
, then pick any
![]() $x\in C_1'$
, such that
$x\in C_1'$
, such that
![]() $xy_1\in C_1$
, and put
$xy_1\in C_1$
, and put
![]() $y=y_1$
. Note that (4.2) implies
$y=y_1$
. Note that (4.2) implies
![]() $x+y\in C_1$
, so
$x+y\in C_1$
, so
![]() $\{x,y,xy,x+y\}\subseteq C_1$
.
$\{x,y,xy,x+y\}\subseteq C_1$
.
Thus, we can assume that
![]() $y_1C_1'\subseteq C_2$
. Since
$y_1C_1'\subseteq C_2$
. Since
![]() $S_2$
is additively IP
$S_2$
is additively IP
![]() $_{r_2}$
, applying Theorem 2.3 to the two homomorphisms
$_{r_2}$
, applying Theorem 2.3 to the two homomorphisms
![]() $x\mapsto y_1 x$
and
$x\mapsto y_1 x$
and
![]() $x\mapsto \frac {1}{y_1}x$
, we find
$x\mapsto \frac {1}{y_1}x$
, we find
![]() $C_1"\subseteq C_1'$
and
$C_1"\subseteq C_1'$
and
![]() $y_2\in S_2$
, such that
$y_2\in S_2$
, such that
Note that
![]() $y_1 y_2\in C_1$
by (4.1).
$y_1 y_2\in C_1$
by (4.1).
If
![]() $y_1 y_2 C_1"\cap C_1\not =\emptyset $
, then put
$y_1 y_2 C_1"\cap C_1\not =\emptyset $
, then put
![]() $y=y_1 y_2$
, and choose
$y=y_1 y_2$
, and choose
![]() $x\in C_1"$
, such that
$x\in C_1"$
, such that
![]() $xy\in C_1$
. Note that (4.3) implies that
$xy\in C_1$
. Note that (4.3) implies that
![]() $x+y\in C_1$
. Thus,
$x+y\in C_1$
. Thus,
![]() $\{x,y,xy,x+y\}\subseteq C_1$
.
$\{x,y,xy,x+y\}\subseteq C_1$
.
Otherwise,
![]() $y_1y_2 C_1"\cap C_2\not =\emptyset $
. Put
$y_1y_2 C_1"\cap C_2\not =\emptyset $
. Put
![]() $y=y_2,$
(which is an element of
$y=y_2,$
(which is an element of
![]() $S_2\subset C_2$
), and let
$S_2\subset C_2$
), and let
![]() $x\in y_1 C_1"$
be such that
$x\in y_1 C_1"$
be such that
![]() $xy\in C_2$
. Since
$xy\in C_2$
. Since
![]() $y_1 C_1"\subseteq y_1 C_1'\subseteq C_2$
, we have
$y_1 C_1"\subseteq y_1 C_1'\subseteq C_2$
, we have
![]() $x\in C_2$
. Note that (4.4) implies that
$x\in C_2$
. Note that (4.4) implies that
![]() $x+y\in C_2$
. Thus, in this case,
$x+y\in C_2$
. Thus, in this case,
![]() $\{x,y,xy,x+y\}\subseteq C_2$
.
$\{x,y,xy,x+y\}\subseteq C_2$
.
To end this subsection, we mention that Claims 4.1 and 4.2 alone can be used to show that any
![]() $2$
-coloring of
$2$
-coloring of
![]() ${\mathbb {Q}}$
contains a monochromatic set of the form
${\mathbb {Q}}$
contains a monochromatic set of the form
![]() $\{x,y,xy,x+y\}$
. This was the original motivation of the proof of Theorem 1.1 given below.
$\{x,y,xy,x+y\}$
. This was the original motivation of the proof of Theorem 1.1 given below.
4.2 The general case
In this subsection, we prove our main result.
Theorem 4.3. For any finite coloring of
![]() ${\mathbb {Q}}$
, there exist nonzero y and infinitely many
${\mathbb {Q}}$
, there exist nonzero y and infinitely many
![]() $x\in {\mathbb {Q}}$
, such that the tuples
$x\in {\mathbb {Q}}$
, such that the tuples
![]() $\{x,y,xy,x+y\}$
are monochromatic.
$\{x,y,xy,x+y\}$
are monochromatic.
Note that the above statement, in particular, implies that all elements in the quadruple can be chosen to be distinct. First, we can assure that
![]() $y\not =1$
by modifying the coloring by giving
$y\not =1$
by modifying the coloring by giving
![]() $1$
a separate color, and then, using the fact that for a fixed
$1$
a separate color, and then, using the fact that for a fixed
![]() $y\not =1$
, the equation
$y\not =1$
, the equation
![]() $xy=x+y$
has one solution, we can choose x so that all numbers
$xy=x+y$
has one solution, we can choose x so that all numbers
![]() $x,y,xy,x+y$
are distinct. In fact, experts may notice from the proof that we may even ensure that we obtain a positive multiplicative density set of y that works for a set of positive multiplicative and additive density
$x,y,xy,x+y$
are distinct. In fact, experts may notice from the proof that we may even ensure that we obtain a positive multiplicative density set of y that works for a set of positive multiplicative and additive density
![]() $x,$
although we will not check this in detail during the proof.
$x,$
although we will not check this in detail during the proof.
In the proof, we will use Lemma 3.3 to carry out the proofs of Claims 4.1 and 4.2 simultaneously.
Proof of Theorem 4.3.
Let d be an additive invariant mean on
![]() ${\mathbb {Q}}$
. Suppose
${\mathbb {Q}}$
. Suppose
![]() ${\mathbb {Q}}$
is colored into n colors, and write
${\mathbb {Q}}$
is colored into n colors, and write
![]() ${\mathbb {Q}}\setminus \{0\}= C_1\cup \ldots \cup C_n$
. Using Lemma 3.3 for the colors
${\mathbb {Q}}\setminus \{0\}= C_1\cup \ldots \cup C_n$
. Using Lemma 3.3 for the colors
![]() $C_i$
, find
$C_i$
, find
![]() $k\in \mathbb {N}$
and finite sets
$k\in \mathbb {N}$
and finite sets
![]() $F\subseteq {\mathbb {Q}}\setminus \{0\}$
and
$F\subseteq {\mathbb {Q}}\setminus \{0\}$
and
![]() $Y_1,\ldots ,Y_k\subseteq [n]$
, such that
$Y_1,\ldots ,Y_k\subseteq [n]$
, such that
-
(i) for each
 $l \leq k$
, the set
$l \leq k$
, the set
 $\bigcup _{m\in Y_l} C_m$
is multiplicatively thick,
$\bigcup _{m\in Y_l} C_m$
is multiplicatively thick, -
(ii) for each
 $x\in {\mathbb {Q}}\setminus \{0\}$
, there exists
$x\in {\mathbb {Q}}\setminus \{0\}$
, there exists
 $l\leq k$
, such that for each
$l\leq k$
, such that for each
 $m\in Y_l$
, we have
$m\in Y_l$
, we have
 $x\in \bigcup _{f\in F} C_m/ f$
.
$x\in \bigcup _{f\in F} C_m/ f$
.
This means that for each
![]() $x\in {\mathbb {Q}}\setminus \{0\}$
, there is
$x\in {\mathbb {Q}}\setminus \{0\}$
, there is
![]() $l\leq k$
and a tuple
$l\leq k$
and a tuple
![]() $f_1,\ldots ,f_n\in F$
, so that for each
$f_1,\ldots ,f_n\in F$
, so that for each
![]() $m\in Y_l$
, we have
$m\in Y_l$
, we have
![]() $x\in C_m/ f_m$
.
$x\in C_m/ f_m$
.
Note that there are finitely many tuples
![]() $(l,f_1,\ldots ,f_n)$
with
$(l,f_1,\ldots ,f_n)$
with
![]() $l\leq k$
and
$l\leq k$
and
![]() $f_1,\ldots ,f_n\in F$
. This allows us to define a new finite coloring of
$f_1,\ldots ,f_n\in F$
. This allows us to define a new finite coloring of
![]() ${\mathbb {Q}}\setminus \{0\}$
, where for each tuple
${\mathbb {Q}}\setminus \{0\}$
, where for each tuple
![]() $(l,f_1,\ldots ,f_n)$
as above, we have a color
$(l,f_1,\ldots ,f_n)$
as above, we have a color
![]() $D_{(l,f_1, \ldots ,f_n)}$
, and we put
$D_{(l,f_1, \ldots ,f_n)}$
, and we put
Write K for the number of colors in the above coloring. These colors do not need to be disjoint, but we can always disjointify them.
Pick via the pigeonhole principle
![]() $N\in \mathbb {N}$
large enough so that given any sequence
$N\in \mathbb {N}$
large enough so that given any sequence
![]() $\vec {v}_1,\ldots \vec {v}_N$
in
$\vec {v}_1,\ldots \vec {v}_N$
in
![]() $[k]\times F^n$
, there exist i and j with
$[k]\times F^n$
, there exist i and j with
![]() $i<j-1<N-1$
, such that
$i<j-1<N-1$
, such that
![]() $\vec {v}_i=\vec {v}_j$
. Let
$\vec {v}_i=\vec {v}_j$
. Let
![]() $s={N\choose 2}\cdot |F|$
. We define a sequence of positive numbers
$s={N\choose 2}\cdot |F|$
. We define a sequence of positive numbers
![]() $\alpha _1,\alpha _1',\ldots ,\alpha _N,\alpha _N'$
with
$\alpha _1,\alpha _1',\ldots ,\alpha _N,\alpha _N'$
with
![]() $\alpha _1=\frac {1}{K}$
and a sequence
$\alpha _1=\frac {1}{K}$
and a sequence
![]() $r_1,\ldots ,r_N$
in
$r_1,\ldots ,r_N$
in
![]() $\mathbb {N}$
. At the j-th step, given
$\mathbb {N}$
. At the j-th step, given
![]() $\alpha _j$
, we apply Theorem 2.3 and obtain
$\alpha _j$
, we apply Theorem 2.3 and obtain
![]() $\alpha _j'$
and
$\alpha _j'$
and
![]() $r_j$
, such that for any set
$r_j$
, such that for any set
![]() $A\subseteq {\mathbb {Q}}$
with
$A\subseteq {\mathbb {Q}}$
with
![]() $d(A)\geq \alpha _j$
and any
$d(A)\geq \alpha _j$
and any
![]() $q_1,\ldots ,q_s$
, the set
$q_1,\ldots ,q_s$
, the set
We put
![]() $\alpha _{j+1}=\frac {\alpha _j'}{K}$
. When the construction is complete, we write
$\alpha _{j+1}=\frac {\alpha _j'}{K}$
. When the construction is complete, we write
![]() $r=\max \{r_1,\ldots ,r_N\}$
so that any set which is additively IP
$r=\max \{r_1,\ldots ,r_N\}$
so that any set which is additively IP
![]() $_{r_j}^*$
for some
$_{r_j}^*$
for some
![]() $j\in [N]$
is additively IP
$j\in [N]$
is additively IP
![]() $_{r}^*$
.
$_{r}^*$
.
Since the sets
![]() $\bigcup _{m\in Y_1} C_m,\ldots , \bigcup _{m\in Y_k} C_m$
are multiplicatively thick, by Lemma 3.2, there are additively IP
$\bigcup _{m\in Y_1} C_m,\ldots , \bigcup _{m\in Y_k} C_m$
are multiplicatively thick, by Lemma 3.2, there are additively IP
![]() $_r$
sets
$_r$
sets
for each
![]() $j<N$
, such that
$j<N$
, such that
 $$ \begin{align} S_{l_i,i}\cdot S_{l_{i+1},i+1}\cdot\ldots\cdot S_{l_j,j}\subseteq \bigcup_{m\in Y_{l_i}}C_m \end{align} $$
$$ \begin{align} S_{l_i,i}\cdot S_{l_{i+1},i+1}\cdot\ldots\cdot S_{l_j,j}\subseteq \bigcup_{m\in Y_{l_i}}C_m \end{align} $$
for any
![]() $i\leq j\leq N$
and any choice
$i\leq j\leq N$
and any choice
![]() $l_i,l_{i+1},\ldots ,l_j\leq k$
.
$l_i,l_{i+1},\ldots ,l_j\leq k$
.
We inductively define
-
• a sequence of subsets
 $A_1\supseteq \ldots \supseteq A_N$
of
$A_1\supseteq \ldots \supseteq A_N$
of
 ${\mathbb {Q}}$
,
${\mathbb {Q}}$
, -
• finite sets
 $Q_1,\ldots ,Q_N\subseteq {\mathbb {Q}}$
,
$Q_1,\ldots ,Q_N\subseteq {\mathbb {Q}}$
, -
• tuples
 $(l_1,f_{1,1},\ldots ,f_{n,1}),\ldots , (l_N,f_{1,N},\ldots ,f_{n,N})$
, such that
$(l_1,f_{1,1},\ldots ,f_{n,1}),\ldots , (l_N,f_{1,N},\ldots ,f_{n,N})$
, such that
 $l_j\leq k$
and
$l_j\leq k$
and
 $f_{1,j},\ldots ,f_{n,j}\in F$
for every
$f_{1,j},\ldots ,f_{n,j}\in F$
for every
 $j\leq N$
,
$j\leq N$
, -
• and elements
 $y_1,\ldots ,y_{N-1}\in {\mathbb {Q}}\setminus \{0\}$
,
$y_1,\ldots ,y_{N-1}\in {\mathbb {Q}}\setminus \{0\}$
,
such that for every
![]() $j< N$
, we have
$j< N$
, we have
-
1.
 $A_{j+1}\subseteq A_j\cap \bigcap _{q\in Q_j}(A_j-qy_j)$
,
$A_{j+1}\subseteq A_j\cap \bigcap _{q\in Q_j}(A_j-qy_j)$
, -
2.
 $A_{j+1}\subseteq \{x\in A_j: xy_1\cdot \ldots \cdot y_j\in D_{(l_{j+1},f_{1,j+1},\ldots ,f_{n,j+1})}\}$
,
$A_{j+1}\subseteq \{x\in A_j: xy_1\cdot \ldots \cdot y_j\in D_{(l_{j+1},f_{1,j+1},\ldots ,f_{n,j+1})}\}$
, -
3.
 $y_j\in S_{l_{j},j}$
.
$y_j\in S_{l_{j},j}$
.
and
![]() $d(A_j)\geq \alpha _j$
for every
$d(A_j)\geq \alpha _j$
for every
![]() $j<N$
with
$j<N$
with
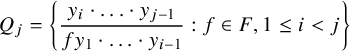 $$ \begin{align*}Q_j=\left\{\frac{y_i\cdot\ldots\cdot y_{j-1}}{fy_1\cdot\ldots\cdot y_{i-1}}: f\in F, 1\leq i<j\right\}\end{align*} $$
$$ \begin{align*}Q_j=\left\{\frac{y_i\cdot\ldots\cdot y_{j-1}}{fy_1\cdot\ldots\cdot y_{i-1}}: f\in F, 1\leq i<j\right\}\end{align*} $$
for every
![]() $j< N$
, where by convention, we write
$j< N$
, where by convention, we write
![]() $y_1\cdot \ldots \cdot y_{0}=1$
and
$y_1\cdot \ldots \cdot y_{0}=1$
and
![]() $Q_1=\{\frac {1}{f}:f\in F\}$
. Note that
$Q_1=\{\frac {1}{f}:f\in F\}$
. Note that
![]() $|Q_j|\leq |F|\cdot {j-1\choose 2}<s$
.
$|Q_j|\leq |F|\cdot {j-1\choose 2}<s$
.
To start off our inductive construction, we choose
![]() $(l_1,f_{1,1},\ldots ,f_{n,1})$
, such that
$(l_1,f_{1,1},\ldots ,f_{n,1})$
, such that
![]() $d(D_{(l_1,f_{1,1},\ldots ,f_{n,1})})>\alpha _1$
and put
$d(D_{(l_1,f_{1,1},\ldots ,f_{n,1})})>\alpha _1$
and put
![]() $A_1= D_{(l_1,f_{1,1},\ldots ,f_{n,1})}$
. Such tuple
$A_1= D_{(l_1,f_{1,1},\ldots ,f_{n,1})}$
. Such tuple
![]() $(l_1,f_{1,1},\ldots ,f_{n,1})$
can be found by our choice of
$(l_1,f_{1,1},\ldots ,f_{n,1})$
can be found by our choice of
![]() $\alpha _1$
.
$\alpha _1$
.
Now we describe the induction. Suppose that
![]() $A_j$
,
$A_j$
,
![]() $Q_j$
,
$Q_j$
,
![]() $(l_j,f_{1,j}\ldots ,f_{n,j})$
as well as
$(l_j,f_{1,j}\ldots ,f_{n,j})$
as well as
![]() $y_{j-1}$
have been constructed. We proceed to find
$y_{j-1}$
have been constructed. We proceed to find
![]() $y_j$
as well as
$y_j$
as well as
![]() $A_{j+1}$
,
$A_{j+1}$
,
![]() $Q_{j+1}$
and
$Q_{j+1}$
and
![]() $(l_{j+1},f_{1,j+1}\ldots ,f_{n,j+1})$
.
$(l_{j+1},f_{1,j+1}\ldots ,f_{n,j+1})$
.
First, since we can assume that s is chosen big enough so that
![]() $|Q_j|\leq s$
, and since the set
$|Q_j|\leq s$
, and since the set
![]() $S_{l_j,j}$
is additively IP
$S_{l_j,j}$
is additively IP
![]() $_r$
, by (4.5), we can find
$_r$
, by (4.5), we can find
![]() $y_j\in S_{l_{j},j}$
and
$y_j\in S_{l_{j},j}$
and
![]() $A_j'\subseteq A_j$
, such that
$A_j'\subseteq A_j$
, such that
![]() $d(A_j')=\alpha _j'$
and for every
$d(A_j')=\alpha _j'$
and for every
![]() $x\in A_j'$
, we have
$x\in A_j'$
, we have
Second, look at
![]() $y_1\cdot \ldots \cdot y_j A_j'$
, and note that for some
$y_1\cdot \ldots \cdot y_j A_j'$
, and note that for some
![]() $(l_{j+1},f_{1,j+1},\ldots ,f_{n,j+1})$
, the set
$(l_{j+1},f_{1,j+1},\ldots ,f_{n,j+1})$
, the set
![]() $\{x\in A_j': xy_1\cdot \ldots \cdot y_j\in D_{(l_{j+1},f_{1,j+1},\ldots ,f_{n,j+1})}\}$
has density at least
$\{x\in A_j': xy_1\cdot \ldots \cdot y_j\in D_{(l_{j+1},f_{1,j+1},\ldots ,f_{n,j+1})}\}$
has density at least
![]() $\alpha _{j+1}$
, by our choice of
$\alpha _{j+1}$
, by our choice of
![]() $\alpha _{j+1}$
. Put
$\alpha _{j+1}$
. Put
We find
![]() $i < j-1 < N-1$
so that for some
$i < j-1 < N-1$
so that for some
![]() $(l, f_1,. .. , f_n)$
, we have
$(l, f_1,. .. , f_n)$
, we have
Let
![]() $y=y_i\cdot \ldots \cdot y_{j-1}$
. By the property (3) and (4.6), there exists
$y=y_i\cdot \ldots \cdot y_{j-1}$
. By the property (3) and (4.6), there exists
![]() $m\in Y_{l}$
, such that
$m\in Y_{l}$
, such that
![]() $y\in C_m$
. Let
$y\in C_m$
. Let
![]() $x'\in A_{j}$
, and put
$x'\in A_{j}$
, and put
![]() $x=f_m x' y_1\cdot \ldots \cdot y_{i-1}$
.
$x=f_m x' y_1\cdot \ldots \cdot y_{i-1}$
.
Since
![]() $A_{j}\subseteq A_{i}$
, by the property (2) at step i of the construction, and we know that
$A_{j}\subseteq A_{i}$
, by the property (2) at step i of the construction, and we know that
so
![]() $x=f_m x'y_1\cdot \ldots \cdot y_{i-1}\in C_m$
by (4.7).
$x=f_m x'y_1\cdot \ldots \cdot y_{i-1}\in C_m$
by (4.7).
By property (2) at step j, we know that
so
![]() $xy=f_m x' y_1\cdot \ldots \cdot y_{j-1}\in C_m$
.
$xy=f_m x' y_1\cdot \ldots \cdot y_{j-1}\in C_m$
.
Finally, by property (1), we have
![]() $A_{j}\subseteq A_{j-1}\cap \bigcap _{q\in Q_{j-1}}(A_{j-1}-qy_{j-1})\subseteq A_{i}\cap \bigcap _{q\in Q_{j-1}}(A_i-qy_{j-1})$
, so
$A_{j}\subseteq A_{j-1}\cap \bigcap _{q\in Q_{j-1}}(A_{j-1}-qy_{j-1})\subseteq A_{i}\cap \bigcap _{q\in Q_{j-1}}(A_i-qy_{j-1})$
, so
for every
![]() $q\in Q_{j-1}$
. Put
$q\in Q_{j-1}$
. Put
Then by (2) again, since
![]() $x'+q y_{j-1}\in A_i$
, we have
$x'+q y_{j-1}\in A_i$
, we have
![]() $y_1\cdot \ldots \cdot y_{i-1}(x'+q y_{j-1})\in D_{(l,f_1,\ldots ,f_n)}$
, that is,
$y_1\cdot \ldots \cdot y_{i-1}(x'+q y_{j-1})\in D_{(l,f_1,\ldots ,f_n)}$
, that is,
which means that
![]() $x+y\in C_m$
.
$x+y\in C_m$
.
4.3 Other fields
Now, we give the short proof of Corollary 1.2 using a standard compactness argument.
Proof of Corollary 1.2.
Write
![]() $T_F$
for the theory of fields. Fix n, and let L be the language of the theory of fields together with n unary predicates
$T_F$
for the theory of fields. Fix n, and let L be the language of the theory of fields together with n unary predicates
![]() $C_1,\ldots , C_n$
. By Theorem 4.3, the sentence
$C_1,\ldots , C_n$
. By Theorem 4.3, the sentence
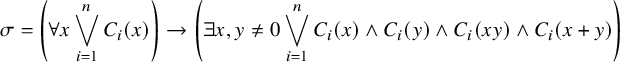 $$ \begin{align*}\sigma=\left(\forall x\bigvee_{i=1}^n C_i(x)\right)\to\left(\exists x,y\not=0 \bigvee_{i=1}^n C_i(x)\wedge C_i(y)\wedge C_i(xy)\wedge C_i(x+y)\right)\end{align*} $$
$$ \begin{align*}\sigma=\left(\forall x\bigvee_{i=1}^n C_i(x)\right)\to\left(\exists x,y\not=0 \bigvee_{i=1}^n C_i(x)\wedge C_i(y)\wedge C_i(xy)\wedge C_i(x+y)\right)\end{align*} $$
is satisfied in
![]() $\mathbb {Q}$
and hence in any field of characteristic zero. Thus,
$\mathbb {Q}$
and hence in any field of characteristic zero. Thus,
![]() $\sigma $
is provable in the theory of fields of characteristic zero
$\sigma $
is provable in the theory of fields of characteristic zero
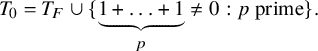 $$ \begin{align*}T_0=T_F\cup\{\underbrace{1+\ldots+1}_{p}\not=0:p\text{ prime}\}.\end{align*} $$
$$ \begin{align*}T_0=T_F\cup\{\underbrace{1+\ldots+1}_{p}\not=0:p\text{ prime}\}.\end{align*} $$
By the first-order logic compactness theorem [Reference Tent and ZieglerTZ12, Theorem 2.2.1],
![]() $\sigma $
is provable from a finite subset of
$\sigma $
is provable from a finite subset of
![]() $T_0$
, hence there exists
$T_0$
, hence there exists
![]() $p_0$
, such that any field of characteristic greater than
$p_0$
, such that any field of characteristic greater than
![]() $p_0$
satisfies
$p_0$
satisfies
![]() $\sigma $
.
$\sigma $
.
5 Generalizations
Here, we prove a generalization of Theorem 1.1 to the setting of more variables and more complicated monochromatic patterns.
Theorem 5.1. Let
![]() $H\subseteq \{h:{\mathbb {Q}}^i\to {\mathbb {Q}}: i\in \mathbb {N}\}$
be a finite set of functions, and let
$H\subseteq \{h:{\mathbb {Q}}^i\to {\mathbb {Q}}: i\in \mathbb {N}\}$
be a finite set of functions, and let
![]() $t\in \mathbb {N}$
. In any finite coloring of
$t\in \mathbb {N}$
. In any finite coloring of
![]() ${\mathbb {Q}}$
, there are
${\mathbb {Q}}$
, there are
![]() $x_0,\ldots ,x_t\in {\mathbb {Q}}$
, such that the following numbers have the same color:
$x_0,\ldots ,x_t\in {\mathbb {Q}}$
, such that the following numbers have the same color:
for all
![]() $0\leq i\leq j\leq t$
and any
$0\leq i\leq j\leq t$
and any
![]() $h_{i+1},\ldots ,h_t\in H$
(of appropriate arity).
$h_{i+1},\ldots ,h_t\in H$
(of appropriate arity).
Note in the above that the functions from H do not take
![]() $x_0$
as an input.
$x_0$
as an input.
Example 5.2. Considering the constant
![]() $0$
and constant
$0$
and constant
![]() $1$
function together with
$1$
function together with
![]() $h_1(y,z)=y$
,
$h_1(y,z)=y$
,
![]() $h_2(y,z)=z$
and
$h_2(y,z)=z$
and
![]() $h_3(y,z)=yz$
, we get the following monochromatic pattern:
$h_3(y,z)=yz$
, we get the following monochromatic pattern:
 $$ \begin{align*} \{x,y,z,xy,yz,xyz, \\ x+y,x+z,x+y+z,x + y + yz, x+yz,\\ xy+z,xy+yz\}. \end{align*} $$
$$ \begin{align*} \{x,y,z,xy,yz,xyz, \\ x+y,x+z,x+y+z,x + y + yz, x+yz,\\ xy+z,xy+yz\}. \end{align*} $$
Example 5.3. For a given k, considering the constant functions
![]() $1,\ldots , k$
, we get the following monochromatic pattern:
$1,\ldots , k$
, we get the following monochromatic pattern:
The proof is essentially the same as that of Theorem 1.1, but now we will need to consider more complicated sets
![]() $Q_i$
in the proof and use Ramsey’s theorem together with the pigeonhole principle. We repeat the first part of the proof for the sake of completeness.
$Q_i$
in the proof and use Ramsey’s theorem together with the pigeonhole principle. We repeat the first part of the proof for the sake of completeness.
Proof. Suppose
![]() ${\mathbb {Q}}$
is colored into n colors, and write
${\mathbb {Q}}$
is colored into n colors, and write
![]() ${\mathbb {Q}}\setminus \{0\}= C_1\cup \ldots \cup C_n$
. Let d be an invariant mean on
${\mathbb {Q}}\setminus \{0\}= C_1\cup \ldots \cup C_n$
. Let d be an invariant mean on
![]() $({\mathbb {Q}},+)$
. By Lemma 3.3, we get
$({\mathbb {Q}},+)$
. By Lemma 3.3, we get
![]() $k\in \mathbb {N}$
and finite sets
$k\in \mathbb {N}$
and finite sets
![]() $F\subseteq {\mathbb {Q}}$
and
$F\subseteq {\mathbb {Q}}$
and
![]() $Y_1,\ldots ,Y_k\subseteq [n],$
such that
$Y_1,\ldots ,Y_k\subseteq [n],$
such that
-
(i) for each
 $l \leq k$
, the set
$l \leq k$
, the set
 $\bigcup _{m\in Y_l} C_m$
is multiplicatively thick,
$\bigcup _{m\in Y_l} C_m$
is multiplicatively thick, -
(ii) for each
 $x\in {\mathbb {Q}}\setminus \{0\}$
, there exists
$x\in {\mathbb {Q}}\setminus \{0\}$
, there exists
 $l\leq k$
, such that for each
$l\leq k$
, such that for each
 $m\in Y_l$
, we have
$m\in Y_l$
, we have
 $x\in \bigcup _{f\in F} C_m/ f$
.
$x\in \bigcup _{f\in F} C_m/ f$
.
This gives the coloring of
![]() ${\mathbb {Q}}\setminus \{0\}$
with colors
${\mathbb {Q}}\setminus \{0\}$
with colors
![]() $D_{(l,f_1,\ldots ,f_n)}$
for each tuple
$D_{(l,f_1,\ldots ,f_n)}$
for each tuple
![]() $(l,f_1,\ldots ,f_n)$
where
$(l,f_1,\ldots ,f_n)$
where
These colors do not need to be disjoint, but we can always disjointify them. Write K for the number of colors in the above coloring.
Similarly, as in the proof of Theorem 4.3, we find large numbers
![]() $N,s\in \mathbb {N}$
with s depending on N, and
$N,s\in \mathbb {N}$
with s depending on N, and
![]() $r\in \mathbb {N}$
obtained by iteratively applying Theorem 2.3 N many times.
$r\in \mathbb {N}$
obtained by iteratively applying Theorem 2.3 N many times.
We define a sequence of positive numbers
![]() $\alpha _1,\alpha _1'\ldots ,\alpha _N,\alpha _N'$
with
$\alpha _1,\alpha _1'\ldots ,\alpha _N,\alpha _N'$
with
![]() $\alpha _1=\frac {1}{K}$
. At the j-th step, given
$\alpha _1=\frac {1}{K}$
. At the j-th step, given
![]() $\alpha _j$
and s, we apply Theorem 2.3 and obtain
$\alpha _j$
and s, we apply Theorem 2.3 and obtain
![]() $\alpha _j'$
, such that for any set
$\alpha _j'$
, such that for any set
![]() $A\subseteq {\mathbb {Q}}$
with
$A\subseteq {\mathbb {Q}}$
with
![]() $d(A)\geq \alpha _j$
and for any
$d(A)\geq \alpha _j$
and for any
![]() $q_1,\ldots ,q_s\in {\mathbb {Q}}$
, the set
$q_1,\ldots ,q_s\in {\mathbb {Q}}$
, the set
We put
![]() $\alpha _{j+1}=\frac {\alpha _j'}{K}$
.
$\alpha _{j+1}=\frac {\alpha _j'}{K}$
.
Lemma 3.2 gives us additively IP
![]() $_r$
sets
$_r$
sets
![]() $S_{1,j}\subseteq \bigcup _{m\in Y_1} C_m,\ldots ,S_{k,j}\subseteq \bigcup _{m\in Y_k} C_m$
for each
$S_{1,j}\subseteq \bigcup _{m\in Y_1} C_m,\ldots ,S_{k,j}\subseteq \bigcup _{m\in Y_k} C_m$
for each
![]() $j<N$
, such that
$j<N$
, such that
 $$ \begin{align} S_{l_i,i}\cdot S_{l_{i+1},i+1}\cdot\ldots\cdot S_{l_j,j}\subseteq \bigcup_{m\in Y_{l_i}}C_m \end{align} $$
$$ \begin{align} S_{l_i,i}\cdot S_{l_{i+1},i+1}\cdot\ldots\cdot S_{l_j,j}\subseteq \bigcup_{m\in Y_{l_i}}C_m \end{align} $$
for any
![]() $i\leq j\leq N$
and any choice of
$i\leq j\leq N$
and any choice of
![]() $l_i,l_{i+1},\ldots ,l_j\leq k$
$l_i,l_{i+1},\ldots ,l_j\leq k$
Inductively define a sequence of subsets
![]() $A_1\supseteq \ldots \supseteq A_N$
of
$A_1\supseteq \ldots \supseteq A_N$
of
![]() ${\mathbb {Q}}$
as well as finite sets
${\mathbb {Q}}$
as well as finite sets
![]() $Q_1,\ldots ,Q_N\subseteq {\mathbb {Q}}$
, tuples
$Q_1,\ldots ,Q_N\subseteq {\mathbb {Q}}$
, tuples
![]() $(l_1,f_{1,1},\ldots ,f_{n,1}),\ldots , (l_N,f_{1,N},\ldots ,f_{n,N})$
with
$(l_1,f_{1,1},\ldots ,f_{n,1}),\ldots , (l_N,f_{1,N},\ldots ,f_{n,N})$
with
![]() $l_j\leq k$
and
$l_j\leq k$
and
![]() $f_{1,j},\ldots ,f_{n,j}\in F$
for every
$f_{1,j},\ldots ,f_{n,j}\in F$
for every
![]() $j\leq N$
, as well as elements
$j\leq N$
, as well as elements
![]() $y_1,\ldots ,y_{N-1}\in {\mathbb {Q}}\setminus \{0\}$
, such that for every
$y_1,\ldots ,y_{N-1}\in {\mathbb {Q}}\setminus \{0\}$
, such that for every
![]() $j\leq N$
, we have
$j\leq N$
, we have
-
1.
 $A_{j+1}\subseteq A_j\cap \bigcap _{q\in Q_j}(A_j-qy_j)$
,
$A_{j+1}\subseteq A_j\cap \bigcap _{q\in Q_j}(A_j-qy_j)$
, -
2.
 $A_{j+1}\subseteq \{x\in A_j: xy_1\cdot \ldots \cdot y_j\in D_{(l_{j+1},f_{1,j+1},\ldots ,f_{n,j+1})}\}$
,
$A_{j+1}\subseteq \{x\in A_j: xy_1\cdot \ldots \cdot y_j\in D_{(l_{j+1},f_{1,j+1},\ldots ,f_{n,j+1})}\}$
, -
3.
 $y_j\in S_{l_{j},j}$
.
$y_j\in S_{l_{j},j}$
.
and
![]() $d(A_j)\geq \alpha _j$
for every
$d(A_j)\geq \alpha _j$
for every
![]() $j\leq N$
and
$j\leq N$
and
 $$ \begin{align*} Q_j=\left\{\frac{h(y_1\cdot\ldots\cdot y_{i_1-1},,\ldots,y_{i_{s-1}}\cdot\ldots\cdot y_{i_s-1})y_{i_s}\cdot\ldots\cdot y_{j-1}}{fy_1\cdot\ldots\cdot y_{i_q-1}}\right.: \\ \left.\vphantom{\frac{A^A}{A^A}}f\in F, h\in H, s\leq j, 0\leq i_1<\ldots<i_s\leq j, q\leq s\right\}, \end{align*} $$
$$ \begin{align*} Q_j=\left\{\frac{h(y_1\cdot\ldots\cdot y_{i_1-1},,\ldots,y_{i_{s-1}}\cdot\ldots\cdot y_{i_s-1})y_{i_s}\cdot\ldots\cdot y_{j-1}}{fy_1\cdot\ldots\cdot y_{i_q-1}}\right.: \\ \left.\vphantom{\frac{A^A}{A^A}}f\in F, h\in H, s\leq j, 0\leq i_1<\ldots<i_s\leq j, q\leq s\right\}, \end{align*} $$
where by convention, we write
![]() $y_1\cdot \ldots \cdot y_{0}=1$
and
$y_1\cdot \ldots \cdot y_{0}=1$
and
![]() $Q_1=\{\frac {1}{f}:f\in F\}$
.
$Q_1=\{\frac {1}{f}:f\in F\}$
.
Now, we describe the induction. Suppose that
![]() $A_j$
,
$A_j$
,
![]() $Q_j$
,
$Q_j$
,
![]() $(l_j,f_{1,j}\ldots ,f_{n,j})$
as well as
$(l_j,f_{1,j}\ldots ,f_{n,j})$
as well as
![]() $y_{j-1}$
have been constructed. We proceed to find
$y_{j-1}$
have been constructed. We proceed to find
![]() $y_j$
as well as
$y_j$
as well as
![]() $A_{j+1}$
,
$A_{j+1}$
,
![]() $Q_{j+1}$
and
$Q_{j+1}$
and
![]() $(l_{j+1},f_{1,j+1}\ldots ,f_{n,j+1})$
.
$(l_{j+1},f_{1,j+1}\ldots ,f_{n,j+1})$
.
First, since we can assume that s is chosen big enough so that
![]() $|Q_j|\leq s$
, and since the set
$|Q_j|\leq s$
, and since the set
![]() $S_{l_j,j}$
is additively IP
$S_{l_j,j}$
is additively IP
![]() $_r$
, by (4.5), we can find
$_r$
, by (4.5), we can find
![]() $y_j\in S_{l_{j},j}$
and
$y_j\in S_{l_{j},j}$
and
![]() $A_j'\subseteq A_j$
, such that
$A_j'\subseteq A_j$
, such that
![]() $d(A_j')=\alpha _j'$
and for every
$d(A_j')=\alpha _j'$
and for every
![]() $x\in A_j'$
, we have
$x\in A_j'$
, we have
Second, look at
![]() $y_1\ldots y_j A_j'$
, and note that for some
$y_1\ldots y_j A_j'$
, and note that for some
![]() $(l_{j+1},f_{1,j+1},\ldots ,f_{n,j+1})$
, the set
$(l_{j+1},f_{1,j+1},\ldots ,f_{n,j+1})$
, the set
![]() $\{x\in A_j': xy_1\cdot \ldots \cdot y_j\in D_{(l_{j+1},f_{1,j+1},\ldots ,f_{n,j+1})}\}$
has density at least
$\{x\in A_j': xy_1\cdot \ldots \cdot y_j\in D_{(l_{j+1},f_{1,j+1},\ldots ,f_{n,j+1})}\}$
has density at least
![]() $\alpha _{j+1}$
, by our choice of
$\alpha _{j+1}$
, by our choice of
![]() $\alpha _{j+1}$
. Put
$\alpha _{j+1}$
. Put
So long as N was chosen large enough, by the pigeonhole principle, we find
![]() $j_1,\ldots ,j_M$
so that for some
$j_1,\ldots ,j_M$
so that for some
![]() $(l,f_1,\ldots ,f_n)$
, we have
$(l,f_1,\ldots ,f_n)$
, we have
for each
![]() $i\leq M$
. For simplicity of notation, suppose
$i\leq M$
. For simplicity of notation, suppose
![]() $j_1=1,\ldots , j_M=M$
.
$j_1=1,\ldots , j_M=M$
.
Note that if
![]() $i<j\leq M$
, then by (3) and (5.2), there exists
$i<j\leq M$
, then by (3) and (5.2), there exists
![]() $m\in Y_l$
, such that
$m\in Y_l$
, such that
![]() $y_i\cdot \ldots \cdot y_{j-1}\in C_m$
. Now, consider the coloring of
$y_i\cdot \ldots \cdot y_{j-1}\in C_m$
. Now, consider the coloring of
![]() $[M]\times [M]$
, where we give
$[M]\times [M]$
, where we give
![]() $(i,j)$
with
$(i,j)$
with
![]() $i<j$
the color m if
$i<j$
the color m if
So long as M is large enough, by Ramsey’s theorem, there is a color m and subsequence
![]() $j_1,\ldots ,j_{t+1}$
so that all pairs from the subsequence have the same color.
$j_1,\ldots ,j_{t+1}$
so that all pairs from the subsequence have the same color.
Put
![]() $x_1=y_{j_1}\cdot \ldots \cdot y_{j_2-1}, \ \ldots ,\ x_t=y_{j_{t}}\cdot \ldots \cdot y_{j_{t+1}-1}$
.
$x_1=y_{j_1}\cdot \ldots \cdot y_{j_2-1}, \ \ldots ,\ x_t=y_{j_{t}}\cdot \ldots \cdot y_{j_{t+1}-1}$
.
First, note that by the choice of the subsequence
![]() $j_1,\ldots ,j_t$
, we have
$j_1,\ldots ,j_t$
, we have
for every
![]() $1\leq i\leq j$
.
$1\leq i\leq j$
.
Choose
![]() $x_0'\in A_{j_t}$
, and put
$x_0'\in A_{j_t}$
, and put
![]() $x_0= f_m x_0' y_1\cdot \ldots \cdot y_{j_1-1}$
. Since
$x_0= f_m x_0' y_1\cdot \ldots \cdot y_{j_1-1}$
. Since
![]() $A_{j}\subseteq A_{i}$
for
$A_{j}\subseteq A_{i}$
for
![]() $i<j$
, by property (1), we know that by (5.3), we have
$i<j$
, by property (1), we know that by (5.3), we have
![]() $x_0' y_1\cdot \ldots \cdot y_{j_i-1}\in D_{(l,f_1,\ldots ,f_n)}$
, so
$x_0' y_1\cdot \ldots \cdot y_{j_i-1}\in D_{(l,f_1,\ldots ,f_n)}$
, so
for each
![]() $0\leq i\leq n$
.
$0\leq i\leq n$
.
Now, fix i and
![]() $h_{i+1},\ldots ,h_t\in H$
. By property (1), we know that if
$h_{i+1},\ldots ,h_t\in H$
. By property (1), we know that if
![]() $i<j$
, then
$i<j$
, then
![]() $A_{j}\subseteq A_{j-1}\cap \bigcap _{q\in Q_{j-1}}(A_{j-1}-qy_{j-1})\subseteq A_{i}\cap \bigcap _{q\in Q_{j-1}}(A_i-qy_{j-1})$
, so
$A_{j}\subseteq A_{j-1}\cap \bigcap _{q\in Q_{j-1}}(A_{j-1}-qy_{j-1})\subseteq A_{i}\cap \bigcap _{q\in Q_{j-1}}(A_i-qy_{j-1})$
, so
for every
![]() $q\in Q_{j-1}$
.
$q\in Q_{j-1}$
.
Put
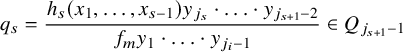 $$ \begin{align*}q_{s}=\frac{h_s(x_1,\ldots,x_{s-1})y_{j_{s}}\cdot\ldots\cdot y_{j_{s+1}-2}}{f_m y_1\cdot\ldots\cdot y_{j_i-1}}\in Q_{j_{s+1}-1}\end{align*} $$
$$ \begin{align*}q_{s}=\frac{h_s(x_1,\ldots,x_{s-1})y_{j_{s}}\cdot\ldots\cdot y_{j_{s+1}-2}}{f_m y_1\cdot\ldots\cdot y_{j_i-1}}\in Q_{j_{s+1}-1}\end{align*} $$
for every s, such that
![]() $i<s\leq t$
. Then, by iterating (5.4), we have
$i<s\leq t$
. Then, by iterating (5.4), we have
for every
![]() $s\leq t$
, so
$s\leq t$
, so
![]() $x_0'+ q_{i+1}y_{j_{i+2}-1}+\ldots +q_{t}y_{j_{t+1}-1} \in A_{j_t}$
. Since
$x_0'+ q_{i+1}y_{j_{i+2}-1}+\ldots +q_{t}y_{j_{t+1}-1} \in A_{j_t}$
. Since
![]() $A_{j_t}\subseteq A_{j_i}$
, we get
$A_{j_t}\subseteq A_{j_i}$
, we get
![]() $y_1\cdot \ldots \cdot y_{j_i-1}(x_0'+ q_{i+1}y_{j_{i+2}-1}+\ldots +q_{t}y_{j_{t+1}-1} )\in D_{(l,,f_1\ldots ,f_n)}$
, which means that
$y_1\cdot \ldots \cdot y_{j_i-1}(x_0'+ q_{i+1}y_{j_{i+2}-1}+\ldots +q_{t}y_{j_{t+1}-1} )\in D_{(l,,f_1\ldots ,f_n)}$
, which means that
![]() $f_m y_1\cdot \ldots \cdot y_{j_i-1}(x_0'+ q_{i+1}y_{j_{i+2}-1}+\ldots +q_{t}y_{j_{t+1}-1} )\in C_m$
, and so
$f_m y_1\cdot \ldots \cdot y_{j_i-1}(x_0'+ q_{i+1}y_{j_{i+2}-1}+\ldots +q_{t}y_{j_{t+1}-1} )\in C_m$
, and so
as needed.
6 Open problems
Our main result is a common extension of Hindman’s conjecture and the van der Waerden theorem [Reference van der WaerdenWae27], so it is natural to wonder if our approach might extend to generalize the polynomial van der Waerden theorem [Reference Bergelson and LeibmanBL96] as well.
Question 6.1. Let P be a finite set of integral polynomials. Does any finite coloring of
![]() $\mathbb {Q}$
contain a monochromatic set of the form
$\mathbb {Q}$
contain a monochromatic set of the form
![]() $\{x,y,xy,x+p(y):p\in P\}?$
$\{x,y,xy,x+p(y):p\in P\}?$
This is known to hold even for
![]() $\mathbb {N}$
if the y term is dropped [Reference MoreiraMor17]. Our approach would immediately extend to prove this if the IP
$\mathbb {N}$
if the y term is dropped [Reference MoreiraMor17]. Our approach would immediately extend to prove this if the IP
![]() $^*_r$
polynomial theorem were known to be true, but perhaps finding the right quantitative version of the polynomial van der Waerden theorem [Reference Bergelson and LeibmanBL96] will suffice.
$^*_r$
polynomial theorem were known to be true, but perhaps finding the right quantitative version of the polynomial van der Waerden theorem [Reference Bergelson and LeibmanBL96] will suffice.
Another potential direction is to extend our results to generalize the geometric theorem as well. Currently, even the following is open.
Question 6.2. Does every finite coloring of
![]() $\mathbb {Q}$
contain a monochromatic set of the form
$\mathbb {Q}$
contain a monochromatic set of the form
![]() $\{xy,xy^2,x+y\}?$
$\{xy,xy^2,x+y\}?$
Finally, let us mention that Hindman also conjectured stronger statements, namely, that any finite coloring of
![]() $\mathbb {N}$
contains monochromatic sets of the form
$\mathbb {N}$
contains monochromatic sets of the form
![]() $FS(A)\cup FP(A)$
for
$FS(A)\cup FP(A)$
for
![]() $A\subseteq \mathbb {N}$
arbitrarily large. Our approach can deal with some subsets of these configurations in
$A\subseteq \mathbb {N}$
arbitrarily large. Our approach can deal with some subsets of these configurations in
![]() $\mathbb {Q}$
(see Theorem 5.1 and Example 5.2), but the problem still seems difficult even for
$\mathbb {Q}$
(see Theorem 5.1 and Example 5.2), but the problem still seems difficult even for
![]() $|A|=3$
in
$|A|=3$
in
![]() $\mathbb {Q}.$
$\mathbb {Q}.$
Acknowledgments
The authors would like to thank the participants of the UltraMath 2022 conference for many useful comments. Thanks are also due to the anonymous referees for their detailed suggestions that improved the presentation of the present paper. Both authors are partly funded by the Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant RGPIN-2020-05445, NSERC Discovery Accelerator Supplement RGPAS-2020-00097, the National Science Centre (Poland) (NCN) Grant Harmonia 2018/30/M/ST1/00668, and thank the Centre de Recherches Mathémathiques (CRM) for its support. The first author was also partially supported by Ben Green’s Simons Investigator Grant number 376201. The second author thanks also the Fondation Sciences Mathématiques de Paris (FSMP) for its support.
Competing interests
The authors have no competing interest to declare.