I. INTRODUCTION
In this paper, we study a social dynamics of the General Equilibrium Theory (GET) through a collective biography of its practitioners in a dozen different countries. Having emerged at the margins of the community of academic economists, it quickly became a powerful research program and was believed to be a “mother structure” (Mirowski Reference Mirowski2002, p. 394) for contemporary neoclassical economics.Footnote 1 While GET was sharply criticized by some economists and other scholars for the lack of realism and dismissed as merely “blackboard economics,” indulging in the “rhetoric of mathematical formalism” (McCloskey Reference McCloskey1994; Blaug Reference Blaug2003), it was admired by many others for its mathematical rigor and its powerful insights.
This highly influential research program became the theoretical centerpiece of the discipline in the early 1950s with the seminal works published by Kenneth Arrow, Gérard Debreu, Lionel McKenzie, David Gale, Tjalling Koopmans, and many others, giving a purely formal and axiomatic frame to the Walrasian model of competitive markets dating back to 1874 (Ingrao and Israel Reference Ingrao and Israel1990; Düppe and Weintraub Reference Düppe and Weintraub2014). By the late 1950s, the GET had been accepted by a wider community of economists, first in the United States and later in other countries. The standard GE (general equilibrium) results included existence, uniqueness, stability, and efficiency properties (“Pareto-optimality”) of competitive economic equilibrium in the abstract model of market economy, in which decentralized interaction of rational agents and corresponding allocation of resources could yield optimal results. Familiar associations of Adam Smith’s “invisible hand” were incorporated into the new theory of perfect competition that could provide rigorous results on the highest level of mathematical sophistication and abstraction. For the first time in history, the Walrasian system of general equilibrium, which Joseph Schumpeter ([1954] Reference Schumpeter2006, p. 233) once called “the Magna Carta of economic theory,” could finally be codified, so that by the 1970s it was considered to be “the most complete existing model of economic behavior” (Weintraub Reference Roy1974, p. 18). The generality and elegance of this research program were, for a long time, important arguments in its favor (Geanakoplos Reference Geanakoplos1990).
Diffusion of the particular style of economic reasoning associated with the GET is concomitant with a relative theoretical unification (the “neoclassical synthesis”) and mathematization of economic analysis, which largely contributes to internationalization of the American economics and to a greater intellectual and public prestige of economic sciences. However, as standard accounts go, the GE theoretical program washes out after the publication of Sonnenschein-Mantel-Debreu’s results in the 1970s, revealing unfixable conceptual difficulties in the foundation of the GET (see, on that, section II herein, and general historical accounts in Rizvi Reference Rizvi1994, Reference Rizvi, Samuels, Biddle and Davis2003). The economists’ attention shifted since then, for insight and support, to more local models in game theory and mechanism design, to an evolutionary approach, behavioral and experimental methods, and other alternative theoretical programs. In addition, since the 1970s, the weight and the prestige of the applied/empirical work in economics in relation to “pure theory” (Hamermesh Reference Hamermesh2013; Backhouse and Cherrier Reference Backhouse and Cherrier2014; Cherrier Reference Cherrier2017; Harris et al. Reference Harris, Myers, Briol, Carlen, D”Amico and Martin2022) have significantly increased as the shift “from models to methods” has occurred (Panhans and Singleton Reference Panhans and Singleton2017). All these tendencies mark a decline of the “pure theory” and the particular style of work in economics symbolized by the GET. At the same time, accounts of emergence, as well as of a presumable running out of steam, of this research program rarely address the recent developments of the discipline.
Despite apparent theoretical dead ends encountered by GE scholars, the approach in terms of “general equilibrium” is still largely used by economists interested both in theory and in many applied fields. Classical topics in the GET—under the keywords such as “competitive equilibrium,” “incomplete markets,” “tâtonnement,” etc.—do not seem to be at the center of economists’ preoccupations anymore. Nonetheless, the GET still proves to be a vigorous research field attracting young scholars with theoretical ambitions and maintaining its places of practice, transmission, and sociability.Footnote 2 As we shall see below, there is still a group of economists identifying themselves with this research domain and engaging in this type of “high theory.”
Philosophers and historians of economic thought generally limit themselves to tracing the emergence and development of the most significant figures and contributions to the GET roughly until the publication of the Sonnenschein-Mantel-Debreu theorem (Ingrao and Israel Reference Ingrao and Israel1990; Rizvi Reference Rizvi, Samuels, Biddle and Davis2003) and sometimes focusing on its aftermath (Kirman Reference Kirman2006; Rizvi Reference Rizvi2006). However, the afterlife of the GET,Footnote 3 no more than its quick and impressive rise, cannot be sufficiently explained in internalist terms as a spontaneous diffusion of inherently powerful ideas. Borrowing from the sociology of science, and of theoretical work in particular (Warwick Reference Warwick2003; Rosental Reference Rosental2003), as well as from the Bourdieusian socio-analysis of fields of cultural production (Bourdieu Reference Bourdieu1975, Reference Bourdieu1976, [1984] Reference Bourdieu1988), this article aims to understand the social dynamics of the Walrasian program in economics in relation to its intellectual development: How did a research program resurrecting Walrasian ideas become “the most prestigious economics of all” that “set standards that all economists aspire to reach” (Blaug [1980] Reference Blaug1992, p. 169)? What were the forms and factors of its large diffusion, legitimation in a larger field of economics, and reproduction over time, in spite of theoretical limitations?
To answer these questions, we chose to approach the GET not as a set of concepts and models without history but as a body of knowledge supported by a group of individuals having different national and educational backgrounds and linked to each other in various ways: through teaching and studying, oral communication, and co-authorship, sharing working space, reading and citing each other’s work, and so on. In other words, in order to understand how this new research program was formed, diffused, and reproduced itself, we consider a social history of a “scientific community” (Crane Reference Crane1972; Shapin and Thackray Reference Shapin and Thackray1974; Bulpin and Molyneux-Hodgson Reference Bulpin and Molyneux-Hodgson2013) of the GET scholars, understood as a network of interacting scientists with its own epistemic standards, acquired through training and various forms of academic sociability, professional culture, and practices.
This analysis relies on a prosopography, i.e., an investigation of common properties of social and professional trajectories of the GET scholars on the basis of relevant biographical data, which we used as a tool to identify relational patterns defining the structure of this scientific community, its longevity, and success in a broader field of economics. Although most historiographic accounts of economics traditionally focus on intellectual contributions and careers of individual thinkers, in recent years prosopography is gaining momentum in this field of research (Hagemann Reference Hagemann2011; Cherrier Reference Cherrier2014; Svorenčik Reference Svorenčik2014, Reference Svorenčik2018). A comprehensive analysis of students and faculties, through several decades, associated with an economics department or a comparison of several departments or schools provides useful insights into social dynamics of the discipline. An approach by biographies is more common in the sociology of economics, particularly in that of Bourdieusian inspiration (Lebaron Reference Lebaron2001; Rossier Reference Rossier2020; Rossier and Benz Reference Rossier, Benz, Maesse, Pühringer, Rossier and Benz2021), where prosopographical data are used to construct a social space defined by “structural distributions of power and meaning as well as of technics, artefacts and other objectifications” of the discipline (Schmidt-Wellenburg and Lebaron Reference Schmidt-Wellenburg and Lebaron2018, p. 21). These studies question the forms of acquisition and conversion of various types of scientific capital (academic, administrative, expert-political, and so on), and allow the understanding of the role of these capitals in the careers of economists in different countries.
As compared with the aforementioned studies, our object is specific in at least two respects: (1) we are dealing with a corpus of theoretical contributions with no clear borders, (2) created by scholars coming from different institutions, disciplines, and countries, yet constituting a sort of “community,” whose nature (form of coherence) we will try to clarify. To understand a quick rise of the GET in the field of economics and its transnational diffusion well beyond the 1970s, we have tried to link the reconstruction of a conceptual development of the GET with a systematic study of biographies of its contributors. We compiled a prosopographical database containing about 150 individuals, recognized as “GE theorists” by a community of peers (see Appendix Part I for a detailed presentation of how this list was produced).Footnote 4 Then we collected and coded, as different kinds of variables, some of their biographical details, educational and academic trajectories, their work in the GET, various forms of professional activity, and recognition. Basic statistical analysis of this data allows us to reconstruct a temporal and institutional dynamics of the GET since the 1950s, to identify its most productive periods and important academic centers—engaged in the most significant conceptual developments (section II). Comparing the key moments in the individual trajectories helps identify typical career patterns, as well as the forms of interdisciplinary and international transmission, that facilitated a geographical expansion of the GET research program (section III). We apply to this dataset a technique of geometric analysis, a Multiple Correspondence Analysis or MCA (Lebaron Reference Lebaron2010), to investigate the relational patterns between attribution of scientific credit and biographical properties in a transnational space of the GET scholars. We interpret these geographical and disciplinary patterns of scientific recognition as principles of intellectual legitimation of the GET research in a larger field of economics and beyond (section IV).
II. A CONCEPTUAL DEVELOPMENT OF THE WALRASIAN GET: FROM ABSTRACTION TO “REAL” MARKETS
In some ways, the GET existed long before WW II, but the attempts to work in the Walrasian tradition (by, e.g., Gustav Cassel or Abraham Wald) could not exert a significant influence on economics until the GET was formalized and contributed itself to the formalization of other branches of economics (see the history of formalizing the GET in Weintraub Reference Roy1983). As a part of a larger movement for the mathematization of social sciences, the GET research program benefitted directly from support from the US government and the military interested in the development of mathematical economics, operations research, and game theory. The role of the RAND Corporation and US defense departments in supporting research in these areas in the US and abroad, particularly during the Cold War years, cannot be underestimated, and resulted in propagation of a particular research style and rationality (Amadae Reference Amadae2003; Erickson et al. Reference Erickson, Klein, Daston, Lemov, Sturm and Gordin2013).Footnote 5 It comes as no surprise that the postwar story of the GET is heavily dominated by US institutions and researchers, although this field has been progressively internationalized throughout the period under study.
First and foremost, it was a development of an abstract formal framework, which, once shown to demonstrate technically tractable and economically appealing results in a fairly general form (Nash Reference Nash1950; Arrow and Debreu Reference Arrow and Debreu1954; Debreu Reference Debreu1959; McKenzie Reference McKenzie1954, Reference McKenzie1959), was further refined to include many market imperfections. The first decade of work on formalizing the GET was crowned by the publication of Debreu’s Theory of Value in 1959, the most general Bourbakist axiomatics for economic theory (Weintraub and Mirowski Reference Weintraub and Mirowski1994), followed by its acceptance, legitimation, and a large diffusion within the economics profession in the United States, Europe, Japan, and in other regions of the world (the most well-known “textbook” codification being Arrow and Hahn Reference Arrow and Hahn1971).
The real significance of the standard Walrasian general equilibrium was thus of providing an ideal benchmark and exemplary techniques, securing some familiar results, and allowing the possibility to achieve them, once a problem at hand could be reformulated. In this, it followed largely the logic of mathematical practice: first, it involved finding in which way—and under which conditions—the “good” or “smooth” results of an original Arrow-Debreu model and its ramifications could be preserved in different frameworks; and, second, it implied that certain initial conditions in the ideal world could be meaningfully analyzed in a “negative,” counterfactual way, that is, in demonstrating precisely the correspondences between imperfections in the real world and deviations from assumptions leading to Pareto-efficiency.
However, there are also more descriptive and substantive interpretations of the general equilibrium framework. It is still regarded by many economists to be the best instrument for the theoretical analysis of the workings of markets. Wherever there are reasons to believe that certain markets are plausibly represented as anonymous and “large,” in the sense of a negligible impact of one agent on the structure and workings of the whole economy, and the low level of strategic interaction between the agents (Mas-Colell 1999; Shannon Reference Shannon2002), the analysis in terms of general equilibrium appears valid. Another rationale is the interconnectedness of markets, the situation making “partial equilibrium” models (taking those markets, which are not considered, as given) irrelevant. In fact, this can be seen as the broadest definition of general equilibrium analysis: “that good analytical models must be closed” (Mas-Colell 1999, p. 208), the most formalized pole of the spectrum being the Walrasian theory.
What were the main developments in the discipline since the famous existence proof (Arrow and Debreu Reference Arrow and Debreu1954; Debreu Reference Debreu1959)? In this discussion, which should demonstrate the conceptual challenges and intellectual driving forces behind the GE program (Zame Reference Zame, Durlauf and Blume2008), we will explore the complexity and diversity of the approaches that appeared since then. This helps define the very object of our study and does not “black box” the GET or reduce it to the set of well-known problems.
Once we have shown that under some plausible conditions a general equilibrium of an abstract economy exists, it has to be in some sense robust or stable: a system should return to equilibrium once it was disturbed (on the history of stability, see Weintraub Reference Roy1991; Hands Reference Hands1994; Boldyrev and Ushakov Reference Boldyrev and Ushakov2016; and Lenfant Reference Lenfant2022). Related to the stability question are the issues of falsifiability of the GET. Some negative results—such as the examples of instability due to Scarf (Reference Scarf1960) and the famous Sonnenschein-Mantel-Debreu (SMD) theory (Sonnenschein Reference Sonnenschein1973; Mantel Reference Mantel1974; Debreu Reference Debreu1974)—demonstrated that standard neoclassical microeconomic assumptions for the properties of individual economic agents put very few restrictions on—and thus create arbitrariness for—the aggregate excess demand function of the economy, the major object GE theorists are working with (allowing the drawing of conclusions about the structure of the general equilibrium on the “macro” level). Hence, under fairly common-sense conditions the general equilibrium dynamics can be, in the aggregate, essentially arbitrary (see the overview of the more recent developments of the SMD theory in Rizvi Reference Rizvi2006, and Chiappori and Ekeland Reference Chiappori and Ekeland2011).
The SMD theory was significant because it clarified the limits to general equilibrium analysis and was widely perceived as claiming that it cannot, in the aggregate, generate falsifiable results. According to this perception, Walrasian GET was demonstrated to be a framework, a powerful and widely adopted method, a set of techniques and insights, but not a theory that describes any real economy.
However, the investigation of the GE model continued, and the central theoretical question concerned what is now called the determinacy of equilibrium—the way it depends on the parameters of the model (Zame Reference Zame, Durlauf and Blume2008). And here, as elsewhere in the GET, the assumptions necessary for “good” results to persist are excessively strong and unrealistic. It was Debreu (Reference Debreu1970) who launched a new research program in the study of GE determinacy. He used new techniques of differential topology to show that for some not-so-restrictive conditions, equilibrium determinacy may be demonstrated (the number of equilibria in the model is finite and, in a local case, comparative statics analysis yields determinate results). This was an important step forward and initiated the new research focusing on “generic” (that is, in some sense, typical) properties of the equilibria.
Another stream of literatures (starting with Debreu and Scarf Reference Debreu and Scarf1963, and Aumann Reference Aumann1964; see the recent history in Cogliano Reference Cogliano2019) showed how, using the techniques of measure theory, general equilibrium results and price-taking behavior can be justified by making agents in the model infinitely small, that is, in modeling their impact on the market parameters as infinitely negligible. Indeed, the very term “Walrasian” is sometimes understood as synonymous to “perfectly competitive,” and the logic of perfect competition thus itself needed to be clarified, defended, and put to a (at least conceptual) test (Makowski and Ostroy Reference Makowski and Ostroy2001). This association of the GET and cooperative game theory has become quite popular (which is also visible in our data).
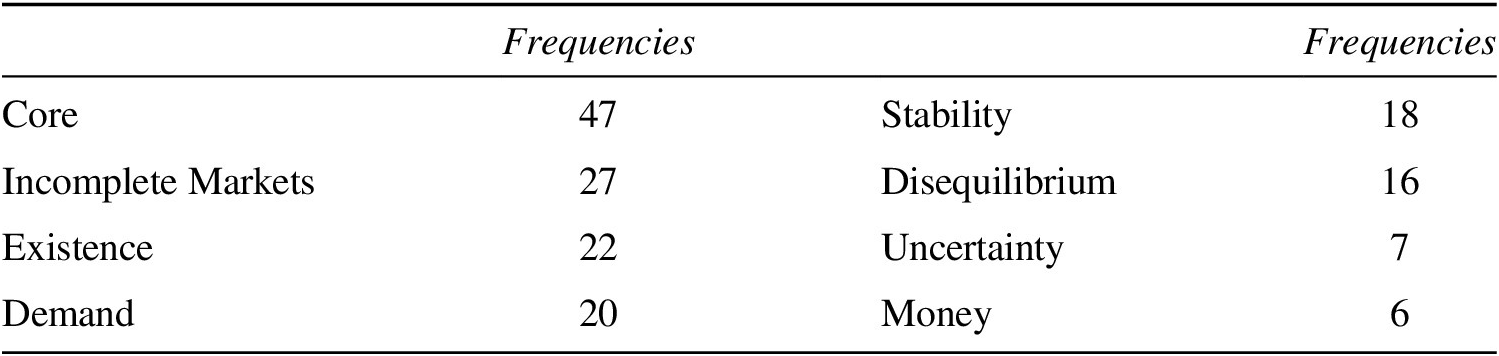
Another significant literature—or, better to say, set of literatures—concerns the elaboration of Arrow’s (Reference Arrow1953) extension of GET to the case of uncertainty. Here, the well-known world of commodities is generalized to the world of assets that allow trading across future dates and states of the world and thus efficiently sharing risks associated with the future uncertainties. This analysis is mostly done within the framework of incomplete markets theory—“incomplete” meaning that assets available in the economy do not allow trading across all possible states of the world and future dates (as in the benchmark model provided by Arrow).Footnote 6 In general, this literature examines the potentials and limits of financial markets in dealing with risks and in improving welfare (Hart Reference Hart1975; Geanakoplos and Polemarchakis Reference Geanakoplos, Polemarchakis, Heller, Starr and Starrett1986). Its overall significance and popularity among GE theorists (Table 1) is understandable: it promised the way out of the sterile world of perfect markets without sacrificing the rigor of the basic GE methodology. Not only financial assets (Harrison and Kreps Reference Harrison and Kreps1979) but also (non-neutrality of) money, bankruptcy, default, or government intervention could be rationalized within this new framework. As John Geanakoplos (Reference Geanakoplos1990, p. 2) remarked, the new incomplete markets model “is important in freeing one’s thinking from the automatic association of competitive equilibrium with Pareto optimality.” Essentially, the popularity of the incomplete markets theory could be explained by the fact that it linked a rigorous Walrasian general equilibrium framework to the concerns of macroeconomics and finance (see more on these concerns in Mehrling Reference Mehrling, Kurz and Faccarello2016; Boldyrev Reference Boldyrev2021).
Table 1. Topics of Interest (Multiple Choice, Most Frequent)
A related research direction involves the extension of the GET to the cases of asymmetric information; here, the concepts of Walrasian expectations equilibrium (assuming that agents have limited private information) and rational expectations equilibrium (assuming that agents have limited private information and rely on prices) (Radner Reference Radner1968, Reference Radner1979) were introduced. A further approach focuses on the dynamization of Walrasian theory and revives the Hicksian notion of “temporary equilibrium” (Grandmont Reference Grandmont1977), in which agents form their expectations on the future states of the economy by constantly adjusting them in every period, whereby the economy is treated as a sequence of temporary equilibria. Many scholars attempted to generalize the GE results for wider types of preferences (see the overview and the recent contribution in He and Yannelis Reference He and Yannelis2016).
On a more mathematical scale, extension of general equilibrium to the case of infinitely many commodities (starting with Bewley Reference Bewley1972) appears to have been a significant step forward, introducing various new formal techniques that allowed, for example, the modeling of differentiated commodities (Mas-Colell Reference Mas-Colell1975) or allocation problems under uncertainty that are typical for finance (Kreps Reference Kreps1981).
We see that, despite being explicitly abstract and unrealistic, Walrasian GET developed as a framework that allowed posing certain questions addressing the structural characteristics of the competitive markets. We single out three important patterns of theoretical development. First, theory developed by handling deviations from the ideal benchmark advanced in the beginning or by reformulating the benchmark itself (what Weintraub Reference Roy1985 called “the hardening of the hard core”). Second, the GET framework allowed for occasionally fruitful contacts with mathematics. One could mention the attempts at dynamization of GET undertaken by famous mathematician and Fields Medalist Stephen Smale (Reference Smale, Arrow and Intrilligator1981) or the adoption of differential topology by Debreu (Reference Debreu1970) and Mas-Colell (1985). Third, the conceptual development of the GET has been decisively stimulated by applying the GET framework to the analysis of asset markets, as well as to the exploration of such issues as the role of money and government intervention. The keywords that guide our prosopographic analysis and help us understand the topics GE theorists were working on originate from this vision of the GE conceptual development.
We should also add that Walrasian GET has become a starting point for more applied policy models, notably the “computable general equilibrium” (CGE) ones and the rational expectations representative-agent macromodels, of which the DSGE, the centerpiece of modern macro, is arguably a product.Footnote 7 But including both directions would not correspond to our specific aim of tracing the development of specifically Walrasian GET as a theoretical program. It is, of course, connected to this more applied and macro-oriented work but should not be identified with it.
Thus, from the 1950s to the 2000s, the Walrasian theory—which was becoming increasingly complex to handle various deviations from the original construction—attracted many economists interested in the pure logic of competitive markets. It is to the social and institutional logics behind this development that we now turn.
III. INSTITUTIONAL DIFFUSION OF THE GET RESEARCH PROGRAM
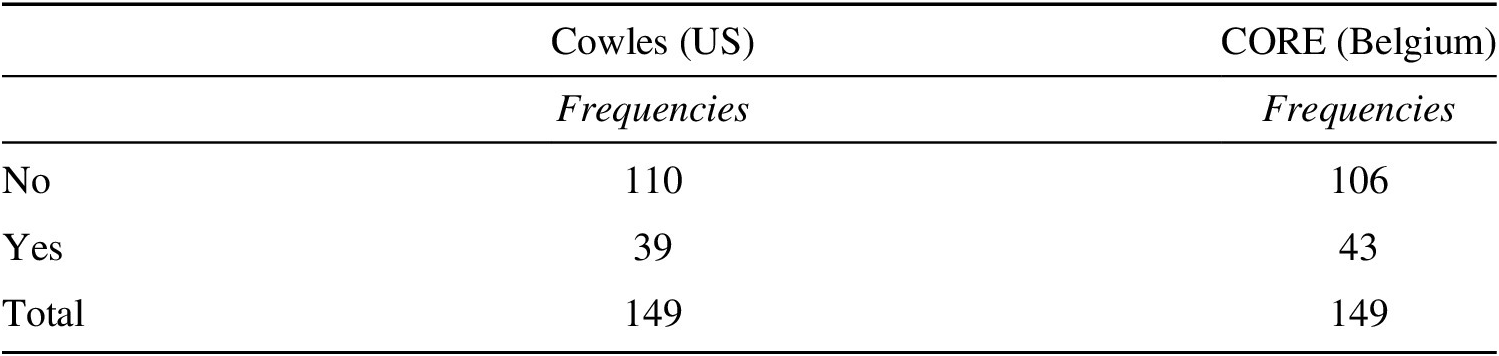
The early work on formalization of the GET was not carried out in an institutional and intellectual vacuum. It built upon previous developments in different disciplines: linear programming (Koopmans’s activity analysis), mathematics (convexity theory and topology), microeconomics (increasingly parsimonious formalizations of consumer and producer behaviors), welfare economics (Pareto, Bergson, Hicks), and game theory (von Neumann, Nash). These different but interconnected lines of development converged within one institution, the Cowles Commission. Its role in the emergence and diffusion of the GET research program has already been highlighted in a few historical accounts.Footnote 8 This institutional support was crucial especially during the 1950s when the biggest part of the economics profession was still hostile towards the idea of mathematical economics and general equilibrium, in particular. However, as our analysis shows, Cowles continued to serve as an institutional base for GE theoristsFootnote 9 for many years to come. First, it provided job opportunities to many of them, starting with Arrow and Debreu, but also to other key figures belonging to younger generations who were spending some time as researchers there. According to our data, Cowles was particularly important for socialization of GE theorists between 1963 and 1977 (the average years of beginning and ending of affiliation with Cowles in our dataset). It also provided a context for academic sociability through summer schools and short academic visits (thirty-nine scholars in our dataset participated in some kind of mobility offered by Cowles; see Table 5). Cowles served as a model for other specialized research centers in mathematical economics in the US and abroad (see, in particular, Düppe Reference Düppe2017 on Belgium, and Mirowski Reference Mirowski2002, pp. 490–503, on Israel).
Thus, the first stage of development and early reception of the Walrasian program in economics takes place almost exclusively on American soil. Stanford (with Arrow coming from Cowles in 1949)Footnote 10 and Berkeley (recruiting Debreu, after a decade spent at Cowles, in 1960)Footnote 11 remained the main centers of mathematical economics and GET in the US during this period, hosting, alternately, a joint Berkeley–Stanford Mathematical Economics Seminar. Only a few other universities, such as Minnesota (with Leonid Hurwicz), Rochester (with Lionel McKenzie recruited to create a doctorate school in mathematical economics), MIT, Chicago, and Cornell, employed important GE theorists during this early period. Outside the US, independent lines of theoretical research on the GE could be found at this point only in Cambridge, UK (Frank Hahn), and France (with major contributions from Maurice Allais and Edmond Malinvaud). Remarkable Japanese contributions to the GET literature (coming most notably from Michio Morishima, Takashi Negishi, and Hirofumi Uzawa) were intellectually, and, in the two latter cases, institutionally, related to the American tradition.Footnote 12 Important centers of the GET appeared, a few years later, in all these countries.
The second stage, that of the intense intellectual development and institutional expansion of the GET research program, opens up with the foundation of the Center for Operations Research and Econometrics (CORE) in Louvain, Belgium, in 1966, and the Center for Economic Research and Its Applications (CEPREMAP) in Paris in 1967. The CORE, created with financial support from American private foundations, has been immensely important for the legitimation and diffusion of the GET outside the US (the story of its foundation and early activities is provided in Düppe Reference Düppe2017). Organized and for a long time presided by a prominent Belgian economist, Jacques Drèze, it has played a very similar role to Cowles in the socialization of GE theorists in the European context (forty-three GE scholars in our dataset, most often from France, Israel, and Germany, were at some point of their careers affiliated with the CORE). The Parisian CEPREMAP, founded only a year later as a think tank providing economic advice to government, became another important center of the French-speaking mathematical economics. Along with INSEE, École Nationale de la Statistique et de l’Administration Économique (ENSAE), École Polytechnique, and later Sorbonne and École des Hautes Études en Sciences Sociales (EHESS), the CEPREMAP made France the second most important country in the field of the GET and, generally, formal economic theory, during this period. Among other notable geographical extensions, the Hebrew University in Jerusalem emerged as one of the prominent centers in the GET and related areas (game theory, operations research) during this second stage. It now hosts the famous Center for the Study of Rationality associated with the work of Robert Aumann and Menahem Yaari, both contributors to the development of the GET research program. In addition, the range of European institutional affiliations of the GET theorists was extended, most notably, to Copenhagen, Bonn, and London. Institutions specialized in mathematical economics also appeared, during the same period, in Eastern Europe and the Soviet Union. In the US, besides Berkeley, Stanford, and a few other pioneers in the field of mathematical economics mentioned above, the GET was at this time developed at Yale and Harvard, but also at Pennsylvania, Northwestern, UCLA, and a number of other top universities.
The first half of the 1970s became a period of the most intensive internationalization of the GE research program—judging by the numbers of non-US newcomers to the field. If we confront this finding with concomitant conceptual developments in the GET, this geographical expansion corresponds to the growing non-American (i.e., from scholars affiliated with non-American institutions) contribution to the “hardening of the hard core” and the emergence of incomplete markets theory, which represented one of the most researched topics by the theorists in our dataset (see Table 1). Significantly, European theorists (especially French, German, Dutch, and Israeli) represented half of all the contributors to the “Core” (Table 2). In support of a hypothesis that incomplete markets theory has become a rejuvenating force for the GET, we can observe that it benefitted from a further internationalization with twenty-one contributing countries (against twelve for the “Core”), most importantly France, Japan, and UK (but also Germany, Israel, Spain, and other European nations).
Table 2. Topics of Interest Most Frequently Addressed by GET Theorists

Between 1955 and 1980, the share of non-American-affiliated GET scholars grew from 21% to 46%, and has remained stable ever since, although their geography continued to diversify. In the following period, the list of institutional affiliations of the GET scholars increased dramatically and included seventy universities and research centers from 1981 to 1995, and eighty-three from 1996 to 2010.Footnote 13 Based on this observation, one could suggest an institutional scattering of the Walrasian research program, but at a closer look it still maintains its coherence and unity. In order to demonstrate this point, we now consider forms of transmission and legitimation of the GET during the whole period under study.
IV. BECOMING A GE THEORIST: FORMS OF KNOWLEDGE TRANSMISSION AND SOCIABILITY
One of the most important findings of this study concerns geographic and institutional patterns of the GE theorists’ careers. In other words, becoming a “GE theorist” most often requires a combination of a few key elements.
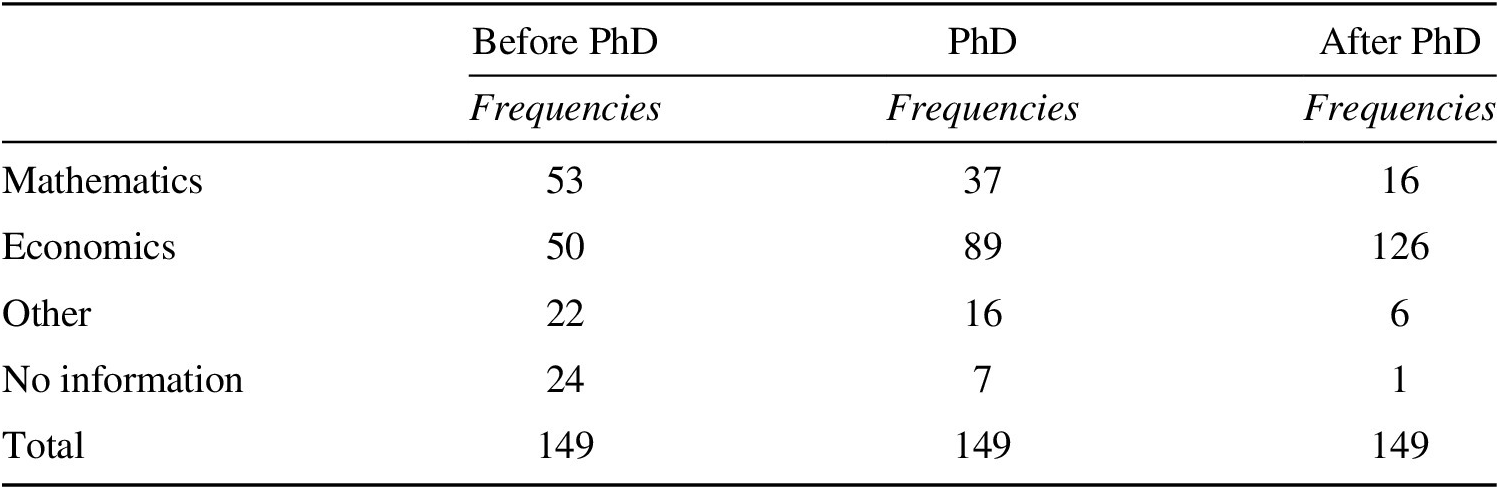
First, a strong mathematical training is necessary to excel at this mathematically sophisticated domain. Mathematics (with physics and engineering) is the main discipline of study before PhD for nearly half of GE theorists, and almost a quarter of them obtained a doctorate degree in mathematics. At the same time, only about a third of GE theorists majored in economics (see Table 3).Footnote 14 Nearly a quarter maintained this double disciplinary affiliation throughout their professional activity (mathematics being the first or secondary discipline of research and teaching). Mathematics was especially important during the first stage of the GET formalization and diffusion in the United States. Since the 1960s, mathematics as the main discipline of graduate studies and research appears more often within the European pole (in particular, scholars from France, Germany, Israel, and the CORE fellows and visitors) as compared with the American one, where mathematization of economics occurred earlier and on a larger scale. Thus, the GET represents an interdiscipline between mathematics and economics, contributing to the transfer of technical competencies and formalization of the latter. However, this double professional identification becomes more rare with time, as more advanced mathematical techniques colonize larger space in the graduate economics curriculum. The professional identity of a GE theorist as economist solidified especially in the 1990s when, for the first time, those who defended their thesis in the specialty “economics” were statistically overrepresented. This finding illustrates a larger trend of the transformation of economists’ training around the globe.
Table 3. Main Discipline of Study
Encounter with the GET is a second key step in the career of a GE theorist. The forms of direct transmission (teacher-to-student relation, or direct contact with leading GE theorists during longer stays at the main GET centers) seem to be the most common way of initiation in the field, even in recent decades. With a notable exception of some leading British and French theorists of the first generation (belonging, as we have already mentioned, to long-established national traditions), and researchers from the other side of the Iron Curtain,Footnote 15 transfers of the GET to other national contexts involved different forms of professional sociability at American universities.
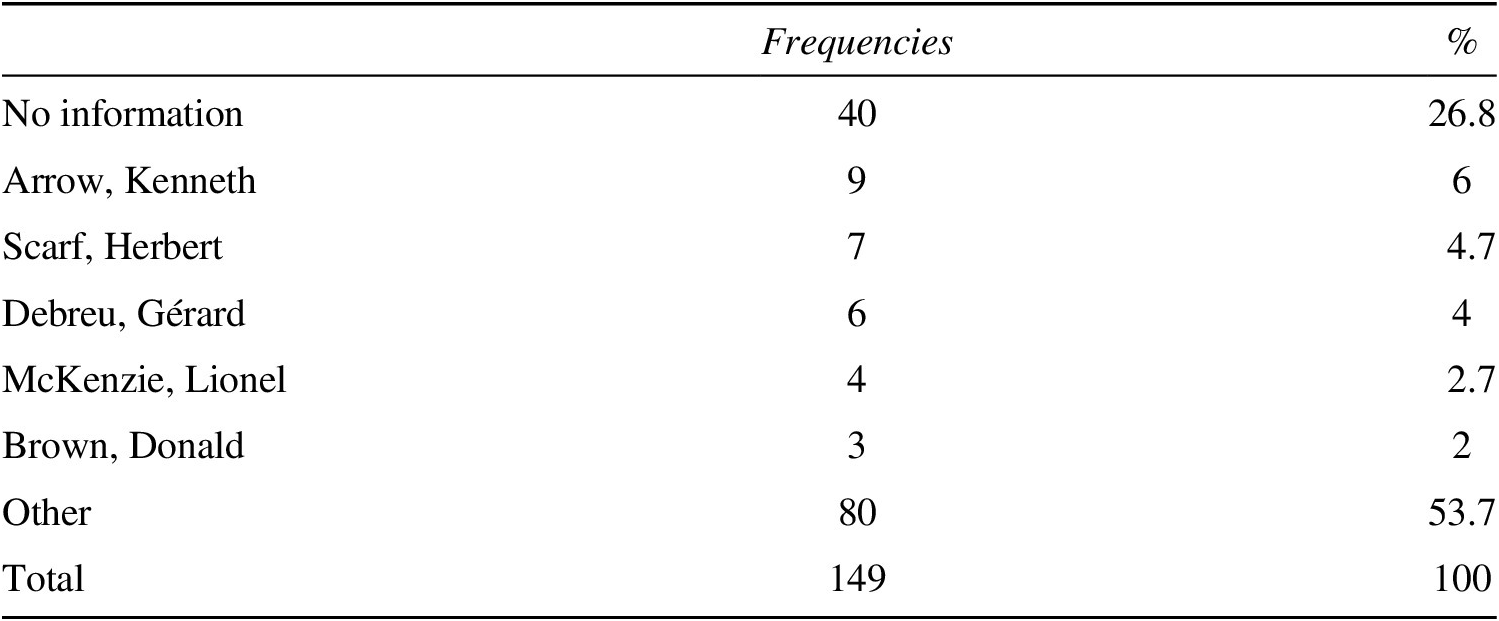
A PhD training is obviously the most important form of relation building in any academic community (on the role of PhD, the advisor–advisee relation in particular, in top American economics departments, see Svorenčik Reference Svorenčik2018; on the importance of graduate training, for instance, in life sciences, see Bulpin and Molyneux-Hodgson Reference Bulpin and Molyneux-Hodgson2013). In fact, a great geographical and institutional diversity, which characterizes the field of GET in the last decades, conceals a relative homogeneity of educational trajectories and a clear domination of a few American universities.Footnote 16 Nearly two-thirds of the theorists obtained their doctorate degrees in the United States, followed, far behind, by France, Germany, and the UK. The doctorate degrees were mainly obtained at eight universities identified in our analysis as the main “GET centers”: UC Berkeley, Yale, Stanford, Harvard, MIT, Minnesota, Princeton, and Rochester (see Table A4 in the online appendix). The founding GET figures (Kenneth Arrow, Gérard Debreu, Lionel McKenzie) and some other prominent GE theorists of the first and second generations (such as Herbert Scarf, see Table 4) proved to be active as advisors of PhD students. Thus, a few “family trees” of intergenerational transmission can be identified within this field.Footnote 17
Table 4. PhD Advisor
Third, academic visits to the key GET centers are another point de passage obligé for a “GE theorist” in the post-doctoral period and at later stages of his career. Such visits served sometimes as initiation to the research program as well as means to maintain interest in contributing to it. Patterns of professional mobility of the GE theorists reveal the existence of a network of academic institutions that serve as places of professional sociability, exchange of information, and mutual recognition. Interestingly, the two most important research centers for post-doctoral mobility are not the same as the institutions for PhD training of GE theorists: the Cowles Commission in the United States (first in Chicago and then at Yale) and the CORE in Belgium (Université Catholique de Louvain) (Table 5). The Center for Advanced Study of the Behavioral Sciences, CASBS, in Stanford (founded in 1954) was also important for the GET sociability, especially during the first stages of the diffusion of this research program. It is significant that all these research centers (also IAS Vienna and EUI in Florence, but later and less importantly) were the places of interdisciplinary and international encounters. These institutions played a key role in the successful diffusion and legitimation of the GET research program. Besides the top American universities, the most important places for academic mobility of the GE theorists include Paris (Paris I, IX, XII, and CEPREMAP), Cambridge (UK) and LSE, the Hebrew University in Jerusalem and Tel Aviv University, Barcelona and Madrid, but also Bonn, Copenhagen, Tilburg, and some other centers in Europe, Japan, Australia, and Latin America.
Table 5. Mobility, Most Important Centers
Thus, a typical academic trajectory of a leader of what would later become a national center of mathematical economics involved obtaining a graduate degree in the United States (often having as a supervisor one of the first-generation GE theorists), being first employed by the alma mater or another American school, and then going back to one’s own country while continuing to have short or longer stays at one of the main GET centers during his career. In some cases, it is precisely a stay at UC Berkeley or Stanford in the United States, or at CORE (but also at CEPREMAP or Cambridge) in Europe, that was the turning point in a professional trajectory when a scholar became engaged with the GET research program. GE theorists identified as national leaders outside the US often became supervisors of doctorate degrees for a younger generation of researchers recognized, in their turn, as contributors to the GET literature.
This typical trajectory can be exemplified by a biography of Jean-Michel Grandmont, one of the most important French mathematical economists of the second generation. Having obtained an engineering diploma from the prestigious École Polytechnique in Paris (graduated among the ten best students and the first in mathematics), and then from the École des Ponts et Chaussées, also providing a strong training in mathematics, he became interested in economics. Impressed with Theory of Value by Gérard Debreu, he went to the USA to get his PhD at Berkeley. Although Debreu himself did not help him much with his thesis, this stay in the United States was a turning point in his intellectual and professional career, and it allowed him to meet and establish lifelong contacts with other leading theorists of his generation (notably with the German mathematician and economist Werner Hildenbrand).Footnote 18 Back to France in the early 1970s, he worked at the CNRS and the CEPREMAP. Later in his career, as did many GE theorists, he often visited other important GET centers as a visiting professor or a research associate (CORE, Stanford, Yale, University of Bonn, LSE, and many others). He also was an active contributor to the activities of the Econometric Society, the main learned society in his field. Recognized for his multiple contributions to the field, he received the highest national academic honors. As we will see below, like many other non-American scholars in the GET, Grandmont did not receive the highest recognition internationally (such as a Nobel Memorial or other important prizes in economics, or presidency of international professional societies), but the accumulated international academic capital (multiple visiting positions, editorships, fellowships, and so on) contributed to his national reputation and institutional recognition.
A very similar career pattern is observed in many other cases as well. For instance, one of the most acclaimed Argentinean economists, Rolf Mantel, received his doctorate degree in 1965 at Yale, under the prominent mathematical economists Tjalling Koopmans and Herbert Scarf (Tohmé Reference Tohmé2006). After that he returned to Argentina, where he became a chief investigator at the Center for Economic Research of the Torcuato Di Tella Institute. During his very successful national career, he returned a few times to the US as a visiting professor and researcher (in particular, he stayed as a research associate at Cowles in the 1970s). Similar patterns characterize the careers of Aloisio Araujo (Brazil), Werner Hildenbrand (Germany), Andreu Mas-Colell (Spain), Takashi Negishi and Hukukane Nikaido (Japan), Karl Vind (Denmark), and Menahem Yaari (Israel).
Thus, the social dynamics of the Walrasian GE research program can be best represented as a moving group, in time and space, of individuals connected to each other horizontally and vertically (as members of different generations). The aggregate of ideas, different forms of written and oral communication,Footnote 19 and other professional practices constantly produced by this group of individuals has assured a reproduction and an even larger diffusion of the research program.
V. STRUCTURE OF THE GLOBAL SPACE OF THE GET: DISTRIBUTION OF SYMBOLIC CAPITAL
A marginal subfield at the time of its emergence, the GET research program acquired its American and international recognition in the 1960s. It appeared, under the rubric “General Economic Theory” (which did not pre-exist in the rise of the GET), in the NSF classification in 1965, and in the AEA classification in 1967 (Cherrier Reference Cherrier2017, p. 566). Although initially some significant results appeared in less known economic and mathematical outlets, after 1960, GET was disseminated in a handful of journals: most prestigious were Econometrica and Review of Economic Studies (with Christopher Bliss, David Cass, Franklin Fisher, David Gale, William Gorman, Oliver Hart, Guy Laroque, Hirofumi Uzawa, and other GE theorists and mathematical economists being on the latter’s editorial board from 1960 to the 1970s); and other quite visible journals, mostly International Economic Review (founded by GE theorist Michio Morishima and Lawrence Klein in 1960); Journal of Economic Theory (founded in 1968 by Karl Shell, the student of Arrow and Uzawa, with, among others, Arrow, Cass, Peter Diamond, Edmond Malinvaud, and Roy Radner as associate editors); and Journal of Mathematical Economics (founded in 1974 by Werner Hildenbrand, the student of Debreu).Footnote 20
Furthermore, as a sign of the highest academic recognition, the GET brought to two of its founding figures, Arrow and Debreu, the Nobel Memorial Prize in Economics, in 1972 and 1983, respectively.Footnote 21 Other Nobel Memorial Prize winners who made significant contributions to various aspects of the GET include John Hicks, John Nash, Robert J. Aumann, and Leonid Hurwicz. Other Nobelists whose work was, to a various degree, connected to the Walrasian GET research program include Tjalling Koopmans, Maurice Allais, Oliver Hart, Lloyd Shapley, and Daniel McFadden. The recognition of the GET by the economics profession undeniably contributed to the legitimation, at least for some time, of the Bourbaki-style “pure theory” in economics (Weintraub and Mirowski Reference Weintraub and Mirowski1994). This collective belief constituted a fundamental illusio of this field necessarily shared by its participants. Of course, this style of theoretical work is limited to a relatively small disciplinary elite, whereas numerically more important segments of the profession rather engage in empirical and applied research. Yet the GET was important in the way that it changed the status and the understanding of what “theory” is in economics, and brought new criteria of rigor and excellence to this academic field.
However, all contributors to the development and diffusion of the GET did not receive equally high academic and institutional recognition. This research domain, where female researchers were rare and never received the highest recognition,Footnote 22 is heavily dominated by American universities (mostly top-ranked economics departments). These features are of course not unique to the GET, not even to economics. Generally, the more “pure” and “theoretical” a knowledge domain is, the higher it used to be situated in the hierarchy of academic prestige (Bourdieu Reference Bourdieu, Halsey, Lauder, Brown and Wells1997, pp. 46–47). Even if, since a few past decades, more empirically oriented work gained greater prestige in economics, theoretical contributions do generally have a higher status in the disciplinary hierarchy than the ones that yield empirical and not generalizable results.
As in any other field of symbolic production, different kinds of capitals, and therefore power, are distributed very unevenly between its members (Bourdieu Reference Bourdieu1976, [1984] Reference Bourdieu1988). According to Pierre Bourdieu, members engage in competition for a specific form of capital that can be defined as a recognition of one’s scientific excellence, or, as in our case, of one’s contribution to advancement of economic theory. We have measured the amount of this specific scientific capital possessed by the GE theorists, which is visible in the different forms of institutional recognition. Based on honors and distinctions received by GE theorists, we have distinguished different categories of scientific prestige: the recognition from the field of economics (membership in learned societies, etc., and, at the highest level, the Nobel Memorial Prize and John Bates Clark Medal) but also from the connected fields of operations research (the John von Neumann Theory Prize), and mathematics (Fields Medal); national academic capital including academic and public distinctions or awards from academic institutions and the highest public authorities of their respective countries; and international academic capital (presidency of international societies, and so on).
These awards, as well as other signs of recognition, do not necessarily come directly from the work in the GET; they certainly reflect broader achievements in formal economics and related fields (like game theory). For purposes of this study, we have measured the overall amount of recognition possessed by a theorist identified as a contributor to the GET. (In fact, a typical GE theorist made contributions to other fields in economics and mathematics as well.) We have made this methodological choice because it is often not easy to separate clearly rewards for contribution to one domain or another. Successes in different domains tend to reinforce each other, thus amplifying the overall amount of recognition of an individual (as a form of a “Matthew effect”).Footnote 23 And, most importantly, our goal here is not to identify how contribution to the GET affects the career and visibility of its single contributors but, on the contrary, to understand to what extent the reputation of a theorist contributes to diffusion and success of this research program (although in many cases it undeniably did have an effect on the career and the degree of recognition of a given theorist; especially, it ensured the status of second-generation GET contributors as leading figures in their national academes, while also attracting younger talents).
The principles of distribution of these capitals can be illustrated by clustering the individuals in the space constructed using the prosopographical data (see Appendix Part II for description of the Multiple Correspondence Analysis, MCA, used in this study). Four clusters present the subclouds of GE theorists endowed with different volumes and types of academic and institutional recognition (see Figure A3 in the online appendix).
Cluster 1 regroups GE theorists of younger generations, belonging to non-American and/or less prestigious academic institutions, having no direct relation with the most prominent figures and academic centers in the field, and women, possessing relatively lower amounts of recognition of all types.Footnote 24 They represent roughly half of the population under study. Nearly one-third of the GE theorists in our dataset possess the signs of higher recognition, including honorary degrees, prestigious awards and prizes, fellowships and presidency of important learned societies (Econometric Society, SAET), and memberships in honorary societies and academies. Significantly, these top theorists subdivide into two different clusters: distinguished economists affiliated with American academic institutions; and theorists whose institutional recognition is exceptionally high but mostly limited to a national context.
Cluster 2 is thus best represented by the economists Robert Wilson, Peter Diamond, Oliver Hart, Daniel McFadden, David Gale, David Kreps, and Herbert Scarf, whose professional trajectories (PhDs, first and last academic affiliations) entirely belong to the United States. Their contribution is recognized both on a national level as members of the most prestigious American honorary societies (such as National Academy of Sciences, American Academy of Arts and Sciences, and so on) and within the field of economics (as distinguished fellows of the American Economic Association [AEA], recipients of the rarest prizes and other honors).
Cluster 3 can be exemplified by the most important non-American contributors to the GET, such as the Japanese economists Hirofumi Uzawa and Michio Morishima, Edmond Malinvaud, and Jean-Lacques Laffont (France), and Andreu Mas-Colell (Spain). With a notable exception of Malinvaud,Footnote 25 these economists spent at least a part, and sometimes a major one, of their educational and career path in the Anglo-American context. All these theorists made a major contribution to the GET recognized by the American economics profession but are especially rewarded in a national context by both the highest academic distinctions (Collège de France, national academies, prizes) and public honors (for instance, Légion d’Honneur in France or Imperial Order of Culture in Japan) of their respective countries. Often, it is the American institutional recognition that reinforced the national, but also regional (European) or international, reputation of these economists.
Cluster 4 is made of a small elite of the GE theorists: Kenneth Arrow, Gérard Debreu, Robert Aumann, Stephen Smale, and Eric Maskin. Significantly, mathematics is a primary discipline for these prominent scholars, with which some of them continued to identify themselves despite recognition from the field of economics. Their contribution to mathematical economics and GET in particular also relates to major mathematical domains (topology, game theory). Except for Maskin, who represents the next generation of scholars and only tangentially worked on the GET, these founding figures and contributors to the GET received their doctoral degree in the 1950s, and, partly due to this unique position, received the highest amounts of intellectual recognition in the fields of economics, mathematics, and related domains. Being endowed with the highest national (American) honors and distinctions, they are distinguished (especially from Cluster 2) by the biggest volume of international scientific capital (as recipients of the highest international awards and of high distinctions from foreign states, as presidents of international learned societies, and members of foreign or international academies).
Although very unevenly distributed, the overall volume of scientific capital—in both national and internationalized forms—and public recognition accumulated by members of this group of GE theorists looks quite important: more than half of the scholars in our dataset can be put into the categories of the “highest” and “higher” recognition. As we have seen, the recognition from the American institutions is central for building a theorist’s reputation in the field of economics. However, mutual conversion and reinforcement of national and international scientific capitals illustrate a circular character of academic influence and, to some degree, an extreme concentration of academic power and scientific authority among a relatively compact disciplinary elite.
VI. CONCLUSION: A SCHOOL, AN INVISIBLE COLLEGE, OR A FIELD?
The Walrasian GET program became prominent in economics in the 1950s, was recognized and institutionalized in the international context in the 1960s, and had the highest academic consecration (most notably with the Nobel Memorial Prize) in the 1970s and the early 1980s—which, interestingly, coincides with the upsurge of the work in applied GE modeling (Ballard and Johnson Reference Ballard and Johnson2017). The program, however, became most prolific during the period from the mid-1970s to the late 1990s, and it has stayed a vibrant research program up to this day. Mathematical language, of course, helped to strengthen the epistemic authority of this group and support its claims of universality and objectivity. The lack of “content” in the theory itself—which can be seen rather as a method, a set of techniques, insights, and benchmarks, than as a well-defined theory with empirically falsifiable claims—also contributed to its adjustment and durability in view of multiple, internal and external, criticisms. The generality and mathematical complexity of the GET allowed for the generation of many interesting extensions (such as, again, the boom of abstract GE modeling in the theory of incomplete markets and asset economies);Footnote 26 for perceiving its problems as significant for the whole of economics; and for the efficient boundary work. Many “classical” problems of the GET were solved, and thus, as far as these problems are concerned, one can think of the GET as a “completed” research program (Hands Reference Hands, Duarte and Lima2012), but it still plays a significant role in the pure economic theory.
The perpetuation of the GET, especially after the publication of discouraging results (SMD theory) in the early 1970s, cannot be fully understood if we do not consider the social mechanisms that assured internal coherence and reproduction of this research program. As we have seen, the GET scholars have come from many institutions in different countries, belonged to different generations (born between 1921 and 1969), and had different disciplinary backgrounds and research interests. Nonetheless, a prosopographical analysis of this field reveals some patterns of its organization and, at the same time, allows the formulation of hypotheses about its successful dissemination and legitimation in a broader field of economics. In particular, the consolidation of this research program and new fruitful developments (such as incomplete markets theory or application of the “core”) benefitted greatly from its export to European academic centers, as well as to other regions of the world. Mobility and communication between these centers seem to be crucial for its survival and durability.
Thus, an heterogeneous network of scholars engaged in the GET has some characteristics of a scientific school, such as a methodological and theoretical unity fixed in a canonical body of early works by founding figures. Forms of direct transmission are also crucial for initiation and the successful career of younger generations of theorists. Similarly to other mono-institutional recognizable scholarly brands (e.g., the Chicago School of economics), the GET research program was, at least at the very early stage, closely associated with a single institution (the Cowles Commission). However, very quickly, it was simultaneously developed (not only diffused) in different institutions by scholars having different disciplinary and theoretical backgrounds and motivations. Notably, the GET developments in the 1960s and 1970s benefitted from different national traditions of the economic thought stemming from specific intellectual and pragmatic concerns. This institutional and national diversity only increased with time, although a few academic centers (in the US but also in Europe) could preserve their importance for the GET research program. The GET also emerged and evolved at the intersection of different disciplines and theoretical languages. This relative openness and heterogeneity—the key GE theorists acting like translators between different research domains and national traditions—also facilitated a wider dissemination and recognition of this research program and its results. To sum it up, what provided success to the research program is a cross-disciplinary fertilization (especially with mathematics, pure and applied), a large dissemination (in terms of institutions and countries), and, at the same time, a strong concentration of control over professional reproduction, sociability, and communication.
So, the GET could rather be seen as an “invisible college” functioning as “a large network of influence and communication,” setting norms of research practice (for more discussion of this term, see Crane Reference Crane1969, Reference Crane1972). Our research also confirms the observation that a few key theorists —occupying the central positions in the network—play a major role in recruiting new members and transmitting the program (Crane Reference Crane1972, p. 67). However, in the case of the GET, the members of a network are not related to each other in informal ways only (citation, coauthorship, communication at conferences, and so on). Our analysis reveals the existence of institutionalized and repeated forms of transmission of the research program (through specialized research centers, training programs, fellowships, journals, and conferences, with their specific distinctions and awards). The concept of a field is thus quite useful to highlight a structured character of this research domain, with its specific illusio, center and periphery, dominating and dominated. As we have seen, the structure of the field (distribution of scientific capital) is still determined across the axes: mathematics vs economics, national vs international (“American” representing a special case as divided into purely domestic and internationally relevant types of scientific capital).
The GET community thus appears to be more than a network of individuals sharing research problems, techniques, and practices. We have shown how this field was constituted and how it managed to reproduce itself and influence larger disciplinary contexts, thanks to its relative cohesion and accumulated scientific capital. Further research is needed to verify whether some of the effects described here belong to the larger field of economics as far as most GE scholars are indeed economists, involved in the everyday professional practices and struggles over the definition of what economics is.
SUPPLEMENTARY MATERIALS
To view supplementary material for this article, please visit http://doi.org/10.1017/S1053837222000712.
COMPETING INTERESTS
The author declares no competing interests exist.
APPENDIX
Part I. Prosopography: Selection of Individuals and Variables
An exploratory research strategy was chosen for this study because a clear definition of “GE theorists” is lacking. First, we created a list of 149 individuals recognized as “GE theorists” by a community of peers. For doing so, we used a multi-stage procedure including browsing bibliographies of authoritative textbooks (such as Mas-Colell Reference Mas-Colell1985), dictionary entries (The New Palgrave), and review articles (Debreu Reference Debreu, Arrow and Intrilligator1981), and getting personal communication feedbacks from GE specialists of different generations. Although the list is almost exhaustive, we emphasize that the research field itself has no clear borders or criteria of inclusion. Some scholars have contributed just one or a few papers to the GE literature and are mostly recognized in other fields of economics (game theory, macroeconomics, finance) or disciplines (pure mathematics, operations research, and so on). The type of contribution may be different as well: it could be a theoretical insight, an exemplary application, or a new mathematical technique. Some scholars might be omitted from the list because they are peripheral to international networks or merely confined to national borders (for instance, most Soviet mathematical economists dealing with GET fall in this case). Thus, our list of the “GE theorists” contains the individuals who are more or less recognized as such by the “internationalized community” of peers. The uncertainty of thematic borders of this research program was another important issue in selecting individuals to be added to the list of “GE theorists.” Are, for example, “computable general equilibrium” (so popular in applied economics) or “dynamic stochastic general equilibrium” models (the basic workhorse of current macroeconomic modeling) “real” GET? We decided to go beyond the classical GET topics (existence, stability, and uniqueness of equilibrium, core, etc.) by including more recent developments such as determinacy of equilibrium, incomplete markets, and some others. This extension allowed us to study different generations of GE theorists, including the younger ones, entering the profession in the 1990s. We decided to exclude the youngest generation of economists from this study mostly because the borders of the research program associated with “General Equilibrium” become even more blurred during this period, while formal signs of academic recognition (honors and rewards in particular) are not applicable to most of these researchers who are still early in their careers. Second, we compiled (mostly from open sources such as curriculum vitae files published on personal or institutional websites, obituaries, and tributes) a prosopographical database aiming to provide structured information on the educational backgrounds and careers of these scholars, their contributions to the field of GET, academic mobility, and various signs of academic recognition and prestige. The database contains different groups of variables related to the year of birth and sex, undergraduate and graduate education (institution, discipline, year, advisor), academic affiliations through the period under study (divided into five time spans) and long academic visits, chronology and main topics of the work on the GET, memberships in professional and honorary societies, and other academic honors and awards.
Part II. Multiple Correspondence Analysis
The dataset contains 149 individuals and fifty-four variables; three quantitative and eighteen qualitative variables are considered as illustrative.
The first two dimensions of analysis express 37.43% of the total dataset inertia; this means that 37.43% of the individuals (or variables) cloud total variability is explained by the plane. This is an intermediate percentage and the first plane represents a part of the data variability. This value is greater than the reference value that equals 19.46%; the variability explained by this plane is thus significant (the reference value is the 0.95-quantile of the inertia percentages distribution obtained by simulating 309 data tables of equivalent size on the basis of a uniform distribution).
The dimension 1 (which can be interpreted as the volume of symbolic capital possessed by individuals) opposes individuals such as 6, 136, 79, 87, 90, 7, 98, 31, 129, and 91 (*Arrow Kenneth*, *Uzawa Hirofumi*, *Laffont Jean-Jacques*, *Malinvaud Edmond*, *Mas-Colell Andreu*, *Aumann Robert*, *Morishima Michio*, *Debreu Gérard*, *Maskin Eric*, and *Smale Stephen*) (to the right of the graph, characterized by a strongly positive coordinate on the axis) to individuals characterized by a strongly negative coordinate on the axis (to the left of the graph).
The dimension 2 (which can be interpreted as the national/international dimension of symbolic capital) opposes individuals such as 6, 7, 31, 129, and 91 (*Arrow Kenneth*, *Aumann Robert*, *Debreu Gérard*, *Maskin Eric*, and *Smale Stephen*) (to the top of the graph, characterized by a strongly positive coordinate on the axis) to individuals such as 136, 79, 87, 90, and 98 (*Uzawa Hirofumi*, *Laffont Jean-Jacques*, *Malinvaud Edmond*, *Mas-Colell Andreu*, and *Morishima Michio*) (to the bottom of the graph, characterized by a strongly negative coordinate on the axis).







