1 INTRODUCTION
Late time cosmic acceleration has been discovered through distance measurements to SNe Ia over a range of redshifts (Riess et al. Reference Riess1998, Perlmutter et al. Reference Perlmutter1999). One explanation for this striking discovery is that the universe is dominated by an unknown energy component, termed dark energy, that is driving the observed acceleration. Although the ΛCDM model of cosmology—in which w, the dark energy equation of state parameter, is exactly − 1—is consistent with observations, the nature of dark energy remains elusive. Another explanation is that the gravity on very large scales behaves differently to that predicted in General Relativity (see the review by Joyce, Lombriser, & Schmidt Reference Joyce, Lombriser and Schmidt2016). Precision cosmological measurements may shed light on the physics that drives the acceleration.
Deriving cosmological parameters using SNe Ia relies on the measurement of two observables: distance and redshift. Distance measurements with a precision of ~ 7% come from the standardisation of SN Ia luminosities (Phillips Reference Phillips1993, Tripp Reference Tripp1998). Recently, ~ 4% precision in distance measurement has been obtained by using a subset of SNe Ia in high-ultraviolet surface brightness hosts (Kelly et al. Reference Kelly, Filippenko, Burke, Hicken, Ganeshalingam and Zheng2015). Redshifts can be obtained from either the host or the SN itself.
In past SN surveys, one confirms the SN type by a spectrum of the SN together with its host while the SN is within a couple of weeks of maximum light. In surveys like the Supernova Legacy Survey (SNLS; Betoule et al. Reference Betoule2014; hereafter B14), the amount of time required to do the spectroscopic confirmation was significantly larger than the amount of time used to obtain SN light curves. On the other hand, obtaining the redshift from a spectrum of the host galaxy with or without the SN is simpler and can be done at any time.
Another advantage of getting the redshift from the host is that the error in the redshift is smaller. The typical error from SN Ia spectra is of the order of 10−2, whereas the typical error from galaxy spectra is of the order of 10−4. While redshifts for host galaxies can be determined with greater precision, there are disadvantages. In addition to not having a spectrum to confirm the SN type spectroscopically, the host may be incorrectly identified or too faint to observe (Gupta et al. Reference Gupta2016).
The next generation of SN surveys will produce many more SNe Ia than past surveys. For example, the ongoing Dark Energy Survey (DES; Bernstein et al. Reference Bernstein2012) will discover ~ 10 times the number of SNe Ia that were discovered in the SNLS. Only a small fraction of the SNe Ia from the new surveys will have spectra of the SNe Ia. We are therefore entering into an era where most SNe Ia will be classified from photometry and most redshifts will be obtained from host galaxies. The efficiency of such a strategy was demonstrated in Lidman et al. (Reference Lidman2013), where host galaxy redshifts of photometrically classified SNe Ia from the SNLS were obtained. An example of a cosmological analysis using photometrically classified SNe Ia from the SDSS-II supernova survey was presented in Campbell et al. (Reference Campbell2013). The cosmological inferences that they obtained with their sample are consistent with those obtained from the spectroscopically confirmed SN Ia sample of B14.
DES is also employing a similar scheme of getting SN Ia redshifts from host galaxies (Yuan et al. Reference Yuan2015). The SN Ia sample they will produce will extend slightly beyond z = 1. These SNe Ia will be biased towards galaxies that are bright and actively forming stars as it is easier to get redshifts for these galaxies. A question then arises as to whether or not the cosmological parameters derived using a sample of SNe Ia, where redshifts are obtained from host galaxies, are different from those using a sample of SNe Ia that contains redshifts from both SNe Ia and hosts.
In this paper, we examine this question using the SN Ia sample presented in B14, where information on the source of the redshift is available and SNe Ia are within the redshift range of 0.01 < z < 1.3. From this sample, we create two types of samples: a host-selected sample, where redshifts come from the host galaxies, and a traditional sample, where the redshift could come from either the SN Ia or its host.
We organise the paper as follows: In Section 2, we describe the SN Ia sample used in this paper. In Section 3, we compare the properties of the SNe Ia in the two samples. In Section 4, we derive constraints on cosmological parameters from the two samples and examine the differences. We discuss effect of Malmquist bias in Section 5. We conclude in Section 6.
2 SNe Ia SAMPLE
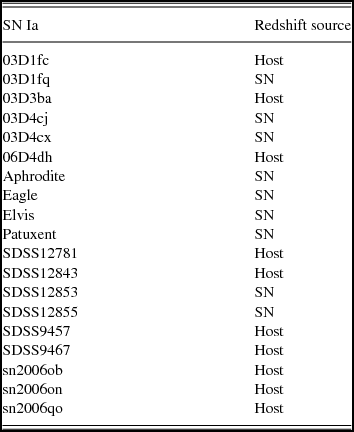
The sample in this work comes from the Joint Light-curve Analysis (JLA; B14). JLA has compiled 740 spectroscopically confirmed SNe Ia from various supernova surveys including SDSS-II (Frieman, Turner, & Huterer Reference Frieman, Turner and Huterer2008, Holtzman et al. Reference Holtzman2008, Zheng et al. Reference Zheng2008, Sako et al. Reference Sako2011, and Sako et al. Reference Sako2014), SNLS (Howell et al. Reference Howell2005, Bronder et al. Reference Bronder2008, Ellis et al. Reference Ellis2008, Balland et al. Reference Balland2009, and Walker et al. Reference Walker2011), CfA (Riess et al. Reference Riess1999, Jha, Riess, & Kirshner Reference Jha, Riess and Kirshner2007, Hicken et al. Reference Hicken2009, and Hicken et al. Reference Hicken2012), CSP (Hamuy et al. Reference Hamuy2006, Contreras et al. Reference Contreras2010, and Stritzinger et al. Reference Stritzinger2011), and HST (Riess et al. Reference Riess2007). Light-curves of all the SNe Ia in this sample are fitted using the SALTFootnote 1 (Guy et al. Reference Guy2010; version 2.4.0) light-curve fitter, as it is the most widely used and tested light-curve fitter in the literature. Of these 740 SNe Ia, there are 537 SNe Ia for which redshifts were derived from the hosts. This means that there were 203 SNe Ia in which the SN Ia redshift could only be derived from the SN Ia itself. Table A1 shows the JLA sample with redshift source information. Throughout the rest of this paper, we will refer to the sample of SNe Ia whose redshifts come from either the host or the SN Ia as the traditional sample, and we will refer to the sample whose SNe Ia are restricted to those that have a spectroscopic redshift from the host as the host-selected sample.
3 COMPARING TRADITIONAL AND HOST-SELECTED SAMPLES
In this section, we want to compare the properties of SNe Ia between traditional and host-selected samples. The JLA sample of 740 SNe Ia described above can act as a traditional sample and the sub-sample of 537 SNe Ia can act as a host-selected sample. But there is 73% overlap between these two samples. Therefore, any statistical comparison between these two is not instructive. We need to develop a way to create traditional and host-selected samples so that there is no overlap between them.
A way to create two independent samples is to take the JLA sample and split it into two equal samples of 370 SNe Ia each in such a way that one sample is a traditional sample and the other is a host-selected sample. First, we divide the JLA sample into low-redshift and high-redshift groups. Low-redshift SNe Ia are from galaxy targeted surveys. Their redshifts are from host galaxies and hence host-selected. We take all low-redshift SNe Ia and randomly select (without replacement) half of them and put in a box labelled A. We put the other half of the low-redshift SNe Ia in a box labelled B. Next, we take the high-redshift SNe Ia and select those SNe Ia that lack a redshift from the host (i.e. the redshift comes from the SN itself). We put them in box A. Now what remains are the high-redshift SNe Ia that have redshifts from the host. We then randomly distribute them into box A and box B in such a way that the total number of SNe Ia in each box becomes 370. Now box A becomes the traditional sample and box B becomes the host-selected sample. The disadvantage of this method is that the traditional sample contains more SNe Ia (55% of the total) that have redshifts from the SNe Ia themselves than would normally be the case.
In Figure 1, we show the distributions of redshifts, colour, stretch, and host mass for these two types of samples for one random realisation. We see that SNe Ia in the traditional sample tend to occur at higher redshift, are bluer, and have narrower light-curve widths. Galaxies in the host-selected sample also tend to be more massive.

Figure 1. Distribution of SN Ia redshift (top left), colour (top right), stretch (bottom left), and mean host stellar mass (bottom right) for both the host-selected (solid red) and traditional (dashed blue) samples. These distributions are shown for one random realisation.
We now compare traditional and host-selected samples by calculating mean properties of SNe Ia and their hosts in each sample. We repeat the process of creating traditional and host-selected samples 100 times, calculating the mean properties of SNe Ia and their hosts of each sample. Figure 2 shows the distributions of SN Ia mean redshift, mean colour, mean stretch, and mean host stellar mass for both the traditional and the host-selected samples.

Figure 2. Distribution of SN Ia mean redshift (top left), mean colour (top right), mean stretch (bottom left), and mean host stellar mass (bottom right) for host-selected (solid red) and traditional (dashed blue) samples. Note how the two distributions differ for each property. See text for details. The mirror symmetry in the figures is a consequence of the way SNe Ia are split between the two samples. The SNe Ia are selected without replacement. This and the even number of SNe Ia in the two subsamples leads to the mirror symmetry.
It is interesting to see from Figure 2 that the distributions of the mean properties are different between two types of samples. SNe Ia in the traditional sample are, on average, bluer and broader. They also have a higher mean redshift. This is not unexpected, as it is harder to get redshifts for galaxies that are further away. However, there may be evolutionary effects that could either drive or mitigate the difference. For example, the number of SNe Ia in star-forming galaxies relative to the number of SNe Ia in passive galaxies is expected to increase with redshift (Mannucci, Della Valle, & Panagia Reference Mannucci, Della Valle and Panagia2006, Childress et al. Reference Childress2013). This would tend to mitigate the difference between the two samples as it is generally easier to measure the redshift of a galaxy that is actively star forming. We also find that the mean host stellar mass in host-selected samples are higher than the traditional samples. This is because it is easy to obtain redshifts of galaxies that are bright and hence more massive.
4 COSMOLOGICAL INFERENCES
We have shown that SNe Ia in the host-selected samples are different to traditional samples in terms of redshift, colour, stretch, and host mass. We now examine if the cosmological parameters derived from these samples differ. For this, we perform fits to both the ΛCDM and wCDM models to the 100 pairs of randomly created traditional and host-selected samples.
We compute the observed distance modulus using the fitted SN Ia rest frame B-band peak apparent magnitude (m B), corrected for stretch (x 1), and colour (c). This correction is needed for standardising SNe Ia as distance indicators (Phillips Reference Phillips1993, Tripp Reference Tripp1998, Astier et al. Reference Astier2006, Goobar & Leibundgut Reference Goobar and Leibundgut2011). The observed distance modulus is given by
The parameters that describe the relationships between SN Ia luminosity (M B), stretch, and colour (α and β) are derived during the cosmological fit. Here, we have used a host mass correction (ΔM B) as suggested by Sullivan et al. (Reference Sullivan2010). It is known that the average SN Ia luminosity after correcting for light curve width and colour correlates with the host mass (e.g., Sullivan et al. Reference Sullivan2010, Childress et al. Reference Childress2013, Uddin Reference Uddin2016) in such a way that massive galaxies host more luminous SNe Ia. Unaccounted for, effects like this might bias the accurate measurement of the properties of dark energy.
For each SN Ia, we compute the model distance modulus using
Here, the cosmological dependence resides in luminosity distance d L. We define the Hubble residual as Δμ ≡ μ o − μm. Following B14, we fit the cosmological parameters (Ωm, w) along with nuisance variables (α, β, M B) by minimising
where C is the covariance matrix that includes all statistical and systematic uncertainties, including terms due to peculiar velocities, gravitational lensing, and intrinsic scatter. The matrix C is defined as
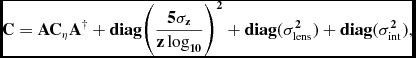 $$\begin{equation}
\bf C = AC_{\eta }A^{\dagger } + diag \bigg (\frac{5\sigma _z}{z\log _{10}}\bigg )^2+diag(\sigma ^2_{\rm {lens}})+diag(\sigma ^2_{\rm {int}}),
\end{equation}$$
$$\begin{equation}
\bf C = AC_{\eta }A^{\dagger } + diag \bigg (\frac{5\sigma _z}{z\log _{10}}\bigg )^2+diag(\sigma ^2_{\rm {lens}})+diag(\sigma ^2_{\rm {int}}),
\end{equation}$$
where Cη is the covariance matrix defined in B14. σ z in the second term of Equation (4) is due to peculiar velocities and is set to cσ z = 150 kms−1 (Conley et al. Reference Conley2011). The third term is due to gravitational lensing, which varies with redshift according to as σlens = 0.055 × z (Jönsson et al. Reference Jönsson2010).
The last term in Equation (4) incorporates the intrinsic dispersion in corrected SN Ia luminosities, σint. This term is needed as SNe Ia are not perfect standard candles. We do not know what causes the extra dispersion in their luminosities (Conley et al. Reference Conley2011). B14 calculates redshift dependent σint for each survey and we use those values here.
Seven different types of systematic uncertainties are considered in B14: uncertainties in the photometric calibration, light-curve model uncertainty, uncertainties in the Malmquist bias correction, mass step error, uncertainties in the extinction correction from Galactic dust, uncertainties in the mean amplitude of peculiar velocities, and contamination from non-SNe Ia.
In our analysis, we assume that the Malmquist bias correction and the associated uncertainty are the same for both the traditional and the host-selected samples. In Section 5.1, we show that this assumption does not make any significant difference in our results. We use the corrections as used in B14, originally calculated in Mosher et al. (Reference Mosher2014). The corrections were calculated for each survey and they are redshift dependent. The mean correction in the JLA sample is − 0.004 mag with maximum and minimum correctionns as 0.002 and − 0.036 g, respectively.
We use Markov Chain Monte Carlo (MCMC) to explore the likelihood defined in Equation (3) and derive best-fit parameters. We use the MCMC sampler called EMCEEFootnote 2 (Foreman-Mackey et al. Reference Foreman-Mackey, Hogg, Lang and Goodman2013). EMCEE is a Python implementation of an affine-invariant ensemble sampler. We fit both the ΛCDM and the wCDM models to the traditional and host-selected samples.
In comparing the results, we follow the procedure described in the previous section. We create 100 pairs of samples and plot best-fit cosmological parameters for each pair. These are shown in Figure 3 for ΛCDM and Figure 4 for wCDM, respectively along with their weighted means. Table 1 summarises mean values and median errors of the cosmological parameters from these samples.

Figure 3. Values of ΩM in the ΛCDM model obtained from 100 random realisations of host-selected and traditional samples. Weighted means are also shown. Although there is a shift in ΩM of 0.046 between these two samples, the shift is not significant (see Table 1 and the discussion in Section 5.2).

Figure 4. Values ΩM (top) and w (bottom) in the wCDM model obtained from 100 random realisations of host-selected and traditional samples. Weighted means are also shown. There are no significant offsets in w and ΩM between these two samples.
Table 1. Weighted mean and 1σ scatter of the 100 samples.
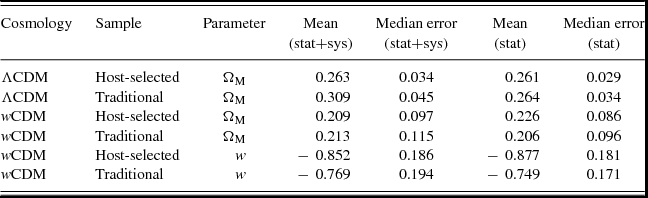
For both cosmological models, we do not find any significant tension in the cosmological parameters, ΩM and w, between the host-selected and traditional samples. The value of ΩM in the ΛCDM model differs by 0.046 between the samples, but this shift is insignificant (0.8σ). These results indicate that cosmological constraints from future SN surveys may remain unbiased in comparison with the current surveys. We check the robustness of this finding in Section 5.2.
We note that the systematic uncertainties of the two randomly drawn samples will be correlated. We investigate the impact this has on our results by redoing the analysis without including systematic uncertainties. The results are listed in Table 1. The impact is minor and our conclusions are unchanged.
5 DISCUSSION
5.1. Effect of Malmquist bias
We have mentioned in Section 4 that we have kept the Malmquist bias unchanged for both types of samples. This is unlikely to be true in detail. To see if a change in the magnitude of the Malmquist bias could change our results, we alter the Malmquist bias correction for the host-selected sample and rerun the analysis as we do in Section 4.
When we double the Malmquist bias correction for the host-selected sample, ΩM changes by less than 1%, which is smaller than our error. Excluding it altogether results in an even smaller change. Our results are therefore not sensitive to the level of Malmquist bias that can be expected for SN samples. Hence, our choice in setting the magnitude of the bias to be the same for both subsamples is reasonable.
5.2. The significance of the offset in ΩM
We have seen in Section 4 that there was an offset in ΩM of 0.046 between the two samples in ΛCDM. Using the median error of the two samples, we determined that the offset was not significant. Here we re-examine the significance of the offset using random subsamples.
To create these subsamples, we take the JLA sample and split it into two equal halves with the constraint that the ratio of low and high redshift SNe Ia in the two subsamples is the same. Let us call these two random samples A and B. We then calculate cosmological parameter in the ΛCDM model. We repeat this 100 times and calculate weighted means in each group of A and B. We show these results in Figure 5.

Figure 5. Left: Values of ΩM in the ΛCDM model obtained from 100 realisations. Weighted means are also shown. We find no significant offset between these two samples. Right: Distribution of the offsets in ΩM for each pair of A and B. Also shown is the offset from the wighted mean of Figure 3—which is 0.046. We see that the offset in ΩM between samples A and B exceeds the mean offset between the host-selected and traditional samples 12% of the time.
We find no significant offset in ΩM between the samples (see Figure 5, left). We then ask how many times the offset in ΩM exceeds the mean offset between host-selected and traditional samples. To answer this, we plot the distribution of the offset in ΩM from 100 realisations (see Figure 5, right). We also mark the mean offset of 0.046 that we have found in Section 4 (also in Figure 3). We find that the offset in ΩM between samples A and B exceeds the mean offset between the host-selected and traditional samples 12% of the time.
6 CONCLUSION
In this paper, we have compared SN Ia properties and cosmological parameters from a traditional SN Ia sample, where redshifts come from either the SNe Ia or the galaxies that host them, and a host-selected SN Ia sample, where redshifts come entirely from the host galaxies. The host selected SN Ia sample is similar to the samples that surveys such as DES are currently obtaining, where most of the redshifts will come from SN host galaxies.
We have found that the mean redshift, colour, stretch, and host galaxy stellar mass of SNe Ia can be different between these two types of samples. Using SNe Ia alone, we find that the two subsamples give consistent cosmological results. In future work, we will examine if this result continues to be true when cross-cutting cosmological constraints from other probes are added.
Future SN Ia samples, such as the sample of SNe Ia from DES, will be several times larger. While extending the analysis presented in this paper to these larger samples will be limited by the number of SNe Ia that are spectroscopically confirmed in these samples (expected to be 20% of the total), our analysis will be an important one to make in these future surveys.
ACKNOWLEDGEMENTS
We thank Chris Blake for helpful discussion regarding statistical analysis. We also thank Tamara Davis and Christophe Balland for their valuable comments. Part of this research was conducted by the Australian Research Council Centre of Excellence for All-sky Astrophysics (CAASTRO), through project number CE110001020. This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration et al. 2013).
A TABLE OF SN Ia REDSHIFT SOURCES
Table A1. Redshift source for SNe Ia in the JLA sample. The full list is available online.