1.0.1 Terminology and History

The study of measurement bias has a rich intellectual history, with many different researchers addressing these issues at many different times in the past century (Reference MillsapMillsap, 2011). The complexity of this landscape has led to a somewhat challenging terminological issue: the terms measurement invariance and differential item functioning effectively refer to the same concept in different ways. In general, researchers using structural equation modeling (SEM), particularly confirmatory factor analysis (CFA), developed the term measurement invariance to describe an assumption: that the items in a given test measure the latent variable equally for all individuals (Reference MeredithMeredith, 1993; Reference MillsapMillsap, 2011; Reference Putnick and BornsteinPutnick et al., 2016). At the same time, research arising mostly from the item response theory (IRT) tradition uses the term differential item functioning, often abbreviated DIF, to describe cases in which this assumption is violated: that is, items or sets thereof in which measurement parameters differ across participants (Reference Holland and ThayerHolland & Thayer, 1986; Reference Osterlind and EversonOsterlind & Everson, 2009; Reference Thissen, Steinberg, Wainer, Holland and WainerThissen et al., 1993). For readers interested in the long history of the study of measurement invariance and DIF, which extends back over a century, are referred to one historical review (Reference Millsap, Meredith, Cudeck and MacCallumMillsap & Meredith, 2007), which provides a fascinating overview of this literature.

However, for the purposes of this Element, there are two important things to note. First is that the study of DIF and measurement invariance have largely come together in the past two decades, perhaps due to the wider adoption of models (e.g., nonlinear factor models, discussed in the next section) which can be extended to accommodate many models within SEM and IRT (Reference BauerBauer, 2017; Reference Knott and BartholomewKnott & Bartholomew, 1999; Reference MillsapMillsap, 2011; Reference Skrondal and Rabe-HeskethSkrondal & Rabe-Hesketh, 2004). The concordance between these two traditions’ treatment of the same phenomenon has been noted many times before (Reference Reise, Widaman and PughReise et al., 1993; Reference Stark, Chernyshenko and DrasgowStark et al., 2004, Reference Stark, Chernyshenko and Drasgow2006), and contemporary modeling tools have been useful in helping researchers to unify these two perspectives. The second thing to note is that the terms will be used interchangeably throughout this Element. In general, measurement invariance will mostly be referred to when discussing an assumption (e.g., ensuring that different types of measurement invariance are satisfied), whereas DIF will be used to describe an effect (e.g., DIF effects were found for some items in this test). However, some slippage between the terms is unavoidable, given that – as we will see shortly – the two refer to virtually identical concepts.

For more information about the terminology used in this Element, readers are referred to the Glossary in Table 1.

1.0.2 Organization of This Element

The main goals of this Element are to give developmental scientists as comprehensive a summary of measurement invariance and DIF research as possible, with the goal of helping them to incorporate the theory and practice of this research area into their own work. We begin with as complete a description of latent variable models as possible. The Element aims to provide a mathematical framework for the specific discussion of exactly what measurement invariance and DIF are. We will then mathematically define the types of DIF effects one might encounter, as well as different fields’ frameworks for studying DIF in general. Readers already familiar with the different types of measurement invariance (e.g., configural, metric, scalar) and DIF (e.g., uniform, nonuniform) may wish to skip this portion, particularly if they are already familiar with nonlinear latent variable models.

The second portion of this Element concerns the different extensions of the nonlinear factor model which can be used to test the assumption of measurement invariance, or detect and account for DIF. First, we discuss the two main modeling frameworks for addressing these questions, with an eye toward comparing and contrasting different fields’ and models’ definitions of DIF. We then move on to an exploration of different algorithms used to locate DIF, with a similar goal of examining differences and similarities between different fields. We will end with a set of recommendations for how to incorporate the study of DIF into one’s measurement-related research.

2.1 The Common Factor Model

Assume that we have a sample of $N$ participants, to whom we administer a set of $J$ items. The response of the $i$ th participant $\left(i=1,\dots ,N\right)$ to the $j\text{th}$ item $\left(j=1,\dots ,J\right)$ is denoted $y_{ij}$ . Note that we will refer to $y_{ij}$ as an “item” or a “response variable” interchangeably throughout this text. We assume that the items are measures of a set of $M$ latent variables $\left(m=1,\dots ,M\right)$ . Each individual has an implicit value of each latent variable, denoted ${\eta }_{im}$ . In a typical common factor model, we assume that the items are related to the latent variables as follows:

$y_{ij}={\nu }_j+\sum _{m=1}^M{\lambda }_{mj}{\eta }_{im}+{ϵ}_{ij}.$(1)

For each item, ${\nu }_j$ is the intercept; this represents the predicted value of $y_{ij}$ for an individual whose value on the latent variable(s) which load on $y_{ij}$ is 0. As with intercepts in linear regression, we can effectively think of it as the overall “level” of the item – we predict that participants will, on average, have high overall levels of ${\nu }_j$ regardless of their level of the latent variable. The effect of the latent variable is conveyed by ${\lambda }_{mj}$ , the factor loading. As with a slope in a linear regression, for each one-unit shift in the $m$ th latent variable we predict a ${\lambda }_{mj}$ -unit shift in the item. Finally, ${ϵ}_{ij}$ represents the error term, which is subject $i$ ’s deviation from their predicted value of item $j$ . These error terms are assumed to have a mean of 0, and a variance of ${\sigma }_j^2$ . Error terms are generally considered to be uncorrelated across items – that is ${\sigma }_{hj}$ , which represents the covariance between the error terms for items $h$ and $j$ , is assumed to be 0.

Latent variables may covary with one another, with an $M\times M$ covariance matrix $\Phi$ . Each diagonal element of $\Phi$ , here denoted ${\varphi }_m^2$ , represents the variance of the $m\text{th}$ latent variable; off-diagonal elements of the matrix, denoted ${\varphi }_{nm}$ , represent the covariance between the $m$ th and $n$ th latent variables. Latent variables may also have their own means; the mean of the $m$ th latent variable is denoted ${\alpha }_m$ .

Some constraints must be imposed on these parameters in order for the model to be identified. There are two common options. First, we can fix one item’s value of ${\nu }_j$ to 0 and its value of ${\lambda }_{mj}$ to 1 for each latent variable. This item is often referred to as the reference variable and, when this approach is used, the latent variable is on the same scale as this item. Alternatively, we could set the variances ${\varphi }_m^2$ to 1 and the mean ${\alpha }_m$ to 0 for all latent variables. In this case, the loading ${\lambda }_{mj}$ may now be considered the predicted change in $y_{ij}$ associated with a one-standard deviation shift in the latent variable ${\eta }_{im}$ ; the intercept ${\nu }_j$ may now be considered the predicted value of $y_{ij}$ when all latent variables are at their means. As we will see shortly, assessing measurement invariance involves adding a number of new parameters to the model, which will complicate model identification; this is discussed in detail below.

2.2 Nonlinear Factor Models

The common factor model presented above is the foundation of most psychological researchers’ understanding of latent variable models. However, in order for us to understand the relations among different latent variable models, it is necessary to extend it. In particular, the above model assumes that items $y_{ij}$ meet the same general assumptions as the dependent variable in a linear regression. For our purpose, the most problematic of these assumptions is that the residuals of the items are normally distributed. This assumption requires, among other things, that our outcome be continuous, which we know many psychological outcomes are not (even if we erroneously treat them that way). In particular, it is common for us to be working with ordinal items resulting from a Likert scale (e.g., responses ranging from 1 to 5 assessing a participant’s agreement with a given statement) or even binary items (e.g., a yes–no response to a question about psychiatric symptoms).

Thus, our discussion of DIF will use a nonlinear factor analysis formulation. Although we will attempt to describe the nonlinear factor analysis formulation, we suggest that this not be the reader’s first introduction to nonlinear factor models and generalized linear models more generally, as mentioned above. However, for review, a brief description follows.

The major advantage of nonlinear factor models is that they allow the relation between items and latent variables (i.e., the one expressed in Equation 1) to take a nonlinear form, corresponding to items $y_{ij}$ of different scales. The shift to nonlinear variables requires two major innovations on the model presented above. The first is what is known as a linear predictor, which we denote ${\omega }_{ij}$ , and which is formulated as follows:

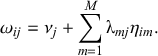${\omega }_{ij}={\nu }_j+\sum _{m=1}^M{\lambda }_{mj}{\eta }_{im}.$(2)

Note that this is basically the exact same equation as Equation 1, except without the error term. The purpose of the linear predictor becomes a bit clearer when we introduce the second component of nonlinear factor models, known as the link function. In order to get to our expected value of $y_{ij}$ , we must take our linear predictor ${\omega }_{ij}$ and place it inside the inverse link function. Let us unpack each term in this statement. The expected value of $y_{ij}$ is whatever value we would predict for subject $i$ on item $j$ . For binary items, this is the probability that that particular subject will give a response of 1 (e.g., say “yes” to a yes–no question, get a question correct on a test of ability, endorse a given symptom on a symptom inventory) based on their level of the latent variable. We will denote this ${\mu }_{ij}$ (following the notation of Reference Bauer and HussongBauer and Hussong (2009)).

As for the inverse link function, let us first define the link function, $g\left(q\right)$ :

$g\left({\mu }_{ij}\right)={\omega }_{ij}.$(3)

To put Equation 3 colloquially, we can define the link function $g\left(x\right)$ as “whatever function we apply to the expected value of $y_{ij}$ to get to ${\omega }_{ij}$ .” Being that the inverse link function, denoted $g^{-1}\left(q\right)$ , is the inverse of $g\left(x\right)$ , it can be colloquially defined as “whatever function we apply to ${\omega }_{ij}$ to get to the expected value of $y_{ij}$ .” Note that the function $g\left(x\right)$ must be bijective in order to have an inverse.

Mathematically, it is defined as follows:

$g^{-1}\left({\omega }_{ij}\right)={\mu }_{ij}.$(4)

Thus, in order to get to ${\mu }_{ij}$ , our expected value for $y_{ij}$ , our model is implicitly estimating the linear predictor ${\omega }_{ij}$ and applying the inverse link function. As far as our choices of link and inverse link functions, they depend on the type of data we are interested in modeling. One reasonable choice for binary data is the logit link function, whose inverse will yield a number between 0 and 1, making it well-suited to modeling a probability. As noted above, when we are working with binary data, the expected value of $y_{ij}$ ( ${\mu }_{ij}$ ) is the probability that a given individual endorses item $y_{ij}$ – that is, $P\left(y_{ij}=1\right)$ . Thus, we will use the logit function to translate ${\mu }_{ij}$ to ${\omega }_{ij}$ , and the inverse of that function to translate ${\omega }_{ij}$ to ${\mu }_{ij}$ . The logit link function is defined as follows:

(5)

where $ln$ denotes the natural logarithm. Conversely, the inverse logit link function is defined as follows:

$g^{-1}\left({\omega }_{ij}\right)=\frac{exp\left({\omega }_{ij}\right)}{1+exp\left({\omega }_{ij}\right)}={\mu }_{ij},$(6)

where $exp\left(q\right)$ is shorthand for $e^q$ . If the reader wishes to see that Equation 6 is indeed the inverse of Equation 5, they may choose a value of ${\mu }_{ij}$ , which can be any number between 0 and 1, and plug it into Equation 5. Then take the value of ${\omega }_{ij}$ obtained from Equation 5 and plug it into Equation 6. This transformation should yield the originally chosen value of ${\mu }_{ij}$ .

Putting it all together, we can now finally formulate how the latent variable itself is related to the expected value of a binary item under a nonlinear factor analysis. Combining the original linear formulation in Equation 2 and the inverse link function in Equation 4 we get the following:

${\mu }_{ij}=\frac{exp\left({\nu }_j+\sum _{m=1}^M{\lambda }_{mj}{\eta }_{im}\right)}{1+exp\left({\nu }_j+\sum _{m=1}^M{\lambda }_{mj}{\eta }_{im}\right)}.$(7)

Note that we have the same exact parameters linking the latent variable ${\eta }_{im}$ to the item $y_{ij}$ : intercept ${\nu }_j$ and loading ${\lambda }_{mj}$ . The difference is that now $y_{ij}$ is related by these parameters to the latent variable through a nonlinear function as opposed to a linear one. If the reader wishes to test this out, an example is given in Table 2, in which we have each individual’s values of ${\eta }_i$ , ${\omega }_{ij}$ , ${\mu }_{ij}$ , and $y_{ij}$ for pre-set values of ${\lambda }_{mj}$ and ${\nu }_j$ .

Table 2 Example values of latent variables ( ${\eta }_i$ ), linear predictors ( ${\omega }_{ij}$ ), endorsement probabilities ( ${\mu }_{ij}$ ), and outcomes (  $y_{ij}$ ), for a nonlinear factor analysis with $\lambda =1.5$ and $\nu =0.25$

ID	${\eta }_i$	${\omega }_{ij}$	${\mu }_{ij}$	$y_{ij}$
1	0.5723	1.1084	0.2482	0
2	− 0.0034	0.245	0.4391	1
3	− 2.7187	− 3.828	0.9787	1
4	− 0.6953	− 0.793	0.6885	0
5	1.3079	2.2118	0.0987	0
6	− 0.9547	− 1.182	0.7653	1
7	− 1.7034	− 2.3051	0.9093	1
8	0.204	0.5559	0.3645	0
9	0.3321	0.7482	0.3212	0
10	0.7218	1.3326	0.2087	0

There is one more step to understanding nonlinear factor analysis, and that is defining the probability function. Note that the inverse link function does not give us $y_{ij}$ but its expected value – that is, for a binary item it will not give us a value of $y_{ij}$ (which can only take a value of 0 or 1) but rather ${\mu }_{ij}$ , the probability that $y_{ij}$ will be 1. Notice also that our linear predictor has no error term in it – we have not accounted for any source of randomness or error. Thus, the probability function is what links the expected value ${\mu }_{ij}$ to the value of $y_{ij}$ we ultimately obtain. In the case of binary response variables, we generally assume that $y_{ij}$ follows a Bernoulli distribution with probability ${\mu }_{ij}$ .

Colloquially, this means the following. The variable $y_{ij}$ is random and we don’t know whether it will be 0 or 1, but we do know the probability with which it will be 1, and that probability is ${\mu }_{ij}$ . A person with ${\mu }_{ij}=0.9$ will most likely give a value of 1, a person with ${\mu }_{ij}=0.2$ will most likely give a value of 0, and a person with ${\mu }_{ij}=0.5$ is just as likely to give a value of 0 or 1, but any one of these people could theoretically give a value of 0 or 1. Note, for instance, in Table 2, that the observed values of $y_{ij}$ take values of 0 or 1, and may even (as in the case of the 8th observation) take a value of 0 if the probability of endorsing the item is over 0.5.

Once we combine all three of these things – the linear predictor, the link function, and the probability function – we have all the information we need to think about factor analysis, and thus DIF, in a way that encompasses many different types of models across disciplines. For instance, the formulation provided above for binary variables, using an inverse logit function to link the linear predictor to the probability of endorsing an item, is actually the same as the two-parameter logistic model in IRT (Reference BirnbaumBirnbaum, 1969). This model is frequently applied to binary data in an IRT setting.

2.2.1 Extensions to Ordinal Data

The above model will suffice for binary data, but ordinal data requires a slightly more complicated extension of this formulation. A model arising from IRT for ordinal data is known as the graded response model (Reference Samejima, Linden and HambletonSamejima, 1997). Like the formulation given in Equation 6, we are modeling probabilities. Given an ordinal item with $K$ categories $\left(k=1,\dots ,K\right)$ , we model the probability of endorsing category $k$ or lower. For instance, in a three-level item, rather than modeling the probability that a participant endorses option 1, 2, or 3, we model the probability that the participant endorses option 1; option 2 or 1; or option 3, 2, or 1. Note that the probability of endorsing option 3, 2, or 1 is exactly 1 – the participant must endorse one of these three options. So we only model $K-1$ probabilities – in this case, the probability of endorsing option 2 or lower, and the probability of endorsing option 1. Note also that the case of binary data is actually a special case of this model – that is, it is a model with $K=2$ categories.

Whereas in binary data we used ${\mu }_{ij}$ to represent the probability of endorsing a given item, here we use $E\left(y_{kij}\right)$ to represent the cumulative probability of endorsing category $k$ or lower. In the three-level example just given, thus, every participant would have an implied value of $E\left(y_{1ij}\right)$ , the probability of endorsing response option 1, and $E\left(y_{2ij}\right)$ , the probability of endorsing response option 2 or response option 1. Each value of $E\left(y_{kij}\right)$ has its own linear predictor, which we will denote ${\omega }_{kij}$ . This linear predictor is given by:

${\omega }_{kij}={\tau }_{kj}-\left({\nu }_j+\sum _{m=1}^M{\lambda }_{mj}{\eta }_{im}\right).$(8)

The new parameter in this equation, ${\tau }_{kj}$ , is the threshold parameter. This parameter represents the value of the latent variable a participant must exceed in order to get a score exceeding $k$ . One critical note is that all possible values of ${\tau }_{kj}$ and the intercept ${\nu }_j$ cannot all be identified; one of these values must be fixed. The typical solution is to set the intercept ${\nu }_j$ to zero in the event that individual thresholds are estimated. Readers who would like a comprehensive description of the ${\tau }_{kj}$ parameter are referred to the original formulation of the model (Reference Bauer and HussongBauer & Hussong, 2009), where it is explained more completely.

3.1 Differences in the Overall Level of the Item: ${\nu }_j$

As noted earlier, the intercept parameter ${\nu }_j$ denotes the intercept for item $j$ . This parameter represents the predicted value of the item for a subject with a value of 0 for all of the latent variables. If there is measurement bias in this parameter for grouping variable $g$ , this means that one of the groups gives higher or lower predicted values of the items than the other, controlling for the latent variable.

The interpretation of this parameter depends on the type of item $y_{ij}$ . If $y_{ij}$ is a continuous item, then the intercept represents the actual value we predict someone with ${\eta }_{im}=0$ for all ${\eta }_{im}$ to endorse. So if members of Group 1 have a higher value of ${\nu }_j$ than members of Group 0, then members of Group 1 are predicted to give higher overall responses to $y_{ij}$ , even if they have the same value of the latent variable ${\eta }_{im}$ . For instance, suppose that we are measuring a single latent variable, responsive parenting, and $y_{ij}$ is the amount of time a parent spends playing with their child during a free-play task. Further suppose that parents in Group 1 (which could be any grouping variable – older parents relative to younger ones, male parents relative to non-male ones, parents in a treatment condition relative to the control group) have higher values of ${\nu }_j$ than those in Group 0. In this case, if we took two parents who had the exact same level of responsiveness, but one parent was from Group 1 and the other was from Group 0, we would predict that the parent from Group 1 plays with their child more than the one from Group 0, even though in reality they are equally responsive. One possible relation between the item and the latent variable is shown in the top left portion of Figure 1. Notice that the lines are parallel: it is only their intercept, representing their overall level of responsiveness, that has changed.

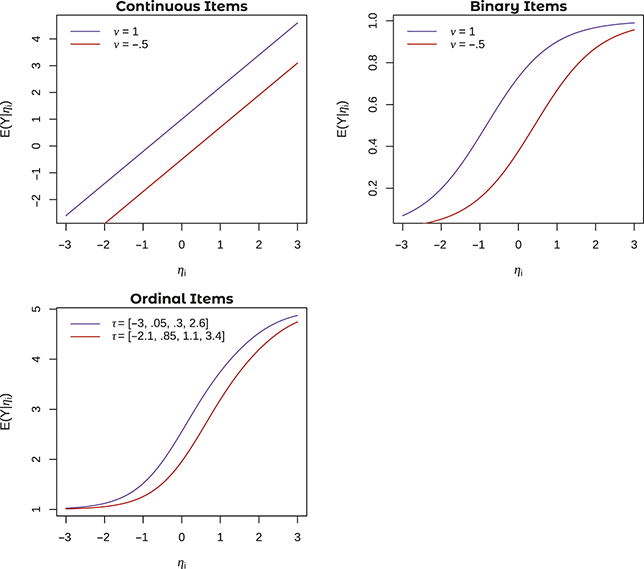
Figure 1 Examples of uniform DIF in continuous, binary, and ordinal items

Note. Figures plot the expected value of $y_{ij}$ against the latent variable ${\eta }_i$ . Note the different intercept values for continuous and binary items, and different threshold values for ordinal items, in the upper left-hand corner of the graphs.

If $y_{ij}$ is binary or ordinal, the interpretation of ${\nu }_j$ changes. If $y_{ij}$ is binary, ${\nu }_j$ represents the probability of endorsing the item. Suppose we are still measuring responsive parenting, but the item $y_{ij}$ in this case is a binary response variable of whether the parent endorses the item: “I try to take my child’s moods into account when interacting with them.” In this case, if members of Group 1 had a higher value of ${\nu }_j$ than those in Group 0, then we would predict that a parent from Group 1 who has the same level of responsiveness as another parent in Group 0, would nevertheless be more likely to endorse this item than their counterpart in Group 0. The interpretation is only slightly different for ordinal items. If the item were instead a five-level ordinal one, a higher value of ${\nu }_j$ in Group 1 would be interpreted as a higher probability of endorsing any category $k$ , relative to category $k-1$ (i.e., the next category down). In this case, we would predict that a parent in Group 1 is more likely than a parent in Group 0 to endorse a higher category, even at the same level of responsiveness. Note that this difference is the exact same across all categories – that is, if Group 1 has a higher value of ${\nu }_j$ , then they are more likely to endorse category 4 relative to category 3, category 3 versus 2, category 2 versus 1, and category 1 versus 0. A possible relation between the item and the latent variable is shown in Figure 1, both for the binary and the ordinal cases. Note that, just as in the case of continuous variables, the difference between the trace lines is best described as a horizontal shift, whereby one trace line is associated with higher values of $E\left(y_{ij}|\eta \right)$ than the other at every value of ${\eta }_{ij}$ . That is, while the expected value of $y_{ij}$ may change, it does so uniformly.

3.2 Differences in the Relation Between the Latent Variable and the Item: ${\lambda }_{jm}$

If ${\nu }_j$ can be considered as the intercept for a given item, the loading ${\lambda }_{jm}$ represents the regression coefficient that conveys the effect of the latent variable ${\eta }_m$ on this item. Thus, if there are differences on the basis of grouping variable $g$ in ${\lambda }_{jm}$ , that means that there are differences in the nature of the relation between the latent variable and the items. As with ${\nu }_j$ , the interpretation of between-group differences in ${\lambda }_{jm}$ differs based on the scale of the item. However, in both cases it can be interpreted as a regression coefficient, with ${\eta }_{im}$ as the predictor and $y_{ij}$ as the outcome. The type of regression coefficient is simply a matter of which type of item we are using – if $y_{ij}$ is continuous, ${\lambda }_{jm}$ is essentially a linear regression coefficient, but if $y_{ij}$ is binary, ${\lambda }_{jm}$ will be a logistic regression coefficient, and so on.

One possible set of relations between ${\eta }_{im}$ and $y_{ij}$ with different values of ${\lambda }_{mj}$ is shown in Figure 2. Notice a critical difference between the lines shown here and those shown for between-group differences in ${\nu }_j$ : here the lines are not parallel, both for continuous and binary values of $y_{ij}$ . The relation between ${\eta }_{im}$ and $y_{ij}$ is stronger in one group than another. Notice that this is the case for all types of items (i.e., continuous, binary, and ordinal). In one group, the predicted value of $y_{ij}$ increases more quickly with corresponding increases in ${\eta }_{im}$ than the other group – that is, the relation between ${\eta }_{im}$ and $y_{ij}$ is stronger in this group.

Figure 2 Examples of nonuniform DIF in continuous, binary, and ordinal items

Note. Figures plot the expected value of $y_{ij}$ against the latent variable ${\eta }_i$ . Note the different loading values for all items in the upper left-hand corners of the graph.

Consider our responsive parenting example from earlier. Suppose that item $y_{ij}$ here is the parent’s recall of the number of times they drove their children to school. (Note that, this being a count variable, it would likely be better modeled using a Poisson or negative binomial regression than the linear regression we are proposing here. This example is just an illustration; we will treat it as normally distributed for the purpose of argument.) Further suppose that $g$ is a grouping variable based on whether the family lived in an urban, suburban, or rural location. In this case, the number of times the parent drove their child to school may not be a particularly good measure of responsiveness, as it would likely show a weaker relation to responsiveness among urban parents. Parents in urban locations may be very responsive but just not have occasion to drive their children to school, opting instead to accompany them on public transit or walk them to school. In this case, the slope linking ${\eta }_{im}$ to $y_{ij}$ , ${\lambda }_{jm}$ , would be smaller among urban parents than rural or suburban ones, indicating that as responsiveness increased we would not expect a corresponding increase in $y_{ij}$ . Similarly, if $y_{ij}$ were a binary item asking a parent to recall the last time they drove their child to school, taking a value of 0 if the occasion was over a week ago and a value of 1 if it was within the past week, ${\lambda }_{jm}$ would also be smaller. In this case, it would simply mean that, relative to rural or suburban parents, urban parents’ probability of driving their children to school does not increase with corresponding increases in responsiveness.

3.3 Differences in the Probability of Endorsing Specific Levels of each Item: ${\tau }_{kj}$

In an item with multiple possible categories a participant could endorse, recall that there are category-specific threshold parameters, denoted ${\tau }_{kjm}$ for category $k$ of item $j$ measuring latent variable $m$ . A difference between groups may mean many different things, depending on the nature of the item and the differences found therein. In general, such differences occur only if one group is more or less likely to endorse a specific category than the other group, over and above differences in the latent variable.

For instance, suppose we have a four-level ordinal item, and one group has a lower threshold for $k=4$ . What this means is that members of this group are more likely to endorse category 4 than the other group. A between-groups difference such as this one may happen, for instance, if category 4 refers to an event which is extremely common in one group due to factors which are unrelated to the latent variable. Suppose that in our responsive parenting example we had a four-level ordinal item which asked the parent how frequently in the past week they had helped their child get dressed, with response options including never (1), occasionally (2), often (3), and always (4). If we created a grouping variable on the basis of the child’s age, putting children under three years in the younger group and children over three years in the older group, we might predict that parents with children in the younger group are more likely to endorse the “always” option than those with children in the younger group. Though many children under three years can do some dressing-related tasks, the majority are not able to complete all of the tasks involved in dressing themselves. Perhaps parents of children in the older group would have more latitude to interpret the question – interpreting it, for instance, as the frequency with which they engaged in age-normative tasks relating to dressing oneself such as helping to pick out a matching outfit or helping the child to tie their shoes. But the parents of children in the younger group would be much more likely to say “always.”

As one might intuit from the very specific nature of this example that differences in individual thresholds are often difficult to hypothesize a priori. As will be seen shortly, they can also be computationally challenging to model, which leads to some methodological researchers recommending that such differences be modeled sparingly (Reference Gottfredson, Cole and GiordanoGottfredson et al., 2019).

Differences That Do Not Represent Measurement Bias

We have stated that measurement bias is present if there are differences between groups in the measurement parameters. However, there is another reason that we may observe differences between groups in the latent variables: it may be the case that there actually are differences in the latent variable. In particular, the latent variable mean ${\alpha }_m$ , as well as latent variable variances ${\psi }_m^2$ and covariances ${\psi }_{lm}$ may differ between groups. We will use the term impact to describe such differences.

Differences between groups in ${\alpha }_m$ , which we will refer to as mean impact, are some of the between-group differences in which researchers are often most interested. Consider our responsive parenting example. In this case, we may be interested in whether one group is actually more responsive on average than the other group. For instance, there is evidence that chaotic home environments (i.e., environments lacking in routine and structure) are conducive to less responsive parenting (Vernon-Feagans et al., 2016; Wachs et al., 2013). If we separated our sample into groups according to household chaos level, we may well find that the mean of responsive parenting was higher among parents who reported living in less chaotic homes, relative to their high-chaos counterparts. Similarly, if we were conducting an intervention trial and measuring postintervention levels of responsiveness, perhaps we would find mean differences on the basis of condition, with those in the treatment condition showing higher means than those in the control condition.

Differences between groups in the variance components, which we refer to as variance impact, is also common. It may be the case, for instance, that certain groups of parents show more variability in their responsiveness than others. For instance, it may be the case that, in addition to being more responsive overall, parents in less-chaotic homes are more uniformly responsive than those in highly chaotic homes. That is, though we do not have evidence to cite here as in the case of latent variable means, we might speculate that parents living in highly predictable environments are generally all highly responsive, which would mean that the variance of responsiveness in that group would be low since all parents show the same high level of responsiveness. By contrast, parents living in chaotic environments could be more variable in their overall level of responsiveness.

We will now map the above-mentioned differences in the parameters, as defined in this section, onto terminologies and conventions from the SEM and IRT traditions of latent variable modeling.

4.1 Types of Invariance in SEM

In general, within SEM the question of invariance is considered at the level of the test, with increasingly stringent invariance conditions which must be met for the results to be interpreted (Reference MeredithMeredith, 1993). These levels are shown in Figure 3. There are a few things to note about the depiction of invariance in Figure 3, some of which reflect broader points about measurement invariance in SEM. First, we are considering a two-group case. The path diagram on the left is for our first group (here denoted Group 0) and the path diagram on the right is our second group (here denoted Group 1). We will discuss multiple-group analysis shortly (“Multiple-groups formulation”). In the meantime, note that the depiction here includes two types of parameters: intercepts ${\nu }_{jg}$ and loadings ${\lambda }_{jmg}$ . This $g$ subscript, which is simply the last number in the subscript of parameters that are allowed to vary across groups, represents group membership. Second, notice that there are no threshold parameters ${\tau }_{ikj}$ here. In general, the original formulation of measurement invariance within an SEM context focuses more on differences in items’ overall levels (i.e., intercepts) and relations to the latent variable (i.e., loadings). Thus, testing for DIF in individual thresholds does not correspond to any of the types of invariance we will name in this section. We will see shortly, however, that it certainly possible to model differences in thresholds at this stage.

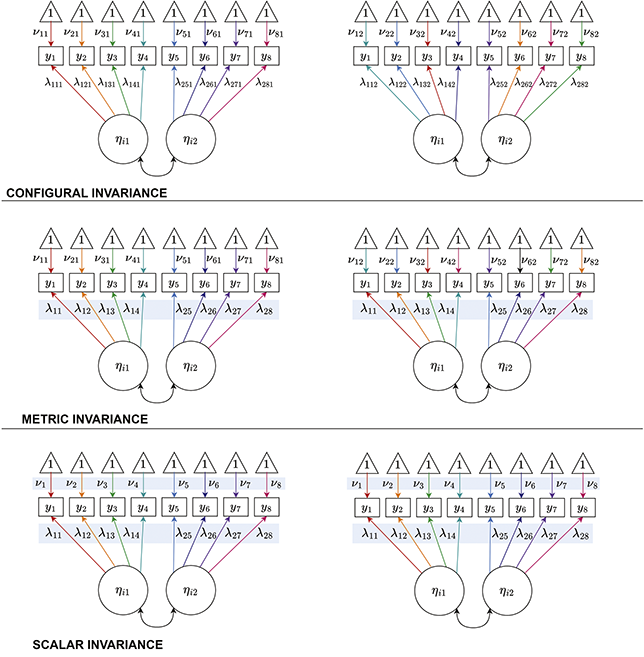
Figure 3 Different types of measurement invariance under the SEM framework

Note. Path diagrams for two-group latent variable models under configural invariance (top), metric invariance (middle), and scalar invariance (bottom). The 1’s in triangles are standard notation for intercepts; the path between the 1 and the indicator, given by ${\nu }_{jg}$ , represents the intercept. Different colored arrows indicate differences across the two groups. Note that both loadings and intercepts differ in configural invariance; only intercepts differ in metric invariance; and neither loadings nor intercepts differ for scalar invariance.

The most fundamental form of invariance, shown in the top panel, is configural invariance, which holds if the same factors account for the same items across groups (Reference Horn and McArdleHorn & McArdle, 1992). The assumption of configural invariance would be violated if, for instance, there are three factors in one group and two factors in the other. In general, absent configural invariance no inferences can be drawn about differences between groups. Having established configural invariance, we then examine metric, scalar, and strict measurement invariance (Reference Steenkamp and BaumgartnerSteenkamp & Baumgartner, 1998; Reference Vandenberg and LanceVandenberg & Lance, 2000). Note that metric invariance is sometimes referred to as “weak metric invariance,” and scalar invariance is sometimes referred to as “strong metric invariance.”

The first two of these conditions are shown in Figure 3. Under metric invariance, the factor loadings $\Lambda$ must be equal across all values of $G$ . That is, we assume that the strength of the relations between the latent variable and the outcomes are the same across groups. Under scalar invariance, metric invariance must hold and, additionally, measurement intercepts $\nu$ must be equal across all values of $G$ . In other words, scalar invariance means that the overall level of the items, over and above the latent variable itself, is the same across groups – members of one group are no more or less likely to endorse the items than the other.

Finally, under strict measurement invariance, both metric and scalar measurement invariance must hold, but the error covariance matrix $\Sigma$ must also be equal across all values of G. Note that strict invariance, thus, is required to fulfill the definition of full invariance offered above in Equation 9. The ramifications of violations of these assumptions are discussed below.

The concept of partial invariance was introduced into the CFA tradition to refer to the case in which some, but not all, measurement parameters are invariant (Reference Byrne, Shavelson and MuthénByrne et al., 1989; Reference Cheung and RensvoldCheung & Rensvold, 2002a). In such a case, for instance, two loadings could be noninvariant, along with three intercepts. The case of partial invariance leads to an important question: How much invariance is “enough” for the groups to be truly comparable in terms of the latent variable? Broadly, there is no one right answer to this question. For one thing, there are many ways in which to measure the overall amount of DIF on an item or a set of items. With respect to partial invariance, however, there are many ways to even consider the question of how much DIF is too much. Should we consider it in terms of the number of items with DIF, the number of unique effects, the magnitude of each DIF effect, or some other way? Though these questions do not have a single answer, some evidence can be drawn from empirical studies of the consequences of DIF. We discuss these studies in the section “Empirical findings: Does DIF actually matter?”.

4.2 Types of DIF in IRT

By contrast to SEM, in IRT DIF is typically explored at the level of individual items. That is, whereas SEM starts from the question of whether all items are invariant and proceeds to test partial invariance only after that omnibus condition has been tested, IRT starts from the question of whether each individual item is invariant (Reference MellenberghMellenbergh, 1989). Consequently, within IRT DIF is typically tested at the level of each item. Uniform DIF refers to differences in the predicted value of $y_{ij}$ that are the same across all levels of the latent variable. In binary or continuous items, this typically corresponds to differences in the ${\nu }_j$ parameter. Recall that, as we noted earlier, the trace lines of two groups who differ in ${\nu }_j$ do not cross – predicted values are simply higher for one group than another. By contrast, nonuniform DIF refers to differences in the predicted values of $y_{ij}$ that differ across levels of the latent variable. Nonuniform DIF typically corresponds to differences across groups in ${\lambda }_{im}$ , indicating a differential relation between the latent variable and the outcome. Note that, as before, this essentially refers to an interaction – as the latent variable’s value changes, differences across groups may be exacerbated or attenuated. Each of these trace lines are depicted with respect to binary and continuous items in Figures 1 and 2, as discussed earlier.

There are a few issues of which readers will want to take note with this terminology. First, though uniform and nonuniform DIF are terms which are typically applied to differences in intercepts ${\nu }_j$ and loadings ${\lambda }_{mj}$ respectively, the broadest definition of nonuniform DIF also includes differences across groups in ${\tau }_{jk}$ . That is, because the predicted value of the item may change across groups to a different extent at different values of ${\eta }_{im}$ , this type of DIF is still nonuniform. Another issue with this terminology is that some authors use the terms uniform and nonuniform to refer to differences in the direction of DIF effects across items within a given test (Reference ChenChen, 2007; Reference Yoon and MillsapYoon & Millsap, 2007). That is, if a test has two items with DIF on ${\nu }_j$ and both are in the same direction (i.e., the differences both favor the same group), that is referred to as uniform DIF. By contrast, if the DIF on ${\nu }_j$ is nonuniform, it may be the case that the difference on one item has a higher value of ${\nu }_j$ in one group, and the other has a higher value of ${\nu }_h$ in the other group, $h\ne j$ . We will not use this terminology here, but readers should know that it is present.

4.3 A Further Note about Similarities and Differences Between SEM- and IRT-Based Methods

Though the terms used by SEM and IRT to describe DIF are different, it is also important to note that they are in many ways the same. Uniform DIF maps relatively well onto a lack of scalar measurement invariance – that is, a uniform difference across groups in the average predicted value of $y_{ij}$ . By contrast, nonuniform DIF maps onto the idea of metric invariance; it represents a difference across groups in the predicted increment in $y_{ij}$ associated with a one-unit shift in ${\eta }_{im}$ . The main difference between the frameworks, as we have reviewed them so far, is in the unit of analysis. Whereas SEM generally treats the whole set of items as potentially noninvariant in terms of all items’ overall endorsement levels and relations to the latent variable (scalar and metric noninvariance, respectively), IRT most often considers whether individual items themselves vary across groups in terms of their overall endorsement levels and relationsips to the latent variable (uniform and nonuniform DIF, respectively). Nevertheless, despite the similarities between them, SEM and IRT have historically been motivated by different considerations, and procedures for testing for measurement noninvariance/DIF vary accordingly.

An important set of distinctions arises from the types of items which SEM and IRT typically consider, as well as the nature of the latent variables they are assumed to measure. Historically, the modal use of IRT has been to measure a single latent variable with a relatively large number (e.g., $>$ 8) of items, which are often binary or ordinal. There are many exceptions to this, with a number of IRT models for more than one latent variable, as well as contexts in which items are continuous (e.g., Reference FerrandoFerrando, 2002; Reference ReckaseReckase, 1997). By contrast, SEM is typically applied when it is presumed that there are multiple latent variables, with the nature of these variables and the relations among them being of primary interest. Additionally, SEM has historically applied the assumption of multivariate normality to items, making it well suited to cases in which items are truly continuous.

The first reason this matters is that, with items of different scales, different sorts of invariance are possible, Notice that, though invariance of parameters ${\nu }_j$ (codified at the single-item level as uniform DIF on ${\nu }_j$ in IRT, at the test level as scalar invariance in $\nu$ in CFA) and ${\lambda }_{jm}$ (nonuniform DIF on ${\lambda }_{jm}$ in IRT, metric invariance in $\Lambda$ in CFA) are described by both frameworks, equivalence of error terms is described only in CFA, as strict invariance. In CFA with continuous items, strict invariance is required to fulfill the definition of full invariance shown in Equation 9. In IRT with dichotomous variables, first-order invariance is equivalent to the full definition of measurement invariance from Equation 9; this is because a conditional variance of $y_{ij}$ is not defined. Given polytomous variables, first-order invariance and full invariance may differ, but under most commonly used IRT models they are the same (Reference Chang and MazzeoChang & Mazzeo, 1994).

The second reason it matters is that, as we will see, the types of models and testing procedures used to find measurement noninvariance/DIF are informed by the types of items and latent variables being considered. Though there are many exceptions to this distinction, in general procedures arising from the CFA tradition focus on establishing the structure of factors across groups, whereas those arising from IRT focus on finding the optimal set of items to measure a construct (Reference Stark, Chernyshenko and DrasgowStark et al., 2004, Reference Stark, Chernyshenko and Drasgow2006; Reference Wirth and EdwardsWirth & Edwards, 2007). We discuss this broadly in the section “Consequences of Measurement Noninvariance and Differential Item Functioning” and specifically when reviewing procedures for locating DIF (“Detecting Measurement Noninvariance and Differential Item Functioning”).

5.1 Data Example: Longitudinal Study of Australian Children

From this point on, we will be demonstrating each model we discuss using real data arising from the Longitudinal Study of Australian Children (LSAC; Reference Sanson, Nicholson and UngererSanson et al., 2002). Data access must be requested from the Australian Institute of Family Studies, but all study scripts are available in the Supplemental Materials of this report, as well as this Git repository: https://github.com/vtcole/element.

Though the data are described completely elsewhere (Reference Gray and SansonGray & Sanson, 2005; Reference Zubrick, Lucas, Westrupp and NicholsonZubrick et al., 2014), we summarize the dataset briefly here. The data ( $N=\mathrm{4,359}$ ; $51\%$ male) come from a nationally representative longitudinal study of children in Australia, whose parents participated in the first wave of the study in 2004. In two-parent households, both parents answered the survey when possible; for each participant, one parent was sampled randomly. There are two cohorts of LSAC, one which started shortly after the child was born and one which started when the child was in kindergarten; we use exclusively the birth cohort here. Data come from the first wave of assessment, when most children were in their first year of life ( $M_{age}=39.90$ weeks; range = 14–103 weeks). Note that the study used complex sampling, and we will use sampling weights in our analyses for demonstration purposes. However, when using only a subset of the sample that has been sampled in this way (as we are here), there are generally a few more data management steps to take; we forego these here as they are not the focus on the current demonstration.

For this analysis, we are interested in parental warmth, which was measured using the six items shown in Table 3 (Reference Cohen, Dibble and GraweCohen et al., 1977). Responses were on a five-point scale, with response options of never/almost never (1), rarely (2), sometimes (3), often (4), and always/almost always (5). Internal consistency for this scale was strong, with $\alpha =0.838$ . We will examine the effects of three covariates: child sex (male vs. female), parent gender (male vs. female), and child age in weeks. Note that we use child sex and parent gender, because parents reported their gender identity but we only have information about biological sex for children. We consider age in two ways: as a grouping variable with four levels corresponding to the four quartiles of age, and as a continuous variable in its original metric (i.e., weeks).

The bulk of this section will introduce two main formulations of models which can be used to answer questions about noninvariance and DIF. Importantly, the purpose of these models is twofold. First, they can be used to assess whether noninvariance or DIF are present. Second, given that noninvariance or DIF are found, they can be used to model those effects, with the goal of eliminating their biasing effects on estimates of the latent variable parameters. However, just as in any analysis, we must conduct a series of exploratory steps before proceeding with the modeling process. We discuss these now.

5.2 A Preliminary Step: Data Visualization and Data Management

As in just about any modeling context, it is critical in the study of measurement invariance to visualize the data before conducting any analyses. We conducted a series of data visualization and management steps with the example data in R, which are given in the Supplemental Materials.

There are two goals of data visualization. The first is to determine which items require further data management before proceeding. In particular, it is critical to make sure that $y_{ij}$ has enough variation, ideally both in the aggregate and at specific levels of the covariate, for us to model. For ordinal items, this means determining whether the endorsement rates of each level are sufficient to keep all levels, or whether we must collapse sparsely endorsed item categories. This decision does entail some loss of information. However, in many cases collapsing across sparsely endorsed categories yields more stable results and greater convergence rates, relative to retaining a level of the item which few subjects endorse (Reference DiStefano, Shi and MorganDiStefano et al., 2021).

In the example data, we find the endorsement rates shown in Figure 4. We notice that for all items except Item 3, the lower two categories (rarely and sometimes) were seldom endorsed. Thus, we collapse all items except Item 3 to a three-level variable, retaining all five levels for Item 3.

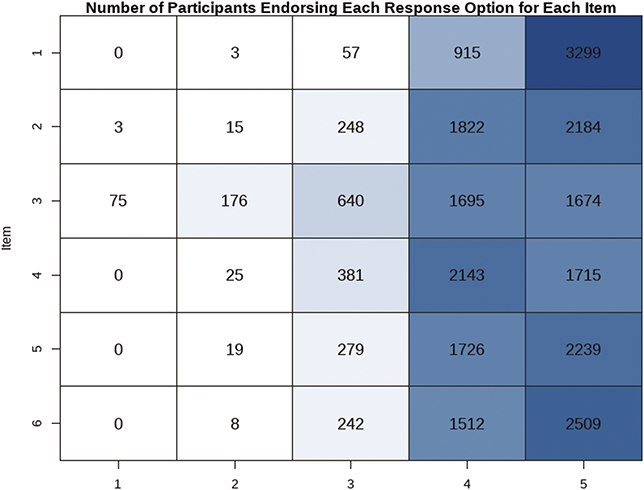
Figure 4 Endorsement rates for each response option for all six items in our data example from the Longitudinal Study of Australian Children (LSAC; $N=4,359$ )

Note. The number in each cell represents the number of participants who endorsed the corresponding response option for the corresponding item.

The second reason to visualize the data is that it may give us some clues about what to expect in our analyses, and give us a sense of what those results will mean in practical terms. Though there are many analyses which may be useful (in addition to the checks for sufficient variance described above), we suggest two. The first is to plot the means (or endorsement probabilities) of each item by levels of the covariates. This step helps us to see whether one or more items does not appear to show the same general behavior as others.

We have done this for the example data in Figure 5. Note that, to get all the item means onto comparable scales, we centered each item’s mean so that the middle response option is zero. There are a few differences between groups, most noticeably that male parents show lower means of all items than female parents. However, here we are looking for items which deviate from the pattern shown by all others. The only potentially suspicious items are Item 3 and, to a lesser extent, Item 5, which appear to be higher among parents of younger children, by contrast to most of the others, which are lower. These may be items on which we can expect to see DIF.

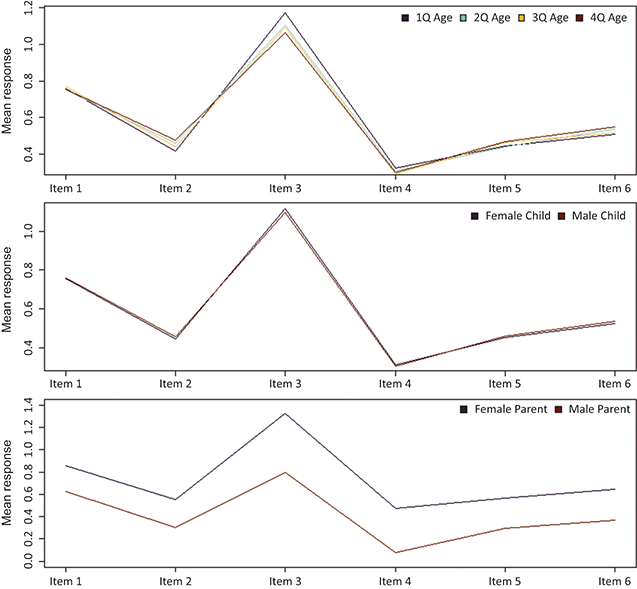
Figure 5 Mean item responses at each level of child age, child sex, and parent gender in our data example from the Longitudinal Study of Australian Children (LSAC; $N=4,359$ )

Note. The number in each cell represents the number of participants who endorsed the corresponding response option for the corresponding item.

We also recommend looking at correlation matrices by levels of each covariate. This step helps to give a sense of whether some relations are weaker or stronger at certain levels of the covariate, which may Lewis as nonuniform DIF later on. We have depicted the correlation matrices in the example data according to each level of age quartile in Figure 6. Corresponding plots for different levels of child sex and parent gender can be obtained using the code in the Supplemental Materials. (Note that researchers do not have to depict each correlation coefficient graphically – merely examining the matrix may be sufficient.) We do not see anything too troubling with the example data, although there may be subtle DIF effects that do not manifest here.

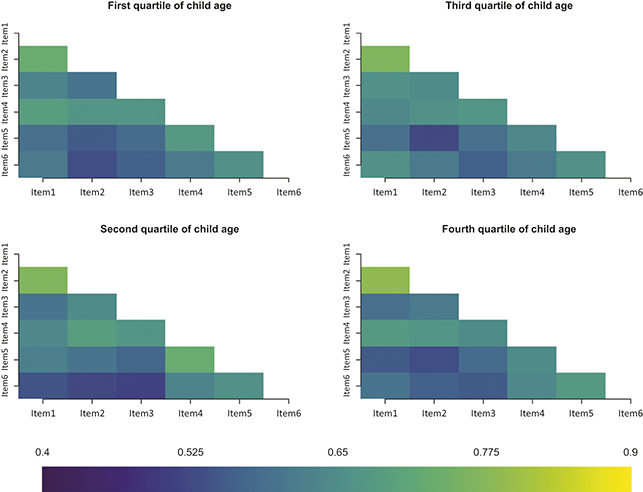
Figure 6 Polychoric correlation matrix for each age quartile in our data example from the Longitudinal Study of Australian Children (LSAC; $N=4,359$ )

Note. Correlations ranged from $r=0.4$ to $r=0.9$ . The relation between color and correlation coefficients is shown in the bottom of the figure.

We are now ready to fit our models to the example data. We articulate the two broad classes of models – multiple-groups and regression-based models – and demonstrate them in the context of this example.

Multiple-groups Formulation

Multiple-groups models are particularly useful in that they allow the same model –in our case, the model outlined in Equations 2–8 – to be fit in multiple different groups, with parameters that may differ across the groups (Reference JöreskogJöreskog, 1971). If we use the same formulation as before, we have measured $J$ items $\left(j=1,\dots ,J\right)$ for $N$ participants $\left(i=1,\dots ,N\right)$ ; each item for each participant is denoted $y_{ij}$ . These items measure $M$ latent variables $\left(m=1,\dots ,M\right)$ ; each participant’s value of the latent variable is denoted ${\eta }_{im}$ . If we extend this to a multiple-groups case, we assume that the participants fall into one of $N_G$ groups $\left(g=1,\dots ,N_G\right)$ .

The multiple groups nonlinear factor model allows us to model $N_G$ sets of parameters. That is, there could be $N_G$ sets of measurement parameters for each group; the parameters for group $g$ are subscripted with $g$ , so that we have item intercepts ${\nu }_{jg}$ , ${\lambda }_{jmg}$ , ${\tau }_{jkg}$ , and so on. Similarly, the latent variable means, variances, and covariances can vary across groups, with the parameters for group $g$ including mean ${\alpha }_{mg}$ , variance ${\psi }_{mg}^2$ , and latent variable covariances ${\psi }_{mqg},q\ne m$ . Taken together, this means that the groups may potentially differ in terms of both the latent variables and the measurement parameters; in other words, they could have completely different relations between the latent variable and the items. The caveat, of course, is that the model must be identified, which precludes all of the item parameters varying across groups. Typically at least one item’s parameters must be the same across groups, and potentially further constrained (e.g., its factor loading set to 1 and its intercept set to 0). However, there are a number of ways to identify the model, as described in greater detail below.

In the multiple-groups context, we would say that there is first-order measurement invariance across the $N_G$ groups if values of the measurement parameters ${\lambda }_{jmg}$ , ${\nu }_{jg}$ , and ${\tau }_{jkg}$ (if estimated) are equal for all values of $g$ . In other words, measurement invariance is codified as the lack of differences in the values of measurement parameters between groups. Similarly, we can test for differences across groups in the mean ${\alpha }_{mg}$ , variance ${\psi }_{mg}^2$ , and latent variable covariances ${\psi }_{mqg},q\ne m$ . These are often the parameter differences that correspond to a researcher’s substantive questions – for example, are there differences in depressive symptoms between subjects of different genders? Are the relation between internalizing and externalizing psychopathology the same across age groups? – and distinguishing these differences from measurement bias is one of the key tasks of measurement invariance analysis.

How exactly do we test whether there are differences across groups? We can use a likelihood ratio test, which assesses whether the fit of one model, which we denote the constrained model, is inferior to that of a more complicated model, which we denote the full model. The log-likelihoods are obtained and a test statistic, equal to -2 times the difference in the log-likelihoods, is computed; this test statistic is roughly ${\chi }^2$ distributed with $df$ equal to the difference between the models in the number of parameters.

The logic of likelihood ratio tests within multiple-groups models is explained fully elsewhere (Reference Satorra and SarisSatorra & Saris, 1985). However, the basic premise is that a model with no differences between groups in parameters is a simpler version of the model which allows these differences. For example, suppose we have two groups, and we are interested in whether the factor loading of the $j^{th}$ item for the $m^{th}$ latent variable is invariant across the groups. If we set all values of ${\lambda }_{jm0}={\lambda }_{jm1}$ for groups 0 and 1, we are estimating fewer parameters than a model in which these parameters are allowed to differ across the two groups. So the model with measurement invariance in ${\lambda }_{jmg}$ is our constrained model; the model without measurement invariance, which allows ${\lambda }_{jmg}$ to differ across groups, is our full model.

There are a number of points of which researchers should be aware when using likelihood ratio tests. First, it is necessary to note that when certain estimators are used (e.g., maximum likelihood estimation for categorical or non-normal continuous response variables, which we use here), a correction factor is applied to the loglikelihoods. Thus, rather than a “standard” likelihood ratio test, we must incorporate these correction factors into the likelihood ratio test statistic (Reference Satorra and BentlerSatorra & Bentler, 2001). If we denote the loglikelihoods of the more restricted and less restricted models $L{L}_0$ and $L{L}_1$ , respectively; the number of parameters in each as $p_0$ and $p_1$ , respectively; and the correction factor for each as $c_0$ and $c_1$ , respectively; we compute the likelihood ratio test statistic as:

$LRT=\frac{-2\left(L{L}_1-L{L}_0\right)}{cd},$(11)

where

$cd=\frac{p_0{c}_0-p_1{c}_1}{p_0-p_1}.$(12)

Note that this correction applies to any loglikelihood calculated using robust maximum likelihood, which we use as a default when estimating nonlinear factor models. Thus, it is our standard approach.

The second major point is a caveat about the potential usefulness of likelihood ratio tests. It has been noted that likelihood ratio tests depend on sample size, with so much statistical power at large sample sizes that even trivial differences between models may be significant (Reference BrannickBrannick, 1995). To get around this issue, some have proposed comparing fit indices commonly used in SEM, between more and less constrained models (Reference Cheung and RensvoldCheung & Rensvold, 2002a). Among others, this includes the comparative fit index (CFI; Reference BentlerBentler, 1990), Tucker–Lewis Index (TLI; Reference Tucker and LewisTucker & Lewis, 1973) and the root mean squared error of approximation (RMSEA; Reference SteigerSteiger, 1998). A researcher might, for instance, note that the CFI values (which takes values between 0 and 1, with values closer to 1 indicating better model fit) are 0.95 and 0.98 for a scalar and metric invariance model, respectively, and favor the model with metric invariance because it improves the CFI substantially. Results from a number of simulation studies have indicated that differences in these fit indices are in many cases more sensitive to noninvariance than likelihood ratio tests (Reference Meade, Johnson and BraddyMeade et al., 2008).

The final major point to note is that likelihood ratio tests (and the fit statistics based on them) are not appropriate for all model testing situations. In particular, the ${\chi }^2$ distribution of likelihood ratio test statistics depends on the less restrictive model being correctly specified (Reference Maydeu-Olivares and CaiMaydeu-Olivares & Cai, 2006; Reference Yuan and BentlerYuan & Bentler, 2004). As such, if neither of the models being compared is the true model, a likelihood ratio test is not suitable for making measurement invariance comparisons (Reference Schneider, Chalmers, Debelak and MerkleSchneider et al., 2020). Another distributional assumption of likelihood ratio tests is that the more restricted model is not on the boundary of the parameter space of the less restricted model. Though a more complete discussion of this phenomenon is available elsewhere (Reference Savalei and KolenikovSavalei & Kolenikov, 2008; Reference Stoel, Garre, Dolan and Van Den WittenboerStoel et al., 2006), one example arises when a researcher is testing whether a variance component is nonzero by comparing a model with the latent variable’s variance set to zero (the restricted model) to one in which this variance is freely estimated. Because all variances must be equal to or greater than zero, the restricted model has fixed the variance to the “boundary” of permissible values such a parameter can take. A more complete and technical presentation of this issue is available at the above-noted references, but researchers should at least be aware that there are some models which cannot be compared (Reference Savalei and KolenikovSavalei & Kolenikov, 2008; Reference Stoel, Garre, Dolan and Van Den WittenboerStoel et al., 2006).

5.3.1 Data Example

We tested the levels of invariance shown in Figure 3 in our example data. Mplus code for fitting all models is available in the Supplemental Materials.

Conducting these tests involved expanding a bit on the series of models shown in Figure 3. First, the classification of measurement invariance shown in Figure 3 does not explicitly refer to measurement invariance in individual thresholds for different categories ( ${\tau }_{kjg}$ ) when using ordinal data. Thus, for models in which intercepts are allowed to vary (i.e., configural and metric invariance) we tested two versions: one in which differences in intercepts were tested, and one in which differences in individual thresholds were tested. We tested models for three grouping variables: child sex (0 = female; 1 = male), parent gender (0 = female; 1 = male), and child age quartile (0 = first quartile; 1 = second quartile; 2 = third quartile; 4 = fourth quartile). Thus, for each of these grouping variables we tested a multiple-group version of the models outlined in Equations 6–8, with the following set of constraints:

1. 1. Configural with thresholds: A model with configural invariance, in which loadings ( ${\lambda }_{mjg}$ ) and individual thresholds ( ${\tau }_{kjg}$ ) are allowed to vary across groups; the intercept parameter ( ${\nu }_{jg}$ ) is constrained to zero in all groups.

2. 2. Configural with intercepts: A model with configural invariance, in which loadings ( ${\lambda }_{mjg}$ ) and intercepts ( ${\nu }_{jg}$ ) are allowed to vary across groups but individual thresholds are not.

3. 3. Metric with thresholds: A model with metric invariance, in which loadings ( ${\lambda }_{mjg}$ ) are constrained to equality across all groups but individual thresholds ( ${\tau }_{kjg}$ ) are allowed to vary across groups; the intercept parameter ( ${\nu }_{jg}$ ) is set to zero in all groups.

4. 4. Metric with intercepts: A model with metric invariance, in which loadings ( ${\lambda }_{mjg}$ ) are constrained to equality across all groups but intercepts ( ${\nu }_{jg}$ ) are allowed to vary across groups.

5. 5. Scalar: A model with scalar invariance, in which loadings ( ${\lambda }_{mjg}$ ), intercepts ( ${\nu }_{jg}$ ), and thresholds ( ${\tau }_{kjg}$ ) are constrained to equality across groups.

Model identification is discussed formally below (“Model identification and anchor items”). However, we note here that each set of models imposed a number of constraints for identification purposes. First, each model in which loadings and/or intercepts were allowed to vary across classes, we used Item 1 as our anchor item. We chose Item 1 on the basis of it appearing to behave similarly across groups in the data visualization step (described in the previous section). However, the importance of anchor items is discussed at greater length below, both by way of a formal definition (“Model identification and anchor items”) and an empirical review of the literature on anchor item selection (“Consequences of measurement noninvariance”). Second, we estimated differences across groups in the latent variable by constraining the latent variable’s mean ${\alpha }_g$ and variance ${\psi }_g^2$ to 0 and 1, respectively, and freely estimating these parameters in other groups.

We conducted likelihood ratio tests comparing each successive level of invariance to the next. For each grouping variable, this entailed four tests: one comparing Models 1 (configural with thresholds) and 3 (metric with thresholds), one comparing Models 2 (configural with intercepts) and 4 (metric with intercepts), one comparing Models 3 (metric with thresholds) and 5 (scalar), and one comparing Models 4 (metric with intercepts) and 5. Note that, as written, models with differences across groups in intercepts (e.g., Models 2 and 4) are not nested within models with differences across groups in individual thresholds (e.g., Models 1 and 3); thus, we do not compare these models in our tables. However, a model with intercept differences can be re-parameterized to show that it is nested within a model with threshold differences; indeed, this is how we parameterize it in the Mplus code in the Supplemental Material. For simplicity’s sake, we do not demonstrate here why this is the case, although it will come up in a few special cases shortly.

Loglikelihoods and model comparisons for each model are shown in Table 4. Note that, due to our use of ordinal response variables with maximum likelihood, we are unable to get the fit indices (e.g., Comparative Fit Index, Tucker–Lewis Index) mentioned earlier. As a reminder, Models 1 and 2 were configural invariance models, allowing between-group differences in loadings and either item thresholds (Model 1) or item intercepts (Model 2); Models 3 and 4 were metric invariance models which constrained Model 1 and 2 respectively by holding loadings equal across groups; and Model 5 was a scalar invariance model which held loadings, intercepts, and thresholds equal across groups.

Table 4 Model fit and model comparisons for all multiple-groups models testing successive levels of invairance in our data example from the Longitudinal Study of Australian Children (LSAC; $N=4,359$ )

	Model fit			Model comparison
Child sex
	$N_{par}$	LL	CF	More restricted model	$\Delta \left(N_{par}\right)$	${\chi }^2$	CF	$p$	Comparison
Model 1	40	− 21627.803	1.140	Model 3	5	5.936	1.191	0.313	Metric vs. configural
Model 2	33	− 21629.616	1.143	Model 4	5	4.859	1.151	0.433	Metric vs. configural
Model 3	35	− 21631.339	1.133	Model 5	12	3.752	1.080	0.988	Scalar vs. metric
Model 4	28	− 21632.437	1.139	Model 5	5	1.782	1.041	0.878	Scalar vs. metric
Model 5	23	− 21633.364	1.161
Parent gender
	$N_{par}$	LL	CF	More restricted model	$\Delta \left(N_{par}\right)$	${\chi }^2$	CF	$p$	Comparison
Model 1	40	− 21292.550	1.166	Model 3	5	8.492	1.198	0.131	Metric vs. configural
Model 2	33	− 21312.932	1.156	Model 4	5	21.914	1.091	$<$ 0.001	Metric vs. configural
Model 3	35	− 21297.636	1.161	Model 5	12	83.609	1.147	$<$ 0.001	Scalar vs. metric
Model 4	28	− 21324.891	1.168	Model 5	5	35.499	1.167	$<$ 0.001	Scalar vs. metric
Model 5	23	− 21345.598	1.168
Child age
	$N_{par}$	LL	CF	More restricted model	$\Delta \left(N_{par}\right)$	${\chi }^2$	CF	$p$	Comparison
Model 1	78	− 24544.744	1.155	Model 3	15	18.047	1.203	0.260	Metric vs. configural
Model 2	57	− 24555.844	1.135	Model 4	15	22.149	1.114	0.104	Metric vs. configural
Model 3	63	− 24555.595	1.144	Model 5	34	52.830	1.107	0.021	Scalar vs. metric
Model 4	44	− 24567.457	1.147	Model 5	15	32.501	1.069	0.006	Scalar vs. metric
Model 5	29	− 24584.835	1.187

Note. $N_{par}$ denotes the number of parameters in a given model; $LL$ denotes the loglikelihood; CF denotes the correction factor; $\Delta \left(N_{par}\right)$ denotes the change in the number of parameters from the more restricted model to the less restricted model.

For child sex, scalar invariance was supported by all model comparisons. In other words, fit was not improved by removing constraints on intercepts (Model 4 vs. Model 5) or thresholds (Model 3 vs. Model 5), nor by removing constraints on factor loadings (Model 1 vs. Model 3; Model 2 vs. Model 4). In other words, we have evidence that Model 5, the simplest model, essentially fits just as well as the more complex models we fit. Thus, Model 5 is the final model; it is shown in Figure 7. In this model, we freely estimate the mean and variance for boys but constrain the mean and variance to 0 and 1 for girls to set the scale of the latent variable. The mean for boys, ${\alpha }_1=-.005$ , is not significantly different from zero, from which we infer that there are no differences in the mean level of parent responsiveness based on child sex.

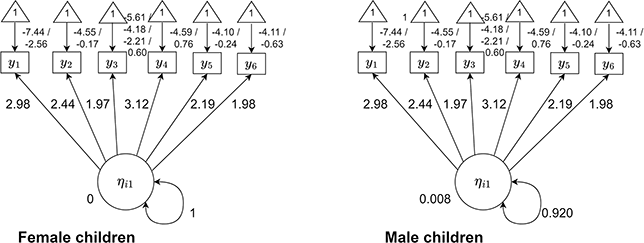
Figure 7 Final multiple-groups model based on child sex in our data example from the Longitudinal Study of Australian Children (LSAC; $N=4,359$ )

Note. No between-group differences in latent variable means and variances were significant at the $\alpha =0.05$ level. Parameter values are given next to the corresponding arrows for loadings, factor means, and factor variances. Item thresholds are given next to the triangle for each item; for instance, the thresholds for endorsing the second and third response options for Item 1 are − 7.44 and − 2.58, respectively, in both groups.

For parent gender a very different story emerges. Here, scalar invariance is not supported in any comparison (Model 3 vs. Model 5 or Model 4 vs. Model 5). Moreover, metric invariance is only supported when we allow thresholds to vary across groups (Model 2 vs. Model 4), not when we only estimate intercept differences (Model 1 vs. Model 3). That is, the nonsignificant LRT comparing Model 2 to Model 4 indicates that allowing thresholds to vary across groups does not improve model fit, whereas the significant LRT comparing Model 1 to Model 3 suggests that allowing intercepts does improve model fit. Taken together, we take these results as a rejection of metric invariance, albeit an equivocal one. Thus, either Model 1 or Model 2 should be our final model. As mentioned earlier, it can be demonstrated that models with between-group differences in thresholds (i.e., Models 1 and 3) can be reparameterized to be nested within models with between-group differences in only intercepts (i.e., Models 2 and 4). Thus, we tested the fit of Model 1 against Model 2, finding that Model 1 fit significantly better, ${\chi }^2\left(7\right)=33.702,p<0.001$ .

Model 1 is, therefore, our final model for parent gender. It is shown in Figure 8. We see that loadings are considerably higher for fathers, relative to mothers, for a number of items. This difference in loadings suggests that these items are more closely related to parental responsiveness among fathers than among mothers. There is less of a consistent pattern among thresholds, with some items (e.g., Item 2) showing lower thresholds (meaning an overall higher likelihood of endorsement) among fathers, and others (e.g., Item 3) showing lower thresholds among mothers. With respect to the latent variable, we see that the mean for fathers is $alph{a}_1=-.818$ and that it is significantly different from zero. We thus conclude that fathers show lower overall levels of responsiveness than mothers.

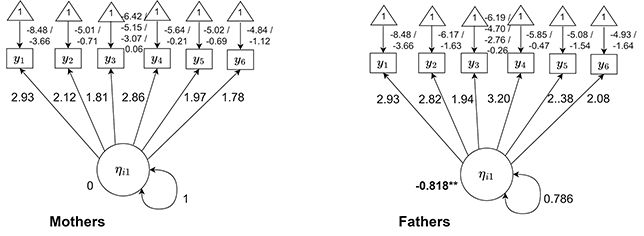
Figure 8 Final multiple-groups model based on parent gender in our data example from the Longitudinal Study of Australian Children (LSAC; $N=4,359$ )

Note. Asterisks denote significant between-group differences in latent variable means. ** $p<0.01$ . * $p<0.05$ . $†p<0.10$ . Parameter values are given next to the corresponding arrows for loadings, factor means, and factor variances. Item thresholds are given next to the triangle for each item; for instance, the thresholds for endorsing the second and third response options for Item 1 are − 8.48 and − 3.66, respectively, in both groups.

Finally, with respect to age grouping, we see that metric invariance is supported by both relevant comparisons (Model 1 vs. Model 3, Model 2 vs. Model 4), and scalar invariance is rejected by both relevant comparisons (Model 3 vs. Model 5, Model 4 vs. Model 5). That is, both sets of LRT’s informing our conclusions about metric invariance were nonsignificant, and both sets of tests informing our conclusions about scalar invariance were significant. Here too, as with parent gender, we are left to interpret either Model 3 or Model 4 – and here too, we can test a reparameterization of Model 4 against Model 3. When we do so, we find that Model 3 does not provide significant improvement in fit over Model 4, ${\chi }^2\left(19\right)=20.8724,p=0.344$ .

Thus, we move forward with Model 4 for age. It is shown in Figure 9. Interestingly, the parameters in Figure 9 give us some insight into the relation between intercept and threshold parameters, as well as why we can reparameterize models with intercept DIF to be nested within those for threshold DIF. Notice that the thresholds differ across age groups, but that they do so uniformly across item categories. For instance, the threshold for choosing the second response option for Item 2 in the youngest quartile, -4.424, is lower than the corresponding threshold in the second-youngest quartile, -4.691. The difference between these groups’ thresholds is -4.424 - (-4.691) = 0.267. That is, the threshold for choosing the second response option is 0.267 units higher in the youngest quartile than in the second-youngest quartile. Now notice these groups’ thresholds for choosing the first response options: -0.024 in the youngest quartile, and -0.291 in the second-youngest quartile. The difference between these two groups’ thresholds is -0.024 - (-0.291) = 0.267. In other words, thresholds for all of the response options for a given item must increase or decrease by the same amount. This formulation is mathematically identical to between-group differences in intercepts.

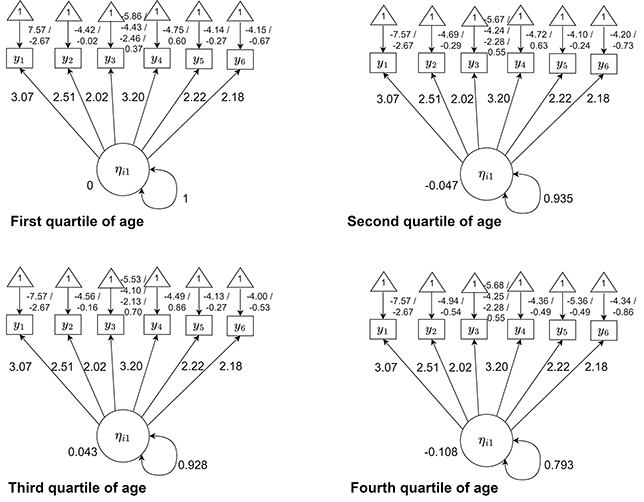
Figure 9 Final multiple-groups model based on child age in our data example from the Longitudinal Study of Australian Children (LSAC; $N=4,359$ )

Note. No between-group differences in latent variable means and variances were significant at the $\alpha =0.05$ level. Parameter values are given next to the corresponding arrows for loadings, factor means, and factor variances. Item thresholds are given next to the triangle for each item; for instance, the thresholds for endorsing the second and third response options for Item 1 are − 7.57 and − 2.67, respectively, in all groups.

Looking at the thresholds, we do not see a clear pattern across ages. Thresholds are generally the lowest in the oldest group, but this pattern is not constant across ages (as thresholds are actually the highest in the second-oldest group). We also see no mean differences across age groups – that is, parents do not show more responsive behavior overall across age groups. Findings like these ones are a great example of why interpreting DIF effects substantively is often a bad idea: there is no particular reason why thresholds should vary in this way (i.e., they do not increase or decrease monotonically across ages), and trying to intuit such a reason is often a fool’s errand that may lead us to an erroneous conclusion. Thus, in a case like this one we would typically include the DIF effects of age on threshold when generating estimates of factor scores, without interpreting what such effects mean. We elaborate on this reasoning below (“Recommendations for best practices”).

Regression-Based Models

Regression-based models take a different approach to modeling between-group differences in parameters, and just about any multiple-groups model can be reparameterized using a regression-based formulation. However, as will be shown momentarily, their real strength is that they can accommodate types of measurement noninvariance/DIF that multiple-groups models cannot. Rather than testing the null hypothesis that parameter values differ between groups, regression-based formulations model parameters as outcomes in a regression equation with group membership – along with any other person-level variable – as a covariate (Reference Bauer and HussongBauer & Hussong, 2009; Reference FinchFinch, 2005).

We start with the formulation of the item response under the nonlinear factor model shown in Equations 2 and 3. As before, ${\lambda }_{jm}$ represents the loading linking the $m^{th}$ factor to the $j^{th}$ item, ${\nu }_j$ represents the intercept of item $j$ , and, if the data are ordinal, ${\tau }_{kj}$ represents the threshold for the $k^{th}$ category for the $j^{th}$ item. We can alter Equation 2 as follows:

${\omega }_{ij}={\nu }_{ij}+\sum _{m=1}^M{\lambda }_{ijm}{\eta }_{im}.$(13)

For ordinal items, we can alter Equation 8 as follows:

${\omega }_{ikj}={\tau }_{ikj}-\left({\nu }_{ij}+\sum _{m=1}^M{\lambda }_{ijm}{\eta }_{im}\right).$(14)

Note that in both cases the only alteration is the addition of the subscript $i$ to the parameters ${\lambda }_{ijm}$ , ${\nu }_{ij}$ , and ${\tau }_{ikj}$ . The addition of this subscript may seem minor, but it represents the crucial modification that defines a regression-based approach: each individual $i$ has their own person-specific value of the measurement parameters. Each of the regression parameters is potentially a function of individual $i$ ’s value on any number of covariates, which can include potentially DIF-generating factors such as age, gender, race, and so on.

Two differences from the multiple-groups approach emerge here. Unlike the multiple-groups approach, these variables may be of any scale; though we could consider group membership as a covariate, we can also consider continuous or ordinal variables. Additionally, we can consider each measurement parameter as a function of multiple covariates at a given time. Note of course that we could combine covariates to create groupings in the multiple-groups approach – for instance, in our data example, we could create a grouping variable that summarizes each combination of child sex, parent gender, and child age quartile. This formulation may be preferable in some cases, such as when we would like to make comparisons across specific levels of these variables (e.g., comparing boys in the first quartile of age to girls in the first quartile of age). However, it would create a large number of groups (in our data example, it would create $2\times 2\times 4=16$ ). One of the approximate methods described below (“Detecting measurement noninvariance”), alignment, is well suited to this case.

We denote the $p^{th}$ covariate for the $i^{th}$ participant $x_{ip}$ , where $P$ refers to the number of covariates $\left(p=1,\dots ,P\right)$ . The regression equation for each of the measurement parameters in Equations 13 and, if relevant, 14 are as follows:

$\begin{array}{c}{\nu }_{ij}={\nu }_{j0}+\sum _{p=1}^P{\nu }_{jp}{x}_{ip},\end{array}$(15)

$\begin{array}{c}{\lambda }_{ijm}={\lambda }_{jm0}+\sum _{p=1}^P{\lambda }_{jmp}{x}_{ip},\end{array}$(16)

$\begin{array}{c}{\tau }_{kij}={\tau }_{kj0}+\sum _{p=1}^P{\tau }_{kjp}{x}_{ip}.\end{array}$(17)

Just as in any regression, there is an intercept to each of these equations. These parameters, denoted ${\nu }_{j0}$ , ${\lambda }_{jm0}$ , and ${\tau }_{jk0}$ represent the predicted values of intercepts, loadings, and thresholds, respectively, when all covariates are equal to 0. The parameters ${\nu }_{jp}$ , ${\lambda }_{jmp}$ , and ${\tau }_{kjp}$ represent the predicted increment in the intercept, loading, and threshold parameters associated with a one-unit increase in covariate $x_{ip}$ .

Just as between-person differences in the measurement parameters can be modeled, so too can between-person differences in the latent variable’s parameters itself – that is, latent variable mean and impact. Specifically, we can think of the mean as a function of covariates as follows:

${\alpha }_{im}={\alpha }_{0m}+\sum _{p=1}^P{\alpha }_{pm}{x}_{ip}.$(18)

Although it may be counterintuitive to think of each individual being characterized by their own mean (which is suggested by the presence of a subscript $i$ for each value of ${\alpha }_{im}$ ), we can instead think of ${\alpha }_{im}$ as the predicted value for individual $i$ on latent variable $m$ , given all their values of the covariates $x_{ip}$ . We typically set ${\alpha }_{0m}$ to 0 for identification. If $x_{ip}$ were a single grouping variable and there were no additional covariates, ${\alpha }_{pm}$ would be equivalent to the difference between groups in means. The difference here is that grouping variables represent just one of the types of covariates we can have. We refer to effects like this one as mean impact, as discussed above (“Differences that do not represent measurement bias”).

Finally, we can also allow the variance of the latent variable to differ over levels of $x_{ip}$ – that is, variance impact. This relation is parameterized in the same way as the other parameters, with one exception: because the variance must always be positive, we apply an exponential function as follows:

${\psi }_{im}^2=\left({\psi }_{0m}+\sum _{p=1}^P{\psi }_{pm}{x}_{ip}\right).$(19)

Because the exponential function yields a positive number in all cases, this alteration allows us to consistently model permissible values of ${\psi }_{im}^2$ . As with ${\alpha }_{0m}$ , we typically set ${\psi }_{0m}$ to zero for identification.

Note that regression-based models offer a major advantage over the multiple-groups formulation: they explicitly allow the incorporation of multiple covariates. Moreover, these covariates may be of any scale; they need not be grouping variables. Thus, in addition to the likelihood ratio test strategy outlined above, we can also simply test the significance of a given parameter. For instance, if there is a significant DIF effect of gender (which, for illustrative purposes, we will say is our first covariate; i.e., $p=1$ ) on the intercept of Item 5, then the parameter ${\nu }_{51}$ will be significant.

A version of this model, the multiple indicator multiple cause (MIMIC; Reference MuthénMuthén, 1989; Reference FinchFinch, 2005) model, introduced as the first major alternative to the multiple-groups formulation. In the MIMIC model, loading DIF (i.e., the equation for ${\lambda }_{ijm}$ ) is not allowed; nor is impact on the latent variable’s variance (i.e., Equation 19). Thus, the MIMIC model generally models only uniform DIF and mean impact, and the model is best applied to cases where only differences in the overall levels of individual items are hypothesized. The full model, with all of the above equations, is typically referred to as moderated nonlinear factor analysis (MNLFA; Reference BauerBauer, 2017; Reference Bauer and HussongBauer & Hussong, 2009). Because this is the most general instance of the model, we will move forward with this parameterization.

5.4.1 Data Example

We fit a series of moderated nonlinear factor analyses to our example data using a specification search approach which is similar to the automated moderated nonlinear factor analysis (aMNLFA) algorithm described in greater detail later on (“Model-based approaches: specification searches”; Reference Gottfredson, Cole and GiordanoGottfredson et al., 2019). In our specification search, we fit one model for each item. In each of these models, all of the other items’ measurement parameters (i.e., ${\lambda }_{ijm}$ , ${\nu }_{ij}$ , and ${\tau }_{ijk}$ if estimated) are assumed noninvariant – that is, no between-participant differences are modeled for these items. For the focal item, the effects of all three covariates (parent gender, child sex, and child age) were modeled simultaneously. Note that, to offset the complexity of adding in multiple variables at once, we did not test between-person differences in thresholds ${\tau }_{ijk}$ here, only differences between intercepts ${\nu }_{ij}$ . As discussed below (“Model identification and anchor items”), a few additional constraints needed to be imposed to ensure model identification. In these models, we estimated each item’s DIF model constraining the mean and variance of the latent variable to 0 and 1, respectively. This approach is not, however, the only identification strategy, as discussed below.

After fitting a series of item-wise models using the approach described above, we tallied all the DIF effects which were significant. We then combined these into a combined model, which contained (1) all of the DIF effects that were significant in the itemwise models, and (2) between-person differences in latent variable means and variances. In this penultimate model, the baseline value of the latent variable mean ( ${\alpha }_0$ ) and variance ( ${\psi }_0)$ were set to zero for identification purposes; the effects of all the covariates (i.e., ${\alpha }_g$ and ${\psi }_g$ for all $g>0$ ) were estimated. Note that we do retain some nonsignificant intercept effects in this model – for each loading we retain the corresponding intercept effect, as is standard to do whenever a loading effect is included. Further note that failing to include an intercept DIF effect in the presence of loading DIF would be much like including an interaction term without the corresponding main effect.

Finally, because the above model combines all the significant effects across items, a number of effects were rendered nonsignificant. Our final model removes any of the effects which were rendered nonsignificant in this penultimate model. Figure 10 shows this final model. When interpreting this figure, note that age was divided by 100 to facilitate model convergence. Because the model contains an exponential parameter (for the variance term), values of age in their original scale (weeks) caused estimation problems. In particular, because the number of weeks could often take the form of a relatively large number (e.g., 60), the parameters associated with this form of age were often small enough (e.g., a 0.0001-unit shift in the variance of parental responsiveness, per week of age) that the covariance matrix of the parameters was difficult for the model to estimate. Dividing age by 100 put it on a similar scale to the other predictors, allowing us to circumvent issues with the parameter covariance matrix.

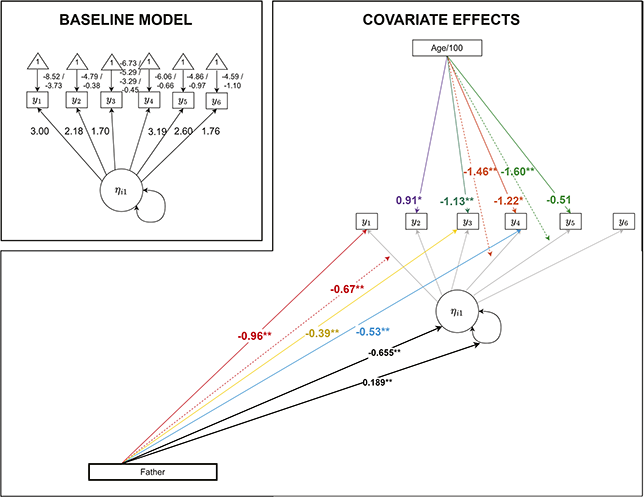
Figure 10 Final moderated nonlinear factor analysis model in our data example from the Longitudinal Study of Australian Children (LSAC; $N=4,359$ )

Note. To simplify presentation, the model is split into two diagrams: the baseline values of parameters, and the covariate effects. In the model for baseline measurement parameters, values of measurement parameters are shown for the case in which all covariates are equal to zero. Item thresholds are given next to the triangle for each item; for instance, the baseline threshold for endorsing the second and third response options for Item 1 is − 8.52 and − 3.73, respectively, in both groups. In the model for covariate effects, all effects for a given covariate-item pair are the same color; for instance, both the intercept and the loading effect for age on item $y_4$ are orange. Loading DIF is shown as a dotted line; intercept DIF is shown as a solid line. Finally, mean and variance impact are shown as bold black arrows. For all parameters, ** $p<0.01$ , * $p<0.05$ , and $†p<0.10$ .

As shown in Figure 10, there were a number of DIF effects on intercepts ${\nu }_{ij}$ . These are represented by arrows pointing from a covariate directly to an item. These effects represent the increment in log-odds in the probability of endorsing one category (i.e., category $k$ ) over the next category down (i.e., category $k-1$ ). For instance, the log-odds of endorsing a higher category (category 3 over category 2; category 2 over category 1) on Item 1 are 0.96 units lower among fathers than mothers. Parent gender shows a similar pattern of negative intercept effects on Items 3 and 4, indicating that fathers are less likely to endorse these items than mothers, even at the same level of responsiveness. Child age showed a less interpretable pattern of intercept effects, with a positive effect on the intercept of Item 2 but negative effects on Item 3; note that some nonsignificant effects of age are included, corresponding to loading effects on the same items.

Figure 10 also shows a number of DIF effects on loadings ${\lambda }_{ij}$ , depicted as arrows pointing to other arrows. They represent the increment in log-odds in the value of ${\lambda }_{ij}$ associated with a one-unit shift in the variable. For instance, the loading for Item 4 decreases by 1.46 units for every 100-week increase in child age (or 0.0146 units for every week increase), indicating a weaker relation between this item and responsive parenting among parents of older children. A similar effect was seen for Item 5, which was also more weakly related to the latent variable among parents of older children. A negative loading effect was seen for parent gender on Item 2, which showed a weaker relation to responsive parenting among fathers than mothers.

Finally, with respect to the latent variable, Figure 10 shows that fathers were both less responsive overall and more variable in their responsiveness than mothers. The lower overall level of responsive parenting among fathers is indicated by the negative mean impact effect. Note that it is challenging to interpret the magnitude of this effect given that the variance impact parameter is also significant; there is no unit in which the coefficient of -0.655 can be placed. Thus, we cannot say that fathers are, for instance, -0.655 standard deviations lower in responsiveness than mothers – we simply know that they are significantly lower. The positive variance effect indicates that fathers showed higher levels of variability in their responsiveness. It represents the increment in log-odds of the variance associated with being a father, relative to being a mother. Following Equation 19, we say that the variance of responsive parenting was 1 in mothers and $e^{0.189}=1.21$ in fathers.

Model Identification and Anchor Items

As noted when we first introduced the common factor model in Equation 1, a number of constraints typically need to be imposed on parameters for a latent variable model to be identified. Ensuring model identification becomes even more complicated when we allow for between-person differences in measurement parameters (i.e., DIF) and latent variable means and variances (i.e., impact).

One possibility is to constrain the latent variable’s mean and variance to 0 and 1 respectively, across all participants. In the multiple-groups formulation, this would be equivalent to setting ${\alpha }_{mg}$ to zero and ${\psi }_{mg}^2$ to 1 for all values of $g$ and $m$ . In a regression-based formulation, it would be equivalent to simply setting ${\alpha }_{im}$ to 0 and ${\psi }_{im}^2$ to 1 for all participants –that is, not estimating any regression effects (i.e., ${\alpha }_{pm}$ or ${\psi }_{pm}$ ) and simply constraining ${\alpha }_{0m}$ and ${\psi }_{0m}^2$ to 0 and 1. The disadvantages of this approach are clear: if there are in fact differences between participants in the means and variances (which, in practice, is often both true and of primary interest), this model will not capture them.

Another possibility is to constrain one item’s loading ${\lambda }_{jm}$ and intercept ${\nu }_j$ to 1 and 0 across all individuals. As with the case of latent variable means and variances discussed above, the parameters associated with this strategy differ between multiple-groups and regression-based approaches. However, in both cases, this is essentially the same as the “reference item” approach in factor analysis more generally, but now it carries an additional implication: this item’s measurement parameters are also assumed to be equal across groups.

Alternatively, there are a number of options which combine the features of these two strategies. One possible approach combines the following two constraints.

1. 1. First, the value of the latent variable’s mean and variance are set to 0 and 1 for some baseline value of a DIF-generating covariate. In the multiple-groups case, the factor means and variances for the reference group, ${\alpha }_{m0}$ and ${\psi }_{m0}^2$ , are set to 0 and 1, and the corresponding values in the other groups are estimated freely. In regression-based approaches, baseline values ${\alpha }_{0m}$ and ${\psi }_{0m}^2$ are set to 0 (with a value of 0 for ${\psi }_{0m}^2$ corresponding to a variance of 1, given the exponential term in Equation 19), while all regression coefficients ${\alpha }_{pm}$ and ${\psi }_{pm}^2,p\ne 0$ are estimated freely. This strategy allows the researcher to estimate impact, while setting a common scale for the latent variable.

2. 2. Second, set one item on which is invariant across levels of each DIF-generating covariate. In multiple-groups models this means that there must be an item whose measurement parameters (including loadings, intercepts, and thresholds, if included) do not vary across groups. In regression-based formulations, this means that, for each covariate $x_{ip}$ , there must be at least one item on which $x_{ip}$ has no DIF effect (loading, intercept, or threshold).

When the above two conditions are met, the multiple-groups and regression-based models are generally identified. This approach is the model identification strategy we have used with the example data in multiple-group formulation discussed earlier in the Element.

Note that, like the reference item strategy mentioned above, this set of constraints does require at least one item to be invariant across all participants. This item is called the anchor item. Though the terms “reference item” and “anchor item” are sometimes used interchangeably, here we will use the former term to refer to any item whose loading and intercept are set to 0 and 1 respectively, and the latter term to refer to any item whose parameters are constrained to equality across participants. In other words, an anchor item’s measurement parameters are estimated freely, with the only requirement being that they do not vary across participants.

A few considerations are important to note. First, recall that all of these different identification strategies result in the same model fit. Neither is “better” than the other; any one of these may be preferable depending on the researcher’s goals and interests. Second, note that a few different constraints must be applied in the case of nonlinear models (see Reference Millsap and Yun-TeinMillsap & Yun-Tein, 2004 for details). For example, if thresholds ${\tau }_{jk}$ are being estimated, all of the thresholds ${\tau }_{jk}$ and intercepts ${\nu }_j$ are not jointly identified, as noted above; at least one threshold, or ${\nu }_j$ , must be set to zero.

Finally, note that in general, unless we set all latent variable parameters to be equal across participants (which, again, is generally an untenable assumption), there must always be at least one anchor item. However, this raises an obvious issue: what happens if the researcher chooses an anchor item (or, if the loading and intercept are set to 0 and 1, reference item) which is actually noninvariant? In the context of specification searches (discussed below: “Model-based methods: specification searches”), there is substantial evidence that choosing an anchor item which is actually noninvariant may cause both type I and type II errors, leading the researcher to erroneously find DIF and miss DIF which is actually present (Reference Cheung and RensvoldCheung & Rensvold, 1999; Reference Meade and WrightMeade & Wright, 2012; Reference Raykov, Marcoulides, Harrison and ZhangRaykov et al., 2020).

Researchers have proposed a number of ways to get around this issue. First, before testing alternate models (as was done in both the data examples above), we could perform a preliminary specification search to find an appropriate anchor item before proceeding to further tests. One proposed solution is an iterative factor ratio testing procedure, which essentially tests every possible combination of anchor and DIF-generating items (Reference Cheung and RensvoldCheung & Rensvold, 1999). Although this strategy is comprehensive, it does become more challenging to find DIF as the number of noninvariant items increases; this is particularly the case if all of the DIF effects are in the same direction (Reference Meade and LautenschlagerMeade & Lautenschlager, 2004; Reference Yoon and MillsapYoon & Millsap, 2007). A less time-consuming and computationally intensive approach is to test itemwise models, as was done in the regression-based modeling example above, and rank items in order of their likelihood ratio test statistic, choosing the one with the smallest value as the anchor item (Reference WoodsWoods, 2009a). These are only a few of the strategies we could use to identify anchor items, and readers are referred to two comprehensive reviews (Reference Kopf, Zeileis and StroblKopf et al., 2015a, Reference Kopf, Zeileis and Strobl2015b) for greater detail. We also discuss a new class of modeling approaches which do not require anchor items below (“Approximate approaches”).

Ramifications for the Interpretations of Between-Groups Comparisons

Within the SEM framework, the question of measurement invariance has historically been framed in terms of the validity of between-group comparisons: at a given level of invariance, what between-group comparisons can be made? Absent configural invariance, no comparisons can be made at all; a lack of configural invariance implies that entirely different constructs are being measured in the two groups. Thus, to attempt to compare the groups in terms of any of the latent variables would be incoherent.

If metric invariance – equivalence across all items in ${\lambda }_{jm}$ – is not satisfied, between-group comparisons in the covariance structure of the latent variable cannot be made. The inability to compare covariance structures between groups means that any inferences about relations among variables – including structural equation model results but also regression coefficients – cannot be compared across groups. Of course, the issue of partial invariance – the idea that some, but not all, measurement parameters may be invariant – complicates this rule.

One argument (Reference Byrne, Shavelson and MuthénByrne et al., 1989) holds that even in the case of some factor loadings being noninvariant, thus causing the researcher to reject the hypothesis of complete metric invariance across all items in $Y$ , some cross-group comparisons may be made as long as noninvariant items are in the minority. The authors, as well as others in later work (Reference Steenkamp and BaumgartnerSteenkamp and Baumgartner, 1998), further argue that if cross-validation work supports the tests’ validity, a lack of metric invariance can often be considered an artifact of the sample.

If scalar invariance – equivalence across groups in ${\nu }_j$ – is not satisfied, between-group comparisons in latent variable means cannot be made (Reference BollenBollen, 1989). This finding was particularly important one in the original context in which measurement invariance analyses were first conducted, because erroneous conclusions of differences between group means (e.g., differences in mean intelligence among members of different races) were often based on findings of differences between groups in mean scores (Reference MillsapMillsap, 1998). In many ways, such conclusions were the raison d’etre of measurement invariance analysis – by showing that a scale lacked scalar invariance, researchers could show that between group means in this scale were a function of differences in item intercepts (i.e., ${\nu }_j$ ) as opposed to differences in the latent variable.

Implicit in these prohibitions on cross-group comparisons are equally stringent prohibitions on cross-group generalization: findings cannot be generalized from one group to another in the absence of measurement invariance. For instance, suppose that a regression links one variable to another in a given group, but the metric invariance assumption is not satisfied for at least one of the variables. Then these regression findings cannot be generalized to the other group.

Ramifications for the Accuracy of Factor Scores

In many applications, the principal goal of applying IRT or factor analysis is to obtain some estimate of a subject’s overall level of the latent variable. Perhaps the most common method is obtaining a sum score for each individual by summing their responses to each item. There are a number of issues associated with sum scores, including their failure to take into account measurement error and implicit assumption that all items load equally onto the factor (Reference McNeish and WolfMcNeish & Wolf, 2020). However, with respect to the question of measurement invariance specifically, one issue becomes obvious: if there is DIF in any item, this DIF will be directly incorporated into the sum score. For instance, suppose that we are working with continuous items, and all but one item, item $j$ , are invariant across groups. For this item the value of ${\nu }_j$ is 1.5 units higher in group 1, relative to group 2. If we create sum scores, these sum scores will be on average 1.5 units higher in group 1 than group 2.

For this and many other reasons, it is preferable to obtain estimates of the latent variable for each participant that incorporate information from the model. These estimates, which we can denote ${\hat{\eta }}_{im}$ , are referred to as $factorscores$ (Grice, 2001). After the latent variable model is estimated, the parameters are then used to generate estimates of ${\hat{\eta }}_{im}$ , which can then be used in subsequent analyses. Importantly, while it may intuitively seem as though there is only one possible value for each person which fits in the model laid out above, in actuality there are an infinite number of sets of ${\eta }_{im}$ values for all $N$ participants which work in a given model. Accordingly, there are many ways in which to calculate factor scores ${\hat{\eta }}_{im}$ . While a full review of factor score calculation methods is beyond the scope of this Element, we note that modal a posteriori (MAP), expected a posteriori (EAP), and plausible value-based scores are three common types of scores arising from the IRT literature (Reference Fischer and RoseFischer & Rose, 2019; Reference Muraki and Engelhard JrMuraki & Engelhard Jr, 1985). There are a number of equivalencies between these methods of calculating factor scores and methods arising from the factor analysis literature which work with continuous indicators, such as Bartlett scores and regression factor scores (Reference DiStefano, Zhu and MindrilaDiStefano et al., 2009; Reference Skrondal and LaakeSkrondal & Laake, 2001), but we do not review them here.

Because estimates of ${\hat{\eta }}_{im}$ are obtained from estimates of the parameters, it stands to reason that bias in the parameters will lead to biases in factor scores. As discussed earlier, strict invariance is often untenable in practice – but in the case of continuous items, it is theoretically necessary if we want to obtain completely unbiased estimates of ${\hat{\eta }}_{im}$ (Reference MillsapMillsap, 1997, Reference Millsap1998). In practice, however, the effects of measurement noninvariance/DIF on factor scores are much less certain than this.

Empirical Findings: Does DIF Actually Matter?

We can make a variety of predictions about the consequences of DIF, based on the known mathematical relations among different model parameters as discussed above. However, even though it is in theory a mathematically demonstrable fact that, for instance, higher values of ${\nu }_j$ in one group will lead to overestimated values of the latent variable means in that group, the actual consequences in real data are unknown. Thus, a large and growing body of research focuses on establishing whether and to what extent DIF biases estimates of between-group differences, as well as scores on the latent variable itself.

With respect to differences between groups, it has been demonstrated that differences across groups in factor loadings and intercepts may indeed lead to erroneous findings of between-group differences in means and covariance structures (Reference ChenChen, 2007; Reference French and FinchFrench & Finch, 2006; Reference MillsapMillsap, 1997). As we might expect, such differences are generally in proportion to the magnitude of the DIF observed, in terms of both the proportion of items with DIF and the size of the DIF effects themselves. Additionally, in the case of multiple groups, sample size differences can lead to less severe bias in the larger group and more severe bias in the smaller group (Reference ChenChen, 2008; Reference Millsap and KwokMillsap & Kwok, 2004). However, it is critical to note that such biases are generally observed only in cases in which the estimated model does not account for DIF. That is to say, when models which model partial noninvariance such as the multiple groups and regression-based models shown above are fit, and the DIF effects which are truly present are accounted for by the model, estimates of differences between groups in latent variable means, variances, and covariances are generally unbiased (Reference French and FinchFrench & Finch, 2006; Reference Millsap and KwokMillsap & Kwok, 2004).

Although it is clear that sum scores for each individual will not be correct in the presence of measurement noninvariance, the magnitude of the issues caused by sum scores in subsequent analyses is more difficult to quantify, as the accuracy of any score must be considered relative to the context in which it is being used (Reference Millsap and KwokMillsap & Kwok, 2004). Selection represents one context in which sum scores arising from noninvariant items can cause a substantial problem. That is, when researchers create sum scores and use some cut point as a selection criterion, the sensitivity and specificity of such criteria may be reduced substantially by measurement noninvariance (Reference Lai, Liu and TseLai et al., 2021; Reference Lai and ZhangLai et al., 2022; Reference Millsap and KwokMillsap & Kwok, 2004). Additionally, when sum scores are used in mean comparisons, Type I error rates (e.g., of $t$ -tests) are inflated in the presence of noninvariance (Reference Li and ZumboLi & Zumbo, 2009). This bias has been shown to be more pronounced if intercepts are noninvariant, relative to loadings (Reference SteinmetzSteinmetz, 2013).

Findings are considerably more complicated when it comes to the accuracy of individual factor scores, ${\hat{\eta }}_{im}$ . A growing body of research investigates this question by simulating data with DIF, fitting a model which fails to account for DIF or accounts for it incompletely, and examining the relation between the true and estimated values of the latent variable for each participant. Under some circumstances, failing to model DIF may be problematic. With binary items, simulation work has shown that failing to account for DIF in estimating factor scores could yield biased estimates of the relations between these factor scores and covariates in subsequent analyses (Reference Curran, Cole, Bauer, Rothenberg and HussongCurran et al., 2018). However, misspecifying the nature of DIF in the model which is used to estimate factor scores may be less of a problem – in other words, as long as some covariate effects on items are estimated, it is not always critical to get the location of these effects correct. Evidence for this is provided by simulation studies which find correlations in excess of $r=0.9$ between factor scores from misspecified models and their true values (Reference Chalmers, Counsell and FloraChalmers et al., 2016; Reference Curran, Cole, Bauer, Hussong and GottfredsonCurran et al., 2016). Additionally, some work using empirical data has shown that models which specify different DIF effects often yield factor scores which are very similar (Reference Cole, Hussong, Gottfredson, Bauer and CurranCole et al., 2022). However, as noted above, the context in which factor scores are to be used is critical. In some high-stakes settings such as state and federal educational testing, two sets of factor scores which are correlated at $r=0.95$ are not sufficiently similar to be interchangeable.

Organization of This Section

As noted above, the majority of this section will focus on three broad groupings of DIF detection strategies: premodel approaches, specification searches, and approximate invariance methods. We will also briefly discuss effect size measures as a supplement to DIF detection procedures. At the end of each section we will review the evidence for all the different subtypes of each method and provide recommendations. All methods are summarized in Table 5, to which we will refer throughout each section. Finally, many of these methods were developed for cases in which there is only one latent variable, and are sufficiently computationally intensive that they are often not run on multiple latent variables at once. Thus, we will consider only the univariate case throughout the section, revisiting the case of multiple latent variables at the end of the section. Thus, the subscript $m$ , which had previously been used to index latent variables, will be dropped.

Pre-estimation Approaches

There are a number of testing procedures for finding DIF which do not depend on the estimation of a model itself. That is, given only participants’ observed responses, we can calculate a number of effect size indices, and in some cases conduct inferential tests, which give insight into whether and where DIF may be present. We refer to these as pre-estimation approaches. In general, they use a proxy for the latent variable ${\eta }_i$ to assess each item for DIF in advance of running the model. The methods we will review are summarized in the top few rows of Table 5.

If pre-estimation approaches have not yet estimated a model for ${\eta }_i$ , how are they able to detect DIF or determine whether the scale measuring ${\eta }_i$ is invariant? Most of these tests instead work with a sum-score of items, $S_i$ . The basic premise of a sum score test for DIF is that $S_i$ may serve as a proxy for ${\eta }_i$ and the relation between $S_i$ and an item $y_{ij}$ should be invariant across groups – i.e., $P(y_{ij}|S_i,g)=P\left(y_{ij}|S_i\right)$ .