Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rhaly, H. C.
2017.
Corrigendum to “Generalized Cesàro Matrices”.
Canadian Mathematical Bulletin,
Vol. 60,
Issue. 1,
p.
196.
Curbera, Guillermo P.
and
Ricker, Werner J.
2022.
Fine spectra and compactness of generalized Cesàro operators in Banach lattices in CN0.
Journal of Mathematical Analysis and Applications,
Vol. 507,
Issue. 2,
p.
125824.
Albanese, Angela A.
Bonet, José
and
Ricker, Werner J.
2023.
Spectral properties of generalized Cesàro operators in sequence spaces.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 117,
Issue. 4,
Albanese, Angela A.
Bonet, José
and
Ricker, Werner J.
2024.
Generalized Cesàro operators in weighted Banach spaces of analytic functions with sup-norms.
Collectanea Mathematica,
Albanese, Angela A.
and
Asensio, Vicente
2024.
Spectra and dynamics of generalized Cesàro operators in (LF) and (PLB) sequence spaces.
Positivity,
Vol. 28,
Issue. 3,
Albanese, Angela A.
Bonet, José
and
Ricker, Werner J.
2025.
Generalized Cesàro operators in the disc algebra and in Hardy spaces.
Advances in Operator Theory,
Vol. 10,
Issue. 1,
Albanese, Angela A.
Bonet, José
and
Ricker, Werner J.
2025.
Mean ergodic and related properties of generalized Cesàro operators in BK-sequence spaces.
Monatshefte für Mathematik,
Vol. 206,
Issue. 1,
p.
1.
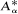 is the operator formally defined on the Hardy space H2 by
is the operator formally defined on the Hardy space H2 by