We define and develop two-level type theory (2LTT), a version of Martin-Löf type theory which combines two different type theories. We refer to them as the ‘inner’ and the ‘outer’ type theory. In our case of interest, the inner theory is homotopy type theory (HoTT) which may include univalent universes and higher inductive types. The outer theory is a traditional form of type theory validating uniqueness of identity proofs (UIP). One point of view on it is as internalised meta-theory of the inner type theory. There are two motivations for 2LTT. Firstly, there are certain results about HoTT which are of meta-theoretic nature, such as the statement that semisimplicial types up to level n can be constructed in HoTT for any externally fixed natural number n. Such results cannot be expressed in HoTT itself, but they can be formalised and proved in 2LTT, where n will be a variable in the outer theory. This point of view is inspired by observations about conservativity of presheaf models. Secondly, 2LTT is a framework which is suitable for formulating additional axioms that one might want to add to HoTT. This idea is heavily inspired by Voevodsky’s Homotopy Type System (HTS), which constitutes one specific instance of a 2LTT. HTS has an axiom ensuring that the type of natural numbers behaves like the external natural numbers, which allows the construction of a universe of semisimplicial types. In 2LTT, this axiom can be assumed by postulating that the inner and outer natural numbers types are isomorphic. After defining 2LTT, we set up a collection of tools with the goal of making 2LTT a convenient language for future developments. As a first such application, we develop the theory of Reedy fibrant diagrams in the style of Shulman. Continuing this line of thought, we suggest a definition of 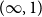 $(\infty,1)$-category and give some examples.
$(\infty,1)$-category and give some examples.