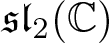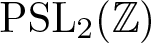1. Introduction
Automorphic Lie algebras are a class of infinite-dimensional Lie algebras over the complex field ![]() $\mathbb{C}$ that emerged in the context of mathematical physics and more precisely in the context of integrable systems [Reference Lombardo19–Reference Lombardo and Mikhailov21]. They originated in the study of algebraic reduction of Lax pairs by Lombardo and Mikhailov [Reference Lombardo19, Reference Lombardo and Mikhailov20], related to the notion of reduction groups, proposed by Mikhailov in [Reference Mikhailov23] and [Reference Mikhailov24]. The first appearance of a notion of automorphic Lie algebras is to be found in the PhD thesis by Lombardo, and subsequently in Lombardo and Mikhailov [Reference Lombardo and Mikhailov21], where a systematic study of these algebras within the theory of integrability began. It then developed independently from this approach into the search and the description of invariant algebras, with contributions by Lombardo and Sanders and later also Knibbeler [Reference Knibbeler, Lombardo and Sanders3, Reference Knibbeler, Lombardo and Sanders4, Reference Knibbeler18, Reference Lombardo and Sanders22]. The subject of automorphic Lie algebras inspired recent research into group theory, by the authors [Reference Knibbeler, Lombardo and Oelen1]. Independently, equivariant map algebras were introduced and studied by representation theorists Neher, Savage and Senesi [Reference Neher, Savage and Senesi6] in order to unify many Lie algebras that appear in mathematical physics. These included automorphic Lie algebras, although they were unaware of this at the time.
$\mathbb{C}$ that emerged in the context of mathematical physics and more precisely in the context of integrable systems [Reference Lombardo19–Reference Lombardo and Mikhailov21]. They originated in the study of algebraic reduction of Lax pairs by Lombardo and Mikhailov [Reference Lombardo19, Reference Lombardo and Mikhailov20], related to the notion of reduction groups, proposed by Mikhailov in [Reference Mikhailov23] and [Reference Mikhailov24]. The first appearance of a notion of automorphic Lie algebras is to be found in the PhD thesis by Lombardo, and subsequently in Lombardo and Mikhailov [Reference Lombardo and Mikhailov21], where a systematic study of these algebras within the theory of integrability began. It then developed independently from this approach into the search and the description of invariant algebras, with contributions by Lombardo and Sanders and later also Knibbeler [Reference Knibbeler, Lombardo and Sanders3, Reference Knibbeler, Lombardo and Sanders4, Reference Knibbeler18, Reference Lombardo and Sanders22]. The subject of automorphic Lie algebras inspired recent research into group theory, by the authors [Reference Knibbeler, Lombardo and Oelen1]. Independently, equivariant map algebras were introduced and studied by representation theorists Neher, Savage and Senesi [Reference Neher, Savage and Senesi6] in order to unify many Lie algebras that appear in mathematical physics. These included automorphic Lie algebras, although they were unaware of this at the time.
While a precise definition will be given in § 2, for now, the reader should think of automorphic Lie algebras as Lie algebras of meromorphic maps (usually with prescribed poles) from a compact Riemann surface X, originally the Riemann sphere, into a finite-dimensional Lie algebra ![]() $\mathfrak{g}$, which are equivariant with respect to a finite group Γ acting on X and on
$\mathfrak{g}$, which are equivariant with respect to a finite group Γ acting on X and on ![]() $\mathfrak{g}$, both by automorphisms. It is therefore not surprising that the study of these objects requires notions from algebra, geometry and analysis. The group Γ plays the role of the reduction group in the context of integrable systems. In this paper, we refer to Γ as the symmetry group of an automorphic Lie algebra.
$\mathfrak{g}$, both by automorphisms. It is therefore not surprising that the study of these objects requires notions from algebra, geometry and analysis. The group Γ plays the role of the reduction group in the context of integrable systems. In this paper, we refer to Γ as the symmetry group of an automorphic Lie algebra.
Considerable work on automorphic Lie algebras based on the Riemann sphere has been carried out in the past decades. More recently, other Riemann surfaces have been investigated in [Reference Duffield, Knibbeler and Lombardo10], where the foundations of a representation theory for automorphic Lie algebras have been developed. Automorphic Lie algebras in the context of modular forms have been investigated in [Reference Knibbeler, Lombardo and Veselov5]. In [Reference Duffield, Knibbeler and Lombardo10], the authors find a local description of automorphic Lie algebras in the vicinity of a point on the compact Riemann surface. That is, the quotient of an automorphic Lie algebra obtained by truncating a local parameter is determined. However, it remains an open problem to have a global description of such Lie algebras on surfaces of positive genus, as we have for the Riemann sphere. First steps in this direction can be found in [Reference Oelen26].
This paper develops those concepts further and presents a first classification in the case where X is a genus 1 Riemann surface and when ![]() ${\mathfrak{g}}=\mathfrak{sl}_2({\mathbb{C}})$; we will refer to
${\mathfrak{g}}=\mathfrak{sl}_2({\mathbb{C}})$; we will refer to ![]() ${\mathfrak{g}}$ as the base Lie algebra. We will exclusively work over the complex numbers, for which reason we use the notation
${\mathfrak{g}}$ as the base Lie algebra. We will exclusively work over the complex numbers, for which reason we use the notation ![]() $\mathfrak{sl}_2:=\mathfrak{sl}_2({\mathbb{C}})$.
$\mathfrak{sl}_2:=\mathfrak{sl}_2({\mathbb{C}})$.
To give a flavour of automorphic Lie algebras to a newcomer, let us start with a classic example. Consider a simple complex, finite-dimensional Lie algebra ![]() $\mathfrak{g}$ and let σ be an automorphism of order N of
$\mathfrak{g}$ and let σ be an automorphism of order N of ![]() $\mathfrak{g}$. Consider the space of Laurent polynomial maps
$\mathfrak{g}$. Consider the space of Laurent polynomial maps ![]() $f:\mathbb{C}^* \rightarrow \mathfrak{g}$ which satisfy
$f:\mathbb{C}^* \rightarrow \mathfrak{g}$ which satisfy ![]() $f(\epsilon z)=\sigma f(z),$ where
$f(\epsilon z)=\sigma f(z),$ where ![]() $\epsilon^N=1.$ Endow this space with the pointwise Lie bracket. This is an example of an automorphic Lie algebra with base Lie algebra
$\epsilon^N=1.$ Endow this space with the pointwise Lie bracket. This is an example of an automorphic Lie algebra with base Lie algebra ![]() $\mathfrak{g}$, and where the Riemann surface X is the Riemann sphere
$\mathfrak{g}$, and where the Riemann surface X is the Riemann sphere ![]() $\mathbb{C}_{\infty}$. The space of meromorphic functions on
$\mathbb{C}_{\infty}$. The space of meromorphic functions on ![]() $\mathbb{C}_{\infty}$ which are holomorphic outside
$\mathbb{C}_{\infty}$ which are holomorphic outside ![]() $\{0,\infty\}$ is given by the space of Laurent polynomials
$\{0,\infty\}$ is given by the space of Laurent polynomials ![]() $\mathbb{C}[z,z^{-1}]$. The group here is CN which acts on
$\mathbb{C}[z,z^{-1}]$. The group here is CN which acts on ![]() $\mathbb{C}_{\infty}$ as
$\mathbb{C}_{\infty}$ as ![]() $z\mapsto \epsilon z$ and on
$z\mapsto \epsilon z$ and on ![]() $\mathfrak{g}$ by the automorphism σ, such that the equivariance condition reads
$\mathfrak{g}$ by the automorphism σ, such that the equivariance condition reads ![]() $f(\epsilon z)=\sigma f(z)$. It is called a twisted loop algebra and is probably best known for the role it plays in the construction of affine Kac–Moody algebras [Reference Kac15]. Automorphic Lie algebras are natural generalisations of this type of algebra, in the sense illustrated below.
$f(\epsilon z)=\sigma f(z)$. It is called a twisted loop algebra and is probably best known for the role it plays in the construction of affine Kac–Moody algebras [Reference Kac15]. Automorphic Lie algebras are natural generalisations of this type of algebra, in the sense illustrated below.
As was recognised only relatively recently [Reference Roan30], another important example of an automorphic Lie algebra can be traced back to the chemistry Nobel Prize winner, Lars Onsager, in his pioneering paper [Reference Onsager27] on the exact solution of the planar Ising model. This is not a loop algebra and is now known as the Onsager algebra. It can be defined as the Lie algebra ![]() $\mathfrak{O}$ with complex basis Ak and Gm where
$\mathfrak{O}$ with complex basis Ak and Gm where ![]() $k\in {\mathbb{Z}}$ and
$k\in {\mathbb{Z}}$ and ![]() $m\in \mathbb{N}.$ The brackets are given by
$m\in \mathbb{N}.$ The brackets are given by
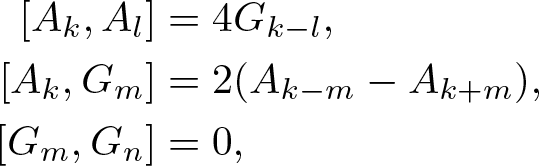 \begin{align*}
[A_k,A_l]&=4G_{k-l},\\
[A_k,G_m]&=2(A_{k-m}-A_{k+m}),\\
[G_m,G_n]&=0,
\end{align*}
\begin{align*}
[A_k,A_l]&=4G_{k-l},\\
[A_k,G_m]&=2(A_{k-m}-A_{k+m}),\\
[G_m,G_n]&=0,
\end{align*} with ![]() $G_{-m}= -G_m$
$G_{-m}= -G_m$ ![]() $(m \gt 0)$ and
$(m \gt 0)$ and ![]() $G_0=0$. Onsager’s work on the 2D Ising model was later simplified using different techniques, cf. [Reference Kaufman and Onsager16], in which there was no appearance of the Onsager algebra. This caused the Onsager algebra to be less studied until the early 1980s, when it began to appear in different contexts and in a different form. In a paper by Grady, [Reference Dolan and Grady9] relations (the Dolan–Grady relations) between two nonlinear operators were found which guarantee the existence of infinitely many commuting charges. The Dolan–Grady relations were later found by Perk in [Reference Perk28] to be connected to the Onsager algebra. For a concise overview, we refer to El-Chaâr [Reference El-Chaâr11].
$G_0=0$. Onsager’s work on the 2D Ising model was later simplified using different techniques, cf. [Reference Kaufman and Onsager16], in which there was no appearance of the Onsager algebra. This caused the Onsager algebra to be less studied until the early 1980s, when it began to appear in different contexts and in a different form. In a paper by Grady, [Reference Dolan and Grady9] relations (the Dolan–Grady relations) between two nonlinear operators were found which guarantee the existence of infinitely many commuting charges. The Dolan–Grady relations were later found by Perk in [Reference Perk28] to be connected to the Onsager algebra. For a concise overview, we refer to El-Chaâr [Reference El-Chaâr11].
In [Reference Knibbeler, Lombardo and Veselov5, Theorem 2.5], it is proven that the Onsager algebra ![]() $\mathfrak{O}$ is isomorphic to the Lie algebra
$\mathfrak{O}$ is isomorphic to the Lie algebra ![]() $\mathfrak{A}={\mathbb{C}}\langle h,e,f\rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[x]$ with the Lie structure that is linear over polynomials in the indeterminate x and
$\mathfrak{A}={\mathbb{C}}\langle h,e,f\rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[x]$ with the Lie structure that is linear over polynomials in the indeterminate x and
This is the form we will encounter when proving that certain automorphic Lie algebras are isomorphic to the Onsager algebra.
The main result of this work is a classification of automorphic Lie algebras on complex tori and the construction of certain normal forms. We will present our classification theorem here and leave the construction of the normal forms, proving our classification theorem, for the main body of the paper.
Besides the Onsager algebra described above, we find two families of Lie algebras parametrised by the (open) modular curve. We denote these families by ![]() $\mathfrak{C}_{\tau}$ and
$\mathfrak{C}_{\tau}$ and ![]() $\mathfrak{S}_{\tau}$ and present them in terms of the traditional elliptic invariants g 2 and g 3 defined as
$\mathfrak{S}_{\tau}$ and present them in terms of the traditional elliptic invariants g 2 and g 3 defined as
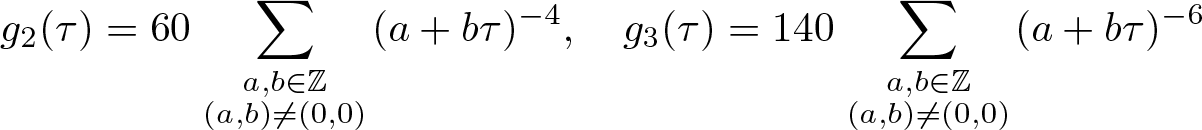 \begin{equation*}g_2(\tau)=60\sum_{a,b\in\mathbb{Z} \atop {(a,b)\ne (0,0)}}(a+b\tau)^{-4},\quad g_3(\tau)=140\sum_{a,b\in\mathbb{Z} \atop {(a,b)\ne (0,0)}}(a+b\tau)^{-6}\end{equation*}
\begin{equation*}g_2(\tau)=60\sum_{a,b\in\mathbb{Z} \atop {(a,b)\ne (0,0)}}(a+b\tau)^{-4},\quad g_3(\tau)=140\sum_{a,b\in\mathbb{Z} \atop {(a,b)\ne (0,0)}}(a+b\tau)^{-6}\end{equation*}where τ is an element of the upper half plane
The Lie algebra ![]() $\mathfrak{C}_{\tau}$ is the current algebra
$\mathfrak{C}_{\tau}$ is the current algebra
where, as usual, the Lie bracket is defined by extending the bracket of ![]() $\mathfrak{sl}_2$ linearly over the polynomials in x and y. The second family is defined by
$\mathfrak{sl}_2$ linearly over the polynomials in x and y. The second family is defined by
where we identify X with ![]() $X\otimes 1$ for
$X\otimes 1$ for ![]() $X=E,F,H$, with the Lie structure that is linear over polynomials in x and satisfies
$X=E,F,H$, with the Lie structure that is linear over polynomials in x and satisfies
The elliptic invariants g 2 and g 3 are usually defined for any lattice ![]() $\Lambda$ in
$\Lambda$ in ![]() $\mathbb{C}$ and we could define families of Lie algebras
$\mathbb{C}$ and we could define families of Lie algebras ![]() $\mathfrak{C}_{\Lambda}$ and
$\mathfrak{C}_{\Lambda}$ and ![]() $\mathfrak{S}_{\Lambda}$ accordingly, but this does not produce any new Lie algebras: homothetic lattices produce isomorphic Lie algebras. Indeed, using the fact that
$\mathfrak{S}_{\Lambda}$ accordingly, but this does not produce any new Lie algebras: homothetic lattices produce isomorphic Lie algebras. Indeed, using the fact that ![]() $g_2(\alpha \Lambda)=\alpha^{-4}g_2(\Lambda)$ and
$g_2(\alpha \Lambda)=\alpha^{-4}g_2(\Lambda)$ and ![]() $g_3(\alpha \Lambda)=\alpha^{-6}g_3(\Lambda)$ for any non-zero complex number α, we can check that the linear extension of
$g_3(\alpha \Lambda)=\alpha^{-6}g_3(\Lambda)$ for any non-zero complex number α, we can check that the linear extension of
descends to an isomorphism from ![]() $\mathfrak{C}_{\Lambda}$ to
$\mathfrak{C}_{\Lambda}$ to ![]() $\mathfrak{C}_{\alpha\Lambda}$. Likewise, we can define an isomorphism from
$\mathfrak{C}_{\alpha\Lambda}$. Likewise, we can define an isomorphism from ![]() $\mathfrak{S}_{\Lambda}$ to
$\mathfrak{S}_{\Lambda}$ to ![]() $\mathfrak{S}_{\alpha\Lambda}$ with the assignments
$\mathfrak{S}_{\alpha\Lambda}$ with the assignments
Hence we can assume that the lattice ![]() $\Lambda$ is scaled to the canonical form
$\Lambda$ is scaled to the canonical form ![]() $\mathbb{Z}\oplus \mathbb{Z}\tau$ for
$\mathbb{Z}\oplus \mathbb{Z}\tau$ for ![]() $\tau\in\mathbb{H}$ if we are only concerned with isomorphism classes of Lie algebras.
$\tau\in\mathbb{H}$ if we are only concerned with isomorphism classes of Lie algebras.
If τ is replaced by  $\tau'=\frac{a\tau+b}{c\tau+d}$ for
$\tau'=\frac{a\tau+b}{c\tau+d}$ for ![]() $a,b,c,d\in\mathbb{Z}$,
$a,b,c,d\in\mathbb{Z}$, ![]() $ad-bc=1$ we arrive at isomorphic Lie algebras again. Indeed,
$ad-bc=1$ we arrive at isomorphic Lie algebras again. Indeed, ![]() $\mathbb{Z}\oplus \mathbb{Z}\tau'=(c+d\tau)^{-1}\left(\mathbb{Z}\oplus \mathbb{Z}\tau\right)$, and we have just shown that homothetic lattices produce isomorphic Lie algebras. Thus, we only need to consider equivalence classes
$\mathbb{Z}\oplus \mathbb{Z}\tau'=(c+d\tau)^{-1}\left(\mathbb{Z}\oplus \mathbb{Z}\tau\right)$, and we have just shown that homothetic lattices produce isomorphic Lie algebras. Thus, we only need to consider equivalence classes ![]() $[\tau]$ in the modular curve
$[\tau]$ in the modular curve ![]() $\mathrm{SL}_2(\mathbb{Z})\backslash\mathbb{H}$ if we are interested in
$\mathrm{SL}_2(\mathbb{Z})\backslash\mathbb{H}$ if we are interested in ![]() $\mathfrak{C}_{\tau}$ and
$\mathfrak{C}_{\tau}$ and ![]() $\mathfrak{S}_{\tau}$ up to isomorphism, and we will occasionally write
$\mathfrak{S}_{\tau}$ up to isomorphism, and we will occasionally write ![]() $\mathfrak{C}_{[\tau]}$ and
$\mathfrak{C}_{[\tau]}$ and ![]() $\mathfrak{S}_{[\tau]}$ accordingly.
$\mathfrak{S}_{[\tau]}$ accordingly.
We know, in fact, that ![]() $\mathfrak{C}_{\tau}\cong \mathfrak{C}_{\tau'}$ if and only if
$\mathfrak{C}_{\tau}\cong \mathfrak{C}_{\tau'}$ if and only if ![]() $[\tau]=[\tau']$ due to Fialowski and Schlichenmaier. In [Reference Fialowski and Schlichenmaier12, Proposition 4.7], they show that if
$[\tau]=[\tau']$ due to Fialowski and Schlichenmaier. In [Reference Fialowski and Schlichenmaier12, Proposition 4.7], they show that if ![]() ${\mathfrak{g}}$ is a semisimple finite-dimensional Lie algebra,
${\mathfrak{g}}$ is a semisimple finite-dimensional Lie algebra, ![]() $\mathcal{A}$ and
$\mathcal{A}$ and ![]() $\mathcal{B}$ two associative, commutative algebras (with units) and if the current algebras
$\mathcal{B}$ two associative, commutative algebras (with units) and if the current algebras ![]() ${\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{A}$ and
${\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{A}$ and ![]() ${\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{B}$ are isomorphic as Lie algebras, then
${\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{B}$ are isomorphic as Lie algebras, then ![]() $\mathcal{A}$ and
$\mathcal{A}$ and ![]() $\mathcal{B}$ are isomorphic as associative algebras. Write
$\mathcal{B}$ are isomorphic as associative algebras. Write ![]() $\mathcal{A}_{\tau}={\mathbb{C}}[x,y]/(y^2-4x^3+g_2(\tau)x+g_3(\tau))$. From algebraic geometry, cf. [Reference Hartshorne14, Corollary 3.7], we learn that
$\mathcal{A}_{\tau}={\mathbb{C}}[x,y]/(y^2-4x^3+g_2(\tau)x+g_3(\tau))$. From algebraic geometry, cf. [Reference Hartshorne14, Corollary 3.7], we learn that ![]() $\mathcal{A}_{\tau}\cong \mathcal{A}_{\tau'}$ implies
$\mathcal{A}_{\tau}\cong \mathcal{A}_{\tau'}$ implies ![]() $[\tau]=[\tau']$ and hence
$[\tau]=[\tau']$ and hence ![]() $\mathfrak{C}_{\tau}\cong \mathfrak{C}_{\tau'}$ implies
$\mathfrak{C}_{\tau}\cong \mathfrak{C}_{\tau'}$ implies ![]() $[\tau]=[\tau']$. It is not known to the authors whether
$[\tau]=[\tau']$. It is not known to the authors whether ![]() $\mathfrak{S}_{[\tau]}\cong \mathfrak{S}_{[\tau']}$ implies
$\mathfrak{S}_{[\tau]}\cong \mathfrak{S}_{[\tau']}$ implies ![]() $[\tau]=[\tau']$.
$[\tau]=[\tau']$.
Now that we know the Lie algebras ![]() $\mathfrak{C}_{\tau},\,\mathfrak{O}$ and
$\mathfrak{C}_{\tau},\,\mathfrak{O}$ and ![]() $\mathfrak{S}_{\tau}$ we can present our classification result.
$\mathfrak{S}_{\tau}$ we can present our classification result.
Theorem 1. Let Γ be a finite group acting faithfully on a complex torus T with biholomorphic maps and also faithfully on ![]() $\mathfrak{sl}_2$ with Lie algebra isomorphisms. Let
$\mathfrak{sl}_2$ with Lie algebra isomorphisms. Let ![]() $\mathbb{T}$ be the torus minus the orbit
$\mathbb{T}$ be the torus minus the orbit ![]() $\Gamma\cdot \{0\}$, and let
$\Gamma\cdot \{0\}$, and let ![]() $\mathbb{T}\rightarrow \mathbb{T}/\Gamma$ be the canonical projection onto the quotient Riemann surface. The isomorphism class of the automorphic Lie algebra consisting of Γ-equivariant holomorphic maps
$\mathbb{T}\rightarrow \mathbb{T}/\Gamma$ be the canonical projection onto the quotient Riemann surface. The isomorphism class of the automorphic Lie algebra consisting of Γ-equivariant holomorphic maps ![]() $\mathbb{T}\to\mathfrak{sl}_2$, meromorphic at the punctures
$\mathbb{T}\to\mathfrak{sl}_2$, meromorphic at the punctures ![]() $\Gamma\cdot \{0\}$, is determined by the number of branch points of
$\Gamma\cdot \{0\}$, is determined by the number of branch points of ![]() $\mathbb{T}\rightarrow \mathbb{T}/\Gamma$ as in Table 1. No other number of branch points occur.
$\mathbb{T}\rightarrow \mathbb{T}/\Gamma$ as in Table 1. No other number of branch points occur.
The class ![]() $[\tau]$ in this table is the element of
$[\tau]$ in this table is the element of ![]() $\mathrm{SL}_2(\mathbb{Z})\backslash\mathbb{H}$ corresponding to the torus
$\mathrm{SL}_2(\mathbb{Z})\backslash\mathbb{H}$ corresponding to the torus ![]() $T/t(\Gamma)$, where
$T/t(\Gamma)$, where ![]() $t(\Gamma)$ is the subgroup of Γ generated by the elements that have no fixed point in T.
$t(\Gamma)$ is the subgroup of Γ generated by the elements that have no fixed point in T.
Table 1. Lie algebra associated to the number of branch points of the quotient map ![]() $\mathbb{T}\rightarrow \mathbb{T}/\Gamma$.
$\mathbb{T}\rightarrow \mathbb{T}/\Gamma$.

Here we use the well-known one-to-one relation between complex tori up to isomorphism and elements of ![]() $\mathrm{SL}_2(\mathbb{Z})\backslash\mathbb{H}$.
$\mathrm{SL}_2(\mathbb{Z})\backslash\mathbb{H}$.
The dimension of the abelianisation ![]() $\mathfrak{A}/[\mathfrak{A},\mathfrak{A}]$ can be computed directly from the definition for
$\mathfrak{A}/[\mathfrak{A},\mathfrak{A}]$ can be computed directly from the definition for ![]() $\mathfrak{A}=\mathfrak{C}_{\tau},\,\mathfrak{O},\,\mathfrak{S}_{\tau}$ and is then seen to be equal to the number of branch points of
$\mathfrak{A}=\mathfrak{C}_{\tau},\,\mathfrak{O},\,\mathfrak{S}_{\tau}$ and is then seen to be equal to the number of branch points of ![]() $\mathbb{T}\rightarrow \mathbb{T}/\Gamma$. In particular, the Lie algebras
$\mathbb{T}\rightarrow \mathbb{T}/\Gamma$. In particular, the Lie algebras ![]() $\mathfrak{C}_{\tau},\mathfrak{O}$ and
$\mathfrak{C}_{\tau},\mathfrak{O}$ and ![]() $\mathfrak{S}_{\tilde{\tau}}$, where
$\mathfrak{S}_{\tilde{\tau}}$, where ![]() $\tau,\tilde{\tau}\in \mathbb{H}$, are pairwise non-isomorphic, and if two automorphic Lie algebras in our classification are isomorphic, then the number of branch points of the corresponding quotient maps are equal.
$\tau,\tilde{\tau}\in \mathbb{H}$, are pairwise non-isomorphic, and if two automorphic Lie algebras in our classification are isomorphic, then the number of branch points of the corresponding quotient maps are equal.
2. Definitions, notations and first examples
In this section, we will define automorphic Lie algebras, introduce notations and present two examples: one where the Riemann surface is the Riemann sphere and one where it is a complex torus.
Let ![]() ${\mathfrak{g}}$ be a complex finite-dimensional Lie algebra and let X be a compact Riemann surface. Suppose Γ is a finite group acting on
${\mathfrak{g}}$ be a complex finite-dimensional Lie algebra and let X be a compact Riemann surface. Suppose Γ is a finite group acting on ![]() ${\mathfrak{g}}$ by Lie algebra isomorphisms and on X by biholomorphisms. We denote the group of Lie algebra isomorphisms by
${\mathfrak{g}}$ by Lie algebra isomorphisms and on X by biholomorphisms. We denote the group of Lie algebra isomorphisms by ![]() $\mathrm{Aut}({\mathfrak{g}})$ and the group of biholomorphisms of X by
$\mathrm{Aut}({\mathfrak{g}})$ and the group of biholomorphisms of X by ![]() $\mathrm{Aut}(X)$. The group actions can be described by homomorphisms
$\mathrm{Aut}(X)$. The group actions can be described by homomorphisms
Consider a finite Γ-invariant set ![]() $\mathcal{S}\subset X$ and denote by
$\mathcal{S}\subset X$ and denote by ![]() $\mathbb{X}$ the complement
$\mathbb{X}$ the complement ![]() $X\setminus \mathcal{S}$. Thus,
$X\setminus \mathcal{S}$. Thus, ![]() $\mathbb{X}$ is a punctured compact Riemann surface. We use the notation
$\mathbb{X}$ is a punctured compact Riemann surface. We use the notation ![]() ${\mathcal{O}_{\mathbb{X}}}$ for the
${\mathcal{O}_{\mathbb{X}}}$ for the ![]() ${\mathbb{C}}$-algebra of meromorphic functions on X holomorphic on
${\mathbb{C}}$-algebra of meromorphic functions on X holomorphic on ![]() $\mathbb{X}$. Denote by
$\mathbb{X}$. Denote by ![]() $\tilde{\sigma}$ the induced homomorphism
$\tilde{\sigma}$ the induced homomorphism ![]() $\Gamma\rightarrow \mathrm{Aut}({\mathcal{O}_{\mathbb{X}}})$ defined by
$\Gamma\rightarrow \mathrm{Aut}({\mathcal{O}_{\mathbb{X}}})$ defined by ![]() $\tilde{\sigma}(\gamma)f=f\circ \sigma(\gamma)^{-1}$ for
$\tilde{\sigma}(\gamma)f=f\circ \sigma(\gamma)^{-1}$ for ![]() $\gamma\in \Gamma$. A current algebra is formed by taking the tensor product over
$\gamma\in \Gamma$. A current algebra is formed by taking the tensor product over ![]() ${\mathbb{C}}$ of
${\mathbb{C}}$ of ![]() ${\mathfrak{g}}$ and
${\mathfrak{g}}$ and ![]() ${\mathcal{O}_{\mathbb{X}}}$. This has a natural structure of a Lie algebra by declaring
${\mathcal{O}_{\mathbb{X}}}$. This has a natural structure of a Lie algebra by declaring
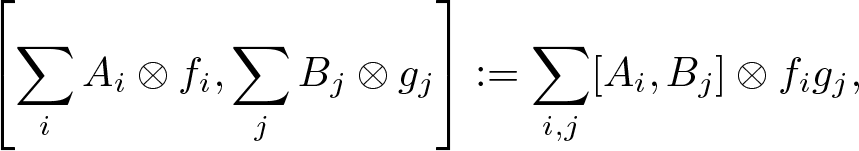 \begin{equation*}\left[\sum_iA_i\otimes f_i, \sum_jB_j\otimes g_j\right]:=\sum_{i,j}[A_i,B_j]\otimes f_ig_j,\end{equation*}
\begin{equation*}\left[\sum_iA_i\otimes f_i, \sum_jB_j\otimes g_j\right]:=\sum_{i,j}[A_i,B_j]\otimes f_ig_j,\end{equation*} where ![]() $A_i,B_j\in {\mathfrak{g}}$,
$A_i,B_j\in {\mathfrak{g}}$, ![]() $f_i,g_j\in {\mathcal{O}_{\mathbb{X}}}$ and the bracket on the right-hand side is the bracket in
$f_i,g_j\in {\mathcal{O}_{\mathbb{X}}}$ and the bracket on the right-hand side is the bracket in ![]() ${\mathfrak{g}}$. We let Γ act naturally on
${\mathfrak{g}}$. We let Γ act naturally on ![]() ${\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}}$ by the diagonal action
${\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}}$ by the diagonal action
We will also write ![]() $\rho\otimes\tilde{\sigma}(\gamma)$ for the homomorphism corresponding to the action defined in (2.1).
$\rho\otimes\tilde{\sigma}(\gamma)$ for the homomorphism corresponding to the action defined in (2.1).
An automorphic Lie algebra is the Lie subalgebra of the current algebra ![]() ${\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}}$ of those elements invariant under the specified action.
${\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}}$ of those elements invariant under the specified action.
Definition 1. The automorphic Lie algebra ![]() $\mathfrak{A}=\mathfrak{A}({\mathfrak{g}}, \mathbb{X},\Gamma,\rho,\sigma)$ is defined as the algebra of fixed points of the action of Γ on
$\mathfrak{A}=\mathfrak{A}({\mathfrak{g}}, \mathbb{X},\Gamma,\rho,\sigma)$ is defined as the algebra of fixed points of the action of Γ on ![]() ${\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}}$. That is,
${\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}}$. That is,
From now onwards, we will use the acronym aLia for ‘automorphic Lie algebra’. We will sometimes simply write ![]() $\mathfrak{A}=({\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}})^{\Gamma}$, suppressing the additional data, if they are clear from the context.
$\mathfrak{A}=({\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}})^{\Gamma}$, suppressing the additional data, if they are clear from the context.
As mentioned in the Introduction, the Onsager algebra is a Lie algebra that appears prominently in the context of aLias. Roan discovered in 1991 [Reference Roan30] that ![]() $\mathfrak{O}$ is in fact an aLia avant la lettre. We will give an example of an aLia, where X is the Riemann sphere, which is isomorphic to the Onsager algebra.
$\mathfrak{O}$ is in fact an aLia avant la lettre. We will give an example of an aLia, where X is the Riemann sphere, which is isomorphic to the Onsager algebra.
Example 2 (The simplest concrete form of the Onsager algebra)
Let ![]() $X={\mathbb{C}}_{\infty}$ be the Riemann sphere and let
$X={\mathbb{C}}_{\infty}$ be the Riemann sphere and let ![]() ${\mathfrak{g}}=\mathfrak{sl}_2$. Take
${\mathfrak{g}}=\mathfrak{sl}_2$. Take ![]() $\mathcal{S}=\{0,\infty\}$. The punctured surface
$\mathcal{S}=\{0,\infty\}$. The punctured surface ![]() $\mathbb{X}$ is given by
$\mathbb{X}$ is given by ![]() ${X}\setminus\mathcal{S}\cong {\mathbb{C}}^*$ and the associated algebra of functions is
${X}\setminus\mathcal{S}\cong {\mathbb{C}}^*$ and the associated algebra of functions is ![]() $\mathcal{O}_{\mathbb{X}}=\mathbb{C}[z,z^{-1}]$, the Laurent polynomials. Let Γ be the group with two elements, generated by γ, and define the homomorphism
$\mathcal{O}_{\mathbb{X}}=\mathbb{C}[z,z^{-1}]$, the Laurent polynomials. Let Γ be the group with two elements, generated by γ, and define the homomorphism ![]() $\sigma:\Gamma\rightarrow \mathrm{Aut}(X)$ by
$\sigma:\Gamma\rightarrow \mathrm{Aut}(X)$ by ![]() $\sigma(\gamma)z= z^{-1}$. The function
$\sigma(\gamma)z= z^{-1}$. The function
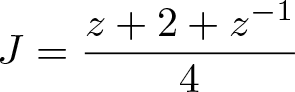 \begin{equation*}J=\frac{z+2+z^{-1}}{4}\end{equation*}
\begin{equation*}J=\frac{z+2+z^{-1}}{4}\end{equation*} is invariant under this action. It is in fact a Hauptmodul, in the sense that any invariant meromorphic function on the Riemann sphere is a rational function in J. This can be shown using the theory of divisors. If we then restrict the poles to ![]() $\{0,\infty\}$ we obtain
$\{0,\infty\}$ we obtain ![]() $\mathbb{C}[z,z^{-1}]^{\Gamma}=\mathbb{C}[J]$. We denote this space by
$\mathbb{C}[z,z^{-1}]^{\Gamma}=\mathbb{C}[J]$. We denote this space by ![]() $\mathbb{C}[z,z^{-1}]^{+}$ as it is the +1 eigenspace of γ. The −1 eigenspace
$\mathbb{C}[z,z^{-1}]^{+}$ as it is the +1 eigenspace of γ. The −1 eigenspace ![]() $\mathbb{C}[z,z^{-1}]^{-}$ is given by
$\mathbb{C}[z,z^{-1}]^{-}$ is given by ![]() $\mathbb{C}[J](z-z^{-1})$. Indeed, if
$\mathbb{C}[J](z-z^{-1})$. Indeed, if ![]() $f\in \mathbb{C}[z,z^{-1}]^{-}$ then it necessarily vanishes at 1 and −1, hence
$f\in \mathbb{C}[z,z^{-1}]^{-}$ then it necessarily vanishes at 1 and −1, hence ![]() $f/(z-z^{-1})$ is an element of
$f/(z-z^{-1})$ is an element of ![]() $\mathbb{C}[z,z^{-1}]^{+}$.
$\mathbb{C}[z,z^{-1}]^{+}$.
Define the homomorphism ![]() $\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ by
$\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ by
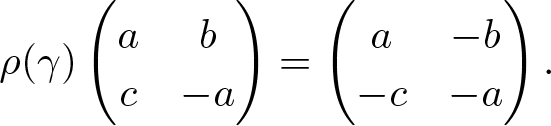 \begin{equation*}
\rho(\gamma)\begin{pmatrix}
a & b\\
c &-a
\end{pmatrix}=\begin{pmatrix}
a & -b\\
-c &-a
\end{pmatrix}.
\end{equation*}
\begin{equation*}
\rho(\gamma)\begin{pmatrix}
a & b\\
c &-a
\end{pmatrix}=\begin{pmatrix}
a & -b\\
-c &-a
\end{pmatrix}.
\end{equation*}Let
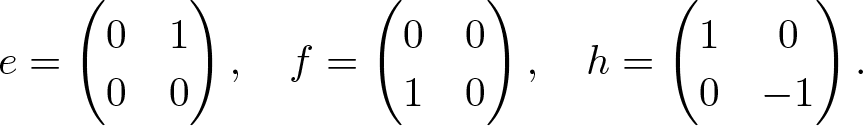 \begin{equation*}e=\begin{pmatrix}
0 & 1\\
0 &0
\end{pmatrix},\quad f=\begin{pmatrix}
0 & 0\\
1 &0
\end{pmatrix},\quad h=\begin{pmatrix}
1 & 0\\
0 &-1
\end{pmatrix}.\end{equation*}
\begin{equation*}e=\begin{pmatrix}
0 & 1\\
0 &0
\end{pmatrix},\quad f=\begin{pmatrix}
0 & 0\\
1 &0
\end{pmatrix},\quad h=\begin{pmatrix}
1 & 0\\
0 &-1
\end{pmatrix}.\end{equation*} This action on ![]() $\mathfrak{sl}_2$ yields the eigenspace decomposition
$\mathfrak{sl}_2$ yields the eigenspace decomposition
We have
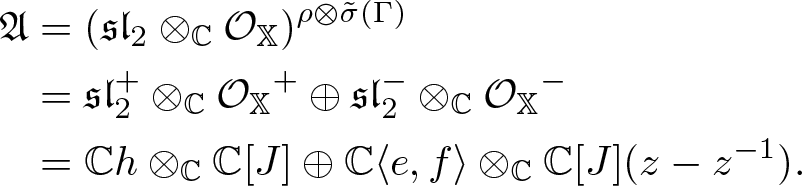 \begin{align*}
\mathfrak{A}&=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{X}})^{\rho\otimes \tilde{\sigma}(\Gamma)}\\
&=\mathfrak{sl}_2^{+}\otimes_{{\mathbb{C}}} {\mathcal{O}_{\mathbb{X}}}^{+}\oplus \mathfrak{sl}_2^{-}\otimes_{{\mathbb{C}}} {\mathcal{O}_{\mathbb{X}}}^{-}\\
&={\mathbb{C}} h \otimes_{{\mathbb{C}}}{\mathbb{C}}[J] \oplus {\mathbb{C}}\langle e,f\rangle \otimes_{{\mathbb{C}}} {\mathbb{C}}[J](z-z^{-1}).
\end{align*}
\begin{align*}
\mathfrak{A}&=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{X}})^{\rho\otimes \tilde{\sigma}(\Gamma)}\\
&=\mathfrak{sl}_2^{+}\otimes_{{\mathbb{C}}} {\mathcal{O}_{\mathbb{X}}}^{+}\oplus \mathfrak{sl}_2^{-}\otimes_{{\mathbb{C}}} {\mathcal{O}_{\mathbb{X}}}^{-}\\
&={\mathbb{C}} h \otimes_{{\mathbb{C}}}{\mathbb{C}}[J] \oplus {\mathbb{C}}\langle e,f\rangle \otimes_{{\mathbb{C}}} {\mathbb{C}}[J](z-z^{-1}).
\end{align*}Define
so that we can write ![]() $\mathfrak{A}= {\mathbb{C}}\langle E,F,H\rangle\otimes_{{\mathbb{C}}} {\mathbb{C}}[J]$ with brackets
$\mathfrak{A}= {\mathbb{C}}\langle E,F,H\rangle\otimes_{{\mathbb{C}}} {\mathbb{C}}[J]$ with brackets
We have chosen the Hauptmodul J with values 0 and 1 at the branch points (−1 and 1), but we could have chosen any other two (distinct) values. They appear as zeros in the last Lie bracket.
This Lie algebra made a lot of appearances in the literature. Roan studied the Onsager algebra and found this aLia (in another basis) as a concrete form of the Onsager algebra which enabled him to classify its finite-dimensional irreducible representations [Reference Roan30]. The work of Lombardo and Sanders [Reference Lombardo and Sanders22], Knibbeler, Lombardo and Sanders [Reference Knibbeler, Lombardo and Sanders2] and Bury and Mikhailov [Reference Bury and Mikhailov7] showed that any aLia of Γ-equivariant meromorphic maps ![]() ${\mathbb{C}_\infty}\to\mathfrak{sl}_2$ with precisely two Γ-orbits of ramification points in its holomorphic domain and precisely one Γ-orbit outside its holomorphic domain, is isomorphic to
${\mathbb{C}_\infty}\to\mathfrak{sl}_2$ with precisely two Γ-orbits of ramification points in its holomorphic domain and precisely one Γ-orbit outside its holomorphic domain, is isomorphic to ![]() $\mathfrak{A}$. Knibbeler, Lombardo and Veselov realised this Lie algebra in terms of modular functions and provided an explicit isomorphism
$\mathfrak{A}$. Knibbeler, Lombardo and Veselov realised this Lie algebra in terms of modular functions and provided an explicit isomorphism ![]() $\mathfrak{O}\to\mathfrak{A}$ by
$\mathfrak{O}\to\mathfrak{A}$ by
cf. [Reference Knibbeler, Lombardo and Veselov5, Theorem 2.5].
We will see in § 6 that the Onsager algebra can also be realised as certain aLias on a complex torus with enough symmetry, that is, tori on which the groups C 4 and C 6 act. As opposed to the case of the Riemann sphere, the symmetry group C 2 will not appear in this context. Instead, the symmetry groups ![]() $C_3,C_4,C_6$ and A 4 are the only ones that give rise to aLias isomorphic to the Onsager algebra.
$C_3,C_4,C_6$ and A 4 are the only ones that give rise to aLias isomorphic to the Onsager algebra.
For our first example of an aLia on a complex torus, we will use the Weierstrass ![]() $\wp$-function. This function is defined as follows. Let
$\wp$-function. This function is defined as follows. Let ![]() $\Lambda$ be a lattice and consider the complex torus
$\Lambda$ be a lattice and consider the complex torus ![]() $T={\mathbb{C}}/{\Lambda}$. The function
$T={\mathbb{C}}/{\Lambda}$. The function ![]() $\wp_{{\Lambda}}:T\rightarrow{\mathbb{C}}$ defined by
$\wp_{{\Lambda}}:T\rightarrow{\mathbb{C}}$ defined by
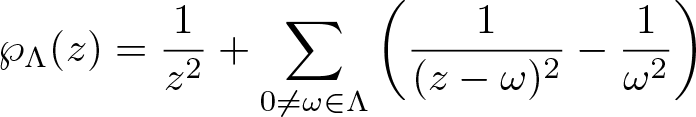 \begin{align}\wp_\Lambda(z) = \frac{1}{z^2}+\sum_{0\neq\omega\in \Lambda}\left(\frac{1}{(z-\omega)^2}-\frac{1}{\omega^2}\right)
\end{align}
\begin{align}\wp_\Lambda(z) = \frac{1}{z^2}+\sum_{0\neq\omega\in \Lambda}\left(\frac{1}{(z-\omega)^2}-\frac{1}{\omega^2}\right)
\end{align} is called the Weierstrass ![]() $\wp$-function associated with the lattice
$\wp$-function associated with the lattice ![]() $\Lambda$. It is a meromorphic function on T with poles precisely at the lattice points
$\Lambda$. It is a meromorphic function on T with poles precisely at the lattice points ![]() $\omega\in {\Lambda}$. The reference to a lattice
$\omega\in {\Lambda}$. The reference to a lattice ![]() $\Lambda$ will be suppressed when there is no confusion. It is clear that
$\Lambda$ will be suppressed when there is no confusion. It is clear that ![]() $\wp(-z)=\wp(z)$ and
$\wp(-z)=\wp(z)$ and ![]() $\wp'(-z)=-\wp'(z)$, where
$\wp'(-z)=-\wp'(z)$, where ![]() $\wp'$ denotes the derivative of
$\wp'$ denotes the derivative of ![]() $\wp$. Furthermore,
$\wp$. Furthermore, ![]() $\wp$ satisfies the equation
$\wp$ satisfies the equation ![]() $(\wp')^2=4\wp^3-g_2\wp-g_3$ where
$(\wp')^2=4\wp^3-g_2\wp-g_3$ where ![]() $g_2,g_3\in {\mathbb{C}}$ are the elliptic invariants. The space of even meromorphic functions on T which are holomorphic on
$g_2,g_3\in {\mathbb{C}}$ are the elliptic invariants. The space of even meromorphic functions on T which are holomorphic on ![]() $T\setminus \{0\}$ is given by the polynomials in
$T\setminus \{0\}$ is given by the polynomials in ![]() $\wp$ with complex coefficients,
$\wp$ with complex coefficients, ![]() ${\mathbb{C}}[\wp]$, cf. [Reference Freitag and Busam13, Proposition V.3.1]. Using this and the relation
${\mathbb{C}}[\wp]$, cf. [Reference Freitag and Busam13, Proposition V.3.1]. Using this and the relation ![]() $(\wp')^2=4\wp^3-g_2\wp-g_3$, it is not difficult to see that any odd meromorphic function on T, holomorphic on
$(\wp')^2=4\wp^3-g_2\wp-g_3$, it is not difficult to see that any odd meromorphic function on T, holomorphic on ![]() $T\setminus \{0\}$, is an element of
$T\setminus \{0\}$, is an element of ![]() ${\mathbb{C}}[\wp]\wp'$. Since any function on T is a sum of an even and odd function, we have established the following fact.
${\mathbb{C}}[\wp]\wp'$. Since any function on T is a sum of an even and odd function, we have established the following fact.
Lemma 1. The algebra of meromorphic function on complex torus T, holomorphic on ![]() $T\setminus\{0\}$, is given by
$T\setminus\{0\}$, is given by ![]() $\mathcal{O}_{T\setminus \{0\}}={\mathbb{C}}[\wp,\wp']$.
$\mathcal{O}_{T\setminus \{0\}}={\mathbb{C}}[\wp,\wp']$.
We now have all the ingredients to present our first, simple example of an aLia on a complex torus with symmetry group C 2. We will write ![]() $\mathbb{T}$ for
$\mathbb{T}$ for ![]() $T\setminus \Gamma\cdot\{0\}$.
$T\setminus \Gamma\cdot\{0\}$.
Example 3. Fix a complex torus ![]() $T={\mathbb{C}}/{\Lambda}$ with
$T={\mathbb{C}}/{\Lambda}$ with ![]() $\Lambda={\mathbb{Z}}\oplus {\mathbb{Z}}\tau$. Let
$\Lambda={\mathbb{Z}}\oplus {\mathbb{Z}}\tau$. Let ![]() ${\mathfrak{g}}=\mathfrak{sl}_2$ and
${\mathfrak{g}}=\mathfrak{sl}_2$ and ![]() $\Gamma =C_2$, generated by γ, where
$\Gamma =C_2$, generated by γ, where ![]() $\sigma:\Gamma\rightarrow \mathrm{Aut}(T)$ is the homomorphism defined by
$\sigma:\Gamma\rightarrow \mathrm{Aut}(T)$ is the homomorphism defined by ![]() $\sigma(\gamma)z= -z.$ The punctured torus
$\sigma(\gamma)z= -z.$ The punctured torus ![]() $\mathbb{T}$ is given by
$\mathbb{T}$ is given by ![]() $T\setminus \{0\}$. Write
$T\setminus \{0\}$. Write ![]() $\wp=\wp_{{\Lambda}}$. Keeping in mind that
$\wp=\wp_{{\Lambda}}$. Keeping in mind that ![]() $\mathcal{O}_{\mathbb{T}}={\mathbb{C}}[\wp,\wp']$ and
$\mathcal{O}_{\mathbb{T}}={\mathbb{C}}[\wp,\wp']$ and ![]() $(\wp')^2=4\wp^3-g_2\wp-g_3$, it is easily seen that the algebra
$(\wp')^2=4\wp^3-g_2\wp-g_3$, it is easily seen that the algebra ![]() $\mathcal{O}_{\mathbb{T}}$ is given by
$\mathcal{O}_{\mathbb{T}}$ is given by ![]() $\mathcal{O}_{\mathbb{T}}=\mathcal{O}_{\mathbb{T}}^{+}\oplus \mathcal{O}_{\mathbb{T}}^{-}$, where
$\mathcal{O}_{\mathbb{T}}=\mathcal{O}_{\mathbb{T}}^{+}\oplus \mathcal{O}_{\mathbb{T}}^{-}$, where
denote the space of even and odd functions, respectively. Define the homomorphism ![]() $\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ by
$\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ by
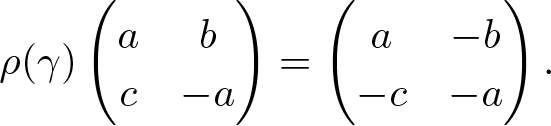 \begin{equation*}
\rho(\gamma)\begin{pmatrix}
a & b\\
c &-a
\end{pmatrix}=\begin{pmatrix}
a & -b\\
-c &-a
\end{pmatrix}.
\end{equation*}
\begin{equation*}
\rho(\gamma)\begin{pmatrix}
a & b\\
c &-a
\end{pmatrix}=\begin{pmatrix}
a & -b\\
-c &-a
\end{pmatrix}.
\end{equation*}Let
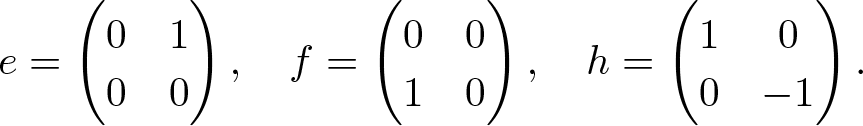 \begin{equation*}e=\begin{pmatrix}
0 & 1\\
0 &0
\end{pmatrix},\quad f=\begin{pmatrix}
0 & 0\\
1 &0
\end{pmatrix},\quad h=\begin{pmatrix}
1 & 0\\
0 &-1
\end{pmatrix}.\end{equation*}
\begin{equation*}e=\begin{pmatrix}
0 & 1\\
0 &0
\end{pmatrix},\quad f=\begin{pmatrix}
0 & 0\\
1 &0
\end{pmatrix},\quad h=\begin{pmatrix}
1 & 0\\
0 &-1
\end{pmatrix}.\end{equation*} This action on ![]() $\mathfrak{sl}_2$ decomposes as
$\mathfrak{sl}_2$ decomposes as ![]() $\mathfrak{sl}_2^{+}\oplus \mathfrak{sl}_2^{-}$, where
$\mathfrak{sl}_2^{+}\oplus \mathfrak{sl}_2^{-}$, where
are the eigenspaces with eigenvalue 1 and −1, respectively. We have
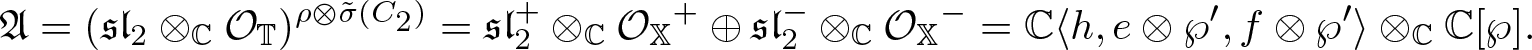 \begin{equation*}\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_2)}=\mathfrak{sl}_2^{+}\otimes_{{\mathbb{C}}} {\mathcal{O}_{\mathbb{X}}}^{+}\oplus \mathfrak{sl}_2^{-}\otimes_{{\mathbb{C}}} {\mathcal{O}_{\mathbb{X}}}^{-}={\mathbb{C}}\langle h,e\otimes \wp',f\otimes \wp'\rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp].\end{equation*}
\begin{equation*}\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_2)}=\mathfrak{sl}_2^{+}\otimes_{{\mathbb{C}}} {\mathcal{O}_{\mathbb{X}}}^{+}\oplus \mathfrak{sl}_2^{-}\otimes_{{\mathbb{C}}} {\mathcal{O}_{\mathbb{X}}}^{-}={\mathbb{C}}\langle h,e\otimes \wp',f\otimes \wp'\rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp].\end{equation*}Define
Then ![]() $\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} {\mathcal{O}_{\mathbb{X}}})^{\rho\otimes \tilde{\sigma}(C_2)}= {\mathbb{C}}\langle E,F,H\rangle\otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp]\cong \mathfrak{S}_{\tau}$ with brackets
$\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} {\mathcal{O}_{\mathbb{X}}})^{\rho\otimes \tilde{\sigma}(C_2)}= {\mathbb{C}}\langle E,F,H\rangle\otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp]\cong \mathfrak{S}_{\tau}$ with brackets
Observe that  $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_2)}\not\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_2)}$, since the right-hand side is perfect, whereas the left-hand side is not.
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_2)}\not\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_2)}$, since the right-hand side is perfect, whereas the left-hand side is not.
In the above example,  $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_2)}\not\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_2)}$. This is a consequence of the fact that with this choice of homomorphism σ, the quotient
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_2)}\not\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_2)}$. This is a consequence of the fact that with this choice of homomorphism σ, the quotient ![]() $T/\sigma(C_2)$ has genus 0 or equivalently, the canonical projection
$T/\sigma(C_2)$ has genus 0 or equivalently, the canonical projection ![]() $\pi:{\mathbb{T}}\rightarrow {\mathbb{T}}/\sigma(C_2)$ has ramification points. It is a general fact, cf. [Reference Duffield, Knibbeler and Lombardo10], that for a punctured compact Riemann surface
$\pi:{\mathbb{T}}\rightarrow {\mathbb{T}}/\sigma(C_2)$ has ramification points. It is a general fact, cf. [Reference Duffield, Knibbeler and Lombardo10], that for a punctured compact Riemann surface ![]() $\mathbb{X}$ and a complex-finite dimensional Lie algebra
$\mathbb{X}$ and a complex-finite dimensional Lie algebra ![]() ${\mathfrak{g}}$, we have
${\mathfrak{g}}$, we have ![]() $({\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}})^{\Gamma}\not\cong {\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}}^{\Gamma}$ whenever
$({\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}})^{\Gamma}\not\cong {\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}}^{\Gamma}$ whenever ![]() $\mathbb{X}\rightarrow \mathbb{X}/\Gamma$ contains a ramification point x 0, when
$\mathbb{X}\rightarrow \mathbb{X}/\Gamma$ contains a ramification point x 0, when ![]() $\Gamma_{x_0}$ acts non-trivially on
$\Gamma_{x_0}$ acts non-trivially on ![]() ${\mathfrak{g}}$. We will later see how choosing a different homomorphism of
${\mathfrak{g}}$. We will later see how choosing a different homomorphism of ![]() $C_2\rightarrow \mathrm{Aut}(T)$ does yield an isomorphism.
$C_2\rightarrow \mathrm{Aut}(T)$ does yield an isomorphism.
3. A classification scheme
The aim of this section is to explain what we will precisely classify. Our objects of interest are aLias of the form
where Γ is a finite group, ![]() $\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and
$\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and ![]() $\sigma:\Gamma\rightarrow \mathrm{Aut}(T)$ homomorphisms,
$\sigma:\Gamma\rightarrow \mathrm{Aut}(T)$ homomorphisms, ![]() ${\mathbb{T}}=T\setminus \mathcal{S}$, where T is a complex torus and
${\mathbb{T}}=T\setminus \mathcal{S}$, where T is a complex torus and ![]() $\mathcal{S}$ an orbit of Γ in T. We would like to determine the isomorphism classes of these aLias, which is the content of Theorem 1. We may assume that
$\mathcal{S}$ an orbit of Γ in T. We would like to determine the isomorphism classes of these aLias, which is the content of Theorem 1. We may assume that ![]() $\mathcal{S}$ is the orbit of 0 because
$\mathcal{S}$ is the orbit of 0 because ![]() $\mathrm{Aut}(T)$ acts transitively on T (using Lemma 4 below), and we may assume that ρ and σ are faithful, almost without losing generality, explained by Lemma 2 and 3. These restrictions constitute our classification scheme.
$\mathrm{Aut}(T)$ acts transitively on T (using Lemma 4 below), and we may assume that ρ and σ are faithful, almost without losing generality, explained by Lemma 2 and 3. These restrictions constitute our classification scheme.
We will first address some general aspects of invariant spaces with respect to some group action. Let X be a compact Riemann surface, ![]() ${\mathfrak{g}}$ a complex finite-dimensional Lie algebra and let
${\mathfrak{g}}$ a complex finite-dimensional Lie algebra and let ![]() $\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{g})$ and
$\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{g})$ and ![]() $\sigma:\Gamma\rightarrow \mathrm{Aut}(X)$ be homomorphisms. Given a finite group Γ and a Γ-module M, a standard technique for obtaining the space of invariants of the action of Γ on M, denoted by
$\sigma:\Gamma\rightarrow \mathrm{Aut}(X)$ be homomorphisms. Given a finite group Γ and a Γ-module M, a standard technique for obtaining the space of invariants of the action of Γ on M, denoted by ![]() $M^{\Gamma}$, is that of averaging over the group Γ. We will explain this method. Define the averaging operator (also known as the Reynolds operator)
$M^{\Gamma}$, is that of averaging over the group Γ. We will explain this method. Define the averaging operator (also known as the Reynolds operator) ![]() $\langle \cdot \rangle_{\Gamma}: M\rightarrow M$ by
$\langle \cdot \rangle_{\Gamma}: M\rightarrow M$ by
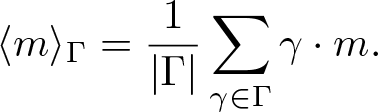 \begin{equation*}\langle m \rangle_{\Gamma}=\frac{1}{|\Gamma|}\sum_{\gamma\in \Gamma}\gamma\cdot m.\end{equation*}
\begin{equation*}\langle m \rangle_{\Gamma}=\frac{1}{|\Gamma|}\sum_{\gamma\in \Gamma}\gamma\cdot m.\end{equation*} Clearly, ![]() $\langle \cdot \rangle_{\Gamma}$ is linear if the action of Γ on M is linear. One sees that its image is
$\langle \cdot \rangle_{\Gamma}$ is linear if the action of Γ on M is linear. One sees that its image is ![]() $M^{\Gamma}$ and
$M^{\Gamma}$ and ![]() $\langle \langle m \rangle_{\Gamma} \rangle_{\Gamma}=\langle m \rangle_{\Gamma}$, thus
$\langle \langle m \rangle_{\Gamma} \rangle_{\Gamma}=\langle m \rangle_{\Gamma}$, thus ![]() $\langle \cdot \rangle_{\Gamma}$ is a projection onto
$\langle \cdot \rangle_{\Gamma}$ is a projection onto ![]() $M^{\Gamma}$. Suppose K is a normal subgroup of Γ, which we denote by
$M^{\Gamma}$. Suppose K is a normal subgroup of Γ, which we denote by ![]() $K\lhd\Gamma$. Then there is an obvious action of the quotient group
$K\lhd\Gamma$. Then there is an obvious action of the quotient group ![]() $\Gamma/K$ on M K and we can check directly that
$\Gamma/K$ on M K and we can check directly that ![]() $\langle \langle \cdot \rangle_{K} \rangle_{\Gamma/K}=\langle \cdot \rangle_{\Gamma}$. In particular, an aLia with symmetry group Γ can be computed making use of the fact that it has a normal subgroup K. Phrased in terms of our setting:
$\langle \langle \cdot \rangle_{K} \rangle_{\Gamma/K}=\langle \cdot \rangle_{\Gamma}$. In particular, an aLia with symmetry group Γ can be computed making use of the fact that it has a normal subgroup K. Phrased in terms of our setting:
Lemma 2. Let ![]() $K\lhd \Gamma$. Then
$K\lhd \Gamma$. Then ![]() $({\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}})^{\Gamma}=(({\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}})^{K})^{\Gamma/K}.$
$({\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}})^{\Gamma}=(({\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}})^{K})^{\Gamma/K}.$
Let ![]() $\tilde{\rho}=\rho\otimes \tilde{\sigma}$ and
$\tilde{\rho}=\rho\otimes \tilde{\sigma}$ and ![]() $\tilde{K}=\ker\rho\cdot\ker\sigma$. First of all, observe that we may replace Γ by
$\tilde{K}=\ker\rho\cdot\ker\sigma$. First of all, observe that we may replace Γ by ![]() $\Gamma/\ker(\rho\otimes \tilde{\sigma})$, making use of the fact that
$\Gamma/\ker(\rho\otimes \tilde{\sigma})$, making use of the fact that ![]() $\ker(\rho\otimes \tilde{\sigma})$ is a normal subgroup of Γ and invoking Lemma 2. Trivially,
$\ker(\rho\otimes \tilde{\sigma})$ is a normal subgroup of Γ and invoking Lemma 2. Trivially, ![]() $({\mathfrak{g}}\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{X}})^{\ker(\rho\otimes \tilde{\sigma})}={\mathfrak{g}}\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{X}}$. We can therefore assume that
$({\mathfrak{g}}\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{X}})^{\ker(\rho\otimes \tilde{\sigma})}={\mathfrak{g}}\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{X}}$. We can therefore assume that ![]() $\ker\rho\cap\ker\tilde\sigma=1$ without losing generality.
$\ker\rho\cap\ker\tilde\sigma=1$ without losing generality.
Lemma 3.  $({\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}})^{\rho\otimes\tilde{\sigma}(\Gamma)}=({\mathfrak{g}}^{\rho(\ker\sigma)}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}}^{\tilde{\sigma}(\ker\rho)})^{\tilde{\rho}(\Gamma)/\tilde{\rho}(\tilde{K})}.$
$({\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}})^{\rho\otimes\tilde{\sigma}(\Gamma)}=({\mathfrak{g}}^{\rho(\ker\sigma)}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}}^{\tilde{\sigma}(\ker\rho)})^{\tilde{\rho}(\Gamma)/\tilde{\rho}(\tilde{K})}.$
Proof. Clearly ![]() $\tilde{\rho}(\tilde{K})\lhd \tilde{\rho}(\Gamma)$ since
$\tilde{\rho}(\tilde{K})\lhd \tilde{\rho}(\Gamma)$ since ![]() $\tilde{K}\lhd \Gamma$ and
$\tilde{K}\lhd \Gamma$ and ![]() $\tilde{\rho}$ is a homomorphism. Suppose
$\tilde{\rho}$ is a homomorphism. Suppose ![]() $A\in {\mathfrak{g}}$ and
$A\in {\mathfrak{g}}$ and ![]() $f\in \mathcal{O}_{\mathbb{X}}$. Now, if
$f\in \mathcal{O}_{\mathbb{X}}$. Now, if ![]() $\tilde{\rho}( \gamma_1 \gamma_2)\in \tilde{\rho}(\tilde{K})$ with
$\tilde{\rho}( \gamma_1 \gamma_2)\in \tilde{\rho}(\tilde{K})$ with ![]() $ \gamma_1\in \ker(\rho)$ and
$ \gamma_1\in \ker(\rho)$ and ![]() $ \gamma_2\in \ker(\sigma)$, then
$ \gamma_2\in \ker(\sigma)$, then
where the homomorphism ![]() $\rho\otimes\tilde{\sigma}$ is defined in (2.1). Hence
$\rho\otimes\tilde{\sigma}$ is defined in (2.1). Hence  $({\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}})^{\tilde{\rho}(\tilde{K})}={\mathfrak{g}}^{\rho(\ker\sigma)}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}}^{\tilde{\sigma}(\ker \rho)}.$ By employing Lemma 2, this proves the claim.
$({\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}})^{\tilde{\rho}(\tilde{K})}={\mathfrak{g}}^{\rho(\ker\sigma)}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}}^{\tilde{\sigma}(\ker \rho)}.$ By employing Lemma 2, this proves the claim.
Assume now the case of X = T and denote again by ![]() $\mathbb{T}$ the punctured complex torus
$\mathbb{T}$ the punctured complex torus ![]() $T\setminus \sigma(\Gamma)\cdot \{0\}$ (see § 2). We know that
$T\setminus \sigma(\Gamma)\cdot \{0\}$ (see § 2). We know that  $\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(\ker\rho)}\cong\mathcal{O}_{\mathbb{T}/\sigma(\ker\rho)}.$ Now,
$\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(\ker\rho)}\cong\mathcal{O}_{\mathbb{T}/\sigma(\ker\rho)}.$ Now, ![]() $\mathbb{T}/\sigma(\ker\rho)$ is a punctured compact Riemann surface of genus 0 or 1. In the former case, we refer to previous literature [Reference Knibbeler, Lombardo and Sanders3, Reference Knibbeler, Lombardo and Sanders4, Reference Bury and Mikhailov7, Reference Lombardo and Sanders22]. In the latter case, we may assume that
$\mathbb{T}/\sigma(\ker\rho)$ is a punctured compact Riemann surface of genus 0 or 1. In the former case, we refer to previous literature [Reference Knibbeler, Lombardo and Sanders3, Reference Knibbeler, Lombardo and Sanders4, Reference Bury and Mikhailov7, Reference Lombardo and Sanders22]. In the latter case, we may assume that ![]() $\sigma(\ker \rho)=\tilde{\sigma}(\ker \rho)=1$. Together with
$\sigma(\ker \rho)=\tilde{\sigma}(\ker \rho)=1$. Together with ![]() $\ker\sigma\cap\ker\rho=1$ this is equivalent to
$\ker\sigma\cap\ker\rho=1$ this is equivalent to ![]() $\ker\rho=1$. Now consider the homomorphism σ. If
$\ker\rho=1$. Now consider the homomorphism σ. If ![]() $\ker\sigma$ is non-trivial, the Lie algebra
$\ker\sigma$ is non-trivial, the Lie algebra  $\mathfrak{sl}_2^{\rho(\ker\sigma)}$ has dimension less than 3 and therefore is abelian, and we will rule out this class.
$\mathfrak{sl}_2^{\rho(\ker\sigma)}$ has dimension less than 3 and therefore is abelian, and we will rule out this class.
The following simple lemma plays an important role in our classification. It appears in a more general setting in the context of equivariant map algebras in [Reference Neher, Savage and Senesi6]. Recall that ![]() $\mathbb{X}$ stands for the punctured compact Riemann surface
$\mathbb{X}$ stands for the punctured compact Riemann surface ![]() $X\setminus \mathcal{S}.$
$X\setminus \mathcal{S}.$
Lemma 4. Suppose ![]() $\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{g})$ and
$\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{g})$ and ![]() $\sigma:\Gamma\rightarrow \mathrm{Aut}(X)$ are homomorphisms and
$\sigma:\Gamma\rightarrow \mathrm{Aut}(X)$ are homomorphisms and ![]() $\tilde{\rho}=\rho\otimes \tilde{\sigma}:\Gamma\rightarrow \mathrm{Aut}({\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}})$. Let
$\tilde{\rho}=\rho\otimes \tilde{\sigma}:\Gamma\rightarrow \mathrm{Aut}({\mathfrak{g}}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{X}})$. Let ![]() $\mathfrak{A}$ be the aLia defined by these actions:
$\mathfrak{A}$ be the aLia defined by these actions:
where ![]() $a=A\otimes f$, with
$a=A\otimes f$, with ![]() $A\in {\mathfrak{g}}$ and
$A\in {\mathfrak{g}}$ and ![]() $f\in {\mathcal{O}_{\mathbb{X}}}$. Define a second action of Γ on
$f\in {\mathcal{O}_{\mathbb{X}}}$. Define a second action of Γ on ![]() ${\mathfrak{g}}$ and X by
${\mathfrak{g}}$ and X by ![]() $\rho'(\gamma)=\tau_1\rho(\gamma)\tau_1^{-1}$ and
$\rho'(\gamma)=\tau_1\rho(\gamma)\tau_1^{-1}$ and ![]() $\sigma'(\gamma)=\tau_2\sigma(\gamma)\tau_2^{-1}$, where
$\sigma'(\gamma)=\tau_2\sigma(\gamma)\tau_2^{-1}$, where ![]() $\tau_1\in \mathrm{Aut}({\mathfrak{g}})$ and
$\tau_1\in \mathrm{Aut}({\mathfrak{g}})$ and ![]() $\tau_2\in \mathrm{Aut}(X)$ such that
$\tau_2\in \mathrm{Aut}(X)$ such that ![]() $\tau_2(\mathcal{S})=\mathcal{S}$. Let
$\tau_2(\mathcal{S})=\mathcal{S}$. Let ![]() $\tilde{\rho}'$ be given by
$\tilde{\rho}'$ be given by ![]() $\tilde{\rho}'=\rho'\otimes \tilde{\sigma}'$ and define
$\tilde{\rho}'=\rho'\otimes \tilde{\sigma}'$ and define
Then ![]() $\mathfrak{A}\cong \mathfrak{A}'$ as Lie algebras.
$\mathfrak{A}\cong \mathfrak{A}'$ as Lie algebras.
Proof. Define ![]() $\varphi: {\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}}\rightarrow {\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}}$ on simple tensors by
$\varphi: {\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}}\rightarrow {\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}}$ on simple tensors by ![]() $\varphi(A\otimes f)=\tau_1(A)\otimes \tilde{\tau}_2f$, where
$\varphi(A\otimes f)=\tau_1(A)\otimes \tilde{\tau}_2f$, where ![]() $A\in {\mathfrak{g}}$,
$A\in {\mathfrak{g}}$, ![]() $f\in {\mathcal{O}_{\mathbb{X}}}$ and
$f\in {\mathcal{O}_{\mathbb{X}}}$ and ![]() $\tilde{\tau}_2f(z)=f(\tau_2^{-1}z)$ for
$\tilde{\tau}_2f(z)=f(\tau_2^{-1}z)$ for ![]() $z\in \mathbb{X}$, and extend φ
$z\in \mathbb{X}$, and extend φ ![]() ${\mathbb{C}}$-linearly to the whole space. It is a straightforward verification that φ is Lie algebra isomorphism and that
${\mathbb{C}}$-linearly to the whole space. It is a straightforward verification that φ is Lie algebra isomorphism and that ![]() $\varphi\circ\tilde{\rho}(\gamma)=\tilde{\rho}'(\gamma)\circ \varphi$ for all
$\varphi\circ\tilde{\rho}(\gamma)=\tilde{\rho}'(\gamma)\circ \varphi$ for all ![]() $\gamma\in \Gamma$, that is, it intertwines
$\gamma\in \Gamma$, that is, it intertwines ![]() $\tilde{\rho}$ and
$\tilde{\rho}$ and ![]() $\tilde{\rho}'$. This implies that
$\tilde{\rho}'$. This implies that ![]() $a\in {\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}}$ is invariant with respect to the action defined by
$a\in {\mathfrak{g}}\otimes_{{\mathbb{C}}}{\mathcal{O}_{\mathbb{X}}}$ is invariant with respect to the action defined by ![]() $\tilde{\rho}$ if and only if
$\tilde{\rho}$ if and only if ![]() $\varphi(a)$ is invariant with respect to the action defined by
$\varphi(a)$ is invariant with respect to the action defined by ![]() $\tilde{\rho}'$. Thus φ restricts to an isomorphism between
$\tilde{\rho}'$. Thus φ restricts to an isomorphism between ![]() $\mathfrak{A}$ and
$\mathfrak{A}$ and ![]() $\mathfrak{A}'.$
$\mathfrak{A}'.$
4. Symmetry groups with  ${\mathfrak{g}}=\mathfrak{sl}_2$
${\mathfrak{g}}=\mathfrak{sl}_2$
In this section, we will investigate which symmetry groups Γ will play a role in the confined context of our classification scheme. This requires an understanding of the finite subgroups of ![]() $\mathrm{Aut}(\mathfrak{sl}_2)$ and of
$\mathrm{Aut}(\mathfrak{sl}_2)$ and of ![]() $\mathrm{Aut}_{}\!\left(T \right)$.
$\mathrm{Aut}_{}\!\left(T \right)$.
Lemma 5 (Klein)
Finite subgroups of ![]() $\mathrm{Aut}(\mathfrak{sl}_2)$ are classified by the list
$\mathrm{Aut}(\mathfrak{sl}_2)$ are classified by the list
If two finite subgroups of ![]() $\mathrm{Aut}(\mathfrak{sl}_2)$ are isomorphic, then they are conjugate.
$\mathrm{Aut}(\mathfrak{sl}_2)$ are isomorphic, then they are conjugate.
Proof. The group ![]() $\mathrm{Aut}(\mathfrak{sl}_2)$ is isomorphic to
$\mathrm{Aut}(\mathfrak{sl}_2)$ is isomorphic to ![]() $\mathrm{PSL}_2({\mathbb{C}})$ by the adjoint representation. A finite subgroup of
$\mathrm{PSL}_2({\mathbb{C}})$ by the adjoint representation. A finite subgroup of ![]() $\mathrm{PSL}_2({\mathbb{C}})$ leaves a Hermitian inner product invariant and is therefore conjugate to a subgroup of
$\mathrm{PSL}_2({\mathbb{C}})$ leaves a Hermitian inner product invariant and is therefore conjugate to a subgroup of ![]() $\mathrm{PSU}_2$ which in turn is isomorphic to
$\mathrm{PSU}_2$ which in turn is isomorphic to ![]() $\mathrm{SO}_3$. Therefore, the statement of the lemma is equivalent to the analogue statement for the Lie group
$\mathrm{SO}_3$. Therefore, the statement of the lemma is equivalent to the analogue statement for the Lie group ![]() $\mathrm{SO}_3$ instead of
$\mathrm{SO}_3$ instead of ![]() $\mathrm{Aut}(\mathfrak{sl}_2)$. Klein showed that the subgroups of
$\mathrm{Aut}(\mathfrak{sl}_2)$. Klein showed that the subgroups of ![]() $\mathrm{SO}_3$ are precisely the orientation preserving isometries of
$\mathrm{SO}_3$ are precisely the orientation preserving isometries of ![]() $\mathbb{R}^3$ that fix the regular pyramids, regular polygons, regular tetrahedrons, regular octahedrons and regular icosahedrons, centred at the origin [Reference Klein17]. This yields the groups listed in the statement, respectively. We may moreover assume that the vertices of the polyhedra have norm 1. If we then take two polyhedra of the same type, there is an element of
$\mathbb{R}^3$ that fix the regular pyramids, regular polygons, regular tetrahedrons, regular octahedrons and regular icosahedrons, centred at the origin [Reference Klein17]. This yields the groups listed in the statement, respectively. We may moreover assume that the vertices of the polyhedra have norm 1. If we then take two polyhedra of the same type, there is an element of ![]() $\mathrm{SO}_3$ that transforms one to the other. This group element conjugates the symmetry groups of the two polyhedra and proves the last statement of the lemma.
$\mathrm{SO}_3$ that transforms one to the other. This group element conjugates the symmetry groups of the two polyhedra and proves the last statement of the lemma.
Lemma 6. A finite group G embeds in ![]() $\mathrm{Aut}(\mathfrak{sl}_2)$ and
$\mathrm{Aut}(\mathfrak{sl}_2)$ and ![]() $\mathrm{Aut}_{}\!\left(T \right)$ if and only if G equals
$\mathrm{Aut}_{}\!\left(T \right)$ if and only if G equals
(1)
 $C_N,\quad N\geqslant 1$
$C_N,\quad N\geqslant 1$(2)
 $D_N,\quad N\geqslant 2$
$D_N,\quad N\geqslant 2$(3)
 $A_4,\quad (g_2(\tau)=0)$
$A_4,\quad (g_2(\tau)=0)$
Proof. By Lemma 5, we know that the finite subgroups of ![]() $\mathrm{Aut}(\mathfrak{sl}_2)$ are given by
$\mathrm{Aut}(\mathfrak{sl}_2)$ are given by
We will show that only the subgroups as given in the statement are simultaneously subgroups of ![]() $\mathrm{Aut}(T)$ as well.
$\mathrm{Aut}(T)$ as well.
Let T be a complex torus. It follows from [Reference Miranda25, Proposition III.1.11] that any automorphism σ of T is of the form ![]() $\sigma(z)=\epsilon z+\alpha$, where ϵ is a suitable root of unity (for which T has multiplication by ϵ) and
$\sigma(z)=\epsilon z+\alpha$, where ϵ is a suitable root of unity (for which T has multiplication by ϵ) and ![]() $\alpha\in T$. This immediately gives a semi-direct product structure
$\alpha\in T$. This immediately gives a semi-direct product structure ![]() $\mathrm{Aut}(T)=\mathrm{Aut}_0(T) \ltimes t(T)$ where
$\mathrm{Aut}(T)=\mathrm{Aut}_0(T) \ltimes t(T)$ where ![]() $\mathrm{Aut}_0(T)$ is the group of automorphisms fixing zero and t(T) is the group of translations of T. Now, take two automorphisms
$\mathrm{Aut}_0(T)$ is the group of automorphisms fixing zero and t(T) is the group of translations of T. Now, take two automorphisms ![]() $\sigma,\sigma'$ defined by
$\sigma,\sigma'$ defined by ![]() $\sigma(z)=\epsilon z+\alpha$ and
$\sigma(z)=\epsilon z+\alpha$ and ![]() $\sigma'(z)=\epsilon'z+\alpha'$. Then
$\sigma'(z)=\epsilon'z+\alpha'$. Then ![]() $[\sigma,\sigma'](z)=z-\alpha'-\epsilon'\alpha+\epsilon\alpha'+\alpha$, so that
$[\sigma,\sigma'](z)=z-\alpha'-\epsilon'\alpha+\epsilon\alpha'+\alpha$, so that ![]() $[\sigma,\sigma']$ is indeed a translation. Hence
$[\sigma,\sigma']$ is indeed a translation. Hence ![]() $[\mathrm{Aut}(T),\mathrm{Aut}(T)]\subset t(T)$.
$[\mathrm{Aut}(T),\mathrm{Aut}(T)]\subset t(T)$.
Now, let ![]() $r\in t(T)$ be any translation of T, say
$r\in t(T)$ be any translation of T, say ![]() $r(z)=z+\alpha$. We will show that there are
$r(z)=z+\alpha$. We will show that there are ![]() $s\in \mathrm{Aut}_0(T)$ and
$s\in \mathrm{Aut}_0(T)$ and ![]() $r'\in \mathrm{Aut}(T)$ such that
$r'\in \mathrm{Aut}(T)$ such that ![]() $r=[s,r']$. Suppose
$r=[s,r']$. Suppose ![]() $s(z)=-z$ (any torus has multiplication by −1) and let
$s(z)=-z$ (any torus has multiplication by −1) and let ![]() $r'(z)=z-\frac{\alpha}{2}$. Then
$r'(z)=z-\frac{\alpha}{2}$. Then ![]() $sr'(z)=-z+\frac{\alpha}{2}$. Hence
$sr'(z)=-z+\frac{\alpha}{2}$. Hence ![]() $[s,r'](z)=-(-z-\frac{\alpha}{2}-\frac{\alpha}{2})=z+\alpha=r(z)$. This proves the claim that
$[s,r'](z)=-(-z-\frac{\alpha}{2}-\frac{\alpha}{2})=z+\alpha=r(z)$. This proves the claim that ![]() $[\mathrm{Aut}(T),\mathrm{Aut}(T)]=t(T)$.
$[\mathrm{Aut}(T),\mathrm{Aut}(T)]=t(T)$.
For the proof that CN, DN are subgroups of ![]() $\mathrm{Aut}(T)$, as well as A 4 for a suitable torus T, we refer to Lemma 7.
$\mathrm{Aut}(T)$, as well as A 4 for a suitable torus T, we refer to Lemma 7.
Let us now argue that S 4 and A 5 are not subgroups of ![]() $\mathrm{Aut}(T)$ for any complex torus T. To see that S 4 is not a subgroup of
$\mathrm{Aut}(T)$ for any complex torus T. To see that S 4 is not a subgroup of ![]() $\mathrm{Aut}(T)$, note that
$\mathrm{Aut}(T)$, note that ![]() $[S_4,S_4]=A_4$, which is non-abelian, whereas for
$[S_4,S_4]=A_4$, which is non-abelian, whereas for ![]() $\Gamma\subset \mathrm{Aut}(T)$, the commutator subgroup
$\Gamma\subset \mathrm{Aut}(T)$, the commutator subgroup ![]() $[\Gamma,\Gamma]\subset t(T)$ is abelian.
$[\Gamma,\Gamma]\subset t(T)$ is abelian.
Finally, suppose for a contradiction that ![]() $A_5\subset \mathrm{Aut}(T)$ for some complex torus T. Then
$A_5\subset \mathrm{Aut}(T)$ for some complex torus T. Then ![]() $A_5\cong C_{\ell} \ltimes H$ for some normal subgroup H ≠ 1, since
$A_5\cong C_{\ell} \ltimes H$ for some normal subgroup H ≠ 1, since ![]() $\mathrm{Aut}(T)=\mathrm{Aut}_0(T) \ltimes t(T)$. However, A 5 is simple and thus it cannot have a proper normal subgroup. This shows that the list above is all there is in the intersection of finite subgroups of
$\mathrm{Aut}(T)=\mathrm{Aut}_0(T) \ltimes t(T)$. However, A 5 is simple and thus it cannot have a proper normal subgroup. This shows that the list above is all there is in the intersection of finite subgroups of ![]() $\mathrm{Aut}(\mathfrak{sl}_2)$ and
$\mathrm{Aut}(\mathfrak{sl}_2)$ and ![]() $\mathrm{Aut}(T)$, for all complex tori T.
$\mathrm{Aut}(T)$, for all complex tori T.
Remark 1. Observe that we can write the groups from Lemma 6 in terms of semidirect products as follows:
where ![]() $\ell\in \{1,2,3,4,6\}$ and
$\ell\in \{1,2,3,4,6\}$ and ![]() $N\in \mathbb{N}.$ When we write
$N\in \mathbb{N}.$ When we write ![]() $G \ltimes K\subset \mathrm{Aut}_0(T) \ltimes t(T)$, we shall tacitly assume that
$G \ltimes K\subset \mathrm{Aut}_0(T) \ltimes t(T)$, we shall tacitly assume that ![]() $G\subset \mathrm{Aut}_0(T)$ and
$G\subset \mathrm{Aut}_0(T)$ and ![]() $K\subset t(T)$.
$K\subset t(T)$.
Lemma 7. The subgroups of ![]() $\mathrm{Aut}_{}\!\left(T \right)$ which are isomorphic to one of the finite groups of Lemma 6 are classified by the following list, up to conjugation.
$\mathrm{Aut}_{}\!\left(T \right)$ which are isomorphic to one of the finite groups of Lemma 6 are classified by the following list, up to conjugation.
(1)
 $C_N=\langle r: r^N=1\rangle$,
$C_N=\langle r: r^N=1\rangle$,(a)
 $C_{\ell}\subset \mathrm{Aut}_0(T),\quad r(z)=\mathrm{e}^{ 2\pi {i}/\ell}z\quad (\ell\in\{2,3,4,6)\}).$
$C_{\ell}\subset \mathrm{Aut}_0(T),\quad r(z)=\mathrm{e}^{ 2\pi {i}/\ell}z\quad (\ell\in\{2,3,4,6)\}).$(b)
 $C_N \subset t(T),\quad r(z)=z+\alpha \quad (\alpha\,\,\text{is a}\,\, N\text{-torsion point in }T).$
$C_N \subset t(T),\quad r(z)=z+\alpha \quad (\alpha\,\,\text{is a}\,\, N\text{-torsion point in }T).$
(2)
 $D_N=\langle s,r:s^2=r^N=1, \, (sr)^2=1\rangle$,
$D_N=\langle s,r:s^2=r^N=1, \, (sr)^2=1\rangle$,(a)
 $C_2\times C_2\subset t(T),\quad s(z)=z+\tau/2, \quad r(z)=z+1/2.$
$C_2\times C_2\subset t(T),\quad s(z)=z+\tau/2, \quad r(z)=z+1/2.$(b)
 $C_2 \ltimes C_N\subset \mathrm{Aut}_0(T) \ltimes t(T), s(z)=-z, r(z)=z+\alpha\,(\alpha {\,is \,a}\, N\text{-torsion point in }T)$.
$C_2 \ltimes C_N\subset \mathrm{Aut}_0(T) \ltimes t(T), s(z)=-z, r(z)=z+\alpha\,(\alpha {\,is \,a}\, N\text{-torsion point in }T)$.
(3)
 $A_4=\langle s, r_1,r_2: s^3=r_1^2=r_2^2=1,\, sr_1s^{-1}=r_1r_2=r_2r_1,\, sr_2s^{-1}=r_1\rangle$,
$A_4=\langle s, r_1,r_2: s^3=r_1^2=r_2^2=1,\, sr_1s^{-1}=r_1r_2=r_2r_1,\, sr_2s^{-1}=r_1\rangle$,  $\tau=\mathrm{e}^{2\pi {i}/3}$,
$\tau=\mathrm{e}^{2\pi {i}/3}$, $s(z)=\mathrm{e}^{2\pi {i}/3}z,\quad r_1(z)= z+1/2.$
$s(z)=\mathrm{e}^{2\pi {i}/3}z,\quad r_1(z)= z+1/2.$
Here we recall that the case 1a with ![]() $\ell=3,4$ or 6 and the case 3 only occurs for special tori, cf. [Reference Miranda25, Proposition III.1.12], and the other cases occur in any torus.
$\ell=3,4$ or 6 and the case 3 only occurs for special tori, cf. [Reference Miranda25, Proposition III.1.12], and the other cases occur in any torus.
Proof. We leave it to the reader to verify that the subgroups in the statements satisfy the group relations and thus are indeed of the mentioned isomorphism class.
We start with the cyclic groups. If an element r of ![]() $\mathrm{Aut}(T)$ fixes an element p of T, then
$\mathrm{Aut}(T)$ fixes an element p of T, then ![]() $t(p) r t(p)^{-1}\in \mathrm{Aut}_0(T)$ (where
$t(p) r t(p)^{-1}\in \mathrm{Aut}_0(T)$ (where ![]() $t(p)(z)=z+p$) and
$t(p)(z)=z+p$) and ![]() $t(p) \langle r\rangle t(p)^{-1}$ is as described in 1a. If on the other hand r has no fixed points, then it is as described in 1b.
$t(p) \langle r\rangle t(p)^{-1}$ is as described in 1a. If on the other hand r has no fixed points, then it is as described in 1b.
Now for the dihedral groups, consider first the abelian case ![]() $D_2=C_2\times C_2$. This group occurs precisely once in t(T), as in 2a, since both groups have precisely three elements of order 2.
$D_2=C_2\times C_2$. This group occurs precisely once in t(T), as in 2a, since both groups have precisely three elements of order 2.
Suppose now that ![]() $D_2\subset \mathrm{Aut}(T)$ has an element s which is not contained in t(T). Using a conjugation as we did to classify the cyclic groups, we may assume that
$D_2\subset \mathrm{Aut}(T)$ has an element s which is not contained in t(T). Using a conjugation as we did to classify the cyclic groups, we may assume that ![]() $s\in\mathrm{Aut}_0(T)$, so that
$s\in\mathrm{Aut}_0(T)$, so that ![]() $s(z)=-z$. There must also be a non-trivial element of D 2, say r, contained in t(T). Indeed, the elements of order 2 in
$s(z)=-z$. There must also be a non-trivial element of D 2, say r, contained in t(T). Indeed, the elements of order 2 in ![]() $\mathrm{Aut}(T)\setminus t(T)$ are the maps
$\mathrm{Aut}(T)\setminus t(T)$ are the maps ![]() $z\mapsto -z+b$. A product of two such maps is in t(T). Thus the group D 2 is as described in 2b with N = 2.
$z\mapsto -z+b$. A product of two such maps is in t(T). Thus the group D 2 is as described in 2b with N = 2.
For the remaining dihedral groups ![]() $D_N\subset\mathrm{Aut}(T)$ (
$D_N\subset\mathrm{Aut}(T)$ (![]() $N\ge 3$), we notice that
$N\ge 3$), we notice that ![]() $[D_N,D_N]=\langle r^2\rangle\subset [\mathrm{Aut}(T),\mathrm{Aut}(T)]\subset t(T)$ implies that
$[D_N,D_N]=\langle r^2\rangle\subset [\mathrm{Aut}(T),\mathrm{Aut}(T)]\subset t(T)$ implies that ![]() $r\in t(T)$. At least one of the order 2 elements
$r\in t(T)$. At least one of the order 2 elements ![]() $D_N\setminus\langle r \rangle$ must be outside of t(T) because DN is non-abelian. Taking a conjugate of the group, we may again assume that such an element, say s, fixes 0. Thus, we arrive at the remaining groups described in 1b.
$D_N\setminus\langle r \rangle$ must be outside of t(T) because DN is non-abelian. Taking a conjugate of the group, we may again assume that such an element, say s, fixes 0. Thus, we arrive at the remaining groups described in 1b.
Finally, for the group A 4, we argue as follows. The derived subgroup ![]() $[A_4,A_4]=\langle r_1,r_2\rangle\subset [\mathrm{Aut}(T),\mathrm{Aut}(T)]\subset t(T)$ is uniquely determined by the only three elements in t(T) of order 2. The element s must be outside of t(T) for A 4 is non-abelian. Taking a conjugate of the group, we may assume that s fixes zero, which leaves two options:
$[A_4,A_4]=\langle r_1,r_2\rangle\subset [\mathrm{Aut}(T),\mathrm{Aut}(T)]\subset t(T)$ is uniquely determined by the only three elements in t(T) of order 2. The element s must be outside of t(T) for A 4 is non-abelian. Taking a conjugate of the group, we may assume that s fixes zero, which leaves two options: ![]() $s(z)=\mathrm{e}^{2\pi {i}/3}z$ and
$s(z)=\mathrm{e}^{2\pi {i}/3}z$ and ![]() $s(z)=\mathrm{e}^{4\pi {i}/3}z$. Both options generate the same group, since there is an automorphism of A 4 sending s to s 2.
$s(z)=\mathrm{e}^{4\pi {i}/3}z$. Both options generate the same group, since there is an automorphism of A 4 sending s to s 2.
Remark 2. The lemma above gives a classification of subgroups ![]() $\Gamma\subset\mathrm{Aut}(T)$. One may be interested in a classification of embeddings (injective homomorphisms)
$\Gamma\subset\mathrm{Aut}(T)$. One may be interested in a classification of embeddings (injective homomorphisms) ![]() $\Gamma\to\mathrm{Aut}(T)$ instead. The difference is in the consideration of
$\Gamma\to\mathrm{Aut}(T)$ instead. The difference is in the consideration of ![]() $\mathrm{Aut}(\Gamma)$: two embeddings
$\mathrm{Aut}(\Gamma)$: two embeddings ![]() $\Gamma\to\mathrm{Aut}(T)$ have the same image if and only if one is the composition of the other with an automorphism of Γ.
$\Gamma\to\mathrm{Aut}(T)$ have the same image if and only if one is the composition of the other with an automorphism of Γ.
Lemma 8. Let ![]() $\Gamma\subset \mathrm{Aut}_0(T) \ltimes t(T)$ be a finite subgroup and
$\Gamma\subset \mathrm{Aut}_0(T) \ltimes t(T)$ be a finite subgroup and ![]() ${\mathbb{T}}=T\setminus \Gamma\cdot\{0\}$. Then for the canonical projection
${\mathbb{T}}=T\setminus \Gamma\cdot\{0\}$. Then for the canonical projection ![]() $\pi:{\mathbb{T}}\rightarrow {\mathbb{T}}/\Gamma$, we have
$\pi:{\mathbb{T}}\rightarrow {\mathbb{T}}/\Gamma$, we have
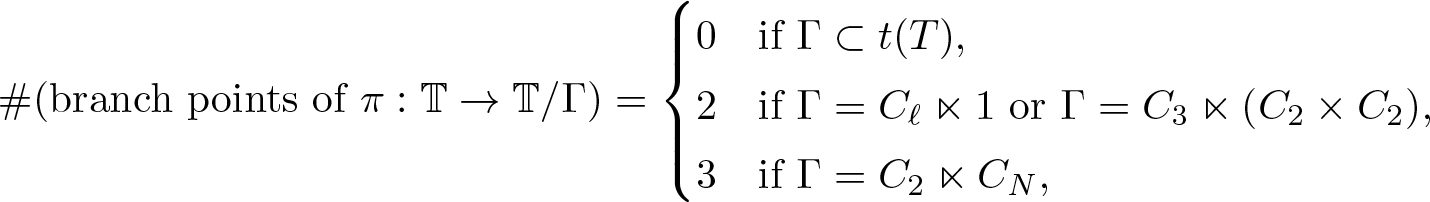 \begin{equation*}\#(\text{branch points of }\pi:{\mathbb{T}}\rightarrow {\mathbb{T}}/\Gamma)=\begin{cases} 0\quad \text{if}\,\, \Gamma\subset t(T),\\
2\quad \text{if}\,\, \Gamma=C_{\ell} \ltimes 1\,\, \text{or} \,\, \Gamma=C_3 \ltimes (C_2\times C_2),\\
3\quad \text{if}\,\, \Gamma=C_2 \ltimes C_N,
\end{cases}\end{equation*}
\begin{equation*}\#(\text{branch points of }\pi:{\mathbb{T}}\rightarrow {\mathbb{T}}/\Gamma)=\begin{cases} 0\quad \text{if}\,\, \Gamma\subset t(T),\\
2\quad \text{if}\,\, \Gamma=C_{\ell} \ltimes 1\,\, \text{or} \,\, \Gamma=C_3 \ltimes (C_2\times C_2),\\
3\quad \text{if}\,\, \Gamma=C_2 \ltimes C_N,
\end{cases}\end{equation*} where ![]() $\ell\in \{3,4,6\}$.
$\ell\in \{3,4,6\}$.
Proof. A point ![]() $p\in T$ is a ramification point of π if the multiplicity of π at p, denoted by
$p\in T$ is a ramification point of π if the multiplicity of π at p, denoted by ![]() $\mathrm{mult}_p(\pi)$, is at least 2. By [Reference Miranda25, Theorem III.3.4],
$\mathrm{mult}_p(\pi)$, is at least 2. By [Reference Miranda25, Theorem III.3.4], ![]() $\mathrm{mult}_p(\pi)$ equals
$\mathrm{mult}_p(\pi)$ equals ![]() $|\Gamma_p|$, where
$|\Gamma_p|$, where ![]() $\Gamma_p=\{\gamma\in\Gamma: \gamma\cdot p=p\}$. It is clear there are no branch points if
$\Gamma_p=\{\gamma\in\Gamma: \gamma\cdot p=p\}$. It is clear there are no branch points if ![]() $\Gamma\subset t(T)$ since a translation has no fixed points. Let now
$\Gamma\subset t(T)$ since a translation has no fixed points. Let now ![]() $\Gamma=C_3\subset \mathrm{Aut}_0(T)$ where
$\Gamma=C_3\subset \mathrm{Aut}_0(T)$ where ![]() $T={\mathbb{C}}/{\mathbb{Z}}\oplus {\mathbb{Z}}\omega_6$. It is straightforward to check that
$T={\mathbb{C}}/{\mathbb{Z}}\oplus {\mathbb{Z}}\omega_6$. It is straightforward to check that ![]() $|\Gamma_p| \gt 1$ if and only if
$|\Gamma_p| \gt 1$ if and only if ![]() $p\in \{0,1/2,\omega_6/2,(1+\omega_6)/2\}$. The only points that are in the same Γ-orbit, are
$p\in \{0,1/2,\omega_6/2,(1+\omega_6)/2\}$. The only points that are in the same Γ-orbit, are ![]() $1/2$ and
$1/2$ and ![]() $\omega_6/2$. Hence the total number of branch points of π after deleting
$\omega_6/2$. Hence the total number of branch points of π after deleting ![]() $\Gamma\cdot \{0\}$ equals 2. The other cases follow by similar arguments.
$\Gamma\cdot \{0\}$ equals 2. The other cases follow by similar arguments.
5. Functional aspects of aLia on complex tori
We will now discuss the functional aspects of aLias on complex tori. Since we are considering meromorphic ![]() $\mathfrak{sl}_2$-valued maps on a complex torus, a starting point is to understand meromorphic functions on a complex torus. There are multiple (equivalent) approaches to this, e.g. via Jacobi theta-functions or Weierstrass functions. We shall further develop the approach with the Weierstrass
$\mathfrak{sl}_2$-valued maps on a complex torus, a starting point is to understand meromorphic functions on a complex torus. There are multiple (equivalent) approaches to this, e.g. via Jacobi theta-functions or Weierstrass functions. We shall further develop the approach with the Weierstrass ![]() $\wp$-function, as we have started to do before Example 3.
$\wp$-function, as we have started to do before Example 3.
Below we will formulate some elementary properties of the Weierstrass ![]() $\wp$-function. Define the values of the half lattice points of a given lattice
$\wp$-function. Define the values of the half lattice points of a given lattice ![]() ${\Lambda}_{\tau}={\mathbb{Z}}\oplus {\mathbb{Z}}\tau$, under
${\Lambda}_{\tau}={\mathbb{Z}}\oplus {\mathbb{Z}}\tau$, under ![]() $\wp_{{\Lambda}_{\tau}}$:
$\wp_{{\Lambda}_{\tau}}$:
Observe that ![]() $\wp_{{\Lambda}_{\tau}}'$ vanishes at the half lattice points, since
$\wp_{{\Lambda}_{\tau}}'$ vanishes at the half lattice points, since ![]() $\wp_{{\Lambda}_{\tau}}'(-z)=-\wp_{{\Lambda}_{\tau}}'(z)$.
$\wp_{{\Lambda}_{\tau}}'(-z)=-\wp_{{\Lambda}_{\tau}}'(z)$.
As we have remarked before Example 3, there is the relation between the square of the derivative ![]() $\wp'$ and
$\wp'$ and ![]() $\wp$ itself, where we now write
$\wp$ itself, where we now write ![]() $\wp$ without specifying the lattice:
$\wp$ without specifying the lattice:
Because ![]() $\wp'$ vanishes at the half lattice points, the right-hand side of (5.2) factors as
$\wp'$ vanishes at the half lattice points, the right-hand side of (5.2) factors as ![]() $4(\wp-e_1)(\wp-e_2)(\wp-e_3)$. From this, one gets the following relations between the ei:
$4(\wp-e_1)(\wp-e_2)(\wp-e_3)$. From this, one gets the following relations between the ei:
The next basic lemma records how Weierstrass ![]() $\wp$-functions associated to homothetic lattices are related.
$\wp$-functions associated to homothetic lattices are related.
Lemma 9. For ![]() $\alpha\in\mathbb{C}^{*}$, we have
$\alpha\in\mathbb{C}^{*}$, we have ![]() $\wp_{\alpha\Lambda}(z)=\alpha^{-2}\wp_{\Lambda}\left(\alpha^{-1}z\right).$
$\wp_{\alpha\Lambda}(z)=\alpha^{-2}\wp_{\Lambda}\left(\alpha^{-1}z\right).$
We write out explicitly two special cases of Lemma 9 that will play an important role in the course of the paper. These cases correspond to the square lattice ![]() ${\Lambda}_i={\mathbb{Z}}\oplus {\mathbb{Z}} i$ and the hexagonal lattice
${\Lambda}_i={\mathbb{Z}}\oplus {\mathbb{Z}} i$ and the hexagonal lattice ![]() ${\Lambda}_{\omega_6}={\mathbb{Z}}\oplus {\mathbb{Z}}\omega_6$, which are the only lattices (up to homothety) that satisfy the property
${\Lambda}_{\omega_6}={\mathbb{Z}}\oplus {\mathbb{Z}}\omega_6$, which are the only lattices (up to homothety) that satisfy the property ![]() $\alpha {\Lambda}={\Lambda}$ for some
$\alpha {\Lambda}={\Lambda}$ for some ![]() $\alpha\neq \pm 1$:
$\alpha\neq \pm 1$:
 \begin{align}
\wp_{{\Lambda}_i}(i^{-1}z)&=-\wp_{{\Lambda}_i}(z), &\wp_{{\Lambda}_i}'(i^{-1}z)&=-i\wp_{{\Lambda}_i}'(z),
\end{align}
\begin{align}
\wp_{{\Lambda}_i}(i^{-1}z)&=-\wp_{{\Lambda}_i}(z), &\wp_{{\Lambda}_i}'(i^{-1}z)&=-i\wp_{{\Lambda}_i}'(z),
\end{align} \begin{align}
\wp_{{\Lambda}_{\omega_6}}(\omega_6^{-1}z)&=\omega_6^{2}\wp_{{\Lambda}_{\omega_6}}(z),&\wp_{{\Lambda}_{\omega_6}}'(\omega_6^{-1}z)&=-\wp_{{\Lambda}_{\omega_6}}'(z).
\end{align}
\begin{align}
\wp_{{\Lambda}_{\omega_6}}(\omega_6^{-1}z)&=\omega_6^{2}\wp_{{\Lambda}_{\omega_6}}(z),&\wp_{{\Lambda}_{\omega_6}}'(\omega_6^{-1}z)&=-\wp_{{\Lambda}_{\omega_6}}'(z).
\end{align} The next lemma describes the isotypical components of the action ![]() $C_{\ell}\subset \mathrm{Aut}_0(T)$ on
$C_{\ell}\subset \mathrm{Aut}_0(T)$ on ![]() $\mathcal{O}_{\mathbb{T}}$, where
$\mathcal{O}_{\mathbb{T}}$, where ![]() $\ell\in \{2,3,4,6\}$ and T is a suitable complex torus. These decompositions will be used in Theorem 5, where we construct a basis for aLias with symmetry group
$\ell\in \{2,3,4,6\}$ and T is a suitable complex torus. These decompositions will be used in Theorem 5, where we construct a basis for aLias with symmetry group ![]() $C_{\ell}$. We denote by χj,
$C_{\ell}$. We denote by χj, ![]() $j=0,\ldots,\ell-1$ the characters of the group
$j=0,\ldots,\ell-1$ the characters of the group ![]() $C_{\ell}$, which are defined as
$C_{\ell}$, which are defined as  $\chi_j(r^k)=\omega_\ell^{jk}$, where r generates
$\chi_j(r^k)=\omega_\ell^{jk}$, where r generates ![]() $C_{\ell}$.
$C_{\ell}$.
Lemma 10. Let ![]() $\sigma_{\ell}:C_{\ell}\rightarrow \mathrm{Aut}_0(T)$ be the homomorphism
$\sigma_{\ell}:C_{\ell}\rightarrow \mathrm{Aut}_0(T)$ be the homomorphism ![]() $\sigma_{\ell}(r)(z)=\omega_{\ell}z$ and let
$\sigma_{\ell}(r)(z)=\omega_{\ell}z$ and let ![]() $\wp:=\wp_{{\Lambda}}$. Suppose that
$\wp:=\wp_{{\Lambda}}$. Suppose that ![]() $\mathcal{S}=\{0\}$ and
$\mathcal{S}=\{0\}$ and ![]() $\mathbb{T}=T\setminus \mathcal{S}$. Then for
$\mathbb{T}=T\setminus \mathcal{S}$. Then for ![]() $\Gamma=C_2$ we have
$\Gamma=C_2$ we have
For ![]() $\Gamma=C_3$ we have
$\Gamma=C_3$ we have
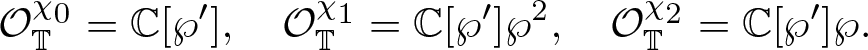 \begin{equation*}
\mathcal{O}_{\mathbb{T}}^{\chi_0}={\mathbb{C}}[\wp'],\quad \mathcal{O}_{\mathbb{T}}^{\chi_1}={\mathbb{C}}[\wp']\wp^2,\quad \mathcal{O}_{\mathbb{T}}^{\chi_2}={\mathbb{C}}[\wp']\wp.
\end{equation*}
\begin{equation*}
\mathcal{O}_{\mathbb{T}}^{\chi_0}={\mathbb{C}}[\wp'],\quad \mathcal{O}_{\mathbb{T}}^{\chi_1}={\mathbb{C}}[\wp']\wp^2,\quad \mathcal{O}_{\mathbb{T}}^{\chi_2}={\mathbb{C}}[\wp']\wp.
\end{equation*} For ![]() $\Gamma=C_4$ we have
$\Gamma=C_4$ we have
 \begin{align*}
\mathcal{O}_{\mathbb{T}}^{\chi_0}&={\mathbb{C}}[\wp^2], &
\mathcal{O}_{\mathbb{T}}^{\chi_1}&={\mathbb{C}}[\wp^2]\wp \wp',\\
\mathcal{O}_{\mathbb{T}}^{\chi_2}&={\mathbb{C}}[\wp^2]\wp, &
\mathcal{O}_{\mathbb{T}}^{\chi_3}&={\mathbb{C}}[\wp^2]\wp'.
\end{align*}
\begin{align*}
\mathcal{O}_{\mathbb{T}}^{\chi_0}&={\mathbb{C}}[\wp^2], &
\mathcal{O}_{\mathbb{T}}^{\chi_1}&={\mathbb{C}}[\wp^2]\wp \wp',\\
\mathcal{O}_{\mathbb{T}}^{\chi_2}&={\mathbb{C}}[\wp^2]\wp, &
\mathcal{O}_{\mathbb{T}}^{\chi_3}&={\mathbb{C}}[\wp^2]\wp'.
\end{align*} For ![]() $\Gamma=C_6$ we have
$\Gamma=C_6$ we have
 \begin{align*}
\mathcal{O}_{\mathbb{T}}^{\chi_0}&={\mathbb{C}}[\wp^3], &
\mathcal{O}_{\mathbb{T}}^{\chi_1}&={\mathbb{C}}[\wp^3]\wp^2 \wp',\\
\mathcal{O}_{\mathbb{T}}^{\chi_2}&={\mathbb{C}}[\wp^3]\wp, &
\mathcal{O}_{\mathbb{T}}^{\chi_3}&={\mathbb{C}}[\wp^3]\wp',\\
\mathcal{O}_{\mathbb{T}}^{\chi_4}&={\mathbb{C}}[\wp^3]\wp^2,&
\mathcal{O}_{\mathbb{T}}^{\chi_5}&={\mathbb{C}}[\wp^3]\wp\wp'.
\end{align*}
\begin{align*}
\mathcal{O}_{\mathbb{T}}^{\chi_0}&={\mathbb{C}}[\wp^3], &
\mathcal{O}_{\mathbb{T}}^{\chi_1}&={\mathbb{C}}[\wp^3]\wp^2 \wp',\\
\mathcal{O}_{\mathbb{T}}^{\chi_2}&={\mathbb{C}}[\wp^3]\wp, &
\mathcal{O}_{\mathbb{T}}^{\chi_3}&={\mathbb{C}}[\wp^3]\wp',\\
\mathcal{O}_{\mathbb{T}}^{\chi_4}&={\mathbb{C}}[\wp^3]\wp^2,&
\mathcal{O}_{\mathbb{T}}^{\chi_5}&={\mathbb{C}}[\wp^3]\wp\wp'.
\end{align*}Proof. We will only prove the claims for ![]() $\Gamma=C_3$; the rest follows in the same way. We know by Lemma 1 that
$\Gamma=C_3$; the rest follows in the same way. We know by Lemma 1 that ![]() $\mathcal{O}_{\mathbb{T}}=\mathbb{C}[\wp,\wp']$. Using (5.4) we see that
$\mathcal{O}_{\mathbb{T}}=\mathbb{C}[\wp,\wp']$. Using (5.4) we see that ![]() ${\mathbb{C}}[\wp']\subset \mathcal{O}_{\mathbb{T}}^{\chi_0}$,
${\mathbb{C}}[\wp']\subset \mathcal{O}_{\mathbb{T}}^{\chi_0}$, ![]() ${\mathbb{C}}[\wp']\wp^2\subset \mathcal{O}_{\mathbb{T}}^{\chi_1}$ and
${\mathbb{C}}[\wp']\wp^2\subset \mathcal{O}_{\mathbb{T}}^{\chi_1}$ and ![]() ${\mathbb{C}}[\wp']\wp\subset \mathcal{O}_{\mathbb{T}}^{\chi_2}.$ It remains to show that
${\mathbb{C}}[\wp']\wp\subset \mathcal{O}_{\mathbb{T}}^{\chi_2}.$ It remains to show that ![]() $\mathbb{C}[\wp,\wp']$ is a subset of
$\mathbb{C}[\wp,\wp']$ is a subset of ![]() ${\mathbb{C}}[\wp']\oplus {\mathbb{C}}[\wp']\wp^2\oplus {\mathbb{C}}[\wp']\wp$. If
${\mathbb{C}}[\wp']\oplus {\mathbb{C}}[\wp']\wp^2\oplus {\mathbb{C}}[\wp']\wp$. If ![]() $\wp^a\wp'^b$ is a monomial with
$\wp^a\wp'^b$ is a monomial with ![]() $a\ge 3$, then we can substitute
$a\ge 3$, then we can substitute  $\wp^3=\frac{1}{4}(\wp')^2+\frac{g_2}{4}\wp+\frac{g_3}{4}$, using (5.2), to obtain a polynomial in
$\wp^3=\frac{1}{4}(\wp')^2+\frac{g_2}{4}\wp+\frac{g_3}{4}$, using (5.2), to obtain a polynomial in ![]() $\wp$ and
$\wp$ and ![]() $\wp'$ where all exponents of
$\wp'$ where all exponents of ![]() $\wp$ are less than a. Repeating this substitution finitely many times, we see that
$\wp$ are less than a. Repeating this substitution finitely many times, we see that ![]() $\wp^a\wp'^b$ is an element of
$\wp^a\wp'^b$ is an element of ![]() ${\mathbb{C}}[\wp']\oplus {\mathbb{C}}[\wp']\wp^2\oplus {\mathbb{C}}[\wp']\wp$. Hence
${\mathbb{C}}[\wp']\oplus {\mathbb{C}}[\wp']\wp^2\oplus {\mathbb{C}}[\wp']\wp$. Hence ![]() $\mathbb{C}[\wp,\wp']$ is indeed a subset of
$\mathbb{C}[\wp,\wp']$ is indeed a subset of ![]() ${\mathbb{C}}[\wp']\oplus {\mathbb{C}}[\wp']\wp^2\oplus {\mathbb{C}}[\wp']\wp$.
${\mathbb{C}}[\wp']\oplus {\mathbb{C}}[\wp']\wp^2\oplus {\mathbb{C}}[\wp']\wp$.
ALias on complex tori with symmetry group Γ and base Lie algebra ![]() $\mathfrak{sl}_2$, as in our classification, turn out to be generated by three generators over their algebra of invariants, as we will establish in § 6. We would therefore like to know what the algebra of invariants
$\mathfrak{sl}_2$, as in our classification, turn out to be generated by three generators over their algebra of invariants, as we will establish in § 6. We would therefore like to know what the algebra of invariants ![]() $\mathcal{O}_{\mathbb{T}}^{\Gamma}$ is, to obtain explicit forms of the Lie algebras. For aLias with symmetry group
$\mathcal{O}_{\mathbb{T}}^{\Gamma}$ is, to obtain explicit forms of the Lie algebras. For aLias with symmetry group ![]() $C_N\subset t(T)$, this is described in the following lemma. For
$C_N\subset t(T)$, this is described in the following lemma. For ![]() $\alpha\in T$ of finite order, let
$\alpha\in T$ of finite order, let ![]() ${\Lambda}_{(\alpha)}={\mathbb{Z}}+{\mathbb{Z}}\alpha+{\mathbb{Z}}\tau$ and
${\Lambda}_{(\alpha)}={\mathbb{Z}}+{\mathbb{Z}}\alpha+{\mathbb{Z}}\tau$ and ![]() $T_{(\alpha)}={\mathbb{C}}/{\Lambda}_{(\alpha)}$.
$T_{(\alpha)}={\mathbb{C}}/{\Lambda}_{(\alpha)}$.
Lemma 11. Let ![]() $\sigma_{\alpha}:C_N\rightarrow \mathrm{Aut}(T)$ be given by
$\sigma_{\alpha}:C_N\rightarrow \mathrm{Aut}(T)$ be given by ![]() $\sigma_{\alpha}(r)(z)=z+\alpha$. Then
$\sigma_{\alpha}(r)(z)=z+\alpha$. Then
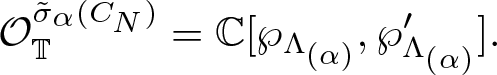 \begin{equation*}\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}_{\alpha}(C_N)}= {\mathbb{C}}[\wp_{\Lambda_{(\alpha)}}, \wp_{\Lambda_{(\alpha)}}'].\end{equation*}
\begin{equation*}\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}_{\alpha}(C_N)}= {\mathbb{C}}[\wp_{\Lambda_{(\alpha)}}, \wp_{\Lambda_{(\alpha)}}'].\end{equation*}Proof. We know that  $\mathcal{O}^{\tilde{\sigma}_\alpha(C_N)}_{\mathbb{T}}$ is the space of
$\mathcal{O}^{\tilde{\sigma}_\alpha(C_N)}_{\mathbb{T}}$ is the space of ![]() $\Lambda_{(\alpha)}$-periodic meromorphic functions which are holomorphic on
$\Lambda_{(\alpha)}$-periodic meromorphic functions which are holomorphic on ![]() $T\setminus \Lambda_{(\alpha)}$. With this perspective,
$T\setminus \Lambda_{(\alpha)}$. With this perspective,  $\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}_{\alpha}(C_N)}=\mathcal{O}_{\mathbb{T}/\sigma_{\alpha}(C_N)}$. Now use Lemma 1 with T taken to be the complex torus
$\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}_{\alpha}(C_N)}=\mathcal{O}_{\mathbb{T}/\sigma_{\alpha}(C_N)}$. Now use Lemma 1 with T taken to be the complex torus ![]() $T/\sigma_{\alpha}(C_N)$. Thus
$T/\sigma_{\alpha}(C_N)$. Thus  $\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}_{\alpha}(C_N)}=\mathbb{C}[\wp_{\Lambda_{(\alpha)}}, \wp_{\Lambda_{(\alpha)}}'].$
$\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}_{\alpha}(C_N)}=\mathbb{C}[\wp_{\Lambda_{(\alpha)}}, \wp_{\Lambda_{(\alpha)}}'].$
We will now construct meromorphic functions on complex tori that will play a fundamental role throughout, especially in the construction of normal forms. Given a meromorphic function f on T, the divisor (f) of f is defined as the following formal ![]() ${\mathbb{Z}}$-linear combination of points
${\mathbb{Z}}$-linear combination of points ![]() $p\in T$,
$p\in T$,  $(f)=\sum_{p\in T}\mathrm{ord}_p(f)(p)$, where
$(f)=\sum_{p\in T}\mathrm{ord}_p(f)(p)$, where ![]() $\mathrm{ord}_p(f)$ is the order of a zero or pole of f at p (if p is neither a zero nor a pole,
$\mathrm{ord}_p(f)$ is the order of a zero or pole of f at p (if p is neither a zero nor a pole, ![]() $\mathrm{ord}_p(f)=0$). Let
$\mathrm{ord}_p(f)=0$). Let ![]() $\{\chi_0,\dots, \chi_{N-1}\}$ denote the set of characters of the cyclic group CN. Embed this group as
$\{\chi_0,\dots, \chi_{N-1}\}$ denote the set of characters of the cyclic group CN. Embed this group as ![]() $\sigma(C_N)\subset \mathrm{Aut}(T)$, where
$\sigma(C_N)\subset \mathrm{Aut}(T)$, where ![]() $\sigma(r)z=z+\alpha.$ Let
$\sigma(r)z=z+\alpha.$ Let ![]() $\tilde{\wp}=\wp-\wp(\alpha)$. Let
$\tilde{\wp}=\wp-\wp(\alpha)$. Let ![]() $\pi_{\chi_j}$ denote the projection
$\pi_{\chi_j}$ denote the projection  $\mathcal{O}_{\mathbb{T}}\rightarrow \mathcal{O}_{\mathbb{T}}^{\chi_j}$ given by
$\mathcal{O}_{\mathbb{T}}\rightarrow \mathcal{O}_{\mathbb{T}}^{\chi_j}$ given by
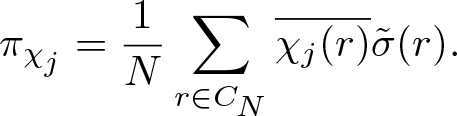 \begin{equation*}\pi_{\chi_j}=\frac{1}{N}\sum_{r\in C_N}\overline{\chi_j(r)}\tilde{\sigma}(r).\end{equation*}
\begin{equation*}\pi_{\chi_j}=\frac{1}{N}\sum_{r\in C_N}\overline{\chi_j(r)}\tilde{\sigma}(r).\end{equation*} We shall sometimes drop the notation that includes σ and only write ![]() $\gamma f$ for a group action of Γ on some
$\gamma f$ for a group action of Γ on some ![]() $f\in \mathcal{O}_{\mathbb{T}}$. However, when this notation causes potential confusion, we opt for readability and write a dot. Consider the function
$f\in \mathcal{O}_{\mathbb{T}}$. However, when this notation causes potential confusion, we opt for readability and write a dot. Consider the function ![]() $\wp'/\tilde{\wp}$. By (5.2) and the fact that
$\wp'/\tilde{\wp}$. By (5.2) and the fact that ![]() $\wp'$ is odd, we have
$\wp'$ is odd, we have ![]() $(\wp')=-3(0)+(1/2)+(\tau/2)+((1+\tau)/2)$. If we assume
$(\wp')=-3(0)+(1/2)+(\tau/2)+((1+\tau)/2)$. If we assume ![]() $N\geqslant 3$, then α cannot be a half lattice point and thus
$N\geqslant 3$, then α cannot be a half lattice point and thus ![]() $\alpha\neq -\alpha$. The divisor of
$\alpha\neq -\alpha$. The divisor of ![]() $\wp'/\tilde{\wp}$ is then given by
$\wp'/\tilde{\wp}$ is then given by
and thus we see that ![]() $\wp'/\tilde{\wp}\in \mathcal{O}_{\mathbb{T}}$. If N = 2, then one can verify that
$\wp'/\tilde{\wp}\in \mathcal{O}_{\mathbb{T}}$. If N = 2, then one can verify that ![]() $\wp'/\tilde{\wp}$ has poles in
$\wp'/\tilde{\wp}$ has poles in ![]() $\{0,\alpha\}$ and thus again
$\{0,\alpha\}$ and thus again ![]() $\wp'/\tilde{\wp}\in \mathcal{O}_{\mathbb{T}}$.
$\wp'/\tilde{\wp}\in \mathcal{O}_{\mathbb{T}}$.
We define ![]() $P_j:T\rightarrow {\mathbb{C}}$ to be the projection of
$P_j:T\rightarrow {\mathbb{C}}$ to be the projection of ![]() $\wp'/\tilde{\wp}$ under
$\wp'/\tilde{\wp}$ under ![]() $\pi_{\chi_j}$, multiplied by N:
$\pi_{\chi_j}$, multiplied by N:
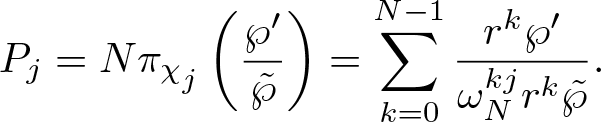 \begin{align}
P_j=N\pi_{\chi_j}\left(\frac{\wp'}{\tilde{\wp}}\right)=\sum_{k=0}^{N-1}\frac{r^k\wp'}{\omega_N^{kj}r^k\tilde{\wp}}.
\end{align}
\begin{align}
P_j=N\pi_{\chi_j}\left(\frac{\wp'}{\tilde{\wp}}\right)=\sum_{k=0}^{N-1}\frac{r^k\wp'}{\omega_N^{kj}r^k\tilde{\wp}}.
\end{align} Notice that indeed ![]() $r\cdot P_j=\chi_j(r)P_j$. We would like to stress that Pj depends both on a choice of a homomorphism
$r\cdot P_j=\chi_j(r)P_j$. We would like to stress that Pj depends both on a choice of a homomorphism ![]() $\sigma:C_N\rightarrow \mathrm{Aut}(T)$ and the character χj of CN, while the notation only shows j dependence. To avoid any confusion, we could write
$\sigma:C_N\rightarrow \mathrm{Aut}(T)$ and the character χj of CN, while the notation only shows j dependence. To avoid any confusion, we could write  $P_{\sigma, \chi_j}$ instead – now risking an overload of notation however.
$P_{\sigma, \chi_j}$ instead – now risking an overload of notation however.
The next lemma states how Pj transforms under the action of ![]() $s:z\mapsto -z$. It is a simple consequence of the fact that
$s:z\mapsto -z$. It is a simple consequence of the fact that ![]() $\wp'/\tilde{\wp}$ is odd and that if r is a translation of the torus, then
$\wp'/\tilde{\wp}$ is odd and that if r is a translation of the torus, then ![]() $sr^k=r^{-k}s$.
$sr^k=r^{-k}s$.
Lemma 12. Consider the action on T given by ![]() $s:z\mapsto -z$. Then s acts on Pj as
$s:z\mapsto -z$. Then s acts on Pj as ![]() $sP_j=-P_{-j}.$
$sP_j=-P_{-j}.$
We will now list some basic properties of the functions Pj. Recall that if a function f has a Laurent expansion ![]() $f(z)=\sum_{n\in {\mathbb{Z}}}c_n(z-z_0)^n$ about
$f(z)=\sum_{n\in {\mathbb{Z}}}c_n(z-z_0)^n$ about ![]() $z=z_0$, then the residue of f at
$z=z_0$, then the residue of f at ![]() $z=z_0$ is given by the coefficient c −1. Notation:
$z=z_0$ is given by the coefficient c −1. Notation: ![]() $\mathrm{Res}_{z=z_0}(f)=c_{-1}.$
$\mathrm{Res}_{z=z_0}(f)=c_{-1}.$
Proposition 1. Let α be an N-torsion point with ![]() $N\geqslant 2$, and let
$N\geqslant 2$, and let ![]() $\mathcal{S}=\{0,\alpha,2\alpha,\dots,(N-1)\alpha\}$. Then
$\mathcal{S}=\{0,\alpha,2\alpha,\dots,(N-1)\alpha\}$. Then
(1) Pj is a meromorphic function on T for all j, with at most order 1 poles in
 $\mathcal{S}$.
$\mathcal{S}$.(2) If Pj has a pole, then it has poles everywhere in
 $\mathcal{S}$.
$\mathcal{S}$.(3) The residue of Pj about z = 0 is given by
 \begin{equation*}\mathrm{Res}_{z=0}(P_j)=-2+\omega_N^{-j}+\omega_N^{j}.\end{equation*}
\begin{equation*}\mathrm{Res}_{z=0}(P_j)=-2+\omega_N^{-j}+\omega_N^{j}.\end{equation*}
In particular Pj is constant if and only if ![]() $j\equiv0 \mod N$. In fact,
$j\equiv0 \mod N$. In fact, ![]() $P_{0}=0$.
$P_{0}=0$.
Proof. Let  $v=\frac{\wp'}{\tilde{\wp}}$ and first take
$v=\frac{\wp'}{\tilde{\wp}}$ and first take ![]() $N\geqslant 3$. Assume r is given by
$N\geqslant 3$. Assume r is given by ![]() $r:z\mapsto z+\alpha$. To prove the first item, note that
$r:z\mapsto z+\alpha$. To prove the first item, note that ![]() $(r^k\tilde{\wp}) = -2(k\alpha)+ ((k+1)\alpha)+((k-1)\alpha)$ and hence
$(r^k\tilde{\wp}) = -2(k\alpha)+ ((k+1)\alpha)+((k-1)\alpha)$ and hence
Using the divisor in (5.5), we see that  $r^kv=r^k\left(\frac{\wp'}{\tilde{\wp}}\right)$ has order 1 poles at
$r^kv=r^k\left(\frac{\wp'}{\tilde{\wp}}\right)$ has order 1 poles at ![]() $(k-1)\alpha$,
$(k-1)\alpha$, ![]() $k\alpha$ and
$k\alpha$ and ![]() $(k+1)\alpha$, which are distinct when
$(k+1)\alpha$, which are distinct when ![]() $N\geqslant 3$. Therefore,
$N\geqslant 3$. Therefore,  $P_j=\sum_{k=0}^{N-1}\frac{r^k\wp'}{\omega_N^{kj}r^k\tilde{\wp}}$ has at most order 1 poles in
$P_j=\sum_{k=0}^{N-1}\frac{r^k\wp'}{\omega_N^{kj}r^k\tilde{\wp}}$ has at most order 1 poles in ![]() $\mathcal{S}=\{0,\alpha,2\alpha,\dots,(N-1)\alpha\}$.
$\mathcal{S}=\{0,\alpha,2\alpha,\dots,(N-1)\alpha\}$.
To prove the second statement, we observe that the divisor ![]() $(P_j)$ is invariant under r, since r acts by a non-zero scalar on Pj. Hence if Pj has a pole, then it has poles of order 1 everywhere in
$(P_j)$ is invariant under r, since r acts by a non-zero scalar on Pj. Hence if Pj has a pole, then it has poles of order 1 everywhere in ![]() $\mathcal{S}$.
$\mathcal{S}$.
For the third item, we consider a number of expansions about z = 0. The summands of Pj that are responsible for the potential occurrence of pole at z = 0 are ![]() $r^{-1}v, v$ and rv. It follows from the definition of
$r^{-1}v, v$ and rv. It follows from the definition of ![]() $\wp$ in (2.2) that about z = 0, we have
$\wp$ in (2.2) that about z = 0, we have
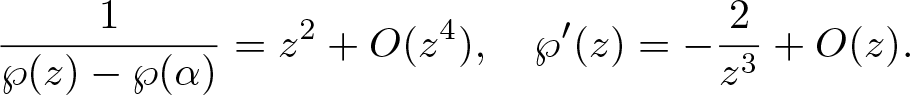 \begin{equation*}\frac{1}{\wp(z)-\wp(\alpha)}=z^2+O(z^4),\quad \wp'(z)=-\frac{2}{z^3}+O(z).\end{equation*}
\begin{equation*}\frac{1}{\wp(z)-\wp(\alpha)}=z^2+O(z^4),\quad \wp'(z)=-\frac{2}{z^3}+O(z).\end{equation*}Thus,
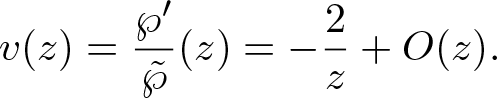 \begin{align}
v(z)=\frac{\wp'}{\tilde{\wp}}(z)= -\frac{2}{z}+O(z).
\end{align}
\begin{align}
v(z)=\frac{\wp'}{\tilde{\wp}}(z)= -\frac{2}{z}+O(z).
\end{align} For ![]() $N\geqslant 3$, we have
$N\geqslant 3$, we have ![]() $r\tilde{\wp}(z)=-\wp'(\alpha)z+O(z^2).$ Observe that
$r\tilde{\wp}(z)=-\wp'(\alpha)z+O(z^2).$ Observe that ![]() $\wp'(\alpha)\neq 0$ as soon as
$\wp'(\alpha)\neq 0$ as soon as ![]() $N\geqslant 3$, because zeros of
$N\geqslant 3$, because zeros of ![]() $\wp'$ appear at half lattice points (i.e. 2-torsion points). We see
$\wp'$ appear at half lattice points (i.e. 2-torsion points). We see  $\frac{1}{r\tilde{\wp}}(z)= -\frac{1}{\wp'(\alpha)}\frac{1}{z}+O(1)$ and
$\frac{1}{r\tilde{\wp}}(z)= -\frac{1}{\wp'(\alpha)}\frac{1}{z}+O(1)$ and ![]() $r\tilde{\wp}'(z)=-\wp'(\alpha)+O(z)$ from which we infer
$r\tilde{\wp}'(z)=-\wp'(\alpha)+O(z)$ from which we infer
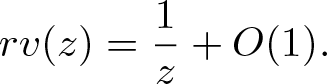 \begin{equation*}rv(z)=\frac{1}{z}+O(1).\end{equation*}
\begin{equation*}rv(z)=\frac{1}{z}+O(1).\end{equation*} Similarly, one argues that  $r^{-1}v(z)=\frac{1}{z}+O(1).$ Thus indeed
$r^{-1}v(z)=\frac{1}{z}+O(1).$ Thus indeed
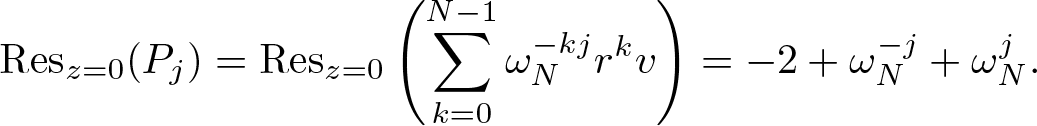 \begin{equation*}\mathrm{Res}_{z=0}(P_j)=\mathrm{Res}_{z=0}\left(\sum_{k=0}^{N-1}\omega_N^{-kj}r^kv\right)=-2+\omega_N^{-j}+\omega_N^{j}.\end{equation*}
\begin{equation*}\mathrm{Res}_{z=0}(P_j)=\mathrm{Res}_{z=0}\left(\sum_{k=0}^{N-1}\omega_N^{-kj}r^kv\right)=-2+\omega_N^{-j}+\omega_N^{j}.\end{equation*} If N = 2, then  $P_{1}=\frac{\wp'}{\tilde{\wp}}-r\frac{\wp'}{\tilde{\wp}}$ and it is easy to see that it has order 1 poles in
$P_{1}=\frac{\wp'}{\tilde{\wp}}-r\frac{\wp'}{\tilde{\wp}}$ and it is easy to see that it has order 1 poles in ![]() $\{0,\alpha\}$. The expansion in (5.7) still holds, thus
$\{0,\alpha\}$. The expansion in (5.7) still holds, thus  $\frac{\wp'}{\tilde{\wp}}(z)=-\frac{2}{z}+O(z)$ and one can show that
$\frac{\wp'}{\tilde{\wp}}(z)=-\frac{2}{z}+O(z)$ and one can show that  $r\frac{\wp'}{\tilde{\wp}}(z)=\frac{2}{z}+O(1)$ about z = 0.
$r\frac{\wp'}{\tilde{\wp}}(z)=\frac{2}{z}+O(1)$ about z = 0.
Now consider Pj for ![]() $j\equiv 0\mod N$. Observe that it is invariant under r. Thus P 0 descends to a function
$j\equiv 0\mod N$. Observe that it is invariant under r. Thus P 0 descends to a function ![]() $\tilde{P}_0$ on the torus
$\tilde{P}_0$ on the torus ![]() $\tilde{T}=T/\langle r\rangle$. If P 0 has poles, they are of order 1 and if this is the case, then
$\tilde{T}=T/\langle r\rangle$. If P 0 has poles, they are of order 1 and if this is the case, then ![]() $\tilde{P}_0$ would have a simple pole on
$\tilde{P}_0$ would have a simple pole on ![]() $\tilde{T}$. This is not possible due to the well-known fact that if a compact Riemann surface has a meromorphic function with a single simple pole, it must be isomorphic to the Riemann sphere, cf. [Reference Miranda25, Proposition II.4.11]. Hence P 0 is constant.
$\tilde{T}$. This is not possible due to the well-known fact that if a compact Riemann surface has a meromorphic function with a single simple pole, it must be isomorphic to the Riemann sphere, cf. [Reference Miranda25, Proposition II.4.11]. Hence P 0 is constant.
Finally, ![]() $sP_{0}=-P_{0}$ from which it follows that
$sP_{0}=-P_{0}$ from which it follows that ![]() $P_{0}=0$. This concludes the proof.
$P_{0}=0$. This concludes the proof.
In § 6, we will introduce intertwining maps which will be used in the construction of bases of aLias. These maps are constructed via the Pj’s. As a consequence, the bases will be formulated in terms of the functions Pj. These functions are also important in another way: they generate the ring ![]() $\mathcal{O}_{\mathbb{T}}$ over the complex numbers, as we will prove now.
$\mathcal{O}_{\mathbb{T}}$ over the complex numbers, as we will prove now.
Proposition 2. Let ![]() $r\in \mathrm{Aut}(T)$ be defined by
$r\in \mathrm{Aut}(T)$ be defined by ![]() $r(z)=z+\alpha$ with α an N-torsion point, where
$r(z)=z+\alpha$ with α an N-torsion point, where ![]() $N\geqslant 3$. Define Pj with respect to this r. Then
$N\geqslant 3$. Define Pj with respect to this r. Then
where ![]() ${\mathbb{T}}=T\setminus \langle r\rangle\cdot \{0\}.$ Furthermore, for any integer
${\mathbb{T}}=T\setminus \langle r\rangle\cdot \{0\}.$ Furthermore, for any integer ![]() $j\not\equiv 0\mod N$, we have
$j\not\equiv 0\mod N$, we have
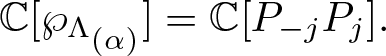 \begin{equation*}{\mathbb{C}}[\wp_{{\Lambda}_{(\alpha)}}]={\mathbb{C}}[P_{-j}P_j].\end{equation*}
\begin{equation*}{\mathbb{C}}[\wp_{{\Lambda}_{(\alpha)}}]={\mathbb{C}}[P_{-j}P_j].\end{equation*} Formulated differently, ![]() $P_{-j}P_j$ is a generator for the algebra of even meromorphic functions on the torus
$P_{-j}P_j$ is a generator for the algebra of even meromorphic functions on the torus ![]() $T'={\mathbb{C}}/{\Lambda}_{(\alpha)}$, holomorphic on
$T'={\mathbb{C}}/{\Lambda}_{(\alpha)}$, holomorphic on ![]() $T'\setminus\{0\}$.
$T'\setminus\{0\}$.
Proof. The space of meromorphic functions on a complex torus T is denoted by ![]() $\mathcal{M}(T)$. Let D be a divisor on T. The degree
$\mathcal{M}(T)$. Let D be a divisor on T. The degree ![]() $\deg(D)$ of
$\deg(D)$ of  $D=\sum_{p\in T}n_p(p)$ is defined as
$D=\sum_{p\in T}n_p(p)$ is defined as  $\deg(D)=\sum_{p\in T}n_p.$ Introduce the space of meromorphic functions on T with poles bounded by D, denoted by L(D):
$\deg(D)=\sum_{p\in T}n_p.$ Introduce the space of meromorphic functions on T with poles bounded by D, denoted by L(D):
Note that L(D) is a complex vector space. The Riemann–Roch theorem, specialised to genus 1 Riemann surfaces [Reference Miranda25, Proposition V.3.14], says that if D is a divisor on a complex torus T and ![]() $\deg(D) \gt 0$, then
$\deg(D) \gt 0$, then ![]() $\dim_{{\mathbb{C}}}L(D)=\deg(D)$. Let
$\dim_{{\mathbb{C}}}L(D)=\deg(D)$. Let  $D=\sum_{j=0}^{N-1}(j\alpha).$ We see that
$D=\sum_{j=0}^{N-1}(j\alpha).$ We see that ![]() $\dim_{{\mathbb{C}}}L(D)=\deg(D)=N$. By construction, we have
$\dim_{{\mathbb{C}}}L(D)=\deg(D)=N$. By construction, we have ![]() $P_j\in L(D)^{\chi_j}$, and hence
$P_j\in L(D)^{\chi_j}$, and hence ![]() $\dim_{{\mathbb{C}}}L(D)^{\chi_j}= 1$ if
$\dim_{{\mathbb{C}}}L(D)^{\chi_j}= 1$ if ![]() $j\not\equiv 0\mod N$. Therefore,
$j\not\equiv 0\mod N$. Therefore, ![]() $L(D)={\mathbb{C}}\langle 1,P_{1},\ldots, P_{N-1}\rangle.$ We proceed inductively. For each
$L(D)={\mathbb{C}}\langle 1,P_{1},\ldots, P_{N-1}\rangle.$ We proceed inductively. For each ![]() $k\in \{1,\ldots, N-1\}$, going from
$k\in \{1,\ldots, N-1\}$, going from ![]() $L((m-1)D)^{\chi_k}$ to
$L((m-1)D)^{\chi_k}$ to ![]() $L(mD)^{\chi_k}$, we add the one-dimensional subspace generated by a product of Pj’s such that
$L(mD)^{\chi_k}$, we add the one-dimensional subspace generated by a product of Pj’s such that  $0\neq \prod_{j\in \{j_1,\ldots, j_m\}}P_j\in L(mD)^{\chi_k}$ to
$0\neq \prod_{j\in \{j_1,\ldots, j_m\}}P_j\in L(mD)^{\chi_k}$ to ![]() $L((m-1)D)^{\chi_k}$. In particular, for
$L((m-1)D)^{\chi_k}$. In particular, for ![]() $k\not\equiv 0\mod N/2$ and letting
$k\not\equiv 0\mod N/2$ and letting  $Q=(P_{-j}P_j)^{\lfloor \frac{m-1}{2}\rfloor}$ (where
$Q=(P_{-j}P_j)^{\lfloor \frac{m-1}{2}\rfloor}$ (where ![]() $\lfloor x\rfloor$ denotes the integer part of x), we claim that
$\lfloor x\rfloor$ denotes the integer part of x), we claim that
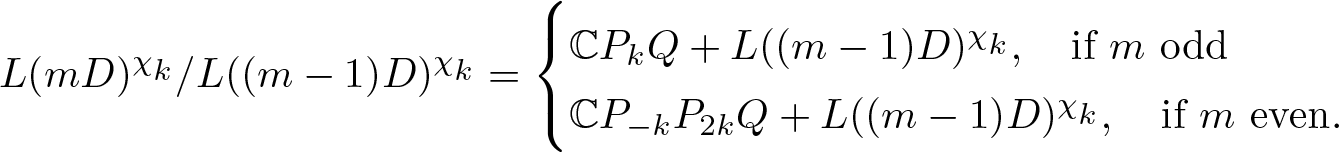 \begin{equation*}L(mD)^{\chi_k}/L((m-1)D)^{\chi_k}=\begin{cases} {\mathbb{C}} P_kQ+L((m-1)D)^{\chi_k},\quad \text{if}\,\, m\,\, \text{odd}\\
{\mathbb{C}} P_{-k}P_{2k}Q+L((m-1)D)^{\chi_k},\quad \text{if}\,\, m\,\, \text{even}.
\end{cases}\end{equation*}
\begin{equation*}L(mD)^{\chi_k}/L((m-1)D)^{\chi_k}=\begin{cases} {\mathbb{C}} P_kQ+L((m-1)D)^{\chi_k},\quad \text{if}\,\, m\,\, \text{odd}\\
{\mathbb{C}} P_{-k}P_{2k}Q+L((m-1)D)^{\chi_k},\quad \text{if}\,\, m\,\, \text{even}.
\end{cases}\end{equation*} Here we used that ![]() $N\geqslant 3$, so that there are enough integers k such that
$N\geqslant 3$, so that there are enough integers k such that ![]() $P_{2k}\neq 0$. For
$P_{2k}\neq 0$. For ![]() $k\equiv 0\mod N/2$ and m even, we need to change
$k\equiv 0\mod N/2$ and m even, we need to change ![]() $P_{-k}P_{2k}$ to
$P_{-k}P_{2k}$ to  $P_{-k-n}P_{2k+n}\in\mathcal{O}_{\mathbb{T}}^{\chi_k}$ for some suitable
$P_{-k-n}P_{2k+n}\in\mathcal{O}_{\mathbb{T}}^{\chi_k}$ for some suitable ![]() $n\in{\mathbb{Z}}$. This shows that
$n\in{\mathbb{Z}}$. This shows that  $\mathcal{O}_{\mathbb{T}}=\bigcup_{j\in \mathbb{N}}L(jD)$ is generated as a
$\mathcal{O}_{\mathbb{T}}=\bigcup_{j\in \mathbb{N}}L(jD)$ is generated as a ![]() ${\mathbb{C}}$-algebra by
${\mathbb{C}}$-algebra by ![]() $P_{1},\ldots, P_{N-1}$ whenever
$P_{1},\ldots, P_{N-1}$ whenever ![]() $N\geqslant 3$.
$N\geqslant 3$.
To prove the second claim, notice that ![]() $r P_{-j}P_j=P_{-j}P_j$ and that it has poles of order 2 in
$r P_{-j}P_j=P_{-j}P_j$ and that it has poles of order 2 in ![]() ${\Lambda}_{(\alpha)}$ if and only if
${\Lambda}_{(\alpha)}$ if and only if ![]() $j\not\equiv 0\mod N$. If z 0 is a zero of P −j, then
$j\not\equiv 0\mod N$. If z 0 is a zero of P −j, then ![]() $-z_0$ is a zero of Pj since
$-z_0$ is a zero of Pj since ![]() $P_{-j}(z_0)=-P_j(-z_0)$ by Lemma 12. Hence the divisor of
$P_{-j}(z_0)=-P_j(-z_0)$ by Lemma 12. Hence the divisor of ![]() $P_{-j}P_j$ equals
$P_{-j}P_j$ equals ![]() $(P_{-j}P_j)=-2(0)+(z_0)+(-z_0)$. Now recall that
$(P_{-j}P_j)=-2(0)+(z_0)+(-z_0)$. Now recall that ![]() $\wp_{{\Lambda}_{(\alpha)}}$ has an order 2 pole at z = 0 and is even, hence
$\wp_{{\Lambda}_{(\alpha)}}$ has an order 2 pole at z = 0 and is even, hence  $(\wp_{{\Lambda}_{(\alpha)}})=-2(0)+(w_0)+(-w_0)$ for some
$(\wp_{{\Lambda}_{(\alpha)}})=-2(0)+(w_0)+(-w_0)$ for some ![]() $w_0\in T'$. We see that indeed
$w_0\in T'$. We see that indeed  $P_{-j}P_j=c_1\wp_{{\Lambda}_{(\alpha)}}+c_2$ for some
$P_{-j}P_j=c_1\wp_{{\Lambda}_{(\alpha)}}+c_2$ for some ![]() $c_1,c_2\in {\mathbb{C}}$ and
$c_1,c_2\in {\mathbb{C}}$ and ![]() $c_1\neq 0$ if and only if
$c_1\neq 0$ if and only if ![]() $j\not\equiv 0\mod N$. Therefore,
$j\not\equiv 0\mod N$. Therefore,  ${\mathbb{C}}[\wp_{{\Lambda}_{(\alpha)}}]={\mathbb{C}}[P_{-j}P_j]$ if and only if
${\mathbb{C}}[\wp_{{\Lambda}_{(\alpha)}}]={\mathbb{C}}[P_{-j}P_j]$ if and only if ![]() $j\not\equiv 0\mod N$.
$j\not\equiv 0\mod N$.
The following identities related to the Pj’s are recorded in the next lemma. These will play an important role in the construction of intertwiners in § 6.
Lemma 13. Let ![]() $N\in \mathbb{N}$. For every
$N\in \mathbb{N}$. For every ![]() $j\in {\mathbb{Z}}$ and
$j\in {\mathbb{Z}}$ and ![]() $k\not\equiv 0\mod N$, there are
$k\not\equiv 0\mod N$, there are ![]() $\lambda,\mu\in {\mathbb{C}}$ such that
$\lambda,\mu\in {\mathbb{C}}$ such that
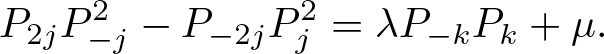 \begin{equation*}P_{2j}P_{-j}^2-P_{-2j}P_j^2=\lambda P_{-k}P_{k}+\mu.\end{equation*}
\begin{equation*}P_{2j}P_{-j}^2-P_{-2j}P_j^2=\lambda P_{-k}P_{k}+\mu.\end{equation*} If in addition ![]() $N\geqslant 3$,
$N\geqslant 3$, ![]() $k=\pm j$ and
$k=\pm j$ and ![]() $j\not \equiv 0 \mod N/2$, then µ is non-zero.
$j\not \equiv 0 \mod N/2$, then µ is non-zero.
Proof. Let ![]() $j\in {\mathbb{Z}}$ and write
$j\in {\mathbb{Z}}$ and write  $f=P_{2j}P_{-j}^2-P_{-2j}P_j^2$. Clearly
$f=P_{2j}P_{-j}^2-P_{-2j}P_j^2$. Clearly ![]() $\gamma f=f$ for all
$\gamma f=f$ for all ![]() $\gamma\in \langle s,r\rangle\cong D_N$ for any
$\gamma\in \langle s,r\rangle\cong D_N$ for any ![]() $N\in \mathbb{N}$. In particular, f is even and hence has at most order 2 poles, for any choice of j. By Proposition 2, we see that for all
$N\in \mathbb{N}$. In particular, f is even and hence has at most order 2 poles, for any choice of j. By Proposition 2, we see that for all ![]() $k\not\equiv 0\mod N$ we have that
$k\not\equiv 0\mod N$ we have that ![]() $f=\lambda P_{-k}P_{k}+\mu$ for some
$f=\lambda P_{-k}P_{k}+\mu$ for some ![]() $\lambda,\mu\in {\mathbb{C}}$.
$\lambda,\mu\in {\mathbb{C}}$.
Assume now that ![]() $N\geqslant 3$,
$N\geqslant 3$, ![]() $k=\pm j$ and
$k=\pm j$ and ![]() $j\not \equiv 0 \mod N/2$. If µ would be zero and
$j\not \equiv 0 \mod N/2$. If µ would be zero and ![]() $z_0\in T$ is a zero of Pj, then
$z_0\in T$ is a zero of Pj, then  $f(z_0)=P_{2j}(z_0)P_{-j}^2(z_0)=0.$ Thus, z 0 would also be a zero of P −j or
$f(z_0)=P_{2j}(z_0)P_{-j}^2(z_0)=0.$ Thus, z 0 would also be a zero of P −j or ![]() $P_{2j}$. However, since the set of zeros of Pk is invariant under r, the set of zeros of Pj must then coincide with the zero set of P −j or
$P_{2j}$. However, since the set of zeros of Pk is invariant under r, the set of zeros of Pj must then coincide with the zero set of P −j or ![]() $P_{2j}$. Since the order and location of the poles of Pj, P −j and
$P_{2j}$. Since the order and location of the poles of Pj, P −j and ![]() $P_{2j}$ already coincide, this means that
$P_{2j}$ already coincide, this means that ![]() $(P_j)=(P_{-j})$ or
$(P_j)=(P_{-j})$ or ![]() $(P_j)=(P_{2j})$, that is, Pj is either a constant multiple of P −j or
$(P_j)=(P_{2j})$, that is, Pj is either a constant multiple of P −j or ![]() $P_{2j}$. This is absurd, which therefore means that µ cannot be zero.
$P_{2j}$. This is absurd, which therefore means that µ cannot be zero.
Remark 3. One could find explicit formulas for λ and µ using Proposition 1 and more detailed expansions. However, the obtained formulas are unlikely to benefit the transparency of the normal form we will later obtain. Related constructions will be carried out for ![]() $\Gamma=C_2\times C_2$ in § 6.2, and here it does seem appropriate to keep track of the constants, mainly because there is simply one group instead of a collection of groups, and the constants have transparent formulas in terms of well-known functions.
$\Gamma=C_2\times C_2$ in § 6.2, and here it does seem appropriate to keep track of the constants, mainly because there is simply one group instead of a collection of groups, and the constants have transparent formulas in terms of well-known functions.
6. Construction of normal forms
In § 2, we have seen a basic example of an aLia on a complex torus with symmetry group C 2, embedded inside ![]() $\mathrm{Aut}(T)$ as
$\mathrm{Aut}(T)$ as ![]() $z\mapsto -z$, and developed a number of functional aspects of the theory. We have observed that this C 2-aLia has a particularly transparent structure – it is generated over its algebra of invariants and its Cartan subalgebra has eigenvalues in
$z\mapsto -z$, and developed a number of functional aspects of the theory. We have observed that this C 2-aLia has a particularly transparent structure – it is generated over its algebra of invariants and its Cartan subalgebra has eigenvalues in ![]() ${\mathbb{C}}$ (in fact, in this case it is a constant matrix). We will see that this is a general feature of aLias on complex tori with base Lie algebra
${\mathbb{C}}$ (in fact, in this case it is a constant matrix). We will see that this is a general feature of aLias on complex tori with base Lie algebra ![]() $\mathfrak{sl}_2$.
$\mathfrak{sl}_2$.
In this section, we shall give explicit realisations of aLias and determine their isomorphism type. It turns out that if the symmetry group acts on a complex torus without fixed points, then we obtain aLias that are isomorphic to a current algebra. Formulated differently, they are untwisted. If on the other end the group acts with fixed points, the corresponding aLias are twisted. The twisted aLias turn out to be isomorphic to either the Onsager algebra ![]() $\mathfrak{O}$ or
$\mathfrak{O}$ or ![]() $\mathfrak{S}_{\tau}$.
$\mathfrak{S}_{\tau}$.
We will bring the aLias into a normal form, which will allow us to decide the isomorphism type of the aLias in question. The normal form will be defined in Definition 3. As a consequence, we settle the question whether the aLias are hereditary [Reference Knibbeler, Lombardo and Sanders4], as defined in Definition 2.
Our main tools in constructing bases for aLias are certain ![]() $SL_2({\mathbb{C}})$-valued maps on a complex torus
$SL_2({\mathbb{C}})$-valued maps on a complex torus ![]() ${\mathbb{T}}=T\setminus \Gamma\cdot \{0\}$ whose composition with
${\mathbb{T}}=T\setminus \Gamma\cdot \{0\}$ whose composition with ![]() $\mathrm{Ad}:SL_2({\mathbb{C}})\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ will intertwine the actions of Γ on T and
$\mathrm{Ad}:SL_2({\mathbb{C}})\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ will intertwine the actions of Γ on T and ![]() $\mathfrak{sl}_2$.
$\mathfrak{sl}_2$.
Definition 2 (Hereditary aLias [Reference Knibbeler, Lombardo and Sanders4])
An aLia is said to be hereditary if it contains a constant spectrum Cartan subalgebra (CSA). This is a Cartan subalgebra which is generated by an element H with constant ![]() $\mathrm{ad}(H)$-eigenvalues.
$\mathrm{ad}(H)$-eigenvalues.
Definition 3 (Normal form of aLias)
We say that an aLia ![]() $\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\Gamma}$ is in normal form if
$\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\Gamma}$ is in normal form if
such that
where ![]() $p\in \mathcal{O}_{\mathbb{T}}^{\Gamma}$.
$p\in \mathcal{O}_{\mathbb{T}}^{\Gamma}$.
We remark that for the normal form as in Definition 3, we automatically have that H has eigenvalues in ![]() ${\mathbb{C}}$. The CSA
${\mathbb{C}}$. The CSA ![]() $\mathfrak{h}={\mathbb{C}} H\otimes \mathcal{O}_{\mathbb{T}}^{\Gamma}$ is a constant spectrum CSA.
$\mathfrak{h}={\mathbb{C}} H\otimes \mathcal{O}_{\mathbb{T}}^{\Gamma}$ is a constant spectrum CSA.
In the upcoming sections, we will construct normal forms for all aLias on complex tori with base Lie algebra ![]() $\mathfrak{sl}_2$, in our classification. This will, therefore, also establish the property of being hereditary of this class of aLias.
$\mathfrak{sl}_2$, in our classification. This will, therefore, also establish the property of being hereditary of this class of aLias.
Let the symmetry group be given by ![]() $\Gamma=G \ltimes K\subset \mathrm{Aut}_0(T) \ltimes t(T)$, where we recall the notation t(T) for the normal subgroup of translations of the torus T. We start with a lemma that says that, under certain circumstances, a normal form for the aLia with symmetry group K automatically determines a normal form for Γ as well.
$\Gamma=G \ltimes K\subset \mathrm{Aut}_0(T) \ltimes t(T)$, where we recall the notation t(T) for the normal subgroup of translations of the torus T. We start with a lemma that says that, under certain circumstances, a normal form for the aLia with symmetry group K automatically determines a normal form for Γ as well.
Lemma 14. Let ![]() $\Gamma=G \ltimes K\subset \mathrm{Aut}_0(T) \ltimes t(T)$. If
$\Gamma=G \ltimes K\subset \mathrm{Aut}_0(T) \ltimes t(T)$. If ![]() $\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{K}$ has a normal form, and
$\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{K}$ has a normal form, and ![]() $H\in \mathfrak{A}$ is G-invariant, such that it generates a CSA of
$H\in \mathfrak{A}$ is G-invariant, such that it generates a CSA of ![]() $\mathfrak{A}$, then
$\mathfrak{A}$, then ![]() $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\Gamma}$ has a normal form as well.
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\Gamma}$ has a normal form as well.
Proof. First recall that ![]() $G=C_{\ell}\subset \mathrm{Aut}_0(T)$ and that K consists of translations of T. By Lemma 11, we, therefore, have
$G=C_{\ell}\subset \mathrm{Aut}_0(T)$ and that K consists of translations of T. By Lemma 11, we, therefore, have ![]() $\mathcal{O}_{\mathbb{T}}^K={\mathbb{C}}[\wp,\wp']$ for some
$\mathcal{O}_{\mathbb{T}}^K={\mathbb{C}}[\wp,\wp']$ for some ![]() $\wp$ associated to a suitable lattice. Observe that the statement is trivially true for
$\wp$ associated to a suitable lattice. Observe that the statement is trivially true for ![]() $\ell=1$, hence we take
$\ell=1$, hence we take ![]() $\ell\in \{2,3,4,6\}$.
$\ell\in \{2,3,4,6\}$.
Assume the normal form of ![]() $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{K}$ to be
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{K}$ to be
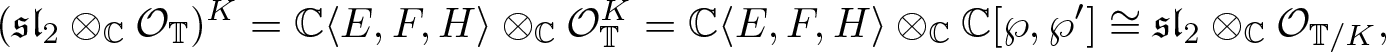 \begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{K}={\mathbb{C}}\langle E,F,H\rangle \otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^K={\mathbb{C}}\langle E,F,H\rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp,\wp']\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}/K},\end{equation*}
\begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{K}={\mathbb{C}}\langle E,F,H\rangle \otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^K={\mathbb{C}}\langle E,F,H\rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp,\wp']\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}/K},\end{equation*} with ![]() $\mathcal{O}_{\mathbb{T}}^K$-linear brackets
$\mathcal{O}_{\mathbb{T}}^K$-linear brackets ![]() $[H,E]=2E$,
$[H,E]=2E$, ![]() $[H,F]=-2F$ and
$[H,F]=-2F$ and ![]() $[E,F]=H$. Now, since K is normal in Γ,
$[E,F]=H$. Now, since K is normal in Γ, ![]() $g\in G$ acts on
$g\in G$ acts on ![]() ${\mathbb{C}}\langle E,F,H\rangle \otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^K$ and
${\mathbb{C}}\langle E,F,H\rangle \otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^K$ and ![]() $\{g\cdot E,g\cdot F,g\cdot H\}$ forms again a standard
$\{g\cdot E,g\cdot F,g\cdot H\}$ forms again a standard ![]() $\mathfrak{sl}_2$-triple, where the action is defined in (2.1). By assumption,
$\mathfrak{sl}_2$-triple, where the action is defined in (2.1). By assumption, ![]() $g\cdot H=H$. Furthermore,
$g\cdot H=H$. Furthermore, ![]() $[H,g\cdot E]=2g\cdot E$, so
$[H,g\cdot E]=2g\cdot E$, so ![]() $g\cdot E=E\otimes k_1$ for some function
$g\cdot E=E\otimes k_1$ for some function ![]() $k_1\in \mathcal{O}_{\mathbb{T}}^K$. Similarly,
$k_1\in \mathcal{O}_{\mathbb{T}}^K$. Similarly, ![]() $g\cdot F=F\otimes k_2$ for some
$g\cdot F=F\otimes k_2$ for some ![]() $k_2\in \mathcal{O}_{\mathbb{T}}^K$. We have
$k_2\in \mathcal{O}_{\mathbb{T}}^K$. We have ![]() $[g\cdot E,g\cdot F]=H$ and this implies that
$[g\cdot E,g\cdot F]=H$ and this implies that ![]() $k_2=k_1^{-1}$. The only units in
$k_2=k_1^{-1}$. The only units in ![]() $\mathcal{O}_{\mathbb{T}}^K={\mathbb{C}}[\wp,\wp']$ are the non-zero constants. Therefore,
$\mathcal{O}_{\mathbb{T}}^K={\mathbb{C}}[\wp,\wp']$ are the non-zero constants. Therefore,  $g\cdot E=\omega_{\ell}^jE$ and
$g\cdot E=\omega_{\ell}^jE$ and  $g\cdot F=\omega_{\ell}^{-j}F$, for some
$g\cdot F=\omega_{\ell}^{-j}F$, for some ![]() $j\in \{1,\ldots, \ell-1\}$ such that
$j\in \{1,\ldots, \ell-1\}$ such that ![]() $\gcd(j,\ell)=1$. Notice that this forces
$\gcd(j,\ell)=1$. Notice that this forces ![]() $j\in \{1,\ell-1\}$, due to the limited amount of choices for
$j\in \{1,\ell-1\}$, due to the limited amount of choices for ![]() $\ell$.
$\ell$.
We now decompose ![]() ${\mathbb{C}}\langle E,F,H\rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp,\wp']$ into its
${\mathbb{C}}\langle E,F,H\rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp,\wp']$ into its ![]() $C_{\ell}$ isotypical components:
$C_{\ell}$ isotypical components:
where ![]() $p_1\in {\mathbb{C}}[\wp,\wp']^{\chi_{\ell-j}}$,
$p_1\in {\mathbb{C}}[\wp,\wp']^{\chi_{\ell-j}}$, ![]() $p_2\in {\mathbb{C}}[\wp,\wp']^{\chi_j}$ and J generates
$p_2\in {\mathbb{C}}[\wp,\wp']^{\chi_j}$ and J generates ![]() $\mathcal{O}_{\mathbb{T}}^{\Gamma}$, which follows from Lemma 10.
$\mathcal{O}_{\mathbb{T}}^{\Gamma}$, which follows from Lemma 10.
Its Lie structure is given by
where ![]() $p_1p_2\in {\mathbb{C}}[J]$. We may assume that
$p_1p_2\in {\mathbb{C}}[J]$. We may assume that ![]() $g\cdot E=\omega_{\ell}E$ and
$g\cdot E=\omega_{\ell}E$ and  $g\cdot F=\omega_{\ell}^{-1}F$ after applying an automorphism that interchanges the isotypical components if necessary (e.g.
$g\cdot F=\omega_{\ell}^{-1}F$ after applying an automorphism that interchanges the isotypical components if necessary (e.g.  $\mathrm{Ad}\begin{pmatrix}
0 & 1\\
-1 &0
\end{pmatrix}$) and assume therefore that
$\mathrm{Ad}\begin{pmatrix}
0 & 1\\
-1 &0
\end{pmatrix}$) and assume therefore that ![]() $p_1\in {\mathbb{C}}[\wp,\wp']^{\chi_{\ell-1}}$,
$p_1\in {\mathbb{C}}[\wp,\wp']^{\chi_{\ell-1}}$, ![]() $p_2\in {\mathbb{C}}[\wp,\wp']^{\chi_{1}}$.
$p_2\in {\mathbb{C}}[\wp,\wp']^{\chi_{1}}$.
Observe that Lemma 14 implies that in order to understand aLias with non-abelian symmetry groups ![]() $\Gamma=G \ltimes K$, it is sufficient to understand the aLias with abelian symmetry groups G and K separately, granted that we have found a K-invariant element H in a CSA, which is simultaneously G-invariant.
$\Gamma=G \ltimes K$, it is sufficient to understand the aLias with abelian symmetry groups G and K separately, granted that we have found a K-invariant element H in a CSA, which is simultaneously G-invariant.
The proof of Lemma 14 gives us a construction to obtain the normal for the aLia with symmetry group Γ as well, if the condition on a generator of the CSA is being satisfied.
The next proposition gives a criterion for the existence of normal forms of aLias and extends Lemma 14 by providing a normal form of the full group ![]() $\Gamma=G \ltimes K$.
$\Gamma=G \ltimes K$.
Proposition 3. Let ![]() $\Gamma=G \ltimes K\subset \mathrm{Aut}_0(T) \ltimes t(T)$ and let
$\Gamma=G \ltimes K\subset \mathrm{Aut}_0(T) \ltimes t(T)$ and let ![]() $\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ be a monomorphism and
$\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ be a monomorphism and ![]() $\tilde{\rho}:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ a homomorphism whose kernel equals K. If there exists an inner automorphism
$\tilde{\rho}:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ a homomorphism whose kernel equals K. If there exists an inner automorphism ![]() $\Psi\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})$ such that for all
$\Psi\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})$ such that for all ![]() $z\in {\mathbb{T}}$ and
$z\in {\mathbb{T}}$ and ![]() $\gamma\in \Gamma$, we have
$\gamma\in \Gamma$, we have
then
(1)
 $\mathfrak{K}:=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{K}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}}^{K},$
$\mathfrak{K}:=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{K}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}}^{K},$(2) There exists a normal form for
 $\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\Gamma}$ and if the normal form of
$\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\Gamma}$ and if the normal form of  $\mathfrak{K}$ is given by
$\mathfrak{K}$ is given by  ${\mathbb{C}}\langle E,F,H \rangle \otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}}^{K}$, with its Lie structure inherited from
${\mathbb{C}}\langle E,F,H \rangle \otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}}^{K}$, with its Lie structure inherited from  $\mathfrak{sl}_2$, then the normal form for
$\mathfrak{sl}_2$, then the normal form for  $\mathfrak{A}$ given by
$\mathfrak{A}$ given by
 \begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\Gamma}={\mathbb{C}}\langle E\otimes p_1,F\otimes p_2,H \rangle \otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}}^{\Gamma},\end{equation*}
\begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\Gamma}={\mathbb{C}}\langle E\otimes p_1,F\otimes p_2,H \rangle \otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}}^{\Gamma},\end{equation*}with Lie structure
 \begin{equation*}[H,E\otimes p_1]=2E\otimes p_1,\quad [H,F\otimes p_2]=-2F\otimes p_2,\quad [E\otimes p_1,F\otimes p_2]=H\otimes p_1p_2,\end{equation*}
\begin{equation*}[H,E\otimes p_1]=2E\otimes p_1,\quad [H,F\otimes p_2]=-2F\otimes p_2,\quad [E\otimes p_1,F\otimes p_2]=H\otimes p_1p_2,\end{equation*}where p 1 generates
 $\mathcal{O}_{\mathbb{T}}^{\chi_{\ell-1}}$, where
$\mathcal{O}_{\mathbb{T}}^{\chi_{\ell-1}}$, where  $|G|=\ell$, p 2 generates
$|G|=\ell$, p 2 generates  $\mathcal{O}_{\mathbb{T}}^{\chi_{1}}$ and
$\mathcal{O}_{\mathbb{T}}^{\chi_{1}}$ and  $p_1p_2\in \mathcal{O}_{\mathbb{T}}^{\Gamma}$.
$p_1p_2\in \mathcal{O}_{\mathbb{T}}^{\Gamma}$.
Proof. First of all, we would like to stress that we can view ![]() $\Psi\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})$ as a holomorphic
$\Psi\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})$ as a holomorphic ![]() $\mathrm{Aut}(\mathfrak{sl}_2)$-valued function on
$\mathrm{Aut}(\mathfrak{sl}_2)$-valued function on ![]() $\mathbb{T}$, in which case we use the notation
$\mathbb{T}$, in which case we use the notation ![]() $\Psi(z)$. We shall use both interpretations interchangeably and let the argument of Ψ be either an element of
$\Psi(z)$. We shall use both interpretations interchangeably and let the argument of Ψ be either an element of ![]() $\mathbb{T}$ or an element of
$\mathbb{T}$ or an element of ![]() $\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}$.
$\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}$.
The first part claims that for ![]() $k\in K$, if we have
$k\in K$, if we have ![]() $\Psi(k\cdot z)=\rho(k)\Psi(z)$, then there is a normal form for
$\Psi(k\cdot z)=\rho(k)\Psi(z)$, then there is a normal form for ![]() $\mathfrak{K}$. Let
$\mathfrak{K}$. Let ![]() $\{x_1,x_2,x_3\}$ be a basis for
$\{x_1,x_2,x_3\}$ be a basis for ![]() $\mathfrak{sl}_2$. Then for
$\mathfrak{sl}_2$. Then for ![]() $j=1,2,3,$ we have that
$j=1,2,3,$ we have that ![]() $X_j(z):=\Psi(z)x_j$ is K-invariant:
$X_j(z):=\Psi(z)x_j$ is K-invariant:
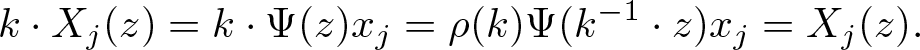 \begin{equation*}k\cdot X_j(z)=k\cdot \Psi(z)x_j=\rho(k)\Psi(k^{-1}\cdot z)x_j=X_j(z).\end{equation*}
\begin{equation*}k\cdot X_j(z)=k\cdot \Psi(z)x_j=\rho(k)\Psi(k^{-1}\cdot z)x_j=X_j(z).\end{equation*} Since ![]() $\Psi\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})$ is an inner automorphism, we have
$\Psi\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})$ is an inner automorphism, we have
Taking the invariants, we obtain a normal form
with the brackets inherited from ![]() $\mathfrak{sl}_2$ and where
$\mathfrak{sl}_2$ and where ![]() $\wp,\wp'$ generate
$\wp,\wp'$ generate ![]() $\mathcal{O}_{\mathbb{T}}^K$.
$\mathcal{O}_{\mathbb{T}}^K$.
To prove the second item, we will argue as follows. Let ![]() $\gamma=gk\in \Gamma=G \ltimes K$ and
$\gamma=gk\in \Gamma=G \ltimes K$ and ![]() $x\in \mathfrak{sl}_2$. By (6.1),
$x\in \mathfrak{sl}_2$. By (6.1),
Since G is cyclic, it leaves a CSA of ![]() $\mathfrak{sl}_2$ invariant. Hence there is a basis
$\mathfrak{sl}_2$ invariant. Hence there is a basis ![]() $\{X_1,X_2,X_3\}\subset \mathfrak{sl}_2$, with X 1 a generator in the CSA, such that with respect to this basis,
$\{X_1,X_2,X_3\}\subset \mathfrak{sl}_2$, with X 1 a generator in the CSA, such that with respect to this basis, ![]() $\tilde{\rho}(\gamma)=\tilde{\rho}(gk)=\mathrm{diag}(1,\chi_1(g),\chi_{\ell-1}(g))$, where χj are the characters of G, g generates G and
$\tilde{\rho}(\gamma)=\tilde{\rho}(gk)=\mathrm{diag}(1,\chi_1(g),\chi_{\ell-1}(g))$, where χj are the characters of G, g generates G and ![]() $k\in K$. Now,
$k\in K$. Now, ![]() $\Psi(X_1\otimes 1)$ generates a CSA of
$\Psi(X_1\otimes 1)$ generates a CSA of ![]() $\mathfrak{K}$ and
$\mathfrak{K}$ and ![]() $g\cdot \Psi(X_1\otimes 1)=\Psi(X_1\otimes 1)$ for all
$g\cdot \Psi(X_1\otimes 1)=\Psi(X_1\otimes 1)$ for all ![]() $g\in G$ by (6.1). We can, therefore, apply Lemma 14 to arrive at the conclusion of the existence of a normal form for
$g\in G$ by (6.1). We can, therefore, apply Lemma 14 to arrive at the conclusion of the existence of a normal form for ![]() $\mathfrak{A}$ and the stated form of it.
$\mathfrak{A}$ and the stated form of it.
Recall that the groups ![]() $\Gamma=G \ltimes K\subset \mathrm{Aut}_0(T) \ltimes t(T)$ considered in our classification are isomorphic to one of the following groups:
$\Gamma=G \ltimes K\subset \mathrm{Aut}_0(T) \ltimes t(T)$ considered in our classification are isomorphic to one of the following groups:
where ![]() $\ell\in \{1,2,3,4,6\}$ and
$\ell\in \{1,2,3,4,6\}$ and ![]() $N\in \mathbb{N}$. The main object of our considerations for the rest of the paper is finding a suitable
$N\in \mathbb{N}$. The main object of our considerations for the rest of the paper is finding a suitable ![]() $\Psi\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})$ such that (6.1) holds. § 6.1 is devoted to the cases
$\Psi\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})$ such that (6.1) holds. § 6.1 is devoted to the cases ![]() $\Gamma=C_N$ and
$\Gamma=C_N$ and ![]() $\Gamma=D_N\cong C_2 \ltimes C_N$ while § 6.2 concerns
$\Gamma=D_N\cong C_2 \ltimes C_N$ while § 6.2 concerns ![]() $\Gamma=C_2\times C_2$ and
$\Gamma=C_2\times C_2$ and ![]() $\Gamma=A_4\cong C_3 \ltimes (C_2\times C_2)$.
$\Gamma=A_4\cong C_3 \ltimes (C_2\times C_2)$.
6.1. The cases  $\Gamma=C_N$ and
$\Gamma=C_N$ and  $\Gamma=D_N$
$\Gamma=D_N$
We will start with the case ![]() $\Gamma=C_N$ where CN is embedded into
$\Gamma=C_N$ where CN is embedded into ![]() $\mathrm{Aut}(T)$ as translations by the homomorphism
$\mathrm{Aut}(T)$ as translations by the homomorphism ![]() $\sigma_{\alpha}:C_N\rightarrow \mathrm{Aut}(T)$, defined by
$\sigma_{\alpha}:C_N\rightarrow \mathrm{Aut}(T)$, defined by ![]() $\sigma_{\alpha}(r)z=z+\alpha$ for some N-torsion point
$\sigma_{\alpha}(r)z=z+\alpha$ for some N-torsion point ![]() $\alpha\in T$. The main tool we use in the construction of aLias with symmetry group CN is the construction of map
$\alpha\in T$. The main tool we use in the construction of aLias with symmetry group CN is the construction of map ![]() $\Phi_j:{\mathbb{T}}\rightarrow SL_2({\mathbb{C}})$ (
$\Phi_j:{\mathbb{T}}\rightarrow SL_2({\mathbb{C}})$ (![]() $j\not\equiv0\mod N/2)$ for which the
$j\not\equiv0\mod N/2)$ for which the ![]() $\mathcal{O}_{\mathbb{T}}$-linear automorphism
$\mathcal{O}_{\mathbb{T}}$-linear automorphism ![]() $\mathrm{Ad}(\Phi_j)$ will map a basis of
$\mathrm{Ad}(\Phi_j)$ will map a basis of ![]() $\mathfrak{sl}_2$ to a subalgebra of the current algebra
$\mathfrak{sl}_2$ to a subalgebra of the current algebra ![]() $\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}$. The automorphism
$\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}$. The automorphism ![]() $\mathrm{Ad}(\Phi_j)$ is designed such that it satisfies the equivariance condition (6.3) for a given homomorphism
$\mathrm{Ad}(\Phi_j)$ is designed such that it satisfies the equivariance condition (6.3) for a given homomorphism ![]() $\rho:C_N\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$, which will imply that we obtain a basis of invariant matrices (with respect to the action induced by the homomorphism
$\rho:C_N\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$, which will imply that we obtain a basis of invariant matrices (with respect to the action induced by the homomorphism ![]() $\rho\otimes \tilde{\sigma})$. From here, one quickly obtains normal forms for aLias with symmetry group CN. Having established the relevant results, one easily obtains aLias with symmetry group DN, since
$\rho\otimes \tilde{\sigma})$. From here, one quickly obtains normal forms for aLias with symmetry group CN. Having established the relevant results, one easily obtains aLias with symmetry group DN, since ![]() $D_N\cong C_2 \ltimes C_N$. Due to Lemma 5 and 4, we can choose any faithful action of CN on
$D_N\cong C_2 \ltimes C_N$. Due to Lemma 5 and 4, we can choose any faithful action of CN on ![]() $\mathfrak{sl}_2$ without loss of generality.
$\mathfrak{sl}_2$ without loss of generality.
A crucial step in our construction of normal forms relies on the existence of intertwining operators between the actions of a symmetry group Γ on ![]() $\mathfrak{sl}_2$ and T. Let us briefly mention some general facts about these intertwiners to provide some motivation on the choice of these maps. Consider monomorphisms (that is, faithful homomorphisms)
$\mathfrak{sl}_2$ and T. Let us briefly mention some general facts about these intertwiners to provide some motivation on the choice of these maps. Consider monomorphisms (that is, faithful homomorphisms) ![]() $\sigma:\Gamma\rightarrow \mathrm{Aut}(T)$ and
$\sigma:\Gamma\rightarrow \mathrm{Aut}(T)$ and ![]() $\delta:\Gamma\rightarrow SL_2({\mathbb{C}})$. We would like to construct a matrix-valued map
$\delta:\Gamma\rightarrow SL_2({\mathbb{C}})$. We would like to construct a matrix-valued map ![]() $\Phi:T\rightarrow SL_2({\mathbb{C}})$,
$\Phi:T\rightarrow SL_2({\mathbb{C}})$,
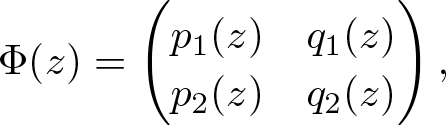 \begin{align}
\Phi(z)=\begin{pmatrix}
p_1(z)& q_1(z)\\
p_2(z) & q_2(z)
\end{pmatrix},
\end{align}
\begin{align}
\Phi(z)=\begin{pmatrix}
p_1(z)& q_1(z)\\
p_2(z) & q_2(z)
\end{pmatrix},
\end{align} where ![]() $p_j,q_j\in \mathcal{O}_{\mathbb{T}}$, such that
$p_j,q_j\in \mathcal{O}_{\mathbb{T}}$, such that ![]() $\Phi(\sigma(\gamma)z)=\delta(\gamma)\Phi(z)$ for all
$\Phi(\sigma(\gamma)z)=\delta(\gamma)\Phi(z)$ for all ![]() $\gamma\in \Gamma$ and
$\gamma\in \Gamma$ and ![]() $z\in \mathbb{T}$. Taking the adjoint
$z\in \mathbb{T}$. Taking the adjoint ![]() $\mathrm{Ad}$ of both sides, gives us the equivariance property with respect to the actions induced by
$\mathrm{Ad}$ of both sides, gives us the equivariance property with respect to the actions induced by ![]() $\sigma: \Gamma\rightarrow \mathrm{Aut}(T)$ and
$\sigma: \Gamma\rightarrow \mathrm{Aut}(T)$ and ![]() $\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$, with
$\rho:\Gamma\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$, with ![]() $\rho=\mathrm{Ad}\circ\delta$:
$\rho=\mathrm{Ad}\circ\delta$:
Notice that ![]() $\mathrm{Ad}(\Phi)$ is an element of
$\mathrm{Ad}(\Phi)$ is an element of ![]() $\mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})$ – the group of
$\mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})$ – the group of ![]() $\mathcal{O}_{\mathbb{T}}$-linear automorphisms of
$\mathcal{O}_{\mathbb{T}}$-linear automorphisms of ![]() $\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}$. The difficult part in constructing such an equivariant map is designing it in such a way that it is invertible over
$\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}$. The difficult part in constructing such an equivariant map is designing it in such a way that it is invertible over ![]() ${\mathbb{C}}$. We will present a procedure for the group CN below. The case of
${\mathbb{C}}$. We will present a procedure for the group CN below. The case of ![]() $C_2\times C_2$ will be dealt with in § 6.2. As we will see later, it will be enough to consider these two cases in the construction of normal forms.
$C_2\times C_2$ will be dealt with in § 6.2. As we will see later, it will be enough to consider these two cases in the construction of normal forms.
Take an element ![]() $\gamma\in \Gamma$ of order N and let
$\gamma\in \Gamma$ of order N and let ![]() $\delta:\Gamma\rightarrow SL_2({\mathbb{C}})$ and
$\delta:\Gamma\rightarrow SL_2({\mathbb{C}})$ and ![]() $\sigma:\Gamma\rightarrow \mathrm{Aut}(T)$ be monomorphisms. We call a vector
$\sigma:\Gamma\rightarrow \mathrm{Aut}(T)$ be monomorphisms. We call a vector ![]() $v=(v_1,v_2)^T$ consisting of functions
$v=(v_1,v_2)^T$ consisting of functions ![]() $v_j\in \mathcal{O}_{\mathbb{T}}$ an equivariant vector with respect to the actions defined by δ and σ, if
$v_j\in \mathcal{O}_{\mathbb{T}}$ an equivariant vector with respect to the actions defined by δ and σ, if
The columns of ![]() $\Phi$ consist of equivariant vectors
$\Phi$ consist of equivariant vectors ![]() $p:=(p_1,p_2)^T$ and
$p:=(p_1,p_2)^T$ and ![]() $q:=(q_1,q_2)^T$ as in (6.2). We will now fix a choice of δ, without loss of generality as we will see later. Let
$q:=(q_1,q_2)^T$ as in (6.2). We will now fix a choice of δ, without loss of generality as we will see later. Let ![]() $\delta=\delta_j:\Gamma\rightarrow SL_2({\mathbb{C}})$ be the monomorphism defined by
$\delta=\delta_j:\Gamma\rightarrow SL_2({\mathbb{C}})$ be the monomorphism defined by  $\delta_j(\gamma)=\mathrm{diag}(\omega_N^j,\omega_N^{-j})$ for some j coprime to N. The condition
$\delta_j(\gamma)=\mathrm{diag}(\omega_N^j,\omega_N^{-j})$ for some j coprime to N. The condition ![]() $\Phi(\sigma(\gamma)z)=\delta_j(\gamma)\Phi(z)$ implies that
$\Phi(\sigma(\gamma)z)=\delta_j(\gamma)\Phi(z)$ implies that  $p_1,q_1\in \mathcal{O}_{\mathbb{T}}^{\chi_{N-j}}$ and
$p_1,q_1\in \mathcal{O}_{\mathbb{T}}^{\chi_{N-j}}$ and  $p_2,q_2\in \mathcal{O}_{\mathbb{T}}^{\chi_{j}}$.
$p_2,q_2\in \mathcal{O}_{\mathbb{T}}^{\chi_{j}}$.
We will now present a construction for the matrix ![]() $\Phi$ as defined in (6.2), which will be used in the construction of normal forms of both CN and DN.
$\Phi$ as defined in (6.2), which will be used in the construction of normal forms of both CN and DN.
Let ![]() $N\geqslant 3$ and fix some integer
$N\geqslant 3$ and fix some integer ![]() $j\not\equiv 0\mod N/2$. Take
$j\not\equiv 0\mod N/2$. Take ![]() $\lambda,\mu\in {\mathbb{C}}$ such that
$\lambda,\mu\in {\mathbb{C}}$ such that  $P_{2j}P_{-j}^2-P_{-2j}P_j^2=\lambda P_{-j}P_j+\mu.$ Lemma 13 guarantees that µ is non-zero. Let the columns of
$P_{2j}P_{-j}^2-P_{-2j}P_j^2=\lambda P_{-j}P_j+\mu.$ Lemma 13 guarantees that µ is non-zero. Let the columns of ![]() $\Phi$ be given by p and q. In a sense, the simplest CN-equivariant vector we can choose for p is
$\Phi$ be given by p and q. In a sense, the simplest CN-equivariant vector we can choose for p is ![]() $(P_{-j}, P_j)^T$. Given this choice for p, for q we need to find
$(P_{-j}, P_j)^T$. Given this choice for p, for q we need to find  $q_1\in \mathcal{O}_{\mathbb{T}}^{\chi_{N-j}}$ and
$q_1\in \mathcal{O}_{\mathbb{T}}^{\chi_{N-j}}$ and  $q_2\in \mathcal{O}_{\mathbb{T}}^{\chi_{j}}$ such that
$q_2\in \mathcal{O}_{\mathbb{T}}^{\chi_{j}}$ such that ![]() $\det(\Phi)=P_{-j}q_2-P_jq_1=1$. Let s be given by
$\det(\Phi)=P_{-j}q_2-P_jq_1=1$. Let s be given by ![]() $s(z)=-z$ and recall that
$s(z)=-z$ and recall that ![]() $s\cdot P_j=-P_{-j}$ (cf. Lemma 12). One finds
$s\cdot P_j=-P_{-j}$ (cf. Lemma 12). One finds
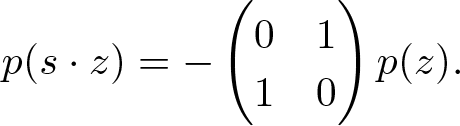 \begin{equation*}p(s\cdot z)=-\begin{pmatrix}
0& 1\\
1 &0
\end{pmatrix} p(z).\end{equation*}
\begin{equation*}p(s\cdot z)=-\begin{pmatrix}
0& 1\\
1 &0
\end{pmatrix} p(z).\end{equation*} Let  $S=\begin{pmatrix}
0& 1\\
1 &0
\end{pmatrix}$. In light of the equivariance condition (6.1), we will impose the condition
$S=\begin{pmatrix}
0& 1\\
1 &0
\end{pmatrix}$. In light of the equivariance condition (6.1), we will impose the condition ![]() $q(s\cdot z)=Sq(z),$ from which we get
$q(s\cdot z)=Sq(z),$ from which we get
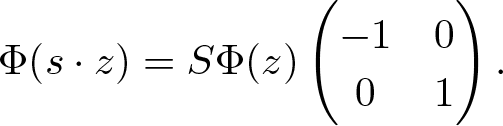 \begin{align}
\Phi(s\cdot z)=S\Phi(z)\begin{pmatrix}
-1& 0\\
0 & 1
\end{pmatrix}.
\end{align}
\begin{align}
\Phi(s\cdot z)=S\Phi(z)\begin{pmatrix}
-1& 0\\
0 & 1
\end{pmatrix}.
\end{align} Adding this condition to the equation ![]() $P_{-j}q_2-P_jq_1=1$ yields a unique solution in the space
$P_{-j}q_2-P_jq_1=1$ yields a unique solution in the space ![]() $L(2D)\subset \mathcal{O}_{\mathbb{T}}$, where D is the divisor
$L(2D)\subset \mathcal{O}_{\mathbb{T}}$, where D is the divisor  $D=\Gamma\cdot(0)=\sum_{j=0}^{N-1}(j\alpha)$. The solution to this equation in
$D=\Gamma\cdot(0)=\sum_{j=0}^{N-1}(j\alpha)$. The solution to this equation in ![]() $L(2D)$ is provided by Lemma 13. By the proof of Proposition 2, we deduce that for each integer
$L(2D)$ is provided by Lemma 13. By the proof of Proposition 2, we deduce that for each integer ![]() $j\not\equiv 0\mod N/2$, we have the vector space decomposition
$j\not\equiv 0\mod N/2$, we have the vector space decomposition ![]() $L(2D)^{\chi_j}={\mathbb{C}} P_j\oplus {\mathbb{C}} P_{-j}P_{2j}$. Then, if we choose
$L(2D)^{\chi_j}={\mathbb{C}} P_j\oplus {\mathbb{C}} P_{-j}P_{2j}$. Then, if we choose
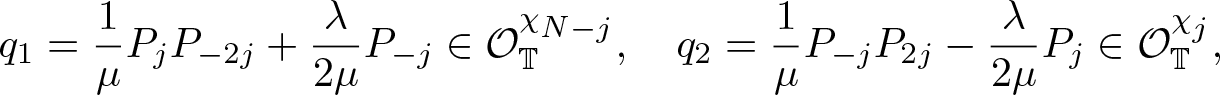 \begin{equation*}q_1=\frac{1}{\mu}P_jP_{-2j}+\frac{\lambda}{2\mu} P_{-j}\in \mathcal{O}_{\mathbb{T}}^{\chi_{N-j}},\quad q_2=\frac{1}{\mu}P_{-j}P_{2j}-\frac{\lambda}{2\mu} P_j\in \mathcal{O}_{\mathbb{T}}^{\chi_{j}},\end{equation*}
\begin{equation*}q_1=\frac{1}{\mu}P_jP_{-2j}+\frac{\lambda}{2\mu} P_{-j}\in \mathcal{O}_{\mathbb{T}}^{\chi_{N-j}},\quad q_2=\frac{1}{\mu}P_{-j}P_{2j}-\frac{\lambda}{2\mu} P_j\in \mathcal{O}_{\mathbb{T}}^{\chi_{j}},\end{equation*} we satisfy the requirement by Lemma 13, and this solution is unique by considering the vector space decompositions of ![]() $L(2D)^{\chi_j}$ and
$L(2D)^{\chi_j}$ and ![]() $L(2D)^{\chi_{N-j}}$. Thus, the matrix
$L(2D)^{\chi_{N-j}}$. Thus, the matrix ![]() $\Phi$ with the pj and qj defined above is the unique matrix with lowest order poles satisfying the intertwining condition.
$\Phi$ with the pj and qj defined above is the unique matrix with lowest order poles satisfying the intertwining condition.
We can summarise this as follows: given a complex torus T, define a faithful homomorphism ![]() $\sigma:C_N\rightarrow t(T)$. Set
$\sigma:C_N\rightarrow t(T)$. Set ![]() ${\mathbb{T}}=T\setminus C_N\cdot \{0\}$ and consider the functions Pj defined with respect to the choice of σ. For every integer
${\mathbb{T}}=T\setminus C_N\cdot \{0\}$ and consider the functions Pj defined with respect to the choice of σ. For every integer ![]() $j\not\equiv 0\mod N/2$, we associate with δj and σ a meromorphic, CN-equivariant map
$j\not\equiv 0\mod N/2$, we associate with δj and σ a meromorphic, CN-equivariant map ![]() $\Phi_j:T\rightarrow SL_2({\mathbb{C}})$, holomorphic on
$\Phi_j:T\rightarrow SL_2({\mathbb{C}})$, holomorphic on ![]() ${\mathbb{T}}$, given by
${\mathbb{T}}$, given by
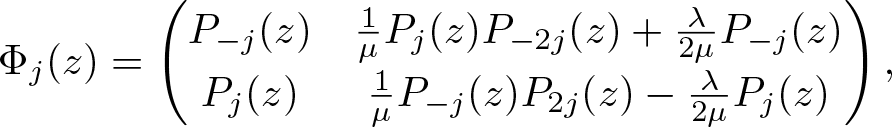 \begin{align}
\Phi_j(z)=\begin{pmatrix}
P_{-j}(z) & \frac{1}{\mu}P_j(z)P_{-2j}(z)+\frac{\lambda}{2\mu} P_{-j}(z)\\
P_j(z) &\frac{1}{\mu}P_{-j}(z)P_{2j}(z)-\frac{\lambda}{2\mu} P_j(z)
\end{pmatrix},
\end{align}
\begin{align}
\Phi_j(z)=\begin{pmatrix}
P_{-j}(z) & \frac{1}{\mu}P_j(z)P_{-2j}(z)+\frac{\lambda}{2\mu} P_{-j}(z)\\
P_j(z) &\frac{1}{\mu}P_{-j}(z)P_{2j}(z)-\frac{\lambda}{2\mu} P_j(z)
\end{pmatrix},
\end{align}where λ and µ are constants defined in Lemma 13. We will record our discussion below in two lemmata.
Lemma 15. For any integer ![]() $j\not\equiv 0\mod N/2$ it holds that
$j\not\equiv 0\mod N/2$ it holds that ![]() $\det(\Phi_j)=1$.
$\det(\Phi_j)=1$.
Lemma 16. Let ![]() $\sigma:C_N\rightarrow \mathrm{Aut}(T)$ be a monomorphism and
$\sigma:C_N\rightarrow \mathrm{Aut}(T)$ be a monomorphism and ![]() $\delta_{j,N}:C_N\rightarrow SL_2({\mathbb{C}})$ be defined by
$\delta_{j,N}:C_N\rightarrow SL_2({\mathbb{C}})$ be defined by  $\delta_{j,N}(r)=\mathrm{diag}(\omega_N^j,\omega_N^{-j})$. For all integers
$\delta_{j,N}(r)=\mathrm{diag}(\omega_N^j,\omega_N^{-j})$. For all integers ![]() $j\not\equiv 0\mod N/2$,
$j\not\equiv 0\mod N/2$, ![]() $z\in \mathbb{T}$ and
$z\in \mathbb{T}$ and ![]() $r\in C_N$, we have
$r\in C_N$, we have
Define ![]() $\rho_{j,N}=\mathrm{Ad}\circ \delta_{j,N}$. Taking the adjoint of both sides of
$\rho_{j,N}=\mathrm{Ad}\circ \delta_{j,N}$. Taking the adjoint of both sides of ![]() $\Phi_j(\sigma(r) z)=\delta_{j,N}(r)\Phi_j(z)$, we obtain
$\Phi_j(\sigma(r) z)=\delta_{j,N}(r)\Phi_j(z)$, we obtain ![]() $\mathrm{Ad}(\Phi_j(\sigma(r) z))=\rho_{j,N}(r)\mathrm{Ad}(\Phi_j(z))$. Notice that
$\mathrm{Ad}(\Phi_j(\sigma(r) z))=\rho_{j,N}(r)\mathrm{Ad}(\Phi_j(z))$. Notice that ![]() $\ker\rho_{j,N}\cong C_2$ if N is even and
$\ker\rho_{j,N}\cong C_2$ if N is even and ![]() $\gcd(j,N)=1$.
$\gcd(j,N)=1$.
We have that for any integer ![]() $j\not\equiv 0\mod N/2$,
$j\not\equiv 0\mod N/2$, ![]() $\mathrm{Ad}(\Phi_j)\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})$ by Lemma 15. We can also consider
$\mathrm{Ad}(\Phi_j)\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})$ by Lemma 15. We can also consider ![]() $\mathrm{Ad}(\Phi_j)$ to be a meromorphic map from T to
$\mathrm{Ad}(\Phi_j)$ to be a meromorphic map from T to ![]() $\mathrm{Aut}(\mathfrak{sl}_2)$,
$\mathrm{Aut}(\mathfrak{sl}_2)$, ![]() $z\mapsto \mathrm{Ad}(\Phi_j(z))$ holomorphic on
$z\mapsto \mathrm{Ad}(\Phi_j(z))$ holomorphic on ![]() ${\mathbb{T}}$. The map
${\mathbb{T}}$. The map ![]() $\mathrm{Ad}(\Phi_j)$ intertwines the actions defined by σ and ρ, or stated differently, it is equivariant with respect the action of CN.
$\mathrm{Ad}(\Phi_j)$ intertwines the actions defined by σ and ρ, or stated differently, it is equivariant with respect the action of CN.
Remark 4. The matrix ![]() $\Phi(z):=\Phi_j(z)$ is constructed via a particular choice of ρ. If
$\Phi(z):=\Phi_j(z)$ is constructed via a particular choice of ρ. If ![]() $\rho'$ is an equivalent representation of CN,
$\rho'$ is an equivalent representation of CN, ![]() $\rho'(r)=B\rho(r) B^{-1}$ for all
$\rho'(r)=B\rho(r) B^{-1}$ for all ![]() $r\in C_N$ for some
$r\in C_N$ for some ![]() $B\in \mathrm{Aut}(\mathfrak{sl}_2)$, and we define
$B\in \mathrm{Aut}(\mathfrak{sl}_2)$, and we define ![]() $\Phi'=B\Phi B^{-1}$, then one can verify that
$\Phi'=B\Phi B^{-1}$, then one can verify that ![]() $\rho'(r)\mathrm{Ad}(\Phi'(z))=\mathrm{Ad}(\Phi'(\sigma(r)z))$.
$\rho'(r)\mathrm{Ad}(\Phi'(z))=\mathrm{Ad}(\Phi'(\sigma(r)z))$.
The next two theorems describe the aLias with a cyclic symmetry group. We split the results according to the genus g of ![]() $T/\sigma(C_N)$. First, we consider
$T/\sigma(C_N)$. First, we consider ![]() $g(T/\sigma(C_N))=1$.
$g(T/\sigma(C_N))=1$.
Theorem 4 (Genus 1 case)
Let ![]() $\rho:C_N\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and
$\rho:C_N\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and ![]() $\sigma:C_N\rightarrow t(T)$ be monomorphisms. Then
$\sigma:C_N\rightarrow t(T)$ be monomorphisms. Then
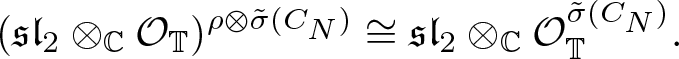 \begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_N)}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_N)}.\end{equation*}
\begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_N)}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_N)}.\end{equation*}A normal form is given by
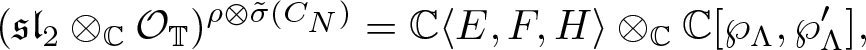 \begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_N)}={\mathbb{C}}\langle E,F,H\rangle\otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{{\Lambda}},\wp_{{\Lambda}}'],\end{equation*}
\begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_N)}={\mathbb{C}}\langle E,F,H\rangle\otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{{\Lambda}},\wp_{{\Lambda}}'],\end{equation*} where ![]() $\Lambda$ is a suitable lattice, and with brackets
$\Lambda$ is a suitable lattice, and with brackets
where ![]() $E,F$ and H are the images under
$E,F$ and H are the images under ![]() $\mathrm{Ad}(\Phi_j)$, for some integer
$\mathrm{Ad}(\Phi_j)$, for some integer ![]() $j\not\equiv 0\mod N/2$, of
$j\not\equiv 0\mod N/2$, of ![]() $e\otimes 1$,
$e\otimes 1$, ![]() $f\otimes 1$ and
$f\otimes 1$ and ![]() $h\otimes 1$, respectively.
$h\otimes 1$, respectively.
Proof. The main ingredients are Proposition 3 and Lemma 16. Fix a lattice ![]() ${\Lambda}={\mathbb{Z}}\oplus {\mathbb{Z}}\tau$ and let
${\Lambda}={\mathbb{Z}}\oplus {\mathbb{Z}}\tau$ and let ![]() $T={\mathbb{C}}/{\Lambda}$. Let
$T={\mathbb{C}}/{\Lambda}$. Let ![]() $\alpha'\in {\mathbb{C}}$ be such that the projection of
$\alpha'\in {\mathbb{C}}$ be such that the projection of ![]() $\alpha'$ under
$\alpha'$ under ![]() $\pi_{{\Lambda}}:{\mathbb{C}}\rightarrow {\mathbb{C}}/{\Lambda}$,
$\pi_{{\Lambda}}:{\mathbb{C}}\rightarrow {\mathbb{C}}/{\Lambda}$, ![]() $\alpha:=\pi(\alpha')$ is an N-torsion point of T. Thus α satisfies
$\alpha:=\pi(\alpha')$ is an N-torsion point of T. Thus α satisfies ![]() $N\alpha=0 \mod {\Lambda}$. We may assume that σ is given by
$N\alpha=0 \mod {\Lambda}$. We may assume that σ is given by ![]() $\sigma_{\alpha}(r)z=z+\alpha$.
$\sigma_{\alpha}(r)z=z+\alpha$.
First, let N be odd. We may also assume that  $\delta(r)=\delta_{j,N}(r):=\mathrm{diag}(\omega_N^j,\omega_N^{-j})$ for some j with
$\delta(r)=\delta_{j,N}(r):=\mathrm{diag}(\omega_N^j,\omega_N^{-j})$ for some j with ![]() $\gcd(j,N)\neq 1$ and that ρ is given by
$\gcd(j,N)\neq 1$ and that ρ is given by ![]() $\mathrm{Ad}\circ\delta$. The explanation is that if
$\mathrm{Ad}\circ\delta$. The explanation is that if ![]() $\delta'$ is another monomorphism, and
$\delta'$ is another monomorphism, and ![]() $\rho'=\mathrm{Ad}\circ\delta'$, then we know by Lemma 5 that
$\rho'=\mathrm{Ad}\circ\delta'$, then we know by Lemma 5 that ![]() $\rho(C_N)$ and
$\rho(C_N)$ and ![]() $\rho'(C_N)$ are conjugated subgroups. Lemma 4 then tells us that the aLias defined by ρ and
$\rho'(C_N)$ are conjugated subgroups. Lemma 4 then tells us that the aLias defined by ρ and ![]() $\rho'$ are isomorphic.
$\rho'$ are isomorphic.
The algebra of invariants  $\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}_{\alpha}(C_N)}$ is given by
$\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}_{\alpha}(C_N)}$ is given by  ${\mathbb{C}}[\wp_{{\Lambda}_{(\alpha)}},\wp_{{\Lambda}_{(\alpha)}}']$ by Lemma 11. Now,
${\mathbb{C}}[\wp_{{\Lambda}_{(\alpha)}},\wp_{{\Lambda}_{(\alpha)}}']$ by Lemma 11. Now, ![]() $\mathrm{Ad}(\Phi_j)$ satisfies (6.1) because of Lemma 15 and Lemma 16, for which reason we can apply Proposition 3. We, therefore, have, as in the proof of Proposition 3, that the following elements form a basis of
$\mathrm{Ad}(\Phi_j)$ satisfies (6.1) because of Lemma 15 and Lemma 16, for which reason we can apply Proposition 3. We, therefore, have, as in the proof of Proposition 3, that the following elements form a basis of ![]() $\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{C_N}$ over
$\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{C_N}$ over  ${\mathbb{C}}[\wp_{\Lambda_{(\alpha)}},\wp_{\Lambda_{(\alpha)}}']$:
${\mathbb{C}}[\wp_{\Lambda_{(\alpha)}},\wp_{\Lambda_{(\alpha)}}']$:
where ![]() $\Phi_j$ is given in (6.5). Remark 4 can be used to find a normal form if instead of δ, we had chosen
$\Phi_j$ is given in (6.5). Remark 4 can be used to find a normal form if instead of δ, we had chosen ![]() $\delta'$ as defined in the beginning of the proof.
$\delta'$ as defined in the beginning of the proof.
Assume now N is even. We may assume that ρ is given by
 \begin{equation*}\rho(r)\begin{pmatrix}
a&b\\
c&-a
\end{pmatrix}=
\begin{pmatrix}a&\omega_Nb\\
\omega_N^{-1}c&-a
\end{pmatrix}.\end{equation*}
\begin{equation*}\rho(r)\begin{pmatrix}
a&b\\
c&-a
\end{pmatrix}=
\begin{pmatrix}a&\omega_Nb\\
\omega_N^{-1}c&-a
\end{pmatrix}.\end{equation*} Observe that the image of ρ and ![]() $\hat{\rho}=\mathrm{Ad}\circ \delta_{j,2N}$ coincide. Notice that
$\hat{\rho}=\mathrm{Ad}\circ \delta_{j,2N}$ coincide. Notice that ![]() $\ker\hat{\rho}=\langle r^{N}\rangle\cong C_2$, where
$\ker\hat{\rho}=\langle r^{N}\rangle\cong C_2$, where ![]() $r\in C_{2N}$. Define
$r\in C_{2N}$. Define
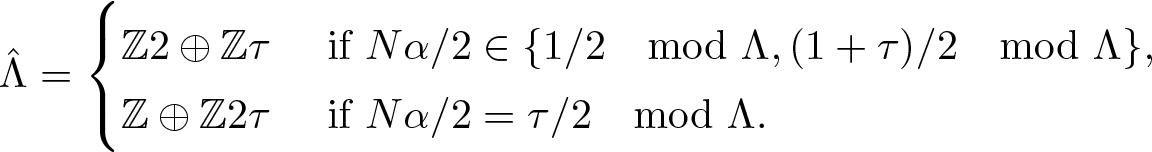 \begin{equation*}\hat{{\Lambda}}=\begin{cases}
{\mathbb{Z}}2\oplus {\mathbb{Z}}\tau &\,\,\text{if}\,\, N\alpha/2\in \{1/2 \mod {\Lambda}, (1+\tau)/2\mod {\Lambda}\},\\
{\mathbb{Z}}\oplus {\mathbb{Z}}2\tau &\,\,\text{if}\,\, N\alpha/2=\tau/2\mod {\Lambda}.
\end{cases}\end{equation*}
\begin{equation*}\hat{{\Lambda}}=\begin{cases}
{\mathbb{Z}}2\oplus {\mathbb{Z}}\tau &\,\,\text{if}\,\, N\alpha/2\in \{1/2 \mod {\Lambda}, (1+\tau)/2\mod {\Lambda}\},\\
{\mathbb{Z}}\oplus {\mathbb{Z}}2\tau &\,\,\text{if}\,\, N\alpha/2=\tau/2\mod {\Lambda}.
\end{cases}\end{equation*} Let ![]() $\hat{T}={\mathbb{C}}/\hat{{\Lambda}}$ and define
$\hat{T}={\mathbb{C}}/\hat{{\Lambda}}$ and define ![]() $\hat{{\mathbb{T}}}$ accordingly. Define
$\hat{{\mathbb{T}}}$ accordingly. Define ![]() $\sigma_1:C_{2N}\rightarrow \mathrm{Aut}(\hat{T})$ by
$\sigma_1:C_{2N}\rightarrow \mathrm{Aut}(\hat{T})$ by ![]() $\sigma_1(r)z=z+\pi_{\hat{{\Lambda}}}(\alpha')$ and notice that
$\sigma_1(r)z=z+\pi_{\hat{{\Lambda}}}(\alpha')$ and notice that ![]() $\pi_{\hat{{\Lambda}}}(N\alpha')=N\alpha$ is a half lattice point of
$\pi_{\hat{{\Lambda}}}(N\alpha')=N\alpha$ is a half lattice point of ![]() $\hat{{\Lambda}}$.
$\hat{{\Lambda}}$.
Recall that in the proof of Lemma 11 we used that for any ![]() $\alpha\in T$,
$\alpha\in T$,  $\mathcal{O}^{\tilde{\sigma}_\alpha(C_N)}_{\mathbb{T}}$ is the space of
$\mathcal{O}^{\tilde{\sigma}_\alpha(C_N)}_{\mathbb{T}}$ is the space of ![]() $\Lambda_{(\alpha)}$-periodic meromorphic functions which are holomorphic on
$\Lambda_{(\alpha)}$-periodic meromorphic functions which are holomorphic on ![]() $T\setminus \Lambda_{(\alpha)}$. This allowed us to say that
$T\setminus \Lambda_{(\alpha)}$. This allowed us to say that  $\mathcal{O}_{\mathbb{T}}^{\Gamma}=\mathcal{O}_{{\mathbb{T}}/\Gamma}$. We adopt this perspective again. Suppose
$\mathcal{O}_{\mathbb{T}}^{\Gamma}=\mathcal{O}_{{\mathbb{T}}/\Gamma}$. We adopt this perspective again. Suppose ![]() $N\alpha/2=1/2\mod {\Lambda}$. Then
$N\alpha/2=1/2\mod {\Lambda}$. Then ![]() $\hat{T}/\sigma_1(C_{2N})= {\mathbb{C}}/({\mathbb{Z}}2+{\mathbb{Z}}\tau+{\mathbb{Z}}\alpha')$. Notice that
$\hat{T}/\sigma_1(C_{2N})= {\mathbb{C}}/({\mathbb{Z}}2+{\mathbb{Z}}\tau+{\mathbb{Z}}\alpha')$. Notice that ![]() $N\alpha'=1+2n_1+2n_2\tau$ for some
$N\alpha'=1+2n_1+2n_2\tau$ for some ![]() $n_1,n_2\in {\mathbb{Z}}$. We see that
$n_1,n_2\in {\mathbb{Z}}$. We see that ![]() $1\in {\mathbb{Z}}2+{\mathbb{Z}}\tau+{\mathbb{Z}}\alpha'$ and hence
$1\in {\mathbb{Z}}2+{\mathbb{Z}}\tau+{\mathbb{Z}}\alpha'$ and hence
Also observe that ![]() $T/\sigma(C_N)= {\mathbb{C}}/({\mathbb{Z}}+{\mathbb{Z}}\tau+{\mathbb{Z}}\alpha')$. Therefore
$T/\sigma(C_N)= {\mathbb{C}}/({\mathbb{Z}}+{\mathbb{Z}}\tau+{\mathbb{Z}}\alpha')$. Therefore ![]() $\hat{T}/\sigma_1(C_{2N})=T/\sigma(C_N)$. Similarly, we have
$\hat{T}/\sigma_1(C_{2N})=T/\sigma(C_N)$. Similarly, we have  $\hat{{\mathbb{T}}}/\langle r^N\rangle={\mathbb{T}}$. The same claim holds in the cases where
$\hat{{\mathbb{T}}}/\langle r^N\rangle={\mathbb{T}}$. The same claim holds in the cases where ![]() $N\alpha/2\in \{\tau/2,(1+\tau)/2\}$.
$N\alpha/2\in \{\tau/2,(1+\tau)/2\}$.
Define ![]() $\Phi:=\Phi_j$ associated to
$\Phi:=\Phi_j$ associated to ![]() $\delta_{j,2N}$ and σ 1, for some integer
$\delta_{j,2N}$ and σ 1, for some integer ![]() $j\not\equiv N/2$. It is clear that
$j\not\equiv N/2$. It is clear that  $\mathrm{Ad}(\Phi)\in \mathrm{Aut}_{\mathcal{O}_{\hat{{\mathbb{T}}}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\hat{{\mathbb{T}}}})$. By similar reasoning as in Proposition 3, we have that
$\mathrm{Ad}(\Phi)\in \mathrm{Aut}_{\mathcal{O}_{\hat{{\mathbb{T}}}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\hat{{\mathbb{T}}}})$. By similar reasoning as in Proposition 3, we have that ![]() $\mathrm{Ad}(\Phi)$ establishes an isomorphism
$\mathrm{Ad}(\Phi)$ establishes an isomorphism
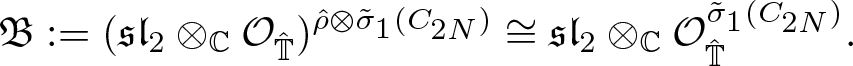 \begin{equation*}\mathfrak{B}:=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\hat{{\mathbb{T}}}})^{\hat{\rho}\otimes\tilde{\sigma}_1(C_{2N})}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\hat{{\mathbb{T}}}}^{\tilde{\sigma}_1(C_{2N})}.\end{equation*}
\begin{equation*}\mathfrak{B}:=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\hat{{\mathbb{T}}}})^{\hat{\rho}\otimes\tilde{\sigma}_1(C_{2N})}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\hat{{\mathbb{T}}}}^{\tilde{\sigma}_1(C_{2N})}.\end{equation*} We know ![]() $\hat{T}/\sigma_1(C_{2N})= T/\sigma(C_N)$ and therefore
$\hat{T}/\sigma_1(C_{2N})= T/\sigma(C_N)$ and therefore  $\mathcal{O}_{\hat{{\mathbb{T}}}}^{\tilde{\sigma}_1(C_{2N})}= \mathcal{O}_{{\mathbb{T}}}^{\tilde{\sigma}(C_{N})}.$ Hence
$\mathcal{O}_{\hat{{\mathbb{T}}}}^{\tilde{\sigma}_1(C_{2N})}= \mathcal{O}_{{\mathbb{T}}}^{\tilde{\sigma}(C_{N})}.$ Hence  $\mathfrak{B}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{{\mathbb{T}}}^{\tilde{\sigma}(C_{N})}.$ We claim that
$\mathfrak{B}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{{\mathbb{T}}}^{\tilde{\sigma}(C_{N})}.$ We claim that ![]() $\mathfrak{B}$ is precisely
$\mathfrak{B}$ is precisely ![]() $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_{N})}.$ By Lemma 3, we have that
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_{N})}.$ By Lemma 3, we have that  $\mathfrak{B}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\hat{\mathbb{T}}/\langle r^N\rangle})^{\hat{\Gamma}}$, where
$\mathfrak{B}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\hat{\mathbb{T}}/\langle r^N\rangle})^{\hat{\Gamma}}$, where ![]() $\hat{\Gamma}=\langle r\rangle/\langle r^N\rangle \cong C_N$. Now, since
$\hat{\Gamma}=\langle r\rangle/\langle r^N\rangle \cong C_N$. Now, since  $\hat{{\mathbb{T}}}/\langle r^N\rangle={\mathbb{T}}$ and the action of
$\hat{{\mathbb{T}}}/\langle r^N\rangle={\mathbb{T}}$ and the action of ![]() $\hat{\Gamma}$ is the same as the one induced from σ, we conclude that
$\hat{\Gamma}$ is the same as the one induced from σ, we conclude that ![]() $\mathfrak{B}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_{N})}.$
$\mathfrak{B}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_{N})}.$
We know ![]() $\mathrm{Ad}(\Phi(r^N\cdot z))=\mathrm{Ad}(\Phi(z))$, since
$\mathrm{Ad}(\Phi(r^N\cdot z))=\mathrm{Ad}(\Phi(z))$, since ![]() $r^N\in \ker(\hat{\rho})$. Therefore, any invariant element
$r^N\in \ker(\hat{\rho})$. Therefore, any invariant element ![]() $X:=\mathrm{Ad}(\Phi)x$, with
$X:=\mathrm{Ad}(\Phi)x$, with ![]() $x\in \mathfrak{sl}_2$, consists of entries which are invariant under
$x\in \mathfrak{sl}_2$, consists of entries which are invariant under ![]() $\langle r^N\rangle\cong C_2$. The remainder of the proof for N is even, follows as it did for N odd. A normal form is given by
$\langle r^N\rangle\cong C_2$. The remainder of the proof for N is even, follows as it did for N odd. A normal form is given by
This proves the claim.
Explicitly, the generators ![]() $H_j:=\mathrm{Ad}(\Phi_j)h\otimes 1$,
$H_j:=\mathrm{Ad}(\Phi_j)h\otimes 1$, ![]() $E_j:=\mathrm{Ad}(\Phi_j)e\otimes 1$ and
$E_j:=\mathrm{Ad}(\Phi_j)e\otimes 1$ and ![]() $F_j:=\mathrm{Ad}(\Phi_j)f\otimes 1$ (
$F_j:=\mathrm{Ad}(\Phi_j)f\otimes 1$ (![]() $j\not\equiv 0 \mod N/2$) are given by
$j\not\equiv 0 \mod N/2$) are given by
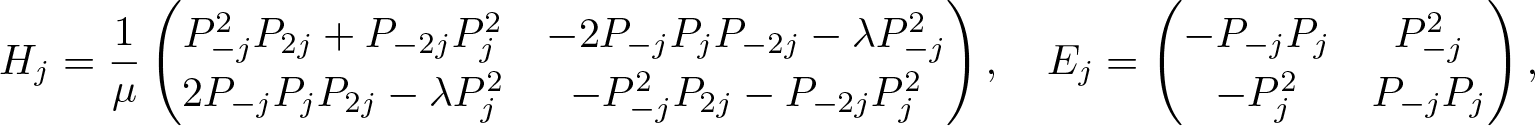 \begin{align}
H_j = \frac{1}{\mu}\begin{pmatrix}
P_{-j}^2 P_{2j} + P_{-2j} P_j^2 & -2 P_{-j} P_j P_{-2j} -\lambda P_{-j}^{2} \\
2 P_{-j} P_j P_{2j} - \lambda P_j^{2} & -P_{-j}^2 P_{2j} - P_{-2j} P_j^2
\end{pmatrix},
\quad E_j=\begin{pmatrix}
-P_{-j} P_j& P_{-j}^{2} \\
-P_j^{2}& P_{-j} P_j
\end{pmatrix},
\end{align}
\begin{align}
H_j = \frac{1}{\mu}\begin{pmatrix}
P_{-j}^2 P_{2j} + P_{-2j} P_j^2 & -2 P_{-j} P_j P_{-2j} -\lambda P_{-j}^{2} \\
2 P_{-j} P_j P_{2j} - \lambda P_j^{2} & -P_{-j}^2 P_{2j} - P_{-2j} P_j^2
\end{pmatrix},
\quad E_j=\begin{pmatrix}
-P_{-j} P_j& P_{-j}^{2} \\
-P_j^{2}& P_{-j} P_j
\end{pmatrix},
\end{align}and
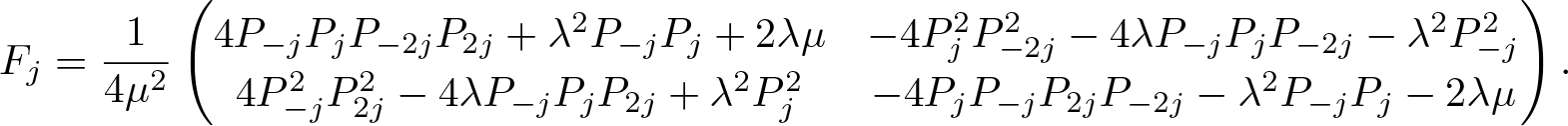 \begin{align}
F_j=\frac{1}{4\mu^2}\begin{pmatrix}
4P_{-j} P_j P_{-2j} P_{2j} + \lambda^{2}P_{-j} P_j + 2\lambda \mu & -4P_j^{2} P_{-2j}^{2} - 4 \lambda P_{-j} P_j P_{-2j} - \lambda^{2}P_{-j}^{2} \\
4P_{-j}^2 P_{2j}^{2} - 4 \lambda P_{-j} P_j P_{2j} + \lambda^{2}P_j^{2} & -4P_j P_{-j} P_{2j} P_{-2j} - \lambda^{2} P_{-j} P_j- 2\lambda \mu\end{pmatrix}.
\end{align}
\begin{align}
F_j=\frac{1}{4\mu^2}\begin{pmatrix}
4P_{-j} P_j P_{-2j} P_{2j} + \lambda^{2}P_{-j} P_j + 2\lambda \mu & -4P_j^{2} P_{-2j}^{2} - 4 \lambda P_{-j} P_j P_{-2j} - \lambda^{2}P_{-j}^{2} \\
4P_{-j}^2 P_{2j}^{2} - 4 \lambda P_{-j} P_j P_{2j} + \lambda^{2}P_j^{2} & -4P_j P_{-j} P_{2j} P_{-2j} - \lambda^{2} P_{-j} P_j- 2\lambda \mu\end{pmatrix}.
\end{align} In the next corollary, we shall omit the j-dependence of ![]() $E,F,H$ and assume this implicitly.
$E,F,H$ and assume this implicitly.
Corollary 1. Let ![]() $\rho:D_N\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and
$\rho:D_N\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and ![]() $\sigma:D_N\rightarrow \mathrm{Aut}(T)$ be monomorphisms. Then
$\sigma:D_N\rightarrow \mathrm{Aut}(T)$ be monomorphisms. Then
for some ![]() $\tau\in \mathbb{H}$. A normal form is given by
$\tau\in \mathbb{H}$. A normal form is given by
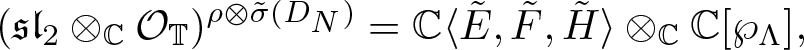 \begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(D_N)}={\mathbb{C}}\langle \tilde{E}, \tilde{F}, \tilde{H}\rangle\otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp_{\Lambda}],\end{equation*}
\begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(D_N)}={\mathbb{C}}\langle \tilde{E}, \tilde{F}, \tilde{H}\rangle\otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp_{\Lambda}],\end{equation*} where ![]() $\Lambda$ is a suitable lattice and
$\Lambda$ is a suitable lattice and  $
\tilde{E}=E\otimes \wp_{\Lambda}'$,
$
\tilde{E}=E\otimes \wp_{\Lambda}'$,  $\tilde{F}=F\otimes \wp_{\Lambda}'$ and
$\tilde{F}=F\otimes \wp_{\Lambda}'$ and ![]() $\tilde{H}=H$, where
$\tilde{H}=H$, where ![]() $E,F,H$ are defined in the proof of Theorem 4. The Lie structure is given by
$E,F,H$ are defined in the proof of Theorem 4. The Lie structure is given by
Proof. We may assume that σ is given by ![]() $\sigma(s)z=-z$ and
$\sigma(s)z=-z$ and ![]() $\sigma(r)z=z+\alpha$ for some N-torsion point
$\sigma(r)z=z+\alpha$ for some N-torsion point ![]() $\alpha\in T$. Let
$\alpha\in T$. Let  $S=\begin{pmatrix}
0& 1\\
1 & 0
\end{pmatrix}$. We will use Proposition 3. Recall
$S=\begin{pmatrix}
0& 1\\
1 & 0
\end{pmatrix}$. We will use Proposition 3. Recall ![]() $H=\mathrm{Ad}(\Phi)h,$ where
$H=\mathrm{Ad}(\Phi)h,$ where ![]() $\Phi=\Phi_j$ for some
$\Phi=\Phi_j$ for some ![]() $j\not\equiv 0\mod N/2$. To satisfy condition (6.1), we only need to verify condition (6.4):
$j\not\equiv 0\mod N/2$. To satisfy condition (6.1), we only need to verify condition (6.4):
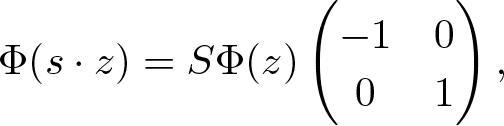 \begin{equation*}\Phi(s\cdot z)=S\Phi(z)\begin{pmatrix}
-1& 0\\
0 & 1
\end{pmatrix},\end{equation*}
\begin{equation*}\Phi(s\cdot z)=S\Phi(z)\begin{pmatrix}
-1& 0\\
0 & 1
\end{pmatrix},\end{equation*} where s generates ![]() $C_2\subset\mathrm{Aut}_0(T)$. This holds as a result of the construction of
$C_2\subset\mathrm{Aut}_0(T)$. This holds as a result of the construction of ![]() $\Phi$ in the beginning of this section. Thus, H is a DN-invariant as well. Hence we can apply Lemma 14 and use Example 3 to obtain the stated normal form.
$\Phi$ in the beginning of this section. Thus, H is a DN-invariant as well. Hence we can apply Lemma 14 and use Example 3 to obtain the stated normal form.
Notice that above corollary also covers the aLia ![]() $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{C_2}$, where
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{C_2}$, where ![]() $g(T/C_2)=0$, since
$g(T/C_2)=0$, since ![]() $D_1=C_2 \ltimes 1\cong C_2.$
$D_1=C_2 \ltimes 1\cong C_2.$
So far, we have considered the groups CN and ![]() $D_N\cong C_2 \ltimes C_N$ for which CN is embedded as translations in
$D_N\cong C_2 \ltimes C_N$ for which CN is embedded as translations in ![]() $\mathrm{Aut}(T)$. There are a number of cyclic groups of small order which also allow an embedding as a rotation in
$\mathrm{Aut}(T)$. There are a number of cyclic groups of small order which also allow an embedding as a rotation in ![]() $\mathrm{Aut}(T)$ for a torus T with more symmetry than the generic case, cf. Proposition 7. The groups
$\mathrm{Aut}(T)$ for a torus T with more symmetry than the generic case, cf. Proposition 7. The groups ![]() $C_{\ell}$ for
$C_{\ell}$ for ![]() $\ell\in \{3,4,6\}$ can be embedded inside
$\ell\in \{3,4,6\}$ can be embedded inside ![]() $\mathrm{Aut}(T)$ as rotations, for tori either isomorphic to Ti or
$\mathrm{Aut}(T)$ as rotations, for tori either isomorphic to Ti or ![]() $T_{\omega_6}$. The following theorem describes the aLias with these symmetry groups.
$T_{\omega_6}$. The following theorem describes the aLias with these symmetry groups.
Theorem 5 (Genus 0 case)
Let ![]() $\rho:C_{\ell}\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and
$\rho:C_{\ell}\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and ![]() $\sigma:C_{\ell}\rightarrow \mathrm{Aut}(T)$ be monomorphisms and assume that
$\sigma:C_{\ell}\rightarrow \mathrm{Aut}(T)$ be monomorphisms and assume that ![]() $g(T/\sigma(C_{\ell}))=0$. Then
$g(T/\sigma(C_{\ell}))=0$. Then
if and only if ![]() $\ell\in \{3,4,6\}.$
$\ell\in \{3,4,6\}.$
Proof. By Lemma 4, we only have to prove the statement for a particular choice of monomorphisms. Let ![]() $\ell=3$ and define the homomorphism
$\ell=3$ and define the homomorphism ![]() $\rho: C_{3}\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ by
$\rho: C_{3}\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ by
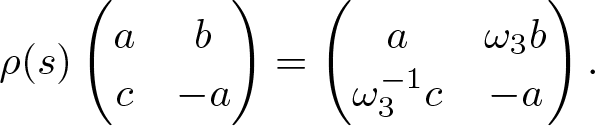 \begin{equation*}
\rho(s)\begin{pmatrix}
a & b\\
c &-a
\end{pmatrix}=\begin{pmatrix}
a & \omega_3b\\
\omega_{3}^{-1}c &-a
\end{pmatrix}.
\end{equation*}
\begin{equation*}
\rho(s)\begin{pmatrix}
a & b\\
c &-a
\end{pmatrix}=\begin{pmatrix}
a & \omega_3b\\
\omega_{3}^{-1}c &-a
\end{pmatrix}.
\end{equation*} Let ![]() $s\in C_{3}$ act on
$s\in C_{3}$ act on ![]() $T\cong T_{\omega_6}$ as
$T\cong T_{\omega_6}$ as ![]() $s\cdot z=\omega_3z$. Recall that
$s\cdot z=\omega_3z$. Recall that ![]() $s\cdot \wp(z)=\wp(\omega_{3}^{-1}z)=\omega_3^2\wp(z)$ and
$s\cdot \wp(z)=\wp(\omega_{3}^{-1}z)=\omega_3^2\wp(z)$ and ![]() $s\cdot \wp'=\wp'$ by Equations (5.3) and (5.4). By Proposition 10, we have
$s\cdot \wp'=\wp'$ by Equations (5.3) and (5.4). By Proposition 10, we have
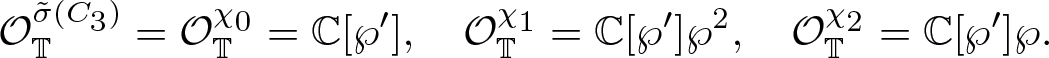 \begin{equation*}
\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_3)}=\mathcal{O}_{\mathbb{T}}^{\chi_0}={\mathbb{C}}[\wp'],\quad
\mathcal{O}_{\mathbb{T}}^{\chi_1}={\mathbb{C}}[\wp']\wp^2,\quad
\mathcal{O}_{\mathbb{T}}^{\chi_2}={\mathbb{C}}[\wp']\wp.
\end{equation*}
\begin{equation*}
\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_3)}=\mathcal{O}_{\mathbb{T}}^{\chi_0}={\mathbb{C}}[\wp'],\quad
\mathcal{O}_{\mathbb{T}}^{\chi_1}={\mathbb{C}}[\wp']\wp^2,\quad
\mathcal{O}_{\mathbb{T}}^{\chi_2}={\mathbb{C}}[\wp']\wp.
\end{equation*}Define the matrices
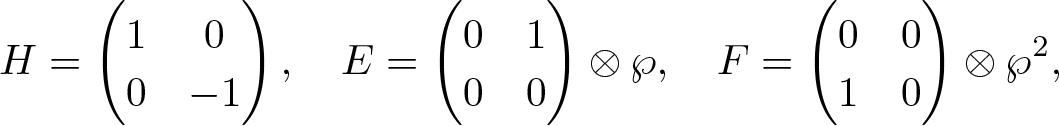 \begin{equation*}H=\begin{pmatrix}
1& 0\\
0 &-1
\end{pmatrix},\quad E=\begin{pmatrix}
0 & 1\\
0 &0
\end{pmatrix}\otimes \wp,\quad F=\begin{pmatrix}
0 & 0\\
1 &0
\end{pmatrix}\otimes \wp^2,\end{equation*}
\begin{equation*}H=\begin{pmatrix}
1& 0\\
0 &-1
\end{pmatrix},\quad E=\begin{pmatrix}
0 & 1\\
0 &0
\end{pmatrix}\otimes \wp,\quad F=\begin{pmatrix}
0 & 0\\
1 &0
\end{pmatrix}\otimes \wp^2,\end{equation*} which are easily seen to be invariant. By decomposing the action of C 3 on both factors of the tensor product, we get  $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_3)}=\bigoplus_{j=0}^2\mathfrak{sl}_2^{\chi_j}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^{\overline{\chi_j}}$, where
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_3)}=\bigoplus_{j=0}^2\mathfrak{sl}_2^{\chi_j}\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^{\overline{\chi_j}}$, where  $\overline{\chi_j}(g)=\overline{\chi_j(g)}$, and we obtain
$\overline{\chi_j}(g)=\overline{\chi_j(g)}$, and we obtain
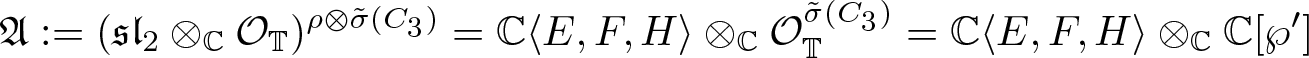 \begin{equation*}\mathfrak{A}:=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_3)}= {\mathbb{C}}\langle E,F,H\rangle\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_3)}={\mathbb{C}}\langle E,F,H\rangle\otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp']\end{equation*}
\begin{equation*}\mathfrak{A}:=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_3)}= {\mathbb{C}}\langle E,F,H\rangle\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_3)}={\mathbb{C}}\langle E,F,H\rangle\otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp']\end{equation*}with brackets
We will show that after performing a sequence of scalings and translations, ![]() $[E,F]$ can be written as
$[E,F]$ can be written as ![]() $[E,F]=H\otimes \wp'(\wp'-1)$, after which we will recognise Onsager’s algebra
$[E,F]=H\otimes \wp'(\wp'-1)$, after which we will recognise Onsager’s algebra ![]() $\mathfrak{O}$ in it.
$\mathfrak{O}$ in it.
By Lemma 10, a generator J of  $\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_3)}$ can be chosen to be
$\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_3)}$ can be chosen to be ![]() $\wp'$. The last bracket can be rewritten as
$\wp'$. The last bracket can be rewritten as
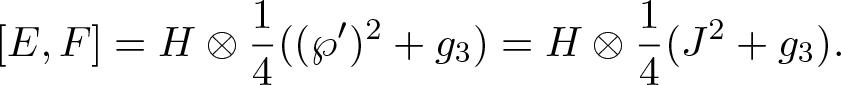 \begin{align*}
[E,F]=H\otimes \frac{1}{4}((\wp')^2+g_3)=H\otimes \frac{1}{4}(J^2+g_3).
\end{align*}
\begin{align*}
[E,F]=H\otimes \frac{1}{4}((\wp')^2+g_3)=H\otimes \frac{1}{4}(J^2+g_3).
\end{align*} Notice that ![]() $g_3\neq 0$ since
$g_3\neq 0$ since ![]() $g_2=0$ and they cannot be both zero. Let
$g_2=0$ and they cannot be both zero. Let  $E'=-\frac{4}{g_3}E$. Then
$E'=-\frac{4}{g_3}E$. Then  $[E',F]=H\otimes (-\frac{1}{g_3}J^2-1).$ Replace
$[E',F]=H\otimes (-\frac{1}{g_3}J^2-1).$ Replace  $-\frac{1}{g_3}J^2$ by J 2 to obtain
$-\frac{1}{g_3}J^2$ by J 2 to obtain ![]() $ [E',F]=H\otimes (J^2-1)$. Replace J − 1 by J to get
$ [E',F]=H\otimes (J^2-1)$. Replace J − 1 by J to get ![]() $[E',F]=H\otimes J(J+2)$ and transform further to obtain
$[E',F]=H\otimes J(J+2)$ and transform further to obtain ![]() $[E',F]=H\otimes J(J-1)$ to see that
$[E',F]=H\otimes J(J-1)$ to see that ![]() $\mathfrak{A}$ is isomorphic to the Onsager algebra, cf. [Reference Knibbeler, Lombardo and Veselov5, Theorem 2.5].
$\mathfrak{A}$ is isomorphic to the Onsager algebra, cf. [Reference Knibbeler, Lombardo and Veselov5, Theorem 2.5].
Another possibility for embedding C 3 is given by ![]() $\sigma'(r)(z)=\omega_3^{-1}z.$ The χ 1 and χ 2 isotypical components interchange when we consider this action. Define the elements
$\sigma'(r)(z)=\omega_3^{-1}z.$ The χ 1 and χ 2 isotypical components interchange when we consider this action. Define the elements
 \begin{equation*}\tilde{H}=-\begin{pmatrix}
1& 0\\
0 &-1
\end{pmatrix},\quad\tilde{E}=-\begin{pmatrix}
0 & 1\\
0 &0
\end{pmatrix}\otimes \wp^2,\quad \tilde{F}=-\begin{pmatrix}
0 & 0\\
1 &0
\end{pmatrix}\otimes \wp.\end{equation*}
\begin{equation*}\tilde{H}=-\begin{pmatrix}
1& 0\\
0 &-1
\end{pmatrix},\quad\tilde{E}=-\begin{pmatrix}
0 & 1\\
0 &0
\end{pmatrix}\otimes \wp^2,\quad \tilde{F}=-\begin{pmatrix}
0 & 0\\
1 &0
\end{pmatrix}\otimes \wp.\end{equation*} Observe how  $\mathrm{Ad}\begin{pmatrix}
0 & 1\\
-1 &0
\end{pmatrix}$ maps
$\mathrm{Ad}\begin{pmatrix}
0 & 1\\
-1 &0
\end{pmatrix}$ maps ![]() $H,E,F$ to
$H,E,F$ to ![]() $\tilde{H},\tilde{F},\tilde{E}$, respectively. By Lemma 4, we see that
$\tilde{H},\tilde{F},\tilde{E}$, respectively. By Lemma 4, we see that
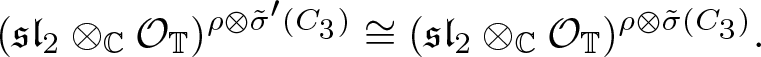 \begin{align*}
(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}'(C_3)}\cong (\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_3)}.
\end{align*}
\begin{align*}
(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}'(C_3)}\cong (\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_3)}.
\end{align*} The cases of ![]() $\ell=4$ and
$\ell=4$ and ![]() $\ell=6$ follow in an analogous manner. By Example 2,
$\ell=6$ follow in an analogous manner. By Example 2, ![]() $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{C_2}\not\cong \mathfrak{O}$. This proves the claim.
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{C_2}\not\cong \mathfrak{O}$. This proves the claim.
The proof of Theorem 5 shows that a normal form of ![]() $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_{3})}$ is given by
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_{3})}$ is given by ![]() ${\mathbb{C}}\langle E_3,F_3,H\rangle \otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp']$, where H = h,
${\mathbb{C}}\langle E_3,F_3,H\rangle \otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp']$, where H = h, ![]() $E_3=e\otimes \wp$,
$E_3=e\otimes \wp$, ![]() $F_3=f\otimes \wp^2$ and
$F_3=f\otimes \wp^2$ and ![]() $\wp=\wp_{{\Lambda}_{\omega_6}}$. In a similar fashion, one can obtain normal forms for remaining aLias with
$\wp=\wp_{{\Lambda}_{\omega_6}}$. In a similar fashion, one can obtain normal forms for remaining aLias with ![]() $\Gamma=C_4$ and
$\Gamma=C_4$ and ![]() $\Gamma=C_6$ using Proposition 10. For
$\Gamma=C_6$ using Proposition 10. For ![]() $\ell\in \{4,6\}$, choose the homomorphism
$\ell\in \{4,6\}$, choose the homomorphism ![]() $\rho_{\ell}:C_{\ell}\rightarrow \mathrm{Aut}(T_{\omega_{\ell}})$ defined by
$\rho_{\ell}:C_{\ell}\rightarrow \mathrm{Aut}(T_{\omega_{\ell}})$ defined by
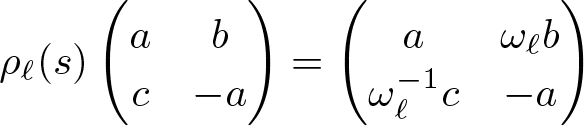 \begin{equation*}\rho_{\ell}(s)\begin{pmatrix}
a & b\\
c &-a
\end{pmatrix}=\begin{pmatrix}
a & \omega_{\ell}b\\
\omega_{\ell}^{-1}c &-a
\end{pmatrix}\end{equation*}
\begin{equation*}\rho_{\ell}(s)\begin{pmatrix}
a & b\\
c &-a
\end{pmatrix}=\begin{pmatrix}
a & \omega_{\ell}b\\
\omega_{\ell}^{-1}c &-a
\end{pmatrix}\end{equation*} and ![]() $\sigma_{\ell}:C_{\ell}\rightarrow \mathrm{Aut}(T_{\omega_{\ell}})$ defined by
$\sigma_{\ell}:C_{\ell}\rightarrow \mathrm{Aut}(T_{\omega_{\ell}})$ defined by ![]() $\sigma(s)z=\omega_{\ell}z$. Then
$\sigma(s)z=\omega_{\ell}z$. Then
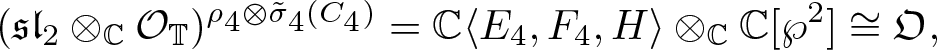 \begin{align}
(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho_4\otimes \tilde{\sigma}_4(C_{4})}={\mathbb{C}}\langle E_4,F_4,H\rangle \otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp^2]\cong \mathfrak{O},
\end{align}
\begin{align}
(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho_4\otimes \tilde{\sigma}_4(C_{4})}={\mathbb{C}}\langle E_4,F_4,H\rangle \otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp^2]\cong \mathfrak{O},
\end{align} where ![]() $E_4=e\otimes \wp\wp'$,
$E_4=e\otimes \wp\wp'$, ![]() $F_4=f\otimes \wp'$ and
$F_4=f\otimes \wp'$ and ![]() $\wp=\wp_{{\Lambda}_i}$.
$\wp=\wp_{{\Lambda}_i}$.
Finally, for C 6, we have the following normal form:
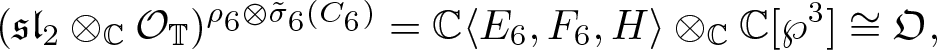 \begin{align}
(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho_6\otimes \tilde{\sigma}_6(C_{6})}={\mathbb{C}}\langle E_6,F_6,H\rangle \otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp^3]\cong \mathfrak{O},
\end{align}
\begin{align}
(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho_6\otimes \tilde{\sigma}_6(C_{6})}={\mathbb{C}}\langle E_6,F_6,H\rangle \otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp^3]\cong \mathfrak{O},
\end{align} where ![]() $E_6=e\otimes \wp\wp'$,
$E_6=e\otimes \wp\wp'$, ![]() $F_6=f\otimes \wp^2\wp'$ and
$F_6=f\otimes \wp^2\wp'$ and ![]() $\wp=\wp_{{\Lambda}_{\omega_6}}$.
$\wp=\wp_{{\Lambda}_{\omega_6}}$.
6.2. The cases  $\Gamma=C_2\times C_2$ and
$\Gamma=C_2\times C_2$ and  $\Gamma=A_4$
$\Gamma=A_4$
We will now consider the final two aLias in our classification, namely those with symmetry group ![]() $C_2\times C_2$ and a homomorphism
$C_2\times C_2$ and a homomorphism ![]() $\sigma:C_2\times C_2\rightarrow \mathrm{Aut}(T)$, such that
$\sigma:C_2\times C_2\rightarrow \mathrm{Aut}(T)$, such that ![]() $g(T/\sigma(C_2\times C_2))=1$, where
$g(T/\sigma(C_2\times C_2))=1$, where ![]() $T={\mathbb{C}}/{\mathbb{Z}}\oplus{\mathbb{Z}}\tau$, and those with symmetry group A 4. We may assume that the homomorphism σ is given by
$T={\mathbb{C}}/{\mathbb{Z}}\oplus{\mathbb{Z}}\tau$, and those with symmetry group A 4. We may assume that the homomorphism σ is given by  $\sigma(r_1)z=z+\frac{1}{2}$ and
$\sigma(r_1)z=z+\frac{1}{2}$ and ![]() $\sigma(r_2)z=z+\frac{\tau}{2}$, where
$\sigma(r_2)z=z+\frac{\tau}{2}$, where ![]() $r_1,r_2$ generate
$r_1,r_2$ generate ![]() $C_2\times C_2$, cf. Lemma 7.
$C_2\times C_2$, cf. Lemma 7.
Let ![]() $\{\alpha_{00},\alpha_{01},\alpha_{10},\alpha_{11}\}$ denote the set of characters of
$\{\alpha_{00},\alpha_{01},\alpha_{10},\alpha_{11}\}$ denote the set of characters of ![]() $C_2\times C_2$, defined by
$C_2\times C_2$, defined by ![]() $\alpha_{ij}(r_1,r_2)=\chi_i(r_1)\chi_j(r_2)$, where χ 0, χ 1 are the characters of C 2. Let
$\alpha_{ij}(r_1,r_2)=\chi_i(r_1)\chi_j(r_2)$, where χ 0, χ 1 are the characters of C 2. Let ![]() $\mathbb{T}=T\setminus \mathcal{S}$, with
$\mathbb{T}=T\setminus \mathcal{S}$, with ![]() $\mathcal{S}=\sigma(C_2\times C_2)\cdot \{0\}=\{0,1/2,\tau/2,(1+\tau)/2\}$ and write
$\mathcal{S}=\sigma(C_2\times C_2)\cdot \{0\}=\{0,1/2,\tau/2,(1+\tau)/2\}$ and write ![]() $\wp=\wp_{{\Lambda}}$. The divisor of
$\wp=\wp_{{\Lambda}}$. The divisor of ![]() $1/\wp'$ is given by
$1/\wp'$ is given by
and therefore ![]() $1/\wp'\in \mathcal{O}_{\mathbb{T}}$. Let
$1/\wp'\in \mathcal{O}_{\mathbb{T}}$. Let  $\pi_{\alpha_{ij}}=\frac{1}{4}\sum_{r\in C_2\times C_2}\overline{\alpha_{ij}(r)}r$ be the projection of
$\pi_{\alpha_{ij}}=\frac{1}{4}\sum_{r\in C_2\times C_2}\overline{\alpha_{ij}(r)}r$ be the projection of ![]() $\mathcal{O}_{\mathbb{T}}$ onto the isotypical component
$\mathcal{O}_{\mathbb{T}}$ onto the isotypical component  $\mathcal{O}_{\mathbb{T}}^{\alpha_{ij}}$. Define
$\mathcal{O}_{\mathbb{T}}^{\alpha_{ij}}$. Define  $p_{ij}:=4\pi_{\alpha_{ij}}(1/\wp')$. Concretely, we have
$p_{ij}:=4\pi_{\alpha_{ij}}(1/\wp')$. Concretely, we have
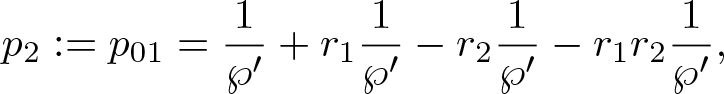 \begin{align}
p_2:=p_{01}&=\frac{1}{\wp'} +r_1\frac{1}{\wp'}-r_2\frac{1}{\wp'}-r_1r_2\frac{1}{\wp'},
\end{align}
\begin{align}
p_2:=p_{01}&=\frac{1}{\wp'} +r_1\frac{1}{\wp'}-r_2\frac{1}{\wp'}-r_1r_2\frac{1}{\wp'},
\end{align}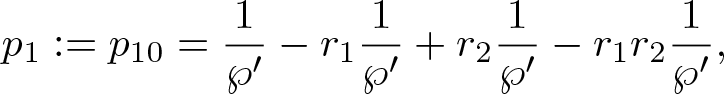 \begin{align}
p_1:=p_{10}&=\frac{1}{\wp'} -r_1\frac{1}{\wp'}+r_2\frac{1}{\wp'}-r_1r_2\frac{1}{\wp'},
\end{align}
\begin{align}
p_1:=p_{10}&=\frac{1}{\wp'} -r_1\frac{1}{\wp'}+r_2\frac{1}{\wp'}-r_1r_2\frac{1}{\wp'},
\end{align}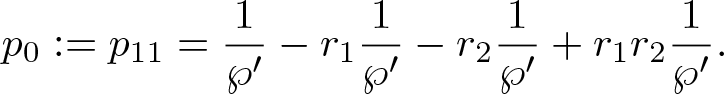 \begin{align}
p_0:=p_{11}&=\frac{1}{\wp'} -r_1\frac{1}{\wp'}-r_2\frac{1}{\wp'}+r_1r_2\frac{1}{\wp'}.
\end{align}
\begin{align}
p_0:=p_{11}&=\frac{1}{\wp'} -r_1\frac{1}{\wp'}-r_2\frac{1}{\wp'}+r_1r_2\frac{1}{\wp'}.
\end{align} By construction, the functions pij are elements of  $\mathcal{O}_{\mathbb{T}}^{\alpha_{ij}}$. Observe that they have at most order 1 poles in the set
$\mathcal{O}_{\mathbb{T}}^{\alpha_{ij}}$. Observe that they have at most order 1 poles in the set ![]() $\mathcal{S}$. Furthermore, they are odd functions since
$\mathcal{S}$. Furthermore, they are odd functions since ![]() $\wp'$ is odd and s (with
$\wp'$ is odd and s (with ![]() $s(z)=-z$) and
$s(z)=-z$) and ![]() $r_1,r_2$ commute. The definition of the pi is motivated in Lemma 19.
$r_1,r_2$ commute. The definition of the pi is motivated in Lemma 19.
Remark 5. The pj can also be defined in terms of theta functions, as is done in [Reference Carey, Hannabuss, Mason and Singer8]. They define
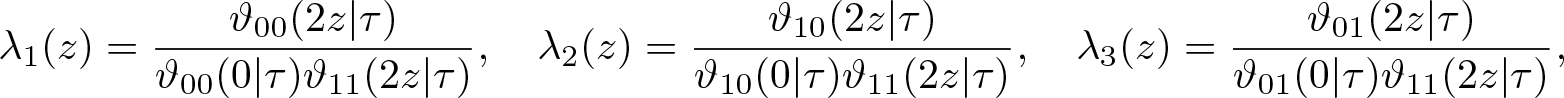 \begin{equation*}\lambda_1(z)=\frac{\vartheta_{00}(2z|\tau)}{\vartheta_{00}(0|\tau)\vartheta_{11}(2z|\tau)},\quad \lambda_2(z)=\frac{\vartheta_{10}(2z|\tau)}{\vartheta_{10}(0|\tau)\vartheta_{11}(2z|\tau)},\quad \lambda_3(z)=\frac{\vartheta_{01}(2z|\tau)}{\vartheta_{01}(0|\tau)\vartheta_{11}(2z|\tau)},\end{equation*}
\begin{equation*}\lambda_1(z)=\frac{\vartheta_{00}(2z|\tau)}{\vartheta_{00}(0|\tau)\vartheta_{11}(2z|\tau)},\quad \lambda_2(z)=\frac{\vartheta_{10}(2z|\tau)}{\vartheta_{10}(0|\tau)\vartheta_{11}(2z|\tau)},\quad \lambda_3(z)=\frac{\vartheta_{01}(2z|\tau)}{\vartheta_{01}(0|\tau)\vartheta_{11}(2z|\tau)},\end{equation*} where  $\vartheta_{ab}(z|\tau)=\sum_{n\in {\mathbb{Z}}}\exp(2\pi {i}[\tau(n+a/2)^2/2+(n+a/2)(z+b/2)])$, and where
$\vartheta_{ab}(z|\tau)=\sum_{n\in {\mathbb{Z}}}\exp(2\pi {i}[\tau(n+a/2)^2/2+(n+a/2)(z+b/2)])$, and where ![]() $(a,b)=(0,0), (1,0), (0,1), (1,1)$. The relations between our projected
$(a,b)=(0,0), (1,0), (0,1), (1,1)$. The relations between our projected ![]() $1/\wp'$ are, up to a scaling, as follows:
$1/\wp'$ are, up to a scaling, as follows:
Written out explicitly, the group ![]() $C_2\times C_2$ acts on the pi as
$C_2\times C_2$ acts on the pi as
Let us obtain the series expansion of  $\frac{1}{r\wp'}$ about z = 0, for
$\frac{1}{r\wp'}$ about z = 0, for ![]() $r\in \langle r_1,r_2\rangle\setminus 1$, which we will use to derive the expansions of the
$r\in \langle r_1,r_2\rangle\setminus 1$, which we will use to derive the expansions of the ![]() $p_i^2$ about z = 0 in Lemma 18. First of all, for
$p_i^2$ about z = 0 in Lemma 18. First of all, for ![]() $r\in \langle r_1,r_2\rangle\setminus 1$, we find for
$r\in \langle r_1,r_2\rangle\setminus 1$, we find for  $\frac{1}{r\wp'}$ the following expansion about z = 0:
$\frac{1}{r\wp'}$ the following expansion about z = 0:
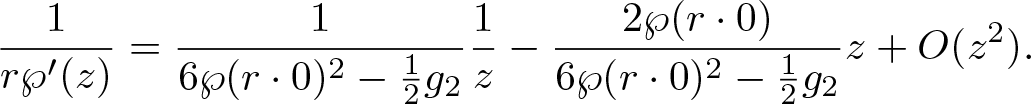 \begin{align}
\frac{1}{r\wp'(z)}= \frac{1}{6\wp(r\cdot 0)^2-\frac{1}{2}g_2}\frac{1}{z}-\frac{2\wp(r\cdot 0)}{6\wp(r\cdot 0)^2-\frac{1}{2}g_2}z+O(z^2).
\end{align}
\begin{align}
\frac{1}{r\wp'(z)}= \frac{1}{6\wp(r\cdot 0)^2-\frac{1}{2}g_2}\frac{1}{z}-\frac{2\wp(r\cdot 0)}{6\wp(r\cdot 0)^2-\frac{1}{2}g_2}z+O(z^2).
\end{align} For example, for ![]() $r=r_1$, we can simplify this to
$r=r_1$, we can simplify this to
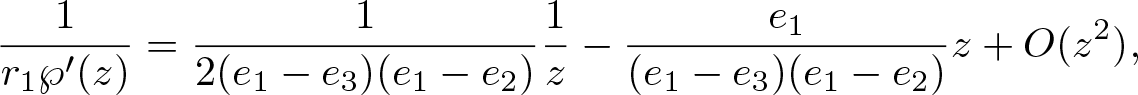 \begin{equation*}\frac{1}{r_1\wp'(z)}= \frac{1}{2(e_1-e_3)(e_1-e_2)}\frac{1}{z}-\frac{e_1}{(e_1-e_3)(e_1-e_2)}z+O(z^2),\end{equation*}
\begin{equation*}\frac{1}{r_1\wp'(z)}= \frac{1}{2(e_1-e_3)(e_1-e_2)}\frac{1}{z}-\frac{e_1}{(e_1-e_3)(e_1-e_2)}z+O(z^2),\end{equation*} using that ![]() $6\wp(1/2)^2-g_2/2=2(e_1-e_3)(e_1-e_2)$. Notice that the denominators of the coefficients are indeed non-zero, since for lattices
$6\wp(1/2)^2-g_2/2=2(e_1-e_3)(e_1-e_2)$. Notice that the denominators of the coefficients are indeed non-zero, since for lattices ![]() $\Lambda$, the discriminant
$\Lambda$, the discriminant ![]() $\Delta({\Lambda}):=g_2^3-27g_3^2$ is non-zero and can be shown to be equal to
$\Delta({\Lambda}):=g_2^3-27g_3^2$ is non-zero and can be shown to be equal to ![]() $16(e_1-e_2)^2(e_1-e_3)^2(e_2-e_3)^2$.
$16(e_1-e_2)^2(e_1-e_3)^2(e_2-e_3)^2$.
Let us argue that the pj are not identically zero. To this end, consider  $p_{00}=4\pi_{\alpha_{00}}(1/\wp')=\frac{1}{\wp'} +r_1\frac{1}{\wp'}+r_2\frac{1}{\wp'}+r_1r_2\frac{1}{\wp'}$. This function is invariant under
$p_{00}=4\pi_{\alpha_{00}}(1/\wp')=\frac{1}{\wp'} +r_1\frac{1}{\wp'}+r_2\frac{1}{\wp'}+r_1r_2\frac{1}{\wp'}$. This function is invariant under ![]() $C_2\times C_2$ and hence descends to a function on
$C_2\times C_2$ and hence descends to a function on ![]() $\tilde{T}:=T/\sigma(C_2\times C_2)$. Now, p 00 has at most order 1 poles and on
$\tilde{T}:=T/\sigma(C_2\times C_2)$. Now, p 00 has at most order 1 poles and on ![]() $\tilde{T}$, there is, therefore, at most a single pole. Thus p 00 must be constant. In fact, since
$\tilde{T}$, there is, therefore, at most a single pole. Thus p 00 must be constant. In fact, since ![]() $\wp'$ is odd, p 00 is odd as well. Hence
$\wp'$ is odd, p 00 is odd as well. Hence ![]() $p_{00}=0.$ Knowing that p 00 is constant allows us to draw conclusions about the pi. By considering the divisor of
$p_{00}=0.$ Knowing that p 00 is constant allows us to draw conclusions about the pi. By considering the divisor of ![]() $\frac{1}{\wp'}$ in (6.12), we see that the sets of poles of
$\frac{1}{\wp'}$ in (6.12), we see that the sets of poles of  $r_1\frac{1}{\wp'}, r_2\frac{1}{\wp'}$ and
$r_1\frac{1}{\wp'}, r_2\frac{1}{\wp'}$ and  $r_1r_2\frac{1}{\wp'}$ have pairwise precisely two poles in common. We, therefore, see that the three functions
$r_1r_2\frac{1}{\wp'}$ have pairwise precisely two poles in common. We, therefore, see that the three functions
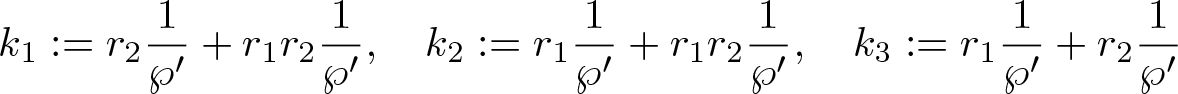 \begin{align*}
k_1:=r_2\frac{1}{\wp'}+r_1r_2\frac{1}{\wp'}, \quad k_2:=r_1\frac{1}{\wp'}+r_1r_2\frac{1}{\wp'}, \quad k_3:=r_1\frac{1}{\wp'}+r_2\frac{1}{\wp'}
\end{align*}
\begin{align*}
k_1:=r_2\frac{1}{\wp'}+r_1r_2\frac{1}{\wp'}, \quad k_2:=r_1\frac{1}{\wp'}+r_1r_2\frac{1}{\wp'}, \quad k_3:=r_1\frac{1}{\wp'}+r_2\frac{1}{\wp'}
\end{align*} are all non-constant. As a consequence we get that ![]() $p_0=p_{00}-2k_3=-2k_3$,
$p_0=p_{00}-2k_3=-2k_3$, ![]() $ p_1=p_{00}-2k_2=-2k_2$ and
$ p_1=p_{00}-2k_2=-2k_2$ and ![]() $ p_2=p_{00}-2k_1=-2k_1$ are all non-zero.
$ p_2=p_{00}-2k_1=-2k_1$ are all non-zero.
The next lemma describes the algebra of ![]() $C_2\times C_2$-invariant subspace of
$C_2\times C_2$-invariant subspace of ![]() $\mathcal{O}_{\mathbb{T}}$.
$\mathcal{O}_{\mathbb{T}}$.
Lemma 17. We have  $\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_2\times C_2)}={\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}']$.
$\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_2\times C_2)}={\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}']$.
Proof. By definition,  $\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_2\times C_2)}$ is the algebra of all
$\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_2\times C_2)}$ is the algebra of all  $\frac{1}{2}{\Lambda}$-periodic meromorphic functions on T that are holomorphic on
$\frac{1}{2}{\Lambda}$-periodic meromorphic functions on T that are holomorphic on  $T\setminus\frac{1}{2}{\Lambda}$, which corresponds to
$T\setminus\frac{1}{2}{\Lambda}$, which corresponds to  ${\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}']$ by Lemma 1.
${\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}']$ by Lemma 1.
We now record the relations between the ![]() $p_i^2$ and
$p_i^2$ and ![]() $\wp_{\frac{1}{2}{\Lambda}}$ in a lemma for later purposes.
$\wp_{\frac{1}{2}{\Lambda}}$ in a lemma for later purposes.
Lemma 18. We have
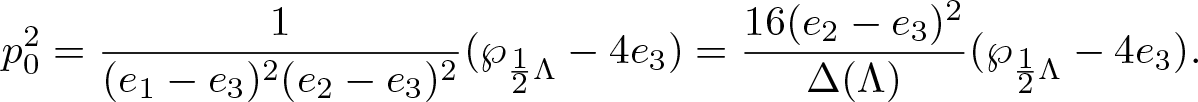 \begin{align*}
p_0^2&=\frac{1}{(e_1-e_3)^2(e_2-e_3)^2}(\wp_{\frac{1}{2}{\Lambda}}-4e_3)=\frac{16(e_2-e_3)^2}{\Delta({\Lambda})}(\wp_{\frac{1}{2}{\Lambda}}-4e_3).
\end{align*}
\begin{align*}
p_0^2&=\frac{1}{(e_1-e_3)^2(e_2-e_3)^2}(\wp_{\frac{1}{2}{\Lambda}}-4e_3)=\frac{16(e_2-e_3)^2}{\Delta({\Lambda})}(\wp_{\frac{1}{2}{\Lambda}}-4e_3).
\end{align*} Similarly, the relations of ![]() $p_j^2$ and
$p_j^2$ and ![]() $\wp_{\frac{1}{2}{\Lambda}}$ for
$\wp_{\frac{1}{2}{\Lambda}}$ for ![]() $j=1,2$ are obtained from
$j=1,2$ are obtained from ![]() $p_0^2$ by cyclic permutations of the ei. Consequently, there are the following relations:
$p_0^2$ by cyclic permutations of the ei. Consequently, there are the following relations: ![]() $ p_1^2=\alpha_1 p_2^2+\alpha_2$,
$ p_1^2=\alpha_1 p_2^2+\alpha_2$, ![]() $ p_0^2=\beta_1 p_2^2+\beta_2$, where
$ p_0^2=\beta_1 p_2^2+\beta_2$, where
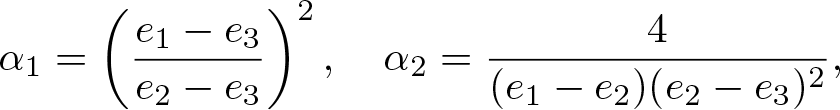 \begin{equation*}\alpha_1=\left(\frac{e_1-e_3}{e_2-e_3}\right)^2,\quad \alpha_2=\frac{4}{(e_1-e_2)(e_2-e_3)^2},\end{equation*}
\begin{equation*}\alpha_1=\left(\frac{e_1-e_3}{e_2-e_3}\right)^2,\quad \alpha_2=\frac{4}{(e_1-e_2)(e_2-e_3)^2},\end{equation*}and
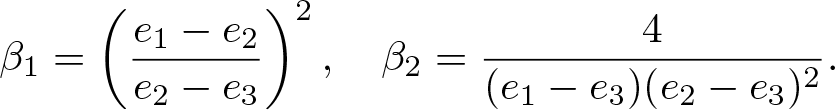 \begin{equation*}\beta_1=\left(\frac{e_1-e_2}{e_2-e_3}\right)^2,\quad \beta_2=\frac{4}{(e_1-e_3)(e_2-e_3)^2}.\end{equation*}
\begin{equation*}\beta_1=\left(\frac{e_1-e_2}{e_2-e_3}\right)^2,\quad \beta_2=\frac{4}{(e_1-e_3)(e_2-e_3)^2}.\end{equation*} Thus ![]() $\alpha_1,\alpha_2,\beta_1,\beta_2\in {\mathbb{C}}^*$.
$\alpha_1,\alpha_2,\beta_1,\beta_2\in {\mathbb{C}}^*$.
Proof. Using the expansion in (6.19), we obtain for ![]() $r,\tilde{r}\in \langle r_1,r_2\rangle\setminus 1$:
$r,\tilde{r}\in \langle r_1,r_2\rangle\setminus 1$:
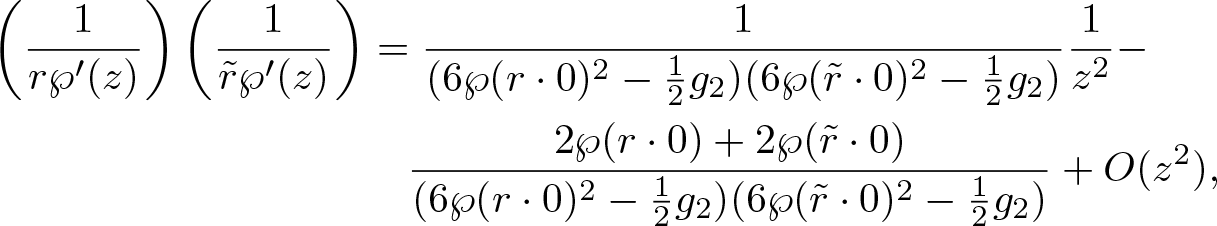 \begin{align*}\left(\frac{1}{r\wp'(z)}\right)\left(\frac{1}{\tilde{r}\wp'(z)}\right)&=\frac{1}{(6\wp(r\cdot 0)^2-\frac{1}{2}g_2)(6\wp(\tilde{r}\cdot 0)^2-\frac{1}{2}g_2)}\frac{1}{z^2}-\\
&\quad \frac{2\wp(r\cdot 0)+2\wp(\tilde{r}\cdot 0)}{(6\wp(r\cdot 0)^2-\frac{1}{2}g_2)(6\wp(\tilde{r}\cdot 0)^2-\frac{1}{2}g_2)}+O(z^2),
\end{align*}
\begin{align*}\left(\frac{1}{r\wp'(z)}\right)\left(\frac{1}{\tilde{r}\wp'(z)}\right)&=\frac{1}{(6\wp(r\cdot 0)^2-\frac{1}{2}g_2)(6\wp(\tilde{r}\cdot 0)^2-\frac{1}{2}g_2)}\frac{1}{z^2}-\\
&\quad \frac{2\wp(r\cdot 0)+2\wp(\tilde{r}\cdot 0)}{(6\wp(r\cdot 0)^2-\frac{1}{2}g_2)(6\wp(\tilde{r}\cdot 0)^2-\frac{1}{2}g_2)}+O(z^2),
\end{align*} where we use that ![]() $\wp'$ is odd, and hence the above product is even. Hence, for
$\wp'$ is odd, and hence the above product is even. Hence, for ![]() $r=r_1$ and
$r=r_1$ and ![]() $\tilde{r}=r_2$, we get
$\tilde{r}=r_2$, we get
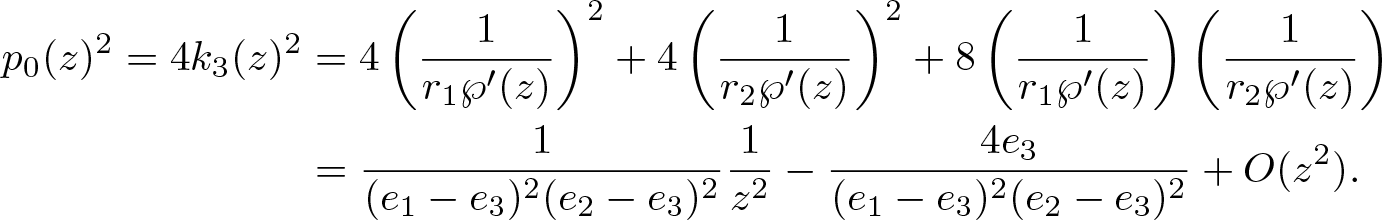 \begin{align*}
p_0(z)^2=4k_3(z)^2&=4\left(\frac{1}{r_1\wp'(z)}\right)^2+4\left(\frac{1}{r_2\wp'(z)}\right)^2+8\left(\frac{1}{r_1\wp'(z)}\right)\left(\frac{1}{r_2\wp'(z)}\right)\\
&=\frac{1}{(e_1-e_3)^2(e_2-e_3)^2}\frac{1}{z^2}-\frac{4e_3}{(e_1-e_3)^2(e_2-e_3)^2}+O(z^2).
\end{align*}
\begin{align*}
p_0(z)^2=4k_3(z)^2&=4\left(\frac{1}{r_1\wp'(z)}\right)^2+4\left(\frac{1}{r_2\wp'(z)}\right)^2+8\left(\frac{1}{r_1\wp'(z)}\right)\left(\frac{1}{r_2\wp'(z)}\right)\\
&=\frac{1}{(e_1-e_3)^2(e_2-e_3)^2}\frac{1}{z^2}-\frac{4e_3}{(e_1-e_3)^2(e_2-e_3)^2}+O(z^2).
\end{align*} Similarly, one can show that ![]() $p_j^2$
$p_j^2$ ![]() $(j=1,2)$ is obtained from
$(j=1,2)$ is obtained from ![]() $p_0^2$ by changing ei to
$p_0^2$ by changing ei to ![]() $e_{i-j}$ in the expansions for
$e_{i-j}$ in the expansions for ![]() $i=1,2,3$.
$i=1,2,3$.
It is clear from the definition of ![]() $\wp$ as given in (2.2), that about z = 0,
$\wp$ as given in (2.2), that about z = 0, ![]() $\wp$ has the expansion
$\wp$ has the expansion  $\wp(z)=\frac{1}{z^2}+O(z^2)$. Since
$\wp(z)=\frac{1}{z^2}+O(z^2)$. Since ![]() $p_j^2$ has order 2 poles and is invariant under
$p_j^2$ has order 2 poles and is invariant under ![]() $C_2\times C_2$, we know that
$C_2\times C_2$, we know that  $p_j^2=c_1\wp_{\frac{1}{2}{\Lambda}}+c_2$ for some
$p_j^2=c_1\wp_{\frac{1}{2}{\Lambda}}+c_2$ for some ![]() $c_1,c_2\in {\mathbb{C}}$. The last statement follows now directly. This completes the proof.
$c_1,c_2\in {\mathbb{C}}$. The last statement follows now directly. This completes the proof.
The symmetry groups for ![]() $\mathfrak{sl}_2$-based aLias having
$\mathfrak{sl}_2$-based aLias having ![]() $C_2\times C_2$ as a subgroup of translations are limited to
$C_2\times C_2$ as a subgroup of translations are limited to ![]() $A_4\cong C_3 \ltimes(C_2\times C_2)$ (for hexagonal lattices) and
$A_4\cong C_3 \ltimes(C_2\times C_2)$ (for hexagonal lattices) and ![]() $C_2\times C_2$ itself. We are, therefore, interested in how C 3 acts on functions in
$C_2\times C_2$ itself. We are, therefore, interested in how C 3 acts on functions in  $\mathcal{O}_{\mathbb{T}}^{C_2\times C_2}$. This is the content of the following lemma.
$\mathcal{O}_{\mathbb{T}}^{C_2\times C_2}$. This is the content of the following lemma.
Lemma 19. Suppose ![]() $\Lambda$ is homothetic to
$\Lambda$ is homothetic to ![]() ${\Lambda}_{\omega_6}$ and s acts on
${\Lambda}_{\omega_6}$ and s acts on ![]() ${\mathbb{C}}/{\Lambda}$ as
${\mathbb{C}}/{\Lambda}$ as ![]() $s\cdot z=\omega_3z$. Then
$s\cdot z=\omega_3z$. Then
where the subscripts are taken modulo 3. Furthermore, ![]() $\alpha_1=\omega_3, \beta_1=\omega_3^2$ if and only if
$\alpha_1=\omega_3, \beta_1=\omega_3^2$ if and only if ![]() $\Lambda$ is homothetic to
$\Lambda$ is homothetic to ![]() ${\Lambda}_{\omega_6}$.
${\Lambda}_{\omega_6}$.
Proof. Assume that ![]() $\Lambda$ is homothetic to
$\Lambda$ is homothetic to ![]() ${\Lambda}_{\omega_6}.$ Recall
${\Lambda}_{\omega_6}.$ Recall ![]() $\langle s\rangle \ltimes \langle r_1,r_2\rangle \cong C_3 \ltimes (C_2\times C_2)\cong A_4$, where
$\langle s\rangle \ltimes \langle r_1,r_2\rangle \cong C_3 \ltimes (C_2\times C_2)\cong A_4$, where ![]() $s(z)=\omega_3z$ and
$s(z)=\omega_3z$ and ![]() $r_1(z)=z+1/2$ and
$r_1(z)=z+1/2$ and ![]() $r_2(z)=z+\omega_3/2$, cf. Lemma 7. The following relations hold:
$r_2(z)=z+\omega_3/2$, cf. Lemma 7. The following relations hold: ![]() $s r_1=r_1r_2s$ and
$s r_1=r_1r_2s$ and ![]() $s r_2=r_1s.$ Using that
$s r_2=r_1s.$ Using that ![]() $s\cdot \wp'=\wp'$, we compute
$s\cdot \wp'=\wp'$, we compute
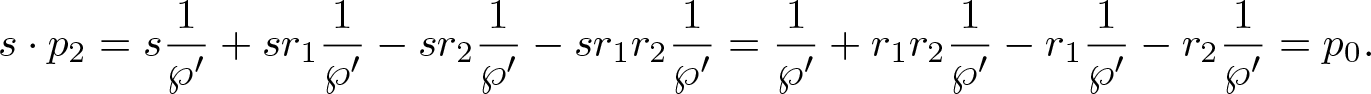 \begin{equation*}
s\cdot p_2=s\frac{1}{\wp'} +sr_1\frac{1}{\wp'}-sr_2\frac{1}{\wp'}-sr_1r_2\frac{1}{\wp'}=\frac{1}{\wp'} +r_1r_2\frac{1}{\wp'}-r_1\frac{1}{\wp'}-r_2\frac{1}{\wp'}= p_0.
\end{equation*}
\begin{equation*}
s\cdot p_2=s\frac{1}{\wp'} +sr_1\frac{1}{\wp'}-sr_2\frac{1}{\wp'}-sr_1r_2\frac{1}{\wp'}=\frac{1}{\wp'} +r_1r_2\frac{1}{\wp'}-r_1\frac{1}{\wp'}-r_2\frac{1}{\wp'}= p_0.
\end{equation*}The other identities follow in the same way.
We now prove the second claim. We have
and we thus see that ![]() $\alpha_1\beta_1=1$ and
$\alpha_1\beta_1=1$ and ![]() $\alpha_1\beta_2=-\alpha_2$. By Lemma 18, we see
$\alpha_1\beta_2=-\alpha_2$. By Lemma 18, we see ![]() $ p_0^2+ p_1^2+ p_2^2=(1+\alpha_1+\beta_1) p_2^2+\alpha_2+\beta_2$. Therefore, the function
$ p_0^2+ p_1^2+ p_2^2=(1+\alpha_1+\beta_1) p_2^2+\alpha_2+\beta_2$. Therefore, the function ![]() $ p_0^2+ p_1^2+ p_2^2$ is constant if and only if
$ p_0^2+ p_1^2+ p_2^2$ is constant if and only if ![]() $g_2=0$. Indeed, a computation shows that
$g_2=0$. Indeed, a computation shows that  $1+\alpha_1+\beta_1=\frac{g_2}{2(e_2-e_3)^2}.$ We conclude that α 1 and β 1 are distinct third roots of unity if and only if
$1+\alpha_1+\beta_1=\frac{g_2}{2(e_2-e_3)^2}.$ We conclude that α 1 and β 1 are distinct third roots of unity if and only if ![]() $\Lambda$ is homothetic to a hexagonal lattice. Using that
$\Lambda$ is homothetic to a hexagonal lattice. Using that ![]() $e_1^2+e_1e_2+e_2^2=0$ if and only if
$e_1^2+e_1e_2+e_2^2=0$ if and only if ![]() $\Lambda$ is homothetic to
$\Lambda$ is homothetic to ![]() ${\Lambda}_{\omega_6}$, one can show that
${\Lambda}_{\omega_6}$, one can show that ![]() $\alpha_1=(2e_1+e_2)^2/(2e_2+e_1)^2=e_2^2/e_1^2.$ Now,
$\alpha_1=(2e_1+e_2)^2/(2e_2+e_1)^2=e_2^2/e_1^2.$ Now, ![]() $e_1=\omega_3 e_2$ by (5.4). Thus, we get
$e_1=\omega_3 e_2$ by (5.4). Thus, we get ![]() $\alpha_1=\omega_3$ and
$\alpha_1=\omega_3$ and ![]() $\beta_1=\omega_3^2$.
$\beta_1=\omega_3^2$.
Define
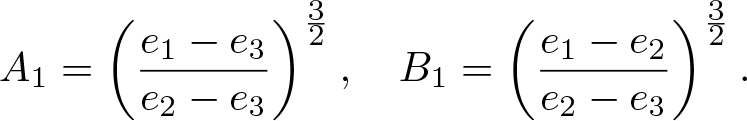 \begin{align}
A_1=\left(\frac{e_1-e_3}{e_2-e_3}\right)^{\frac{3}{2}},\quad B_1=\left(\frac{e_1-e_2}{e_2-e_3}\right)^{\frac{3}{2}}.
\end{align}
\begin{align}
A_1=\left(\frac{e_1-e_3}{e_2-e_3}\right)^{\frac{3}{2}},\quad B_1=\left(\frac{e_1-e_2}{e_2-e_3}\right)^{\frac{3}{2}}.
\end{align}We note that
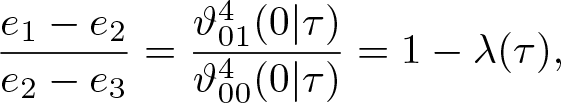 \begin{equation*}\frac{e_1-e_2}{e_2-e_3}=\frac{\vartheta_{01}^4(0|\tau)}{\vartheta_{00}^4(0|\tau)}=1-\lambda(\tau),\end{equation*}
\begin{equation*}\frac{e_1-e_2}{e_2-e_3}=\frac{\vartheta_{01}^4(0|\tau)}{\vartheta_{00}^4(0|\tau)}=1-\lambda(\tau),\end{equation*} where ![]() $\vartheta_{00},\vartheta_{01}$ are the Jacobi theta functions defined in Remark 5 and λ is the modular lambda function, see for example [Reference Rankin29, § 7.2].
$\vartheta_{00},\vartheta_{01}$ are the Jacobi theta functions defined in Remark 5 and λ is the modular lambda function, see for example [Reference Rankin29, § 7.2].
Also,  $\frac{e_1-e_3}{e_2-e_3}=1+\frac{e_1-e_2}{e_2-e_3},$ and hence
$\frac{e_1-e_3}{e_2-e_3}=1+\frac{e_1-e_2}{e_2-e_3},$ and hence  $\frac{e_1-e_3}{e_2-e_3}=2-\lambda(\tau).$ In particular, we can express α 1, β 1, A 1 and B 1 in terms of λ as follows:
$\frac{e_1-e_3}{e_2-e_3}=2-\lambda(\tau).$ In particular, we can express α 1, β 1, A 1 and B 1 in terms of λ as follows: ![]() $\alpha_1=(2-\lambda)^2$,
$\alpha_1=(2-\lambda)^2$, ![]() $\beta_1=(1-\lambda)^2$,
$\beta_1=(1-\lambda)^2$, ![]() $A_1=(2-\lambda)^{3/2}$ and
$A_1=(2-\lambda)^{3/2}$ and ![]() $B_1=(1-\lambda)^{3/2}$.
$B_1=(1-\lambda)^{3/2}$.
For later reference, we will record the following identities.
Lemma 20. The following identities hold:
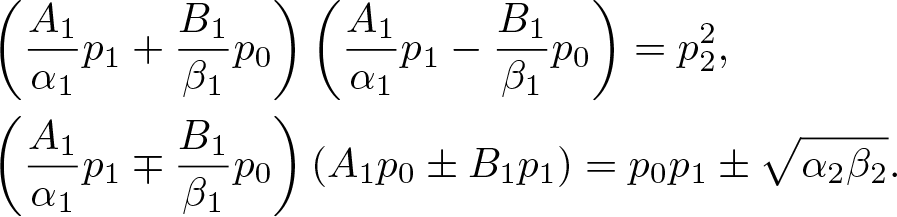 \begin{align*}
&\left(\frac{A_1}{\alpha_1} p_1+\frac{B_1}{\beta_1} p_0\right)\left(\frac{A_1}{\alpha_1} p_1-\frac{B_1}{\beta_1} p_0\right)= p_2^2,\\
&\left(\frac{A_1}{\alpha_1} p_1\mp\frac{B_1}{\beta_1} p_0\right)(A_1 p_0\pm B_1 p_1)= p_0 p_1\pm\sqrt{\alpha_2\beta_2}.
\end{align*}
\begin{align*}
&\left(\frac{A_1}{\alpha_1} p_1+\frac{B_1}{\beta_1} p_0\right)\left(\frac{A_1}{\alpha_1} p_1-\frac{B_1}{\beta_1} p_0\right)= p_2^2,\\
&\left(\frac{A_1}{\alpha_1} p_1\mp\frac{B_1}{\beta_1} p_0\right)(A_1 p_0\pm B_1 p_1)= p_0 p_1\pm\sqrt{\alpha_2\beta_2}.
\end{align*} Furthermore, if ![]() $\Lambda$ is homothetic to
$\Lambda$ is homothetic to ![]() ${\Lambda}_{\omega_6}$, then
${\Lambda}_{\omega_6}$, then ![]() $A_1^2=-1$ and
$A_1^2=-1$ and ![]() $B_1^2=1$.
$B_1^2=1$.
Proof. Using Lemma 19, we compute
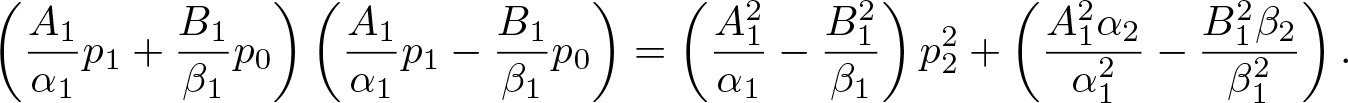 \begin{equation*}
\left(\frac{A_1}{\alpha_1} p_1+\frac{B_1}{\beta_1} p_0\right)\left(\frac{A_1}{\alpha_1} p_1-\frac{B_1}{\beta_1} p_0\right)=\left(\frac{A_1^2}{\alpha_1}-\frac{B_1^2}{\beta_1}\right) p_2^2+\left(\frac{A_1^2\alpha_2}{\alpha_1^2}-\frac{B_1^2\beta_2}{\beta_1^2}\right).
\end{equation*}
\begin{equation*}
\left(\frac{A_1}{\alpha_1} p_1+\frac{B_1}{\beta_1} p_0\right)\left(\frac{A_1}{\alpha_1} p_1-\frac{B_1}{\beta_1} p_0\right)=\left(\frac{A_1^2}{\alpha_1}-\frac{B_1^2}{\beta_1}\right) p_2^2+\left(\frac{A_1^2\alpha_2}{\alpha_1^2}-\frac{B_1^2\beta_2}{\beta_1^2}\right).
\end{equation*}Another computation shows that
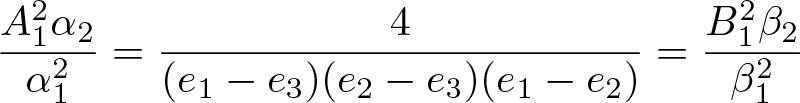 \begin{equation*}\frac{A_1^2\alpha_2}{\alpha_1^2}=\frac{4}{(e_1-e_3)(e_2-e_3)(e_1-e_2)}=\frac{B_1^2\beta_2}{\beta_1^2}\end{equation*}
\begin{equation*}\frac{A_1^2\alpha_2}{\alpha_1^2}=\frac{4}{(e_1-e_3)(e_2-e_3)(e_1-e_2)}=\frac{B_1^2\beta_2}{\beta_1^2}\end{equation*}and
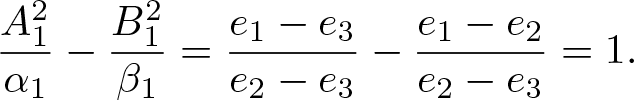 \begin{equation*}\frac{A_1^2}{\alpha_1}-\frac{B_1^2}{\beta_1}=\frac{e_1-e_3}{e_2-e_3}-\frac{e_1-e_2}{e_2-e_3}=1.\end{equation*}
\begin{equation*}\frac{A_1^2}{\alpha_1}-\frac{B_1^2}{\beta_1}=\frac{e_1-e_3}{e_2-e_3}-\frac{e_1-e_2}{e_2-e_3}=1.\end{equation*} This proves the first claim. The other identities follow by similar calculations, whereby we note that the sign of ![]() $\sqrt{\alpha_2\beta_2}$ comes from the choice of the square roots in the definition of A 1 and B 1. Notice that
$\sqrt{\alpha_2\beta_2}$ comes from the choice of the square roots in the definition of A 1 and B 1. Notice that ![]() $\sqrt{\alpha_2\beta_2}\neq 0$ since
$\sqrt{\alpha_2\beta_2}\neq 0$ since ![]() $\Delta({\Lambda})=16(e_1-e_3)^2(e_2-e_3)^2(e_1-e_2)^2\neq 0$ for any lattice
$\Delta({\Lambda})=16(e_1-e_3)^2(e_2-e_3)^2(e_1-e_2)^2\neq 0$ for any lattice ![]() $\Lambda$. The final claim follows from the definition of A 1 and B 1, cf. (6.20), and using that in this case,
$\Lambda$. The final claim follows from the definition of A 1 and B 1, cf. (6.20), and using that in this case, ![]() $e_1=\omega_3e_2$.
$e_1=\omega_3e_2$.
We will now define two functions which arise in the construction of an intertwiner Ψ. The intertwiner will be used to construct a basis for the ![]() $C_2\times C_2$-aLia with
$C_2\times C_2$-aLia with ![]() $g(T/C_2\times C_2)=1$. Define
$g(T/C_2\times C_2)=1$. Define
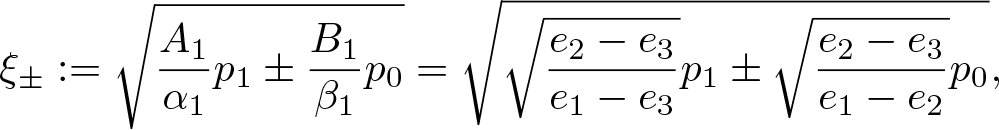 \begin{align}
\xi_{\pm}:=\sqrt{\frac{A_1}{\alpha_1} p_1\pm\frac{B_1}{\beta_1} p_0}=\sqrt{\sqrt{\frac{e_2-e_3}{e_1-e_3}} p_1\pm\sqrt{\frac{e_2-e_3}{e_1-e_2}} p_0},
\end{align}
\begin{align}
\xi_{\pm}:=\sqrt{\frac{A_1}{\alpha_1} p_1\pm\frac{B_1}{\beta_1} p_0}=\sqrt{\sqrt{\frac{e_2-e_3}{e_1-e_3}} p_1\pm\sqrt{\frac{e_2-e_3}{e_1-e_2}} p_0},
\end{align} where we choose the branches in such way that ![]() $\xi_-\xi_+=p_2$ (having Lemma 20 in mind). Notice that
$\xi_-\xi_+=p_2$ (having Lemma 20 in mind). Notice that ![]() $\xi_{\pm}$ are not functions on any complex torus.
$\xi_{\pm}$ are not functions on any complex torus.
We will now turn our attention to finding an intertwiner ![]() $\mathrm{Ad}(\Phi)$ as we have done for
$\mathrm{Ad}(\Phi)$ as we have done for ![]() $\Gamma=C_N$, cf. § 6.1. Recall that we constructed an
$\Gamma=C_N$, cf. § 6.1. Recall that we constructed an ![]() $SL_2({\mathbb{C}})$-valued map
$SL_2({\mathbb{C}})$-valued map ![]() $\Phi$ such that
$\Phi$ such that ![]() $\Phi(r\cdot z)=\delta(r)\Phi(z)$, where
$\Phi(r\cdot z)=\delta(r)\Phi(z)$, where ![]() $r\in C_N$ and δ is a monomorphism
$r\in C_N$ and δ is a monomorphism ![]() $C_N\rightarrow SL_2({\mathbb{C}})$. Composing
$C_N\rightarrow SL_2({\mathbb{C}})$. Composing ![]() $\Phi$ with
$\Phi$ with ![]() $\mathrm{Ad}$ yields a map equivariant with respect to the action of CN on a torus T and
$\mathrm{Ad}$ yields a map equivariant with respect to the action of CN on a torus T and ![]() $\mathfrak{sl}_2$. Let us now argue that a similar construction, that is, obtaining an intertwiner via conjugation of some CN-equivariant
$\mathfrak{sl}_2$. Let us now argue that a similar construction, that is, obtaining an intertwiner via conjugation of some CN-equivariant ![]() $SL_2({\mathbb{C}})$-valued map, cannot be carried out for
$SL_2({\mathbb{C}})$-valued map, cannot be carried out for ![]() $\Gamma=C_2\times C_2$. A necessary condition for carrying out this construction is that
$\Gamma=C_2\times C_2$. A necessary condition for carrying out this construction is that ![]() $\delta:\Gamma\rightarrow SL_2({\mathbb{C}})$ should be a monomorphism. However, by considering the character table of
$\delta:\Gamma\rightarrow SL_2({\mathbb{C}})$ should be a monomorphism. However, by considering the character table of ![]() $C_2\times C_2$, one concludes that there does not exist a faithful representation
$C_2\times C_2$, one concludes that there does not exist a faithful representation ![]() $C_2\times C_2\rightarrow SL_2({\mathbb{C}})$, and hence there is no monomorphism δ such that the above condition holds for non-zero
$C_2\times C_2\rightarrow SL_2({\mathbb{C}})$, and hence there is no monomorphism δ such that the above condition holds for non-zero ![]() $\Lambda$. However, there does exist a faithful representation
$\Lambda$. However, there does exist a faithful representation ![]() $C_2\times C_2\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$, which is the context in which we will look for an intertwiner below.
$C_2\times C_2\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$, which is the context in which we will look for an intertwiner below.
Define ![]() $\rho: C_2\times C_2\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ by
$\rho: C_2\times C_2\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ by
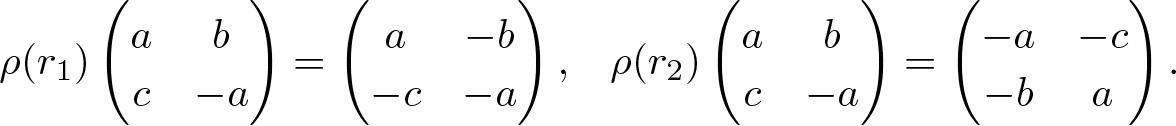 \begin{align}
\rho(r_1)\begin{pmatrix}
a & b\\
c &-a
\end{pmatrix}=\begin{pmatrix}
a & -b\\
-c &-a
\end{pmatrix}, &\quad
\rho(r_2)\begin{pmatrix}
a & b\\
c &-a
\end{pmatrix}=\begin{pmatrix}
-a & -c\\
-b &a
\end{pmatrix}.
\end{align}
\begin{align}
\rho(r_1)\begin{pmatrix}
a & b\\
c &-a
\end{pmatrix}=\begin{pmatrix}
a & -b\\
-c &-a
\end{pmatrix}, &\quad
\rho(r_2)\begin{pmatrix}
a & b\\
c &-a
\end{pmatrix}=\begin{pmatrix}
-a & -c\\
-b &a
\end{pmatrix}.
\end{align}Remark 6. We have used the quaternions Q 8 as a double cover of ![]() $C_2\times C_2$ in (6.22). The matrices
$C_2\times C_2$ in (6.22). The matrices  $R_1=\begin{pmatrix}
i& 0\\
0&-i
\end{pmatrix}$ and
$R_1=\begin{pmatrix}
i& 0\\
0&-i
\end{pmatrix}$ and  $R_2=\begin{pmatrix}
0& 1\\
-1&0
\end{pmatrix}$ generate Q 8 inside
$R_2=\begin{pmatrix}
0& 1\\
-1&0
\end{pmatrix}$ generate Q 8 inside ![]() $SL_2({\mathbb{C}})$, which define a homomorphism
$SL_2({\mathbb{C}})$, which define a homomorphism ![]() $\zeta:Q_8\rightarrow SL_2({\mathbb{C}})$. Then
$\zeta:Q_8\rightarrow SL_2({\mathbb{C}})$. Then ![]() $\mathrm{Ad}(\zeta(Q_8))\cong C_2\times C_2$ inside
$\mathrm{Ad}(\zeta(Q_8))\cong C_2\times C_2$ inside ![]() $\mathrm{Aut}(\mathfrak{sl}_2)$.
$\mathrm{Aut}(\mathfrak{sl}_2)$.
Introduce the following matrix, which will play an important role in the construction of the intertwiner:
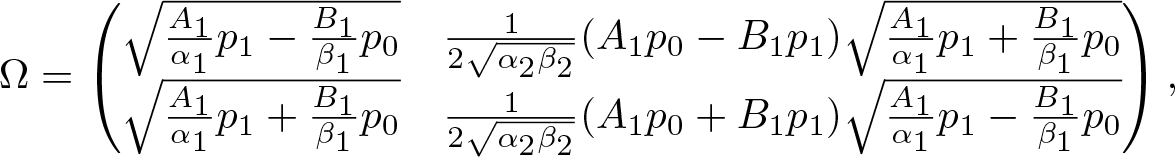 \begin{align}
\Omega=\begin{pmatrix}
\sqrt{\frac{A_1}{\alpha_1} p_1-\frac{B_1}{\beta_1} p_0}&\frac{1}{2\sqrt{\alpha_2\beta_2}}(A_1 p_0-B_1 p_1)\sqrt{\frac{A_1}{\alpha_1} p_1+\frac{B_1}{\beta_1} p_0}\\
\sqrt{\frac{A_1}{\alpha_1} p_1+\frac{B_1}{\beta_1} p_0}&\frac{1}{2\sqrt{\alpha_2\beta_2}}(A_1 p_0+B_1 p_1)\sqrt{\frac{A_1}{\alpha_1} p_1-\frac{B_1}{\beta_1} p_0}
\end{pmatrix},
\end{align}
\begin{align}
\Omega=\begin{pmatrix}
\sqrt{\frac{A_1}{\alpha_1} p_1-\frac{B_1}{\beta_1} p_0}&\frac{1}{2\sqrt{\alpha_2\beta_2}}(A_1 p_0-B_1 p_1)\sqrt{\frac{A_1}{\alpha_1} p_1+\frac{B_1}{\beta_1} p_0}\\
\sqrt{\frac{A_1}{\alpha_1} p_1+\frac{B_1}{\beta_1} p_0}&\frac{1}{2\sqrt{\alpha_2\beta_2}}(A_1 p_0+B_1 p_1)\sqrt{\frac{A_1}{\alpha_1} p_1-\frac{B_1}{\beta_1} p_0}
\end{pmatrix},
\end{align} where we recall that ![]() $\alpha_j,\beta_j$ are defined in Lemma 19 and
$\alpha_j,\beta_j$ are defined in Lemma 19 and ![]() $A_1,B_1$ in (6.20).
$A_1,B_1$ in (6.20).
The following two simple lemmata establish that ![]() $\mathrm{Ad}(\Omega)$ is a
$\mathrm{Ad}(\Omega)$ is a ![]() $C_2\times C_2$-equivariant automorphism of
$C_2\times C_2$-equivariant automorphism of ![]() $\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}$. First of all, conjugation with Ω is an automorphism of
$\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}$. First of all, conjugation with Ω is an automorphism of ![]() $\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}$:
$\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}$:
Lemma 21. We have ![]() $\Psi:=\mathrm{Ad}(\Omega)\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}).$ Explicitly, the matrix of Ψ with respect to the basis
$\Psi:=\mathrm{Ad}(\Omega)\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}).$ Explicitly, the matrix of Ψ with respect to the basis ![]() $\mathcal{B}=\{h,e,f\}$ is given by
$\mathcal{B}=\{h,e,f\}$ is given by
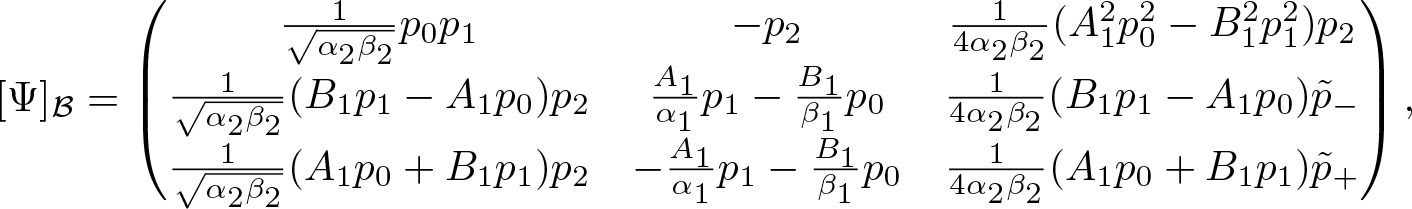 \begin{align*}[\Psi]_{\mathcal{B}}=\begin{pmatrix}
\frac{1}{\sqrt{\alpha_2\beta_2}} p_0 p_1 & - p_2 & \frac{1}{4\alpha_2\beta_2}(A_1^2 p_0^2-B_1^2 p_1^2) p_2\\
\frac{1}{\sqrt{\alpha_2\beta_2}}(B_1 p_1-A_1 p_0) p_2 & \frac{A_1}{\alpha_1} p_1-\frac{B_1}{\beta_1} p_0 & \frac{1}{4\alpha_2\beta_2}(B_1 p_1-A_1 p_0)\tilde{p}_-\\
\frac{1}{\sqrt{\alpha_2\beta_2}}(A_1 p_0+B_1 p_1) p_2 & -\frac{A_1}{\alpha_1} p_1-\frac{B_1}{\beta_1} p_0 &\frac{1}{4\alpha_2\beta_2} (A_1 p_0+B_1 p_1)\tilde{p}_+
\end{pmatrix},
\end{align*}
\begin{align*}[\Psi]_{\mathcal{B}}=\begin{pmatrix}
\frac{1}{\sqrt{\alpha_2\beta_2}} p_0 p_1 & - p_2 & \frac{1}{4\alpha_2\beta_2}(A_1^2 p_0^2-B_1^2 p_1^2) p_2\\
\frac{1}{\sqrt{\alpha_2\beta_2}}(B_1 p_1-A_1 p_0) p_2 & \frac{A_1}{\alpha_1} p_1-\frac{B_1}{\beta_1} p_0 & \frac{1}{4\alpha_2\beta_2}(B_1 p_1-A_1 p_0)\tilde{p}_-\\
\frac{1}{\sqrt{\alpha_2\beta_2}}(A_1 p_0+B_1 p_1) p_2 & -\frac{A_1}{\alpha_1} p_1-\frac{B_1}{\beta_1} p_0 &\frac{1}{4\alpha_2\beta_2} (A_1 p_0+B_1 p_1)\tilde{p}_+
\end{pmatrix},
\end{align*} where ![]() $\tilde{p}_{\pm}:=p_0 p_1\pm \sqrt{\alpha_2\beta_2}$.
$\tilde{p}_{\pm}:=p_0 p_1\pm \sqrt{\alpha_2\beta_2}$.
Proof. We will first argue that ![]() $\det(\Omega)=1$. Recall
$\det(\Omega)=1$. Recall  $\xi_{\pm}=\sqrt{\frac{A_1}{\alpha_1} p_1\pm\frac{B_1}{\beta_1} p_0}$. Using Lemma 20, we compute
$\xi_{\pm}=\sqrt{\frac{A_1}{\alpha_1} p_1\pm\frac{B_1}{\beta_1} p_0}$. Using Lemma 20, we compute
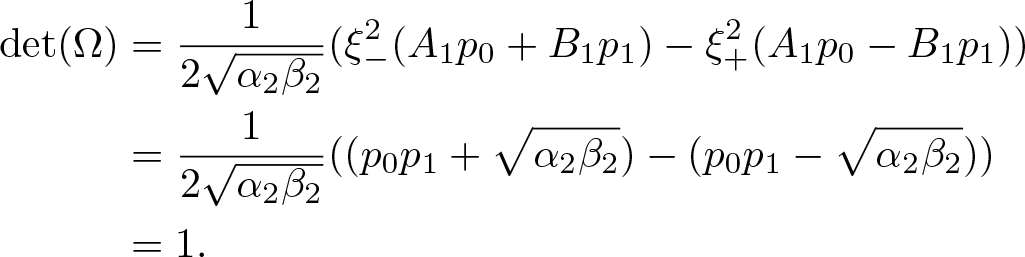 \begin{align*}
\det(\Omega)&=\frac{1}{2\sqrt{\alpha_2\beta_2}}(\xi_-^2(A_1 p_0+B_1 p_1)-\xi_+^2(A_1 p_0-B_1p_1))\\
&=\frac{1}{2\sqrt{\alpha_2\beta_2}}(( p_0 p_1+\sqrt{\alpha_2\beta_2})-( p_0 p_1-\sqrt{\alpha_2\beta_2}))\\
&=1.
\end{align*}
\begin{align*}
\det(\Omega)&=\frac{1}{2\sqrt{\alpha_2\beta_2}}(\xi_-^2(A_1 p_0+B_1 p_1)-\xi_+^2(A_1 p_0-B_1p_1))\\
&=\frac{1}{2\sqrt{\alpha_2\beta_2}}(( p_0 p_1+\sqrt{\alpha_2\beta_2})-( p_0 p_1-\sqrt{\alpha_2\beta_2}))\\
&=1.
\end{align*} Let  $m=\begin{pmatrix}
a&b\\
c&d
\end{pmatrix}\in SL_2(R)$, where R is some unital ring. The matrix of
$m=\begin{pmatrix}
a&b\\
c&d
\end{pmatrix}\in SL_2(R)$, where R is some unital ring. The matrix of ![]() $\mathrm{Ad}(m)$ with respect to
$\mathrm{Ad}(m)$ with respect to ![]() $\mathcal{B}$ is given by
$\mathcal{B}$ is given by
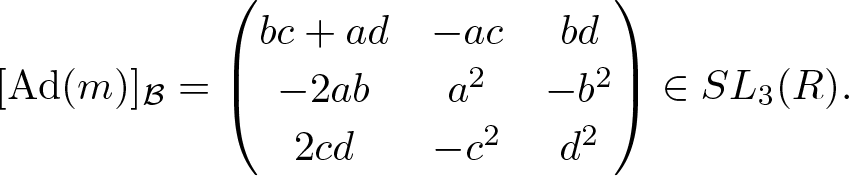 \begin{equation*}[\mathrm{Ad}(m)]_{\mathcal{B}}=\begin{pmatrix}bc+ad&-ac&bd\\
-2ab&a^2&-b^2\\
2cd&-c^2&d^2\end{pmatrix}\in SL_3(R).\end{equation*}
\begin{equation*}[\mathrm{Ad}(m)]_{\mathcal{B}}=\begin{pmatrix}bc+ad&-ac&bd\\
-2ab&a^2&-b^2\\
2cd&-c^2&d^2\end{pmatrix}\in SL_3(R).\end{equation*} Take ![]() $m=\Omega$ and after some work, using Lemma 20, one arrives at the matrix in the claim. Since
$m=\Omega$ and after some work, using Lemma 20, one arrives at the matrix in the claim. Since ![]() $\det(\Omega)=1$, the same holds for Ψ and we see that all the entries are in
$\det(\Omega)=1$, the same holds for Ψ and we see that all the entries are in ![]() $\mathcal{O}_{\mathbb{T}}$. This shows that
$\mathcal{O}_{\mathbb{T}}$. This shows that ![]() $\Psi\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}).$
$\Psi\in \mathrm{Aut}_{\mathcal{O}_{\mathbb{T}}}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}).$
Lemma 22. The map Ψ intertwines the actions of ![]() $C_2\times C_2$ on T and
$C_2\times C_2$ on T and ![]() $\mathfrak{sl}_2$:
$\mathfrak{sl}_2$: ![]() $\Psi (r\cdot z)=\rho(r)\Psi (z)$ for all
$\Psi (r\cdot z)=\rho(r)\Psi (z)$ for all ![]() $r\in C_2\times C_2$ and
$r\in C_2\times C_2$ and ![]() $z\in {\mathbb{T}}$.
$z\in {\mathbb{T}}$.
Proof. Using that
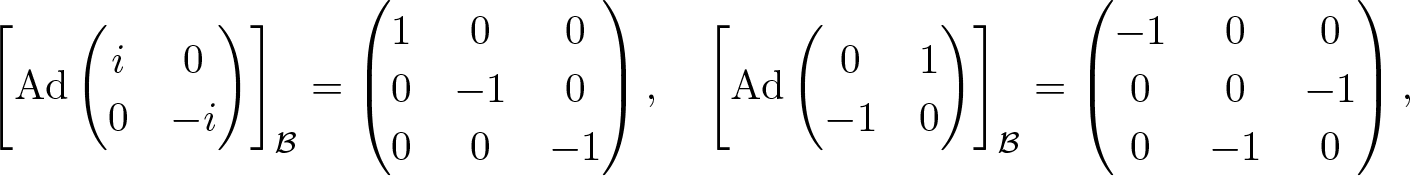 \begin{equation*}\left[\mathrm{Ad}\begin{pmatrix}
i& 0\\
0&-i
\end{pmatrix}\right]_{\mathcal{B}}=\begin{pmatrix}
1&0&0\\
0&-1&0\\
0&0&-1
\end{pmatrix},\quad \left[\mathrm{Ad}\begin{pmatrix}
0& 1\\
-1&0
\end{pmatrix}\right]_{\mathcal{B}}=\begin{pmatrix}
-1&0&0\\
0&0&-1\\
0&-1&0
\end{pmatrix},\end{equation*}
\begin{equation*}\left[\mathrm{Ad}\begin{pmatrix}
i& 0\\
0&-i
\end{pmatrix}\right]_{\mathcal{B}}=\begin{pmatrix}
1&0&0\\
0&-1&0\\
0&0&-1
\end{pmatrix},\quad \left[\mathrm{Ad}\begin{pmatrix}
0& 1\\
-1&0
\end{pmatrix}\right]_{\mathcal{B}}=\begin{pmatrix}
-1&0&0\\
0&0&-1\\
0&-1&0
\end{pmatrix},\end{equation*} it is straightforward to verify the claim for r 1 and r 2, and hence for all ![]() $r\in C_2\times C_2$.
$r\in C_2\times C_2$.
Remark 7. Notice that in the definition of Ω in (6.23), the choice of signs of the constants A 1 and B 1 does not matter. Indeed, one could verify that changing the signs corresponds to compose ![]() $\Psi=\mathrm{Ad}(\Omega)$ with commuting (order 2) elements of
$\Psi=\mathrm{Ad}(\Omega)$ with commuting (order 2) elements of ![]() $\mathrm{Aut}(\mathfrak{sl}_2)$, which in turn also commute with
$\mathrm{Aut}(\mathfrak{sl}_2)$, which in turn also commute with ![]() $\rho(r)$, for any
$\rho(r)$, for any ![]() $r\in C_2\times C_2$.
$r\in C_2\times C_2$.
Define the following elements of ![]() $\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}$:
$\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}$:
By the equivariance property of Ψ, cf. Lemma 22, the elements ![]() $h',e'$ and fʹ are invariant with respect to the action of
$h',e'$ and fʹ are invariant with respect to the action of ![]() $C_2\times C_2$. In fact, they will form a basis of the
$C_2\times C_2$. In fact, they will form a basis of the ![]() $C_2\times C_2$-aLia as we will see in the following theorem.
$C_2\times C_2$-aLia as we will see in the following theorem.
Theorem 6. Let ![]() $\rho:C_2\times C_2\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and
$\rho:C_2\times C_2\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and ![]() $\sigma:C_2\times C_2\rightarrow \mathrm{Aut}(T)$ be monomorphisms and assume that
$\sigma:C_2\times C_2\rightarrow \mathrm{Aut}(T)$ be monomorphisms and assume that ![]() $g(T/\sigma(C_2\times C_2))=1$. Then
$g(T/\sigma(C_2\times C_2))=1$. Then
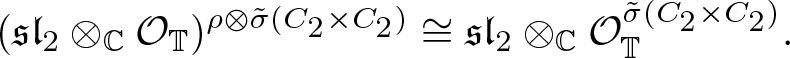 \begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_2\times C_2)}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_2\times C_2)}.\end{equation*}
\begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_2\times C_2)}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_2\times C_2)}.\end{equation*}A normal form is given by
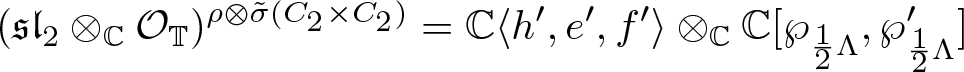 \begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_2\times C_2)}={\mathbb{C}}\langle h',e',f' \rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}'] \end{equation*}
\begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_2\times C_2)}={\mathbb{C}}\langle h',e',f' \rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}'] \end{equation*}with
where ![]() $h',e',f'$ are defined in (6.24).
$h',e',f'$ are defined in (6.24).
Proof. By Lemma 17 , we know that  $\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_2\times C_2)}={\mathbb{C}}[\wp_{\frac{1}{2}\Lambda},\wp_{\frac{1}{2}\Lambda}']$. Now, by Lemma 22, we are in a position to apply Proposition 3 to
$\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}(C_2\times C_2)}={\mathbb{C}}[\wp_{\frac{1}{2}\Lambda},\wp_{\frac{1}{2}\Lambda}']$. Now, by Lemma 22, we are in a position to apply Proposition 3 to ![]() $\Psi=\mathrm{Ad}(\Omega) $ with
$\Psi=\mathrm{Ad}(\Omega) $ with ![]() $K=C_2\times C_2$. Hence
$K=C_2\times C_2$. Hence
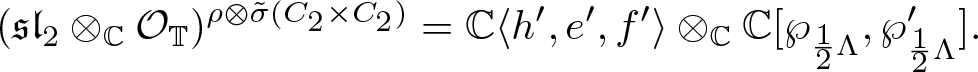 \begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_2\times C_2)}={\mathbb{C}}\langle h',e',f' \rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}'] .\end{equation*}
\begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_2\times C_2)}={\mathbb{C}}\langle h',e',f' \rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}'] .\end{equation*} The Lie structure is the same as the Lie structure of ![]() ${\mathbb{C}}\langle e,f,h\rangle$ and is, therefore, given by
${\mathbb{C}}\langle e,f,h\rangle$ and is, therefore, given by
In particular, we see that  $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_2\times C_2)}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}']= \mathfrak{C}_{\frac{1}{2}{\Lambda}}.$
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(C_2\times C_2)}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}']= \mathfrak{C}_{\frac{1}{2}{\Lambda}}.$
Explicitly, the generators of the ![]() $C_2\times C_2$-aLia in normal form are given by
$C_2\times C_2$-aLia in normal form are given by
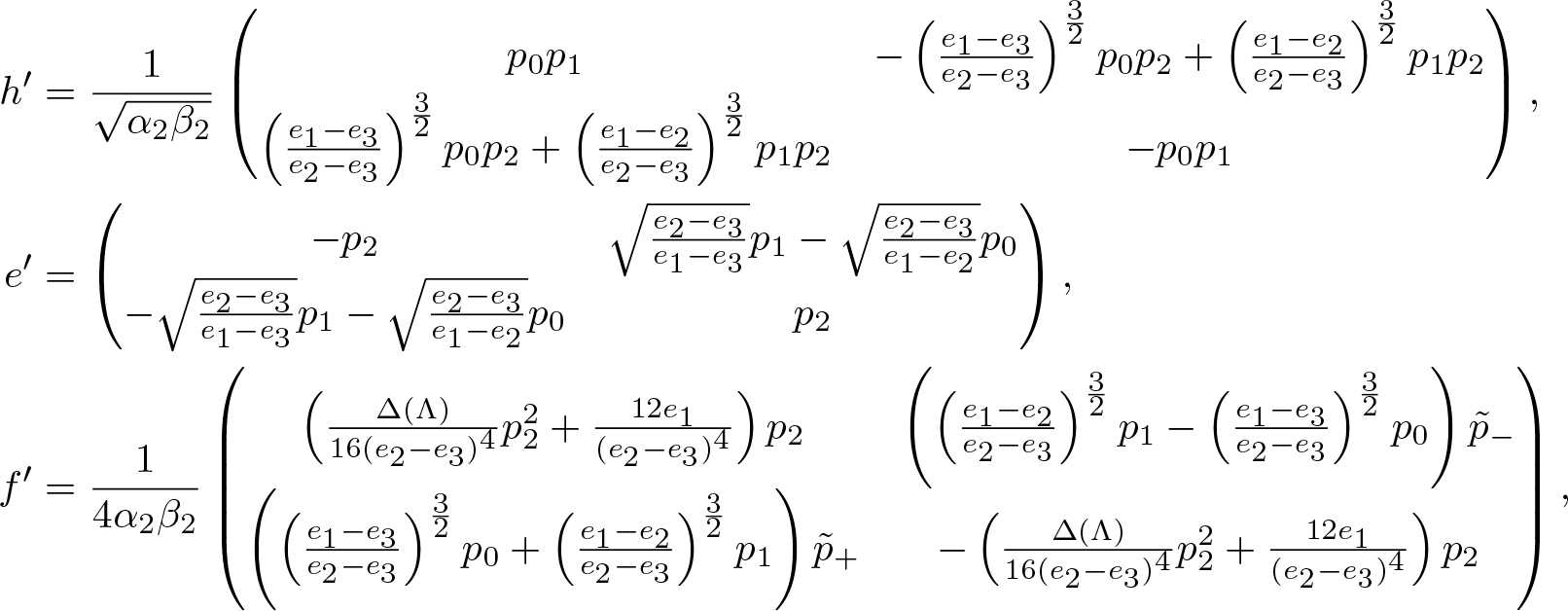 \begin{align*}
h'&=\frac{1}{\sqrt{\alpha_2\beta_2}}\begin{pmatrix}
p_0 p_1 & -\left(\frac{e_1-e_3}{e_2-e_3}\right)^{\frac{3}{2}} p_0 p_2+\left(\frac{e_1-e_2}{e_2-e_3}\right)^{\frac{3}{2}} p_1 p_2\\
\left(\frac{e_1-e_3}{e_2-e_3}\right)^{\frac{3}{2}} p_0 p_2+\left(\frac{e_1-e_2}{e_2-e_3}\right)^{\frac{3}{2}} p_1 p_2 & - p_0 p_1
\end{pmatrix},\\
e'&=\begin{pmatrix}
- p_2&\sqrt{\frac{e_2-e_3}{e_1-e_3}} p_1-\sqrt{\frac{e_2-e_3}{e_1-e_2}} p_0\\
-\sqrt{\frac{e_2-e_3}{e_1-e_3}} p_1-\sqrt{\frac{e_2-e_3}{e_1-e_2}} p_0 & p_2
\end{pmatrix},\\
f'&=\frac{1}{4\alpha_2\beta_2}\begin{pmatrix}
\left(\frac{\Delta({\Lambda})}{16(e_2-e_3)^4} p_2^2+\frac{12e_1}{(e_2-e_3)^4}\right) p_2& \left(\left(\frac{e_1-e_2}{e_2-e_3}\right)^{\frac{3}{2}} p_1-\left(\frac{e_1-e_3}{e_2-e_3}\right)^{\frac{3}{2}} p_0\right)\tilde{p}_-\\
\left(\left(\frac{e_1-e_3}{e_2-e_3}\right)^{\frac{3}{2}} p_0+\left(\frac{e_1-e_2}{e_2-e_3}\right)^{\frac{3}{2}} p_1\right)\tilde{p}_+ & -\left(\frac{\Delta({\Lambda})}{16(e_2-e_3)^4} p_2^2+\frac{12e_1}{(e_2-e_3)^4}\right) p_2\end{pmatrix},
\end{align*}
\begin{align*}
h'&=\frac{1}{\sqrt{\alpha_2\beta_2}}\begin{pmatrix}
p_0 p_1 & -\left(\frac{e_1-e_3}{e_2-e_3}\right)^{\frac{3}{2}} p_0 p_2+\left(\frac{e_1-e_2}{e_2-e_3}\right)^{\frac{3}{2}} p_1 p_2\\
\left(\frac{e_1-e_3}{e_2-e_3}\right)^{\frac{3}{2}} p_0 p_2+\left(\frac{e_1-e_2}{e_2-e_3}\right)^{\frac{3}{2}} p_1 p_2 & - p_0 p_1
\end{pmatrix},\\
e'&=\begin{pmatrix}
- p_2&\sqrt{\frac{e_2-e_3}{e_1-e_3}} p_1-\sqrt{\frac{e_2-e_3}{e_1-e_2}} p_0\\
-\sqrt{\frac{e_2-e_3}{e_1-e_3}} p_1-\sqrt{\frac{e_2-e_3}{e_1-e_2}} p_0 & p_2
\end{pmatrix},\\
f'&=\frac{1}{4\alpha_2\beta_2}\begin{pmatrix}
\left(\frac{\Delta({\Lambda})}{16(e_2-e_3)^4} p_2^2+\frac{12e_1}{(e_2-e_3)^4}\right) p_2& \left(\left(\frac{e_1-e_2}{e_2-e_3}\right)^{\frac{3}{2}} p_1-\left(\frac{e_1-e_3}{e_2-e_3}\right)^{\frac{3}{2}} p_0\right)\tilde{p}_-\\
\left(\left(\frac{e_1-e_3}{e_2-e_3}\right)^{\frac{3}{2}} p_0+\left(\frac{e_1-e_2}{e_2-e_3}\right)^{\frac{3}{2}} p_1\right)\tilde{p}_+ & -\left(\frac{\Delta({\Lambda})}{16(e_2-e_3)^4} p_2^2+\frac{12e_1}{(e_2-e_3)^4}\right) p_2\end{pmatrix},
\end{align*} where we recall that ![]() $\tilde{p}_{\pm}=p_0 p_1\pm\sqrt{\alpha_2\beta_2}$. We could rewrite/simplify the term
$\tilde{p}_{\pm}=p_0 p_1\pm\sqrt{\alpha_2\beta_2}$. We could rewrite/simplify the term  $\frac{\Delta({\Lambda})}{16(e_2-e_3)^4} p_2^2$ to
$\frac{\Delta({\Lambda})}{16(e_2-e_3)^4} p_2^2$ to  $\wp_{\frac{1}{2}{\Lambda}}-4e_1$ due to Corollary 18.
$\wp_{\frac{1}{2}{\Lambda}}-4e_1$ due to Corollary 18.
Remark 8. The aLia ![]() $\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_2\times C_2)}$ is the Lie algebra of holomorphic
$\mathfrak{A}=(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_2\times C_2)}$ is the Lie algebra of holomorphic ![]() $K=C_2\times C_2$-equivariant maps from a punctured torus to
$K=C_2\times C_2$-equivariant maps from a punctured torus to ![]() $\mathfrak{sl}_2$. In [Reference Carey, Hannabuss, Mason and Singer8], the authors study holomorphic K-equivariant maps from some K-invariant subset of a complex torus
$\mathfrak{sl}_2$. In [Reference Carey, Hannabuss, Mason and Singer8], the authors study holomorphic K-equivariant maps from some K-invariant subset of a complex torus ![]() ${\mathbb{C}}/{\mathbb{Z}}\oplus{\mathbb{Z}}\tau$ to
${\mathbb{C}}/{\mathbb{Z}}\oplus{\mathbb{Z}}\tau$ to ![]() $SL_2({\mathbb{C}})$. They give expansions of the functions that appear in these matrices in terms of
$SL_2({\mathbb{C}})$. They give expansions of the functions that appear in these matrices in terms of ![]() $\lambda_1,\lambda_2$ and λ 3, which are related to our functions
$\lambda_1,\lambda_2$ and λ 3, which are related to our functions ![]() $p_0,p_1$ and p 2 defined in (6.13)–(6.15). With these functions, they construct K-equivariant maps with values in
$p_0,p_1$ and p 2 defined in (6.13)–(6.15). With these functions, they construct K-equivariant maps with values in ![]() $\mathfrak{sl}_2$ which they use in the context of integrable systems, in particular in an algebraic description of the Landau-Lifshitz hierarchy. For example, a Lax pair, which is the Lax pair found in [Reference Sklyanin31], is constructed for the Landau–Lifshitz equation, using elements of
$\mathfrak{sl}_2$ which they use in the context of integrable systems, in particular in an algebraic description of the Landau-Lifshitz hierarchy. For example, a Lax pair, which is the Lax pair found in [Reference Sklyanin31], is constructed for the Landau–Lifshitz equation, using elements of ![]() $\mathfrak{A}$. Furthermore, they present a result about a factorisation of smooth K-equivariant loops
$\mathfrak{A}$. Furthermore, they present a result about a factorisation of smooth K-equivariant loops ![]() $\gamma:\mathcal{C}\rightarrow SL_2({\mathbb{C}})$, where
$\gamma:\mathcal{C}\rightarrow SL_2({\mathbb{C}})$, where ![]() $\mathcal{C}$ is a union of disjoint circles around the points
$\mathcal{C}$ is a union of disjoint circles around the points ![]() $0,1/2,\tau/2,(1+\tau)/2$, analogues to Birkhoff factorisation.
$0,1/2,\tau/2,(1+\tau)/2$, analogues to Birkhoff factorisation.
The last symmetry group in our classification is ![]() $\Gamma=A_4$, which we will discuss now.
$\Gamma=A_4$, which we will discuss now.
Theorem 7. Let ![]() $T\cong T_{\omega_6}$ and
$T\cong T_{\omega_6}$ and ![]() $\rho:A_4\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and
$\rho:A_4\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and ![]() $\sigma:A_4\rightarrow \mathrm{Aut}(T)$ be monomorphisms. Let
$\sigma:A_4\rightarrow \mathrm{Aut}(T)$ be monomorphisms. Let ![]() $\mathbb{T}=T\setminus A_4\cdot \{0\}.$ There is the following isomorphism of Lie algebras:
$\mathbb{T}=T\setminus A_4\cdot \{0\}.$ There is the following isomorphism of Lie algebras:
where ![]() $\mathfrak{O}$ is the Onsager algebra. A normal form is given by
$\mathfrak{O}$ is the Onsager algebra. A normal form is given by
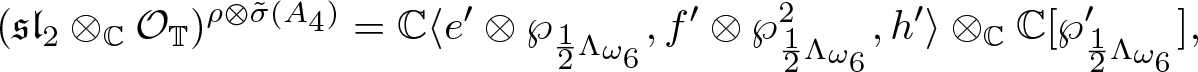 \begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(A_4)}={\mathbb{C}}\langle e'\otimes \wp_{\frac{1}{2}{\Lambda}_{\omega_6}},f'\otimes \wp_{\frac{1}{2}{\Lambda}_{\omega_6}}^2,h'\rangle \otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}_{\omega_6}}'],\end{equation*}
\begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{\rho\otimes \tilde{\sigma}(A_4)}={\mathbb{C}}\langle e'\otimes \wp_{\frac{1}{2}{\Lambda}_{\omega_6}},f'\otimes \wp_{\frac{1}{2}{\Lambda}_{\omega_6}}^2,h'\rangle \otimes_{{\mathbb{C}}} {\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}_{\omega_6}}'],\end{equation*} where ![]() $e',f',h'$ are the generators of the
$e',f',h'$ are the generators of the ![]() $C_2\times C_2$-aLia, cf. Theorem 6.
$C_2\times C_2$-aLia, cf. Theorem 6.
Proof. Assume A 4 is generated by ![]() $r_1,r_2$ and s as in Lemma 7 and notice that
$r_1,r_2$ and s as in Lemma 7 and notice that ![]() $A_4\cong C_3 \ltimes (C_2\times C_2)$. Define
$A_4\cong C_3 \ltimes (C_2\times C_2)$. Define ![]() $\rho:A_4\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ by
$\rho:A_4\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ by
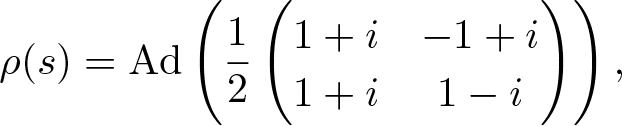 \begin{equation*}\rho(s)=\mathrm{Ad}\left(\frac{1}{2}\begin{pmatrix}
1+i &-1+i\\
1+i&1-i
\end{pmatrix}\right),\end{equation*}
\begin{equation*}\rho(s)=\mathrm{Ad}\left(\frac{1}{2}\begin{pmatrix}
1+i &-1+i\\
1+i&1-i
\end{pmatrix}\right),\end{equation*} and ![]() $\rho(r_1)$,
$\rho(r_1)$, ![]() $\rho(r_2)$ as we have done for
$\rho(r_2)$ as we have done for ![]() $C_2\times C_2$, see (6.22). Define
$C_2\times C_2$, see (6.22). Define ![]() $\sigma:A_4\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ by
$\sigma:A_4\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ by ![]() $\sigma(s)z=\omega_3z$,
$\sigma(s)z=\omega_3z$, ![]() $\sigma(r_1)z=z+1/2$ and
$\sigma(r_1)z=z+1/2$ and ![]() $\sigma(r_2)z=z+\omega_3/2$. Theorem 6 gives us the normal form
$\sigma(r_2)z=z+\omega_3/2$. Theorem 6 gives us the normal form  ${\mathbb{C}}\langle h',e',f' \rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}']$ for the
${\mathbb{C}}\langle h',e',f' \rangle \otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}']$ for the ![]() $C_2\times C_2$-aLia. We will verify that hʹ is C 3-invariant, where
$C_2\times C_2$-aLia. We will verify that hʹ is C 3-invariant, where ![]() $C_3\subset \mathrm{Aut}(\mathfrak{sl}_2)$ is generated by
$C_3\subset \mathrm{Aut}(\mathfrak{sl}_2)$ is generated by ![]() $\rho(s)$, after which we can invoke Lemma 14 and Proposition 3. By Lemma 10, we know that
$\rho(s)$, after which we can invoke Lemma 14 and Proposition 3. By Lemma 10, we know that  ${\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}_{\omega_6}},\wp_{\frac{1}{2}{\Lambda}_{\omega_6}}']^{\langle s\rangle}\cong {\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}_{\omega_6}}'].$ Again, there is no loss of generality by our choice of ρ and σ by Lemma 5 combined with Lemma 4.
${\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}_{\omega_6}},\wp_{\frac{1}{2}{\Lambda}_{\omega_6}}']^{\langle s\rangle}\cong {\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}_{\omega_6}}'].$ Again, there is no loss of generality by our choice of ρ and σ by Lemma 5 combined with Lemma 4.
Recall that by Lemma 20 ![]() $A_1^2=-1$ and
$A_1^2=-1$ and ![]() $B_1^2=1$ in case of a hexagonal lattice. We choose
$B_1^2=1$ in case of a hexagonal lattice. We choose ![]() $A_1=-i$ and
$A_1=-i$ and ![]() $B_1=1$. The intertwiner Ψ with respect to the basis
$B_1=1$. The intertwiner Ψ with respect to the basis ![]() $\{h,e,f\}$ becomes
$\{h,e,f\}$ becomes
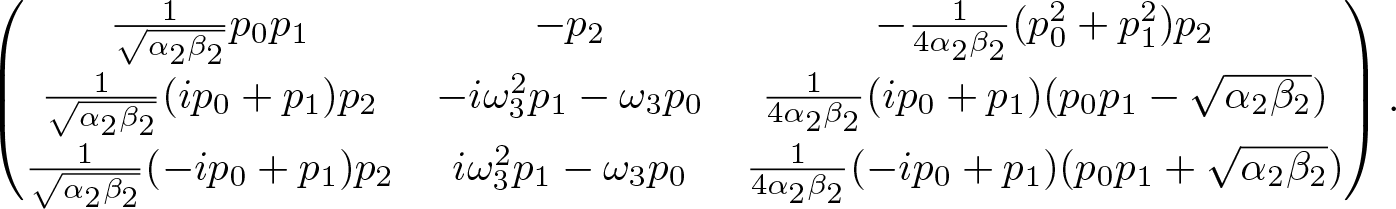 \begin{equation*}\begin{pmatrix}
\frac{1}{\sqrt{\alpha_2\beta_2}} p_0 p_1 & - p_2 & -\frac{1}{4\alpha_2\beta_2}(p_0^2+ p_1^2) p_2\\
\frac{1}{\sqrt{\alpha_2\beta_2}}(i p_0+ p_1) p_2 & -i\omega_3^2 p_1-\omega_3p_0 & \frac{1}{4\alpha_2\beta_2}(i p_0+ p_1)( p_0 p_1-\sqrt{\alpha_2\beta_2})\\
\frac{1}{\sqrt{\alpha_2\beta_2}}(-i p_0+ p_1) p_2 & i\omega_3^2 p_1-\omega_3 p_0 &\frac{1}{4\alpha_2\beta_2} (-i p_0+p_1)( p_0 p_1+\sqrt{\alpha_2\beta_2})
\end{pmatrix}.\end{equation*}
\begin{equation*}\begin{pmatrix}
\frac{1}{\sqrt{\alpha_2\beta_2}} p_0 p_1 & - p_2 & -\frac{1}{4\alpha_2\beta_2}(p_0^2+ p_1^2) p_2\\
\frac{1}{\sqrt{\alpha_2\beta_2}}(i p_0+ p_1) p_2 & -i\omega_3^2 p_1-\omega_3p_0 & \frac{1}{4\alpha_2\beta_2}(i p_0+ p_1)( p_0 p_1-\sqrt{\alpha_2\beta_2})\\
\frac{1}{\sqrt{\alpha_2\beta_2}}(-i p_0+ p_1) p_2 & i\omega_3^2 p_1-\omega_3 p_0 &\frac{1}{4\alpha_2\beta_2} (-i p_0+p_1)( p_0 p_1+\sqrt{\alpha_2\beta_2})
\end{pmatrix}.\end{equation*} We will show, given our choice of A 1 and B 1, that ![]() $\rho(s)\Psi (z)h=\Psi (s\cdot z)h$, which will imply that
$\rho(s)\Psi (z)h=\Psi (s\cdot z)h$, which will imply that ![]() $\Psi h$ is C 3-invariant. Write
$\Psi h$ is C 3-invariant. Write ![]() $[\cdot]$ for a vector or matrix with respect to the basis
$[\cdot]$ for a vector or matrix with respect to the basis ![]() $\mathcal{B}=\{h,e,f\}$ and let
$\mathcal{B}=\{h,e,f\}$ and let
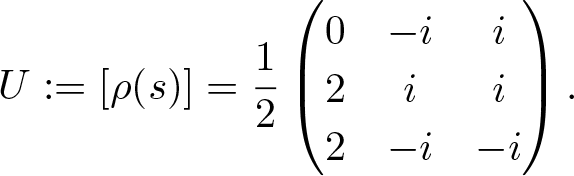 \begin{equation*}U:=\left[\rho(s)\right]=\frac{1}{2}\begin{pmatrix}
0&-i&i\\
2&i&i\\
2&-i&-i
\end{pmatrix}.\end{equation*}
\begin{equation*}U:=\left[\rho(s)\right]=\frac{1}{2}\begin{pmatrix}
0&-i&i\\
2&i&i\\
2&-i&-i
\end{pmatrix}.\end{equation*}We compute
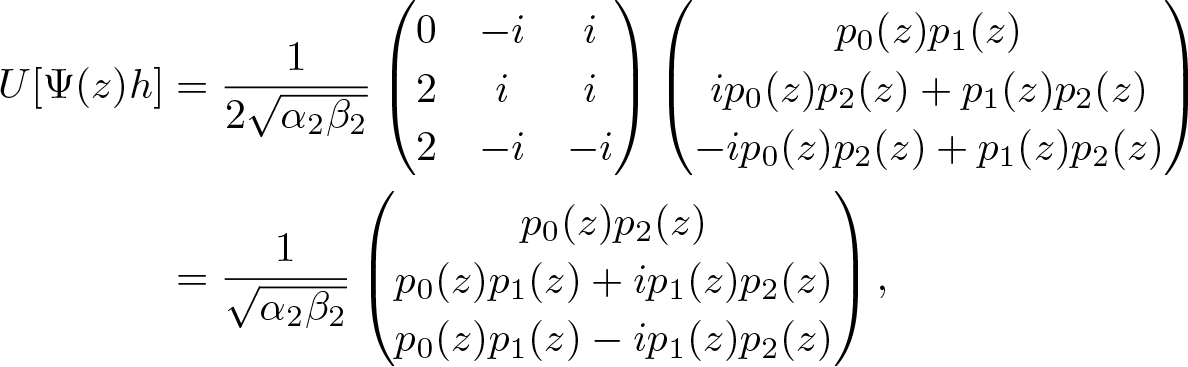 \begin{align*}U[\Psi (z)h]&=\frac{1}{2\sqrt{\alpha_2\beta_2}}\begin{pmatrix}
0&-i&i\\
2&i&i\\
2&-i&-i
\end{pmatrix} \begin{pmatrix}
p_0(z) p_1(z) \\
i p_0(z)p_2(z)+ p_1(z)p_2(z)\\
-i p_0(z)p_2(z)+ p_1(z)p_2(z)\end{pmatrix}\\
&=\frac{1}{\sqrt{\alpha_2\beta_2}}\begin{pmatrix}p_0(z)p_2(z)\\
p_0(z)p_1(z)+ip_1(z)p_2(z)\\
p_0(z)p_1(z)-ip_1(z)p_2(z) \end{pmatrix},
\end{align*}
\begin{align*}U[\Psi (z)h]&=\frac{1}{2\sqrt{\alpha_2\beta_2}}\begin{pmatrix}
0&-i&i\\
2&i&i\\
2&-i&-i
\end{pmatrix} \begin{pmatrix}
p_0(z) p_1(z) \\
i p_0(z)p_2(z)+ p_1(z)p_2(z)\\
-i p_0(z)p_2(z)+ p_1(z)p_2(z)\end{pmatrix}\\
&=\frac{1}{\sqrt{\alpha_2\beta_2}}\begin{pmatrix}p_0(z)p_2(z)\\
p_0(z)p_1(z)+ip_1(z)p_2(z)\\
p_0(z)p_1(z)-ip_1(z)p_2(z) \end{pmatrix},
\end{align*} and, using ![]() $p_j(s\cdot z)=p_{j-1}(z)$,
$p_j(s\cdot z)=p_{j-1}(z)$,
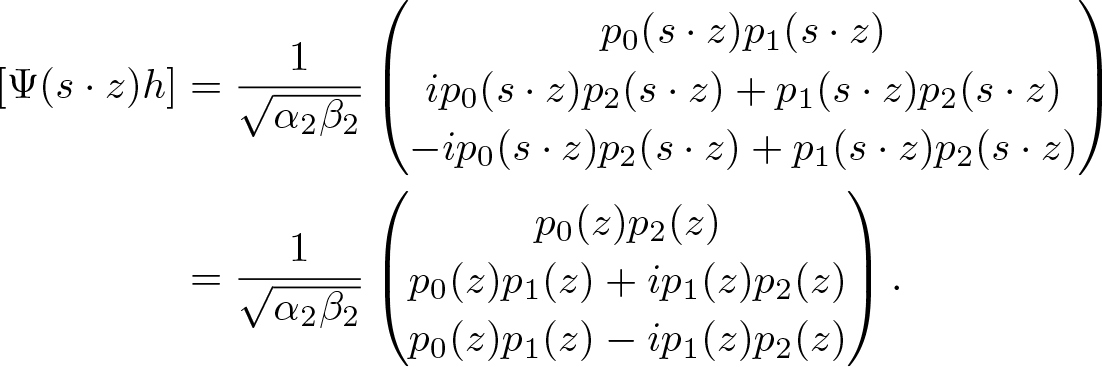 \begin{align*}
[\Psi (s\cdot z)h]&=\frac{1}{\sqrt{\alpha_2\beta_2}}\begin{pmatrix}p_0(s\cdot z)p_1(s\cdot z)\\
i p_0(s\cdot z)p_2(s\cdot z)+ p_1(s\cdot z)p_2(s\cdot z)\\
-i p_0(s\cdot z)p_2(s\cdot z)+ p_1(s\cdot z)p_2(s\cdot z)\end{pmatrix}\\
&=\frac{1}{\sqrt{\alpha_2\beta_2}}\begin{pmatrix}p_0(z)p_2(z)\\
p_0(z)p_1(z)+ip_1(z)p_2(z)\\
p_0(z)p_1(z)-ip_1(z)p_2(z) \end{pmatrix}.
\end{align*}
\begin{align*}
[\Psi (s\cdot z)h]&=\frac{1}{\sqrt{\alpha_2\beta_2}}\begin{pmatrix}p_0(s\cdot z)p_1(s\cdot z)\\
i p_0(s\cdot z)p_2(s\cdot z)+ p_1(s\cdot z)p_2(s\cdot z)\\
-i p_0(s\cdot z)p_2(s\cdot z)+ p_1(s\cdot z)p_2(s\cdot z)\end{pmatrix}\\
&=\frac{1}{\sqrt{\alpha_2\beta_2}}\begin{pmatrix}p_0(z)p_2(z)\\
p_0(z)p_1(z)+ip_1(z)p_2(z)\\
p_0(z)p_1(z)-ip_1(z)p_2(z) \end{pmatrix}.
\end{align*} This means that ![]() $h':=\Psi h$ is indeed invariant under the action of C 3. By Lemma 14 and Proposition 3, we see that
$h':=\Psi h$ is indeed invariant under the action of C 3. By Lemma 14 and Proposition 3, we see that
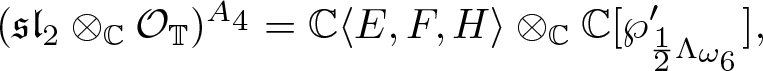 \begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{A_4} ={\mathbb{C}}\langle E,F,H\rangle\otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}_{\omega_6}}'],\end{equation*}
\begin{equation*}(\mathfrak{sl}_2\otimes_{{\mathbb{C}}} \mathcal{O}_{\mathbb{T}})^{A_4} ={\mathbb{C}}\langle E,F,H\rangle\otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}_{\omega_6}}'],\end{equation*}with generators
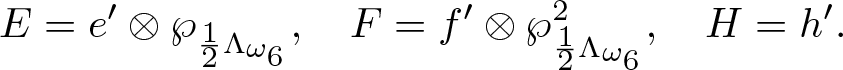 \begin{equation*}E=e'\otimes \wp_{\frac{1}{2}{\Lambda}_{\omega_6}}, \quad F=f'\otimes \wp_{\frac{1}{2}{\Lambda}_{\omega_6}}^2,\quad H=h'.\end{equation*}
\begin{equation*}E=e'\otimes \wp_{\frac{1}{2}{\Lambda}_{\omega_6}}, \quad F=f'\otimes \wp_{\frac{1}{2}{\Lambda}_{\omega_6}}^2,\quad H=h'.\end{equation*} By Theorem 5, this aLia is isomorphic to ![]() $\mathfrak{O}.$
$\mathfrak{O}.$
6.3. Summary
In this section, we will summarise our results. The main results are firstly a classification of aLias on complex tori with base Lie algebra ![]() $\mathfrak{sl}_2$ and secondly, the normal forms (as defined in Definition 3) corresponding to each of the groups in Lemma 6. In Table 1 in the Introduction, we have given a classification in terms of the number of branch points of the canonical projection
$\mathfrak{sl}_2$ and secondly, the normal forms (as defined in Definition 3) corresponding to each of the groups in Lemma 6. In Table 1 in the Introduction, we have given a classification in terms of the number of branch points of the canonical projection ![]() $\mathbb{T}\rightarrow \mathbb{T}/\Gamma$, where
$\mathbb{T}\rightarrow \mathbb{T}/\Gamma$, where ![]() $\mathbb{T}$ is a punctured complex torus. It is a remarkable fact that the Onsager algebra appears only in the case where the complex torus has additional symmetry. We learn from Table 1 that if
$\mathbb{T}$ is a punctured complex torus. It is a remarkable fact that the Onsager algebra appears only in the case where the complex torus has additional symmetry. We learn from Table 1 that if ![]() $\Gamma\subset \mathrm{Aut}(T)$ is such that
$\Gamma\subset \mathrm{Aut}(T)$ is such that ![]() $\mathbb{T}\rightarrow \mathbb{T}/\Gamma$ has two branch points, then
$\mathbb{T}\rightarrow \mathbb{T}/\Gamma$ has two branch points, then ![]() $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\Gamma}$ is isomorphic to
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\Gamma}$ is isomorphic to ![]() $\mathfrak{O}$. Below we will give a more elaborate classification based on the possible symmetry groups, as we have found in § 6.
$\mathfrak{O}$. Below we will give a more elaborate classification based on the possible symmetry groups, as we have found in § 6.
ALias with ![]() $\Gamma=C_{\ell}\subset \mathrm{Aut}_0(T),\,\, \ell=2,3,4,6$
$\Gamma=C_{\ell}\subset \mathrm{Aut}_0(T),\,\, \ell=2,3,4,6$
The classification of aLias with ![]() $C_{\ell}$ (
$C_{\ell}$ (![]() $\ell=3,4,6$) such that
$\ell=3,4,6$) such that ![]() $C_{\ell}\subset \mathrm{Aut}_0(T)$, where T is a suitable torus, has been done in Theorem 5. The normal forms are given in the proof of Theorem 5 and (6.10), (6.11). In particular, for any faithful
$C_{\ell}\subset \mathrm{Aut}_0(T)$, where T is a suitable torus, has been done in Theorem 5. The normal forms are given in the proof of Theorem 5 and (6.10), (6.11). In particular, for any faithful ![]() $\rho:C_{\ell}\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and
$\rho:C_{\ell}\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and ![]() $\sigma:C_{\ell}\rightarrow \mathrm{Aut}(T)$, the aLia
$\sigma:C_{\ell}\rightarrow \mathrm{Aut}(T)$, the aLia ![]() $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_{\ell})}$ is isomorphic to the Onsager algebra.
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(C_{\ell})}$ is isomorphic to the Onsager algebra.
The case of ![]() $\ell=2$ has been done in Example 3 and is isomorphic to
$\ell=2$ has been done in Example 3 and is isomorphic to ![]() $\mathfrak{S}_{\tau}$ for some
$\mathfrak{S}_{\tau}$ for some ![]() $\tau\in \mathbb{H}$.
$\tau\in \mathbb{H}$.
ALias with ![]() $\Gamma=C_{N}\subset t(T),\,\, N\in {\mathbb{Z}}_{\geqslant 1}$
$\Gamma=C_{N}\subset t(T),\,\, N\in {\mathbb{Z}}_{\geqslant 1}$
Fix a complex torus ![]() $T={\mathbb{C}}/{\mathbb{Z}}\oplus{\mathbb{Z}}\tau$ and let
$T={\mathbb{C}}/{\mathbb{Z}}\oplus{\mathbb{Z}}\tau$ and let ![]() $\sigma_{\alpha}:C_N\rightarrow \mathrm{Aut}(T)$ be given by
$\sigma_{\alpha}:C_N\rightarrow \mathrm{Aut}(T)$ be given by ![]() $\sigma_{\alpha}(r)z=z+\alpha$, where α is a N-torsion point of T. In Theorem 4, we proved that for any T it holds that
$\sigma_{\alpha}(r)z=z+\alpha$, where α is a N-torsion point of T. In Theorem 4, we proved that for any T it holds that  $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}_{\alpha}(C_N)}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}_{\alpha}(C_N)}$, regardless of the choice of
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}_{\alpha}(C_N)}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}}^{\tilde{\sigma}_{\alpha}(C_N)}$, regardless of the choice of ![]() $\rho:C_N\rightarrow\mathrm{Aut}(\mathfrak{sl}_2)$. Notice that
$\rho:C_N\rightarrow\mathrm{Aut}(\mathfrak{sl}_2)$. Notice that ![]() $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}_{\alpha}(C_N)}\cong \mathfrak{C}_{\tau'}$ for some
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}_{\alpha}(C_N)}\cong \mathfrak{C}_{\tau'}$ for some ![]() $\tau'$ such that
$\tau'$ such that ![]() $T_{(\alpha)}\cong T_{\tau'}$, where we recall that
$T_{(\alpha)}\cong T_{\tau'}$, where we recall that ![]() $T_{(\alpha)}={\mathbb{C}}/({\mathbb{Z}}+{\mathbb{Z}}\alpha+{\mathbb{Z}}\tau)$.
$T_{(\alpha)}={\mathbb{C}}/({\mathbb{Z}}+{\mathbb{Z}}\alpha+{\mathbb{Z}}\tau)$.
ALias with ![]() $\Gamma=C_2\times C_2\subset t(T)$
$\Gamma=C_2\times C_2\subset t(T)$
Theorem 6 says that for any faithful ![]() $\rho:C_{2}\times C_2\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and
$\rho:C_{2}\times C_2\rightarrow \mathrm{Aut}(\mathfrak{sl}_2)$ and ![]() $\sigma:C_2\times C_2\rightarrow \mathrm{Aut}(T)$, where
$\sigma:C_2\times C_2\rightarrow \mathrm{Aut}(T)$, where ![]() $T={\mathbb{C}}/{\Lambda}$,
$T={\mathbb{C}}/{\Lambda}$,  $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\tilde{\sigma}(C_2\times C_2)}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}']\cong \mathfrak{C}_{\frac{1}{2}{\Lambda}}$. Since the embedding of
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\tilde{\sigma}(C_2\times C_2)}\cong \mathfrak{sl}_2\otimes_{{\mathbb{C}}}{\mathbb{C}}[\wp_{\frac{1}{2}{\Lambda}},\wp_{\frac{1}{2}{\Lambda}}']\cong \mathfrak{C}_{\frac{1}{2}{\Lambda}}$. Since the embedding of ![]() $C_2\times C_2$ inside
$C_2\times C_2$ inside ![]() $\mathrm{Aut}(T)$ is unique, we have that for each
$\mathrm{Aut}(T)$ is unique, we have that for each ![]() $\Lambda$, there is precisely one aLia with base Lie algebra
$\Lambda$, there is precisely one aLia with base Lie algebra ![]() $\mathfrak{sl}_2$ and symmetry group
$\mathfrak{sl}_2$ and symmetry group ![]() $C_2\times C_2$ embedded as translations.
$C_2\times C_2$ embedded as translations.
ALias with ![]() $\Gamma =A_4$
$\Gamma =A_4$
By Theorem 7, ![]() $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(A_4)}\cong \mathfrak{O}$. In particular, this is independent of (faithful) σ and ρ.
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}(A_4)}\cong \mathfrak{O}$. In particular, this is independent of (faithful) σ and ρ.
ALias with ![]() $\Gamma=D_N, \,\, N\in {\mathbb{Z}}_{\geqslant 2}$
$\Gamma=D_N, \,\, N\in {\mathbb{Z}}_{\geqslant 2}$
In Corollary 1, we obtained ![]() $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}_{\alpha}(D_N)}\cong \mathfrak{S}_{\tau}$ for some τ such that
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}_{\alpha}(D_N)}\cong \mathfrak{S}_{\tau}$ for some τ such that ![]() $T_{(\alpha)}\cong T_{\tau}$. For N = 2, we choose the first factor of
$T_{(\alpha)}\cong T_{\tau}$. For N = 2, we choose the first factor of ![]() $C_2 \ltimes C_2$ to be a subgroup of
$C_2 \ltimes C_2$ to be a subgroup of ![]() $\mathrm{Aut}_0(T)$, as opposed to the third item in the above list (
$\mathrm{Aut}_0(T)$, as opposed to the third item in the above list (![]() $C_2\times C_2\subset t(T)$). In this case
$C_2\times C_2\subset t(T)$). In this case ![]() $(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}_{\alpha}(D_2)}\cong \mathfrak{S}_{\tau}$ for some τ.
$(\mathfrak{sl}_2\otimes_{{\mathbb{C}}}\mathcal{O}_{\mathbb{T}})^{\rho\otimes\tilde{\sigma}_{\alpha}(D_2)}\cong \mathfrak{S}_{\tau}$ for some τ.
7. Discussion
Our classification has been formulated in Theorem 1. This section provides a summary in terms of two tables, leading to Table 1, as given in the Introduction. It will also highlight some directions for further research.
To explain how one arrives at Table 1, we will recall a basic fact. We have shown in Lemma 8 that the number of branch points of ![]() $\mathbb{T}\rightarrow \mathbb{T}/\Gamma$ equals 0 if
$\mathbb{T}\rightarrow \mathbb{T}/\Gamma$ equals 0 if ![]() $\Gamma\subset t(T)$. Furthermore, this number equals 2 if
$\Gamma\subset t(T)$. Furthermore, this number equals 2 if ![]() $\Gamma\in \{C_3,C_4,C_6,A_4\}$, where the cyclic groups are subgroups of
$\Gamma\in \{C_3,C_4,C_6,A_4\}$, where the cyclic groups are subgroups of ![]() $\mathrm{Aut}_0(T)$ for a suitable T. For
$\mathrm{Aut}_0(T)$ for a suitable T. For ![]() $\Gamma=D_N\cong C_2 \ltimes C_N$ such that
$\Gamma=D_N\cong C_2 \ltimes C_N$ such that ![]() $C_2\subset \mathrm{Aut}_0(T)$, it holds that the number of branch points equals 3. We summarise our main result in Table 2.
$C_2\subset \mathrm{Aut}_0(T)$, it holds that the number of branch points equals 3. We summarise our main result in Table 2.
Table 2. Isomorphism classes of aLias for each symmetry group Γ and each number of branch points of the quotient map ![]() $\mathbb{T}\rightarrow \mathbb{T}/\Gamma$.
$\mathbb{T}\rightarrow \mathbb{T}/\Gamma$.

The columns of Table 2 are constant, so that we can summarise it further into Table 3.
Table 3. Lie algebra associated to the number of branch points of the quotient map ![]() $\mathbb{T}\rightarrow \mathbb{T}/\Gamma$.
$\mathbb{T}\rightarrow \mathbb{T}/\Gamma$.

We will present some possible directions for completing and extending the results in this paper. We know that ![]() $\mathfrak{C}_{\tau}\cong \mathfrak{C}_{\tau'}$ if and only if
$\mathfrak{C}_{\tau}\cong \mathfrak{C}_{\tau'}$ if and only if ![]() $[\tau]=[\tau']$. Settling how
$[\tau]=[\tau']$. Settling how ![]() $\mathfrak{S}_{\tau}$ breaks down into
$\mathfrak{S}_{\tau}$ breaks down into ![]() ${\mathbb{C}}$-isomorphism classes would result in a more complete classification of our result. Notice that we can interpret this question also as to what extent the algebra determines the geometry in our problem.
${\mathbb{C}}$-isomorphism classes would result in a more complete classification of our result. Notice that we can interpret this question also as to what extent the algebra determines the geometry in our problem.
An obvious extension would be to replace the base Lie algebra ![]() $\mathfrak{sl}_2$ by
$\mathfrak{sl}_2$ by ![]() ${\mathfrak{g}}$, where
${\mathfrak{g}}$, where ![]() ${\mathfrak{g}}$ is a complex semisimple Lie algebra or even reductive
${\mathfrak{g}}$ is a complex semisimple Lie algebra or even reductive ![]() ${\mathfrak{g}}$. The challenge here is to construct intertwining maps; preliminary work shows that this is possible for some classes of higher dimensional base Lie algebras but rather involved for others.
${\mathfrak{g}}$. The challenge here is to construct intertwining maps; preliminary work shows that this is possible for some classes of higher dimensional base Lie algebras but rather involved for others.
This brings us to another question. The construction of intertwiners in § 6 may appear to the reader to be somewhat ad hoc. Can the main classification theorem, Theorem 1, be also proved without constructing bases, but only using the geometry of the problem, as suggested by Table 3?
As we have pointed out in the Introduction, aLias arose in the context of integrable systems. A recent paper by Mikhailov and Bury [Reference Bury and Mikhailov7] sparks renewed interest in the construction of Lax pairs using bases of aLias of the Riemann sphere. An interesting question is to consider what kind of integrable equations can be obtained using aLias on complex tori. In our Remark 8, we have highlighted a development arising in a different context leading to the Landau–Lifshitz hierarchy [Reference Carey, Hannabuss, Mason and Singer8]. We hope that our classification allows for a systematic study of possible integrable systems associated with aLias on complex tori. This question is beyond the scope of this paper and it is research in progress.
Finally, we will make some remarks concerning the Onsager algebra. In this paper, we have realised the Onsager algebra as an aLia in flat geometry. Previously, this algebra was realised in the spherical case [Reference Roan30] and more recently also in hyperbolic geometry, cf. [Reference Knibbeler, Lombardo and Veselov5]. It would be interesting to see how the Onsager algebra can be applied in a wider variety of geometries and what role the symmetry group plays in this context.
Acknowledgements
We are grateful to Marta Mazzocco, Artie Prendergast, Jan Sanders and Alexander Veselov for very helpful and stimulating discussions. VK gratefully acknowledges support by the London Mathematical Society via an Emmy Noether fellowship. This work was supported by the Engineering and Physical Sciences Research Council (EPSRC): the work of CO is supported by the grant [EP/W522569/1]; the work of SL and VK has been in part supported by the grant [EP/V048546/1].