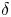1. Introduction
Have you ever wondered how many people you overlap with in a store or retail shop? This is fascinating question on its own, but it is especially important given the current COVID-19 pandemic. Much of the work on COVID-19 has focused on using deterministic compartmentalized style models to estimate the infection rate and dynamics of the spread, see for example Dandekar et al. [Reference Dandekar, Henderson, Jansen, McDonald, Moka, Nazarathy, Rackauckas, Taylor and Vuorinen2], Nguemdjo et al. [Reference Nguemdjo, Meno, Dongfack and Ventelou20], and Kaplan [Reference Kaplan14]. However, we know that stochastic effects can play an important role in determining the spread, see for example Drakopoulos et al. [Reference Drakopoulos, Ozdaglar and Tsitsiklis9], Palomo et al. [Reference Palomo, Pender, Massey and Hampshire22], Pang and Pardoux [Reference Pang and Pardoux23], Forien et al. [Reference Forien, Pang and Pardoux11], and Moein et al. [Reference Moein, Nickaeen, Roointan, Borhani, Heidary, Javanmard, Ghaisari and Gheisari19]. As shoppers crowd a store to stock up on water or large amounts of non-perishable items, it is inevitable that the virus would spread. To combat the spread of the virus, many service facilities and systems have installed new air filters and transparent barriers, and have asked that patrons wear facial masks. Moreover, these service systems also have implemented various forms of social/physical distancing in order to minimize close proximity of one customer to another Bove and Benoit [Reference Bove and Benoit1].
However, there are some places where people work or shop that limiting distance is not feasible. In this case, we really care about how much customers overlap with one another. Recently, there has been new work by Kang et al. [Reference Kang, Doroudi, Delasay and Wickeham13] and Palomo and Pender [Reference Palomo and Pender21] that explores how one can calculate the overlap times of customers in multi-server and single server queues, respectively. More specifically, Kang et al. [Reference Kang, Doroudi, Delasay and Wickeham13] show how to use the overlaps to compute a new ![]() $R_0$ value for understanding infection rates in compartmentalized epidemic models and Palomo and Pender [Reference Palomo and Pender21] prove that the overlap distribution is exponential for the M/M/1 queue and show via simulation that a similar result holds for the non-Markovian setting as well. Our analysis is important because it can demonstrate, exactly, how much overlap occurs and can provide distributional information or prediction intervals for possible overlap. Moreover, it can be used as a tool to prevent large overlaps and as a design tool to construct appropriate overlap by restricting the arrival rate or service distributions.
$R_0$ value for understanding infection rates in compartmentalized epidemic models and Palomo and Pender [Reference Palomo and Pender21] prove that the overlap distribution is exponential for the M/M/1 queue and show via simulation that a similar result holds for the non-Markovian setting as well. Our analysis is important because it can demonstrate, exactly, how much overlap occurs and can provide distributional information or prediction intervals for possible overlap. Moreover, it can be used as a tool to prevent large overlaps and as a design tool to construct appropriate overlap by restricting the arrival rate or service distributions.
In addition to understanding lightly loaded systems with our infinite server queue overlap analysis, there are many other applications where studying overlap times is essential. The first application is from queues with advanced reservations, see for example [Reference Maillardet and Taylor17]. Companies such as AirBnB, HomeAway, and Vrbo all have systems where the arrival process is an incoming stream of customer booking requests from customers and an important object of study is the maximum number of overlapping customers. Moreover, in the context of spot welding in production lines, it is known that multiple welders trying to access the same power source is detrimental to the welding process. In order to understand the interference that is caused when multiple welders are using the same power source, it is important to derive the distribution of the maximum number of overlapping welders at any given instant in a simple closed network, see for example [Reference Rumsewicz and Taylor26]. Thus, the study of overlap times is critical to developing a thorough understanding of these applications.
In this paper, we extend the overlap time analysis to the setting of the infinite server queue. At first glance, the infinite server queue analysis might not seem relevant, however, for service entities such as grocery stores, outlets, restaurants, and retail shops, an infinite server queue is quite relevant as there is not much waiting or the waiting to check out may be insignificant when compared with the shopping time. Moreover, the overlap times in the infinite server queue serve as a lower bound for the overlap times that a customer might experience in systems where there is significant waiting or in a multi-server setting. What also makes the infinite server queue important is that we are able to derive explicit formulas for the overlap distribution and residual overlap distributions as well as the number of people that a customer will overlap with during the duration of their service experience.
1.1. Contributions and organization of the paper
In Section 2, we describe the stochastic model that we will use in this work. We derive an equation for describing the overlap times for customers in the infinite server queue. We use this equation to compute the steady-state distribution of the overlap time of customers such that exactly ![]() $k-1$ other customers arrived between their arrival times. In Section 3, we compute the mean and variance of the number of customers a customer will overlap with during their time in the queue. We also show how to compute a residual version of the overlap time where a customer must overlap at least
$k-1$ other customers arrived between their arrival times. In Section 3, we compute the mean and variance of the number of customers a customer will overlap with during their time in the queue. We also show how to compute a residual version of the overlap time where a customer must overlap at least ![]() $\delta$ units of time. Finally, in Section 4, we provide a conclusion and some future research directions.
$\delta$ units of time. Finally, in Section 4, we provide a conclusion and some future research directions.
2. Infinite server overlap times
In this section, we study the infinite server queue with the intention of understanding how much time consecutive customers spend in the system together. A similar type of analysis has been completed [Reference Kang, Doroudi, Delasay and Wickeham13,Reference Palomo and Pender21] albeit in Markovian systems.
2.1. Overlap time distribution
In this section, we consider the ![]() $GI/GI/\infty$ queue starting with 0 customers at time 0. Let
$GI/GI/\infty$ queue starting with 0 customers at time 0. Let ![]() $A_i$ be the arrival time of the
$A_i$ be the arrival time of the ![]() $i$th customer and we define the inter-arrival time between the
$i$th customer and we define the inter-arrival time between the ![]() $i$th and
$i$th and ![]() $(i+1)$th customers to be
$(i+1)$th customers to be ![]() $A_{i+1} - A_i$, which are i.i.d. random variables with cumulative distribution function (cdf)
$A_{i+1} - A_i$, which are i.i.d. random variables with cumulative distribution function (cdf) ![]() $F(x)$. We also assume that
$F(x)$. We also assume that ![]() $S_i$ is the service time of the
$S_i$ is the service time of the ![]() $i$th customer and the service times are i.i.d. with cdf
$i$th customer and the service times are i.i.d. with cdf ![]() $G(x)$. In the infinite server queue, by definition, no customer will wait. Thus, the departure time for the
$G(x)$. In the infinite server queue, by definition, no customer will wait. Thus, the departure time for the ![]() $n$th customer is given by the following equation
$n$th customer is given by the following equation
We can now construct an equation for the overlap time between consecutive customers. The overlap time between the ![]() $n$th and
$n$th and ![]() $(n+k)$th customers is given by
$(n+k)$th customers is given by
 \begin{align} O_{n,n+k} & = ( \min( D_n , D_{n+k} ) - A_{n+k} )^+ \nonumber\\ & = ( \min( A_n + S_n , A_{n+k} + S_{n+k} ) - A_{n+k} )^+ \nonumber\\ & = ( (S_n - ( A_{n+k} - A_{n}) )^+{\wedge} S_{n+k} ) . \end{align}
\begin{align} O_{n,n+k} & = ( \min( D_n , D_{n+k} ) - A_{n+k} )^+ \nonumber\\ & = ( \min( A_n + S_n , A_{n+k} + S_{n+k} ) - A_{n+k} )^+ \nonumber\\ & = ( (S_n - ( A_{n+k} - A_{n}) )^+{\wedge} S_{n+k} ) . \end{align}
It is important to observe that the overlap time between the ![]() $n$th and
$n$th and ![]() $(n+k)$th customers can be decomposed into two parts. The first part (the left term in the minimum) is the time that the
$(n+k)$th customers can be decomposed into two parts. The first part (the left term in the minimum) is the time that the ![]() $n$th customer overlaps with the
$n$th customer overlaps with the ![]() $(n+k)$th customer given that the
$(n+k)$th customer given that the ![]() $n$th customer stays longer. The second part is the service time of the
$n$th customer stays longer. The second part is the service time of the ![]() $(n+k)$th customer if the service time of the
$(n+k)$th customer if the service time of the ![]() $(n+k)$th stay is shorter than the
$(n+k)$th stay is shorter than the ![]() $n$th customer's service time minus the inter-arrival time gap. We will leverage this representation when considering the steady-state overlap time and the fact that all of the random variables are independent from one another in the
$n$th customer's service time minus the inter-arrival time gap. We will leverage this representation when considering the steady-state overlap time and the fact that all of the random variables are independent from one another in the ![]() $GI/GI/\infty$ queue.
$GI/GI/\infty$ queue.
Theorem 2.1. Let ![]() $O_k$ have the steady-state distribution of
$O_k$ have the steady-state distribution of ![]() $O_{n,n+k}$ in the
$O_{n,n+k}$ in the ![]() $GI/GI/\infty$ queue, and let
$GI/GI/\infty$ queue, and let ![]() $\mathcal {S}$ and
$\mathcal {S}$ and ![]() $\tilde {\mathcal {S}}$ be two independent service times with cdf
$\tilde {\mathcal {S}}$ be two independent service times with cdf ![]() $G(x)$, then the tail distribution of
$G(x)$, then the tail distribution of ![]() $O_k = \lim _{n \to \infty } O_{n,n+k}$ is given by
$O_k = \lim _{n \to \infty } O_{n,n+k}$ is given by
where ![]() $h_k(x)$ is the density of the sum of
$h_k(x)$ is the density of the sum of ![]() $k$ i.i.d. inter-arrival times.
$k$ i.i.d. inter-arrival times.
Proof. First, we need to decompose the overlap probability into two probabilities by using a property of the minimum of two independent random variables, that is,
 \begin{align*} \mathbb{P} ( O_{k} \gt t) & = \mathbb{P} ( ( (\mathcal{S} - \mathcal{A}_k )^+{\wedge} \tilde{\mathcal{S}}) \gt t ) \\ & = \mathbb{P} ( (\mathcal{S} - \mathcal{A}_k )^+{\gt} t ) \cdot \mathbb{P} ( \tilde{\mathcal{S}} \gt t ) \\ & = \mathbb{P} ( (\mathcal{S} -\mathcal{A}_k )^+{\gt} t ) \cdot \overline{G}(t) \\ & = \overline{G}(t) \int^{\infty}_{0}\mathbb{P} ( \mathcal{S} \gt t + x ) h_k(x) \,dx \\ & = \overline{G}(t) \int^{\infty}_{0}\overline{G}( t + x ) h_k(x) \,dx . \end{align*}
\begin{align*} \mathbb{P} ( O_{k} \gt t) & = \mathbb{P} ( ( (\mathcal{S} - \mathcal{A}_k )^+{\wedge} \tilde{\mathcal{S}}) \gt t ) \\ & = \mathbb{P} ( (\mathcal{S} - \mathcal{A}_k )^+{\gt} t ) \cdot \mathbb{P} ( \tilde{\mathcal{S}} \gt t ) \\ & = \mathbb{P} ( (\mathcal{S} -\mathcal{A}_k )^+{\gt} t ) \cdot \overline{G}(t) \\ & = \overline{G}(t) \int^{\infty}_{0}\mathbb{P} ( \mathcal{S} \gt t + x ) h_k(x) \,dx \\ & = \overline{G}(t) \int^{\infty}_{0}\overline{G}( t + x ) h_k(x) \,dx . \end{align*}
This completes the proof.
Corollary 2.2. Let ![]() $O_k$ have the steady-state distribution of
$O_k$ have the steady-state distribution of ![]() $O_{n,n+k}$ in the
$O_{n,n+k}$ in the ![]() $GI/M/\infty$ queue with service rate
$GI/M/\infty$ queue with service rate ![]() $\mu$ and let
$\mu$ and let ![]() $\mathcal {A}_1$ be an inter-arrival time. Then, the tail distribution of
$\mathcal {A}_1$ be an inter-arrival time. Then, the tail distribution of ![]() $O_k = \lim _{n \to \infty } O_{n,n+k}$ is given by
$O_k = \lim _{n \to \infty } O_{n,n+k}$ is given by
It is clear from this result that the functional form of the tail distribution of the overlap time is given by the service time distribution, which is exponential in this case. The inter-arrival times do not impact the decay rate of the tail distribution, which implies that it does not depend on the time parameter ![]() $t$. Moreover, the inter-arrival time distribution only emerges as a constant that determines how many of the overlap times are zero. Thus, the service time governs the tail behavior of the overlap time while the inter-arrival distribution controls the probability of a specific overlap time being equal to zero.
$t$. Moreover, the inter-arrival time distribution only emerges as a constant that determines how many of the overlap times are zero. Thus, the service time governs the tail behavior of the overlap time while the inter-arrival distribution controls the probability of a specific overlap time being equal to zero.
3. Computing the number of overlaps
In addition to knowing how much time consecutive customers will spend together in a service system, it is important to also know how many customers one expects to overlap with. In the context of epidemics, the more customers that one actually overlaps with the greater chance that one might contract the disease. In this section, we restrict our analysis to that of the ![]() $M_t/G/\infty$ queue and leverage results from Eick et al. [Reference Eick, Massey and Whitt10] to compute the exact distribution of overlapping customers. In what follows, we assume without loss of generality that all queues start with zero customers. Under this assumption, we know that the number in the
$M_t/G/\infty$ queue and leverage results from Eick et al. [Reference Eick, Massey and Whitt10] to compute the exact distribution of overlapping customers. In what follows, we assume without loss of generality that all queues start with zero customers. Under this assumption, we know that the number in the ![]() $M_t/G/\infty$ queue at time
$M_t/G/\infty$ queue at time ![]() $t$ is given by the following expression
$t$ is given by the following expression
 $$Q(t) = \sum_{j=1}^{N(t)} \{A_j \lt t \lt A_j + S_j\},$$
$$Q(t) = \sum_{j=1}^{N(t)} \{A_j \lt t \lt A_j + S_j\},$$
where ![]() $N(t)$ is the number of arrivals in the interval
$N(t)$ is the number of arrivals in the interval ![]() $(0,t]$ and we define
$(0,t]$ and we define ![]() $\{ \mathcal {A} \}$ as an indicator function of the set
$\{ \mathcal {A} \}$ as an indicator function of the set ![]() $\mathcal {A}$. Thus, the number of customers in the system at the time of arrival of the
$\mathcal {A}$. Thus, the number of customers in the system at the time of arrival of the ![]() $k$th customer is given by
$k$th customer is given by
 $$Q(A_{k}-) = \sum_{j=1}^{N(A_{k}-)} \{A_j \lt A_{k} \lt A_j + S_j\}.$$
$$Q(A_{k}-) = \sum_{j=1}^{N(A_{k}-)} \{A_j \lt A_{k} \lt A_j + S_j\}.$$
In order to compute the total number of overlapping customers, we also need to calculate the number of customers that arrive during the service time of the ![]() $k$th customer, which is
$k$th customer, which is
Adding the number of customers upon arrival and the number that arrive during service, we arrive at an expression for ![]() $M_k$, the total number of customers that the
$M_k$, the total number of customers that the ![]() $k$th customer will overlap with.
$k$th customer will overlap with.
 \begin{equation} M_k = N(A_{k} + S_k) - N(A_{k}) + \sum_{j=1}^{N(A_{k}-)} \{A_j \lt A_{k} \lt A_j + S_j\} . \end{equation}
\begin{equation} M_k = N(A_{k} + S_k) - N(A_{k}) + \sum_{j=1}^{N(A_{k}-)} \{A_j \lt A_{k} \lt A_j + S_j\} . \end{equation}
Theorem 3.1. The mean number of overlaps for the ![]() $k$th arrival in the
$k$th arrival in the ![]() $M/G/\infty$ queue is equal to
$M/G/\infty$ queue is equal to
 $$\mathbb{E}[M_k] = \lambda \mathbb{E}[ \mathcal{S} ] + \sum_{j=1}^{k-1} \frac{\lambda^{k-j} }{\Gamma(k-j)}\int^{\infty}_{0} \overline{G}(x) e^{-\lambda x} x^{k-j-1} \,dx .$$
$$\mathbb{E}[M_k] = \lambda \mathbb{E}[ \mathcal{S} ] + \sum_{j=1}^{k-1} \frac{\lambda^{k-j} }{\Gamma(k-j)}\int^{\infty}_{0} \overline{G}(x) e^{-\lambda x} x^{k-j-1} \,dx .$$
Proof.
 \begin{align*} \mathbb{E}[M_k] & = \mathbb{E}[ N(A_{k} + S_k) - N(A_{k}) ] + \mathbb{E}\left[\sum_{j=1}^{N(A_{k}-)} \{A_j \lt A_{k} \lt A_j + S_j\} \right] \\ & = \lambda \mathbb{E}[ \mathcal{S} ] + \mathbb{E}\left[\sum_{j=1}^{k-1} \{A_j \lt A_{k} \lt A_j + S_j\} \right]\\ & = \lambda \mathbb{E}[\mathcal{S} ] + \sum_{j=1}^{k-1} \mathbb{E} [ \overline{G}( A_k - A_j)] \\ & = \lambda \mathbb{E}[ \mathcal{S} ] + \sum_{j=1}^{k-1} \frac{\lambda^{k-j} }{\Gamma(k-j)}\int^{\infty}_{0} \overline{G}(x) e^{-\lambda x} x^{k-j-1} \,dx. \end{align*}
\begin{align*} \mathbb{E}[M_k] & = \mathbb{E}[ N(A_{k} + S_k) - N(A_{k}) ] + \mathbb{E}\left[\sum_{j=1}^{N(A_{k}-)} \{A_j \lt A_{k} \lt A_j + S_j\} \right] \\ & = \lambda \mathbb{E}[ \mathcal{S} ] + \mathbb{E}\left[\sum_{j=1}^{k-1} \{A_j \lt A_{k} \lt A_j + S_j\} \right]\\ & = \lambda \mathbb{E}[\mathcal{S} ] + \sum_{j=1}^{k-1} \mathbb{E} [ \overline{G}( A_k - A_j)] \\ & = \lambda \mathbb{E}[ \mathcal{S} ] + \sum_{j=1}^{k-1} \frac{\lambda^{k-j} }{\Gamma(k-j)}\int^{\infty}_{0} \overline{G}(x) e^{-\lambda x} x^{k-j-1} \,dx. \end{align*}
This completes the proof.
Corollary 3.2. When the service distribution is given by an exponential with rate ![]() $\mu$, we have that the mean number of overlaps for the
$\mu$, we have that the mean number of overlaps for the ![]() $k$th arrival is equal to
$k$th arrival is equal to
 $$\mathbb{E}[M_k] = \frac{\lambda}{\mu} + \frac{\lambda}{\mu} \cdot \left( 1 - \left( \frac{\lambda}{\lambda +\mu} \right)^{k-1} \right) .$$
$$\mathbb{E}[M_k] = \frac{\lambda}{\mu} + \frac{\lambda}{\mu} \cdot \left( 1 - \left( \frac{\lambda}{\lambda +\mu} \right)^{k-1} \right) .$$
It is important to note that the total number of overlapping customers for the ![]() $k$th arrival can be only computed when the
$k$th arrival can be only computed when the ![]() $k$th arrival departs the queue and it is not known at the time of arrival. Thus, the representation of Eq. (2) for the number of overlaps provides a methodology for computing the number of overlaps for each customer via simulation. However, this representation is customer-centered and not time-centered. In what follows, we provide a time-centered perspective of the number of overlaps.
$k$th arrival departs the queue and it is not known at the time of arrival. Thus, the representation of Eq. (2) for the number of overlaps provides a methodology for computing the number of overlaps for each customer via simulation. However, this representation is customer-centered and not time-centered. In what follows, we provide a time-centered perspective of the number of overlaps.
If a customer arrives at time ![]() $t$, then we define
$t$, then we define ![]() $O(t)$ as the number of customers that the arriving customer will overlap with.
$O(t)$ as the number of customers that the arriving customer will overlap with. ![]() $O(t)$ has the following expression
$O(t)$ has the following expression
where ![]() $\mathcal {S}$ is a generic service time, which is independent of the arrival process.
$\mathcal {S}$ is a generic service time, which is independent of the arrival process.
It is important to note here that the number of overlapping customers ![]() $O(t)$ is not completely known at time
$O(t)$ is not completely known at time ![]() $t$. It is only fully known after the service of the customer that arrives at time
$t$. It is only fully known after the service of the customer that arrives at time ![]() $t$. However, we can use the expression of
$t$. However, we can use the expression of ![]() $O(t)$ to compute the distribution of the number of customers that an arrival will overlap with at time
$O(t)$ to compute the distribution of the number of customers that an arrival will overlap with at time ![]() $t$. In this way, it is time-centered as the expression depends on time and not the specific number of the customer arriving. In addition to knowing the exact number of customers, an arrival at time
$t$. In this way, it is time-centered as the expression depends on time and not the specific number of the customer arriving. In addition to knowing the exact number of customers, an arrival at time ![]() $t$ would overlap with for each sample path, we can also describe the distribution of the number of customers that an arrival at time
$t$ would overlap with for each sample path, we can also describe the distribution of the number of customers that an arrival at time ![]() $t$ would overlap. One important ingredient to describing the exact distribution is knowing that the number of customers upon arrival is independent of the number of arrivals that arrive during service. We provide the exact distribution in the following theorem.
$t$ would overlap. One important ingredient to describing the exact distribution is knowing that the number of customers upon arrival is independent of the number of arrivals that arrive during service. We provide the exact distribution in the following theorem.
Theorem 3.3. The distribution of overlapping customers for a customers arriving at time ![]() $t$ in the
$t$ in the ![]() $M_t/G/\infty$ queue is
$M_t/G/\infty$ queue is
 $$O(t) \stackrel{D}{=} {\rm Poisson} \left( \int^{t+\mathcal{S}}_{t}\lambda(s)\,ds + \int^{t}_{0} \lambda(u) \overline{G}(t-u) \,du \right) .$$
$$O(t) \stackrel{D}{=} {\rm Poisson} \left( \int^{t+\mathcal{S}}_{t}\lambda(s)\,ds + \int^{t}_{0} \lambda(u) \overline{G}(t-u) \,du \right) .$$
This result follows easily from the representation given in Eq. (2).
Corollary 3.4. The overlap distribution at time ![]() $t$ in the
$t$ in the ![]() $M/M/\infty$ queue is equal to
$M/M/\infty$ queue is equal to
and ![]() $O(t)$ can be decomposed into a sum of geometric and Poisson random variables, that is,
$O(t)$ can be decomposed into a sum of geometric and Poisson random variables, that is,
where ![]() $q(t) = \lambda \int ^{t}_{0} \overline {G}(t-u)\, du$.
$q(t) = \lambda \int ^{t}_{0} \overline {G}(t-u)\, du$.
In addition to understanding the distribution of the number of overlapping customers at any point in time, one might be interested in counting the number of customers that overlap by at least ![]() $\delta$ amount of time. In this case, we can define the thinned arrival process counting only the customers with service times that exceed
$\delta$ amount of time. In this case, we can define the thinned arrival process counting only the customers with service times that exceed ![]() $\delta$ so
$\delta$ so ![]() $\lambda _\delta (t) = \lambda (t) \cdot \overline {G}(\delta )$ and
$\lambda _\delta (t) = \lambda (t) \cdot \overline {G}(\delta )$ and ![]() $\overline {G}_\delta (x) = G(x)/ G(\delta )$ for
$\overline {G}_\delta (x) = G(x)/ G(\delta )$ for ![]() $x \geq \delta$. Then, the thinned process
$x \geq \delta$. Then, the thinned process ![]() $O(t,\delta )$ has the same distribution as Eq. (3.4) where
$O(t,\delta )$ has the same distribution as Eq. (3.4) where ![]() $\mathcal {S}$ is replaced by
$\mathcal {S}$ is replaced by ![]() $(\mathcal {S}-\delta )^+$,
$(\mathcal {S}-\delta )^+$, ![]() $\lambda$ is replaced by
$\lambda$ is replaced by ![]() $\lambda _\delta$, and
$\lambda _\delta$, and ![]() $G(x)$ is replaced by
$G(x)$ is replaced by ![]() $G_\delta (x)$.
$G_\delta (x)$.
4. Conclusion and future work
In this paper, we consider the overlap times for customers in an infinite server queue. The infinite server model is appropriate in retail settings where the time a customer waits is small relative to their shopping experience. We derive the steady-state distribution for the overlap time of customers that are ![]() $k$ arrivals apart. We also compute explicitly the distribution of the number of customers that a randomly arriving customer will overlap with as the sum of a Poisson random variable and Poisson with a random arrival rate. Finally, we compute an expression for the number of customers that a random arrival will overlap at least
$k$ arrivals apart. We also compute explicitly the distribution of the number of customers that a randomly arriving customer will overlap with as the sum of a Poisson random variable and Poisson with a random arrival rate. Finally, we compute an expression for the number of customers that a random arrival will overlap at least ![]() $\delta$ time units. We compute the mean and variance for this quantity and are able to provide a prediction interval for a randomly arriving customer at any time. Our analysis has implications for understanding the interaction time between customers in a pandemic setting and sheds light on the interactions of customers.
$\delta$ time units. We compute the mean and variance for this quantity and are able to provide a prediction interval for a randomly arriving customer at any time. Our analysis has implications for understanding the interaction time between customers in a pandemic setting and sheds light on the interactions of customers.
Despite our analysis, there are many avenues for additional research. First, we would like to complete our analysis by analyzing the ![]() $G/G/\infty$ queue in explicit detail. Issues like dependent arrivals or service times like in Pang and Whitt [Reference Pang and Whitt24,Reference Pang and Whitt25], Daw and Pender [Reference Daw and Pender5,Reference Daw and Pender6], Koops et al. [Reference Koops, Boxma and Mandjes15,Reference Koops, Saxena, Boxma and Mandjes16], and Daw et al. [Reference Daw, Castellanos, Yom-Tov, Pender and Gruendlinger3] would be interesting to explore as well. Second, we would like to extend our analysis to more complicated queueing systems like the Erlang-A, see for example Daw and Pender [Reference Daw and Pender7], Massey and Pender [Reference Massey and Pender18], and Hampshire et al. [Reference Hampshire, Bao, Lasecki, Daw and Pender12] where customers can abandon the system. Abandoning customers clearly reduces the number of overlapping customers, but by how much? It would also be great to extend our analysis to queueing systems with batch arrivals. In this case, the scaled Poisson decomposition of Daw and Pender [Reference Daw and Pender8] and Daw et al. [Reference Daw, Fralix and Pender4] might be helpful in replicating our analysis in the batch setting. Finally, we would like to extend our analysis to spatial point processes and think about the overlap in terms of not only time, number, but spatial distance as well.
$G/G/\infty$ queue in explicit detail. Issues like dependent arrivals or service times like in Pang and Whitt [Reference Pang and Whitt24,Reference Pang and Whitt25], Daw and Pender [Reference Daw and Pender5,Reference Daw and Pender6], Koops et al. [Reference Koops, Boxma and Mandjes15,Reference Koops, Saxena, Boxma and Mandjes16], and Daw et al. [Reference Daw, Castellanos, Yom-Tov, Pender and Gruendlinger3] would be interesting to explore as well. Second, we would like to extend our analysis to more complicated queueing systems like the Erlang-A, see for example Daw and Pender [Reference Daw and Pender7], Massey and Pender [Reference Massey and Pender18], and Hampshire et al. [Reference Hampshire, Bao, Lasecki, Daw and Pender12] where customers can abandon the system. Abandoning customers clearly reduces the number of overlapping customers, but by how much? It would also be great to extend our analysis to queueing systems with batch arrivals. In this case, the scaled Poisson decomposition of Daw and Pender [Reference Daw and Pender8] and Daw et al. [Reference Daw, Fralix and Pender4] might be helpful in replicating our analysis in the batch setting. Finally, we would like to extend our analysis to spatial point processes and think about the overlap in terms of not only time, number, but spatial distance as well.
We are also interested in knowing the overlap distribution for more than two customers. For example, if one considers the overlap time of three customers ![]() $(n,n+j,n+k)$ where
$(n,n+j,n+k)$ where ![]() $1 \leq j \lt k$, then one obtains the following overlap time for the
$1 \leq j \lt k$, then one obtains the following overlap time for the ![]() $n$th,
$n$th, ![]() $(n+j)$th, and the
$(n+j)$th, and the ![]() $(n+k)$th customers as
$(n+k)$th customers as
 \begin{align*} O_{n,n+j,n+k} & = ( \min( D_n , D_{n+j}, D_{n+k} ) - A_{n+k} )^+ \\ & = ( \min( A_n +S_n , A_{n+j} + S_{n+j}, A_{n+k} + S_{n+k} ) - A_{n+k} )^+ \\ & = (S_n + A_{n} - A_{n+k} )^+\boldsymbol{\wedge} (S_{n+j} + A_{n+j} - A_{n+k} )^+ \boldsymbol{\wedge} S_{n+k} \\ & = (S_n + A_{n} - A_{n+k} )^+ \boldsymbol{\wedge} (S_{n+j} + A_n + (A_{n+j} - A_n) - A_{n+k} )^+ \boldsymbol{\wedge} S_{n+k} . \end{align*}
\begin{align*} O_{n,n+j,n+k} & = ( \min( D_n , D_{n+j}, D_{n+k} ) - A_{n+k} )^+ \\ & = ( \min( A_n +S_n , A_{n+j} + S_{n+j}, A_{n+k} + S_{n+k} ) - A_{n+k} )^+ \\ & = (S_n + A_{n} - A_{n+k} )^+\boldsymbol{\wedge} (S_{n+j} + A_{n+j} - A_{n+k} )^+ \boldsymbol{\wedge} S_{n+k} \\ & = (S_n + A_{n} - A_{n+k} )^+ \boldsymbol{\wedge} (S_{n+j} + A_n + (A_{n+j} - A_n) - A_{n+k} )^+ \boldsymbol{\wedge} S_{n+k} . \end{align*}
Unlike the two customer situation, it is clear here that the random variables are not independent anymore. This presents a new issue that must be resolved in future work.
Acknowledgments
J.P. would like to acknowledge the gracious support of the National Science Foundation DMS Award # 2206286. S.P. would like to acknowledge the gracious support of the Sloan Foundation for supporting his graduate studies.