No CrossRef data available.
Article contents
A novel morphing soft robot design to minimize deviations
Published online by Cambridge University Press: 10 October 2024
Abstract
Soft robotics is rapidly advancing, particularly in medical device applications. A particular miniaturized manipulator design that offers high dexterity, multiple degrees-of-freedom, and better lateral force rendering than competing designs, has great potential for minimally invasive surgery. However, it faces challenges such as the tendency to suddenly and unpredictably deviate in bending plane orientation at higher pressures. In this work, we identified the cause of this deviation as the buckling of the partition wall and proposed design alternatives along with their manufacturing process to address the problem without compromising the original design features. In both simulation and experiment, the novel design managed to achieve a better bending performance in terms of stiffness and reduced deviation of the bending plane. We also developed an artificial neural network-based inverse kinematics model to further improve the performance of the prototype during vectorization. This approach yielded mean absolute errors in orientation of the bending plane below 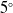 $5^{\circ }$.
$5^{\circ }$.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press


