2.1. Human understanding of complex systems

Studies in measuring human understanding of emergent systems with micro-/macrolevels have demonstrated that misunderstandings of emergent behaviors (e.g., diffusive fluid flow) are more strongly held than misunderstandings of direct behaviors (e.g., blood flow in the circulatory system) (Chi Reference Chi2005). People who lack understanding of emergent systems often have fragmented system understandings, such as being able to understand aspects of component behaviors but not how they relate across scales. Most commonly, this fragmented understanding occurs through attempts to explain emergent systems as direct processes, rather than distributed behaviors. Studies comparing expert and novice understandings of ecosystems and lungs have demonstrated that experts have greater understandings of behaviors within and across levels, which enables them to more effectively reason about how perturbations affect system functioning (Hmelo-Silver et al. Reference Hmelo-Silver, Marathe and Liu2007). Such findings are relevant to design problems because engineers must be capable of effectively manipulating a system and its components toward a desirable goal state. These considerations can significantly aid in human design endeavors concerning parametric design, which is known to be difficult for humans even when only a few coupled parameters are involved (Hirschi & Frey Reference Hirschi and Frey2002). Typically, humans find success in these systems when approaching them utilizing simple decision-making rules, such as manipulating one variable at a time while leaving other design variables constant (Kuhn et al. Reference Kuhn, Iordanou, Pease and Wirkala2008). Using these strategies, designers may be able to effectively learn and make decisions that improve design outcomes (Egan et al. Reference Egan, Cagan, Schunn and LeDuc2015a ).

2.2. Software interfaces for engineering design

Past engineering design interfaces have been constructed to address the challenges of complex systems design, especially the need to consider multiple objectives in searches with visualizations (Zhang et al. Reference Zhang, Simpson, Frecker and Lesieutre2012; Woodruff et al. Reference Woodruff, Reed and Simpson2013) and trade-offs in multi-dimensional and multivariate data (German et al. Reference German, Feigh and Daskilewicz2013). Progress in effective GUI approaches is relevant to design because engineers must be capable of effectively manipulating a system and its components toward a desirable goal state—an effective GUI should enable the engineer to learn essential aspects of complex systems that aid in design. One successful GUI approach utilized the parameterization of designs such that engineers could manipulate design variables to design a system toward an optimal state (Simpson et al. Reference Simpson, Frecker, Barton and Rothrock2007), which is a strategy adopted in this present study. This study expands on the findings from these previous studies through considering systems that are highly stochastic in nature with multiple outputs. These systems are then communicated to users via an agent-based simulation rendering that can provide parametric insights to a user in addition to behavior concerning the structures, behaviors, and functions of a system (Vattam et al. Reference Vattam, Goel, Rugaber, Hmelo-Silver, Jordan, Gray and Sinha2011). Such an approach of including cognitive considerations in the GUI design is similar to previous engineering interfaces for investigating design trade-offs that pinpoint designs based on human cognitive principles (Li & Gunal Reference Li and Gunal2012). There is also a need for modeling complex biological systems, as evidenced by recent GUIs developed for cell and gene modeling in synthetic biology contexts, which could contribute to engineering design of bio-based technologies (Villalobos et al. Reference Villalobos, Ness, Gustafsson, Minshull and Govindarajan2006; Chandra, Bergmann & Sauro Reference Chandra, Bergmann and Sauro2009). These recent synthetic biology interfaces motivate the need for an effective GUI approach for myosin-based complex systems as they are mechanical in nature, which contrasts with these past bio-based GUI approaches that have concentrated on biochemical system modeling.

2.3. Agent-based simulations as teaching supports

Inter-level causal mechanisms can be learned through software tools, such as agent-based simulations, which is demonstrated in studies focusing on users’ understanding of multi-level phenomena relating to fluid diffusion (Chi et al. Reference Chi, Roscoe, Slotta, Roy and Chase2012) and aquarium ecosystems (Vattam et al. Reference Vattam, Goel, Rugaber, Hmelo-Silver, Jordan, Gray and Sinha2011; Jordan et al. Reference Jordan, Hmelo-Silver, Liu and Gray2013). Agent-based simulations, in this context, operate through graphically rendering the actions of independent autonomous computational objects in a virtual environment representative of a physical system (Dessalles, Ferber & Phan Reference Dessalles, Ferber and Phan2008). These simulations are particularly well-suited for representing multi-level phenomena because individual agents can represent the bottom-most level of a system, such as molecules in the case of fluid diffusion. Agents then perform actions during each simulation step according to rule-based logic, and the results of their interactions may produce recognizable patterns of global emergent behavior, such as two liquids mixing. One of the greatest benefits of agent-based simulations is that users can manipulate a system by altering parameters among agents and receive visual feedback of emergent behaviors, which greatly supports understanding of complex multi-level systems and may be extendible to aiding in the design of complex bio-based systems.

2.4. Animations as teaching supports

Medical education has had great success in utilizing animations for learning, which present an alternate route for utilizing software tools to maximize learning in comparison to agent-based methods (Ruiz, Cook & Levinson Reference Ruiz, Cook and Levinson2009; Van Merriënboer & Sweller Reference Van Merriënboer and Sweller2010). Animations can present users with the critical information they need to learn, rather than requiring them to actively search and manipulate a system while learning. Animations are more effective when optimized through cognitive load theory (Van Merriënboer & Sweller Reference Van Merriënboer and Sweller2010), which suggests that a user has a restricted amount of information that they can accommodate at a time, due to possessing a limited amount of working memory. To optimize learning, intrinsic cognitive load (i.e., complexity of information in the given problem that must be processed) and extrinsic cognitive load (i.e., any information that does not contribute to learning) should be minimized while germane cognitive load (i.e., the resources a user has for learning and building of cognitive schemas) is maximized. In the case of myosin systems where two contrasting global behaviors may emerge, side-by-side animations are possibly an effective tool (Alfieri, Nokes-Malach & Schunn Reference Alfieri, Nokes-Malach and Schunn2013) because they reduce cognitive load as a user no longer has to compare the current state of a system to a representation in their working memory, as required in agent-based learning environments.

2.5. Emergent behaviors of myosin systems

Myosins are nanoscale motor proteins that often work in groups to mechanically drive emergent behavior in biological systems (Howard Reference Howard2001). Individual myosins operate by converting chemical to mechanical energy and stochastically attaching and detaching to an actin protein filament they propel—the propulsion of the filament is essential for contracting muscles or moving molecules across locations. The emergent propulsion behavior depends on how often at least one myosin in a system is attached to the protein filament it is propelling; during periods of time when at least one myosin is attached, the filament is assumed to translate due to the myosin exerting force on the filament, but during times when no myosins are attached, the filament remains static (Harada et al. Reference Harada, Sakurada, Aoki, Thomas and Yanagida1990; Egan et al. Reference Egan, Moore, Schunn, Cagan and LeDuc2015b ).

A general finding from biological studies (that may also be considered an engineering heuristic) suggests that a filament has continuous emergent behavior when the probability that at least one myosin is attached, $P_{\mathit{att}}$ , is greater than 90%, which generally occurs when at least two myosins are attached to a filament on average (Harada et al. Reference Harada, Sakurada, Aoki, Thomas and Yanagida1990). This heuristic implies that emergent translation behavior may be considered continuous when $P_{\mathit{att}}>90\%$ and intermittent when $P_{\mathit{att}}<90\%$ , thus presenting two contrasting systems level behaviors. In intermittent systems, the time-average velocity of the system is much lower than the instantaneous velocity of the filament because of the many periods of time when no translation is occurring—filament translation occurs less frequently for lower values of $P_{\mathit{att}}$ . These assumptions are only valid for myosin systems that operate in a highly viscous environment; in low viscosity environments, the system terminates due to diffusion when myosins do not maintain contact with actin. The contrast in time-average velocity for continuous and intermittent systems is illustrated graphically with our agent-based simulation (Egan et al. Reference Egan, Cagan, Schunn and LeDuc2013, Reference Egan, Moore, Schunn, Cagan and LeDuc2015b ) in Figure 1. In the agent-based simulation, myosins obey stochastic rules that enable their chemical and mechanical interactions with an actin filament in a virtual environment.

Figure 1. Simulated (A) continuous and (B) intermittent myosin filament translation. Each frame consists of an actin filament and myosins anchored on a microscope slide. Animations are available at http://youtu.be/BEqoOBddteI.

These emergent behaviors present an interesting design challenge, namely that design parameters have different influences on performance based on the emergent behavior of the system (Egan et al. Reference Egan, Cagan, Schunn and LeDuc2013, Reference Egan, Moore, Schunn, Cagan and LeDuc2015b ). For instance, designing myosins with higher chances of attaching to a filament has little effect on time-average system velocity when emergent behavior is continuous, but greatly increases time-average velocity for intermittent systems because at least one myosin is attached more often. Therefore, the ability to recognize a system’s emergent behavior and understand effects of design variables on performance within and across levels may greatly improve a human designer’s proficiency in optimizing these systems.

2.6. Myosin modeling and design

Biological studies have demonstrated techniques for synthetically altering myosins (Manstein Reference Manstein2004), which affect their mechanical (Anson et al. Reference Anson, Geeves, Kurzawa and Manstein1996) and chemical (Murphy & Spudich Reference Murphy and Spudich1998) behaviors, and we recently developed engineering models for exploring the optimization of myosin systems (Egan et al. Reference Egan, Cagan, Schunn and LeDuc2013, Reference Egan, Cagan, Schunn and LeDuc2015a ). In our model, myosins were represented through a structure–behavior–function paradigm, which required design of individual myosin structures to be followed by agent-based simulations that recreated their behaviors in order to predict global performance (i.e., function). Three myosin design parameters were considered: (1) a myosin’s lever arm length $\boldsymbol{l}$ , (2) a myosin’s attachment rate $\boldsymbol{k}_{\mathit{on}}$ , and (3) a myosin’s detachment rate $\boldsymbol{k}_{\mathit{off}}$ , in addition to the number of myosins $N_{\mathit{myo}}$ interacting with a filament. It was found that each parameter has unique effects on performance, for metrics including system velocity, energy use, and the average number of attached myosins. The agent-based simulations agreed with predictions from mathematical models and were suggested to offer a more complete perspective for how changes in myosin structures and behavior affect emergent system performance. Therefore, it is possible that users exposed to agent-based simulations could learn inter-level relationships that extend beyond basic input/output parametric models where underlying behavior is obscured.

2.7. Myosin-based design with GUIs

Parametric modeling of myosin design inputs and influences was analyzed in our past GUI studies to assess engineering students’ capabilities in searching for optimal solutions in myosin design tasks (Egan et al. Reference Egan, Cagan, Schunn and LeDuc2015a ) (Figure 2). Details are presented here because we adapt those tools in the current study. In the prior study, the maximum values for each input were a myosin lever arm length $\boldsymbol{l}$ of 20 nm, myosin attachment rate $\boldsymbol{k}_{\mathit{on}}$ of $4000~\text{s}^{-1}$ , myosin detachment rate $\boldsymbol{k}_{\mathit{off}}$ of $2000~\text{s}^{-1}$ , and a maximum number of myosins $\boldsymbol{n}_{\mathit{myo}}$ of 100. The lever arm, attachment rate, and detachment rate were represented in a non-dimensionalized quantity to avoid overly confusing units and values for users unfamiliar with the system. These variables were weighted from 0.2 to 1.0 of the parameter’s maximum value according to the five possible input possibilities tied to each slider. The sliders were tuned such that a user increasing a slider input linearly resulted in its corresponding myosin design input increasing linearly (e.g., if a slider was at its lowest value of 0.2 and then moved to its value of 0.8, and the corresponding myosin input was lever arm length, it would increase from 4 to 16 nm). Because there were four sliders and five input positions for each slider, 625 designs were possible, which is a fairly complex search space for a user who is limited by time and number of total design evaluations. As a user searched for an optimal design, their search was recorded on plots and tabulated for easy reference.

Figure 2. Myosin GUI with demonstration available at http://youtu.be/fJTZX1JfRXw.

The resulting design space was quite difficult for users to navigate when considering the counter-intuitive parameter interactions present and limited time a user had to search the space during our timed user studies (users were allowed to input only ten designs). The feedback provided from the GUI improved users’ design proficiency; however, users still improved their design less often than expected by random chance. The study also demonstrated that users did not learn parametric relationships across problems. Users had improved performance when the GUI enforced the utilization of greedy search logic according to relationships learned while solving a given optimization problem, thus suggesting that parametric knowledge is beneficial to solving design problems.

3.1. Aims for investigating proposed cognitive model

Our goals are to investigate from a cognitive perspective how engineers may learn information to improve their parametric and multi-level understanding of a system, and whether such understanding translates to improved design proficiency. Our past myosin GUI study empirically demonstrates that users may be capable of obtaining parametric knowledge and implementing it within a design problem for improved performance (Egan et al. Reference Egan, Cagan, Schunn and LeDuc2015a ). Additionally, past studies with our agent-based simulations have suggested that they could improve a user’s proficiency in reasoning across levels (Egan et al. Reference Egan, Cagan, Schunn and LeDuc2013), which is supported by findings from other cognitive studies of agent-based learning supports for aquarium ecosystems (Vattam et al. Reference Vattam, Goel, Rugaber, Hmelo-Silver, Jordan, Gray and Sinha2011; Jordan et al. Reference Jordan, Hmelo-Silver, Liu and Gray2013). These prior studies did not examine whether inter-level understanding improves a user’s ability to design a system. We therefore propose a cognitive-based model for how human design proficiency could be improved through exposure to differing GUIs that emphasize the learning of parametric design relationships or inter-level causal mechanisms. Through having two GUIs with different types of information presented and measurements of the understanding gained by each user, it is possible to study how each type of information contributes to design proficiency.

In particular, to test parametric learning effects, a GUI could enable users to explore and learn the parametric relationships among design variables by demonstrating how inputs affect performance outputs through graphical changes across many plots in a chart-oriented interface similar to the GUI in Figure 2. To test inter-level learning effects, a GUI could enable user discovery of how changes in design inputs affect intermittent and continuous global system behaviors through an animation-oriented interface, where users could change design inputs and receive visual feedback of how myosin behavior changes in an agent-based rendering akin to Figure 1. Both of these types of reasoning are then expected to lead to improved optimization design task proficiency as suggested by the cognitive-based model shown in Figure 3. It describes how strategies in presenting different information via GUIs enables different types of learning that may result in improved design proficiency.

Figure 3. Cognitive-based model for how differing GUIs enable learning that aids design.

In Figure 3, large arrows indicate the primary learning tracks targeted by each GUI interface. However, it is difficult to completely decouple these types of learning from each other as the exposure to charts could improve a user’s understanding of inter-level causal mechanisms or the exposure to animations could improve a user’s learning of parametric design relationships (as indicated by the small arrows). Because each GUI presents different forms of information to a user, it is essential to conduct multiple types of measurements at multiple points in time to determine the types of learning that take place throughout the study and how they affect design outcomes. A challenge in our development of hypotheses and testing is to determine the effect of these phenomena through separate assessments of optimization design task proficiency and a user’s learning of inter-level causal mechanisms. In Sections 4.1 and 4.2, we further elaborate on GUI construction and cognitive study protocols for evaluating the following three hypotheses that test the Figure 3 model: (1) learning via charts or interactive simulations will improve user design task performance, (2) users exposed to animated renderings of agent-based simulation behavior will demonstrate understanding of inter-level causal relationships, while users exposed to chart GUIs will not demonstrate such understanding, and (3) users who demonstrate an understanding of inter-level causalities will perform better on design tasks.

Through these three hypotheses, all arrows in the diagram representing effects are evaluated either directly or indirectly, thus validating or refuting the proposed Figure 3 cognitive-based model. More specifically, the first hypothesis tests the overall tracks with large arrows stating that exposure to the GUI results in learning that improves design task proficiency, without regard to whether that improved performance was a result of learning parametric or inter-level relationships. The second hypothesis specifically tests whether each GUI leads to learned inter-level causal mechanisms; here it is only expected that the animation GUI supports inter-level causal learning because it reveals underlying mechanics that influence emergent system behaviors hidden in parametric representations. The final hypothesis tests whether improved design performance is achieved through learning of inter-level relationships, as opposed to all gains in performance being due to increased parametric knowledge, which has already been studied and suggested to improve user design proficiency (Egan et al. Reference Egan, Cagan, Schunn and LeDuc2015a ).

The assessment of these hypotheses is essential as it enables the decoupling of the types of relationships users learned throughout the study (i.e., parametric or inter-level), which highlights how the different types of information presented by the contrasting GUIs affect user design proficiency. It is possible to assess these hypotheses using a combination of between-subject and within-subject comparisons. Between-subject comparisons among users exposed to different interfaces enable inferences concerning how information types influence design proficiency, while within-subject comparisons of users throughout the study can demonstrate the effects of learning on improvements in individuals’ reasoning. Through these measurements, it is possible to infer which types of information users learned, and how it affects their design outcomes.

3.2. Significance

This study seeks to understand how engineers can learn and understand types of information that result in improved proficiency in designing complex multi-level systems. Through measuring the effects on GUI exposure on user design proficiency, it is possible to infer what types of information a user learned and how specific understandings contribute to searching for optimal solutions in myosin-based design tasks. Each of the three proposed hypotheses tests the magnitude of different learning and application pathways in Figure 3, which serves to validate the Figure 3 cognitive-based model and reveal effective routes for presenting information through software tools that aid engineers in complex multi-level system design. If the aims of this study are achieved, then new insights will be reached concerning learning and design of complex systems from a cognitive perspective, which could translate toward new strategies for developing software aids for instructing and improving engineering design performance.

4.1. Graphical user interfaces

Two GUIs that emphasized learning through charts (Figure 4A) and animations (Figure 4B) were developed to conduct a cognitive study and validate the Figure 3 model. To maintain consistency with past myosin GUI studies (Figure 2) and to compare effects of learning from each interface, all interfaces were constructed similar to past myosin design GUIs. Modifications were made to the GUIs to produce two contrasting interfaces that facilitate the testing of different Figure 3 cognitive-based pathways through altering how graphical output of the GUIs is presented to a user. These design GUIs consist of four design inputs and up to two performance outputs in the chart interface or an agent-based rendering that updates in real time for the animation interface. All design inputs are manipulated by users via sliders that have five possible values for each myosin and systems design input, with maximum values for each parameter being a myosin lever arm length $\boldsymbol{l}$ of 20 nm, myosin attachment rate $\boldsymbol{k}_{\mathit{on}}$ of $4000~\text{s}^{-1}$ , myosin detachment rate $\boldsymbol{k}_{\mathit{off}}$ of $4000~\text{s}^{-1}$ , and a maximum number of myosins $N_{\mathit{myo}}$ of 100 or 30 depending on the task (tasks prior to learning support have a 100 myosin maximum so that intermittent behavior is uncommon). The performance of evaluated systems was calculated using mathematical equations (§ A.1) that predicted the global time-average filament velocity, the energy utilized via adenosine triphosphate (ATP) use of the myosins, and the average number of myosins attached to the filament.

The chart GUI was configured through supplying users quantitative feedback of system performance via plots of independent design inputs and dependent performance outputs, thus allowing the user to change myosin design inputs and see measured changes in emergent system behavior, as demonstrated in Figure 4(A) screen capture (video available at http://youtu.be/6Ke5I-Rm1Co). In Figure 4(A), directions for learning are in the top left, the time a user is allowed to utilize the scene before it is advanced automatically is in the bottom left, and the design inputs with a static graphical representation of the current system are in the center left. The middle portion of the screen consists of eight plots that represent each of the four independent design variables and two performance outputs that are calculated via mathematical equations. On the right of the screen is a summary that provides users a basis for what parametric relationships they should learn for their next task, which aids in maximizing a user’s germane cognitive load.

The second GUI configuration presented users animated feedback of the agent-based molecular simulation when design inputs are varied (video available at http://youtu.be/f0G7uc3Empk), as demonstrated in Figure 4(B) screen capture. The animation GUI is similar to the chart GUI of Figure 4(A), except that the plots and static myosin representation are replaced with an agent-based simulation that updates in real time as users manipulate design inputs. During periods of time when no myosins are attached during the simulation, the system becomes transparent, which should draw the attention of the user to the intermittent system behavior that occurs when less than two myosins are attached on average, thus highlighting crucial information indicative of inter-level relationships.

Through each of these two interfaces, a user is expected to learn different types of information about the system by manipulating inputs and recognizing their effects on output performance. For instance, with the animation interface, a user could add more myosins to the system and notice that if the filament was originally intermittently moving, it would begin moving more often as there are more periods of at least one myosin being attached. In the chart interface, a user would see the filament velocity parameter increase on the $y$ -axis as the number of myosins is increased in the system if it was changing from intermittent to continuous emergent behavior. However, it may not be obvious to the user in the chart interface why the velocity increased in this intermittent case, but not when the system is already continuous since they do not directly observe simulated myosin and global filament behaviors—such inter-level revelations are more apparent from the animation interface. Further details about how users may expect parameter changes to influence the performance of a system are available in § A.2. A drawback to the animation interface is that the user must view the simulation for a period of time before recognizing how a perturbed design input has affected the behavior of the system. Such a delay leads to a greater effort and less opportunity for the user to gain insights concerning parametric relationships within the same time period as a user with the chart interface.

Thus, in each interface, users have some chance to learn both parametric and inter-level causal mechanisms but the effort required to infer (i.e., cognitive load) and availability of information differ. These differences in information presented by the interfaces are an intentional aspect of the experimental design. Specifically, it enables comparison of how different types of information learned from the contrasting interfaces influence design proficiency and shows how the decoupling of parametric learning differs from that of inter-level causal learning with regard to design outcomes. Without these differences in the GUIs and experimental approaches, it would be difficult to determine whether users gained better design proficiency as a result of gained parametric knowledge or inter-level causal understanding.

4.2. Cognitive study protocol

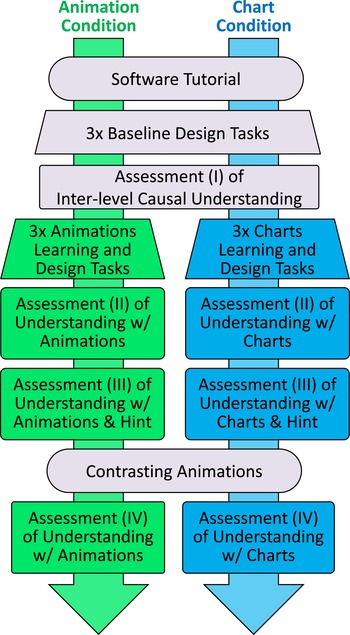
In order to conduct cognitive studies with the contrasting GUIs, each user follows a sequence of scenes that present useful information, design tasks, learning interfaces, or multiple-choice/free response questions. To test the hypotheses proposed in Section 3.1, there are one of two scene sequences presented to each user that are identical except for users being exposed to the animation or chart GUI during particular learning scenes and question/answer scenes. In our study, 31 mechanical engineering undergraduates in a senior design class participated for course credit and were randomly assigned to either track, resulting in 15 participants in the chart condition and 16 participants in the animation condition. Details concerning each track are illustrated in Figure 5 and elaborated on throughout this section.

Figure 5. Flow chart of cognitive study protocol.

Users in both conditions begin with a software tutorial that explains how to use the interface to design myosins and answer questions. Next, three baseline myosin design tasks are presented to the user via generic variable names of Input A/B/C/D and Output A/B instead of the different myosin design inputs and outputs they represent. The purpose of the generic variable names is to minimize learning of parametric relationships prior to exposing users to learning scenes. The mapping of the generic names to myosin parameters is changed for each task. The maximum number of myosins for these tasks is set to 100, such that intermittent filament behavior is not significant and therefore not learned by a user. Users are allowed to input ten designs within 4 min and receive feedback immediately upon evaluation of that design. All users throughout this study successfully input ten designs for all tasks. These design tasks are provided in Table 1 and consist of the functional requirements considered during a user’s optimization task that represent a myosin technology.

The table shows the output goal (users are instructed to minimize or maximize their design performance with respect to this output) and the additional constraints on output performance (users are instructed that their designs cannot violate any output constraints) for each design task. If a design violates a constraint, it is designated infeasible and given a score of zero. Three design task difficulties were created by increasing the number of output variables and constraints (although only one output is graded as the goal output, additional constraints on secondary output variables inherently reduce the set of acceptable possibilities in the larger design space). The three types of difficulties are 1-output–1-constraint, 2-outputs–1-constraint, and 2-outputs–2-constraints. To create a benchmark for later comparisons against user scores, a random solver was used to propose ten unique designs for each task and provided an average score on a scale of 0 to 1, which is normalized to the global optimum for each task; the average solution of the random solver was found by having it solve the task repeatedly until the standard error in the measurement of its mean score for a given task was negligible. A score of 1 is the highest score possible, and user scores were also normalized according to this metric (e.g., if the global optimum solution is a maximum velocity of $4~{\rm\mu}\text{m}~\text{s}^{-1}$ , and a user’s best design has a velocity of $1~{\rm\mu}\text{m}~\text{s}^{-1}$ , they receive a score of 0.25; the reciprocal is taken for minimization tasks).

A baseline assessment of whether users could demonstrate inter-level causal reasoning was taken by asking them to answer what would happen to system velocity if an unloaded system of 100 myosins was redesigned with only 10 myosins or with myosins of a higher attachment rate. This question is an assessment of their understanding of inter-level causal relations because a system with many myosins should have a large number of myosins attached on average (and therefore be continuous), so removing a large number of myosins would likely slow the system and drive it toward the intermittent regime, while increasing the myosin attachment rate would have no effect. In all of the qualitative assessment sections, the inter-level relationship of global velocity to the average number of myosins attached to a system is used as a metric because it is easily defined using the heuristic regarding how many myosins are attached on average (two or more lead to a continuous system, less than two leads to intermittent behavior). Whether a system is continuous or intermittent has profound effects on parameter sensitivities essential for effectively searching the design space (§ A.2).

Users are then provided one of the learning interfaces based on their assigned condition before solving their next set of learning tasks with functional requirements provided in Table 1. The maximum number of myosins in each design is reduced to 30, which means that the system is much more likely to become intermittent. Afterward, users’ ability to describe inter-level causalities is assessed a second time by asking several multiple-choice questions about a system presented according to their study condition.

These questions are shown in Table 2, and present the user a system either in the intermittent or continuous regimes and ask how the time-average filament velocity should change based on perturbing a system from an initial state of being continuous or intermittent; design perturbations in the questions were designed to have an obvious effect on a user who understands the inter-level causal mechanisms of the system. In Table 2, the design input values in the table reflect the slider value in the GUI for the myosin design variables and how many myosins were present in the system. At this point in the experimental design, users who demonstrate an understanding of the inter-level causality are assumed to have also had that knowledge for their final design task (completed just before the second assessment of inter-level understanding). This assumption enables an examination of how inter-level causal knowledge affects design task proficiency (which is necessary for answering the third hypothesis from Section 3.1). A third qualitative assessment was then conducted in which users were given a hint through provision of the correct parametric answer to the multiple-choice questions prior to demonstrating their reasoning in support of that answer. This hint enables the determination of whether improved parametric knowledge may support proper description of inter-level causalities (second hypothesis from Section 3.1).

Questions were designed as in Table 2 for a balance in difficulty across each assessment, but questions varied in specifics to avoid users becoming familiar with specific questions being asked. All questions were tuned to test a user’s inter-level causal reasoning through asking how a change in system design may result in a change in filament velocity, although the precise variables for each question changed. Balancing of questions was controlled through having one question in each assessment require knowledge that the time-average filament velocity should change notably, while the other question in each phase required knowledge that the design perturbation would not significantly alter filament velocity. Additionally, users were not provided feedback concerning whether their answer was correct or not at the end of each assessment, which further promotes the independence of measurements gathered from each phase. The purpose of having multiple assessment phases is to determine the growth in user understanding of inter-level causalities throughout the course of the experiment, and to specifically address the second hypothesis of the study.

Additionally, as a control, parametric questions were asked during the second and fourth assessment phases to determine whether users properly understood whether changes in attachment rate or numbers of myosins affected system outputs. Including such questions enabled an assessment of whether students misunderstood inter-level causal mechanisms due to the non-obvious nature of the emergent behavior, or because they did not understand parametrically how changes in design inputs affect design outputs. Examples of questions for these controls are ‘Does adding more myosins to a system increase the average number of attached myosins in a system?’ and ‘Does increasing the attachment rate of each myosin increase the average number of attached myosins in a system?’ Users answered these questions through checkboxes to indicate ‘yes’ or ‘no’ answers.

Last, users in both groups are presented contrasting animations before a final qualitative reasoning assessment. The animations show users the systems side by side in the intermittent and continuous emergent behavioral regime, thus providing a clear distinction to the user for how systems designed in two different ways produce two different global patterns of behavior. Users are also provided the engineering heuristic that if about two myosins are attached on average, the system will remain continuous while systems with much fewer myosins attached on average have intermittent behavior (and therefore lower time-average velocity). The purpose of the contrasting animations is to determine what percentage of users are able to correctly learn and explain these crucial inter-level causal mechanisms from a learning interface with reduced cognitive load and salient characteristics highlighted. The question details for this final assessment are also provided in Table 2. The complete sequence of scenes for the two study conditions provides an opportunity for testing each proposed hypothesis, through comparison of effects of each learning interface, as well as how users learn and apply parametric and inter-level causal knowledge of the system.

5.1. Both types of learning improve design proficiency

The first hypothesis was learning via charts or interactive simulations will improve user design task performance. The hypothesis was analyzed by aggregating data from each optimization task separately, and then averaging the solution quality of a user’s best solution for that task with all other users in their condition. Solution quality was determined by first comparing a user’s goal output value to the global optimum for a task and providing it a relative score between 0 and 1 (all designs that did not meet constraints had a score of 0; the global optimum has a score of 1). The solution quality was then calculated by finding the difference between the user average relative objective function and the average score found by a random solver (Table 1) to facilitate absolute evaluation and performance comparison across problem types. Each problem type is defined by the number of outputs/constraints that describe its design space. Tasks were generated such that those of the same type are representative of similar search difficulties (Egan et al. Reference Egan, Cagan, Schunn and LeDuc2015a ), thus providing a means of comparison on pre-/post-learning tasks. The average solution quality of users is presented in Figure 6 for each task and learning condition.

Figure 6. Average user solution quality in each learning condition for all tasks.

In comparing baseline and post-learning tasks, the average solution quality improved post-learning for all tasks, which supports the hypothesis, as demonstrated by Figure 6 pair-wise comparisons with $p$ -values reported. When $p\leqslant 0.05$ , it is suggested that the error rate in reporting a false positive is less than 5%, which is generally considered as statistically significant. The results suggest that the information conveyed by each GUI resulted in nearly equal improvement in design proficiency. Improvement of users increased as task complexity grew, thus motivating an ever increasing need for software tools as systems grow increasingly more complex, which remains consistent with previous findings for myosin GUI studies (Egan et al. Reference Egan, Cagan, Schunn and LeDuc2015a ). Interestingly, the charts and animations did not appear to support design performance by changing design strategies, at least not on the strategies previously shown to improve performance on these tasks (e.g., only changing one input at a time, searching near their current best design, minimizing/maximizing inputs), which were assessed through post-processing of user input data in relation to their received output (Egan et al. Reference Egan, Cagan, Schunn and LeDuc2015a ). Thus, the benefit may occur through the knowledge used in existing strategies rather than via changing strategies. The difference in performance among those in different chart/animation conditions is not significant for any pair-wise measurement.

These results demonstrate the overall influence of each GUI for improving design task proficiency. They demonstrate that agent-based models, which past studies have shown to improve user understanding of systems (Vattam et al. Reference Vattam, Goel, Rugaber, Hmelo-Silver, Jordan, Gray and Sinha2011), can also improve user design proficiency of the systems. The relatively equal impact of each method on design quality has limited theoretical importance, as it does not imply that the two methods have equal influences on users since it is possible that different underlying cognitive mechanisms of users are affected by each interface (such as performing better due to gains in parametric relationships or qualitative understanding). Further analysis of the user performance with regard to the Figure 3 cognitive-based model is required to determine how gains in design performance are attained by users in each of the study groups, despite differing types of information being emphasized by each GUI.

5.2. Animations support inter-level understanding

Throughout the cognitive study, user understanding of inter-level causalities was assessed to address the second hypothesis: users exposed to animated renderings of agent-based simulation behavior will demonstrate understanding of inter-level causal relationships, while users exposed to chart GUIs will not demonstrate such understanding. In each assessment phase, users were asked two questions of how filament velocity of a system would change if redesigned, as presented in Table 2. The questions were designed such that the perturbations would obviously have a large effect or negligible effect on system velocity to a user with knowledge of how inter-level relationships of the system affect its emergent behavior.

Users indicated their answer via a multiple-choice box (either filament velocity increases notably or remains about the same) and typed their reasoning in a free response box that was only analyzed for users who correctly answered the multiple-choice question (with the exception of assessment phase one, where no multiple-choice question was given). Free response answers were tagged as a correct demonstration of understanding inter-level causality if users referred to the stopping/starting behavior of the filament being related to having at least one myosin attached. Examples of user responses that were tagged as correct were The increased number of myosins results in more time during which at least 1 myosin is attached and therefore the filament is being pushed forward and Average filament velocity increases because when there are more myosins there is less of a chance the filament will not be moving as a result of no present myosins. These were deemed as correct because both answers relate the individual myosin level (that one must be attached) to the emergent phenomenon of continuous or intermittent filament motion. Some examples of answers tagged as incorrect, despite users indicating the correct parametric relationship, were Since the amount of force is increased and On average the filament is going to move at the rate at which the myosin pulls, which is independent of how often it attaches. The first of these answers is incorrect because the force of the system has no influence on its velocity in our model where time-average force among myosins equals zero. The second answer is incorrect because it fails to take into account the average velocity of the filament, which requires consideration of times when it is translating and static, despite it having the same instantaneous velocity every time at least one myosin is attached.

Understanding of inter-level causalities was measured four times through averaging the percentage of correct free response answers of users in each condition during each phase. No users indicated a proper understanding during the baseline assessment phase prior to learning sessions. The next two assessments occurred after the learning sessions (the first being directly after, and the second occurring once users were provided the correct parametric relationship via the correct multiple-choice answer but still had to provide an explanation). The final assessment occurred immediately after the contrasting animations were presented. The percentage of correct answers for users in each condition is presented in Figure 7.

Figure 7. Percentage of correct responses from users in both learning conditions for demonstration of inter-level causal understanding.

Users in the animation group correctly demonstrated understanding of inter-level causality about 33% of the time directly after the learning tasks, thus indicating that a significant number of users learned $(p\leqslant .02)$ as a result of interacting with the animation interface, when compared to none of the users demonstrating an understanding during the baseline assessment. No users in the chart condition demonstrated understanding at this point, thus supporting the hypothesis that the agent-based simulation supports learning inter-level relationships while the chart-based GUI does not support learning inter-level relationships $(p\leqslant .04)$ . However, despite supporting the hypothesis, only a small portion of users demonstrated understanding. After the parametric hint was provided, there was no significant improvement; one user in the chart condition explained the stochastic system behavior correctly, which suggests that it was not entirely implausible for users in that condition to formulate theories in line with correctly explaining the inter-level causal mechanisms. However, such a result suggests that parametric reasoning processes are not sufficient to teach users inter-level causal mechanisms.

After the contrasting animations were presented to users, approximately half of the users in each condition correctly explained the inter-level causality, which is a significant increase for both the chart $(p\leqslant .001)$ and the animation condition $(p\leqslant .03)$ . This pattern further supports the hypothesis that agent-based simulation renderings are effective in teaching inter-level causality, and are more effective when cognitive load is reduced via contrasting animations (Alfieri et al. Reference Alfieri, Nokes-Malach and Schunn2013). Because average user score was only about 50%, our findings reinforce prior reports that emergent systems are difficult to understand (even for engineering students) and misconceptions about these systems are robust to learning interventions. The growth of user understanding in both groups, however, shows the success in the software interface’s capabilities for producing a cognitive shift in how some users in each group understand and reason about inter-level causal mechanisms essential to system performance.

Past research has also found that inter-level causal understanding is particularly difficult for learners (Chi et al. Reference Chi, Roscoe, Slotta, Roy and Chase2012). In that prior work, most students were able to learn about molecular diffusion using agent-based simulations along with other instructional tools. The lower number of learners gaining proper understanding from simulations in this study may be attributed to shorter overall learning periods, in addition to the greater complexity of the myosin system in design contexts when compared to diffusion systems.

Additionally, control questions (Section 4.2) were asked to determine whether users understood parametric influences of the system, such that they knew an increase in the number of myosins or their attachment rate resulted in an increase in the average number of attached myosins in the system. User groups scored between 73% and 94% correct on these types of questions, which further demonstrates the difficulties in learning inter-level causal behaviors even when correct parametric understanding of the system is achieved.

5.3. Inter-level understanding improves design performance

The final hypothesis tested was users who demonstrate an understanding of inter-level causalities will perform better on design tasks. This hypothesis was investigated by separating the users in the animation condition into those who did and did not demonstrate an understanding during the second assessment. Users in the chart group were ignored for testing this hypothesis because they demonstrated no inter-level causal understanding immediately after the design tasks and had access to differing information compared to users in the animation groups, which would not enable a controlled comparison of how inter-level understanding influences design task performance independent of a user’s gained parametric knowledge. Group performance was then compared on the final design task (Figure 8). Only the final design task was selected because the first qualitative assessment immediately followed it and thus was the closest measure of inter-level understanding during design. Performance on the baseline task was also investigated to rule out variable differences among participants related to design ability.

Figure 8. Design performance of users from animation condition who did/did not demonstrate inter-level causal understanding.

The results show that during the baseline, there was not a significant difference $(p\leqslant .47)$ in design performance among the two groups; thus when no users understood inter-level causality their design task performance was similar. Afterward, users who had demonstrated understanding of inter-level causal relationships performed better and found designs very close to the global optimum when compared to users who had not demonstrated understanding $(p\leqslant .01)$ . This finding is statistically significant and supports the hypothesis that users who demonstrate an understanding of inter-level causality perform better in design applications related to that understanding. The result is particularly important because it isolates the understanding of inter-level causal mechanisms of the system as beneficial to the design process, in comparison to learning parametric relationships among variables. This finding also highlights inter-level causal relationships as an important form of information that can improve engineers’ ability to design, as opposed to learning other types of information about the system that improve a user’s understanding (e.g., learning the detailed mechanochemistry of myosin motors would improve user understanding, but not necessarily translate into improvements in designing a system effectively).