1. Introduction

Precise mapping and monitoring of the elements of the cryosphere, including the ice sheets, ice caps and mountain glaciers, is important to assess their sensitivity to local and global climate changes and their impact on sea-level variations. It is especially important to monitor the vast ice sheets of Antarctica and Greenland. They cover almost 10% of the Earth’s land surface, and their mass balance is a sensitive indicator of global changes. A direct indication of the mass balance can be obtained by comparing repeat surface elevation measurements. Laser altimetry is an emerging new technology that measures surface elevation of snow and ice surfaces with minimal human intervention, high accuracy and spatial resolution, providing precise surface topography and description of surface statistics (roughness, crevasses).

A number of publications report successful applications of airborne laser altimetry for mass-balance studies. Repeat aircraft laser-altimeter surveys over the Greenland ice sheets show that the ice sheet is in balance at high elevations, although thinning, with rates exceeding 1ma^–1 close to the coast (Reference KrabillKrabill and others, 2000). Laser-altimetry surveys are used to map changes on the West Antarctic ice streams (Reference Spikes, Csathö and WhillansSpikes and others, 1999), on mountain glaciers in Alaska (Echel-meyer and others, 1996; Reference Aðalgeirsdóttir, Echelmeyer and HarrisonAðalgeirsdóttir and others, 1998) and in the Swiss Alps (Reference Favey, Pateraki, Baltsavias, Bauder and BöschFavey and others, 2000). Other applications of laser altimetry include the mapping of detailed surface relief (sastrugi) to estimate the contribution of spatial noise to the stratigraphic record (Reference Van der Veen, Krabill, Csathó and BolzanVan der Veen and others, 1998).

The reported accuracy of state-of-the-art laser altimetry systems is 0.1–0.15m (e.g. Reference FloodFlood, 1999; Reference KrabillKrabill and others, 2000). To achieve this accuracy, in-flight calibration must be performed. Current calibration techniques require overflights of large, smooth, flat surfaces (lakes, ocean, runways), usually using pitch and roll maneuvers, to resolve the misalignment between the inertial navigation system (INS) and the laser (e.g. Reference Krabill, Thomas, Martin, Swift and FrederickKrabill and others, 1995; Reference HoftonHofton and others, 2000). The 0.1 –0.15merror estimate refers to ideal (good) target surfaces, such as the flat or gently sloping, bright surface of the ice sheets. Larger errors are expected over steep slopes and at large off-nadir pointing angles. For example, Reference Favey, Pateraki, Baltsavias, Bauder and BöschFavey and others (2000) identified a difference of a few decimeters with an rms difference of >1m between overlapping laser swaths over the steep, rugged surface of an alpine glacier. The authors attribute this error, which is much larger than that determined from the overflight of the known runway, to unmodeled errors in attitude angles. The magnitude of the errors reveals that the current approaches may not model the errors properly.

The algorithm presented here provides a comprehensive tool for laser system calibration. It ties together the modeling of the laser system and the surface, and also includes a detailed analysis of the solution. This calibration scheme facilitates calibration over arbitrary surfaces, making it possible to precisely calibrate systems where no flat surfaces are available, for example in the interior of the ice sheets. The applied analytical approach provides reliable estimates of calibration parameters, resulting in high-precision laser spot geolocation.

Theapproachwas applied to calibrating the U.S.National Science Foundation Support Office for Aerogeophysical Research (NSF-SOAR) laser altimetry systemthat was flown in Antarctica to map surface elevation changes on the West Antarctica Ice Shelf (WAIS) ice streams (Reference Spikes, Csathö and WhillansSpikes and others, 1999). Precise calibration of the SOAR laser system poses a problem for traditional calibration approaches since the whole mission was performed in the interior of the WAIS where no flat surfaces were available for applying the regular methods.

In the next section we present the calibration algorithm. Following in section 3 is the application of the approach for precise calibration of the SOAR laser altimeter system, along with results and evaluation of the calibration. Several aspects of the algorithm are discussed in section 4. The application of our in-flight calibration method significantly improves the accuracy of the SOAR system.

2. The Analytical Model

In-flight calibration of laser systems is complicated. The geometric realization of the system that transmits a single laser beam from each firing location suggests that no intrinsic redundancy exists in the system. An error in the system position, attitude or ranging cannot be noticed, in general. In addition, the calibration procedure involves more than the formulation of an analytical model for the systematic effects. System calibration belongs, in general, to the class of inverse problems. For many of them knowledge about the relation between the target and domain data (here referred to as the correspondence) is assumed, so the focus is on solving the simple inverse problem. With laser mapping it is impossible to know exactly where the laser beam illuminated the ground. The only information available at the outset is a cloud of three-dimensional laser points, deformed by the biases. The unknown relation between the domain (a laser point) and the target data (the true location of the illuminated surface patch) suggests that solving the inverse problem requires first finding the correspondence by some method.

The approachpresented here is focused on the geolocation of the laser footprint on the ground. The goal is to find the best geolocation of the laser points in terms of minimizing the differences between the laser-point coordinates and the ground. Two spatial relations are involved in this modeling: the laser geolocation equation and the surface model.

The laser geolocation equation incorporates the different components of a laser altimeter system. As the laser altimeter measures only the range between the laser firing point and the footprint, the position and the attitude of the system should be obtained from external sources, usually globalpositioning system (GPS) receivers and inertial mapping units (IMU). The integration of the three components involves handling three different reference coordinate frames: the laser altimeter reference frame in which the laser ranging is measured, the inertial frame in which the attitude angles are measured, and the Earth-centered reference frame in which position is measured. Derivation of the geolocation laser point as a function of these components and the transformation among them is given, for example, in Reference Vaughn, Bufton, Krabill and RabineVaughn and others (1996):

(1)

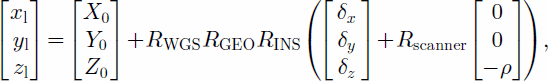
where x_l; y_l; z_l is the location of the footprint in the World Geodetic System 1984 (WGS84) geocentric coordinate system, X₀; Y₀;Z₀ is the location of the phase center of the GPS receiver, R_WGS is the rotation from the local ellipsoidal reference system at the position of the GPS antenna into the Earth-centered WGS84 reference frame, R_GEO is the rotation from the Earth-tangential reference system, defined by the local vertical, to the local ellipsoidal reference frame (the angle between the local vertical and the vector normal to the WGS ellipsoid is also calleddeflection of the vertical), R_INS is the rotation from the body reference system to the Earthtangential system centered at the GPS antenna, defined by the INS angles, δ_x, δ_y, δ_z is the offset vector between the GPS antenna and laser firing point, R_scanner is the rotation between laser beam and laser system defined by scanning angles, and ρ is the range measured by the laser system.

The mounting bias and the range bias are considered the systematic biases that contribute most to the geolocation errors. The mounting bias models the difference in alignment between the laser altimeter reference frame and the inertial reference frame; it is considered a major error source (Reference Vaughn, Bufton, Krabill and RabineVaughn and others, 1996; Reference Ridgway, Minster, Williams, Bufton and KrabillRidgway and others, 1997; Reference HoftonHofton and others, 2000). The range bias models a constant offset in the range determination. An interesting effect of the range bias is that it may result in a non-linear surface deformation (Reference Filin, Csathö and SchenkFilin and others, 2001). Incorporation of the two systematic errors into the laser geolocation equation is given by

(2)

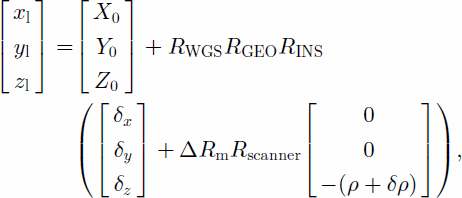
where δρ is the range bias and ΔR_m is the mounting-bias rotation matrix. The geometry of the system is illustrated in Figure 1.

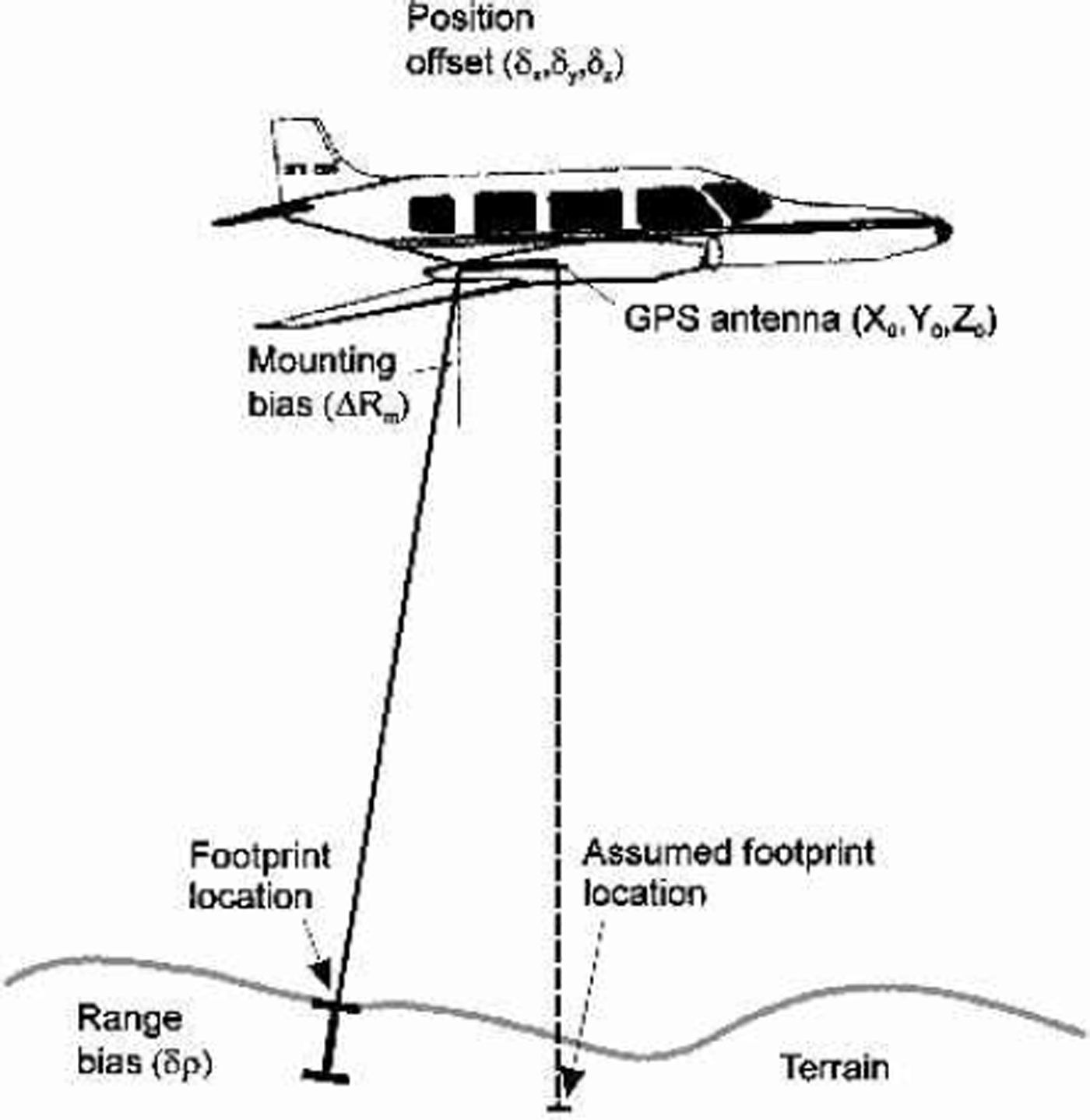
Fig. 1. Geometry of laser altimetry system.

The misalignment between the laser reference frame and the navigation frame, captured by the mounting bias, can be described by the three Euler angles that describe rotation along the x axis (roll), the y axis (pitch) and the z axis (yaw). The mounting bias therefore encompasses three unknowns. Together with the range bias, there are four unknowns.

Recovering the systematic biases involves the second spatial relation. A general expression for a surface is given by

(3)

The laser-point geolocation equation provides the ground-point coordinates in the form of Substituting the laser coordinates into Equation (3) leads to

where δ is the difference between the laser-point coordinates and the ground. Notice that in an error-free world the equality f (x_l; y_l; z_l) = 0 would result, but the systematic errors and the random noise alter this equality. Introducing the laser points as a function into the surface model generates an analytical form that ties the two spatial relations together.

In reality, an explicit form of the surface function is not known. We assume that the surface can be approximated by a set of surface patches, each with its analytical form. The current implementation assumes that the surface is represented by a set of a planar surfaces

(4)

although any other surface model can be used. In this form S = [s₁s₂s₃] is the surface normal direction and s₄ is the intercept point. The current modeling considers the surface parameters to be known a priori. Incorporation of the surface constraint and geolocation Equation (2) is given by

(5)

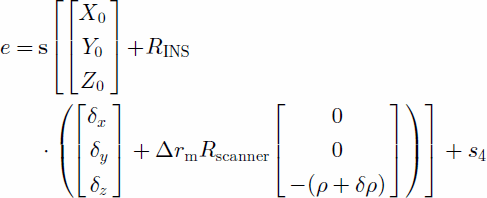
with e as the random error. The relation in Equation (5) is the dot product between the representation of the laser point in homogeneous coordinates and the surface, namely,

with and

Linearization of this form is given in Equation (6). The biases are expected to be small (order of a few degrees for the mounting-bias angles and a few decimeters for the range bias), so the first approximations can be set to zero.

(6)

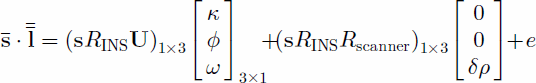
with ω; ϕ; κ the bias angles along the x; y and z axes, respectively, the approximation for the geolocation of the laser point (according to the current knowledge of the biases), and U₃£₃ a matrix of the form

(7)

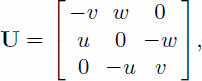
where

(8)

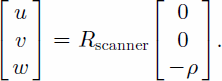
Each laser point contributes one equation, with the parameters of the appropriate surface patch. The parameters are solved with the Gauss–Markov model

(9)

where w is the observation vector (according to Equation (6)), A is the coefficient matrix, ξ is the vector of unknowns that consists of the three mounting-bias angles, ω; ϕ; κ, and the range bias δρ, e is the system noise, P is the weight matrix, n is the number of observations and m is the number of unknowns. The minimum norm criterion that also provides the best linear uniformly unbiased estimator for ξ gives the following solution:

(10)

with

(11)

(12)

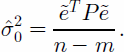
3. Calibration Of The Soar System Laser Altimeter

The SOAR system is a unique suite of geophysical, mapping and navigational instruments mounted in a ski-equipped Twin Otter aircraft operated by NSF-SOAR. The combination of laser profiling, ice-penetrating radar, airborne gravity and magnetic measurements was designed to investigate the geologic control on the ice flow. The laser altimeter system is reported to have 0.1–0.4m internal accuracy (Reference Blankenship, Alley and BindschadlerBlankenship and others, 2001) that indicates that the suite works to an adequate level of precision for detection of ice-sheet surface elevation changes. To establish the absolute accuracy of the system a calibration-validation project was carried out using flights over known surfaces to remove the systematic biases and to assess the absolute accuracy of the system. In addition, a small science program was carried out to map changes in surface elevation on selected parts of Whillans Ice Stream (formerly known as Ice Stream B) and Ice Streams C and E in the West Antarctic ice sheet over a 2 year time period (Reference Spikes, Csathö and WhillansSpikes and others, 1999).

The SOAR laser system is a profiling system using an Azimuth Model LRY 500 pulsed-laser transceiver with a diode-pumped Nd:YAG pulsed, near-infrared (1064 nm) laser. The beam divergence angle is 4.5 mrad, resulting in a footprint size of 1.5 m from the 300 m nominal flight altitude. The quoted single-pulse range accuracy is 10 cm. The laser was operated at 1000 Hz frequency, and 64 pulses were averaged eight times per second providing ranges approximately every 8 m.

A Litton Aero Products LTN92 INS unit, a laser gyroscope, was used for measuring the aircraft attitude angles. The INS has a quoted accuracy of 0.05³in all three angles (Reference Vaughn, Bufton, Krabill and RabineVaughn and others, 1996).

The aircraft position was determined by differential carrier-phase GPS surveys from data collected by Astech Z-12 and Turborouge receivers operating at 2 Hz at the base camp and on the aircraft.

Time-tagged range and attitude data together with information for converting the time tags into Universal Time Co-ordinated (UTC) time were provided by SOAR. Theyalso computed the GPS base-station positions by using the automated GYPSY system developedby the Jet Propulsion Laboratory, Pasadena, CA. The base stations were on moving ice, and their position changed as a function of time. Since ice motions at the sites were relatively small and uncomplicated, SOAR applied linear regression to estimate the base-station location for each flight. We used GPSurvey software (Trimble, Inc.) to process the kinematic GPS surveys to determine the accurate position of the aircraft during the laser altimetry missions. Although the maximum distance from the base station has reached 500 km, 0.1 m or better maximum rms was reported by GPSurvey for most of the flights. To assess the performance of the GPSurvey software, one of the surveys was processed with GUITAR (GPS Inferred Trajectories for Aircrafts and Rockets, courtesy of J. Sonntag, EG&G). GUITAR can provide aircraft positions with an accuracy of 0.2 mor better over baselines of >700 km (Reference Krabill, Thomas, Martin, Swift and FrederickKrabill and others, 1995). The two solutions agree well, having a maximum difference of 1cm in the horizontal and 8 cm in the vertical.

To map surface elevation changes over the ice streams, repeat flights were conducted by SOAR during the 1997/98 and 1999/2000 field seasons. System calibration was performed over aircraft landing strips (skiways) at the Siple Dome (1997/98) and Byrd Station (1999/2000) camps. To provide ground control, snowmobile-mounted GPS surveys were conducted along the skiways and in their surroundings. The ground-survey pattern at Byrd Station is shown in Figure 2. The calibration sites were overflown several times, including flights with constant attitude as well as with pitch or roll maneuvers. Figure 3 shows the variation in pitch and roll during one of the flights over the Byrd Station camp skiway.

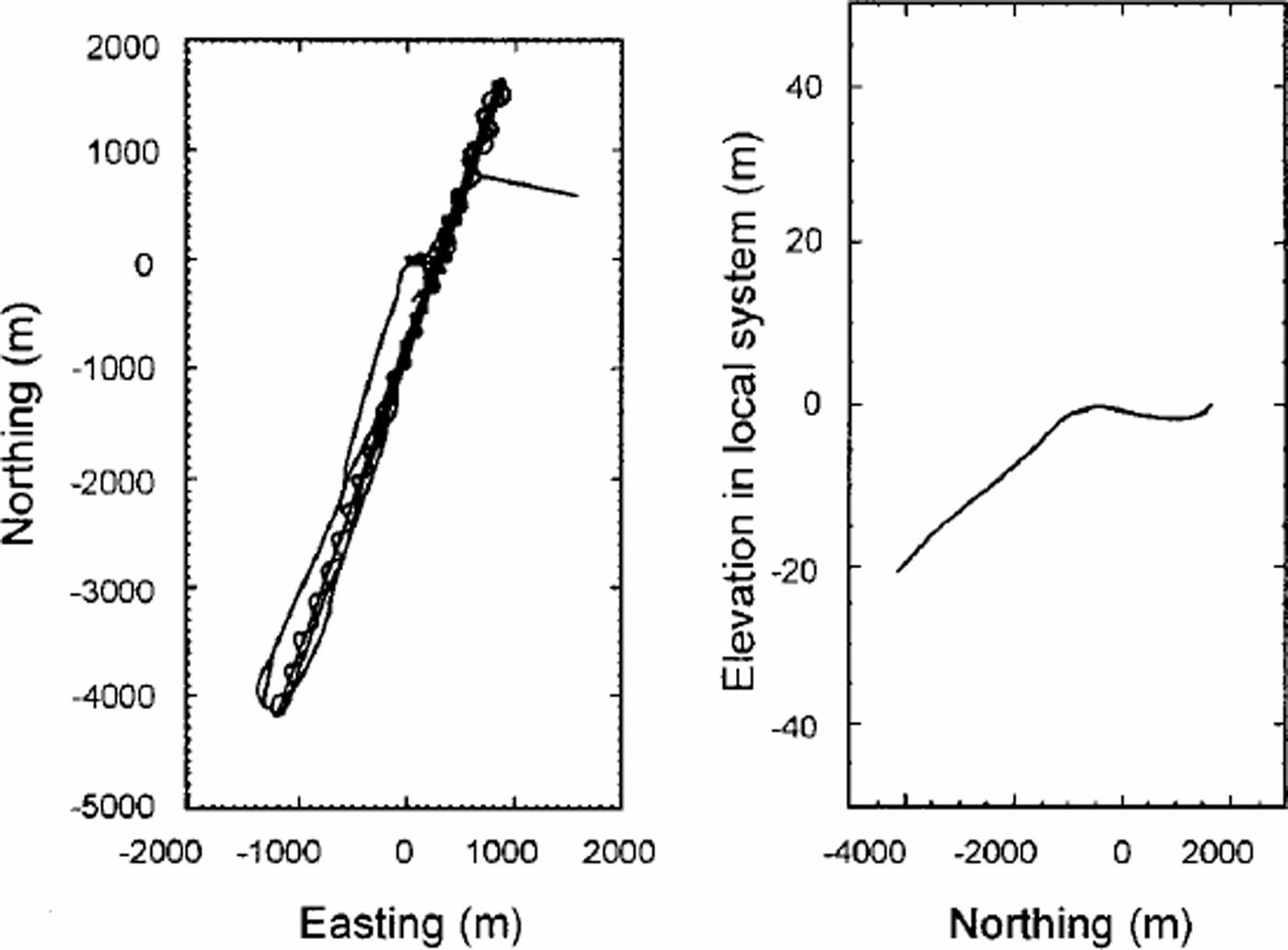
Fig. 2. Ground survey pattern at Byrd Station.

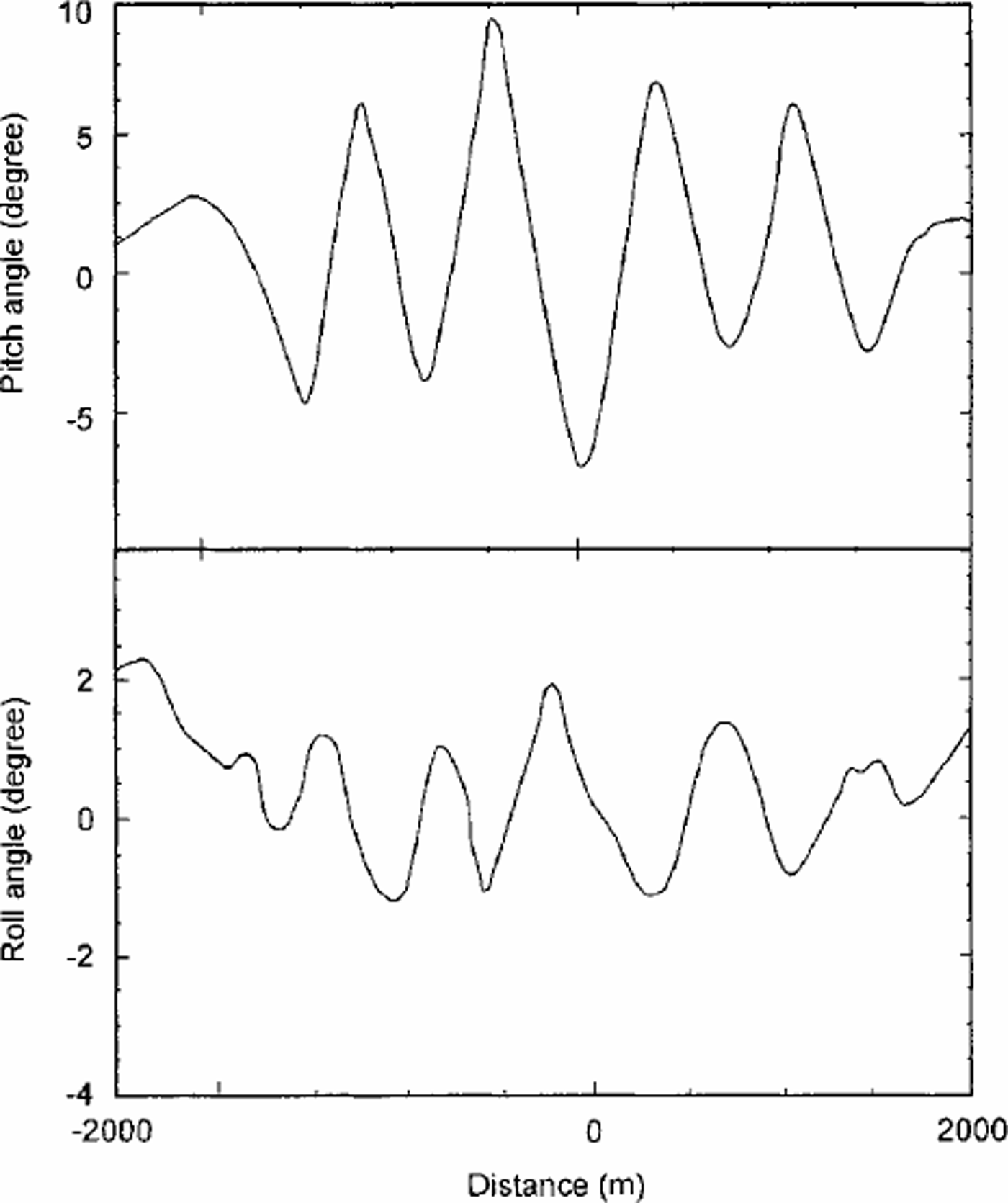
Fig. 3. Aircraft roll and pitch angles during pitch maneuvers.

The control surface model was formed by triangulating the points collected by the ground survey. The relatively high density of points resulted in a good description of the terrain, and the properties of the Delaunay Triangulation (DT) algorithm provided an optimal tesselation of the surface. Although a regular grid description is a more convenient pattern to process than an irregular network of triangles, the latter enables working with the original observations instead of a resampled set. Planar surface parameters were computed using plane fitting.

For a more convenient analysis of the results, the data were converted into a local coordinate system. Equation (1) shows that the laser points are given in a WGS84 reference frame. A geocentered reference frame is not very meaningful for evaluating orthometric elevation differences. Conversion to a local frame consists of a constant translation of the origin, usually to the centroid of the control coordinates, and rotations along the z axis, to coincide with the xz plane and the meridian plane, and along the y axis turning the z axis to point along the normal direction. Equation (5) shows that a constant translation and rotation do not affect the parameters. The same conversion was applied on the control surface.

For a profiler system the effect of the yaw bias is absorbed in the other two biases, and so cannot be recovered. The biases recovered here include the pitch and roll mounting biases and the range bias. Figure 4 presents the distribution of the residuals before system calibration. The existence of a constant offset, the range bias effect, is evident. The wide distribution of the errors indicates that the error modeling is more involved.

Fig. 4. Histogram of residuals before system calibration.

Figure 5 presents the residuals after the system calibration. The mean of the residual is zero, and its standard deviation is 0.06 m. The recovered laser-system biases are listed in Table 1. Analysis of the different flight configurations shows that the use of flight patterns with varying pitch and roll angles decorrelates the estimated parameters. In addition, bigger off-nadir angles improve the robustness of the solution. Table 2 presents the correlation matrix between the parameters. The low correlation suggests that the recovery of the different biases is almost independent. Evaluation of the robustness of the calibration configuration can also be analyzed via the condition number. The condition number (the ratio between the biggest and smallest eigenvalues of the dispersion matrix) for this calibration configuration is C = 800. This value indicates that the system has a fairly strong configuration. In summary, the calibration configuration resulted in a set of calibration parameters with very desirable properties, such as low variance, low correlation between the parameters, and a relatively low condition number.

Fig. 5. Histogram of residuals after system calibration.

Table 1. Estimated calibration parameters

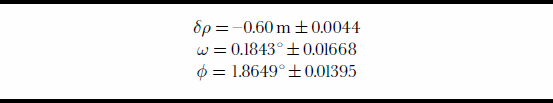
Table 2. Correlation matrix

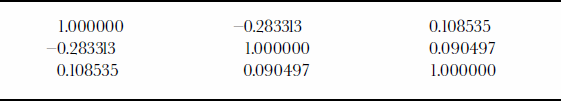
4. Discussion

The problem formulation presented in this paper has many advantages. From a theoretical standpoint, it models the essence of the problem, i.e. tying together the two relevant elements: the three-dimensional laser points and the surface. No point-to-point correspondence is needed; the terrain is used as a constraint and not as a source for extracting elevation for control points. Furthermore, no restriction on the surface type (e.g. flat surfaces) is needed. Since the analytical solution models the errors directly, inclusion of other error types in the model is not too complicated.

The analytical approach provides the best calibration parameters, in terms of having minimum dispersion, in the group of the unbiased estimators. Therefore this approach provides the best solution in the sense of minimum variances. The small estimated standard deviation of the residuals and its narrow distribution (see Fig. 5) suggest that the systematic errors of the system have been removed. This is also indicated by the fact that the magnitude of the residuals is similar to the approximated surface roughness (sastrugi) of the surveyed area.

The expected accuracy of the laser-point geolocation can be derived via error propagation. Therefore the accuracy of the surface elevation can be assessed analytically. The estimates can also be utilized in conjunction with the crossover method, which is generally used to assess accuracy when no ground control is available. Test statistics can be used to evaluate whether the differences obtained over crossovers are in the range of measurement error.

When repeat surveys are performed for detecting changes, precise system calibration becomes very important. Calibration is mandatory every time the laser system is mounted into the aircraft. The installation affects the calibration parameters, such as the mounting bias and the offset vector between the laser system and the GPS antenna. Calibration parameters may even change for the same installation from one mission to another, and it is advantageous to establish a time series of system calibration parameters by repeat calibrations. Analysis of the time series increases the confidence, reliability and understanding of the system.

Finally, the accuracy we obtained with the current configuration shows that in-flight, field, calibration is not too difficult to perform. The non-sophisticatedmanner in which the calibration site was surveyed, and the fact that no restriction on the surface was imposed, suggests that relatively high accuracy can be obtained even in less than optimal conditions.