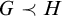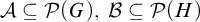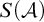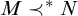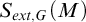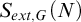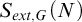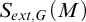1 Introduction
Assume M is a model for a relational language L,
![]() $T=Th(M)$
and
$T=Th(M)$
and
![]() $G=G(M)$
is an infinite group
$G=G(M)$
is an infinite group
![]() $0$
-definable in M. All models of T we consider are elementary submodels of a monster model
$0$
-definable in M. All models of T we consider are elementary submodels of a monster model
![]() ${\cal M}$
of T. In this paper we are interested in topological dynamics of some G-flows of types over M. We assume the reader is familiar with the basic notions of topological dynamics [Reference Ellis1, 2, Reference Glasner4] and model theory [Reference Hodges5, Reference Lascar7, Reference Pillay13] as well as topological dynamics of definable groups [Reference Newelski9], although we shall recall some of them.
${\cal M}$
of T. In this paper we are interested in topological dynamics of some G-flows of types over M. We assume the reader is familiar with the basic notions of topological dynamics [Reference Ellis1, 2, Reference Glasner4] and model theory [Reference Hodges5, Reference Lascar7, Reference Pillay13] as well as topological dynamics of definable groups [Reference Newelski9], although we shall recall some of them.
Let
![]() ${\mathrm {Def}}_{ext,G}(M)$
be the algebra of externally definable subsets of G and let
${\mathrm {Def}}_{ext,G}(M)$
be the algebra of externally definable subsets of G and let
![]() $S_{ext,G}(M)$
be the Stone space of ultrafilters in
$S_{ext,G}(M)$
be the Stone space of ultrafilters in
![]() ${\mathrm {Def}}_{ext,G}(M)$
, called external G-types over M.
${\mathrm {Def}}_{ext,G}(M)$
, called external G-types over M.
![]() $S_{ext,G}(M)$
is a G-flow, in model theory it is a counterpart of the universal G-flow
$S_{ext,G}(M)$
is a G-flow, in model theory it is a counterpart of the universal G-flow
![]() $\beta G$
in topological dynamics. In particular, the G-flow
$\beta G$
in topological dynamics. In particular, the G-flow
![]() $S_{ext,G}(M)$
is isomorphic to its Ellis semigroup, hence it carries the induced semigroup operation
$S_{ext,G}(M)$
is isomorphic to its Ellis semigroup, hence it carries the induced semigroup operation
![]() $*$
that is continuous in the first coordinate (a semigroup like that is called left-continuous).
$*$
that is continuous in the first coordinate (a semigroup like that is called left-continuous).
There is a question, how are the flows
![]() $S_{ext,G}(M)$
related for various models M of T, in particular, are the semigroups
$S_{ext,G}(M)$
related for various models M of T, in particular, are the semigroups
![]() $(S_{ext,G}(M),*)$
and their Ellis groups related algebraically? [Reference Newelski10, Reference Newelski11] contain some results on these questions. The results of [Reference Newelski9] and [Reference Krupinski and Pillay6, Proposition 3.1] indicate that the quotient groups of
$(S_{ext,G}(M),*)$
and their Ellis groups related algebraically? [Reference Newelski10, Reference Newelski11] contain some results on these questions. The results of [Reference Newelski9] and [Reference Krupinski and Pillay6, Proposition 3.1] indicate that the quotient groups of
![]() $G({\cal M})$
by its model theoretic M-connected components are homomorphic images of the semigroup
$G({\cal M})$
by its model theoretic M-connected components are homomorphic images of the semigroup
![]() $S_{ext,G}(M)$
and also of its Ellis groups.
$S_{ext,G}(M)$
and also of its Ellis groups.
In order to compare the G-flow
![]() $S_{ext,G}(M)$
and the
$S_{ext,G}(M)$
and the
![]() $G(N)$
-flow
$G(N)$
-flow
![]() $S_{ext,G}(N)$
for
$S_{ext,G}(N)$
for
![]() $M,N\models T$
we need to be able to compare the algebras
$M,N\models T$
we need to be able to compare the algebras
![]() ${\mathrm {Def}}_{ext,G}(M)$
and
${\mathrm {Def}}_{ext,G}(M)$
and
![]() ${\mathrm {Def}}_{ext,G}(N)$
. So it is natural to assume that
${\mathrm {Def}}_{ext,G}(N)$
. So it is natural to assume that
![]() $M\prec N$
, but it is not enough. We need a stronger relation between M and N, called
$M\prec N$
, but it is not enough. We need a stronger relation between M and N, called
![]() $*$
-elementary inclusion
$*$
-elementary inclusion
![]() $\prec ^*$
, we recall it later.
$\prec ^*$
, we recall it later.
Assume
![]() $M\prec ^* N$
. In [Reference Newelski10, Theorem 4.1] we proved that if there is a generic type in
$M\prec ^* N$
. In [Reference Newelski10, Theorem 4.1] we proved that if there is a generic type in
![]() $S_{ext,G}(N)$
(equivalently,
$S_{ext,G}(N)$
(equivalently,
![]() $S_{ext,G}(N)$
has a unique minimal subflow [Reference Newelski9]), then the Ellis groups of
$S_{ext,G}(N)$
has a unique minimal subflow [Reference Newelski9]), then the Ellis groups of
![]() $S_{ext,G}(M)$
are homomorphic images of subgroups of the Ellis groups of
$S_{ext,G}(M)$
are homomorphic images of subgroups of the Ellis groups of
![]() $S_{ext,G}(N)$
. Here we prove that if every minimal left ideal in
$S_{ext,G}(N)$
. Here we prove that if every minimal left ideal in
![]() $S_{ext,G}(N)$
is a group, then the Ellis groups of
$S_{ext,G}(N)$
is a group, then the Ellis groups of
![]() $S_{ext,G}(M)$
are isomorphic to closed subgroups of the Ellis groups of
$S_{ext,G}(M)$
are isomorphic to closed subgroups of the Ellis groups of
![]() $S_{ext,G}(N)$
. The assumption that every minimal left ideal in
$S_{ext,G}(N)$
. The assumption that every minimal left ideal in
![]() $S_{ext,G}(N)$
is a group is dual to the assumption that
$S_{ext,G}(N)$
is a group is dual to the assumption that
![]() $S_{ext,G}(N)$
contains a generic type.
$S_{ext,G}(N)$
contains a generic type.
We present our results in a general combinatorial set up, making the presentation easier. So we consider infinite groups
![]() $G\prec H$
, a G-algebra
$G\prec H$
, a G-algebra
![]() ${\cal A}\subseteq {\cal P}({\cal G})$
and an H-algebra
${\cal A}\subseteq {\cal P}({\cal G})$
and an H-algebra
![]() ${\cal B}\subseteq {\cal P}(H)$
and under some additional assumptions we find some algebraic connections between the Ellis [semi]groups of
${\cal B}\subseteq {\cal P}(H)$
and under some additional assumptions we find some algebraic connections between the Ellis [semi]groups of
![]() $S({\cal A})$
and
$S({\cal A})$
and
![]() $S({\cal B})$
. The important tools in our proofs are the notions of weak heir from [Reference Newelski10] and weak coheir (introduced here). We think they are of independent interest, so we elaborate on them. We characterize them in the case where T is stable, by means of local forking. We provide some examples.
$S({\cal B})$
. The important tools in our proofs are the notions of weak heir from [Reference Newelski10] and weak coheir (introduced here). We think they are of independent interest, so we elaborate on them. We characterize them in the case where T is stable, by means of local forking. We provide some examples.
2 Preliminaries
Assume G is an infinite (discrete) group. We use e to denote the identity element of G and also of any other group. Assume that
![]() ${\cal A}$
is a G-algebra, that is an algebra of subsets of G closed under left translation by elements of G. In this case its Stone space
${\cal A}$
is a G-algebra, that is an algebra of subsets of G closed under left translation by elements of G. In this case its Stone space
![]() $S({\cal A})$
is naturally a G-flow, with G acting on
$S({\cal A})$
is naturally a G-flow, with G acting on
![]() $S({\cal A})$
by left translation. For
$S({\cal A})$
by left translation. For
![]() $A\in {\cal A}$
,
$A\in {\cal A}$
,
![]() $S({\cal A})\cap [A]$
denotes the set
$S({\cal A})\cap [A]$
denotes the set
![]() $\{p\in S({\cal A}):A\in p\}$
, a clopen subset of
$\{p\in S({\cal A}):A\in p\}$
, a clopen subset of
![]() $S({\cal A})$
. When
$S({\cal A})$
. When
![]() $p\in S({\cal A})$
then
$p\in S({\cal A})$
then
![]() $cl(Gp)$
is the subflow of
$cl(Gp)$
is the subflow of
![]() $S({\cal A})$
generated by p.
$S({\cal A})$
generated by p.
For
![]() $g\in G$
let
$g\in G$
let
![]() $l_g:S({\cal A})\to S({\cal A})$
be the left translation by g. Let
$l_g:S({\cal A})\to S({\cal A})$
be the left translation by g. Let
![]() $E(S({\cal A}))$
be the topological closure of the set
$E(S({\cal A}))$
be the topological closure of the set
![]() $\{l_g:g\in G\}$
in the space of functions
$\{l_g:g\in G\}$
in the space of functions
![]() $S({\cal A})\to S({\cal A})$
with the topology of pointwise convergence.
$S({\cal A})\to S({\cal A})$
with the topology of pointwise convergence.
![]() $E(S({\cal A}))$
is a G-flow, where
$E(S({\cal A}))$
is a G-flow, where
![]() $g\cdot f = l_g\circ f$
for
$g\cdot f = l_g\circ f$
for
![]() $g\in G$
and
$g\in G$
and
![]() $f\in E(S({\cal A}))$
.
$f\in E(S({\cal A}))$
.
![]() $E(S({\cal A}))$
is also a compact left-continuous semigroup, with respect to composition of functions, called the Ellis semigroup of
$E(S({\cal A}))$
is also a compact left-continuous semigroup, with respect to composition of functions, called the Ellis semigroup of
![]() $S({\cal A})$
.
$S({\cal A})$
.
Assume S is a semigroup. We write
![]() $I\triangleleft S$
[
$I\triangleleft S$
[
![]() $I\triangleleft _m S$
] when I is a [minimal] left ideal in S. We say that
$I\triangleleft _m S$
] when I is a [minimal] left ideal in S. We say that
![]() $u\in S$
is an idempotent if
$u\in S$
is an idempotent if
![]() $u^2=u$
. The next fact is a fundamental structural result of Ellis.
$u^2=u$
. The next fact is a fundamental structural result of Ellis.
Fact 2.1 [Reference Ellis2],[Reference Ellis, Ellis and Nerurkar3, Proposition 4.2].
Assume S is a compact Hausdorff left-continuous semigroup and let J be the set of idempotents in S.
![]() $(1)$
Given
$(1)$
Given
![]() $I\triangleleft _m S$
, the set
$I\triangleleft _m S$
, the set
![]() $J(I)=I\cap J$
is non-empty.
$J(I)=I\cap J$
is non-empty.
![]() $(2)$
For every
$(2)$
For every
![]() $I\triangleleft _m S$
and
$I\triangleleft _m S$
and
![]() $u\in J(I)$
, the set
$u\in J(I)$
, the set
![]() $uI$
is a subgroup of I and I is a disjoint union of such subgroups.
$uI$
is a subgroup of I and I is a disjoint union of such subgroups.
![]() $(3)$
The groups
$(3)$
The groups
![]() $uI,I\triangleleft _m S,u\in J(I)$
, are all isomorphic.
$uI,I\triangleleft _m S,u\in J(I)$
, are all isomorphic.
![]() $(4)$
If
$(4)$
If
![]() $a\in S$
and
$a\in S$
and
![]() $I\triangleleft _m S$
, then
$I\triangleleft _m S$
, then
![]() $Ia\triangleleft _m S$
.
$Ia\triangleleft _m S$
.
The groups
![]() $uI$
appearing in Fact 2.1 are called the Ellis subgroups of S.
$uI$
appearing in Fact 2.1 are called the Ellis subgroups of S.
![]() $E(S({\cal A}))$
is a compact left-continuous semigroup, hence Fact 2.1 applies. We call its Ellis subgroups the Ellis groups of the flow
$E(S({\cal A}))$
is a compact left-continuous semigroup, hence Fact 2.1 applies. We call its Ellis subgroups the Ellis groups of the flow
![]() $S({\cal A})$
.
$S({\cal A})$
.
When
![]() ${\cal A}={\cal P}(G)$
, then
${\cal A}={\cal P}(G)$
, then
![]() $S({\cal A})=\beta G$
is naturally isomorphic to
$S({\cal A})=\beta G$
is naturally isomorphic to
![]() $E(\beta G)$
. This fact has been generalized in [Reference Newelski12] to some other G-algebras as follows.
$E(\beta G)$
. This fact has been generalized in [Reference Newelski12] to some other G-algebras as follows.
Definition 2.2 [Reference Newelski12, Definition 2.2].
![]() $(1)$
For
$(1)$
For
![]() $p\in S({\cal A})$
we define a function
$p\in S({\cal A})$
we define a function
![]() $d_p:{\cal A}\to {\cal P}(G)$
by
$d_p:{\cal A}\to {\cal P}(G)$
by
Clearly
![]() $d_p:{\cal A}\to {\cal P}(G)$
is a homomorphism of G-algebras.
$d_p:{\cal A}\to {\cal P}(G)$
is a homomorphism of G-algebras.
![]() $(2)$
We say that
$(2)$
We say that
![]() ${\cal A}$
is d-closed if
${\cal A}$
is d-closed if
![]() ${\cal A}$
is closed under
${\cal A}$
is closed under
![]() $d_p$
for every
$d_p$
for every
![]() $p\in S({\cal A})$
, that is
$p\in S({\cal A})$
, that is
![]() $d_p[{\cal A}]\subseteq {\cal A}$
. Notice that in this case
$d_p[{\cal A}]\subseteq {\cal A}$
. Notice that in this case
![]() $d_p$
belongs to
$d_p$
belongs to
![]() ${\mathrm {End}}({\cal A})$
, the semigroup of endomorphisms of G-algebra
${\mathrm {End}}({\cal A})$
, the semigroup of endomorphisms of G-algebra
![]() ${\cal A}$
.
${\cal A}$
.
![]() $(3)$
If
$(3)$
If
![]() ${\cal A}$
is d-closed, then let
${\cal A}$
is d-closed, then let
![]() $d:S({\cal A})\to {\mathrm {End}}({\cal A})$
be the function mapping p to
$d:S({\cal A})\to {\mathrm {End}}({\cal A})$
be the function mapping p to
![]() $d_p$
.
$d_p$
.
So the algebra
![]() ${\cal P}(G)$
is d-closed. By [Reference Newelski10, Lemma 1.2] also the G-algebra
${\cal P}(G)$
is d-closed. By [Reference Newelski10, Lemma 1.2] also the G-algebra
![]() ${\mathrm {Def}}_{ext,G}(M)$
is d-closed. The next fact lists the basic properties of d-closed G-algebras.Footnote
1
${\mathrm {Def}}_{ext,G}(M)$
is d-closed. The next fact lists the basic properties of d-closed G-algebras.Footnote
1
Fact 2.3 [Reference Newelski12, Proposition 2.4].
Assume
![]() ${\cal A}$
is d-closed.
${\cal A}$
is d-closed.
![]() $(1)$
The function
$(1)$
The function
![]() $d:S({\cal A})\to {\mathrm {End}}({\cal A})$
is a bijection.
$d:S({\cal A})\to {\mathrm {End}}({\cal A})$
is a bijection.
![]() $(2)$
d induces on
$(2)$
d induces on
![]() $S({\cal A})$
a semigroup operation
$S({\cal A})$
a semigroup operation
![]() $*$
so that
$*$
so that
![]() $d:S({\cal A})\to {\mathrm {End}}({\cal A})$
becomes an isomorphism of semigroups and for
$d:S({\cal A})\to {\mathrm {End}}({\cal A})$
becomes an isomorphism of semigroups and for
![]() $p,q\in S({\cal A})$
we have
$p,q\in S({\cal A})$
we have
![]() $d_{p*q}=d_p\circ d_q$
. Also for
$d_{p*q}=d_p\circ d_q$
. Also for
![]() $A\in {\cal A}$
we have
$A\in {\cal A}$
we have
(3) For
![]() $p\in S({\cal A})$
let
$p\in S({\cal A})$
let
![]() $l_p:S({\cal A})\to S({\cal A})$
be the left translation by p, that is,
$l_p:S({\cal A})\to S({\cal A})$
be the left translation by p, that is,
![]() $l_p(q)=p*q$
. Then
$l_p(q)=p*q$
. Then
![]() $E(S({\cal A}))=\{l_p:p\in S({\cal A})\}$
and the function
$E(S({\cal A}))=\{l_p:p\in S({\cal A})\}$
and the function
![]() $l:S({\cal A})\to E(S({\cal A}))$
mapping p to
$l:S({\cal A})\to E(S({\cal A}))$
mapping p to
![]() $l_p$
is an isomorphism of G-flows and of semigroups. In particular,
$l_p$
is an isomorphism of G-flows and of semigroups. In particular,
![]() $(S({\cal A}),*)$
is a compact left-continuous semigroup.
$(S({\cal A}),*)$
is a compact left-continuous semigroup.
When
![]() ${\cal A}$
is d-closed and
${\cal A}$
is d-closed and
![]() $p\in S({\cal A})$
, we associate with
$p\in S({\cal A})$
, we associate with
![]() $d_p\in {\mathrm {End}}({\cal A})$
its kernel
$d_p\in {\mathrm {End}}({\cal A})$
its kernel
![]() ${\mathrm {Ker}} d_p$
and image
${\mathrm {Ker}} d_p$
and image
![]() ${\mathrm {Im}} d_p$
. Clearly
${\mathrm {Im}} d_p$
. Clearly
![]() ${\mathrm {Ker}} d_p$
is a G-ideal in
${\mathrm {Ker}} d_p$
is a G-ideal in
![]() ${\cal A}$
and
${\cal A}$
and
![]() ${\mathrm {Im}} d_p$
is a G-subalgebra of
${\mathrm {Im}} d_p$
is a G-subalgebra of
![]() ${\cal A}$
.
${\cal A}$
.
Fact 2.4 [Reference Newelski10, Reference Newelski12].
Assume
![]() ${\cal A}$
is d-closed.
${\cal A}$
is d-closed.
![]() $(1)$
Assume
$(1)$
Assume
![]() $p,q\in S({\cal A})$
. Then
$p,q\in S({\cal A})$
. Then
![]() ${\mathrm {Ker}} d_p\subseteq {\mathrm {Ker}} d_q$
iff
${\mathrm {Ker}} d_p\subseteq {\mathrm {Ker}} d_q$
iff
![]() $cl(Gp)\supseteq cl(Gq)$
.
$cl(Gp)\supseteq cl(Gq)$
.
![]() $(2)$
If S is a subgroup of
$(2)$
If S is a subgroup of
![]() $S({\cal A})$
, then the endomorphisms
$S({\cal A})$
, then the endomorphisms
![]() $d_p,p\in S$
have common kernel
$d_p,p\in S$
have common kernel
![]() $K(S)={\mathrm {Ker}} d_p$
and image
$K(S)={\mathrm {Ker}} d_p$
and image
![]() $R(S)={\mathrm {Im}} d_p$
.
$R(S)={\mathrm {Im}} d_p$
.
![]() $R(S)$
is a section of the family of
$R(S)$
is a section of the family of
![]() $K(S)$
-cosets in
$K(S)$
-cosets in
![]() ${\cal A}$
, hence
${\cal A}$
, hence
![]() $R(S)\cong {\cal A} / K(S)$
. Also, every
$R(S)\cong {\cal A} / K(S)$
. Also, every
![]() $d_p,p\in S$
restricted to
$d_p,p\in S$
restricted to
![]() $R(S)$
is a G-algebra automorphism of
$R(S)$
is a G-algebra automorphism of
![]() $R(S)$
and the mapping
$R(S)$
and the mapping
![]() $p\mapsto d_p|_{R(S)}$
is a group monomorphism
$p\mapsto d_p|_{R(S)}$
is a group monomorphism
![]() $S\to {\mathrm {Aut}}(R(S))\cong {\mathrm {Aut}}({\cal A}/ K(S))$
.
$S\to {\mathrm {Aut}}(R(S))\cong {\mathrm {Aut}}({\cal A}/ K(S))$
.
![]() $(3)$
Let
$(3)$
Let
![]() ${\cal K} = \{{\mathrm {Ker}} d_p: p\in I\triangleleft _m S({\cal A})\}$
and
${\cal K} = \{{\mathrm {Ker}} d_p: p\in I\triangleleft _m S({\cal A})\}$
and
![]() ${\cal R} = \{{\mathrm {Im}} d_p:p\in I\triangleleft _m S({\cal A})\}$
. Then the mapping
${\cal R} = \{{\mathrm {Im}} d_p:p\in I\triangleleft _m S({\cal A})\}$
. Then the mapping
![]() $uI\mapsto (K(uI), R(uI))$
is a bijection between the Ellis subgroups of
$uI\mapsto (K(uI), R(uI))$
is a bijection between the Ellis subgroups of
![]() $S({\cal A})$
and the product
$S({\cal A})$
and the product
![]() ${\cal K}\times {\cal R}$
. Moreover,
${\cal K}\times {\cal R}$
. Moreover,
![]() $K(uI)=K(u'I')$
iff
$K(uI)=K(u'I')$
iff
![]() $I=I'$
and for every
$I=I'$
and for every
![]() $I\triangleleft _mS({\cal A})$
and
$I\triangleleft _mS({\cal A})$
and
![]() $R\in {\cal R}$
there is a unique
$R\in {\cal R}$
there is a unique
![]() $u\in J(I)$
with
$u\in J(I)$
with
![]() $R=R(uI)$
.
$R=R(uI)$
.
We shall need a characterization of the algebras from
![]() ${\cal R}$
. We say that
${\cal R}$
. We say that
![]() $A\in {\cal A}$
is generic (in G) if some finitely many left translates of A cover G. We say that a point
$A\in {\cal A}$
is generic (in G) if some finitely many left translates of A cover G. We say that a point
![]() $p\in S({\cal A})$
is generic if every set in p is generic. We say that a G-subalgebra R of
$p\in S({\cal A})$
is generic if every set in p is generic. We say that a G-subalgebra R of
![]() ${\cal A}$
is generic if every non-empty element of R is a generic subset of G. We say that
${\cal A}$
is generic if every non-empty element of R is a generic subset of G. We say that
![]() $A\in {\cal A}$
is strongly generic if it generates a generic G-subalgebra of
$A\in {\cal A}$
is strongly generic if it generates a generic G-subalgebra of
![]() ${\cal A}$
.
${\cal A}$
.
Fact 2.5 [Reference Newelski11, Reference Newelski12].
Assume
![]() ${\cal A}$
is d-closed. The G-algebras in
${\cal A}$
is d-closed. The G-algebras in
![]() ${\cal R}$
are exactly the maximal generic G-subalgebras of
${\cal R}$
are exactly the maximal generic G-subalgebras of
![]() ${\cal A}$
.
${\cal A}$
.
The combinatorial set-up. From now on in this paper usually we assume G is an infinite group (possibly with an additional first order structure) and
![]() $L_G$
is the language of G. Also we assume that
$L_G$
is the language of G. Also we assume that
![]() $G\prec H$
.
$G\prec H$
.
![]() ${\mathrm {Def}}(G)$
denotes the G-algebra of subsets of G definable by formulas of
${\mathrm {Def}}(G)$
denotes the G-algebra of subsets of G definable by formulas of
![]() $L_G$
, using parameters from G.
$L_G$
, using parameters from G.
Given
![]() $A\in {\mathrm {Def}}(G)$
definable by an
$A\in {\mathrm {Def}}(G)$
definable by an
![]() $L_G$
-formula
$L_G$
-formula
![]() $\varphi (x)$
, let
$\varphi (x)$
, let
![]() $A^{\#}$
be the subset of H defined by
$A^{\#}$
be the subset of H defined by
![]() $\varphi (x)$
. Throughout,
$\varphi (x)$
. Throughout,
![]() ${\cal A}$
denotes a d-closed G-algebra contained in
${\cal A}$
denotes a d-closed G-algebra contained in
![]() ${\mathrm {Def}}(G)$
and
${\mathrm {Def}}(G)$
and
![]() ${\cal B}$
a d-closed H-algebra containing
${\cal B}$
a d-closed H-algebra containing
![]() $A^{\#}$
for all
$A^{\#}$
for all
![]() $A\in {\cal A}$
. We also assume that
$A\in {\cal A}$
. We also assume that
![]() ${\cal B}|_G:=\{B\cap G:B\in {\cal B}\}$
equals
${\cal B}|_G:=\{B\cap G:B\in {\cal B}\}$
equals
![]() ${\cal A}$
.
${\cal A}$
.
Clearly, the function
![]() $\mbox {}^{\#}:{\cal A}\to {\cal B}$
mapping A to
$\mbox {}^{\#}:{\cal A}\to {\cal B}$
mapping A to
![]() $A^{\#}$
is a Boolean algebra monomorphism respecting left translation by elements of G. So we have a dual continuous surjection
$A^{\#}$
is a Boolean algebra monomorphism respecting left translation by elements of G. So we have a dual continuous surjection
![]() $r:S({\cal B})\to S({\cal A})$
, called restriction. When
$r:S({\cal B})\to S({\cal A})$
, called restriction. When
![]() $r(q)=p$
, we say that q extends p and write
$r(q)=p$
, we say that q extends p and write
![]() $p\subseteq q$
.
$p\subseteq q$
.
Remark 2.6. For every
![]() $q\in S({\cal B})$
and
$q\in S({\cal B})$
and
![]() $A\in {\cal A}$
we have that
$A\in {\cal A}$
we have that
![]() $d_qA^{\#}\cap G=d_{r(q)}A$
.
$d_qA^{\#}\cap G=d_{r(q)}A$
.
The model theoretic set-up. This set-up appeared already in Introduction. So we have an L-structure M and
![]() $T=Th(M)$
.
$T=Th(M)$
.
![]() $G=G(M)$
is an infinite group
$G=G(M)$
is an infinite group
![]() $0$
-definable in M and we are interested in the G-flow
$0$
-definable in M and we are interested in the G-flow
![]() $S_{ext,G}(M)$
of external G-types over M. We show how to reduce this set-up to the combinatorial one described above. We proceed as in [Reference Newelski10, Section 2].
$S_{ext,G}(M)$
of external G-types over M. We show how to reduce this set-up to the combinatorial one described above. We proceed as in [Reference Newelski10, Section 2].
For every
![]() $U\in {\mathrm {Def}}_{ext}(M)$
let
$U\in {\mathrm {Def}}_{ext}(M)$
let
![]() $P_U$
be a new relational symbol and let
$P_U$
be a new relational symbol and let
![]() $L_{ext,M}= L\cup \{P_U:U\in {\mathrm {Def}}_{ext}(M)\}$
. Let
$L_{ext,M}= L\cup \{P_U:U\in {\mathrm {Def}}_{ext}(M)\}$
. Let
![]() $M_{ext}$
be the expansion of M to an
$M_{ext}$
be the expansion of M to an
![]() $L_{ext,M}$
-structure, where
$L_{ext,M}$
-structure, where
![]() $P_U$
is interpreted as U.
$P_U$
is interpreted as U.
To compare topological dynamics of flows
![]() $S_{ext,G}(M)$
for various models M of T we need to consider not just elementary, but rather
$S_{ext,G}(M)$
for various models M of T we need to consider not just elementary, but rather
![]() $*$
-elementary extensions. We say that an L-structure N is a
$*$
-elementary extensions. We say that an L-structure N is a
![]() $*$
-elementary extension of M (and write
$*$
-elementary extension of M (and write
![]() $M\prec ^* N$
) if
$M\prec ^* N$
) if
![]() $M\prec N$
and the new relational symbols of
$M\prec N$
and the new relational symbols of
![]() $L_{ext,M}$
are identified with some relational symbols of
$L_{ext,M}$
are identified with some relational symbols of
![]() $L_{ext,N}$
so that
$L_{ext,N}$
so that
![]() $M_{ext}\prec N_{ext}|_{L_{ext,M}}$
.
$M_{ext}\prec N_{ext}|_{L_{ext,M}}$
.
It is easy to construct
![]() $*$
-elementary extensions of M. Namely, let
$*$
-elementary extensions of M. Namely, let
![]() $N^0$
be any elementary extension of
$N^0$
be any elementary extension of
![]() $M_{ext}$
and let
$M_{ext}$
and let
![]() $N=N^0|_L$
. For
$N=N^0|_L$
. For
![]() $U\in {\mathrm {Def}}_{ext}(M)$
let
$U\in {\mathrm {Def}}_{ext}(M)$
let
![]() $U^N=P_U(N^0)$
. By [Reference Newelski10, Lemma 2.1],
$U^N=P_U(N^0)$
. By [Reference Newelski10, Lemma 2.1],
![]() $U^N\in {\mathrm {Def}}_{ext}(N)$
, so the identification of
$U^N\in {\mathrm {Def}}_{ext}(N)$
, so the identification of
![]() $P_U$
with
$P_U$
with
![]() $P_{U^N }$
witnesses that
$P_{U^N }$
witnesses that
![]() $M\prec ^* N$
.
$M\prec ^* N$
.
Assume
![]() $M\prec ^* N$
and let
$M\prec ^* N$
and let
![]() $H=G(N)$
. Then
$H=G(N)$
. Then
![]() $G\prec H$
, where G and H are considered with the structure induced from
$G\prec H$
, where G and H are considered with the structure induced from
![]() $M_{ext}$
and
$M_{ext}$
and
![]() $N_{ext}|_{L_{ext,M}}$
, respectively. Let
$N_{ext}|_{L_{ext,M}}$
, respectively. Let
![]() ${\cal A}={\mathrm {Def}}_{ext,G}(M)$
and
${\cal A}={\mathrm {Def}}_{ext,G}(M)$
and
![]() ${\cal B}={\mathrm {Def}}_{ext,G}(N)$
. For
${\cal B}={\mathrm {Def}}_{ext,G}(N)$
. For
![]() $A\in {\cal A}$
let
$A\in {\cal A}$
let
![]() $A^{\#}= P_A(N)$
. By [Reference Newelski10, Lemma 1.2],
$A^{\#}= P_A(N)$
. By [Reference Newelski10, Lemma 1.2],
![]() $G,H,{\cal A}$
and
$G,H,{\cal A}$
and
![]() ${\cal B}$
satisfy the assumptions of combinatorial set-up. So the results on
${\cal B}$
satisfy the assumptions of combinatorial set-up. So the results on
![]() $S({\cal A})$
and
$S({\cal A})$
and
![]() $S({\cal B})$
in the combinatorial set-up will be valid also in the model theoretic set-up.
$S({\cal B})$
in the combinatorial set-up will be valid also in the model theoretic set-up.
3 Weak heirs and weak coheirs
We work in the combinatorial set-up.
Definition 3.1. Assume
![]() $p\in S({\cal A})$
and
$p\in S({\cal A})$
and
![]() $q\in S({\cal B})$
.
$q\in S({\cal B})$
.
![]() $(1)\ q$
is a weak heir of p if
$(1)\ q$
is a weak heir of p if
![]() $d_qA^{\#} = (d_pA)^{\#}$
for every
$d_qA^{\#} = (d_pA)^{\#}$
for every
![]() $A\in {\cal A}$
.
$A\in {\cal A}$
.
![]() $(2)\ q$
is a weak coheir of p if for every
$(2)\ q$
is a weak coheir of p if for every
![]() $A\in {\cal A}$
and
$A\in {\cal A}$
and
![]() $s\in S({\cal B})$
we have that
$s\in S({\cal B})$
we have that
In (2) “
![]() $\iff $
” may be equivalently replaced by “
$\iff $
” may be equivalently replaced by “
![]() $\Rightarrow $
” and also by Remark 2.6,
$\Rightarrow $
” and also by Remark 2.6,
![]() $d_sA^{\#}\cap G=d_{r(s)}A$
. In the model-theoretic set-up the definition of weak heir appeared already in [Reference Newelski10].
$d_sA^{\#}\cap G=d_{r(s)}A$
. In the model-theoretic set-up the definition of weak heir appeared already in [Reference Newelski10].
Lemma 3.2. Assume q is a weak heir or weak coheir of p. Then
![]() $p\subseteq q$
.
$p\subseteq q$
.
Proof Suppose that
![]() $p\not \subseteq q$
. Hence for some
$p\not \subseteq q$
. Hence for some
![]() $A\in p$
we have that
$A\in p$
we have that
![]() $A^{\#}\not \in q$
. Therefore
$A^{\#}\not \in q$
. Therefore
![]() $e\in d_pA$
and
$e\in d_pA$
and
![]() $e\not \in d_qA^{\#}$
. So also
$e\not \in d_qA^{\#}$
. So also
![]() $e\in (d_pA)^{\#}$
and
$e\in (d_pA)^{\#}$
and
![]() $(d_pA)^{\#}\neq d_qA^{\#}$
, showing that q is not a weak heir of p.
$(d_pA)^{\#}\neq d_qA^{\#}$
, showing that q is not a weak heir of p.
Let
![]() $\hat {e}=\{B\in {\cal B}: e\in {\cal B}\}$
. So
$\hat {e}=\{B\in {\cal B}: e\in {\cal B}\}$
. So
![]() $\hat {e}\in S({\cal B})$
. We have that
$\hat {e}\in S({\cal B})$
. We have that
![]() $d_{\hat {e}}A^{\#}=A^{\#}\not \in q$
and
$d_{\hat {e}}A^{\#}=A^{\#}\not \in q$
and
![]() $d_{\hat {e}}A^{\#}\cap G=d_{r(\hat {e})}A=A\in p$
, so q is not a weak coheir of p.
$d_{\hat {e}}A^{\#}\cap G=d_{r(\hat {e})}A=A\in p$
, so q is not a weak coheir of p.
By Lemma 3.2, in Definition 3.1 if q is a weak heir or weak coheir of p, then
![]() $p=r(q)$
. Therefore in this situation we say also that q is a weak [co]heir over
$p=r(q)$
. Therefore in this situation we say also that q is a weak [co]heir over
![]() ${\cal A}$
. Regarding Definition 3.1(2),
${\cal A}$
. Regarding Definition 3.1(2),
![]() $d_{r(s)}A\in r(q)$
is equivalent to
$d_{r(s)}A\in r(q)$
is equivalent to
![]() $(d_{r(s)}A)^{\#}\in q$
.
$(d_{r(s)}A)^{\#}\in q$
.
In the model theoretic set-up, when
![]() $p\in S_{ext,G}(M)$
and
$p\in S_{ext,G}(M)$
and
![]() $q\in S_{ext,G}(N)$
is a weak [co]heir of p, we say that q is a weak [co]heir over N.
$q\in S_{ext,G}(N)$
is a weak [co]heir of p, we say that q is a weak [co]heir over N.
The next lemma provides an alternative definition of weak heir and weak coheir.
Lemma 3.3. Assume
![]() $p\in S({\cal A})$
and
$p\in S({\cal A})$
and
![]() $q\in S({\cal B})$
.
$q\in S({\cal B})$
.
![]() $(1)\ q$
is a weak heir of p iff for every
$(1)\ q$
is a weak heir of p iff for every
![]() $A,B\in {\cal A}$
and
$A,B\in {\cal A}$
and
![]() $h\in H$
, if
$h\in H$
, if
![]() $h\in B^{\#}$
and
$h\in B^{\#}$
and
![]() $h^{-1}A^{\#}\in q$
, then for some
$h^{-1}A^{\#}\in q$
, then for some
![]() $g\in G$
,
$g\in G$
,
![]() $g\in B$
and
$g\in B$
and
![]() $g^{-1}A\in p$
.
$g^{-1}A\in p$
.
![]() $(2)\ q$
is a weak coheir of p iff
$(2)\ q$
is a weak coheir of p iff
![]() $p=r(q)$
and for every
$p=r(q)$
and for every
![]() $A,B\in {\cal A}$
and
$A,B\in {\cal A}$
and
![]() $s\in S({\cal B})$
, if
$s\in S({\cal B})$
, if
![]() $d_sA^{\#}\cap B^{\#}\in q$
, then
$d_sA^{\#}\cap B^{\#}\in q$
, then
![]() $d_sA^{\#}\cap B^{\#}\cap G\neq \emptyset $
.
$d_sA^{\#}\cap B^{\#}\cap G\neq \emptyset $
.
Proof (1)
![]() $\Rightarrow $
Assume q is a weak heir of p. By Lemma 3.2,
$\Rightarrow $
Assume q is a weak heir of p. By Lemma 3.2,
![]() $p=r(q)$
. Take any
$p=r(q)$
. Take any
![]() $A,B\in {\cal A}$
and
$A,B\in {\cal A}$
and
![]() $h\in H$
satisfying
$h\in H$
satisfying
![]() $h\in B^{\#}$
and
$h\in B^{\#}$
and
![]() $h^{-1}A^{\#}\in q$
. Then
$h^{-1}A^{\#}\in q$
. Then
Since
![]() $G\prec H$
, there is
$G\prec H$
, there is
![]() $g\in G$
with
$g\in G$
with
![]() $g\in d_{r(q)}A\cap B$
. It follows that
$g\in d_{r(q)}A\cap B$
. It follows that
![]() $g\in B$
and
$g\in B$
and
![]() $g^{-1}A\in r(q)$
, as required.
$g^{-1}A\in r(q)$
, as required.
![]() $\Leftarrow $
Suppose for contradiction that the right-hand side condition holds and q is not a weak heir of p. Hence
$\Leftarrow $
Suppose for contradiction that the right-hand side condition holds and q is not a weak heir of p. Hence
![]() $(d_pA)^{\#}\neq d_qA^{\#}$
for some
$(d_pA)^{\#}\neq d_qA^{\#}$
for some
![]() $A\in {\cal A}$
. Replacing A with
$A\in {\cal A}$
. Replacing A with
![]() $G\setminus A$
if necessary, we can assume that there is
$G\setminus A$
if necessary, we can assume that there is
![]() $h\in d_qA^{\#}\setminus (d_pA)^{\#}$
.
$h\in d_qA^{\#}\setminus (d_pA)^{\#}$
.
Let
![]() $B=G\setminus d_pA$
. Then
$B=G\setminus d_pA$
. Then
![]() $h\in B^{\#}$
and
$h\in B^{\#}$
and
![]() $h^{-1}A^{\#}\in q$
, so by our assumptions there is
$h^{-1}A^{\#}\in q$
, so by our assumptions there is
![]() $g\in G$
satisfying
$g\in G$
satisfying
![]() $g\in B$
and
$g\in B$
and
![]() $g^{-1}A\in p$
. It follows that
$g^{-1}A\in p$
. It follows that
![]() $g\in B$
and
$g\in B$
and
![]() $g\in d_pA$
, a contradiction.
$g\in d_pA$
, a contradiction.
(2)
![]() $\Rightarrow $
Assume q is a weak coheir of p. By Lemma 3.2,
$\Rightarrow $
Assume q is a weak coheir of p. By Lemma 3.2,
![]() $p=r(q)$
. Take any
$p=r(q)$
. Take any
![]() $A,B\in {\cal A}$
and
$A,B\in {\cal A}$
and
![]() $s\in S({\cal B})$
with
$s\in S({\cal B})$
with
![]() $d_sA^{\#}\cap B^{\#}\in q$
. By the definition of weak coheir we get that
$d_sA^{\#}\cap B^{\#}\in q$
. By the definition of weak coheir we get that
hence
![]() $d_{r(s)}A\cap B\neq \emptyset $
. So the right-hand side condition holds.
$d_{r(s)}A\cap B\neq \emptyset $
. So the right-hand side condition holds.
![]() $\Leftarrow $
Suppose for contradiction that the right-hand side condition holds and q is not a weak coheir of
$\Leftarrow $
Suppose for contradiction that the right-hand side condition holds and q is not a weak coheir of
![]() $p=r(q)$
. Hence for some
$p=r(q)$
. Hence for some
![]() $A\in {\cal A}$
and
$A\in {\cal A}$
and
![]() $s\in S({\cal B})$
we have
$s\in S({\cal B})$
we have
Replacing A with
![]() $G\setminus A$
if necessary, we can assume that
$G\setminus A$
if necessary, we can assume that
![]() $d_sA^{\#}\setminus (d_{r(s)}A)^{\#}\in q$
. Let
$d_sA^{\#}\setminus (d_{r(s)}A)^{\#}\in q$
. Let
![]() $B=G\setminus d_{r(s)}A$
. Then
$B=G\setminus d_{r(s)}A$
. Then
![]() $d_sA^{\#}\cap B^{\#}\in q$
, but
$d_sA^{\#}\cap B^{\#}\in q$
, but
![]() $d_sA^{\#}\cap B^{\#}\cap G=d_{r(s)}A\cap B=\emptyset $
, a contradiction.
$d_sA^{\#}\cap B^{\#}\cap G=d_{r(s)}A\cap B=\emptyset $
, a contradiction.
We define coheirs in the standard way.
Definition 3.4.
![]() $($
1
$($
1
![]() $)$
Let
$)$
Let
![]() $q\in S({\cal B})$
. We say that q is a coheir over
$q\in S({\cal B})$
. We say that q is a coheir over
![]() ${\cal A}$
if
${\cal A}$
if
![]() $B\cap G\neq \emptyset $
for every
$B\cap G\neq \emptyset $
for every
![]() $B\in q$
.
$B\in q$
.
![]() $(2)$
For
$(2)$
For
![]() $p\in S({\cal A})$
let
$p\in S({\cal A})$
let
So
![]() $p^{{\cal B}}\in S({\cal B})$
is a coheir over
$p^{{\cal B}}\in S({\cal B})$
is a coheir over
![]() ${\cal A}$
extending p.
${\cal A}$
extending p.
Remark 3.5. Assume
![]() $q\in S({\cal B})$
. Then q is a coheir over
$q\in S({\cal B})$
. Then q is a coheir over
![]() ${\cal A}$
iff
${\cal A}$
iff
![]() $q=p^{{\cal B}}$
, where
$q=p^{{\cal B}}$
, where
![]() $p=r(q)$
. In particular, every ultrafilter
$p=r(q)$
. In particular, every ultrafilter
![]() $p\in S({\cal A})$
has a unique coheir extension
$p\in S({\cal A})$
has a unique coheir extension
![]() $p^{{\cal B}}$
in
$p^{{\cal B}}$
in
![]() $S({\cal B})$
and the function
$S({\cal B})$
and the function
![]() $p\mapsto p^{{\cal B}}$
is a continuous embedding
$p\mapsto p^{{\cal B}}$
is a continuous embedding
![]() $S({\cal A})\to S({\cal B})$
.
$S({\cal A})\to S({\cal B})$
.
So if
![]() $q\in S({\cal B})$
is a coheir over
$q\in S({\cal B})$
is a coheir over
![]() ${\cal A}$
, we say also that q is a coheir extension of
${\cal A}$
, we say also that q is a coheir extension of
![]() $p=r(q)$
.
$p=r(q)$
.
We can identify formulas
![]() $\varphi (x)$
of
$\varphi (x)$
of
![]() $L_G$
with parameters from H with the subsets of H they define. For
$L_G$
with parameters from H with the subsets of H they define. For
![]() $A,B\in {\cal A}$
let
$A,B\in {\cal A}$
let
![]() $\varphi _{A,B}(x,y)$
be a formula of
$\varphi _{A,B}(x,y)$
be a formula of
![]() $L_G$
(with parameters from G) saying that “
$L_G$
(with parameters from G) saying that “
![]() $x\in y^{-1}A\land y\in B$
”. The condition in Lemma 3.3(1) characterizing weak heirs says that if there is
$x\in y^{-1}A\land y\in B$
”. The condition in Lemma 3.3(1) characterizing weak heirs says that if there is
![]() $h\in H$
with
$h\in H$
with
![]() $\varphi _{A,B}(x,h)\in q$
, then there is
$\varphi _{A,B}(x,h)\in q$
, then there is
![]() $g\in G$
with
$g\in G$
with
![]() $\varphi _{A,B}(x,g)\in q$
. This shows that the notion of weak heir is indeed a weakening of the notion of heir. Similarly by Lemmas 3.5 and 3.3(2) we see that every coheir is a weak coheir. Consequently we get the following lemma.
$\varphi _{A,B}(x,g)\in q$
. This shows that the notion of weak heir is indeed a weakening of the notion of heir. Similarly by Lemmas 3.5 and 3.3(2) we see that every coheir is a weak coheir. Consequently we get the following lemma.
Lemma 3.6. Every
![]() $p\in S({\cal A})$
extends to a weak heir and to a weak coheir in
$p\in S({\cal A})$
extends to a weak heir and to a weak coheir in
![]() $S({\cal B})$
.
$S({\cal B})$
.
Proof Let
![]() $q_0=p^{{\cal B}}$
. By Remark 3.5 and Lemma 3.3(2),
$q_0=p^{{\cal B}}$
. By Remark 3.5 and Lemma 3.3(2),
![]() $q_0$
is a coheir of p, hence a weak coheir of p. Regarding the weak heir case, first extend p to a complete type
$q_0$
is a coheir of p, hence a weak coheir of p. Regarding the weak heir case, first extend p to a complete type
![]() $p'\in S(G)$
and let
$p'\in S(G)$
and let
![]() $q_1'\in S(H)$
be a heir extension of
$q_1'\in S(H)$
be a heir extension of
![]() $p'$
. We can regard
$p'$
. We can regard
![]() $q_1'$
as an ultrafilter in the algebra
$q_1'$
as an ultrafilter in the algebra
![]() ${\mathrm {Def}}(H)$
. Extend
${\mathrm {Def}}(H)$
. Extend
![]() $q_1'$
to
$q_1'$
to
![]() $q_1"\in \beta H$
and let
$q_1"\in \beta H$
and let
![]() $q_1=q_1"\cap {\cal B}$
. By the discussion before Lemma 3.6,
$q_1=q_1"\cap {\cal B}$
. By the discussion before Lemma 3.6,
![]() $q_1\in S({\cal B})$
is a weak heir of p.
$q_1\in S({\cal B})$
is a weak heir of p.
Let
![]() $CH({\cal B}/{\cal A})=\{q\in S({\cal B}): q \mbox { is a coheir over }{\cal A}\}$
and similarly define the sets
$CH({\cal B}/{\cal A})=\{q\in S({\cal B}): q \mbox { is a coheir over }{\cal A}\}$
and similarly define the sets
![]() $WCH({\cal B}/{\cal A})$
and
$WCH({\cal B}/{\cal A})$
and
![]() $WH({\cal B}/{\cal A})$
of weak coheirs and weak heirs, respectively.
$WH({\cal B}/{\cal A})$
of weak coheirs and weak heirs, respectively.
Remark 3.7.
![]() $CH({\cal B}/{\cal A})$
and
$CH({\cal B}/{\cal A})$
and
![]() $WCH({\cal B}/{\cal A})$
are closed subsets of
$WCH({\cal B}/{\cal A})$
are closed subsets of
![]() $S({\cal B})$
and
$S({\cal B})$
and
![]() $CH({\cal B}/{\cal A})\subseteq WCH({\cal B}/{\cal A})$
. The sets
$CH({\cal B}/{\cal A})\subseteq WCH({\cal B}/{\cal A})$
. The sets
![]() $CH({\cal B}/{\cal A}), WCH({\cal B}/{\cal A})$
and
$CH({\cal B}/{\cal A}), WCH({\cal B}/{\cal A})$
and
![]() $WH({\cal B}/{\cal A})$
are non-empty.
$WH({\cal B}/{\cal A})$
are non-empty.
Even though the set
![]() $WH({\cal B}/{\cal A})$
need not be closed (see an example at the end of this paper), it is a union of certain closed sets. For
$WH({\cal B}/{\cal A})$
need not be closed (see an example at the end of this paper), it is a union of certain closed sets. For
![]() $p\in S({\cal A})$
let
$p\in S({\cal A})$
let
![]() $WH_p({\cal B})=\{q\in WH({\cal B}/{\cal A}): p\subseteq q\}$
.
$WH_p({\cal B})=\{q\in WH({\cal B}/{\cal A}): p\subseteq q\}$
.
Lemma 3.8. The set
![]() $WH_p({\cal B})$
is closed and non-empty.
$WH_p({\cal B})$
is closed and non-empty.
![]() $WH({\cal B}/{\cal A})=\bigcup _{p\in S({\cal A})}WH_p({\cal B})$
.
$WH({\cal B}/{\cal A})=\bigcup _{p\in S({\cal A})}WH_p({\cal B})$
.
Proof
![]() $WH_p({\cal B})\neq \emptyset $
by Lemma 3.6. Let
$WH_p({\cal B})\neq \emptyset $
by Lemma 3.6. Let
By Definition 3.1(1),
![]() $WH_p({\cal B})=\{q\in S({\cal B}): p_{{\cal B}}\subseteq q\}$
, so it is closed. The last part of the lemma is obvious.
$WH_p({\cal B})=\{q\in S({\cal B}): p_{{\cal B}}\subseteq q\}$
, so it is closed. The last part of the lemma is obvious.
We see that our definitions of weak heir and weak coheir consist in restricting the definitions of heir and coheir to some special formulas. The next proposition justifies this particular restriction.
Proposition 3.9. Assume
![]() $q\in S({\cal B})$
.
$q\in S({\cal B})$
.
![]() $(1)\ q$
is a weak heir over
$(1)\ q$
is a weak heir over
![]() ${\cal A}$
iff
${\cal A}$
iff
![]() $r(s*q)=r(s)*r(q)$
for every
$r(s*q)=r(s)*r(q)$
for every
![]() $s\in S({\cal B})$
.
$s\in S({\cal B})$
.
![]() $(2)\ q$
is a weak coheir over
$(2)\ q$
is a weak coheir over
![]() ${\cal A}$
iff
${\cal A}$
iff
![]() $r(q*s)=r(q)*r(s)$
for every
$r(q*s)=r(q)*r(s)$
for every
![]() $s\in S({\cal B})$
.
$s\in S({\cal B})$
.
Proof Note that for any
![]() $A\in {\cal A}$
and
$A\in {\cal A}$
and
![]() $s\in S({\cal B})$
,
$s\in S({\cal B})$
,
(1) If q is a weak heir over
![]() ${\cal A}$
, then the right-hand sides of the above equivalences are equivalent for each
${\cal A}$
, then the right-hand sides of the above equivalences are equivalent for each
![]() $A,s$
, so
$A,s$
, so
![]() $r(s*q)=r(s)*r(q)$
. On the other hand, if q is not a weak heir over
$r(s*q)=r(s)*r(q)$
. On the other hand, if q is not a weak heir over
![]() ${\cal A}$
, then
${\cal A}$
, then
![]() $d_qA^{\#}\neq (d_{r(q)}A)^{\#}$
for some
$d_qA^{\#}\neq (d_{r(q)}A)^{\#}$
for some
![]() $A\in {\cal A}$
. Thus we can find
$A\in {\cal A}$
. Thus we can find
![]() $s\in S({\cal B})$
with
$s\in S({\cal B})$
with
![]() $d_qA^{\#}\triangle (d_{r(q)}A)^{\#}\in s$
and then
$d_qA^{\#}\triangle (d_{r(q)}A)^{\#}\in s$
and then
![]() $r(s*q)\neq r(s)*r(q)$
.
$r(s*q)\neq r(s)*r(q)$
.
(2) follows directly from definition.
In fact, Proposition 3.9(1)
![]() $\Rightarrow $
was already proved in [Reference Newelski10] in the model theoretic set-up.
$\Rightarrow $
was already proved in [Reference Newelski10] in the model theoretic set-up.
For
![]() $h\in H$
let
$h\in H$
let
![]() $\hat {h}=\{B\in {\cal B}: h\in H\}$
and
$\hat {h}=\{B\in {\cal B}: h\in H\}$
and
![]() $\hat {H}=\{\hat {h}:h\in H\}$
. Clearly
$\hat {H}=\{\hat {h}:h\in H\}$
. Clearly
![]() $\hat {H}$
is a dense subset of
$\hat {H}$
is a dense subset of
![]() $S({\cal B})$
. It is easy to see that the function
$S({\cal B})$
. It is easy to see that the function
![]() $f:H\to \hat {H}$
mapping h to
$f:H\to \hat {H}$
mapping h to
![]() $\hat {h}$
is a
$\hat {h}$
is a
![]() $*$
-homomorphism, so
$*$
-homomorphism, so
![]() $\hat {H}$
is a dense subgroup of
$\hat {H}$
is a dense subgroup of
![]() $S({\cal B})$
and f is a group epimorphism. Since
$S({\cal B})$
and f is a group epimorphism. Since
![]() $*$
is a continuous in the first coordinate we get the following corollary.
$*$
is a continuous in the first coordinate we get the following corollary.
Corollary 3.10. Assume
![]() $q\in S({\cal B})$
. Then q is a weak heir over
$q\in S({\cal B})$
. Then q is a weak heir over
![]() ${\cal A}$
iff
${\cal A}$
iff
![]() $r(\hat {h}*q)=r(\hat {h}) * r(q)$
for every
$r(\hat {h}*q)=r(\hat {h}) * r(q)$
for every
![]() $h\in H$
.
$h\in H$
.
Notice also that
![]() $\hat {h}*q=hq$
.
$\hat {h}*q=hq$
.
Corollary 3.11. The sets
![]() $CH({\cal B}/{\cal A})\subseteq WCH({\cal B}/{\cal A})$
and
$CH({\cal B}/{\cal A})\subseteq WCH({\cal B}/{\cal A})$
and
![]() $WH({\cal B}/{\cal A})$
are sub-semigroups of
$WH({\cal B}/{\cal A})$
are sub-semigroups of
![]() $S({\cal B})$
and restrictions
$S({\cal B})$
and restrictions
![]() $r:WCH({\cal B}/{\cal A})\to S({\cal A})$
and
$r:WCH({\cal B}/{\cal A})\to S({\cal A})$
and
![]() $r:WH({\cal B}/{\cal A})\to S({\cal A})$
are
$r:WH({\cal B}/{\cal A})\to S({\cal A})$
are
![]() $*$
-epimorphisms. The restriction
$*$
-epimorphisms. The restriction
![]() $r:CH({\cal B}/{\cal A})\to S({\cal A})$
is a semigroup isomorphism and homeomorphism. Its inverse is the function
$r:CH({\cal B}/{\cal A})\to S({\cal A})$
is a semigroup isomorphism and homeomorphism. Its inverse is the function
![]() $j:S({\cal A})\to CH({\cal B}/{\cal A})$
mapping p to
$j:S({\cal A})\to CH({\cal B}/{\cal A})$
mapping p to
![]() $p^{{\cal B}}$
.
$p^{{\cal B}}$
.
Proof We prove that the set
![]() $CH({\cal B}/{\cal A})$
is closed under
$CH({\cal B}/{\cal A})$
is closed under
![]() $*$
, the other claims of the corollary follow directly from earlier results. First, for every
$*$
, the other claims of the corollary follow directly from earlier results. First, for every
![]() $q\in CH({\cal B}/{\cal A})$
and
$q\in CH({\cal B}/{\cal A})$
and
![]() $A\in {\cal B}$
we have that
$A\in {\cal B}$
we have that
Therefore for
![]() $p,q\in CH({\cal B}/{\cal A})$
and
$p,q\in CH({\cal B}/{\cal A})$
and
![]() $A\in {\cal B}$
we have that
$A\in {\cal B}$
we have that
Hence
![]() $A\in p*q$
implies
$A\in p*q$
implies
![]() $A\cap G\neq \emptyset $
and
$A\cap G\neq \emptyset $
and
![]() $p*q\in CH({\cal B}/{\cal A})$
.
$p*q\in CH({\cal B}/{\cal A})$
.
Even though the left-continuous semigroup
![]() $WH({\cal B}/{\cal A})$
may not be closed, still it has the properties from Fact 2.1 (see Proposition 4.5). In the model theoretic set-up Corollary 3.11 was already partially noticed in earlier papers. Namely in [Reference Newelski9] it was mentioned that the semigroup
$WH({\cal B}/{\cal A})$
may not be closed, still it has the properties from Fact 2.1 (see Proposition 4.5). In the model theoretic set-up Corollary 3.11 was already partially noticed in earlier papers. Namely in [Reference Newelski9] it was mentioned that the semigroup
![]() $S({\cal A})$
is isomorphic to
$S({\cal A})$
is isomorphic to
![]() $CH({\cal B}/{\cal A})$
(suitably rephrased in the model theoretic context) and in [Reference Newelski10] it was proved that
$CH({\cal B}/{\cal A})$
(suitably rephrased in the model theoretic context) and in [Reference Newelski10] it was proved that
![]() $WH({\cal B}/{\cal A})$
is a semigroup and
$WH({\cal B}/{\cal A})$
is a semigroup and
![]() $r:WH({\cal B}/{\cal A})\to S({\cal A})$
is an epimorphism. We shall use Corollary 3.11 later to relate algebraically the Ellis groups of
$r:WH({\cal B}/{\cal A})\to S({\cal A})$
is an epimorphism. We shall use Corollary 3.11 later to relate algebraically the Ellis groups of
![]() $S({\cal A})$
and
$S({\cal A})$
and
![]() $S({\cal B})$
. The semigroup
$S({\cal B})$
. The semigroup
![]() $WH({\cal B}/{\cal A})\cap CH({\cal B}/A)$
contains an important subgroup.
$WH({\cal B}/{\cal A})\cap CH({\cal B}/A)$
contains an important subgroup.
Lemma 3.12. Let
![]() $\hat {G}=\{\hat {h}\in \hat {H}: h\in G\}$
.
$\hat {G}=\{\hat {h}\in \hat {H}: h\in G\}$
.
(1)
![]() $\hat {G}$
is a subgroup of
$\hat {G}$
is a subgroup of
![]() $S({\cal B})$
and the mapping
$S({\cal B})$
and the mapping
![]() $g\mapsto \hat {g}$
is a group epimorphism
$g\mapsto \hat {g}$
is a group epimorphism
![]() $G\to \hat {G}$
.
$G\to \hat {G}$
.
(2)
![]() $\hat {G}\subseteq WH({\cal B}/{\cal A})\cap CH({\cal B}/A)$
,
$\hat {G}\subseteq WH({\cal B}/{\cal A})\cap CH({\cal B}/A)$
,
![]() $\hat {e}$
is the unique identity element in
$\hat {e}$
is the unique identity element in
![]() $S({\cal B})$
.
$S({\cal B})$
.
![]() $(3)$
For every
$(3)$
For every
![]() $q\in S({\cal B})$
and
$q\in S({\cal B})$
and
![]() $g\in G$
we have that
$g\in G$
we have that
![]() $(4)$
Like
$(4)$
Like
![]() $(3)$
, but with
$(3)$
, but with
![]() $WH$
replaced by
$WH$
replaced by
![]() $WCH$
[or
$WCH$
[or
![]() $CH$
].
$CH$
].
Proof The proof is by revealing the definitions and applying Proposition 3.9 in (3) and (4).
By Fact 2.3(3), elements of
![]() $S({\cal A})$
and
$S({\cal A})$
and
![]() $S({\cal B})$
may be regarded as functions from the Ellis semigroups
$S({\cal B})$
may be regarded as functions from the Ellis semigroups
![]() $E(S({\cal A}))$
and
$E(S({\cal A}))$
and
![]() $E(S({\cal B}))$
. In Proposition 3.13 we give yet another characterization of weak [co]heirs in terms of functions from
$E(S({\cal B}))$
. In Proposition 3.13 we give yet another characterization of weak [co]heirs in terms of functions from
![]() $E(S({\cal A}))$
and
$E(S({\cal A}))$
and
![]() $E(S({\cal B}))$
.
$E(S({\cal B}))$
.
Let
![]() ${\cal A}^{\#}$
be the H-subalgebra of
${\cal A}^{\#}$
be the H-subalgebra of
![]() ${\cal B}$
generated by the set
${\cal B}$
generated by the set
![]() $\{ A^{\#} : A \in {\cal A} \}$
. So
$\{ A^{\#} : A \in {\cal A} \}$
. So
![]() ${\cal A}^{\#}$
need not be d-closed. Each
${\cal A}^{\#}$
need not be d-closed. Each
![]() $q_0 \in S({\cal A})$
has a unique weak heir in
$q_0 \in S({\cal A})$
has a unique weak heir in
![]() $S({\cal A}^{\#})$
, that is, a type
$S({\cal A}^{\#})$
, that is, a type
![]() $q \in S({\cal A}^{\#})$
such that
$q \in S({\cal A}^{\#})$
such that
![]() $d_q A^{\#} = (d_{q_0} A)^{\#}$
for each
$d_q A^{\#} = (d_{q_0} A)^{\#}$
for each
![]() $A \in {\cal A}$
. We write
$A \in {\cal A}$
. We write
![]() $(q_0)^{\#} := q$
.
$(q_0)^{\#} := q$
.
Consider any
![]() $p_0 \in S({\cal A}),p \in S({\cal B})$
and let
$p_0 \in S({\cal A}),p \in S({\cal B})$
and let
![]() $f_0 \in E(S({\cal A}))$
,
$f_0 \in E(S({\cal A}))$
,
![]() $f \in E(S({\cal B}))$
correspond to
$f \in E(S({\cal B}))$
correspond to
![]() $p_0$
and p via the standard isomorphisms from Fact 2.3(3). p determines a function
$p_0$
and p via the standard isomorphisms from Fact 2.3(3). p determines a function
![]() $f^{\#}:S({\cal A}^{\#})\to S({\cal A}^{\#})$
defined by
$f^{\#}:S({\cal A}^{\#})\to S({\cal A}^{\#})$
defined by
![]() $f^{\#}(q) = p * q$
, where
$f^{\#}(q) = p * q$
, where
![]() $p*q\in S({\cal A}^{\#})$
is defined by the formula from Fact 2.3(2). Since
$p*q\in S({\cal A}^{\#})$
is defined by the formula from Fact 2.3(2). Since
![]() $p*q=\lim _{h\to p}hq$
, we have that
$p*q=\lim _{h\to p}hq$
, we have that
![]() $f^{\#}\in E(S({\cal A}^{\#}))$
and
$f^{\#}\in E(S({\cal A}^{\#}))$
and
![]() $f^{\#}$
is the unique function from
$f^{\#}$
is the unique function from
![]() $E(S({\cal A}^{\#}))$
such that the following diagram commutes.
$E(S({\cal A}^{\#}))$
such that the following diagram commutes.

Also using the formula for
![]() $*$
from Fact 2.3(2) we get that
$*$
from Fact 2.3(2) we get that
![]() $d_{p*q}=d_p\circ d_q$
for
$d_{p*q}=d_p\circ d_q$
for
![]() $p\in S({\cal B})$
and
$p\in S({\cal B})$
and
![]() $q\in S({\cal A}^{\#})$
.
$q\in S({\cal A}^{\#})$
.
Proposition 3.13. Assume
![]() $p_0\in S({\cal A}),p\in S({\cal B})$
and
$p_0\in S({\cal A}),p\in S({\cal B})$
and
![]() $f_0,f,f^{\#}$
are defined as above.
$f_0,f,f^{\#}$
are defined as above.
(1)
![]() $p$
extends
$p$
extends
![]() $p_0$
iff the following diagram commutes.
$p_0$
iff the following diagram commutes.

(2)
![]() $p$
is a weak heir of
$p$
is a weak heir of
![]() $p_0$
iff the following diagram commutes.
$p_0$
iff the following diagram commutes.

(3)
![]() $p$
is a weak coheir of
$p$
is a weak coheir of
![]() $p_0$
iff the following diagram commutes.
$p_0$
iff the following diagram commutes.

Proof (1) We have that
 $$ \begin{align*} p \text{ extends } p_0 & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, \big( d_q A \in p_0 \Leftrightarrow (d_q A)^{\#} \in p \big) \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, \big( d_q A \in p_0 \Leftrightarrow d_{q^{\#}} A^{\#} \in p \big) \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, \big( A \in p_0 \ast q \Leftrightarrow A^{\#} \in p \ast q^{\#} \big) \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, \big( A \in f_0(q) \Leftrightarrow A^{\#} \in f^{\#}(q^{\#}) \big) \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, \big( A \in f_0(q) \Leftrightarrow A \in r(f^{\#}(q^{\#})) \big) \end{align*} $$
$$ \begin{align*} p \text{ extends } p_0 & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, \big( d_q A \in p_0 \Leftrightarrow (d_q A)^{\#} \in p \big) \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, \big( d_q A \in p_0 \Leftrightarrow d_{q^{\#}} A^{\#} \in p \big) \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, \big( A \in p_0 \ast q \Leftrightarrow A^{\#} \in p \ast q^{\#} \big) \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, \big( A \in f_0(q) \Leftrightarrow A^{\#} \in f^{\#}(q^{\#}) \big) \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, \big( A \in f_0(q) \Leftrightarrow A \in r(f^{\#}(q^{\#})) \big) \end{align*} $$
and the last condition means that the corresponding diagram commutes.
(2) We have that
 $$ \begin{align*} p \text{ is a weak heir of } p_0 & \iff (\forall B \in {\cal A}) \, (d_{p_0} B)^{\#} = d_p B^{\#} \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, (d_{p_0} d_q A)^{\#} = d_p (d_q A)^{\#} \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, (d_{p_0} d_q A)^{\#} = d_p d_{q^{\#}} A^{\#} \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, (d_{p_0 * q} A)^{\#} = d_{p * q^{\#}} A^{\#} \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, d_{(p_0 * q)^{\#}} A^{\#} = d_{p * q^{\#}} A^{\#} \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, d_{f_0(q)^{\#}} A^{\#} = d_{f^{\#}(q^{\#})} A^{\#}. \end{align*} $$
$$ \begin{align*} p \text{ is a weak heir of } p_0 & \iff (\forall B \in {\cal A}) \, (d_{p_0} B)^{\#} = d_p B^{\#} \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, (d_{p_0} d_q A)^{\#} = d_p (d_q A)^{\#} \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, (d_{p_0} d_q A)^{\#} = d_p d_{q^{\#}} A^{\#} \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, (d_{p_0 * q} A)^{\#} = d_{p * q^{\#}} A^{\#} \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, d_{(p_0 * q)^{\#}} A^{\#} = d_{p * q^{\#}} A^{\#} \\[1ex] & \iff (\forall q \in S({\cal A}))(\forall A \in {\cal A}) \, d_{f_0(q)^{\#}} A^{\#} = d_{f^{\#}(q^{\#})} A^{\#}. \end{align*} $$
The last condition holds exactly when
![]() $f_0(q)^{\#} = f^{\#}(q^{\#})$
for each
$f_0(q)^{\#} = f^{\#}(q^{\#})$
for each
![]() $q \in S({\cal A})$
, which is equivalent to the commutativity of the corresponding diagram.
$q \in S({\cal A})$
, which is equivalent to the commutativity of the corresponding diagram.
(3) By Proposition 3.9 we have that
 $$ \begin{align*} p \text{ is a weak coheir of } p_0 & \iff (\forall q \in S({\cal B})) \, r(p * q) = p_0 * r(q) \\[1ex] & \iff (\forall q \in S({\cal B})) \, r(f(q)) = f_0(r(q)), \end{align*} $$
$$ \begin{align*} p \text{ is a weak coheir of } p_0 & \iff (\forall q \in S({\cal B})) \, r(p * q) = p_0 * r(q) \\[1ex] & \iff (\forall q \in S({\cal B})) \, r(f(q)) = f_0(r(q)), \end{align*} $$
where
![]() $r:S({\cal B})\to S({\cal A})$
is restriction. The last condition is equivalent to the commutativity of the outer rectangle in the following diagram.
$r:S({\cal B})\to S({\cal A})$
is restriction. The last condition is equivalent to the commutativity of the outer rectangle in the following diagram.

Since the upper rectangle is commutative and
![]() $r : S({\cal B}) \to S({\cal A}^{\#})$
is surjective, the condition is equivalent to the commutativity of the lower rectangle.
$r : S({\cal B}) \to S({\cal A}^{\#})$
is surjective, the condition is equivalent to the commutativity of the lower rectangle.
In order to be able to compare the flows
![]() $S({\cal A})$
and
$S({\cal A})$
and
![]() $S({\cal B})$
we need a way to lift minimal left ideals in
$S({\cal B})$
we need a way to lift minimal left ideals in
![]() $S({\cal A})$
to minimal left ideals in
$S({\cal A})$
to minimal left ideals in
![]() $S({\cal B})$
. This uses weak heirs and was already done in [Reference Newelski10, Lemma 2.4] in the model theoretic set-up. Here we easily adapt the argument from [Reference Newelski10]. Recall from topological dynamics that a point p in a G-flow X is called almost periodic if p belongs to a minimal subflow of X, equivalently the subflow
$S({\cal B})$
. This uses weak heirs and was already done in [Reference Newelski10, Lemma 2.4] in the model theoretic set-up. Here we easily adapt the argument from [Reference Newelski10]. Recall from topological dynamics that a point p in a G-flow X is called almost periodic if p belongs to a minimal subflow of X, equivalently the subflow
![]() $cl(Gp)\subseteq X$
generated by p is minimal. In our situation the minimal flows in
$cl(Gp)\subseteq X$
generated by p is minimal. In our situation the minimal flows in
![]() $S({\cal A})$
and
$S({\cal A})$
and
![]() $S({\cal B})$
are exactly the minimal left ideals. Their elements are exactly the almost periodic points. The next lemma is the main place where we use the assumption that
$S({\cal B})$
are exactly the minimal left ideals. Their elements are exactly the almost periodic points. The next lemma is the main place where we use the assumption that
![]() $G\prec H$
in the combinatorial set-up and
$G\prec H$
in the combinatorial set-up and
![]() $M\prec ^* N$
in the model theoretic set-up.
$M\prec ^* N$
in the model theoretic set-up.
Lemma 3.14.
![]() $(1)$
Assume
$(1)$
Assume
![]() $q\in S({\cal B})$
is a weak heir of
$q\in S({\cal B})$
is a weak heir of
![]() $p\in S({\cal A})$
. Then
$p\in S({\cal A})$
. Then
![]() $r[cl(Hq)]=cl(Gp)$
. If moreover p is almost periodic, then
$r[cl(Hq)]=cl(Gp)$
. If moreover p is almost periodic, then
![]() $r[cl(Hq')]=cl(Gp)$
for every
$r[cl(Hq')]=cl(Gp)$
for every
![]() $q'\in cl(Hq)$
.
$q'\in cl(Hq)$
.
![]() $(2)$
Assume
$(2)$
Assume
![]() $I\triangleleft _mS({\cal A})$
. Then there is
$I\triangleleft _mS({\cal A})$
. Then there is
![]() $I'\triangleleft _mS({\cal B})$
with
$I'\triangleleft _mS({\cal B})$
with
![]() $r[I']=I$
. In particular, every almost periodic
$r[I']=I$
. In particular, every almost periodic
![]() $p\in S({\cal A})$
extends to an almost periodic
$p\in S({\cal A})$
extends to an almost periodic
![]() $q\in S({\cal B})$
.
$q\in S({\cal B})$
.
Proof (1) For
![]() $h\in H$
we have that
$h\in H$
we have that
![]() $hq=\hat {h}*q$
. Since
$hq=\hat {h}*q$
. Since
![]() $*$
is left-continuous and the set
$*$
is left-continuous and the set
![]() $\{\hat {h}:h\in H\}$
is dense in
$\{\hat {h}:h\in H\}$
is dense in
![]() $S({\cal B})$
, we have that
$S({\cal B})$
, we have that
![]() $cl(Hq)=S({\cal B})*q$
. Proposition 3.9(1) implies that
$cl(Hq)=S({\cal B})*q$
. Proposition 3.9(1) implies that
In the case where p is almost periodic,
![]() $cl(Gp)$
is a minimal left ideal in
$cl(Gp)$
is a minimal left ideal in
![]() $S({\cal A})$
. Since
$S({\cal A})$
. Since
![]() $r[cl(Hq')]$
is a G-invariant closed subset of
$r[cl(Hq')]$
is a G-invariant closed subset of
![]() $cl(Gp)$
, we get that
$cl(Gp)$
, we get that
![]() $r[cl(Hq)]=cl(Gp)$
.
$r[cl(Hq)]=cl(Gp)$
.
(2) Let
![]() $p\in I$
and let
$p\in I$
and let
![]() $q_0\in S({\cal B})$
be a weak heir of p. Let
$q_0\in S({\cal B})$
be a weak heir of p. Let
![]() $I'\triangleleft _mS(B)$
be a minimal subflow of
$I'\triangleleft _mS(B)$
be a minimal subflow of
![]() $cl(Hq_0)$
. By (1),
$cl(Hq_0)$
. By (1),
![]() $r[I']=I$
.
$r[I']=I$
.
4 Transfer between
 $S({\cal A})$
and
$S({\cal A})$
and
 $S({\cal B})$
: the Ellis groups
$S({\cal B})$
: the Ellis groups
In this section we shall relate algebraically the Ellis groups of
![]() $S({\cal A})$
and
$S({\cal A})$
and
![]() $S({\cal B})$
, under some additional assumptions. Let
$S({\cal B})$
, under some additional assumptions. Let
![]() $I\triangleleft _mS({\cal A})$
and
$I\triangleleft _mS({\cal A})$
and
![]() $u\in J(I)$
. First we lift the group
$u\in J(I)$
. First we lift the group
![]() $uI$
to a group in
$uI$
to a group in
![]() $S({\cal B})$
, possibly not an Ellis group. We do it in two ways, using the coheir and weak heir extensions.
$S({\cal B})$
, possibly not an Ellis group. We do it in two ways, using the coheir and weak heir extensions.
First let
![]() ${\cal G}=j[uI]$
, where
${\cal G}=j[uI]$
, where
![]() $j:S({\cal A})\to CH({\cal B}/{\cal A})$
is the
$j:S({\cal A})\to CH({\cal B}/{\cal A})$
is the
![]() $*$
-isomorphism from Corollary 3.11. So
$*$
-isomorphism from Corollary 3.11. So
![]() ${\cal G}$
is a subgroup of
${\cal G}$
is a subgroup of
![]() $S({\cal B})$
such that
$S({\cal B})$
such that
![]() $r:{\cal G}\to uI$
is a group isomorphism. The group
$r:{\cal G}\to uI$
is a group isomorphism. The group
![]() ${\cal G}$
is determined by the choice of
${\cal G}$
is determined by the choice of
![]() $u\in J(I)$
, so we may write
$u\in J(I)$
, so we may write
![]() ${\cal G}={\cal G}_u$
. The groups
${\cal G}={\cal G}_u$
. The groups
![]() ${\cal G}_u,u\in J(I),I\triangleleft _mS({\cal A})$
are all isomorphic and their choice is canonical.
${\cal G}_u,u\in J(I),I\triangleleft _mS({\cal A})$
are all isomorphic and their choice is canonical.
Next, we find a subgroup
![]() ${\cal H}$
of
${\cal H}$
of
![]() $WH({\cal B}/{\cal A})$
with the property that
$WH({\cal B}/{\cal A})$
with the property that
![]() $r:{\cal H}\to uI$
is a group epimorphism. In the model theoretic set-up this has been done in [Reference Newelski10, Section 3]. The construction from [Reference Newelski10] is easily adapted to our combinatorial set-up. We describe it briefly here, referring the reader to [Reference Newelski10, Section 3] for details.
$r:{\cal H}\to uI$
is a group epimorphism. In the model theoretic set-up this has been done in [Reference Newelski10, Section 3]. The construction from [Reference Newelski10] is easily adapted to our combinatorial set-up. We describe it briefly here, referring the reader to [Reference Newelski10, Section 3] for details.
By Lemma 3.8 and Corollary 3.11, the set
![]() $WH_u({\cal B})$
is a closed subset of
$WH_u({\cal B})$
is a closed subset of
![]() $S({\cal A})$
and a sub-semigroup. Fix an
$S({\cal A})$
and a sub-semigroup. Fix an
![]() $I'\triangleleft _mWH_u({\cal B})$
. By [Reference Newelski10, Lemma 3.3(2)] there is a common kernel
$I'\triangleleft _mWH_u({\cal B})$
. By [Reference Newelski10, Lemma 3.3(2)] there is a common kernel
![]() $K'\subseteq {\cal B}$
of all
$K'\subseteq {\cal B}$
of all
![]() $d_{q'},q'\in I'$
. Also let
$d_{q'},q'\in I'$
. Also let
![]() ${\cal R}^{\prime }_u=\{{\mathrm {Im}} d_{q'}:q'\in I'\}$
. By Fact 2.1,
${\cal R}^{\prime }_u=\{{\mathrm {Im}} d_{q'}:q'\in I'\}$
. By Fact 2.1,
![]() $I'$
is a disjoint union of isomorphic groups
$I'$
is a disjoint union of isomorphic groups
![]() $u'I',u'\in J(I')$
. By [Reference Newelski10, Lemma 3.3] there is
$u'I',u'\in J(I')$
. By [Reference Newelski10, Lemma 3.3] there is
![]() $I^+\triangleleft S({\cal B})$
with
$I^+\triangleleft S({\cal B})$
with
![]() $I'=WH_u({\cal B})\cap I^+$
(in fact,
$I'=WH_u({\cal B})\cap I^+$
(in fact,
![]() $I^+=cl(Hs)$
for any
$I^+=cl(Hs)$
for any
![]() $s\in I'$
). Notice also that by Fact 3.14,
$s\in I'$
). Notice also that by Fact 3.14,
![]() $r[I^+]=I$
.
$r[I^+]=I$
.
By [Reference Newelski10, Lemma 3.6], for every
![]() $q\in I$
the set
$q\in I$
the set
![]() $I_q':= WH_q({\cal B})\cap I^+$
is nonempty and for every
$I_q':= WH_q({\cal B})\cap I^+$
is nonempty and for every
![]() $q'\in I_q'$
we have that
$q'\in I_q'$
we have that
![]() ${\mathrm {Ker}} d_{q'}=K'$
. Also for every
${\mathrm {Ker}} d_{q'}=K'$
. Also for every
![]() $q\in uI$
we have that
$q\in uI$
we have that
![]() ${\cal R}^{\prime }_u={\cal R}^{\prime }_q$
, where
${\cal R}^{\prime }_u={\cal R}^{\prime }_q$
, where
![]() ${\cal R}^{\prime }_q:=\{{\mathrm {Im}} d_{q'}: q'\in I_q'\}$
. Now fix an idempotent
${\cal R}^{\prime }_q:=\{{\mathrm {Im}} d_{q'}: q'\in I_q'\}$
. Now fix an idempotent
![]() $u'\in J(I')$
and let
$u'\in J(I')$
and let
![]() $R'={\mathrm {Im}} d_{u'}$
. Let
$R'={\mathrm {Im}} d_{u'}$
. Let
Clearly,
![]() ${\cal H}\subseteq WH({\cal B}/{\cal A})\cap I^+$
. By [Reference Newelski10, Proposition 3.7],
${\cal H}\subseteq WH({\cal B}/{\cal A})\cap I^+$
. By [Reference Newelski10, Proposition 3.7],
![]() ${\cal H}$
is a subgroup of
${\cal H}$
is a subgroup of
![]() $S({\cal B})$
and
$S({\cal B})$
and
![]() $r:{\cal H}\to uI$
is a group epimorphism, with kernel
$r:{\cal H}\to uI$
is a group epimorphism, with kernel
![]() $u'I'$
. The group
$u'I'$
. The group
![]() ${\cal H}$
is determined by the choice of
${\cal H}$
is determined by the choice of
![]() $u'$
, hence we may write
$u'$
, hence we may write
![]() ${\cal H}$
as
${\cal H}$
as
![]() ${\cal H}_{u'}$
.
${\cal H}_{u'}$
.
Using
![]() ${\cal H}$
, in [Reference Newelski10] we proved in the model-theoretic set-up that the Ellis groups of
${\cal H}$
, in [Reference Newelski10] we proved in the model-theoretic set-up that the Ellis groups of
![]() $S_{ext,G}(M)$
are homomorphic images of some subgroups of the Ellis groups of
$S_{ext,G}(M)$
are homomorphic images of some subgroups of the Ellis groups of
![]() $S_{ext,G}(N)$
, under the assumption that there are generic types in
$S_{ext,G}(N)$
, under the assumption that there are generic types in
![]() $S_{ext,G}(N)$
(equivalently, in
$S_{ext,G}(N)$
(equivalently, in
![]() $S_{ext,G}(N)$
there is exactly one minimal left ideal [Reference Newelski9]). We will recall this result later in the combinatorial set-up, with an easier proof. Notice that the choice of the group
$S_{ext,G}(N)$
there is exactly one minimal left ideal [Reference Newelski9]). We will recall this result later in the combinatorial set-up, with an easier proof. Notice that the choice of the group
![]() ${\cal H}={\cal H}_{u'}$
is canonical. We mentioned it in [Reference Newelski10], here we make this claim precise in Proposition 4.5, that is a structural result on the semigroup
${\cal H}={\cal H}_{u'}$
is canonical. We mentioned it in [Reference Newelski10], here we make this claim precise in Proposition 4.5, that is a structural result on the semigroup
![]() $WH({\cal B}/{\cal A})$
parallel to Fact 2.1. Let
$WH({\cal B}/{\cal A})$
parallel to Fact 2.1. Let
![]() $I_0^+=WH({\cal B}/{\cal A})\cap I^+$
. Hence
$I_0^+=WH({\cal B}/{\cal A})\cap I^+$
. Hence
![]() $I_0^+\triangleleft WH({\cal B}/{\cal A})$
.
$I_0^+\triangleleft WH({\cal B}/{\cal A})$
.
Lemma 4.1. (1)
![]() $r[I^+]=r[I_0^+]=I$
.
$r[I^+]=r[I_0^+]=I$
.
(2) For every
![]() $q'\in I^+_0,\ I^+=cl(Hq')$
and
$q'\in I^+_0,\ I^+=cl(Hq')$
and
![]() ${\mathrm {Ker}} d_{q'}=K'$
.
${\mathrm {Ker}} d_{q'}=K'$
.
(3) If
![]() $q\in I$
, then
$q\in I$
, then
![]() $I_q'\neq \emptyset $
and if
$I_q'\neq \emptyset $
and if
![]() $q\in J(I)$
, then
$q\in J(I)$
, then
![]() $I_q'\triangleleft _m WH_q({\cal B})$
.
$I_q'\triangleleft _m WH_q({\cal B})$
.
(4) For
![]() $q\in I$
let
$q\in I$
let
![]() ${\cal R}_q'=\{{\mathrm {Im}} d_{q'}:q'\in I_q'\}$
. If
${\cal R}_q'=\{{\mathrm {Im}} d_{q'}:q'\in I_q'\}$
. If
![]() $u_0\in J(I)$
and
$u_0\in J(I)$
and
![]() $q\in u_0I$
, then
$q\in u_0I$
, then
![]() ${\cal R}_q'={\cal R}_{u_0}'$
.
${\cal R}_q'={\cal R}_{u_0}'$
.
(5) For
![]() $v_0\in J(I_0^+)$
let
$v_0\in J(I_0^+)$
let
where
![]() $u_0=r(v_0)$
. Then
$u_0=r(v_0)$
. Then
![]() $u_0\in J(I),\ {\cal H}_{v_0}\subseteq I_0^+$
is a group and
$u_0\in J(I),\ {\cal H}_{v_0}\subseteq I_0^+$
is a group and
![]() $I_0^+$
is a disjoint union of the groups
$I_0^+$
is a disjoint union of the groups
![]() ${\cal H}_{v_0},v_0\in J(I_0^+)$
.
${\cal H}_{v_0},v_0\in J(I_0^+)$
.
(6) If
![]() $v_0\neq v_1\in J(I_0^+)$
, then
$v_0\neq v_1\in J(I_0^+)$
, then
![]() ${\mathrm {Im}} d_{v_0}\neq {\mathrm {Im}} d_{v_1}$
.
${\mathrm {Im}} d_{v_0}\neq {\mathrm {Im}} d_{v_1}$
.
(7) The groups
![]() ${\cal H}_v,v\in J(I^+_0)$
are isomorphic and
${\cal H}_v,v\in J(I^+_0)$
are isomorphic and
![]() ${\cal H}_v=vI_0^+$
.
${\cal H}_v=vI_0^+$
.
(8)
![]() $I_0^+\triangleleft _m WH({\cal B}/{\cal A})$
.
$I_0^+\triangleleft _m WH({\cal B}/{\cal A})$
.
Proof (2) and (3) are [Reference Newelski10, Lemma 3.6(1),(2)]. Together with Lemma 3.14 they imply (1).
(4) is [Reference Newelski10, Lemma 3.6(3)] when
![]() $u_0=u$
. However every
$u_0=u$
. However every
![]() $u_0\in J(I)$
can play the role of u in generating
$u_0\in J(I)$
can play the role of u in generating
![]() $I^+$
. Namely, by (3)
$I^+$
. Namely, by (3)
![]() $I_{u_0}'\triangleleft _m WH_{u_0}({\cal B})$
and by (2),
$I_{u_0}'\triangleleft _m WH_{u_0}({\cal B})$
and by (2),
![]() $I^+=cl(Hu_0')$
for any
$I^+=cl(Hu_0')$
for any
![]() $u_0'\in J(I_{u_0}')$
. So the roles of u and
$u_0'\in J(I_{u_0}')$
. So the roles of u and
![]() $u_0$
in
$u_0$
in
![]() $I^+$
are symmetrical hence [Reference Newelski10, Lemma 3.6(3)] holds for arbitrary
$I^+$
are symmetrical hence [Reference Newelski10, Lemma 3.6(3)] holds for arbitrary
![]() $u_0\in J(I)$
. So (4) follows.
$u_0\in J(I)$
. So (4) follows.
(5) Let
![]() $v_0{\kern-1pt}\in{\kern-1pt} J(I_0^+)$
and
$v_0{\kern-1pt}\in{\kern-1pt} J(I_0^+)$
and
![]() $u_0{\kern-1pt}={\kern-1pt}r(v_0)$
. We have that
$u_0{\kern-1pt}={\kern-1pt}r(v_0)$
. We have that
![]() $u_0{\kern-1pt}\in{\kern-1pt} J(I)$
because
$u_0{\kern-1pt}\in{\kern-1pt} J(I)$
because
![]() $r:I_0^+{\kern-1pt}\to{\kern-1pt} I$
is a
$r:I_0^+{\kern-1pt}\to{\kern-1pt} I$
is a
![]() $*$
-homomorphism. That
$*$
-homomorphism. That
![]() ${\cal H}_{v_0}$
is a group with
${\cal H}_{v_0}$
is a group with
![]() $r:{\cal H}_{v_0}\to u_0I$
being a group epimorphism follows from [Reference Newelski10, Proposition 3.7] and the symmetrical role of
$r:{\cal H}_{v_0}\to u_0I$
being a group epimorphism follows from [Reference Newelski10, Proposition 3.7] and the symmetrical role of
![]() $u_0$
and u in
$u_0$
and u in
![]() $I^+$
.
$I^+$
.
To see that the groups
![]() ${\cal H}_{v_0},v_0\in J(I_0^+)$
are disjoint, consider
${\cal H}_{v_0},v_0\in J(I_0^+)$
are disjoint, consider
![]() $v_0\neq v_1\in J(I_0^+)$
. Let
$v_0\neq v_1\in J(I_0^+)$
. Let
![]() $u_i=r(v_i)\in J(I),\ i=0,1$
.
$u_i=r(v_i)\in J(I),\ i=0,1$
.
If
![]() $u_0\neq u_1$
, then
$u_0\neq u_1$
, then
![]() $r[{\cal H}_{v_0}]=u_0I$
,
$r[{\cal H}_{v_0}]=u_0I$
,
![]() $r[{\cal H}_{v_1}]=u_1I$
and
$r[{\cal H}_{v_1}]=u_1I$
and
![]() $u_0I\cap u_1I=\emptyset $
, hence also
$u_0I\cap u_1I=\emptyset $
, hence also
![]() ${\cal H}_{v_0}\cap {\cal H}_{v_1}=\emptyset $
.
${\cal H}_{v_0}\cap {\cal H}_{v_1}=\emptyset $
.
If
![]() $u_0=u_1$
, then
$u_0=u_1$
, then
![]() $v_0,v_1\in J(I_{u_0}')$
and
$v_0,v_1\in J(I_{u_0}')$
and
![]() $I_{u_0}'\triangleleft _m WH_{u_0}({\cal B})$
, so
$I_{u_0}'\triangleleft _m WH_{u_0}({\cal B})$
, so
![]() $v_0\neq v_1$
implies
$v_0\neq v_1$
implies
![]() ${\mathrm {Im}} d_{v_0}\neq {\mathrm {Im}} d_{v_1}$
. But
${\mathrm {Im}} d_{v_0}\neq {\mathrm {Im}} d_{v_1}$
. But
![]() ${\mathrm {Im}} d_{v_i}={\mathrm {Im}} d_x$
for every
${\mathrm {Im}} d_{v_i}={\mathrm {Im}} d_x$
for every
![]() $x\in {\cal H}_{v_i}$
, hence
$x\in {\cal H}_{v_i}$
, hence
![]() ${\cal H}_{v_0}$
and
${\cal H}_{v_0}$
and
![]() ${\cal H}_{v_1}$
are disjoint also in this case.
${\cal H}_{v_1}$
are disjoint also in this case.
By (4) every
![]() $q'\in I_0^+$
belongs to some
$q'\in I_0^+$
belongs to some
![]() ${\cal H}_{v_0},v_0\in J(I_0^+)$
, so we are done.
${\cal H}_{v_0},v_0\in J(I_0^+)$
, so we are done.
(6) Assume
![]() $v_0\neq v_1\in J(I_0^+)$
. By (5) the groups
$v_0\neq v_1\in J(I_0^+)$
. By (5) the groups
![]() ${\cal H}_{v_0}$
and
${\cal H}_{v_0}$
and
![]() ${\cal H}_{v_1}$
are disjoint and
${\cal H}_{v_1}$
are disjoint and
![]() ${\mathrm {Ker}} d_{v_0}={\mathrm {Ker}} d_{v_1}=K'$
, hence by Fact 2.4,
${\mathrm {Ker}} d_{v_0}={\mathrm {Ker}} d_{v_1}=K'$
, hence by Fact 2.4,
![]() ${\mathrm {Im}} d_{v_0}\neq {\mathrm {Im}} d_{v_1}$
.
${\mathrm {Im}} d_{v_0}\neq {\mathrm {Im}} d_{v_1}$
.
(7) Let
![]() $v_0\neq v_1\in J(I_0^+)$
. Since
$v_0\neq v_1\in J(I_0^+)$
. Since
![]() $K({\cal H}_{v_0})=K({\cal H}_{v_1})=K'$
, the groups
$K({\cal H}_{v_0})=K({\cal H}_{v_1})=K'$
, the groups
![]() ${\cal H}_{v_i}$
may be regarded as subgroups of
${\cal H}_{v_i}$
may be regarded as subgroups of
![]() ${\mathrm {Aut}}({\cal B}/K')$
(via the function d, since
${\mathrm {Aut}}({\cal B}/K')$
(via the function d, since
![]() $R({\cal H}_{v_i})$
is a section of the family of
$R({\cal H}_{v_i})$
is a section of the family of
![]() $K'$
-cosets in
$K'$
-cosets in
![]() ${\cal B}$
). Hence the function mapping x to
${\cal B}$
). Hence the function mapping x to
![]() $v_1x$
is a group isomorphism
$v_1x$
is a group isomorphism
![]() ${\cal H}_{v_0}\to {\cal H}_{v_1}$
. We see also that
${\cal H}_{v_0}\to {\cal H}_{v_1}$
. We see also that
![]() ${\cal H}_{v_0}=v_0I_0^+$
.
${\cal H}_{v_0}=v_0I_0^+$
.
(8) Let
![]() $x,y\in I_0^+$
. Choose
$x,y\in I_0^+$
. Choose
![]() $v_0,v_1\in J(I_0^+)$
such that
$v_0,v_1\in J(I_0^+)$
such that
![]() $x\in {\cal H}_{v_0}$
and
$x\in {\cal H}_{v_0}$
and
![]() $y\in {\cal H}_{v_1}$
. It is enough to show that
$y\in {\cal H}_{v_1}$
. It is enough to show that
![]() $y=zx$
for some
$y=zx$
for some
![]() $z\in I_0^+$
.
$z\in I_0^+$
.
When
![]() $v_0=v_1$
, then
$v_0=v_1$
, then
![]() $x,y\in {\cal H}_{v_0}$
and
$x,y\in {\cal H}_{v_0}$
and
![]() $z=yx^{-1}$
calculated in the group
$z=yx^{-1}$
calculated in the group
![]() ${\cal H}_{v_0}$
will do. Otherwise,
${\cal H}_{v_0}$
will do. Otherwise,
![]() $v_1x\in {\cal H}_{v_1}$
and
$v_1x\in {\cal H}_{v_1}$
and
![]() $z=z_0v_1$
will do, where
$z=z_0v_1$
will do, where
![]() $z_0=y(v_1x)^{-1}$
calculated in the group
$z_0=y(v_1x)^{-1}$
calculated in the group
![]() ${\cal H}_{v_1}$
.
${\cal H}_{v_1}$
.
Lemma 4.2. Assume
![]() $I^*\triangleleft _m WH({\cal B}/{\cal A})$
. Then
$I^*\triangleleft _m WH({\cal B}/{\cal A})$
. Then
![]() $I^*$
is of the form
$I^*$
is of the form
![]() $I_0^+$
for some
$I_0^+$
for some
![]() $I\triangleleft _m S({\cal A}),\ u\in J(I),\ I'\triangleleft _m WH_u({\cal B})$
and
$I\triangleleft _m S({\cal A}),\ u\in J(I),\ I'\triangleleft _m WH_u({\cal B})$
and
![]() $u'\in J(I')$
.
$u'\in J(I')$
.
Proof Let
![]() $I=r[I^*]$
. Since
$I=r[I^*]$
. Since
![]() $r:WH({\cal B}/{\cal A})\to S({\cal A})$
is a
$r:WH({\cal B}/{\cal A})\to S({\cal A})$
is a
![]() $*$
-epimorphism, we have that
$*$
-epimorphism, we have that
![]() $I\triangleleft _m S({\cal A})$
. Choose
$I\triangleleft _m S({\cal A})$
. Choose
![]() $u\in J(I)$
and then
$u\in J(I)$
and then
![]() $I'\subseteq I^*\cap WH_u({\cal B})$
with
$I'\subseteq I^*\cap WH_u({\cal B})$
with
![]() $I'\triangleleft _m WH_u({\cal B})$
. Let
$I'\triangleleft _m WH_u({\cal B})$
. Let
![]() $u'\in J(I'),\ I^+=cl(Hu')$
and
$u'\in J(I'),\ I^+=cl(Hu')$
and
![]() $I_0^+=I^+\cap WH({\cal B}/{\cal A})$
. By Lemma 4.1 and the minimality of
$I_0^+=I^+\cap WH({\cal B}/{\cal A})$
. By Lemma 4.1 and the minimality of
![]() $I^*$
we have that
$I^*$
we have that
![]() $I_0^+=WH({\cal B}/{\cal A})u'=I^*$
.
$I_0^+=WH({\cal B}/{\cal A})u'=I^*$
.
Lemma 4.3. Assume
![]() $I_i^+\triangleleft _m WH({\cal B}/{\cal A})$
and
$I_i^+\triangleleft _m WH({\cal B}/{\cal A})$
and
![]() ${\cal R}_i=\{{\mathrm {Im}} d_{q'}:q'\in I_i^+\},i=0,1$
.
${\cal R}_i=\{{\mathrm {Im}} d_{q'}:q'\in I_i^+\},i=0,1$
.
(1) If
![]() $R_0,R_1\in {\cal R}_i$
and
$R_0,R_1\in {\cal R}_i$
and
![]() $R_0\subseteq R_1$
, then
$R_0\subseteq R_1$
, then
![]() $R_0=R_1$
.
$R_0=R_1$
.
(2)
![]() ${\cal R}_0={\cal R}_1$
.
${\cal R}_0={\cal R}_1$
.
Proof (1) Let K be the common kernel of
![]() $d_x,x\in I^+_i$
. By Fact 2.4, the algebras
$d_x,x\in I^+_i$
. By Fact 2.4, the algebras
![]() $R_0,R_1$
are sections of the family of K-cosets in
$R_0,R_1$
are sections of the family of K-cosets in
![]() ${\cal B}$
, so
${\cal B}$
, so
![]() $R_0\subseteq R_1$
implies
$R_0\subseteq R_1$
implies
![]() $R_0=R_1$
.
$R_0=R_1$
.
(2) Choose
![]() $v_i\in J(I_i^+),i=0,1$
. Let
$v_i\in J(I_i^+),i=0,1$
. Let
![]() $x\in I_0^+$
. Hence
$x\in I_0^+$
. Hence
![]() $xv_1\in I_1^+$
and
$xv_1\in I_1^+$
and
![]() $xv_1v_0\in I_0^+$
. Therefore
$xv_1v_0\in I_0^+$
. Therefore
![]() ${\mathrm {Im}} d_x,{\mathrm {Im}} d_{xv_1v_0}\in {\cal R}_0$
and
${\mathrm {Im}} d_x,{\mathrm {Im}} d_{xv_1v_0}\in {\cal R}_0$
and
![]() ${\mathrm {Im}} d_{xv_1}\in {\cal R}_1$
. We have that
${\mathrm {Im}} d_{xv_1}\in {\cal R}_1$
. We have that
hence
![]() ${\mathrm {Im}} d_{xv_1v_0}\subseteq {\mathrm {Im}} d_x$
and by (1)
${\mathrm {Im}} d_{xv_1v_0}\subseteq {\mathrm {Im}} d_x$
and by (1)
![]() ${\mathrm {Im}} d_{xv_1v_0}={\mathrm {Im}} d_x$
. Therefore also
${\mathrm {Im}} d_{xv_1v_0}={\mathrm {Im}} d_x$
. Therefore also
![]() ${\mathrm {Im}} d_x={\mathrm {Im}} d_{xv_1}\in {\cal R}_1$
. So
${\mathrm {Im}} d_x={\mathrm {Im}} d_{xv_1}\in {\cal R}_1$
. So
![]() ${\cal R}_0\subseteq {\cal R}_1$
. By symmetry,
${\cal R}_0\subseteq {\cal R}_1$
. By symmetry,
![]() ${\cal R}_0={\cal R}_1$
.
${\cal R}_0={\cal R}_1$
.
Lemma 4.4. Assume for
![]() $i=0,1,\ I_i^+\triangleleft _m WH({\cal B}/{\cal A}),\ v_i\in J(I_i^+)$
and let
$i=0,1,\ I_i^+\triangleleft _m WH({\cal B}/{\cal A}),\ v_i\in J(I_i^+)$
and let
![]() ${\cal H}_i={\cal H}_{v_i}=v_iI_i^+$
,
${\cal H}_i={\cal H}_{v_i}=v_iI_i^+$
,
![]() $I_i=r[I_i^+]\triangleleft _m S({\cal A})$
and
$I_i=r[I_i^+]\triangleleft _m S({\cal A})$
and
![]() $u_i=r(v_i)\in J(I_i)$
. Then there are group isomorphisms
$u_i=r(v_i)\in J(I_i)$
. Then there are group isomorphisms
![]() $f:{\cal H}_0\to {\cal H}_1$
and
$f:{\cal H}_0\to {\cal H}_1$
and
![]() $\delta :u_0I_0\to u_1I_1$
such that the following diagram commutes.
$\delta :u_0I_0\to u_1I_1$
such that the following diagram commutes.

Proof Let
![]() $K_i={\mathrm {Ker}} d_{v_i}$
and
$K_i={\mathrm {Ker}} d_{v_i}$
and
![]() $R_i={\mathrm {Im}} d_{v_i}, i=0,1$
. First we consider two special cases.
$R_i={\mathrm {Im}} d_{v_i}, i=0,1$
. First we consider two special cases.
Case 1.
![]() $K_0=K_1$
. In this case by Fact 2.4 and Lemma 4.1(2) we have that
$K_0=K_1$
. In this case by Fact 2.4 and Lemma 4.1(2) we have that
![]() $cl(Hv_0)=cl(Hv_1)$
and
$cl(Hv_0)=cl(Hv_1)$
and
Hence also
![]() $I_0=r[I_0^+]=r[I_1^+]=I_1$
. By Fact 2.4(2) and Lemma 4.1(5), the groups
$I_0=r[I_0^+]=r[I_1^+]=I_1$
. By Fact 2.4(2) and Lemma 4.1(5), the groups
![]() ${\cal H}_i$
are isomorphic to some subgroups of
${\cal H}_i$
are isomorphic to some subgroups of
![]() ${\mathrm {Aut}}(R_i)\cong {\mathrm {Aut}}({\cal B}/K_i)$
. Hence, considering the elements of
${\mathrm {Aut}}(R_i)\cong {\mathrm {Aut}}({\cal B}/K_i)$
. Hence, considering the elements of
![]() ${\cal H}_i$
as automorphisms of
${\cal H}_i$
as automorphisms of
![]() ${\cal B}/K_i$
(via the function d) we see that the functions
${\cal B}/K_i$
(via the function d) we see that the functions
![]() $f:{\cal H}_0\to {\cal H}_1$
and
$f:{\cal H}_0\to {\cal H}_1$
and
![]() $\delta :u_0I_0\to u_1I_1$
defined by
$\delta :u_0I_0\to u_1I_1$
defined by
![]() $f(x)=v_1x$
and
$f(x)=v_1x$
and
![]() $\delta (x)=u_1x$
are group isomorphisms and the diagram from the lemma commutes.
$\delta (x)=u_1x$
are group isomorphisms and the diagram from the lemma commutes.
Case 2.
![]() $R_0=R_1$
. In this case we have that
$R_0=R_1$
. In this case we have that
![]() $v_0v_1=v_1$
and
$v_0v_1=v_1$
and
![]() $v_1v_0=v_0$
. Therefore by Corollary 3.11,
$v_1v_0=v_0$
. Therefore by Corollary 3.11,
![]() $u_0u_1=u_1$
and
$u_0u_1=u_1$
and
![]() $u_1u_0=u_0$
, which gives that also
$u_1u_0=u_0$
, which gives that also
![]() ${\mathrm {Im}} d_{u_0}={\mathrm {Im}} d_{u_1}$
. Here the groups
${\mathrm {Im}} d_{u_0}={\mathrm {Im}} d_{u_1}$
. Here the groups
![]() ${\cal H}_i$
are isomorphic to some subgroups of
${\cal H}_i$
are isomorphic to some subgroups of
![]() ${\mathrm {Aut}}(R_0)={Aut}(R_1)$
, the functions
${\mathrm {Aut}}(R_0)={Aut}(R_1)$
, the functions
![]() $f:{\cal H}_0\to {\cal H}_1$
and
$f:{\cal H}_0\to {\cal H}_1$
and
![]() $\delta :u_0I_0\to u_1I_1$
defined by
$\delta :u_0I_0\to u_1I_1$
defined by
![]() $f(x)=xv_1$
and
$f(x)=xv_1$
and
![]() $\delta (x)=xu_1$
are group isomorphisms and the diagram from the lemma commutes.
$\delta (x)=xu_1$
are group isomorphisms and the diagram from the lemma commutes.
In general, by Lemma 4.3 there is
![]() $v_2\in J(I_0^+)$
with
$v_2\in J(I_0^+)$
with
![]() ${\mathrm {Im}} d_{v_2}=R_1$
and
${\mathrm {Im}} d_{v_2}=R_1$
and
![]() ${\mathrm {Ker}} d_{v_2}=K_0$
. Let
${\mathrm {Ker}} d_{v_2}=K_0$
. Let
![]() ${\cal H}_2={\cal H}_{v_2}=v_2I_0^+$
and
${\cal H}_2={\cal H}_{v_2}=v_2I_0^+$
and
![]() $u_2=r(v_2)\in J(I_0)$
. By Cases 1 and 2 we get group isomorphisms
$u_2=r(v_2)\in J(I_0)$
. By Cases 1 and 2 we get group isomorphisms
![]() $f_0:{\cal H}_0\to {\cal H}_2$
,
$f_0:{\cal H}_0\to {\cal H}_2$
,
![]() $\delta _0:u_0I_0\to u_2I_0$
,
$\delta _0:u_0I_0\to u_2I_0$
,
![]() $f_1:{\cal H}_2\to {\cal H}_1$
and
$f_1:{\cal H}_2\to {\cal H}_1$
and
![]() $\delta _1: u_2I_0\to u_1I_1$
such that the corresponding diagrams commute. Then the functions
$\delta _1: u_2I_0\to u_1I_1$
such that the corresponding diagrams commute. Then the functions
![]() $f=f_1\circ f_0$
and
$f=f_1\circ f_0$
and
![]() $\delta =\delta _1\circ \delta _0$
satisfy our demands.
$\delta =\delta _1\circ \delta _0$
satisfy our demands.
The next proposition summarizes the previous four lemmas.
Proposition 4.5. There are minimal left ideals in
![]() $WH({\cal B}/{\cal A})$
. Assume
$WH({\cal B}/{\cal A})$
. Assume
![]() $I^*\triangleleft _m WH({\cal B}/{\cal A})$
. Then the following hold.
$I^*\triangleleft _m WH({\cal B}/{\cal A})$
. Then the following hold.
(1) The set
![]() $J(I^*)$
is nonempty.
$J(I^*)$
is nonempty.
(2)
![]() $I^*$
is a disjoint union of groups
$I^*$
is a disjoint union of groups
![]() $u'I^*,u'\in J(I^*)$
.
$u'I^*,u'\in J(I^*)$
.
(3) The groups of the form
![]() $u'I^*$
, where
$u'I^*$
, where
![]() $I^*\triangleleft _m WH({\cal B}/{\cal A})$
and
$I^*\triangleleft _m WH({\cal B}/{\cal A})$
and
![]() $u'\in J(I^*)$
, are isomorphic.
$u'\in J(I^*)$
, are isomorphic.
(4) Assume
![]() $u'\in J(I^*)$
. Then the restriction function
$u'\in J(I^*)$
. Then the restriction function
![]() $r:u'I^*\to uI$
is a group epimorphism, where
$r:u'I^*\to uI$
is a group epimorphism, where
![]() $I=r[I^*]\triangleleft _m S({\cal A})$
and
$I=r[I^*]\triangleleft _m S({\cal A})$
and
![]() $u=r(u')\in J(I)$
. Also
$u=r(u')\in J(I)$
. Also
![]() ${\mathrm {Ker}} (r) = I'\triangleleft _m WH({\cal B}/{\cal A})$
, where
${\mathrm {Ker}} (r) = I'\triangleleft _m WH({\cal B}/{\cal A})$
, where
![]() $I'=I^*\cap WH_u({\cal B})$
.
$I'=I^*\cap WH_u({\cal B})$
.
(5) The minimal ideals
![]() $I^*\triangleleft _m WH({\cal B}/{\cal A})$
are relatively closed in
$I^*\triangleleft _m WH({\cal B}/{\cal A})$
are relatively closed in
![]() $WH({\cal B}/{\cal A})$
and determined by the common kernel of
$WH({\cal B}/{\cal A})$
and determined by the common kernel of
![]() $d_x,x\in I^*$
.
$d_x,x\in I^*$
.
We see that the group
![]() ${\cal H}={\cal H}_{u'}$
from the beginning of this section is of the form
${\cal H}={\cal H}_{u'}$
from the beginning of this section is of the form
![]() $u'I^*$
, where
$u'I^*$
, where
![]() $I^*\triangleleft _m WH({\cal B}/{\cal A})$
and
$I^*\triangleleft _m WH({\cal B}/{\cal A})$
and
![]() $u'\in J(I^*)$
. We call such groups the Ellis subgroups of
$u'\in J(I^*)$
. We call such groups the Ellis subgroups of
![]() $WH({\cal B}/{\cal A})$
. All of them are isomorphic.
$WH({\cal B}/{\cal A})$
. All of them are isomorphic.
In this paper we show an algebraic connection between the Ellis groups of
![]() $S({\cal A})$
and the Ellis groups of
$S({\cal A})$
and the Ellis groups of
![]() $S({\cal B})$
under an assumption dual to the genericity assumption considered in [Reference Newelski10]. By Fact 2.4 there is a bijection between the Ellis groups of
$S({\cal B})$
under an assumption dual to the genericity assumption considered in [Reference Newelski10]. By Fact 2.4 there is a bijection between the Ellis groups of
![]() $S({\cal B})$
and the set
$S({\cal B})$
and the set
![]() ${\cal K}\times {\cal R}$
(defined as in Fact 2.4). Every Ellis subgroup
${\cal K}\times {\cal R}$
(defined as in Fact 2.4). Every Ellis subgroup
![]() $u"I"$
of
$u"I"$
of
![]() $S({\cal B})$
is determined uniquely by the pair
$S({\cal B})$
is determined uniquely by the pair
![]() $(K(u"I"), R(u"I"))\in {\cal K}\times {\cal R}$
, where
$(K(u"I"), R(u"I"))\in {\cal K}\times {\cal R}$
, where
![]() $K(u"I")$
is the same for all Ellis subgroups
$K(u"I")$
is the same for all Ellis subgroups
![]() $u"I"$
of
$u"I"$
of
![]() $I"$
, and for every
$I"$
, and for every
![]() $I"\triangleleft _mS({\cal B})$
, all
$I"\triangleleft _mS({\cal B})$
, all
![]() $R\in {\cal R}$
appear as
$R\in {\cal R}$
appear as
![]() $R(u"I")$
for
$R(u"I")$
for
![]() $u"\in J(I")$
. Hence the genericity assumption that in
$u"\in J(I")$
. Hence the genericity assumption that in
![]() $S({\cal B})$
there is exactly one minimal left ideal
$S({\cal B})$
there is exactly one minimal left ideal
![]() $I"$
is equivalent to
$I"$
is equivalent to
![]() $|{\cal K}|=1$
. Here we consider a dual assumption that
$|{\cal K}|=1$
. Here we consider a dual assumption that
![]() $|{\cal R}|=1$
which means that every (equivalently some) minimal left ideal of
$|{\cal R}|=1$
which means that every (equivalently some) minimal left ideal of
![]() $S({\cal B})$
is a group Footnote
2
.
$S({\cal B})$
is a group Footnote
2
.
Theorem 4.6. Assume every minimal left ideal in
![]() $S({\cal B})$
is a group. Then the Ellis groups of
$S({\cal B})$
is a group. Then the Ellis groups of
![]() $S({\cal A})$
are isomorphic to some closed subgroups of the Ellis groups of
$S({\cal A})$
are isomorphic to some closed subgroups of the Ellis groups of
![]() $S({\cal B})$
.
$S({\cal B})$
.
Before the proof we shall prove two lemmas.
Lemma 4.7. Assume
![]() $I"\triangleleft _mS({\cal B})$
is a group and
$I"\triangleleft _mS({\cal B})$
is a group and
![]() $u"$
is the only idempotent in
$u"$
is the only idempotent in
![]() $I"$
. Then the function
$I"$
. Then the function
![]() $\varphi :S({\cal B})\to I"$
mapping x to
$\varphi :S({\cal B})\to I"$
mapping x to
![]() $x*u"$
is a
$x*u"$
is a
![]() $*$
-epimorphism and a continuous retraction.
$*$
-epimorphism and a continuous retraction.
Proof Let
![]() $x,y\in S({\cal B})$
. Since
$x,y\in S({\cal B})$
. Since
![]() $yu"\in I"$
and
$yu"\in I"$
and
![]() $u"$
is the identity element of
$u"$
is the identity element of
![]() $I"$
, we have that
$I"$
, we have that
![]() $yu"=u"yu"$
. Therefore
$yu"=u"yu"$
. Therefore
hence
![]() $\varphi $
is a
$\varphi $
is a
![]() $*$
-homomorphism. The rest is easy.
$*$
-homomorphism. The rest is easy.
Lemma 4.8. Assume every minimal left ideal in
![]() $S({\cal B})$
is a group. Then every minimal left ideal in
$S({\cal B})$
is a group. Then every minimal left ideal in
![]() $S({\cal A})$
is a group.
$S({\cal A})$
is a group.
Proof Let
![]() $I\triangleleft _m S({\cal A})$
and by Lemma 3.14(2) choose
$I\triangleleft _m S({\cal A})$
and by Lemma 3.14(2) choose
![]() $I"\triangleleft _m S({\cal B})$
with
$I"\triangleleft _m S({\cal B})$
with
![]() $r[I"]=I$
. Let
$r[I"]=I$
. Let
![]() $u"\in J(I")$
and then let
$u"\in J(I")$
and then let
![]() $u\in J(I)$
be such that
$u\in J(I)$
be such that
![]() $r(u")\in uI$
. By Corollary 3.11
$r(u")\in uI$
. By Corollary 3.11
![]() $r:CH({\cal B}/{\cal A})\to S({\cal A})$
is a
$r:CH({\cal B}/{\cal A})\to S({\cal A})$
is a
![]() $*$
-isomorphism. Let
$*$
-isomorphism. Let
![]() $I'$
be a minimal left ideal in
$I'$
be a minimal left ideal in
![]() $CH({\cal B}/{\cal A})$
with
$CH({\cal B}/{\cal A})$
with
![]() $r[I']=I$
and choose
$r[I']=I$
and choose
![]() $u'\in J(I')$
with
$u'\in J(I')$
with
![]() $r(u')=u$
.
$r(u')=u$
.
Suppose for contradiction that I is not a group. So there is
![]() $u_0\in J(I)$
distinct from u. Choose
$u_0\in J(I)$
distinct from u. Choose
![]() $u_0'\in J(I')$
with
$u_0'\in J(I')$
with
![]() $r(u_0')=u_0$
. We have that both
$r(u_0')=u_0$
. We have that both
![]() $u'u"$
and
$u'u"$
and
![]() $u"$
belong to
$u"$
belong to
![]() $I"$
that is a group, hence there is a
$I"$
that is a group, hence there is a
![]() $p\in I"$
with
$p\in I"$
with
![]() $u'u"p=u"$
. Therefore
$u'u"p=u"$
. Therefore
and similarly
![]() $u_0'u"=u"$
.
$u_0'u"=u"$
.
By Proposition 3.9,
Since
![]() $u\neq u_0\in J(I)$
,
$u\neq u_0\in J(I)$
,
![]() $uI$
and
$uI$
and
![]() $u_0I$
are disjoint groups and
$u_0I$
are disjoint groups and
![]() $ur(u")\neq u_0r(u")$
. Hence
$ur(u")\neq u_0r(u")$
. Hence
![]() $u'u"\neq u_0'u"$
, a contradiction.
$u'u"\neq u_0'u"$
, a contradiction.
Proof of Theorem 4.6
Let
![]() $I\triangleleft _m S({\cal A})$
,
$I\triangleleft _m S({\cal A})$
,
![]() $u\in J(I)$
and
$u\in J(I)$
and
![]() ${\cal G}$
be as in the beginning of this section. Due to the assumptions of Theorem 4.6 and by Lemma 4.8 we have that
${\cal G}$
be as in the beginning of this section. Due to the assumptions of Theorem 4.6 and by Lemma 4.8 we have that
![]() ${\cal G}\subseteq CH({\cal B}/{\cal A})$
is a closed subgroup of
${\cal G}\subseteq CH({\cal B}/{\cal A})$
is a closed subgroup of
![]() $S({\cal B})$
and
$S({\cal B})$
and
![]() $r:{\cal G}\to I$
is a continuous group isomorphism. By Lemma 3.14(2) choose
$r:{\cal G}\to I$
is a continuous group isomorphism. By Lemma 3.14(2) choose
![]() $I"\triangleleft _m S({\cal B})$
with
$I"\triangleleft _m S({\cal B})$
with
![]() $r[I"]=I$
and pick
$r[I"]=I$
and pick
![]() $u"\in J(I")$
. By Lemma 4.7 the function
$u"\in J(I")$
. By Lemma 4.7 the function
![]() $\varphi :{\cal G}\to I"$
mapping x to
$\varphi :{\cal G}\to I"$
mapping x to
![]() $x*u"$
is a continuous group homomorphism. Let
$x*u"$
is a continuous group homomorphism. Let
![]() ${\cal G}'=\varphi [{\cal G}]$
. So
${\cal G}'=\varphi [{\cal G}]$
. So
![]() ${\cal G}'$
is a closed subgroup of
${\cal G}'$
is a closed subgroup of
![]() $I"$
and
$I"$
and
![]() $\varphi :{\cal G}\to {\cal G}'$
is a group epimorphism. Let
$\varphi :{\cal G}\to {\cal G}'$
is a group epimorphism. Let
![]() $p=r(u")$
and
$p=r(u")$
and
![]() $p'$
be the group inverse of p in the group I. Let
$p'$
be the group inverse of p in the group I. Let
![]() $\chi :I\to I$
be the right translation by
$\chi :I\to I$
be the right translation by
![]() $p'$
.
$p'$
.
![]() ${\cal G}\subseteq WCH({\cal B}/{\cal A})$
, so by Proposition 3.9, for
${\cal G}\subseteq WCH({\cal B}/{\cal A})$
, so by Proposition 3.9, for
![]() $x\in {\cal G}$
we have that
$x\in {\cal G}$
we have that
Therefore the following diagram commutes.

Since in this diagram
![]() $r:{\cal G}\to I$
is a bijection and
$r:{\cal G}\to I$
is a bijection and
![]() $r=\chi r\varphi $
, also
$r=\chi r\varphi $
, also
![]() $\varphi $
is a bijection, hence a group isomorphism. Let
$\varphi $
is a bijection, hence a group isomorphism. Let
![]() $f:{\cal G}'\to I$
be the composition
$f:{\cal G}'\to I$
be the composition
![]() $\chi r$
. So also
$\chi r$
. So also
![]() $f=r\varphi ^{-1}$
. We see that f is a continuous group isomorphism.
$f=r\varphi ^{-1}$
. We see that f is a continuous group isomorphism.
Notice that the function
![]() $r:{\cal G}'\to I$
in the proof of Theorem 4.6 is a twisted isomorphism, that is, r is the composition of isomorphism f with right translation by p. The group
$r:{\cal G}'\to I$
in the proof of Theorem 4.6 is a twisted isomorphism, that is, r is the composition of isomorphism f with right translation by p. The group
![]() ${\cal G}'$
in the proof of Theorem 4.6 depends on the choice of
${\cal G}'$
in the proof of Theorem 4.6 depends on the choice of
![]() $I"\triangleleft _mS({\cal B})$
. However, it is independent of this choice up to isomorphism.
$I"\triangleleft _mS({\cal B})$
. However, it is independent of this choice up to isomorphism.
In the model theoretic set-up Theorem 4.6 translates into the following.
Theorem 4.9. Assume every minimal left ideal in
![]() $S_{ext,G}(N)$
is a group. Then the Ellis groups of
$S_{ext,G}(N)$
is a group. Then the Ellis groups of
![]() $S_{ext,G}(M)$
are isomorphic to some closed subgroups of the Ellis groups of
$S_{ext,G}(M)$
are isomorphic to some closed subgroups of the Ellis groups of
![]() $S_{ext,G}(N)$
.
$S_{ext,G}(N)$
.
Under the dual genericity assumption we have the following theorem.
Theorem 4.10. Assume
![]() $S({\cal B})$
has a unique minimal left ideal. Then the Ellis groups of
$S({\cal B})$
has a unique minimal left ideal. Then the Ellis groups of
![]() $S({\cal A})$
are homomorphic images of subgroups of the Ellis groups of
$S({\cal A})$
are homomorphic images of subgroups of the Ellis groups of
![]() $S({\cal B})$
.
$S({\cal B})$
.
This theorem has been proved in [Reference Newelski10, Theorem 4.1] in the model theoretic set-up and the proof translates directly into the combinatorial set-up. However, using the group
![]() ${\cal H}$
described in the beginning of this section we shall give an easier proof, in a way dual to the proof of Theorem 4.6. The only properties of the group
${\cal H}$
described in the beginning of this section we shall give an easier proof, in a way dual to the proof of Theorem 4.6. The only properties of the group
![]() ${\cal H}$
we shall use will be that
${\cal H}$
we shall use will be that
![]() ${\cal H}\subseteq WH({\cal B}/{\cal A})$
and
${\cal H}\subseteq WH({\cal B}/{\cal A})$
and
![]() $r:{\cal H}\to uI$
is a group epimorphism. We shall need the following lemma.
$r:{\cal H}\to uI$
is a group epimorphism. We shall need the following lemma.
Lemma 4.11. Assume in
![]() $S({\cal B})$
there is a unique minimal left ideal
$S({\cal B})$
there is a unique minimal left ideal
![]() $I"$
and let
$I"$
and let
![]() $u"\in J(I")$
. Then the function
$u"\in J(I")$
. Then the function
![]() $\psi :S({\cal B})\to S({\cal B})$
mapping x to
$\psi :S({\cal B})\to S({\cal B})$
mapping x to
![]() $u"*x$
is a
$u"*x$
is a
![]() $*$
-homomorphism with the image
$*$
-homomorphism with the image
![]() $u"I"$
.
$u"I"$
.
Proof Let
![]() $x,y\in S({\cal B})$
. By Fact 2.1(4),
$x,y\in S({\cal B})$
. By Fact 2.1(4),
![]() $u"x$
is almost periodic, hence it belongs to the only minimal left ideal
$u"x$
is almost periodic, hence it belongs to the only minimal left ideal
![]() $I"$
in
$I"$
in
![]() $S({\cal B})$
. Also
$S({\cal B})$
. Also
![]() $u"x=u"(u"x)\in u"I$
. If
$u"x=u"(u"x)\in u"I$
. If
![]() $x\in u"I"$
, then
$x\in u"I"$
, then
![]() $u"x=x$
, hence the group
$u"x=x$
, hence the group
![]() $u"I"$
is the image of
$u"I"$
is the image of
![]() $\psi $
.
$\psi $
.
Since
![]() $u"I"$
is a group and
$u"I"$
is a group and
![]() $u"x\in u"I"$
, we get that
$u"x\in u"I"$
, we get that
![]() $u"x=u"xu"$
. Therefore,
$u"x=u"xu"$
. Therefore,
and
![]() $\psi $
is a homomorphism.
$\psi $
is a homomorphism.
Proof of Theorem 4.10
Let
![]() $I\triangleleft _mS({\cal A}),\ u\in J(I)$
and
$I\triangleleft _mS({\cal A}),\ u\in J(I)$
and
![]() ${\cal H}\subseteq WH({\cal B}/{\cal A})$
be as in the beginning of this section. So
${\cal H}\subseteq WH({\cal B}/{\cal A})$
be as in the beginning of this section. So
![]() ${\cal H}$
is a group and
${\cal H}$
is a group and
![]() $r:{\cal H}\to uI$
is a group epimorphism. Let
$r:{\cal H}\to uI$
is a group epimorphism. Let
![]() $I"\triangleleft _m S({\cal B})$
and
$I"\triangleleft _m S({\cal B})$
and
![]() $u"\in J(I")$
. Since
$u"\in J(I")$
. Since
![]() $I"$
is the only minimal left ideal in
$I"$
is the only minimal left ideal in
![]() $S({\cal B})$
, by Lemma 3.14(2) we have that
$S({\cal B})$
, by Lemma 3.14(2) we have that
![]() $r[I"]=I$
. Replacing u by another element of
$r[I"]=I$
. Replacing u by another element of
![]() $J(I)$
if necessary (and modifying
$J(I)$
if necessary (and modifying
![]() ${\cal H}$
accordingly), we may assume that
${\cal H}$
accordingly), we may assume that
![]() $r(u")\in uI$
. Let
$r(u")\in uI$
. Let
![]() $\psi :{\cal H}\to u"I"$
be as in Lemma 4.11 and let
$\psi :{\cal H}\to u"I"$
be as in Lemma 4.11 and let
![]() ${\cal H}'=\psi [{\cal H}]$
. So
${\cal H}'=\psi [{\cal H}]$
. So
![]() $\psi :{\cal H}\to {\cal H}'$
is a group epimorphism. Let
$\psi :{\cal H}\to {\cal H}'$
is a group epimorphism. Let
![]() $p=r(u")$
and let
$p=r(u")$
and let
![]() $p'$
be the group inverse of p in
$p'$
be the group inverse of p in
![]() $uI$
. Let
$uI$
. Let
![]() $\chi :uI\to uI$
be the left translation by
$\chi :uI\to uI$
be the left translation by
![]() $p'$
.
$p'$
.
![]() ${\cal H}\subseteq WH({\cal B}/{\cal A})$
, so by Proposition 3.9 we have that
${\cal H}\subseteq WH({\cal B}/{\cal A})$
, so by Proposition 3.9 we have that
Therefore the following diagram commutes.

Since in this diagram
![]() $r:{\cal H}\to uI$
is “onto”,
$r:{\cal H}\to uI$
is “onto”,
![]() $r=\chi r\psi $
and
$r=\chi r\psi $
and
![]() $\chi $
is a bijection, we get that
$\chi $
is a bijection, we get that
![]() $r:{\cal H}'\to uI$
is “onto” and
$r:{\cal H}'\to uI$
is “onto” and
![]() $f:{\cal H}'\to uI$
defined as
$f:{\cal H}'\to uI$
defined as
![]() $\chi r$
is a group epimorphism.
$\chi r$
is a group epimorphism.
Notice that the function
![]() $r:{\cal H}'\to uI$
is a twisted group epimorphism, namely it is the epimorphism f composed with left translation by p, similarly as in the proof of Theorem 4.6 and also as in [Reference Newelski11], where under another assumption it is proved that the Ellis groups in
$r:{\cal H}'\to uI$
is a twisted group epimorphism, namely it is the epimorphism f composed with left translation by p, similarly as in the proof of Theorem 4.6 and also as in [Reference Newelski11], where under another assumption it is proved that the Ellis groups in
![]() $S_{ext,G}(M)$
and
$S_{ext,G}(M)$
and
![]() $S_{ext,G}(N)$
are isomorphic and in the proof restrictions are twisted isomorphisms. However, in the model theoretic set-up no example is known where the twist is really needed. So, given
$S_{ext,G}(N)$
are isomorphic and in the proof restrictions are twisted isomorphisms. However, in the model theoretic set-up no example is known where the twist is really needed. So, given
![]() $M\prec ^* N,\ I\triangleleft _mS_{ext,G}(M)$
and
$M\prec ^* N,\ I\triangleleft _mS_{ext,G}(M)$
and
![]() $I"\triangleleft _m S_{ext,G}(N)$
with
$I"\triangleleft _m S_{ext,G}(N)$
with
![]() $r[I"]=I$
, is it true that there are
$r[I"]=I$
, is it true that there are
![]() $u\in J(I)$
and
$u\in J(I)$
and
![]() $u"\in J(I")$
with
$u"\in J(I")$
with
![]() $u=r(u")$
?
$u=r(u")$
?
Also, the group
![]() ${\cal H}'$
in the proof of Theorem 4.10 is independent on the choice of
${\cal H}'$
in the proof of Theorem 4.10 is independent on the choice of
![]() $u"$
, up to isomorphism.
$u"$
, up to isomorphism.
We conclude this section considering some special cases.
Remark 4.12. Assume
![]() $S({\cal B})$
contains a unique minimal left ideal and
$S({\cal B})$
contains a unique minimal left ideal and
![]() $CH({\cal B}/{\cal A})\subseteq WH({\cal B}/{\cal A})$
. Let
$CH({\cal B}/{\cal A})\subseteq WH({\cal B}/{\cal A})$
. Let
![]() $f:{\cal H}'\to uI$
be the group epimorphism from the proof of Theorem 4.10. Then f splits, that is there is a subgroup
$f:{\cal H}'\to uI$
be the group epimorphism from the proof of Theorem 4.10. Then f splits, that is there is a subgroup
![]() ${\cal H}"$
of
${\cal H}"$
of
![]() ${\cal H}'$
such that
${\cal H}'$
such that
![]() $f|_{{\cal H}"}:{\cal H}"\to uI$
is an isomorphism and
$f|_{{\cal H}"}:{\cal H}"\to uI$
is an isomorphism and
![]() ${\cal H}'={\mathrm {Ker}} f\rtimes {\cal H}"$
.
${\cal H}'={\mathrm {Ker}} f\rtimes {\cal H}"$
.
Proof We consider the situation from the proof of Theorem 4.10. By Lemma 4.11 we have a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\psi :S({\cal B})\to u"I"$
(mapping x to
$\psi :S({\cal B})\to u"I"$
(mapping x to
![]() $u"x$
) and
$u"x$
) and
![]() ${\cal H}'=\psi [{\cal H}]$
.
${\cal H}'=\psi [{\cal H}]$
.
Now we have additionally a group
![]() ${\cal G}=\{p^{{\cal B}}:p\in uI\}\subseteq CH({\cal B}/{\cal A})\subseteq WH({\cal B}/{\cal A})$
such that
${\cal G}=\{p^{{\cal B}}:p\in uI\}\subseteq CH({\cal B}/{\cal A})\subseteq WH({\cal B}/{\cal A})$
such that
![]() $r:{\cal G}\to uI$
is an isomorphism. Let
$r:{\cal G}\to uI$
is an isomorphism. Let
![]() ${\cal H}"=\psi [{\cal G}]$
. So
${\cal H}"=\psi [{\cal G}]$
. So
![]() ${\cal H}"$
is a subgroup of
${\cal H}"$
is a subgroup of
![]() $u"I"$
and as in the proof of Theorem 4.6 we get that
$u"I"$
and as in the proof of Theorem 4.6 we get that
![]() $r:{\cal H}"\to uI$
is a bijection. We claim that
$r:{\cal H}"\to uI$
is a bijection. We claim that
![]() ${\cal H}"\subseteq {\cal H}'$
.
${\cal H}"\subseteq {\cal H}'$
.
Indeed, let
![]() $x\in {\cal G}$
. We have that
$x\in {\cal G}$
. We have that
![]() $u"$
is the identity element of the group
$u"$
is the identity element of the group
![]() ${\cal H}'$
and let
${\cal H}'$
and let
![]() $u'$
be the identity element of the group
$u'$
be the identity element of the group
![]() ${\cal H}$
(as in the proof of Theorem 4.10). Since
${\cal H}$
(as in the proof of Theorem 4.10). Since
![]() $\psi (u')=u"$
, we have that
$\psi (u')=u"$
, we have that
![]() $\psi (x)=\psi (u'xu')$
. By Lemma 4.1,
$\psi (x)=\psi (u'xu')$
. By Lemma 4.1,
![]() ${\cal H}_{u'}=u'I_0^+$
, where
${\cal H}_{u'}=u'I_0^+$
, where
![]() $I_0^+=cl(Hu')\cap WH({\cal B}/{\cal A})\triangleleft _m WH({\cal B}/{\cal A})$
. Hence
$I_0^+=cl(Hu')\cap WH({\cal B}/{\cal A})\triangleleft _m WH({\cal B}/{\cal A})$
. Hence
![]() $u'xu'\in {\cal H}_{u'}$
and
$u'xu'\in {\cal H}_{u'}$
and
![]() $\psi (x)\in {\cal H}'$
.
$\psi (x)\in {\cal H}'$
.
Therefore
![]() $f|_{{\cal H}"}$
is an isomorphism
$f|_{{\cal H}"}$
is an isomorphism
![]() ${\cal H}"\to uI$
and we are done.
${\cal H}"\to uI$
and we are done.
Proposition 4.13. Assume the semigroup
![]() $S({\cal B})$
is commutative.Footnote
3
$S({\cal B})$
is commutative.Footnote
3
(1) The assumptions of both Theorems 4.6 and 4.10 are satisfied.
(2) The semigroup
![]() $S({\cal A})$
is also commutative.
$S({\cal A})$
is also commutative.
(3)
![]() $WCH({\cal B}/{\cal A})=WH({\cal B}/{\cal A})$
In particular,
$WCH({\cal B}/{\cal A})=WH({\cal B}/{\cal A})$
In particular,
![]() $CH({\cal B}/{\cal A})\subseteq WH({\cal B}/{\cal A})$
and the assumptions of Remark 4.12 hold. Also the group
$CH({\cal B}/{\cal A})\subseteq WH({\cal B}/{\cal A})$
and the assumptions of Remark 4.12 hold. Also the group
![]() ${\cal G}'$
from the proof of Theorem 4.6 is contained in the group
${\cal G}'$
from the proof of Theorem 4.6 is contained in the group
![]() ${\cal H}'$
from the proof of Theorem 4.10 and
${\cal H}'$
from the proof of Theorem 4.10 and
![]() ${\cal H}'={\mathrm {Ker}} f\rtimes {\cal G}'$
, where
${\cal H}'={\mathrm {Ker}} f\rtimes {\cal G}'$
, where
![]() $f:{\cal H}'\to uI$
is the group epimorphism from the proof of Theorem 4.10.
$f:{\cal H}'\to uI$
is the group epimorphism from the proof of Theorem 4.10.
Proof (1) Assume
![]() $I_0,I_1\triangleleft _mS({\cal B})$
and
$I_0,I_1\triangleleft _mS({\cal B})$
and
![]() $u_0,u_1\in J(I_0)$
. Then
$u_0,u_1\in J(I_0)$
. Then
![]() $u_0=u_0u_1=u_1u_0=u_1$
, hence
$u_0=u_0u_1=u_1u_0=u_1$
, hence
![]() $I_0$
is a group. Also
$I_0$
is a group. Also
![]() $I_0=I_1I_0=I_0I_1=I_1$
, hence
$I_0=I_1I_0=I_0I_1=I_1$
, hence
![]() $S({\cal B})$
contains a unique minimal left ideal.
$S({\cal B})$
contains a unique minimal left ideal.
(2) By Corollary 3.11
![]() $S({\cal A})\cong CH({\cal B}/{\cal A})\subseteq S({\cal B})$
.
$S({\cal A})\cong CH({\cal B}/{\cal A})\subseteq S({\cal B})$
.
(3) Assume
![]() $q,s\in S({\cal B})$
. Using commutativity of
$q,s\in S({\cal B})$
. Using commutativity of
![]() $S({\cal B})$
and
$S({\cal B})$
and
![]() $S({\cal A})$
we see that
$S({\cal A})$
we see that
hence we are done by Proposition 3.9.
For the last clause we work in the situations of the proofs of Theorems 4.6 and 4.10. So we have a unique
![]() $I"\triangleleft _m S({\cal B})$
that is a group with identity element
$I"\triangleleft _m S({\cal B})$
that is a group with identity element
![]() $u"\in J(I")$
. By Lemmas 4.9 and 4.11 we have
$u"\in J(I")$
. By Lemmas 4.9 and 4.11 we have
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $\varphi ,\psi :S({\cal B})\to I"$
mapping x to
$\varphi ,\psi :S({\cal B})\to I"$
mapping x to
![]() $xu"$
and
$xu"$
and
![]() $u"x$
, respectively. Since
$u"x$
, respectively. Since
![]() $I"$
is a group we have that
$I"$
is a group we have that
hence
![]() $\varphi =\psi $
. Now
$\varphi =\psi $
. Now
![]() ${\cal G}'=\varphi [{\cal G}]=\psi [{\cal G}]$
equals
${\cal G}'=\varphi [{\cal G}]=\psi [{\cal G}]$
equals
![]() ${\cal H}"$
from the proof of Remark 4.12, hence it is contained in
${\cal H}"$
from the proof of Remark 4.12, hence it is contained in
![]() ${\cal H}'$
. The rest follows from Remark 4.12.
${\cal H}'$
. The rest follows from Remark 4.12.
5 The model theoretic set-up
In this section we elaborate on the results from Sections 2 and 3 in the model theoretic set-up. So again we assume M is an L-structure,
![]() $T=Th(M)$
,
$T=Th(M)$
,
![]() $G=G(M)$
is an infinite
$G=G(M)$
is an infinite
![]() $0$
-definable group in M,
$0$
-definable group in M,
![]() $M\prec ^*N$
and
$M\prec ^*N$
and
![]() $H=G(N)$
. We are interested in the G-flow
$H=G(N)$
. We are interested in the G-flow
![]() $S_{ext,G}(M)$
and the H-flow
$S_{ext,G}(M)$
and the H-flow
![]() $S_{ext,G}(N)$
. This situation fits into the combinatorial set-up, with
$S_{ext,G}(N)$
. This situation fits into the combinatorial set-up, with
![]() ${\cal A}={\mathrm {Def}}_{ext,G}(M)$
and
${\cal A}={\mathrm {Def}}_{ext,G}(M)$
and
![]() ${\cal B}={\mathrm {Def}}_{ext,G}(N)$
. For
${\cal B}={\mathrm {Def}}_{ext,G}(N)$
. For
![]() $A\in {\mathrm {Def}}_{ext,G}(M)$
we define
$A\in {\mathrm {Def}}_{ext,G}(M)$
we define
![]() $A ^{\#}\in {\mathrm {Def}}_{ext,G}(N)$
as in Section 1. We apply the definitions of weak heir and weak coheir here. When
$A ^{\#}\in {\mathrm {Def}}_{ext,G}(N)$
as in Section 1. We apply the definitions of weak heir and weak coheir here. When
![]() $q\in S_{ext,G}(N)$
is a weak [co]heir of
$q\in S_{ext,G}(N)$
is a weak [co]heir of
![]() $p\in S_{ext,G}(M)$
, we say that q is a weak [co]heir over M. Let
$p\in S_{ext,G}(M)$
, we say that q is a weak [co]heir over M. Let
and let
![]() $WCH_G(N/M)$
and
$WCH_G(N/M)$
and
![]() $WH_G(N/M)$
be the corresponding sets of weak coheirs and weak heirs, respectively.
$WH_G(N/M)$
be the corresponding sets of weak coheirs and weak heirs, respectively.
Assume
![]() $G_1$
is a
$G_1$
is a
![]() $0$
-definable subgroup of G and let
$0$
-definable subgroup of G and let
![]() $H_1=G_1(N)$
. Then we have also a
$H_1=G_1(N)$
. Then we have also a
![]() $G_1$
-flow
$G_1$
-flow
![]() $S_{ext,G_1}(M)$
and
$S_{ext,G_1}(M)$
and
![]() $H_1$
-flow
$H_1$
-flow
![]() $S_{ext,G_1}(N)$
, they are naturally identified with the clopen sets
$S_{ext,G_1}(N)$
, they are naturally identified with the clopen sets
![]() $S_{ext,G}(M)\cap [G_1]$
and
$S_{ext,G}(M)\cap [G_1]$
and
![]() $S_{ext,G}(N)\cap [H_1]$
, respectively. So
$S_{ext,G}(N)\cap [H_1]$
, respectively. So
![]() $S_{ext,G_1}(M)$
and
$S_{ext,G_1}(M)$
and
![]() $S_{ext,G_1}(N)$
are semigroups isomorphic to
$S_{ext,G_1}(N)$
are semigroups isomorphic to
![]() ${\mathrm {End}}({\mathrm {Def}}_{ext,G_1}(M))$
and
${\mathrm {End}}({\mathrm {Def}}_{ext,G_1}(M))$
and
![]() ${\mathrm {End}}({\mathrm {Def}}_{ext,G_1}(N))$
, and as such also closed sub-semigroups of
${\mathrm {End}}({\mathrm {Def}}_{ext,G_1}(N))$
, and as such also closed sub-semigroups of
![]() $S_{ext,G}(M)$
and
$S_{ext,G}(M)$
and
![]() $S_{ext,G}(N)$
, respectively.
$S_{ext,G}(N)$
, respectively.
Lemma 5.1. Assume
![]() $[G:G_1]$
is finite and
$[G:G_1]$
is finite and
![]() $p\in S_{ext,G_1}(N)$
.
$p\in S_{ext,G_1}(N)$
.
(1)
![]() $p\in WH_{G_1}(N/M)$
iff
$p\in WH_{G_1}(N/M)$
iff
![]() $p\in WH_G(N/M)$
.
$p\in WH_G(N/M)$
.
(2)
![]() $p\in WCH_{G_1}(N/M)$
iff
$p\in WCH_{G_1}(N/M)$
iff
![]() $p\in WCH_G(N/M)$
.
$p\in WCH_G(N/M)$
.
Proof (1)
![]() $\Leftarrow $
is immediate by Proposition 3.9. For
$\Leftarrow $
is immediate by Proposition 3.9. For
![]() $\Rightarrow $
, let
$\Rightarrow $
, let
![]() $b_1,\dots ,b_n$
be representatives of the left cosets of
$b_1,\dots ,b_n$
be representatives of the left cosets of
![]() $G_1$
in G. Let
$G_1$
in G. Let
![]() $s\in S_{ext,G}(N)$
. Then there are
$s\in S_{ext,G}(N)$
. Then there are
![]() $s'\in S_{ext,G_1}(N)$
and
$s'\in S_{ext,G_1}(N)$
and
![]() $i\leq n$
such that
$i\leq n$
such that
![]() $\hat {b}_i*s'=s$
. Hence, using the fact that
$\hat {b}_i*s'=s$
. Hence, using the fact that
![]() $\hat {b}_i\in WH_G(N/M)\cap WCH_G(N/M)$
(Lemma 3.12), we have that
$\hat {b}_i\in WH_G(N/M)\cap WCH_G(N/M)$
(Lemma 3.12), we have that
 $$ \begin{align*}&r(s*p)=r(\hat{b}_i*s'*p)=r(\hat{b}_i)*r(s'*p)=r(\hat{b}_i)*r(s')*r(p)\\ & \quad =r(\hat{b}_i*s')*r(p)=r(s)*r(p).\end{align*} $$
$$ \begin{align*}&r(s*p)=r(\hat{b}_i*s'*p)=r(\hat{b}_i)*r(s'*p)=r(\hat{b}_i)*r(s')*r(p)\\ & \quad =r(\hat{b}_i*s')*r(p)=r(s)*r(p).\end{align*} $$
So by Proposition 3.9
![]() $p\in WH_G(N/M)$
. (2) has a similar proof.
$p\in WH_G(N/M)$
. (2) has a similar proof.
Now we shall characterize the notions of weak heirs and weak coheirs in the case where T is stable. So from now on until Lemma 5.8 we assume T is stable and for simplicity also that
![]() $G=M$
. This means that
$G=M$
. This means that
![]() ${\mathrm {Def}}_{ext,G}(M)={\mathrm {Def}}(M)$
, the algebra of definable subsets of M, and
${\mathrm {Def}}_{ext,G}(M)={\mathrm {Def}}(M)$
, the algebra of definable subsets of M, and
![]() $S_{ext,G}(M)=S(M)$
, the space of complete
$S_{ext,G}(M)=S(M)$
, the space of complete
![]() $1$
-types over M. Also now
$1$
-types over M. Also now
![]() $M\prec ^*N$
means just that
$M\prec ^*N$
means just that
![]() $M\prec N$
.
$M\prec N$
.
For
![]() $A\in {\mathrm {Def}}(M)$
let
$A\in {\mathrm {Def}}(M)$
let
![]() $\varphi _A(x;y)$
be an
$\varphi _A(x;y)$
be an
![]() $L(M)$
-formula saying that
$L(M)$
-formula saying that
![]() $x\in y\cdot A$
. Likewise let
$x\in y\cdot A$
. Likewise let
![]() $\psi _A(x;y)$
be an
$\psi _A(x;y)$
be an
![]() $L(M)$
-formula saying that
$L(M)$
-formula saying that
![]() $x\in A\cdot y$
. Let
$x\in A\cdot y$
. Let
We identify formulas that are equivalent in
![]() ${\cal M}$
.
${\cal M}$
.
Remark 5.2. Every L-formula
![]() $\varphi (x)$
over M is equivalent to a
$\varphi (x)$
over M is equivalent to a
![]() $\Delta _M$
-formula over M and to a
$\Delta _M$
-formula over M and to a
![]() $\Delta _M^*$
-formula over M.
$\Delta _M^*$
-formula over M.
Proof Let
![]() $A=\varphi (M)$
. So
$A=\varphi (M)$
. So
![]() $A\in {\mathrm {Def}}(M)$
and
$A\in {\mathrm {Def}}(M)$
and
![]() $A=\varphi _A(M,e)=\psi _A(M;e)$
, where e is the identity element of G. Hence
$A=\varphi _A(M,e)=\psi _A(M;e)$
, where e is the identity element of G. Hence
![]() $\varphi (x)$
is equivalent to
$\varphi (x)$
is equivalent to
![]() $\varphi _A(x;e)$
and to
$\varphi _A(x;e)$
and to
![]() $\psi _A(x;e)$
.
$\psi _A(x;e)$
.
The following theorem characterizes weak heirs and weak coheirs in terms of local forking.
Theorem 5.3. Assume
![]() $q(x)\in S(N)$
.
$q(x)\in S(N)$
.
(1)
![]() $q\in WH_G(N/M)$
iff
$q\in WH_G(N/M)$
iff
![]() $q|_{\Delta _M}$
does not fork over M.
$q|_{\Delta _M}$
does not fork over M.
(2)
![]() $q\in WCH_G(N/M)$
iff
$q\in WCH_G(N/M)$
iff
![]() $q|_{\Delta _M^*}$
does not fork over M.
$q|_{\Delta _M^*}$
does not fork over M.
Before the proof we need some introductory comments. Let
![]() $p\in S(M)$
and
$p\in S(M)$
and
![]() $\varphi (x;y)\in L(M)$
. Let
$\varphi (x;y)\in L(M)$
. Let
![]() $d_p\varphi (y)$
be the
$d_p\varphi (y)$
be the
![]() $L(M)$
-formula defining
$L(M)$
-formula defining
![]() $p|_{\varphi }$
, that is for every
$p|_{\varphi }$
, that is for every
![]() $c\in M$
we have that
$c\in M$
we have that
![]() $\models d_p\varphi (c)$
iff
$\models d_p\varphi (c)$
iff
![]() $\varphi (x,c)\in p$
. On the other hand we have the function
$\varphi (x,c)\in p$
. On the other hand we have the function
![]() $d_p:{\mathrm {Def}}(M)\to {\mathrm {Def}}(M)$
, defined in Definition 2.2.
$d_p:{\mathrm {Def}}(M)\to {\mathrm {Def}}(M)$
, defined in Definition 2.2.
Lemma 5.4. Let
![]() $q(x)\in S(N),\ p=q|_M\in S(M),\ A\in {\mathrm {Def}}(M)$
and let
$q(x)\in S(N),\ p=q|_M\in S(M),\ A\in {\mathrm {Def}}(M)$
and let
![]() $c\in {\cal M}$
realize q.
$c\in {\cal M}$
realize q.
(1)
![]() $d_pA=(d_p\varphi _A(M))^{-1}$
.
$d_pA=(d_p\varphi _A(M))^{-1}$
.
(2)
![]() $(d_pA)^{\#}=d_qA^{\#}$
iff
$(d_pA)^{\#}=d_qA^{\#}$
iff
![]() $d_p\varphi _A(y)\equiv d_q\varphi _A(y)$
.
$d_p\varphi _A(y)\equiv d_q\varphi _A(y)$
.
(3)
![]() $d_qA^{\#}=\psi _A(N;c^{-1}).$
$d_qA^{\#}=\psi _A(N;c^{-1}).$
Proof (1) Let
![]() $b\in M$
. We have that
$b\in M$
. We have that
(2) By (1),
![]() $(d_pA)^{\#}=(d_p\varphi _A(N))^{-1}$
and
$(d_pA)^{\#}=(d_p\varphi _A(N))^{-1}$
and
![]() $d_qA^{\#}=(d_q\varphi _{A^{\#}}(N))^{-1}$
. So (2) follows.
$d_qA^{\#}=(d_q\varphi _{A^{\#}}(N))^{-1}$
. So (2) follows.
(3) Let
![]() $b\in N$
. We have that
$b\in N$
. We have that
where
![]() $A^{{\cal M}}$
is the subset of
$A^{{\cal M}}$
is the subset of
![]() ${\cal M}$
defined by the formula defining A in M. So we are done.
${\cal M}$
defined by the formula defining A in M. So we are done.
Proof of Theorem 5.3
Let
![]() $p=q|_M$
. (1)
$p=q|_M$
. (1)
![]() $\Rightarrow $
Assume that q is a weak heir over M. Then for every
$\Rightarrow $
Assume that q is a weak heir over M. Then for every
![]() $A\in {\mathrm {Def}}(M),\ (d_pA)^{\#}=d_qA^{\#}$
, hence by Lemma 5.4(2),
$A\in {\mathrm {Def}}(M),\ (d_pA)^{\#}=d_qA^{\#}$
, hence by Lemma 5.4(2),
![]() $d_q\varphi _A(y)\equiv d_p\varphi _A(y)$
.
$d_q\varphi _A(y)\equiv d_p\varphi _A(y)$
.
Let
![]() $p'\in S({\cal M})$
be the nonforking extension of p. Then for every formula
$p'\in S({\cal M})$
be the nonforking extension of p. Then for every formula
![]() $\chi (x;\bar {y})$
, the formula
$\chi (x;\bar {y})$
, the formula
![]() $d_p\chi (\bar {y})$
defines
$d_p\chi (\bar {y})$
defines
![]() $p'|_{\chi }$
. When
$p'|_{\chi }$
. When
![]() $\chi =\varphi _A$
, we have that
$\chi =\varphi _A$
, we have that
![]() $d_p\chi \equiv d_q\chi $
, hence
$d_p\chi \equiv d_q\chi $
, hence
![]() $q|_{\Delta _M}\subseteq p'$
and
$q|_{\Delta _M}\subseteq p'$
and
![]() $q|_{\Delta _M}$
does not fork over M.
$q|_{\Delta _M}$
does not fork over M.
![]() $\Leftarrow $
Assume that
$\Leftarrow $
Assume that
![]() $q|_{\Delta _M}$
does not fork over M. Let
$q|_{\Delta _M}$
does not fork over M. Let
![]() $q'\in S({\cal M})$
be an extension of
$q'\in S({\cal M})$
be an extension of
![]() $q|_{\Delta _M}$
that does not fork over M. By Remark 5.2,
$q|_{\Delta _M}$
that does not fork over M. By Remark 5.2,
![]() $q|_{\Delta _M}$
contains a complete type over M, hence
$q|_{\Delta _M}$
contains a complete type over M, hence
![]() $p\subseteq q|_{\Delta _M}$
and
$p\subseteq q|_{\Delta _M}$
and
![]() $q'$
is a nonforking extension of p. Therefore for every
$q'$
is a nonforking extension of p. Therefore for every
![]() $A\in {\mathrm {Def}}(M)$
we have
$A\in {\mathrm {Def}}(M)$
we have
Thus by Lemma 5.4(2),
![]() $(d_pA)^{\#}=d_qA^{\#}$
and q is a weak heir of p.
$(d_pA)^{\#}=d_qA^{\#}$
and q is a weak heir of p.
(2)
![]() $\Rightarrow $
Assume q is a weak coheir over M. Hence for every
$\Rightarrow $
Assume q is a weak coheir over M. Hence for every
![]() $s\in S(N)$
and
$s\in S(N)$
and
![]() $A,B\in {\mathrm {Def}}(M)$
, if
$A,B\in {\mathrm {Def}}(M)$
, if
![]() $d_sA^{\#}\cap B^{\#}\in q$
, then
$d_sA^{\#}\cap B^{\#}\in q$
, then
![]() $d_sA^{\#}\cap B^{\#}\cap M\neq \emptyset $
. By Lemma 5.4(3),
$d_sA^{\#}\cap B^{\#}\cap M\neq \emptyset $
. By Lemma 5.4(3),
![]() $d_sA^{\#}=\psi _A(N;c^{-1})$
, where
$d_sA^{\#}=\psi _A(N;c^{-1})$
, where
![]() $c\in {\cal M}$
realizes s. Hence we get that for every
$c\in {\cal M}$
realizes s. Hence we get that for every
![]() $c\in N$
, if
$c\in N$
, if
![]() $\psi _A(x;c^{-1})\in q$
and
$\psi _A(x;c^{-1})\in q$
and
![]() $\varphi (x)\in p$
, then the formula
$\varphi (x)\in p$
, then the formula
![]() $\psi _A(x;c^{-1})\land \varphi (x)$
is realized by an element of M (consider
$\psi _A(x;c^{-1})\land \varphi (x)$
is realized by an element of M (consider
![]() $s=tp(c/M)$
and
$s=tp(c/M)$
and
![]() $B=\varphi (M)$
).
$B=\varphi (M)$
).
Let
![]() $p|N$
be the coheir of p in
$p|N$
be the coheir of p in
![]() $S(N)$
. We see that
$S(N)$
. We see that
![]() $q|_{\Delta _M^*}\subseteq p|N$
. Clearly
$q|_{\Delta _M^*}\subseteq p|N$
. Clearly
![]() $p|N$
does not fork over M, hence neither does
$p|N$
does not fork over M, hence neither does
![]() $q|_{\Delta _M^*}$
.
$q|_{\Delta _M^*}$
.
![]() $\Leftarrow $
Assume that
$\Leftarrow $
Assume that
![]() $q|_{\Delta _M^*}$
does not fork over M. The type
$q|_{\Delta _M^*}$
does not fork over M. The type
![]() $p=q|_M\in S(M)$
is stationary, therefore
$p=q|_M\in S(M)$
is stationary, therefore
![]() $q|_{\Delta _M^*}$
is the only nonforking extension of p in
$q|_{\Delta _M^*}$
is the only nonforking extension of p in
![]() $S_{\Delta _M^*}(N)$
. Let
$S_{\Delta _M^*}(N)$
. Let
![]() $q'\in S(N)$
be a weak coheir of p. By (2)
$q'\in S(N)$
be a weak coheir of p. By (2)
![]() $\Rightarrow $
,
$\Rightarrow $
,
![]() $q'|_{\Delta _M^*}$
does not fork over M. Hence
$q'|_{\Delta _M^*}$
does not fork over M. Hence
![]() $q|_{\Delta _M^*}=q'|_{\Delta _M^*}$
. We shall prove that q is also a weak coheir over M.
$q|_{\Delta _M^*}=q'|_{\Delta _M^*}$
. We shall prove that q is also a weak coheir over M.
Let
![]() $s\in S(N),\ A,B\in {\mathrm {Def}}(M)$
and assume that
$s\in S(N),\ A,B\in {\mathrm {Def}}(M)$
and assume that
![]() $d_sA^{\#}\cap B^{\#}\in q$
. We have that
$d_sA^{\#}\cap B^{\#}\in q$
. We have that
![]() $(*)$
$(*)$
![]() $d_sA^{\#}\cap B^{\#}\in q|_{\Delta _M^*}$
$d_sA^{\#}\cap B^{\#}\in q|_{\Delta _M^*}$
meaning that
![]() $d_sA^{\#}\cap B^{\#}$
is definable (in N) by a
$d_sA^{\#}\cap B^{\#}$
is definable (in N) by a
![]() $\Delta _M^*$
-formula (with parameters from N) belonging to q. Indeed, first notice that obviously
$\Delta _M^*$
-formula (with parameters from N) belonging to q. Indeed, first notice that obviously
![]() $B^{\#}\in q|_{\Delta _M^*}$
. We shall prove that also
$B^{\#}\in q|_{\Delta _M^*}$
. We shall prove that also
![]() $d_sA^{\#}\in q|_{\Delta _M^*}$
.
$d_sA^{\#}\in q|_{\Delta _M^*}$
.
Let
![]() $d\in {\cal M}$
realize s and let
$d\in {\cal M}$
realize s and let
![]() $s^{-1}=tp(d^{-1}/N)$
. By Lemma 5.4(3),
$s^{-1}=tp(d^{-1}/N)$
. By Lemma 5.4(3),
where
![]() $\psi _A^*(y;x)$
is the formula
$\psi _A^*(y;x)$
is the formula
![]() $\psi _A(x;y)$
with the roles of variables
$\psi _A(x;y)$
with the roles of variables
![]() $x,y$
reversed, so that in
$x,y$
reversed, so that in
![]() $\psi _A^*$
, x is the parameter variable. By [Reference Pillay13, Lemma I.2.2],
$\psi _A^*$
, x is the parameter variable. By [Reference Pillay13, Lemma I.2.2],
![]() $d_{s^{-1}}\psi ^*_A (x)$
is equivalent in N to a positive Boolean combination of formulas
$d_{s^{-1}}\psi ^*_A (x)$
is equivalent in N to a positive Boolean combination of formulas
![]() $\psi _A(x,c),c\in N$
, hence it is a
$\psi _A(x,c),c\in N$
, hence it is a
![]() $\Delta _M^*$
-formula over N. This proves
$\Delta _M^*$
-formula over N. This proves
![]() $(*)$
.
$(*)$
.
Since
![]() $q|_{\Delta _M^*}=q'|_{\Delta _M^*}$
, we get that
$q|_{\Delta _M^*}=q'|_{\Delta _M^*}$
, we get that
![]() $d_sA^{\#}\cap B^{\#}\in q'$
. As
$d_sA^{\#}\cap B^{\#}\in q'$
. As
![]() $q'$
is a weak coheir over M, we conclude that
$q'$
is a weak coheir over M, we conclude that
![]() $d_sA^{\#}\cap B^{\#}\cap M\neq \emptyset $
and q is a weak coheir over M.
$d_sA^{\#}\cap B^{\#}\cap M\neq \emptyset $
and q is a weak coheir over M.
By Theorem 5.3, in the stable case both sets
![]() $WCH_G(N/M)$
and
$WCH_G(N/M)$
and
![]() $WH_G(N/M)$
are closed in
$WH_G(N/M)$
are closed in
![]() $S_G(N)$
. Also, in this case the groups
$S_G(N)$
. Also, in this case the groups
![]() ${\cal G},{\cal G}',{\cal H}$
and
${\cal G},{\cal G}',{\cal H}$
and
![]() ${\cal H}'$
from Section 3 are equal to the set
${\cal H}'$
from Section 3 are equal to the set
![]() $CH_G(N/M)$
that is the set if generic types in
$CH_G(N/M)$
that is the set if generic types in
![]() $S_G(N)$
. It is the only minimal left ideal in
$S_G(N)$
. It is the only minimal left ideal in
![]() $S_G(N)$
and the group epimorphisms f from the proof of Theorems 4.6 and 4.9 are restrictions.
$S_G(N)$
and the group epimorphisms f from the proof of Theorems 4.6 and 4.9 are restrictions.
Corollary 5.5. Assume
![]() $a\in {\cal M}$
. Then
$a\in {\cal M}$
. Then
![]() $tp(a/N)\in WH_G(N/M)$
iff
$tp(a/N)\in WH_G(N/M)$
iff
![]() $tp(a^{-1}/N)\in WCH_G(N/M)$
.
$tp(a^{-1}/N)\in WCH_G(N/M)$
.
Proof Let
![]() $i:{\cal M}\to {\cal M}$
be the group inversion, that is
$i:{\cal M}\to {\cal M}$
be the group inversion, that is
![]() $i(x)=x^{-1}$
. So i maps a to
$i(x)=x^{-1}$
. So i maps a to
![]() $a^{-1}$
. Also, given a formula
$a^{-1}$
. Also, given a formula
![]() $\varphi _A(x;y)\in \Delta _M$
and
$\varphi _A(x;y)\in \Delta _M$
and
![]() $b\in {\cal M}$
, i maps
$b\in {\cal M}$
, i maps
![]() $\varphi _A({\cal M};b)$
to the set
$\varphi _A({\cal M};b)$
to the set
![]() $\psi _{A^{-1}}({\cal M};b^{-1})$
, since for
$\psi _{A^{-1}}({\cal M};b^{-1})$
, since for
![]() $x,y\in {\cal M}$
,
$x,y\in {\cal M}$
,
Therefore
![]() $tp(a/B)|_{\Delta _M}$
does not fork over M iff
$tp(a/B)|_{\Delta _M}$
does not fork over M iff
![]() $tp(a^{-1}/N)|_{\Delta _M^*}$
does not fork over M, so we are done by Theorem 5.3.
$tp(a^{-1}/N)|_{\Delta _M^*}$
does not fork over M, so we are done by Theorem 5.3.
We can also prove Corollary 5.5 directly, using Proposition 3.9 and the fact that in the stable case
![]() $*$
is just the independent multiplication of types [Reference Newelski9], that is for
$*$
is just the independent multiplication of types [Reference Newelski9], that is for
![]() $p,q\in S(N)$
,
$p,q\in S(N)$
,
![]() $p*q=tp(ab/N)$
for any N-independent
$p*q=tp(ab/N)$
for any N-independent
![]() $a\models p$
and
$a\models p$
and
![]() $b\models q$
. This fact implies also that in the stable case
$b\models q$
. This fact implies also that in the stable case
![]() $*$
in
$*$
in
![]() $S(N)$
is continuous not only in the first coordinate, but also in the second coordinate. The next corollary corresponds to Corollary 3.10.
$S(N)$
is continuous not only in the first coordinate, but also in the second coordinate. The next corollary corresponds to Corollary 3.10.
Corollary 5.6. Assume T is stable and
![]() $q\in S_G(N)$
. Then
$q\in S_G(N)$
. Then
![]() $q\in WCH_G(N/M)$
iff
$q\in WCH_G(N/M)$
iff
![]() $r(q*\hat {h})=r(q)*r(\hat {h})$
for every
$r(q*\hat {h})=r(q)*r(\hat {h})$
for every
![]() $h\in G(N)$
.
$h\in G(N)$
.
Also the proof of Theorem 5.3(2)
![]() $\Rightarrow $
shows that for
$\Rightarrow $
shows that for
![]() $q\in S(N)$
we have that
$q\in S(N)$
we have that
![]() $q\in WCH_G(N/M)$
iff for every
$q\in WCH_G(N/M)$
iff for every
![]() $c\in N$
and
$c\in N$
and
![]() $A,B\in {\mathrm {Def}}(N)$
, if
$A,B\in {\mathrm {Def}}(N)$
, if
![]() $A^{\#}c\cap B^{\#}\in q$
, then
$A^{\#}c\cap B^{\#}\in q$
, then
![]() $A^{\#}c\cap B^{\#}\cap M\neq \emptyset $
.
$A^{\#}c\cap B^{\#}\cap M\neq \emptyset $
.
Now we assume additionally that
![]() $G=M$
is abelian. Since in a stable theory forking independence is symmetric and
$G=M$
is abelian. Since in a stable theory forking independence is symmetric and
![]() $*$
in
$*$
in
![]() $S(M)$
is the free multiplication of types, we get that
$S(M)$
is the free multiplication of types, we get that
![]() $(S(M),*)$
is a commutative semigroup (in fact,
$(S(M),*)$
is a commutative semigroup (in fact,
![]() $(S(M),*)$
is commutative iff M is abelian). In the combinatorial case this provides examples where
$(S(M),*)$
is commutative iff M is abelian). In the combinatorial case this provides examples where
![]() $(S({\cal B}),*)$
is commutative.
$(S({\cal B}),*)$
is commutative.
By Proposition 4.13 we get that in the stable case, if G is abelian, then
![]() $WH_G(N/M)=WCH_G(N/M)$
. (This follows also from Theorem 5.3, since in the abelian case
$WH_G(N/M)=WCH_G(N/M)$
. (This follows also from Theorem 5.3, since in the abelian case
![]() $\Delta _M=\Delta _M^*$
.) We can do slightly better.
$\Delta _M=\Delta _M^*$
.) We can do slightly better.
Corollary 5.7. If G is abelian-by-finite, then
![]() $WH_G(N/M)=WCH_G(N/M)$
.
$WH_G(N/M)=WCH_G(N/M)$
.
Proof Assume G is abelian-by-finite. So there is an abelian subgroup
![]() $G_1$
of finite index in G and by stability we may assume that
$G_1$
of finite index in G and by stability we may assume that
![]() $G_1$
is definable. Let
$G_1$
is definable. Let
![]() $H_1=G_1(N)$
. By the discussion above,
$H_1=G_1(N)$
. By the discussion above,
![]() $WH_{G_1}(N/M)=WCH_{G_1}(N/M)$
. Let
$WH_{G_1}(N/M)=WCH_{G_1}(N/M)$
. Let
![]() $b_1,\dots ,b_n\in G$
be representatives of the left cosets of
$b_1,\dots ,b_n\in G$
be representatives of the left cosets of
![]() $G_1$
in G and let
$G_1$
in G and let
![]() $p\in S_G(N)$
. Then there are
$p\in S_G(N)$
. Then there are
![]() $p'\in S_{G_1}(N)$
and
$p'\in S_{G_1}(N)$
and
![]() $i\leq n$
such that
$i\leq n$
such that
![]() $p=\hat {b}_i*p'$
. We are done by Lemmas 5.1 and 3.12.
$p=\hat {b}_i*p'$
. We are done by Lemmas 5.1 and 3.12.
Now we waive the assumption that T is stable. We say that G has the group ideals property (shortly gip) if every (equivalently some) minimal left ideal in
![]() $S_{ext,G}(M)$
is a group. Let
$S_{ext,G}(M)$
is a group. Let
![]() ${\cal K}_M,{\cal R}_M$
be the set of kernels and images of the functions
${\cal K}_M,{\cal R}_M$
be the set of kernels and images of the functions
![]() $d_p$
for almost periodic
$d_p$
for almost periodic
![]() $p\in S_{ext,G}(M)$
. So G has the gip iff
$p\in S_{ext,G}(M)$
. So G has the gip iff
![]() ${\cal R}_M$
is a singleton. In the model theoretic set-up Theorem 4.6 translates into Theorem 4.9. Also Lemma 4.8 translates as follows.
${\cal R}_M$
is a singleton. In the model theoretic set-up Theorem 4.6 translates into Theorem 4.9. Also Lemma 4.8 translates as follows.
Lemma 5.8. Assume
![]() $M\prec ^* N$
and the group
$M\prec ^* N$
and the group
![]() $H=G(N)$
has the gip. Then also G has the gip.
$H=G(N)$
has the gip. Then also G has the gip.
Is the gip assumption model theoretic? The next proposition suggests a positive answer.
Proposition 5.9. Assume
![]() $G(x)$
is a formula defining groups in models of T and
$G(x)$
is a formula defining groups in models of T and
![]() $\kappa \geq |T|$
. Then the following are equivalent.
$\kappa \geq |T|$
. Then the following are equivalent.
(1)
![]() $G(M)$
has the gip for every model M of T.
$G(M)$
has the gip for every model M of T.
(2)
![]() $G(M)$
has the gip for every model M of T of power
$G(M)$
has the gip for every model M of T of power
![]() $\kappa $
.
$\kappa $
.
Proof (1)
![]() $\Rightarrow $
(2) is obvious. We prove (2)
$\Rightarrow $
(2) is obvious. We prove (2)
![]() $\Rightarrow $
(1). Suppose for contradiction that (2) holds but (1) fails and in some
$\Rightarrow $
(1). Suppose for contradiction that (2) holds but (1) fails and in some
![]() $N\models T$
, the group
$N\models T$
, the group
![]() $H=G(N)$
does not have the gip. There are two cases, depending on whether
$H=G(N)$
does not have the gip. There are two cases, depending on whether
![]() $\|N\|<\kappa $
.
$\|N\|<\kappa $
.
Case 1.
![]() $\|N\|<\kappa $
Let
$\|N\|<\kappa $
Let
![]() $N'$
be a
$N'$
be a
![]() $*$
-elementary extension of N of power
$*$
-elementary extension of N of power
![]() $>\kappa $
. Since H does not have the gip, by Lemma 5.8 also
$>\kappa $
. Since H does not have the gip, by Lemma 5.8 also
![]() $H':= G(N')$
does not have the gip, so this case reduces to the following Case 2.
$H':= G(N')$
does not have the gip, so this case reduces to the following Case 2.
Case 2.
![]() $\|N\|>\kappa $
Here we need to work harder. Since H does not have the gip, the set
$\|N\|>\kappa $
Here we need to work harder. Since H does not have the gip, the set
![]() ${\cal R}_N$
has at least two distinct elements
${\cal R}_N$
has at least two distinct elements
![]() $R_0$
and
$R_0$
and
![]() $R_1$
. By Fact 2.5
$R_1$
. By Fact 2.5
![]() $R_0\not \subseteq R_1$
. Choose
$R_0\not \subseteq R_1$
. Choose
![]() $A\in R_0$
with
$A\in R_0$
with
![]() $A\not \in R_1$
. Again by Fact 2.5 the set A is strongly generic in H and the H-subalgebra of
$A\not \in R_1$
. Again by Fact 2.5 the set A is strongly generic in H and the H-subalgebra of
![]() ${\mathrm {Def}}_{ext,G}(N)$
generated by
${\mathrm {Def}}_{ext,G}(N)$
generated by
![]() $R_1\cup \{A\}$
is not generic. This means that there are a Boolean term
$R_1\cup \{A\}$
is not generic. This means that there are a Boolean term
![]() $\tau (x_0,\dots ,x_n)$
and some
$\tau (x_0,\dots ,x_n)$
and some
![]() $B_1,\dots ,B_n\in R_1$
and
$B_1,\dots ,B_n\in R_1$
and
![]() $h_1,\dots ,h_n\in H$
such that the set
$h_1,\dots ,h_n\in H$
such that the set
![]() $\tau (A,h_1B_1,\dots ,h_nB_n)$
is nonempty and not generic in H.
$\tau (A,h_1B_1,\dots ,h_nB_n)$
is nonempty and not generic in H.
Let
![]() $L'$
be the language L of T extended by new unary predicates
$L'$
be the language L of T extended by new unary predicates
![]() $P_A,P_{B_1},\dots ,P_{B_n}$
that we interpret in N as
$P_A,P_{B_1},\dots ,P_{B_n}$
that we interpret in N as
![]() $A,B_1,\dots ,B_n$
, respectively, obtaining an
$A,B_1,\dots ,B_n$
, respectively, obtaining an
![]() $L'$
-structure
$L'$
-structure
![]() $N'$
. Let
$N'$
. Let
![]() $M'$
be an elementary substructure of
$M'$
be an elementary substructure of
![]() $N'$
of power
$N'$
of power
![]() $\kappa $
, containing
$\kappa $
, containing
![]() $h_1,\dots ,h_n$
and let
$h_1,\dots ,h_n$
and let
![]() $M=M'|_L$
. Then the sets
$M=M'|_L$
. Then the sets
![]() $A'=A\cap M,B_i'=B_i\cap M,i=1,\dots ,n$
, are subsets of G externally definable in M, the set
$A'=A\cap M,B_i'=B_i\cap M,i=1,\dots ,n$
, are subsets of G externally definable in M, the set
![]() $A'$
is strongly generic in G and the G-algebra
$A'$
is strongly generic in G and the G-algebra
![]() $R'$
generated by the sets
$R'$
generated by the sets
![]() $B_1',\dots B_n'$
is generic.
$B_1',\dots B_n'$
is generic.
Let
![]() $R_0',R_1'$
be some maximal generic G-subalgebras of
$R_0',R_1'$
be some maximal generic G-subalgebras of
![]() ${\mathrm {Def}}_{ext,G}(M)$
containing
${\mathrm {Def}}_{ext,G}(M)$
containing
![]() $A'$
and
$A'$
and
![]() $R'$
, respectively. Since
$R'$
, respectively. Since
![]() $M'\prec N'$
, the set
$M'\prec N'$
, the set
![]() $\tau (A',h_1B_1',\dots ,h_nB_n')$
is nonempty and not generic in G. Hence
$\tau (A',h_1B_1',\dots ,h_nB_n')$
is nonempty and not generic in G. Hence
![]() $A'\not \in R_1'$
and
$A'\not \in R_1'$
and
![]() $R_0'\neq R_1'$
. Therefore G does not have the gip, a contradiction.
$R_0'\neq R_1'$
. Therefore G does not have the gip, a contradiction.
Proposition 5.9 is a counterpart of [Reference Newelski10, Lemma 4.5] that deals with the dual property that G has external generic types.
Given
![]() $M\prec ^* N$
and
$M\prec ^* N$
and
![]() $p\in S_{ext,G}(M)$
that is almost periodic, weak heir and [weak] coheir extensions are distinguished extensions of p in
$p\in S_{ext,G}(M)$
that is almost periodic, weak heir and [weak] coheir extensions are distinguished extensions of p in
![]() $S_{ext,G}(N)$
. Sometimes they are almost periodic, sometimes not.
$S_{ext,G}(N)$
. Sometimes they are almost periodic, sometimes not.
For example, let M be an o-minimal expansion of the ordered field of reals. Since M is Dedekind complete,
![]() ${\mathrm {Def}}_{ext}(M)={\mathrm {Def}}(M)$
[Reference Marker and Steinhorn8], hence
${\mathrm {Def}}_{ext}(M)={\mathrm {Def}}(M)$
[Reference Marker and Steinhorn8], hence
![]() $M\prec ^* N$
means just
$M\prec ^* N$
means just
![]() $M\prec N$
. Let
$M\prec N$
. Let
![]() $G_1=(M,+)$
. Then the only almost periodic types in
$G_1=(M,+)$
. Then the only almost periodic types in
![]() $S_{G_1}(M)$
are the two types at infinity
$S_{G_1}(M)$
are the two types at infinity
![]() $p_{-\infty }$
and
$p_{-\infty }$
and
![]() $p_{+\infty }$
. For every
$p_{+\infty }$
. For every
![]() $N\succ M$
they extend uniquely to almost periodic types
$N\succ M$
they extend uniquely to almost periodic types
![]() $p_{-\infty }',p_{+\infty }'\in S_{ext,G_1}(N)$
. The types
$p_{-\infty }',p_{+\infty }'\in S_{ext,G_1}(N)$
. The types
![]() $p_{-\infty }',p_{+\infty }'$
are weak heirs and not weak coheirs over M, provided
$p_{-\infty }',p_{+\infty }'$
are weak heirs and not weak coheirs over M, provided
![]() $N\neq M$
. In this example the groups
$N\neq M$
. In this example the groups
![]() $G_1(N)$
have the gip for all
$G_1(N)$
have the gip for all
![]() $N\equiv M$
. Also, if N is a proper elementary extension of M, then the set
$N\equiv M$
. Also, if N is a proper elementary extension of M, then the set
![]() $WH_{G_1}(N/M)$
is not closed in
$WH_{G_1}(N/M)$
is not closed in
![]() $S_{ext,G_1}(N)$
.
$S_{ext,G_1}(N)$
.
Next assume
![]() $G_2$
is a definably compact definable group in M. In this case by [Reference Newelski10] the groups
$G_2$
is a definably compact definable group in M. In this case by [Reference Newelski10] the groups
![]() $G_2(N)$
have external generic types for every
$G_2(N)$
have external generic types for every
![]() $N\equiv M$
containing the parameters of the definition of
$N\equiv M$
containing the parameters of the definition of
![]() $G_2$
. Also, for all
$G_2$
. Also, for all
![]() $N\succ M$
the almost periodic types in
$N\succ M$
the almost periodic types in
![]() $S_{ext,G_2}(N)$
are exactly the coheirs of the almost periodic types in
$S_{ext,G_2}(N)$
are exactly the coheirs of the almost periodic types in
![]() $S_{G_2}(M)$
and not weak heirs over M.
$S_{G_2}(M)$
and not weak heirs over M.
Combining these two examples we create a structure
![]() $M'$
with two sorts containing
$M'$
with two sorts containing
![]() $G_1$
and
$G_1$
and
![]() $G_2$
, respectively. Let
$G_2$
, respectively. Let
![]() $G=G_1\times G_2$
. Then G has neither external generic types nor the gip and also if
$G=G_1\times G_2$
. Then G has neither external generic types nor the gip and also if
![]() $p\in S_{ext,G}(M')$
is almost periodic,
$p\in S_{ext,G}(M')$
is almost periodic,
![]() $N'$
is a sufficiently large
$N'$
is a sufficiently large
![]() $*$
-elementary extension of
$*$
-elementary extension of
![]() $M'$
and
$M'$
and
![]() $p'\in S_{ext,G}(N')$
is an almost periodic extension of p, then
$p'\in S_{ext,G}(N')$
is an almost periodic extension of p, then
![]() $p'$
is neither a weak heir nor a weak coheir of p.
$p'$
is neither a weak heir nor a weak coheir of p.
Funding
This research was supported by the Narodowe Centrum Nauki (Grant No. 2018/31/B/ST1/00357).