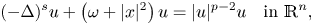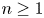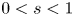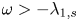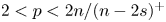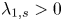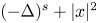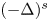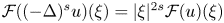1. Introduction
In this paper, we study the uniqueness of ground states to the following fractional nonlinear elliptic equation with harmonic potential,
where $n \geq 1$![]() , $0< s<1$
, $0< s<1$![]() , $\omega >-\lambda _{1,s}$
, $\omega >-\lambda _{1,s}$![]() , $2< p<2_s^*:={2n}/{(n-2s)^+}$
, $2< p<2_s^*:={2n}/{(n-2s)^+}$![]() and $\lambda _{1,s}>0$
and $\lambda _{1,s}>0$![]() is the lowest eigenvalue of $(-\Delta )^s + |x|^2$
is the lowest eigenvalue of $(-\Delta )^s + |x|^2$![]() , which is defined by
, which is defined by
The fractional Laplacian $(-\Delta )^s$![]() is characterized as $\mathcal {F}((-\Delta )^{s}u)(\xi )=|\xi |^{2s} \mathcal {F}(u)(\xi )$
is characterized as $\mathcal {F}((-\Delta )^{s}u)(\xi )=|\xi |^{2s} \mathcal {F}(u)(\xi )$![]() for $\xi \in \mathbb {R}^n$
for $\xi \in \mathbb {R}^n$![]() , where $\mathcal {F}$
, where $\mathcal {F}$![]() denotes the Fourier transform defined by
denotes the Fourier transform defined by
For $0< s<1$![]() , the fractional Sobolev space $H^s(\mathbb {R}^n)$
, the fractional Sobolev space $H^s(\mathbb {R}^n)$![]() is defined by
is defined by
equipped with the norm
The problem under consideration arises in the study of standing waves to the following time-dependent Schrödinger equation,
Here a standing wave to (1.3) is a solution of the form
It is simple to see that $\psi$![]() is a solution to (1.3) if and only if $u$
is a solution to (1.3) if and only if $u$![]() is a solution to (1.1). Equation (1.1) is of particular interest in fractional quantum mechanics and originates from the early work of Laskin [Reference Laskin8, Reference Laskin9].
is a solution to (1.1). Equation (1.1) is of particular interest in fractional quantum mechanics and originates from the early work of Laskin [Reference Laskin8, Reference Laskin9].
For the case $s=1$![]() , the uniqueness of ground states to (1.1) was achieved in [Reference Hirose and Ohta5, Reference Hirose and Ohta6]. However, for the case $0< s<1$
, the uniqueness of ground states to (1.1) was achieved in [Reference Hirose and Ohta5, Reference Hirose and Ohta6]. However, for the case $0< s<1$![]() , the uniqueness of ground states to (1.1) is open so far. The aim of this paper is to make a contribution towards this direction.
, the uniqueness of ground states to (1.1) is open so far. The aim of this paper is to make a contribution towards this direction.
In the present paper, we are only concerned with the uniqueness of ground states to (1.1), the existence of which is a simple consequence of the use of mountain pass theorem, see [Reference Willem11, Theorem 1.15], and the fact that $\Sigma _s$![]() is compactly embedded into $L^q(\mathbb {R}^n)$
is compactly embedded into $L^q(\mathbb {R}^n)$![]() for any $2 \leq q<2_s^*$
for any $2 \leq q<2_s^*$![]() , see [Reference Ding and Hajaiej1, Lemma 3.1]. Moreover, in view of the maximum principle, we can further obtain that any ground state to (1.1) is positive. The main result of the paper reads as follows.
, see [Reference Ding and Hajaiej1, Lemma 3.1]. Moreover, in view of the maximum principle, we can further obtain that any ground state to (1.1) is positive. The main result of the paper reads as follows.
Theorem 1.1 Let $n \geq 1$![]() , $0< s<1$
, $0< s<1$![]() , $\omega >-\lambda _{1,s}$
, $\omega >-\lambda _{1,s}$![]() and $2< p<2_s^*$
and $2< p<2_s^*$![]() . Then ground state to (1.1) is unique up to translations.
. Then ground state to (1.1) is unique up to translations.
Due to the nonlocal feature of the fractional Laplacian operator, the well-known ODE techniques often adapted to discuss the uniqueness of ground states to nonlinear elliptic equations with $s=1$![]() are not applicable to our problem. Therefore, to establish theorem 1.1, we shall make use of the scheme developed in [Reference Frank and Lenzmann3, Reference Frank, Lenzmann and Silvestre4].
are not applicable to our problem. Therefore, to establish theorem 1.1, we shall make use of the scheme developed in [Reference Frank and Lenzmann3, Reference Frank, Lenzmann and Silvestre4].
Remark 1.2 Theorem 1.1 answers an open question posed in [Reference Stanislavova and Stefanov10] with respect to the uniqueness of ground states to (1.1), which also extends the uniqueness results in [Reference Hirose and Ohta5, Reference Hirose and Ohta6] for $s=1$![]() to the case $0< s<1$
to the case $0< s<1$![]() .
.
Notation 1.3 For $1 \leq q \leq \infty$![]() , we denote by $\|\cdot \|_q$
, we denote by $\|\cdot \|_q$![]() the standard norm in the Lebesgue space $L^q(\mathbb {R}^n)$
the standard norm in the Lebesgue space $L^q(\mathbb {R}^n)$![]() . Moreover, we use $X \lesssim Y$
. Moreover, we use $X \lesssim Y$![]() to denote that $X \leq C Y$
to denote that $X \leq C Y$![]() for some proper constant $C>0$
for some proper constant $C>0$![]() and we use $X \sim Y$
and we use $X \sim Y$![]() to denote $X \lesssim Y$
to denote $X \lesssim Y$![]() and $Y \lesssim X$
and $Y \lesssim X$![]() .
.
2. Proof of theorem 1.1
In this section, we are going to establish theorem 1.1. To do this, we first present the nondegeneracy of ground states.
Lemma 2.1 Let $n \geq 1$![]() , $0< s<1$
, $0< s<1$![]() , $\omega >-\lambda _{1,s}$
, $\omega >-\lambda _{1,s}$![]() and $2< p<2_s^*$
and $2< p<2_s^*$![]() . Let $u \in \Sigma _s$
. Let $u \in \Sigma _s$![]() be a ground state to (1.1). Then the linearized operator
be a ground state to (1.1). Then the linearized operator
has a trivial kernel.
Proof. To prove this lemma, one can follow closely the line of the proof of [Reference Stanislavova and Stefanov10, Theorem 2]. Let us now sketch the proof. First we observe that $\mathcal {L}_{+,s} \mid _{\{u\}^{\bot }} \geq 0$![]() . On the other hand, we find that
. On the other hand, we find that
It then follows that $\mathcal {L}_{+,s}$![]() has only one negative eigenvalue. From [Reference Stanislavova and Stefanov10, Proposition 7], we actually know that the eigenvalue is simple. Using spherical harmonics and the representations of fractional Schrödinger operators introduced in [Reference Stanislavova and Stefanov10], we can write that
has only one negative eigenvalue. From [Reference Stanislavova and Stefanov10, Proposition 7], we actually know that the eigenvalue is simple. Using spherical harmonics and the representations of fractional Schrödinger operators introduced in [Reference Stanislavova and Stefanov10], we can write that

where the operator $\mathcal {L}_{+,s, l}$![]() acting on $L_{rad}^2(\mathbb {R}^n)$
acting on $L_{rad}^2(\mathbb {R}^n)$![]() is given by
is given by

It is clear that

At this point, to conclude the proof, we only need to verify that the second smallest eigenvalue of $\mathcal {L}_{+,s, 0}$![]() is positive and $\mathcal {L}_{+,s, \geq 1} \geq \delta >0$
is positive and $\mathcal {L}_{+,s, \geq 1} \geq \delta >0$![]() . This can be achieved by applying [Reference Stanislavova and Stefanov10, Propositions 8–9]. Thus, the proof is completed.
. This can be achieved by applying [Reference Stanislavova and Stefanov10, Propositions 8–9]. Thus, the proof is completed.
In order to establish theorem 1.1, we shall closely follow the strategies developed in [Reference Frank and Lenzmann3, Reference Frank, Lenzmann and Silvestre4]. For this, we now introduce some notations. Let $n \geq 1$![]() , $0< s<1$
, $0< s<1$![]() , $\omega >-\lambda _{1,s}$
, $\omega >-\lambda _{1,s}$![]() and $2< p<2_s^*$
and $2< p<2_s^*$![]() . Define
. Define

equipped with the norm
Lemma 2.2 Let $n \geq 1$![]() , $0< s<1$
, $0< s<1$![]() , $\omega >-\lambda _{1,s}$
, $\omega >-\lambda _{1,s}$![]() and $2< p<2_s^*$
and $2< p<2_s^*$![]() and $u \in X_p$
and $u \in X_p$![]() be a solution to (1.1). Then $u \in H^{s}(\mathbb {R}^n)$
be a solution to (1.1). Then $u \in H^{s}(\mathbb {R}^n)$![]() .
.
Proof. First we show that $u \in H^1(\mathbb {R}^n)$![]() . Since $v \in X_p$
. Since $v \in X_p$![]() be a solution to (1.1), then
be a solution to (1.1), then
where $\lambda >0$![]() satisfies $\omega +\lambda >0$
satisfies $\omega +\lambda >0$![]() . Note that
. Note that
This leads to
It then follows from Young's inequality that

where $H^{-s}(\mathbb {R}^n)$![]() denotes the dual space of $H^s(\mathbb {R}^n)$
denotes the dual space of $H^s(\mathbb {R}^n)$![]() and $\mathcal {K}$
and $\mathcal {K}$![]() is the fundamental solution to the equation
is the fundamental solution to the equation
and $\mathcal {K} \in L^1(\mathbb {R}^n)$![]() by [Reference Frank, Lenzmann and Silvestre4, Lemma C. 1]. This indicates that the operator $((-\Delta )^s + (\omega +|x|^2) +2 \lambda )^{-1}$
by [Reference Frank, Lenzmann and Silvestre4, Lemma C. 1]. This indicates that the operator $((-\Delta )^s + (\omega +|x|^2) +2 \lambda )^{-1}$![]() maps $H^{-s}(\mathbb {R}^n)$
maps $H^{-s}(\mathbb {R}^n)$![]() to $L^2(\mathbb {R}^n)$
to $L^2(\mathbb {R}^n)$![]() . Using dual theory, we then see that $((-\Delta )^s + (\omega +|x|^2) +2 \lambda )^{-1}$
. Using dual theory, we then see that $((-\Delta )^s + (\omega +|x|^2) +2 \lambda )^{-1}$![]() maps $L^2(\mathbb {R}^n)$
maps $L^2(\mathbb {R}^n)$![]() to $H^{s}(\mathbb {R}^n)$
to $H^{s}(\mathbb {R}^n)$![]() . Observe that
. Observe that
where the last inequality is from the dual to the Sobolev embedding $\|u\|_p \lesssim \|u\|_{H^s}$![]() . This indicates that the operator $((-\Delta )^s + (\omega +|x|^2) +2 \lambda )^{-1}$
. This indicates that the operator $((-\Delta )^s + (\omega +|x|^2) +2 \lambda )^{-1}$![]() maps $L^{p'}(\mathbb {R}^n)$
maps $L^{p'}(\mathbb {R}^n)$![]() to $H^{s}(\mathbb {R}^n)$
to $H^{s}(\mathbb {R}^n)$![]() . In fact, this can observe that
. In fact, this can observe that
and
Then the desired result follows. This completes the proof.
Lemma 2.3 Let $s_n \to s$![]() as $n \to \infty$
as $n \to \infty$![]() , then $\lambda _{1,s_n} \to \lambda _{1,s}$
, then $\lambda _{1,s_n} \to \lambda _{1,s}$![]() as $n \to \infty$
as $n \to \infty$![]() .
.
Proof. To prove this, we only need to show that $A_{s_n} \to A_s$![]() in the norm-resolvent sense as $n \to \infty$
in the norm-resolvent sense as $n \to \infty$![]() , where
, where
Let $z \in \mathbb {C}$![]() be such that $\mbox {Im}\ z \neq 0$
be such that $\mbox {Im}\ z \neq 0$![]() , then
, then

Then we see that

Note that
In addition, we see that $(A_s +z)^{-1}$![]() is bounded from $L^2(\mathbb {R}^n)$
is bounded from $L^2(\mathbb {R}^n)$![]() to $L^2(\mathbb {R}^n)$
to $L^2(\mathbb {R}^n)$![]() . As a consequence, from (2.6), we can conclude that
. As a consequence, from (2.6), we can conclude that
This completes the proof.
Lemma 2.4 Let $0< s_0<1$![]() and $2< p<2_{s_0}^*$
and $2< p<2_{s_0}^*$![]() . Suppose that $u_0 \in X_p$
. Suppose that $u_0 \in X_p$![]() solves (2.1) with $s=s_0$
solves (2.1) with $s=s_0$![]() such that the linearized operator
such that the linearized operator
has a trivial kernel on $L^2_{rad}(\mathbb {R}^n)$![]() , where $w>-\lambda _{1, s_0}$
, where $w>-\lambda _{1, s_0}$![]() . Then there exist $\delta _0>0$
. Then there exist $\delta _0>0$![]() and a map $u \in C^1(I; X_p)$
and a map $u \in C^1(I; X_p)$![]() with $I=[s_0,\, s_0+ \delta _0)$
with $I=[s_0,\, s_0+ \delta _0)$![]() such that
such that
Proof. Let $\delta _0>0$![]() be a small constant to be determined later and $\lambda _{1,s}>0$
be a small constant to be determined later and $\lambda _{1,s}>0$![]() be the lowest eigenvalue of $(-\Delta )^s + |x|^2$
be the lowest eigenvalue of $(-\Delta )^s + |x|^2$![]() for $s \in [s_0,\, s_0+\delta _0)$
for $s \in [s_0,\, s_0+\delta _0)$![]() . Define a mapping $F: X_p \times [s_0,\, s_0+ \delta _0) \to X_p$
. Define a mapping $F: X_p \times [s_0,\, s_0+ \delta _0) \to X_p$![]() by
by
where $\omega >0$![]() satisfies $\omega >-\lambda _{1,s}$
satisfies $\omega >-\lambda _{1,s}$![]() and $\lambda >0$
and $\lambda >0$![]() satisfies $\lambda _{1,s}<\lambda$
satisfies $\lambda _{1,s}<\lambda$![]() for any $s \in [s_0,\, s_0+\delta _0)$
for any $s \in [s_0,\, s_0+\delta _0)$![]() . Due to $\omega >-\lambda _{1,s_0}$
. Due to $\omega >-\lambda _{1,s_0}$![]() , by lemma 2.3, then there exists $\delta _0>0$
, by lemma 2.3, then there exists $\delta _0>0$![]() small such that $\omega >-\lambda _{1,s}$
small such that $\omega >-\lambda _{1,s}$![]() is valid for any $s \in [s_0,\, s_0+\delta _0)$
is valid for any $s \in [s_0,\, s_0+\delta _0)$![]() . Moreover, observe that $\Sigma _1 \subset \Sigma _s$
. Moreover, observe that $\Sigma _1 \subset \Sigma _s$![]() , then
, then
where $\lambda _{1,1}>0$![]() is defined by
is defined by
This then justifies that there exists $\lambda >0$![]() such that $\lambda _{1,s}<\lambda$
such that $\lambda _{1,s}<\lambda$![]() for any $s \in [s_0,s_0+\delta _0)$
for any $s \in [s_0,s_0+\delta _0)$![]() .
.
First we check that $F$![]() is well-defined. As an immediate consequence of the proof of lemma 2.2, we see that $F(u,\, s) \in L^2(\mathbb {R}^n) \cap L^p(\mathbb {R}^n)$
is well-defined. As an immediate consequence of the proof of lemma 2.2, we see that $F(u,\, s) \in L^2(\mathbb {R}^n) \cap L^p(\mathbb {R}^n)$![]() for any $u \in X_p$
for any $u \in X_p$![]() and $s\in [s_0,\, s_0 +\delta _0)$
and $s\in [s_0,\, s_0 +\delta _0)$![]() . Let us now check that $F(u,\, s) \in L^2(\mathbb {R}^n; |x|^2 \, {\rm d}x)$
. Let us now check that $F(u,\, s) \in L^2(\mathbb {R}^n; |x|^2 \, {\rm d}x)$![]() for any $u \in X_p$
for any $u \in X_p$![]() and $s\in [s_0,\, s_0 +\delta )$
and $s\in [s_0,\, s_0 +\delta )$![]() . Define
. Define
As the proof of lemma 2.2, we find that $f \in H^s(\mathbb {R}^n)$![]() . This further gives that
. This further gives that
Therefore, we have that

where we used Hölder's inequality for the inequality. It then leads to the desired result.
To apply the implicit function theorem, we are going to check that $F$![]() is of class $C^1$
is of class $C^1$![]() . First we show that ${\partial F}/{\partial u}$
. First we show that ${\partial F}/{\partial u}$![]() exists and
exists and
For simplicity, we shall define
Indeed, it suffices to prove that ${\partial G}/{\partial u}$![]() exists and
exists and
Observe that, for any $h \in X_p$![]() ,
,

where we used the fact that the fundamental solution $\mathcal {K}$![]() to (2.4) satisfies $\mathcal {K} \in L^{p/2}(\mathbb {R}^n) \cap L^{{2p}/{p+2}} (\mathbb {R}^n)$
to (2.4) satisfies $\mathcal {K} \in L^{p/2}(\mathbb {R}^n) \cap L^{{2p}/{p+2}} (\mathbb {R}^n)$![]() and Young's inequality. Define
and Young's inequality. Define
Since
then $g \in H^s(\mathbb {R}^n)$![]() by arguing as the proof of lemma 2.2. Then we write
by arguing as the proof of lemma 2.2. Then we write
It then follows that

Using the fact that $H^s(\mathbb {R}^n)$![]() is continuously embedded into $L^p(\mathbb {R}^n)$
is continuously embedded into $L^p(\mathbb {R}^n)$![]() and Young's inequality, we then obtain that
and Young's inequality, we then obtain that
Consequently, there holds that

Thus, we conclude that

The desired result follows.
Next we are going to verify that ${\partial F}/{\partial u}$![]() is continuous. Indeed, it suffices to show that ${\partial G}/{\partial u}$
is continuous. Indeed, it suffices to show that ${\partial G}/{\partial u}$![]() is continuous. For this aim, we shall demonstrate that, for any $\epsilon >0$
is continuous. For this aim, we shall demonstrate that, for any $\epsilon >0$![]() , there exists $\delta >0$
, there exists $\delta >0$![]() such that $\|u-\tilde {u}\|_{X_p} +|s-\tilde {s}| <\delta$
such that $\|u-\tilde {u}\|_{X_p} +|s-\tilde {s}| <\delta$![]() , then, for any $h \in X_p$
, then, for any $h \in X_p$![]() ,
,

Observe that

where
Note that
Then, by Plancherel's identity, the mean value theorem and Young's inequality, there holds that

In addition, we see that

Notice that
Further, we can conclude that
Note that
and

Consequently, from the calculations above, (2.7) holds true. This implies that ${\partial F}/{\partial u}$![]() is continuous. By a similar argument, we are also able to show that ${\partial F}/{\partial s}$
is continuous. By a similar argument, we are also able to show that ${\partial F}/{\partial s}$![]() exists and
exists and
In addition, we can prove that ${\partial F}/{\partial s}$![]() . Thus, we have that $F$
. Thus, we have that $F$![]() is of class $C^1$
is of class $C^1$![]() .
.
Now we employ the implicit function theorem to establish theorem. Note first that $F(u_0,\, s_0)=0$![]() and
and
It is simple to see that $K$![]() is compact on $L^2_{rad}(\mathbb {R}^n)$
is compact on $L^2_{rad}(\mathbb {R}^n)$![]() . Moreover, from lemma 2.1, we have that $-1 \not \in \sigma (K)$
. Moreover, from lemma 2.1, we have that $-1 \not \in \sigma (K)$![]() . Then $1+ K$
. Then $1+ K$![]() is invertible. Furthermore, arguing as before, we can show that $1+K$
is invertible. Furthermore, arguing as before, we can show that $1+K$![]() is bounded from $X_p$
is bounded from $X_p$![]() to $X_p$
to $X_p$![]() . This implies that $(1+K)^{-1}$
. This implies that $(1+K)^{-1}$![]() is bounded from $X_p$
is bounded from $X_p$![]() to $X_p$
to $X_p$![]() . It then follows from the implicit function theorem that theorem holds true. This completes the proof.
. It then follows from the implicit function theorem that theorem holds true. This completes the proof.
In the following, we shall consider the maximum extension of the branch $u_s$![]() for $s \in [s_0,\, s_*)$
for $s \in [s_0,\, s_*)$![]() , where $s_*>s_0$
, where $s_*>s_0$![]() is given by
is given by

Lemma 2.5 There holds that
for any $s \in [s_0,\, s_*)$![]() .
.
Proof. Define

Since $u_s \in H^s(\mathbb {R}^n)$![]() is a solution to (1.1), then
is a solution to (1.1), then
In addition, we have that $u_s$![]() satisfies the following Pohozaev identity,
satisfies the following Pohozaev identity,
Combining (2.8) and (2.9), we see that
It follows from (2.8) and (2.10) that
and
Consequently, we have that $M_s + H_s \sim V_s$![]() for any $s \in [s_0,\, s_*)$
for any $s \in [s_0,\, s_*)$![]() . It follows from (2.8) and (2.10) that
. It follows from (2.8) and (2.10) that
and
This leads to $T_s \sim V_s$![]() for any $s \in [s_0,\, s_*)$
for any $s \in [s_0,\, s_*)$![]() . Therefore, we obtain that
. Therefore, we obtain that
for any $s \in [s_0,\, s_*)$![]() . Since $2< p< p_{s_0}$
. Since $2< p< p_{s_0}$![]() , there exists $0<\theta <1$
, there exists $0<\theta <1$![]() such that $p=2\theta + (1-\theta ) p_{s_0}$
such that $p=2\theta + (1-\theta ) p_{s_0}$![]() . From Gagliardo–Nirenberg's inequality and Hölder's inequality, we then get that
. From Gagliardo–Nirenberg's inequality and Hölder's inequality, we then get that

In addition, there holds that

Utilizing (2.11), (2.12) and (2.13) then implies that
for any $s \in [s_0,\, s_*)$![]() . Arguing as the proof of [Reference Frank, Lenzmann and Silvestre4, Lemma 8.2], we can obtain that $V_s \lesssim 1$
. Arguing as the proof of [Reference Frank, Lenzmann and Silvestre4, Lemma 8.2], we can obtain that $V_s \lesssim 1$![]() for any $s \in [s_0,\, s_*)$
for any $s \in [s_0,\, s_*)$![]() . This in turn implies that
. This in turn implies that
for any $s \in [s_0,\, s_*)$![]() . This completes the proof.
. This completes the proof.
Lemma 2.6 Let $n \geq 1$![]() , $s_0 \leq s \leq 1$
, $s_0 \leq s \leq 1$![]() , $\omega >-\lambda _{1, s_0}$
, $\omega >-\lambda _{1, s_0}$![]() and $2< p<2_{s_0}^*$
and $2< p<2_{s_0}^*$![]() . Suppose that $u_s \in X_p$
. Suppose that $u_s \in X_p$![]() is a ground state to (1.1). Then there exists $\mu _s>0$
is a ground state to (1.1). Then there exists $\mu _s>0$![]() such that
such that
Proof. Define
Obviously, we have that $\alpha _s \geq 0$![]() . First we shall verify that $\alpha _s>0$
. First we shall verify that $\alpha _s>0$![]() is attained. Let $\{f_k\}$
is attained. Let $\{f_k\}$![]() be a minimizing sequence to (2.15) such that $f_k \bot u_s$
be a minimizing sequence to (2.15) such that $f_k \bot u_s$![]() , $\|f_k\|_2=1$
, $\|f_k\|_2=1$![]() and $\langle \mathcal {L}_{+,s} f_k,\, f_k \rangle =\alpha _s+o_k(1)$
and $\langle \mathcal {L}_{+,s} f_k,\, f_k \rangle =\alpha _s+o_k(1)$![]() . Observe that $\{f_k\}$
. Observe that $\{f_k\}$![]() is bounded in $\Sigma _s$
is bounded in $\Sigma _s$![]() . Therefore, there exists a function $f \in \Sigma _s$
. Therefore, there exists a function $f \in \Sigma _s$![]() such that $f_k \rightharpoonup f$
such that $f_k \rightharpoonup f$![]() in $\Sigma _s$
in $\Sigma _s$![]() and $f_k \to f$
and $f_k \to f$![]() in $L^q(\mathbb {R}^n)$
in $L^q(\mathbb {R}^n)$![]() for any $q \in [2,\, 2_s^*)$
for any $q \in [2,\, 2_s^*)$![]() as $n \to \infty$
as $n \to \infty$![]() . This leads to $f \bot u_s$
. This leads to $f \bot u_s$![]() , $\|f\|_2=1$
, $\|f\|_2=1$![]() and $\langle \mathcal {L}_{+,s} f,\, f \rangle =\alpha _s$
and $\langle \mathcal {L}_{+,s} f,\, f \rangle =\alpha _s$![]() . Contrarily, we assume that $\alpha _s=0$
. Contrarily, we assume that $\alpha _s=0$![]() . When $s<1$
. When $s<1$![]() , using the fact that $Ker [\mathcal {L}_{+, s}]=\{0\}$
, using the fact that $Ker [\mathcal {L}_{+, s}]=\{0\}$![]() by lemma 2.1 and arguing as the proof of [Reference Stanislavova and Stefanov10, Proposition 6], we are able to reach a contradiction. This in turn shows that $\alpha _s>0$
by lemma 2.1 and arguing as the proof of [Reference Stanislavova and Stefanov10, Proposition 6], we are able to reach a contradiction. This in turn shows that $\alpha _s>0$![]() and
and
While $s =1$![]() , using the fact that $Ker[\mathcal {L}_{+, 1}]=\{0\}$
, using the fact that $Ker[\mathcal {L}_{+, 1}]=\{0\}$![]() and following the spirit of the proof of [Reference Stanislavova and Stefanov10, Proposition 6], we can also derive that $\alpha _1>0$
and following the spirit of the proof of [Reference Stanislavova and Stefanov10, Proposition 6], we can also derive that $\alpha _1>0$![]() and
and
Thus, the proof is completed.
Lemma 2.7 Let $u_{s_0}>0$![]() be a solution to (1.1) with $s=s_0$
be a solution to (1.1) with $s=s_0$![]() . Then, for any $s \in [s_0,\, s_*)$
. Then, for any $s \in [s_0,\, s_*)$![]() , there holds that $u_s(x)>0$
, there holds that $u_s(x)>0$![]() for $x \in \mathbb {R}^n$
for $x \in \mathbb {R}^n$![]() and $u_s(x) \lesssim |x|^{-n}$
and $u_s(x) \lesssim |x|^{-n}$![]() for $|x| \gtrsim 1$
for $|x| \gtrsim 1$![]() .
.
Proof. In the spirit of the proof of [Reference Frank, Lenzmann and Silvestre4, Lemma 8.3], we need to verify that the operator $\mathcal {L}_{-, s}$![]() enjoys the Perron–Frobenius type property, where
enjoys the Perron–Frobenius type property, where
In addition, we need to check that $\mathcal {L}_{-, \tilde {s}} \to \mathcal {L}_{-,s}$![]() as $\tilde {s} \to s$
as $\tilde {s} \to s$![]() in norm-resolvent sense.
in norm-resolvent sense.
Define $H:=(-\Delta )^s+|x|^2$![]() , which generates a semigroup ${\rm e}^{-t H}$
, which generates a semigroup ${\rm e}^{-t H}$![]() with positive integral kernel. Then we have that ${\rm e}^{-t H}$
with positive integral kernel. Then we have that ${\rm e}^{-t H}$![]() acting on $L^2(\mathbb {R}^n)$
acting on $L^2(\mathbb {R}^n)$![]() is positivity improving. Next we show that $w+|u|^{p-2}$
is positivity improving. Next we show that $w+|u|^{p-2}$![]() belongs to Kato class, i.e.
belongs to Kato class, i.e.
Note that $H+ \lambda >(-\Delta )^s + \lambda$![]() , then
, then
Let $\mathcal {K}$![]() be the fundamental solution to the equation
be the fundamental solution to the equation
Then we have that
where
From $(A 4)$![]() in [Reference Felmer, Quaas and Tan2, Appendix A], we find that
in [Reference Felmer, Quaas and Tan2, Appendix A], we find that
This gives that, for any $q \geq 1$![]() ,
,

It then follows that
where $q \geq 1$![]() satisfies
satisfies
Using Young's inequality, we then get that, for any $f \in L^{\infty }(\mathbb {R}^n)$![]() ,
,
which readily yields that
Thus, (2.16) holds true and the desired result follows. Arguing as the proof of [Reference Frank and Lenzmann3, Lemma C.2], we conclude that the operator $\mathcal {L}_{-, s}$![]() enjoys Perron–Frobenius type property.
enjoys Perron–Frobenius type property.
Next we prove the convergence of the operator in norm-resolvent sense. Observe first that

Therefore, we have that

As the proof of lemma 2.3, we can show that
This indicates that $\mathcal {L}_{-, \tilde {s}} \to \mathcal {L}_{-, s}$![]() in the norm-resolvent sense as $\tilde {s} \to s$
in the norm-resolvent sense as $\tilde {s} \to s$![]() . Thus, the proof is completed.
. Thus, the proof is completed.
Lemma 2.8 Let $\{s_n\} \subset [s_0,\, s_*)$![]() be a sequence such that $s_n \to s_*$
be a sequence such that $s_n \to s_*$![]() as $n \to \infty$
as $n \to \infty$![]() and $u_{s_n}>0$
and $u_{s_n}>0$![]() for any $n \in \mathbb {N}$
for any $n \in \mathbb {N}$![]() . Then there exists $u_* \in X_p$
. Then there exists $u_* \in X_p$![]() such that $u_{s_n} \to u_*$
such that $u_{s_n} \to u_*$![]() in $X_p$
in $X_p$![]() as $n \to \infty$
as $n \to \infty$![]() . Moreover, there holds that $u_*>0$
. Moreover, there holds that $u_*>0$![]() and it solves the equation
and it solves the equation
Proof. From lemma 2.5, we know that $u_{s_n}$![]() is bounded in $\Sigma _{s_0}$
is bounded in $\Sigma _{s_0}$![]() . Thus, there exists $u_* \in \Sigma _{s_0}$
. Thus, there exists $u_* \in \Sigma _{s_0}$![]() such that $u_{s_n} \rightharpoonup u_*$
such that $u_{s_n} \rightharpoonup u_*$![]() in $\Sigma _{s_0}$
in $\Sigma _{s_0}$![]() and $u_{s_n} \to u_*$
and $u_{s_n} \to u_*$![]() in $L^q(\mathbb {R}^n)$
in $L^q(\mathbb {R}^n)$![]() for any $q \in [2,\, 2_{s_0}^*)$
for any $q \in [2,\, 2_{s_0}^*)$![]() . Since $u_{s_n} >0$
. Since $u_{s_n} >0$![]() , then $u_* \geq 0$
, then $u_* \geq 0$![]() . It follows from lemma 2.5 that $u_* \neq 0$
. It follows from lemma 2.5 that $u_* \neq 0$![]() . Note that
. Note that
Since $u_{s_n} \to u_*$![]() in $L^2(\mathbb {R}^n) \cap L^p(\mathbb {R}^n)$
in $L^2(\mathbb {R}^n) \cap L^p(\mathbb {R}^n)$![]() as $n \to \infty$
as $n \to \infty$![]() , then
, then
This implies that $u_*$![]() solves (2.17) and $u_{s_n} \to u_*$
solves (2.17) and $u_{s_n} \to u_*$![]() in $X_p$
in $X_p$![]() as $n \to \infty$
as $n \to \infty$![]() . Thus, the proof is completed.
. Thus, the proof is completed.
Lemma 2.9 Let $u_0 \in X_p$![]() be a ground state to (1.1) with $s=s_0$
be a ground state to (1.1) with $s=s_0$![]() . Then its maximum branch $u_s$
. Then its maximum branch $u_s$![]() with $s \in [s_0,\, s_*)$
with $s \in [s_0,\, s_*)$![]() extends to $s_*=1$
extends to $s_*=1$![]() .
.
Proof. Define
Reasoning as the proof of the norm-resolvent convergence of $\mathcal {L}_{-, s}$![]() in lemma 2.7, we can also show that $\mathcal {L}_{+, \tilde {s}} \to \mathcal {L}_{+,s}$
in lemma 2.7, we can also show that $\mathcal {L}_{+, \tilde {s}} \to \mathcal {L}_{+,s}$![]() in the norm-resolvent sense as $\tilde {s} \to s$
in the norm-resolvent sense as $\tilde {s} \to s$![]() . This gives that
. This gives that
Let $\{s_n\} \subset [s_0,\, s_*)$![]() be such that $s_n \to s_*$
be such that $s_n \to s_*$![]() . Since $u_0 \in X_p$
. Since $u_0 \in X_p$![]() is a ground state to (1.1) with $s=s_0$
is a ground state to (1.1) with $s=s_0$![]() , then $u_0>0$
, then $u_0>0$![]() . In view of lemma 2.7, then $u_{s_n}>0$
. In view of lemma 2.7, then $u_{s_n}>0$![]() . From lemma 2.8, we know that there exists $u_*>0$
. From lemma 2.8, we know that there exists $u_*>0$![]() solving (2.17). Note that $\mathcal {L}_{+, s_n} \to \mathcal {L}_{+, s_*}$
solving (2.17). Note that $\mathcal {L}_{+, s_n} \to \mathcal {L}_{+, s_*}$![]() in the norm-resolvent sense as $n \to \infty$
in the norm-resolvent sense as $n \to \infty$![]() . By the lower semicontinuity of the Morse index, we have that
. By the lower semicontinuity of the Morse index, we have that
This implies that $\mathcal {N}_{-, rad}(\mathcal {L}_{+, s_*}) \leq 1$![]() . On the other hand, since $u_*$
. On the other hand, since $u_*$![]() solves (2.17), then we see that
solves (2.17), then we see that
Thus, we conclude that $\mathcal {N}_{-, rad}(\mathcal {L}_{+, s_*})=1$![]() , which yields that $u_*$
, which yields that $u_*$![]() is a ground state to (2.17). As a result, we have that $s_*=1$
is a ground state to (2.17). As a result, we have that $s_*=1$![]() . On the other hand, by the nondegeneracy of $\mathcal {L}_{+, s_*}$
. On the other hand, by the nondegeneracy of $\mathcal {L}_{+, s_*}$![]() , then $u_s$
, then $u_s$![]() can be extended beyond $s_*$
can be extended beyond $s_*$![]() . This is impossible and the proof is completed.
. This is impossible and the proof is completed.
Now we are ready to prove theorem 1.1.
Proof of theorem 1.1 Let $n \geq 1$![]() , $0< s_0<1$
, $0< s_0<1$![]() and $2< p<2_{s_0}^*$
and $2< p<2_{s_0}^*$![]() . Let $u_{s_0}>0$
. Let $u_{s_0}>0$![]() and $\tilde {u}_{s_0}>0$
and $\tilde {u}_{s_0}>0$![]() be two different ground states to (1.1) with $s=s_0$
be two different ground states to (1.1) with $s=s_0$![]() , which are indeed radially symmetric. From lemma 2.1, we obtain that the associated linearized operators around $u_{s_0}$
, which are indeed radially symmetric. From lemma 2.1, we obtain that the associated linearized operators around $u_{s_0}$![]() and $\tilde {u}_{s_0}$
and $\tilde {u}_{s_0}$![]() are nondegenerate. Then, by lemmas 2.4 and 2.9, we have that $u_s \in C^1([s_0,\, 1); X_p)$
are nondegenerate. Then, by lemmas 2.4 and 2.9, we have that $u_s \in C^1([s_0,\, 1); X_p)$![]() and $\tilde {u}_s \in C^1([s_0,\, 1); X_p)$
and $\tilde {u}_s \in C^1([s_0,\, 1); X_p)$![]() . Moreover, by the local uniqueness of solutions derived in lemma 2.4, we get that $u_s \neq \tilde {u}_s$
. Moreover, by the local uniqueness of solutions derived in lemma 2.4, we get that $u_s \neq \tilde {u}_s$![]() for any $s \in [s_0,\, 1)$
for any $s \in [s_0,\, 1)$![]() . It follows from lemma 2.8 that there exist $u_* \in X_p$
. It follows from lemma 2.8 that there exist $u_* \in X_p$![]() and $\tilde {u}_* \in X_p$
and $\tilde {u}_* \in X_p$![]() such that $u_s \to u_*$
such that $u_s \to u_*$![]() and $\tilde {u}_{s} \to \tilde {u}_*$
and $\tilde {u}_{s} \to \tilde {u}_*$![]() in $X_p$
in $X_p$![]() as $s \to 1^-$
as $s \to 1^-$![]() . In addition, $u_*>0$
. In addition, $u_*>0$![]() and $\tilde {u}_*>0$
and $\tilde {u}_*>0$![]() solve (2.17) with $s_*=1$
solve (2.17) with $s_*=1$![]() . Thanks to [Reference Hirose and Ohta5, Theorem 1.3] and [Reference Hirose and Ohta6, Theorem1.2], then we have that $u_*=\tilde {u}_*$
. Thanks to [Reference Hirose and Ohta5, Theorem 1.3] and [Reference Hirose and Ohta6, Theorem1.2], then we have that $u_*=\tilde {u}_*$![]() . This implies that $\|u_s-\tilde {u}_s\|_{X_p} \to 0$
. This implies that $\|u_s-\tilde {u}_s\|_{X_p} \to 0$![]() as $s \to 1^-$
as $s \to 1^-$![]() . Note that the linearized operator $\mathcal {L}_{+, 1}$
. Note that the linearized operator $\mathcal {L}_{+, 1}$![]() around $u_*$
around $u_*$![]() is nondegenerate, see [Reference Kabeya and Tanaka7, Theorem 0.2]. Remark that, from the proof of [Reference Kabeya and Tanaka7, Theorem 0.2], it is simple to see that the result also holds true for $n=1$
is nondegenerate, see [Reference Kabeya and Tanaka7, Theorem 0.2]. Remark that, from the proof of [Reference Kabeya and Tanaka7, Theorem 0.2], it is simple to see that the result also holds true for $n=1$![]() . Then, by the implicit function theorem, there exists a unique branch $\hat {u}_{s} \in C^1((1-\delta,\, 1]; X_p)$
. Then, by the implicit function theorem, there exists a unique branch $\hat {u}_{s} \in C^1((1-\delta,\, 1]; X_p)$![]() solving (1.1) with $\hat {u}_1=u^*$
solving (1.1) with $\hat {u}_1=u^*$![]() for some $\delta >0$
for some $\delta >0$![]() . This contradicts with $u_s \neq \tilde {u}_s$
. This contradicts with $u_s \neq \tilde {u}_s$![]() for any $s\in [s_0,\, 1)$
for any $s\in [s_0,\, 1)$![]() . Thus, the proof is completed.
. Thus, the proof is completed.
Acknowledgements
The author was supported by the National Natural Science Foundation of China (No. 12101483) and the Postdoctoral Science Foundation of China (No. 2021M702620). The author would like to thank warmly the referee for the helpful and constructive comments to improve the manuscript.
Competing interest
None.