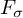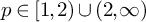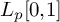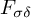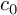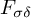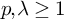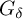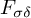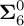Introduction
Descriptive set theoretic approach to Banach spaces has proved to be a powerful tool in solving many problems in Banach space theory; for a wide selection of references ranging from the earliest ones of Bourgain to the most recent ones see e.g. [Reference Antunes, Beanland and Braga3, Reference Argyros and Dodos4, Reference Argyros, Godefroy and Rosenthal5, Reference Bourgain8, Reference Cuellar Carrera12]. Traditionally, and as defined explicitly for the first time in the seminal papers of Bossard ([Reference Bossard6, Reference Bossard7]), one considers the standard Borel space of all separable Banach spaces, which can be defined as an appropriate Borel subspace of the Effros-Borel space of all closed subspaces of some isometrically universal separable Banach space. Since such defined space of Banach spaces is not a topological space, it allows us to study Banach spaces globally only in a Borel way and not topologically, which would be desirable in some cases. This drawback was addressed in a recent paper [Reference Godefroy and Saint-Raymond28] of Godefroy and Saint-Raymond, where they propose to study certain natural topologies on the standard Borel spaces of separable Banach spaces, and they compute Borel complexities, in these topologies, of several important classes of Banach spaces. The authors of this paper initiated in [Reference Cúth, Doležal, Doucha and Kurka14] the study of the Polish spaces of norms and pseudonorms on the countable infinite-dimensional vector space over
![]() $\mathbb {Q}$
, which have additional further advantages:
$\mathbb {Q}$
, which have additional further advantages:
-
• they are almost canonical Polish spaces of separable Banach spaces;
-
• they have very nice topological properties that are connected to local theory of Banach spaces, especially to finite representability;
-
• the computation of Borel complexities of various classes of separable Banach spaces is usually in these spaces as straightforward as possible, which, in particular, allows us to improve several estimates by Godefroy and Saint-Raymond;
-
• this approach to topologizing the space of Banach spaces is somewhat similar to how metric structures are topologized generally in continuous model theory, which could connect descriptive set theory of Banach spaces with the model theory of Banach spaces, which is one of the most developed areas of applications of logic to metric structures.
This paper is a companion and second part to [Reference Cúth, Doležal, Doucha and Kurka14], however, it is completely self-contained and can be read independently. Its aim is to demonstrate the strength of this new approach by computing (in many cases, these computations are sharp) complexities of several classes of Banach spaces, focusing on isomorphism classes, improving several results of Godefroy and Saint-Raymond, and initiating the research of computing the complexities of isometry classes.
First, we focus on the undoubtedly most important separable infinite-dimensional Banach space – the Hilbert space
![]() $\ell _2(\mathbb {N})$
. We uniquely characterize it by both the complexity of its isometry class, as well as the complexity of its isomorphism class.
$\ell _2(\mathbb {N})$
. We uniquely characterize it by both the complexity of its isometry class, as well as the complexity of its isomorphism class.
Theorem A.
-
(1) The separable infinite-dimensional Hilbert space is characterized as the unique separable infinite-dimensional Banach space whose isometry class is closed (see Theorem 2.4).
-
(2) The separable infinite-dimensional Hilbert space is characterized as the unique, up to isomorphism, separable infinite-dimensional Banach space whose isomorphism class is
 $F_\sigma $
(see Theorem 2.10).
$F_\sigma $
(see Theorem 2.10).
Let us briefly comment on the importance of this result. There are many known isometric characterizations of inner product spaces, and several of those may be easily seen to form a closed condition (see, e.g. the monograph [Reference Amir2]). By our isometric characterization from Theorem A, there is no other separable infinite-dimensional Banach space, which can be characterized by a closed condition. Our isomorphic characterization of Hilbert spaces from Theorem A seems to be even more interesting. Recall that Bossard [Reference Bossard7, Problem 2.9] originally asked whether
![]() $\ell _2$
is the unique space with a Borel isomorphism class. Although this is known to be false now (see, e.g. [Reference Godefroy26]), our Theorem A shows that it is arguably the Banach space with the simplest possible isomorphism class. The only other candidate possibly having a simple isomorphism class is the Gurariı̆ space, which might potentially have a
$\ell _2$
is the unique space with a Borel isomorphism class. Although this is known to be false now (see, e.g. [Reference Godefroy26]), our Theorem A shows that it is arguably the Banach space with the simplest possible isomorphism class. The only other candidate possibly having a simple isomorphism class is the Gurariı̆ space, which might potentially have a
![]() $G_\delta $
isomorphism class (see Proposition 2.11). We conjecture that it is not the case (in fact, we do not know whether the isomorphism class of the Gurariı̆ space is even Borel), however, we cannot disprove it at the moment.
$G_\delta $
isomorphism class (see Proposition 2.11). We conjecture that it is not the case (in fact, we do not know whether the isomorphism class of the Gurariı̆ space is even Borel), however, we cannot disprove it at the moment.
Moreover, since our coding of Banach spaces is connected to the local theory of Banach spaces, it is of some interest to notice that there were some attempts to characterize
![]() $\ell _2$
up to isomorphism using its finite-dimensional structure (see, e.g. [Reference Johnson, Lindenstrauss and Schechtman33, Conjecture 7.3] for the conjecture by Johnson et al.). Thus, our setting enables us to formulate and prove a result similar in a spirit to what was conjectured by Johnson et al. We refer the reader to Section 6 for more information in this direction.
$\ell _2$
up to isomorphism using its finite-dimensional structure (see, e.g. [Reference Johnson, Lindenstrauss and Schechtman33, Conjecture 7.3] for the conjecture by Johnson et al.). Thus, our setting enables us to formulate and prove a result similar in a spirit to what was conjectured by Johnson et al. We refer the reader to Section 6 for more information in this direction.
Next, we continue by studying complexities of isometry classes of other Banach spaces, that is how easy/difficult it is to define them uniquely up to isometry. There is an active ongoing research whether for a particular Banach space its isomorphism class is Borel or not (see, e.g. [Reference Godefroy26], [Reference Kurka36], [Reference Ghawadrah22], [Reference Godefroy27]), while it is known that isometry classes of separable Banach spaces are always Borel (note that the linear isometry relation is Borel bireducible with an orbit equivalence relation [Reference Melleray44], and orbit equivalence relations have Borel equivalence classes [Reference Kechris34, Theorem 15.14]). Having a topology at our disposal, we compute complexities of isometry classes of several classical Banach spaces.
Theorem B.
-
(1) For
 $p\in [1,2)\cup (2,\infty )$
, the isometry class of
$p\in [1,2)\cup (2,\infty )$
, the isometry class of
 $L_p[0,1]$
is
$L_p[0,1]$
is
 $G_\delta $
-complete. Moreover, for every
$G_\delta $
-complete. Moreover, for every
 $\lambda \geq 1$
, the class of separable
$\lambda \geq 1$
, the class of separable
 $\mathcal {L}_{p,\lambda +}$
-spaces is a
$\mathcal {L}_{p,\lambda +}$
-spaces is a
 $G_\delta $
-set and the class of separable
$G_\delta $
-set and the class of separable
 $\mathcal {L}_p$
-spaces is a
$\mathcal {L}_p$
-spaces is a
 $G_{\delta \sigma }$
-set, improving the estimate from [Reference Godefroy and Saint-Raymond28] (see Theorems 3.4 and 3.6, and Corollary 3.7).
$G_{\delta \sigma }$
-set, improving the estimate from [Reference Godefroy and Saint-Raymond28] (see Theorems 3.4 and 3.6, and Corollary 3.7). -
(2) For
 $p\in [1,2)\cup (2,\infty )$
, the isometry class of
$p\in [1,2)\cup (2,\infty )$
, the isometry class of
 $\ell _p$
is an
$\ell _p$
is an
 $F_{\sigma \delta }$
-complete set (see Theorem 4.1).
$F_{\sigma \delta }$
-complete set (see Theorem 4.1). -
(3) The isometry class of
 $c_0$
is an
$c_0$
is an
 $F_{\sigma \delta }$
-complete set (see Theorem 4.1).
$F_{\sigma \delta }$
-complete set (see Theorem 4.1). -
(4) The isometry class of the Gurariı̆ space is a
 $G_\delta $
-complete set (see Corollary 3.2).
$G_\delta $
-complete set (see Corollary 3.2).
Let us also present here a few sample results, which involve complexities of more general classes of Banach spaces.
Theorem C.
-
(1) The class of all superreflexive spaces is an
 $F_{\sigma \delta }$
-set (see Theorem 5.3).
$F_{\sigma \delta }$
-set (see Theorem 5.3). -
(2) The class of all spaces with local
 $\Pi $
-basis structure is a
$\Pi $
-basis structure is a
 $\boldsymbol {\Sigma }^0_6$
-set (see Theorem 5.13).
$\boldsymbol {\Sigma }^0_6$
-set (see Theorem 5.13). -
(3) For a fixed ordinal
 $\alpha \in [1,\omega _1)$
, the class of spaces whose Szlenk index is bounded by
$\alpha \in [1,\omega _1)$
, the class of spaces whose Szlenk index is bounded by
 $\omega ^\alpha $
is a
$\omega ^\alpha $
is a
 $\boldsymbol {\Pi }^0_{\omega ^\alpha +1}$
-set (see Theorem 5.7).
$\boldsymbol {\Pi }^0_{\omega ^\alpha +1}$
-set (see Theorem 5.7).
1 Preliminaries
In this section, we set up some notation that will be used throughout the paper and recall the notions and basic results from [Reference Cúth, Doležal, Doucha and Kurka14] that we shall need in this paper.
1.1 Notation
Throughout the paper, we usually denote the Borel classes of low complexity by the traditional notation, such as
![]() $F_\sigma $
and
$F_\sigma $
and
![]() $G_\delta $
, or even
$G_\delta $
, or even
![]() $F_{\sigma \delta }$
(countable intersection of
$F_{\sigma \delta }$
(countable intersection of
![]() $F_\sigma $
sets) and
$F_\sigma $
sets) and
![]() $G_{\delta \sigma }$
(countable union of
$G_{\delta \sigma }$
(countable union of
![]() $G_\delta $
-sets). However, whenever it is more convenient or necessary, we use the notation
$G_\delta $
-sets). However, whenever it is more convenient or necessary, we use the notation
![]() $\boldsymbol {\Sigma }_\alpha ^0$
, respectively,
$\boldsymbol {\Sigma }_\alpha ^0$
, respectively,
![]() $\boldsymbol {\Pi }_\alpha ^0$
, where
$\boldsymbol {\Pi }_\alpha ^0$
, where
![]() $\alpha <\omega _1$
(we refer to [Reference Kechris34, Section 11] for this notation). We emphasize that open sets, respectively, closed sets, are
$\alpha <\omega _1$
(we refer to [Reference Kechris34, Section 11] for this notation). We emphasize that open sets, respectively, closed sets, are
![]() $\boldsymbol {\Sigma }^0_1$
, respectively,
$\boldsymbol {\Sigma }^0_1$
, respectively,
![]() $\boldsymbol {\Pi }^0_1$
, by this notation.
$\boldsymbol {\Pi }^0_1$
, by this notation.
In a few occassions, for a Borel class
![]() $\boldsymbol {\Gamma }$
, we will use the notion of
$\boldsymbol {\Gamma }$
, we will use the notion of
![]() $\boldsymbol {\Gamma }$
-hard and
$\boldsymbol {\Gamma }$
-hard and
![]() $\boldsymbol {\Gamma }$
-complete sets. We refer the reader to [Reference Kechris34, Definition 22.9] for these notions. For a reader not familiar with them, let us emphasize that a set A being
$\boldsymbol {\Gamma }$
-complete sets. We refer the reader to [Reference Kechris34, Definition 22.9] for these notions. For a reader not familiar with them, let us emphasize that a set A being
![]() $\boldsymbol {\Gamma }$
-hard, for a Borel class
$\boldsymbol {\Gamma }$
-hard, for a Borel class
![]() $\boldsymbol {\Gamma }$
, in particular, implies that A is not of a lower complexity than
$\boldsymbol {\Gamma }$
, in particular, implies that A is not of a lower complexity than
![]() $\boldsymbol {\Gamma }$
. Thus, results stating that some set is
$\boldsymbol {\Gamma }$
. Thus, results stating that some set is
![]() $\boldsymbol {\Sigma }^0_\alpha $
-complete means that the set is
$\boldsymbol {\Sigma }^0_\alpha $
-complete means that the set is
![]() $\boldsymbol {\Sigma }^0_\alpha $
and not simpler.
$\boldsymbol {\Sigma }^0_\alpha $
and not simpler.
Let us also state here the following simple lemma. Although it should be well-known, we could not find a proper reference, so we provide a sketch of the proof.
Lemma 1.1. Suppose that X is a Polish space and
![]() $B\subseteq X$
is a Borel set, which is not a
$B\subseteq X$
is a Borel set, which is not a
![]() $G_\delta $
-set. Then B is
$G_\delta $
-set. Then B is
![]() $F_\sigma $
-hard. The same with the roles of
$F_\sigma $
-hard. The same with the roles of
![]() $G_\delta $
and
$G_\delta $
and
![]() $F_\sigma $
interchanged.
$F_\sigma $
interchanged.
Proof. By the Hurewicz theorem (see, e.g. [Reference Kechris34, Theorem 21.18]), there is a set
![]() $C\subseteq X$
homeomorphic to the Cantor space, such that
$C\subseteq X$
homeomorphic to the Cantor space, such that
![]() $C\cap B$
is countable dense in C. Then
$C\cap B$
is countable dense in C. Then
![]() $C\cap B$
is an
$C\cap B$
is an
![]() $F_\sigma $
-set but not a
$F_\sigma $
-set but not a
![]() $G_\delta $
-set in the zero-dimensional Polish space C, and so it is
$G_\delta $
-set in the zero-dimensional Polish space C, and so it is
![]() $F_\sigma $
-complete in C by Wadge’s theorem (see, e.g. [Reference Kechris34, Theorem 22.10]). So for any zero-dimensional Polish space Y and any
$F_\sigma $
-complete in C by Wadge’s theorem (see, e.g. [Reference Kechris34, Theorem 22.10]). So for any zero-dimensional Polish space Y and any
![]() $F_\sigma $
-subset A of Y, there is a Wadge reduction of
$F_\sigma $
-subset A of Y, there is a Wadge reduction of
![]() $A\subseteq Y$
to
$A\subseteq Y$
to
![]() $C\cap B\subseteq C$
. But any such reduction is also a reduction of
$C\cap B\subseteq C$
. But any such reduction is also a reduction of
![]() $A\subseteq Y$
to
$A\subseteq Y$
to
![]() $B\subseteq X$
, and so B is
$B\subseteq X$
, and so B is
![]() $F_\sigma $
-hard.
$F_\sigma $
-hard.
The argument with the roles of
![]() $F_\sigma $
and
$F_\sigma $
and
![]() $G_\delta $
interchanged is similar.
$G_\delta $
interchanged is similar.
Moreover, given a class
![]() $\boldsymbol {\Gamma }$
of sets in metrizable spaces, we say that
$\boldsymbol {\Gamma }$
of sets in metrizable spaces, we say that
![]() $f:X\to Y$
is
$f:X\to Y$
is
![]() $\boldsymbol {\Gamma }$
-measurable if
$\boldsymbol {\Gamma }$
-measurable if
![]() $f^{-1}(U)\in \boldsymbol {\Gamma }$
for every open set
$f^{-1}(U)\in \boldsymbol {\Gamma }$
for every open set
![]() $U\subseteq Y$
.
$U\subseteq Y$
.
Given Banach spaces X and Y, we denote by
![]() $X\equiv Y$
(respectively,
$X\equiv Y$
(respectively,
![]() $X\simeq Y$
) the fact that those two spaces are linearly isometric (respectively, isomorphic). We denote by
$X\simeq Y$
) the fact that those two spaces are linearly isometric (respectively, isomorphic). We denote by
![]() $X\hookrightarrow Y$
the fact that Y contains a subspace isomorphic to X. For
$X\hookrightarrow Y$
the fact that Y contains a subspace isomorphic to X. For
![]() $K\geq 1$
, a K-isomorphism
$K\geq 1$
, a K-isomorphism
![]() $T:X\to Y$
is a linear map with
$T:X\to Y$
is a linear map with
![]() $K^{-1}\|x\|\leq \|Tx\|\leq K\|x\|$
,
$K^{-1}\|x\|\leq \|Tx\|\leq K\|x\|$
,
![]() $x\in X$
. If
$x\in X$
. If
![]() $x_1,\ldots ,x_n$
are linearly independent elements of X and
$x_1,\ldots ,x_n$
are linearly independent elements of X and
![]() $y_1,\ldots ,y_n\in Y$
, we write
$y_1,\ldots ,y_n\in Y$
, we write
![]() $(Y,y_1,\ldots ,y_n){\stackrel {K}{\sim } (X,x_1,\ldots ,x_n)}$
if the linear operator
$(Y,y_1,\ldots ,y_n){\stackrel {K}{\sim } (X,x_1,\ldots ,x_n)}$
if the linear operator
![]() $T:\operatorname {span}\{x_1,\ldots ,x_n\}\to \operatorname {span}\{y_1,\ldots ,y_n\}$
sending
$T:\operatorname {span}\{x_1,\ldots ,x_n\}\to \operatorname {span}\{y_1,\ldots ,y_n\}$
sending
![]() $x_i$
to
$x_i$
to
![]() $y_i$
satisfies
$y_i$
satisfies
![]() $\max \{\|T\|,\|T^{-1}\|\}<K$
. If X has a canonical basis
$\max \{\|T\|,\|T^{-1}\|\}<K$
. If X has a canonical basis
![]() $(x_1,\ldots ,x_n)$
, which is clear from the context, we just write
$(x_1,\ldots ,x_n)$
, which is clear from the context, we just write
![]() $(Y,y_1,\ldots ,y_n){\stackrel {K}{\sim } X}$
instead of
$(Y,y_1,\ldots ,y_n){\stackrel {K}{\sim } X}$
instead of
![]() $(Y,y_1,\ldots ,y_n){\stackrel {K}{\sim } (X,x_1,\ldots ,x_n)}$
. Moreover, if Y is clear from the context, we write
$(Y,y_1,\ldots ,y_n){\stackrel {K}{\sim } (X,x_1,\ldots ,x_n)}$
. Moreover, if Y is clear from the context, we write
![]() $(y_1,\ldots ,y_n){\stackrel {K}{\sim } X}$
instead of
$(y_1,\ldots ,y_n){\stackrel {K}{\sim } X}$
instead of
![]() $(Y,y_1,\ldots ,y_n){\stackrel {K}{\sim } X}$
.
$(Y,y_1,\ldots ,y_n){\stackrel {K}{\sim } X}$
.
Throughout the text,
![]() $\ell _p^n$
denotes the n-dimensional
$\ell _p^n$
denotes the n-dimensional
![]() $\ell _p$
-space, that is the upper index denotes dimension.
$\ell _p$
-space, that is the upper index denotes dimension.
Finally, in order to avoid any confusion, we emphasize that if we write that a mapping is an ‘isometry’ or an ‘isomorphism,’ we do not mean it is surjective if this is not explicitly mentioned.
1.2 Notions and results from [Reference Cúth, Doležal, Doucha and Kurka14]
The most important notion we want to recall is the Polish spaces of Banach spaces. We refer to [Reference Cúth, Doležal, Doucha and Kurka14, Section 2] for a proper introduction.
By V, let us denote the vector space over
![]() $\mathbb {Q}$
of all finitely supported sequences of rational numbers; that is, the unique infinite-dimensional vector space over
$\mathbb {Q}$
of all finitely supported sequences of rational numbers; that is, the unique infinite-dimensional vector space over
![]() $\mathbb {Q}$
with a countable Hamel basis
$\mathbb {Q}$
with a countable Hamel basis
![]() $(e_n)_{n\in \mathbb {N}}$
, which we may view as the vector space of all finitely supported rational sequences.
$(e_n)_{n\in \mathbb {N}}$
, which we may view as the vector space of all finitely supported rational sequences.
Definition 1.2 [Reference Cúth, Doležal, Doucha and Kurka14, Definition 2.1].
Let us denote by
![]() $\mathcal {P}$
the space of all pseudonorms on the vector space V. Since
$\mathcal {P}$
the space of all pseudonorms on the vector space V. Since
![]() $\mathcal {P}$
is a closed subset of
$\mathcal {P}$
is a closed subset of
![]() $\mathbb {R}^V$
, this gives
$\mathbb {R}^V$
, this gives
![]() $\mathcal {P}$
the Polish topology inherited from
$\mathcal {P}$
the Polish topology inherited from
![]() $\mathbb {R}^V$
. The subbasis of this topology is given by sets of the form
$\mathbb {R}^V$
. The subbasis of this topology is given by sets of the form
![]() $U[v,I]:=\{\mu \in \mathcal {P}:\; \mu (v)\in I\}$
, where
$U[v,I]:=\{\mu \in \mathcal {P}:\; \mu (v)\in I\}$
, where
![]() $v\in V$
and I is an open interval.
$v\in V$
and I is an open interval.
We often identify
![]() $\mu \in \mathcal {P}$
with its extension to the pseudonorm on the space
$\mu \in \mathcal {P}$
with its extension to the pseudonorm on the space
![]() $c_{00}$
, that is, on the vector space over
$c_{00}$
, that is, on the vector space over
![]() $\mathbb {R}$
of all finitely supported sequences of real numbers.
$\mathbb {R}$
of all finitely supported sequences of real numbers.
For every
![]() $\mu \in \mathcal {P}$
, we denote by
$\mu \in \mathcal {P}$
, we denote by
![]() $X_\mu $
the Banach space given as the completion of the quotient space
$X_\mu $
the Banach space given as the completion of the quotient space
![]() $X/N$
, where
$X/N$
, where
![]() $X = (c_{00},\mu )$
and
$X = (c_{00},\mu )$
and
![]() $N = \{x\in c_{00}:\; \mu (x) = 0\}$
. In what follows, we often consider V as a subspace of
$N = \{x\in c_{00}:\; \mu (x) = 0\}$
. In what follows, we often consider V as a subspace of
![]() $X_\mu $
, that is, we identify every
$X_\mu $
, that is, we identify every
![]() $v\in V$
with its equivalence class
$v\in V$
with its equivalence class
![]() $[v]_N\in X_\mu $
.
$[v]_N\in X_\mu $
.
By
![]() $\mathcal {P}_\infty $
, we denote the set of those
$\mathcal {P}_\infty $
, we denote the set of those
![]() $\mu \in \mathcal {P}$
for which
$\mu \in \mathcal {P}$
for which
![]() $X_\mu $
is infinite-dimensional Banach space, and by
$X_\mu $
is infinite-dimensional Banach space, and by
![]() $\mathcal {B}$
, we denote the set of those
$\mathcal {B}$
, we denote the set of those
![]() $\mu \in \mathcal {P}_\infty $
for which the extension of
$\mu \in \mathcal {P}_\infty $
for which the extension of
![]() $\mu $
to
$\mu $
to
![]() $c_{00}$
is an actual norm, that is, the vectors
$c_{00}$
is an actual norm, that is, the vectors
![]() $ e_{1}, e_{2}, \dots $
are linearly independent in
$ e_{1}, e_{2}, \dots $
are linearly independent in
![]() $X_\mu $
.
$X_\mu $
.
We endow
![]() $\mathcal {P}_\infty $
and
$\mathcal {P}_\infty $
and
![]() $\mathcal {B}$
with topologies inherited from
$\mathcal {B}$
with topologies inherited from
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
It is rather easy to verify that the topologies on
![]() $\mathcal {P}_\infty $
and
$\mathcal {P}_\infty $
and
![]() $\mathcal {B}$
are Polish, we refer to [Reference Cúth, Doležal, Doucha and Kurka14, Corollary 2.5] for a proof.
$\mathcal {B}$
are Polish, we refer to [Reference Cúth, Doležal, Doucha and Kurka14, Corollary 2.5] for a proof.
Remark 1.3. As we have mentioned in the Introduction, Godefroy and Saint-Raymond [Reference Godefroy and Saint-Raymond28] considered another way of topologizing the class of all separable (infinite-dimensional) Banach spaces. Namely, they consider the set
![]() $SB = \{X\subseteq C(2^\omega )\colon X \text { is a closed linear subspace}\}$
and introduce a class of natural Polish topologies
$SB = \{X\subseteq C(2^\omega )\colon X \text { is a closed linear subspace}\}$
and introduce a class of natural Polish topologies
![]() $\tau $
on
$\tau $
on
![]() $SB$
, which they call ‘admissible’. In [Reference Cúth, Doležal, Doucha and Kurka14], we compared our spaces
$SB$
, which they call ‘admissible’. In [Reference Cúth, Doležal, Doucha and Kurka14], we compared our spaces
![]() $\mathcal {P}_\infty $
and
$\mathcal {P}_\infty $
and
![]() $\mathcal {B}$
with
$\mathcal {B}$
with
![]() $(SB,\tau )$
. In particular, we observed that whenever
$(SB,\tau )$
. In particular, we observed that whenever
![]() $\tau $
is an admissible topology, then there exists a continuous map
$\tau $
is an admissible topology, then there exists a continuous map
![]() $\Phi :(SB,\tau )\to \mathcal {P}$
, such that for every
$\Phi :(SB,\tau )\to \mathcal {P}$
, such that for every
![]() $F\in SB(X)$
, we have
$F\in SB(X)$
, we have
![]() $F\equiv X_{\Phi (F)}$
isometrically (see [Reference Cúth, Doležal, Doucha and Kurka14, Theorem 3.3]). Thus, from our results obtained in the coding
$F\equiv X_{\Phi (F)}$
isometrically (see [Reference Cúth, Doležal, Doucha and Kurka14, Theorem 3.3]). Thus, from our results obtained in the coding
![]() $\mathcal {P}_\infty $
, one may easily deduce also results formulated in the language of admissible topologies.
$\mathcal {P}_\infty $
, one may easily deduce also results formulated in the language of admissible topologies.
The following definition precises the notation
![]() ${\stackrel {K}{\sim }}$
defined earlier.
${\stackrel {K}{\sim }}$
defined earlier.
Definition 1.4. If
![]() $v_1,\ldots ,v_n\in V$
are given, for
$v_1,\ldots ,v_n\in V$
are given, for
![]() $\mu \in \mathcal {P}$
, instead of
$\mu \in \mathcal {P}$
, instead of
![]() $(X_\mu ,v_1,\ldots ,v_n){\stackrel {K}{\sim } X}$
, we shall write
$(X_\mu ,v_1,\ldots ,v_n){\stackrel {K}{\sim } X}$
, we shall write
![]() $(\mu ,v_1,\ldots ,v_n){\stackrel {K}{\sim } X}$
.
$(\mu ,v_1,\ldots ,v_n){\stackrel {K}{\sim } X}$
.
For further purposes, we record here the following lemma from [Reference Cúth, Doležal, Doucha and Kurka14].
Lemma 1.5 [Reference Cúth, Doležal, Doucha and Kurka14, Lemma 2.4].
Let X be a Banach space with
![]() $\{x_1,\ldots ,x_n\}\subseteq X$
linearly independent, and let
$\{x_1,\ldots ,x_n\}\subseteq X$
linearly independent, and let
![]() $v_1,\ldots ,v_n\in V$
. Then for any
$v_1,\ldots ,v_n\in V$
. Then for any
![]() $K>1$
, the set
$K>1$
, the set
is open in
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
In particular, the set of those
![]() $\mu \in \mathcal {P}$
for which the set
$\mu \in \mathcal {P}$
for which the set
![]() $\{v_1,\ldots ,v_n\}$
is linearly independent in
$\{v_1,\ldots ,v_n\}$
is linearly independent in
![]() $X_\mu $
is open in
$X_\mu $
is open in
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
Since we are interested mainly in subsets of
![]() $\mathcal {P}$
closed under isometries, we introduce the following notation.
$\mathcal {P}$
closed under isometries, we introduce the following notation.
Notation 1.6. Let Z be a separable Banach space, and let
![]() $\mathcal {I}$
be a subset of
$\mathcal {I}$
be a subset of
![]() $\mathcal {P}$
. We put
$\mathcal {P}$
. We put
If
![]() $\mathcal {I}$
is clear from the context, we write
$\mathcal {I}$
is clear from the context, we write
![]() ${\langle Z\rangle _{\equiv }}$
and
${\langle Z\rangle _{\equiv }}$
and
![]() $\langle Z\rangle _{\simeq }$
instead of
$\langle Z\rangle _{\simeq }$
instead of
![]() ${\langle Z\rangle _{\equiv }^{\mathcal {I}}}$
and
${\langle Z\rangle _{\equiv }^{\mathcal {I}}}$
and
![]() ${\langle Z\rangle _{\simeq }^{\mathcal {I}}}$
, respectively.
${\langle Z\rangle _{\simeq }^{\mathcal {I}}}$
, respectively.
The connection of the topologies on
![]() $\mathcal {P}$
,
$\mathcal {P}$
,
![]() $\mathcal {P}_\infty $
and
$\mathcal {P}_\infty $
and
![]() $\mathcal {B}$
with finite representability was thoroughly explored in [Reference Cúth, Doležal, Doucha and Kurka14]. Here, we recall what will be useful in this paper.
$\mathcal {B}$
with finite representability was thoroughly explored in [Reference Cúth, Doležal, Doucha and Kurka14]. Here, we recall what will be useful in this paper.
Definition 1.7. We say that a Banach space X is finitely representable in a Banach space Y if given any finite-dimensional subspace E of X and
![]() $\varepsilon> 0$
, there exists a finite-dimensional subspace F of Y, which is
$\varepsilon> 0$
, there exists a finite-dimensional subspace F of Y, which is
![]() $(1+\varepsilon )$
-isomorphic to E.
$(1+\varepsilon )$
-isomorphic to E.
Moreover, if
![]() $\mathcal {F}$
is a family of Banach spaces, we say that a Banach space X is finitely representable in
$\mathcal {F}$
is a family of Banach spaces, we say that a Banach space X is finitely representable in
![]() $\mathcal {F}$
if given any finite-dimensional subspace E of X and any
$\mathcal {F}$
if given any finite-dimensional subspace E of X and any
![]() $\varepsilon> 0$
, there exists a finite-dimensional subspace F of some
$\varepsilon> 0$
, there exists a finite-dimensional subspace F of some
![]() $Y\in \mathcal {F}$
, which is
$Y\in \mathcal {F}$
, which is
![]() $(1+\varepsilon )$
-isomorphic to E.
$(1+\varepsilon )$
-isomorphic to E.
Proposition 1.8 [Reference Cúth, Doležal, Doucha and Kurka14, Proposition 2.9].
If X is a separable infinite-dimensional Banach space, then
and similarly also if we replace
![]() $\mathcal {B}$
with
$\mathcal {B}$
with
![]() $\mathcal {P}_\infty $
or with
$\mathcal {P}_\infty $
or with
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
Moreover, let
![]() $\mathcal {F}\subseteq \mathcal {B}$
be such that
$\mathcal {F}\subseteq \mathcal {B}$
be such that
![]() ${\langle X_\mu \rangle _{\equiv }^{\mathcal {B}}}\subseteq \mathcal {F}$
for every
${\langle X_\mu \rangle _{\equiv }^{\mathcal {B}}}\subseteq \mathcal {F}$
for every
![]() $\mu \in \mathcal {F}$
. Then
$\mu \in \mathcal {F}$
. Then
The same again holds if we replace
![]() $\mathcal {B}$
with
$\mathcal {B}$
with
![]() $\mathcal {P}_\infty $
or with
$\mathcal {P}_\infty $
or with
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
We finish this section by recalling one particular Banach space that will play a fundamental role in certain further results in this paper. That is, we recall what the Gurariı̆ space is. One of the characterizations of the Gurariı̆ space is the following, for more details, we refer the interested reader, for example, to [Reference Cabello Sánchez, Garbulińska-Wȩgrzyn and Kubiś10] (the characterization below is provided by [Reference Cabello Sánchez, Garbulińska-Wȩgrzyn and Kubiś10, Lemma 2.2]).
Definition 1.9. The Gurariı̆ space is the unique (up to isometry) separable Banach space, such that for every
![]() $\varepsilon> 0$
and every isometric embedding
$\varepsilon> 0$
and every isometric embedding
![]() $g:A\to B$
, where B is a finite-dimensional Banach space and A is a subspace of
$g:A\to B$
, where B is a finite-dimensional Banach space and A is a subspace of
![]() $\mathbb {G}$
, there is a
$\mathbb {G}$
, there is a
![]() $(1+\varepsilon )$
-isomorphism
$(1+\varepsilon )$
-isomorphism
![]() $f:B\to \mathbb {G}$
, such that
$f:B\to \mathbb {G}$
, such that
![]() $\|f\circ g - id_A\|\leq \varepsilon $
.
$\|f\circ g - id_A\|\leq \varepsilon $
.
In the sequel, we will need the following result.
Theorem 1.10 [Reference Cúth, Doležal, Doucha and Kurka14, Theorem 4.1].
Let
![]() $\mathbb {G}$
be the Gurariı̆ space. The set
$\mathbb {G}$
be the Gurariı̆ space. The set
![]() ${\langle \mathbb {G\rangle _{\equiv }^{\mathcal I}}}$
is a dense
${\langle \mathbb {G\rangle _{\equiv }^{\mathcal I}}}$
is a dense
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {I}$
for any
$\mathcal {I}$
for any
![]() $\mathcal {I}\in \{\mathcal {P},\mathcal {P}_\infty ,\mathcal {B}\}$
.
$\mathcal {I}\in \{\mathcal {P},\mathcal {P}_\infty ,\mathcal {B}\}$
.
2 Spaces with descriptively simple isometry and isomorphism classes
The topic of this section is to deal with spaces with descriptively simple isometry classes (see Section 2.1) and with spaces with descriptively simple isomorphism classes (see Section 2.3). The main outcome is Theorem A, which follows from Theorems 2.4 and 2.10.
2.1 Spaces with closed isometry classes
In this subsection, we start our investigation of descriptive complexity of isometry classes, with the main goal to prove the first part of Theorem A. Let us first observe that no isometry class can be open, as every isometry class actually has an empty interior. Indeed, it follows from Proposition 1.8 that the isometry class of every isometrically universal separable Banach space is dense. Since there are obviously many pairwise nonisometric universal Banach spaces, we get that every open set (in all
![]() $\mathcal {P}$
,
$\mathcal {P}$
,
![]() $\mathcal {P}_\infty $
and
$\mathcal {P}_\infty $
and
![]() $\mathcal {B}$
) contains norms, respectively, pseudonorms, defining distinct Banach spaces. The same argument can also be used to show that every isomorphism class has an empty interior.
$\mathcal {B}$
) contains norms, respectively, pseudonorms, defining distinct Banach spaces. The same argument can also be used to show that every isomorphism class has an empty interior.
Lemma 2.1.
![]() ${\langle \ell _2\rangle _{\equiv }}$
is closed in
${\langle \ell _2\rangle _{\equiv }}$
is closed in
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Proof. Hilbert spaces are characterized among Banach spaces as those Banach spaces whose norm satisfies the parallelogram law, that is
![]() $\|x+y\|^2+\|x-y\|^2=2(\|x\|^2+\|y\|^2)$
for any pair of elements
$\|x+y\|^2+\|x-y\|^2=2(\|x\|^2+\|y\|^2)$
for any pair of elements
![]() $x,y$
. It is clear that a norm satisfies the parallelogram law if and only if it satisfies it on a dense set of vectors, therefore, every norm, respectively, pseudonorm, from
$x,y$
. It is clear that a norm satisfies the parallelogram law if and only if it satisfies it on a dense set of vectors, therefore, every norm, respectively, pseudonorm, from
![]() $\mathcal {B}$
, respectively,
$\mathcal {B}$
, respectively,
![]() $\mathcal {P}_\infty $
, satisfying the parallelogram law on V defines a Hilbert space. Since norms, respectively, pseudonorms, from
$\mathcal {P}_\infty $
, satisfying the parallelogram law on V defines a Hilbert space. Since norms, respectively, pseudonorms, from
![]() $\mathcal {B}$
, respectively,
$\mathcal {B}$
, respectively,
![]() $\mathcal {P}_\infty $
, define only infinite-dimensional spaces, they define spaces isometric to
$\mathcal {P}_\infty $
, define only infinite-dimensional spaces, they define spaces isometric to
![]() $\ell _2(\mathbb {N})$
. Since the parallelogram law is clearly a closed condition, we are done.
$\ell _2(\mathbb {N})$
. Since the parallelogram law is clearly a closed condition, we are done.
Remark 2.2. We note that here we need to work with the spaces
![]() $\mathcal {B}$
or
$\mathcal {B}$
or
![]() $\mathcal {P}_\infty $
, since in
$\mathcal {P}_\infty $
, since in
![]() $\mathcal {P}$
, the only space with closed isometry class is the trivial space. To show it, first notice that the trivial space is indeed closed. Next, we show that any open neighbourhood of a pseudonorm defining trivial space contains a pseudonorm defining arbitrary Banach space, which will finish our claim. Let such an open neighbourhood be fixed. We may assume that it is of the form
$\mathcal {P}$
, the only space with closed isometry class is the trivial space. To show it, first notice that the trivial space is indeed closed. Next, we show that any open neighbourhood of a pseudonorm defining trivial space contains a pseudonorm defining arbitrary Banach space, which will finish our claim. Let such an open neighbourhood be fixed. We may assume that it is of the form
![]() $\{\mu \in \mathcal {P}\colon \mu (v_i)<\varepsilon , i\leq n\}$
, where
$\{\mu \in \mathcal {P}\colon \mu (v_i)<\varepsilon , i\leq n\}$
, where
![]() $v_1,\ldots ,v_n\in V$
and
$v_1,\ldots ,v_n\in V$
and
![]() $\varepsilon>0$
. Let m be such that all
$\varepsilon>0$
. Let m be such that all
![]() $v_i$
,
$v_i$
,
![]() $i\leq n$
, are in
$i\leq n$
, are in
![]() $\operatorname {span}_{\mathbb {Q}}\{e_j\colon j\leq m\}$
. Let X be an arbitrary separable Banach space, and let
$\operatorname {span}_{\mathbb {Q}}\{e_j\colon j\leq m\}$
. Let X be an arbitrary separable Banach space, and let
![]() $(f_i)_{i\in \mathbb {N}}\subseteq X$
be a sequence whose span is dense in X. We define
$(f_i)_{i\in \mathbb {N}}\subseteq X$
be a sequence whose span is dense in X. We define
![]() $\mu \in \mathcal {P}$
by
$\mu \in \mathcal {P}$
by
![]() $\mu (e_j)=0$
, for
$\mu (e_j)=0$
, for
![]() $j\leq m$
, and
$j\leq m$
, and
![]() $\mu (\sum _{i\in I} \alpha _i e_{m+i})=\|\sum _{i\in I} \alpha _i f_i\|_X$
, where
$\mu (\sum _{i\in I} \alpha _i e_{m+i})=\|\sum _{i\in I} \alpha _i f_i\|_X$
, where
![]() $I\subseteq \mathbb {N}$
is finite and
$I\subseteq \mathbb {N}$
is finite and
![]() $(\alpha _i)_{i\in I}\subseteq \mathbb {Q}$
. This defines
$(\alpha _i)_{i\in I}\subseteq \mathbb {Q}$
. This defines
![]() $\mu $
separately on
$\mu $
separately on
![]() $\operatorname {span}_{\mathbb {Q}}\{e_i\colon i\leq m\}$
and
$\operatorname {span}_{\mathbb {Q}}\{e_i\colon i\leq m\}$
and
![]() $\operatorname {span}_{\mathbb {Q}}\{e_i\colon i>m\}$
, however, the extension to the whole V is unique. It is clear that
$\operatorname {span}_{\mathbb {Q}}\{e_i\colon i>m\}$
, however, the extension to the whole V is unique. It is clear that
![]() $\mu $
is in the fixed open neighbourhood and that
$\mu $
is in the fixed open neighbourhood and that
![]() $X_\mu \equiv X$
.
$X_\mu \equiv X$
.
One may be interested whether there are other Banach spaces whose isometry class is closed. The answer is negative. This follows from another corollary of Proposition 1.8, which we mentioned already in [Reference Cúth, Doležal, Doucha and Kurka14, Corollary 2.11]. Its proof is just an easy application of the Dvoretzky theorem.
Lemma 2.3 [Reference Cúth, Doležal, Doucha and Kurka14, Corollary 2.11].
Let X be a separable infinite-dimensional Banach space. Then,
![]() ${\langle \ell _2\rangle _{\equiv }^{\mathcal {B}}}\subseteq \overline {{\langle X\rangle _{\equiv }^{\mathcal {B}}}}\cap \mathcal {B}$
. The same holds if we replace
${\langle \ell _2\rangle _{\equiv }^{\mathcal {B}}}\subseteq \overline {{\langle X\rangle _{\equiv }^{\mathcal {B}}}}\cap \mathcal {B}$
. The same holds if we replace
![]() $\mathcal {B}$
with
$\mathcal {B}$
with
![]() $\mathcal {P}_\infty $
or
$\mathcal {P}_\infty $
or
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
The following theorem is now an immediate consequence of Lemmas 2.1 and 2.3.
Theorem 2.4.
![]() $\ell _2$
is the only separable infinite-dimensional Banach space whose isometry class is closed in
$\ell _2$
is the only separable infinite-dimensional Banach space whose isometry class is closed in
![]() $\mathcal {B}$
. The same holds if we replace
$\mathcal {B}$
. The same holds if we replace
![]() $\mathcal {B}$
by
$\mathcal {B}$
by
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
2.2
 $QSL_p$
-spaces
$QSL_p$
-spaces
Before embarking on studying spaces with descriptively simple isomorphism classes, let us consider some natural closed subspaces of
![]() $\mathcal {P}$
,
$\mathcal {P}$
,
![]() $\mathcal {P}_\infty $
and
$\mathcal {P}_\infty $
and
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
In [Reference Kwapien37], Kwapień denotes by
![]() $S_p$
, respectively,
$S_p$
, respectively,
![]() $SQ_p$
, for
$SQ_p$
, for
![]() $1\leq p<\infty $
, the class of all Banach spaces isometric to a subspace of
$1\leq p<\infty $
, the class of all Banach spaces isometric to a subspace of
![]() $L_p(\mu )$
, respectively, to a subspace of some quotient of
$L_p(\mu )$
, respectively, to a subspace of some quotient of
![]() $L_p(\mu )$
, for some measure
$L_p(\mu )$
, for some measure
![]() $\mu $
. Note that a separable Banach space X belongs to
$\mu $
. Note that a separable Banach space X belongs to
![]() $S_p$
, respectively,
$S_p$
, respectively,
![]() $SQ_p$
if and only if it is isometric to a subspace of
$SQ_p$
if and only if it is isometric to a subspace of
![]() $L_p[0,1]$
, respectively, to a subspace of a quotient of
$L_p[0,1]$
, respectively, to a subspace of a quotient of
![]() $L_p[0,1]$
, which easily follows from the fact that any separable
$L_p[0,1]$
, which easily follows from the fact that any separable
![]() $L_p(\mu )$
isometrically embeds into
$L_p(\mu )$
isometrically embeds into
![]() $L_p[0,1]$
as a complemented subspace (see, e.g. Theorem 3.8 below).
$L_p[0,1]$
as a complemented subspace (see, e.g. Theorem 3.8 below).
Let us address the class
![]() $S_p$
first. We have the following simple lemma.
$S_p$
first. We have the following simple lemma.
Lemma 2.5. Let
![]() $1\leq p < \infty $
. Put
$1\leq p < \infty $
. Put
Then M is a closed set in
![]() $\mathcal {B}$
, and we have
$\mathcal {B}$
, and we have
The same holds if we replace
![]() $\mathcal {B}$
with
$\mathcal {B}$
with
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Proof. We recall the fact that a separable infinite-dimensional Banach space is isometric to a subspace of
![]() $L_p[0,1]$
if and only if it is finitely representable in
$L_p[0,1]$
if and only if it is finitely representable in
![]() $\ell _p$
(see, e.g. [Reference Albiac and Kalton1, Theorem 12.1.9]). The rest follows from Proposition 1.8. We refer the reader to Section 3 for a definition of the class
$\ell _p$
(see, e.g. [Reference Albiac and Kalton1, Theorem 12.1.9]). The rest follows from Proposition 1.8. We refer the reader to Section 3 for a definition of the class
![]() $\mathcal {L}_{p,1+}$
.
$\mathcal {L}_{p,1+}$
.
In the rest, we focus on the class
![]() $SQ_p$
. Notice that for
$SQ_p$
. Notice that for
![]() $p=1$
, this class coincides with the class of all Banach spaces, and for
$p=1$
, this class coincides with the class of all Banach spaces, and for
![]() $p=2$
, this class consists of Hilbert spaces.
$p=2$
, this class consists of Hilbert spaces.
These Banach spaces are also called
![]() $QSL_p$
-spaces in literature, and since it seems this is the more recent terminology, this is what we will use further. It seems to be well-known, see, for example, [Reference Runde49], that this class of spaces is characterized by Proposition 2.6 below. This result was first essentially proved probably by Kwapien [Reference Kwapien37] (however, in his paper, he considered the isomorphic variant only), for a more detailed explanation of the proof (and even for a generalization), one may consult, for example, the proof in [Reference Le Merdy40, Theorem 3.2], which uses ideas from [Reference Pisier48] and [Reference Hernandez31]. Let us note that, by Proposition 2.6 and [Reference Herz32, Proposition 0], the class of
$QSL_p$
-spaces in literature, and since it seems this is the more recent terminology, this is what we will use further. It seems to be well-known, see, for example, [Reference Runde49], that this class of spaces is characterized by Proposition 2.6 below. This result was first essentially proved probably by Kwapien [Reference Kwapien37] (however, in his paper, he considered the isomorphic variant only), for a more detailed explanation of the proof (and even for a generalization), one may consult, for example, the proof in [Reference Le Merdy40, Theorem 3.2], which uses ideas from [Reference Pisier48] and [Reference Hernandez31]. Let us note that, by Proposition 2.6 and [Reference Herz32, Proposition 0], the class of
![]() $QSL_p$
-spaces coincides with the class of p-spaces considered already in 1971 by Herz [Reference Herz32].
$QSL_p$
-spaces coincides with the class of p-spaces considered already in 1971 by Herz [Reference Herz32].
Proposition 2.6. A Banach space X is a
![]() $QSL_p$
-space, if and only if, for every real valued
$QSL_p$
-space, if and only if, for every real valued
![]() $(n,m)$
-matrix M satisfying
$(n,m)$
-matrix M satisfying
 $$ \begin{align*}\sum_{i=1}^n \left|\sum_{j=1}^m M(i,j) r_j \right|{}^p\leq \sum_{k=1}^m |r_k|^p,\end{align*} $$
$$ \begin{align*}\sum_{i=1}^n \left|\sum_{j=1}^m M(i,j) r_j \right|{}^p\leq \sum_{k=1}^m |r_k|^p,\end{align*} $$
for all m-tuples
![]() $r_1,\ldots ,r_m\in \mathbb {R}$
, we have
$r_1,\ldots ,r_m\in \mathbb {R}$
, we have
 $$ \begin{align*} \sum_{i=1}^n \left\|\sum_{j=1}^m M(i,j) x_j \right\|_X^p\leq \sum_{k=1}^m \|x_k\|_X^p, \end{align*} $$
$$ \begin{align*} \sum_{i=1}^n \left\|\sum_{j=1}^m M(i,j) x_j \right\|_X^p\leq \sum_{k=1}^m \|x_k\|_X^p, \end{align*} $$
for all m-tuples
![]() $x_1,\ldots ,x_m\in X$
.
$x_1,\ldots ,x_m\in X$
.
Since it is clear that it suffices to verify the condition from Proposition 2.6 only on dense tuples of vectors, and that this condition is closed, we immediately obtain the following.
Proposition 2.7. For every
![]() $1< p<\infty $
, the set
$1< p<\infty $
, the set
is closed in
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
The same is true if
![]() $\mathcal {P}_\infty $
is replaced by
$\mathcal {P}_\infty $
is replaced by
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
Denote now the set
![]() $\{\mu \in \mathcal {P}_\infty \colon X_\mu \text { is a }QSL_p\text {-space}\}$
by
$\{\mu \in \mathcal {P}_\infty \colon X_\mu \text { is a }QSL_p\text {-space}\}$
by
![]() $QSL_p$
. By Lemma 2.5, for
$QSL_p$
. By Lemma 2.5, for
![]() $1\leq p<\infty $
, the set
$1\leq p<\infty $
, the set
![]() $M_p:=\{\mu \in \mathcal P_\infty \colon X_\mu \text { is isometric to a subspace of }L_p[0,1]\}$
is closed. Clearly,
$M_p:=\{\mu \in \mathcal P_\infty \colon X_\mu \text { is isometric to a subspace of }L_p[0,1]\}$
is closed. Clearly,
![]() $M_p\subseteq QSL_p$
(and for
$M_p\subseteq QSL_p$
(and for
![]() $p=2$
, there is an equality).
$p=2$
, there is an equality).
If
![]() $p\neq 2$
, then
$p\neq 2$
, then
![]() $M_p\neq QSL_p$
because there exists a separable infinite-dimensional Banach space, which is isomorphic to a quotient of
$M_p\neq QSL_p$
because there exists a separable infinite-dimensional Banach space, which is isomorphic to a quotient of
![]() $L_p[0,1]$
but not to its subspace. Indeed, if
$L_p[0,1]$
but not to its subspace. Indeed, if
![]() $p=1$
, this is easy since every separable Banach space is isomorphic to a quotient of
$p=1$
, this is easy since every separable Banach space is isomorphic to a quotient of
![]() $\ell _1$
(see, e.g. [Reference Albiac and Kalton1, Theorem 2.3.1]). If
$\ell _1$
(see, e.g. [Reference Albiac and Kalton1, Theorem 2.3.1]). If
![]() $2<q<p<\infty $
, then
$2<q<p<\infty $
, then
![]() $\ell _q$
is isometric to a quotient of
$\ell _q$
is isometric to a quotient of
![]() $L_p[0,1]$
(because its dual
$L_p[0,1]$
(because its dual
![]() $\ell _{q'}$
embeds isometrically into
$\ell _{q'}$
embeds isometrically into
![]() $L_{p'}[0,1]$
) but is not isomorphic to a subspace of
$L_{p'}[0,1]$
) but is not isomorphic to a subspace of
![]() $L_p[0,1]$
(see, e.g. [Reference Albiac and Kalton1, Theorem 6.4.18]). Finally, if
$L_p[0,1]$
(see, e.g. [Reference Albiac and Kalton1, Theorem 6.4.18]). Finally, if
![]() $1<p<2$
, then by [Reference Figiel, Kwapień and Pełczyński20, Corollary 2], there exists a subspace X of
$1<p<2$
, then by [Reference Figiel, Kwapień and Pełczyński20, Corollary 2], there exists a subspace X of
![]() $\ell _{p'}\subseteq L_{p'}[0,1]$
, which is not isomorphic to a quotient of
$\ell _{p'}\subseteq L_{p'}[0,1]$
, which is not isomorphic to a quotient of
![]() $L_{p'}[0,1]$
,Footnote
1
and so
$L_{p'}[0,1]$
,Footnote
1
and so
![]() $X^*$
is isometric to a quotient of
$X^*$
is isometric to a quotient of
![]() $L_p[0,1]$
, which is not isomorphic to a subspace of
$L_p[0,1]$
, which is not isomorphic to a subspace of
![]() $L_p[0,1]$
. We would like to thank Bill Johnson for providing us these examples. Moreover, we have the following.
$L_p[0,1]$
. We would like to thank Bill Johnson for providing us these examples. Moreover, we have the following.
Proposition 2.8. For
![]() $p\in \left [1,2\right )\cup \left (2,\infty \right )$
, the set
$p\in \left [1,2\right )\cup \left (2,\infty \right )$
, the set
![]() $M_p$
has an empty interior in
$M_p$
has an empty interior in
![]() $QSL_p$
.
$QSL_p$
.
Proof. Fix
![]() $p\in \left [1,2\right )\cup \left (2,\infty \right )$
. Pick
$p\in \left [1,2\right )\cup \left (2,\infty \right )$
. Pick
![]() $\mu \in QSL_p$
, such that
$\mu \in QSL_p$
, such that
![]() $X_\mu $
does not isometrically embed as a subspace into
$X_\mu $
does not isometrically embed as a subspace into
![]() $L_p[0,1]$
(such a space exists, see the examples above). Let U be now a basic open neighbourhood of some
$L_p[0,1]$
(such a space exists, see the examples above). Let U be now a basic open neighbourhood of some
![]() $\nu \in QSL_p$
. Since the class of
$\nu \in QSL_p$
. Since the class of
![]() $QSL_p$
-spaces is clearly closed under taking
$QSL_p$
-spaces is clearly closed under taking
![]() $\ell _p$
-sums (see, e.g. [Reference Runde49]),
$\ell _p$
-sums (see, e.g. [Reference Runde49]),
![]() $X_\nu \oplus _p X_\mu $
is still a
$X_\nu \oplus _p X_\mu $
is still a
![]() $QSL_p$
-space. It is easy to define
$QSL_p$
-space. It is easy to define
![]() $\nu '\in U$
, so that
$\nu '\in U$
, so that
![]() $X_{\nu '}$
is isometric to
$X_{\nu '}$
is isometric to
![]() $X_\nu \oplus _p X_\mu $
. Now, since
$X_\nu \oplus _p X_\mu $
. Now, since
![]() $X_\mu $
does not isometrically embed as a subspace into
$X_\mu $
does not isometrically embed as a subspace into
![]() $L_p[0,1]$
, neither
$L_p[0,1]$
, neither
![]() $X_{\nu '}$
does. By [Reference Albiac and Kalton1, Theorem 12.1.9],
$X_{\nu '}$
does. By [Reference Albiac and Kalton1, Theorem 12.1.9],
![]() $X_{\nu '}$
is not finitely representable in
$X_{\nu '}$
is not finitely representable in
![]() $\ell _p$
, so also not in
$\ell _p$
, so also not in
![]() $L_p[0,1]$
(by [Reference Albiac and Kalton1, Proposition 12.1.8]). It follows from Proposition 1.8 that there exists a basic open neighbourhood
$L_p[0,1]$
(by [Reference Albiac and Kalton1, Proposition 12.1.8]). It follows from Proposition 1.8 that there exists a basic open neighbourhood
![]() $U'$
of
$U'$
of
![]() $\nu '$
avoiding
$\nu '$
avoiding
![]() $M_p$
. Now,
$M_p$
. Now,
![]() $U\cap U'$
is a nonempty open subset of U avoiding
$U\cap U'$
is a nonempty open subset of U avoiding
![]() $M_p$
, and we are done.
$M_p$
, and we are done.
Corollary 2.9. For
![]() $p\in \left [1,2\right )\cup \left (2,\infty \right )$
,
$p\in \left [1,2\right )\cup \left (2,\infty \right )$
,
![]() $L_p[0,1]$
is not a generic
$L_p[0,1]$
is not a generic
![]() $QSL_p$
-space.
$QSL_p$
-space.
2.3 Spaces with descriptively simple isomorphism classes
The main result of this subsection, and one of the main results of the whole paper, is the second part of Theorem A. That is, we prove the following.
Theorem 2.10. The Hilbert space
![]() $\ell _2$
is characterized as the unique, up to isomorphism, separable infinite-dimensional Banach space X, such that
$\ell _2$
is characterized as the unique, up to isomorphism, separable infinite-dimensional Banach space X, such that
![]() ${\langle X\rangle _{\simeq }}$
is an
${\langle X\rangle _{\simeq }}$
is an
![]() $F_\sigma $
-set in
$F_\sigma $
-set in
![]() $\mathcal {B}$
. The same holds if we replace
$\mathcal {B}$
. The same holds if we replace
![]() $\mathcal {B}$
with
$\mathcal {B}$
with
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Moreover,
![]() ${\langle \ell _2\rangle _{\simeq }}$
is
${\langle \ell _2\rangle _{\simeq }}$
is
![]() $F_\sigma $
-complete.
$F_\sigma $
-complete.
While there are several Banach spaces whose isometry classes have low complexity, as we shall see also in the next sections, there are reasons to suspect that isomorphism classes are rather complicated in general. Theorem 2.10 is a strong evidence that
![]() $\ell _2$
is quite unique with respect to its property of having a simple isomorphism class. Another piece of evidence which we state and prove before proving Theorem 2.10 is the following result.
$\ell _2$
is quite unique with respect to its property of having a simple isomorphism class. Another piece of evidence which we state and prove before proving Theorem 2.10 is the following result.
Proposition 2.11. No isomorphism class can be closed in
![]() $\mathcal {P}_\infty $
,
$\mathcal {P}_\infty $
,
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\mathcal {P}$
, and with the possible exception of spaces isomorphic to
$\mathcal {P}$
, and with the possible exception of spaces isomorphic to
![]() $\mathbb {G}$
, for which we do not know the answer, no isomorphism class can even be a
$\mathbb {G}$
, for which we do not know the answer, no isomorphism class can even be a
![]() $G_\delta $
-set.
$G_\delta $
-set.
Proof. Let X be a separable infinite-dimensional Banach space. We show that
![]() ${\langle X\rangle _{\simeq }}$
is dense (we show the argument only for
${\langle X\rangle _{\simeq }}$
is dense (we show the argument only for
![]() $\mathcal {P}_\infty $
, the other cases are analogous). Let F be a finite-dimensional Banach space. It is well-known that every finite-dimensional space is complemented in any infinite-dimensional Banach space, so we have
$\mathcal {P}_\infty $
, the other cases are analogous). Let F be a finite-dimensional Banach space. It is well-known that every finite-dimensional space is complemented in any infinite-dimensional Banach space, so we have
![]() $X\simeq F\oplus _1 Y$
for some Banach space Y. Since F was arbitrary, it follows that every separable Banach space is finitely representable in
$X\simeq F\oplus _1 Y$
for some Banach space Y. Since F was arbitrary, it follows that every separable Banach space is finitely representable in
![]() ${\langle X\rangle _{\simeq }}$
, so by Proposition 1.8,
${\langle X\rangle _{\simeq }}$
, so by Proposition 1.8,
![]() $\overline {{\langle X\rangle _{\simeq }}}=\mathcal {P}_\infty $
, hence,
$\overline {{\langle X\rangle _{\simeq }}}=\mathcal {P}_\infty $
, hence,
![]() ${\langle X\rangle _{\simeq }}$
is dense.
${\langle X\rangle _{\simeq }}$
is dense.
It follows that
![]() ${\langle X\rangle _{\simeq }}$
cannot be closed for any X because it is dense and there are obviously two nonisomorphic spaces. Moreover, if X is not isomorphic to the Gurariı̆ space, then
${\langle X\rangle _{\simeq }}$
cannot be closed for any X because it is dense and there are obviously two nonisomorphic spaces. Moreover, if X is not isomorphic to the Gurariı̆ space, then
![]() ${\langle X\rangle _{\simeq }}$
cannot be a
${\langle X\rangle _{\simeq }}$
cannot be a
![]() $G_\delta $
-set since by Theorem 1.10, the isometry class of the Gurariı̆ space is a dense
$G_\delta $
-set since by Theorem 1.10, the isometry class of the Gurariı̆ space is a dense
![]() $G_\delta $
-set, so it would have nonempty intersection with
$G_\delta $
-set, so it would have nonempty intersection with
![]() ${\langle X\rangle _{\simeq }}$
otherwise.
${\langle X\rangle _{\simeq }}$
otherwise.
Besides
![]() $\ell _2$
, whose isomorphism class is
$\ell _2$
, whose isomorphism class is
![]() $F_\sigma $
, it is proved in [Reference Godefroy and Saint-Raymond28, Theorem 4.12] that separable Banach spaces determined by their pavings have
$F_\sigma $
, it is proved in [Reference Godefroy and Saint-Raymond28, Theorem 4.12] that separable Banach spaces determined by their pavings have
![]() $\boldsymbol {\Sigma }_4^0$
isomorphism classes in any admissible topology (see Remark 1.3, where we recall some basics about admissible topologies). We refer the interested reader to the text before Theorem 2.13 for a definition of spaces determined by their pavings. Here, we just briefly note that this class of spaces was introduced by Johnson et al. in [Reference Johnson, Lindenstrauss and Schechtman33] and that there are known examples of separable Banach spaces determined by their pavings not isomorphic to
$\boldsymbol {\Sigma }_4^0$
isomorphism classes in any admissible topology (see Remark 1.3, where we recall some basics about admissible topologies). We refer the interested reader to the text before Theorem 2.13 for a definition of spaces determined by their pavings. Here, we just briefly note that this class of spaces was introduced by Johnson et al. in [Reference Johnson, Lindenstrauss and Schechtman33] and that there are known examples of separable Banach spaces determined by their pavings not isomorphic to
![]() $\ell _2$
(e.g. certain
$\ell _2$
(e.g. certain
![]() $\ell _2$
-sums of finite-dimensional spaces are such). The second main result of this section is the following improvement of the estimate mentioned above.
$\ell _2$
-sums of finite-dimensional spaces are such). The second main result of this section is the following improvement of the estimate mentioned above.
Theorem 2.12. Let X be a separable infinite-dimensional Banach space that is determined by its pavings. Then
![]() ${\langle X\rangle _{\simeq }}$
is a
${\langle X\rangle _{\simeq }}$
is a
![]() $G_{\delta \sigma }$
-set in
$G_{\delta \sigma }$
-set in
![]() $\mathcal {P}_\infty $
. In particular, it is a
$\mathcal {P}_\infty $
. In particular, it is a
![]() $G_{\delta \sigma }$
-set in
$G_{\delta \sigma }$
-set in
![]() $\mathcal {P}$
and in any admissible topology.
$\mathcal {P}$
and in any admissible topology.
Let us start with the proof of Theorem 2.10.
Proof of Theorem 2.10.
First, we show that isomorphism class is
![]() $F_\sigma $
. This was proved for an admissible topology on
$F_\sigma $
. This was proved for an admissible topology on
![]() $SB_{\infty} $
in [Reference Godefroy and Saint-Raymond28, Theorem 4.3]. The same proof, which we briefly sketch, works also for
$SB_{\infty} $
in [Reference Godefroy and Saint-Raymond28, Theorem 4.3]. The same proof, which we briefly sketch, works also for
![]() $\mathcal {P}_\infty $
and
$\mathcal {P}_\infty $
and
![]() $\mathcal {B}$
. By Kwapień’s theorem (see, e.g. [Reference Albiac and Kalton1, Theorem 7.4.1]), a separable infinite-dimensional Banach space is isomorphic to
$\mathcal {B}$
. By Kwapień’s theorem (see, e.g. [Reference Albiac and Kalton1, Theorem 7.4.1]), a separable infinite-dimensional Banach space is isomorphic to
![]() $\ell _2$
if and only if it is of type
$\ell _2$
if and only if it is of type
![]() $2$
and of cotype
$2$
and of cotype
![]() $2$
. It is clear from the definition of type and cotype (see, e.g. [Reference Albiac and Kalton1, Definition 6.2.10]) that these properties are
$2$
. It is clear from the definition of type and cotype (see, e.g. [Reference Albiac and Kalton1, Definition 6.2.10]) that these properties are
![]() $F_\sigma $
-conditions. So to show that
$F_\sigma $
-conditions. So to show that
![]() ${\langle \ell _2\rangle _{\simeq }}$
is even
${\langle \ell _2\rangle _{\simeq }}$
is even
![]() $F_\sigma $
-complete, by Lemma 1.1, it suffices to show that
$F_\sigma $
-complete, by Lemma 1.1, it suffices to show that
![]() ${\langle \ell _2\rangle _{\simeq }}$
is not a
${\langle \ell _2\rangle _{\simeq }}$
is not a
![]() $G_\delta $
-set, which we have already proved. An alternative proof showing that the isomorphism class
$G_\delta $
-set, which we have already proved. An alternative proof showing that the isomorphism class
![]() ${\langle \ell _2\rangle _{\simeq }}$
is an
${\langle \ell _2\rangle _{\simeq }}$
is an
![]() $F_\sigma $
-set follows from [Reference Kwapien37, Theorem 2’] (see also Remark 4 therein), which provides a formula defining spaces isomorphic to
$F_\sigma $
-set follows from [Reference Kwapien37, Theorem 2’] (see also Remark 4 therein), which provides a formula defining spaces isomorphic to
![]() $\ell _2$
and which obviously defines an
$\ell _2$
and which obviously defines an
![]() $F_\sigma $
-set (in
$F_\sigma $
-set (in
![]() $\mathcal {P}_\infty $
and
$\mathcal {P}_\infty $
and
![]() $\mathcal {B}$
).
$\mathcal {B}$
).
Next, we show that if a separable infinite-dimensional Banach space X is not isomorphic to
![]() $\ell _2$
, then
$\ell _2$
, then
![]() ${\langle X\rangle _{\simeq }}$
is not
${\langle X\rangle _{\simeq }}$
is not
![]() $F_\sigma $
in
$F_\sigma $
in
![]() $\mathcal {B}$
. In what follows, we denote by
$\mathcal {B}$
. In what follows, we denote by
![]() $\mathcal {T}$
the set of finite tuples (including empty) of natural numbers without repetition. The length of
$\mathcal {T}$
the set of finite tuples (including empty) of natural numbers without repetition. The length of
![]() $\gamma \in \mathcal {T}$
is denoted by
$\gamma \in \mathcal {T}$
is denoted by
![]() $|\gamma |$
, and its range by
$|\gamma |$
, and its range by
![]() $\operatorname {rng}(\gamma )$
. Moreover, for every
$\operatorname {rng}(\gamma )$
. Moreover, for every
![]() $\gamma \in \mathcal {T}$
and every
$\gamma \in \mathcal {T}$
and every
![]() $\mu \in \mathcal {B}$
, we put
$\mu \in \mathcal {B}$
, we put
 $$\begin{align*}\mathbb{M}^{\gamma}_\mu:=\Big\{\nu\in\mathcal{B}\colon \text{for every } (a_i)_{i=1}^{|\gamma|}\in\mathbb{Q}^{|\gamma|} \text{ we have } \nu\Big(\sum_{i=1}^{|\gamma|} a_i e_i\Big) = \mu\Big(\sum_{i=1}^{|\gamma|} a_i e_{\gamma(i)}\Big)\Big\}. \end{align*}$$
$$\begin{align*}\mathbb{M}^{\gamma}_\mu:=\Big\{\nu\in\mathcal{B}\colon \text{for every } (a_i)_{i=1}^{|\gamma|}\in\mathbb{Q}^{|\gamma|} \text{ we have } \nu\Big(\sum_{i=1}^{|\gamma|} a_i e_i\Big) = \mu\Big(\sum_{i=1}^{|\gamma|} a_i e_{\gamma(i)}\Big)\Big\}. \end{align*}$$
In order to get a contradiction, assume that
![]() $(F_n)_{n=1}^\infty $
are closed sets in
$(F_n)_{n=1}^\infty $
are closed sets in
![]() $\mathcal {B}$
such that
$\mathcal {B}$
such that
![]() ${\langle X\rangle _{\simeq }} = \bigcup _{n=1}^\infty F_n$
.
${\langle X\rangle _{\simeq }} = \bigcup _{n=1}^\infty F_n$
.
Claim. For every
![]() $\mu \in \mathcal {B}$
with
$\mu \in \mathcal {B}$
with
![]() ${\langle X_\mu \rangle _{\equiv }}\subseteq \bigcup _{n=1}^\infty F_n$
there exist
${\langle X_\mu \rangle _{\equiv }}\subseteq \bigcup _{n=1}^\infty F_n$
there exist
![]() $\gamma \in \mathcal {T}$
and
$\gamma \in \mathcal {T}$
and
![]() $m\in \mathbb {N}$
, such that we have
$m\in \mathbb {N}$
, such that we have
![]() $\mathbb {M}^{\gamma '}_\mu \cap F_m\neq \emptyset $
for every
$\mathbb {M}^{\gamma '}_\mu \cap F_m\neq \emptyset $
for every
![]() $\gamma '\in \mathcal {T}$
with
$\gamma '\in \mathcal {T}$
with
![]() $\gamma '\supseteq \gamma $
.
$\gamma '\supseteq \gamma $
.
Proof of the claim.
Suppose the statement is not true. In particular, it does not hold for
![]() $\gamma = \emptyset $
and
$\gamma = \emptyset $
and
![]() $m=1$
. That is, there is some
$m=1$
. That is, there is some
![]() $\gamma ^{\prime }_1\in \mathcal {T}$
so that
$\gamma ^{\prime }_1\in \mathcal {T}$
so that
![]() $\mathbb {M}^{\gamma _1^{\prime }}_\mu \cap F_1=\emptyset $
. If
$\mathbb {M}^{\gamma _1^{\prime }}_\mu \cap F_1=\emptyset $
. If
![]() $1\in \operatorname {rng}(\gamma ^{\prime }_1)$
, we set
$1\in \operatorname {rng}(\gamma ^{\prime }_1)$
, we set
![]() $\gamma _1=\gamma ^{\prime }_1$
. Otherwise, we set
$\gamma _1=\gamma ^{\prime }_1$
. Otherwise, we set
![]() $\gamma _1={\gamma ^{\prime }_1}^{\frown } (1)$
.
$\gamma _1={\gamma ^{\prime }_1}^{\frown } (1)$
.
In the next step, we use that the statement is not true for
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $m=2$
to obtain
$m=2$
to obtain
![]() $\gamma ^{\prime }_2\in \mathcal {T}$
,
$\gamma ^{\prime }_2\in \mathcal {T}$
,
![]() $\gamma ^{\prime }_2\supseteq \gamma _1$
so that
$\gamma ^{\prime }_2\supseteq \gamma _1$
so that
![]() $\mathbb {M}^{\gamma ^{\prime }_2}_\mu \cap F_2=\emptyset $
. If
$\mathbb {M}^{\gamma ^{\prime }_2}_\mu \cap F_2=\emptyset $
. If
![]() $2\in \operatorname {rng}(\gamma ^{\prime }_2)$
, we set
$2\in \operatorname {rng}(\gamma ^{\prime }_2)$
, we set
![]() $\gamma _2=\gamma ^{\prime }_2$
. Otherwise, we set
$\gamma _2=\gamma ^{\prime }_2$
. Otherwise, we set
![]() $\gamma _2={\gamma ^{\prime }_2}^\frown {} (2)$
.
$\gamma _2={\gamma ^{\prime }_2}^\frown {} (2)$
.
We continue analogously. At the end of the recursion, we obtain a bijection
![]() $\pi :\mathbb {N}\to \mathbb {N}$
, such that
$\pi :\mathbb {N}\to \mathbb {N}$
, such that
![]() $\pi \supseteq \gamma _n$
for every
$\pi \supseteq \gamma _n$
for every
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\mathbb {M}^{\gamma _n}_\mu \cap F_n=\emptyset $
for every
$\mathbb {M}^{\gamma _n}_\mu \cap F_n=\emptyset $
for every
![]() $n\in \mathbb {N}$
. Consider
$n\in \mathbb {N}$
. Consider
![]() $\mu _0\in \mathcal {B}$
given as
$\mu _0\in \mathcal {B}$
given as
 $$\begin{align*}\mu_0\Big(\sum_{i=1}^k a_i e_i\Big):=\mu\Big(\sum_{i=1}^k a_i e_{\pi(i)}\Big),\quad k\in\mathbb{N},\; (a_i)_{i=1}^k\in \mathbb{Q}^k. \end{align*}$$
$$\begin{align*}\mu_0\Big(\sum_{i=1}^k a_i e_i\Big):=\mu\Big(\sum_{i=1}^k a_i e_{\pi(i)}\Big),\quad k\in\mathbb{N},\; (a_i)_{i=1}^k\in \mathbb{Q}^k. \end{align*}$$
Then the linear mapping given by
![]() $e_i\mapsto e_{\pi (i)}$
,
$e_i\mapsto e_{\pi (i)}$
,
![]() $i\in \mathbb {N}$
, witnesses that
$i\in \mathbb {N}$
, witnesses that
![]() $X_{\mu _0}\equiv X_\mu $
and
$X_{\mu _0}\equiv X_\mu $
and
![]() $\mu _0\in \mathbb {M}^{\gamma _n}_\mu $
for every
$\mu _0\in \mathbb {M}^{\gamma _n}_\mu $
for every
![]() $n\in \mathbb {N}$
. Thus,
$n\in \mathbb {N}$
. Thus,
![]() $\mu _0\notin \bigcup _{n=1}^\infty F_n$
, which is in contradiction with
$\mu _0\notin \bigcup _{n=1}^\infty F_n$
, which is in contradiction with
![]() $\mu _0\in {\langle X_\mu \rangle _{\equiv }}\subseteq \bigcup _{n=1}^\infty F_n$
.
$\mu _0\in {\langle X_\mu \rangle _{\equiv }}\subseteq \bigcup _{n=1}^\infty F_n$
.
Since
![]() $X\not \simeq \ell _2$
, by the celebrated solution to the homogeneous subspace problem following from the results of Komorowski and Tomczak-Jaegermann ([Reference Komorowski and Tomczak-Jaegermann35]) and of Gowers ([Reference Gowers29]), it must contain an infinite-dimensional closed subspace
$X\not \simeq \ell _2$
, by the celebrated solution to the homogeneous subspace problem following from the results of Komorowski and Tomczak-Jaegermann ([Reference Komorowski and Tomczak-Jaegermann35]) and of Gowers ([Reference Gowers29]), it must contain an infinite-dimensional closed subspace
![]() $Y\subseteq X$
that is not isomorphic to X. Let
$Y\subseteq X$
that is not isomorphic to X. Let
![]() $I\subseteq \mathbb {N}$
be an infinite subset and
$I\subseteq \mathbb {N}$
be an infinite subset and
![]() $\{x_n\}_{n\in \mathbb {N}}$
a sequence of linearly independent vectors in X so that
$\{x_n\}_{n\in \mathbb {N}}$
a sequence of linearly independent vectors in X so that
-
(1)
 $\overline {\operatorname {span}}\{x_n\}_{n\in \mathbb {N}}=X$
,
$\overline {\operatorname {span}}\{x_n\}_{n\in \mathbb {N}}=X$
,
 $\overline {\operatorname {span}}\{x_n\colon n\in I\}=Y$
, and
$\overline {\operatorname {span}}\{x_n\colon n\in I\}=Y$
, and -
(2) for every finite set
 $F\subseteq \mathbb {N}$
, we have
$F\subseteq \mathbb {N}$
, we have  $$\begin{align*}\overline{\operatorname{span}}\{x_n\}_{n\in I \cup F} = \overline{\operatorname{span}}\{x_n\}_{n\in F\cap I}\oplus \overline{\operatorname{span}}\{x_n\}_{n\in F\setminus I}\oplus \overline{\operatorname{span}}\{x_n\}_{n\in I \setminus F}.\end{align*}$$
$$\begin{align*}\overline{\operatorname{span}}\{x_n\}_{n\in I \cup F} = \overline{\operatorname{span}}\{x_n\}_{n\in F\cap I}\oplus \overline{\operatorname{span}}\{x_n\}_{n\in F\setminus I}\oplus \overline{\operatorname{span}}\{x_n\}_{n\in I \setminus F}.\end{align*}$$
Such a choice is possible, for example, by finding a Markushevich basis
![]() $\{x_n\}_{n\in I}$
on Y (see [Reference Hájek, Montesinos Santalucía, Vanderwerff and Zizler30, Theorem 1.22]), extending it to a Markushevich basis
$\{x_n\}_{n\in I}$
on Y (see [Reference Hájek, Montesinos Santalucía, Vanderwerff and Zizler30, Theorem 1.22]), extending it to a Markushevich basis
![]() $\{x_n\}_{n\in \mathbb {N}}$
on X (see [Reference Hájek, Montesinos Santalucía, Vanderwerff and Zizler30, Theorem 1.45]) and then observing that for any
$\{x_n\}_{n\in \mathbb {N}}$
on X (see [Reference Hájek, Montesinos Santalucía, Vanderwerff and Zizler30, Theorem 1.45]) and then observing that for any
![]() $J\subseteq \mathbb {N}$
, we have that
$J\subseteq \mathbb {N}$
, we have that
![]() $\{x_n\}_{n\in J}$
is a fundamental biorthogonal system of
$\{x_n\}_{n\in J}$
is a fundamental biorthogonal system of
![]() $\overline {\operatorname {span}}\{x_n\}_{n\in J}$
and so (2) holds (see [Reference Hájek, Montesinos Santalucía, Vanderwerff and Zizler30, Fact 1.5]).
$\overline {\operatorname {span}}\{x_n\}_{n\in J}$
and so (2) holds (see [Reference Hájek, Montesinos Santalucía, Vanderwerff and Zizler30, Fact 1.5]).
We define
![]() $\mu \in \mathcal {B}$
as
$\mu \in \mathcal {B}$
as
 $$\begin{align*}\mu\Big(\sum_{i=1}^k a_i e_i\Big):=\Big\|\sum_{i=1}^k a_i x_i\Big\|_X,\quad k\in\mathbb{N},\;(a_i)_{i=1}^k\in\mathbb{Q}^k. \end{align*}$$
$$\begin{align*}\mu\Big(\sum_{i=1}^k a_i e_i\Big):=\Big\|\sum_{i=1}^k a_i x_i\Big\|_X,\quad k\in\mathbb{N},\;(a_i)_{i=1}^k\in\mathbb{Q}^k. \end{align*}$$
Then
![]() ${\langle X_\mu \rangle _{\equiv }}={\langle X\rangle _{\equiv }}\subseteq \bigcup _{n=1}^\infty F_n$
and so, by the claim above, there exist
${\langle X_\mu \rangle _{\equiv }}={\langle X\rangle _{\equiv }}\subseteq \bigcup _{n=1}^\infty F_n$
and so, by the claim above, there exist
![]() $\gamma \in \mathcal {T}$
and
$\gamma \in \mathcal {T}$
and
![]() $m\in \mathbb {N}$
with
$m\in \mathbb {N}$
with
![]() $\mathbb {M}^{\gamma '}_\mu \cap F_m\neq \emptyset $
for every
$\mathbb {M}^{\gamma '}_\mu \cap F_m\neq \emptyset $
for every
![]() $\gamma '\in \mathcal {T}$
with
$\gamma '\in \mathcal {T}$
with
![]() $\gamma '\supseteq \gamma $
. Consider now the space
$\gamma '\supseteq \gamma $
. Consider now the space
![]() $Z:=(\overline {\operatorname {span}}\{e_i\colon i\in I\cup \operatorname {rng}(\gamma )\},\mu )\subseteq X_\mu $
. Fix some
$Z:=(\overline {\operatorname {span}}\{e_i\colon i\in I\cup \operatorname {rng}(\gamma )\},\mu )\subseteq X_\mu $
. Fix some
![]() $\widetilde I\subseteq I$
such that
$\widetilde I\subseteq I$
such that
![]() $|I\setminus \widetilde I|=|\operatorname {rng}(\gamma )\setminus I|$
and such that
$|I\setminus \widetilde I|=|\operatorname {rng}(\gamma )\setminus I|$
and such that
![]() $(I\setminus \widetilde I)\cap \operatorname {rng}(\gamma )=\emptyset $
. Define
$(I\setminus \widetilde I)\cap \operatorname {rng}(\gamma )=\emptyset $
. Define
![]() $\widetilde Z:=(\overline {\operatorname {span}}\{e_i\colon i\in \widetilde I\cup \operatorname {rng}(\gamma )\},\mu )$
. Then, using (2), we have
$\widetilde Z:=(\overline {\operatorname {span}}\{e_i\colon i\in \widetilde I\cup \operatorname {rng}(\gamma )\},\mu )$
. Then, using (2), we have
and so
![]() $\widetilde Z\not \simeq X$
. Let
$\widetilde Z\not \simeq X$
. Let
![]() $\varphi :\mathbb {N}\to \operatorname {rng}(\gamma )\cup \widetilde I$
be a bijection with
$\varphi :\mathbb {N}\to \operatorname {rng}(\gamma )\cup \widetilde I$
be a bijection with
![]() $\varphi \supseteq \gamma $
. We define
$\varphi \supseteq \gamma $
. We define
![]() $\nu \in \mathcal {B}$
by
$\nu \in \mathcal {B}$
by
 $$\begin{align*}\nu\Big(\sum_{i=1}^k a_i e_i\Big):=\mu\Big(\sum_{i=1}^k a_i e_{\varphi(i)}\Big),\quad k\in\mathbb{N},\;(a_i)_{i=1}^k\in\mathbb{Q}^k. \end{align*}$$
$$\begin{align*}\nu\Big(\sum_{i=1}^k a_i e_i\Big):=\mu\Big(\sum_{i=1}^k a_i e_{\varphi(i)}\Big),\quad k\in\mathbb{N},\;(a_i)_{i=1}^k\in\mathbb{Q}^k. \end{align*}$$
Clearly,
![]() $X_\nu \equiv \widetilde Z\not \simeq X$
.
$X_\nu \equiv \widetilde Z\not \simeq X$
.
We claim that
![]() $\nu \in F_m$
. This will be in contradiction with the fact that
$\nu \in F_m$
. This will be in contradiction with the fact that
![]() $F_m\subseteq {\langle X\rangle _{\simeq }}$
. Since
$F_m\subseteq {\langle X\rangle _{\simeq }}$
. Since
![]() $F_m$
is closed, it suffices to check that each basic open neighbourhood of
$F_m$
is closed, it suffices to check that each basic open neighbourhood of
![]() $\nu $
intersects
$\nu $
intersects
![]() $F_m$
. Pick
$F_m$
. Pick
![]() $v_1,\ldots , v_l\in V$
and
$v_1,\ldots , v_l\in V$
and
![]() $\varepsilon>0$
. We need to find
$\varepsilon>0$
. We need to find
![]() $\mu '\in F_m$
so that
$\mu '\in F_m$
so that
![]() $|\mu '(v_j)-\nu (v_j)|<\varepsilon $
for every
$|\mu '(v_j)-\nu (v_j)|<\varepsilon $
for every
![]() $j\leq l$
.
$j\leq l$
.
Let
![]() $L\in \mathbb {N}$
,
$L\in \mathbb {N}$
,
![]() $L\geq |\gamma |$
, be such that
$L\geq |\gamma |$
, be such that
![]() $v_1,\ldots ,v_l\in \operatorname {span}\{e_i\colon i\leq L\}$
. Since
$v_1,\ldots ,v_l\in \operatorname {span}\{e_i\colon i\leq L\}$
. Since
![]() $\varphi |_{\{1,\ldots ,L\}}\supseteq \gamma $
, we may pick
$\varphi |_{\{1,\ldots ,L\}}\supseteq \gamma $
, we may pick
![]() $\mu '\in \mathbb {M}^{\varphi |_{\{1,\ldots ,L\}}}_\mu \cap F_m$
. Then
$\mu '\in \mathbb {M}^{\varphi |_{\{1,\ldots ,L\}}}_\mu \cap F_m$
. Then
 $$\begin{align*}\mu'\Big(\sum_{i=1}^L a_i e_i\Big) = \mu\Big(\sum_{i=1}^L a_i e_{\varphi(i)}\Big) = \nu\Big(\sum_{i=1}^L a_i e_i\Big),\quad (a_i)_{i=1}^L\in\mathbb{Q}^L. \end{align*}$$
$$\begin{align*}\mu'\Big(\sum_{i=1}^L a_i e_i\Big) = \mu\Big(\sum_{i=1}^L a_i e_{\varphi(i)}\Big) = \nu\Big(\sum_{i=1}^L a_i e_i\Big),\quad (a_i)_{i=1}^L\in\mathbb{Q}^L. \end{align*}$$
In particular,
![]() $\mu '(v_j)=\nu (v_j)$
,
$\mu '(v_j)=\nu (v_j)$
,
![]() $j\leq l$
, as desired.
$j\leq l$
, as desired.
In the remainder of this section, we head towards the proof of Theorem 2.12. Following [Reference Johnson, Lindenstrauss and Schechtman33], we say that an increasing sequence
![]() $E_1\subseteq E_2\subseteq \ldots $
of finite-dimensional subspaces of a separable Banach space X whose union is dense is a paving of X. A separable Banach space X is determined by its pavings if whenever Y is a Banach space for which there are pavings
$E_1\subseteq E_2\subseteq \ldots $
of finite-dimensional subspaces of a separable Banach space X whose union is dense is a paving of X. A separable Banach space X is determined by its pavings if whenever Y is a Banach space for which there are pavings
![]() $\{E_n\}_{n=1}^\infty $
of X and
$\{E_n\}_{n=1}^\infty $
of X and
![]() $\{F_n\}_{n=1}^\infty $
of Y with
$\{F_n\}_{n=1}^\infty $
of Y with
![]() $\sup _{n\in \mathbb {N}}d_{BM}(E_n,F_n)<\infty $
, then Y is isomorphic to X. We refer the reader to [Reference Johnson, Lindenstrauss and Schechtman33] for details and examples.
$\sup _{n\in \mathbb {N}}d_{BM}(E_n,F_n)<\infty $
, then Y is isomorphic to X. We refer the reader to [Reference Johnson, Lindenstrauss and Schechtman33] for details and examples.
We start with a theorem that is interesting on its own.
Theorem 2.13. Let X be a separable infinite-dimensional Banach space,
![]() $\{E_n\}_{n=1}^\infty $
a paving of X and
$\{E_n\}_{n=1}^\infty $
a paving of X and
![]() $\lambda \geq 1$
. Then the set
$\lambda \geq 1$
. Then the set
 $$\begin{align*}\begin{aligned} \mathcal{Z}:=\big\{\mu\in\mathcal{P}\colon & \text{for every } \varepsilon>0, \text{ there is a paving } \{F_k\}_{k=1}^\infty \text{ of } X_\mu \text{ and an increasing } \\ & \text{sequence } (n_k)_{k=1}^\infty\in \mathbb{N}^{\mathbb{N}} \text{ with } \sup _{k\in\mathbb{N}}d_{BM}(F_k,E_{n_k})\leq \lambda+\varepsilon\big\} \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \mathcal{Z}:=\big\{\mu\in\mathcal{P}\colon & \text{for every } \varepsilon>0, \text{ there is a paving } \{F_k\}_{k=1}^\infty \text{ of } X_\mu \text{ and an increasing } \\ & \text{sequence } (n_k)_{k=1}^\infty\in \mathbb{N}^{\mathbb{N}} \text{ with } \sup _{k\in\mathbb{N}}d_{BM}(F_k,E_{n_k})\leq \lambda+\varepsilon\big\} \end{aligned} \end{align*}$$
is a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
In the proof, we will need the following observation, which is well-known and easy to prove. We use the formulation from [Reference Cúth, Doležal, Doucha and Kurka14, Lemma 4.3].
Lemma 2.14. Given a basis
![]() $\mathfrak {b}_E = \{e_1,\ldots ,e_n\}$
of a finite-dimensional Banach space E, there is
$\mathfrak {b}_E = \{e_1,\ldots ,e_n\}$
of a finite-dimensional Banach space E, there is
![]() $C>0$
and a function
$C>0$
and a function
![]() $\phi _2^{\mathfrak {b}_E}:[0,C)\to [0,\infty )$
continuous at zero with
$\phi _2^{\mathfrak {b}_E}:[0,C)\to [0,\infty )$
continuous at zero with
![]() $\phi _2^{\mathfrak {b}_E}(0)=0$
, such that whenever X is a Banach space with
$\phi _2^{\mathfrak {b}_E}(0)=0$
, such that whenever X is a Banach space with
![]() $E\subseteq X$
and
$E\subseteq X$
and
![]() $\{x_i:\; i\leq n\}\subseteq X$
are such that
$\{x_i:\; i\leq n\}\subseteq X$
are such that
![]() $\|x_i-e_i\|<\varepsilon $
,
$\|x_i-e_i\|<\varepsilon $
,
![]() $i\leq n$
, for some
$i\leq n$
, for some
![]() $\varepsilon <C$
, then the linear operator
$\varepsilon <C$
, then the linear operator
![]() $T:E\to X$
given by
$T:E\to X$
given by
![]() $T(e_i):=x_i$
is a
$T(e_i):=x_i$
is a
![]() $(1+\phi _2^{\mathfrak {b}_E}(\varepsilon ))$
-isomorphism and
$(1+\phi _2^{\mathfrak {b}_E}(\varepsilon ))$
-isomorphism and
![]() $\|T-Id_E\|\leq \phi _2^{\mathfrak {b}_E}(\varepsilon )$
.
$\|T-Id_E\|\leq \phi _2^{\mathfrak {b}_E}(\varepsilon )$
.
Proof of Theorem 2.13.
For each
![]() $E_n$
,
$E_n$
,
![]() $n\in \mathbb {N}$
, we fix its basis (which will be used only in order to know what
$n\in \mathbb {N}$
, we fix its basis (which will be used only in order to know what
![]() $Z{\stackrel {K}{\sim } E_n}$
means for a finite-dimensional space Z and
$Z{\stackrel {K}{\sim } E_n}$
means for a finite-dimensional space Z and
![]() $K>1$
). For each finite tuple
$K>1$
). For each finite tuple
![]() $\vec v$
of elements from V, we set
$\vec v$
of elements from V, we set
![]() $S_{\vec v}$
to be the set of all finite tuples
$S_{\vec v}$
to be the set of all finite tuples
![]() $\vec w$
,
$\vec w$
,
![]() $\mathbb {Q}$
-linearly independent in V, such that each element of
$\mathbb {Q}$
-linearly independent in V, such that each element of
![]() $\vec v$
(considered as an element of
$\vec v$
(considered as an element of
![]() $c_{00}$
) lies in
$c_{00}$
) lies in
![]() $\operatorname {span}\vec w$
. For
$\operatorname {span}\vec w$
. For
![]() $m\in \mathbb {N}$
and a finite tuple
$m\in \mathbb {N}$
and a finite tuple
![]() $\vec v$
of elements from V, we set
$\vec v$
of elements from V, we set
 $$\begin{align*}\begin{aligned} P(\vec v,m):=\big\{\mu\in\mathcal{P}\colon & \text{if } \mu \text{ restricted to }\operatorname{span}\{v_1,\ldots,v_{|\vec v|}\}\subseteq c_{00}\text{ is a norm, then }\\ & \text{there exist } \vec w\in S_{\vec v} \text{ and } n\in\mathbb{N}, \text{ such that }\\ &\mu\text{ restricted to }\operatorname{span}\{w_1,\ldots,w_{|\vec w|}\}\subseteq c_{00}\text{ is a norm and }\\ & (((\operatorname{span}\{w_1,\ldots,w_{|\vec w|}\},\mu),\vec w){\stackrel{\sqrt{\lambda + \frac{1}{m}}}{\sim} E_{n}})\big\}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} P(\vec v,m):=\big\{\mu\in\mathcal{P}\colon & \text{if } \mu \text{ restricted to }\operatorname{span}\{v_1,\ldots,v_{|\vec v|}\}\subseteq c_{00}\text{ is a norm, then }\\ & \text{there exist } \vec w\in S_{\vec v} \text{ and } n\in\mathbb{N}, \text{ such that }\\ &\mu\text{ restricted to }\operatorname{span}\{w_1,\ldots,w_{|\vec w|}\}\subseteq c_{00}\text{ is a norm and }\\ & (((\operatorname{span}\{w_1,\ldots,w_{|\vec w|}\},\mu),\vec w){\stackrel{\sqrt{\lambda + \frac{1}{m}}}{\sim} E_{n}})\big\}. \end{aligned} \end{align*}$$
Then, using the observation that
![]() $\{\mu \in \mathcal {P}\colon \mu \text { restricted to }\operatorname {span}\{v_1,\ldots ,v_{|\vec v|}\}\subseteq c_{00}\text { is a norm}\}$
is open due to Lemma 1.5,
$\{\mu \in \mathcal {P}\colon \mu \text { restricted to }\operatorname {span}\{v_1,\ldots ,v_{|\vec v|}\}\subseteq c_{00}\text { is a norm}\}$
is open due to Lemma 1.5,
![]() $P(\vec v,m)$
is the union of a closed and an open set, so it is a
$P(\vec v,m)$
is the union of a closed and an open set, so it is a
![]() $G_\delta $
-set.
$G_\delta $
-set.
Denote by
![]() $LI$
the set of all finite tuples
$LI$
the set of all finite tuples
![]() $\vec v = (v_1,\ldots ,v_{|\vec v|})$
of elements from V, which are linearly independent in
$\vec v = (v_1,\ldots ,v_{|\vec v|})$
of elements from V, which are linearly independent in
![]() $c_{00}$
. We now set
$c_{00}$
. We now set
which is clearly a
![]() $G_{\delta }$
-set. We shall prove that
$G_{\delta }$
-set. We shall prove that
![]() $\mathcal {G}=\mathcal {Z}$
.
$\mathcal {G}=\mathcal {Z}$
.
If
![]() $\mu \in \mathcal {G}$
, it is clear that for every m, we can recursively build an increasing sequence
$\mu \in \mathcal {G}$
, it is clear that for every m, we can recursively build an increasing sequence
![]() $\{F_k\}_{k=1}^\infty $
of finite-dimensional subspaces whose union is dense in
$\{F_k\}_{k=1}^\infty $
of finite-dimensional subspaces whose union is dense in
![]() $X_\mu $
, such that we have
$X_\mu $
, such that we have
![]() $d_{BM}(F_k,E_{n_k})\leq \lambda + \frac {1}{m}$
for every
$d_{BM}(F_k,E_{n_k})\leq \lambda + \frac {1}{m}$
for every
![]() $k\in \mathbb {N}$
. It follows that
$k\in \mathbb {N}$
. It follows that
![]() $\mu \in \mathcal {Z}$
.
$\mu \in \mathcal {Z}$
.
On the other hand, pick
![]() $\mu \in \mathcal {Z}$
. In what follows for
$\mu \in \mathcal {Z}$
. In what follows for
![]() $x\in c_{00}$
, we denote by
$x\in c_{00}$
, we denote by
![]() $[x]\in X_\mu $
the equivalence class corresponding to x. Pick some
$[x]\in X_\mu $
the equivalence class corresponding to x. Pick some
![]() $m\in \mathbb {N}$
and an n-tuple
$m\in \mathbb {N}$
and an n-tuple
![]() $\vec v\in LI$
, such that
$\vec v\in LI$
, such that
![]() $\mu $
restricted to
$\mu $
restricted to
![]() $\operatorname {span}\{v_1,\ldots ,v_n\}\subseteq c_{00}$
is a norm, so
$\operatorname {span}\{v_1,\ldots ,v_n\}\subseteq c_{00}$
is a norm, so
![]() $\{v_1,\ldots ,v_n\}$
is a basis of
$\{v_1,\ldots ,v_n\}$
is a basis of
![]() $\operatorname {span}\{v_1,\ldots ,v_n\}$
. Pick
$\operatorname {span}\{v_1,\ldots ,v_n\}$
. Pick
![]() $\lambda '\in (\lambda ,\lambda + \tfrac {1}{m})$
and
$\lambda '\in (\lambda ,\lambda + \tfrac {1}{m})$
and
![]() $\delta>1$
with
$\delta>1$
with
![]() $\delta \lambda '<\lambda + \frac {1}{m}$
. Since
$\delta \lambda '<\lambda + \frac {1}{m}$
. Since
![]() $\mu \in \mathcal {Z}$
, there is an increasing sequence
$\mu \in \mathcal {Z}$
, there is an increasing sequence
![]() $\{F_k\}_{k=1}^\infty $
of finite-dimensional subspaces whose union is dense in
$\{F_k\}_{k=1}^\infty $
of finite-dimensional subspaces whose union is dense in
![]() $X_\mu $
, such that
$X_\mu $
, such that
![]() $\sup _{k\in \mathbb {N}}d_{BM}(F_k,E_{n_k})\leq \lambda '$
. By [Reference Lacey38, Section 17, Theorem 6], we can find a finite dimensional subspace
$\sup _{k\in \mathbb {N}}d_{BM}(F_k,E_{n_k})\leq \lambda '$
. By [Reference Lacey38, Section 17, Theorem 6], we can find a finite dimensional subspace
![]() $\operatorname {span}\{[v_1],\ldots ,[v_n]\}\subseteq Y\subseteq X_\mu $
and
$\operatorname {span}\{[v_1],\ldots ,[v_n]\}\subseteq Y\subseteq X_\mu $
and
![]() $k\in \mathbb {N}$
, such that
$k\in \mathbb {N}$
, such that
![]() $d_{BM}(Y,F_k)\leq \delta $
so
$d_{BM}(Y,F_k)\leq \delta $
so
![]() $d_{BM}(Y,E_{n_k})\leq \delta \lambda '$
. Select
$d_{BM}(Y,E_{n_k})\leq \delta \lambda '$
. Select
![]() $y_{n+1},\ldots , y_{\dim Y}\in Y$
, such that
$y_{n+1},\ldots , y_{\dim Y}\in Y$
, such that
![]() $\mathfrak {b} = \{[v_1],\ldots , [v_n], y_{n+1},\ldots , y_{\dim Y}\}$
is a basis of Y. Let
$\mathfrak {b} = \{[v_1],\ldots , [v_n], y_{n+1},\ldots , y_{\dim Y}\}$
is a basis of Y. Let
![]() $\phi _2^{\mathfrak {b}}$
be the function from Lemma 2.14, and let
$\phi _2^{\mathfrak {b}}$
be the function from Lemma 2.14, and let
![]() $\eta>0$
be such that
$\eta>0$
be such that
![]() $\delta \lambda '(1+\phi _2^{\mathfrak {b}}(\eta ))^2<\lambda +\frac {1}{m}$
. Further, for every
$\delta \lambda '(1+\phi _2^{\mathfrak {b}}(\eta ))^2<\lambda +\frac {1}{m}$
. Further, for every
![]() $n+1\leq i\leq \dim Y$
, pick
$n+1\leq i\leq \dim Y$
, pick
![]() $v_i\in V$
with
$v_i\in V$
with
![]() $\|[v_i]-y_i\|_{X_\mu }<\eta $
. Then
$\|[v_i]-y_i\|_{X_\mu }<\eta $
. Then
![]() $(\mu ,[v_1],\ldots ,[v_{\dim Y}]){\stackrel {1+\phi _2^{\mathfrak {b}}(\eta )}{\sim } Y}$
so
$(\mu ,[v_1],\ldots ,[v_{\dim Y}]){\stackrel {1+\phi _2^{\mathfrak {b}}(\eta )}{\sim } Y}$
so
![]() $\mu $
restricted to
$\mu $
restricted to
![]() $\operatorname {span}\{v_1,\ldots ,v_{\dim Y}\}\subseteq c_{00}$
is a norm and
$\operatorname {span}\{v_1,\ldots ,v_{\dim Y}\}\subseteq c_{00}$
is a norm and
![]() $\operatorname {span}\{[v_1],\ldots ,[v_{\dim Y}]\}\subseteq X_\mu $
is isometric to
$\operatorname {span}\{[v_1],\ldots ,[v_{\dim Y}]\}\subseteq X_\mu $
is isometric to
![]() $(\operatorname {span}\{v_1,\ldots ,v_{\dim Y}\},\mu )$
. Since
$(\operatorname {span}\{v_1,\ldots ,v_{\dim Y}\},\mu )$
. Since
![]() $d_{BM}((\operatorname {span}\{v_1,\ldots ,v_{\dim Y}\},\mu ),E_{n_k})<\delta \lambda '\cdot (1+\phi _2^{\mathfrak {b}}(\eta ))^2<\lambda + \frac {1}{m}$
, there exists a surjective isomorphism
$d_{BM}((\operatorname {span}\{v_1,\ldots ,v_{\dim Y}\},\mu ),E_{n_k})<\delta \lambda '\cdot (1+\phi _2^{\mathfrak {b}}(\eta ))^2<\lambda + \frac {1}{m}$
, there exists a surjective isomorphism
![]() $T:E_{n_k}\to (\operatorname {span}\{v_1,\ldots ,v_{\dim Y}\},\mu )$
with
$T:E_{n_k}\to (\operatorname {span}\{v_1,\ldots ,v_{\dim Y}\},\mu )$
with
![]() $\max \{\|T\|,\|T^{-1}\|\}<\sqrt {\lambda + \frac {1}{m}}$
. By Lemma 2.14, we may without loss of generality assume that
$\max \{\|T\|,\|T^{-1}\|\}<\sqrt {\lambda + \frac {1}{m}}$
. By Lemma 2.14, we may without loss of generality assume that
![]() $w_i:=T(e_i)\in V$
for every
$w_i:=T(e_i)\in V$
for every
![]() $i\leq \dim Y$
. Then
$i\leq \dim Y$
. Then
![]() $\mu $
restricted to
$\mu $
restricted to
![]() $\operatorname {span}\{w_1,\ldots ,w_{\dim Y}\}\subseteq c_{00}$
is a norm,
$\operatorname {span}\{w_1,\ldots ,w_{\dim Y}\}\subseteq c_{00}$
is a norm,
![]() $\vec w\in S_{\vec v}$
and
$\vec w\in S_{\vec v}$
and
![]() $((\mu ,\vec w){\stackrel {\sqrt {\lambda + \frac {1}{m}}}{\sim } E_{n_k}})$
.
$((\mu ,\vec w){\stackrel {\sqrt {\lambda + \frac {1}{m}}}{\sim } E_{n_k}})$
.
Proof of Theorem 2.12.
Pick a paving
![]() $\{E_n\}_{n=1}^\infty $
of X. It is easy to see that for every
$\{E_n\}_{n=1}^\infty $
of X. It is easy to see that for every
![]() $\mu \in \mathcal {P}_\infty $
, the Banach space
$\mu \in \mathcal {P}_\infty $
, the Banach space
![]() $X_\mu $
is isomorphic to X if and only if
$X_\mu $
is isomorphic to X if and only if
![]() $\mu $
belongs to the set
$\mu $
belongs to the set
![]() $\mathcal {Z}$
from Theorem 2.13 for some
$\mathcal {Z}$
from Theorem 2.13 for some
![]() $\lambda \geq 1$
. The ‘In particular’ part follows, since
$\lambda \geq 1$
. The ‘In particular’ part follows, since
![]() $\mathcal {P}_\infty $
is a
$\mathcal {P}_\infty $
is a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {P}$
. For admissible topologies, the result follows by applying [Reference Cúth, Doležal, Doucha and Kurka14, Theorem 3.3].
$\mathcal {P}$
. For admissible topologies, the result follows by applying [Reference Cúth, Doležal, Doucha and Kurka14, Theorem 3.3].
3 Spaces with
 $G_\delta $
isometry classes
$G_\delta $
isometry classes
In this section, we investigate Banach spaces whose isometry classes are
![]() $G_\delta $
-sets, or even
$G_\delta $
-sets, or even
![]() $G_\delta $
-complete sets. The main results here are Theorems 3.3, 3.4 and 3.6, which imply the first and the last part of Theorem B.
$G_\delta $
-complete sets. The main results here are Theorems 3.3, 3.4 and 3.6, which imply the first and the last part of Theorem B.
Besides
![]() $\ell _2$
, whose isometry class is actually closed, we have already mentioned in Theorem 1.10 that the isometry class of the Gurariı̆ space is a
$\ell _2$
, whose isometry class is actually closed, we have already mentioned in Theorem 1.10 that the isometry class of the Gurariı̆ space is a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {P}_\infty $
and
$\mathcal {P}_\infty $
and
![]() $\mathcal {B}$
. We start the section with some basic corollaries of that result; in particular, that the isometry class of
$\mathcal {B}$
. We start the section with some basic corollaries of that result; in particular, that the isometry class of
![]() $\mathbb {G}$
is even a
$\mathbb {G}$
is even a
![]() $G_\delta $
-complete set.
$G_\delta $
-complete set.
Since for any separable infinite-dimensional Banach space X we obviously have
![]() ${\langle X\rangle _{\equiv }^{\mathcal {B}}} = {\langle X\rangle _{\equiv }^{\mathcal {P}_\infty }}\cap \mathcal {B}$
, it is sufficient to formulate our positive results in the coding of
${\langle X\rangle _{\equiv }^{\mathcal {B}}} = {\langle X\rangle _{\equiv }^{\mathcal {P}_\infty }}\cap \mathcal {B}$
, it is sufficient to formulate our positive results in the coding of
![]() $\mathcal {P}_\infty $
and negative results in the coding of
$\mathcal {P}_\infty $
and negative results in the coding of
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
Lemma 3.1. Let X, Y be separable infinite-dimensional Banach spaces, such that X is finitely representable in Y and Y is finitely representable in X. If
![]() ${\langle X\rangle _{\equiv }}$
is a
${\langle X\rangle _{\equiv }}$
is a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $X\not \equiv Y$
, then
$X\not \equiv Y$
, then
-
(i)
 ${\langle Y\rangle _{\equiv }}$
is not a
${\langle Y\rangle _{\equiv }}$
is not a
 $G_\delta $
-set in
$G_\delta $
-set in
 $\mathcal {B}$
.
$\mathcal {B}$
. -
(ii)
 ${\langle X\rangle _{\equiv }}$
is a
${\langle X\rangle _{\equiv }}$
is a
 $G_\delta $
-complete set in
$G_\delta $
-complete set in
 $\mathcal {B}$
.
$\mathcal {B}$
.
Proof. Recall that by Proposition 1.8, we have that both
![]() ${\langle X\rangle _{\equiv }}$
and
${\langle X\rangle _{\equiv }}$
and
![]() ${\langle Y\rangle _{\equiv }}$
are dense in
${\langle Y\rangle _{\equiv }}$
are dense in
(i): If both
![]() ${\langle X\rangle _{\equiv }}$
and
${\langle X\rangle _{\equiv }}$
and
![]() ${\langle Y\rangle _{\equiv }}$
are
${\langle Y\rangle _{\equiv }}$
are
![]() $G_\delta $
-sets, by the Baire theorem, we have that
$G_\delta $
-sets, by the Baire theorem, we have that
![]() ${\langle X\rangle _{\equiv }}\cap {\langle Y\rangle _{\equiv }}$
is comeager in N. Thus, the intersection cannot be an empty set, and we obtain
${\langle X\rangle _{\equiv }}\cap {\langle Y\rangle _{\equiv }}$
is comeager in N. Thus, the intersection cannot be an empty set, and we obtain
![]() $X\equiv Y$
.
$X\equiv Y$
.
(ii): Since
![]() $X\not \equiv Y$
, we have that
$X\not \equiv Y$
, we have that
![]() ${\langle X\rangle _{\equiv }}$
has empty interior in N. But it is also comeager in N, and so it cannot be
${\langle X\rangle _{\equiv }}$
has empty interior in N. But it is also comeager in N, and so it cannot be
![]() $F_\sigma $
. Therefore, it is a
$F_\sigma $
. Therefore, it is a
![]() $G_\delta $
-complete set by Lemma 1.1.
$G_\delta $
-complete set by Lemma 1.1.
Corollary 3.2.
![]() $\mathbb {G}$
is the only isometrically universal separable Banach space whose isometry class is a
$\mathbb {G}$
is the only isometrically universal separable Banach space whose isometry class is a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {B}$
. The same holds if we replace
$\mathcal {B}$
. The same holds if we replace
![]() $\mathcal {B}$
by
$\mathcal {B}$
by
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Moreover,
![]() ${\langle \mathbb {G\rangle _{\equiv }}}$
is a
${\langle \mathbb {G\rangle _{\equiv }}}$
is a
![]() $G_\delta $
-complete set in both
$G_\delta $
-complete set in both
![]() $\mathcal {P}_\infty $
and
$\mathcal {P}_\infty $
and
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
Proof. By Theorem 1.10, the isometry class of
![]() $\mathbb {G}$
is a
$\mathbb {G}$
is a
![]() $G_\delta $
-set. Let X be an isometrically universal separable Banach space. By Lemma 3.1, if
$G_\delta $
-set. Let X be an isometrically universal separable Banach space. By Lemma 3.1, if
![]() $X\not \equiv \mathbb {G}$
, then
$X\not \equiv \mathbb {G}$
, then
![]() ${\langle X\rangle _{\equiv }^{\mathcal {B}}}$
is not a
${\langle X\rangle _{\equiv }^{\mathcal {B}}}$
is not a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {B}$
(and so neither in
$\mathcal {B}$
(and so neither in
![]() $\mathcal {P}_\infty $
).
$\mathcal {P}_\infty $
).
For the ‘moreover’ part, we use Lemma 3.1 and any Banach space X not isometric to
![]() $\mathbb {G}$
that is finitely representable in
$\mathbb {G}$
that is finitely representable in
![]() $\mathbb {G}$
and vice versa (e.g. any other universal separable Banach space or
$\mathbb {G}$
and vice versa (e.g. any other universal separable Banach space or
![]() $c_0$
).
$c_0$
).
The same proof gives us actually the following strengthening. Let us recall that by Maurey–Pisier theorem, see [Reference Maurey and Pisier43] or [Reference Albiac and Kalton1, Theorem 12.3.14], a Banach space X has no nontrivial cotype if and only if
![]() $\ell _\infty $
is finitely-representable in X (and yet equivalently,
$\ell _\infty $
is finitely-representable in X (and yet equivalently,
![]() $c_0$
is finitely-representable in X).
$c_0$
is finitely-representable in X).
Theorem 3.3.
![]() $\mathbb {G}$
is the only separable Banach space with no nontrivial cotype whose isometry class is a
$\mathbb {G}$
is the only separable Banach space with no nontrivial cotype whose isometry class is a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {B}$
. The same holds if we replace
$\mathcal {B}$
. The same holds if we replace
![]() $\mathcal {B}$
by
$\mathcal {B}$
by
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Proof. Any separable Banach space is finitely representable in
![]() $c_0$
, so by Lemma 3.1, there is at most one Banach space X, such that
$c_0$
, so by Lemma 3.1, there is at most one Banach space X, such that
![]() $c_0$
is finitely representable in X and
$c_0$
is finitely representable in X and
![]() ${\langle X\rangle _{\equiv }}$
is a
${\langle X\rangle _{\equiv }}$
is a
![]() $G_\delta $
-set. By Theorem 1.10,
$G_\delta $
-set. By Theorem 1.10,
![]() ${\langle \mathbb {G\rangle _{\equiv }}}$
is a
${\langle \mathbb {G\rangle _{\equiv }}}$
is a
![]() $G_\delta $
-set.
$G_\delta $
-set.
3.1
 $L_p$
-spaces
$L_p$
-spaces
Let us recall that a Banach space X is said to be an
![]() $\mathcal {L}_{p,\lambda }$
-space (with
$\mathcal {L}_{p,\lambda }$
-space (with
![]() $1\leq p\leq \infty $
and
$1\leq p\leq \infty $
and
![]() $\lambda \geq 1$
) if every finite-dimensional subspace of X is contained in another finite-dimensional subspace of X whose Banach-Mazur distance
$\lambda \geq 1$
) if every finite-dimensional subspace of X is contained in another finite-dimensional subspace of X whose Banach-Mazur distance
![]() $d_{BM}$
to the corresponding
$d_{BM}$
to the corresponding
![]() $\ell _p^n$
is at most
$\ell _p^n$
is at most
![]() $\lambda $
. A space X is said to be an
$\lambda $
. A space X is said to be an
![]() $\mathcal {L}_{p}$
-space, respectively,
$\mathcal {L}_{p}$
-space, respectively,
![]() $\mathcal {L}_{p,\lambda +}$
-space, if it is an
$\mathcal {L}_{p,\lambda +}$
-space, if it is an
![]() $\mathcal {L}_{p,\lambda '}$
-space for some
$\mathcal {L}_{p,\lambda '}$
-space for some
![]() $\lambda '\geq 1$
, respectively, for every
$\lambda '\geq 1$
, respectively, for every
![]() $\lambda '>\lambda $
.
$\lambda '>\lambda $
.
The main result of this subsection is the following.
Theorem 3.4. For every
![]() $1\leq p<\infty $
,
$1\leq p<\infty $
,
![]() $p\neq 2$
, the isometry class of
$p\neq 2$
, the isometry class of
![]() $L_p[0,1]$
is a
$L_p[0,1]$
is a
![]() $G_\delta $
-complete set in
$G_\delta $
-complete set in
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Moreover,
![]() $L_p[0,1]$
is the only separable
$L_p[0,1]$
is the only separable
![]() $\mathcal {L}_{p,1+}$
-space whose isometry class is a
$\mathcal {L}_{p,1+}$
-space whose isometry class is a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {B}$
, and the same holds if we replace
$\mathcal {B}$
, and the same holds if we replace
![]() $\mathcal {B}$
by
$\mathcal {B}$
by
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Remark 3.5. It is easy to see (e.g. using [Reference Lacey38, Section 17, Theorem 6]) that for every
![]() $p\in [1,\infty ]$
and
$p\in [1,\infty ]$
and
![]() $\lambda \geq 1$
, we have that a separable infinite-dimensional Banach space Y is an
$\lambda \geq 1$
, we have that a separable infinite-dimensional Banach space Y is an
![]() $\mathcal {L}_{p,\lambda +}$
-space if and only if, for every
$\mathcal {L}_{p,\lambda +}$
-space if and only if, for every
![]() $\varepsilon>0$
, there is an increasing sequence
$\varepsilon>0$
, there is an increasing sequence
![]() $\{F_k\}_{k=1}^\infty $
of finite-dimensional subspaces whose union is dense in Y, such that
$\{F_k\}_{k=1}^\infty $
of finite-dimensional subspaces whose union is dense in Y, such that
![]() $d_{BM}(\ell _p^{\dim F_k},F_k)\leq \lambda +\varepsilon $
for every
$d_{BM}(\ell _p^{\dim F_k},F_k)\leq \lambda +\varepsilon $
for every
![]() $k\in \mathbb {N}$
.
$k\in \mathbb {N}$
.
The next theorem is a crucial step in proving Theorem 3.4. However, it is also of independent interest, and its corollary improves the related result from [Reference Godefroy and Saint-Raymond28].
Theorem 3.6. Let
![]() $1\leq p\leq \infty $
and
$1\leq p\leq \infty $
and
![]() $\lambda \geq 1$
. The class of separable infinite-dimensional
$\lambda \geq 1$
. The class of separable infinite-dimensional
![]() $\mathcal {L}_{p,\lambda +}$
-spaces is a
$\mathcal {L}_{p,\lambda +}$
-spaces is a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {P}$
. In particular, the class of separable infinite-dimensional
$\mathcal {P}$
. In particular, the class of separable infinite-dimensional
![]() $\mathcal {L}_{p,\lambda +}$
-spaces is a
$\mathcal {L}_{p,\lambda +}$
-spaces is a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Note that for
![]() $1\leq p\leq \infty $
, the class of
$1\leq p\leq \infty $
, the class of
![]() $\mathcal {L}_p$
-spaces is obtained as the union
$\mathcal {L}_p$
-spaces is obtained as the union
![]() $\bigcup _{\lambda \geq 1} \mathcal {L}_{p,\lambda +}$
. It is shown in [Reference Godefroy and Saint-Raymond28, Proposition 4.5] that the class of separable
$\bigcup _{\lambda \geq 1} \mathcal {L}_{p,\lambda +}$
. It is shown in [Reference Godefroy and Saint-Raymond28, Proposition 4.5] that the class of separable
![]() $\mathcal {L}_p$
-spaces is a
$\mathcal {L}_p$
-spaces is a
![]() $\boldsymbol {\Sigma }_4^0$
-set in an admissible topology. It is immediate from Theorem 3.6 (and using [Reference Cúth, Doležal, Doucha and Kurka14, Theorem 3.3]) that we have a better estimate.
$\boldsymbol {\Sigma }_4^0$
-set in an admissible topology. It is immediate from Theorem 3.6 (and using [Reference Cúth, Doležal, Doucha and Kurka14, Theorem 3.3]) that we have a better estimate.
Corollary 3.7. For every
![]() $1\leq p\leq \infty $
, the class of separable
$1\leq p\leq \infty $
, the class of separable
![]() $\mathcal {L}_p$
-spaces is a
$\mathcal {L}_p$
-spaces is a
![]() $G_{\delta \sigma }$
-set in
$G_{\delta \sigma }$
-set in
![]() $\mathcal {P}$
and any admissible topology.
$\mathcal {P}$
and any admissible topology.
Proof. Note that any finite-dimensional space is an
![]() $\mathcal {L}_p$
-space, so the class of separable
$\mathcal {L}_p$
-space, so the class of separable
![]() $\mathcal {L}_p$
-spaces may be written as the union of
$\mathcal {L}_p$
-spaces may be written as the union of
![]() $\mathcal {P}\setminus \mathcal {P}_\infty $
(which is an
$\mathcal {P}\setminus \mathcal {P}_\infty $
(which is an
![]() $F_\sigma $
-set by [Reference Cúth, Doležal, Doucha and Kurka14, Corollary 2.5]) and
$F_\sigma $
-set by [Reference Cúth, Doležal, Doucha and Kurka14, Corollary 2.5]) and
![]() $\{\mu \in \mathcal {P}_\infty \colon X_\mu \text { is an } \mathcal {L}_p\text {-space}\}$
(which is
$\{\mu \in \mathcal {P}_\infty \colon X_\mu \text { is an } \mathcal {L}_p\text {-space}\}$
(which is
![]() $G_{\delta \sigma }$
-set by Theorem 3.6 above).
$G_{\delta \sigma }$
-set by Theorem 3.6 above).
Let us recall the following classical result.
Theorem 3.8 (Lindenstrauss, Pełczyński).
For every
![]() $1\leq p<\infty $
and a separable infinite-dimensional Banach space X, the following assertions are equivalent.
$1\leq p<\infty $
and a separable infinite-dimensional Banach space X, the following assertions are equivalent.
-
• X is an
 $\mathcal {L}_{p,1+}$
-space.
$\mathcal {L}_{p,1+}$
-space. -
• X is isometric to a separable
 $L_p(\mu )$
space for some measure
$L_p(\mu )$
space for some measure
 $\mu $
.
$\mu $
. -
• X is isometric to one of the following spaces
 $$\begin{align*}L_p[0,1],\quad L_p[0,1]\oplus_p \ell_p,\quad \ell_p,\quad L_p[0,1]\oplus_p \ell_p^n\; \text{ (for some }n\in\mathbb{N}). \end{align*}$$
$$\begin{align*}L_p[0,1],\quad L_p[0,1]\oplus_p \ell_p,\quad \ell_p,\quad L_p[0,1]\oplus_p \ell_p^n\; \text{ (for some }n\in\mathbb{N}). \end{align*}$$
Proof. By [Reference Lindenstrauss and Pełczyński41, Section 7, Corollaries 4 and 5], a separable Banach space is an
![]() $\mathcal {L}_{p,1+}$
-space if and only if it is isometric to an
$\mathcal {L}_{p,1+}$
-space if and only if it is isometric to an
![]() $L_p(\mu )$
space for some measure
$L_p(\mu )$
space for some measure
![]() $\mu $
. Finally, note that every separable infinite-dimensional
$\mu $
. Finally, note that every separable infinite-dimensional
![]() $L_p(\mu )$
space is isometric to one of the spaces mentioned above (see, e.g. [Reference Albiac and Kalton1, pages 137–138]).
$L_p(\mu )$
space is isometric to one of the spaces mentioned above (see, e.g. [Reference Albiac and Kalton1, pages 137–138]).
Recall that given a finite sequence
![]() $(z_n)_{n\in N}$
in a Banach space Z, the symbol
$(z_n)_{n\in N}$
in a Banach space Z, the symbol
![]() $(z_n){\stackrel {K}{\sim } \ell _p^N}$
means that
$(z_n){\stackrel {K}{\sim } \ell _p^N}$
means that
![]() $K^{-1}\left (\sum _{i\in N}|a_i|^p\right )^{1/p} < \|\sum _{i\in N} a_i z_i\| < K\left (\sum _{i\in N}|a_i|^p\right )^{1/p}$
for every
$K^{-1}\left (\sum _{i\in N}|a_i|^p\right )^{1/p} < \|\sum _{i\in N} a_i z_i\| < K\left (\sum _{i\in N}|a_i|^p\right )^{1/p}$
for every
![]() $a\in c_{00}^N$
. If
$a\in c_{00}^N$
. If
![]() $(z_n)$
is isometrically equivalent to the
$(z_n)$
is isometrically equivalent to the
![]() $\ell _p^N$
basis (that is,
$\ell _p^N$
basis (that is,
![]() $(z_n){\stackrel {1+\varepsilon }{\sim } \ell _p^N}$
for every
$(z_n){\stackrel {1+\varepsilon }{\sim } \ell _p^N}$
for every
![]() $\varepsilon> 0$
), we write
$\varepsilon> 0$
), we write
![]() $(z_n)\equiv \ell _p^N$
.
$(z_n)\equiv \ell _p^N$
.
Theorem 3.9. Let
![]() $1\leq p<\infty $
,
$1\leq p<\infty $
,
![]() $p\neq 2$
, and let X be a separable infinite-dimensional
$p\neq 2$
, and let X be a separable infinite-dimensional
![]() $\mathcal {L}_{p,1+}$
space. Then the following assertions are equivalent.
$\mathcal {L}_{p,1+}$
space. Then the following assertions are equivalent.
-
(i) X is isometric to
 $L_p[0,1]$
.
$L_p[0,1]$
. -
(ii) For every
 $x\in S_X$
, the following condition is satisfied
$x\in S_X$
, the following condition is satisfied  $$\begin{align*}\forall N\in\mathbb{N}\;\exists x_1,\ldots,x_N\in X:\quad (x_i)_{i=1}^N \equiv \ell_p^N \text{ and }N^{1/p}\cdot x = \sum_{i=1}^N x_i.\end{align*}$$
$$\begin{align*}\forall N\in\mathbb{N}\;\exists x_1,\ldots,x_N\in X:\quad (x_i)_{i=1}^N \equiv \ell_p^N \text{ and }N^{1/p}\cdot x = \sum_{i=1}^N x_i.\end{align*}$$
-
(iii) For every
 $x\in S_X$
, the following condition is satisfied
$x\in S_X$
, the following condition is satisfied  $$\begin{align*}\forall \varepsilon> 0\;\exists x_1,x_2\in X:\quad (x_1,x_2){\stackrel{1+\varepsilon}{\sim} \ell_p^2} \text{ and }2^{1/p}\cdot x = x_1 + x_2.\end{align*}$$
$$\begin{align*}\forall \varepsilon> 0\;\exists x_1,x_2\in X:\quad (x_1,x_2){\stackrel{1+\varepsilon}{\sim} \ell_p^2} \text{ and }2^{1/p}\cdot x = x_1 + x_2.\end{align*}$$
-
(iv) For every
 $x\in S_X$
, the following condition is satisfied
$x\in S_X$
, the following condition is satisfied  $$\begin{align*}\forall \varepsilon> 0\;\forall \delta > 0\;\exists x_1,x_2\in X:\quad (x_1,x_2){\stackrel{1+\varepsilon}{\sim} \ell_p^2} \text{ and }\|2^{1/p}\cdot x - x_1 - x_2\| < \delta.\end{align*}$$
$$\begin{align*}\forall \varepsilon> 0\;\forall \delta > 0\;\exists x_1,x_2\in X:\quad (x_1,x_2){\stackrel{1+\varepsilon}{\sim} \ell_p^2} \text{ and }\|2^{1/p}\cdot x - x_1 - x_2\| < \delta.\end{align*}$$
Proof.
![]() $(i)\implies (ii)$
: Pick
$(i)\implies (ii)$
: Pick
![]() $f\in S_{L_p[0,1]}$
and
$f\in S_{L_p[0,1]}$
and
![]() $N\in \mathbb {N}$
. Then, using the continuity of the mapping
$N\in \mathbb {N}$
. Then, using the continuity of the mapping
![]() $[0,1]\ni x\mapsto \int _0^x |f|$
, we find
$[0,1]\ni x\mapsto \int _0^x |f|$
, we find
![]() $0=x_0<x_1<\ldots <x_N=1$
, such that
$0=x_0<x_1<\ldots <x_N=1$
, such that
![]() $\int _{x_{i-1}}^{x_i} |f|^p = \frac {1}{N} \int _0^1 |f|^p$
for every
$\int _{x_{i-1}}^{x_i} |f|^p = \frac {1}{N} \int _0^1 |f|^p$
for every
![]() $i=1,\ldots ,N$
. We put
$i=1,\ldots ,N$
. We put
![]() $f_i:=N^{1/p}\cdot f\cdot \chi _{[x_{i-1},x_i]}$
,
$f_i:=N^{1/p}\cdot f\cdot \chi _{[x_{i-1},x_i]}$
,
![]() $i=1,\ldots ,N$
. Then, since the supports of
$i=1,\ldots ,N$
. Then, since the supports of
![]() $f_i$
are disjoint and since
$f_i$
are disjoint and since
![]() $f_i$
are normalized, we have
$f_i$
are normalized, we have
![]() $(f_i)_{i=1}^N \equiv \ell _p^N$
. Further, we obviously have
$(f_i)_{i=1}^N \equiv \ell _p^N$
. Further, we obviously have
![]() $N^{1/p}\cdot f = \sum _{i=1}^N f_i$
.
$N^{1/p}\cdot f = \sum _{i=1}^N f_i$
.
Obviously, we have
![]() $(ii)\implies (iii)$
and
$(ii)\implies (iii)$
and
![]() $(iii)\implies (iv)$
.
$(iii)\implies (iv)$
.
![]() $(iii)\implies (i)$
: In order to get a contradiction, let us assume that X is not isometric to
$(iii)\implies (i)$
: In order to get a contradiction, let us assume that X is not isometric to
![]() $L_p[0,1]$
, which, by Theorem 3.8, implies that X is isometric to
$L_p[0,1]$
, which, by Theorem 3.8, implies that X is isometric to
![]() $L_p(\mu )$
, where
$L_p(\mu )$
, where
![]() $(\Omega ,S,\mu )$
is a measure space for which there is
$(\Omega ,S,\mu )$
is a measure space for which there is
![]() $\omega \in \Omega $
with
$\omega \in \Omega $
with
![]() $\mu (\{\omega \}) = 1$
. Fix
$\mu (\{\omega \}) = 1$
. Fix
![]() $\varepsilon> 0$
small enough (to be specified later). Suppose, to the contrary, that there are
$\varepsilon> 0$
small enough (to be specified later). Suppose, to the contrary, that there are
![]() $f,g\in L_p(\mu )$
, such that
$f,g\in L_p(\mu )$
, such that
![]() $(f,g){\stackrel {1+\varepsilon }{\sim } \ell _p^2}$
and
$(f,g){\stackrel {1+\varepsilon }{\sim } \ell _p^2}$
and
![]() $2^{\frac 1p}\cdot \delta _{\omega }=f+g$
, where
$2^{\frac 1p}\cdot \delta _{\omega }=f+g$
, where
![]() $\delta _{\omega }$
is the Dirac function supported by the point
$\delta _{\omega }$
is the Dirac function supported by the point
![]() $\omega $
. For
$\omega $
. For
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in \Omega \setminus \{\omega \}$
, we have
$x\in \Omega \setminus \{\omega \}$
, we have
![]() $f(x)+g(x)=0$
, so we assume this holds for all
$f(x)+g(x)=0$
, so we assume this holds for all
![]() $x\in \Omega \setminus \{\omega \}$
. We without loss of generality assume that
$x\in \Omega \setminus \{\omega \}$
. We without loss of generality assume that
![]() $f(\omega )\geq g(\omega )$
.
$f(\omega )\geq g(\omega )$
.
We claim that both
![]() $f(\omega )$
and
$f(\omega )$
and
![]() $g(\omega )$
are positive and
$g(\omega )$
are positive and
![]() $|f(\omega ) - g(\omega )|^p<\frac {1}{2}$
if
$|f(\omega ) - g(\omega )|^p<\frac {1}{2}$
if
![]() $\varepsilon>0$
is chosen sufficiently small. Indeed, we have
$\varepsilon>0$
is chosen sufficiently small. Indeed, we have
which implies
![]() $||f(\omega )| - |g(\omega )||<2^{-1/p}$
for sufficiently small
$||f(\omega )| - |g(\omega )||<2^{-1/p}$
for sufficiently small
![]() $\varepsilon>0$
. The claim follows, since if both
$\varepsilon>0$
. The claim follows, since if both
![]() $f(\omega )$
and
$f(\omega )$
and
![]() $g(\omega )$
were not positive, we would have
$g(\omega )$
were not positive, we would have
![]() $2^{1/p}> 2^{-1/p} > ||f(\omega )| - |g(\omega )|| = |(f+g)(\omega )| = 2^{1/p}$
, a contradiction.
$2^{1/p}> 2^{-1/p} > ||f(\omega )| - |g(\omega )|| = |(f+g)(\omega )| = 2^{1/p}$
, a contradiction.
First, let us handle the case when
![]() $1\leq p<2$
. We have
$1\leq p<2$
. We have
 $$\begin{align*}\begin{aligned} \|2f\|_p^p & = \int_{\Omega\setminus\{\omega\}} |2f|^p \, \mathrm{d} \mu + (2f(\omega))^p = \int_{\Omega\setminus\{\omega\}} |f-g|^p \, \mathrm{d} \mu + (2f(\omega))^p\\ & = \|f-g\|_p^p + (2f(\omega))^p - ((f-g)(\omega))^p\\ & \geq \|f-g\|_p^p + ((f+g)(\omega))^p = \|f-g\|_p^p + \|f+g\|_p^p, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \|2f\|_p^p & = \int_{\Omega\setminus\{\omega\}} |2f|^p \, \mathrm{d} \mu + (2f(\omega))^p = \int_{\Omega\setminus\{\omega\}} |f-g|^p \, \mathrm{d} \mu + (2f(\omega))^p\\ & = \|f-g\|_p^p + (2f(\omega))^p - ((f-g)(\omega))^p\\ & \geq \|f-g\|_p^p + ((f+g)(\omega))^p = \|f-g\|_p^p + \|f+g\|_p^p, \end{aligned} \end{align*}$$
where in the inequality we used superadditivity of the function
![]() $[0,\infty )\ni t\mapsto t^p$
. Thus,
$[0,\infty )\ni t\mapsto t^p$
. Thus,
![]() $(f,g){\stackrel {1+\varepsilon }{\sim } \ell _2^p}$
implies
$(f,g){\stackrel {1+\varepsilon }{\sim } \ell _2^p}$
implies
 $$\begin{align*}(1+\varepsilon)^p\geq \|f\|_p^p\geq \frac{\|f-g\|_p^p + \|f+g\|_p^p}{2^p}\geq \frac{4}{2^p(1+\varepsilon)^p}; \end{align*}$$
$$\begin{align*}(1+\varepsilon)^p\geq \|f\|_p^p\geq \frac{\|f-g\|_p^p + \|f+g\|_p^p}{2^p}\geq \frac{4}{2^p(1+\varepsilon)^p}; \end{align*}$$
hence, if
![]() $1\leq p<2$
, we get a contradiction for sufficiently small
$1\leq p<2$
, we get a contradiction for sufficiently small
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Finally, let us handle the case when
![]() $p>2$
. Note that since
$p>2$
. Note that since
![]() $f(\omega )\geq g(\omega )\geq 0$
and
$f(\omega )\geq g(\omega )\geq 0$
and
![]() $f(\omega ) + g(\omega ) = 2^{1/p}$
, we have
$f(\omega ) + g(\omega ) = 2^{1/p}$
, we have
![]() $g(\omega )\leq 2^{1/p-1}$
. Further, we have
$g(\omega )\leq 2^{1/p-1}$
. Further, we have
 $$\begin{align*}\begin{aligned} \|2g\|_p^p & = \int_{\Omega\setminus\{\omega\}} |f-g|^p \, \mathrm{d} \mu + (2g(\omega))^p \leq \|f-g\|_p^p + 2. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \|2g\|_p^p & = \int_{\Omega\setminus\{\omega\}} |f-g|^p \, \mathrm{d} \mu + (2g(\omega))^p \leq \|f-g\|_p^p + 2. \end{aligned}\end{align*}$$
Thus,
![]() $(f,g){\stackrel {1+\varepsilon }{\sim } \ell _2^p}$
implies
$(f,g){\stackrel {1+\varepsilon }{\sim } \ell _2^p}$
implies
 $$\begin{align*}\frac{1}{(1+\varepsilon)^p}\leq \|g\|_p^p\leq \frac{\|f-g\|_p^p + 2}{2^p}\leq \frac{2(1+\varepsilon)^p + 2}{2^p}; \end{align*}$$
$$\begin{align*}\frac{1}{(1+\varepsilon)^p}\leq \|g\|_p^p\leq \frac{\|f-g\|_p^p + 2}{2^p}\leq \frac{2(1+\varepsilon)^p + 2}{2^p}; \end{align*}$$
hence, if
![]() $p>2$
, we get a contradiction for sufficiently small
$p>2$
, we get a contradiction for sufficiently small
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
![]() $(iv)\implies (iii)$
: Fix
$(iv)\implies (iii)$
: Fix
![]() $x\in S_X$
and
$x\in S_X$
and
![]() $\varepsilon> 0$
. Pick
$\varepsilon> 0$
. Pick
![]() $\delta>0$
small enough (to be specified later). Applying Condition
$\delta>0$
small enough (to be specified later). Applying Condition
![]() $(iv)$
, we obtain
$(iv)$
, we obtain
![]() $x_1^{\prime },x_2^{\prime }\in X$
, such that
$x_1^{\prime },x_2^{\prime }\in X$
, such that
![]() $(x_1^{\prime},x_2^{\prime}){\stackrel{1 + \tfrac{\varepsilon}{2}}{\sim}} \ell_p^2$
and
$(x_1^{\prime},x_2^{\prime}){\stackrel{1 + \tfrac{\varepsilon}{2}}{\sim}} \ell_p^2$
and
![]() $\|2^{1/p}\cdot x - x_1^{\prime } - x_2^{\prime }\| < \delta $
. Now, set
$\|2^{1/p}\cdot x - x_1^{\prime } - x_2^{\prime }\| < \delta $
. Now, set
![]() $x_1=x^{\prime }_1+(2^{1/p}\cdot x-(x^{\prime }_1+x^{\prime }_2))/2$
and
$x_1=x^{\prime }_1+(2^{1/p}\cdot x-(x^{\prime }_1+x^{\prime }_2))/2$
and
![]() $x_2=x^{\prime }_2+(2^{1/p}\cdot x-(x^{\prime }_1+x^{\prime }_2))/2$
. If
$x_2=x^{\prime }_2+(2^{1/p}\cdot x-(x^{\prime }_1+x^{\prime }_2))/2$
. If
![]() $\delta $
was chosen sufficiently small, we have
$\delta $
was chosen sufficiently small, we have
![]() $(x_1,x_2){\stackrel {1+\varepsilon }{\sim } \ell _p^2}$
, and clearly,
$(x_1,x_2){\stackrel {1+\varepsilon }{\sim } \ell _p^2}$
, and clearly,
![]() $2^{1/p}\cdot x=x_1+x_2$
.
$2^{1/p}\cdot x=x_1+x_2$
.
Let us note the following easy observation. The proof is easy and so omitted.
Fact 3.10. Let
![]() $v,w\in V$
,
$v,w\in V$
,
![]() $v\neq 0$
and
$v\neq 0$
and
![]() $a,b\in \mathbb {R}$
. Then the set
$a,b\in \mathbb {R}$
. Then the set
 $$\begin{align*}\left\{\mu\in\mathcal{P}:\; \mu(v)\neq 0\text{ and }\mu(a\cdot\frac{v}{\mu(v)} - w)<b\right\}\end{align*}$$
$$\begin{align*}\left\{\mu\in\mathcal{P}:\; \mu(v)\neq 0\text{ and }\mu(a\cdot\frac{v}{\mu(v)} - w)<b\right\}\end{align*}$$
is open in
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
Proof of Theorem 3.4.
Let
![]() $\mathcal {F}$
be the set of those
$\mathcal {F}$
be the set of those
![]() $\nu \in \mathcal {P}_\infty $
for which
$\nu \in \mathcal {P}_\infty $
for which
![]() $X_\nu $
is an
$X_\nu $
is an
![]() $\mathcal {L}_{p,1+}$
-space. By Theorem 3.6,
$\mathcal {L}_{p,1+}$
-space. By Theorem 3.6,
![]() $\mathcal {F}\subseteq \mathcal {P}_\infty $
is a
$\mathcal {F}\subseteq \mathcal {P}_\infty $
is a
![]() $G_\delta $
-set. By Theorem 3.9, using the obvious observation that Condition
$G_\delta $
-set. By Theorem 3.9, using the obvious observation that Condition
![]() $(iv)$
may be verified on a dense subset, we have
$(iv)$
may be verified on a dense subset, we have
where
![]() $U_{v,n,k}$
are open sets (using Fact 3.10 and Lemma 1.5) defined as
$U_{v,n,k}$
are open sets (using Fact 3.10 and Lemma 1.5) defined as
 $$\begin{align*}U_{v,n,k}:=\Big\{\mu\in\mathcal{P}_\infty:\; \exists v_1,v_2\in V:\; (v_1,v_2) \stackrel{1+\tfrac{1}{n}}{\sim} \ell_p^2 \text{ and }\mu\big(2^{1/p}\cdot \frac{v}{\mu(v)} - v_1 - v_2\big) < \frac{1}{k}\Big\}.\end{align*}$$
$$\begin{align*}U_{v,n,k}:=\Big\{\mu\in\mathcal{P}_\infty:\; \exists v_1,v_2\in V:\; (v_1,v_2) \stackrel{1+\tfrac{1}{n}}{\sim} \ell_p^2 \text{ and }\mu\big(2^{1/p}\cdot \frac{v}{\mu(v)} - v_1 - v_2\big) < \frac{1}{k}\Big\}.\end{align*}$$
Thus,
![]() ${\langle L_p[0,1]\rangle _{\equiv }^{\mathcal {P}_\infty }}$
is a
${\langle L_p[0,1]\rangle _{\equiv }^{\mathcal {P}_\infty }}$
is a
![]() $G_\delta $
-set.
$G_\delta $
-set.
On the other hand, since any
![]() $L_p(\mu )$
is finitely representable in
$L_p(\mu )$
is finitely representable in
![]() $\ell _p$
and vice versa (see, e.g. [Reference Albiac and Kalton1, Proposition 12.1.8]), from Lemma 3.1 and Theorem 3.8, we obtain that there is at most one (up to isometry)
$\ell _p$
and vice versa (see, e.g. [Reference Albiac and Kalton1, Proposition 12.1.8]), from Lemma 3.1 and Theorem 3.8, we obtain that there is at most one (up to isometry)
![]() $\mathcal {L}_{p,1+}$
space X, such that
$\mathcal {L}_{p,1+}$
space X, such that
![]() ${\langle X\rangle _{\equiv }}$
is a
${\langle X\rangle _{\equiv }}$
is a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {B}$
and that
$\mathcal {B}$
and that
![]() ${\langle L_p[0,1]\rangle _{\equiv }}$
is a
${\langle L_p[0,1]\rangle _{\equiv }}$
is a
![]() $G_\delta $
-complete set.
$G_\delta $
-complete set.
4 Spaces with
 $F_{\sigma \delta }$
isometry classes
$F_{\sigma \delta }$
isometry classes
In this section, we focus on another classical Banach space, namely,
![]() $\ell _p$
spaces, for
$\ell _p$
spaces, for
![]() $p\in [1,2)\cup (2,\infty )$
, and
$p\in [1,2)\cup (2,\infty )$
, and
![]() $c_0$
. The main result of this section is the following, which proves the second and the third part of Theorem B.
$c_0$
. The main result of this section is the following, which proves the second and the third part of Theorem B.
Theorem 4.1. The sets
![]() ${\langle c_0\rangle _{\equiv }}$
and
${\langle c_0\rangle _{\equiv }}$
and
![]() ${\langle \ell _p\rangle _{\equiv }}$
(for
${\langle \ell _p\rangle _{\equiv }}$
(for
![]() $p\in [1,2)\cup (2,\infty )$
) are
$p\in [1,2)\cup (2,\infty )$
) are
![]() $F_{\sigma \delta }$
-complete sets in both
$F_{\sigma \delta }$
-complete sets in both
![]() $\mathcal {P}_\infty $
and
$\mathcal {P}_\infty $
and
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
Note that in order to obtain that result, we prove Proposition 4.6 and Theorem 4.13, which are of independent interest, and where the ‘easiest possible’ isometric characterizations of the Banach spaces
![]() $\ell _p$
, respectively,
$\ell _p$
, respectively,
![]() $c_0$
, among separable
$c_0$
, among separable
![]() $\mathcal L_{p,1+}$
-spaces, respectively, separable
$\mathcal L_{p,1+}$
-spaces, respectively, separable
![]() $\mathcal L_{\infty ,1+}$
-spaces are given. The proof of Theorem 4.1 follows immediately from Propositions 4.3, 4.4 and 4.11.
$\mathcal L_{\infty ,1+}$
-spaces are given. The proof of Theorem 4.1 follows immediately from Propositions 4.3, 4.4 and 4.11.
Let us emphasize that in Section 4.2, we compute the Borel complexity of the operation, assigning to a given Banach space the Szlenk derivative of its dual unit ball, which could be of an independent interest as well. See, for example, Section 5.2 for some consequences. The reason why we need to do it here is obviously that our isometric characterization of the space
![]() $c_0$
involves Szlenk derivatives.
$c_0$
involves Szlenk derivatives.
We start with the part which is common for both cases – that is, for
![]() ${\langle c_0\rangle _{\equiv }}$
and
${\langle c_0\rangle _{\equiv }}$
and
![]() ${\langle \ell _p\rangle _{\equiv }}$
.
${\langle \ell _p\rangle _{\equiv }}$
.
Lemma 4.2. Let
![]() $p\in [1,\infty )$
, and let
$p\in [1,\infty )$
, and let
![]() $X=(\bigoplus _{n\in \mathbb {N}} X_n)_p$
be the
$X=(\bigoplus _{n\in \mathbb {N}} X_n)_p$
be the
![]() $\ell _p$
-sum of a family
$\ell _p$
-sum of a family
![]() $(X_n)_{n\in \mathbb {N}}$
of separable infinite-dimensional Banach spaces. Then,
$(X_n)_{n\in \mathbb {N}}$
of separable infinite-dimensional Banach spaces. Then,
![]() $X\equiv \ell _p$
if and only if
$X\equiv \ell _p$
if and only if
![]() $X_n\equiv \ell _p$
for every
$X_n\equiv \ell _p$
for every
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Similarly, let
![]() $X=(\bigoplus _{n\in \mathbb {N}} X_n)_0$
be the
$X=(\bigoplus _{n\in \mathbb {N}} X_n)_0$
be the
![]() $c_0$
-sum of a family
$c_0$
-sum of a family
![]() $(X_n)_{n\in \mathbb {N}}$
of separable infinite-dimensional Banach spaces. Then,
$(X_n)_{n\in \mathbb {N}}$
of separable infinite-dimensional Banach spaces. Then,
![]() $X\equiv c_0$
if and only if
$X\equiv c_0$
if and only if
![]() $X_n\equiv c_0$
for every
$X_n\equiv c_0$
for every
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Proof. It is easy and well-known that the
![]() $\ell _p$
-sum of countably many
$\ell _p$
-sum of countably many
![]() $\ell _p$
spaces is isometric to
$\ell _p$
spaces is isometric to
![]() $\ell _p$
, and that the
$\ell _p$
, and that the
![]() $c_0$
-sum of countably many
$c_0$
-sum of countably many
![]() $c_0$
spaces is isometric to
$c_0$
spaces is isometric to
![]() $c_0$
. The opposite implications follow from the facts that every
$c_0$
. The opposite implications follow from the facts that every
![]() $1$
-complemented infinite-dimensional subspace of
$1$
-complemented infinite-dimensional subspace of
![]() $\ell _p$
is isometric to
$\ell _p$
is isometric to
![]() $\ell _p$
, and that every
$\ell _p$
, and that every
![]() $1$
-complemented infinite-dimensional subspace of
$1$
-complemented infinite-dimensional subspace of
![]() $c_0$
is isometric to
$c_0$
is isometric to
![]() $c_0$
(see [Reference Lindenstrauss and Tzafriri42, page 54]).
$c_0$
(see [Reference Lindenstrauss and Tzafriri42, page 54]).
Proposition 4.3. Let X be one of the spaces
![]() $\ell _p$
,
$\ell _p$
,
![]() $p\in [1,2)\cup (2,\infty )$
or
$p\in [1,2)\cup (2,\infty )$
or
![]() $c_0$
. Then the set
$c_0$
. Then the set
![]() ${\langle X\rangle _{\equiv }}$
is
${\langle X\rangle _{\equiv }}$
is
![]() $F_{\sigma \delta }$
-hard in
$F_{\sigma \delta }$
-hard in
![]() $\mathcal {B}$
.
$\mathcal {B}$
.
Proof. Our plan is to find a Wadge reduction of a known
![]() $F_{\sigma \delta }$
-hard set to
$F_{\sigma \delta }$
-hard set to
![]() ${\langle X\rangle _{\equiv }^{\mathcal {B}}}$
. For this purpose, we will use the set
${\langle X\rangle _{\equiv }^{\mathcal {B}}}$
. For this purpose, we will use the set
(see, e.g. [Reference Kechris34, Section 23.A] for the fact that
![]() $P_3$
is
$P_3$
is
![]() $F_{\sigma \delta }$
-hard in
$F_{\sigma \delta }$
-hard in
![]() $2^{\mathbb {N}\times \mathbb {N}}$
). But before we start to construct the reduction of
$2^{\mathbb {N}\times \mathbb {N}}$
). But before we start to construct the reduction of
![]() $P_3$
to
$P_3$
to
![]() ${\langle X\rangle _{\equiv }^{\mathcal {B}}}$
, we need to do some preparation.
${\langle X\rangle _{\equiv }^{\mathcal {B}}}$
, we need to do some preparation.
By Theorem 3.4 (in case
![]() $X=\ell _p$
) and Theorem 3.3 (in case
$X=\ell _p$
) and Theorem 3.3 (in case
![]() $X=c_0$
), we know that
$X=c_0$
), we know that
![]() ${\langle X\rangle _{\equiv }^{\mathcal {B}}}$
is not a
${\langle X\rangle _{\equiv }^{\mathcal {B}}}$
is not a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {B}$
. Therefore, it is
$\mathcal {B}$
. Therefore, it is
![]() $F_\sigma $
-hard in
$F_\sigma $
-hard in
![]() $\mathcal {B}$
by Lemma 1.1. Now, as the set
$\mathcal {B}$
by Lemma 1.1. Now, as the set
is an
![]() $F_\sigma $
-set in
$F_\sigma $
-set in
![]() $2^{\mathbb {N}}$
, it is Wadge reducible to
$2^{\mathbb {N}}$
, it is Wadge reducible to
![]() ${\langle X\rangle _{\equiv }^{\mathcal {B}}}$
, so there is a continuous function
${\langle X\rangle _{\equiv }^{\mathcal {B}}}$
, so there is a continuous function
![]() $\varrho \colon 2^{\mathbb {N}}\rightarrow \mathcal {B}$
, such that
$\varrho \colon 2^{\mathbb {N}}\rightarrow \mathcal {B}$
, such that
We fix a bijection
![]() $b\colon \mathbb {N}^2\rightarrow \mathbb {N}$
. For every
$b\colon \mathbb {N}^2\rightarrow \mathbb {N}$
. For every
![]() $x\in 2^{\mathbb {N}}$
and every
$x\in 2^{\mathbb {N}}$
and every
![]() $m\in \mathbb {N}$
, we define
$m\in \mathbb {N}$
, we define
![]() $\varrho _m(x)\in \mathcal {P}_\infty $
as follows. Suppose that
$\varrho _m(x)\in \mathcal {P}_\infty $
as follows. Suppose that
![]() $v=\sum _{n\in \mathbb {N}}\alpha _ne_n$
is an element of V (i.e.
$v=\sum _{n\in \mathbb {N}}\alpha _ne_n$
is an element of V (i.e.
![]() $\alpha _n$
is a rational number for every n, and
$\alpha _n$
is a rational number for every n, and
![]() $\alpha _n\neq 0$
only for finitely many n’s), then we put
$\alpha _n\neq 0$
only for finitely many n’s), then we put
 $$\begin{align*}\varrho_m(x)(v)=\varrho(x)\left(\sum_{n\in\mathbb{N}}\alpha_{b(m,n)}e_n\right). \end{align*}$$
$$\begin{align*}\varrho_m(x)(v)=\varrho(x)\left(\sum_{n\in\mathbb{N}}\alpha_{b(m,n)}e_n\right). \end{align*}$$
Note that the set
![]() $\{e_{b(m,n)}\colon n\in \mathbb {N}\}$
is both linearly independent and linearly dense in
$\{e_{b(m,n)}\colon n\in \mathbb {N}\}$
is both linearly independent and linearly dense in
![]() $X_{\varrho _m(x)}$
, and that
$X_{\varrho _m(x)}$
, and that
![]() $\varrho _m(x)(e_k)=0$
if
$\varrho _m(x)(e_k)=0$
if
![]() $k\notin \{b(m,n)\colon n\in \mathbb {N}\}$
. Also,
$k\notin \{b(m,n)\colon n\in \mathbb {N}\}$
. Also,
![]() $X_{\varrho _m(x)}$
is isometric to
$X_{\varrho _m(x)}$
is isometric to
![]() $X_{\varrho (x)}$
, where the isometry is induced by the operator
$X_{\varrho (x)}$
, where the isometry is induced by the operator
 $$ \begin{align*}e_k\mapsto \begin{cases}e_n & k=b(m,n),\\ 0 & k\notin\{b(m,n)\colon n\in\mathbb{N}\}. \end{cases}\end{align*} $$
$$ \begin{align*}e_k\mapsto \begin{cases}e_n & k=b(m,n),\\ 0 & k\notin\{b(m,n)\colon n\in\mathbb{N}\}. \end{cases}\end{align*} $$
Now, we are ready to construct the required reduction
![]() $f\colon 2^{\mathbb {N}\times \mathbb {N}}\rightarrow \mathcal {B}$
. For every
$f\colon 2^{\mathbb {N}\times \mathbb {N}}\rightarrow \mathcal {B}$
. For every
![]() $x\in 2^{\mathbb {N}\times \mathbb {N}}$
and every
$x\in 2^{\mathbb {N}\times \mathbb {N}}$
and every
![]() $m\in \mathbb {N}$
, we write
$m\in \mathbb {N}$
, we write
![]() $x^{(m)}$
for the sequence
$x^{(m)}$
for the sequence
![]() $(x(m,n))_{n\in \mathbb {N}}$
. If
$(x(m,n))_{n\in \mathbb {N}}$
. If
![]() $X=\ell _p$
, we define
$X=\ell _p$
, we define
 $$\begin{align*}f(x)(v)=\sqrt[p]{\sum_{m\in\mathbb{N}}\left(\varrho_m(x^{(m)})(v)\right)^p},\;\;\;\;\;v\in V, \end{align*}$$
$$\begin{align*}f(x)(v)=\sqrt[p]{\sum_{m\in\mathbb{N}}\left(\varrho_m(x^{(m)})(v)\right)^p},\;\;\;\;\;v\in V, \end{align*}$$
and if
![]() $X=c_0$
, we put
$X=c_0$
, we put
This formula, together with the preceding considerations, easily implies that
![]() $f(x)\in \mathcal {B}$
and that
$f(x)\in \mathcal {B}$
and that
![]() $X_{f(x)}$
is isometric to the
$X_{f(x)}$
is isometric to the
![]() $\ell _p$
-sum, or to the
$\ell _p$
-sum, or to the
![]() $c_0$
-sum (depending on whether
$c_0$
-sum (depending on whether
![]() $X=\ell _p$
or
$X=\ell _p$
or
![]() $X=c_0$
), of the spaces
$X=c_0$
), of the spaces
![]() $X_{\varrho (x^{(m)})}$
,
$X_{\varrho (x^{(m)})}$
,
![]() $m\in \mathbb {N}$
. Continuity of the functions
$m\in \mathbb {N}$
. Continuity of the functions
![]() $\varrho _m$
and
$\varrho _m$
and
![]() $x\mapsto x^{(m)}$
,
$x\mapsto x^{(m)}$
,
![]() $m\in \mathbb {N}$
, immediately implies continuity of f. By Lemma 4.2,
$m\in \mathbb {N}$
, immediately implies continuity of f. By Lemma 4.2,
![]() $f(x)\in {\langle X\rangle _{\equiv }^{\mathcal {B}}}$
if and only if
$f(x)\in {\langle X\rangle _{\equiv }^{\mathcal {B}}}$
if and only if
![]() $\varrho (x^{(m)})\in {\langle X\rangle _{\equiv }^{\mathcal {B}}}$
for every
$\varrho (x^{(m)})\in {\langle X\rangle _{\equiv }^{\mathcal {B}}}$
for every
![]() $m\in \mathbb {N}$
. Hence,
$m\in \mathbb {N}$
. Hence,
4.1 The spaces
 $\ell _p$
$\ell _p$
The purpose of this subsection is to prove the following result.
Proposition 4.4. For every
![]() $p\in [1,2)\cup (2,\infty )$
, we have that
$p\in [1,2)\cup (2,\infty )$
, we have that
![]() ${\langle \ell _p\rangle _{\equiv }}$
is an
${\langle \ell _p\rangle _{\equiv }}$
is an
![]() $F_{\sigma \delta }$
-set in
$F_{\sigma \delta }$
-set in
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
We start with the following classical result, which is sometimes named Clarkson’s inequality. The proof may be found on various places, the original one is in the paper by Clarkson (see [Reference Clarkson11]). In fact, we use only a very special case of Clarkson’s inequality, where
![]() $z,w$
are required to be elements of the real line instead of an
$z,w$
are required to be elements of the real line instead of an
![]() $L_p$
space (and this case is rather straightforward to prove).
$L_p$
space (and this case is rather straightforward to prove).
Lemma 4.5 (Clarkson’s inequality).
Let
![]() $1\leq p < \infty $
,
$1\leq p < \infty $
,
![]() $p\neq 2$
. If
$p\neq 2$
. If
![]() $p>2$
, then for every
$p>2$
, then for every
![]() $z,w\in \mathbb {R}$
, we have
$z,w\in \mathbb {R}$
, we have
If
![]() $p<2$
, then the reverse inequality holds. Moreover, the equality holds if and only if
$p<2$
, then the reverse inequality holds. Moreover, the equality holds if and only if
![]() $zw=0$
.
$zw=0$
.
Proposition 4.6. Let
![]() $1\leq p <\infty $
,
$1\leq p <\infty $
,
![]() $p\neq 2$
, and let X be a separable infinite-dimensional
$p\neq 2$
, and let X be a separable infinite-dimensional
![]() $\mathcal {L}_{p,1+}$
-space. Let D be a dense subset of X. Then the following assertions are equivalent.
$\mathcal {L}_{p,1+}$
-space. Let D be a dense subset of X. Then the following assertions are equivalent.
-
(i) X is isometric to
 $\ell _p$
.
$\ell _p$
. -
(ii) For every
 $x\in S_X$
and every
$x\in S_X$
and every
 $\delta \in (0,1)$
, the following condition is satisfied:
$\delta \in (0,1)$
, the following condition is satisfied:  $$\begin{align*}\exists N\in\mathbb{N}\; \exists \varepsilon>0\;\forall x_1,\ldots,x_N\in X:\quad (N^{1/p}\cdot x_i)_{i=1}^N{\stackrel{1+\varepsilon}{\sim} \ell_p^N} \Rightarrow \|x-\sum_{i=1}^N x_i\|>\delta. \end{align*}$$
$$\begin{align*}\exists N\in\mathbb{N}\; \exists \varepsilon>0\;\forall x_1,\ldots,x_N\in X:\quad (N^{1/p}\cdot x_i)_{i=1}^N{\stackrel{1+\varepsilon}{\sim} \ell_p^N} \Rightarrow \|x-\sum_{i=1}^N x_i\|>\delta. \end{align*}$$
-
(iii) For every
 $x\in S_X$
, the following condition is satisfied:
$x\in S_X$
, the following condition is satisfied:  $$\begin{align*}\exists N\in\mathbb{N}\; \forall x_1,\ldots,x_N\in X:\quad (N^{1/p}\cdot x_i)_{i=1}^N\equiv\ell_p^N \Rightarrow x\neq \sum_{i=1}^N x_i.\end{align*}$$
$$\begin{align*}\exists N\in\mathbb{N}\; \forall x_1,\ldots,x_N\in X:\quad (N^{1/p}\cdot x_i)_{i=1}^N\equiv\ell_p^N \Rightarrow x\neq \sum_{i=1}^N x_i.\end{align*}$$
-
(iv) For every
 $x\in D\setminus \{0\}$
and every
$x\in D\setminus \{0\}$
and every
 $\delta \in (0,1)$
, the following condition is satisfied:
$\delta \in (0,1)$
, the following condition is satisfied:  $$\begin{align*}\exists N\in\mathbb{N}\; \exists \varepsilon>0\;\forall x_1,\ldots,x_N\in D:\quad (N^{1/p}\cdot x_i)_{i=1}^N{\stackrel{1+\varepsilon}{\sim} \ell_p^N} \Rightarrow \Big\|\frac x{\|x\|}-\sum_{i=1}^N x_i\Big\|\ge\delta. \end{align*}$$
$$\begin{align*}\exists N\in\mathbb{N}\; \exists \varepsilon>0\;\forall x_1,\ldots,x_N\in D:\quad (N^{1/p}\cdot x_i)_{i=1}^N{\stackrel{1+\varepsilon}{\sim} \ell_p^N} \Rightarrow \Big\|\frac x{\|x\|}-\sum_{i=1}^N x_i\Big\|\ge\delta. \end{align*}$$
Proof.
![]() $(i)\implies (ii)$
: Fix
$(i)\implies (ii)$
: Fix
![]() $x\in S_{\ell _p}$
and
$x\in S_{\ell _p}$
and
![]() $\delta \in (0,1)$
. Pick
$\delta \in (0,1)$
. Pick
![]() $l\in \mathbb {N}$
with
$l\in \mathbb {N}$
with
![]() $\sum _{k=1}^l |x(k)|^p> \delta ^p$
and
$\sum _{k=1}^l |x(k)|^p> \delta ^p$
and
![]() $N\in \mathbb {N}$
, such that
$N\in \mathbb {N}$
, such that
![]() $\sum _{k=1}^l (|x(k)| - \frac {3}{\sqrt [p]{N}})^p> \delta ^p$
. Fix a sequence
$\sum _{k=1}^l (|x(k)| - \frac {3}{\sqrt [p]{N}})^p> \delta ^p$
. Fix a sequence
![]() $(\varepsilon _m)_{m\in \mathbb {N}}\in (0,1)^{\mathbb {N}}$
with
$(\varepsilon _m)_{m\in \mathbb {N}}\in (0,1)^{\mathbb {N}}$
with
![]() $\varepsilon _m\to 0$
. In order to get a contradiction, for every
$\varepsilon _m\to 0$
. In order to get a contradiction, for every
![]() $m\in \mathbb {N}$
, pick
$m\in \mathbb {N}$
, pick
![]() $x_1^{\varepsilon _m},\ldots ,x_N^{\varepsilon _m}\in \ell _p$
, such that
$x_1^{\varepsilon _m},\ldots ,x_N^{\varepsilon _m}\in \ell _p$
, such that
![]() $(N^{1/p}\cdot x_i^{\varepsilon _m})_{i=1}^N{\stackrel {1+\varepsilon _m}{\sim } \ell _p^N}$
and
$(N^{1/p}\cdot x_i^{\varepsilon _m})_{i=1}^N{\stackrel {1+\varepsilon _m}{\sim } \ell _p^N}$
and
![]() $\|x-\sum _{i=1}^N x_i^{\varepsilon _m}\|\leq \delta $
for every
$\|x-\sum _{i=1}^N x_i^{\varepsilon _m}\|\leq \delta $
for every
![]() $m\in \mathbb {N}$
.
$m\in \mathbb {N}$
.
We claim that there is
![]() $m\in \mathbb {N}$
, such that
$m\in \mathbb {N}$
, such that
![]() $|x_i^{\varepsilon _m}(k)x_j^{\varepsilon _m}(k)|<\eta :=N^{-(2+2/p)}$
for every
$|x_i^{\varepsilon _m}(k)x_j^{\varepsilon _m}(k)|<\eta :=N^{-(2+2/p)}$
for every
![]() $i,j\in \{1,\ldots ,N\}$
,
$i,j\in \{1,\ldots ,N\}$
,
![]() $i\neq j$
, and
$i\neq j$
, and
![]() $k\in \{1,\ldots ,l\}$
. Indeed, otherwise, there are
$k\in \{1,\ldots ,l\}$
. Indeed, otherwise, there are
![]() $i,j,k$
, such that
$i,j,k$
, such that
![]() $|x_i^{\varepsilon _m}(k)x_j^{\varepsilon _m}(k)|\geq \eta $
for infinitely many m’s. By passing to a subsequence, we may assume that this holds for every
$|x_i^{\varepsilon _m}(k)x_j^{\varepsilon _m}(k)|\geq \eta $
for infinitely many m’s. By passing to a subsequence, we may assume that this holds for every
![]() $m\in \mathbb {N}$
. Since the sequences
$m\in \mathbb {N}$
. Since the sequences
![]() $(|x_i^{\varepsilon _m}(k)|)_m$
and
$(|x_i^{\varepsilon _m}(k)|)_m$
and
![]() $(|x_j^{\varepsilon _m}(k)|)_m$
are bounded, by passing to a subsequence, we may assume there are numbers
$(|x_j^{\varepsilon _m}(k)|)_m$
are bounded, by passing to a subsequence, we may assume there are numbers
![]() $a,b\in \mathbb {R}$
with
$a,b\in \mathbb {R}$
with
![]() $x_i^{\varepsilon _m}(k)\to a$
,
$x_i^{\varepsilon _m}(k)\to a$
,
![]() $x_j^{\varepsilon _m}(k)\to b$
and
$x_j^{\varepsilon _m}(k)\to b$
and
![]() $|ab|\geq \eta> 0$
. Since
$|ab|\geq \eta> 0$
. Since
![]() $(N^{1/p}\cdot x_i^{\varepsilon _m},N^{1/p}\cdot x_j^{\varepsilon _m}){\stackrel {1+\varepsilon _m}{\sim } \ell _p^2}$
, using Lemma 4.5, for
$(N^{1/p}\cdot x_i^{\varepsilon _m},N^{1/p}\cdot x_j^{\varepsilon _m}){\stackrel {1+\varepsilon _m}{\sim } \ell _p^2}$
, using Lemma 4.5, for
![]() $p>2$
, we obtain
$p>2$
, we obtain
 $$\begin{align*}\begin{aligned} 0 & \leq |a+b|^p + |a-b|^p - 2|a|^p - 2|b|^p\\ & = \lim_m \big(|x_i^{\varepsilon_m}(k) + x_j^{\varepsilon_m}(k)|^p + |x_i^{\varepsilon_m}(k) - x_j^{\varepsilon_m}(k)|^p - 2|x_i^{\varepsilon_m}(k)|^p - 2|x_j^{\varepsilon_m}(k)|^p\big)\\ & \leq \lim_m \big(\|x_i^{\varepsilon_m} + x_j^{\varepsilon_m}\|^p + \|x_i^{\varepsilon_m} - x_j^{\varepsilon_m}\|^p - 2\|x_i^{\varepsilon_m}\|^p - 2\|x_j^{\varepsilon_m}\|^p\big) = 0; \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} 0 & \leq |a+b|^p + |a-b|^p - 2|a|^p - 2|b|^p\\ & = \lim_m \big(|x_i^{\varepsilon_m}(k) + x_j^{\varepsilon_m}(k)|^p + |x_i^{\varepsilon_m}(k) - x_j^{\varepsilon_m}(k)|^p - 2|x_i^{\varepsilon_m}(k)|^p - 2|x_j^{\varepsilon_m}(k)|^p\big)\\ & \leq \lim_m \big(\|x_i^{\varepsilon_m} + x_j^{\varepsilon_m}\|^p + \|x_i^{\varepsilon_m} - x_j^{\varepsilon_m}\|^p - 2\|x_i^{\varepsilon_m}\|^p - 2\|x_j^{\varepsilon_m}\|^p\big) = 0; \end{aligned} \end{align*}$$
hence,
![]() $|a+b|^p + |a-b|^p=2|a|^p+2|b|^p=0$
, which, by Lemma 4.5, is in contradiction with
$|a+b|^p + |a-b|^p=2|a|^p+2|b|^p=0$
, which, by Lemma 4.5, is in contradiction with
![]() $|ab|>0$
. The case when
$|ab|>0$
. The case when
![]() $p<2$
is similar.
$p<2$
is similar.
From now on, we write
![]() $x_i$
instead of
$x_i$
instead of
![]() $x_i^{\varepsilon _m}$
, where
$x_i^{\varepsilon _m}$
, where
![]() $m\in \mathbb {N}$
is chosen to satisfy the claim above. Fix
$m\in \mathbb {N}$
is chosen to satisfy the claim above. Fix
![]() $k\leq l$
. By the claim above, there is at most one
$k\leq l$
. By the claim above, there is at most one
![]() $i_0\in \{1,\ldots ,N\}$
with
$i_0\in \{1,\ldots ,N\}$
with
![]() $|x_{i_0}(k)| \geq \sqrt {\eta }$
, and for this
$|x_{i_0}(k)| \geq \sqrt {\eta }$
, and for this
![]() $i_0$
, we have
$i_0$
, we have
![]() $|x_{i_0}(k)|\leq \|x_{i_0}\|\leq 2N^{-1/p}$
. Consequently, we have
$|x_{i_0}(k)|\leq \|x_{i_0}\|\leq 2N^{-1/p}$
. Consequently, we have
 $$\begin{align*}\sum_{i=1}^N |x_i(k)|\leq \frac{2}{N^{1/p}} + \sum_{i\in \{1,\ldots,N\}\& |x_i(k)|<\sqrt{\eta}} |x_i(k)|\leq \frac{2}{N^{1/p}} + N\cdot\sqrt{\eta} = \frac{3}{N^{1/p}}. \end{align*}$$
$$\begin{align*}\sum_{i=1}^N |x_i(k)|\leq \frac{2}{N^{1/p}} + \sum_{i\in \{1,\ldots,N\}\& |x_i(k)|<\sqrt{\eta}} |x_i(k)|\leq \frac{2}{N^{1/p}} + N\cdot\sqrt{\eta} = \frac{3}{N^{1/p}}. \end{align*}$$
Thus, we have
 $$\begin{align*}\|x-\sum_{i=1}^N x_i\|^p\geq \sum_{k=1}^l \Big(|x(k)| - \sum_{i=1}^N |x_i(k)|\Big)^p\geq \sum_{k=1}^l \Big(|x(k)| - \frac{3}{N^{1/p}}\Big)^p> \delta^p,\end{align*}$$
$$\begin{align*}\|x-\sum_{i=1}^N x_i\|^p\geq \sum_{k=1}^l \Big(|x(k)| - \sum_{i=1}^N |x_i(k)|\Big)^p\geq \sum_{k=1}^l \Big(|x(k)| - \frac{3}{N^{1/p}}\Big)^p> \delta^p,\end{align*}$$
which is in contradiction with
![]() $\|x-\sum _{i=1}^N x_i\| = \|x-\sum _{i=1}^N x_i^{\varepsilon _m}\|\leq \delta $
.
$\|x-\sum _{i=1}^N x_i\| = \|x-\sum _{i=1}^N x_i^{\varepsilon _m}\|\leq \delta $
.
![]() $(ii)\implies (iii)$
is obvious.
$(ii)\implies (iii)$
is obvious.
![]() $(iii)\implies (i)$
: Suppose that X is not isometric to
$(iii)\implies (i)$
: Suppose that X is not isometric to
![]() $\ell _p$
. By Theorem 3.8, X is isometric to
$\ell _p$
. By Theorem 3.8, X is isometric to
![]() $L_p[0,1]\oplus _p Y$
for some (possibly trivial) Banach space Y. By abusing the notation, we may assume that
$L_p[0,1]\oplus _p Y$
for some (possibly trivial) Banach space Y. By abusing the notation, we may assume that
![]() $X=L_p[0,1]\oplus _p Y$
. Let
$X=L_p[0,1]\oplus _p Y$
. Let
![]() $\mathbf {1}\in L_p[0,1]$
be the constant 1 function, and define
$\mathbf {1}\in L_p[0,1]$
be the constant 1 function, and define
![]() $x\in X=L_p[0,1]\oplus _p Y$
by
$x\in X=L_p[0,1]\oplus _p Y$
by
![]() $x=(\mathbf {1},0)$
. Now, fix
$x=(\mathbf {1},0)$
. Now, fix
![]() $N\in \mathbb {N}$
arbitrarily. Define
$N\in \mathbb {N}$
arbitrarily. Define
![]() $x_1,\ldots ,x_N\in X$
by
$x_1,\ldots ,x_N\in X$
by
![]() $x_i=(\chi _{[\frac {i-1}n,\frac in]},0)$
. Clearly,
$x_i=(\chi _{[\frac {i-1}n,\frac in]},0)$
. Clearly,
![]() $(N^{1/p}\cdot x_i)_{i=1}^N\equiv \ell ^n_p$
, and we have
$(N^{1/p}\cdot x_i)_{i=1}^N\equiv \ell ^n_p$
, and we have
![]() $x = \sum _{i=1}^N x_i$
.
$x = \sum _{i=1}^N x_i$
.
![]() $(ii)\implies (iv)$
is obvious, so it only remains to show that
$(ii)\implies (iv)$
is obvious, so it only remains to show that
![]() $(iv)\implies (ii)$
. For every
$(iv)\implies (ii)$
. For every
![]() $x\in X\setminus \{0\}$
,
$x\in X\setminus \{0\}$
,
![]() $\delta \in (0,1)$
,
$\delta \in (0,1)$
,
![]() $N\in \mathbb {N}$
,
$N\in \mathbb {N}$
,
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $x_1,\ldots ,x_N\in X$
, we denote by
$x_1,\ldots ,x_N\in X$
, we denote by
![]() $V(x,\delta ,N,\varepsilon ,(x_i)_{i=1}^N)$
the assertion that if
$V(x,\delta ,N,\varepsilon ,(x_i)_{i=1}^N)$
the assertion that if
![]() $(N^{1/p}\cdot x_i)_{i=1}^N{\stackrel {1+\varepsilon }{\sim } \ell _p^N}$
, then
$(N^{1/p}\cdot x_i)_{i=1}^N{\stackrel {1+\varepsilon }{\sim } \ell _p^N}$
, then
![]() $\|\frac x{\|x\|}-\sum _{i=1}^N x_i\|\ge \delta $
. The desired implication straightforwardly follows by the following two easy observations. First, if
$\|\frac x{\|x\|}-\sum _{i=1}^N x_i\|\ge \delta $
. The desired implication straightforwardly follows by the following two easy observations. First, if
![]() $x\in D\setminus \{0\}$
,
$x\in D\setminus \{0\}$
,
![]() $\delta $
, N and
$\delta $
, N and
![]() $\varepsilon $
are given, such that
$\varepsilon $
are given, such that
![]() $V(x,\delta ,N,\varepsilon ,(x_i)_{i=1}^N)$
holds for every
$V(x,\delta ,N,\varepsilon ,(x_i)_{i=1}^N)$
holds for every
![]() $x_1,\ldots ,x_N\in D$
, then
$x_1,\ldots ,x_N\in D$
, then
![]() $V(x,\delta ,N,\varepsilon ,(x_i)_{i=1}^N)$
holds for every
$V(x,\delta ,N,\varepsilon ,(x_i)_{i=1}^N)$
holds for every
![]() $x_1,\ldots ,x_N\in X$
. Second, if for every
$x_1,\ldots ,x_N\in X$
. Second, if for every
![]() $x\in D\setminus \{0\}$
and
$x\in D\setminus \{0\}$
and
![]() $\delta $
, there are N and
$\delta $
, there are N and
![]() $\varepsilon $
, such that
$\varepsilon $
, such that
![]() $V(x,\frac {1+\delta }2,N,\varepsilon ,(x_i)_{i=1}^N)$
holds for every
$V(x,\frac {1+\delta }2,N,\varepsilon ,(x_i)_{i=1}^N)$
holds for every
![]() $x_1,\ldots ,x_N\in X$
, then for every
$x_1,\ldots ,x_N\in X$
, then for every
![]() $x\in X\setminus \{0\}$
and
$x\in X\setminus \{0\}$
and
![]() $\delta $
, there are N and
$\delta $
, there are N and
![]() $\varepsilon $
, such that
$\varepsilon $
, such that
![]() $V(x,\delta ,N,\varepsilon ,(x_i)_{i=1}^N)$
holds for every
$V(x,\delta ,N,\varepsilon ,(x_i)_{i=1}^N)$
holds for every
![]() $x_1,\ldots ,x_N\in X$
.
$x_1,\ldots ,x_N\in X$
.
Proof of Proposition 4.4.
Let
![]() $\mathcal {F}$
be the set of those
$\mathcal {F}$
be the set of those
![]() $\nu \in \mathcal {P}_\infty $
for which
$\nu \in \mathcal {P}_\infty $
for which
![]() $X_\nu $
is an
$X_\nu $
is an
![]() $\mathcal {L}_{p,1+}$
-space. By Theorem 3.6,
$\mathcal {L}_{p,1+}$
-space. By Theorem 3.6,
![]() $\mathcal {F}\subseteq \mathcal {P}_\infty $
is a
$\mathcal {F}\subseteq \mathcal {P}_\infty $
is a
![]() $G_\delta $
-set. By Proposition 4.6
$G_\delta $
-set. By Proposition 4.6
![]() $(i)\Leftrightarrow (iv)$
, we have
$(i)\Leftrightarrow (iv)$
, we have
 $$\begin{align*}{\langle \ell_p\rangle_{\equiv}^{\mathcal{P}_\infty}} = \mathcal{F}\cap\bigcap_{v\in V\setminus\{0\}}\bigcap_{m\in\mathbb{N}}\bigcup_{n,k\in\mathbb{N}}V_{v,m,n,k},\end{align*}$$
$$\begin{align*}{\langle \ell_p\rangle_{\equiv}^{\mathcal{P}_\infty}} = \mathcal{F}\cap\bigcap_{v\in V\setminus\{0\}}\bigcap_{m\in\mathbb{N}}\bigcup_{n,k\in\mathbb{N}}V_{v,m,n,k},\end{align*}$$
where the closed (see Fact 3.10 and Lemma 1.5) sets
![]() $V_{v,m,n,k}$
are given by
$V_{v,m,n,k}$
are given by
 $$\begin{align*}\begin{aligned} V_{v,m,n,k}:=\Big\{\mu\in\mathcal{P}_\infty:\; & \mu(v)=0\text{, or for every } (v_i)_{i=1}^n\in V^n, \text{ we have}\\ & \neg\left((\sqrt[p]nv_i)_{i=1}^n{\stackrel{1+\frac 1k}{\sim} \ell_p^n}\right) \text{ or }\mu\big(\frac{v}{\mu(v)} - \sum_{i=1}^nv_i\big)\ge\frac 1m\Big\}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} V_{v,m,n,k}:=\Big\{\mu\in\mathcal{P}_\infty:\; & \mu(v)=0\text{, or for every } (v_i)_{i=1}^n\in V^n, \text{ we have}\\ & \neg\left((\sqrt[p]nv_i)_{i=1}^n{\stackrel{1+\frac 1k}{\sim} \ell_p^n}\right) \text{ or }\mu\big(\frac{v}{\mu(v)} - \sum_{i=1}^nv_i\big)\ge\frac 1m\Big\}. \end{aligned} \end{align*}$$
Thus,
![]() ${\langle \ell _p\rangle _{\equiv }^{\mathcal {P}_\infty }}$
is an
${\langle \ell _p\rangle _{\equiv }^{\mathcal {P}_\infty }}$
is an
![]() $F_{\sigma \delta }$
-set.
$F_{\sigma \delta }$
-set.
4.2 Dual unit balls and the Szlenk derivative
The purpose here is to show that mappings, which assign the dual unit ball and its Szlenk derivative to a separable Banach space, may be realized as Borel maps (see Lemmas 4.9 and 4.10). This will be later used in order to estimate the Borel complexity of the isometry class of the space
![]() $c_0$
because the isometric characterization of the space
$c_0$
because the isometric characterization of the space
![]() $c_0$
we use involves Szlenk derivatives (see Theorem 4.13). Note that the issue of handling Szlenk derivations as Borel maps was previously considered also by Bossard in [Reference Bossard7, page 141], but our approach is slightly different, as we prefer to work with the coding
$c_0$
we use involves Szlenk derivatives (see Theorem 4.13). Note that the issue of handling Szlenk derivations as Borel maps was previously considered also by Bossard in [Reference Bossard7, page 141], but our approach is slightly different, as we prefer to work with the coding
![]() $\mathcal {P}$
, and we also need to obtain an estimate on the Borel class of the mapping.
$\mathcal {P}$
, and we also need to obtain an estimate on the Borel class of the mapping.
Let us recall that given a real Banach space X, a
![]() $w^*$
-compact set
$w^*$
-compact set
![]() $F\subseteq X^*$
and
$F\subseteq X^*$
and
![]() $\varepsilon>0$
, the Szlenk derivative is given as
$\varepsilon>0$
, the Szlenk derivative is given as
We start by coding dual unit balls as closed subsets of
![]() $ B_{\ell _{\infty }} $
equipped with the weak* topology, that is the topology generated by elements of the unique predual
$ B_{\ell _{\infty }} $
equipped with the weak* topology, that is the topology generated by elements of the unique predual
![]() $\ell _1$
.
$\ell _1$
.
Lemma 4.7. Let X be a separable Banach space, and let
![]() $\{x_n\colon n\in \mathbb {N}\}$
be a dense set in
$\{x_n\colon n\in \mathbb {N}\}$
be a dense set in
![]() $B_X$
. Then the mapping
$B_X$
. Then the mapping
![]() $B_{X^{*}}\ni x^*\mapsto (x^*(x_n))_{n=1}^\infty \in B_{\ell _\infty }$
is
$B_{X^{*}}\ni x^*\mapsto (x^*(x_n))_{n=1}^\infty \in B_{\ell _\infty }$
is
![]() $\|\cdot \|$
-
$\|\cdot \|$
-
![]() $\|\cdot \|$
isometry and
$\|\cdot \|$
isometry and
![]() $w^*$
-
$w^*$
-
![]() $w^*$
homeomorphism onto the set
$w^*$
homeomorphism onto the set
 $$\begin{align*}\Omega(X):=\Big\{ (a_{n})_{n=1}^{\infty} \in B_{\ell_{\infty}} : M \subseteq \mathbb{N} \text{ finite} \Rightarrow \Big| \sum_{n \in M} a_{n} \Big| \leq \Big\Vert \sum_{n \in M} x_{n} \Big\Vert \Big\}. \end{align*}$$
$$\begin{align*}\Omega(X):=\Big\{ (a_{n})_{n=1}^{\infty} \in B_{\ell_{\infty}} : M \subseteq \mathbb{N} \text{ finite} \Rightarrow \Big| \sum_{n \in M} a_{n} \Big| \leq \Big\Vert \sum_{n \in M} x_{n} \Big\Vert \Big\}. \end{align*}$$
Proof. That the mapping is
![]() $w^*$
-
$w^*$
-
![]() $w^*$
homeomorphism onto its image follows from the fact that
$w^*$
homeomorphism onto its image follows from the fact that
![]() $B_{X^*}$
is
$B_{X^*}$
is
![]() $w^*$
-compact and the mapping is one-to-one (because
$w^*$
-compact and the mapping is one-to-one (because
![]() $(x_n)$
separate the points of
$(x_n)$
separate the points of
![]() $B_{X^*}$
) and
$B_{X^*}$
) and
![]() $w^*$
-
$w^*$
-
![]() $w^*$
continuous (because on
$w^*$
continuous (because on
![]() $B_{\ell _\infty }$
, the
$B_{\ell _\infty }$
, the
![]() $w^*$
-topology coincides with the topology of pointwise convergence). It is also straightforward to see that the mapping is isometry. Thus, it suffices to prove that
$w^*$
-topology coincides with the topology of pointwise convergence). It is also straightforward to see that the mapping is isometry. Thus, it suffices to prove that
The inclusion
![]() $ \subseteq $
is easy, let us prove
$ \subseteq $
is easy, let us prove
![]() $ \supseteq $
. Given numbers
$ \supseteq $
. Given numbers
![]() $ a_{1}, a_{2}, \dots $
satisfying
$ a_{1}, a_{2}, \dots $
satisfying
![]() $ | \sum _{n \in M} a_{n} | \leq \Vert \sum _{n \in M} x_{n} \Vert $
for any finite
$ | \sum _{n \in M} a_{n} | \leq \Vert \sum _{n \in M} x_{n} \Vert $
for any finite
![]() $ M \subseteq \mathbb {N} $
, we need to find
$ M \subseteq \mathbb {N} $
, we need to find
![]() $ x^{*} \in B_{X^{*}} $
, such that
$ x^{*} \in B_{X^{*}} $
, such that
![]() $ x^{*}(x_{n}) = a_{n} $
for each
$ x^{*}(x_{n}) = a_{n} $
for each
![]() $ n $
.
$ n $
.
Let us realize first that
-
•
 $ |a_{n} - a_{m}| \leq \Vert x_{n} - x_{m} \Vert $
for every
$ |a_{n} - a_{m}| \leq \Vert x_{n} - x_{m} \Vert $
for every
 $ n, m $
,
$ n, m $
, -
•
 $ |a_{n} + a_{m} - a_{l}| \leq \Vert x_{n} + x_{m} - x_{l} \Vert $
for every
$ |a_{n} + a_{m} - a_{l}| \leq \Vert x_{n} + x_{m} - x_{l} \Vert $
for every
 $ n, m, l $
.
$ n, m, l $
.
We check the first inequality only, the second inequality can be checked in the same way. Given
![]() $ \varepsilon> 0 $
, let
$ \varepsilon> 0 $
, let
![]() $ n' $
different from
$ n' $
different from
![]() $ n $
and
$ n $
and
![]() $ m $
be such that
$ m $
be such that
![]() $ \Vert x_{n} + x_{n'} \Vert < \varepsilon $
. We obtain
$ \Vert x_{n} + x_{n'} \Vert < \varepsilon $
. We obtain
![]() $ |a_{n} - a_{m}| = |(a_{n} + a_{n'}) - (a_{m} + a_{n'})| \leq |a_{n} + a_{n'}| + |a_{m} + a_{n'}| \leq \Vert x_{n} + x_{n'} \Vert + \Vert x_{m} + x_{n'} \Vert \leq 2 \Vert x_{n} + x_{n'} \Vert + \Vert x_{m} - x_{n} \Vert < 2 \varepsilon + \Vert x_{m} - x_{n} \Vert $
. Since
$ |a_{n} - a_{m}| = |(a_{n} + a_{n'}) - (a_{m} + a_{n'})| \leq |a_{n} + a_{n'}| + |a_{m} + a_{n'}| \leq \Vert x_{n} + x_{n'} \Vert + \Vert x_{m} + x_{n'} \Vert \leq 2 \Vert x_{n} + x_{n'} \Vert + \Vert x_{m} - x_{n} \Vert < 2 \varepsilon + \Vert x_{m} - x_{n} \Vert $
. Since
![]() $ \varepsilon> 0 $
was chosen arbitrarily, we arrive at
$ \varepsilon> 0 $
was chosen arbitrarily, we arrive at
![]() $ |a_{n} - a_{m}| \leq \Vert x_{m} - x_{n} \Vert $
. It follows that there is a function
$ |a_{n} - a_{m}| \leq \Vert x_{m} - x_{n} \Vert $
. It follows that there is a function
![]() $ f : B_{X} \to \mathbb {R} $
with the Lipschitz constant
$ f : B_{X} \to \mathbb {R} $
with the Lipschitz constant
![]() $ 1 $
, such that
$ 1 $
, such that
![]() $ f(x_{n}) = a_{n} $
for each
$ f(x_{n}) = a_{n} $
for each
![]() $ n $
. We claim that
$ n $
. We claim that
![]() $ f(u + v) = f(u) + f(v) $
and
$ f(u + v) = f(u) + f(v) $
and
![]() $f(\alpha u)=\alpha f(u)$
, whenever
$f(\alpha u)=\alpha f(u)$
, whenever
![]() $ u, \alpha u, v, u + v \in B_{X} $
. Given
$ u, \alpha u, v, u + v \in B_{X} $
. Given
![]() $ \varepsilon> 0 $
, we pick
$ \varepsilon> 0 $
, we pick
![]() $ n, m, l $
, such that
$ n, m, l $
, such that
![]() $ \Vert x_{n} - u \Vert < \varepsilon , \Vert x_{m} - v \Vert < \varepsilon $
and
$ \Vert x_{n} - u \Vert < \varepsilon , \Vert x_{m} - v \Vert < \varepsilon $
and
![]() $ \Vert x_{l} - (u + v) \Vert < \varepsilon $
. Then,
$ \Vert x_{l} - (u + v) \Vert < \varepsilon $
. Then,
![]() $ |f(u) + f(v) - f(u + v)| < |a_{n} + a_{m} - a_{l}| + 3\varepsilon \leq \Vert x_{n} + x_{m} - x_{l} \Vert + 3\varepsilon \leq \Vert u + v - (u + v) \Vert + 3\varepsilon + 3\varepsilon = 6\varepsilon $
. Since
$ |f(u) + f(v) - f(u + v)| < |a_{n} + a_{m} - a_{l}| + 3\varepsilon \leq \Vert x_{n} + x_{m} - x_{l} \Vert + 3\varepsilon \leq \Vert u + v - (u + v) \Vert + 3\varepsilon + 3\varepsilon = 6\varepsilon $
. Since
![]() $ \varepsilon> 0 $
was chosen arbitrarily, we arrive at
$ \varepsilon> 0 $
was chosen arbitrarily, we arrive at
![]() $ |f(u) + f(v) - f(u + v)| = 0 $
. This also shows that
$ |f(u) + f(v) - f(u + v)| = 0 $
. This also shows that
![]() $f(u/2)=f(u)/2$
, therefore,
$f(u/2)=f(u)/2$
, therefore,
![]() $f(\alpha u)=\alpha f(u)$
, provided that
$f(\alpha u)=\alpha f(u)$
, provided that
![]() $\alpha $
is a dyadic rational number. For a general
$\alpha $
is a dyadic rational number. For a general
![]() $\alpha $
, we use density of dyadic rationals and continuity of f.
$\alpha $
, we use density of dyadic rationals and continuity of f.
Now, it is easy to see that f uniquely extends to a linear functional on X.
By the above, every dual unit ball of a separable Banach space may be realized as a subset of the unit ball of
![]() $\ell _\infty $
. Thus, in what follows, we use the following convention.
$\ell _\infty $
. Thus, in what follows, we use the following convention.
Convention. Whenever we talk about open (closed,
![]() $F_\sigma $
, etc.) subsets of
$F_\sigma $
, etc.) subsets of
![]() $B_{l_\infty }$
, we always mean open (closed,
$B_{l_\infty }$
, we always mean open (closed,
![]() $F_\sigma $
, etc.) subsets in the weak* topology. On the other hand, whenever we talk about the diameter of a subset of
$F_\sigma $
, etc.) subsets in the weak* topology. On the other hand, whenever we talk about the diameter of a subset of
![]() $B_{l_\infty }$
, or about the distance of two subsets of
$B_{l_\infty }$
, or about the distance of two subsets of
![]() $B_{l_\infty }$
, we always mean the diameter, or the distance, with respect to the metric given by the norm of
$B_{l_\infty }$
, we always mean the diameter, or the distance, with respect to the metric given by the norm of
![]() $\ell _\infty $
. Also, we write only
$\ell _\infty $
. Also, we write only
![]() $\mathcal K(B_{l_\infty })$
instead of
$\mathcal K(B_{l_\infty })$
instead of
![]() $\mathcal K(B_{l_\infty },w^*)$
.
$\mathcal K(B_{l_\infty },w^*)$
.
Let us note the following easy observation for further references.
Lemma 4.8. Let P be a Polish space, X a metrizable compact,
![]() $\alpha \in [1,\omega _1)$
and
$\alpha \in [1,\omega _1)$
and
![]() $f:P\to \mathcal K(X)$
a mapping, such that
$f:P\to \mathcal K(X)$
a mapping, such that
![]() $\{p\in P\colon f(p)\subseteq W\}\in \boldsymbol {\Sigma }_\alpha ^0(P)\cup \boldsymbol {\Pi }_\alpha ^0(P)$
for every open
$\{p\in P\colon f(p)\subseteq W\}\in \boldsymbol {\Sigma }_\alpha ^0(P)\cup \boldsymbol {\Pi }_\alpha ^0(P)$
for every open
![]() $W\subseteq X$
. Then, f is
$W\subseteq X$
. Then, f is
![]() $\boldsymbol {\Sigma }_{\alpha +1}^0$
-measurable.
$\boldsymbol {\Sigma }_{\alpha +1}^0$
-measurable.
Proof. The sets of the form
where W ranges over all open subsets of X, form a subbasis of the topology of
![]() $\mathcal K(X)$
. So we only need to check that
$\mathcal K(X)$
. So we only need to check that
![]() $f^{-1}(U)$
is a
$f^{-1}(U)$
is a
![]() $\boldsymbol {\Sigma }_{\alpha +1}^0$
-set for every open set U of one of these forms. For the first case, this follows immediately from the assumptions, and for the second case, if
$\boldsymbol {\Sigma }_{\alpha +1}^0$
-set for every open set U of one of these forms. For the first case, this follows immediately from the assumptions, and for the second case, if
![]() $\{W_n\colon n\in \mathbb {N}\}$
is an open basis for the topology of X, we have
$\{W_n\colon n\in \mathbb {N}\}$
is an open basis for the topology of X, we have
 $$\begin{align*}f^{-1}(\{F\in\mathcal K(X)\colon F\cap W\neq\emptyset\}) = \bigcup _{n\in\mathbb{N} \text{, such that } \overline{W_n}\subseteq W} P\setminus \{p\in P\colon f(p)\subseteq X\setminus \overline{W_n}\}, \end{align*}$$
$$\begin{align*}f^{-1}(\{F\in\mathcal K(X)\colon F\cap W\neq\emptyset\}) = \bigcup _{n\in\mathbb{N} \text{, such that } \overline{W_n}\subseteq W} P\setminus \{p\in P\colon f(p)\subseteq X\setminus \overline{W_n}\}, \end{align*}$$
which, by the assumptions, is the countable union of sets from
![]() $\boldsymbol {\Sigma }_\alpha ^0(P)\cup \boldsymbol {\Pi }_\alpha ^0(P)$
.
$\boldsymbol {\Sigma }_\alpha ^0(P)\cup \boldsymbol {\Pi }_\alpha ^0(P)$
.
Lemma 4.9. For every
![]() $\nu \in \mathcal P$
, we can choose a countable dense subset
$\nu \in \mathcal P$
, we can choose a countable dense subset
![]() $\{x_n^\nu \colon n\in \mathbb N\}$
of
$\{x_n^\nu \colon n\in \mathbb N\}$
of
![]() $B_{X_\nu }$
in such a way that the mapping
$B_{X_\nu }$
in such a way that the mapping
![]() $\Omega \colon \mathcal P\rightarrow \mathcal K(B_{l_\infty },w^*)$
given by
$\Omega \colon \mathcal P\rightarrow \mathcal K(B_{l_\infty },w^*)$
given by
 $$\begin{align*}\Omega(\nu)=\left\{(a_n)_{n=1}^\infty\in B_{l_\infty}\colon M\subseteq\mathbb N\text{ finite} \Rightarrow\left|\sum\limits_{n\in M}a_n\right|\le \nu\left(\sum\limits_{n\in M}x_n^\nu\right)\right\} \end{align*}$$
$$\begin{align*}\Omega(\nu)=\left\{(a_n)_{n=1}^\infty\in B_{l_\infty}\colon M\subseteq\mathbb N\text{ finite} \Rightarrow\left|\sum\limits_{n\in M}a_n\right|\le \nu\left(\sum\limits_{n\in M}x_n^\nu\right)\right\} \end{align*}$$
is continuous.
Proof. First of all, we describe the choice of the sets
![]() $\{x_n^\nu \colon n\in \mathbb N\}$
,
$\{x_n^\nu \colon n\in \mathbb N\}$
,
![]() $\nu \in \mathcal P$
. Let
$\nu \in \mathcal P$
. Let
![]() $g\colon [0,\infty )\rightarrow [1,\infty )$
be given by
$g\colon [0,\infty )\rightarrow [1,\infty )$
be given by
![]() $g(t)=1$
for
$g(t)=1$
for
![]() $t\le 1$
and
$t\le 1$
and
![]() $g(t)=t$
for
$g(t)=t$
for
![]() $t>1$
. Let
$t>1$
. Let
![]() $\{v_n\colon n\in \mathbb N\}$
be an enumeration of all elements of the vector space V (which is naturally embedded into all Banach spaces
$\{v_n\colon n\in \mathbb N\}$
be an enumeration of all elements of the vector space V (which is naturally embedded into all Banach spaces
![]() $X_\nu $
,
$X_\nu $
,
![]() $\nu \in \mathcal P$
). Now, for every
$\nu \in \mathcal P$
). Now, for every
![]() $\nu \in \mathcal P$
and every
$\nu \in \mathcal P$
and every
![]() $n\in \mathbb N$
, we define
$n\in \mathbb N$
, we define
![]() $x_n^\nu \in B_{X_\nu }$
by
$x_n^\nu \in B_{X_\nu }$
by
![]() $x_n^\nu =\frac {v_n}{g(\nu (v_n))}$
. Then, for every
$x_n^\nu =\frac {v_n}{g(\nu (v_n))}$
. Then, for every
![]() $\nu \in \mathcal P$
, we have that
$\nu \in \mathcal P$
, we have that
![]() $\{x_n^\nu \colon n\in \mathbb N\}$
is a dense subset of
$\{x_n^\nu \colon n\in \mathbb N\}$
is a dense subset of
![]() $B_{X_\nu }$
. Note also that the set
$B_{X_\nu }$
. Note also that the set
 $$\begin{align*}\left\{\left(\nu,(a_n)_{n=1}^\infty\right)\in\mathcal P\times B_{l_\infty}\colon\left|\sum\limits_{n\in M}a_n\right|>\nu\left(\sum\limits_{n\in M}x_n^\nu\right)\right\} \end{align*}$$
$$\begin{align*}\left\{\left(\nu,(a_n)_{n=1}^\infty\right)\in\mathcal P\times B_{l_\infty}\colon\left|\sum\limits_{n\in M}a_n\right|>\nu\left(\sum\limits_{n\in M}x_n^\nu\right)\right\} \end{align*}$$
is open in
![]() $\mathcal P\times (B_{l_\infty },w^*)$
for every
$\mathcal P\times (B_{l_\infty },w^*)$
for every
![]() $M\subseteq \mathbb {N}$
finite (the proof is easy and is omitted).
$M\subseteq \mathbb {N}$
finite (the proof is easy and is omitted).
Pick an open subset U of
![]() $B_{\ell _{\infty }}$
. We have
$B_{\ell _{\infty }}$
. We have
 $$ \begin{align*} &\Omega^{-1}\left(\{F\in\mathcal K(B_{l_\infty})\colon F\subseteq U\}\right)\\ & \quad =\left\{\nu\in\mathcal P\colon\mathop{\forall}\limits_{(a_n)_{n=1}^\infty\in B_{l_\infty}}\left(\left(\mathop{\exists}\limits_{\substack{M\subseteq\mathbb N\\ \text{finite}}}\left|\sum\limits_{n\in M}a_n\right|>\nu\left(\sum\limits_{n\in M}x_n^\nu\right)\right)\text{ or }\left((a_n)_{n=1}^\infty\in U\right) \right)\right\}. \end{align*} $$
$$ \begin{align*} &\Omega^{-1}\left(\{F\in\mathcal K(B_{l_\infty})\colon F\subseteq U\}\right)\\ & \quad =\left\{\nu\in\mathcal P\colon\mathop{\forall}\limits_{(a_n)_{n=1}^\infty\in B_{l_\infty}}\left(\left(\mathop{\exists}\limits_{\substack{M\subseteq\mathbb N\\ \text{finite}}}\left|\sum\limits_{n\in M}a_n\right|>\nu\left(\sum\limits_{n\in M}x_n^\nu\right)\right)\text{ or }\left((a_n)_{n=1}^\infty\in U\right) \right)\right\}. \end{align*} $$
The complement of the last set is the projection of a closed subset of
![]() $\mathcal P\times (B_{l_\infty },w^*)$
onto the first coordinate. As the space
$\mathcal P\times (B_{l_\infty },w^*)$
onto the first coordinate. As the space
![]() $(B_{l_\infty },w^*)$
is compact, the complement is a closed subset of
$(B_{l_\infty },w^*)$
is compact, the complement is a closed subset of
![]() $\mathcal P$
. It remains to show that the set
$\mathcal P$
. It remains to show that the set
![]() $\{\nu \in \mathcal {P}\colon \Omega (\nu )\cap U\neq \emptyset \}$
is open. Pick
$\{\nu \in \mathcal {P}\colon \Omega (\nu )\cap U\neq \emptyset \}$
is open. Pick
![]() $\nu \in \mathcal {P}$
with
$\nu \in \mathcal {P}$
with
![]() $\Omega (\nu )\cap U\neq \emptyset $
. By Lemma 4.7, there exists
$\Omega (\nu )\cap U\neq \emptyset $
. By Lemma 4.7, there exists
![]() $x^*\in B_{X_\nu ^*}$
, such that the sequence
$x^*\in B_{X_\nu ^*}$
, such that the sequence
![]() $(a_n)_{n=1}^\infty $
given by
$(a_n)_{n=1}^\infty $
given by
![]() $a_n=x^*(x_n^\nu )$
,
$a_n=x^*(x_n^\nu )$
,
![]() $n\in \mathbb {N}$
, satisfies
$n\in \mathbb {N}$
, satisfies
![]() $(a_n)_{n=1}^\infty \in \Omega (\nu )\cap U$
. Let
$(a_n)_{n=1}^\infty \in \Omega (\nu )\cap U$
. Let
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $N\in \mathbb {N}$
be such that
$N\in \mathbb {N}$
be such that
![]() $(b_n)_{n=1}^\infty \in \ell _\infty $
is an element of U whenever
$(b_n)_{n=1}^\infty \in \ell _\infty $
is an element of U whenever
![]() $|b_n-a_n|<\varepsilon $
for every
$|b_n-a_n|<\varepsilon $
for every
![]() $1\leq n\leq N$
. Let us consider subspaces of
$1\leq n\leq N$
. Let us consider subspaces of
![]() $c_{00}$
, given as
$c_{00}$
, given as
![]() $E=\operatorname {span}\{v_1,\ldots ,v_N\}$
and
$E=\operatorname {span}\{v_1,\ldots ,v_N\}$
and
![]() $F=\{x\in E\colon \nu (x)=0\}$
. Let G be such that
$F=\{x\in E\colon \nu (x)=0\}$
. Let G be such that
![]() $F\oplus G = E$
and
$F\oplus G = E$
and
![]() $\overline {G\cap V}=G$
(it is enough to pick a basis of E consisting of vectors from V, and using the Gauss elimination to determine which vectors from the basis generate the algebraic complement to F). Let
$\overline {G\cap V}=G$
(it is enough to pick a basis of E consisting of vectors from V, and using the Gauss elimination to determine which vectors from the basis generate the algebraic complement to F). Let
![]() $P_F:E\to F$
and
$P_F:E\to F$
and
![]() $P_G:E\to G$
be linear projections onto F and G, respectively. Pick
$P_G:E\to G$
be linear projections onto F and G, respectively. Pick
![]() $\delta < \min \{1,\tfrac {\varepsilon }{3}\}$
, such that
$\delta < \min \{1,\tfrac {\varepsilon }{3}\}$
, such that
![]() $ \delta \cdot | x^{*}(P_{G}v_{n}) | < \varepsilon / 3 $
for every
$ \delta \cdot | x^{*}(P_{G}v_{n}) | < \varepsilon / 3 $
for every
![]() $1\leq n\leq N$
. Finally, put
$1\leq n\leq N$
. Finally, put
 $$\begin{align*}\begin{aligned} \mathcal{O}:=& \{\nu'\in\mathcal{P}\colon \frac{1}{1-\delta}\nu(x)>\nu'(x)>(1-\delta)\nu(x)\text{ for every } x\in G\setminus \{ 0 \}\}\cap\\ & \qquad \bigcap_{n=1}^N\{\nu'\in\mathcal{P}\colon \nu'(P_{F}v_{n}) < \delta, | \nu'(v_{n}) - \nu(v_{n}) | < \delta\}. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \mathcal{O}:=& \{\nu'\in\mathcal{P}\colon \frac{1}{1-\delta}\nu(x)>\nu'(x)>(1-\delta)\nu(x)\text{ for every } x\in G\setminus \{ 0 \}\}\cap\\ & \qquad \bigcap_{n=1}^N\{\nu'\in\mathcal{P}\colon \nu'(P_{F}v_{n}) < \delta, | \nu'(v_{n}) - \nu(v_{n}) | < \delta\}. \end{aligned}\end{align*}$$
Then,
![]() $\mathcal {O}$
is an open neighbourhood of
$\mathcal {O}$
is an open neighbourhood of
![]() $\nu $
, which easily follows from Lemma 1.5 and the fact that
$\nu $
, which easily follows from Lemma 1.5 and the fact that
![]() $G\cap V$
is dense in G.
$G\cap V$
is dense in G.
We will show that
![]() $\mathcal {O}\subseteq \{\nu '\in \mathcal {P}\colon \Omega (\nu ')\cap U\neq \emptyset \}$
. Pick
$\mathcal {O}\subseteq \{\nu '\in \mathcal {P}\colon \Omega (\nu ')\cap U\neq \emptyset \}$
. Pick
![]() $\nu '\in \mathcal {O}$
. If we put
$\nu '\in \mathcal {O}$
. If we put
![]() $y^*(x):= (1-\delta )x^*(x)$
for
$y^*(x):= (1-\delta )x^*(x)$
for
![]() $x\in G$
, then
$x\in G$
, then
![]() $|y^*(x)|=(1-\delta )|x^*(x)| \leq (1 - \delta ) \nu (x) \leq \nu '(x) $
for every
$|y^*(x)|=(1-\delta )|x^*(x)| \leq (1 - \delta ) \nu (x) \leq \nu '(x) $
for every
![]() $ x \in G $
, and so by the Hahn-Banach theorem, we may extend
$ x \in G $
, and so by the Hahn-Banach theorem, we may extend
![]() $y^*$
to a functional (denoted again by
$y^*$
to a functional (denoted again by
![]() $y^*$
) from the dual unit ball of
$y^*$
) from the dual unit ball of
![]() $X_{\nu '}$
. By Lemma 4.7, the sequence
$X_{\nu '}$
. By Lemma 4.7, the sequence
![]() $(b_n)_{n=1}^\infty $
given by
$(b_n)_{n=1}^\infty $
given by
![]() $b_n:=y^*(x_n^{\nu '})$
,
$b_n:=y^*(x_n^{\nu '})$
,
![]() $n\in \mathbb {N}$
, is in
$n\in \mathbb {N}$
, is in
![]() $\Omega (\nu ')$
. Moreover, for every
$\Omega (\nu ')$
. Moreover, for every
![]() $1\leq n\leq N$
, we have
$1\leq n\leq N$
, we have
 $$\begin{align*}\begin{aligned} |b_n-a_n| & = \big| \tfrac{1}{g(\nu'(v_{n}))} y^{*}(v_{n}) - \tfrac{1}{g(\nu(v_{n}))} x^{*}(v_{n}) \big|\\[3pt] & = \big| \tfrac{1}{g(\nu'(v_{n}))} y^{*}(P_{F}v_{n}) + \tfrac{1}{g(\nu'(v_{n}))} y^{*}(P_{G}v_{n}) - \tfrac{1}{g(\nu(v_{n}))} x^{*}(P_{F}v_{n} + P_{G}v_{n}) \big|\\[3pt] & = \big| \tfrac{1}{g(\nu'(v_{n}))} y^{*}(P_{F}v_{n}) + \tfrac{1}{g(\nu'(v_{n}))} (1-\delta)x^*(P_{G}v_{n}) - \tfrac{1}{g(\nu(v_{n}))} x^{*}(P_{G}v_{n}) \big|\\[3pt] & \leq \tfrac{1}{g(\nu'(v_{n}))} |y^{*}(P_{F}v_{n})| + \big| \tfrac{1}{g(\nu'(v_{n}))} (1 - \delta) - \tfrac{1}{g(\nu(v_{n}))} \big| | x^{*}(P_{G}v_{n}) |\\[3pt] & \leq \delta + \big(|g(\nu(v_{n})) - g(\nu'(v_{n}))| + \delta\big)|x^{*}(P_{G}v_{n})|\\[3pt] & \leq \delta + 2\delta |x^*(P_{G}v_{n})| < \varepsilon, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} |b_n-a_n| & = \big| \tfrac{1}{g(\nu'(v_{n}))} y^{*}(v_{n}) - \tfrac{1}{g(\nu(v_{n}))} x^{*}(v_{n}) \big|\\[3pt] & = \big| \tfrac{1}{g(\nu'(v_{n}))} y^{*}(P_{F}v_{n}) + \tfrac{1}{g(\nu'(v_{n}))} y^{*}(P_{G}v_{n}) - \tfrac{1}{g(\nu(v_{n}))} x^{*}(P_{F}v_{n} + P_{G}v_{n}) \big|\\[3pt] & = \big| \tfrac{1}{g(\nu'(v_{n}))} y^{*}(P_{F}v_{n}) + \tfrac{1}{g(\nu'(v_{n}))} (1-\delta)x^*(P_{G}v_{n}) - \tfrac{1}{g(\nu(v_{n}))} x^{*}(P_{G}v_{n}) \big|\\[3pt] & \leq \tfrac{1}{g(\nu'(v_{n}))} |y^{*}(P_{F}v_{n})| + \big| \tfrac{1}{g(\nu'(v_{n}))} (1 - \delta) - \tfrac{1}{g(\nu(v_{n}))} \big| | x^{*}(P_{G}v_{n}) |\\[3pt] & \leq \delta + \big(|g(\nu(v_{n})) - g(\nu'(v_{n}))| + \delta\big)|x^{*}(P_{G}v_{n})|\\[3pt] & \leq \delta + 2\delta |x^*(P_{G}v_{n})| < \varepsilon, \end{aligned} \end{align*}$$
and so
![]() $(b_n)_{n=1}^\infty \in \Omega (\nu ')\cap U$
. Hence,
$(b_n)_{n=1}^\infty \in \Omega (\nu ')\cap U$
. Hence,
![]() $\mathcal {O}\subseteq \{\nu '\in \mathcal {P}\colon \Omega (\nu ')\cap U\neq \emptyset \}$
, so
$\mathcal {O}\subseteq \{\nu '\in \mathcal {P}\colon \Omega (\nu ')\cap U\neq \emptyset \}$
, so
![]() $\{\nu \in \mathcal {P}\colon \Omega (\nu )\cap U\neq \emptyset \}$
is an open set and
$\{\nu \in \mathcal {P}\colon \Omega (\nu )\cap U\neq \emptyset \}$
is an open set and
![]() $\Omega $
is a continuous mapping.
$\Omega $
is a continuous mapping.
We close this subsection by realizing that the mapping which assigns to every compact subset of
![]() $B_{\ell _\infty }$
its Szlenk derivative is Borel. Let us note that the result is almost optimal, as the mapping from Lemma 4.10 is not
$B_{\ell _\infty }$
its Szlenk derivative is Borel. Let us note that the result is almost optimal, as the mapping from Lemma 4.10 is not
![]() $F_\sigma $
-measurable (see Corollary 4.14).
$F_\sigma $
-measurable (see Corollary 4.14).
Lemma 4.10. For every
![]() $\varepsilon>0$
, the function
$\varepsilon>0$
, the function
![]() $s_\varepsilon \colon \mathcal K(B_{l_\infty },w^*)\rightarrow \mathcal K(B_{l_\infty },w^*)$
given by
$s_\varepsilon \colon \mathcal K(B_{l_\infty },w^*)\rightarrow \mathcal K(B_{l_\infty },w^*)$
given by
![]() $s_\varepsilon (F)=F^{\prime }_\varepsilon $
is
$s_\varepsilon (F)=F^{\prime }_\varepsilon $
is
![]() $\boldsymbol {\Sigma }_3^0$
-measurable.
$\boldsymbol {\Sigma }_3^0$
-measurable.
Proof. First, we claim that the set
is an
![]() $F_\sigma $
-set for every open subset U of
$F_\sigma $
-set for every open subset U of
![]() $B_{l_\infty }$
. Indeed, the set above equals
$B_{l_\infty }$
. Indeed, the set above equals
 $$ \begin{align*} &\bigcup_{k=1}^\infty\{F\in\mathcal K(B_{l_\infty})\colon\text{diam}(U\cap F)\le\varepsilon-\tfrac 1k\}\\ & \quad =\bigcup_{k=1}^\infty\;\bigcap_{\substack{O_1,O_2\text{ open subsets of }U\\ \text{dist}(O_1,O_2)\ge\varepsilon-\tfrac 1k}}\;\{F\in\mathcal K(B_{l_\infty})\colon F\cap O_1=\emptyset\text{ or }F\cap O_2=\emptyset\}, \end{align*} $$
$$ \begin{align*} &\bigcup_{k=1}^\infty\{F\in\mathcal K(B_{l_\infty})\colon\text{diam}(U\cap F)\le\varepsilon-\tfrac 1k\}\\ & \quad =\bigcup_{k=1}^\infty\;\bigcap_{\substack{O_1,O_2\text{ open subsets of }U\\ \text{dist}(O_1,O_2)\ge\varepsilon-\tfrac 1k}}\;\{F\in\mathcal K(B_{l_\infty})\colon F\cap O_1=\emptyset\text{ or }F\cap O_2=\emptyset\}, \end{align*} $$
and our claim immediately follows.
Now, let W be an open subset of
![]() $B_{l_\infty }$
. Let
$B_{l_\infty }$
. Let
![]() $\{U_n\colon n\in \mathbb N\}$
be an open basis for the weak* topology of
$\{U_n\colon n\in \mathbb N\}$
be an open basis for the weak* topology of
![]() $B_{l_\infty }$
. Then, we have (using a compactness argument in the last equality) that
$B_{l_\infty }$
. Then, we have (using a compactness argument in the last equality) that
 $$ \begin{align*} &s_\varepsilon^{-1}(\{F\in\mathcal K(B_{l_\infty})\colon F\subseteq W\})\\ & \quad =\{F\in\mathcal K(B_{l_\infty})\colon\mathop{\exists}\limits_{M\subseteq\mathbb N}\big(\big(\mathop{\forall}\limits_{n\in M}\text{diam}(U_n\cap F)<\varepsilon\big)\text{ and }\big(F\subseteq W\cup\bigcup_{n\in M}U_n\big)\big)\}\\ & \quad =\{F\in\mathcal K(B_{l_\infty})\colon\mathop{\exists}\limits_{\substack{M\subseteq\mathbb N\\ \text{finite}}}\big(\big(\mathop{\forall}\limits_{n\in M}\text{diam}(U_n\cap F)<\varepsilon\big)\text{ and }\big(F\subseteq W\cup\bigcup_{n\in M}U_n\big)\big)\}, \end{align*} $$
$$ \begin{align*} &s_\varepsilon^{-1}(\{F\in\mathcal K(B_{l_\infty})\colon F\subseteq W\})\\ & \quad =\{F\in\mathcal K(B_{l_\infty})\colon\mathop{\exists}\limits_{M\subseteq\mathbb N}\big(\big(\mathop{\forall}\limits_{n\in M}\text{diam}(U_n\cap F)<\varepsilon\big)\text{ and }\big(F\subseteq W\cup\bigcup_{n\in M}U_n\big)\big)\}\\ & \quad =\{F\in\mathcal K(B_{l_\infty})\colon\mathop{\exists}\limits_{\substack{M\subseteq\mathbb N\\ \text{finite}}}\big(\big(\mathop{\forall}\limits_{n\in M}\text{diam}(U_n\cap F)<\varepsilon\big)\text{ and }\big(F\subseteq W\cup\bigcup_{n\in M}U_n\big)\big)\}, \end{align*} $$
and our previous claim implies that the last set is an
![]() $F_\sigma $
-set.
$F_\sigma $
-set.
Thus, by Lemma 4.8, the mapping
![]() $s_\varepsilon $
is
$s_\varepsilon $
is
![]() $\boldsymbol {\Sigma }_3^0$
-measurable.
$\boldsymbol {\Sigma }_3^0$
-measurable.
4.3 The space
 $c_0$
$c_0$
The main goal of this subsection is to prove the following.
Proposition 4.11.
![]() ${\langle c_0\rangle _{\equiv }}$
is an
${\langle c_0\rangle _{\equiv }}$
is an
![]() $F_{\sigma \delta }$
-set in
$F_{\sigma \delta }$
-set in
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Our estimate on the Borel complexity of the isometry class of
![]() $c_0$
is based on an isometric characterization of
$c_0$
is based on an isometric characterization of
![]() $c_0$
among
$c_0$
among
![]() $\mathcal {L}_{\infty ,1+}$
-spaces. Let us recall that
$\mathcal {L}_{\infty ,1+}$
-spaces. Let us recall that
![]() $\mathcal {L}_{\infty ,1+}$
-spaces are often called the Lindenstrauss spaces or
$\mathcal {L}_{\infty ,1+}$
-spaces are often called the Lindenstrauss spaces or
![]() $L_1$
predual spaces. There are many different characterizations of this class of spaces. Let us recall one which we will use further (see, e.g. [Reference Lacey38, page 232], the ‘in particular’ part follows from the easy part of Theorem 3.8 applied to
$L_1$
predual spaces. There are many different characterizations of this class of spaces. Let us recall one which we will use further (see, e.g. [Reference Lacey38, page 232], the ‘in particular’ part follows from the easy part of Theorem 3.8 applied to
![]() $X^*$
and the fact that
$X^*$
and the fact that
![]() $L_1[0,1]$
is not isomorphic to a subspace of a separable dual Banach space, see, e.g. [Reference Albiac and Kalton1, Theorem 6.3.7]).
$L_1[0,1]$
is not isomorphic to a subspace of a separable dual Banach space, see, e.g. [Reference Albiac and Kalton1, Theorem 6.3.7]).
Theorem 4.12. Let X be a Banach space. Then the following conditions are equivalent.
-
(i) X is an
 $\mathcal {L}_{\infty ,1+}$
-space.
$\mathcal {L}_{\infty ,1+}$
-space. -
(ii)
 $X^*$
is isometric to
$X^*$
is isometric to
 $L_1(\mu )$
for some measure
$L_1(\mu )$
for some measure
 $\mu $
.
$\mu $
.
In particular, if X is an
![]() $\mathcal {L}_{\infty ,1+}$
-space with
$\mathcal {L}_{\infty ,1+}$
-space with
![]() $X^*$
separable, then
$X^*$
separable, then
![]() $X^*$
is isometric to
$X^*$
is isometric to
![]() $\ell _1$
.
$\ell _1$
.
The isometric characterization of
![]() $c_0$
, which we use for our upper estimate, follows.
$c_0$
, which we use for our upper estimate, follows.
Theorem 4.13. Let
![]() $ X $
be a separable
$ X $
be a separable
![]() $ \mathcal {L}_{\infty , 1+} $
-space, and let
$ \mathcal {L}_{\infty , 1+} $
-space, and let
![]() $ 0 < \varepsilon < 1 $
. Then
$ 0 < \varepsilon < 1 $
. Then
![]() $ X $
is isometric to
$ X $
is isometric to
![]() $ c_{0} $
if and only if
$ c_{0} $
if and only if
Proof. First, we show that
![]() $ (B_{c_{0}^{*}})^{\prime }_{2\varepsilon } = (1 - \varepsilon ) B_{c_{0}^{*}} $
(this must be known, but we were unable to find any reference). By a standard argument,
$ (B_{c_{0}^{*}})^{\prime }_{2\varepsilon } = (1 - \varepsilon ) B_{c_{0}^{*}} $
(this must be known, but we were unable to find any reference). By a standard argument,
![]() $ (1 - \varepsilon ) B_{X^{*}} \subseteq (B_{X^{*}})^{\prime }_{2\varepsilon } $
for any infinite-dimensional
$ (1 - \varepsilon ) B_{X^{*}} \subseteq (B_{X^{*}})^{\prime }_{2\varepsilon } $
for any infinite-dimensional
![]() $ X $
. (Let
$ X $
. (Let
![]() $ x^{*} \in (1 - \varepsilon ) B_{X^{*}} $
. Any
$ x^{*} \in (1 - \varepsilon ) B_{X^{*}} $
. Any
![]() $ w^{*} $
-open set
$ w^{*} $
-open set
![]() $ U $
containing
$ U $
containing
![]() $ 0 $
contains also both
$ 0 $
contains also both
![]() $ y^{*} $
and
$ y^{*} $
and
![]() $ -y^{*} $
for some
$ -y^{*} $
for some
![]() $ y^{*} \in S_{X^{*}} $
, and so
$ y^{*} \in S_{X^{*}} $
, and so
![]() $ \mathrm {diam}(U \cap B_{X^{*}}) = 2 $
. For this reason, any
$ \mathrm {diam}(U \cap B_{X^{*}}) = 2 $
. For this reason, any
![]() $ w^{*} $
-open set
$ w^{*} $
-open set
![]() $ V $
containing
$ V $
containing
![]() $ x^{*} $
fulfils
$ x^{*} $
fulfils
![]() $ \mathrm {diam}(V \cap (x^{*} + \varepsilon B_{X^{*}})) = 2\varepsilon $
, in particular,
$ \mathrm {diam}(V \cap (x^{*} + \varepsilon B_{X^{*}})) = 2\varepsilon $
, in particular,
![]() $ \mathrm {diam}(V \cap B_{X^{*}}) \geq 2\varepsilon $
. This proves that
$ \mathrm {diam}(V \cap B_{X^{*}}) \geq 2\varepsilon $
. This proves that
![]() $ x^{*} \in (B_{X^{*}})^{\prime }_{2\varepsilon } $
.)
$ x^{*} \in (B_{X^{*}})^{\prime }_{2\varepsilon } $
.)
Let us show that the opposite inclusion takes place for
![]() $ X = c_{0} $
. Assuming
$ X = c_{0} $
. Assuming
![]() $ 1 - \varepsilon < \Vert x^{*} \Vert \leq 1 $
, we need to check that
$ 1 - \varepsilon < \Vert x^{*} \Vert \leq 1 $
, we need to check that
![]() $ x^{*} \notin (B_{c_{0}^{*}})^{\prime }_{2\varepsilon } $
. Let
$ x^{*} \notin (B_{c_{0}^{*}})^{\prime }_{2\varepsilon } $
. Let
![]() $ e_{1}, e_{2}, \dots $
be the canonical basis of
$ e_{1}, e_{2}, \dots $
be the canonical basis of
![]() $ c_{0} $
. Let
$ c_{0} $
. Let
![]() $ n $
be large enough that
$ n $
be large enough that
![]() $ \sum _{i=1}^{n} |x^{*}(e_{i})|> 1 - \varepsilon $
, and let
$ \sum _{i=1}^{n} |x^{*}(e_{i})|> 1 - \varepsilon $
, and let
![]() $ \delta> 0 $
satisfy
$ \delta> 0 $
satisfy
![]() $ 2 \delta n < [\sum _{i=1}^{n} |x^{*}(e_{i})|] - (1 - \varepsilon ) $
. Let
$ 2 \delta n < [\sum _{i=1}^{n} |x^{*}(e_{i})|] - (1 - \varepsilon ) $
. Let
For
![]() $ y^{*}, z^{*} \in U \cap B_{c_{0}^{*}} $
, we have
$ y^{*}, z^{*} \in U \cap B_{c_{0}^{*}} $
, we have
 $$ \begin{align*}\sum_{i=n+1}^{\infty} |y^{*}(e_{i})| = \Vert y^{*} \Vert - \sum_{i=1}^{n} |y^{*}(e_{i})| \leq 1 - \sum_{i=1}^{n} |x^{*}(e_{i})| + \delta n,\end{align*} $$
$$ \begin{align*}\sum_{i=n+1}^{\infty} |y^{*}(e_{i})| = \Vert y^{*} \Vert - \sum_{i=1}^{n} |y^{*}(e_{i})| \leq 1 - \sum_{i=1}^{n} |x^{*}(e_{i})| + \delta n,\end{align*} $$
and the same for
![]() $ z^{*} $
, thus
$ z^{*} $
, thus
 $$ \begin{align*}\Vert y^{*} - z^{*} \Vert &\leq \sum_{i=1}^{n} |y^{*}(e_{i}) - z^{*}(e_{i})| + \sum_{i=n+1}^{\infty} |y^{*}(e_{i})| + \sum_{i=n+1}^{\infty} |z^{*}(e_{i})|\\&\leq 2 \delta n + 2 \Big[ 1 - \sum_{i=1}^{n} |x^{*}(e_{i})| \Big] + 2 \delta n. \end{align*} $$
$$ \begin{align*}\Vert y^{*} - z^{*} \Vert &\leq \sum_{i=1}^{n} |y^{*}(e_{i}) - z^{*}(e_{i})| + \sum_{i=n+1}^{\infty} |y^{*}(e_{i})| + \sum_{i=n+1}^{\infty} |z^{*}(e_{i})|\\&\leq 2 \delta n + 2 \Big[ 1 - \sum_{i=1}^{n} |x^{*}(e_{i})| \Big] + 2 \delta n. \end{align*} $$
We get
![]() $ \mathrm {diam}(U \cap B_{c_{0}^{*}}) \leq 4 \delta n + 2 [ 1 - \sum _{i=1}^{n} |x^{*}(e_{i})| ] < 2 \varepsilon $
.
$ \mathrm {diam}(U \cap B_{c_{0}^{*}}) \leq 4 \delta n + 2 [ 1 - \sum _{i=1}^{n} |x^{*}(e_{i})| ] < 2 \varepsilon $
.
Now, let us assume that
![]() $ X $
satisfies
$ X $
satisfies
![]() $ (B_{X^{*}})^{\prime }_{2\varepsilon } = (1 - \varepsilon ) B_{X^{*}} $
. Clearly,
$ (B_{X^{*}})^{\prime }_{2\varepsilon } = (1 - \varepsilon ) B_{X^{*}} $
. Clearly,
![]() $ X $
is infinite-dimensional, as
$ X $
is infinite-dimensional, as
![]() $ (B_{X^{*}})^{\prime }_{2\varepsilon } $
is nonempty. Moreover,
$ (B_{X^{*}})^{\prime }_{2\varepsilon } $
is nonempty. Moreover,
![]() $ X^{*} $
is separable because the Szlenk index of X is
$ X^{*} $
is separable because the Szlenk index of X is
![]() $ \omega $
(see, e.g. [Reference Lancien39, Proposition 3 and Theorem 1]). Thus, by Theorem 4.12, the dual
$ \omega $
(see, e.g. [Reference Lancien39, Proposition 3 and Theorem 1]). Thus, by Theorem 4.12, the dual
![]() $ X^{*} $
is isometric to
$ X^{*} $
is isometric to
![]() $ \ell _{1} $
. Let
$ \ell _{1} $
. Let
![]() $ e^{*}_{1}, e^{*}_{2}, \dots $
be a basis of
$ e^{*}_{1}, e^{*}_{2}, \dots $
be a basis of
![]() $ X^{*} $
that is
$ X^{*} $
that is
![]() $ 1 $
-equivalent to the canonical basis of
$ 1 $
-equivalent to the canonical basis of
![]() $ \ell _{1} $
, and let
$ \ell _{1} $
, and let
![]() $ e^{**}_{1}, e^{**}_{2}, \dots $
be the dual basic sequence in
$ e^{**}_{1}, e^{**}_{2}, \dots $
be the dual basic sequence in
![]() $ X^{**} $
. We claim that the functionals
$ X^{**} $
. We claim that the functionals
![]() $ e^{**}_{n} $
are
$ e^{**}_{n} $
are
![]() $ w^{*} $
-continuous. Suppose that
$ w^{*} $
-continuous. Suppose that
![]() $ e^{**}_{n} $
is not
$ e^{**}_{n} $
is not
![]() $ w^{*} $
-continuous for some
$ w^{*} $
-continuous for some
![]() $ n $
. It means that
$ n $
. It means that
![]() $ \{ x^{*} \in X^{*} : e^{**}_{n}(x^{*}) = 0 \} $
is not
$ \{ x^{*} \in X^{*} : e^{**}_{n}(x^{*}) = 0 \} $
is not
![]() $ w^{*} $
-closed. By the Banach-Dieudonné theorem, the set
$ w^{*} $
-closed. By the Banach-Dieudonné theorem, the set
![]() $ \{ x^{*} \in B_{X^{*}} : e^{**}_{n}(x^{*}) = 0 \} $
is not
$ \{ x^{*} \in B_{X^{*}} : e^{**}_{n}(x^{*}) = 0 \} $
is not
![]() $ w^{*} $
-closed, too. The space
$ w^{*} $
-closed, too. The space
![]() $ (B_{X^{*}}, w^{*}) $
is metrizable, so there is a sequence
$ (B_{X^{*}}, w^{*}) $
is metrizable, so there is a sequence
![]() $ x^{*}_{k} $
in
$ x^{*}_{k} $
in
![]() $ B_{X^{*}} $
with
$ B_{X^{*}} $
with
![]() $ e^{**}_{n}(x^{*}_{k}) = 0 $
, which
$ e^{**}_{n}(x^{*}_{k}) = 0 $
, which
![]() $ w^{*} $
-converges to some
$ w^{*} $
-converges to some
![]() $ x^{*} $
with
$ x^{*} $
with
![]() $ e^{**}_{n}(x^{*}) \neq 0 $
. Without loss of generality, let us assume that
$ e^{**}_{n}(x^{*}) \neq 0 $
. Without loss of generality, let us assume that
![]() $ e^{**}_{n}(x^{*})> 0 $
and that
$ e^{**}_{n}(x^{*})> 0 $
and that
![]() $ e^{**}_{i}(x^{*}_{k}) $
converges to some
$ e^{**}_{i}(x^{*}_{k}) $
converges to some
![]() $ a_{i} $
for every
$ a_{i} $
for every
![]() $ i $
. Then, clearly,
$ i $
. Then, clearly,
![]() $ a_{n} = 0 $
. Note that
$ a_{n} = 0 $
. Note that
![]() $ \sum _{i=1}^{\infty } |a_{i}| \leq 1 $
, which follows from the fact that
$ \sum _{i=1}^{\infty } |a_{i}| \leq 1 $
, which follows from the fact that
![]() $ \sum _{i=1}^{\infty } |e^{**}_{i}(x^{*}_{k})| = \Vert x^{*}_{k} \Vert \leq 1 $
for every
$ \sum _{i=1}^{\infty } |e^{**}_{i}(x^{*}_{k})| = \Vert x^{*}_{k} \Vert \leq 1 $
for every
![]() $ k $
. Let us put
$ k $
. Let us put
![]() $ a^{*} = \sum _{i=1}^{\infty } a_{i} e^{*}_{i} $
,
$ a^{*} = \sum _{i=1}^{\infty } a_{i} e^{*}_{i} $
,
![]() $ y^{*}_{k} = x^{*}_{k} - a^{*} $
and
$ y^{*}_{k} = x^{*}_{k} - a^{*} $
and
![]() $ y^{*} = x^{*} - a^{*} $
. Then,
$ y^{*} = x^{*} - a^{*} $
. Then,
![]() $ e^{**}_{n}(y^{*}_{k}) = 0, e^{**}_{n}(y^{*})> 0 $
, the sequence
$ e^{**}_{n}(y^{*}_{k}) = 0, e^{**}_{n}(y^{*})> 0 $
, the sequence
![]() $ y^{*}_{k} $
is
$ y^{*}_{k} $
is
![]() $ w^{*} $
-convergent to
$ w^{*} $
-convergent to
![]() $ y^{*} $
and, moreover,
$ y^{*} $
and, moreover,
![]() $ e^{**}_{i}(y^{*}_{k}) $
converges to
$ e^{**}_{i}(y^{*}_{k}) $
converges to
![]() $ 0 $
for every
$ 0 $
for every
![]() $ i $
. Choosing a subsequence and making a small perturbation, we can find a sequence
$ i $
. Choosing a subsequence and making a small perturbation, we can find a sequence
![]() $ z^{*}_{l} $
which is a block sequence with respect to the basis
$ z^{*}_{l} $
which is a block sequence with respect to the basis
![]() $ e^{*}_{i} $
and which still
$ e^{*}_{i} $
and which still
![]() $ w^{*} $
-converges to
$ w^{*} $
-converges to
![]() $ y^{*} $
. Without loss of generality, let us assume that
$ y^{*} $
. Without loss of generality, let us assume that
![]() $ \Vert z^{*}_{l} \Vert $
converges to some
$ \Vert z^{*}_{l} \Vert $
converges to some
![]() $ \lambda $
, clearly, with
$ \lambda $
, clearly, with
![]() $ \lambda \geq \Vert y^{*} \Vert> 0 $
, and let us consider
$ \lambda \geq \Vert y^{*} \Vert> 0 $
, and let us consider
![]() $ u^{*}_{l} = \frac {1}{\Vert z^{*}_{l} \Vert } z^{*}_{l} $
and
$ u^{*}_{l} = \frac {1}{\Vert z^{*}_{l} \Vert } z^{*}_{l} $
and
![]() $ u^{*} = \frac {1}{\lambda } y^{*} $
.
$ u^{*} = \frac {1}{\lambda } y^{*} $
.
So, we have seen that there is a normalized block sequence
![]() $ u^{*}_{l} $
in
$ u^{*}_{l} $
in
![]() $ X^{*} $
which
$ X^{*} $
which
![]() $ w^{*} $
-converges to some
$ w^{*} $
-converges to some
![]() $ u^{*} $
with
$ u^{*} $
with
![]() $ e^{**}_{n}(u^{*})> 0 $
. We put
$ e^{**}_{n}(u^{*})> 0 $
. We put
Then,
![]() $ v^{*}_{l} $
is a sequence in
$ v^{*}_{l} $
is a sequence in
![]() $ B_{X^{*}} $
that
$ B_{X^{*}} $
that
![]() $ w^{*} $
-converges to
$ w^{*} $
-converges to
![]() $ v^{*} $
. Since
$ v^{*} $
. Since
![]() $ \Vert v^{*}_{l} - v^{*}_{l'} \Vert = 2 \varepsilon $
for
$ \Vert v^{*}_{l} - v^{*}_{l'} \Vert = 2 \varepsilon $
for
![]() $ l \neq l' $
, any
$ l \neq l' $
, any
![]() $ w^{*} $
-open set
$ w^{*} $
-open set
![]() $ U $
containing
$ U $
containing
![]() $ v^{*} $
fulfils
$ v^{*} $
fulfils
![]() $ \mathrm {diam}(U \cap B_{X^{*}}) \geq 2\varepsilon $
. It follows that
$ \mathrm {diam}(U \cap B_{X^{*}}) \geq 2\varepsilon $
. It follows that
![]() $ v^{*} \in (B_{X^{*}})^{\prime }_{2\varepsilon } $
, and, by our assumption,
$ v^{*} \in (B_{X^{*}})^{\prime }_{2\varepsilon } $
, and, by our assumption,
![]() $ v^{*} \in (1 - \varepsilon ) B_{X^{*}} $
. At the same time,
$ v^{*} \in (1 - \varepsilon ) B_{X^{*}} $
. At the same time,
which is not possible.
Hence, the functionals
![]() $ e^{**}_{n} $
are
$ e^{**}_{n} $
are
![]() $ w^{*} $
-continuous indeed. Every
$ w^{*} $
-continuous indeed. Every
![]() $ e^{**}_{n} $
is therefore the evaluation of some
$ e^{**}_{n} $
is therefore the evaluation of some
![]() $ e_{n} \in X $
. Finally, it is easy to check that
$ e_{n} \in X $
. Finally, it is easy to check that
![]() $ e_{1}, e_{2}, \dots $
is a basis of
$ e_{1}, e_{2}, \dots $
is a basis of
![]() $ X $
that is
$ X $
that is
![]() $ 1 $
-equivalent to the canonical basis of
$ 1 $
-equivalent to the canonical basis of
![]() $ c_{0} $
.
$ c_{0} $
.
Proof of Proposition 4.11.
Let
![]() $\mathcal {F}$
be the set of those
$\mathcal {F}$
be the set of those
![]() $\mu \in \mathcal {P}_\infty $
for which
$\mu \in \mathcal {P}_\infty $
for which
![]() $X_\mu $
is an
$X_\mu $
is an
![]() $ \mathcal {L}_{\infty , 1+} $
-space. By Theorem 3.6,
$ \mathcal {L}_{\infty , 1+} $
-space. By Theorem 3.6,
![]() $\mathcal {F}$
is a
$\mathcal {F}$
is a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {P}_\infty $
. Let
$\mathcal {P}_\infty $
. Let
![]() $\Omega $
be the mapping from Lemma 4.9, and let us denote by
$\Omega $
be the mapping from Lemma 4.9, and let us denote by
![]() $\triangle $
the closed set
$\triangle $
the closed set
![]() $\{(x,x)\colon x\in \mathcal K(\ell _\infty )\}$
in
$\{(x,x)\colon x\in \mathcal K(\ell _\infty )\}$
in
![]() $\mathcal K(\ell _\infty )\times \mathcal K(\ell _\infty )$
. By Lemma 4.7 and Theorem 4.13, we have that
$\mathcal K(\ell _\infty )\times \mathcal K(\ell _\infty )$
. By Lemma 4.7 and Theorem 4.13, we have that
By Lemmas 4.9 and 4.10, the mapping
![]() $\mathcal {P}\ni \nu \mapsto (\tfrac {1}{2}\Omega (\nu ),\Omega ^{\prime }_1(\nu ))\in \mathcal K(\ell _\infty )\times \mathcal K(\ell _\infty )$
is
$\mathcal {P}\ni \nu \mapsto (\tfrac {1}{2}\Omega (\nu ),\Omega ^{\prime }_1(\nu ))\in \mathcal K(\ell _\infty )\times \mathcal K(\ell _\infty )$
is
![]() $\boldsymbol {\Sigma }_3^0$
-measurable, so we obtain that
$\boldsymbol {\Sigma }_3^0$
-measurable, so we obtain that
![]() ${\langle c_0\rangle _{\equiv }}$
is an
${\langle c_0\rangle _{\equiv }}$
is an
![]() $F_{\sigma \delta }$
-set in
$F_{\sigma \delta }$
-set in
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Corollary 4.14. Let
![]() $\varepsilon>0$
. Then, the mapping
$\varepsilon>0$
. Then, the mapping
![]() $s_\varepsilon $
from Lemma 4.10 is not
$s_\varepsilon $
from Lemma 4.10 is not
![]() $\boldsymbol {\Sigma }_2^0$
-measurable.
$\boldsymbol {\Sigma }_2^0$
-measurable.
5 Miscellaneous
5.1 Superreflexive spaces
Recall that a map
![]() $f:M\to N$
between metric spaces is called a C-bi-Lipschitz embedding if
$f:M\to N$
between metric spaces is called a C-bi-Lipschitz embedding if
Lemma 5.1. Let M be a finite metric space and
![]() $C>0$
. The set
$C>0$
. The set
![]() $E(M,C)$
consisting of those
$E(M,C)$
consisting of those
![]() $\mu \in \mathcal {P}$
, such that M admits a C-bi-Lipschitz embedding into
$\mu \in \mathcal {P}$
, such that M admits a C-bi-Lipschitz embedding into
![]() $X_\mu $
is open in
$X_\mu $
is open in
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
Proof. Let
![]() $\mu \in E(M,C)$
. Thus, there is a C-bi-Lipschitz embedding
$\mu \in E(M,C)$
. Thus, there is a C-bi-Lipschitz embedding
![]() $f:M\to X_\mu $
. By perturbing the image of f if necessary, we may without loss of generality assume that
$f:M\to X_\mu $
. By perturbing the image of f if necessary, we may without loss of generality assume that
![]() $f(M)\subseteq V$
.
$f(M)\subseteq V$
.
Consider
![]() $\varepsilon>0$
and the open neighbourhood
$\varepsilon>0$
and the open neighbourhood
![]() $U_\varepsilon $
of
$U_\varepsilon $
of
![]() $\mu $
consisting of those
$\mu $
consisting of those
![]() $\mu '\in \mathcal {P}$
for which
$\mu '\in \mathcal {P}$
for which
![]() $|\mu (f(x)-f(y)) - \mu '(f(x)-f(y))|<\varepsilon $
for every
$|\mu (f(x)-f(y)) - \mu '(f(x)-f(y))|<\varepsilon $
for every
![]() $x,y\in M$
. Then,
$x,y\in M$
. Then,
![]() $U_\varepsilon \subseteq E(M,C)$
for
$U_\varepsilon \subseteq E(M,C)$
for
![]() $\varepsilon>0$
small enough. Indeed, it suffices to choose
$\varepsilon>0$
small enough. Indeed, it suffices to choose
![]() $\varepsilon $
smaller than
$\varepsilon $
smaller than
The easy verification is left to the reader.
Proposition 5.2. Let
![]() $(M_n)_{n\in \mathbb {N}}$
be a sequence of finite metric spaces, and let
$(M_n)_{n\in \mathbb {N}}$
be a sequence of finite metric spaces, and let
![]() $\mathcal {X}$
be the class of those Banach spaces X for which there exists a constant C, such that for every
$\mathcal {X}$
be the class of those Banach spaces X for which there exists a constant C, such that for every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $M_n$
admits a C-bi-Lipschitz embedding into X.
$M_n$
admits a C-bi-Lipschitz embedding into X.
Then,
![]() $\mathcal {F}:=\{\mu \in \mathcal {P}_\infty :\; X_\mu \text { is in }\mathcal {X}\}$
is a
$\mathcal {F}:=\{\mu \in \mathcal {P}_\infty :\; X_\mu \text { is in }\mathcal {X}\}$
is a
![]() $G_{\delta \sigma }$
-set in
$G_{\delta \sigma }$
-set in
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Proof. Follows immediately from Lemma 5.1, because we have
Bourgain in his seminal paper [Reference Bourgain9] found a sequence of finite metric spaces
![]() $(M_n)_{n\in \mathbb {N}}$
, such that a separable Banach space is not superreflexive if and only if there exists a constant C, such that for every
$(M_n)_{n\in \mathbb {N}}$
, such that a separable Banach space is not superreflexive if and only if there exists a constant C, such that for every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $M_n$
admits a C-bi-Lipschitz embedding into X. We refer the interested reader to [Reference Ostrovskii47, Section 9] for some more related facts and results. Thus, combining this result with Proposition 5.2, we obtain immediately the following.
$M_n$
admits a C-bi-Lipschitz embedding into X. We refer the interested reader to [Reference Ostrovskii47, Section 9] for some more related facts and results. Thus, combining this result with Proposition 5.2, we obtain immediately the following.
Theorem 5.3. The class of all superreflexive spaces is an
![]() $F_{\sigma \delta }$
-set in
$F_{\sigma \delta }$
-set in
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
A metric space M is called locally finite if it is uniformly discrete and all balls in M are finite sets (in particular, every such M is at most countable). Let us mention a result by Ostrovskii by which a locally finite metric space bi-Lipschitz embeds into a Banach space X if and only if all of its finite subsets admit uniformly bi-Lipschitz embeddings into X (see [Reference Ostrovskii46] or [Reference Ostrovskii47, Theorem 2.6]). Thus, from Proposition 5.2, we obtain also the following.
Corollary 5.4. Let M be a locally finite metric space. Then, the set of those
![]() $\mu \in \mathcal {P}_\infty $
for which M admits a bi-Lipschitz embedding into
$\mu \in \mathcal {P}_\infty $
for which M admits a bi-Lipschitz embedding into
![]() $X_\mu $
is a
$X_\mu $
is a
![]() $G_{\delta \sigma }$
-set in
$G_{\delta \sigma }$
-set in
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
It is well-known that many important classes of separable Banach spaces are not Borel. This concerns, for example, reflexive spaces, spaces with separable dual, spaces containing
![]() $\ell _1$
, spaces with the Radon-Nikodým property, spaces isomorphic to
$\ell _1$
, spaces with the Radon-Nikodým property, spaces isomorphic to
![]() $L_p[0,1]$
for
$L_p[0,1]$
for
![]() $p\in (1,2)\cup (2,\infty )$
, or spaces isomorphic to
$p\in (1,2)\cup (2,\infty )$
, or spaces isomorphic to
![]() $c_0$
. We refer to [Reference Bossard7, page 130 and Corollary 3.3] and [Reference Kurka36, Theorem 1.1] for papers which contain the corresponding results and to the monograph [Reference Dodos17] and the survey [Reference Godefroy26] for some more information. Thus, for example, in combination with Corollary 5.4, we see that none of those classes might be characterized as a class into which a given locally finite metric space bi-Lipchitz embeds. Let us give an example of such a result, which is related to [Reference Motakis and Schlumprecht45, Problem 12.5(b)]. This is an elementary but interesting application of the whole theory.
$c_0$
. We refer to [Reference Bossard7, page 130 and Corollary 3.3] and [Reference Kurka36, Theorem 1.1] for papers which contain the corresponding results and to the monograph [Reference Dodos17] and the survey [Reference Godefroy26] for some more information. Thus, for example, in combination with Corollary 5.4, we see that none of those classes might be characterized as a class into which a given locally finite metric space bi-Lipchitz embeds. Let us give an example of such a result, which is related to [Reference Motakis and Schlumprecht45, Problem 12.5(b)]. This is an elementary but interesting application of the whole theory.
Corollary 5.5. There does not exist a locally finite metric space M, such that any separable Banach space X is not reflexive if and only if M admits a bi-Lipschitz embeddings into X.
Remark 5.6. Let us draw the attention of the reader once more to the remarkable paper [Reference Motakis and Schlumprecht45], where the authors found a metric characterization of reflexivity, even though such a condition is necessarily non-Borel (as mentioned above).
5.2 Szlenk indices
In this subsection, we give estimates on the Borel classes of spaces with Szlenk index less than or equal to a given ordinal number. Note that it is a result by Bossard, see [Reference Bossard7, Section 4], that those sets are Borel and their Borel classes are unbounded. So our contribution here is that we provide certain quantitative estimates from above. Similarly, we give an estimate on the Borel class of spaces with summable Szlenk index, which is a quantitative improvement of the result mentioned in [Reference Godefroy25, page 367]. Let us start with the corresponding definitions. Let X be a real Banach space and
![]() $K\subseteq X^*$
a
$K\subseteq X^*$
a
![]() $w^*$
-compact set. Following [Reference Lancien39], for
$w^*$
-compact set. Following [Reference Lancien39], for
![]() $\varepsilon>0$
, we define
$\varepsilon>0$
, we define
![]() $s_\varepsilon (K)$
as the Szlenk derivative of the set K (see Section 4.2), and then we inductively define
$s_\varepsilon (K)$
as the Szlenk derivative of the set K (see Section 4.2), and then we inductively define
![]() $s_\varepsilon ^\alpha (K)$
for an ordinal
$s_\varepsilon ^\alpha (K)$
for an ordinal
![]() $\alpha $
by
$\alpha $
by
![]() $s_\varepsilon ^{\alpha +1}(K):=s_\varepsilon (s_\varepsilon ^\alpha (K))$
and
$s_\varepsilon ^{\alpha +1}(K):=s_\varepsilon (s_\varepsilon ^\alpha (K))$
and
![]() $s_\varepsilon ^\alpha (K):=\bigcap _{\beta <\alpha } s_\varepsilon ^\beta (K)$
if
$s_\varepsilon ^\alpha (K):=\bigcap _{\beta <\alpha } s_\varepsilon ^\beta (K)$
if
![]() $\alpha $
is a limit ordinal. Given a real Banach space X,
$\alpha $
is a limit ordinal. Given a real Banach space X,
![]() $Sz(X,\varepsilon )$
is the least ordinal
$Sz(X,\varepsilon )$
is the least ordinal
![]() $\alpha $
, such that
$\alpha $
, such that
![]() $s_\varepsilon ^\alpha (B_{X^*})=\emptyset $
, if such an ordinal exists (otherwise, we write
$s_\varepsilon ^\alpha (B_{X^*})=\emptyset $
, if such an ordinal exists (otherwise, we write
![]() $Sz(X,\varepsilon ) = \infty $
). The Szlenk index is defined by
$Sz(X,\varepsilon ) = \infty $
). The Szlenk index is defined by
![]() $Sz(X) = \sup _{\varepsilon> 0} Sz(X,\varepsilon )$
.
$Sz(X) = \sup _{\varepsilon> 0} Sz(X,\varepsilon )$
.
Recall that for a separable infinite-dimensional Banach space X, the Szlenk index is either
![]() $\infty $
or
$\infty $
or
![]() $\omega ^\alpha $
for some
$\omega ^\alpha $
for some
![]() $\alpha \in [1,\omega _1)$
(see [Reference Lancien39, Section 3]).
$\alpha \in [1,\omega _1)$
(see [Reference Lancien39, Section 3]).
Theorem 5.7. Let
![]() $\alpha \in [1,\omega _1)$
be an ordinal. Then
$\alpha \in [1,\omega _1)$
be an ordinal. Then
is a
![]() $\boldsymbol {\Pi }_{\omega ^\alpha + 1}^0$
-set in
$\boldsymbol {\Pi }_{\omega ^\alpha + 1}^0$
-set in
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Proof. Using Lemma 4.10, it is easy to prove by induction on n that the mapping
![]() $\mathcal K(B_{\ell _\infty })\ni F\mapsto s_\varepsilon ^n(F)\in \mathcal K(B_{\ell _\infty })$
is
$\mathcal K(B_{\ell _\infty })\ni F\mapsto s_\varepsilon ^n(F)\in \mathcal K(B_{\ell _\infty })$
is
![]() $\boldsymbol {\Sigma }_{2n+1}^0$
-measurable for every
$\boldsymbol {\Sigma }_{2n+1}^0$
-measurable for every
![]() $n\in \mathbb {N}$
. Further, the mapping
$n\in \mathbb {N}$
. Further, the mapping
![]() $\mathcal K(B_{\ell _\infty })\ni F\mapsto s_\varepsilon ^\omega (F)\in \mathcal K(B_{\ell _\infty })$
is
$\mathcal K(B_{\ell _\infty })\ni F\mapsto s_\varepsilon ^\omega (F)\in \mathcal K(B_{\ell _\infty })$
is
![]() $\boldsymbol {\Sigma }_{\omega +1}^0$
-measurable. Indeed, for every open
$\boldsymbol {\Sigma }_{\omega +1}^0$
-measurable. Indeed, for every open
![]() $V\subseteq B_{\ell _\infty }$
, by compactness argument, we have
$V\subseteq B_{\ell _\infty }$
, by compactness argument, we have
 $$\begin{align*}\{F\colon s_\varepsilon^\omega(F)\subseteq V\} = \bigcup_{n=1}^\infty \{F\colon s_\varepsilon^n(F)\subseteq V\} \end{align*}$$
$$\begin{align*}\{F\colon s_\varepsilon^\omega(F)\subseteq V\} = \bigcup_{n=1}^\infty \{F\colon s_\varepsilon^n(F)\subseteq V\} \end{align*}$$
which is a
![]() $\boldsymbol {\Sigma }_{\omega }^0$
-set, so by Lemma 4.8, the mapping
$\boldsymbol {\Sigma }_{\omega }^0$
-set, so by Lemma 4.8, the mapping
![]() $s_\varepsilon ^\omega $
is
$s_\varepsilon ^\omega $
is
![]() $\boldsymbol {\Sigma }_{\omega +1}^0$
-measurable. Similarly, we prove by transfinite induction that
$\boldsymbol {\Sigma }_{\omega +1}^0$
-measurable. Similarly, we prove by transfinite induction that
![]() $s_\varepsilon ^\beta $
is
$s_\varepsilon ^\beta $
is
![]() $\boldsymbol {\Sigma }_{\beta +1}^0$
-measurable whenever
$\boldsymbol {\Sigma }_{\beta +1}^0$
-measurable whenever
![]() $\beta \in [\omega ,\omega _1)$
is a limit ordinal.
$\beta \in [\omega ,\omega _1)$
is a limit ordinal.
Let
![]() $\Omega $
be the mapping from Lemma 4.9. Then, by Lemma 4.7, we have
$\Omega $
be the mapping from Lemma 4.9. Then, by Lemma 4.7, we have
 $$\begin{align*}\begin{aligned} \{\mu\in\mathcal{P}_\infty\colon Sz(X_{\mu})\leq \omega^\alpha\} & = \bigcap_{k\in\mathbb{N}} \{\mu\in\mathcal{P}_\infty\colon Sz(X_{\mu},\tfrac{1}{k})\leq \omega^\alpha\}\\ & = \bigcap_{k\in\mathbb{N}} \{\mu\in\mathcal{P}_\infty\colon s_{1/k}^{\omega^\alpha}(\Omega(\mu)) = \emptyset\}, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \{\mu\in\mathcal{P}_\infty\colon Sz(X_{\mu})\leq \omega^\alpha\} & = \bigcap_{k\in\mathbb{N}} \{\mu\in\mathcal{P}_\infty\colon Sz(X_{\mu},\tfrac{1}{k})\leq \omega^\alpha\}\\ & = \bigcap_{k\in\mathbb{N}} \{\mu\in\mathcal{P}_\infty\colon s_{1/k}^{\omega^\alpha}(\Omega(\mu)) = \emptyset\}, \end{aligned} \end{align*}$$
which, by the above and Lemma 4.9, is the countable intersection of preimages of closed sets under
![]() $\boldsymbol {\Sigma }_{\omega ^\alpha + 1}^0$
-measurable mapping, so it is a
$\boldsymbol {\Sigma }_{\omega ^\alpha + 1}^0$
-measurable mapping, so it is a
![]() $\boldsymbol {\Pi }_{\omega ^\alpha + 1}^0$
-set in
$\boldsymbol {\Pi }_{\omega ^\alpha + 1}^0$
-set in
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Let us recall that a Banach space X has a summable Szlenk index if there is a constant M, such that for all positive
![]() $\varepsilon _1,\ldots ,\varepsilon _n$
with
$\varepsilon _1,\ldots ,\varepsilon _n$
with
![]() $s_{\varepsilon _1}\ldots s_{\varepsilon _n}B_{X^*}\neq \emptyset $
, we have
$s_{\varepsilon _1}\ldots s_{\varepsilon _n}B_{X^*}\neq \emptyset $
, we have
![]() $\sum _{i=1}^n \varepsilon _i\leq M$
.
$\sum _{i=1}^n \varepsilon _i\leq M$
.
Proposition 5.8. The set
![]() $\{\mu \in \mathcal {P}_\infty \colon X_{\mu }\text { has a summable Szlenk index}\}$
is a
$\{\mu \in \mathcal {P}_\infty \colon X_{\mu }\text { has a summable Szlenk index}\}$
is a
![]() $\boldsymbol {\Sigma }_{\omega +2}^0$
-set in
$\boldsymbol {\Sigma }_{\omega +2}^0$
-set in
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Proof. Let
![]() $\Omega $
be the mapping from Lemma 4.9. It is easy to see that the set
$\Omega $
be the mapping from Lemma 4.9. It is easy to see that the set
![]() $\{\mu \in \mathcal {P}_\infty \colon X_{\mu }\text { has a summable Szlenk index}\}$
is equal to
$\{\mu \in \mathcal {P}_\infty \colon X_{\mu }\text { has a summable Szlenk index}\}$
is equal to
 $$\begin{align*}\bigcup_{M\in\mathbb{N}}\quad \bigcap_{\substack{\varepsilon_1,\ldots,\varepsilon_n\in\mathbb{Q}_+\\ \sum_{i=1}^n \varepsilon_i> M}} \{\mu\in\mathcal{P}_\infty\colon s_{\varepsilon_1}\ldots s_{\varepsilon_n}\Omega(\mu)=\emptyset\}, \end{align*}$$
$$\begin{align*}\bigcup_{M\in\mathbb{N}}\quad \bigcap_{\substack{\varepsilon_1,\ldots,\varepsilon_n\in\mathbb{Q}_+\\ \sum_{i=1}^n \varepsilon_i> M}} \{\mu\in\mathcal{P}_\infty\colon s_{\varepsilon_1}\ldots s_{\varepsilon_n}\Omega(\mu)=\emptyset\}, \end{align*}$$
which by Lemmas 4.9 and 4.10 is a
![]() $\boldsymbol {\Sigma }_{\omega +2}^0$
-set in
$\boldsymbol {\Sigma }_{\omega +2}^0$
-set in
![]() $\mathcal {P}_\infty $
.
$\mathcal {P}_\infty $
.
Finally, let us note that similarly, one can of course estimate Borel complexity of various other classes of spaces related to Szlenk derivations, for example, spaces with Szlenk power type at most p etc.
5.3 Spaces having Schauder basis-like structures
It is an open problem whether the class of spaces with Schauder basis is a Borel set in
![]() $\mathcal {B}$
(see, e.g. [Reference Dodos17, Problem 8]), and note that by the results from [Reference Cúth, Doležal, Doucha and Kurka14, Section 3], it does not matter whether we use the coding
$\mathcal {B}$
(see, e.g. [Reference Dodos17, Problem 8]), and note that by the results from [Reference Cúth, Doležal, Doucha and Kurka14, Section 3], it does not matter whether we use the coding
![]() $SB(C([0,1]))$
or
$SB(C([0,1]))$
or
![]() $\mathcal {B}$
. However, it was proved by Ghawadrah that the class of spaces with
$\mathcal {B}$
. However, it was proved by Ghawadrah that the class of spaces with
![]() $\pi $
-property is Borel (actually, it is a
$\pi $
-property is Borel (actually, it is a
![]() $\boldsymbol {\Sigma }_6^0$
-set in
$\boldsymbol {\Sigma }_6^0$
-set in
![]() $\mathcal {P}_\infty $
, which follows immediately from [Reference Ghawadrah21, Lemma 2.1], see also [Reference Ghawadrah24]) and that the class of spaces with the bounded approximation property (BAP) is Borel (actually, it is a
$\mathcal {P}_\infty $
, which follows immediately from [Reference Ghawadrah21, Lemma 2.1], see also [Reference Ghawadrah24]) and that the class of spaces with the bounded approximation property (BAP) is Borel (actually, it is a
![]() $\boldsymbol {\Sigma }_7^0$
-set in
$\boldsymbol {\Sigma }_7^0$
-set in
![]() $\mathcal {P}_\infty $
, which follows immediately from [Reference Ghawadrah23, Lemma 2.1], and this estimate has recently been improved to a
$\mathcal {P}_\infty $
, which follows immediately from [Reference Ghawadrah23, Lemma 2.1], and this estimate has recently been improved to a
![]() $\boldsymbol {\Sigma }_6^0$
-set in any admissible topology, see [Reference Ghawadrah24]). One is therefore led to the question of finding examples of Banach spaces having BAP but not Schauder basis. Such an example was constructed by Szarek [Reference Szarek50]. Actually, Szarek considered classes of separable spaces with local basis structure (LBS) and local
$\boldsymbol {\Sigma }_6^0$
-set in any admissible topology, see [Reference Ghawadrah24]). One is therefore led to the question of finding examples of Banach spaces having BAP but not Schauder basis. Such an example was constructed by Szarek [Reference Szarek50]. Actually, Szarek considered classes of separable spaces with local basis structure (LBS) and local
![]() $\Pi $
-basis structure (L
$\Pi $
-basis structure (L
![]() $\Pi $
BS) for which we have
$\Pi $
BS) for which we have
and he proved that the converses to the second and the third implication do not hold in general. The problem of whether the converse to the first implication holds seems to be open (see [Reference Szarek50, Problem 1.8]). In this subsection, we prove that both (LBS) and (L
![]() $\Pi $
BS) give rise to a Borel class of separable Banach spaces (we even compute an upper bound on their Borel complexities, see Theorem 5.13). Note that this result somehow builds a bridge between both open problems mentioned above, that is, between the problem of whether
$\Pi $
BS) give rise to a Borel class of separable Banach spaces (we even compute an upper bound on their Borel complexities, see Theorem 5.13). Note that this result somehow builds a bridge between both open problems mentioned above, that is, between the problem of whether
![]() $\langle \text {spaces with Schauder basis} \rangle $
is a Borel set in
$\langle \text {spaces with Schauder basis} \rangle $
is a Borel set in
![]() $\mathcal {B}$
and the problem of whether every separable Banach space with (L
$\mathcal {B}$
and the problem of whether every separable Banach space with (L
![]() $\Pi $
BS) has a basis.
$\Pi $
BS) has a basis.
Let us start with the definitions as they are given in [Reference Szarek50].
Definition 5.9. By the basis constant of a basis
![]() $ (x_{i})_{i=1}^{d} $
of a Banach space
$ (x_{i})_{i=1}^{d} $
of a Banach space
![]() $ X $
of dimension
$ X $
of dimension
![]() $ d \in [0, \infty ] $
, we mean the least number
$ d \in [0, \infty ] $
, we mean the least number
![]() $ C \geq 1 $
, such that
$ C \geq 1 $
, such that
![]() $ \Vert \sum _{i=1}^{n} a_{i} x_{i} \Vert \leq C \Vert \sum _{i=1}^{m} a_{i} x_{i} \Vert $
whenever
$ \Vert \sum _{i=1}^{n} a_{i} x_{i} \Vert \leq C \Vert \sum _{i=1}^{m} a_{i} x_{i} \Vert $
whenever
![]() $ n , m \in \mathbb {N} $
,
$ n , m \in \mathbb {N} $
,
![]() $ n \leq m \leq d $
and
$ n \leq m \leq d $
and
![]() $ a_{1}, \dots , a_{m} \in \mathbb {R} $
. The basis constant of
$ a_{1}, \dots , a_{m} \in \mathbb {R} $
. The basis constant of
![]() $ (x_{i})_{i=1}^{d} $
is denoted by
$ (x_{i})_{i=1}^{d} $
is denoted by
![]() $ \mathrm {bc}( (x_{i})_{i=1}^{d} ) $
. We further denote
$ \mathrm {bc}( (x_{i})_{i=1}^{d} ) $
. We further denote
Definition 5.10. A Banach space
![]() $ X $
is said to have the local basis structure (LBS) if
$ X $
is said to have the local basis structure (LBS) if
![]() $ X = \overline {\bigcup _{n=1}^{\infty } E_{n}} $
, where
$ X = \overline {\bigcup _{n=1}^{\infty } E_{n}} $
, where
![]() $ E_{1} \subseteq E_{2} \subseteq \dots $
are finite-dimensional subspaces satisfying
$ E_{1} \subseteq E_{2} \subseteq \dots $
are finite-dimensional subspaces satisfying
![]() $ \sup _{n \in \mathbb {N}} \mathrm {bc}(E_{n}) < \infty $
.
$ \sup _{n \in \mathbb {N}} \mathrm {bc}(E_{n}) < \infty $
.
Further,
![]() $ X $
is said to have the local
$ X $
is said to have the local
![]() $\Pi $
-basis structure (L
$\Pi $
-basis structure (L
![]() $\Pi $
BS) if
$\Pi $
BS) if
![]() $ X = \overline {\bigcup _{n=1}^{\infty } E_{n}} $
, where
$ X = \overline {\bigcup _{n=1}^{\infty } E_{n}} $
, where
![]() $ E_{1} \subseteq E_{2} \subseteq \dots $
are finite-dimensional subspaces satisfying
$ E_{1} \subseteq E_{2} \subseteq \dots $
are finite-dimensional subspaces satisfying
![]() $ \sup _{n \in \mathbb {N}} \mathrm {bc}(E_{n}) < \infty $
for which there are projections
$ \sup _{n \in \mathbb {N}} \mathrm {bc}(E_{n}) < \infty $
for which there are projections
![]() $ P_{n} : X \to E_{n} $
, such that
$ P_{n} : X \to E_{n} $
, such that
![]() $ P_{n}(X) = E_{n} $
and
$ P_{n}(X) = E_{n} $
and
![]() $ \sup _{n \in \mathbb {N}} \Vert P_{n} \Vert < \infty $
.
$ \sup _{n \in \mathbb {N}} \Vert P_{n} \Vert < \infty $
.
Lemma 5.11. Whenever E is a finite-dimensional subspace of a Banach space X,
![]() $\delta \in (0,1)$
,
$\delta \in (0,1)$
,
![]() $K>0$
,
$K>0$
,
![]() $T:E\to X$
is a
$T:E\to X$
is a
![]() $(1+\delta )$
-isomorphism (not necessarily surjective) with
$(1+\delta )$
-isomorphism (not necessarily surjective) with
![]() $\|T-I\|<\delta $
and
$\|T-I\|<\delta $
and
![]() $P:X\to E$
is a projection with
$P:X\to E$
is a projection with
![]() $P(X)=E$
and
$P(X)=E$
and
![]() $\|P\|\leq K$
, then, for every subspace F of E, we have
$\|P\|\leq K$
, then, for every subspace F of E, we have
![]() $\|TP|_{T(F)} - I_{T(F)}\|\leq 4\delta K$
.
$\|TP|_{T(F)} - I_{T(F)}\|\leq 4\delta K$
.
Moreover, whenever
![]() $\|TP|_{T(E)} - I_{T(E)}\|\leq q <1$
, then
$\|TP|_{T(E)} - I_{T(E)}\|\leq q <1$
, then
![]() $T(E)$
is
$T(E)$
is
![]() $\frac {(1+\delta ) K}{1-q}$
-complemented in X.
$\frac {(1+\delta ) K}{1-q}$
-complemented in X.
Proof. Let
![]() $\{f_1,\ldots ,f_n\}$
be a basis of F. Then, for every
$\{f_1,\ldots ,f_n\}$
be a basis of F. Then, for every
![]() $x=\sum _{i=1}^n a_i T(f_i)\in T(F)$
, we have
$x=\sum _{i=1}^n a_i T(f_i)\in T(F)$
, we have
 $$\begin{align*}\|TPx-x\|=\|TP(\sum_{i=1}^n a_i(T(f_i)-f_i))\|\leq (1+\delta)K\|(T-I)T^{-1}x\|\leq (1+\delta)^2\delta K \|x\|. \end{align*}$$
$$\begin{align*}\|TPx-x\|=\|TP(\sum_{i=1}^n a_i(T(f_i)-f_i))\|\leq (1+\delta)K\|(T-I)T^{-1}x\|\leq (1+\delta)^2\delta K \|x\|. \end{align*}$$
Moreover, if
![]() $\|TP|_{T(E)} - I_{T(E)}\|<1$
, then the mapping
$\|TP|_{T(E)} - I_{T(E)}\|<1$
, then the mapping
![]() $TP|_{T(E)}$
is an isomorphism with
$TP|_{T(E)}$
is an isomorphism with
![]() $\|(TP|_{T(E)})^{-1}\|\leq \sum _{i=0}^\infty q^i = \frac {1}{1-q}$
. It is now straightforward to prove that
$\|(TP|_{T(E)})^{-1}\|\leq \sum _{i=0}^\infty q^i = \frac {1}{1-q}$
. It is now straightforward to prove that
![]() $P':=(TP|_{T(E)})^{-1} TP:X\to T(E)$
is a projection onto
$P':=(TP|_{T(E)})^{-1} TP:X\to T(E)$
is a projection onto
![]() $T(E)$
with
$T(E)$
with
![]() $\|P'\|\leq \frac {(1+\delta ) K}{1-q}$
.
$\|P'\|\leq \frac {(1+\delta ) K}{1-q}$
.
Lemma 5.12. For every
![]() $\mu \in \mathcal {B}$
,
$\mu \in \mathcal {B}$
,
![]() $K,l\in \mathbb {N}$
and
$K,l\in \mathbb {N}$
and
![]() $v_1,\ldots ,v_m\in V$
, let us denote by
$v_1,\ldots ,v_m\in V$
, let us denote by
![]() $\Phi (\mu ,K,v_1,\ldots ,v_m)$
and
$\Phi (\mu ,K,v_1,\ldots ,v_m)$
and
![]() $\Psi (\mu ,K,l,v_1,\ldots ,v_m)$
the formulae
$\Psi (\mu ,K,l,v_1,\ldots ,v_m)$
the formulae
 $$ \begin{align*}\Phi(\mu,K,v_1,\ldots,v_m)=\forall a_{1}, \dots, a_{m} \in \mathbb{R} : \max_{1 \leq k \leq m} \mu \Big( \sum_{i=1}^{k} a_{i} v_{i} \Big) \leq K \mu \Big( \sum_{i=1}^{m} a_{i} v_{i} \Big)\end{align*} $$
$$ \begin{align*}\Phi(\mu,K,v_1,\ldots,v_m)=\forall a_{1}, \dots, a_{m} \in \mathbb{R} : \max_{1 \leq k \leq m} \mu \Big( \sum_{i=1}^{k} a_{i} v_{i} \Big) \leq K \mu \Big( \sum_{i=1}^{m} a_{i} v_{i} \Big)\end{align*} $$
and
 $$ \begin{align*}\mu \Big( \sum_{i=1}^{m} a_{i} v_{i} + \sum_{i=1}^{l} b_{i} u_{i} \Big) \leq K \mu \Big( \sum_{i=1}^{m} a_{i} v_{i} + \sum_{i=1}^{l} b_{i} e_{i} \Big).\end{align*} $$
$$ \begin{align*}\mu \Big( \sum_{i=1}^{m} a_{i} v_{i} + \sum_{i=1}^{l} b_{i} u_{i} \Big) \leq K \mu \Big( \sum_{i=1}^{m} a_{i} v_{i} + \sum_{i=1}^{l} b_{i} e_{i} \Big).\end{align*} $$
Then, for every
![]() $\nu \in \mathcal {B}$
, the following holds.
$\nu \in \mathcal {B}$
, the following holds.
-
(a) The space
 $ X_{\nu } $
has LBS if and only if
$ X_{\nu } $
has LBS if and only if  $$\begin{align*}\exists K \in \mathbb{N} \, \forall n \in \mathbb{N} \, \exists m \in \mathbb{N} \, \exists v_{1}, \dots, v_{m} \in V, \, \{ e_{1}, \dots, e_{n} \} \subseteq \mathrm{span} \{ v_{1}, \dots, v_{m} \}\end{align*}$$
$$\begin{align*}\exists K \in \mathbb{N} \, \forall n \in \mathbb{N} \, \exists m \in \mathbb{N} \, \exists v_{1}, \dots, v_{m} \in V, \, \{ e_{1}, \dots, e_{n} \} \subseteq \mathrm{span} \{ v_{1}, \dots, v_{m} \}\end{align*}$$
 $$\begin{align*}\Phi(\nu,K,v_1,\ldots,v_m). \end{align*}$$
$$\begin{align*}\Phi(\nu,K,v_1,\ldots,v_m). \end{align*}$$
-
(b) The space
 $ X_{\nu } $
has L
$ X_{\nu } $
has L
 $\Pi $
BS if and only if
$\Pi $
BS if and only if  $$ \begin{align*}\exists K \in \mathbb{N} \, \forall n \in \mathbb{N} \, \exists m \in \mathbb{N} \, \exists v_{1}, \dots, v_{m} \in V, \, \{ e_{1}, \dots, e_{n} \} \subseteq \mathrm{span} \{ v_{1}, \dots, v_{m} \}\end{align*} $$
$$ \begin{align*}\exists K \in \mathbb{N} \, \forall n \in \mathbb{N} \, \exists m \in \mathbb{N} \, \exists v_{1}, \dots, v_{m} \in V, \, \{ e_{1}, \dots, e_{n} \} \subseteq \mathrm{span} \{ v_{1}, \dots, v_{m} \}\end{align*} $$
 $$ \begin{align*}\Phi(\nu,K,v_1,\ldots,v_m) \wedge \forall l\in\mathbb{N} \Psi(\nu,K,l,v_1,\ldots,v_m).\end{align*} $$
$$ \begin{align*}\Phi(\nu,K,v_1,\ldots,v_m) \wedge \forall l\in\mathbb{N} \Psi(\nu,K,l,v_1,\ldots,v_m).\end{align*} $$
Proof. We prove only the more difficult part (b). Since
![]() $ \nu \in \mathcal {B} $
, the space
$ \nu \in \mathcal {B} $
, the space
![]() $ X_{\nu } $
is just the completion of
$ X_{\nu } $
is just the completion of
![]() $ (c_{00}, \nu ) $
(it is not necessary to consider a quotient). So, the notions of linear span and of linear independence have the same meaning in
$ (c_{00}, \nu ) $
(it is not necessary to consider a quotient). So, the notions of linear span and of linear independence have the same meaning in
![]() $ c_{00} $
and in
$ c_{00} $
and in
![]() $ X_{\nu } $
, if performed on subsets of
$ X_{\nu } $
, if performed on subsets of
![]() $ c_{00} $
.
$ c_{00} $
.
Let us suppose that
![]() $ \nu \in \mathcal {B} $
satisfies the formula in (b) for some
$ \nu \in \mathcal {B} $
satisfies the formula in (b) for some
![]() $ K \in \mathbb {N} $
. We put
$ K \in \mathbb {N} $
. We put
![]() $ E_{0} = \{ 0 \} $
and choose recursively subspaces
$ E_{0} = \{ 0 \} $
and choose recursively subspaces
![]() $ E_{1} \subseteq E_{2} \subseteq \dots $
of
$ E_{1} \subseteq E_{2} \subseteq \dots $
of
![]() $ X_{\nu } $
, each of which is generated by a finite number of elements of
$ X_{\nu } $
, each of which is generated by a finite number of elements of
![]() $ V $
, in the following way. Assuming that
$ V $
, in the following way. Assuming that
![]() $ E_{j} $
has been already chosen, we pick first
$ E_{j} $
has been already chosen, we pick first
![]() $ n_{j+1} \geq j + 1 $
, such that
$ n_{j+1} \geq j + 1 $
, such that
![]() $ E_{j} \subseteq \mathrm {span} \{ e_{1}, \dots , e_{n_{j+1}} \} $
. Then, we can pick
$ E_{j} \subseteq \mathrm {span} \{ e_{1}, \dots , e_{n_{j+1}} \} $
. Then, we can pick
![]() $ m_{j+1} \in \mathbb {N} $
and
$ m_{j+1} \in \mathbb {N} $
and
![]() $ v^{j+1}_{1}, \dots , v^{j+1}_{m_{j+1}} \in V $
with
$ v^{j+1}_{1}, \dots , v^{j+1}_{m_{j+1}} \in V $
with
![]() $ \{ e_{1}, \dots , e_{n_{j+1}} \} \subseteq \mathrm {span} \{ v^{j+1}_{1}, \dots , v^{j+1}_{m_{j+1}} \} $
, such that
$ \{ e_{1}, \dots , e_{n_{j+1}} \} \subseteq \mathrm {span} \{ v^{j+1}_{1}, \dots , v^{j+1}_{m_{j+1}} \} $
, such that
![]() $\Phi (\nu ,K,v^{j+1}_{1}, \ldots , v^{j+1}_{m_{j+1}})$
and for every
$\Phi (\nu ,K,v^{j+1}_{1}, \ldots , v^{j+1}_{m_{j+1}})$
and for every
![]() $l\in \mathbb {N}$
,
$l\in \mathbb {N}$
,
![]() $\Psi (\nu ,K,l,v^{j+1}_{1}, \ldots , v^{j+1}_{m_{j+1}})$
hold.
$\Psi (\nu ,K,l,v^{j+1}_{1}, \ldots , v^{j+1}_{m_{j+1}})$
hold.
We put
![]() $E_{j+1} = \mathrm {span} \big \{ v^{j+1}_{1}, \dots , v^{j+1}_{m_{j+1}} \big \}$
. In this way, we obtain
$E_{j+1} = \mathrm {span} \big \{ v^{j+1}_{1}, \dots , v^{j+1}_{m_{j+1}} \big \}$
. In this way, we obtain
![]() $ E_{j} \subseteq E_{j+1} $
. Also,
$ E_{j} \subseteq E_{j+1} $
. Also,
![]() $ X_{\nu } = \overline {\bigcup _{n=1}^{\infty } E_{n}} $
(we have
$ X_{\nu } = \overline {\bigcup _{n=1}^{\infty } E_{n}} $
(we have
![]() $ e_{j+1} \in E_{j+1} $
, as
$ e_{j+1} \in E_{j+1} $
, as
![]() $ n_{j+1} \geq j + 1 $
). If we take all nonzero vectors
$ n_{j+1} \geq j + 1 $
). If we take all nonzero vectors
![]() $ v^{j+1}_{i}, 1 \leq i \leq m_{j+1} $
, we obtain a basis of
$ v^{j+1}_{i}, 1 \leq i \leq m_{j+1} $
, we obtain a basis of
![]() $ E_{j+1} $
with the basis constant at most
$ E_{j+1} $
with the basis constant at most
![]() $ K $
.
$ K $
.
To show that the sequence
![]() $ E_{1} \subseteq E_{2} \subseteq \dots $
witnesses that
$ E_{1} \subseteq E_{2} \subseteq \dots $
witnesses that
![]() $ X_{\nu } $
has L
$ X_{\nu } $
has L
![]() $\Pi $
BS, it remains to find a projection
$\Pi $
BS, it remains to find a projection
![]() $ P_{j+1} $
of
$ P_{j+1} $
of
![]() $ X_{\nu } $
onto
$ X_{\nu } $
onto
![]() $ E_{j+1} $
, such that
$ E_{j+1} $
, such that
![]() $ \Vert P_{j+1} \Vert \leq K $
. Let us pick some
$ \Vert P_{j+1} \Vert \leq K $
. Let us pick some
![]() $ l \in \mathbb {N} $
and put
$ l \in \mathbb {N} $
and put
![]() $ E^{(l)} = \mathrm {span} \{ v^{j+1}_{1}, \dots , v^{j+1}_{m_{j+1}}, e_{1}, \dots , e_{l} \} $
. By
$ E^{(l)} = \mathrm {span} \{ v^{j+1}_{1}, \dots , v^{j+1}_{m_{j+1}}, e_{1}, \dots , e_{l} \} $
. By
![]() $\Psi (\nu ,K,l,v^{j+1}_{1}, \ldots , v^{j+1}_{m_{j+1}})$
, there exists a projection
$\Psi (\nu ,K,l,v^{j+1}_{1}, \ldots , v^{j+1}_{m_{j+1}})$
, there exists a projection
![]() $P^{(l)}$
of
$P^{(l)}$
of
![]() $E^{(l)}$
onto
$E^{(l)}$
onto
![]() $E_{j+1}$
with
$E_{j+1}$
with
![]() $\|P^{(l)}\|\leq K$
. Since the norms of
$\|P^{(l)}\|\leq K$
. Since the norms of
![]() $P^{(l)}$
, for
$P^{(l)}$
, for
![]() $l\in \mathbb {N}$
, are uniformly bounded and have a fixed finite-dimensional range, there exists their accumulation point in strong operator topology (SOT) which is a projection
$l\in \mathbb {N}$
, are uniformly bounded and have a fixed finite-dimensional range, there exists their accumulation point in strong operator topology (SOT) which is a projection
![]() $P_{j+1}: X_\nu \rightarrow E_{j+1}$
of norm bounded by K as desired.
$P_{j+1}: X_\nu \rightarrow E_{j+1}$
of norm bounded by K as desired.
Conversely, suppose that
![]() $X_\nu $
has L
$X_\nu $
has L
![]() $\Pi $
BS as witnessed by some
$\Pi $
BS as witnessed by some
![]() $C>1$
and a sequence
$C>1$
and a sequence
![]() $(E_n)_{n\in \mathbb {N}}$
of finite-dimensional subspaces satisfying
$(E_n)_{n\in \mathbb {N}}$
of finite-dimensional subspaces satisfying
![]() $X_\nu =\overline {\bigcup _n E_n}$
and
$X_\nu =\overline {\bigcup _n E_n}$
and
![]() $ \sup _{n \in \mathbb {N}} \mathrm {bc}(E_{n}) <C$
, for which there are projections
$ \sup _{n \in \mathbb {N}} \mathrm {bc}(E_{n}) <C$
, for which there are projections
![]() $ P_{n} : X_\nu \to E_{n} $
, such that
$ P_{n} : X_\nu \to E_{n} $
, such that
![]() $ P_{n}(X_\nu ) = E_{n} $
and
$ P_{n}(X_\nu ) = E_{n} $
and
![]() $ \sup _{n \in \mathbb {N}} \Vert P_{n} \Vert < C$
. Pick
$ \sup _{n \in \mathbb {N}} \Vert P_{n} \Vert < C$
. Pick
![]() $D>0$
, such that
$D>0$
, such that
![]() $H_n:=(\operatorname {span}\{e_1,\ldots ,e_n\},\nu )$
is D-complemented in
$H_n:=(\operatorname {span}\{e_1,\ldots ,e_n\},\nu )$
is D-complemented in
![]() $X_\nu $
, and let
$X_\nu $
, and let
![]() $\phi _1:=\phi _2^{e_1,\ldots ,e_n}$
be the function from Lemma 2.14. Fix
$\phi _1:=\phi _2^{e_1,\ldots ,e_n}$
be the function from Lemma 2.14. Fix
![]() $\varepsilon>0$
, such that
$\varepsilon>0$
, such that
![]() $\phi _1(t)$
is small enough (to be specified later) whenever
$\phi _1(t)$
is small enough (to be specified later) whenever
![]() $t<\varepsilon $
. Find
$t<\varepsilon $
. Find
![]() $k\in \mathbb {N}$
, such that there are
$k\in \mathbb {N}$
, such that there are
![]() $h_1,\ldots ,h_n\in E_k$
with
$h_1,\ldots ,h_n\in E_k$
with
![]() $\nu (e_i-h_i)<\varepsilon $
. If
$\nu (e_i-h_i)<\varepsilon $
. If
![]() $\phi _1(\varepsilon )$
is small enough, we have
$\phi _1(\varepsilon )$
is small enough, we have
![]() $\frac {(1+\phi _1(\varepsilon ))D}{1-4\phi _1(\varepsilon )D}\leq 2D$
(this value refers to the ‘Moreover’ part in Lemma 5.11). By Lemma 5.11,
$\frac {(1+\phi _1(\varepsilon ))D}{1-4\phi _1(\varepsilon )D}\leq 2D$
(this value refers to the ‘Moreover’ part in Lemma 5.11). By Lemma 5.11,
![]() $\operatorname {span}\{h_i\colon i\leq n\}$
is
$\operatorname {span}\{h_i\colon i\leq n\}$
is
![]() $2D$
-complemented in
$2D$
-complemented in
![]() $X_\nu $
, so let
$X_\nu $
, so let
![]() $Q:X_\nu \to \operatorname {span}\{h_i\colon i\leq n\}$
be the corresponding projection. Pick a basis
$Q:X_\nu \to \operatorname {span}\{h_i\colon i\leq n\}$
be the corresponding projection. Pick a basis
![]() $h_{n+1},\ldots ,h_{\dim E_k}$
of the space
$h_{n+1},\ldots ,h_{\dim E_k}$
of the space
![]() $E_k\cap Q^{-1}(0)$
, which is
$E_k\cap Q^{-1}(0)$
, which is
![]() $(2D+1)$
-complemented in
$(2D+1)$
-complemented in
![]() $E_k$
. Let
$E_k$
. Let
![]() $\phi _2:=\phi _2^{h_{n+1},\ldots ,h_{\dim E_k}}$
be the function from Lemma 2.14. Fix
$\phi _2:=\phi _2^{h_{n+1},\ldots ,h_{\dim E_k}}$
be the function from Lemma 2.14. Fix
![]() $\delta>0$
, such that
$\delta>0$
, such that
![]() $\phi _2(t)$
is small enough (to be specified later) whenever
$\phi _2(t)$
is small enough (to be specified later) whenever
![]() $t<\delta $
. Finally, find
$t<\delta $
. Finally, find
![]() $f_{n+1},\ldots ,f_{\dim E_k}\in V$
with
$f_{n+1},\ldots ,f_{\dim E_k}\in V$
with
![]() $\nu (f_j-h_j)<\delta $
for
$\nu (f_j-h_j)<\delta $
for
![]() $j=n+1,\ldots ,\dim E_k$
.
$j=n+1,\ldots ,\dim E_k$
.
We claim that the space
![]() $F_n:=(\operatorname {span}\{e_1,\ldots ,e_n,f_{n+1},\ldots ,f_{\dim E_k}\},\nu )$
is
$F_n:=(\operatorname {span}\{e_1,\ldots ,e_n,f_{n+1},\ldots ,f_{\dim E_k}\},\nu )$
is
![]() $2C$
-complemented in
$2C$
-complemented in
![]() $X_\nu $
and
$X_\nu $
and
![]() $d_{BM}(F_n,E_k)<2$
. If we denote by
$d_{BM}(F_n,E_k)<2$
. If we denote by
![]() $T:E_k\to F_n$
the linear mapping given by
$T:E_k\to F_n$
the linear mapping given by
![]() $h_i\mapsto e_i$
,
$h_i\mapsto e_i$
,
![]() $i\leq n$
, and
$i\leq n$
, and
![]() $h_j\mapsto f_j$
,
$h_j\mapsto f_j$
,
![]() $n+1\leq j\leq \dim E_k$
, then for every
$n+1\leq j\leq \dim E_k$
, then for every
![]() $y\in \operatorname {span}\{h_i\colon i\leq n\}$
and
$y\in \operatorname {span}\{h_i\colon i\leq n\}$
and
![]() $z\in \operatorname {span}\{h_j\colon j=n+1,\ldots ,\dim E_k\}$
, we have
$z\in \operatorname {span}\{h_j\colon j=n+1,\ldots ,\dim E_k\}$
, we have
 $$\begin{align*}\begin{aligned} \nu(T(y+z)-y-z) & \leq \nu(Ty-y) + \nu(Tz-z)\leq \phi_1(\varepsilon)\nu(y) + \phi_2(\delta)\nu(z)\\ & \leq \Big(\phi_1(\varepsilon)2D + \phi_2(\delta)(2D+1)\Big)\nu(y+z); \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \nu(T(y+z)-y-z) & \leq \nu(Ty-y) + \nu(Tz-z)\leq \phi_1(\varepsilon)\nu(y) + \phi_2(\delta)\nu(z)\\ & \leq \Big(\phi_1(\varepsilon)2D + \phi_2(\delta)(2D+1)\Big)\nu(y+z); \end{aligned} \end{align*}$$
hence, if
![]() $\eta :=\Big (\phi _1(\varepsilon )2D + \phi _2(\delta )(2D+1)\Big )<1$
, we obtain
$\eta :=\Big (\phi _1(\varepsilon )2D + \phi _2(\delta )(2D+1)\Big )<1$
, we obtain
![]() $\|T\|\leq 1 + \|I-T\|\leq 1+\eta $
and
$\|T\|\leq 1 + \|I-T\|\leq 1+\eta $
and
![]() $\|Tx\|\geq \|x\|-\|(I-T)x\|\geq (1-\eta )\|x\|$
for every
$\|Tx\|\geq \|x\|-\|(I-T)x\|\geq (1-\eta )\|x\|$
for every
![]() $x\in E_k$
, so T is an isomorphism with
$x\in E_k$
, so T is an isomorphism with
![]() $\|T\|^{-1}\leq (1-\eta )^{-1}$
. Thus, by Lemma 5.11, if
$\|T\|^{-1}\leq (1-\eta )^{-1}$
. Thus, by Lemma 5.11, if
![]() $\phi _1(\varepsilon )$
and
$\phi _1(\varepsilon )$
and
![]() $\phi _2(\delta )$
are small enough (and so
$\phi _2(\delta )$
are small enough (and so
![]() $\eta $
is small enough), we obtain
$\eta $
is small enough), we obtain
![]() $\|T\|\|T^{-1}\|<2$
and
$\|T\|\|T^{-1}\|<2$
and
![]() $F_n$
is
$F_n$
is
![]() $2C$
-complemented in
$2C$
-complemented in
![]() $X_\nu $
.
$X_\nu $
.
Thus,
![]() $\mathrm {bc}(F_n)\leq \mathrm {bc}(E_k)d_{BM}(E_k,F_n)<2C$
, which is witnessed by some basis
$\mathrm {bc}(F_n)\leq \mathrm {bc}(E_k)d_{BM}(E_k,F_n)<2C$
, which is witnessed by some basis
![]() $v_1,\ldots ,v_m\in V$
of
$v_1,\ldots ,v_m\in V$
of
![]() $F_n$
. This shows that
$F_n$
. This shows that
![]() $\Phi (\nu ,2C,v_1,\ldots ,v_m)$
holds. Let
$\Phi (\nu ,2C,v_1,\ldots ,v_m)$
holds. Let
![]() $P:X_\nu \rightarrow F_n$
be a projection with
$P:X_\nu \rightarrow F_n$
be a projection with
![]() $P[X_\nu ]=F_n$
and
$P[X_\nu ]=F_n$
and
![]() $\|P\|\leq 2C$
. Given
$\|P\|\leq 2C$
. Given
![]() $ l \in \mathbb {N} $
, let
$ l \in \mathbb {N} $
, let
![]() $ T \subseteq \{ 1, \dots , l \} $
be a set, such that
$ T \subseteq \{ 1, \dots , l \} $
be a set, such that
![]() $ (e_{i})_{i \in T} $
together with
$ (e_{i})_{i \in T} $
together with
![]() $ (v_{i})_{i=1}^{m} $
form a basis of
$ (v_{i})_{i=1}^{m} $
form a basis of
![]() $ \operatorname {span} (\{ v_{1}, \dots , v_{m} \} \cup \{ e_{1}, \dots , e_{l} \}) $
. Pick
$ \operatorname {span} (\{ v_{1}, \dots , v_{m} \} \cup \{ e_{1}, \dots , e_{l} \}) $
. Pick
![]() $A>0$
, such that
$A>0$
, such that
![]() $(v_i)_{i=1}^m\cup (e_i)_{i\in T} {\stackrel {A}{\sim } \ell _1^{m+|T|}}$
. For
$(v_i)_{i=1}^m\cup (e_i)_{i\in T} {\stackrel {A}{\sim } \ell _1^{m+|T|}}$
. For
![]() $i\in T$
pick
$i\in T$
pick
![]() $u_i\in \operatorname {span}_{\mathbb {Q}} \{v_1,\ldots ,v_m\}$
, such that
$u_i\in \operatorname {span}_{\mathbb {Q}} \{v_1,\ldots ,v_m\}$
, such that
![]() $\nu (u_i-P(e_i))<\frac {C}{A}$
. Then, for every
$\nu (u_i-P(e_i))<\frac {C}{A}$
. Then, for every
![]() $a_1,\ldots ,a_m\in \mathbb {R}$
and every
$a_1,\ldots ,a_m\in \mathbb {R}$
and every
![]() $(b_i)_{i\in T}\in \mathbb {R}^T$
, we have
$(b_i)_{i\in T}\in \mathbb {R}^T$
, we have
 $$\begin{align*}\begin{aligned} \nu \Big( \sum_{i=1}^{m} a_{i} v_{i} + \sum_{i\in T} b_{i} u_{i} \Big) & \leq 2C \nu \Big( \sum_{i=1}^{m} a_{i} v_{i} + \sum_{i\in T} b_{i} e_{i} \Big) + \nu(\sum_{i\in T} b_{i} (u_{i} - P(e_i)))\\ & \leq 3C \nu \Big( \sum_{i=1}^{m} a_{i} v_{i} + \sum_{i\in T} b_{i} e_{i} \Big). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \nu \Big( \sum_{i=1}^{m} a_{i} v_{i} + \sum_{i\in T} b_{i} u_{i} \Big) & \leq 2C \nu \Big( \sum_{i=1}^{m} a_{i} v_{i} + \sum_{i\in T} b_{i} e_{i} \Big) + \nu(\sum_{i\in T} b_{i} (u_{i} - P(e_i)))\\ & \leq 3C \nu \Big( \sum_{i=1}^{m} a_{i} v_{i} + \sum_{i\in T} b_{i} e_{i} \Big). \end{aligned} \end{align*}$$
Thus, the linear mapping
![]() $O:\operatorname {span} (\{ v_{1}, \dots , v_{m} \} \cup \{ e_{1}, \dots , e_{l} \})\to \operatorname {span} \{ v_{1}, \dots , v_{m} \}$
given by
$O:\operatorname {span} (\{ v_{1}, \dots , v_{m} \} \cup \{ e_{1}, \dots , e_{l} \})\to \operatorname {span} \{ v_{1}, \dots , v_{m} \}$
given by
![]() $v_i\mapsto v_i$
,
$v_i\mapsto v_i$
,
![]() $i\leq m$
, and
$i\leq m$
, and
![]() $e_i\mapsto u_i$
,
$e_i\mapsto u_i$
,
![]() $i\in T$
, is a linear projection, and if we put
$i\in T$
, is a linear projection, and if we put
![]() $u_i:=O(e_i)\in V$
for every
$u_i:=O(e_i)\in V$
for every
![]() $i\in \{1,\ldots ,l\}$
, we see that
$i\in \{1,\ldots ,l\}$
, we see that
![]() $\Psi (\nu ,3C,l,v_1,\ldots ,v_m)$
holds and the formula in
$\Psi (\nu ,3C,l,v_1,\ldots ,v_m)$
holds and the formula in
![]() $(b)$
is satisfied with
$(b)$
is satisfied with
![]() $K=3C$
.
$K=3C$
.
Theorem 5.13.
-
(a) The class of spaces which have LBS is a
 $ \boldsymbol {\Sigma }^{0}_{4} $
-set in
$ \boldsymbol {\Sigma }^{0}_{4} $
-set in
 $ \mathcal {B} $
.
$ \mathcal {B} $
. -
(b) The class of spaces which have L
 $\Pi $
BS is a
$\Pi $
BS is a
 $ \boldsymbol {\Sigma }^{0}_{6} $
-set in
$ \boldsymbol {\Sigma }^{0}_{6} $
-set in
 $ \mathcal {B} $
.
$ \mathcal {B} $
.
Proof. This follows from Lemma 5.12 because the conditions given by formulas
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
are obviously closed and
$\Psi $
are obviously closed and
![]() $F_\sigma $
, respectively.
$F_\sigma $
, respectively.
6 Open questions and remarks
In Theorem 2.10, we proved that
![]() $\ell _2$
is the unique separable infinite-dimensional Banach space (up to isomorphism) whose isomorphism class is an
$\ell _2$
is the unique separable infinite-dimensional Banach space (up to isomorphism) whose isomorphism class is an
![]() $F_\sigma $
-set. Following [Reference Johnson, Lindenstrauss and Schechtman33], we say that a separable infinite-dimensional Banach space X is determined by its finite dimensional subspaces if it is isomorphic to every separable Banach space Y, which is finitely crudely representable in X and for which X is finitely crudely representable in Y. Note that
$F_\sigma $
-set. Following [Reference Johnson, Lindenstrauss and Schechtman33], we say that a separable infinite-dimensional Banach space X is determined by its finite dimensional subspaces if it is isomorphic to every separable Banach space Y, which is finitely crudely representable in X and for which X is finitely crudely representable in Y. Note that
![]() $\ell _2$
is determined by its finite dimensional subspaces and that if a separable infinite-dimensional Banach space is determined by its finite dimensional subspaces, then it is obviously determined by its pavings and so, by Theorem 2.12, its isomorphism class is
$\ell _2$
is determined by its finite dimensional subspaces and that if a separable infinite-dimensional Banach space is determined by its finite dimensional subspaces, then it is obviously determined by its pavings and so, by Theorem 2.12, its isomorphism class is
![]() $G_{\delta \sigma }$
. Johnson et al. conjectured (see [Reference Johnson, Lindenstrauss and Schechtman33, Conjecture 7.3]) that
$G_{\delta \sigma }$
. Johnson et al. conjectured (see [Reference Johnson, Lindenstrauss and Schechtman33, Conjecture 7.3]) that
![]() $\ell _2$
is the unique, up to isomorphism, separable infinite-dimensional Banach space which is determined by its finite dimensional subspaces. We believe that Theorem 2.10 could be instrumental for proving this conjecture, since it follows from this theorem that the conjecture is equivalent to the positive answer to the following question. We thank Gilles Godefroy who suggested to us that there might be a relation between having
$\ell _2$
is the unique, up to isomorphism, separable infinite-dimensional Banach space which is determined by its finite dimensional subspaces. We believe that Theorem 2.10 could be instrumental for proving this conjecture, since it follows from this theorem that the conjecture is equivalent to the positive answer to the following question. We thank Gilles Godefroy who suggested to us that there might be a relation between having
![]() $F_\sigma $
isomorphism class and being determined by finite dimensional subspaces.
$F_\sigma $
isomorphism class and being determined by finite dimensional subspaces.
Question 1. Let X be a separable infinite-dimensional Banach space determined by its finite dimensional subspaces. Is
![]() ${\langle X\rangle _{\simeq }}$
an
${\langle X\rangle _{\simeq }}$
an
![]() $F_\sigma $
-set in
$F_\sigma $
-set in
![]() $\mathcal {B}$
?
$\mathcal {B}$
?
It would be interesting to know whether there is a separable infinite-dimensional Banach space X, such that
![]() ${\langle X\rangle _{\simeq }}$
is a
${\langle X\rangle _{\simeq }}$
is a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {B}$
or in
$\mathcal {B}$
or in
![]() $\mathcal {P}_\infty $
. Note that the only possible candidate is the Gurariı̆ space (see Section 2.1 for more details). One of the possible strategies to answer Question 2 in negative for
$\mathcal {P}_\infty $
. Note that the only possible candidate is the Gurariı̆ space (see Section 2.1 for more details). One of the possible strategies to answer Question 2 in negative for
![]() $\mathcal {P}_\infty $
would be to find an admissible topology
$\mathcal {P}_\infty $
would be to find an admissible topology
![]() $\tau $
on
$\tau $
on
![]() $SB(X)$
, such that
$SB(X)$
, such that
![]() ${\langle \mathbb {G\rangle _{\simeq }}}$
is a dense and meagre set in
${\langle \mathbb {G\rangle _{\simeq }}}$
is a dense and meagre set in
![]() $(SB(X),\tau )$
. However, we do not even know whether
$(SB(X),\tau )$
. However, we do not even know whether
![]() ${\langle \mathbb {G\rangle _{\simeq }}}$
is Borel.
${\langle \mathbb {G\rangle _{\simeq }}}$
is Borel.
Question 2. Is
![]() ${\langle \mathbb {G\rangle _{\simeq }}}$
a
${\langle \mathbb {G\rangle _{\simeq }}}$
a
![]() $G_\delta $
-set in
$G_\delta $
-set in
![]() $\mathcal {P}_\infty $
or in
$\mathcal {P}_\infty $
or in
![]() $\mathcal {B}$
? Is it at least Borel?
$\mathcal {B}$
? Is it at least Borel?
Solving the homogeneous Banach space problem, Komorowski and Tomczak-Jaegermann ([Reference Komorowski and Tomczak-Jaegermann35]), and Gowers ([Reference Gowers29]) proved that if a separable infinite-dimensional Banach space is isomorphic to all of its closed infinite-dimensional subspaces, then it is isomorphic to
![]() $\ell _2$
. It seems that the isometric variant of this result is open; that is, whether
$\ell _2$
. It seems that the isometric variant of this result is open; that is, whether
![]() $\ell _2$
is the only (up to isometry) separable infinite-dimensional Banach space that is isometric to all of its infinite-dimensional closed subspaces. We note that any Banach space satisfying this criterion must be, by the Gowers’s result, isomorphic to
$\ell _2$
is the only (up to isometry) separable infinite-dimensional Banach space that is isometric to all of its infinite-dimensional closed subspaces. We note that any Banach space satisfying this criterion must be, by the Gowers’s result, isomorphic to
![]() $\ell _2$
. Our initial interest in this problem was that we observed that a positive answer implies that whenever
$\ell _2$
. Our initial interest in this problem was that we observed that a positive answer implies that whenever
![]() ${\langle X\rangle _{\equiv }}$
is closed in
${\langle X\rangle _{\equiv }}$
is closed in
![]() $\mathcal {P}_\infty $
, then
$\mathcal {P}_\infty $
, then
![]() $X\equiv \ell _2$
. Eventually, we found another argument (see Section 2.1), but the question is clearly of independent interest.
$X\equiv \ell _2$
. Eventually, we found another argument (see Section 2.1), but the question is clearly of independent interest.
Question 3. Let X be a separable infinite-dimensional Banach space which is isometric to all of its closed infinite-dimensional subspaces. Is then X isometric to
![]() $\ell _2$
?
$\ell _2$
?
We note here that Question 3 was already attacked by de Rancourt [Reference de Rancourt15], who was able to prove that if X is as above (that is, isometric to all of its closed infinite-dimensional subspaces), then, for every
![]() $\varepsilon>0$
, X admits a
$\varepsilon>0$
, X admits a
![]() $(1+\varepsilon )$
-unconditional basis.
$(1+\varepsilon )$
-unconditional basis.
In Theorem B, we proved that
![]() ${\langle \mathbb {G\rangle _{\equiv }}}$
, respectively,
${\langle \mathbb {G\rangle _{\equiv }}}$
, respectively,
![]() ${\langle L_p[0,1]\rangle _{\equiv }}$
, for
${\langle L_p[0,1]\rangle _{\equiv }}$
, for
![]() $p\in [1,\infty )$
, are
$p\in [1,\infty )$
, are
![]() $G_\delta $
-sets; we even proved that they are dense
$G_\delta $
-sets; we even proved that they are dense
![]() $G_\delta $
-sets in
$G_\delta $
-sets in
![]() $\mathcal {P}_\infty $
, respectively, in
$\mathcal {P}_\infty $
, respectively, in
![]() $\mathcal {L}_{p,1+}\cap \mathcal {P}_\infty $
. Coincidentally, all these spaces are Fraïssé limits (we refer to [Reference Ferenczi, Lopez-Abad, Mbombo and Todorcevic18, Proposition 3.7] for this statement about
$\mathcal {L}_{p,1+}\cap \mathcal {P}_\infty $
. Coincidentally, all these spaces are Fraïssé limits (we refer to [Reference Ferenczi, Lopez-Abad, Mbombo and Todorcevic18, Proposition 3.7] for this statement about
![]() $L_p[0,1]$
). According to [Reference Ferenczi, Lopez-Abad, Mbombo and Todorcevic18], no other examples of separable Banach spaces which are Fraïssé limits seem to be known. We remark that a characterization of separable Banach spaces with
$L_p[0,1]$
). According to [Reference Ferenczi, Lopez-Abad, Mbombo and Todorcevic18], no other examples of separable Banach spaces which are Fraïssé limits seem to be known. We remark that a characterization of separable Banach spaces with
![]() $G_\delta $
isometry classes has been obtained in [Reference Cúth, de Rancourt and Doucha13], where some new examples are presented.
$G_\delta $
isometry classes has been obtained in [Reference Cúth, de Rancourt and Doucha13], where some new examples are presented.
It also follows that for
![]() $1\leq p<\infty $
,
$1\leq p<\infty $
,
![]() $L_p[0,1]$
is a generic
$L_p[0,1]$
is a generic
![]() $\mathcal {L}_{p,1+}$
-space. On the other hand, by Corollary 2.9, for
$\mathcal {L}_{p,1+}$
-space. On the other hand, by Corollary 2.9, for
![]() $p\in \left [1,2\right )\cup \left (2,\infty \right )$
,
$p\in \left [1,2\right )\cup \left (2,\infty \right )$
,
![]() $L_p[0,1]$
is not a generic
$L_p[0,1]$
is not a generic
![]() $QSL_p$
-space. For
$QSL_p$
-space. For
![]() $p=2$
,
$p=2$
,
![]() $\ell _2$
is obviously the generic
$\ell _2$
is obviously the generic
![]() $QSL_2$
-space, and since
$QSL_2$
-space, and since
![]() $QSL_1$
-spaces coincide with the class of all Banach spaces, for
$QSL_1$
-spaces coincide with the class of all Banach spaces, for
![]() $p=1$
,
$p=1$
,
![]() $\mathbb {G}$
is the generic
$\mathbb {G}$
is the generic
![]() $QSL_1$
-space. This leaves open the next question.
$QSL_1$
-space. This leaves open the next question.
Question 4. For
![]() $p\in \left (1,2\right )\cup \left (2,\infty \right )$
, does there exist a generic
$p\in \left (1,2\right )\cup \left (2,\infty \right )$
, does there exist a generic
![]() $QSL_p$
-space in
$QSL_p$
-space in
![]() $\mathcal {B}$
or
$\mathcal {B}$
or
![]() $\mathcal {P}_\infty $
?
$\mathcal {P}_\infty $
?
In Theorem 5.3, we have computed that the class of superreflexive spaces is an
![]() $F_{\sigma \delta }$
-set. It is easy to check that the class of superreflexive spaces is dense in
$F_{\sigma \delta }$
-set. It is easy to check that the class of superreflexive spaces is dense in
![]() $\mathcal {P}_\infty $
and
$\mathcal {P}_\infty $
and
![]() $\mathcal {B}$
, so it cannot be a
$\mathcal {B}$
, so it cannot be a
![]() $G_\delta $
-set, as then this class would have a nonempty intersection with the isometry class of
$G_\delta $
-set, as then this class would have a nonempty intersection with the isometry class of
![]() $\mathbb {G}$
which is not superreflexive. However, the following is not known to us.
$\mathbb {G}$
which is not superreflexive. However, the following is not known to us.
Question 5. Is the class of all superreflexive spaces
![]() $F_{\sigma \delta }$
-complete in
$F_{\sigma \delta }$
-complete in
![]() $\mathcal {P}_\infty $
or
$\mathcal {P}_\infty $
or
![]() $\mathcal {B}$
?
$\mathcal {B}$
?
Taking into account that spaces with a summable Szlenk index form a class of spaces which is a
![]() $\boldsymbol {\Sigma }^0_{\omega +2}$
-set, see Proposition 5.8, the following seems to be an interesting problem.
$\boldsymbol {\Sigma }^0_{\omega +2}$
-set, see Proposition 5.8, the following seems to be an interesting problem.
Question 6. Is the set
![]() $\{\mu \in \mathcal {P}_\infty \colon X_{\mu }\text { has a summable Szlenk index}\}$
of a finite Borel class?
$\{\mu \in \mathcal {P}_\infty \colon X_{\mu }\text { has a summable Szlenk index}\}$
of a finite Borel class?
Even though we do not formulate it as a numbered question, a natural project to consider is to determine at least upper bounds for isometry classes of other (classical or less classical) separable infinite-dimensional Banach spaces, such as
![]() $C[0,1]$
,
$C[0,1]$
,
![]() $C([0,\alpha ])$
with
$C([0,\alpha ])$
with
![]() $\alpha $
countable ordinal, Orlicz sequence spaces, Orlicz function spaces, spaces of absolutely continuous functions, Tsirelson’s space, etc.
$\alpha $
countable ordinal, Orlicz sequence spaces, Orlicz function spaces, spaces of absolutely continuous functions, Tsirelson’s space, etc.
Kechris in [Reference Kechris34, page 189] mentions that there are not known any natural examples of Borel sets from topology or analysis that are
![]() $\boldsymbol {\Pi }^0_\xi $
or
$\boldsymbol {\Pi }^0_\xi $
or
![]() $\boldsymbol {\Sigma }^0_\xi $
, for
$\boldsymbol {\Sigma }^0_\xi $
, for
![]() $\xi \geq 5$
, and not of lower complexity. We think that the area of research investigated in this paper is a good one to find such examples.
$\xi \geq 5$
, and not of lower complexity. We think that the area of research investigated in this paper is a good one to find such examples.
Acknowledgments
We would like to thank William B. Johnson for his helpful advice concerning the structure of subspaces and quotients of
![]() $L_p$
spaces (see Section 2), Gilles Godefroy for his suggestion to have a look at the paper [Reference Johnson, Lindenstrauss and Schechtman33] and Ghadeer Ghawadrah for sending us a preliminary version of her paper [Reference Ghawadrah24]. M. Cúth was supported by Charles University Research program no. UNCE/SCI/023. M. Doležal was supported by the Grantová agentura České Republiky (GAČR) project 20-22230L and by the Czech Academy of Sciences (RVO 67985840). M. Doucha and O. Kurka were supported by the GAČR project 22-07833K and by the Czech Academy of Sciences (RVO 67985840).
$L_p$
spaces (see Section 2), Gilles Godefroy for his suggestion to have a look at the paper [Reference Johnson, Lindenstrauss and Schechtman33] and Ghadeer Ghawadrah for sending us a preliminary version of her paper [Reference Ghawadrah24]. M. Cúth was supported by Charles University Research program no. UNCE/SCI/023. M. Doležal was supported by the Grantová agentura České Republiky (GAČR) project 20-22230L and by the Czech Academy of Sciences (RVO 67985840). M. Doucha and O. Kurka were supported by the GAČR project 22-07833K and by the Czech Academy of Sciences (RVO 67985840).
Competing interests
The authors have no competing interest to declare.