Hostname: page-component-f554764f5-nqxm9 Total loading time: 0 Render date: 2025-04-20T10:19:42.608Z Has data issue: false hasContentIssue false
  • English
  • Français

THE OPTIMAL MALLIAVIN-TYPE REMAINDER FOR BEURLING GENERALIZED INTEGERS

Part of: Zeta and $L$-functions: analytic theory Multiplicative number theory

Published online by Cambridge University Press:  09 August 2022

Frederik Broucke ,
Gregory Debruyne  and
Jasson Vindas Open the ORCID record for Jasson Vindas [Opens in a new window]
Frederik Broucke
Affiliation:
Department of Mathematics: Analysis, Logic and Discrete Mathematics, Ghent University, Krijgslaan 281, 9000 Gent, Belgium ([email protected], [email protected])
Gregory Debruyne
Affiliation:
Department of Mathematics: Analysis, Logic and Discrete Mathematics, Ghent University, Krijgslaan 281, 9000 Gent, Belgium ([email protected], [email protected])
Jasson Vindas*
Affiliation:
Department of Mathematics: Analysis, Logic and Discrete Mathematics, Ghent University, Krijgslaan 281, 9000 Gent, Belgium ([email protected], [email protected])
*
[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish the optimal order of Malliavin-type remainders in the asymptotic density approximation formula for Beurling generalized integers. Given 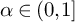$\alpha \in (0,1]$ and 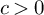$c>0$ (with 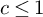$c\leq 1$ if 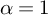$\alpha =1$), a generalized number system is constructed with Riemann prime counting function 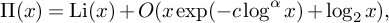$ \Pi (x)= \operatorname {\mathrm {Li}}(x)+ O(x\exp (-c \log ^{\alpha } x ) +\log _{2}x), $ and whose integer counting function satisfies the extremal oscillation estimate 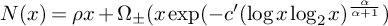$N(x)=\rho x + \Omega _{\pm }(x\exp (- c'(\log x\log _{2} x)^{\frac {\alpha }{\alpha +1}})$ for any 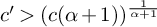$c'>(c(\alpha +1))^{\frac {1}{\alpha +1}}$, where 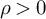$\rho>0$ is its asymptotic density. In particular, this improves and extends upon the earlier work [Adv. Math. 370 (2020), Article 107240].

Keywords

Malliavin-type error termsGeneralized integers with large oscillationPrime number theoremSaddle point methodRandom prime approximation

MSC classification

Primary: 11M41: Other Dirichlet series and zeta functions 11N80: Generalized primes and integers
Secondary: 11N05: Distribution of primes
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 23 , Issue 1 , January 2024 , pp. 249 - 278
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

F. Broucke was supported by the Ghent University BOF-grant 01J04017. G. Debruyne acknowledges support by Postdoctoral Research Fellowships of the Research Foundation–Flanders (grant number 12X9719N) and the Belgian American Educational Foundation. The latter one allowed him to do part of this research at the University of Illinois at Urbana-Champaign. J. Vindas was partly supported by Ghent University through the BOF-grant 01J04017 and by the Research Foundation–Flanders through the FWO-grant 1510119N.

References

Balazard, M., ‘La version de Diamond de la méthode de l’hyperbole de Dirichlet’, Enseign. Math. 45 (1999), 253–270.Google Scholar
Bateman, P. T. and Diamond, H. G., ‘Asymptotic distribution of Beurling’s generalized prime numbers ’, in Studies in Number Theory , W. J. LeVeque (ed.) (Mathematical Association of America, Buffalo, N.Y., 1969), 152–210.Google Scholar
Beurling, A., ‘Analyse de la loi asymptotique de la distribution des nombres premiers généralisés’, Acta Math. 68 (1937), 255–291.CrossRefGoogle Scholar
Broucke, F., ‘Note on a conjecture of Bateman and Diamond concerning the abstract PNT with Malliavin-type remainder’, Monatsh. Math. 196 (2021), 456–470.CrossRefGoogle Scholar
Broucke, F., Debruyne, G. and Vindas, J., ‘Beurling integers with RH and large oscillation’, Adv. Math. 370 (2020), Article 107240.CrossRefGoogle Scholar
Broucke, F. and Vindas, J., ‘A new generalized prime random approximation procedure and some of its applications’, Preprint, 2022, arXiv:2102.08478.Google Scholar
de Bruijn, N. G., Asymptotic Methods in Analysis, third edn. (Dover Publications, Inc. New York, 1981).Google Scholar
Diamond, H. G., ‘Asymptotic distribution of Beurling’s generalized integers’, Illinois J. Math. 14 (1970), 12–28.Google Scholar
Diamond, H. G., Montgomery, H. L. and Vorhauer, U. M. A., ‘Beurling primes with large oscillation’, Math. Ann. 334 (2006), 1–36.CrossRefGoogle Scholar
Diamond, H. G. and Zhang, W.-B., Beurling Generalized Numbers, Mathematical Surveys and Monographs Series, (American Mathematical Society, Providence, RI, 2016).CrossRefGoogle Scholar
Estrada, R., Kanwal, R. P., ‘A distributional approach to asymptotics ’, in Theory and Applications , second edn. (Birkhäuser, Boston, 2002).CrossRefGoogle Scholar
Hilberdink, T. W. and Lapidus, M. L., ‘Beurling zeta functions, generalised primes, and fractal membranes’, Acta Appl. Math 94 (2006), 21–48.CrossRefGoogle Scholar
Landau, E., ‘Neuer Beweis des Primzahlsatzes und Beweis des Primidealsatzes’, Math. Ann. 56 (1903), 645–670.CrossRefGoogle Scholar
Malliavin, P., ‘Sur le reste de la loi asymptotique de répartition des nombres premiers généralisés de Beurling’, Acta Math. 106 (1961), 281–298.CrossRefGoogle Scholar
Tenenbaum, G., Introduction to Analytic and Probabilistic Number Theory, third edn, Graduate Studies in Mathematics, vol. 163 (American Mathematical Society, Providence, RI, 2015).CrossRefGoogle Scholar
Zhang, W.-B., ‘Beurling primes with RH and Beurling primes with large oscillation’, Math. Ann. 337 (2007), 671–704.CrossRefGoogle Scholar