Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-25T22:34:15.323Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical analysis of dynamic acoustic resonance with deformed liquid surfaces: the acoustic fountain

Published online by Cambridge University Press:  22 December 2023

William Cailly ,
Jun Yin  and
Simon Kuhn Open the ORCID record for Simon Kuhn [Opens in a new window]
William Cailly
Affiliation:
KU Leuven, Department of Chemical Engineering, Celestijnenlaan 200F, 3001 Leuven, Belgium
Jun Yin
Affiliation:
KU Leuven, Department of Chemical Engineering, Celestijnenlaan 200F, 3001 Leuven, Belgium
Simon Kuhn*
Affiliation:
KU Leuven, Department of Chemical Engineering, Celestijnenlaan 200F, 3001 Leuven, Belgium
*
†Email address for correspondence: simon.kuhn@kuleuven.be
Get access Rights & Permissions [Opens in a new window]

Abstract

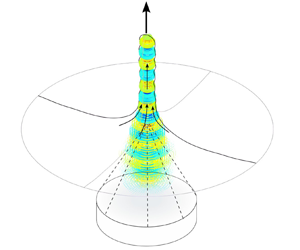
Applying a focused ultrasonic field on a free liquid surface results in its growth eventually leading to the so-called acoustic fountain. In this work, a numerical approach is presented to further increase the understanding of the acoustic fountain phenomenon. The developed simulation method enables the prediction of the free surface motion and the dynamic acoustic field in the moving liquid. The dynamic system is a balance between inertia, surface tension and the acoustic radiation force, and its nonlinearity is demonstrated by studying the relation between the ultrasonic excitation amplitude and corresponding liquid deformation. We show that dynamic resonance is the main mechanism causing the specific acoustic fountain shapes, and the analysis of the dynamic acoustic pressure allows us to predict Faraday-instability atomisation. We show that strong resonance peaks cause atomisation bursts and strong transient deformations corresponding to previously reported experimental observations. The quantitative prediction of the dynamic acoustic pressure enables us to assess the potential of cavitation generation in acoustic fountains. The observed local high acoustic pressures above both the cavitation and the atomisation threshold hint at the coexistence of these two phenomena in acoustic fountains.

JFM classification

Drops and Bubbles: Aerosols/atomization
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 977 , 25 December 2023 , A44
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bachu, V.S., Kedda, J., Suk, I., Green, J.J. & Tyler, B. 2021 High-intensity focused ultrasound: a review of mechanisms and clinical applications. Ann. Biomed. Engng 49 (9), 1975–1991.CrossRefGoogle ScholarPubMed
Barreras, F., Amaveda, H. & Lozano, A. 2002 Transient high-frequency ultrasonic water atomization. Exp. Fluids 33 (3), 405–413.CrossRefGoogle Scholar
Baudoin, M. & Thomas, J.-L. 2020 Acoustic tweezers for particle and fluid micromanipulation. Annu. Rev. Fluid Mech. 52 (1), 205–234.CrossRefGoogle Scholar
Brakke, K.A. 1992 The surface evolver. Exp. Math. 1 (2), 141–165.CrossRefGoogle Scholar
Cailly, W., Mc Carogher, K., Bolze, H., Yin, J. & Kuhn, S. 2023 Analysis of dynamic acoustic resonance effects in a sonicated gas–liquid flow microreactor. Ultrason. Sonochem. 93, 106300.CrossRefGoogle Scholar
Canney, M.S., Bailey, M.R., Crum, L.A., Khokhlova, V.A. & Sapozhnikov, O.A. 2008 Acoustic characterization of high intensity focused ultrasound fields: a combined measurement and modeling approach. J. Acoust. Soc. Am. 124 (4), 2406–2420.CrossRefGoogle Scholar
Carter, C. 1996 ‘Surface Evolver’ as a Tool for Materials Science Research. National Institute of Standards and Technology.Google Scholar
Dong, Z., Wen, Z., Zhao, F., Kuhn, S. & Noël, T. 2021 Scale-up of micro- and milli-reactors: an overview of strategies, design principles and applications. Chem. Engng Sci. X 10, 100097.Google Scholar
Duc, N.M. & Keserci, B. 2019 Emerging clinical applications of high-intensity focused ultrasound. Diagn. Interv. Radiol. 25 (5), 398–409.CrossRefGoogle ScholarPubMed
Ewins, D.J. 2009 Modal Testing: Theory, Practice and Application, 2nd edn. Research Studies Press.Google Scholar
Fernandez Rivas, D. & Kuhn, S. 2016 Synergy of microfluidics and ultrasound. Top. Curr. Chem. 374 (5), 70.CrossRefGoogle ScholarPubMed
Friend, J. & Yeo, L.Y. 2011 Microscale acoustofluidics: microfluidics driven via acoustics and ultrasonics. Rev. Mod. Phys. 83, 647–704.CrossRefGoogle Scholar
Galtier, S. 2021 Wave turbulence: the case of capillary waves. Geophys. Astrophys. Fluid Dyn. 115 (3), 234–257.CrossRefGoogle Scholar
Goodridge, C.L., Hentschel, H.G.E. & Lathrop, D.P. 1999 Breaking faraday waves: critical slowing of droplet ejection rates. Phys. Rev. Lett. 82, 3062–3065.CrossRefGoogle Scholar
Goodridge, C.L., Shi, W.T., Hentschel, H.G.E. & Lathrop, D.P. 1997 Viscous effects in droplet-ejecting capillary waves. Phys. Rev. E 56, 472–475.CrossRefGoogle Scholar
Herbert, E., Balibar, S. & Caupin, F. 2006 Cavitation pressure in water. Phys. Rev. E 74, 041603.CrossRefGoogle ScholarPubMed
Kim, G., Cheng, S., Hong, L., Kim, J.T., Li, K.C. & Chamorro, L.P. 2021 On the acoustic fountain types and flow induced with focused ultrasound. J. Fluid Mech. 909, R2.CrossRefGoogle Scholar
Kooij, S., Astefanei, A., Corthals, G.L. & Bonn, D. 2019 Size distributions of droplets produced by ultrasonic nebulizers. Sci. Rep. 9 (1), 6128.CrossRefGoogle ScholarPubMed
Kudo, T., Sekiguchi, K., Sankoda, K., Namiki, N. & Nii, S. 2017 Effect of ultrasonic frequency on size distributions of nanosized mist generated by ultrasonic atomization. Ultrason. Sonochem. 37, 16–22.CrossRefGoogle ScholarPubMed
Kumar, K. & Tuckerman, L.S. 1994 Parametric instability of the interface between two fluids. J. Fluid Mech. 279, 49–68.CrossRefGoogle Scholar
Lang, R.J. 1962 Ultrasonic atomization of liquids. J. Acoust. Soc. Am. 34 (1), 6–8.CrossRefGoogle Scholar
Lei, J., Glynne-Jones, P. & Hill, M. 2017 Comparing methods for the modelling of boundary-driven streaming in acoustofluidic devices. Microfluid Nanofluid 21 (2), 23.CrossRefGoogle ScholarPubMed
Lim, S., Kim, M. & Kim, J. 2019 Analysis of an acoustic fountain generated by using an ultrasonic plane wave for different water depths. J. Korean Phys. Soc. 74 (4), 336–339.CrossRefGoogle Scholar
Louisnard, O. & Garcia-Vargas, I. 2022 Simulation of sonoreactors accounting for dissipated power. In Energy Aspects of Acoustic Cavitation and Sonochemistry (ed. O. Hamdaoui & K. Kerboua), chap. 13, pp. 219–249. Elsevier.CrossRefGoogle Scholar
Mc Carogher, K., Dong, Z., Stephens, D.S., Leblebici, M.E., Mettin, R. & Kuhn, S. 2021 Acoustic resonance and atomization for gas-liquid systems in microreactors. Ultrason. Sonochem. 75, 105611.CrossRefGoogle ScholarPubMed
Modarres-Gheisari, S.M.M., Gavagsaz-Ghoachani, R., Malaki, M., Safarpour, P. & Zandi, M. 2019 Ultrasonic nano-emulsification – a review. Ultrason. Sonochem. 52, 88–105.CrossRefGoogle ScholarPubMed
Muller, P.B. & Bruus, H. 2014 Numerical study of thermoviscous effects in ultrasound-induced acoustic streaming in microchannels. Phys. Rev. E 90, 043016.CrossRefGoogle ScholarPubMed
Naidu, H., Kahraman, O. & Feng, H. 2022 Novel applications of ultrasonic atomization in the manufacturing of fine chemicals, pharmaceuticals, and medical devices. Ultrason. Sonochem. 86, 105984.CrossRefGoogle ScholarPubMed
Pavlic, A. & Dual, J. 2021 On the streaming in a microfluidic Kundt's tube. J. Fluid Mech. 911, A28.CrossRefGoogle Scholar
Settnes, M. & Bruus, H. 2012 Forces acting on a small particle in an acoustical field in a viscous fluid. Phys. Rev. E 85, 016327.CrossRefGoogle Scholar
Simon, J.C., Sapozhnikov, O.A., Khokhlova, V.A., Crum, L.A. & Bailey, M.R. 2015 Ultrasonic atomization of liquids in drop-chain acoustic fountains. J. Fluid Mech. 766, 129–146.CrossRefGoogle ScholarPubMed
Simon, J.C., Sapozhnikov, O.A., Khokhlova, V.A., Wang, Y.-N., Crum, L.A. & Bailey, M.R. 2012 Ultrasonic atomization of tissue and its role in tissue fractionation by high intensity focused ultrasound. Phys. Med. Biol. 57 (23), 8061–8078.CrossRefGoogle ScholarPubMed
Sisombat, F., Devaux, T., Haumesser, L. & Callé, S. 2022 Water–air interface deformation by transient acoustic radiation pressure. J. Appl. Phys. 132 (17), 174901.CrossRefGoogle Scholar
Sitta, J. & Howard, C.M. 2021 Applications of ultrasound-mediated drug delivery and gene therapy. Intl J. Mol. Sci. 22 (21), 11491.CrossRefGoogle ScholarPubMed
Strani, M. & Sabetta, F. 1984 Free vibrations of a drop in partial contact with a solid support. J. Fluid Mech. 141, 233–247.CrossRefGoogle Scholar
Suryawanshi, P.L., Gumfekar, S.P., Bhanvase, B.A., Sonawane, S.H. & Pimplapure, M.S. 2018 A review on microreactors: reactor fabrication, design, and cutting-edge applications. Chem. Engng Sci. 189, 431–448.CrossRefGoogle Scholar
Tharkar, P., Varanasi, R., Wong, W.S.F., Jin, C.T. & Chrzanowski, W. 2019 Nano-enhanced drug delivery and therapeutic ultrasound for cancer treatment and beyond. Front. Bioengng Biotechnol. 7.Google ScholarPubMed
Tomita, Y. 2014 Jet atomization and cavitation induced by interactions between focused ultrasound and a water surface. Phys. Fluids 26 (9), 097105.CrossRefGoogle Scholar
Udepurkar, A.P., Clasen, C. & Kuhn, S. 2023 Emulsification mechanism in an ultrasonic microreactor: influence of surface roughness and ultrasound frequency. Ultrason. Sonochem. 94, 106323.CrossRefGoogle Scholar
Vlaisavljevich, E., et al. 2016 Effects of temperature on the histotripsy intrinsic threshold for cavitation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 63 (8), 1064–1077.CrossRefGoogle ScholarPubMed
Wang, X., Mori, Y. & Tsuchiya, K. 2022 Periodicity in ultrasonic atomization involving beads-fountain oscillations and mist generation: effects of driving frequency. Ultrason. Sonochem. 86, 105997.CrossRefGoogle ScholarPubMed
Xu, Z., Yasuda, K. & Liu, X. 2016 Simulation of the formation and characteristics of ultrasonic fountain. Ultrason. Sonochem. 32, 241–246.CrossRefGoogle ScholarPubMed
Yao, R., Hu, J., Zhao, W., Cheng, Y. & Feng, C. 2022 A review of high-intensity focused ultrasound as a novel and non-invasive interventional radiology technique. J. Interv. Med. 5 (3), 127–132.Google ScholarPubMed
Yin, J. & Kuhn, S. 2022 Numerical simulation of droplet formation in a microfluidic T-junction using a dynamic contact angle model. Chem. Engng Sci. 261, 117874.CrossRefGoogle Scholar
Zhang, Y., Yuan, S. & Gao, Y. 2023 Spatial distribution and transient evolution of sub-droplet velocity and size in ultrasonic atomization. Exp. Therm. Fluid Sci. 140, 110761.CrossRefGoogle Scholar
Zhang, Y., Yuan, S. & Wang, L. 2021 Investigation of capillary wave, cavitation and droplet diameter distribution during ultrasonic atomization. Exp. Therm. Fluid Sci. 120, 110219.CrossRefGoogle Scholar
Supplementary material: File

Cailly et al. supplementary movie 1

Simulation of the Magnitude 1 case. Top: Shape of the moving liquid surface. The vertical velocity in the centre of the fountain is displayed and the colour scale characterizes the acoustic vibration with respect to the following thresholds: Light blue: below the Faraday threshold, Red: above the Faraday threshold and below the atomisation threshold, Orange: above the atomisation threshold. Bottom: Evolution of the maximum absolute pressure over time.
Download Cailly et al. supplementary movie 1(File)
File 3.5 MB
Supplementary material: File

Cailly et al. supplementary movie 2

Simulation of the Magnitude 2 case. Top: Shape of the moving liquid surface. The vertical velocity in the centre of the fountain is displayed and the colour scale characterizes the acoustic vibration with respect to the following thresholds: Light blue: below the Faraday threshold, Red: above the Faraday threshold and below the atomisation threshold, Orange: above the atomisation threshold. Bottom: Evolution of the maximum absolute pressure over time.
Download Cailly et al. supplementary movie 2(File)
File 3.3 MB
Supplementary material: File

Cailly et al. supplementary movie 3

Simulation of the Magnitude 3 case. Top: Shape of the moving liquid surface. The vertical velocity in the centre of the fountain is displayed and the colour scale characterizes the acoustic vibration with respect to the following thresholds: Light blue: below the Faraday threshold, Red: above the Faraday threshold and below the atomisation threshold, Orange: above the atomisation threshold. Bottom: Evolution of the maximum absolute pressure over time.
Download Cailly et al. supplementary movie 3(File)
File 3.1 MB
Supplementary material: File

Cailly et al. supplementary movie 4

Simulation of the Magnitude 4 case. Top: Shape of the moving liquid surface. The vertical velocity in the centre of the fountain is displayed and the colour scale characterizes the acoustic vibration with respect to the following thresholds: Light blue: below the Faraday threshold, Red: above the Faraday threshold and below the atomisation threshold, Orange: above the atomisation threshold. Bottom: Evolution of the maximum absolute pressure over time.
Download Cailly et al. supplementary movie 4(File)
File 3.8 MB
Supplementary material: File

Cailly et al. supplementary movie 5

Simulation of the Magnitude 5 case. Top: Shape of the moving liquid surface. The vertical velocity in the centre of the fountain is displayed and the colour scale characterizes the acoustic vibration with respect to the following thresholds: Light blue: below the Faraday threshold, Red: above the Faraday threshold and below the atomisation threshold, Orange: above the atomisation threshold. Bottom: Evolution of the maximum absolute pressure over time.
Download Cailly et al. supplementary movie 5(File)
File 3.3 MB
Supplementary material: File

Cailly et al. supplementary movie 6

Simulation of the Magnitude 6 case. Top: Shape of the moving liquid surface. The vertical velocity in the centre of the fountain is displayed and the colour scale characterizes the acoustic vibration with respect to the following thresholds: Light blue: below the Faraday threshold, Red: above the Faraday threshold and below the atomisation threshold, Orange: above the atomisation threshold. Bottom: Evolution of the maximum absolute pressure over time.
Download Cailly et al. supplementary movie 6(File)
File 3.8 MB
Supplementary material: File

Cailly et al. supplementary movie 7

Simulation of the Magnitude 7 case. Top: Shape of the moving liquid surface. The vertical velocity in the centre of the fountain is displayed and the colour scale characterizes the acoustic vibration with respect to the following thresholds: Light blue: below the Faraday threshold, Red: above the Faraday threshold and below the atomisation threshold, Orange: above the atomisation threshold. Bottom: Evolution of the maximum absolute pressure over time.
Download Cailly et al. supplementary movie 7(File)
File 3.3 MB
Supplementary material: File

Cailly et al. supplementary movie 8

Simulation of the Magnitude 8 case. Top: Shape of the moving liquid surface. The vertical velocity in the centre of the fountain is displayed and the colour scale characterizes the acoustic vibration with respect to the following thresholds: Light blue: below the Faraday threshold, Red: above the Faraday threshold and below the atomisation threshold, Orange: above the atomisation threshold. Bottom: Evolution of the maximum absolute pressure over time.
Download Cailly et al. supplementary movie 8(File)
File 6.5 MB
Supplementary material: File

Cailly et al. supplementary movie 9

Simulation of the Magnitude 9 case. Top: Shape of the moving liquid surface. The vertical velocity in the centre of the fountain is displayed and the colour scale characterizes the acoustic vibration with respect to the following thresholds: Light blue: below the Faraday threshold, Red: above the Faraday threshold and below the atomisation threshold, Orange: above the atomisation threshold. Bottom: Evolution of the maximum absolute pressure over time.
Download Cailly et al. supplementary movie 9(File)
File 5.1 MB
Supplementary material: File

Cailly et al. supplementary movie 10

Simulation of the Magnitude 10 case. Top: Shape of the moving liquid surface. The vertical velocity in the centre of the fountain is displayed and the colour scale characterizes the acoustic vibration with respect to the following thresholds: Light blue: below the Faraday threshold, Red: above the Faraday threshold and below the atomisation threshold, Orange: above the atomisation threshold. Bottom: Evolution of the maximum absolute pressure over time.
Download Cailly et al. supplementary movie 10(File)
File 2.5 MB
Supplementary material: File

Cailly et al. supplementary movie 11

Simulation of the Magnitude 11 case. Top: Shape of the moving liquid surface. The vertical velocity in the centre of the fountain is displayed and the colour scale characterizes the acoustic vibration with respect to the following thresholds: Light blue: below the Faraday threshold, Red: above the Faraday threshold and below the atomisation threshold, Orange: above the atomisation threshold. Bottom: Evolution of the maximum absolute pressure over time.
Download Cailly et al. supplementary movie 11(File)
File 7 MB
Supplementary material: File

Cailly et al. supplementary movie 12

Simulation of the Magnitude 12 case. Top: Shape of the moving liquid surface. The vertical velocity in the centre of the fountain is displayed and the colour scale characterizes the acoustic vibration with respect to the following thresholds: Light blue: below the Faraday threshold, Red: above the Faraday threshold and below the atomisation threshold, Orange: above the atomisation threshold. Bottom: Evolution of the maximum absolute pressure over time.
Download Cailly et al. supplementary movie 12(File)
File 2 MB
Supplementary material: File

Cailly et al. supplementary movie 13

Simulation of the Magnitude 13 case. Top: Shape of the moving liquid surface. The vertical velocity in the centre of the fountain is displayed and the colour scale characterizes the acoustic vibration with respect to the following thresholds: Light blue: below the Faraday threshold, Red: above the Faraday threshold and below the atomisation threshold, Orange: above the atomisation threshold. Bottom: Evolution of the maximum absolute pressure over time.
Download Cailly et al. supplementary movie 13(File)
File 3.9 MB